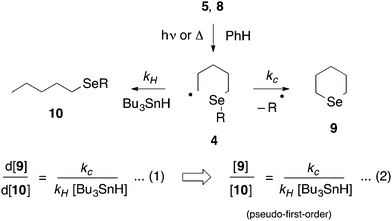
The kinetics of alkyl radical ring closures at selenium: formation of selenane†‡
Amber N.
Hancock
ab,
Yvonne
Kavanagh
ab and
Carl H.
Schiesser
*ab
aARC Centre of Excellence for Free Radical Chemistry and Biotechnology, Australia
bSchool of Chemistry and Bio21 Molecular Science and Biotechnology Institute, The University of Melbourne, Victoria, 3010, Australia. E-mail: carlhs@unimelb.edu.au; Fax: +61 3 9347 8189; Tel: +61 3 8344 2432
First published on 16th May 2014
Abstract
Intramolecular homolytic substitution reactions of 5-(alkylseleno)pentyl radicals 4 have been investigated by competition kinetics as well as computational techniques. B3LYP/6-31G(d) calculations predict that cyclizations of radicals 4 proceed through unremarkable transition states 11 in which the attacking and leaving radicals follow trajectories that deviate some 10–20° from co-linearity with distances in the expected 2.1–2.4 Å range. Competition kinetic experiments provide activation energies (Ea) that lie in the range: 20–36 kJ mol−1, and depend on the nature of the leaving radical, while G3(MP2)-RAD calculations provide data that are in good agreement with those obtained experimentally. Values of log(A/s−1) lie in the expected range of ∼9–11. These data provide rate constants for cyclization that span three orders of magnitude at 25°, namely: 103–106 s−1. This work also provides valuable Arrhenius data for the benzyl-substituted system 4 (R = Bn) (kc = 5.8 × 104 s−1 in benzene at 25°) and is important because the benzyl radical has become the “workhorse” for radical ring closures at selenium.
Introduction
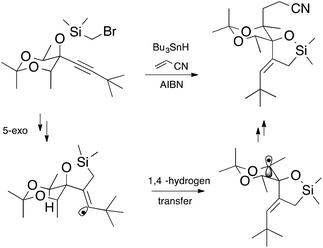
Free radical methods in synthesis abound;1 indeed there are over 20,000 references to this methodology according to a recent web search,2 and this figure does not include polymer chemistry. It is somewhat astonishing that this chemistry could have risen to the levels that it has in such a relatively short time. There have been waves of intense activity in the field. The First Renaissance Period (1980s)§ was built on the solid foundations established as a consequence of critical kinetic and mechanistic studies of fundamental radical reactions.3,4 The understanding and guidelines that followed allowed the synthetic practitioner to avoid the “demons” associated with chemistry under kinetic control5 and led to a period of prosperity during which free radical syntheses blossomed to include transformations under high regio- and stereocontrol, and evolved to include cascade chemistry.1 Many argue that the field is currently undergoing a second renaissance (Renaissance II) in which stable radicals, catalysis and efficiency have become key drivers of innovation.4An example of synthetic elegance following Renaissance I comes from the laboratories of Malacria.† The transformation depicted in Scheme 1 involves a 5-exo cyclization followed by a 1,4-hydrogen atom transfer and is finished off by an intermolecular addition (Giese reaction) and would have been unthinkable only a couple of decades ago.6
The early 1990s were dominated by new carbon–carbon bond forming methodology, with intramolecular homolytic addition chemistry finding a comfortable home in the synthetic chemists’ toolbox. In contrast, with the exception of reactions involving sulfur, almost no attention was given to intramolecular homolytic substitution chemistry that might be useful for constructing interesting heterocyclic molecules, and consequently this methodology lay dormant for quite a considerable length of time.7
This was the essentially state of play in 1992; the field had recently exited the First Period and enthusiasm for meticulous kinetic studies was waning; instead, practitioners became more interested in applying their “shiny new toys” to more and more complex scenarios. This evolution is a direct measure of the success of the advances made in the two previous decades.
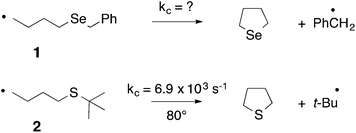
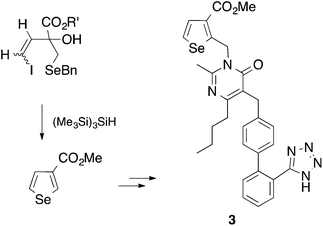
In 1992 we were particularly interested in developing free radical methods for the preparation of selenium-containing ring systems, and homolytic substitution seemed an appropriate chemistry to achieve this aim. Unfortunately, we were hampered by the lack of critical kinetic data for this chemistry; consequently we relied on inspired guesswork to estimate a rate constant for the cyclization of the 4-(benzylseleno)butyl radical 1 to give tetrahydroselenophene (Scheme 2).7,8 We reasoned that since the cyclization of the 4-(tert-butylthio)butyl radical 2 proceeded with a rate constant of 6.9 × 103 s−1 (80°),9 and given that phenylselenides react two to three orders of magnitude faster with tributyltin radical than the corresponding phenylsulfide,10 the rate constant (kc) for the ring closure of 1 had to be of the order of 105–106 s−1 at 80°. These assumptions ultimately proved to be helpful, and since these early days we have utilized homolytic substitution chemistry at benzylselenides to construct a large variety of selenium-containing ring systems,11–16 some of which have proven to be useful in medicinal chemistry. An example is selenomilfasartan 3, an antihypertensive, in which the selenophene ring is constructed using this chemistry (Scheme 3).17
Despite these successes, it has always been a goal of ours to provide a kinetic scale for intramolecular homolytic substitution chemistry in much that same way that exists for other cyclization reactions.18 This paper partly fills this gap; herein we show how competition kinetic experiments together with high-level computational chemistry can provide rate constants and Arrhenius parameters for the intramolecular attack of primary alkyl radicals at the selenium atom in a variety of substituted 5-(alkylseleno)pentyl radicals 4.
Computational methods
Ab initio and DFT calculations were carried out using Gaussian 09.19 Systematic conformational searches were carried out to ensure global rather than local minima were studied. Rotational increments of 120° were employed as this resolution has been reported to adequately explore molecular conformations.20 Geometry optimizations were performed utilizing standard gradient techniques at the B3LYP/6-31G(d) level of theory using restricted and unrestricted wavefunctions for closed and open shell systems, respectively.21 Values of <s2> never exceeded 0.77 before annihilation of the first spin contaminant. After annihilation of quartet contamination <s2> values were 0.75. Zero point energy corrections have been applied to all optimized structures and all ground and transition state structures have been verified by vibrational frequency analysis. Optimized geometries and energies for all transition structures in this study are available in the ESI.‡ Kinetic parameters were determined using the Eyring equation and energies obtained using the G3(MP2)-RAD method. G3(MP2)-RAD is a high-level composite method that has been shown to perform within chemical accuracy for radical reaction, hence it was selected for our study.22Results and discussion
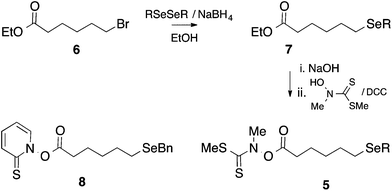
Except for the benzylseleno derivative (4, R = Bn), we chose to generate radicals 4 from the corresponding thiohydroximate (Kim) ester precursor 5,23 themselves prepared from the corresponding 6-(alkylseleno)hexanoic acid by well-established procedures (Scheme 4).24 Accordingly, the required dialkyl diselenide25 was reacted with sodium borohydride in ethanol; the alkylselenoate generated in this manner was further reacted with ethyl 6-bromohexanoate 6 to give the corresponding alkylseleno ester 7 in ∼70–90% yield. Subsequent hydrolysis and coupling with N-methylhydroxydithiocarbamate afforded the required Kim esters 5.Radicals 4 were generated by photolysis of a benzene solution of 5, at the required temperature, by a low pressure (broad spectrum) mercury lamp (Scheme 5). In the case of the benzyl-substituted system (R = Bn) we chose to generate 4 by thermolysis of the corresponding pyridinethioneoxycarbonyl (PTOC, Barton) ester 8,26 because, in related systems, we have observed cleavage of the Se–Bn bond upon photolysis;278 was prepared from 7 (R = Bn) as described previously.28
The 5-(n-octylseleno)pentyl radical (4, R = n-octyl)
Gas chromatography (GC) of the reaction mixture obtained when 5 (R = n-octyl) was photolysed as described above in the presence of 10 equivalents of tributyltin hydride (0.03–0.5 M) in benzene revealed the presence of selenane 9 and octyl pentyl selenide 10 (R = n-octyl) by comparison with authentic samples. Integration of the appropriate rate equation (eqn (1), Scheme 5) leads to eqn (2), which is valid under “pseudo-first-order” conditions in stannane.Initial experiments were carried out at 23° employing a variety of stannane concentrations; application of eqn (2) provided the rate constant data listed in Table 1. Each data point is the average of three individual experiments and the linearity of the data shown in Fig. 1, provides confidence that the kinetic model (Scheme 5) is correct and that we are monitoring free radical processes. Reactions at other temperatures were carried out at one concentration (0.1 M), in triplicate.
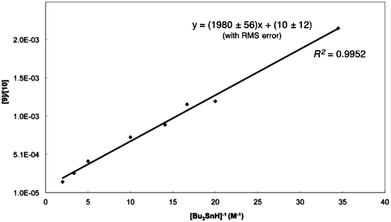 | ||
| Fig. 1 Dependence of [9]/[10] on Bu3SnH concentration at 23° for the cyclization of 4 (R = n-octyl) in benzene. | ||
| Temp (°C) | [Bu3SnH] (m) | [9]/[10]a |
k
H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (M−1 s−1) b (M−1 s−1) |
k c (s−1) |
|---|---|---|---|---|
| a Average of three experiments. b Taken from ref. 29. c Determined from the slope of the line in Fig. 1. | ||||
| 23 | 0.029 | 1.4 × 10−2 | 3.2 × 106 | 1.7 × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
| 0.050 | 7.9 × 10−3 | |||
| 0.060 | 7.6 × 10−3 | |||
| 0.071 | 5.9 × 10−3 | |||
| 0.10 | 4.9 × 10−3 | |||
| 0.30 | 1.7 × 10−3 | |||
| 0.50 | 9.7 × 10−4 | |||
| 47 | 0.10 | 8.0 × 10−3 | 5.3 × 106 | 4.2 × 103 |
| 65 | 0.10 | 1.06 × 10−2 | 6.8 × 106 | 7.5 × 103 |
| 75 | 0.10 | 1.35 × 10−3 | 8.4 × 106 | 1.1 × 104 |
| 85 | 0.10 | 2.12 × 10−2 | 9.0 × 106 | 1.9 × 104 |
| 95 | 0.10 | 2.44 × 10−2 | 1.2 × 107 | 2.8 × 104 |
Linear regression analysis of the [9]/[10] ratios presented in Table 1 (Fig. 2) provides the following (relative) Arrhenius expression (errors are expressed to 90% confidence and include random but not systematic variations):
| log(kc/kH) = 0.22 ± 0.54 − (20.2 ± 3.4)/θ | (3) |
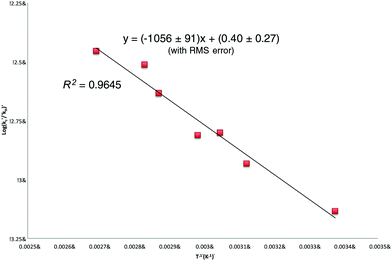 | ||
| Fig. 2 Relative Arrhenius expression (log(kc/kH)) vs. T−1) for the ring-closure of the 5-(octylseleno)pentyl radical 4 (R = n-octyl). | ||
Combining eqn (3) with the best available Arrhenius expression (eqn (4)) for the transfer of hydrogen atom from tributyltinhydride to a primary alkyl radical in hydrocarbon solvent,29 namely:
| log kH = 9.07 ± 0.24 − (15.4 ± 1.3)/θ | (4) |
| log kc = 9.3 ± 0.7 − (35.6 ± 4.7)/θ. | (5) |
This Arrhenius expression can be compared to the only available experimental kinetic data for the ring closure of a 5-(alkylseleno)pentyl radical; the diphenylmethyl derivative 4 (R = Ph2CH) was determined by laser-flash experiments to cyclize with an activation energy (Ea) of 15.2 ± 0.6 kJ mol−1 and log A of 8.9 ± 0.1, leading to a rate constant kc of 1.7 × 106 s−1 at 25°,30 some three orders of magnitude faster than our system (4, R = n-octyl). This difference in rate constant is to be expected on the basis of the difference in leaving group stability.31
To provide further comfort in our experimentally determined Arrhenius data, we chose to examine the ring closure of 4 by computational means. In recent years, our group has effectively employed high-level (G3(MP2)-RAD) techniques to provide rate data that are in good-to-excellent agreement with experimentally derived rate coefficients.31–34
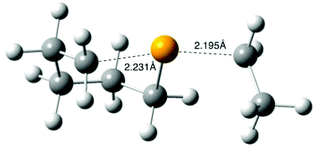
For computational expedience, the n-octyl leaving radical in 4 was replaced with the simplest primary alkyl leaving group, namely ethyl. Extensive searching of the B3LYP/6-31G(d) energy surface, as recommended for the G3(MP2)-RAD method,22 located transition structure 11 (R = Et) for the cyclization of 4 (R = Et) to give selenane 9 (Scheme 5); 11 is depicted in Fig. 3, full geometric data are available in the ESI.‡ Transition state 11 is somewhat unremarkable,35 with B3LYP/6-31G(d) transition state separations of 2.231 and 2.195 Å and the expected 15–20° deviation of attacking and leaving radical trajectory from linearity;32,3511 is calculated to lie 34.7 kJ mol−1 (ΔE‡) above the starting radical 4 (R = Et) at G3(MP2)-RAD.
G3(MP2)-RAD also provided a gas-phase rate constant (kc) of 4.8 × 103 s−1 at 25°, for the cyclization of 4, in good agreement with our experimentally determined value of 1.7 × 103 s−1 (23°) (Table 1) for 4 (R = n-octyl). When rate constants were calculated across the 25–80° temperature range, the following Arrhenius expression could be calculated for the cyclization of 4 (R = Et) in the gas phase:
| log kc = 10.2 − 37.2/θ | (6) |
The remaining radicals (4, R ≠ n-octyl)
Other radicals in this study (4, R = 2-octyl, tert-butyl, benzyl) were generated through photolysis (or thermolysis, R = Bn) and reacted as described above, using 0.1 M tert-dodecanethiol (instead of tributyltin hydride)¶ in benzene; values of [9]/[10] derived from this work are available in Table S1 in the ESI.‡ B3LYP/6-31G(d) optimised transition structures 11 (R = Me, iso-Pr, tert-Bu, Bn)|| were determined as described above and are depicted in Fig. 4, with full data available in the ESI.‡ The transition structures 11 depicted in Fig. 3 and 4 show the expected distance dependence observed as the leaving group ability increases, with R = Me exhibiting the “latest” structure, with attacking and leaving distances of 2.164 and 2.241 Å respectively, and R = Bn being the “earliest” (2.421, 2.122 Å).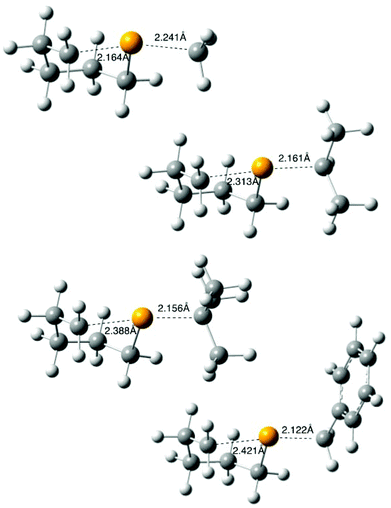 | ||
| Fig. 4 B3LYP/6-31G(d) calculated transition states 11 for the cyclization of radical 4 (R = Me, iso-Pr, tert-Bu, Bn). | ||
When the product ratios in Table S1‡ are combined with values of kH for the transfer of hydrogen atom from a tertiary thiol,36 Arrhenius data for the ring-closure of radicals 4 are obtained and are listed in Table 2 together with those obtained using G3(MP2)-RAD. Also included in this table are calculated data for 4 (R = Me), a system that we were unable to explore experimentally, as well as data for the previously measured diphenylmethyl substituted system 4 (R = Ph2CH). These Arrhenius data are depicted graphically in Fig. 5.
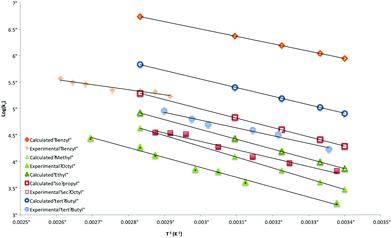 | ||
| Fig. 5 Overlay of calculated and experimentally-determined Arrhenius expressions for the cyclization of radicals 4. | ||
| Experimentala | G3(MP2)-RADb | |||||||
|---|---|---|---|---|---|---|---|---|
| Radical 4 | Log(A/s−1) | E act/kJ mol−1 | Log(kc/s−1) (25°)c | k c/s−1 (25°)c | Log(A/s−1) | E act/kJ mol−1 | Log(kc/s−1) (25°)c | k c/s−1 (25°)c |
| a In benzene unless otherwise states. b Gas phase. c Calculated from the Arrhenius expression. d 0.2 × 104 < kc < 7.4 × 104 s−1. e Calculated for R = Et. f 0.5 × 104 < kc < 4.4 × 105 s−1. g Calculated for R = iso-propyl. h 1.0 × 104 < kc < 1.2 × 106 s−1. i 1.5 × 104 < kc < 2.7 × 106 s−1. j Determined by laser flash experiments in tert-butylbenzene: see ref. 30. k 2.0 × 106 < kc < 9.8 × 106 s−1. | ||||||||
| R = Me | — | — | — | — | 10.2 | 38.9 | 3.38 | 2.4 × 103 |
| n-Oct | 9.3 ± 0.7 | 35.6 ± 4.7 | 3.06 ± 0.63 | 1.2 × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
10.2e | 37.2e | 3.68e | 4.8 × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
| 2-Oct | 9.1 ± 0.6 | 30.0 ± 4.3 | 3.84 ± 0.80 | 7.0 × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
10.3g | 33.6g | 4.41g | 2.6 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
| tert-Bu | 9.2 ± 0.5 | 28.0 ± 4.2 | 4.29 ± 0.88 | 2.0 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h h |
10.4 | 30.9 | 4.98 | 9.7 × 104 |
| Bn | 8.3 ± 0.8 | 20.2 ± 2.3 | 4.76 ± 1.00 | 5.8 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i i |
10.7 | 26.5 | 6.06 | 1.1 × 106 |
| Ph2CHj | 8.9 ± 0.1 | 15.2 ± 0.6 | 6.24 ± 0.32 | 1.7 × 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
— | — | — | — |
Inspection of Table 2 reveals good agreement between experimentally and computationally determined values of activation energy (Eact) and log kc, with G3(MP2)-RAD data generally falling within the 90% confidence limits of the experimentally-determined data. Activation energies range from 38.9 kJ mol−1 for the worst leaving group (Me) through to ∼30 kJ mol−1 (tert-Bu), ∼20 kJ mol−1 (Bn), and ∼15 kJ mol−1 (Ph2CH). Inclusion of the entropy (log A) terms lead to rate constants that span three orders of magnitude; from 103 s−1 (n-Oct) to 106 s−1 (Ph2CH) at 25°. It is interesting to note that the computationally determined rate constants generally sit at the high end of the experimentally determined confidence windows and this is predominately due to higher values of calculated log A compared to those obtained in benzene. Importantly, the experimental log A numbers from this work are consistent with those obtained experimentally for other intramolecular homolytic substitution reactions at sulfur and selenium,30 while the G3(MP2)-RAD data are consistent with other calculated log A values.31,32 These observed differences presumably reflect entropy changes between solution and gas phase reactions.
Conclusions
The work described in this paper provides important kinetic data for the intramolecular homolytic substitution reactions of 5-(alkylseleno)pentyl radicals 4. Competition kinetic experiments together with high-level G3(MP2)-RAD calculations provide rate constants for cyclization (kc) that span three orders of magnitude at 25° (103–106 s−1) and depend strongly on the nature of the leaving group. B3LYP/6-31G(d) calculations reveal that transition states 11 for cyclization are unremarkable and resemble those calculated previously for intermolecular and intramolecular SH2 chemistry. This work also provides valuable Arrhenius data for the benzyl-substituted system 4 (R = Bn) leading to a rate constant (kc) of 5.8 × 104 s−1 in benzene at 25° and is important because the benzyl radical has become the “workhorse” for radical ring closures at selenium.Experimental
Ethyl 6-(benzylseleno)hexanoate 7 (R = Bn) and its PTOC ester were prepared as reported previously.8 General procedures for the preparation of the remaining selenides 7 (R ≠ Bn), thiohydroximate (Kim) esters 5 and authentic products 10 are provided in the ESI.‡ An authentic sample of selenane 9 was prepared as described previously.37Ethyl 6-(1-octylseleno)hexanoate 7 (R = 1-Oct) was isolated in 71% yield. δH (500 MHz, CDCl3) 4.10 (q, J = 7.3 Hz, 2H, CH2), 2.52 (t, J = 7.4 Hz, 4H, CH2), 2.27 (t, J = 7.5 Hz, 2H, CH2), 1.69–1.58 (m, 6H), 1.46–1.10 (m, 15H), and 0.86 (t, J = 6.9 Hz, 3H, CH3); δC (125 MHz, CDCl3) 173.5, 60.1, 34.1, 31.8, 30.6, 30.2, 29.9, 29.4, 29.1, 29.0, 24.4, 24.0, 23.5, 22.6, 14.2 and 14.0; δSe (95 MHz, CDCl3) 161.1; νmax (neat) 2925, 2856, 1734, 1186 and 758 cm−1; HRMS C16H32O2SeNa requires 359.14604; found 359.14645.
Ethyl 6-(2-octylseleno)hexanoate 7 (R = 2-Oct) was isolated in 92% yield. δH (500 MHz, CDCl3) 4.13 (q, J = 7.1 Hz, 2H, CH2), 2.93 (sex, J = 6.8 Hz, 1H, CH), 2.56 (t, 7.4 Hz, 2H, CH2), 2.30 (t, J = 7.5 Hz, 2H, CH2), 1.83–1.11 (m, 22H) and 0.89 (t, J = 6.3 Hz, 3H, CH3); δC (125 MHz, CDCl3) 173.6, 60.2, 38.1, 34.9, 34.2, 31.8, 30.43, 29.6, 29.1, 27.8, 24.5, 22.6, 22.5, 22.3, 14.2 and 14.1 ppm; δSe (95 MHz, CDCl3) 265.6; νmax (neat) 2923, 1735, 1459, 1372, 1250, 1183, 1029, 802 and 722 cm−1; HRMS C16H32O2SeNa requires 359.14604, found 359.14588.
Ethyl 6-(tert-butylseleno)hexanoate 7 (R = tert-butyl) was isolated in 89% yield. δH 4.09 (q, J = 7.0 Hz, 2H, CH2), 2.54 (t, J = 7.5 Hz, 2H, CH2), 2.25 (t, J = 7.8 Hz, 2H, CH2), 1.61–1.71 (m, 4H), 1.49–1.28 (m, 2H), 1.40 (s, 9H, tBu) and 1.22 (t, J = 7.1 Hz, 3H, CH3); δC (125 MHz, CDCl3) 173.5, 60.1, 38.4, 34.1, 32.5, 30.2, 29.7, 24.4, 21.6 and 14.2; δSe (95 MHz, CDCl3) 376.9; νmax (neat) 2935, 1733, 1456, 1365, 1250, 1185, 1156, 1119, 857 and 732 cm−1; HRMS C12H24O2SeNa requires 303.08341; found 303.08328.
Kim ester 5 (R = 1-Oct) was isolated in 36% yield. δH (500 MHz, CDCl3) 3.79 (s, 3H, CH3), 2.81–2.23 (m, 9H), 1.77 (dt, J = 20.7, 7.5 Hz, 6H), 1.70 (m, 2H), 1.64 (dt, J = 15.1, 7.7 Hz, 2H CH2), 1.56–1.46 (m, 2H), 1.38–1.25 (10H, m) and 0.88 (t, J = 7.0 Hz, CH3); δC (125 MHz, CDCl3) 196.7, 169.8, 42.7, 31.8, 31.3, 30.6, 30.1, 30.0, 29.2, 29.2, 29.1, 24.2, 24.0, 23.4, 22.6, 18.7 and 14.1 ppm; δSe (95 MHz, CDCl3) 160.5; νmax (neat) 2933, 1796, 1457, 1362, 1049, 1010, 870 and 729 cm−1; HRMS C17H33NO2S2Se + H requires 428.11901; found 428.11901.
Kim ester 5 (R = 2-Oct) was isolated in 66% yield. δH (500 MHz, CDCl3) 3.79 (3H, s, CH3), 2.93 (sex, J = 13.7, 6.8 Hz, 1H, CH), 2.56 (3H, s, CH3), 2.55–2.58 (2H, m, CH2), 2.51 (2H, t, J = 7.5 Hz, CH2), 1.48–1.79 (8H, m), 1.40–1.44 (5H, m), 1.25–1.33 (6H, m) and 0.88 (3H, t, J = 7.0 Hz, CH3); δC (125 MHz, CDCl3) 196.7, 169.8, 42.7, 38.1, 35.1, 31.7, 31.3, 30.2, 29.3, 29,1, 27.8, 24.0, 22.6, 22.5, 22.1, 18.6 and 14.1; δSe (95 MHz, CDCl3) 266.2; νmax (neat) 2923, 1797, 1457, 1359, 1049, 1010, 870 and 724 cm−1; HRMS C17H33NO2S2SeNa requires 450.10096, found 450.10092.
Kim ester 5 (R = tert-Butyl) was isolated in 41% yield. δH (500 MHz, CDCl3) 3.79 (s, 3H), 2.64–2.48 (dt, J = 42.5, 7.4, 2H), 2.57 (s, 3H), 1.75–1.41, 8H) and 1.49 (s, 9H); δC (125 MHz, CDCl3) 196.7, 169.8, 42.7, 38.7, 32.5, 31.3, 30.1, 29.5, 24.0, 21.5 and 18.7; δSe (95 MHz, CDCl3) 376.6; νmax (neat) 2933, 1796, 1455, 1362, 1155, 1048, 1009, 870 and 870 cm−1; HRMS C13H25NO2S2SeNa requires 394.03833, found 394.03946.
Octyl pentyl selenide 10 (R = 1-Oct) was isolated in 81% yield. δH (500 MHz, CDCl3) 0.87–0.91 (6H, m), 1.27–1.43 (14H, m), 1.63–1.67 (4H, m) and 2.2–2.57 (4H, m); δC (125 MHz, CDCl3) 13.8, 13.9, 22.2, 22.6, 23.8, 29.0, 29.1, 29.9, 30.3, 31.8 and 32.0; νmax (neat) 2922, 1465, 1245, 1184 and 722 cm−1; δSe (95 MHz, CDCl3) 162.3. HRMS C13H28SeAg requires 371.04043; found 371.04140.
2-Octyl pentyl selenide 10 (R = 2-Oct) was isolated in 62% yield. δH (500 MHz, CDCl3) δ 0.88–0.91 (6H, m), 1.27–1.45 (15H, m), 1.51–1.55 (1H, m), 1.61–1.67 (3H, m), 2.53–2.57 (2H, m) and 2.91–2.95 (1H, m); δC (125 MHz, CDCl3) 13.9, 14.0, 22.2, 22.4, 22.5, 22.6, 22.7, 29.1, 30.5, 31.7, 32.3, 34.7 and 38.1; νmax (neat) 2924, 1457, 1376, 1193 and 724 cm−1; δSe (95 MHz, CDCl3) 265.5. HRMS C13H28SeAg requires 371.04049; found 371.04093.
tert-Butyl pentyl selenide 10 (R = tert-butyl) was isolated in 65% yield. δH (500 MHz, CDCl3) δ 2.58 (2H, t, J = 7.5 Hz), 1.66–1.70 (2H, m, CH2), 1.44 (9H, s, CH3), 1.32–1.37 (4H, m) and 0.89 (3H, t, J = 7.0 Hz, CH3); δC (125 MHz, CDCl3) 38.2, 32.5, 32.4, 30.4, 22.2, 21.9 and 13.9; νmax (neat) 2956, 2928, 1455, 1364, 1244, 1156, 1020 and 727 cm−1; δSe (95 MHz, CDCl3) 376.9. HRMS C9H20SeAg requires 314.97778; found 314.97760.
Acknowledgements
Generous support of the Australian Research Council through the Centres of Excellence Scheme is gratefully acknowledged. Allocations of computing resources by the National Computing Infrastructure (NCI) National Facility and the Victorian Life Science Computation Initiative (VLSCI) are also gratefully acknowledged.Notes and references
- B. Giese, B. Kopping, T. Gobel, J. Dickhaut, G. Thoma, K. J. Kulicke and O. R. F. Trach, Radical Cyclization Reactions, Wiley and Sons, New York, 1996, vol. 48, pp. 301–340 Search PubMed.
- SciFinder search performed on 19 March 2014. For a comprehensive overview of the richness and diversity of modern free radical methods in synthesis see: Encyclopedia of Radicals in Chemistry, Biology and Materials, ed. C. Chatgilialoglu and A. Studer, John Wiley & Sons Ltd, Chichester, UK, 2012, vol. 2 and 4 Search PubMed.
- A. L. J. Beckwith and C. H. Schiesser, Org. Biomol. Chem., 2011, 9, 1736–1743 CAS.
- C. R. J. Stephenson, A. Studer and D. P. Curran, Beilstein J. Org. Chem., 2013, 9, 2778–2780 CrossRef CAS PubMed.
- A. N. Hancock and C. H. Schiesser, Chem. Commun., 2013, 49, 9892–9895 RSC . See also: A. L. J. Beckwith, C. J. Easton and A. K. Serelis, J. Chem. Soc., Chem. Commun., 1980, 482–483 RSC.
- M. Gulea, J. M. López-Romero, L. Fensterbank and M. Malacria, Org. Lett., 2000, 2, 2591–2594 CrossRef CAS.
- K. Sutej and C. H. Schiesser, J. Chem. Soc., Chem. Commun., 1992, 57–58 Search PubMed.
- L. J. Benjamin, C. H. Schiesser and K. Sutej, Tetrahedron, 1993, 49, 2557–2566 CrossRef CAS.
- J. A. Franz, D. H. Roberts and K. F. Ferris, J. Org. Chem., 1987, 52, 2256–2262 CrossRef CAS.
- A. L. J. Beckwith and P. E. Pigou, Aust. J. Chem., 1986, 39, 77–87 CrossRef CAS.
- J. E. Lyons, C. H. Schiesser and K. Sutej, J. Org. Chem., 1993, 58, 5632–5638 CrossRef CAS.
- C. H. Schiesser, Chem. Commun., 2006, 4055–4065 RSC.
- S. Lobachevsky, C. H. Schiesser and V. Gupta, Tetrahedron Lett., 2007, 48, 9077–9079 CrossRef CAS PubMed.
- M. K. Staples and C. H. Schiesser, Chem. Commun., 2010, 46, 565–567 RSC.
- M. K. Staples, R. L. Grange, J. A. Angus, J. Ziogas, N. P. H. Tan, M. K. Taylor and C. H. Schiesser, Org. Biomol. Chem., 2011, 9, 473–479 CAS.
- P. E. Macdougall, H. M. Aitken, Y. Kavanagh, P. J. Scammells, S. H. Kyne and C. H. Schiesser, Chem. Commun., 2012, 48, 9126–9128 RSC.
- R. L. Grange, J. Ziogas, A. J. North, J. A. Angus, C. H. Schiesser and C. H, Bioorg. Med. Chem. Lett., 2008, 18, 1241–1244 CrossRef CAS PubMed.
- M. Newcomb, Tetrahedron, 1993, 49, 1151–1176 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsujo, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavarachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jarramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C. 01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- E. I. Izgorodina, C.-Y. Lin and M. L. Coote, Phys. Chem. Chem. Phys., 2007, 9, 2507–2516 RSC.
- W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- D. J. Henry, M. B. Sullivan and L. Radom, J. Chem. Phys., 2003, 118, 4849–4860 CrossRef CAS PubMed.
- S. Kim, C. J. Lim, S. Song and H. Kang, Synlett, 2001, 688–690 Search PubMed.
- M. W. Carland, R. L. Martin and C. H. Schiesser, Org. Biomol. Chem., 2004, 2, 2612–2618 CAS.
- The Chemistry of Organic Selenium and Tellurium Compounds, ed. S. Patai and Z. Rappoport, Wiley and Sons, Chichester, 1986 Search PubMed.
- D. H. R. Barton, D. Crich and W. B. Motherwell, Tetrahedron, 1985, 41, 3901–3924 CrossRef CAS.
- S. Lobachevsky, PhD Thesis, The University of Melbourne, 2008.
- L. J. Benjamin, C. H. Schiesser and K. Sutej, Tetrahedron, 1993, 49, 2557–2566 CrossRef CAS.
- L. J. Johnston, J. Lusztyk, D. D. M. Wayner, A. N. Abeywickrema, A. L. J. Beckwith, J. C. Scaiano and K. U. Ingold, J. Am. Chem. Soc., 1985, 107, 4594–4596 CrossRef CAS.
- L. M. Wild, PhD Thesis, The University of Melbourne, 1998. See also; S. H. Kyne and C. H. Schiesser, in Encyclopedia of Radicals in Chemistry, Biology and Materials, ed. C. Chatgilialoglu and A. Studer, John Wiley & Sons Ltd, Chichester, UK, 2012, pp. 629–654 Search PubMed.
- H. M. Aitken, S. M. Horvat, C. H. Schiesser, C. Y. Lin and M. L. Coote, Int. J. Chem. Kinet., 2012, 44, 51–58 CrossRef CAS.
- H. M. Aitken, A. N. Hancock and C. H. Schiesser, Chem. Commun., 2012, 48, 8326–8328 RSC.
- S. H. Kyne, C.-Y. Lin, I. Ryu, M. L. Coote and C. H. Schiesser, Chem. Commun., 2010, 46, 6521–6523 RSC.
- A. N. Hancock and C. H. Schiesser, Chem. Sci., 2014, 5, 1967–1973 RSC.
- C. H. Schiesser and L. M. Wild, J. Org. Chem., 1999, 64, 1131–1139 CrossRef CAS.
- M. Newcomb, A. G. Glenn and M. B. Manek, J. Org. Chem., 1989, 54, 4603–4606 CrossRef CAS.
- G. T. Morgan and F. H. Burstall, J. Chem. Soc., 1929, 2197–2202 RSC.
Footnotes |
| † Dedicated to Professor Max Malacria on the occasion of his 65th birthday. Happy birthday Max! |
| ‡ Electronic supplementary information (ESI) available: General procedures for the preparation of 5, 7, and 10 (R ≠ Bn). Table S1. Gaussian archive entries for all transitions states 11 calculated in this study. 1H, 13C and 77Se spectra of 5, 7, and 10 (R ≠ Bn). (35 pages). See DOI: 10.1039/c4qo00108g |
| § Also referred to as the Free Radical Renaissance Period, or Renaissance I. See ref. 3,4. |
| ¶ tert-Dodecanethiol provided reaction mixtures that proved to be easier to analyse than those obtained using tributyltin hydride. |
| || For computational expedience, the 2-octyl substituent was replaced with iso-propyl. |
| This journal is © the Partner Organisations 2014 |