Descriptor-based identification of bimetallic-derived catalysts for selective activation of ethane with CO₂

Abstract

The selective activation of ethane with CO₂ offers a promising strategy to simultaneously reduce the greenhouse gas and upgrade the underutilized ethane to value-added chemicals. Herein, the catalytic reactions of ethane and CO₂ over a series of indium (In)-based bimetallic-derived catalysts were investigated by combining catalytic evaluation, in situ characterization and Density Functional Theory (DFT) calculations. The DFT-calculated energetics along the dry reforming of ethane pathway to produce syngas and oxidative dehydrogenation of ethane to produce ethylene were consistent with the trend in experimentally observed selectivity. Combining the results currently collected for In-based bimetallic catalysts with those previously reported for other bimetallic systems, a descriptor-based model was used to scale the ethylene selectivity over a wide range of bimetallic systems. Furthermore, results from the current study enhanced the mechanistic understanding of the importance that the binding strength of the initial reaction intermediates played in controlling the selective activation of ethane with CO₂.

---

Broader context

In recent decades, increasing anthropogenic CO₂ emissions and verified huge shale gas reserves have attracted intensive interests in simultaneously upgrading CO₂ and C₂+ light alkanes into different types of important industrial feedstocks (e.g., syngas, olefins, aromatics and oxygenates) at ambient pressure. One of the challenges is how to control the selective scission of C–H/C–C bonds in alkanes. However, the development of selective catalysts, such as those from the bimetallic-derived systems, is hindered by the ambiguous structure–function relationship due to the structural complexity of supported catalysts. The present work is motivated to identify general descriptors not only to predict the thermodynamically favorable bimetallic-derived structures under CO₂-assisted alkane activation conditions, but also to provide mechanistic insights into the selective bond cleavage in alkanes. Herein, ethane–CO₂ reaction over a wide range of bimetallic-derived catalysts was adopted as a case study to unravel the structure–function relationship over two types of representative structures. Two general descriptors, formation energy of alloy surfaces and the corresponding binding energy to oxygen, were utilized to correlate catalytic performance with DFT-calculated values. The identification of these two general descriptors opens new opportunities to the rational design of highly selective catalysts for simultaneously upgrading light alkanes and CO₂.

1. Introduction

The rapid increase of carbon dioxide (CO₂) emissions in the past decades has contributed to the global climate change.¹ To reduce CO₂ emissions, several strategies such as CO₂ capture and catalytic conversion have been proposed.^2–6 One promising route is the utilization of light alkanes to directly activate CO₂ to value-added products, such as syngas, olefins, aromatics and oxygenates.^7–10 The recent shale gas boom has significantly increased the supply of light alkanes, with the fraction of ethane (C₂H₆) being up to 10 vol%.¹¹ Therefore, the catalytic reactions between CO₂ and C₂H₆ provide a promising strategy to simultaneously reduce the greenhouse gas emissions and upgrade the underutilized C₂H₆ to important industrial chemicals. Depending on the selective bond cleavage of C₂H₆, there are mainly two pathways, i.e., dry reforming of ethane (DRE) to produce syngas (C₂H₆ + 2CO₂ → 4CO + 3H₂) via C–C and C–H bond cleavage and oxidative dehydrogenation of ethane (ODHE) to produce ethylene (C₂H₆ + CO₂ → C₂H₄ + CO + H₂O) via selective C–H bond session while protecting the C–C bond.^7–10

Bimetallic-derived catalysts, either in the metallic or oxidized form, typically feature distinct catalytic properties and are often superior to those of either monometallic component due to the ligand, ensemble and strain effects.¹² A number of bimetallic-derived catalysts have been used for the reactions of C₂H₆ with CO₂, such as Co–Mo,¹³ Ni–Mo,¹³ Ni–Al,^14,15 Ni–Fe,^13,16,17 Pt–Co,¹³ Pt–Ni,^18,19 Pt–Ga,²⁰ Pt–Ce,²¹ Pt–In,²⁰ Pt–Sn,²² Pd–Fe,²³ Pd–Co²⁴ and Pd–In.²⁴ The enhanced catalytic properties have been proposed to be associated with changes in the compositions and structures.^25–27 For example, Yan et al.¹⁶ reported that by changing the ratio of bimetallic components, the active phases under reaction conditions can be transformed, leading to the distinguished reaction pathways: Ni₃Fe prefers to stay as mixed alloy during the activation of C₂H₆ by CO₂ and is more favorable for C–C bond scission; while NiFe₃ prefers to form the Ni/FeO_x interface, which is the active site for C–H bond scission. Recently, Xie et al. revealed that the reaction-induced surface phase transformation can tune the selectivity in the scission of the C–C and C–H bonds of C₂H₆ on PdCo_x/CeO₂ and PdIn_x/CeO₂ catalysts, respectively.²⁴ Based on the case studies of a series of Pd-based bimetallic catalysts, the interplay of two descriptors was proposed:²⁴ the formation energy of the alloy surface and the reactive oxygen binding energy, which scaled well with the C₂H₄ selectivity. However, it remains unclear whether the previously identified descriptors can be employed universally to capture the CO₂-assisted C₂H₆ activation beyond the Pd-based catalysts.

Herein, the selective activation of C₂H₆ with CO₂ was studied over a series of In-based bimetallic catalysts. The C₂H₄ selectivity was investigated using experimental studies of synthesis, catalytic testing and in situ characterization, followed by DFT calculations to gain better mechanistic understanding, validate the descriptors previously identified for Pd-based bimetallic catalysts and eventually use them as universal descriptors for identifying promising bimetallic-derived catalysts. The selection of In-based bimetallic catalysts was primarily inspired by their intriguing performance for CO₂-assisted propane dehydrogenation, where the catalytic activity was attributed to the In redox activity (In⁰ and In^III) and the associated transfer of chemisorbed oxygen (*O).^28–31 Moreover, previously the change in the ratio of Pt : In in bimetallic Pt–In derived catalysts was also found to influence the active phases and therefore the performance during the direct dehydrogenation of C₂H₆.²⁰

The present experimental and DFT studies of In-based catalysts provided insights into controlling the DRE and ODHE pathways to produce syngas and C₂H₄, respectively. The combination of results of In-based systems from current study with those of other bimetallic-derived catalysts reported previously, a descriptor-based prediction of selectivity was achieved for the simultaneous upgrading of C₂H₆ and CO₂ over a wide range of bimetallic catalysts. It not only facilitates the discovery of new catalysts, but also promotes the mechanistic understanding of selectivity-tuning introduced by forming different bimetallic-derived structures. Furthermore, a volcano relationship was observed between the binding difference of *CH₃CH₂O and *CH₃CH₂ intermediates and the corresponding C₂H₄ selectivity over diverse bimetallic systems.

2. Methods

2.1. Experimental methods

All In-based bimetallic catalysts were synthesized using a slurry method. For each synthesis, desired amounts of metal precursors [Rh(NO₃)₃·2H₂O, Pt(NH₃)₄(NO₃)₂, Co(NO₃)₂·6H₂O, Ni(NO₃)₂·6H₂O, or Cu(NO₃)₂·3H₂O] were simultaneously dissolved with In(NO₃)₃·xH₂O in 30 ml of DI water to achieve a M/In atomic ratio of 1 : 3 at room temperature. Afterwards, the solution was ultrasonicated for 15 min before adding the CeO₂ support, followed by another ultrasonication of 30 min. The slurry suspension was continuously stirred and dried at 343 K overnight, after which the dried sample was calcined in static air at 673 K for 4 h with a heating rate of 1.0 K min⁻¹. More details about the loading amounts of each metal elements can be found in the ESI.†

All the catalysts were evaluated using a flow reactor (quartz tube, 4 mm ID, 6.35 mm OD) at ambient pressure. For each test, unless specified, approximately 100 mg of catalyst (60–80 mesh) was loaded into the isothermal zone of the quartz tube and fixed by two pieces of quartz wool on both ends. The catalyst was reduced in 50 vol% H₂ in Ar (total 40 ml min⁻¹) at 723 K for 1 h and then heated to 873 K under Ar (40 ml min⁻¹) in 15 min. The catalyst was subsequently exposed to C₂H₆/CO₂/Ar (10/10/20 ml min⁻¹) at 873 K for catalytic evaluation for 12 h. The gas line from the reactor outlet to the gas chromatography (GC) inlet was wrapped by heating tapes and maintained at 423 K to avoid any condensation of water vapor. The product stream was analyzed by an Agilent 7890B GC (PLOT Q and MOLESEIVE columns) equipped with a thermal conductivity detector (TCD) and a flame ionized detector (FID). The elemental (C, H, O) balances were within 100 ± 2% for all the experiments. Procedures for calculating conversion (X), C₂H₆-based selectivity (S) and yield (Y) were the same to those described in a previous study.²⁴

The in situ X-ray absorption fine structure (XAFS) spectra of the Pt L₃-edge, Rh K-edge and In K-edge were collected at Beamline 7-BM (QAS) of the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory, following the same experimental methods described in a previous study.²⁴ XAFS spectra were continuously collected in situ under Helium at 298 K, 50 vol% H₂ at 723 K, He purging at 823 K, and the reaction stream of CO₂ and C₂H₆ at 823 K. Rh, Pt and In foils were used as standard references for energy calibrations as well as to obtain the passive electron reduction factor (S₀²) used for the fitting of the extended X-ray absorption fine structure (EXAFS) spectra. The EXAFS fittings were performed with the scattering information (amplitude and phase functions) extracted from the model compounds (see more details in Fig. S1 and S2 in ESI†). Metal oxide references (Rh₂O₃, PtO₂, and In₂O₃) were also measured for identifying oxidation states using the X-ray absorption near edge structure (XANES) results. Data processing was performed using the IFEFFIT package.

2.2. DFT calculations

Spin-polarized DFT calculations were performed with the projector-augmented-wave (PAW) approach^32,33 and the generalized gradient approximation (GGA) exchange–correlation functional by Perdew, Burke and Ernzerhof (PBE)³⁴ as implemented in the Vienna Ab Initio Simulation Package (VASP).^32,35 A kinetic energy cutoff for the plane wave basis of 400 eV was employed. The Methfessel–Paxton order I method was used to describe the Fermi-distribution of electronic states in the metallic systems with an artificial electronic temperature of k_BT = 0.2 eV. The total energy was converged better than 10⁻⁷ eV per atom, and the final force on each atom was less than 0.03 eV Å⁻¹. To calculate the descriptors for the CO₂-assisted activation of ethane, a 4-layer 2 × 2 surface slab was constructed to describe the (111) surface phases of AB₃ bimetallic alloys, where the first Brillouin zone was sampled on a Γ-centered 3 × 3 × 1 k-mesh. Following our previous study,²⁴ three surface models were considered for bare AB₃(111): the bulk-terminated surface to simulate the stoichiometric structure AB₃(111), the skin A/B(111) or the sandwich B/A/B(111) models to describe the two extreme cases of surface segregation. In addition, the configurations under activation of ethane with CO₂, where chemisorbed oxygen (*O) was likely formed via CO₂ dissociation,²³ were also considered by the saturate adsorption of a layer of *O on top of the three types of alloy surfaces and formation of oxide–metal interfaces.

To describe the potential energy diagram on the selected bimetallic-derived interfaces, InO_x/Rh(111) and InO_x/Pt(111) were modeled by placing a small InO_x cluster on a 4-layer 5 × 5 Rh(111) and Pt(111) surfaces, respectively. The choice of such small cluster was a compromise between the computational cost and reasonable size to account for the characterized nanoparticles experimentally. The formation energies of the InO_x cluster on the metal surfaces were calculated with reference to the corresponding metal surface, metallic In and gaseous oxygen. The variation in formation energy with the increasing ratio of O : In, x, was calculated for InO_x/Pt(111) or InO_x/Rh(111) and the surface with the lowest formation energy was selected for further catalytic studies.

A 20 Å thick vacuum was added along the direction perpendicular to the surface to avoid the interactions between the slabs. During geometry optimization, the bottom two layers were fixed at the bulk positions while the remaining layers were allowed to relax, and dipole corrections were included in the calculations. The formation energies of alloy surfaces and the reactive oxygen binding energies were calculated following the previous study.²⁴ Wherein, the formation energies of alloy surfaces were calculated referenced to each metal surface. The reactive oxygen binding energies were determined by referring to the most stable alloy surface and gaseous oxygen, accounting for possible phase transitions. The binding energy of an adsorbate is calculated as E_b = E_{adsorbate/slab} − E_slab − E_adsorbate, where E_{adsorbate/slab}, E_slab and E_adsorbate are the DFT-calculated total energies of slab with the adsorbate, bare slab and the adsorbate species in the gas phase, respectively.

3. Results and discussion

3.1. Experimental evaluation of activity and selectivity

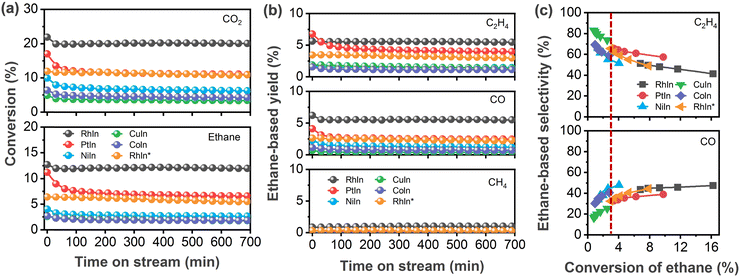
Several CeO₂-supported AIn₃ (A = Co, Ni, Cu, Rh, Pd, Pt) were synthesized, characterized, and tested for the CO₂-assisted activation of C₂H₆. As shown in Fig. 1a, all the In-based catalysts exhibited stable conversion of CO₂ and C₂H₆ after the initial 2 h. Among the catalysts investigated in the current study, RhIn₃/CeO₂ showed the highest conversion (20.0%) of CO₂ at the steady state, followed by PtIn₃/CeO₂ (11.0%), NiIn₃/CeO₂ (6.3%), PdIn₃/CeO₂ (4.5%),²⁴ CoIn₃/CeO₂ (4.3%), and CuIn₃/CeO₂ (3.4%) in a decreasing sequence. Likewise, the C₂H₆ conversion followed a similar trend: RhIn₃/CeO₂ (12.0%) > PtIn₃/CeO₂ (6.6%) > PdIn₃/CeO₂ (3.1%)²⁴ ≈ NiIn₃/CeO₂ (2.7%) > CoIn₃/CeO₂ (1.8%) ≈ CuIn₃/CeO₂ (1.8%). Fig. 1b showed that the main products were C₂H₄ and CO as well as a minor amount of methane (CH₄). RhIn₃/CeO₂ (5.5%) and PtIn₃/CeO₂ (4.0%) exhibited higher yields of C₂H₄ than the previously reported PdIn₃/CeO₂ catalyst (2.8%) as well as the other MIn₃/CeO₂ (M = Ni, Co and Cu) catalysts (1.1–1.4%). The highest and lowest CO yields were observed over RhIn₃/CeO₂ (5.5%) and PdIn₃/CeO₂ (0.3%), respectively. Given the different conversions among different catalysts, for the sake of properly comparing selectivity, the C₂H₆ conversion was varied by changing the space velocity at the same reaction temperature (873 K) to obtain comparable values (around 3% conversion, denoted by the dashed line in Fig. 1c). As summarized in Table 1, the C₂H₄ selectivity followed the trend of PdIn₃/CeO₂ (89.0%) > CuIn₃/CeO₂ (73.9%) > RhIn₃/CeO₂ (65.6%) ≈ PtIn₃/CeO₂ (65.6%) > CoIn₃/CeO₂ (59.0%) > NiIn₃/CeO₂ (55.3%) in a decreasing sequence, while it followed the reverse trend for the C₂H₆-based CO selectivity.

Fig. 1 Catalytic performance of In-based bimetallic catalysts for the CO₂–ethane reaction. (a) Conversion of CO₂ and ethane as a function of time on stream; (b) ethane-based yield of ethylene, CO and methane along with time on stream; (c) ethane-based selectivity of ethylene and CO at different conversion of ethane. Reaction conditions: (a and b) 100 mg of catalyst, 1 atm, 873 K, C₂H₆/CO₂/Ar = 10/10/20 ml min⁻¹; (c) 100 mg of catalyst, 1 atm, 873 K, C₂H₆/CO₂/Ar = 5/5/10, 10/10/20, 15/15/30, 20/20/40, 25/25/50 ml min⁻¹. Notes: the catalyst loading for RhIn* was 40 mg; the ethane-based yield or selectivity of ethylene and CO means that such products were ethane-derived species.

Table 1 Summary of catalytic performance over different MIn₃/CeO₂ catalysts for the CO₂–ethane reaction at 873 K with comparable ethane conversion

Catalysts	Conversion (%)	Selectivity (%)
	C2H6	CH4	CO	C2H4
Notes: unless denoted, the catalysts were evaluated with the reaction conditions of 1 atm, 100 mg of catalyst, 873 K.a C2H6/CO2/Ar = 25/25/50 ml min^−1.b C2H6/CO2/Ar = 10/10/20 ml min^−1.c C2H6/CO2/Ar = 5/5/10 ml min^−1.d C2H6/CO2/Ar = 5/5/10 ml min^−1.e 40 mg of catalyst, C2H6/CO2/Ar = 25/25/50 ml min^−1.f C2H6/CO2/Ar = 10/10/20 ml min^−1.g The data were collected from ref. 24.
PtIn3/CeO2^a	3.4	1.4	33.0	65.6
NiIn3/CeO2^b	2.6	0.2	44.5	55.3
CuIn3/CeO2^c	2.5	0.6	25.5	73.9
CoIn3/CeO2^d	2.8	0.4	40.6	59.0
RhIn3/CeO2^e	2.9	1.9	32.5	65.6
PdIn3/CeO2^f^g	3.1	0.0	11.0	89.0

---

3.2. Characterization using in situ XAFS

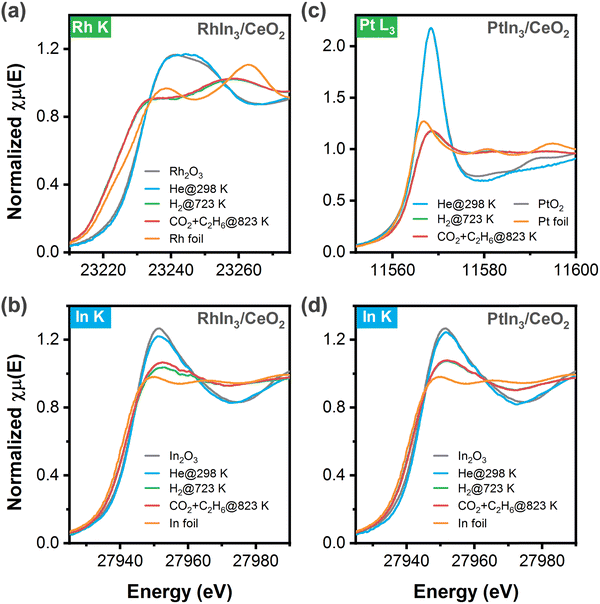
Because RhIn₃/CeO₂ and PtIn₃/CeO₂ showed the highest activity for CO₂ and C₂H₆ conversions, the chemical states of these two catalysts under different conditions were characterized using in situ XAFS measurements. According to the Rh K-edge XANES results (Fig. 2a), Rh in the fresh sample retained a chemical state resembling Rh³⁺ in Rh₂O₃, which was reduced at 723 K under the hydrogen atmosphere as indicated by the diminished white line and a shift to lower energy. It should be noted that the XANES feature was much different from that of Rh foil, suggesting the formation of Rh–In bonds where the orbitals rehybridized. Meanwhile, the In K-edge XANES features (Fig. 2b) indicated that In was reduced to a state between In⁰ and In³⁺, likely due to the co-presence of InO_x oxides and metallic (or Rh_xIn_y) species. Upon exposure to the reaction stream (C₂H₆ and CO₂) at 823 K, both the XANES features of Rh and In K-edges remained nearly unchanged, suggesting the robust feature of the above structures. Likewise, as shown in Fig. 2c and d, after reduction at 723 K the Pt L₃-edge and In K-edge XANES results of PtIn₃/CeO₂ also revealed that a metallic character of Pt, but different from that of Pt foil, while In was in a mixed state with both oxidic and metallic features, again suggesting the co-presence of the InO_x and PtIn alloy structures, which remained unchanged in the presence of C₂H₆ and CO₂ at 823 K. Overall, the XANES results indicated the presence of both InO_x and RhIn (or PtIn) under reaction conditions, consistent with the corresponding EXAFS results (Fig. S1, S2 and Table S1, ESI†) that revealed the presence of both In–O and In–Rh (or In–Pt) coordination.

Fig. 2 In situ XANES spectra of RhIn₃/CeO₂ and PtIn₃/CeO₂ catalysts as well as reference samples: (a and b) referred to the in situ XANES spectra of Rh and In K-edges, respectively, of RhIn₃/CeO₂ under different conditions; (c and d) referred to the in situ XANES spectra of Pt L₃-edge and In K-edge, respectively, of PtIn₃/CeO₂ under different conditions. Note: standard referential samples (metal foils: Rh, Pt, and In; metal oxides: Rh₂O₃, PtO₂, and In₂O₃) were also measured for comparison in XANES.

3.3. Mechanistic understanding using DFT calculations

DFT calculations were performed on the highly active In-based catalysts observed experimentally (Fig. 1), RhIn₃ and PtIn₃, to gain a mechanistic understanding of the activation of C₂H₆ with CO₂. Wherein, the CeO₂ support for the bimetallic catalysts was found experimentally to play similar roles, i.e. facilitating the CO₂ dissociation and providing reactive oxygen species, *O, during the reaction.^{13,16,18,23,24} Thus, as shown previously, it is reasonable to compare the theoretical predictions based on unsupported bimetallic AB₃ model surfaces with the experimentally measured trends on supported AB₃/CeO₂ catalysts.^{13,16,18,23,24}

The stable surface structures of RhIn₃ and PtIn₃ under reaction condition were firstly determined using DFT calculations (Fig. S3, ESI†). The results showed the preference to the inverse model with InO_x oxide supported on the Rh(111) (Fig. S4, ESI†) and Pt(111) (Fig. S5, ESI†) surfaces due to the strong interaction between *O, likely produced from CO₂ dissociation, and the surface In atoms, while the subsurface remained as the bimetallic. This is consistent with the in situ XAFS results showing the mixture of In in both oxidative and metallic states (Fig. 2 and Fig. S1, S2, ESI†). For the inverse model, a small InO_x cluster containing two In atoms was chosen as a compromise of computational cost and reasonable size to depict the InO_x nanostructures formed on the metal surface under the reaction conditions. The effect of In : O ratio on the relative cluster stability was evaluated based on the formation energies (Fig. S4 and S5, ESI†). On Rh(111) (Fig. S4, ESI†), the most stable configuration is In₂O₅/Rh(111) with the additional *O locating at the interfacial fcc hollow site of Rh(111), rather than that on In₂O₅ cluster. In comparison, the interaction of the InO_x cluster on Pt(111) (Fig. S5, ESI†) is much weaker and In₂O₇/Pt(111) is preferred. Yet, the additional *O still favors the interfacial fcc hollow site of Pt(111).

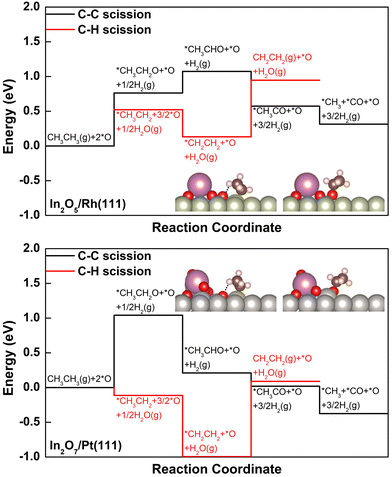
The DRE (C–C bond scission), and the ODHE (C–H bond scission) reaction pathways were calculated to describe the observed variation in C₂H₄ selectivity from the CO₂–ethane reaction over the stable surfaces under reaction conditions (Fig. 3). We note here that only the reaction energies for the elementary steps involved were calculated, by assuming a BEP-like correlation between the reaction energy and the corresponding activation barrier according to our previous DFT studies on the activation of light alkanes with CO₂.^24,36 On In₂O₅/Rh(111), with the presence of *O at the interfacial fcc hollow site of Rh and in a binding energy of −1.72 eV (Fig. 3 and Fig. S6 and Table S2, ESI†), the initial dissociative adsorption of C₂H₆ to produce *CH₃CH₂ along the ODHE pathway is slightly more favorable (ΔE = 0.52 eV) than the formation of *CH₃CH₂O along the DRE pathway (ΔE = 0.76 eV, Fig. 3). The further dehydrogenation of *CH₃CH₂ to *CH₂CH₂ along the ODHE pathway is exothermic (ΔE = −0.39 eV), and the most endothermic process is the desorption of *CH₂CH₂ (ΔE = 0.82 eV), which is likely overcome under the reaction temperature at 823 K. It is noticed that the elementary steps involved in the DRE pathway show a different energy profile from that along the ODHE pathway (Fig. 3). Once *CH₃CH₂O is formed, not only its further dehydrogenations to *CH₃CHO (ΔE = 0.31 eV) and *CH₃CO (ΔE = −0.50 eV), but also the following C–C bond cleavage to produce *CO (ΔE = −0.26 eV) are facile (Fig. 3). Overall, the DFT results suggest that, although the initial reaction step on In₂O₅/Rh(111) favors the ODHE leading to the C₂H₄ production, the DRE resulting in syngas production is also feasible due to the facile subsequent steps after the initial formation of *CH₃CH₂O, which reasonably agrees with the experimentally measured intermediate C₂H₄ selectivity of 65.6%.

Fig. 3 Potential energy diagrams for dry reforming reaction of ethane (DRE or C–C bond scission) and oxidative dehydrogenation reaction of ethane (ODHE or C–H bond scission) on In₂O₅/Rh(111) (top) and In₂O₇/Pt(111) (bottom). The DFT-optimized structures of selected key intermediates *CH₃CH₂ + *O (left) and *CH₃CH₂O (right) were included as insets and the hydrogen bonds were shown by dotted lines (In: pink; Pt: gray; Rh: ivory; O: red; C: brown; H: white).

Compared to In₂O₅/Rh(111), with the lower In : O ratio In₂O₇/Pt(111) enables the significant bond weakening for *O located at the interfacial fcc hollow site of Pt(111) (Fig. S7, ESI†), going from −1.72 eV to −0.86 eV in binding energy (Table S2, ESI†). While the preference to form *CH₃CH₂ (ΔE = −0.11 eV) along the ODHE pathway over *CH₃CH₂O (ΔE = 1.04 eV) along the DRE pathway is greatly increased. In considering the energetics for the initial C₂H₆ dissociative adsorption, the preference of ODHE over DRE is more significant (−0.11 eV vs. 1.04 eV) for In₂O₇/Pt(111) than that of In₂O₅/Rh(111) (0.52 eV vs. 0.76 eV), and thus, a higher C₂H₄ selectivity on In₂O₇/Pt(111) should be expected (Fig. 3). However, the *CH₂CH₂ desorption along the ODHE pathway is more facile on In₂O₅/Rh(111) than In₂O₇/Pt(111) (0.82 eV vs. 1.08 eV), and therefore a lower C₂H₄ selectivity on In₂O₇/Pt(111) is likely observed. The interplay of the two factors operating in an opposite direction likely contributes to a similar C₂H₄ selectivity for the two catalysts as observed experimentally.

3.4. Identifying selective bimetallic-derived catalysts using descriptors

Our previous study of 14 Pd-based bimetallic catalysts²⁴ identified a contour plot, which described well the relationship between the two identified descriptors (formation energies of alloy surfaces and the reactive oxygen binding energies) and experimentally measured C₂H₄ selectivity. The current study showed that in general such contour plot can be expanded to describe the In-based systems, confirming the universality of the descriptor-selectivity relationship identified previously (Fig. 4). That is, depending on the value of calculated descriptors, the bimetallic-derived surfaces can be classified into three major regions: (i) blue region where the bimetallic systems prefer to segregate before reaction due to the high alloy surface formation energy (>−0.5 eV), while under the reaction the reactive oxygen binding energy is too weak (>−2 eV) to form metal oxides, leading to low C₂H₄ selectivity; (ii) red region where the metal/oxide interfaces during the reaction are preferentially formed by featuring strong oxygen binding and low alloy surface formation energy, yielding high C₂H₄ selectivity; (iii) green region where the mixed alloys with the bulk-terminated configuration are favored despite the interaction with the reactive environment, and the transition to metal/oxide interface is hindered by either the oxygen binding not being strong enough or the alloy surface formation not being favorable enough, featuring intermediate C₂H₄ selectivity. Besides, the addition of the results for In-based bimetallic catalysts also enhances the predictive capability, which features the expansion to describe the systems with more negative (<−1.25 eV) or positive (>0.25 eV) alloy surface formation energy (Fig. 4).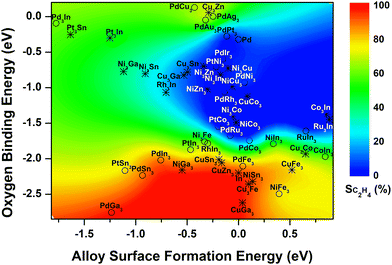

Fig. 4 Descriptor-based contour map (circles: bimetallic systems where C₂H₄ selectivity have been measured experimentally; asterisks: bimetallic systems that have not been explored yet). The selectivity of Pd-based catalysts was cited from ref. 24.

Based on the color-coded contour plot (Fig. 4), one can roughly estimate the corresponding C₂H₄ selectivity from CO₂-activation of C₂H₆ over a bimetallic system, simply using the DFT-calculated values for the two descriptors, reactive oxygen binding energy and alloy surface formation energy. Accordingly, the C₂H₄ selectivity measured previously for bimetallic-derived systems, such as NiFe₃ (experiment: 78%¹⁶vs. descriptor-based estimation: ∼75%), PdFe₃ (86%²³vs. ∼85%), PtCo₃ (1%¹³vs. ∼0%), PtNi₃ (1%^18,19vs. ∼0%), and PtSn₃ (83%³⁶vs. ∼75%) can be estimated, which reproduced the experimental values reasonably well. Therefore, the DFT-calculated formation energies of alloy surfaces and the reactive oxygen binding energies can be used as universal descriptors to screen the bimetallic-derived catalysts for the selective activation of C₂H₆ with CO₂.

In addition, the two descriptors were also calculated for other bimetallic catalysts based on the stable surface structures (Fig. S3, ESI†), which have not been studied previously, aiming to predict the C₂H₄ selectivity during activation of C₂H₆ with CO₂ based on the contour plot in Fig. 4. One group involved the In-based bimetallic alloys, including RuIn₃ and series of M₃In (M = Pd, Pt, Rh, Cu, Ni, Co, Ru) (asterisk, Fig. 4). However, none of these candidates falls into the red region with the possible high C₂H₄ selectivity. The other group considered the earth abundant elements, Ni-based (MNi₃ and M₃Ni, M = Cu, Ni, Co, Zn, Ga, Sn, Fe) and Cu-based (MCu₃ and M₃Cu) bimetallic catalysts (asterisk, Fig. 4). Among the 20 Ni- and Cu-based systems, NiGa₃, NiSn₃, CuGa₃, CuSn₃, CuZn₃ and Cu₃Fe prefer to form the metal/oxide interfaces and fall into the red region featuring strong binding to oxygen and thus a high C₂H₄ selectivity is expected. Some other catalysts likely maintain the bulk-terminated mixed alloy surface during the reaction, i.e. Ni₃Fe, Ni₃Ga, Ni₃Sn, Cu₃Co and Cu₃Zn, and are featured with either relatively high oxygen binding energy or high surface formation energy in the green region, which should possess a moderate C₂H₄ selectivity and can be potential catalysts for the tandem reactions, e.g., hydroformylation^17,37 and aromatization.^38–40 The remaining bimetallic systems are located in the blue region. Due to both high oxygen binding energy and high alloy surface formation energy, these systems likely segregate, favoring the DRE pathway and thus a low C₂H₄ selectivity.

The descriptor-based scaling (Fig. 4) not only allows the effective prediction of C₂H₄ selectivity during C₂H₆ activation with CO₂ over a large range of bimetallic catalysts, but also provides a database to gain general mechanistic understanding and thus extraction of design principle, which requires the well-dispersion in C₂H₄ selectivity values for potential data mining. Indeed, a group of In or Pd-based bimetallic catalysts was selected from the systems with the predicted C₂H₄ selectivity using DFT-calculated descriptors, making sure the diversity and dispersion over a large range of selectivity. As a result, the difference in binding energy of initial reaction intermediates, *CH₃CH₂O for the DRE pathway and *CH₃CH₂ for the ODHE pathway, was found to scale well with the C₂H₄ selectivity during C₂H₆ activation with CO₂. Specifically, a relationship between the binding difference and the C₂H₄ selectivity was observed (Fig. 5), which remained valid by including more systems with reported C₂H₄ selectivity previously, i.e., Fe₃O₇/Ni(111) (Fig. S8, ESI†) as a model to describe NiFe₃¹⁶ and Fe₃O₆/Pd(111) (Fig. S9, ESI†) to describe PdFe₃.²³ With the binding difference decreasing via weakening *CH₃CH₂O and/or strengthening *CH₃CH₂ interaction with the surfaces, the ODHE pathway becomes more favorable over the DRE pathway, and thus the C₂H₄ selectivity increases in a sequence: Ni₃In < Pd₃Co < PdIn₃ or In₂O₅/Pd(111) < PdGa₃ or Ga₂O₅/Pd(111) (the solid line region in Fig. 5). PdGa₃ before the reaction or Ga₂O₅/Pd(111) under the reaction is able to balance the binding difference well at the metal–oxide interface (Fig. S10, ESI†), which shows the highest C₂H₄ selectivity among the catalysts investigated. On the other hand, if the strengthening in *CH₃CH₂ binding is too strong, it can lower the C₂H₄ selectivity. For example, in the case of In₂O₇/Pt(111), the highly stabilized *CH₃CH₂ and *CH₂CH₂ hinder the desorption of the product and reduce the C₂H₄ selectivity. However, in order to determine whether a volcano-type relationship exists, more bimetallic-derived catalysts need to be studied, especially those with binding energy difference of *CH₃CH₂O and *CH₃CH₂ between that of Ga₂O₅/Pd and In₂O₇/Pt (the dashed line region in Fig. 5). In addition, depending on the nature of active sites the key intermediates responsible for the C₂H₄ selectivity may not necessarily be *CH₃CH₂O and *CH₃CH₂, which seem to scale well with the C₂H₄ selectivity for the bimetallic systems studied in Fig. 5. Further studies of a wide range of bimetallic catalysts should be carried out for verification.

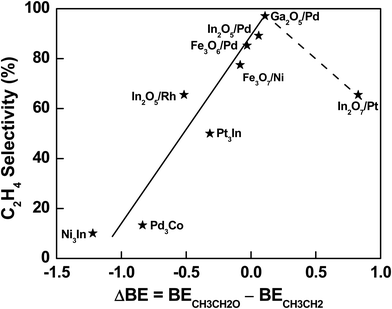Fig. 5 Correlation between C₂H₄ selectivity and binding energy difference of *CH₃CH₂O and *CH₃CH₂, which is the initial intermediate for DRE or C–C bond scission and ODHE or C–H bond scission, respectively. The labels correspond to the most stable structures according to DFT calculations. Note: the selectivity associated with different structures in Fig. 5 was predicted from the descriptor-based contour plot in Fig. 4, which was established based on experimentally measured selectivity reported in Table 1 and our previous studies under similar conditions.^16,23,24

In general, for bimetallic alloys that maintain the bulk-terminated alloy surface during the activation of C₂H₆ with CO₂, a low C₂H₄ selectivity is expected. While for those that prefer the phase transformation to metal/oxide interfaces, a higher C₂H₄ selectivity is likely achieved (Fig. 5). The preferential formation of oxide/metal interfaces weakens the binding of *O at the interface where the metal sites are partially oxidized upon interaction with oxides. It also leads to a destabilization for the adsorbed oxygenate (*C₂H_xO) species and thus the hindered DRE pathway leading to syngas production. While the presence of *O at the interface enhances the binding of hydrocarbon (*C₂H_x) intermediates via the formation of hydrogen bonds (Fig. 3), giving rise to the C₂H₄ selectivity by facilitating the ODHE pathway. To achieve a high C₂H₄ selectivity, bimetallic-derived catalysts offer opportunities to tune the reaction pathways. With an appropriate bimetallic combination, the catalyst can bind *O strongly enough to overcome the formation energy of alloy and transform the metallic surface to oxide/metal interfaces under reaction conditions, enabling the selective tuning of *C₂H_x binding more strongly than *C₂H_xO, but still moderate enough to allow facile desorption of C₂H₄ from the bimetallic-derived surfaces.

4. Conclusions

The selective CO₂-assisted activation of ethane was investigated on a series of In-based bimetallic-derived catalysts by combining experimental synthesis, catalytic test, in situ characterization and DFT calculations. The mechanistic study on In-based catalysts provided insights into the origin of the observed C₂H₄ selectivity. A scaling relationship was established based on the results for In-based bimetallic catalysts from the current work and others from previous studies, being able to well predict the C₂H₄ selectivity based on the descriptors (DFT-calculated formation energies of alloy surfaces and the reactive oxygen binding energies) for a wide range of bimetallic systems. Furthermore, our study also opens the opportunity to extract the design principles of bimetallic catalysts for the activation of ethane with CO₂, indicating that the selectivity of bimetallic-derived catalysts between the ODHE and DRE pathways or C₂H₄ and syngas production can be tuned by the relative binding strength of the initial reaction intermediates. Bimetallic-derived catalysts with high C₂H₄ selectivity should bind oxygen strongly to enable the formation of oxide/metal interfaces under reaction conditions, which favor ODHE rather than DRE by binding the *C₂H_x species more strongly than *C₂H_xO, but moderately to allow facile removal of *C₂H₄.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was financially supported by the Division of Chemical Sciences, Geosciences, & Biosciences, Office of Basic Energy Sciences and carried out at Brookhaven National Laboratory (BNL), operated under contract DE-SC0012704 with the US Department of Energy. The DFT calculations were performed using computational resources at the Center for Functional Nanomaterials, a user facility at BNL supported by the U.S. DOE under Contract No. DE-SC0012704, and at the National Energy Research Scientific Computing Center (NERSC), a U.S. DOE Office of Science User Facility located at Lawrence Berkeley National Laboratory (LBNL), supported by the Office of Science of the U.S. DOE under Contract No. DE-AC02-05CH11231. This work used resources at the 7-BM (QAS) beamline of the National Synchrotron Light Source-II at BNL and was supported in part by the Synchrotron Catalysis Consortium under U.S. Department of Energy, Office of Basis Energy Sciences (Grant No. DE-SC0012704 and DE-SC0012653). Authors also thank Dr Erwei Huang for help with formatting.

References

1. J. Rogelj, P. M. Forster, E. Kriegler, C. J. Smith and R. Séférian, Nature, 2019, 571, 335–342.
2. X. Zhang, S. Han, B. Zhu, G. Zhang, X. Li, Y. Gao, Z. Wu, B. Yang, Y. Liu, W. Baaziz, O. Ersen, M. Gu, J. T. Miller and W. Liu, Nat. Catal., 2020, 3, 411–417.
3. Y. Nian, Y. Wang, A. N. Biswas, X. Chen, Y. Han and J. G. Chen, Chem. Eng. J., 2021, 426, 130781.
4. Q. Chang, J. H. Lee, Y. Liu, Z. Xie, S. Hwang, N. S. Marinkovic, A.-H. A. Park, S. Kattel and J. G. Chen, JACS Au, 2022, 2, 214–222.
5. X. Wang, P. J. Ramírez, W. Liao, J. A. Rodriguez and P. Liu, J. Am. Chem. Soc., 2021, 143, 13103–13112.
6. J. V. Kildgaard, H. A. Hansen and T. Vegge, J. Phys. Chem. C, 2021, 125, 14221–14227.
7. E. Gomez, B. Yan, S. Kattel and J. G. Chen, Nat. Rev. Chem., 2019, 3, 638–649.
8. Z. Xie, E. Gomez and J. G. Chen, AIChE J., 2021, 67, e17249.
9. A. N. Biswas, Z. Xie and J. G. Chen, Joule, 2022, 6, 269–273.
10. Z. Xie, E. Gomez and J. G. Chen, AIChE J., 2021, 67, e17249.
11. A. V. Milkov, S. Schwietzke, G. Allen, O. A. Sherwood and G. Etiope, Sci. Rep., 2020, 10, 4199.
12. J. H. Sinfelt, Sci. Am., 1985, 253, 90–101.
13. M. Myint, B. Yan, J. Wan, S. Zhao and J. G. Chen, J. Catal., 2016, 343, 168–177.
14. Y. Zhou, J. Lin, L. Li, M. Tian, X. Li, X. Pan, Y. Chen and X. Wang, J. Catal., 2019, 377, 438–448.
15. Y. Zhou, F. Wei, J. Lin, L. Li, X. Li, H. Qi, X. Pan, X. Liu, C. Huang, S. Lin and X. Wang, ACS Catal., 2020, 10, 7619–7629.
16. B. Yan, S. Yao, S. Kattel, Q. Wu, Z. Xie, E. Gomez, P. Liu, D. Su and J. G. Chen, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8278–8283.
17. Z. Xie, Y. Xu, M. Xie, X. Chen, J. H. Lee, E. Stavitski, S. Kattel and J. G. Chen, Nat. Commun., 2020, 11, 1887.
18. B. Yan, X. Yang, S. Yao, J. Wan, M. Myint, E. Gomez, Z. Xie, S. Kattel, W. Xu and J. G. Chen, ACS Catal., 2016, 6, 7283–7292.
19. Z. Xie, B. Yan, J. H. Lee, Q. Wu, X. Li, B. Zhao, D. Su, L. Zhang and J. G. Chen, Appl. Catal., B, 2019, 245, 376–388.
20. N. J. Escorcia, N. J. LiBretto, J. T. Miller and C. W. Li, ACS Catal., 2020, 10, 9813–9823.
21. M. Numan, E. Eom, A. Li, M. Mazur, H. W. Cha, H. C. Ham, C. Jo and S.-E. Park, ACS Catal., 2021, 11, 9221–9232.
22. T. Ma, S. Wang, M. Chen, R. V. Maligal-Ganesh, L.-L. Wang, D. D. Johnson, M. J. Kramer, W. Huang and L. Zhou, Chem, 2019, 5, 1235–1247.
23. Z. Xie, D. Tian, M. Xie, S.-Z. Yang, Y. Xu, N. Rui, J. H. Lee, S. D. Senanayake, K. Li, H. Wang, S. Kattel and J. G. Chen, Chem, 2020, 6, 2703–2716.
24. Z. Xie, X. Wang, X. Chen, P. Liu and J. G. Chen, J. Am. Chem. Soc., 2022, 144, 4186–4195.
25. Z. Wei, J. Sun, Y. Li, A. K. Datye and Y. Wang, Chem. Soc. Rev., 2012, 41, 7994–8008.
26. E. Gomez, S. Kattel, B. Yan, S. Yao, P. Liu and J. G. Chen, Nat. Commun., 2018, 9, 1398.
27. N. Artrith, Z. Lin and J. G. Chen, ACS Catal., 2020, 10, 9438–9444.
28. M. Chen, J. Xu, Y.-M. Liu, Y. Cao, H.-Y. He and J.-H. Zhuang, Appl. Catal., A, 2010, 377, 35–41.
29. M. Chen, J. Xu, Y. Cao, H.-Y. He, K.-N. Fan and J.-H. Zhuang, J. Catal., 2010, 272, 101–108.
30. M. Chen, J.-L. Wu, Y.-M. Liu, Y. Cao, L. Guo, H.-Y. He and K.-N. Fan, Appl. Catal., A, 2011, 407, 20–28.
31. J. Ye, C. Liu and Q. Ge, J. Phys. Chem. C, 2012, 116, 7817–7825.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
36. Z. Xie, H. Guo, E. Huang, Z. Mao, X. Chen, P. Liu and J. G. Chen, ACS Catal., 2022, 12, 8279–8290.
37. Z. Mao, Z. Xie and J. G. Chen, ACS Catal., 2021, 11, 14575–14585.
38. E. Gomez, X. Nie, J. H. Lee, Z. Xie and J. G. Chen, J. Am. Chem. Soc., 2019, 141, 17771–17782.
39. C. Tu, H. Fan, D. Wang, N. Rui, Y. Du, S. D. Senanayake, Z. Xie, X. Nie and J. G. Chen, Appl. Catal., B, 2022, 304, 120956.
40. Z. Xie, E. Gomez, D. Wang, J. Hoon Lee, T. Wang and J. G. Chen, J. Energy Chem., 2022, 66, 210–217.

---

Footnotes

† Electronic supplementary information (ESI) available: EXAFS spectra of bimetallic-derived catalyst; DFT-optimized structures and corresponding energies for bimetallic surfaces with/without adsorption of reaction intermediates. See DOI: https://doi.org/10.1039/d2ey00051b

‡ Haoyue Guo and Zhenhua Xie contributed equally.

---