Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Partitioning into phosphatidylcholine–cholesterol membranes: liposome measurements, coarse-grained simulations, and implications for bioaccumulation†
Thomas D.
Potter
 a,
Nicola
Haywood
a,
Nicola
Haywood
 b,
Alexandre
Teixeira
b,
Alexandre
Teixeira
 b,
Geoff
Hodges
b,
Geoff
Hodges
 b,
Elin L.
Barrett
b,
Elin L.
Barrett
 b and
Mark A.
Miller
b and
Mark A.
Miller
 *a
*a
aDepartment of Chemistry, Durham University, South Road, Durham DH1 3LE, United Kingdom. E-mail: m.a.miller@durham.ac.uk
bSafety and Environmental Assurance Centre, Unilever, Colworth Science Park, Sharnbrook, Bedfordshire MK44 1LQ, United Kingdom
First published on 2nd May 2023
Abstract
Membrane–water partitioning is an important physical property for the assessment of bioaccumulation and environmental impact. Here, we advance simulation methodology for predicting the partitioning of small molecules into lipid membranes and compare the computational predictions to experimental measurements in liposomes. As a step towards high-throughput screening, we present an automated mapping and parametrization procedure to produce coarse-grained models compatible with the Martini 3 force field. The methodology is general and can also be used for other applications where coarse-grained simulations are appropriate. This article addresses the effect on membrane–water partitioning of adding cholesterol to POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) membranes. Nine contrasting neutral, zwitterionic and charged solutes are tested. Agreement between experiment and simulation is generally good, with the most challenging cases being permanently charged solutes. For all solutes, partitioning is found to be insensitive to membrane cholesterol concentration up to 25% mole fraction. Hence, for assessment of bioaccumulation into a range of membranes (such as those found in fish), partitioning data measured in pure lipid membranes are still informative.
Environmental significanceIntegral to regulatory environmental safety assessment of chemicals is the need to quantify the potential for bioaccumulation in fish, typically characterized using metrics such as the whole-body bioconcentration factor (BCF). For some compound types, octanol–water partitioning is unsuitable for BCF assessment and so membrane–water partitioning/distribution (KMW/DMW) can be used. Most methods to determine KMW/DMW represent the membrane using pure phospholipid. However, biological membranes are significantly more complex. We present experimental and in silico data for partitioning of a set of diverse compounds into a phospholipid membrane with 0%, 15% and 25% cholesterol. Results indicate that the extent of partitioning does not vary significantly with cholesterol, meaning that partitioning estimates using pure-phospholipid membranes are sufficient for BCF. |
1 Introduction
A global regulatory paradigm shift is currently underway to reduce or even eliminate the use of animal testing for assessing the safety of chemicals.1 Changes to legislation banning animal testing for cosmetic safety have been introduced in many countries.2 Historically, legislation has been focussed on in vivo studies to understand chemical toxicity endpoints (hazard) which are then contextualized within an assessment of risk through consideration of exposure.3 Integral to this regulatory assessment when considering environmental impacts is the need to assess and understand the potential for bioaccumulation of a chemical in fish.4 In the European Union under REACH regulations, for example, chemicals manufactured at more than 100 tonnes per year require an assessment of bioaccumulation.5 This is typically characterized using metrics such as the whole-body bioconcentration factor (BCF), historically using in vivo studies. However, recent efforts now provide tangible options for replacing in vivo studies with computational approaches to assess bioaccumulation.4,6For organic chemicals, the BCF is positively correlated with the octanol–water partition coefficient KOW (which refers to the charge-neutral form of a solute) and the octanol–water distribution coefficient DOW (which accounts for all relevant charge-states at a given pH).7,8 However, for many ionizable compounds these constants are difficult to measure or predict. Surface-active compounds (surfactants) tend to accumulate at the interface between hydrophobic and hydrophilic phases and form aggregates in solution, making experimental determination challenging.9 Furthermore, octanol–water partitioning does not fully reflect the interactions of a molecule with the phospholipid bilayers in biological membranes. This is particularly notable for ionizable chemicals, which can have hydrophobic, polar and charge–charge interactions with the chemical.10
Such simple models for estimating BCF using octanol–water partitioning and one-compartment partitioning are suitable only for non-polar substances that are not biotransformed. In silico bioconcentration models such as BIONIC6 and others11 use hepatic and whole-body biotransformation clearance rates derived from in vitro methods combined with partitioning information to account for biotransformation and ionization. The membrane–water partition coefficient KMW and pH-dependent membrane–water distribution coefficient DMW are used by these models as key descriptors of sorption to phospholipids instead of only considering their octanol–water counterparts KOW and DOW. The membrane–water coefficients overcome many of the challenges associated with octanol–water partitioning, are more biologically relevant, and have been demonstrated to be an accurate alternative for estimating bioaccumulation and baseline toxicity.12–15
The most common experimental methods for determining KMW and DMW include (1) liposomes,16–18 (2) solid-supported lipid membranes (SSLM)19 and (3) retention on a chromatographic column coated with immobilized artificial membrane phospholipids (IAM-HPLC).20–22 Each has its strengths and weaknesses.
Liposomes or lipid vesicles provide the closest analogue to a cell membrane and there are several analytical methods for measuring the partitioning of a compound into a liposome–water system.23 However, it can be difficult and time-consuming to prepare and store the liposomes.
Solid supported lipid membranes (SSLM)24 consist of lipid bilayers, non-covalently bound to silica beads. These SSLM beads are commercially available, which allows for simpler and more consistent experiments. The results have been shown to correlate well with liposome experiments for drug-like molecules.25
In immobilized artificial membrane (IAM) chromatography, a lipid monolayer is bound covalently to a HPLC column, and the retention factor is measured as in other HPLC methods.26 This method is efficient, and has been used to estimate lipophilicity in several ecotoxological studies.15,27 However, the environment in an HPLC column does not perfectly represent the structure of a real lipid membrane. In particular, the interactions of charged species with the silica surface can affect the results, and conversion of retention factors to partition or distribution coefficients requires empirical correction factors.10,22 Additionally, IAM columns generally consist of one-component lipid membranes, limiting their use in investigating how membrane composition affects solute partitioning.
Computational approaches are attractive alternatives to experimental methods, due to their efficiency, ability to overcome some of the practical limitations in experimental approaches, and lower cost. Several methods for calculating KMW exist, with varying levels of accuracy and complexity. Simple fragment-based approaches8,28 and polyparameter linear free energy relationships (pp-LFER) – where partition coefficients are related to solute descriptors via an empirically fitted linear equation29,30 – are accessible and easy to apply but have limited coverage of chemical domain. As pp-LFERs require measured data to create the model, they often do not cover materials for which it is difficult to measure KMW, such as ionizable chemicals. More comprehensive approaches include COSMOmic,31 which is an extension of the COnductor-like Screening MOdel for Realistic Solvation (COSMO-RS)32 to consider micelles and membranes. In COSMOmic, a lipid bilayer–water system is represented as layers of isotropic solvents with differing compositions. Membrane–solute interactions are calculated by applying COSMO-RS to each layer to calculate the change in free energy across the system. COSMOmic works well for most neutral organic molecules,33 but has issues with some families of molecules like perfluorinated surfactants.19 Both pp-LFERs and COSMOmic can struggle to model ionic compounds,34 although COSMOmic can be improved using an additional empirical membrane potential.35
Molecular dynamics (MD) is a general-purpose simulation method where a system is studied by propagating Newton's equations of motion. Atomistic MD, where molecules are modeled at the atomic level by ‘ball-and-spring’ representations, has been applied to lipid membranes and their interactions with small molecules,36 and gives good results for KMW.37 However, a notable disadvantage of atomistic MD compared to the other computational methods discussed here is its high computational cost, which prevents its use in high-throughput screening. This cost can be alleviated using coarse-grained (CG) MD, where groups of atoms are combined into interaction sites known as ‘beads’. The Martini force field is a prominent CG model for biological systems.38,39 It uses a building-block approach, where the interactions between CG beads are defined by selecting from a list of predefined bead types. We have recently developed an efficient algorithm for automatic parametrization of solute models in Martini version 2,38 and have applied it to membrane–water partitioning.40 The most recent version of the force field, Martini 3, has more flexibility in its bead types,41 and as been shown to capture the thermodynamic properties of small organic molecules well.42 A more detailed explanation of our latest Martini scheme is given in Computational methods below.
Real cell membranes are more complex than the one-component model membranes usually used to estimate KMW and DMW. They contain multiple lipid types, as well as sterols, proteins, and other biomolecules.43 In particular, cholesterol is prevalent in most mammalian and fish cell membranes, and is essential for their biological function.44 Lipid content (including cholesterol) varies considerably between membranes. This is as true between different cell, tissue and organelle types within an organism as between species. Further temporal and geographic variability is also observed with organisms where compensatory lipid mechanisms exist to maintain membrane functions (such as fluidity, ion transport and permeability) under changing stress and environmental factors such as diet and temperature.45,46 Cell membranes in fish typically contain 2 to 38 mol% cholesterol;45–49 for example, liver cells and erythrocytes in trout lie in the range 15–22 mol%.50 Adding sufficient cholesterol to pure phospholipid bilayers induces a phase transition from the liquid-disordered to the liquid-ordered phase via an intermediate region,51 the nature of which continues to be investigated.52–55
While some experimental data for partitioning into cholesterol-containing membranes do exist, few studies have looked at a wide chemical space using consistent methodology. The aim of this study is to help address this gap and gain greater understanding of the influence of the presence of cholesterol on partitioning. We have, therefore, determined experimental liposome–water partitioning values in both pure 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) and POPC–cholesterol membranes, for a varied set of chemicals using cholesterol levels of 0–25 mol%, which align with those typical of fish membranes. We have also updated our CG simulation protocol for Martini 3 and assessed it against the experimental measurements. The conclusions from this study will be useful in informing chemical risk assessment methodology, notably for parametrizing bioaccumulation models, and whether including realistic membrane compositions is likely to be beneficial over single-component phospholipid bilayers. The results will also help determine whether KMW and DMW measures of partitioning sufficiently capture the interactions of chemicals in a phospholipid–cholesterol model.
2 Experimental
2.1 Liposome preparation and measurements
Liposomes were prepared based on the small-volume extrusion method for the preparation of large, unilamellar liposome vesicles.56 Cholesterol was added where necessary, to make up liposomes with 0, 10–15 and 20–25 mol% cholesterol. Liposome solutions were stored at 4 °C for up to 2 weeks before use. See ESI† for additional details of liposome preparation.The following nine molecules were tested for partitioning to cover a range of ionization states under pH-neutral conditions, to reflect their predominant state in the environment: 3-nitroaniline, diclofenac, sulfobetaine 3-10 (SB3-10), dodecyldimethylamine oxide (DDAO-C12), propranolol, dihexylamine, octyl sulfate, decyl sulfate and dodecyl sulfate. An additional seven molecules – tryptophan, urea, diethyl adipate, hexylamine, dodecylamine, trihexylamine, and tridecyl sulfate – were also tested, but for reasons explained in the Discussion section, difficulties were encountered for these cases and the study proceeded with the remaining nine. The materials were clustered into four sets according to their suitability for analysis under the same analytical method, and tested in these groups. This procedure is described in the ESI.†
The liposome–water partitioning was determined in a 96-well plate rapid equilibrium dialysis (RED) device (by Thermo Fisher Scientific) based on a protein-binding protocol.57 Each well in the RED device contains a donor cell (red cell) and a receptor (white cell) separated by a 8 kDa molecular weight cut-off cellulose membrane, through which the liposomes cannot permeate. The liposome solutions were diluted to approximately 4 mM with PBS solution (pH 7.4) and dosed with the test chemicals at three different nominal concentrations of 10, 20 and 50 μM. Analysis was carried out by liquid chromatography coupled to electrospray ionization mass spectrometry (LC-MS/MS) using an Agilent 1200 LC system coupled to an Agilent 6460 Triple Quadrupole Mass Spectrometer. Further details of the method are detailed in the ESI.†
2.2 Calculation of experimental liposome–water partitioning
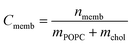
K MW is the ratio of the concentrations of a particular species between the membrane and water phases,| KMW = CM/CW, | (1) |
| nmemb = (Cnom − Cfree)Vwell | (2) |
 | (3) |
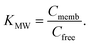 | (4) |
3 Computational methods
3.1 Coarse-grained models
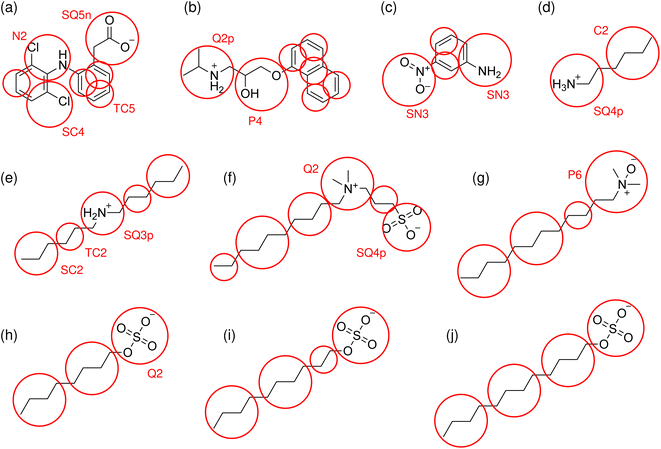
CG models were built using the Martini 3 force field.41 The POPC model was taken from the standard Martini 3 library of lipids. The cholesterol model was adapted from the virtual-site Martini 2 model,58 by changing the bead types to their closest Martini 3 equivalents, based on existing Martini 3 solvent models.Solute models were parametrized for the nine compounds studied experimentally in this work, and additionally for hexylamine. The models were constructed using a new version of our cg_param tool,40 to take advantage of the Martini 3 force field. The mapping algorithm for dividing molecules into CG beads is unchanged from the previous version, but the subsequent assignment of bead types now reflects the expanded choice in Martini 3. The version of cg_param used in this work supports the range of beads from C1 to P6, but no subtypes or halogenated beads. The regular, small and tiny (R, S, T) bead sizes available in Martini 3 are automatically assigned using the maximum number of bonds spanning the fragment. Bead types are now assigned based on experimental ΔGOW of the fragment where available, falling back on the predictions of the ALOGPS algorithm59,60 only when direct measurements are not available. Certain neutral fragments now have their optimal bead assignments hard-coded, with ethyl, propyl and butyl fragments assigned as TC2, SC2 and C2 respectively.
The mapping of anionic charged groups based on pre-defined fragments has been updated, with the SO4− group assigned as a Q2 bead, and the SO3− group as SQ4. These assignments were based on matching existing experimental (SSLM) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW data for octyl sulfate and octyl sulfonate,19 analogously to the approach in our Martini 2 version.40
KMW data for octyl sulfate and octyl sulfonate,19 analogously to the approach in our Martini 2 version.40
The tetramethyl ammonium fragment NC4+ was assigned as Q2, and the acetate fragment C2O2− as SQ5n, using existing bead assignments from the Martini 3 ions library.41 Other primary and secondary ammonium fragments from the automated mapping were parametrized manually using the general guidelines for charged bead assignments from the Martini 3 ESI.41
Mappings of the solute molecules tested in this work, and their bead assignments, are shown diagrammatically in Fig. 1. The bead assignments are also listed in ESI† and the updated cg_param is available at https://github.com/cgkmw-durham/cg_param_m3/tree/martini3_v1. While this new version of the algorithm takes advantage of several important new features in Martini 3, full exploitation of Martini 3 is a larger piece of work which is still underway.
3.2 Coarse-grained simulations
The insane tool was used for building initial configurations of all POPC–cholesterol systems.61 The water phase consisted of Martini 3 regular water (4 molecules per bead), with 0.15 molar NaCl. All bilayers contained a total of 162 molecules (2 monolayers of 9 × 9 molecules), at varying ratios of POPC and cholesterol. Partition coefficients were calculated for all solutes using membranes containing 0, 10–15 and 20–25 mol% cholesterol, to match the individual experimental liposome measurements. A wider range of concentrations was used to validate the cholesterol-dependence of membrane properties, and of partitioning for a subset of solutes.All simulations in this study were carried out using Gromacs 2021.1.62 and the new-RF set of Martini simulation parameters.63 The leapfrog integrator, with a 20 fs timestep, was used. The velocity-rescale thermostat and Parrinello–Rahman barostat were used to keep the simulation at 310 K and 1 bar pressure (for equilibration and constant pressure simulations). The reaction field method,64 with a relative permittivity of 15.0 and a cutoff of 1.1 nm, was used to calculate electrostatic interactions. Van der Waals interactions were cut off at 1.1 nm using the potential shift method, which shifts the potential to zero at the cutoff. LINCS was used to constrain bond lengths within CG ring systems, with an order of 12 and 2 iterations. These LINCS parameters are recommended for cholesterol simulations to avoid artificial temperature gradients.65
The same umbrella sampling setup was used as in our previous work.40 Two solute molecules were simulated in each umbrella window. The simulations were set up so that while one molecule is in the center of the membrane, the other is in the water. For neutral molecules, the umbrella windows were at 0.1 nm intervals between the center of the membrane and 5.0 nm away from the center, and the molecule was restrained using a harmonic potential with a 1000 kJ mol−1 nm−2 force constant. For charged molecules, umbrella windows were at 0.05 nm intervals, using a 2000 kJ mol−1 nm−2 force constant. The distance between a solute and the membrane center was defined using the cylinder method, to remove the effect of undulations in the membrane.66
The umbrella sampling simulations were analyzed in the same way as in our previous work.40 The weighted histogram analysis method (WHAM) was used to estimate the probability P of finding the solute at a given position zi between the center of the membrane (z0 = 0.0 nm) and the water (zn = 5.0 nm). The water and bilayer parts of the profile were determined using a hard cut-off, zR which was determined separately for each profile. zR was defined as the point where the RMSD of the free energy profile between zn and that position first increases above 0.1 kJ mol−1. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW was then calculated using:
KMW was then calculated using:
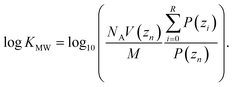 | (5) |
Strictly speaking, KMW refers to a particular charge state (neutral or ionized) of a given solute. In contrast, the distribution coefficient DMW takes into account the possibility that more than one charge state may be relevant at a given pH, and the overall partitioning is a weighted sum of state-specific KMW values:
| DMW = f(Q)KMW(Q) + f(N)KMW(N). | (6) |
The pKa and f values at pH = 7.4 (the pH of our experimental measurements) for the molecules in this study are given in Table 1. In each case, the simulations have been conducted using a fixed charge state corresponding to the dominant species in aqueous solution, as indicated in the final column of the table. For compounds that are charged at pH 7.4, the experiments are effectively measuring DMW rather than KMW, but for convenience both KMW and DMW values are referred to as KMW throughout. In practice, the distribution of charge states in the membrane may differ from that in water. Methods for constant-pH Martini simulations – where the explicit charge state of a molecule can change during a simulation – are under development.67,68 Such techniques may provide scope for further refinement of KMW predictions in the future and make it possible to extend the approach to species where no single charge state dominates.
| Molecule | pKa | f(Q−) | f(N) | f(Q+) | Model charge |
|---|---|---|---|---|---|
| 3-Nitroaniline71 | 2.47* | 0.000 | 1.000 | 0.000 | 0 |
| Diclofenac72 | 4.15 | 0.999 | 0.001 | 0.000 | −1 |
| Propranolol72 | 9.42* | 0.000 | 0.009 | 0.991 | +1 |
| Hexylamine73 | 10.64* | 0.000 | 0.001 | 0.999 | +1 |
| Dihexylamine74 | 11.31* | 0.000 | 0.000 | 1.000 | +1 |
| SB3-10 (ref. 74) | 1.275 | 0.000 | 1.000 | 0.000 | 0 |
| DDAO-C12 (ref. 74) | 4.79* | 0.000 | 0.998 | 0.002 | 0 |
| Octyl sulfate75 | 1.9 | 1.000 | 0.000 | 0.000 | −1 |
| Decyl sulfate75 | 1.9 | 1.000 | 0.000 | 0.000 | −1 |
| Dodecyl sulfate75 | 1.9 | 1.000 | 0.000 | 0.000 | −1 |
3.3 All-atom simulations
All-atom simulations were also carried out, using the CHARMM36 force field,76 to help validate the CG membrane properties. Gromacs input files were generated using the CHARMM-GUI.77 The same set of cholesterol concentrations and system sizes were used as for the CG simulations.For each bilayer, equilibration was carried out using the default series of parameters from the CHARMM-GUI, which involves a minimization followed by a series of short equilibrations in which position restraints on the membrane are removed, and the time-step increased. A production run lasting 100 μs was then carried out using the default CHARMM-GUI production parameters. A 2 fs time step was used with the leapfrog integrator. The temperature was kept constant at 310 K using the Nosé–Hoover thermostat, with a coupling constant of 1.0 ps. The pressure was kept constant at 1.0 bar with the Parrinello–Rahman barostat, with a coupling constant of 5.0 ps. Electrostatic interactions were calculated using the particle mesh Ewald (PME) method, with a 1.2 nm short-range cutoff. Van der Waals interactions were cut off by switching the forces to zero between 1.0 and 1.2 nm. The LINCS algorithm, with an order of 4 and 1 iteration, was used to constrain all bonds containing hydrogens.
4 Results
4.1 Validation of membrane models
The Martini 3 POPC/cholesterol system in this work is closely based on its widely used predecessor58 in Martini 2. We have validated the present version by comparing density and lipid ordering to results from all-atom simulations. Results were obtained at 0, 15 and 30 mol% cholesterol to cover the range at which partition coefficients were calculated, as well as at 40, 50 and 60 mol% cholesterol to assess the transferability of the CG models to membranes with higher cholesterol content.The condensing effect of cholesterol on the lipid structure was examined by comparing the area per lipid, Alipid, with respect to cholesterol concentration (Fig. S1†). For the pure POPC membrane, both CG and atomistic models agree well with the experimental value78 of 0.643 nm2. The all-atom simulations show a steady decrease in Alipid with cholesterol concentration up to 40% cholesterol, after which the gradient decreases. The Martini 3 model shows a steady decrease at a comparable rate to the all-atom simulations, but the gradient is uniform over the concentration range. Additionally, the ordering of the lipid molecules in the membranes was determined by calculating the bond order parameter for each inter-bead bond in the CG molecule. For more detail on the simulated condensing and ordering effect of cholesterol, see ESI.†
The liquid structure of the lipid bilayers was investigated by calculating 2D radial distribution functions (RDFs) of the lipid tails of POPC (see ESI†). Overall, the qualitative trend of increased ordering on adding cholesterol is followed by the Martini models of POPC/cholesterol mixtures. At around 40 mol% cholesterol there is a transition to the liquid-ordered phase from the liquid-disordered/liquid-ordered coexistence region, which is captured by atomistic simulations but not Martini 3 models. However, physiological cholesterol concentrations in fish are mostly less than 40 mol% and our experimental measurements are all below 40 mol%. Hence, an accurate description of the transition region is not required for the present study. Nevertheless, there is scope for further reparametrization of the bead types and bonded structure of the lipid and sterol models in Martini 3 in order to improve the phase behavior of mixed bilayers in the future.79
4.2 Partitioning data
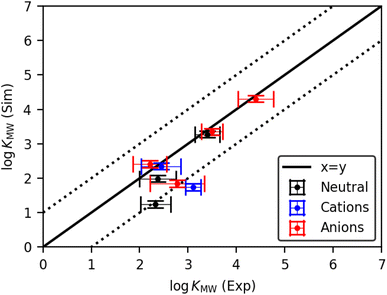
The experimental and simulated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW values for all molecules in the pure POPC bilayer are shown in Fig. 2. There is good agreement between the two approaches for many of the solutes, both neutral and charged, indicating that the CG solute models are a good representation of the molecules in question. Nevertheless, there are some outliers among the charged molecules, highlighting the greater difficulty in parametrizing this class of solute. Where a well-validated bead assignment was available for the charge-bearing fragment, including SO3−, SO4− and NC4+, good results were achieved. However, the primary and secondary ammonium fragments were challenging due to the lack of specific bead assignments in the literature. For these fragments, we followed the general guidelines for ammonium fragments by the Martini 3 developers.41 Using this approach, the dihexylamine model achieved a very good match with experiment. However, propranolol was significantly underestimated with respect to the experimental values. This indicates that whilst the model works well for many compounds with charged moieties, including SO3−, SO4− and NC4+, further development is still required before consistently good models can be achieved for ammonium-containing compounds.
KMW values for all molecules in the pure POPC bilayer are shown in Fig. 2. There is good agreement between the two approaches for many of the solutes, both neutral and charged, indicating that the CG solute models are a good representation of the molecules in question. Nevertheless, there are some outliers among the charged molecules, highlighting the greater difficulty in parametrizing this class of solute. Where a well-validated bead assignment was available for the charge-bearing fragment, including SO3−, SO4− and NC4+, good results were achieved. However, the primary and secondary ammonium fragments were challenging due to the lack of specific bead assignments in the literature. For these fragments, we followed the general guidelines for ammonium fragments by the Martini 3 developers.41 Using this approach, the dihexylamine model achieved a very good match with experiment. However, propranolol was significantly underestimated with respect to the experimental values. This indicates that whilst the model works well for many compounds with charged moieties, including SO3−, SO4− and NC4+, further development is still required before consistently good models can be achieved for ammonium-containing compounds.
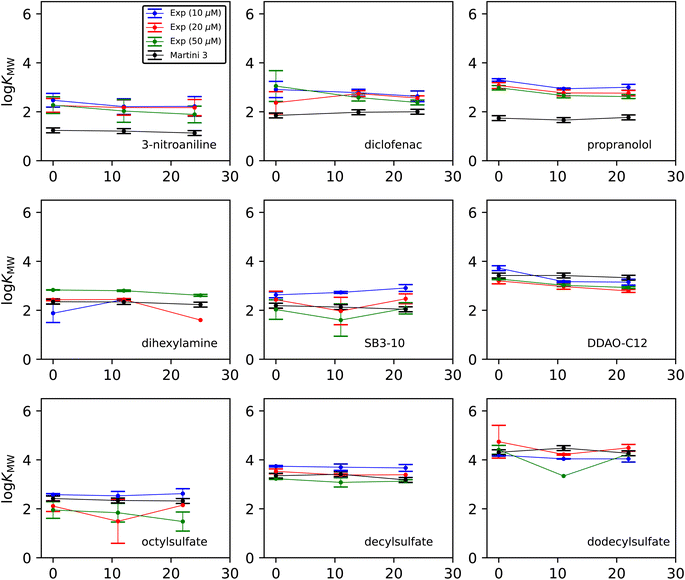
Fig. 3 shows how the experimental and simulated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW values vary with cholesterol concentration. The experimental results are separated in order to illustrate the effect of the initial dosing concentration. Each experimental point is the average of three concentration measurements taken from the same experiment, and the error bars are the standard deviations of those three measurements. Each simulation point is the calculated value from a single set of umbrella-sampling simulations. The error bars are the maximum observed standard deviation when 10 replicate simulations were carried out for two test cases (dodecyl sulfate and diclofenac) at all cholesterol concentrations. The resulting uncertainty of 0.10 in log
KMW values vary with cholesterol concentration. The experimental results are separated in order to illustrate the effect of the initial dosing concentration. Each experimental point is the average of three concentration measurements taken from the same experiment, and the error bars are the standard deviations of those three measurements. Each simulation point is the calculated value from a single set of umbrella-sampling simulations. The error bars are the maximum observed standard deviation when 10 replicate simulations were carried out for two test cases (dodecyl sulfate and diclofenac) at all cholesterol concentrations. The resulting uncertainty of 0.10 in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW has been taken as representative for all the simulation points.
KMW has been taken as representative for all the simulation points.
The change in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW with cholesterol concentration is generally small from both experimental and computational methods. There is most often a small overall downward trend on adding cholesterol in the experimental results, although there is variation from molecule to molecule. In the experimental measurements, the difference between results at different dose concentrations is often larger than the difference with respect to cholesterol. There is no consistent trend with respect to dose concentration across all molecules, suggesting that the choice of dosing does not introduce any systematic bias in the results. Nevertheless, the differences between the three batches of results for each molecule indicate that a statistical analysis of the data from any one dosing may not reflect the true uncertainty in the result. We therefore take the mean of all individual measurements at all three dose concentrations as the most reliable value of the solute partitioning at a given cholesterol concentration. This gives values for each solute and cholesterol combination based on a minimum of 4 and a maximum of 9 measurements. These consolidated figures and their uncertainties, along with the corresponding simulation predictions, are summarized in Table 2. Additionally in Table 2 are simulation data for hexylamine, which has a log
KMW with cholesterol concentration is generally small from both experimental and computational methods. There is most often a small overall downward trend on adding cholesterol in the experimental results, although there is variation from molecule to molecule. In the experimental measurements, the difference between results at different dose concentrations is often larger than the difference with respect to cholesterol. There is no consistent trend with respect to dose concentration across all molecules, suggesting that the choice of dosing does not introduce any systematic bias in the results. Nevertheless, the differences between the three batches of results for each molecule indicate that a statistical analysis of the data from any one dosing may not reflect the true uncertainty in the result. We therefore take the mean of all individual measurements at all three dose concentrations as the most reliable value of the solute partitioning at a given cholesterol concentration. This gives values for each solute and cholesterol combination based on a minimum of 4 and a maximum of 9 measurements. These consolidated figures and their uncertainties, along with the corresponding simulation predictions, are summarized in Table 2. Additionally in Table 2 are simulation data for hexylamine, which has a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW value too low to be measurable by this experiment (see Discussion).
KMW value too low to be measurable by this experiment (see Discussion).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW in POPC membranes as a function of cholesterol content. Experimental values are averaged over all measurements a minimum of 4 and up to 9 for each cholesterol concentration. See ESI for raw data. Statistical uncertainties in the final digit(s) of the experimental results are given in parentheses. The statistical uncertainty in the simulation results is 0.10
KMW in POPC membranes as a function of cholesterol content. Experimental values are averaged over all measurements a minimum of 4 and up to 9 for each cholesterol concentration. See ESI for raw data. Statistical uncertainties in the final digit(s) of the experimental results are given in parentheses. The statistical uncertainty in the simulation results is 0.10
| Molecule | Experiment | Simulation | ||||
|---|---|---|---|---|---|---|
| 0% cholesterol | 10–15% cholesterol | 20–25% cholesterol | 0% cholesterol | 10–15% cholesterol | 20–25% cholesterol | |
| 3-Nitroaniline | 2.3(4) | 2.1(4) | 2.1(4) | 1.24 | 1.21 | 1.13 |
| Diclofenac | 2.8(6) | 2.7(2) | 2.5(2) | 1.85 | 1.98 | 2.00 |
| Propranolol | 3.1(2) | 2.8(2) | 2.8(2) | 1.74 | 1.66 | 1.77 |
| Hexylamine | — | — | — | 0.29 | 0.37 | 0.34 |
| Dihexylamine | 2.4(5) | 2.6(2) | 2.4(6) | 2.35 | 2.34 | 2.23 |
| SB3-10 | 2.4(4) | 2.0(7) | 2.5(4) | 1.99 | 2.08 | 1.94 |
| DDAO-C12 | 3.4(3) | 3.05(10) | 2.95(16) | 3.28 | 3.19 | 3.35 |
| Octyl sulfate | 2.2(4) | 2.0(7) | 2.2(6) | 2.42 | 2.34 | 2.32 |
| Decyl sulfate | 3.5(3) | 3.4(3) | 3.4(3) | 3.35 | 3.41 | 3.18 |
| Dodecyl sulfate | 4.4(4) | 4.0(4) | 4.2(3) | 4.31 | 4.48 | 4.27 |
5 Discussion
The simulated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW results presented here differ from those in our previous work using the Martini 2 force field to model POPC/cholesterol and DMPC/cholesterol membranes.40 In that paper, log
KMW results presented here differ from those in our previous work using the Martini 2 force field to model POPC/cholesterol and DMPC/cholesterol membranes.40 In that paper, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW of aromatic molecules generally decreased on adding cholesterol, whereas it increased by a small amount for many aliphatic molecules. This effect comes from the way interactions between differently sized beads are handled in Martini 2. The Martini 2 models for all aliphatic models were built using R beads, while cholesterol and all ring compounds are modeled using S beads. R–S interactions are not scaled relative to R–R interactions in Martini 2, resulting in an overestimation of the attraction between aliphatic molecules and cholesterol. This was a recognized shortcoming80 of Martini 2 and has been rectified in Martini 3 by proper scaling of the Lennard–Jones interactions between different bead sizes.41 The results presented in this article benefit from this improvement in the force field.
KMW of aromatic molecules generally decreased on adding cholesterol, whereas it increased by a small amount for many aliphatic molecules. This effect comes from the way interactions between differently sized beads are handled in Martini 2. The Martini 2 models for all aliphatic models were built using R beads, while cholesterol and all ring compounds are modeled using S beads. R–S interactions are not scaled relative to R–R interactions in Martini 2, resulting in an overestimation of the attraction between aliphatic molecules and cholesterol. This was a recognized shortcoming80 of Martini 2 and has been rectified in Martini 3 by proper scaling of the Lennard–Jones interactions between different bead sizes.41 The results presented in this article benefit from this improvement in the force field.
The driving force for reduced solute partitioning into cholesterol-containing membranes is generally understood to be changes in membrane ordering on the addition of cholesterol. Cholesterol increases the lipid ordering for membranes composed of phospholipids, but the extent of this ordering depends on the nature of the acyl chain. Fully saturated lipids show a significantly greater increase in ordering than those with one or two unsaturated acyl chains.81 In the case of POPC, which has one fully saturated chain, there is a moderate ordering effect, as shown in our atomistic results, which explains the small decrease in partitioning in the experimental results. This underestimation of ordering in the CG simulations could indicate why this change in partitioning, where experimentally detectable, is also underestimated. Nevertheless, the effect of cholesterol on partitioning even in the experimental POPC system is small.
Experimental liposome measurements are well established for estimating log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW and are considered the closest representation of a real biological environment within a controlled experimental setting. As such, they are extremely valuable when assessing the bioaccumulation of important chemicals. The history of their use gives a good understanding of the method's limitations, such as the difficulties in measuring values for certain molecules. Some chemicals which we intended to study could not be assessed experimentally. Urea, which is very hydrophilic (and so would be expected to have a high concentration in the water phase) could not be quantified using LC-MS, highlighting the difficulty of finding general analytical methods when studying a varied set of molecules. Dodecylamine, on the other hand, was insoluble in the dosing solution. Even though it most likely can accumulate in the bilayer, it was not possible to accurately determine its concentration in the aqueous phase.
KMW and are considered the closest representation of a real biological environment within a controlled experimental setting. As such, they are extremely valuable when assessing the bioaccumulation of important chemicals. The history of their use gives a good understanding of the method's limitations, such as the difficulties in measuring values for certain molecules. Some chemicals which we intended to study could not be assessed experimentally. Urea, which is very hydrophilic (and so would be expected to have a high concentration in the water phase) could not be quantified using LC-MS, highlighting the difficulty of finding general analytical methods when studying a varied set of molecules. Dodecylamine, on the other hand, was insoluble in the dosing solution. Even though it most likely can accumulate in the bilayer, it was not possible to accurately determine its concentration in the aqueous phase.
Finally, the amount of hexylamine in the liposomes at equilibrium could not be determined accurately. This problem occurs when the bound concentration is smaller than the variability of the bound concentration measurement, and sets a lower limit on the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW values that can be reliably calculated using a particular analytical method. This limitation does not exist in simulations, because the umbrella sampling technique can force a molecule to sample unfavorable environments. This is one of the areas where simulation can complement experiment. For example, simulations may be validated using experimental results for the more soluble members of a chemical series, and then trends with respect to, for example, alkyl chain length can be examined using simulation. In the experimentally marginal case of hexylamine, the CG model shown in Fig. 1(d) returns log
KMW values that can be reliably calculated using a particular analytical method. This limitation does not exist in simulations, because the umbrella sampling technique can force a molecule to sample unfavorable environments. This is one of the areas where simulation can complement experiment. For example, simulations may be validated using experimental results for the more soluble members of a chemical series, and then trends with respect to, for example, alkyl chain length can be examined using simulation. In the experimentally marginal case of hexylamine, the CG model shown in Fig. 1(d) returns log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW values in the range 0.29 to 0.37, as listed in Table 2. Such low values correspond to a difference between dosed concentration and free concentration in the liposome system of less than 3%, which is indeed below the resolution of the present experiments. Hence, the simulations correctly predict that an experimental measurement of log
KMW values in the range 0.29 to 0.37, as listed in Table 2. Such low values correspond to a difference between dosed concentration and free concentration in the liposome system of less than 3%, which is indeed below the resolution of the present experiments. Hence, the simulations correctly predict that an experimental measurement of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW would be challenging for hexylamine and, in the process, provide a prediction of what the value would be.
KMW would be challenging for hexylamine and, in the process, provide a prediction of what the value would be.
It is also important to bear in mind the assumptions associated with liposome experiments. The calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW is based on measuring the free aqueous concentration in the dialysis receptor cell and the assumption that any remaining solute must be in the liposome. Concentrations during control experiments (with no liposome) show a loss of material in some cases (recovery less than 80%). Stability assessment in the same matrix and under the same conditions were carried out as part of the method development for all chemicals and did not show significant degradation, which rules this out as the main loss. It is proposed that losses result from binding to the RED plate. In the case of diethyl adipate, tryptophan, trihexylamine and tridecyl sulfate, the recovery was substantially lower (less than 25%) in the reference compound or the solute itself, and we have therefore been unable to obtain reliable log
KMW is based on measuring the free aqueous concentration in the dialysis receptor cell and the assumption that any remaining solute must be in the liposome. Concentrations during control experiments (with no liposome) show a loss of material in some cases (recovery less than 80%). Stability assessment in the same matrix and under the same conditions were carried out as part of the method development for all chemicals and did not show significant degradation, which rules this out as the main loss. It is proposed that losses result from binding to the RED plate. In the case of diethyl adipate, tryptophan, trihexylamine and tridecyl sulfate, the recovery was substantially lower (less than 25%) in the reference compound or the solute itself, and we have therefore been unable to obtain reliable log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW values for these molecules. Scaling of the measured concentrations to the respective control values gave unphysical results where the scaled concentration was higher than the initial dosed concentration. There may be a more complex three-way equilibrium between the water, liposome and the binding of solute to the experimental equipment but it is not clear how best to account for this.
KMW values for these molecules. Scaling of the measured concentrations to the respective control values gave unphysical results where the scaled concentration was higher than the initial dosed concentration. There may be a more complex three-way equilibrium between the water, liposome and the binding of solute to the experimental equipment but it is not clear how best to account for this.
6 Conclusions
In summary, we have presented membrane–water partitioning data for a varied set of charged and neutral molecules, calculated using experimental liposome measurements and coarse-grained molecular dynamics simulations. The two methods were found to agree well for most molecules, and where there were discrepancies there are clear reasons from either the simulation or experimental side. This adds weight to the use of simulation to complement other methods, for example for molecules where experiments are difficult to carry out, or to fill in gaps in the data for series of similar molecules, or by way of initial high-throughput screening.Another key aim of this study was to determine whether it is appropriate to include cholesterol in model membranes for helping to determine bioaccumulation. Many of the solutes studied do show a slight reduction in partitioning for cholesterol-containing membranes compared to pure POPC. However, this change is small, and is generally less than the difference between, for example, measurements from different dose concentrations or methods for calculating KMW and DMW. For the purposes of a risk assessment, where several other factors in addition to bioaccumulation must be taken into account, this small change may not be significant. Some chemicals, e.g., perfluoroalkyl surfactants, are known to have specific affinity for other membrane components such as certain proteins, and so require more specific consideration.19 However, even for these chemicals, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW for pure membranes has been demonstrated to provide improved correspondence with BCF values.19 We conclude that KMW determined for pure phospholipid membranes is a suitable surrogate for partitioning into cholesterol-containing membranes characteristic of fish as part of an overall assessment of bioaccumulation.
KMW for pure membranes has been demonstrated to provide improved correspondence with BCF values.19 We conclude that KMW determined for pure phospholipid membranes is a suitable surrogate for partitioning into cholesterol-containing membranes characteristic of fish as part of an overall assessment of bioaccumulation.
The present study highlights the need for further work in several directions. In this article we have considered the influence of cholesterol on partitioning, but other membrane components also have the potential to influence the uptake of ionizable compounds, despite being present at lower levels. For example, acidic phospholipids are able to attract positively charged molecules and repel negatively charged molecules.82 While these phospholipids may be present only in small concentrations, their overall impact has not yet been fully quantified across a broad chemical space (including those chemicals considered in this study). Additionally, the agreement between experiment and simulation for 3-nitroaniline in this study is poor. Considering the large amount of experimental data for this compound, the disagreement suggests that further development is needed for simulations of compounds containing nitro groups and zwitterions in general. Finally, another priority is the development of consistently good models for compounds containing ammonium, especially quaternary nitrogen. As log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW for these molecules often proves difficult to measure experimentally, the development of simulation models for such compounds is a focus for future research opportunities.
KMW for these molecules often proves difficult to measure experimentally, the development of simulation models for such compounds is a focus for future research opportunities.
Author contributions
All authors contributed to the writing. Additionally, TDP developed simulation methodology and carried out all simulations. NH designed, executed and validated liposome measurements, with assistance from AT. GH and ELB conceptualized the project; additionally, ELB is the project manager. MAM supervised the computational work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support of Unilever.Notes and references
- C. A. LaLone, N. Basu, P. Browne, S. W. Edwards, M. Embry, F. Sewell and G. Hodges, International Consortium to Advance Cross-Species Extrapolation of the Effects of Chemicals in Regulatory Toxicology, Environ. Toxicol. Chem., 2021, 40, 3226–3233 CrossRef CAS PubMed.
- N. Burden, F. Sewell and K. Chapman, Testing Chemical Safety: What Is Needed to Ensure the Widespread Application of Non-animal Approaches?, PLoS Biol., 2015, 13, e1002156 CrossRef PubMed.
- E. K. Brockmeier, G. Hodges, T. H. Hutchinson, E. Butler, M. Hecker, K. E. Tollefsen, N. Garcia-Reyero, P. Kille, D. Becker, K. Chipman, J. Colbourne, T. W. Collette, A. Cossins, M. Cronin, P. Graystock, S. Gutsell, D. Knapen, I. Katsiadaki, A. Lange, S. Marshall, S. F. Owen, E. J. Perkins, S. Plaistow, A. Schroeder, D. Taylor, M. Viant, G. Ankley and F. Falciani, The Role of Omics in the Application of Adverse Outcome Pathways for Chemical Risk Assessment, Toxicol. Sci., 2017, 158, 252–262 CrossRef CAS PubMed.
- J. M. Armitage, R. J. Erickson, T. Luckenbach, C. A. Ng, R. S. Prosser, J. A. Arnot, K. Schirmer and J. W. Nichols, Assessing the bioaccumulation potential of ionizable organic compounds: current knowledge and research priorities: bioaccumulation of IOCs: current knowledge, Environ. Toxicol. Chem., 2017, 36, 882–897 CrossRef CAS PubMed.
- Regulation (EC) No 1907/2006 - Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH), https://osha.europa.eu/en/legislation/directives/regulation-ec-no-1907-2006-of-the-european-parliament-and-of-the-council, Accessed: 26-08-2022.
- J. M. Armitage, J. A. Arnot, F. Wania and D. Mackay, Development and evaluation of a mechanistic bioconcentration model for ionogenic organic chemicals in fish, Environ. Toxicol. Chem., 2013, 32, 115–128 CrossRef CAS PubMed.
- S. G. Abernethy, D. MacKay and L. S. McCarty, “Volume fraction” correlation for narcosis in aquatic organisms: the key role of partitioning, Environ. Toxicol. Chem., 1988, 7, 469–481 CrossRef CAS.
- S. T. J. Droge, P. Scherpenisse, J. A. Arnot, J. M. Armitage, M. S. McLachlan, P. C. von der Ohe and G. Hodges, Screening the baseline fish bioconcentration factor of various types of surfactants using phospholipid binding data, Environ. Sci.: Processes Impacts, 2021, 23, 1930–1948 RSC.
- G. Hodges, C. Eadsforth, B. Bossuyt, A. Bouvy, M.-H. Enrici, M. Geurts, M. Kotthoff, E. Michie, D. Miller, J. Müller, G. Oetter, J. Roberts, D. Schowanek, P. Sun and J. Venzmer, A comparison of log Kow (n-octanol–water partition coefficient) values for non-ionic, anionic, cationic and amphoteric surfactants determined using predictions and experimental methods, Environ. Sci. Eur., 2019, 31, 1 CrossRef CAS.
- S. T. J. Droge, J. L. M. Hermens, S. Gutsell, J. Rabone and G. Hodges, Predicting the phospholipophilicity of monoprotic positively charged amines, Environ. Sci.: Processes Impacts, 2017, 19, 307–323 RSC.
- A. Ribbenstedt, J. M. Armitage, F. Günther, J. A. Arnot, S. T. J. Droge and M. S. McLachlan, In Vivo Bioconcentration of 10 Anionic Surfactants in Rainbow Trout Explained by In Vitro Data on Partitioning and S9 Clearance, Environ. Sci. Technol., 2022, 56, 6305–6314 CrossRef CAS PubMed.
- B. I. Escher and R. P. Schwarzenbach, Partitioning of Substituted Phenols in Liposome−Water, Biomembrane−Water, and Octanol−Water Systems, Environ. Sci. Technol., 1996, 30, 260–270 CrossRef CAS.
- B. I. Escher, R. I. L. Eggen, U. Schreiber, Z. Schreiber, E. Vye, B. Wisner and R. P. Schwarzenbach, Baseline Toxicity (Narcosis) of Organic Chemicals Determined by In Vitro Membrane Potential Measurements in Energy-Transducing Membranes, Environ. Sci. Technol., 2002, 36, 1971–1979 CrossRef CAS PubMed.
- B. I. Escher, A. Baumer, K. Bittermann, L. Henneberger, M. König, C. Kühnert and N. Klüver, General baseline toxicity QSAR for nonpolar, polar and ionisable chemicals and their mixtures in the bioluminescence inhibition assay with Aliivibrio fischeri, Environ. Sci.: Processes Impacts, 2017, 19, 414–428 RSC.
- S. T. J. Droge, G. Hodges, M. Bonnell, S. Gutsell, J. Roberts, A. Teixeira and E. L. Barrett, Using membrane–water partition coefficients in a critical membrane burden approach to aid the identification of neutral and ionizable chemicals that induce acute toxicity below narcosis levels, Environ. Sci.: Processes Impacts, 2023, 25, 621–647 RSC.
- B. I. Escher, R. P. Schwarzenbach and J. C. Westall, Evaluation of Liposome−Water Partitioning of Organic Acids and Bases. 1. Development of a Sorption Model, Environ. Sci. Technol., 2000, 34, 3954–3961 CrossRef CAS.
- S. D. Kramer, B. Testa, H. van de Waterbeemd, G. Folkers and R. Guy, Pharmacokinetic Optimization in Drug Research: Biological, Physicochemical, and Computational Strategies, Wiley, Zürich, Switzerland, 2001 Search PubMed.
- S. Van Der Heijden and M. Jonker, Evaluation of liposome-water partitioning for predicting bioaccumulation potential of hydrophobic organic chemicals, Environ. Sci. Technol., 2009, 43, 8854–8859 CrossRef CAS PubMed.
- S. T. J. Droge, Membrane–Water Partition Coefficients to Aid Risk Assessment of Perfluoroalkyl Anions and Alkyl Sulfates, Environ. Sci. Technol., 2019, 53, 760–770 CrossRef CAS PubMed.
- S. Ong, H. Liu, X. Qiu, G. Bhat and C. Pidgeon, Membrane Partition Coefficients Chromatographically Measured Using Immobilized Artificial Membrane Surfaces, Anal. Chem., 1995, 67, 755–762 CrossRef CAS PubMed.
- C. Giaginis and A. Tsantili-Kakoulidou, Alternative Measures of Lipophilicity: From Octanol–Water Partitioning to IAM Retention, J. Pharm. Sci., 2008, 97, 2984–3004 CrossRef CAS PubMed.
- S. T. J. Droge, J. L. M. Hermens, J. Rabone, S. Gutsell and G. Hodges, Phospholipophilicity of CxHyN+ amines: chromatographic descriptors and molecular simulations for understanding partitioning into membranes, Environ. Sci.: Processes Impacts, 2016, 18, 1011–1023 RSC.
- G. P. van Balen, C. a. M. Martinet, G. Caron, G. Bouchard, M. Reist, P.-A. Carrupt, R. Fruttero, A. Gasco and B. Testa, Liposome/water lipophilicity: methods, information content, and pharmaceutical applications, Med. Res. Rev., 2004, 24, 299–324 CrossRef CAS PubMed.
- A. Loidl-Stahlhofen, T. Hartmann, M. Schöttner, C. Röhring, H. Brodowsky, J. Schmitt and J. Keldenich, Multilamellar Liposomes and Solid-Supported Lipid Membranes (TRANSIL): Screening of Lipid-Water Partitioning Toward a High-Throughput Scale, Pharm. Res., 2001, 18, 1782–1788 CrossRef CAS PubMed.
- A. Loidl-Stahlhofen, A. Eckert, T. Hartmann and M. Schöttner, Solid-supported lipid membranes as a tool for determination of membrane affinity: high-throughput screening of a physicochemical parameter, J. Pharm. Sci., 2001, 90, 599–606 CrossRef CAS PubMed.
- S. Ong, H. Liu and C. Pidgeon, Immobilized-artificial-membrane chromatography: measurements of membrane partition coefficient and predicting drug membrane permeability, J. Chromatogr. A, 1996, 728, 113–128 CrossRef CAS PubMed.
- F. Tsopelas, C. Stergiopoulos and A. Tsantili-Kakoulidou, Immobilized artificial membrane chromatography: from medicinal chemistry to environmental sciences, ADMET and DMPK, 2018, 6, 225–241 CrossRef.
- M. R. Ledbetter, S. Gutsell, G. Hodges, S. O'Connor, J. C. Madden, P. H. Rowe and M. Cronin, Prediction of immobilised artificial membrane chromatography retention factors using theoretical molecular fragments and structural features, SAR QSAR Environ. Res., 2013, 24, 661–678 CrossRef CAS PubMed.
- S. Endo, B. I. Escher and K.-U. Goss, Capacities of Membrane Lipids to Accumulate Neutral Organic Chemicals, Environ. Sci. Technol., 2011, 45, 5912–5921 CrossRef CAS PubMed.
- S. Endo and K.-U. Goss, Applications of Polyparameter Linear Free Energy Relationships in Environmental Chemistry, Environ. Sci. Technol., 2014, 48, 12477–12491 CrossRef CAS PubMed.
- A. Klamt, U. Huniar, S. Spycher and J. Keldenich, COSMOmic: a mechanistic approach to the calculation of membrane-water partition coefficients and internal distributions within membranes and micelles, J. Phys. Chem. B, 2008, 112, 12148–12157 CrossRef CAS PubMed.
- A. Klamt, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- S. Jakobtorweihen, T. Ingram and I. Smirnova, Combination of COSMOmic and molecular dynamics simulations for the calculation of membrane–water partition coefficients, J. Comput. Chem., 2013, 34, 1332–1340 CrossRef CAS PubMed.
- K. Bittermann, S. Spycher and K.-U. Goss, Comparison of different models predicting the phospholipid-membrane water partition coefficients of charged compounds, Chemosphere, 2016, 144, 382–391 CrossRef CAS PubMed.
- K. Bittermann, S. Spycher, S. Endo, L. Pohler, U. Huniar, K.-U. Goss and A. Klamt, Prediction of Phospholipid–Water Partition Coefficients of Ionic Organic Chemicals Using the Mechanistic Model COSMOmic, J. Phys. Chem. B, 2014, 118, 14833–14842 CrossRef CAS PubMed.
- F. Di Meo, G. Fabre, K. Berka, T. Ossman, B. Chantemargue, M. Paloncýová, P. Marquet, M. Otyepka and P. Trouillas, In silico pharmacology: drug membrane partitioning and crossing, Pharmacol. Res., 2016, 111, 471–486 CrossRef CAS PubMed.
- S. Jakobtorweihen, A. C. Zuniga, T. Ingram, T. Gerlach, F. J. Keil and I. Smirnova, Predicting solute partitioning in lipid bilayers: free energies and partition coefficients from molecular dynamics simulations and COSMOmic, J. Chem. Phys., 2014, 141, 045102 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Perspective on the Martini model, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- T. D. Potter, E. L. Barrett and M. A. Miller, Automated Coarse-Grained Mapping Algorithm for the Martini Force Field and Benchmarks for Membrane–Water Partitioning, J. Chem. Theory Comput., 2021, 17, 5777–5791 CrossRef CAS PubMed.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: a general purpose force field for coarse-grained molecular dynamics, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- R. Alessandri, J. Barnoud, A. S. Gertsen, I. Patmanidis, A. H. de Vries, P. C. T. Souza and S. J. Marrink, Martini 3 Coarse-Grained Force Field: Small Molecules, Adv. Theory Simul., 2022, 5, 2100391 CrossRef CAS.
- T. Harayama and H. Riezman, Understanding the diversity of membrane lipid composition, Nat. Rev. Mol. Cell Biol., 2018, 19, 281–296 CrossRef CAS PubMed.
- P. Goluszko and B. Nowicki, Membrane Cholesterol: A Crucial Molecule Affecting Interactions of Microbial Pathogens with Mammalian Cells, Infect. Immun., 2005, 73, 7791–7796 CrossRef CAS PubMed.
- L. Bolis and R. Fänge, Lipid composition of the erythrocyte membrane of some marine fish, Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 1979, 62, 345–348 CrossRef.
- S. Murzina, Z. Nefedova, S. Falk-Petersen, P. Ripatti, T. Ruokolainen, S. Pekkoeva and N. Nemova, Lipid Status of the Two High Latitude Fish Species, Leptoclinus maculatus and Lumpenus fabricii, Int. J. Mol. Sci., 2013, 14, 7048–7060 CrossRef CAS PubMed.
- K. Thompson, R. Henderson and M. Tatner, A comparison of the lipid composition of peripheral blood cells and head kidney leucocytes of Atlantic salmon (Salmo salar L.), Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 1995, 112, 83–92 CrossRef.
- P. V. Velansky and E. Y. Kostetsky, Lipids of marine cold-water fishes, Russ. J. Mar. Biol., 2008, 34, 51–56 CrossRef CAS.
- M. V. Lizenko, T. I. Regerand, A. M. Bakhirev and E. I. Lizenko, Lipid composition of cells and low-density lipoproteins in blood serum of human and some vertebrate species, J. Evol. Biochem. Physiol., 2011, 47, 428–437 CrossRef CAS.
- J. C. Robertson and J. R. Hazel, Cholesterol content of trout plasma membranes varies with acclimation temperature, Am. J. Physiol., 1995, 269, R1113–R1119 CAS.
- D. Marsh, Liquid-ordered phases induced by cholesterol: a compendium of binary phase diagrams, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 688–699 CrossRef CAS PubMed.
- R. F. M. de Almeida, A. Fedorov and M. Prieto, Sphingomyelin/Phosphatidylcholine/Cholesterol Phase Diagram: Boundaries and Composition of Lipid Rafts, Biophys. J., 2003, 85, 2406–2416 CrossRef CAS PubMed.
- I. V. Ionova, V. A. Livshits and D. Marsh, Phase Diagram of Ternary Cholesterol/Palmitoylsphingomyelin/Palmitoyloleoyl-Phosphatidylcholine Mixtures: Spin-Label EPR Study of Lipid-Raft Formation, Biophys. J., 2012, 102, 1856–1865 CrossRef CAS PubMed.
- M. C. Rheinstädter and O. G. Mouritsen, Small-scale structure in fluid cholesterol–lipid bilayers, Curr. Opin. Colloid Interface Sci., 2013, 18, 440–447 CrossRef.
- F. Favela-Rosales, A. Galván-Hernández, J. Hernández-Cobos, N. Kobayashi, M. D. Carbajal-Tinoco, S. Nakabayashi and I. Ortega-Blake, A molecular dynamics study proposing the existence of statistical structural heterogeneity due to chain orientation in the POPC-cholesterol bilayer, Biophys. Chem., 2020, 257, 106275 CrossRef CAS PubMed.
- R. C. MacDonald, R. I. MacDonald, B. P. Menco, K. Takeshita, N. K. Subbarao and L.-r. Hu, Small-volume extrusion apparatus for preparation of large, unilamellar vesicles, Biochim. Biophys. Acta, Biomembr., 1991, 1061, 297–303 CrossRef CAS PubMed.
- N. J. Waters, R. Jones, G. Williams and B. Sohal, Validation of a Rapid Equilibrium Dialysis Approach for the Measurement of Plasma Protein Binding, J. Pharm. Sci., 2008, 97, 4586–4595 CrossRef CAS PubMed.
- M. N. Melo, H. I. Ingólfsson and S. J. Marrink, Parameters for Martini sterols and hopanoids based on a virtual-site description, J. Chem. Phys., 2015, 143, 243152 CrossRef CAS PubMed.
- I. V. Tetko and V. Y. Tanchuk, Application of Associative Neural Networks for Prediction of Lipophilicity in ALOGPS 2.1 Program, J. Chem. Inf. Comput. Sci., 2002, 42, 1136–1145 CrossRef CAS PubMed.
- I. Sushko, S. Novotarskyi, R. Körner, A. K. Pandey, M. Rupp, W. Teetz, S. Brandmaier, A. Abdelaziz, V. V. Prokopenko, V. Y. Tanchuk, R. Todeschini, A. Varnek, G. Marcou, P. Ertl, V. Potemkin, M. Grishina, J. Gasteiger, C. Schwab, I. I. Baskin, V. A. Palyulin, E. V. Radchenko, W. J. Welsh, V. Kholodovych, D. Chekmarev, A. Cherkasov, J. Aires-de Sousa, Q.-Y. Zhang, A. Bender, F. Nigsch, L. Patiny, A. Williams, V. Tkachenko and I. V. Tetko, Online chemical modeling environment (OCHEM): web platform for data storage, model development and publishing of chemical information, J. Comput.-Aided Mol. Des., 2011, 25, 533–554 CrossRef CAS PubMed.
- T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, Computational Lipidomics with Insane: A Versatile Tool for Generating Custom Membranes for Molecular Simulations, J. Chem. Theory Comput., 2015, 11, 2144–2155 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- D. H. de Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Martini straight: boosting performance using a shorter cutoff and GPUs, Comput. Phys. Commun., 2016, 199, 1–7 CrossRef CAS.
- J. A. Barker and R. O. Watts, Monte Carlo studies of the dielectric properties of water-like models, Mol. Phys., 1973, 26, 789–792 CrossRef CAS.
- S. Thallmair, M. Javanainen, B. Fábián, H. Martinez-Seara and S. J. Marrink, Nonconverged Constraints Cause Artificial Temperature Gradients in Lipid Bilayer Simulations, J. Phys. Chem. B, 2021, 125, 9537–9546 CrossRef CAS PubMed.
- N. Nitschke, K. Atkovska and J. S. Hub, Accelerating potential of mean force calculations for lipid membrane permeation: system size, reaction coordinate, solute-solute distance, and cutoffs, J. Chem. Phys., 2016, 145, 125101 CrossRef PubMed.
- W. D. Bennett, A. W. Chen, S. Donnini, G. Groenhof and D. P. Tieleman, Constant pH simulations with the coarse-grained MARTINI model — application to oleic acid aggregates, Can. J. Chem., 2013, 91, 839–846 CrossRef CAS.
- F. Grünewald, P. C. T. Souza, H. Abdizadeh, J. Barnoud, A. H. de Vries and S. J. Marrink, Titratable Martini model for constant pH simulations, J. Chem. Phys., 2020, 153, 024118 CrossRef PubMed.
- L. J. Henderson, Concerning the relationship between the strength of acids and their capacity to preserve neutrality, Am. J. Physiol., 1908, 21, 173–179 CrossRef CAS.
- K. A. Hasselbalch, Die Berechnung der Wasserstoffzahl des Blutes aus der freien und gebundenen Kohlensäure desselben, und die Sauerstoffbindung des Blutes als Funktion der Wasserstoffzahl, Biochem. Z., 1917, 78, 112–144 Search PubMed.
- R. C. Weast, Handbook of data on organic compounds, 1985 Search PubMed.
- J. M. Sangster, Octanol-Water Partition Coefficients: Fundamentals and Physical Chemistry, John Wiley & Sons, 1997 Search PubMed.
- D. D. Perrin, Dissociation Constants of Organic Bases in Aqueous Solution, Butterworths, 1965 Search PubMed.
- Advanced Chemistry Development (ACD/Labs), Chemistry software for analytical and chemical knowledge management, 2019, https://www.acdlabs.com/ Search PubMed.
- S. Chakraborty, D. Shukla, A. Jain, B. Mishra and S. Singh, Assessment of solubilization characteristics of different surfactants for carvedilol phosphate as a function of pH, J. Colloid Interface Sci., 2009, 335, 242–249 CrossRef CAS PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field, J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef CAS PubMed.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef PubMed.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Two decades of Martini: better beads, broader scope, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1620 Search PubMed.
- R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, Pitfalls of the Martini Model, J. Chem. Theory Comput., 2019, 15, 5448–5460 CrossRef CAS PubMed.
- J. Pan, S. Tristram-Nagle and J. F. Nagle, Effect of cholesterol on structural and mechanical properties of membranes depends on lipid chain saturation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021931 CrossRef PubMed.
- W. Schmitt, General approach for the calculation of tissue to plasma partition coefficients, Toxicol. in Vitro, 2008, 22, 457–467 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3em00081h |
| This journal is © The Royal Society of Chemistry 2023 |