Open Access Article
Open Access ArticleMolecular packing structure of fibrin fibers resolved by X-ray scattering and molecular modeling†
Karin A.
Jansen‡
 ab,
Artem
Zhmurov‡
cd,
Bart E.
Vos
ab,
Artem
Zhmurov‡
cd,
Bart E.
Vos
 ae,
Giuseppe
Portale
ae,
Giuseppe
Portale
 f,
Daniel
Hermida-Merino
g,
Rustem I.
Litvinov
f,
Daniel
Hermida-Merino
g,
Rustem I.
Litvinov
 hi,
Valerie
Tutwiler
h,
Nicholas A.
Kurniawan
hi,
Valerie
Tutwiler
h,
Nicholas A.
Kurniawan
 aj,
Wim
Bras
aj,
Wim
Bras
 gk,
John W.
Weisel
gk,
John W.
Weisel
 h,
Valeri
Barsegov
*l and
Gijsje H.
Koenderink
h,
Valeri
Barsegov
*l and
Gijsje H.
Koenderink
 *am
*am
aAMOLF, Biological Soft Matter Group, Amsterdam, The Netherlands
bUMC Utrecht, Department of Pathology, 3508 GA Utrecht, The Netherlands
cKTH Royal Institute of Technology, Stockholm, Sweden
dSechenov University, Moscow 119991, Russian Federation
eInstitute of Cell Biology, Center of Molecular Biology of Inflammation, University of Münster, Münster, Germany
fMacromolecular Chemistry and New Polymeric Materials, Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands
gNetherlands Organization for Scientific Research (NWO), DUBBLE CRG at the ESRF, 71 Avenue des Martyrs, 38000 Grenoble Cedex, France
hDepartment of Cell and Developmental Biology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, Pennsylvania, USA
iInstitute of Fundamental Medicine and Biology, Kazan Federal University, 18 Kremlyovskaya St., Kazan 420008, Russian Federation
jDepartment of Biomedical Engineering and Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven, The Netherlands
kChemical Sciences Division, Oak Ridge National Laboratory, One Bethel Valley Road, Oak Ridge Tennessee, 37831, USA
lDepartment of Chemistry, University of Massachusetts, 1 University Ave., Lowell, MA, 01854, USA. E-mail: Valeri_Barsegov@uml.edu
mDepartment of Bionanoscience, Kavli Institute of Nanoscience Delft, Delft University of Technology, Van der Maasweg 9, Delft, 2629 HZ, The Netherlands. E-mail: g.h.koenderink@tudelft.nl
First published on 17th August 2020
Abstract
Fibrin is the major extracellular component of blood clots and a proteinaceous hydrogel used as a versatile biomaterial. Fibrin forms branched networks built of laterally associated double-stranded protofibrils. This multiscale hierarchical structure is crucial for the extraordinary mechanical resilience of blood clots, yet the structural basis of clot mechanical properties remains largely unclear due, in part, to the unresolved molecular packing of fibrin fibers. Here the packing structure of fibrin fibers is quantitatively assessed by combining Small Angle X-ray Scattering (SAXS) measurements of fibrin reconstituted under a wide range of conditions with computational molecular modeling of fibrin protofibrils. The number, positions, and intensities of the Bragg peaks observed in the SAXS experiments were reproduced computationally based on the all-atom molecular structure of reconstructed fibrin protofibrils. Specifically, the model correctly predicts the intensities of the reflections of the 22.5 nm axial repeat, corresponding to the half-staggered longitudinal arrangement of fibrin molecules. In addition, the SAXS measurements showed that protofibrils within fibrin fibers have a partially ordered lateral arrangement with a characteristic transverse repeat distance of 13 nm, irrespective of the fiber thickness. These findings provide fundamental insights into the molecular structure of fibrin clots that underlies their biological and physical properties.
1 Introduction
Fibrin forms the polymeric mechanical scaffold of blood clots and thrombi. Fibrin networks, along with platelets and erythrocytes, serve to seal sites of vascular injury and promote wound healing.1 In addition, fibrin hydrogels have been extensively used as biomaterials in tissue engineering due to their unique biological and physical characteristics, such as porosity, deformability, elasticity and biodegradability.2 Fibrin networks have a complex hierarchical structure that is crucial for their material properties.3 At the network scale, fibrin fibers form a branched, space-filling elastic network that is able to withstand large mechanical deformations exerted by flowing blood, platelet-induced contraction, and deformations of the vessel wall. The fibers are in turn made up of laterally associated protofibrils,4 which themselves are two-stranded linear filaments of half-staggered fibrin monomers.5 The molecular packing of fibrin fibers, together with the structural flexibility of individual fibrin molecules, results in remarkable mechanical properties. For example, an individual fibrin fiber can be stretched by about twice its length before changes in elastic properties occur.6,7 Whole fibrin clots are similarly deformable and resilient.8–10 Furthermore, the molecular packing of fibrin fibers affects the susceptibility of fibrin to enzymatic lysis, a process called fibrinolysis that dissolves fully or partially obstructive blood clots (thrombi) to restore impaired blood flow.11,12The structure of fibrin networks has been studied at various structural levels. The structure of the monomers has been elucidated by X-ray crystallography,13 electron microscopy14 and atomic force microscopy15,16 and has been modeled by full-atom Molecular Dynamics (MD) simulations.17–21 The structure and assembly mechanism of fibrin protofibrils has likewise been studied by electron microscopy and atomic force microscopy22–24 and through full-atom MD simulations.22,25 The structure at the network level has been characterized mostly by light scattering,23,26–28 confocal light microscopy,29,30 and scanning electron microscopy.31
The least well understood aspect of the hierarchical structure of fibrin is the three-dimensional molecular packing of protofibrils within fibrin fibers. Along the fiber axis, fibrin monomers are known to be half-staggered, as evident from cross-striations with a 22.5 nm repeat in high-resolution images of fibers taken by electron or atomic force microscopy.14–16,23 Transverse to the fiber axis, it is less clear how protofibrils are organized. Most of what we know about the 3D packing structure of fibrin fibers comes from small angle X-ray scattering (SAXS) because it allows the molecular arrangement of fibrin fibers to be probed in their native hydrated state. Early on, SAXS was used to demonstrate the half-staggered molecular packing structure of fibrin fibers, which shows up in the form of a Bragg peak at a wave vector corresponding to the 22.5 nm repeat distance.14,32 Later measurements by SAXS4,32–35 and neutron diffraction36 confirmed that the axial packing order is long-ranged, and reasonably well ordered, along a fiber, as evident from the presence of quite narrow peaks corresponding to higher-order reflections of the 22.5 nm axial repeat distance. Surprisingly, while the third and higher-order reflections are often observed in the SAXS spectra, the second order reflection is usually missing or very faint,32,36,37 although the origin of this peak suppression is unclear. The suppression of such a low angle peak usually indicates a higher symmetry or a form factor scattering that has a minimum at this q value, but so far the source of this long range ordering has remained elusive.
Transverse to the fiber axis, the packing of protofibrils inside the fibrin fiber was shown by SAXS to be less ordered than the axial packing, but there is controversy about the degree of disorder. Some X-ray scattering studies concluded that there was no order in the lateral packing of fibrin fibers,4,32 while others found evidence of considerable lateral crystallinity.34,36,38 It was proposed that fibrin fibers might be partially crystalline as a consequence of defects in the radial packing structure, and that the degree of order might depend on the conditions of fibrin self-assembly.39 The lateral packing order might also vary for fibers with different dimensions.14
One of the main challenges in resolving the three-dimensional packing of protofibrils within fibrin fibers in SAXS experiments is the lack of experimental data about the detailed structure of the protofibril, because it is a short-lived intermediate oligomer formed at the early stages of fibrin formation. This makes it difficult to relate the positions, intensities, and widths of low angle diffraction peaks, which for brevity we will refer to as ‘Bragg peaks’, observed in SAXS spectra to structural signatures originating from molecular packing within fibrin fibers. As a powerful methodological advantage, here we provide a structural model-based interpretation of experimental SAXS spectra for fibrin based on the full-atomic modeling of fibrin protofibril fragments in silico. By coupling experiments and computational molecular modeling, we resolve the axial and radial packing arrangements of fibrin fibers. The theoretically reconstructed SAXS spectra captured the number, positions and intensities of the Bragg peaks observed by experimental SAXS and explain the long-standing riddle as to why the second order reflection of the 22.5 nm axial repeat is suppressed. By systematically varying the fibrin fiber thickness, we found that the range of axial order reflected by the width of the Bragg peaks in the SAXS spectra of isotropic fibrin networks is determined by the protein packing density of the fibers. Furthermore, our results confirm predictions of proposed model that the radial packing of fibrin fibers is partially ordered39 with a newly determined characteristic repeat distance of 13 nm that is independent of the fiber thickness.
2 Materials & methods
2.1 Formation of fibrin clots with varying structure
Human fibrinogen (FIB 3) and human α-thrombin were obtained from Enzyme Research Laboratories (Swansea, UK). FIB 3 was depleted of plasminogen, von Willebrand Factor, and fibronectin and delivered at a concentration of 13.64 mg ml−1 in a 20 mM sodium citrate–HCl buffer, pH 7.4 (stock solution). To vary the fiber thickness (quantified as the average number of protofibrils per cross-section of the fiber, Np) and fiber protein density ρ (in units of mass per volume), we used 4 different fibrin assembly conditions (see Table S1, ESI†):(1) Fine clot conditions: networks with Np = 2 were obtained from the fibrinogen stock preparation dialyzed against buffer with a high ionic strength and alkaline pH (50 mM Tris–HCl, 400 mM NaCl, pH 8.5). Fibrin was formed after diluting fibrinogen to the desired concentration in the same buffer supplemented with 3.2 mM CaCl2 followed by addition of thrombin to a final concentration of 0.5 U ml−1 and incubation for 2 hours at 37 °C. These conditions were previously shown to result in so-called fine clots with extremely thin fibers due to a minimal degree of protofibril lateral association.40
(2) Assembly from as-received stock: networks with Np = 47 and ρ = 11.6 mg ml−1 at a fibrinogen concentration of 8 mg ml−1 were obtained after diluting the fibrinogen stock preparation in an assembly buffer (pH 7.4) with final concentrations of 20 mM HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), 150 mM NaCl and 5 mM CaCl2. Fibrin formation was initiated by adding 0.5 U ml−1 thrombin (final concentration) and the network was allowed to form for 4 hours at 37 °C before measurements.
(3) Assembly from dialyzed stock fibrinogen preparation: fibrin networks with thicker fibers were obtained from the fibrinogen stock solution dialyzed against the assembly buffer (20 mM HEPES, 150 mM NaCL, pH 7.4) without CaCl2. We prepared networks with Np = 291 and ρ = 148 mg ml−1 by adding thrombin (0.5 U ml−1 final concentration) and CaCl2 (5 mM final concentration) to fibrinogen at 4 mg ml−1 and networks with Np = 435 and ρ = 190 mg ml−1 by clotting fibrinogen at 8 mg ml−1 with thrombin (0.5 U ml−1) and calcium (5 mM). The protein concentration after dialysis was determined using a NanoDrop spectrophotometer from the absorbance at a wavelength of 280 nm with correction for scattering at 320 nm as described.41
(4) Assembly from gel-filtered monomeric fibrinogen: networks with Np = 368 and ρ = 255 mg ml−1 at a 4 mg ml−1 fibrinogen concentration were prepared from monomeric fibrinogen obtained after removing contaminating fibrinogen oligomers from the fibrinogen stock solution by gel-filtration on Superdex-200 as described.42 The assembly buffer (pH 7.4) contained 20 mM HEPES, 150 mM NaCl, and 5 mM CaCl2 with addition of thrombin at 0.5 U ml−1 final concentration.
2.2 Confocal microscopy
Fibrin networks prepared as described above were imaged on a Nikon Eclipse Ti inverted confocal fluorescence microscope equipped with a 100× oil immersion objective lens (NA 1.49), a 488 nm laser (Coherent, Utrecht, The Netherlands) for illumination, and a photomultiplier tube detector (A1; Nikon, Amsterdam, the Netherlands). We collected stacks of confocal slices over a total depth of 10 μm and with a spacing of 0.125 μm. We performed confocal reflectance microscopy on unlabeled fibrin samples (see Fig. 2) and fluorescence imaging (see Fig. 4) on networks polymerized from unlabeled fibrinogen and Alexa488-labeled human fibrinogen (Life Technologies, Bleiswijk, the Netherlands) mixed in a 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio.
1 molar ratio.
2.3 Turbidimetry
To characterize the fibrin fibers in terms of the number of protofibrils per fiber Np and the protein mass density ρ, we performed turbidity measurements using a UV1 Spectrophotometer (Thermo Optek). Fibrin samples were prepared as described in disposable plastic cuvettes (UV-Cuvette micro, Plastibrand) with an optical path length of 1 cm for low-turbidity samples and 2 mm for high-turbidity samples. The optical density (OD) for wavelengths between 400 and 900 nm with 1 nm intervals was measured relative to a blank sample consisting of just buffer. The turbidity (in units of cm−1) follows from the optical density by multiplication by ln(10) times the path length.39We analyzed the data using a custom-written Python script (available upon request) that fits the wavelength dependence of the turbidity to an analytical model describing light scattering of fibrous networks,28 as explained in detail in the Supplementary Methods section in the ESI.† The model involves the two structural parameters characteristic of the fibers that we aim to determine, namely their radius R and mass-length ratio ν, and two parameters characterizing the network structure, namely its fractal dimension Dm and mesh size ξ. We determined Dm by Fourier analysis of confocal reflection microscopy images of fibrin networks,9–30,60 giving values between 1.4 and 1.5. Since ξ and ν are interrelated according to ξ = (c/ν)−1/2, we used an iterative fitting procedure to determine both parameters (see Fig. S1, ESI†). We fitted the turbidity data using an initial guess for ξ from the confocal data. From the resulting best-fit value for ν, we calculated an updated estimate of ξ and then repeated the fitting procedure. We typically needed fewer than 5 iterations until ξ and ν changed less than <1% (see example fits in Fig. S2, ESI†). From the mass-per-length ν and corresponding fiber radius R obtained by this iterative fitting procedure, we calculated the fiber mass density ρ = ν/πR2.
In the case of fine clots, the fiber radius is smaller than the wavelength, so the wavelength-dependent turbidity was fitted to the Carr model for thin fibers43 to determine ν. The fiber radius was estimated in earlier work from our lab to be in the range of ∼7.5–15 nm based on electron microscopy imaging.9
2.4 Small angle X-ray scattering of fibrin networks
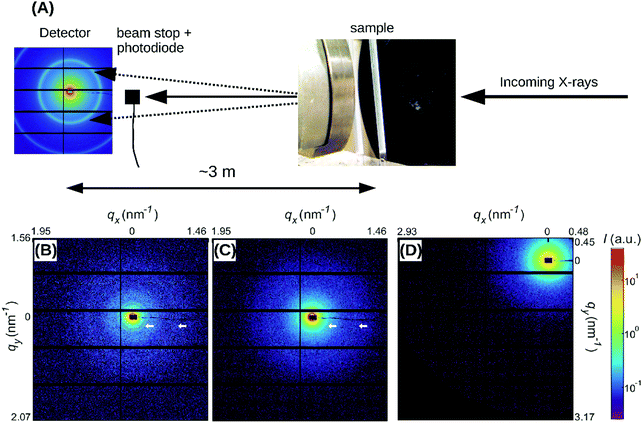
Small Angle X-ray Scattering (SAXS) was performed at the DUBBLE Beamline (BM26B) of the European Synchrotron Radiation Facility (ESRF, Grenoble, France).44 The range of the wave vector q was calibrated using silver behenate powder as a standard. The sample-to-detector (P1M) distance was about 3 m and the energy of the beam was 12 keV. The beam dimensions on the sample were about 900 × 700 μm. The fibrin samples were prepared as described earlier inside 2 mm borosilicate glass capillaries with 0.01 mm wall thickness (Hilgenberg, Germany). Capillaries filled with buffer were used to determine background scattering. Since there can be variations in capillary thickness, we ensured that a background was taken for every capillary and on every spot we measured, before we polymerized the fibrin gels in the same capillaries.2.5 Atomic structural models of fibrin protofibrils
To interpret the experimental SAXS spectra, we used the complete atomic models of two-stranded fibrin oligomer with 6 fibrin monomers in one strand and 5 in the other complementary strand (abbreviated as FO6-5) and protofibril with 10 and 9 fibrin monomers (abbreviated as FP10-9). The fibrin molecule is composed of three polypeptide chains denoted Aα, Bβ and γ, which fold into a symmetric trinodular structure that is 45 nm in length.45 The central nodule is formed by the N-terminal portions of all the six chains, and is connected to the globular β- and γ-nodules formed by the C-terminal parts of the β- and γ-chains, respectively, via triple α-helical coiled-coils.46 Half-staggered assembly into protofibrils is driven by specific interactions between knobs ‘A’ and ‘B’ in the central E region and holes ‘a’ and ‘b’ in the lateral D-regions of adjacent fibrin molecules.5,47 The flexible C-terminal portions of the Aα chains known as the αC regions form compact αC-domains that are tethered to the molecule by flexible αC-connectors.48The complete atomic structures of fibrin oligomer (FO6-5) and protofibril (FP10-9), with A:a and B:b knob–hole bonds, γ–γ covalent crosslinking, and the αC regions, were reconstructed in silico as described elsewhere.25 In all structural models, the two strands inside the protofibril are twisted around one another, forming a superhelical structure. This is an important property that affects the lateral aggregation of protofibrils into fibrin fibers and sets the limit of fibers’ thickness.49 In this superhelical structure, fibrin monomers are slightly tilted with respect to the helical axis, which reduces the scattering periodicity.
To obtain the atomic model of a protofibril without the αC-domain (FP10-9/αC), the complete atomic structures were truncated at residue αGln221 in both α-chains in all 19 fibrin monomers. To reconstruct the model of a protofibril without the γ-nodules (FP10-9/γ), both γ-chains in all fibrin monomers in both strands were truncated past residue γCys137. To obtain the structural model of a protofibril without the β-nodules (FP10-9/β), the β-chains were truncated in all 19 fibrin monomers starting from residue βCys197.
A single-stranded fibrin oligomer Fnm with m = 10 fibrin monomers connected longitudinally at the D:D interface was constructed using resolved crystallographic structures by connecting monomers end-to-end at the D–D junction. To build a single-stranded fibrinogen dimer, the double-D structure (PDB structure501FZG) was aligned with the full-length fibrinogen (PDB structure 3GHG13) so that one of the D regions of the double-D fragment overlapped with one of the D regions of the fibrin molecule. We used the Kabsch algorithm51 to align the globular parts of the molecules. Here, we superimposed the Cα-atoms of resolved residues Bβ197-461 in the β-nodule and γ139-411 in the γ-nodule. The procedure was then repeated to incorporate the third, fourth, etc. fibrin monomer until the desired length of the single-stranded oligomer was reached. Data visualization was done using VMD.52
2.6 Theoretical reconstruction of SAXS spectra
The one-dimensional SAXS scattering spectrum I(q) of a collection of single fibrin fibers was calculated in the limit of a large number of scattering particles N, using the following relation: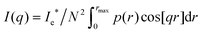 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ψ)/λ is the momentum transfer, λ is the wavelength of scattered radiation, and 2ψ is the scattering angle.
sin(ψ)/λ is the momentum transfer, λ is the wavelength of scattered radiation, and 2ψ is the scattering angle.
Since the fibrin networks are isotropic as evidenced from the isotropic SAXS patterns (Fig. 1B–D) and from the confocal images (Fig. 2B–D), we averaged the scattering intensity of single fibers over all orientations in 3D, according to:
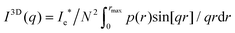 | (2) |
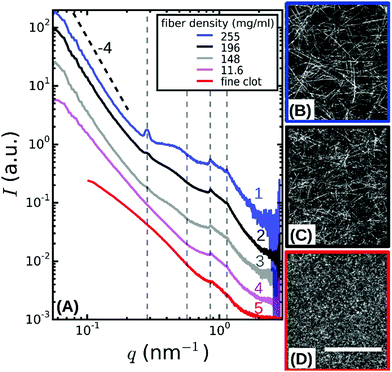 | ||
| Fig. 2 (A) SAXS spectra obtained by radial integration of the 2D SAXS patterns of fibrin networks with fibers of varying protofibril number Np. For fine clots (red curve), Np = 2. The other curves represent coarse (thick-fiber) clots with different protein mass densities ρ as specified in the legend (see Table S1, ESI†). The curves are shifted along the y-axis for clarity. Vertical dotted lines indicate the expected positions of the first, second, third and fourth order reflections of the axial packing distance (22.5 nm), while the dotted black line indicates the Porod scattering regime where I(q) ∝ q−4 for reference. (B–D) Confocal reflectance images of coarse fibrin networks with fiber mass densities of 255 and 148 mg ml−1, and for fine clots. Images show maximum intensity projections over a total depth of 20 μm. The scale bar is 20 μm. | ||
3 Results
3.1 Probing the axial packing of fibrin fibers with SAXS
To probe the sensitivity of the small angle X-ray diffraction to subtle differences in the fiber structure, we performed SAXS measurements on isotropic fibrin networks assembled using different polymerization conditions inside glass capillaries (Fig. 1A). By changing the fibrinogen concentration and buffer composition (see Materials and methods), we varied the fiber thickness, expressed as the average number of protofibrils per cross-section of a fibrin fiber (Np), over a wide range from Np = 2 up to Np = 435, as determined by light scattering measurements (see Table S1, ESI,† and confocal reflectance images in Fig. 2B–D). Light scattering measurements showed that the variation in fiber thickness was accompanied by strong variations in the protein mass density of the fibers, as summarized in Table S1, ESI.† The mass density ranged from ρ = 11.6 mg ml−1 for Np = 47 up to ρ = 255 mg ml−1 for Np = 368. This observation is qualitatively consistent with earlier reports of strong variations in fibrin fiber density with assembly conditions.39,55,56 Note that for the Np = 2 networks we could only determine the mass-length ratio (and thus Np) of the fibers from light scattering and not the fiber radius (and thus ρ), because these thin fibers have radii of only 7.5–15 nm, smaller than the wavelength of light.9The 2D SAXS patterns of fibrin were isotropic in all cases, showing concentric reflection rings (cf. white arrows in Fig. 1B and C), as would be expected for a random fibrous network. The intensities of the reflections were larger for thick fibers (Np = 368 and 435 in Fig. 1B and C, respectively) than for thin fibers (Np = 2 in Fig. 1D). The Np-dependence of the scattering was more evident from the SAXS 1D profiles obtained by the radial integration of the 2D scattering patterns (Fig. 2A). For the fibers with the highest mass density (ρ = 255 mg ml−1) we observe a clear Bragg peak at a wave number q = 0.285 nm−1 (labeled as curve 1). This peak corresponds to a repeat distance of 22.2 nm and it can thus be assigned as the first-order reflection of the fibrin half-staggered axial packing repeat.32 In case of long-range axial packing order, higher-order reflections are expected at q = 0.57 (second), q = 0.855 (third) and q = 1.14 nm−1 (fourth) (denoted by dashed vertical lines). Interestingly, we only observed the third and fourth order reflections. For fibers with a slightly lower mass density (ρ = 196 mg ml−1), we again observed first, third and fourth order reflections, but with a smaller peak height (curve 2 in Fig. 2A). The same reflections were still faintly visible for even less dense fibers (ρ = 148 mg ml−1, curve 3). For the thinnest fibers with ρ = 11.6 mg ml−1 (curve 4) or fine clots (curve 5), the first order reflection was not visible at all, but we could still faintly discern the third and fourth order reflections. Qualitatively, these observations are consistent with prior SAXS measurements, where the first order reflection was clearly observed for fibrin networks composed of thick fibers,8,34,36,38,39,57,58 but not for networks of protofibrils formed at high ionic strength.58 The absence of the second order reflection from the SAXS spectra is also consistent with earlier SAXS studies,32,39 but the reason for the suppression of this peak is not clear.
3.2 Molecular origin of fibrin SAXS spectra
To understand the molecular origin of the Bragg peaks in the SAXS spectra of fibrin, we performed a structure-based theoretical reconstruction of SAXS spectra using a complete atomic model of the two-stranded fibrin protofibril with 10 fibrin monomers in one strand and 9 in the other complementary strand (abbreviated as FP10-9). First, we computed the theoretical SAXS spectra using the distribution of atomic pair distances p(r) for protofibril FP10-9 as described in Materials and methods (Fig. 3, curve 2). Here, the dashed vertical lines indicate the expected positions of the first, second, third and fourth order reflections of the half-staggered repeat distance. Consistent with the experimental data, the second order reflection was absent in the theoretical spectrum for FP10-9. Hence, the complete structural model of two-stranded fibrin protofibrils FP10-9 accounts for the suppression of the second order reflection observed in the SAXS experiments.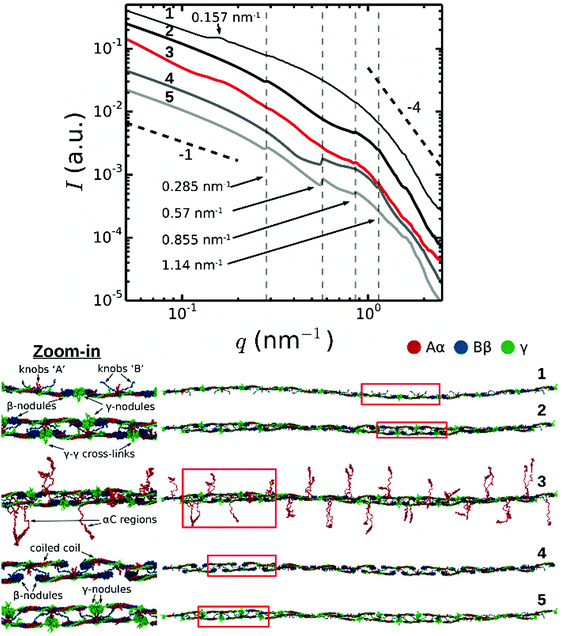 | ||
| Fig. 3 Theoretically reconstructed SAXS spectra (top) based on full atomic structural models of a fibrin protofibril and its variants (bottom). Numbers correspond to: (1) single-stranded fibrin polymer Fnm with m = 10 fibrin monomers connected longitudinally at the D:D interface; (2) twisted double-stranded protofibril without the αC regions; (3) same protofibril as in 2, but with αC regions (shown in red) incorporated in a random coil conformation; (4) same structure as in 2, but with the γ-nodules removed; (5) same structure as in 2, but with the β-nodules removed. The black dashed lines indicate a power law with exponent −1 for low q-numbers (expected for cylinders, see Fig. S3, ESI†) and −4 for high q-numbers (corresponding to the Porod regime). Red boxes in the structural models in the bottom indicate regions where we zoomed in (displayed on the left) to show more structural detail. | ||
Next, to understand the origin of the suppression of the second order reflection, we systematically modified the protofibril structure by removing selected structural elements, i.e. the αC regions (FP10-9/αC), γ-nodules (FP10-9/γ), and β-nodules (FP10-9/β), and recalculating the corresponding SAXS spectrum for each truncated construct. The results presented in Fig. 3 clearly demonstrate that the second order reflection is suppressed altogether in all SAXS spectra for fragment FP10-9 containing αC regions (curve 3) and without αC regions (curve 2). Nevertheless, the presence of αC regions does influence other reflections corresponding to the half-staggering distance, causing a reduced peak intensity and increased peak width. By contrast, with either all the γ-nodules removed (FP10-9/γ, curve 4) or β-nodules removed (FP10-9/β, curve 5) from the protofibril structure, the second order reflection appears.
Analysis of the symmetries of the protofibril structure reveals that the β-nodules are separated by ∼11.25 nm along the protofibril axis (see Fig. S4 in ESI†). This length corresponds to the second order reflection peak. This weaker signal (only β-nodules contribute) can interfere with the main signal, thus changing the height of the second order reflection peak. In the case of protofibrils made of full-length fibrin monomers, this interference is destructive and the second order peak is not visible (modelled curves 2 and 3). However, the removal of all γ-nodules from fibrin monomers weakens the first order peak and makes the periodicity associated with the distance between the β-nodules more pronounced, with a clear peak at the position of the second order reflection (modelled curve 4). The removal of all β-nodules from fibrin monomers destroys the negative interference and reveals the second order reflection peak in the modelled SAXS profile.
As an additional control, we calculated a SAXS spectrum for a hypothetical single-stranded fibrin oligomer, composed of a linear strand of 10 fibrin monomers connected end-to-end through the D:D self-association interface (Fig. 3; curve 1). In this case, a new peak appeared at q = 0.157 nm−1 corresponding to a typical distance of 40 nm between the centers of mass of the two symmetrical globular D regions. Each fibrin monomer is ∼45 nm long and has two globular ends of 6 nm each.13,44 In the single-stranded fibrin oligomer, fibrin monomers form a spiral and make a 25 degree angle with respect to the helical axis. As a result, the projected distance between the centers of mass of the two globular ends of the molecule is 40 nm (see Fig. S5, ESI†). This 0.157 nm−1 peak is suppressed for the double-stranded fibrin protofibrils. Hence, we conclude that the second order reflection is not present in the SAXS spectra of fibrin due to destructive interference from the symmetric structure of fibrin monomers. This resolves a long standing puzzle in the interpretation of X-ray scattering data from fibrin fibers.
3.3 Probing the radial packing of fibrin fibers with SAXS
In addition to the Bragg peaks discussed above, the q-dependence of the X-ray scattering patterns contains information on the radial (transverse) packing structure of fibrin fibers. However, this information is more difficult to infer from the spectra than the axial packing order because the radial packing is more disordered. To determine the q-range where the SAXS spectra are sensitive to the radial packing structure, we first consider the length scales covered by the SAXS spectra based on an analytical model proposed by Ferri and co-workers26,27,29 that treats the network as a collection of “blobs” of size ξblob with network fractal dimension Dm (see schematic in Fig. 4). Fibrin fibers have a persistence length of hundreds of micrometers,59,60 much larger than the typical distance between adjacent branch points. We therefore assume that each blob contains fiber segments that can be approximated by cylinders of a certain length (l) and diameter (d). In the absence of any internal packing structure, this model predicts three distinct scattering regimes as a function of q (black curve in Fig. 4). At small q, the spectrum should exhibit a peak at q = q1, which is related to the long-range network order.61 The position of this peak is inversely proportional to the average blob size26,27 according to q1 ≃ 4.4/ξblob. In the middle range, q1 < q < q2, the scattering intensity is determined by the fractal network structure within the blobs, i.e. I ∝ q−Dm. Finally, in the limit of large q > q2, the Porod regime is reached. In this regime, scattering occurs from the interface between the fibers and the solvent. Hence, the onset of the Porod regime is set by the fiber diameter26,27,39 according to q2 ≃ 2.2/d. In the case of smooth filaments that lack internal structure, the scattering intensity is expected to decay as a power law with q with an exponent αs = −4.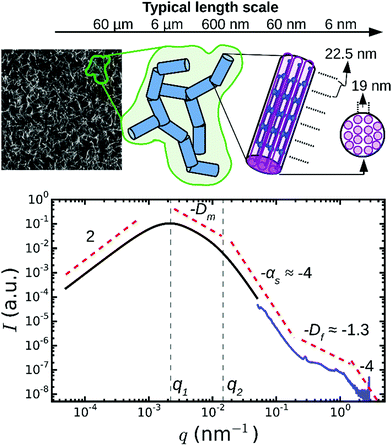 | ||
| Fig. 4 Model to distinguish between network and fiber structural features in light/X-ray scattering data. On large length scales (q < 10−1 nm−1), fibrin networks behave as a collection of blobs (shown in green in the schematic) of rigid fiber segments (blue). For fibers lacking any internal structure, this model predicts three q-regimes (black curve). Experimentally, SAXS curves (blue curve, for Np = 368/ρ = 255 mg ml−1) show additional fine structure at high q, which therefore provides information on the internal structure of the fibers. The model curve was calculated from the model of Ferri and co-workers,27,29 using as input a blob size ξblob = 10 μm, fiber segment length l = 0.5 μm, fiber diameter d = 0.2 μm, fractal dimension Dm = 1.3, and Porod exponent αs = 4. The two curves are shifted along the y-axis for clarity (note arbitrary units). The top-left image shows a typical confocal fluorescence image of a fibrin network (100 μm × 100 μm). | ||
When we compared this calculation with SAXS spectra measured for thick fibrin fibers (Np = 368, blue curve in Fig. 4), we saw that the low q-regime (q < 0.2 nm−1) of the SAXS spectrum corresponded to the Porod regime, where the scattering intensity decreased as I ∼ q−4. However, the high q-regime (q > 0.2 nm−1) of the spectra displayed features not predicted by the scattering model. It is this regime that carries information about the internal structure of the fibers, and that will be considered below. Note that for networks of very thin fibers, with Np = 2 (curve 5 in Fig. 2), we did not observe the Porod regime. Indeed, for these thin fibers the Porod regime should start only once q reaches ∼1 nm−1. In this case, the SAXS measurements can therefore not access the internal structure of the fibers, but they only access the q-regime where scattering is determined by the fractal structure of the network (I ∼ q−Dm). We found a value for the network fractal dimension Dm of around 1.5.
To infer the radial packing structure of the fibers from the high-q regime of the SAXS spectra, we need to assume a structural model for the cross-sectional packing. So far three different models have been proposed (Fig. 5A). The first model assumes that protofibrils are packed in an ordered lattice46 that should give rise to a Bragg peak at a q-vector corresponding to the average spacing between the protofibrils. Indeed, some measurements by SAXS,35,38 SANS,36 neutron diffraction57,62 and energy-dispersive X-ray diffraction34,38 revealed broad Bragg peaks, indicating partial disorder, but other SAXS studies found no evidence for lateral crystalline order.32 The second model instead assumes that the fibers are completely disordered assemblies of protofibrils (Fig. 5A), which should give rise to a power-law decay of the scattering intensity I ∝ q−Df with Df the fractal dimension of the fibers characterizing their radial mass distribution.63 Physically, this means that fibrin fibers would have a dense core and a loose periphery with sparsely arranged protofibrils. This model is supported by measurements of the fluorescence intensity64 and stiffness55 of fibrin fibers as a function of their diameter. The third model is essentially a hybrid of the other two models, because it considers the lateral packing as crystalline but with defects (Fig. 5A).39 This arrangement would result in a superposition of a fractal-like scattering pattern with broad peak(s) due to locally crystalline regions.
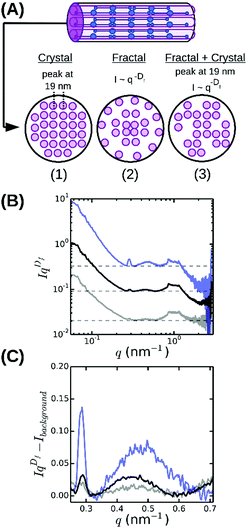 | ||
| Fig. 5 Radial (cross-sectional) packing structure of fibrin fibers. (A) Current models assume either (1) a crystalline array46 with a unit cell measuring 19 × 19 × 46 nm, or (2) a disordered structure64 characterized by a fractal dimension Df = 1.3 characterizing the internal mass distribution, or (3) a superposition of a crystalline and a fractal structure, with disorder stemming from missing protofibrils.39 (B) Rescaled SAXS spectra for fibrin networks with varying bundle size, obtained by multiplying SAXS spectra with qDf, reveal that fibrin fibers combine a fractal structure with partial radial order (broad peak at q ≈ 0.47 nm−1). (C) Magnified views of a small region of the rescaled spectra after subtraction of the background level (horizontal dashed lines in B). Spectra are shown for networks with ρ = 255 mg ml−1 (blue), 196 mg ml−1 (black) and 148 mg ml−1 (grey). Spectra in (A) and (B) were shifted along the y-axis for clarity. | ||
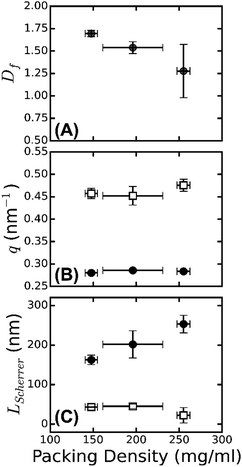
The spectrum shown in Fig. 4 is most consistent with the third model: we observe a superposition of an overall I ∼ q−Df power-law decay with an exponent Df close to −1.3 (indicated by the red dashed line between 0.2 and 1 nm−1) with a broad and weak superimposed bump centered around q = 0.47 nm−1. This was more visible when we multiplied the scattering intensities by qDf and adjust Df to make the resulting curves flat between q = 0.2 and 1 nm−1 (see Fig. 5B). The best-fit values for Df varied between 1.3 and 1.7 (Fig. 6A), consistent with prior measurements based on SAXS,39 fluorescence microscopy,64 and single-fiber stretching.55,65 As shown in Fig. 5C, the IqDf-curves nicely revealed the narrow Bragg peak at q = 0.29 nm−1 corresponding to the axial half-staggered packing order of fibrin, as well as a much broader peak centered around q = 0.47 nm−1. We observed the broader peak only for the thick fibers (Np = 291, 368, and 435) and not for the thinner fibers (Np = 2 and 47). Given the results obtained from the atomic molecular modeling in silico described above, it is unlikely that this peak is the second order peak originating from the axial packing. We therefore propose that it corresponds to lateral packing order, with a characteristic repeat distance between protofibrils of 13 nm. This spacing is in reasonable agreement with previous studies reporting repeat distances of ∼19 nm based on scattering methods or electron microscopy.14,34–38,57
As shown in Fig. 6B, the peak position from the axial packing order (solid circles) is constant, while the peak position from the radial order (open squares) shows a slight shift with the fiber mass density, from 0.45 nm−1 for ρ = 148 mg ml−1 to 0.47 nm−1 for ρ = 255 mg ml−1. The packing density of fibrin fibers thus varies with assembly conditions. This is even clearer from the turbidity data, which show that fibers of a similar radius can differ by an order of magnitude in protein mass density (Table S1, ESI†). This behavior is rather different from that of collagen fibers, which have a similar diameter as fibrin fibers and serve a similar biological function as an extracellular scaffold. Collagen has a much smaller and more constant lateral intermolecular Bragg spacing (∼4 nm66). This difference highlights the unique molecular structure of the fibrin monomer, which combines an ordered trinodular structure that directs longitudinal association with protruding long, flexible, unstructured αC-regions that mediate lateral interactions of protofibrils. By contrast, collagen monomers laterally associate by specific interactions of their rod-like triple helical domains, which only have short unstructured end regions (telopeptides, less than 5% of the overall molecular weight).67
The large width of the q = 0.47 nm−1 peak suggests that the radial ordering is only short-ranged. Indeed, the fiber diameter poses a strict upper limit on the range of order. In a perfectly crystalline system, the average crystal size can be approximately quantified by the Scherrer peak broadening, which sets the full width at half maximum of a Bragg's peak Δq, i.e. LScherrer = 2π/Δq.68 We used this expression to estimate the apparent crystal size as a function of fiber protein density from the width of the peak determined by Gaussian peak fits (Fig. S6, ESI†). As shown in Fig. 6C (open squares), LScherrer was ∼40 nm and independent of fiber density. This observation suggests that the extent of (crystalline) cross-sectional ordering is limited not by the fiber diameter, but rather by the intrinsic disorder. By dividing LScherrer for the radial distance, we find that the average number of protofibrils per domain, Navg = LScherrer/(2π/qmax) is 3 ± 0.2 for all the samples. The presence of intrinsic disorder is consistent with the existence of a fractal dimension, and also agrees with reported electron microscopy data.14 By contrast, the Scherrer length associated with the axial packing periodicity systematically increases with increasing fiber mass density (Fig. 6C, solid circles). This finding suggests that the axial ordering becomes more pronounced as the fibrin fibers become more densely packed.
4 Discussion
Here, we have investigated the internal packing structures of fibrin fibers by performing SAXS measurements on fibrin networks with structural variations induced by changing the fibrin assembly conditions. To interpret the results in terms of the molecular packing structure, we complemented the experimental SAXS measurements with the theoretical reconstruction of SAXS patterns performed using full atomic structural models of fibrin oligomers and protofibrils. The theory correctly predicted the number and positions of the Bragg peaks observed in the SAXS experiments, which validates our in silico molecular modeling approach.We have shown that the SAXS spectra of fibrin networks reveal both longitudinal and lateral (i.e. axial and radial) molecular packing within fibrin fibers. The axial packing gave rise to a sharp reflection at q = 0.285 nm−1 and several higher-order reflections (Bragg peaks) indicative of long-range 22.5 nm packing periodicity of fibrin. This periodicity corresponds with findings in a number of X-ray and neutron scattering experiments35,36,38,57,62,74 as well as electron microscopy14,23 and atomic force microscopy15,16 of individual fibrin fibers. Our work advances this well known structural characteristic of fibrin assembly and structure by revealing that the axial packing in fibrin fibers is sensitive to the fiber protein density. In particular, these axial reflections are only seen when the fibers are thick enough, i.e., the number of protofibrils per cross-section, Np, is larger than ∼40. Moreover, the denser the fiber is, the more intense and narrow the first order Bragg peak. Strikingly, the second order reflection of the axial packing order is missing in all fibrin samples tested. With the help of full-atom modeling of fibrin protofibrils (Fig. 3), we were able to determine that the origin of this phenomenon is the symmetry arising as a result of the spacing of the γ- and β-nodules. Indeed, the second order reflection shows up in the calculated SAXS spectra only after either all the γ- or all the β-nodules are computationally removed from the fibrin molecules forming protofibrils. Accordingly, the appearance of the second order reflection could serve as a signature of potential unfolding transitions in fibrin networks under tensile mechanical stress, given that prior simulation studies uncovered forced unfolding of the γ-nodules.17,18 Furthermore, molecular modeling in silico shows that the disordered αC regions emanating from the protofibrils broaden the Bragg peaks.
We observed a systematic increase of the apparent axial packing order with increasing mass density of the fibers. A possible explanation is that the densest fibrin fibers in our study were prepared from gel-filtered fibrinogen (see Materials and methods) containing non-aggregated monomeric fibrinogen molecules of uniform molecular length. In support of this explanation, the presence of fibrinogen aggregates in the clotting mixture has been shown to alter the kinetics of polymerization, impair the assembly of monomers into protofibrils and fibers42 and reduce the protein density of fiber fibers and lessen coherency of the 22.5 nm axial packing.69 Another possible source of variability in the fibrin fiber packing and their structural arrangement is that the presence of the fibrinogen γ′ chain splicing variant in plasma and plasma-derived fibrinogen preparations affects the number of protofibrils and protein density within fibers.70
Whether protofibrils within a fibrin fiber are ordered or disordered in the direction transverse to the fiber axis has been a matter of debate. Our results show that fibrin fibers are partially ordered with elements of a fractal structure, giving rise to a power-law decay of the scattering intensity with q, and of a crystalline-like structure, with a broad superimposed peak centered around q = 0.47 nm−1. The peak position reveals a 13 nm repeat distance between protofibrils, close to values reported elsewhere.14,34,36–38,57 We found that the fractal dimension of the fibers is on the order of Df = 1.5, well within the range of other reported fractal dimensions for fibrin obtained by atomic force microscopy and SAXS.39,55,64 However, we find that the fractal dimension is dependent on the fiber mass density. To the best of our knowledge, no one has looked at the fractal dimension of the fibrin fiber with systematic changes in the packing densities experimentally. However, an increase of fractal dimension with increasing protein density can be expected based on the model presented by Yeromonahos et al.39 In this model, the lateral packing of a fibrin fiber is effectively fractal because not all the crystalline positions are used by protofibrils (Fig. 5A). In the context of this model, an increase in fiber protein density means physically that more empty spaces in the crystal structure are filled by protofibrils, bringing the overall structure closer to a homogeneous packing with a limiting Df value of 2.
The major in vivo manifestation of fibrin is in clots and thrombi. Fibrin is the main structural component of arterial thrombi and is nearly as prevalent in venous thrombi.71 Recent SAXS data on clots formed from human plasma35 revealed a close correspondence between the fibrin structure formed from purified fibrin and from human plasma. Specifically, both systems show the same axial packing order with a periodicity of 22.5 nm and a suppression of the second order Bragg peak, and they also show similar radial packing order characterized by a broad equatorial diffraction. The equatorial spacing was ≈19 nm for the human plasma clots, somewhat larger than the 13 nm spacing we find for reconstituted fibrin, suggesting a difference in packing density. This difference could be due to differences in buffer conditions and plasma proteins such as albumin, fibrinogen and thrombin concentrations, or to the presence of many covalently and non-covalently fibrin-attached proteins present in plasma and not in our model system.72,73 We conclude that our findings are indeed relevant to in vivo blood clots.
5 Conclusions
To obtain insight into the structural hierarchy of fibrin clots, we have performed SAXS measurements on fibrin networks composed of fibers with varying thickness and internal protein mass density in combination with computational molecular modeling of fibrin oligomers and protofibrils. We carried out the first systematic study of the effects of axial and lateral packing on the scattering patterns by varying the fiber protein density from 3.4 mg ml−1 up to 250 mg ml−1. We show that the Bragg peaks corresponding to axial order are much more pronounced for denser fibers and that the peak width also depends on the fiber protein density. Furthermore, we show, for the first time, that the axially symmetric molecular packing structure of fibrin can explain the suppression of the second order reflection of the 22 nm axial repeat observed here as well as in previous publications.When we artificially perturb the symmetry by computational removal of the γ- or β-nodules, the second order peak appears. An interesting prediction from this study is that SAXS could be used to probe whether the γ-nodules in fibrin monomers unfold upon fibrin network deformation, since unfolding should result in the appearance of the second order peak. Moreover, we demonstrate that fibrin fibers have a partially ordered lateral packing with a characteristic repeat distance of 13 nm, independent of the fiber thickness or the number of protofibrils per fiber cross-section. Taken together, our findings demonstrate that SAXS in combination with computational molecular modeling provides a powerful method to extract structural information at different spatial scales. In the future, this approach may be used to explore the force response of fibrin networks to external mechanical factors and to probe how mutations, polymorphisms, and posttranslational modifications of fibrinogen impact fibrin network structure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Baldomero Alonso Latorre (AMOLF) for help with SAXS data analysis, and Federica Burla (AMOLF) and Fabio Ferri (Università dell'Insubria) for help with analysis of the turbidimetry data. This work was part of the research program of the Foundation for Fundamental Research on Matter (FOM), which is financially supported by the Netherlands Organization for Scientific Research (NWO). We gratefully acknowledge access to the DUBBLE BM26B beamline at the ESRF made possible by NWO. WB's contribution is based upon work supported by Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U.S. Department of Energy. NK was supported by a Marie Curie IIF fellowship and a grant from the European Research Council (851960). This work was further supported by the American Heart Association grants 15GRNT23150000 and 13GRNT16960013, NIH grants HL135254 and UO1-HL116330, the University of Pennsylvania Perelman School of Medicine Bridge Funding, the NSF grants DMR 1505662 and DMR 1505316, and the Program for Competitive Growth at Kazan Federal University.Notes and references
- M. Pieters and A. S. Wolberg, Res. Pract. Thromb. Haemostasis, 2019, 3, 161–172 CrossRef PubMed.
- O. V. Kim, R. I. Litvinov, J. Chen, D. Z. Chen, J. W. Weisel and M. S. Alber, Matrix Biol., 2017, 60–61, 141–156 CrossRef CAS PubMed.
- R. I. Litvinov and J. W. Weisel, Matrix Biol., 2017, 60–61, 110–123 CrossRef CAS PubMed.
- W. Voter, C. Lucaveche, A. Blaurock and H. Erickson, Biopolymers, 1986, 25, 2359–2373 CrossRef CAS PubMed.
- W. E. Fowler, R. R. Hantgan, J. Hermans and H. P. Erickson, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 4872–4876 CrossRef CAS PubMed.
- W. Liu, L. Jawerth, E. Sparks, M. Falvo, R. Hantgan, R. Superfine, S. Lord and M. Guthold, Science, 2006, 313, 634–638 CrossRef CAS PubMed.
- C. C. Helms, R. A. Ariens, S. Uitte de Willige, K. F. Standeven and M. Guthold, Biophys. J., 2012, 102, 168–175 CrossRef CAS.
- A. Brown, R. Litvinov, D. Discher, P. Purohit and J. Weisel, Science, 2009, 325, 741–744 CrossRef CAS PubMed.
- I. Piechocka, R. Bacabac, M. Potters, F. MacKintosh and G. Koenderink, Biophys. J., 2010, 98, 2281–2289 CrossRef CAS PubMed.
- N. A. Kurniawan, B. E. Vos, A. Biebricher, G. J. Wuite, E. J. Peterman and G. H. Koenderink, Biophys. J., 2016, 111, 1026–1034 CrossRef CAS PubMed.
- C. Longstaff and K. Kolev, J. Thromb. Haemostasis, 2015, 13(suppl. 1), S98–S105 CrossRef CAS PubMed.
- B. E. Bannish, I. N. Chernysh, J. P. Keener, A. L. Fogelson and J. W. Weisel, Sci. Rep., 2017, 7, 6914 CrossRef PubMed.
- J. M. Kollman, L. Pandi, M. R. Sawaya, M. Riley and R. F. Doolittle, Biochemistry, 2009, 48, 3877–3886 CrossRef CAS PubMed.
- J. Weisel, Biophys. J., 1986, 50, 1079–1093 CrossRef CAS PubMed.
- I. S. Yermolenko, V. K. Lishko, T. P. Ugarova and S. N. Magonov, Biomacromolecules, 2011, 12, 370–379 CrossRef CAS PubMed.
- A. D. Protopopova, N. A. Barinov, E. G. Zavyalova, A. M. Kopylov, V. I. Sergienko and D. V. Klinov, J. Thromb. Haemostasis, 2015, 13, 570–579 CrossRef CAS PubMed.
- A. Zhmurov, A. E. Brown, R. I. Litvinov, R. I. Dima, J. W. Weisel and V. Barsegov, Structure, 2011, 19, 1615–1624 CrossRef CAS PubMed.
- A. Zhmurov, O. Kononova, R. I. Litvinov, R. I. Dima, V. Barsegov and J. W. Weisel, J. Am. Chem. Soc., 2012, 134, 20396–20402 CrossRef CAS PubMed.
- Y. F. Zuev, R. I. Litvinov, A. E. Sitnitsky, B. Z. Idiyatullin, D. R. Bakirova, D. K. Galanakis, A. Zhmurov, V. Barsegov and J. W. Weisel, J. Phys. Chem. B, 2017, 121, 7833–7843 CrossRef CAS PubMed.
- S. Kohler, F. Schmid and G. Settanni, Langmuir, 2015, 31, 13180–13190 CrossRef PubMed.
- S. Kohler, F. Schmid and G. Settanni, PLoS Comput. Biol., 2015, 11, e1004346 CrossRef PubMed.
- A. Zhmurov, A. D. Protopopova, R. I. Litvinov, P. Zhukov, J. W. Weisel and V. Barsegov, Structure, 2018, 26, 857–868 CrossRef CAS PubMed.
- R. Hantgan, W. Fowler, H. Erickson and J. Hermans, Thromb. Haemostasis, 1980, 44, 119–124 CrossRef CAS.
- I. N. Chernysh, C. Nagaswami and J. W. Weisel, Blood, 2011, 117, 4609–4614 CrossRef CAS PubMed.
- A. Zhmurov, A. D. Protopopova, R. I. Litvinov, P. Zhukov, A. R. Mukhitov, J. W. Weisel and V. Barsegov, Structure, 2016, 24, 1907–1917 CrossRef CAS PubMed.
- F. Ferri, M. Greco, G. Arcovito, F. A. Bassi, M. De Spirito, E. Paganini and M. Rocco, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031401 CrossRef CAS PubMed.
- F. Ferri, M. Greco, G. Arcovito, M. DeSpirito and M. Rocco, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011913 CrossRef PubMed.
- F. Ferri, G. R. Calegari, M. Molteni, B. Cardinali, D. Magatti and M. Rocco, Macromolecules, 2015, 48, 5423–5432 CrossRef CAS.
- D. Magatti, M. Molteni, B. Cardinali, M. Rocco and F. Ferri, Biophys. J., 2013, 104, 1151–1159 CrossRef CAS PubMed.
- A. Takahashi, R. Kita, T. Shinozaki, K. Kubota and M. Kaibara, Colloid Polym. Sci., 2003, 281, 832–838 CrossRef CAS.
- E. A. Ryan, L. F. Mockros, J. W. Weisel and L. Lorand, Biophys. J., 1999, 77, 2813–2826 CrossRef CAS PubMed.
- L. Stryer, C. Cohen and R. Langridge, Nature, 1963, 197, 793–794 CrossRef CAS PubMed.
- F. J. Roska, J. D. Ferry, J. S. Lin and J. W. Anderegg, Biopolymers, 1982, 21, 1833–1845 CrossRef CAS PubMed.
- G. Caracciolo, M. DeSpirito, A. Castellano, D. Pozzi, G. Amiconi, A. DePascalis, R. Caminiti and G. Arcovito, Thromb. Haemostasis, 2003, 89, 632–636 CrossRef CAS.
- G. Portale and J. Torbet, Nanoscale, 2018, 10, 10063–10072 RSC.
- J. Torbet, J. Freyssinet and G. Hudry-Clergeon, Nature, 1981, 289, 91–93 CrossRef CAS.
- C. Longstaff, I. Varjú, P. Sótonyi, L. Szabó, M. Krumrey, A. Hoell, A. Bóta, Z. Varga, E. Komorowicz and K. Kolev, J. Biol. Chem., 2013, 288, 6946–6956 CrossRef CAS.
- M. Missori, M. Papi, G. Maulucci, G. Arcovito, G. Boumis, A. Bellelli, G. Amiconi and M. DSpirito, Eur. Biophys. J., 2010, 39, 1001–1006 CrossRef CAS.
- C. Yeromonahos, B. Polack and F. Caton, Biophys. J., 2010, 99, 2018–2027 CrossRef CAS.
- I. K. Piechocka, K. A. Jansen, C. P. Broedersz, N. A. Kurniawan, F. C. MacKintosh and G. H. Koenderink, Soft Matter, 2016, 12, 2145–2156 RSC.
- M. D. Bale and J. D. Ferry, Thromb. Res., 1988, 52, 565–572 CrossRef CAS.
- L. Huang and S. T. Lord, Thromb. Res., 2013, 131, e258–e263 CrossRef CAS PubMed.
- M. Carr and J. Hermans, Macromolecules, 1978, 11, 46–50 CrossRef CAS PubMed.
- W. Bras, I. P. Dolbnya, D. Detollenaere, R. VanTol, M. Malfois, G. N. Greaves, A. J. Ryan and E. Heeley, J. Appl. Crystallogr., 2003, 36, 791–794 CrossRef CAS.
- C. E. Hall and H. S. Slayter, J. Biophys. Biochem. Cytol., 1959, 5, 11–16 CrossRef CAS PubMed.
- Z. Yang, I. Mochalkin and R. Doolittle, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 14156–14161 CrossRef CAS PubMed.
- R. I. Litvinov, O. V. Gorkun, S. F. Owen, H. Shuman and J. W. Weisel, Blood, 2005, 106, 2944–2951 CrossRef CAS PubMed.
- J. W. Weisel and L. Medved, Ann. N. Y. Acad. Sci., 2001, 936, 312–327 CrossRef CAS PubMed.
- J. W. Weisel, C. Nagaswami and L. Makowski, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 8991–8995 CrossRef CAS PubMed.
- S. J. Everse, G. Spraggon, L. Veerapandian and R. F. Doolittle, Biochemistry, 1999, 38, 2941–2946 CrossRef CAS PubMed.
- W. Kabsch, Acta Crystallogr., 1976, 32, 922–923 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14(33–38), 27–38 Search PubMed.
- P. Debye, Ann. Phys., 1915, 351, 809–823 CrossRef.
- D. K. Putnam, E. W. Lowe, Jr. and J. Meiler, Comput. Struct. Biotechnol. J., 2013, 8, e201308006 CrossRef PubMed.
- W. Li, J. Sigley, S. R. Baker, C. C. Helms, M. T. Kinney, M. Pieters, P. H. Brubaker, R. Cubcciotti and M. Guthold, BioMed Res. Int., 2017, 2017, 6385628 Search PubMed.
- N. A. Kurniawan, T. H. S. van Kempen, S. Sonneveld, T. T. Rosalina, B. E. Vos, K. A. Jansen, G. W. M. Peters, F. N. van de Vosse and G. H. Koenderink, Langmuir, 2017, 33, 6342–6352 CrossRef CAS PubMed.
- J. Freyssinet, J. Torbet, G. Hudry-Clergeon and G. Maret, Proc. Natl. Acad. Sci. U. S. A., 1983, 80, 1616–1620 CrossRef CAS PubMed.
- M. Müller, J. Ferry and J. Lin, Biopolymers, 1989, 28, 1011–1018 CrossRef PubMed.
- I. Piechocka, R. Bacabac, M. Potters, F. C. Mackintosh and G. Koenderink, Biophys J., 2010, 98(10), 2281–2289 CrossRef CAS PubMed.
- I. Piechocka, K. Jansen, C. P. Broedersz, N. A. Kurniawan, F. C. MacKintosh and G. Koenderink, Soft Matter, 2016, 12, 2145–2156 RSC.
- A. E. Gonzalez and G. Ramirez-Santiago, Phys. Rev. Lett., 1995, 74, 1238–1241 CrossRef CAS PubMed.
- K. Weigandt, D. Pozzo and L. Porcar, Soft Matter, 2009, 5, 4321–4330 RSC.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- M. Guthold, W. Liu, B. Stephens, S. Lord, R. Hantgan, D. Erie, R. Taylor and R. Superfine, Biophys. J., 2004, 87, 4226–4236 CrossRef CAS PubMed.
- W. Li, J. Sigley, M. Pieters, C. C. Helms, C. Nagaswami, J. W. Weisel and M. Guthold, Biophys. J., 2016, 110, 1400–1410 CrossRef CAS PubMed.
- D. J. Hulmes, T. J. Wess, D. J. Prockop and P. Fratzl, Biophys. J., 1995, 68, 1661–1670 CrossRef CAS PubMed.
- J. P. Orgel, T. C. Irving, A. Miller and T. J. Wess, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9001–9005 CrossRef CAS PubMed.
- L. Alexander, X-ray diffraction methods in polymer science, Wiley-Interscience, New York, 1969 Search PubMed.
- X. Garcia, L. Seyve, Z. Tellier, G. Chevreux, N. Bihoreau, B. Polack and F. Caton, Biophys. J., 2019, 118(1), 172–181 CrossRef PubMed.
- M. M. Domingues, F. L. Macrae, C. Duval, H. R. McPherson, K. I. Bridge, R. A. Ajjan, V. C. Ridger, S. D. Connell, H. Philippou and R. A. Ariens, Blood, 2016, 127, 487–495 CrossRef CAS PubMed.
- I. N. Chernysh, C. Nagaswami, S. Kosolapova, A. D. Peshkova, A. Cuker, D. B. Cines, C. L. Cambor, R. I. Litvinov and J. W. Weisel, Sci. Rep., 2020, 10, 5112 CrossRef CAS PubMed.
- S. Talens, F. W. Leebeek, J. A. Demmers and D. C. Rijken, PLoS One, 2012, 7, e41966 CrossRef CAS PubMed.
- J. W. Weisel and R. I. Litvinov, Subcell. Biochem., 2017, 82, 405–456 CrossRef CAS PubMed.
- B. E. Vos, C. Martinez-Torres, F. Burla, J. W. Weisel and G. H. Koenderink, Acta Biomater., 2020, 104, 39–52 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00916d |
| ‡ K. A. Jansen and A. Zhmurov contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |