Prediction on the origin of selectivities of NHC-catalyzed asymmetric dearomatization (CADA) reactions†
Yang
Wang
 a,
Qiu-Yu
Wu
a,
Tian-Hua
Lai
a,
Kai-Jun
Zheng
a,
Ling-Bo
Qu
*b and
Donghui
Wei
a,
Qiu-Yu
Wu
a,
Tian-Hua
Lai
a,
Kai-Jun
Zheng
a,
Ling-Bo
Qu
*b and
Donghui
Wei
 *b
*b
aDepartment of Material and Chemical Engineering, Zhengzhou University of Light Industry, Zhengzhou, Henan Province 450002, P.R. China
bCollege of Chemistry and Molecular Engineering, Center of Computational Chemistry, Zhengzhou University, Zhengzhou, Henan Province 450001, P.R. China. E-mail: qulingbo@zzu.edu.cn; donghuiwei@zzu.edu.cn
First published on 14th December 2018
Abstract
Prediction of the regioselectivities (i.e., the active sites) of dearomatization reactions has been and continues to be one of the most challenging issues in the modern synthesis field. In this work, we provide a valuable case for predicting the origin of the chemoselectivity for organocatalyst-catalyzed asymmetric dearomatization (CADA) reactions. Herein, the possible mechanisms and the origin of selectivities of NHC-catalyzed asymmetric dearomatization reaction of isoquinoline have been systematically investigated using density functional theory (DFT) for the first time. Computational results show that the intermolecular Mannich-type transformation was both the stereoselectivity- and chemoselectivity-determining step. The NCI analysis reveals that C–H⋯Br and π⋯π interactions contribute significantly to the control of the stereoselectivity. Furthermore, the origin of regioselectivities on NHC-catalyzed asymmetric dearomatization reactions of other aromatic rings has been accurately predicted by performing the local reactivity index analysis. This work would provide valuable clues for predicting the origin of the selectivities and designing more effective organocatalysts for these kinds of reactions with high and special selectivities.
Introduction
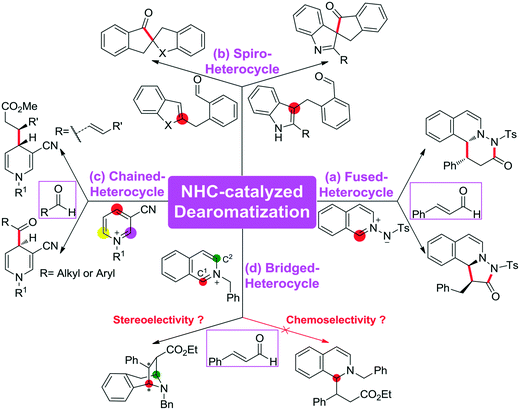
The C–C bond is one of the most fundamental bonds involved in organic compounds. The catalytic enantioselective construction of C–C bonds is one of the hottest topics in organic chemistry to rapidly access stereoenriched skeletons. In particular, catalytic asymmetric dearomatization (CADA) reactions are important transformations of aromatic compounds leading to a variety of ring systems through C–C bond construction. Recently, the CADA reactions, which have emerged as powerful organic transformation for the construction of complex molecules from the wide availability of cheap and versatile aromatic compounds, have gained increasing attention.1 During the dearomatization reaction, the formation of quaternary carbon centers would facilitate the construction of three-dimensional spiro or bridged heterocyclic compounds.2 Despite the high potential of this strategy, the main challenge of such an approach is the low reactivity of substrates and the difficult control of the chemo-, regio-, and stereoselectivities in the formation of the desired products.For the CADA reactions, transition-metal catalytic strategies have been extensively applied for highly stereoselective dearomatization of aromatic compounds,3 while the utilization of organocatalytic approaches remains underdeveloped. Recently, the use of organocatalysis has opened up various kinds of new and exciting opportunities for providing different reactive modes. Pioneered by MacMillan, Jørgensen, and Jacobsen, the dearomatization reaction of (iso)quinolines, indoles, and pyridines catalyzed by organocatalysts has already attracted considerable attention in experiment.4 Noteworthily, N-heterocyclic carbene (NHC), which has an increasing number of applications as a nucleophilic organocatalyst to access an impressive set of reactions,5 such as the annulation reaction,6 cross-coupling reaction,7 and Stetter reaction8 as well as the C–X (X = C, F, Br, H, etc.) bond activation reaction,9 was widely employed to promote the CADA reactions of (hetero)aromatic compounds to construct various types of heterocycles.
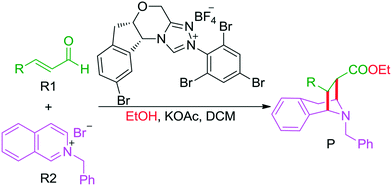
Scheme 1 summarizes some of the recently reported examples of NHC-catalyzed CADA reactions of (hetero)aromatic compounds. Glorius and co-workers reported that the dearomatization reaction of aromatic azomethine imines can be achieved for the construction of fused-heterocycles (Scheme 1a).10 Later on, Glorius11 and Studer12 developed the intramolecular dearomatization of benzofurans/benzothiophenes by hydroacylation and of indoles by oxidative NHC catalysis to afford spiro-heterocycles (Scheme 1b). In 2017, Rovis13 and Massi14 groups independently described the enantio- and diastereoselective addition of enals to N-alkylpyridinium salts to generate chained 1,4-dihydropyridines (DHPs) with good regioselectivity under NHC catalysis (Scheme 1c). Furthermore, Tan and co-workers reported an example of an NHC organocatalytic route for the construction of a bridged tropane framework with special chemoselectivity and high stereoselectivity through the CADA reaction (Scheme 1d),15 in which the isoquinoline provided two reactive sites for a double Mannich-type transformation. In these reactions, one can find that the regioselective sites (i.e., the ortho- or para-position of the aromatic ring) would participate in those CADA reactions, thus it should be important to identify and predict the potential active sites of the aromatic rings in theory for rational design. To the best of our knowledge, computational investigation on the detailed mechanism and origin of selectivities of NHC-catalyzed dearomatization reactions has remained hitherto unreported.
To shed light on the general mechanism and predict the origin of the selectivities of these kinds of reactions, we selected Tan's experimental work15 as a computational model (Scheme 1d) to perform a theoretical investigation, and we aimed to pursue the exact pictures of the reaction mechanism and disclose the origin of selectivities. This computational work would provide valuable clues for the rational design of the organocatalytic CADA reactions with controllable chemoselectivities and excellent stereoselectivities. The density functional theory (DFT) method, which has become one of the most powerful and efficient tools for clarifying the reaction mechanism and predicting the selectivities in NHC catalyzed reactions16,17 as well as other asymmetric reactions,18 was employed to perform the theoretical simulations.
Results and discussion
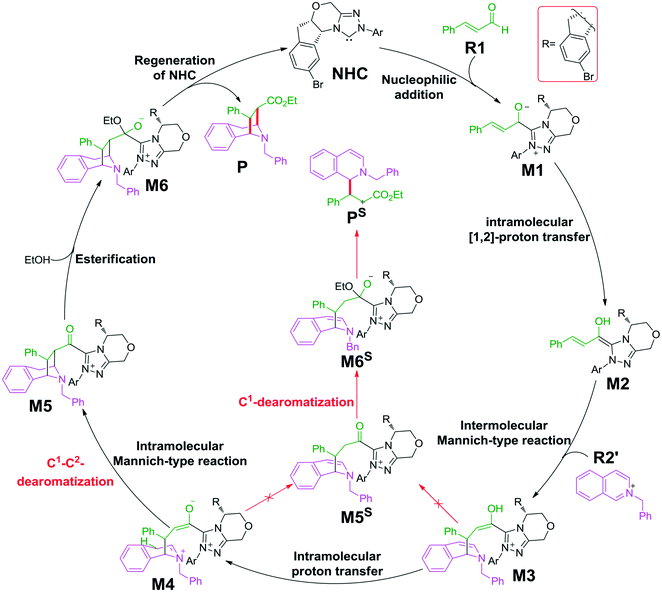
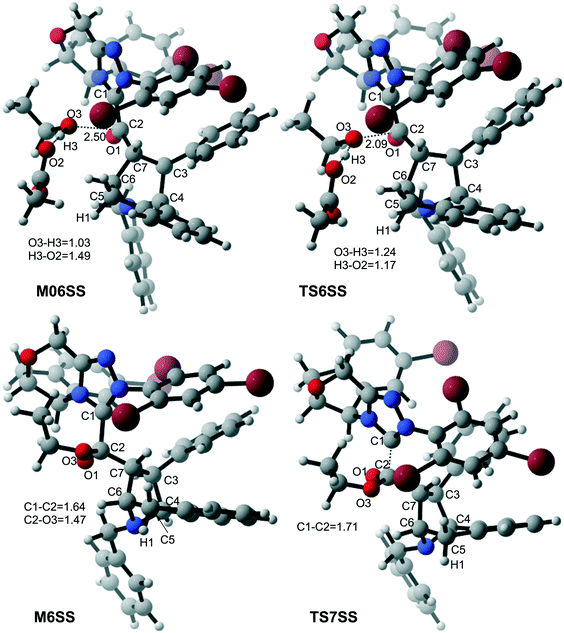
As shown in Scheme 2, the possible catalytic pathways for the NHC-catalyzed CADA reaction of isoquinoline, including C1–C2-dearomatization and C1-dearomatization pathways, have been suggested. The C1–C2-dearomatization pathway mainly contains three stages, i.e., formation of the Breslow intermediate (stage 1), Mannich-type transformations (stage 2), and regeneration of NHC (stage 3). Alternatively, the C1-dearomatization reaction may proceed via another active intermediate M5S, in which the α-carbon is protonated from intermediate M3 or M4.Reaction mechanism of C1–C2-dearomatization
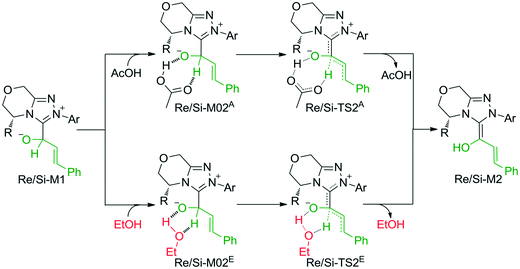
The second step is the [1,2]-proton transfer to give the well-known Breslow intermediate M2. The traditional direct proton transfer mechanism is difficult to occur under mild experimental conditions because the proton transfer process associated with a three-membered ring transition state requires an extremely high energy (Fig. S1 of the ESI†), which has been reported by various computational studies.19 Thus, the protic media-assisted proton transfer mechanism should be invoked to lower the energy barrier of the proton transfer process. Based on the details of Tan's experiment,15 ethanol (EtOH) is included in the reaction conditions, which should be viewed as a proton transfer medium. Moreover, the additive base NaOAc would be transformed to its conjugate acid AcOH by means of deprotonation of the triazolium salt, and the AcOH can also work as a protic medium to assist the proton transfer. As shown in Scheme 3, two possible protic media-assisted proton transfer pathways have been suggested for the formation of the Breslow intermediate, i.e., AcOH-assisted and EtOH-assisted proton transfer pathways.
As depicted in Fig. 1, the energy barriers of AcOH-assisted proton transfer pathways are 12.4/14.7 kcal mol−1, respectively, and those of EtOH-assisted proton transfer processes are 35.6/33.9 kcal mol−1, which are much lower than those of the direct proton transfer pathways (ΔG≠ = 55.6/58.1 kcal mol−1, Fig. S1 of the ESI†). Comparing the three proton transfer pathways, the high energy barrier involved in the direct proton transfer pathway is mainly due to the large strain of the three-membered ring structure of the transition state. Meanwhile for the media-assisted proton transfer pathways, the energy barrier of the AcOH-assisted proton transfer pathway (12.4/14.7 kcal mol−1, Fig. 1) is obviously lower than that of the EtOH-assisted proton transfer pathway (35.6/33.9 kcal mol−1, Fig. 1), since the acidity of AcOH (pKa = 5.0) is much stronger than that of EtOH (pKa = 16.0). Moreover, the reaction pathway associated with the Re face addition (Re-TS1 → Re-M1 → Re-TS2A → Re-M2) is calculated to be more energetically favorable than that associated with the Si face addition (Si-TS1 → Si-M1 → Si-TS2A → Si-M2). Thus, it is reasonable to exclude the Si face addition pathway in the following sections.
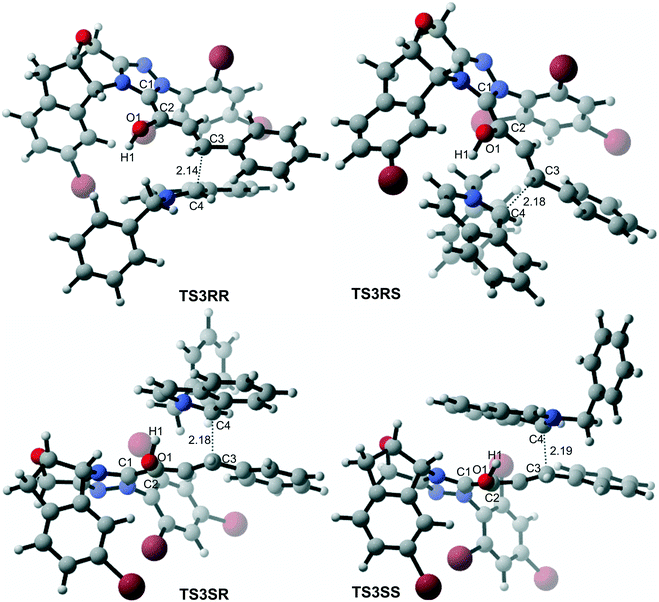
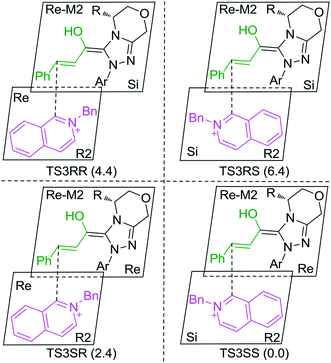
In the intermolecular Mannich-type transformation, two continuous chiral centers are formed in intermediate M3via transition state TS3. During the formation of C–C bonds, reactant R2′ can attack on either the Re or Si face of Re-M2 by Re or Si face addition to give four diastereoselective intermediates M3RR/RS/SR/SS through transition states TS3RR/RS/SR/SS, respectively. As an important note, the first letter after TS3 represents the chirality of the C3 atom, and the second letter represents the chirality of the C4 atom (Fig. 2). The energy barriers viaTS3RR/RS/SR/SS, as depicted in Fig. 3, are 13.9, 15.9, 11.9, and 9.5 kcal mol−1, respectively. From Fig. 3, one can conclude that the reaction pathway associated with SS-configuration is more energetically favorable than the other three pathways, thus, we only take the SS-configurational pathway as reference for discussion in the following sections.
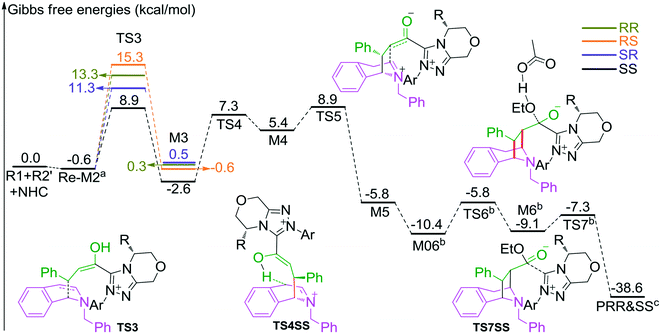 | ||
| Fig. 3 The most energetically favorable pathway involved in stages 2 and 3 of the NHC-catalyzed asymmetric dearomatization reaction of isoquinolines (the superscripts “a”, “b”, and “c” represent addition of the free energies of R2′, AcO−–EtOH, and NHC, respectively. The whole energy profile is provided in Fig. S2 of the ESI†). | ||
The next step is the proton transfer process for the formation of intermediate M4via transition state TS4. The energy barrier of this step is only 9.9 kcal mol−1 (Fig. 3), indicating that this step can occur smoothly under experimental conditions.
Subsequently, the intramolecular Mannich-type transformation occurs via transition state TS5 for the formation of intermediate M5. The energy barrier of this step is only 3.5 kcal mol−1 (Fig. 3), showing that this step is also a facile process.
With the aid of AcO−, the oxygen atom of ethanol nucleophilically attacks on the carbonyl carbon atom, which is coupled with the abstraction of the hydrogen atom of ethanol by the oxygen atom of AcO− to afford the ester M6 (Fig. 4). The energy barrier of this step is 4.6 kcal mol−1 (Fig. 3), which can be easily overcome under the experimental conditions. The last step of this reaction is the dissociation of the catalyst with the final product via transition state TS7, and the energy barrier of this step is only 1.8 kcal mol−1 (Fig. 3), implying that the NHC catalyst can easily regenerate.
Chemoselective C1-dearomatization
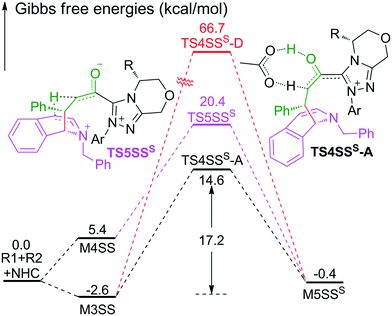
As shown in Scheme 2, the intermediate M3 can undergo an alternative type of dearomatization reaction to give intermediate M5S, in which the protonation of the α-carbon of R1 is involved. Moreover, the intermediate M4 can also transform to M5S. This is because the main catalytic reaction and the C1-dearomatization share the same formation process of M3 or M4 and diverge afterward. On the other hand, the SS-configurational pathway has been revealed to be the most energy favorable. Thus, we only studied the process of C1-dearomatization following from M3 or M4 associated with the SS-configurational pathway. During the protonation of the α-carbon, the direct proton transfer pathway associated with four-membered ring transition state TS4SSS-D requires an energy barrier of 69.3 kcal mol−1 (Fig. 5), which is too high for the pathway to occur under the experimental conditions. Meanwhile the energy barrier of the AcOH-assisted proton transfer pathway associated with transition state TS4SSS-A is 17.2 kcal mol−1 (Fig. 5). In addition, the energy barrier viaTS5SSS is 20.4 kcal mol−1 (Fig. 5). Obviously, the AcOH-assisted proton transfer pathway is the most energy favorable for the formation of intermediate M5SSS (ΔG = −0.4 kcal mol−1, Fig. 5). Compared with the reaction pathways associated with TS5SS and TS4SSS-A, the C1–C2-dearomatization reaction pathway viaTS5SS (ΔG≠ = 11.5 kcal mol−1, Fig. 3) is more energy favorable than the C1-dearomatization reaction pathway associated with TS4SSS-A (ΔG≠ = 17.2 kcal mol−1, Fig. 5), and the intermediate M5SS (ΔG = −5.8 kcal mol−1, Fig. 3) is more stable than M5SSS (ΔG = −0.4 kcal mol−1, Fig. 5). Thus, it is unnecessary to further explore the subsequent process involved in the C1-dearomatization.Origin of stereoselectivity
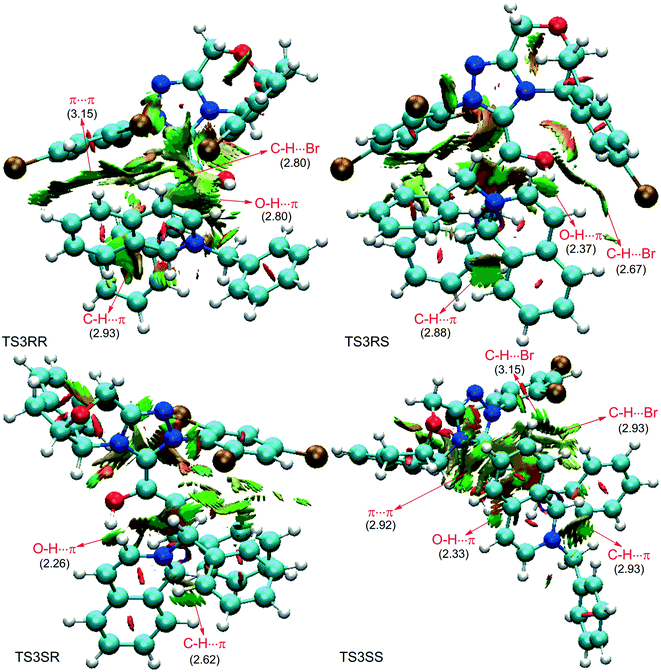
As discussed above, the intermolecular Mannich-type transformation was calculated to be the stereoselectivity-determining step, which was further confirmed by the benchmark calculations (more details are provided in Table S1 of the ESI†). The addition to different prochiral faces of Re-M2 by different faces of R2′ will lead to four diastereomeric intermediates, and concurrently, the chiralities of C3 and C4 atoms appear during the C3–C4 bond formation process. As shown in Scheme 4, the addition of the Re face of R2′ to the Re or Si face of Re-M2 results in the formation of M3SR and M3RRvia transition states TS3SR and TS3RR, respectively. Correspondingly, the addition of the Si face of R2′ to the Re or Si face of Re-M2 leads to the formation of M3SS and M3RS associated with transition states TS3SS and TS3RS, separately. The computational results show that the addition of the Re-face of Re-M2 to the Si-face of the R2′ is the most preferred mode for C–C bond formation. Moreover, the Re–Si transition state TS3SS is the most energetically favorable, and its energy barrier is 4.4 kcal mol−1 lower than that via the Si–Re transition state TS3RR. Based on the Boltzmann distribution analysis, this value corresponds to an enantiomeric excess of 99.9%, which aligns well with the experimentally reported ee value of 93%.17Having identified the most preferred stereochemical modes of the approach between the reactant and intermediates on the basis of the energies of the corresponding transition states, we then turned our attention toward discovering the origin of the stereoselectivity by using the non-covalent interaction (NCI) analysis. In the NCI pictures, the regions of attractive non-covalent interactions appear as green colored regions, while red regions represent repulsive interactions.
As depicted in Fig. 6, the NCI plots of the stereocontrolling transition states show that the non-covalent interactions are more preferred in the lowest energy barrier transition state TS3SS. There are more C–H⋯Br interactions in TS3SS than in the other three transition states (i.e., TS3RR, TS3RS, and TS3SS). Moreover, the π⋯π interaction is found to be stronger in TS3SS than in its enantioselective transition state TS3RR (the distances between two aryl groups are 2.92 and 3.15 Å in TS3SS and TS3RR, respectively), and is absent in transition states TS3RS and TS3SR. As an important note, other kinds of interactions such as O–H⋯π and C–H⋯π exist in the four transition states and have little difference between these transition states. As mentioned above, the more effective C–H⋯Br and π⋯π interactions stabilize the transition state TS3SS.
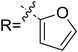
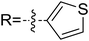
In order to further verify the reliability of the above predictions on the stereocontrolling transition states, we have investigated other three kinds of enals with R = 4-MePh, furan, and thiopene groups (Table 1). The computational results show that the selectivities of the reaction associated with different groups are in good agreement with the experimental observations, which indicates that the computational models would be reliable to predict the stereoselectivity for this kind of reaction. Moreover, NCI analysis has also been studied (the NCI pictures of the transition states with different substrates are provided in Fig. S3–S5 of the ESI†). According to the non-covalent interaction analysis, we can find that the π⋯π interaction is responsible for the origin of stereoselectivity.
Global reactivity index and Parr function analyses
As shown in Table 2, the GRI analysis shows that the electrophilicity of intermediates Re-M1 and Re-M2 is decreased after complexation of NHC and [1,2]-proton transfer, while the nucleophilicity of Re-M1 and Re-M2 is increased. This phenomenon reveals that the addition of the NHC catalyst strengthens the nucleophilicity of the substrate R1, which can facilitate the addition of another reactant R2′. After the formation of M3SS and M4SS, the electrophilicity values of the intermediates M3SS and M4SS are enhanced and the nucleophilicity values of M3SS and M4SS are slightly weakened. This result indicates that the intermediates M3SS and M4SS are hard to protonate via transition states TS4SSS-A and TS5SSS.
| E H | E L | μ | η | ω | N | |
|---|---|---|---|---|---|---|
| a E (TCNE)HOMO = −0.37826 a.u. (HOMO energy is calculated at the M06-2X/6-31G(d, p)//IEF-PCMDCM level). | ||||||
| R1 | −0.29 | −0.04 | −0.17 | 0.25 | 1.57 | 2.45 |
| R2′ | −0.32 | −0.08 | −0.20 | 0.24 | 2.27 | 1.63 |
| Re-M1 | −0.25 | −0.02 | −0.14 | 0.23 | 1.16 | 3.54 |
| Re-M2 | −0.21 | −0.02 | −0.12 | 0.19 | 1.03 | 4.63 |
| M3SS | −0.26 | −0.06 | −0.16 | 0.20 | 1.74 | 3.27 |
| M4SS | −0.25 | −0.05 | −0.15 | 0.20 | 1.53 | 3.54 |
Parr function analysis
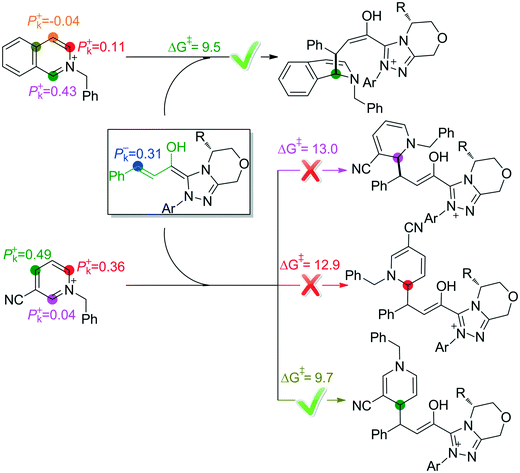
The above discussions show that the protonation of α-carbon is less favorable than the intramolecular Mannich reaction (17.2 kcal mol−1vs. 9.9 kcal mol−1). Herein, we intended to carry out the Parr function analysis22 to disclose the origin of chemoselectivity and the role of NHC by analyzing the local electrophilicity and nucleophilicity of active sites.Table 3 and Fig. S6 summarize the electrophilic and nucleophilic Parr functions of R1, R2′, Re-M1, Re-M2, M3SS, and M4SS. As can be seen in Table 3, one can find that the electrophilic Parr function (Pk+) of the C4 atom in R2′ is 0.43 and the nucleophilic Parr function (Pk−) of the C3 atom in Re-M2 is 0.31, which is in line with the GRI analysis. In intermediate M3SS, the nucleophilic Parr function (Pk−) of C5, C6, and C7 atoms is 0.36, −0.03, and 0.00 respectively, indicating that the nucleophilicity of the C5 atom is stronger than that of the C6 and C7 atoms. This phenomenon shows that the C5 atom accepts the proton more easily than the C6 and C7 atoms. In intermediate M4SS, the nucleophilic Parr function (Pk−) of the C7 atom is 0.65, which seems that the C7 atom has stronger proton accepting ability. Meanwhile the electrophilic Parr function (Pk+) of C5 (or hydrogen located on the C5 atom) and C6 atoms in M4SS is 0.00 and 0.74, respectively, revealing that the C6 atom should be more reactive than the C5 atom and can easily react with the C7 atom to occur the intramolecular Mannich reaction.
| R1 | R2′ | Re-M1 | Re-M2 | M3SS | M4SS | ||
|---|---|---|---|---|---|---|---|
| a Values in parentheses refer to the local nucleophilic Pk− and electrophilic Pk+ Parr functions of hydrogen located on the C5 atom. | |||||||
| C2 | P k + | 0.13 | — | 0.00 | −0.10 | −0.05 | 0.01 |
| P k − | −0.09 | — | 0.02 | 0.40 | 0.00 | −0.11 | |
| C3 | P k + | 0.28 | — | 0.03 | 0.10 | −0.02 | 0.02 |
| P k − | −0.11 | — | 0.02 | 0.31 | 0.07 | −0.06 | |
| C4 | P k + | — | 0.43 | — | — | 0.02 | −0.01 |
| P k − | — | 0.07 | — | — | −0.03 | 0.04 | |
| C5 | P k + | — | 0.11 | — | — | 0.00 | 0.00 (0.00) |
| P k − | — | 0.06 | — | — | 0.36 | 0.00 (0.00) | |
| C6 | P k + | — | −0.04 | — | — | 0.00 | 0.74 |
| P k − | — | 0.18 | — | — | −0.03 | 0.01 | |
| C7 | P k + | 0.10 | — | −0.01 | 0.20 | 0.29 | −0.01 |
| P k − | 0.41 | — | 0.07 | −0.13 | 0.00 | 0.65 | |
As mentioned above, the C1-dearomatization is impossible to occur, mainly because the C7 atom in M3SS is less reactive in accepting a proton and the C5 atom is deactivated after protonation. Additionally, the possible reactive sites have also been predicted by using the Parr function on the basis of Rovis'13 and Tan's15 work. As shown in Fig. 7, the active site is the C4 atom when the isoquinoline is used as the substrate, while the para-carbon is the most active when the pyridine is used as the substrate. The predictions are in good accordance with Rovis' and Tan's experimental results, respectively.
Conclusions
In summary, the possible reaction mechanisms and selectivities of NHC-catalyzed dearomatization reaction have been systematically investigated. The computational results suggest that the main catalytic mechanism consists of three major stages: (1) formation of the Breslow intermediate, (2) two sequential Mannich-type reactions (C1–C2-dearomatization) for forming a tropane-skeleton intermediate, and (3) dissociation of the catalyst. The intermolecular Mannich-type reaction step is identified to be both the stereoselectivity- and regioselectivity-determining steps, in which the Re–Si addition leading to SS-configured products is predominant. The NCI analysis shows that the more effective C–H⋯Br and π⋯π interactions are the key factors that govern the stereoselectivity. Furthermore, the C1-dearomatization is calculated to be less favorable, which is mainly due to the less reactivity in accepting the proton of β-carbon by using the Parr function analysis. Thus, one can predict the possible reactive sites through local reactivity analysis to provide valuable insights into rational design of potential catalysts in organocatalytic dearomatization reaction with excellent selectivities.Computational details
All the calculations involved in the reaction were performed by using the density functional theory (DFT) method with the Gaussian 09 (ref. 23) suite of programs, which has been identified to be a powerful and widely used method for exploring the mechanisms of organic reactions.24 The solution-phase structure optimization of all the stationary points was carried out at the M06-2X25/6-31G(d, p)26 level in DCM solvent using the integral equation formalism polarizable continuum model (IEF-PCM).27 The energies discussed in this work were obtained by the addition of the thermal correction at the M06-2X/6-31G(d, p)//IEF-PCMDCM level to the corresponding single-point energy at the M06-2X-D3/6-31++G (2df, 2pd)//IEF-PCMDCM level. Non-covalent interaction (NCI) analysis was plotted by using Multiwfn (version 3.3.8)28 and the computed 3D-structures were rendered using the CYLView software.29Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work described in this paper was supported by the National Natural Science Foundation of China (No. 21773214), the Outstanding Young Talent Research Fund of Zhengzhou University (No. 1521316001), the China Postdoctoral Science Foundation (No. 2015T80776), and the Startup Fund of Zhengzhou University of Light Industry (No. 13501050070).References
- For related reviews: (a) W.-T. Wu, L. M. Zhang and S.-L. You, Chem. Soc. Rev., 2016, 45, 1570–1580 RSC; (b) Z.-P. Yang, Q.-F. Wu, W. Shang and S.-L. You, J. Am. Chem. Soc., 2015, 137, 15899–15906 CrossRef CAS PubMed; (c) X.-W. Liang, C. Zheng and S.-L. You, Chem. – Eur. J., 2016, 22, 1–17 CrossRef; (d) Q. P. Ding, X. L. Zhou and R. H. Fan, Org. Biomol. Chem., 2014, 12, 4807–4815 RSC; (e) J. A. Bull, J. J. Mousseau, G. Pelletier and A. B. Charette, Chem. Rev., 2012, 112, 2642–2713 CrossRef CAS PubMed; (f) W. C. Wertjes, E. H. Southgate and D. Sarlah, Chem. Soc. Rev., 2018, 47, 7996–8017 RSC; (g) W. S. Sun, G. F. Li, L. Hong and R. Wang, Org. Biomol. Chem., 2016, 14, 2164–2176 RSC; (h) M. Zhang, W. S. Sun, G. M. Zhu, G. J. Bao, B. Z. Zhang, L. Hong, M. Li and R. Wang, ACS Catal., 2016, 6, 5290–5294 CrossRef CAS.
- C.-X. Zhuo, W. Zhang and S.-L. You, Angew. Chem., Int. Ed., 2012, 51, 12662–12686 CrossRef.
- For selected reviews: (a) C. Zheng and S.-L. You, Chem, 2016, 1, 830–857 CrossRef CAS; (b) A. R. Pape, K. P. Kaliappan and E. P. Kündig, Chem. Rev., 2000, 100, 2917–2940 CrossRef CAS PubMed; (c) C.-X. Zhuo, C. Zheng and S.-L. You, Acc. Chem. Res., 2014, 47, 2558–2573 CrossRef CAS PubMed.
- (a) S. P. Brown, N. C. Goodwin and D. W. C. MacMillan, J. Am. Chem. Soc., 2003, 125, 1192–1194 CrossRef CAS PubMed; (b) K. Frisch, A. Landa, S. Saaby and K. A. Jørgensen, Angew. Chem., Int. Ed., 2005, 44, 6058–6063 CrossRef CAS PubMed; (c) M. S. Taylor, N. Tokunaga and E. N. Jacobsen, Angew. Chem., Int. Ed., 2005, 44, 6700–6704 CrossRef CAS PubMed.
- For some related reviews: (a) A. Grossmann and D. Enders, Angew. Chem., Int. Ed., 2011, 51, 314–325 CrossRef PubMed; (b) S. J. Ryan, L. Candish and D. W. Lupton, Chem. Soc. Rev., 2013, 42, 4906–4917 RSC; (c) M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496 CrossRef CAS PubMed; (d) R. S. Menon, A. T. Biju and V. Nair, Chem. Soc. Rev., 2015, 44, 5040–5052 RSC; (e) D. M. Flanigan, F. Romanov-Michailidis, N. A. White and T. Rovis, Chem. Rev., 2015, 115, 9307–9387 CrossRef CAS PubMed; (f) X.-Y. Chen, Q. Liu, P. Chauhan and D. Enders, Angew. Chem., Int. Ed., 2017, 57, 3862–3873 CrossRef PubMed; (g) Y. Wang, D. H. Wei and W. J. Zhang, ChemCatChem, 2018, 10, 338–360 CrossRef CAS; (h) K. J. R. Murauski, A. A. Jaworski and K. A. Scheidt, Chem. Soc. Rev., 2018, 47, 1773–1782 RSC.
- For selected articles: (a) J. Izquierdo, A. Orue and K. A. Scheidt, J. Am. Chem. Soc., 2013, 135, 10634–10637 CrossRef CAS PubMed; (b) Z. Q. Fu, H. Sun, S. J. Chen, B. Tiwari, G. H. Li and Y. R. Chi, Chem. Commun., 2013, 49, 261–263 RSC; (c) P. C. Chiang, J. Kaeobamrung and J. W. Bode, J. Am. Chem. Soc., 2007, 129, 3520–3521 CrossRef CAS; (d) B. Cardinal-David, D. E. A. Raup and K. A. Scheidt, J. Am. Chem. Soc., 2010, 132, 5345–5347 CrossRef CAS PubMed.
- For selected articles: (a) J. F. Xu, C. L. Mou, T. S. Zhu, B. A. Song and Y. R. Chi, Org. Lett., 2014, 16, 3272–3275 CrossRef CAS PubMed; (b) P. Haghshenas, J. W. Quail and M. Gravel, J. Org. Chem., 2016, 81, 12075–12083 CrossRef CAS PubMed; (c) P. Haghshenas and M. Gravel, Org. Lett., 2016, 18, 4518–4521 CrossRef CAS PubMed; (d) S. M. Langdon, C. Y. Legault and M. Gravel, J. Org. Chem., 2015, 80, 3597–3610 CrossRef CAS PubMed.
- For selected articles: (a) X. Q. Fang, X. K. Chen, H. Lv and Y. R. Chi, Angew. Chem., Int. Ed., 2011, 50, 11782–11785 CrossRef CAS PubMed; (b) D. A. DiRocco and T. Rovis, J. Am. Chem. Soc., 2011, 133, 10402–10405 CrossRef CAS PubMed; (c) T. Jousseaume, N. E. Wurz and F. Glorius, Angew. Chem., Int. Ed., 2011, 50, 1410–1414 CrossRef CAS PubMed.
- (a) B. S. Li, Y. H. Wang, Z. C. Jin, P. C. Zheng, R. Ganguly and Y. R. Chi, Nat. Commun., 2015, 6, 6207–6211 CrossRef PubMed; (b) Y. Wang, B. H. Wu, H. Y. Zhang, D. H. Wei and M. S. Tang, Phys. Chem. Chem. Phys., 2016, 18, 19933–19943 RSC; (c) Z. Q. Fu, J. F. Xu, T. S. Zhu, W. W. Y. Leong and Y. R. Chi, Nat. Chem., 2013, 5, 835–839 CrossRef CAS; (d) Z. C. Jin, S. J. Chen, Y. H. Wang, P. C. Zheng, S. Yang and Y. R. Chi, Angew. Chem., Int. Ed., 2014, 53, 13506–13509 CrossRef CAS PubMed; (e) L. Hao, S. J. Chen, J. F. Xu, B. Tiwari, Z. Q. Fu, T. Li, J. Lim and Y. R. Chi, Org. Lett., 2013, 15, 4956–4959 CrossRef CAS; (f) Y. Y. Wang, D. H. Wei, Y. Wang, W. J. Zhang and M. S. Tang, ACS Catal., 2016, 6, 279–289 CrossRef CAS; (g) J. Yan, K. X. Shi, C. T. Zhao, L. Y. Ding, S. S. Jiang, L. M. Yang and G. F. Zhong, Chem. Commun., 2018, 54, 1567–1570 RSC; (h) Z. X. Xiao, C. X. Yu, T. J. Li, X.-S. Wang and C. S. Yao, Org. Lett., 2014, 16, 3632–3635 CrossRef CAS PubMed; (i) Q. Q. Shi, Y. Wang, Y. Y. Wang, L.-B. Qu, Y. Qiao and D. H. Wei, Org. Chem. Front., 2018, 5, 2739–2748 RSC.
- C. Guo, M. Fleige, D. Janssen-Müller, C. G. Daniliuc and F. Glorius, Nat. Chem., 2015, 7, 842–847 CrossRef CAS PubMed.
- D. Janssen-Müller, M. Fleige, D. Schlüns, M. Wollenburg, C. G. Daniliuc, J. Neugebauer and F. Glorius, ACS Catal., 2016, 6, 5735–5739 CrossRef.
- S. Bera, C. G. Daniliuc and A. Studer, Angew. Chem., Int. Ed., 2017, 56, 7402–7406 CrossRef CAS PubMed.
- D. M. Flanigan and T. Rovis, Chem. Sci., 2017, 8, 6566–6569 RSC.
- G. D. Carmine, D. Ragno, O. Bortolini, P. P. Giovannini, A. Mazzanti, A. Massi and M. Fogagnolo, J. Org. Chem., 2018, 83, 2050–2057 CrossRef PubMed.
- J. H. Xu, S. C. Zheng, J. W. Zhang, X. Y. Liu and B. Tan, Angew. Chem., Int. Ed., 2016, 55, 11834–11839 CrossRef CAS PubMed.
- For selected articles: (a) Y. Wang, D. H. Wei and M. S. Tang, J. Org. Chem., 2017, 82, 13043–13050 CrossRef CAS PubMed; (b) Y. Wang, Y. Qiao, D. H. Wei and M. S. Tang, Org. Chem. Front., 2017, 4, 1987–1998 RSC; (c) Y. Wang, S.-R. Zhang, Y. Y. Wang, L.-B. Qu and D. H. Wei, Org. Chem. Front., 2018, 5, 2065–2072 RSC; (d) Y. Wang, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2015, 2, 874–884 RSC; (e) Y. Wang, Y. Y. Wang, X. H. Wang, X. Li, L.-B. Qu and D. H. Wei, Catal. Sci. Technol., 2018, 8, 4229–4240 RSC.
- (a) X. X. Wei, R. Fang and L. Z. Yang, Catal. Sci. Technol., 2015, 5, 3352–3362 RSC; (b) P.-C. Tu, L. Zhou, A. M. Kirillov, R. Fang and L. Z. Yang, Org. Chem. Front., 2018, 5, 1356–1365 RSC; (c) Y. Reddi and R. B. Sunoj, ACS Catal., 2017, 7, 530–537 CrossRef CAS; (d) Y. Qiao, D. H. Wei and J. B. Chang, J. Org. Chem., 2015, 80, 8619–8630 CrossRef CAS PubMed.
- (a) C.-X. Yan, F. Yang, X. Yang, D.-G. Zhou and P.-P. Zhou, J. Org. Chem., 2017, 82, 3046–3061 CrossRef CAS PubMed; (b) Q. Q. Shi, W. Zhang, Y. Wang, L.-B. Qu and D. H. Wei, Org. Biomol. Chem., 2018, 16, 2301–2311 RSC; (c) L. J. Zheng, M. S. Tang, Y. Wang, X. K. Guo, D. H. Wei and Y. Qiao, Org. Biomol. Chem., 2016, 14, 3130–3141 RSC.
- (a) Y. Z. Xia, Y. Liang, Y. Y. Chen, M. Wang, L. Jiao, F. Huang, S. Liu, Y. H. Li and Z.-X. Yu, J. Am. Chem. Soc., 2007, 129, 3470–3471 CrossRef CAS PubMed; (b) Y. Wang and Z.-X. Yu, J. Org. Chem., 2018, 83, 5384–5391 CrossRef CAS PubMed; (c) Y. Wang, B. H. Wu, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2016, 3, 190–203 RSC; (d) Y. Wang, M. S. Tang, Y. Y. Wang and D. H. Wei, J. Org. Chem., 2016, 81, 5370–5380 CrossRef CAS PubMed.
- (a) Y. Wang, X. K. Guo, M. S. Tang and D. H. Wei, J. Phys. Chem. A, 2015, 119, 8422–8431 CrossRef CAS PubMed; (b) Y. Wang, D. H. Wei, Z. Y. Li, Y. Y. Zhu and M. S. Tang, J. Phys. Chem. A, 2014, 118, 4288–4300 CrossRef CAS PubMed; (c) C. X. Yan, P.-P. Zhou, F.-L. Yang, R.-Z. Wu, X. Yang, F. Yang and X. F. Shao, Org. Chem. Front., 2018, 5, 2692–2709 RSC; (d) X. Li, Y. Y. Wang, Y. Wang, M. S. Tang, L.-B. Qu, Z. J. Li and D. H. Wei, J. Org. Chem., 2018, 83, 8543–8555 CrossRef CAS PubMed; (e) X. Li, M. S. Tang, Y. Y. Wang, Y. Wang, Z. J. Li, L.-B. Qu and D. H. Wei, Chem. – Asian J., 2018, 13, 1710–1718 CrossRef CAS PubMed; (f) W. Zhang, Y. Wang, D. H. Wei, M. S. Tang and X. J. Zhu, Org. Biomol. Chem., 2016, 14, 6577–6590 RSC.
- (a) L. R. Domingo, J. A. Sáez, J. A. Joule, L. Rhyman and P. Ramasami, J. Org. Chem., 2013, 78, 1621–1629 CrossRef CAS PubMed; (b) L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, J. Org. Chem., 2018, 83, 2182–2197 CrossRef CAS PubMed.
- (a) L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC; (b) L. J. Zheng, Y. Wang, D. H. Wei and Y. Qiao, Chem. – Asian J., 2016, 11, 3046–3054 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford, CT, 2010 Search PubMed.
- (a) Y. Wang, C. Du, Y. Y. Wang, X. K. Guo, L. Fang, M.-P. Song, J.-L. Niu and D. H. Wei, Adv. Synth. Catal., 2018, 360, 2668–2677 CrossRef CAS; (b) X. K. Guo, L.-B. Zhang, D. H. Wei and J.-L. Niu, Chem. Sci., 2015, 6, 7059–7071 RSC; (c) Y. Z. Lv, A. A. Ogunlana, H. L. Li, D. F. Gao, C. L. Wang and X. G. Bao, Catal. Sci. Technol., 2018, 8, 3379–3386 RSC; (d) Z. Y. Yu, X. T. Qi, Y. Z. Li, S. Liu and Y. Lan, Org. Chem. Front., 2016, 3, 209–216 RSC; (e) J. Y. Zhang, J. S. Lin, Y. W. Li, Y. X. Shao, X. Huang, C. Y. Zhao and Z. F. Ke, Catal. Sci. Technol., 2017, 7, 4866–4878 RSC; (f) X. Y. Lv, Y.-B. Wu and G. Lu, Catal. Sci. Technol., 2017, 7, 5049–5054 RSC.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS; (b) W. Sang-Aroon and V. Ruangpornvisuti, Int. J. Quantum Chem., 2007, 108, 1181–1188 CrossRef.
- (a) B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS; (b) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2011, 33, 580–592 CrossRef.
- C. Y. Legault, CYLview, 1.0b, Universit'e de Sherbrooke, 2009, http://www.cylview.org Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cy02238k |
| This journal is © The Royal Society of Chemistry 2019 |