Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coming full circle: constructing a [Gd6] wheel dimer by dimer and the importance of spin topology†
Thomas N.
Hooper
a,
Stuart K.
Langley‡
b,
Silvia
Gómez-Coca
c,
Giulia
Lorusso
 d,
Eliseo
Ruiz
c,
Keith S.
Murray
d,
Eliseo
Ruiz
c,
Keith S.
Murray
 *b,
Marco
Evangelisti
*b,
Marco
Evangelisti
 *d and
Euan K.
Brechin
*d and
Euan K.
Brechin
 *a
*a
aEaStCHEM School of Chemistry, The University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ, UK. E-mail: ebrechin@ed.ac.uk
bSchool of Chemistry, Monash University, Clayton, Victoria, 3800, Australia. E-mail: keith.murray@monash.edu
cDepartament de Química Inorgànica I Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain
dInstituto de Ciencia de Materiales de Aragón, CSIC-Universidad de Zaragoza, 50009 Zaragoza, Spain. E-mail: evange@unizar.es
First published on 18th July 2017
Abstract
The syntheses, structures, magnetic and thermodynamic properties of three related triethanolamine-based GdIII complexes are described. The smallest, a dimer ([Gd2]), can be viewed as the subunit from which the two larger complexes, a linear tetramer ([Gd2]2) and a cyclic hexamer ([Gd2]3), are composed by further deprotonation of the triethanolamine ligand. In all cases, nearest neighbour magnetic ions are weakly correlated by antiferromagnetic isotropic exchange, whose strength does not change significantly from one complex to another; J ranging from −0.10 to −0.13 cm−1. Therefore, rather than the strength of the coupling, it is the spin topology that is the dominant factor in determining the differences between the physical properties – specifically, the nuclearity and the transition from open (dimer and tetramer) to cyclic (hexamer) boundary conditions. Indeed the hexanuclear wheel reaches the continuum limit of classical Heisenberg spin chains. In terms of the magnetocaloric properties, the smaller the nuclearity, the larger the magnetic entropy and adiabatic temperature changes.
Introduction
Molecule-based materials consist of molecular building blocks that can be linked together in various ways to create larger, more complex 0–3D species. The type and magnitude of the interactions between the molecular units is crucial in determining their physical properties. If magnetic ions are involved, then molecule-based magnetic materials can provide a route for testing model spin systems.1 In this regard, chemical synthesis is a powerful tool because it can lead to a bottom-up approach to examining magnetic interactions in a controlled fashion and, as such, to materials with designer properties.2 Here, we focus on isotropic metal ions, namely GdIII, whose quenched orbital momentum implies that crystal field effects are extremely small, if not negligible.3 Furthermore, gadolinium possesses the largest spin (s = 7/2) of any ion in the periodic table. Under these circumstances, classical spin models can provide a good approximation to systems of interacting quantum spins.From an applications perspective, the aforementioned characteristics contribute to making gadolinium the most widely employed element in magnetocaloric materials.4 The magnetocaloric effect (MCE) is based on the changes of magnetic entropy (ΔSm) and adiabatic temperature (ΔTad) upon application of a magnetic field and is of interest for refrigeration via a process known as adiabatic demagnetization.5 Although the MCE is intrinsic to all magnetic materials, in only a few of these are the changes sufficiently large to make them commercially suitable. Molecular magnetic refrigerants are amongst the most promising candidates in this regard, with recent examples demonstrating an MCE comparable to materials conventionally employed for low- and ultra-low-temperature cooling applications.6 These improvements have allowed the desired physical characteristics of the ideal molecule-based materials to be identified.4b These are: (1) A large spin s, since the magnetic entropy is related to it by Sm = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2s + 1), where R is the gas constant. (2) Molecular isotropy, since zero-field splitting promotes spin ordering, limiting the MCE at the lowest temperatures. (3) Weak magnetic interactions, which lead to low-lying excited states each of which contribute to the field dependence of the MCE. (4) A (relatively) low molecular mass, and thus a large magnetic density. These four prerequisites therefore dictate the synthetic strategy towards constructing good magnetic refrigerants. A sensible approach is based on the synthesis of homo- and heterometallic GdIII clusters. The inherently weak exchange mediated through the core-like f-orbitals of GdIII and its isotropic f7 configuration guarantee the presence of multiple low-lying spin states. Heterometallic complexes (e.g., GdIII–TMn+; TM = transition metal) can be guaranteed to afford non-zero spin ground states on account of their differing dn/fn electron configurations and on the basis of literature precedents that show certain combinations, e.g., GdIII–CuII, favour ferromagnetic exchange.7 Molecular isotropy can be controlled through the use of isotropic metals ions (GdIII, CrIII, MnII, FeIII), or via the synthesis of highly symmetric molecules. The latter usually result from high temperature/high pressure reactions, i.e., they are the thermodynamic products of solvothermal or microwave synthesis, and this then allows the use of anisotropic metal ions.8
ln(2s + 1), where R is the gas constant. (2) Molecular isotropy, since zero-field splitting promotes spin ordering, limiting the MCE at the lowest temperatures. (3) Weak magnetic interactions, which lead to low-lying excited states each of which contribute to the field dependence of the MCE. (4) A (relatively) low molecular mass, and thus a large magnetic density. These four prerequisites therefore dictate the synthetic strategy towards constructing good magnetic refrigerants. A sensible approach is based on the synthesis of homo- and heterometallic GdIII clusters. The inherently weak exchange mediated through the core-like f-orbitals of GdIII and its isotropic f7 configuration guarantee the presence of multiple low-lying spin states. Heterometallic complexes (e.g., GdIII–TMn+; TM = transition metal) can be guaranteed to afford non-zero spin ground states on account of their differing dn/fn electron configurations and on the basis of literature precedents that show certain combinations, e.g., GdIII–CuII, favour ferromagnetic exchange.7 Molecular isotropy can be controlled through the use of isotropic metals ions (GdIII, CrIII, MnII, FeIII), or via the synthesis of highly symmetric molecules. The latter usually result from high temperature/high pressure reactions, i.e., they are the thermodynamic products of solvothermal or microwave synthesis, and this then allows the use of anisotropic metal ions.8
We, and others, have demonstrated that, upon deprotonation, triethanolamine (H3tea) is an excellent ligand for constructing high spin, high nuclearity compounds,9 including a [Cu5Gd4] cluster displaying a large cryogenic MCE.10 Herein we extend the coordination chemistry of triethanolamine to homometallic GdIII species and show that stepwise structural variation can be provided by progressive deprotonation of the ligand, and that the initial compound made, a dimer, can be regarded as the building block from which a tetramer and hexamer can be constructed. The structure of the hexamer has been previously communicated.9f We construct the magnetic and thermodynamic properties of these compounds in the same manner, since the exchange interaction that characterizes the dimeric subunit remains effectively unchanged in the tetramer and hexamer.
Results and discussion
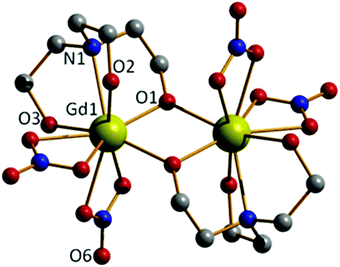
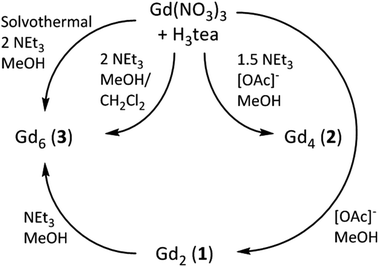
The reaction of Gd(NO3)3·6H2O with H3tea in the presence of 1 equivalent of base (acetate) in methanol results in the formation of the alkoxide bridged gadolinium dimer [Gd(H2tea)(NO3)2]2·2MeOH (1·2MeOH, Fig. 1; see the Experimental section for full details). This is the basic building block common to all the clusters reported herein. Crystals suitable for X-ray diffraction were grown from diffusion of diethyl ether into the alcoholic reaction mixture.The GdIII ions are bridged by two μ-O-atoms (O1 and symmetry equivalent (s.e.)) derived from the sole deprotonated arm of two triethanolamine ligands to form a planar [Gd2O2]4+ motif. Each GdIII ion is 9-coordinate in capped square-antiprismatic geometry with a [GdO8N] coordination sphere. The eight remaining coordination sites are filled by a combination of two chelating nitrate ions, two terminally bonded O-atoms (O2, O3) from the protonated arms of the H2tea ligand, and the N-atom (N1) from the H2tea ligand. The bond lengths in the [Gd2O2] core show slight asymmetry {Gd(1)–O(1) 2.301(4) Å and Gd(1)–O(1A) 2.250(4) Å} and the Gd(1)–O(1)–Gd(1A) bond angle of 109.11(16)° means the Gd⋯Gd distance of 3.706(7) Å is one the shortest reported for a planar [Gd2O2] motif. This small Gd⋯Gd distance is consistent with known alkoxide-bridged GdIII dimers,11–15 with carboxylate bridged dimers tending to show larger Gd⋯Gd separations, as would be expected from the presence of a three atom O–C–O bridge.16
In the crystal molecules of 1 pack in chains in the bc plane as directed by H-bonding interactions between the alcohols from the triethanolamine ligands to both the non-coordinated O-atoms of the nitrate anions {O(3)⋯(O6) 2.762 Å} and the MeOH solvate molecules {O(2)⋯(O10) 2.644 Å, O(3)⋯(O10) 2.953 Å} that sit between neighbouring clusters (Fig. S1†).
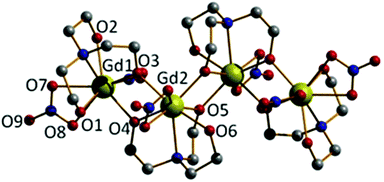
A similar reaction between Gd(NO3)3·6H2O and H3tea in MeOH with 1 equivalent of acetate and 1.5 equivalents of NEt3 yields the tetrametallic cluster [Gd2(H2tea)(Htea)(NO3)3]2·MeOH (2·MeOH; Fig. 2). Complex 2 can be regarded as the linear dimer of complex 1. Single crystals of 2 suitable for X-ray diffraction were formed from diffusion of diethyl ether into the methanolic reaction mixture. The structure describes a zig-zag like chain structure in which two molecules of 1 have dimerised in a head-to-tail fashion via the “further” deprotonation of two of the triethanolamine ligands (i.e., H2tea to Htea). The doubly deprotonated Htea2− ligands chelate to the central GdIII ions (Gd2 and s.e.), using one alkoxide arm each to bridge between Gd2–Gd2A (O5 and s.e.), and the other (O4 and s.e.) to bridge to the peripheral GdIII ions (Gd1 and s.e.). The singly deprotonated H2tea− ligands chelate to Gd1 (and s.e.), with the protonated arms terminally bonded, and the sole deprotonated arm (O3 and s.e.) μ–bridging to Gd2 (and s.e.). The remaining two coordination sites on each GdIII ion are completed by the presence of one chelating NO3− anion, resulting in each of the GdIII ions being in a capped square-antiprismatic geometry with a [GdO8N] coordination sphere. This arrangement is reinforced by an intra-molecular H-bond between the OH of the triethanolamine attached to the central GdIII centre (Gd2) and the coordinated oxygen of a nitrate anion attached to the terminal GdIII centre {O(6)⋯(O11) 2.736 Å}. The bond lengths and angles found in 2 are similar to those in 1 with asymmetry observed in the planar [Gd2O2] bridge and short Gd⋯Gd distances.
There are numerous inter-molecular interactions in the crystal, with each molecule of 2 being H-bonded to its four nearest neighbours, two above and two below opposite ends of the Gd4 plane. As in 1 these are directed by one NO3−⋯HO(triethanolamine) {O(8)⋯(O2) 2.760 Å} interaction, and by O(NO3−)⋯O(MeOH solvate)⋯OH(triethanolamine) contacts {O(12)⋯(O16A) 2.990 Å, O(16A)⋯(O1) 2.626 Å}. The result is the formation of H-bonded 2-D sheets running across the diagonal of the ac plane (Fig. S2†). The [Gd4] zig-zag chain structure in 2 is somewhat similar to that observed in the complex [Dy4L4(MeOH)6] (H3L = 2-hydroxy-3-methoxybenzoic acid [(2-hydroxy-3-methoxyphenyl)methylene] hydrazide).17,18
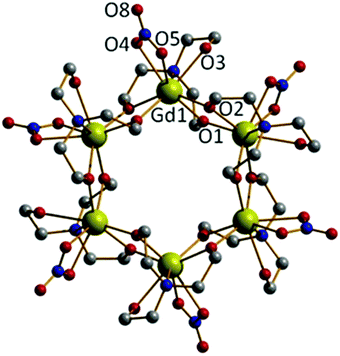
Repeating the reaction that produced 2, but increasing the molar ratio of NEt3 to 2 equivalents (per mole of Gd), produces the cluster [Gd(Htea)(NO3)]6·8MeOH (3·8MeOH; Fig. 3) Complex 3 (which some of us have reported previously9f) can be regarded as the cyclic trimer of complex 1. Single crystals of 3 suitable for X-ray diffraction were formed from the slow evaporation of a MeOH/CH2Cl2 solution. The structure is that of a hexametallic wheel in which three molecules of 1 have oligomerised in a head-to-tail fashion via the double deprotonation of all of the triethanolamine ligands. Each Htea2− ligand thus chelates to one GdIII ion and bridges to two others, forming a [Gd6O12]6+ magnetic core. As for complex 2, each GdIII ion sits in a capped square antiprismatic geometry with a [GdO8N] coordination sphere, the remaining sites per metal being occupied by one chelating NO3− ion. The planar asymmetric [Gd2O2] motif is again present with the Gd⋯Gd distance being 3.775 Å, and the Gd⋯Gd distance across the diameter of the wheel measuring 7.549 Å. Each of the six Htea2− ligands is H-bonded to a MeOH solvate molecule (e.g. O3⋯O6, 2.682 Å) which in turn is H-bonded to either another MeOH solvate molecule or a neighbouring [Gd6] wheel {O(MeOH)⋯O(Htea), 2.682 Å}. The result of these inter-molecular interactions is the formation of aesthetically pleasing 2D honeycomb-like sheets in the ab plane (Fig. S3†). The closest inter-molecular interactions between sheets (down the c-axis) are between O-atoms from the NO3− ions and C-atoms from the Htea2− ligands {O⋯C, ∼3.7 Å}.
The idea that complexes 1 and 2 are simply ‘kinetic’ products reached on the road to the ‘thermodynamic’ end-product 3 is strengthened by the observation that 3 can also be synthesised by simple addition of 1 equivalent of triethylamine to 1 in a mixture of methanol and dichloromethane, and that 3 can be made (in higher yield) via the solvothermal reaction of Gd(NO3)3·6H2O and H3tea in the complete absence of base. The relatively poor yield of 2 has prevented us from ‘completing the cycle’, and no attempt has yet been made to reverse the oligomerisation (Gd6 → Gd4 → Gd2) via addition of, for example, acid. The reaction pathways are summarised in Scheme 1.
Magnetometry
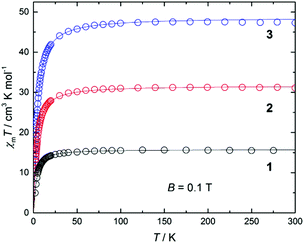
DC magnetic susceptibility measurements were carried out on powdered crystalline samples of 1–3 in the 300–5 K temperature range in an applied magnetic field of 0.1 T. Plots of the χmT vs. T response are given in Fig. 4. All three complexes show similar behaviour, as one might expect given their structural similarity. Their room-temperature χmT values are consistent with the presence of 2 (15.5 cm3 mol−1 K, 1), 4 (32.1 cm3 mol−1 K, 2) and 6 (48.7 cm3 mol−1 K, 3) non-interacting s = 7/2 centres. These values remain constant as the temperature is lowered down to approximately 50 K when a sharp decrease is seen in each case, resulting in minimum values of ∼10, 18 and 27 cm3 K mol−1, respectively. This is clearly indicative of rather weak antiferromagnetic nearest neighbour exchange interactions, consistent with previously published examples of alkoxide-bridged GdIII ions.11–15 Isothermal DC magnetization curves were also measured for powdered crystalline samples of 1–3 up to an applied magnetic field of 5 T and for several temperatures between 2 and 10 K (Fig. S4†).The experimental susceptibility and magnetization data in each case (1–3) were fitted using the isotropic Hamiltonians given in Scheme 2 and eqn (1)–(3), respectively.19 Note that we identify two different coupling constants J and J′ for complex 2, on account of the slightly different coordination environments of the GdIII ions involved: the Gd(1)⋯Gd(2) distance is 3.735 Å, while the Gd(2)⋯Gd(3) distance is 3.785 Å; the Gd(1)–O–Gd(2) bond angles are 107.9° and 109.8°, while the Gd(2)–O–Gd(3) bond angles are both 110.2°. This affords, g = 2.00 J = −0.13 cm−1 for 1; g = 2.01 J = −0.12 cm−1, J′ = −0.10 cm−1 for 2; and g = 2.02 J = −0.10 cm−1 for 3 (see solid lines in Fig. 4 and S4† for the susceptibility and magnetization data, respectively). These values are comparable with another alkoxide bridged GdIII dimer [Gd(Hsabhea)(NO3)]2 (where H3sabhea = N-salicylidene-2-(bis-(2-hydroxyethyl)amino)ethylamine)11 which displayed antiferromagnetic coupling of J = −0.198 cm−1 (g = 1.975); but is larger in absolute magnitude than that observed in carboxylate bridged dimers.16 Note that the three complexes have very similar values of the exchange coupling constant. Thus, the magnetic properties are determined chiefly by the different spin topologies.
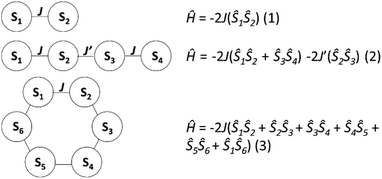 | ||
| Scheme 2 The exchange interaction schemes employed to fit the susceptibility data for (top to bottom) 1–3. | ||
Electronic structure calculations
To investigate the magnetic properties of 1–3 in a little more detail, electronic structure calculations based on density functional theory (DFT) have been performed. Two different computational approaches were employed: the SIESTA code20 with the PBE functional,21 and FHI-Aims22 with implemented hybrid B3LYP23 functional which also allows us to include relativistic effects using the ZORA approach (see Computational details in the ESI†). Both methodologies have been successfully employed to calculate exchange coupling constants.24 The DFT calculated J values are collected in Table 1. Both computational approaches correctly reproduce the weak antiferromagnetic exchange interactions typically observed for GdIII ions bridged by alkoxide ligands. Taking into account the very weak nature of these interactions, they reproduce the observed coupling constants remarkably well, although the SIESTA code with PBE functional tends to overestimate the J values somewhat.24 Interestingly, the inclusion of scalar relativistic effects together with a hybrid functional is necessary to obtain J values close to the experimental values.| J exp | J PBE | J B3LYP | J B3LYP+ZORA | ||
|---|---|---|---|---|---|
| 1 | J | −0.13 | −0.22 | −0.20 | −0.16 |
| 2 | J | −0.12 | −0.24 | −0.18 | −0.15 |
| J′ | −0.10 | −0.17 | −0.14 | −0.13 | |
| 3 | J | −0.10 | −0.20 | −0.15 | −0.13 |
For the sake of completeness, we have also studied the dependence of the exchange coupling constant on the bridging Gd–O–Gd angle. Calculations were performed on a model complex (Fig. 5) derived from 1 in which the ‘second’ –CH2– moiety of the triethanolamine arm linking the bridging O-atom to the N-atom has been replaced with two H-atoms, thus forming independent bridging (methoxide) and terminal ligands. The results, for a symmetric model with Gd–O bond distances fixed at 2.3 Å, are summarized in Fig. 6. They show that the strength of the antiferromagnetic coupling increases on lowering the Gd–O–Gd angle, and that this coupling is weakly antiferromagnetic in the range of bridging angle values employed.
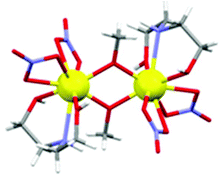 | ||
| Fig. 5 The model complex employed to calculate the exchange interactions between GdIII ions upon changing Gd–O–Gd angle. Colour code: Gd, yellow; O, red; N, blue; C, grey; H, white. | ||
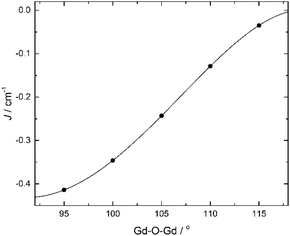 | ||
| Fig. 6 Calculated B3LYP J-values vs. Gd–O–Gd angle for a symmetric [GdIII2] model (Fig. 5) with Gd–O bond distances fixed at 2.3 Å. | ||
Heat capacity
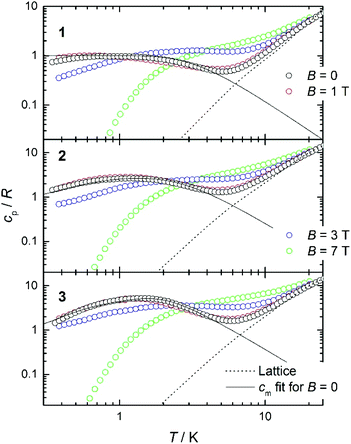
Heat capacity experiments were carried out in the 0.3–30 K temperature range in applied magnetic fields of 0, 1, 3 and 7 T. Plots of the cpvs. T response are given in Fig. 7. Above ca. 6 K, cp is dominated by lattice phonon modes of the crystal, which can be described by the Debye model (dotted line) and simplify to cp/T3 = 1.1 × 10−3, 3.3 × 10−3 and 3.0 × 10−3 K−3 at the lowest temperatures for 1, 2 and 3, respectively.The magnetic field-dependent contribution to the heat capacity (cm) develops at the lowest temperatures and shows characteristics that are common to all three complexes. For each complex, the cm curves collected for B = 0 and 1 T are essentially indistinguishable from one another. This behaviour is consistent with dominant antiferromagnetism, in agreement with the magnetization data. For the highest field used (B = 7 T), all spins are fully decoupled and the magnetic anomaly is therefore equivalent to a Schottky curve originating from the field-splitting of non-interacting GdIII spins. Comparing the three complexes, the only difference between the cm curves for B = 7 T is the height of the anomaly, which is proportional to the number of spins per mole involved. In addition to the height, what differs in the magnetic heat capacity from one compound to another is the temperature at which the zero-field cm has its maximum – this temperature is clearly higher in 3 than in 2 and 1, respectively (see Fig. 7). Note that intermolecular (dipolar) interactions play a negligible role, at least at the relatively high temperatures investigated. The experimental zero-field cm curves are indeed satisfactorily modelled (solid lines) by the isotropic Hamiltonians given in Scheme 2 and eqn (1)–(3), using the same parameters obtained from the fits of the magnetization data.
Spin topology
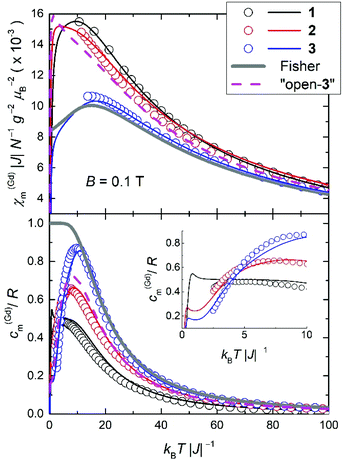
In order to highlight the role of the spin topology and to facilitate comparison between the physical properties of 1, 2 and 3, we normalize the susceptibility and heat capacity data per GdIII ion and plot the χ(Gd)m and c(Gd)m in Fig. 8. Furthermore, we normalize χm and T per |J|, whose values were obtained from the fits of the experimental data to the Hamiltonians of eqn (1)–(3). For 2, we assume |J| = 0.11 cm−1, as a mean value between 0.10 and 0.12 cm−1 (see fit). Note that since all the J values involved are very close to one another, normalization of the temperature is not strictly necessary for comparison. Importantly, Fig. 8 reveals strikingly different behaviours depending on the spin topology. Complex 1 has a larger χ(Gd)m with respect to 2 and 3, while the opposite trend applies to the c(Gd)m data. For comparison, we also plot the susceptibility and heat capacity calculated on basis of Fisher's model for isotropic Heisenberg infinite chains in the classical limit of infinite spins.25 Bear in mind that the so-obtained heat capacity is unrealistic for the lowest temperatures since in the classical limit the calculation necessarily flattens and goes to a nonzero value for T → 0. As can be seen in Fig. 8, both χ(Gd)m and c(Gd)m of 1, 2 and 3 gradually approach the classical limit on increasing the number of spin sites. It indeed turns out that complex 3 can be described well by Fisher's model, at least down to kBT|J|−1 ∼ 10, i.e., T ∼ 1 K. This comparison suggests that s = 7/2 spins can be regarded as classical ‘infinite’ spins and that the Heisenberg 1D chain of classical spins can be efficiently mapped onto a molecular wheel motif based on six GdIII spins, as for 3. Finally, to investigate the role of boundary conditions, we have considered a hypothetical molecular analogue of 3 but with an open-wheel structure, viz., we break the cyclic boundary condition by omitting a J-pair in our calculations for 3. We have calculated the susceptibility and heat capacity of “open-3” (dashed lines in Fig. 8), which are rather different from Fisher's model, and relatively close to the corresponding contributions for 2. We conclude therefore that boundary conditions play a determinant role in the magnetic and thermodynamic properties of these compounds.For kBT|J|−1 ≤ 3, thus beyond the temperature window of our experiments, the calculations show that the fewer the spin sites, the higher is the corresponding c(Gd)m (inset of Fig. 8), which corresponds to an entropy (S) content higher in 1 than 2 and 3, respectively, at the lowest temperatures. The temperature and field dependence of the entropy can be obtained by applying 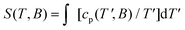 to the heat capacity.
to the heat capacity.
Magnetocalorics
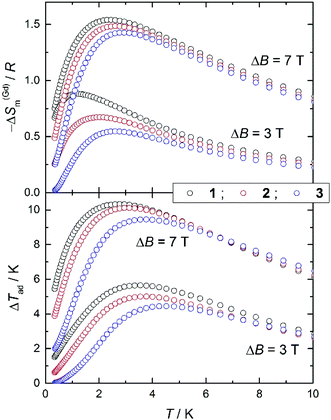
We employ the experimental magnetization and heat capacity data (Fig. S4† and Fig. 7, respectively) to calculate the magnetocaloric effect for 1, 2 and 3, using standard procedures.4a,b Fig. S5† shows the magnetic entropy change, as derived by applying the Maxwell equation to the magnetization data. Likewise, Fig. 9 shows −ΔSm(T, ΔB) data for applied-field changes ΔB = (3–0) and (7–0) T, as derived from the entropy curves (Fig. S6†). Both calculations of the −ΔSm(T, ΔB) sets of data provide identical results, that we plot separately (Fig. 9 and Fig. S5†) for the sake of clarity, validating the procedures employed. To facilitate the comparison between 1, 2 and 3, we normalize the magnetic entropy change data per molar Gd content. Similarly, we employ the entropy curves in Fig. S6† to derive the adiabatic temperature changes plotted in Fig. 9. We restrict our analysis to the ΔB = (3–0) and (7–0) T applied changes, thus omitting the data collected for 1 T since these are indistinguishable from the equivalent sets of zero-field data.For ΔB = 7 T, Fig. 9 shows that complex 1 attains the maximum −ΔS(Gd)m = 1.54R, equivalent to 27.8 J kg−1 K−1 per unit mass, at T = 2.3 K and ΔTad = 10.3 K at T = 2.8 K; complex 2 attains −ΔS(Gd)m = 1.48R = 29.8 J kg−1 K−1 at T = 2.6 K and ΔTad = 10.1 K at T = 3.1 K; complex 3 attains −ΔS(Gd)m = 1.43R = 29.0 J kg−1 K−1 at T = 2.9 K and ΔTad = 9.4 K at T = 3.8 K. Finally, for ΔB = 3 T, complex 1 attains −ΔS(Gd)m = 0.88R = 15.9 J kg−1 K−1 at T = 1.2 K and ΔTad = 5.6 K at T = 3.5 K; complex 2 attains −ΔS(Gd)m = 0.67R = 13.5 J kg−1 K−1 at T = 1.9 K and ΔTad = 5.0 K at T = 3.6 K; complex 3 attains −ΔS(Gd)m = 0.55R = 11.1 J kg−1 K−1 at T = 2.6 K and ΔTad = 4.4 K at T = 4.5 K. Although these values are relatively large for magnetic molecules based purely on GdIII ions,4c they are much smaller than, for example, that reported for the ferromagnetic molecular dimer gadolinium acetate tetrahydrate.26 It is interesting to compare the different behaviours in connection with the number of GdIII spin centres involved, while holding ‘constant’ the exchange coupling. Clearly, one can notice the relatively lower MCE for complex 3, or by analogy, for an infinite chain of classical spins. The effect can be made larger by localizing the exchange interactions into smaller spin segments, such as in 2 and 1. This behaviour is entirely determined by the zero-field cm and hence by the zero-field magnetic entropy. As already observed, the zero-field magnetic entropy develops closer to absolute zero for the smaller molecules.
Conclusions
We have shown that three related gadolinium complexes can be synthesised using triethanolamine as a supporting ligand, with the structural variation provided by the extent of deprotonation of the ligand. The simplest of these, a dimer (1), can be viewed as the building block from which the tetramer (2) and the hexamer (3) were formed in solution by further deprotonation of the triethanolamine. Complex 3 can also be synthesised by simple addition of 1 equivalent of triethylamine to 1 in a mixture of methanol and dichloromethane, and (in higher yield) via the solvothermal reaction of Gd(NO3)3·6H2O and H3tea in the complete absence of base. The complexes show short Gd⋯Gd distances and a magnetic core comprising planar [Gd2O2] moieties. Each exhibits weak antiferromagnetic nearest neighbour exchange. Topological size effects are responsible for the magnetic and thermodynamic properties of these compounds. By decreasing the nuclearity, the magnetocaloric effect becomes larger at relatively lower temperatures, being more prominent for the dimer that reaches −ΔSm = 27.8 J kg−1 K−1 at T = 2.3 K and ΔTad = 10.3 K at T = 2.8 K.Experimental
[Gd(H2tea)(NO3)2]2·2MeOH (1·2MeOH)
Triethanolamine (0.5 cm3, 1.0 M solution in MeOH, 0.5 mmol) was added to a solution of Gd(NO3)3·6H2O (0.226 g, 0.5 mmol) in MeOH (25 cm3). [NEt4][OAc]·4H2O (0.131 g, 0.5 mmol) was added and the solution stirred for 1 h. Colourless blocks of 1 were crystallised by vapour diffusion of Et2O over 7 d and isolated in ∼50% yield. Elemental analysis (%) calculated for C14H36N6O20Gd2: C 18.22, H 3.93, N 9.11; found: C 18.28, H 3.67, N 8.66. Crystal data for 1: C14H36Gd2N6O20, M = 922.99, triclinic, a = 8.2904(3), b = 8.6272(3), c = 10.2877(3) Å, α = 86.684(3), β = 79.434(3), γ = 84.336(3)°, V = 719.20(4) Å3, T = 100 K, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2), Z = 1, reflections measured 11
(no. 2), Z = 1, reflections measured 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286, 2823 unique (Rint = 0.0421) which were used in all calculations. The final R1 was 0.0343 [for 2669 reflections with I > 2σ(I)] and the final wR(F2) was 0.0889 (all data). CCDC 1520393.†
286, 2823 unique (Rint = 0.0421) which were used in all calculations. The final R1 was 0.0343 [for 2669 reflections with I > 2σ(I)] and the final wR(F2) was 0.0889 (all data). CCDC 1520393.†
[Gd2(H2tea)(Htea)(NO3)3]2·MeOH (2·MeOH)
Triethanolamine (0.5 cm3, 1.0 M solution in MeOH, 0.5 mmol) and [NEt4][OAc]·4H2O (0.131 g, 0.5 mmol) were added to a solution of Gd(NO3)3·6H2O (0.226 g, 0.5 mmol) in MeOH (25 cm3). NEt3 (0.10 cm3, 0.75 mmol) was added and the solution stirred for 1 h. Colourless prisms of 2 were crystallised by vapour diffusion of Et2O over 14 d and isolated in 20% yield. Elemental analysis (%) calculated for Gd4C26H62N10O32: C 18.85, H 3.77, N 8.46; found: C 18.48, H 3.78, N 8.21. Crystal data for 2: C26H62Gd4N10O32, M = 1655.86, monoclinic, a = 14.0518(4), b = 11.2346(3), c = 16.6847(5) Å, β = 103.776(3)°, V = 2558.18(13) Å3, T = 100 K, space group P21/c (no. 14), Z = 2, reflections measured 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816, 5041 unique (Rint = 0.0853) which were used in all calculations. The final R1 was 0.0752 [for 4333 reflections with I > 2σ(I)] and the final wR(F2) was 0.1991 (all data). CCDC 1520394.†
816, 5041 unique (Rint = 0.0853) which were used in all calculations. The final R1 was 0.0752 [for 4333 reflections with I > 2σ(I)] and the final wR(F2) was 0.1991 (all data). CCDC 1520394.†
[Gd(Htea)(NO3)]6·8MeOH (3·8MeOH)
3 was prepared in a slight adaptation of the procedure described by Murray et al.9f Triethanolamine (0.5 cm3, 1.0 M solution in MeOH, 0.5 mmol) was added to a solution of Gd(NO3)3·6H2O (0.226 g, 0.5 mmol) in MeOH/CH2Cl2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) (25 cm3). NEt3 (0.14 cm3, 1.0 mmol) was added and the solution stirred for 10 min. A white precipitate was removed by filtration and colourless plates of 3 were crystallised by slow evaporation over 2 d and isolated in 35% yield. Alternatively, 3 was also prepared by solvothermal methods by sealing Gd(NO3)3·6H2O (0.226 g, 0.5 mmol), triethanolamine (0.5 cm3, 1.0 M solution in MeOH, 0.5 mmol), NEt3 (0.14 cm3, 1.0 mmol) and MeOH (8 cm3) in a Teflon lined bomb and heating to 130 °C for 24 h. After slow cooling 3 was isolated as large colourless crystals in ∼60% yield. 3 can also be prepared without the addition of NEt3, but the yield drops to approximately 30%. Elemental analysis (%) calculated for Gd6C44H110N12O44: C 21.53, H 4.52, N 6.85; found: C 21.18, H 4.12, N 6.66. CCDC 751870.†
1 v/v) (25 cm3). NEt3 (0.14 cm3, 1.0 mmol) was added and the solution stirred for 10 min. A white precipitate was removed by filtration and colourless plates of 3 were crystallised by slow evaporation over 2 d and isolated in 35% yield. Alternatively, 3 was also prepared by solvothermal methods by sealing Gd(NO3)3·6H2O (0.226 g, 0.5 mmol), triethanolamine (0.5 cm3, 1.0 M solution in MeOH, 0.5 mmol), NEt3 (0.14 cm3, 1.0 mmol) and MeOH (8 cm3) in a Teflon lined bomb and heating to 130 °C for 24 h. After slow cooling 3 was isolated as large colourless crystals in ∼60% yield. 3 can also be prepared without the addition of NEt3, but the yield drops to approximately 30%. Elemental analysis (%) calculated for Gd6C44H110N12O44: C 21.53, H 4.52, N 6.85; found: C 21.18, H 4.12, N 6.66. CCDC 751870.†
Acknowledgements
EKB thanks the EPSRC for funding. SGC, GL, ER and ME thank the Spanish Ministry of Economy, Industry and Competitiveness (MAT2015-68204-R and CTQ2015-64579-C3-1-P) and for a postdoctoral grant (to GL). ER acknowledges the Generalitat de Catalunya for an ICREA Academia grant and the BSC (Barcelona Supercomputer Center) for computational resources. KSM thanks the Australian Research Council for a Discovery grant.Notes and references
- (a) L. Engelhardt, M. Luban and C. Schröder, Phys. Rev. B: Condens. Matter, 2006, 74, 054413 CrossRef; (b) A. Ghirri, A. Candini, M. Evangelisti, M. Affronte, S. Carretta, P. Santini, G. Amoretti, R. S. G. Davies, G. Timco and R. E. P. Winpenny, Phys. Rev. B: Condens. Matter, 2007, 76, 214405 CrossRef; (c) A. Machens, N. P. Konstantinidis, O. Waldmann, I. Schneider and S. Eggert, Phys. Rev. B: Condens. Matter, 2013, 87, 144409 CrossRef; (d) F. Adelnia, A. Chiesa, S. Bordignon, S. Carretta, A. Ghirri, A. Candini, C. Cervetti, M. Evangelisti, M. Affronte, I. Sheikin, R. Winpenny, G. Timco, F. Borsa and A. Lascialfari, J. Chem. Phys., 2016, 143, 244321 CrossRef PubMed.
- NanoScience and Technology, in Molecular Magnets: Physics and Applications, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer-Verlag, Berlin, Heidelberg, 2014 Search PubMed.
- F. Luis and M. Evangelisti, Struct. Bonding, 2015, 164, 431 CrossRef CAS.
- (a) K. A. Gschneidner Jr. and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387 CrossRef; (b) M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672 RSC; (c) J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91 CrossRef CAS.
- (a) P. Debye, Ann. Phys., 1926, 386, 1154 CrossRef; (b) W. F. Giauque, J. Am. Chem. Soc., 1927, 49, 1864 CrossRef CAS.
- (a) G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653 CrossRef CAS PubMed; (b) M.-J. Martínez-Pérez, O. Montero, M. Evangelisti, F. Luis, J. Sesé, S. Cardona-Serra and E. Coronado, Adv. Mater., 2012, 24, 4301 CrossRef PubMed.
- See, e.g.: (a) A. Benelli, C. Benelli, A. Caneschi, R. Carlin, A. Dei and D. Gatteschi, J. Am. Chem. Soc., 1985, 107, 8128 CrossRef; (b) M. Andruh, I. Ramade, E. Codjovi, O. Guillou, O. Kahn and J. C. Trombe, J. Am. Chem. Soc., 1993, 115, 1823 CrossRef; (c) J. P. Costes, F. Dahan, A. Dupuis and J. P. Laurent, Inorg. Chem., 1997, 36, 3429 CrossRef CAS PubMed; (d) A. J. Blake, R. O. Gould, C. M. Grant, P. E. Y. Milne, S. Parsons and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 1997, 485 RSC; (e) C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369 CrossRef CAS PubMed; (f) M. Evangelisti, M. L. Khan, J. Bartolomé, L. J. de Jongh, C. Meyers, J. Leandri, Y. Leroyer and C. Mathonière, Phys. Rev. B: Condens. Matter, 2003, 68, 184405 CrossRef; (g) B. W. Wang, S. D. Jiang, X. T. Wang and S. Gao, Sci. China Ser. B: Chem., 2009, 52, 1739 CrossRef CAS.
- (a) R. H. Laye and E. J. L. McInnes, Eur. J. Inorg. Chem., 2004, 2811 CrossRef CAS; (b) R. Shaw, R. H. Laye, L. F. Jones, D. M. Low, C. Talbot-Eeckelaers, Q. Wei, C. J. Milios, S. Teat, M. Helliwell, J. Raftery, M. Evangelisti, M. Affronte, D. Collison, E. K. Brechin and E. J. L. McInnes, Inorg. Chem., 2007, 46, 4968 CrossRef CAS PubMed.
- See for example: (a) N. F. Chilton, S. K. Langley, B. Moubaraki and K. S. Murray, Dalton Trans., 2010, 46, 7787 CAS; (b) S. K. Langley, N. F. Chilton, M. Massi, K. J. Berry and K. S. Murray, Dalton Trans., 2010, 39, 7236 RSC; (c) S. K. Langley, B. Moubaraki and K. S. Murray, Dalton Trans., 2010, 39, 5066 RSC; (d) S. K. Langley, B. Moubaraki, K. J. Berry and K. S. Murray, Dalton Trans., 2010, 39, 4848 RSC; (e) S. K. Langley, K. J. Berry, B. Moubaraki and K. S. Murray, Dalton Trans., 2009, 973 RSC; (f) S. K. Langley, B. Moubaraki, C. M. Forsyth, I. A. Gass and K. S. Murray, Dalton Trans., 2010, 39, 1705 RSC; (g) T. C. Stamatatos, D. Foguet-Albiol, W. Wernsdorfer, K. A. Abboud and G. Christou, Chem. Commun., 2011, 47, 274 RSC.
- S. K. Langley, N. F. Chilton, B. Moubaraki, T. Hooper, E. K. Brechin, M. Evangelisti and K. S. Murray, Chem. Sci., 2011, 2, 1166 RSC.
- W. Plass and G. Fries, Z. Anorg. Allg. Chem., 1997, 623, 1205 CrossRef CAS.
- K. Manseki, H. Sakiyama, M. Sakamoto, Y. Nishida, H. Aono, Y. Sadaoka, M. Ohba and H. Okawa, Synth. React. Inorg. Met.-Org. Chem., 2001, 31, 1443 CrossRef CAS.
- S. Mathur, H. Shen, N. Lecerf, A. Kjekshus, H. Fjellvag and G. F. Goya, Adv. Mater., 2002, 14, 1405 CrossRef CAS.
- N. G. Naumov, M. S. Tarasenko, A. V. Virovets, Y. Kim, S. J. Kim and V. E. Fedorov, Eur. J. Inorg. Chem., 2006, 298 CrossRef CAS.
- S. D. Daniel, J. S. M. Lehn, P. van der Heide, Y. Q. Wang and D. M. Hoffman, Inorg. Chim. Acta, 2006, 359, 257 CrossRef CAS.
- L. Canadillas-Delgado, O. Fabelo, J. Pasan, F. S. Delgado, F. Lloret, M. Julve and C. Ruiz-Perez, Dalton Trans., 2010, 39, 7286 RSC.
- Y. N. Guo, G. F. Xu, P. Gamez, L. Zhao, S. Y. Lin, R. P. Deng, J. K. Tang and H. J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538 CrossRef CAS PubMed.
- H. S. Ke, G. F. Xu, Y. N. Guo, P. Gamez, C. M. Beavers, S. J. Teat and J. K. Tang, Chem. Commun., 2010, 46, 6057 RSC.
- J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, J. Comput. Chem., 2001, 22, 985 CrossRef.
- (a) M. S. José, A. Emilio, D. G. Julian, G. Alberto, J. Javier, O. Pablo and S.-P. Daniel, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef; (b) E. Artacho, E. Anglada, O. Diéguez, J. D. Gale, A. García, J. Junquera, R. M. Martin, P. Ordejón, J. M. Pruneda, D. Sánchez-Portal and J. M. Soler, J. Phys.: Condens. Matter, 2008, 20, 064208 CrossRef PubMed; L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- (a) E. Cremades, S. Gómez-Coca, D. Aravena, S. Alvarez and E. Ruiz, J. Am. Chem. Soc., 2012, 134, 10532 CrossRef CAS PubMed; (b) D. Aravena, D. Venegas-Yazigi and E. Ruiz, Sci. Rep., 2016, 6, 23847 CrossRef CAS PubMed.
- (a) M. E. Fisher, Am. J. Phys., 1964, 32, 343 CrossRef; J. H. Luscombe, M. Luban and F. Borsa, J. Chem. Phys., 1998, 108, 7266 Search PubMed.
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Packing diagrams, magnetization data, magnetic entropy data, computational details. CCDC 1520393 and 1520394. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02281f |
| ‡ Current address: School of Science and the Environment, Division of Chemistry, Manchester Metropolitan University, Manchester M15 6BH, UK. |
| This journal is © The Royal Society of Chemistry 2017 |