Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effective transport properties of porous composites applied to MIEC SOC electrodes†
Philip
Marmet
 *ab,
Lorenz
Holzer
*ab,
Lorenz
Holzer
 a,
Thomas
Hocker
a,
Gernot K.
Boiger
a,
Thomas
Hocker
a,
Gernot K.
Boiger
 a and
Joseph M.
Brader
a and
Joseph M.
Brader
 b
b
aZurich University of Applied Sciences, Institute of Computational Physics, CH-8400 Winterthur, Switzerland. E-mail: mame@zhaw.ch
bDepartment of Physics, University of Fribourg, CH-1700 Fribourg, Switzerland
First published on 3rd July 2024
Abstract
Semi-analytical models describing transport phenomena governed by the Laplace equation (like conduction of charge carriers or heat) are presented for the case of a porous composite with two solid phases and one pore-phase (i.e., two conducting and one insulating phase), closing the existing gap in the literature for fast and accurate predictions for this particular case. The models allow for an efficient screening of promising concepts and material combinations, as they are computationally much more efficient compared to numerical simulations on a 3D geometry. Three different semi-analytical models (Maxwell, Xu and MST models) are compared and validated using a microstructure dataset of perovskite–CGO solid oxide cell electrodes obtained by stochastic modeling. Based on the results from both numerical and semi-analytical models, the effects of the resulting composite transport properties are discussed for the application example of these fully ceramic electrodes. CGO and the used LSTN perovskite are both mixed ionic and electronic conductors (MIECs), which leads to different reaction mechanisms and associated requirements for the microstructure design compared to, e.g., Ni–YSZ. Due to the MIEC-property of both solid phases, the transport of neither electrons nor oxygen ions is limited to a single phase. Consequently, the composite conductivity, which is inherent to MIEC electrodes, opens a much larger design space for microstructure optimization compared to the single-phase conductivity of conventional electrodes, which are prone to percolation failure.
1 Introduction
Transport phenomena in composite materials are relevant for many technical applications. There is a class of transport phenomena, which can be described by the Laplace equation, like the conduction of heat (e.g., in electronic components), the conduction of charged species (e.g., electrons and oxygen ions in solid oxide cell electrodes) or diffusion in solids. Typically, the components of a composite have different intrinsic transport properties. However, the resulting effective transport properties not only depend on the intrinsic material properties, but also on the volume fractions and the morphological arrangement of the components (e.g., microstructure limitations). A conceptually straightforward way to determine the effective transport properties of such transport phenomena is to solve the Laplace equation numerically on a specific 3D geometry using a software package like GeoDict1 or TauFactor.2 However, for this simulation-based approach, an exact 3D representation of the microstructure needs to be available, e.g., from tomography. Alternatively, analytical approaches are reported in the literature. Especially the effective thermal conductivity of two-phase systems is widely discussed3 because of its technical relevance for the engineering of thermal components. However, composites with three phases are rarely studied, despite the fact that they are frequently used in applications such as battery and fuel cell electrodes. Thus, a framework for the systematic study of porous composite three-phase materials (i.e., two solid phases and one pore phase) shall be elaborated in this publication. Hence, the scenario considered in the present study considers the special case, where the transport can happen in two phases of the composite to a different extent, due to different intrinsic transport properties. The third phase (pore-phase) does not contribute to the transport process and thus represents a microstructural obstacle. In this paper, the term “composite conductivity” will be used to describe the resulting effective property describing the ability of the composite to transport a certain quantity. Thus, the term “composite conductivity” is used for effective transport of different physical phenomena that can be described by the Laplace equation like charge transport, heat transport and diffusion. Thereby, we consider three different semi-analytical models from the literature, which are capable of predicting the composite conductivity in composite materials with two phases (Section 2.3). These three models are studied and reformulated, so that they are applicable to three phase materials (i.e., porous composites).An application example for this scenario is heat transport in a porous composite. Thereby, the analytical models typically consider cases where the heat transport (conduction, radiation, convection) in the pore-phase is negligible compared to the heat transport in the solid phases. Moreover, the analytical models equally describe solid-phase diffusion or conduction processes in porous composites. Another relevant example concerns solid oxide cell (SOC) electrodes consisting of two solid phases with mixed ionic electronic conducting (MIEC) properties. In these MIEC electrodes, the transport of both charge carriers (electrons and oxygen ions) extends to both solid phases. Note that in practice there exist composite SOC electrodes with zero, one or two MIEC materials. An example for zero MIEC materials is Ni–YSZ (i.e., a combination of two single-phase conductors). In this electrode, Ni is the electronic conducting phase and YSZ is the ionic conducting phase. In Ni–YSZ, there is thus no composite conductivity taking place. An example for composite SOC electrodes with one MIEC material is Ni–CGO. This electrode owns composite conductivity properties only for the transport of electrons, but not for ions. Finally, an example for composite SOC electrodes with two MIEC materials is LSTN–CGO, which owns composite conductivity properties for the transport of electrons and ions (see discussion in Section 2.4.1). Moreover, in the emerging semiconductor electrochemistry, composite conductivity can also be relevant for recent semiconductor-ionic composite materials, e.g., used for electrolyte-layer-free fuel cells (EFFCs). Thereby, the electrolyte of a conventional SOFC design is replaced by a p–n junction forming in situ under a fuel cell atmosphere. For example, Zhu et al.4 reported a functional EEFC with a high power density (ca. 1000 mW cm−2 at 550 °C) using a MIEC-based semiconductor–ionic composite with La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF) and Sm–Ca co-doped ceria (SCDC). An overview of this recent topic can be found in the review by Zhu et al.5
The composite conductivity of porous SOC-electrodes with two MIEC phases and using a conventional electrolyte based design will be used in this paper as the main application example. Thereby, perovskite–CGO composites represent one of the most important material combinations for Ni-free fuel electrodes (e.g., ref. 6–9), which show promising results concerning improved stability and degradation behavior. The ionic and electronic composite conductivities specific for MIEC-based SOC electrodes and their implications for microstructure optimization will be thoroughly discussed in Section 2.4. For this purpose, a microstructure dataset consisting of numerous compositional variations is available from a previous study (Marmet et al.10). These virtual microstructure variations were constructed with a model of stochastic geometry, which was fitted to real tomography data from experimental LSTN–CGO electrodes. This set of virtual 3D structures (with realistic properties) is used as input for numerical transport simulations (solving the Laplace equation), whereby the different intrinsic ionic or electronic conductivities of the two MIEC phases are considered. In this way, accurate numerical determination of the composite conductivity is achieved, and these numerical results will be used as a reference for calibration and validation of the three analytical models (Section 3.3). Hence, the numerical simulations are typically much more reliable, but they are also more expensive in terms of the required microstructure input and also regarding the computational resources. The question thus arises, how precise and reliable the prediction with analytical models can be, and whether or not these analytical models can be used to replace the more expensive numerical models. Moreover, only a few analytical models are available, which can consistently be applied to a material system with a phase without conductivity (pore-phase) as, e.g., the quadratic parallel model,11 while many mixing models12–14 are not well defined in this particular case (see also literature discussion in Section 2.3).
Besides the introduction of the semi-analytical models, a further goal of this paper is to discuss the implications of the composite conductivity effects for the microstructure and material design for the specific example of SOC electrodes. However, the discussion of absolute performance data is out of scope of this paper, as this involves a thorough consideration of additional effects like gas transport in pores and reaction kinetics calibrated to dedicated experiments, e.g., on the basis of a multiscale-multiphysics electrode model as reported in Marmet et al.56 and in the PhD-thesis by Ph. Marmet15 (Sections 9 and 10). Hence, a simple analytical model will be used to demonstrate the impact of the composite conductivity on the performance of solid oxide fuel cell (SOFC) electrodes in a qualitative way. Thereby, microstructure design regions are discussed and compared for three different anode material systems (Section 3.2): perovskite–CGO (with composite conductivities), Ni–YSZ (with single-phase conductivities), and Ni–CGO (with single-phase ionic and composite electronic conductivities). Finally, important guidelines on how to optimize perovskite–CGO anode composition and its constituents are provided (Section 3.4). For this purpose, the semi-analytical Xu-model is used for an efficient screening of optimization strategies related to the phase compositions and intrinsic conductivities.
Additional details about composite conductivity effects including the semi-analytic models and their validation can be found in the ESI,† and in Chapter 6 of the PhD-thesis of Ph. Marmet.15
2 Methods and models
2.1 From single-phase to composite conductivity
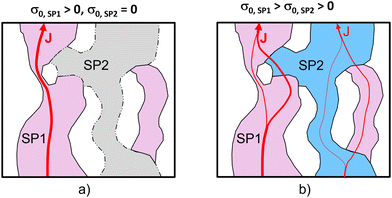
We study the conductivity of a porous composite (two solid phases and one pore-phase) as illustrated in Fig. 1. We first consider the case in Fig. 1(a), where only the solid-phase 1 (SP1) is conductive, while the solid-phase 2 (SP2) is an insulator. Hence, the conductive transport takes place in a single solid phase (SP1). The corresponding effective single-phase conductivity can be expressed as| σeff = σrel,SP1·σ0,SP1, | (1) |
For (a) the simulated relative conductivity σsimrel (or simulated M-factor Msim) is defined as
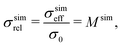 | (2) |
(b) On the other hand, prediction based on the knowledge of microstructure characteristics requires morphological analysis of phase volume fraction ϕ, geodesic tortuosity τdir,geod and constrictivity β of the transporting phase, as described by Stenzel et al.:17
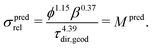 | (3) |
(a) For the single-phase conductivities, the impact of intrinsic properties (σ0) and microstructure limitations (σrel) can be described separately from each other. The relative conductivity is therefore also called microstructure factor (M-factor)17 since it describes purely geometric effects. To emphasize this fact, the M-factor notations Msim and Mpred are also stated in eqn (2) and (3), respectively.
(b) For the case of single-phase conductivity (Fig. 1(a)), it is also important to note that disconnected components (i.e., islands) of SP1 do not contribute to the transport at all. This is expressed by a reduced value for the effective phase volume fraction (ϕeff). Furthermore, the bottlenecks within the phase network of SP1 have a strongly limiting effect on the relative conductivity, which is expressed by a small value for constrictivity (β).
We now consider the case of a porous composite illustrated in Fig. 1(b), where also SP2 contributes to the conductive transport of the same species (e.g., ions) as in SP1, but to a lower extent (i.e., σ0,SP1 > σ0,SP2). As the transport is no more limited to a single phase, the transport limitations due to the microstructure of the single phases are less restrictive. Disconnected components (islands), bottlenecks and tortuous pathways in one solid-phase can be bridged by the second solid-phase (and vice versa). This can result in a significantly higher composite conductivity compared to the single-phase conductivity, even for cases where the intrinsic conductivity of SP2 is significantly lower compared to SP1. As will be shown later, this improvement is particularly strong for cases where SP1 suffers from pronounced microstructural limitations such as disconnected islands and narrow bottlenecks.
2.2 Definition of the composite conductivity
The effective composite conductivity depends on the intrinsic conductivities of both solid phases and on the microstructure (including obstacles from the insulating pore phase). However, the microstructure-effect cannot be determined as easily as for material systems with single-phase conductivity only. In contrast to the effective single-phase conductivity, the effects of intrinsic properties and of the microstructure on the effective composite conductivity cannot be strictly separated. This is because the transport pathways extend over both solid phases and are a result of combined effects of the intrinsic conductivities and microstructure effects of both phases. For example, if the transport pathway between two disconnected regions (e.g., separate grains) of a solid-phase (e.g., SP1) is bridged with another material with poorer conductivity (e.g., SP2), the effect on the total conductivity depends on both, the shape of the bridge and the intrinsic conductivity of the bridging material.In order to provide a measure similar to the relative single-phase conductivity (or M-factor) of eqn (1), a relative composite conductivity σrel,comp is defined in eqn (4). The definition is valid for a composite with two solid phases, where the first solid-phase (SP1) has a higher conductivity compared to the second solid-phase (SP2).
| σeff,comp = σrel,comp·σ0,SP1, | (4) |
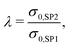 | (5) |
| σrel,comp = f(λ). | (6) |
The total relative composite conductivity (σrel,comp) can be subdivided into three distinct components (see also the illustration in Fig. 4), which are (a) the single-phase contribution from SP1 (σrel,SP1), (b) the single-phase contribution from SP2 (λ·σrel,SP2), and (c) a particular contribution, which is specific to composite conductivity scenarios (σrel,comp-part). The latter contribution is, for example, due to the bridging of islands in the phase network of SP1 via pathways in SP2. These islands would not contribute to transport in single-phase conducting scenarios. This particular contribution (σrel,comp-part) becomes very important, for example, when the porosity increases and/or when the phase volume fraction of SP1 decreases. An illustration of some basic microstructure effects like the influence of porosity, composition and wetting behavior on the total composite conductivity and the three mentioned components is illustrated in Section A of the ESI.†
2.3 Models to predict the composite conductivity
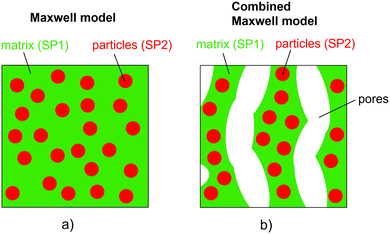
The relative composite conductivities can be determined by numerical simulation (solving the Laplace equation) on the 3D geometry of a microstructure for a specific conductivity ratio λ of the two solid phases, as described in a previous publication (Marmet et al.16). However, the result is only valid for a specific conductivity ratio λ and the computationally expensive simulation needs to be repeated for every λ of interest. Moreover, this approach only provides limited conceptual insight. Therefore, a more efficient (semi) analytical model for prediction of composite conductivity of porous composites is of high interest, allowing for a fast screening of promising material combinations and microstructure designs and at the same time providing a more fundamental understanding of the complex microstructure phenomena involved.In the literature, some models for the conductivity of porous composites are available in the context of solid oxide cells, which are also the main application example in this paper. There are many studies available for the conductivity of SOFC anodes, where electrons and ions are transported in separate phases. Many of them are based on percolation theory (e.g., ref. 20–22), which is an important concept for this electrode type with only single-phase conductivities. In contrast, studies about composite conductivity are rare. Specifically, a few publications are available for MIEC cathodes. Chen et al.23 presented a model for SOFC cathodes to treat composite conductivities for a combination of pure ion conducting materials like YSZ and CGO (in a cathodic environment) and MIEC-phases like LSCF or LSCM. Their approach is based on the percolation theory. More general literature is available for two-phase systems without porosity, which is especially of importance for the thermal conductivity of composite materials. Wang et al.24 and Karol et al.3 provided an overview of different models in such scenarios. Basically, the models can be grouped into two main classes based on the criteria of phase percolation of both phases. A very common model for non-percolating and even non-touching particles in a continuous matrix is the Maxwell model.25 Models with two continuous phases have, e.g., been formulated by Agari and Uno26 and by Xu et al.27
Moreover, also models for the composite conductivity for three-phase systems are available. Woodside and Messmer11 proposed the quadratic parallel (QP) model for the effective composite conductivity:
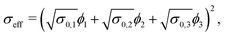 | (7) |
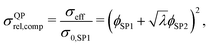 | (8) |
There are also more sophisticated multiphase models available, where a multiphase material is divided into a combination of several two-phase systems24 like the Maxwell–DeLoor model.12,13 Like the QP model, no geometric parameters are required for these mixture models. Dobson et al.14 formulated this model for a four-phase system. However, this model is not well defined for a case with vanishing conductivity (i.e., pore-phase), as the equation includes division by the vanishing intrinsic conductivity, resulting in division by zero. Therefore, a direct comparison with our models and for our microstructure and material scenarios is not possible.
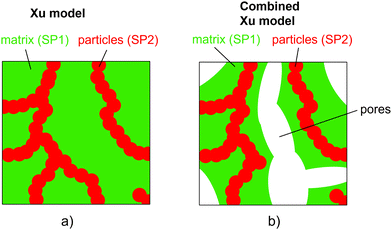
In the following, the Maxwell model and the model of Xu et al.27 will be discussed in more detail and modifications will be introduced in order to make them usable for three-phase electrodes with two solid MIEC-phases and one pore-phase. In contrast to the QP model and the mixture models, geometrical parameters will be used.
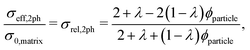 | (9) |
The assumptions of the Maxwell model in its original form are violated if applied for porous composite electrodes and thus some modifications are needed. The assumption of a continuous matrix is violated because of the porosity. This scenario is shown in Fig. 2(b). Thereby, the insulating pore-phase does not contribute to the conductivity. Hence, the effect of the pore-phase can be captured by multiplying the relative two-phase composite conductivity σrel,2ph (eqn (9)) according to the conventional Maxwell model with the relative conductivity σrel,SPtot of the total solid-phase in order to obtain an estimation for the relative composite conductivity of the three-phase system as formulated in eqn (10):
| σrel,3ph = σrel,2ph·σrel,SPtot | (10) |
Note that the relative conductivity (M-factor) according to eqn (1) is normally only applicable to single-phase conductivity scenarios. For example, in a porous medium with a single conducting solid phase, the relative conductivity describes microstructure limitations induced by the pore-phase. In the combined Maxwell model of eqn (10), σrel,2ph can be considered as a homogenization approach for the composite solid-phase. In this way, the application of the relative conductivity similar to a single-phase scenario is justified. Thereby, σrel,SPtot is determined numerically for the total solid-phase according to eqn (2) (i.e., the corresponding simulated property σsimrel,SPtot is used as defined in Marmet et al.16). Alternatively, the relative conductivity can also be estimated based on eqn (3). Hence, the morphology of the total solid-phase (i.e., the effects of total solid-phase volume fraction, tortuosity and constrictivity) is respected with σrel,SPtot and the contributions of the two solid phases with individual intrinsic conductivities with the Maxwell model. In the pore-phase, no charge transport takes place. The porosity ε represents the inactive phase volume fraction and is considered in the model via the total solid-phase volume fraction (i.e., ϕtot = 1 − ε), while tortuosity and constrictivity are not of importance for the insulating pore-phase.
However, the assumption of sparse particles forming isolated islands within the matrix (as shown in Fig. 2(a) and (b)) is often violated in composite materials. In addition, the particles will sometimes also be located at the pore-interface and thus are not totally enclosed within the matrix. The latter issue cannot at all be accounted for within this model framework. On the other hand, the issue with the dilute approximation of the particles can be partially resolved. The assumption of isolated particles approximately holds for very low volume fractions of the minor phase (SP2), far below the percolation threshold. In eqn (11), the relative two-phase conductivity σrel,2ph,M1 is formulated using SP1 as the matrix-phase and SP2 as the particle-phase. Thus, this equation can be expected to provide a good approximation for low relative volume fractions of SP2 ϕSP2,rel ≪ 0.5 but to be inaccurate for large ϕSP2,rel > 0.5. Additionally, eqn (11) can also be formulated using SP2 as the matrix-phase and SP1 as the particle-phase, as reported in eqn (12). The two terms of eqn (11) and (12) are then blended according to the relative volume-fractions in eqn (13), resulting in the prediction for the composite conductivity σMaxrel,comp. Therewith, always the term with the larger volume fraction for the matrix is dominant, which is in accordance with the Maxwell model assumptions. However, it has to be expected that the prediction is less accurate around the relative volume fractions of ϕSP1,rel = ϕSP2,rel = 0.5, as will be discussed in Section 3.3. Note that in eqn (12) for the relative two-phase conductivity σrel,2ph,M2 with SP2 as the matrix-phase, the intrinsic conductivity ratio λ has to be inverted. Moreover, the multiplication with λ is needed in order to establish the correct relationship between σrel,2ph,M2 and the intrinsic conductivity of SP1 (according to the definition in eqn (4)), as derived in Section C.1 of the ESI.† Thus, the set of equations for the prediction of the relative composite conductivity σMaxrel,comp using the (modified) Maxwell model reads (eqn (11)–(13))
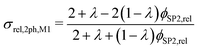 | (11) |
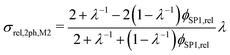 | (12) |
| σMaxrel,comp = (ϕSP1,rel·σrel,2ph,M1 + ϕSP2,rel·σrel,2ph,M2)·σrel,SPtot, | (13) |
The prediction power and limitation of this modeling approach will be discussed in the results Section 3.3.
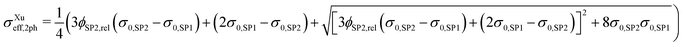 | (14) |
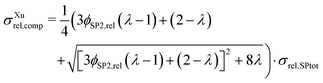 | (15) |
Note that because in the formulation in eqn (14) and (15) the interface resistance between the grains is neglected, the formulation is symmetrical with respect to SP1 and SP2. Hence, it does not matter which solid-phase is chosen as the matrix-phase or particle-phase. Therewith, a procedure with blending to equations using SP1 and SP2 as the matrix-phase as used for the Maxwell model (described in Section 2.3.1) is not necessary. In contrast to the Maxwell model, the Xu model assumes percolating phases. This assumption is violated for very low volume fractions of the minor phase, as will be discussed in the results Section 3.3.
The effective composite conductivity can be interpreted to be composed of three parts: (1) single-phase conductivity of SP1, (2) single-phase conductivity of SP2 and (3) a composite conductivity part, originating from transport pathways crossing the phase boundaries (e.g., using islands and dead-ends). These three conductivity components constitute the relative composite conductivity, as formulated in eqn (16).
| σrel,comp = σrel,SP1 + λ·σrel,SP2 + σrel,comp-part,Rint, | (16) |
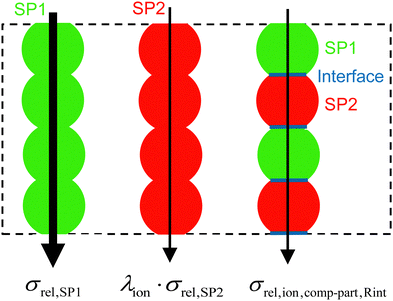 | ||
| Fig. 4 Illustration of the MST model for an artificial microstructure example, where the single-phase and composite conductivity parts can be easily distinguished. | ||
The breakdown of the relative composite conductivity into these three parts is the basis for the MST model to predict the relative composite conductivity reported in eqn (17). Thereby, the formulation of the contributions of the single-phase conductivities is straightforward and can be directly used as stated in eqn (16):
| σMSTrel,comp = σrel,SP1 + λ·σrel,SP2 + σMSTrel,comp-part,Rint, | (17) |
| σMST,ν→0rel,comp-part,Rint = σMSTrel,comp-part = λa·(σrel,SPtot − (σrel,SP1 + σrel,SP2)), | (18) |
The expression for composite conductivity needs to be modified for material scenarios, where interface resistance becomes relevant:
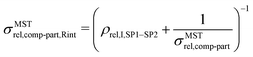 | (19) |
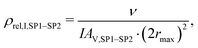 | (20) |
| ν = ρint·σ0,SP1 | (21) |
Note that the MST model provides correct values for the extreme cases of the relative composite conductivity (eqn (17):
• σMSTrel,comp = σrel,SP1 for λ = 0
• σMSTrel,comp = σrel,SPtot for λ = 1 and ν = 0
• σMSTrel,comp = σrel,SP1 + σrel,SP2 for ν → ∞ (i.e., perfect insulation between SP1 and SP2)
2.4 Composite conductivity in porous MIEC SOC composite electrodes
In this section, the composite conductivity is discussed for the specific application example of SOC electrodes consisting of two conductive solid phases (i.e., two MIEC phases conducting electrons and oxygen ions) and an insulating pore-phase. Thereby, the effect of composite conductivity on the functionality of MIEC-based electrodes is illustrated qualitatively and compared to conventional SOC electrodes (Section 2.4.1). Moreover, the semi-analytical models shall be validated based on numerical calculations on a dataset of SOC microstructures. Thus, the corresponding methodological framework for this validation is introduced (Section 2.4.2). Finally, the methodical approach is critically evaluated including a discussion on limitations and the validation concept for the semi-analytical models is presented (Section 2.4.3).| Material | MIEC | Intrinsic electronic conductivity (S cm−1) | Intrinsic ionic conductivity (S cm−1) | Ref. |
|---|---|---|---|---|
| a Hypothetical MIEC perovskite with the same electronic conductivity as LSTN and with relatively high ionic conductivity (half the value of CGO) and. b Hypothetical MIEC perovskite with the same electronic conductivity as LSTN and with relatively low ionic conductivity (factor 10 lower than LSTN) used for the validation of the composite conductivity models only. | ||||
| Ni | No |
σ
0,eon,Ni = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
σ 0,ion,Ni = 0 | 37 |
| YSZ ((ZrO2)0.92(Y2O3)0.08) | No | σ 0,eon,Ni = 0 | σ 0,ion,YSZ = 0.07 | 38 |
| CGO (Ce0.9Gd0.1O1.95−δ) | Yes | σ 0,eon,CGO = 1.83 | σ 0,ion,CGO = 0.13 | 39 |
| LSTN (La0.3Sr0.55Ti0.95Ni0.05O3−δ) | Yes | σ 0,eon,LSTN = 18.3 | σ 0,ion,LSTN = 0.013 | 7 and 40 |
| Perovskite 1a | Yes | σ 0,eon,Per1 = 18.3 | σ 0,ion,Per1 = 0.065 | — |
| Perovskite 2b | Yes | σ 0,eon,Per2 = 18.3 | σ 0,ion,Per2 = 0.0013 | — |
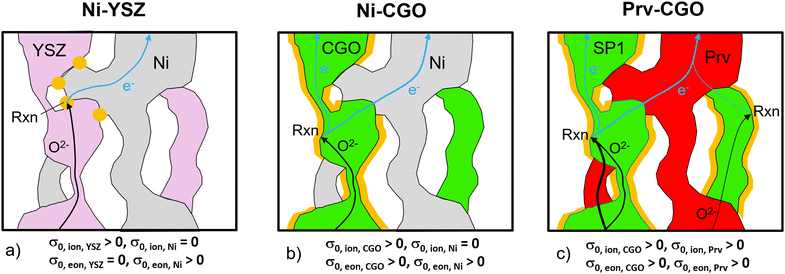
As an alternative anode concept, mixed ionic and electronic conductive (MIEC) materials are drawing much attention. An already well-established MIEC material system is Ni–CGO. As illustrated in Fig. 5(b), the fuel oxidation reaction can take place on the contiguous pore-CGO interface, i.e., the contiguous double-phase boundaries (DPBs), because not only the ions but also the electrons can pass through the CGO-phase (see also Table 1). In addition, CGO has oxygen donor properties. However, because ions cannot pass through the Ni-phase, disconnected CGO-features do not contribute to the fuel oxidation. In addition, bottlenecks and tortuous pathways within the CGO-phase limit the effective ionic conductivity. Hence, this anode has beneficial properties due to the composite electronic conductivity of Ni and CGO. But for ions, it remains a single-phase conducting anode. In practice, even though Ni–CGO anodes show higher tolerance for carbon deposition41 and sulfur poisoning42 compared to Ni–YSZ, some of the issues associated with the Ni-degradation persist in these Ni–CGO anodes.43–45
The third alternative is perovskite–CGO composites, which represent one of the most important material combinations for anodes (e.g., ref. 6–9). Thereby, the Ni-phase is replaced by a perovskite with the goal to get rid of the harmful degradation phenomena associated with Ni. In fact, a high robustness against carbon coking, sulfur poisoning and redox-cycling is reported for many perovskite oxides.6 It is important to mention that the intrinsic transport properties of perovskites can vary greatly, depending on their chemical composition and stoichiometry. For SOFC anodes, La–Sr–titanates (+/-Ni, Ca, Co, Fe) are often used, because these perovskites show relatively high electronic conductivity, but also some minor ionic conductivity (see Table 1). Hence, when combined with CGO, these anodes exhibit composite conductivities for both ionic and electronic transport, in contrast to the Ni–CGO anodes. The successful application of perovskite–CGO anodes has been frequently reported in the literature. Typically, a perovskite backbone is infiltrated with nano-sized CGO. In addition, in some studies a metal catalyst is added, in order to enhance the reactivity for fuel oxidation.8,40,46–50 As an alternative structural architecture, perovskite–CGO composite backbones are fabricated, with or without additional metal catalyst infiltration. This type is also reported as a promising SOFC anode.7,9,51–54 The inclusion of CGO in the backbone has the advantage that it increases the ionic conductivity of the backbone, as CGO in general shows a much higher intrinsic ionic conductivity (0.13 S cm−1) compared to the available perovskites (see Table 1). The composite conductivities (both for ions and electrons) of such perovskite–CGO composite structures will be thoroughly studied in the following. A more detailed discussion of perovskite materials (especially titanates) and their application as perovskite–CGO composite anodes is reported in Chapter 3 of the PhD thesis by Ph. Marmet.15 Fully ceramic anodes such as titanate-CGO offer some specific advantages compared to conventional cermet anodes, even beyond the improved degradation behavior that is typically associated with Ni. Ceria- and perovskite-based phases are both mixed ionic and electronic conductors (MIEC), which leads to very different reaction mechanisms and associated requirements for the microstructure design compared to, e.g., Ni–YSZ. Due to the MIEC-property of both solid phases, the transport of neither electrons nor oxygen ions is limited to a single phase, as illustrated in Fig. 5(c). As a consequence, composite MIEC electrodes show composite conductivities for electrons as well as for ions, which are typically much higher than the (hypothetical) single-phase conductivities of the same microstructure (i.e., assuming the same phase morphologies, but with different intrinsic transport properties, as shown in Fig. 5). In composite MIEC anodes, the charge carriers can reach the reaction sites even when the volume fraction of one or even both MIEC-phases is below the percolation threshold, because the missing single-phase contiguity is automatically bridged by the second MIEC-phase. The MIEC properties thus open a much larger design space for microstructure optimization of composite electrodes.
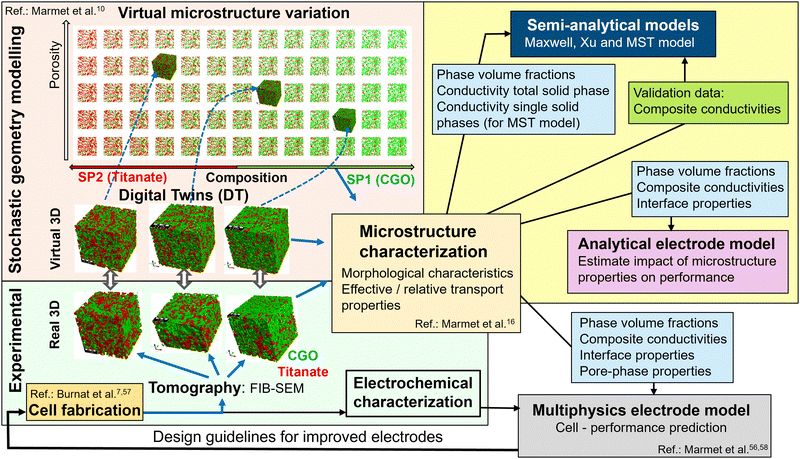 | ||
| Fig. 6 Overview of digital material design (DMD) methodologies for model-based optimization of SOC electrodes (and illustration of data flow in the present study). The field with yellow background (top right) marks the methodologies and the data flow used in this paper for prediction/validation of composite conductivity and electrode performance. A set of virtual 3D structures from stochastic modelling (in a previous study10) was extensively characterized with image analysis and with numerical transport simulation (see the ‘microstructure characterization’-box in the center). The light blue boxes represent output from microstructure characterization (i.e., microstructure characteristics and effective/relative conductivities), which are used as input for various models (to predict composite conductivity as well as electrode performance). Furthermore, the numerically determined composite conductivities (green box) are used in the present study for validation of the semi-analytical models. The other methodological modules of the DMD workflow are described in great detail in separate papers, such as the module including material processing and cell fabrication (see Burnat et al.7,57), the modules for imaging and standardized microstructure characterization (Marmet et al.16 and Holzer et al.18), the module of stochastic geometry modeling and associated realization of digital twins (Marmet et al.10), and the module for performance prediction with a multiphysics electrode model (Marmet et al.56,58). A detailed description of the entire DMD workflow, including all the different modules, is also given in the PhD thesis of Ph. Marmet.15 | ||
The determined microstructure properties can also serve as an input for multiphysics electrode models to predict the impact of the microstructure variation on the electrode performance (see also Marmet et al.56,58). This model-based performance prediction enables one to establish the relationship between fabrication parameters, material choice, microstructure properties and cell-performance and thus to provide design guidelines for the fabrication of electrodes with improved performance, as illustrated in Fig. 6. Such a detailed study was reported in Marmet et al.56 and in the PhD-thesis by Ph. Marmet15 (Sections 9 and 10) including a thorough consideration of additional effects like gas transport in pores and reaction kinetics calibrated to dedicated experiments. However, such an extensive study is out of scope of the current publication. Hence, a simple analytical model will be used in the results Section 3.2 to demonstrate the impact of the composite conductivity on the performance of solid oxide fuel cell (SOFC) electrodes in a qualitative way, including a comparison to conventional electrodes. Thereby, the characterized microstructure properties, namely the phase volume fractions, the ionic and electronic composite conductivities and the interface properties (i.e., TPB density and volume specific interface areas), are used as model inputs (see also Fig. 6).
Furthermore, this dataset is also used for the validation of the semi-analytical models for composite conductivity. Thereby, the phase volume fractions and the relative single-phase conductivity (or M-factor) of the total solid-phase are used as model inputs for the Maxwell and the Xu model. For the MST-model, the relative single-phase conductivities of the individual solid phases are additional model inputs (see also Fig. 6). The results of the semi-analytical models can then be compared and validated against the numerical results of the composite conductivity for specific conductivity ratio λ of the intrinsic conductivities. It must be emphasized that the numerical calculations need to be repeated for every conductivity ratio λ of interest, which is computationally demanding. In contrast, the semi-analytical models can predict the composite conductivity for arbitrary λ without the need of numerical re-calculation.
Note that the terms anode and cathode are used in this paper referring to an SOFC. However, these terms can equally be associated with fuel electrodes and air electrodes including the applications for SOEC, even if it is not explicitly mentioned further on. Moreover, the methodologies presented for MIEC-based SOFC anodes can equally be used for MIEC-based SOFC cathodes as, e.g., LSCF–CGO with single-phase electronic and composite ionic conductivity (note that CGO conducts only oxygen ions and not electrons under cathodic conditions).
The methodological approach can be summarized as follows: composite conductivities are predicted with semi-analytical models, which are derived partly by the authors and partly from the literature. The predicted composite conductivities are compared with the results from numerical simulations. For this purpose, a set of 150 virtual 3D structures with two solid-phases and a pore-phase are created with stochastic geometry modelling. This stochastic model was developed in a previous study (Marmet et al.10). In this way, a wide range of microstructures can be covered, representing hypothetical but realistic SOFC electrode microstructures. Furthermore, different material scenarios can be simulated by attributing hypothetical but realistic phase compositions (e.g., Ni–YSZ, Ni–CGO, LSTN–CGO, hypothetical perovskite(s)-CGO) to the two solid phases. Hence, the attributed material combinations are covering a wide range of intrinsic conductivities, which are listed in Table 1.
Validation of semi-analytical models (a): the validation of semi-analytical models for the prediction of composite conductivity is presented with the following three steps:
(1) A suitable reference dataset for validation needs to be used. The use of an experimental dataset is not feasible because of the needed large amount of data. Hence, our large dataset of virtual SOFC electrodes is an ideal basis for the validation. Moreover, the numerical model solving the Laplace equation is exactly consistent with the underlying assumptions of the semi-analytical models, without any additional side-effects. Note that the numerical calculation on the voxel grid based on the finite element method is very accurate and reliable. This has been shown in numerous studies using tomography data as structural input (Holzer et al.18). Hence the comparison of composite conductivities predicted with the analytical model vs. numerical simulation can be considered as a reasonable (model based) validation, which does not require further experimental validation.
(2) Moreover, the accuracy of the semi-analytical models also depends on the structure type (see also Section 3.3). Hence, the validation needs to be performed for the specific structure type of interest. This is ensured in the current study by using microstructures generated with a stochastic model, which was fitted to real SOFC microstructures.
(3) To justify the use of the models for prediction (and validation) of composite conductivity, the underlying model assumptions need to be a reasonable approximation for the specific applications of interest. The discussed models (numerical as well as semi-analytical) are restricted to effects of simple conduction described by the Laplace equation. Especially, the following effects are not considered:
• The effects of grain boundaries within the same phase are not included for all the models. However, for the MST-model, a resistance can be introduced at the interfaces of the two solid phases.
• Drift–diffusion phenomena are not considered. However, as drift and diffusion are restricted by the same microstructure obstacles, the presented models still provide good approximations for this case.
• The effect of space charge regions that might develop at the interfaces between the two solid phases is not considered.
For the application for SOC electrodes, it must be emphasized that the charge transport in MIECs is governed by drift and diffusion, which can, e.g., be modelled by the Nernst Planck Poisson equation (see, e.g., Marmet et al.58). However, to the best of our knowledge, there are no studies available yet about the exact mechanisms of the drift diffusion transport in perovskite–CGO composites. For example, it is not clear if there is a significant interface resistance between the perovskite- and CGO-phase. Consequently, no interface resistance is considered in the current study. Moreover, the approach of using a lumped description for the microstructure effects of drift and diffusion seems to be appropriate in the sense that drift and diffusion are both limited by the same microstructure obstacles. Furthermore, the effect of the grain boundaries can be neglected for the high reference temperature of T = 850 °C used in this work, where volume transport is dominant. In summary, the presented models for composite conductivity are a reasonable approximation for MIEC-based SOC electrodes, even if the simplifications are significant. Hence, the focus of the presented models is to incorporate the microstructure effects of porous composites for the prediction of the composite conductivity, while further research is needed to incorporate all possible effects in detail.
Validation of the performance prediction (b): it must be emphasized that Section 3.2 dealing with electrode performance is presented as an example, which illustrates how semi-analytical models for composite conductivity can be used by material engineers for efficient screening of microstructure effects. This illustration can be done with relatively simple and well established analytical models for performance prediction (adapted from Adler et al.59). However, the present study is by no means a detailed investigation on material and microstructure optimization. In such a study the precise prediction of electrode performance would be more critical. Hence, considering the illustrative aspect of the performance prediction in the present study, the lack of an extensive experimental validation of the electrode model can be justified. However, a detailed study including predictions of absolute electrode performance for a similar material system (i.e., LSCT-CGO) can be found in Marmet et al.56 and in the PhD-thesis by Ph. Marmet15 (Sections 9 and 10).
3 Results and discussion
3.1 Quantitative example for composite conductivity in titanate-CGO anodes
In this section, a quantitative example of composite conductivity is provided for MIEC-based SOFC anodes. In a porous composite with two MIEC phases like LSTN–CGO (illustrated in Fig. 5(c)), electrons and ions can be transported in both phases. Hence, the composite conductivity defined in eqn (4) needs to be distinguished for an electronic and ionic composite conductivity:| σeff,ion,comp = σrel,ion,comp·σ0,ion,SP1 | (22) |
| σeff,eon,comp = σrel,eon,comp·σ0,eon,SP2, | (23) |
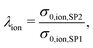 | (24) |
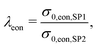 | (25) |
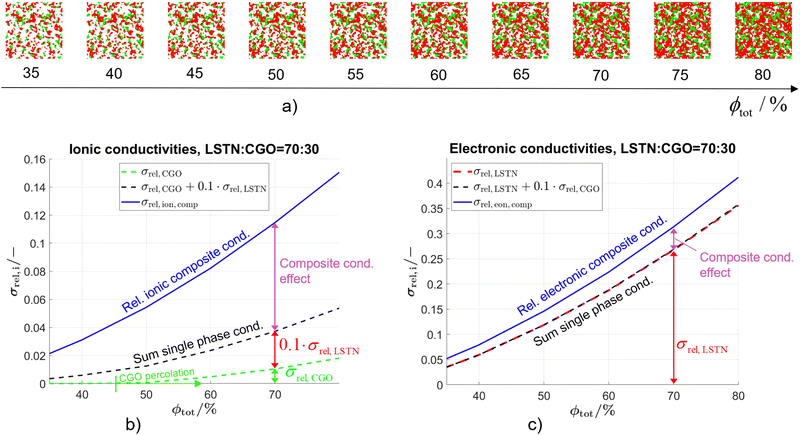
The composite conductivity effects shall be further illustrated using a subset of the data presented in a previous publication (Marmet et al.10), consisting of virtual but realistic PGM structures constructed on the basis of three digital microstructure twins fitted to real tomography data of LSTN–CGO electrodes. The data subset is obtained by fixing the composition to LSTN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CGO = 70
CGO = 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (i.e., constant relative phase volume fractions), while still varying the total solid volume fraction (or porosity, respectively), as illustrated in Fig. 7(a). Even though both phases can transport electrons and ions, the intrinsic conductivities of the titanate and CGO are very different as listed in Table 1. Note that a reference temperature of 850 °C is used for the material properties because this is the typical operating temperature of the electrolyte supported SOFC system of our industrial partner Hexis. A relevant amount of research work related to the Hexis system using this reference temperature is reported in the literature.7,8,49,56,58,60–66 Moreover, there are numerous additional research results reported at T = 850 °C (e.g., ref. 47, 50 and 67–70) or slightly below at T = 800 °C (e.g., ref. 9, 45, 53, 54 and 71–73) in the literature using CGO-based SOFC electrodes. Nevertheless, it is worth mentioning that ceria (especially CGO) is also a typical material used for intermediate temperature SOFCs (see e.g., ref. 39 and 74–76) in an operating temperature range of 500–750 °C (as defined by Steele74). However, the properties of titanates vary widely and precise experimental data are rare. For currently available titanates,40 the intrinsic electronic conductivity is about one order of magnitude higher than the intrinsic electronic conductivity of CGO for an operating temperature of 850 °C. In contrast the intrinsic ionic conductivity of titanate is about one order of magnitude lower than the intrinsic ionic conductivity of CGO. Nevertheless, the limiting effects from the microstructure are much weaker in composite MIEC electrodes compared to electrodes with only single-phase conductivity (e.g., Ni–YSZ cermets, see discussion in Section 2.4.1 in context with Fig. 5). For each 3D microstructure in Fig. 7(a), the resulting composite and single-phase conductivities are determined with numerical simulation, using the intrinsic transport properties from Table 1. As a result, the contributions of single-phase conductivities to the total composite conductivity can be determined. The effective composite conductivities (for electrons as well as for ions) with two MIECs are much higher than the (hypothetical) single-phase conductivities of the same microstructure, as shown in Fig. 7(b) and (c). As a concrete example, we select a fixed value for the total solid-phase volume fraction ϕtot = 70% in Fig. 7(b) to illustrate different contributions to the relative ionic composite conductivity. The contribution from the relative single-phase ionic conductivity of CGO (green) is very low (σrel,CGO = 0.010). In contrast, the relative single-phase conductivity of the titanate-phase (red) would be considerably higher (σrel,LSTN = 0.268). However, because the intrinsic ionic conductivity of the titanate is one order of magnitude lower than that of CGO, the true contribution of the isolated titanate-phase is 10 times smaller (i.e., 0.027). Hence, we still have a missing part of 0.077 to the total ionic composite conductivity σrel,ion,comp = 0.115. This difference between the ionic composite conductivity and the sum of the single-phase ionic conductivities from CGO and titanate can be interpreted as the composite conductivity effect. Compared to the hypothetical single-phase conductivity of CGO, the ionic composite conductivity is 12 times higher (see Fig. 7(b), blue vs. green lines). The composite conductivity effects due to MIEC properties can be explained by different transport pathways (compared to single-phase transport), which are shown in Fig. 5(b) and (c), respectively. CGO-particles that would otherwise (i.e., in materials with single-phase conductivity) be disconnected from the main CGO-phase network (Fig. 5(b)) are now connected over the titanate-phase (resulting in higher effective volume fraction). Furthermore, the bottlenecks in the CGO-phase are less restrictive for ion transport because these bottlenecks can be by-passed via pathways through the neighboring titanate-phase (resulting in higher constrictivity). Finally, the ionic charge-carriers do not need to detour the obstacles represented by the titanate-phase but can directly cross these obstacles. Therefore, the bridging effects in MIEC composites also result in shorter pathways for composite conduction (i.e., lower tortuosity). In the introduction it was shown that the three main effects from microstructure limiting charge transport in solids (see eqn (3)) are associated with narrow bottlenecks (small constrictivity), increased transport pathlengths (high tortuosity) and low effective phase volume fraction (e.g., due to the formation of disconnected islands). As illustrated in Fig. 5, these three limiting effects are decreased in MIEC materials with composite conductivity, which explains the specific composite conductivity component that is detected in the quantitative data (Fig. 7, magenta).
30 (i.e., constant relative phase volume fractions), while still varying the total solid volume fraction (or porosity, respectively), as illustrated in Fig. 7(a). Even though both phases can transport electrons and ions, the intrinsic conductivities of the titanate and CGO are very different as listed in Table 1. Note that a reference temperature of 850 °C is used for the material properties because this is the typical operating temperature of the electrolyte supported SOFC system of our industrial partner Hexis. A relevant amount of research work related to the Hexis system using this reference temperature is reported in the literature.7,8,49,56,58,60–66 Moreover, there are numerous additional research results reported at T = 850 °C (e.g., ref. 47, 50 and 67–70) or slightly below at T = 800 °C (e.g., ref. 9, 45, 53, 54 and 71–73) in the literature using CGO-based SOFC electrodes. Nevertheless, it is worth mentioning that ceria (especially CGO) is also a typical material used for intermediate temperature SOFCs (see e.g., ref. 39 and 74–76) in an operating temperature range of 500–750 °C (as defined by Steele74). However, the properties of titanates vary widely and precise experimental data are rare. For currently available titanates,40 the intrinsic electronic conductivity is about one order of magnitude higher than the intrinsic electronic conductivity of CGO for an operating temperature of 850 °C. In contrast the intrinsic ionic conductivity of titanate is about one order of magnitude lower than the intrinsic ionic conductivity of CGO. Nevertheless, the limiting effects from the microstructure are much weaker in composite MIEC electrodes compared to electrodes with only single-phase conductivity (e.g., Ni–YSZ cermets, see discussion in Section 2.4.1 in context with Fig. 5). For each 3D microstructure in Fig. 7(a), the resulting composite and single-phase conductivities are determined with numerical simulation, using the intrinsic transport properties from Table 1. As a result, the contributions of single-phase conductivities to the total composite conductivity can be determined. The effective composite conductivities (for electrons as well as for ions) with two MIECs are much higher than the (hypothetical) single-phase conductivities of the same microstructure, as shown in Fig. 7(b) and (c). As a concrete example, we select a fixed value for the total solid-phase volume fraction ϕtot = 70% in Fig. 7(b) to illustrate different contributions to the relative ionic composite conductivity. The contribution from the relative single-phase ionic conductivity of CGO (green) is very low (σrel,CGO = 0.010). In contrast, the relative single-phase conductivity of the titanate-phase (red) would be considerably higher (σrel,LSTN = 0.268). However, because the intrinsic ionic conductivity of the titanate is one order of magnitude lower than that of CGO, the true contribution of the isolated titanate-phase is 10 times smaller (i.e., 0.027). Hence, we still have a missing part of 0.077 to the total ionic composite conductivity σrel,ion,comp = 0.115. This difference between the ionic composite conductivity and the sum of the single-phase ionic conductivities from CGO and titanate can be interpreted as the composite conductivity effect. Compared to the hypothetical single-phase conductivity of CGO, the ionic composite conductivity is 12 times higher (see Fig. 7(b), blue vs. green lines). The composite conductivity effects due to MIEC properties can be explained by different transport pathways (compared to single-phase transport), which are shown in Fig. 5(b) and (c), respectively. CGO-particles that would otherwise (i.e., in materials with single-phase conductivity) be disconnected from the main CGO-phase network (Fig. 5(b)) are now connected over the titanate-phase (resulting in higher effective volume fraction). Furthermore, the bottlenecks in the CGO-phase are less restrictive for ion transport because these bottlenecks can be by-passed via pathways through the neighboring titanate-phase (resulting in higher constrictivity). Finally, the ionic charge-carriers do not need to detour the obstacles represented by the titanate-phase but can directly cross these obstacles. Therefore, the bridging effects in MIEC composites also result in shorter pathways for composite conduction (i.e., lower tortuosity). In the introduction it was shown that the three main effects from microstructure limiting charge transport in solids (see eqn (3)) are associated with narrow bottlenecks (small constrictivity), increased transport pathlengths (high tortuosity) and low effective phase volume fraction (e.g., due to the formation of disconnected islands). As illustrated in Fig. 5, these three limiting effects are decreased in MIEC materials with composite conductivity, which explains the specific composite conductivity component that is detected in the quantitative data (Fig. 7, magenta).
In a scenario with constant composition (e.g., 70% titanate, 30% CGO), the composite conductivity effect is particularly important for compensating the transport limitations in the phase with the lower volume fraction, as illustrated in section A of the ESI.† The charge carriers can reach the reaction sites even when the single-phase volume fraction(s) is/are below the percolation threshold, or when islands are formed, which is more probable for the minor phase. As shown in Fig. 7(b), the CGO-phase only percolates for ϕtot > 45%, but already for total volume fractions below this percolation threshold, the composite conductivity effect (magenta) contributes significantly to the total (ionic) conductivity due to the bridging effect. When comparing ionic and electronic conductivities for the same microstructure scenario, the resulting composite conductivities show very different behavior, due to the different intrinsic conductivities (see Table 1). For the electronic composite conductivity reported in Fig. 7(c), the CGO-phase does not provide any remarkable single-phase contribution (green) to the total conductivity, because of its lower volume fraction and its lower intrinsic electronic conductivity, compared to LSTN. There is thus only a moderate composite conductivity effect (magenta), which supports the electronic charge transport in the titanate-phase. Hence, the composite conductivity effect for electronic transport (magenta part in Fig. 7(c)) is much smaller than for ionic transport (magenta part in Fig. 7(b)). This difference can be attributed to the fact that the electronic transport in the LSTN-phase is relatively high, since it has 10 times higher intrinsic conductivity compared to CGO, and it also represents the larger volume fraction (70% LSTN vs. 30% CGO). Compensating the electronic transport limitations in the less important CGO-phase does not make such a big difference, which is in contrast to the ionic transport, where CGO is the main transporting phase.
3.2 Microstructure design regions of classical and novel SOC-electrodes
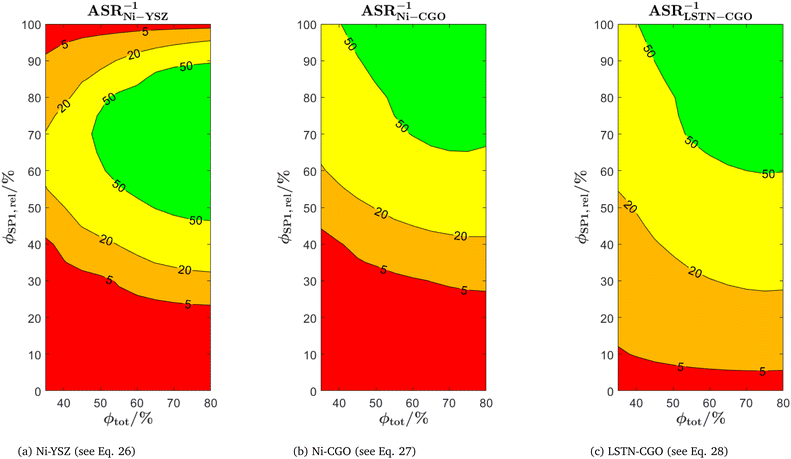
The use of MIEC materials and the resulting composite conductivity lead to very different restriction for a suitable microstructure design compared to the common Ni–YSZ electrodes. Thus, the different design regions in terms of porosity and composition shall be illustrated for Ni–YSZ, Ni–CGO and LSTN–CGO composites. However, a quantitative description of the electrode performance requires sophisticated multiphysics electrode models including gas species transport and reaction kinetics with experimental calibration on specific material systems, as, e.g., reported in Marmet et al.56 and in the PhD-thesis of Ph. Marmet15 (Sections 9 and 10). While such complex models are out of scope of this publication, qualitative figures of merit for the electrode performances associated with the simulated microstructure variations can be estimated with a simplified approach according to the analytical model presented by Adler et al.,59 as already discussed in a previous publication in this journal.10 Note that this estimate is formulated for the case that the transport of gas species and the transport of electrons are not limiting (see also Marmet et al.10 for a more detailed discussion). Moreover, the microstructures of the LSTN–CGO data set are also used to illustrate the effects for Ni–YSZ (using the LSTN-phase for the Ni-phase and the CGO-phase for the YSZ-phase) and Ni–CGO (using the LSTN-phase for the Ni-phase). Hence, the effect of the different materials can be discussed for the same microstructure scenarios. For each 3D microstructure (from stochastic modeling), the relative conductivities (single-phase and composite) and the relevant microstructure characteristics (TPB-lengths and interface areas) were then computed by numerical transport simulation and by quantitative image analysis, respectively. All these microstructure properties used for the figures of merit were reported and discussed in a previous publication (Marmet et al.10) in this journal. The figures of merit for the three composites according to this approach are presented in the following.Figure of merit for Ni–YSZ:
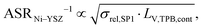 | (26) |
Figure of merit for Ni–CGO
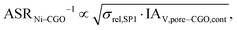 | (27) |
Figure of merit for LSTN–CGO:
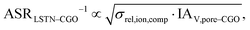 | (28) |
The figures of merit are reported in Fig. 8 as a function of porosity and composition for the three composite electrodes. The ASR−1-values are normalized to values between 0 and 100. The red regions correspond to performance values below 5% with respect to the highest possible performance and can thus be considered as non-functional. The regions above 50% highlighted in green can be considered as the main design regions for the corresponding type of composite electrode.
The Ni–YSZ system exhibits red zones on both ends of the compositional variation, as the three-phase boundary length vanishes for pure YSZ- and for pure Ni-electrodes. Moreover, low YSZ-contents lead to an insufficient ionic single-phase conductivity due to the percolation loss of the YSZ-phase. For the Ni–CGO system, the same restriction applies for the ionic conductivity of the CGO-phase, which is the only phase with ionic conductivity in this type of electrode. However, as the fuel oxidation reaction takes place on the entire pore-CGO interface area (i.e., not limited to TPB), there is no limitation of reaction sites towards high CGO-contents (in contrast to Ni–YSZ). In fact, the performance increases towards 100% CGO because of the increasing pore-CGO interface area. For the titanate-CGO composite, almost the entire compositional space covered in this study belongs to the potential design space. The performance is only dropping into the red range for low CGO-contents, because of the vanishing pore-CGO surface area (note that for certain perovskites and especially for the case of additional catalyst impregnation,8,46,48,54,70 also the pore-perovskite interface area might be active for the fuel oxidation, which must be then considered in the computation of performance and figure of merit). Most importantly, the green and the yellow zones are significantly larger in LSTN–CGO anodes compared to the other two anode material systems. It must be emphasized that this larger microstructure design-space not only opens new possibilities for the design of well performing electrodes, but it also documents a certain tolerance (and associated robustness) for eventual deviations from the optimal design-points, which can originate from variations in the manufacturing process and/or from microstructure degradation (e.g., reduction of porosity and active surface area upon coarsening/grain growth). Hence, this example illustrates the benefits of novel anode material concepts based on MIEC materials, which are largely due to (ionic) composite conductivity.
3.3 Validation of the models predicting the composite conductivity
The studies presented in Sections 3.1 and 3.2 based on the virtual microstructure variation using stochastic modeling and numerical characterization allow for accurate studies of the composite conductivities. However, this approach is quite time consuming and computationally expensive. Especially, the calculations need to be repeated for every conductivity ratio λ of interest and for every 3D microstructure. For the present study, 54 microstructures (i.e., a subset of the 150 microstructures, as the variation with respect to composition and porosity is rather smooth) with 5 λ-values (see Table 2) were studied, which results in a total number of 270 composite conductivity values determined by numerical simulations. Thus, semi-analytical models for the prediction of the composite conductivity are useful for a fast and efficient screening of potential material systems. Hence, the three models to predict the composite conductivity (based on the Maxwell, Xu and MST models) introduced in Section 2.3 are tested in this section for different microstructure datasets.| Conductivity ratio λ | Maxwell (%) | Xu (%) | MST (%) | QP (%) |
|---|---|---|---|---|
| λ ion = 0.1 | 3.65 | 6.03 | 5.44 | 19.50 |
| λ eon = 0.1 | 4.13 | 6.56 | 5.69 | 19.57 |
| λ ion = 0.5 | 0.84 | 0.88 | 2.38 | 8.81 |
| λ ion = 0.01 | 28.53 | 19.02 | 8.76 | 83.95 |
| λ eon = 0.0001 | 692.1 | 65.82 | 53.8 | 1371 |
The predictive capabilities of the three models are analysed with statistical methods, i.e., by comparison with the results from numerical transport simulations. Thereby, we consider the relative error in percent between predicted and simulated relative composite conductivities, which is given by the so-called mean absolute percentage error (MAPE)17 as reported in eqn (29):
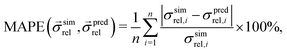 | (29) |
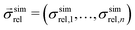 is a vector of simulated relative composite conductivities using GeoDict1 for n microstructures and
is a vector of simulated relative composite conductivities using GeoDict1 for n microstructures and 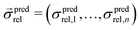 is a vector of the corresponding predicted relative composite conductivities by one of the three models (Maxwell, Xu, MST).
is a vector of the corresponding predicted relative composite conductivities by one of the three models (Maxwell, Xu, MST).
First, the three models are tested for the virtual LSTN–CGO microstructures. The characterization of the virtual microstructures by numerical simulation, which reveals the relative ionic and electronic composite conductivities for λion = λeon = 0.1 (among many other microstructure properties), was reported in a previous publication (Marmet et al.10). These results are already used as a basis for the studies reported in Sections 3.1 and 3.2. Composite conductivities with further conductivity ratios λ are additionally calculated using the same methods as reported in Marmet et al.16,77 (i.e., numerical transport simulation) and the simulated and predicted conductivities are then compared with each other. An overview of the resulting MAPEs for the different models and conductivity ratios λ is provided in Table 2. A detailed presentation and discussion of these tests can be found in the ESI,† Sections D.1–D.3. In the following section we only present a short summary.
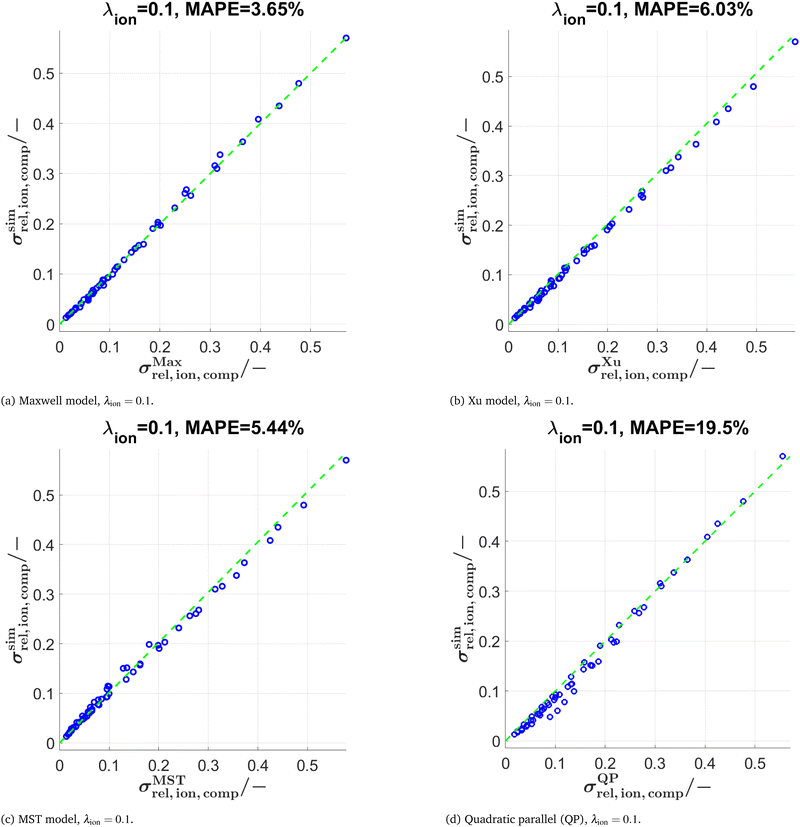
In Fig. 9, the scatter plots are reported for (a) the Maxwell model, (b) the Xu model and (c) the MST model using a conductivity ratio λion = 0.1. All three models show a very good agreement with respect to the numerical simulations. The MAPE of the Maxwell model is slightly lower compared to the Xu and MST model, but within the same order of magnitude. Note that the Maxwell model shows larger deviations compared to the Xu model for similar volume fractions of the two solid phases (see Section D.1.1 in the ESI†), where the model-assumption of isolated spheres is considerably violated. In contrast, for low total solid volume fractions and for compositions with very different phase volume fractions of SP1 und SP2, the prediction of the Xu model is worse compared to the Maxwell model, because the assumption of two percolating solid phases does not hold in these compositional regions (see Section D.2.1 in the ESI†). For the MST model, the exponent a in eqn (18) needs to be fitted. A fixed exponent a = 0.6 (obtained by manual fitting) provides good prediction qualities for all the data used in this work. As a reference, the results of the simple QP model are reported in Fig. 9(d) and 10(d). The error of the QP model (MAPE = 19.5% for λ = 0.1 and 83.95% for λ = 0.01) is approximately 4 times larger compared to the semi-analytical models (MAPE = 3–6% for λ = 0.1 and 8–29% for λ = 0.01). The prediction errors for the QP model are particularly large for low relative composite conductivities, where the influence of the microstructure morphology is especially large.
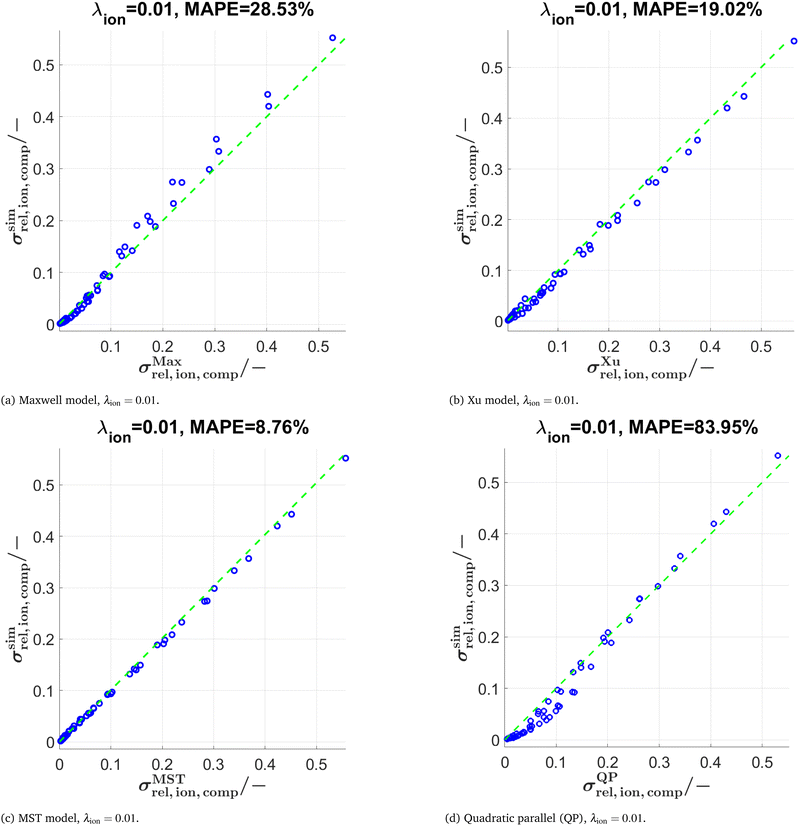
The predictions with the three models are also tested for further conductivity ratios λ = 0.5, 0.01, and 0.0001 as summarized in Table 2. The scatter plots for λion = 0.01 are presented in Fig. 10 for the models (Maxwell, Xu, MST, QP). The main findings are:
• Comparing results for λion = 0.5 vs. λion = 0.1: For the Maxwell and Xu models, the MAPE < 1% is considerably smaller compared to λion = 0.1. This is probably because the inherent relative conductivity (M-factor) of the total solid-phase is already a good approximation of the total composite conductivity, since the intrinsic conductivities of the two solid phases are quite close to each other (for λion = 0.5). The same tendency can also be observed, but to a lower extent, for the MST and the QP model.
• The differences in prediction power among the models are becoming more apparent when lowering the conductivity ratios. For λion = 0.01 (see also Fig. 10), the MST model still shows a good prediction performance with a MAPE = 8.76%, while the deviations with the Maxwell model (MAPE = 28.53%) and the Xu model (MAPE = 19.02%) are already quite large. The simple QP model shows a poor performance with a MAPE = 83.95%.
• For λion = 0.0001, the Maxwell model (MAPE = 692.1%) and the QP model (MAPE = 1371%) are no more capable of describing the data appropriately, while the Xu model still provides a reasonable estimation (MAPE = 65.82%). However, there are large prediction errors around the percolation thresholds of the single solid-phases for the Xu model, which are visible in the corresponding scatter plots presented in Section D.2.2 in the ESI† (Fig. S15). The best prediction is again achieved with the MST model (MAPE = 53.8%).
In summary, the MST model shows similar prediction errors for λ ≥ 0.1 but performs considerably better for λ < 0.1 compared to the Maxwell and Xu models, because the geometrical details of the single phases are captured better due to the inclusion of the relative conductivities (M-factors) of the single phases. This comes at the cost of additional computational expenses for the characterization of the single phases and an additional fit-factor (a). The three semi-analytical (Maxwell, Xu, MST) models clearly outperform the QP model. Nevertheless, the QP model can still be useful as a fast initial guess, as it does not need any geometrical input parameters.
In order to check the sensitivity of the three semi-analytical models with respect to the type of microstructure and to evaluate the corresponding prediction power, these models are tested for two further datasets from stochastic modeling, representing pure PGM and sphere-packing structures. The dataset of pure PGM structures was presented in a previous publication (Marmet et al.10). In contrast to the PGM dataset that is fitted to real LSTN–CGO anodes (see Fig. 7), a neutral wetting behavior of the solid phases and no modifications by morphological operations were used for the realization of the pure PGM structure. Apart from that, the two PGM structure types are quite similar. As presented in Table 3, the MAPEs for the predictions are very similar for the pure PGM dataset compared to the LSTN–CGO dataset (Table 2). This confirms a certain robustness of the prediction models (i.e., consistency of prediction power) when varying the type of microstructure moderately. Further details are reported in section D.4.1 in the ESI.† More interesting is the comparison with the dataset of 65 virtual sphere-packing structures with different compositions and porosities, shown in Section D.4.2 (Fig. S24) in the ESI.† These sphere-packing structures represent a very different type of microstructure, which are characterized by much more pronounced bottlenecks within the solid-phase networks, compared to the LSTN–CGO and pure PGM datasets. The MAPEs for the prediction of relative ionic composite conductivity are reported in Table 4 for the three prediction models and for λion = 0.1. The MAPEs for the sphere-packing dataset are generally by a factor of about 4 higher than the MAPEs for the predictions for the PGM structures (i.e., the LSTN–CGO dataset, Table 2 and the pure PGM dataset, Table 3). This is most probably a result of the pronounced bottlenecks of the sphere-packing structures. In the sphere-packing structures, the difference between single-phase conduction and the total composite conduction is particularly large (i.e., there is a strong composite conductivity effect, similar to that in Fig. 7(b)). Consistently, the MAPE for the MST model including information of the single solid-phases is considerably lower than for the other two prediction models, which only take into account the morphology of the total solid-phase. However, for the Maxwell and the Xu model, the predictions systematically overestimate the relative ionic composite conductivity and thus, these predictions can be improved with a correction factor. These results for the sphere-packing structures are presented in more detail in Section D.4.2 in the ESI.†
| Conductivity ratio λ | Maxwell model (%) | Xu model (%) | MST model (%) |
|---|---|---|---|
| λ ion = 0.1 | 4.9 | 4.73 | 3.83 |
| λ ion = 0.5 | 1.02 | 1.04 | 2.2 |
| Conductivity ratio λ | Maxwell model (%) | Xu model (%) | MST model (%) |
|---|---|---|---|
| λ ion = 0.1 | 19.8 | 23.63 | 13.66 |
As a summary, the prediction power of the three prediction models is not independent of the type of microstructure. The most reliable results can be obtained with the MST model, especially for low λ-values (see Fig. 9, 10 and Table 2). However, the MST model is also the most expensive one concerning the needed input parameters. Nevertheless, all three models show a reasonable agreement with the simulation data and the deviations are in a good range with respect to other uncertainties like those from intrinsic conductivities and from contact and interface resistances. Moreover, especially the predictions based on the Maxwell and the Xu models provide a fast and inexpensive possibility to estimate the composite conductivities of MIEC-based electrodes. As an input, these models are only requiring the composition (i.e., volume fractions of solid phases), the porosity, the intrinsic conductivities of the solid phases, and the relative conductivity (M-factor) of the total solid-phase. Composition and porosity can be determined based on 2D images. The relative conductivity of the total solid-phase generally requires a 3D-image for an accurate representation. However, it can be estimated with reasonable accuracy using (empirical) reference datasets, as for example the data reported in this and in previous publications (see Marmet et al.10,16). Thus, the prediction models for composite conductivity are especially helpful for a fast screening of suitable material systems.
3.4 Application example of the analytical model for optimization of perovskite–CGO electrodes
The synthesis of suitable perovskites for SOC electrodes is still a topic of ongoing research (see e.g., reviews6,40,62,78–81). For the performance of SOC electrodes, typically the ionic conductivity of a perovskite–CGO composite is a limiting factor.15 As an application example of the analytical model, the relevance of the intrinsic ionic conductivity of a perovskite used for SOC composite electrodes shall be illustrated. Furthermore, in this application example, we take into consideration the possibility that the intrinsic ionic conductivity of the perovskite phase can be changed within certain limits (e.g., by varying the level of dopants and/or oxygen vacancy concentration). As a consequence, variation of the conductivity ratio λion becomes an additional optimization parameter.In Fig. 11 the relative ionic composite conductivity σrel,ion,comp is predicted based on the Xu model (eqn (15)) as a function of the conductivity ratio λ (y-axis), and for anodes with different phase compositions (x-axis), but with fixed porosity ε = 30% (i.e., ϕtot = 70%, respectively) using a subset of the virtual LSTN–CGO dataset.10 Note that a porosity of 30% is a reasonable value to ensure sufficient gas transport. As all microstructures of this subset have the same total volume fraction ϕtot, the relative conductivity of the total solid-phase varies only marginally for the different microstructures (with different phase compositions) and is thus fixed to a value of σrel,SPtot = 0.605 for simplicity.
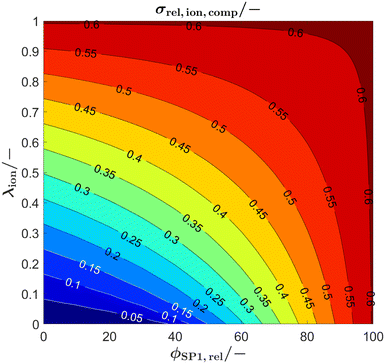 | ||
| Fig. 11 Prediction of the relative ionic composite conductivities σrel,ion,comp with the Xu model (eqn (15)) as a function of the conductivity ratio (λion), for anode microstructures with varying solid-phase compositions (ϕSP1,rel) and fixed porosity of ε = 30% (i.e., ϕtot = 70%, respectively). | ||
The maximal possible relative ionic composite conductivity max(σrel,ion,comp) = σrel,SPtot = 0.605 can be achieved for the case of 100% CGO-content (i.e., ϕSP1,rel = 100%) or for a perovskite with equal intrinsic ionic conductivity as that of CGO (i.e., λion = 1). Even though it is known that pure nanoporous CGO-anodes show a very good performance (e.g., reported by Nenning et al.82 and Graves et al.83), Sciazko et al.9 have documented that the addition of a perovskite (i.e., 30 wt% LSCM) leads to a significant improvement of the degradation behavior by preventing the formation of nano-cracks in the CGO-phase, which otherwise were present in pure CGO-anodes. Thus, for the following discussion, we focus on crack resistant anode compositions and we thus consider the case of a perovskite–CGO anode with 40 vol% perovskite and 60 vol% CGO (i.e., ϕSP1,rel = 60%, note that CGO has typically higher density than perovskite and thus wt% ≠ vol%). For a realistic intrinsic ionic conductivity ratio of λion = 0.1, a relative ionic composite conductivity of about σrel,ion,comp = 0.3 can be expected, which is already a relatively high value. For a considerable increase of the relative ionic composite conductivity for this scenario, the intrinsic ionic conductivity of the perovskite would need to be drastically increased. For example, for an increase of the relative ionic composite conductivity by 50 vol% to σrel,ion,comp = 0.45, the intrinsic ionic composite conductivity would need to be improved by a factor of 4.5 to λion = 0.45. On the other hand, a lower intrinsic ionic conductivity of the perovskite does not lead to a tremendous decrease of the ionic composite conductivity. In fact, a total loss of the intrinsic ionic conductivity of the perovskite-phase (i.e., λion = 0, which corresponds to a Ni–CGO composite) only leads to a decrease of about 20% to σrel,ion,comp = 0.24. In summary, the plot (Fig. 11) that can be easily extracted with the Xu model gives us important guidelines on how to optimize the anode composition and its constituents. The Xu model indicates that the addition of 40 vol% perovskite (for the sake of improved durability) with 10 times lower intrinsic ionic conductivity than CGO (i.e., λion = 0.1) does not lead to a tremendous loss in the total ionic composite conductivity of the anode. Hence, we gain stability, without losing much performance. Furthermore, there exists the possibility to search for different chemical/stoichiometric compositions of the perovskite, which may lead to better intrinsic ionic conductivity. But for this strategy, the Xu model indicates that the intrinsic conductivity needs to be increased by factors in order to improve the anode performance significantly. An improvement of, e.g., 50% in the intrinsic ionic conductivity of the perovskite has nearly no impact on the total relative composite conductivity. Hence, this strategy might not be efficient for the chosen anode composition (i.e., 40 vol% perovskite).
Another concept is to choose a higher perovskite content in order to potentially obtain a very robust electrode. For a scenario of a perovskite content of, e.g., 70 vol% (i.e., ϕSP1,rel = 30%), and still assuming 30% porosity, only a relative ionic composite conductivity of about σrel,ion,comp = 0.135 can be expected. However, Fig. 11 also illustrates that for anodes with increased perovskite content, the total composite conductivity is much more sensitive to the intrinsic properties of the perovskite. For example, to achieve the same ionic composite conductivity compared to the anode with ϕSP1,rel = 60%, a λion = 0.35 would be needed (i.e., enhancement of the intrinsic ionic conductivity of the perovskite by a factor of Section 3.5). Vice versa, the ionic composite conductivity is sensitive to a decrease of the intrinsic ionic conductivity of the perovskite. A reduction of the intrinsic ionic conductivity of the perovskite by 50% (i.e., λion = 0.05) leads to a reduction of the relative composite conductivity of about 35% to σrel,ion,comp = 0.09. Moreover, when the intrinsic ionic conductivity of the perovskite is completely lost, this also leads to a complete loss of the ionic composite conductivity, as the percolation of the CGO-phase is not ensured due to the low CGO-content. Consequently, an improvement of the ionic conductivity of perovskites would be very beneficial for the concept with high perovskite content, while possible improvement is only moderate for the concept two with larger CGO-content.
A more detailed discussion about possible design concepts of perovskite–CGO anodes also supported by multiphysics electrode models can be found in the PhD thesis by Ph. Marmet.15
4 Conclusion
A framework for the systematic study and prediction of the effective composite conductivity in porous three-phase materials (two conductive solid phases and one insulating pore-phase) has been presented. The issue of composite conductivity is typically relevant when MIEC based materials are involved. But it also applies to other types of transport (e.g., thermal conduction in composite materials). A definition for the relative composite conductivity has been established, which describes the involved microstructure effects as a function of the intrinsic conductivity ratio λ of the two solid phases. This property can be determined in a straightforward way by using direct numerical simulation (e.g., using GeoDict1) on a 3D geometry obtained from tomography or virtual construction by stochastic modeling. However, this numerical approach is computationally quite expensive, especially for large parameter variations. Therefore, three different semi-analytical models for the prediction of the composite conductivity as a function of the conductivity ratio λ have been introduced, which allow for a fast screening of promising material combinations and microstructure designs. Two models based on the mean-field theory (Maxwell and Xu model) are presented, which include a correction factor to account for the non-conductive pore-phase. Both models provide good prediction results for moderate conductivity ratios in the range of 0.1 ≤ λ ≤ 1. The third model, i.e., the MST model, based on an empirical approach using the relative conductivities (M-factors, respectively) of the single and total solid phases provides even more robust predictions, especially for low λ-values (i.e., very different intrinsic conductivities of the solid phases) as well as for phase volume fractions near the percolation threshold. Furthermore, an interface resistance between the two solid phases can be easily introduced for the MST model. The advantages of the MST model come at the cost of additional computational expenses for the characterization of the single phases and an additional fit-factor. The three semi-analytical (Maxwell, Xu, MST) models introduced in this work clearly outperform the analytical quadratic parallel (QP) model available in the literature, which uses no geometrical parameters.The composite conductivity framework is illustrated and validated for a microstructure dataset of LSTN–CGO electrodes, where both solid phases exhibit MIEC properties. Thereby a large number of 3D microstructures was generated by stochastic modeling, as described in a previous publication (Marmet et al.10). To illustrate the effects of composite conductivity, the design regions for SOFC electrodes with two MIEC-phases (i.e., LSTN–CGO anodes) were compared with those for conventional anode compositions (i.e., Ni–YSZ, Ni–CGO). Thereby, the design space is characterized by performance variation as a function of composition and porosity. The results from numerical simulation document that the performance and associated design space of Ni–YSZ are limited by the percolation of both solid phases, while for Ni–CGO, only CGO needs to percolate to ensure the anode functionality. For the LSTN–CGO composite, neither the LSTN nor the CGO-phase needs to percolate for a minimal functionality of the electrode, as the transport of neither electrons nor oxygen ions is limited to a single phase. Hence, MIEC material concepts and associated composite conductivity open a much larger design space for microstructure optimization.
Furthermore, by using semi-analytical models, possible optimization routes for SOC electrodes including perovskite materials were discussed. A perovskite with considerably higher intrinsic ionic conductivity would be very beneficial for perovskite–CGO electrodes with a high perovskite-content. On the other hand, the intrinsic ionic conductivity of the currently available perovskites is sufficient for electrodes with a high CGO-content (e.g., 60 vol%). For these compositions, the contribution of the perovskite-phase is largely limited to electronic current collection and structural support (i.e., improved degradation behavior).
While the presented models provide good approximations for the incorporation of microstructure effects on the composite conductivity, further research is needed for additional physical effects at grain boundaries and solid-phase interfaces including space charge regions. Moreover, for the application for SOC electrodes, more precise measurements for specific material combinations are needed, especially for the ionic conductivity.
The established framework is relevant for many applications of porous composites as, e.g., SOC MIEC electrodes like perovskite–CGO fuel electrodes and LSCF–CGO air electrodes. In this context, the introduced semi-analytical models enable a fast screening of microstructure features like porosity and solid-phase composition as well as material combinations with different intrinsic conductivities, towards sufficient effective ionic and electronic conductivities. This allows one to considerably reduce the needed amount of experimental testing. Moreover, the presented approach is also relevant for other transport mechanisms such as the thermal conductivity of porous composites.
Data availability
Data will be made available on request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is based mainly on two research projects that received financial support from the Swiss Federal Office of Energy (SFOE, grant SI/501792-01-8100076) and from Eurostars (grant E!115455), which are gratefully acknowledged. Furthermore, we would like to thank our industrial partners Hexis AG and Math2Market GmbH for the excellent collaboration within these projects. A special thanks is dedicated to Holger Bausinger, Jan G. Grolig and Andreas Mai from Hexis and to Mathias Fingerle, Sarah Reeb and Dominik Michel from Math2Market.Notes and references
- GeoDict simulation software Release 2023 (Revision 61624), by Math2Market GmbH, Germany DOI:10.30423/release.geodict2023.
- S. J. Cooper, A. Bertei, P. R. Shearing, J. A. Kilner and N. P. Brandon, SoftwareX, 2016, 5, 203–210 CrossRef.
- K. Pietrak and T. S. Wiśniewski, J. Power Technol., 2014, 95(1), 14–24 Search PubMed.
- B. Zhu, B. Wang, Y. Wang, R. Raza, W. Tan, J. S. Kim, P. A. van Aken and P. Lund, Nano Energy, 2017, 37, 195–202 CrossRef CAS.
- B. Zhu, L. Fan, N. Mushtaq, R. Raza, M. Sajid, Y. Wu, W. Lin, J. S. Kim, P. D. Lund and S. Yun, Semiconductor Electrochemistry for Clean Energy Conversion and Storage, Springer, Singapore, 2021, vol. 4, pp. 757–792 Search PubMed.
- L. Shu, J. Sunarso, S. S. Hashim, J. Mao, W. Zhou and F. Liang, Int. J. Hydrogen Energy, 2019, 44, 31275–31304 CrossRef CAS.
- D. Burnat, G. Nasdaurk, L. Holzer, M. Kopecki and A. Heel, J. Power Sources, 2018, 385, 62–75 CrossRef CAS.
- R. Price, M. Cassidy, J. G. Grolig, A. Mai and J. T. S. Irvine, J. Electrochem. Soc., 2019, 166, F343–F349 CAS.
- A. Sciazko, Y. Komatsu, R. Yokoi, T. Shimura and N. Shikazono, J. Eur. Ceram. Soc., 2022, 42, 1556–1567 CrossRef CAS.
- P. Marmet, L. Holzer, T. Hocker, V. Muser, G. K. Boiger, M. Fingerle, S. Reeb, D. Michel and J. M. Brader, Energy Adv., 2023, 2, 1942–1967 CAS.
- W. Woodside and J. H. Messmer, J. Appl. Phys., 1961, 32, 1688–1699 CrossRef.
- G. Loor, The Netherlands Remote Sensing Board: bcrs Rep. 90-13, 1990, pp. 1–39 Search PubMed.
- G. P. De Loor, Appl. Sci. Res., 1965, 11, 310–320 CrossRef.
- M. C. Dobson, F. T. Ulaby, M. T. Hallikainen and M. A. El-Rayes, IEEE Trans. Geosci. Remote Sens., 1985, GE-23, 35–46 Search PubMed.
- P. Marmet, PhD thesis, Digital Materials Design of Solid Oxide Fuel Cell Anodes, University of Fribourg, Switzerland, 2023 DOI:10.21256/zhaw-28430.
- P. Marmet, L. Holzer, T. Hocker, G. K. Boiger, H. Bausinger, A. Mai, M. Fingerle, S. Reeb, D. Michel and J. M. Brader, Energy Adv., 2023, 2, 980–1013 CAS.
- O. Stenzel, O. Pecho, L. Holzer, M. Neumann and V. Schmidt, AIChE J., 2016, 62, 1834–1843 CrossRef CAS.
- L. Holzer, P. Marmet, M. Fingerle, A. Wiegmann, M. Neumann and V. Schmidt, Tortuosity and microstructure effects in porous media: classical theories, empirical data and modern methods, Springer, Cham, ISBN: 978-3-031-30477-4, 1st edn, 2023 Search PubMed.
- L. Holzer, P. Marmet, M. Fingerle, A. Wiegmann, M. Neumann and V. Schmidt, Towards a Quantitative Understanding of Microstructure-Property Relationships, Springer, Cham, 1st edn, 2023 DOI:10.1007/978-3-031-30477-4_5.
- D. Chen, Z. Lin, H. Zhu and R. J. Kee, J. Power Sources, 2009, 191, 240–252 CrossRef CAS.
- J. Ott, B. Völker, Y. Gan, R. M. McMeeking and M. Kamlah, Acta Mech. Sin., 2013, 29, 682–698 CrossRef CAS.
- K. Zheng and M. Ni, Sci. Bull., 2016, 61, 78–85 CrossRef.
- D. Chen, H. He, D. Zhang, H. Wang and M. Ni, Energies, 2013, 6, 1632–1656 CrossRef CAS.
- M. Wang and N. Pan, Mater. Sci. Eng., R, 2008, 63, 1–30 CrossRef.
- J. C. Maxwell, A treatise on Electricity and Magnetism, Oxford University Press, Cambridge, UK, 1904 Search PubMed.
- Y. Agari and T. Uno, J. Appl. Polym. Sci., 1986, 32, 5705–5712 CrossRef CAS.
- J. Z. Xu, B. Z. Gao and F. Y. Kang, Appl. Therm. Eng., 2016, 102, 972–979 CrossRef.
- N. Dib and G. P. Zéhil, Mater. Today Commun., 2021, 27, 102283 CrossRef CAS.
- I. Sevostianov, S. G. Mogilevskaya and V. I. Kushch, Int. J. Eng. Sci., 2019, 140, 35–88 CAS.
- M. S. Khan, S. B. Lee, R. H. Song, J. W. Lee, T. H. Lim and S. J. Park, Ceram. Int., 2016, 42, 35–48 CAS.
- L. Holzer, B. Iwanschitz, T. Hocker, B. Münch, M. Prestat, D. Wiedenmann, U. Vogt, P. Holtappels, J. Sfeir, A. Mai and T. Graule, J. Power Sources, 2011, 196, 1279–1294 CAS.
- H. He and J. M. Hill, Appl. Catal., A, 2007, 317, 284–292 CrossRef CAS.
- G. Brus, R. Nowak, J. S. Szmyd, Y. Komatsu and S. Kimijima, J. Theor. Appl. Mech., 2015, 53, 273–284 CrossRef.
- F. Yu, J. Xiao, Y. Zhang, W. Cai, Y. Xie, N. Yang, J. Liu and M. Liu, Appl. Energy, 2019, 256, 113910 CAS.
- Y. Matsuzaki and I. Yasuda, Solid State Ionics, 2000, 132, 261–269 CrossRef CAS.
- D. Fouquet, A. C. Müller, A. Weber and E. Ivers-Tiffée, Ionics, 2003, 9, 103–108 CrossRef CAS.
- P. Costamagna, P. Costa and V. Antonucci, Electrochim. Acta, 1998, 43, 375–394 CrossRef CAS.
- S. Dierickx, J. Joos, A. Weber and E. Ivers-Tiffée, Electrochim. Acta, 2018, 265, 736–750 CrossRef CAS.
- B. C. Steele, Solid State Ionics, 2000, 129, 95–110 CrossRef CAS.
- X. Zhou, N. Yan, K. T. Chuang and J. Luo, RSC Adv., 2014, 4, 118–131 RSC.
- J. Kubota, S. Hashimoto, T. Shindo, K. Yashiro, T. Matsui, K. Yamaji, H. Kishimoto and T. Kawada, Fuel Cells, 2017, 17, 402–406 CrossRef CAS.
- A. Weber, S. Dierickx, N. Russner and E. Ivers-Tiffée, ECS Trans., 2017, 77, 141–147 CrossRef CAS.
- A. Zekri, M. Knipper, J. Parisi and T. Plaggenborg, Phys. Chem. Chem. Phys., 2017, 19, 13767–13777 RSC.
- A. Zekri, K. Herbrig, M. Knipper, J. Parisi and T. Plaggenborg, Fuel Cells, 2017, 17, 359–366 CrossRef CAS.
- A. Sciazko, Y. Komatsu, T. Shimura and N. Shikazono, J. Power Sources, 2020, 478, 228710 CrossRef CAS.
- M. C. Verbraeken, B. Iwanschitz, A. Mai and J. T. S. Irvine, J. Electrochem. Soc., 2012, 159, F757–F762 CrossRef CAS.
- P. Blennow, K. Kammer Hansen, L. R. Wallenberg and M. Mogensen, ECS Trans., 2008, 13, 181–194 CrossRef CAS.
- C. D. Savaniu and J. T. Irvine, Solid State Ionics, 2011, 192, 491–493 CrossRef CAS.
- M. C. Verbraeken, B. Iwanschitz, E. Stefan, M. Cassidy, U. Weissen, A. Mai and J. T. Irvine, Fuel Cells, 2015, 15, 682–688 CrossRef CAS.
- N. Muzaffar, N. Arshad, D. B. Drasbæk, B. R. Sudireddy and P. Holtappels, Catalysts, 2019, 9, 269 CrossRef CAS.
- X. Sun, S. Wang, Z. Wang, X. Ye, T. Wen and F. Huang, J. Power Sources, 2008, 183, 114–117 CAS.
- K. B. Yoo and G. M. Choi, Solid State Ionics, 2009, 180, 867–871 CrossRef CAS.
- S. Futamura, Y. Tachikawa, J. Matsuda, S. M. Lyth, Y. Shiratori, S. Taniguchi and K. Sasaki, J. Electrochem. Soc., 2017, 164, F3055–F3063 CrossRef CAS.
- S. Futamura, A. Muramoto, Y. Tachikawa, J. Matsuda, S. M. Lyth, Y. Shiratori, S. Taniguchi and K. Sasaki, Int. J. Hydrogen Energy, 2019, 44, 8502–8518 CrossRef CAS.
- P. Marmet, L. Holzer, T. Hocker, V. Muser, G. K. Boiger, M. Fingerle, S. Reeb, D. Michel and J. M. Brader, Python app for stochastic microstructure modeling of SOC electrodes based on a pluri-Gaussian method, 2023 DOI:10.5281/zenodo.7744110.
- P. Marmet, L. Holzer, T. Hocker, H. Bausinger, J. G. Grolig, A. Mai, J. M. Brader and G. K. Boiger, Int. J. Multiphys., 2024, 18(2s), 58–83 Search PubMed.
- D. Burnat, R. Kontic, L. Holzer, P. Steiger, D. Ferri and A. Heel, J. Mater. Chem. A, 2016, 4, 11939–11948 RSC.
- P. Marmet, L. Holzer, J. G. Grolig, H. Bausinger, A. Mai, J. M. Brader and T. Hocker, Phys. Chem. Chem. Phys., 2021, 23, 23042–23074 RSC.
- S. B. Adler, J. Lane and B. Steele, J. Electrochem. Soc., 1996, 143, 3554–3564 CrossRef CAS.
- R. Price, J. G. Grolig, A. Mai and J. T. Irvine, Solid State Ionics, 2020, 347, 115254 CrossRef CAS.
- R. Price, U. Weissen, J. G. Grolig, M. Cassidy, A. Mai and J. T. Irvine, J. Mater. Chem. A, 2021, 9, 10404–10418 RSC.
- R. Price, M. Cassidy, J. G. Grolig, G. Longo, U. Weissen, A. Mai and J. T. Irvine, Adv. Energy Mater., 2021, 11, 2003951 CrossRef CAS.
- M. Riegraf, V. Yurkiv, R. Costa, G. Schiller and K. A. Friedrich, ChemSusChem, 2017, 10, 587–599 CrossRef CAS PubMed.
- M. Linder, T. Hocker, C. Meier, L. Holzer, K. A. Friedrich, B. Iwanschitz, A. Mai and J. A. Schuler, J. Power Sources, 2015, 288, 409–418 CrossRef CAS.
- M. Linder, T. Hocker, R. Denzler, A. Mai and B. Iwanschitz, Fuel Cells, 2011, 11, 573–580 CrossRef CAS.
- P. Marmet, T. Hocker, J. G. Grolig, H. Bausinger, A. Mai, J. M. Brader and L. Holzer, 14th European SOFC & SOE Forum, EFCF, Luzern, 2020, p. A1514 Search PubMed.
- S. Primdahl and M. Mogensen, Solid State Ionics, 2002, 152–153, 597–608 CrossRef CAS.
- S. Primdahl and Y. L. Liu, J. Electrochem. Soc., 2002, 149, A1466–A1472 CrossRef CAS.
- C. D. Savaniu, D. N. Miller and J. T. Irvine, J. Am. Ceram. Soc., 2013, 96, 1718–1723 CrossRef CAS.
- T. Ramos, S. Veltzé, B. R. Sudireddy, P. S. Jørgensen, L. Theil Kuhn and P. Holtappels, Fuel Cells, 2014, 14, 1062–1065 CrossRef CAS.
- T. Nakamura, K. Yashiro, A. Kaimai, T. Otake, K. Sato, T. Kawada and J. Mizusaki, J. Electrochem. Soc., 2008, 155, B1244–B1250 CrossRef CAS.
- T. Nakamura, T. Kobayashi, K. Yashiro, A. Kaimai, T. Otake, K. Sato, J. Mizusaki and T. Kawada, J. Electrochem. Soc., 2008, 155, B563–B569 CrossRef CAS.
- A. Nenning, M. Holzmann, J. Fleig and A. K. Opitz, Mater. Adv., 2021, 2, 5422–5431 RSC.
- B. C. Steele, J. Mater. Sci., 2001, 36, 1053–1068 CrossRef CAS.
- D. J. Brett, A. Atkinson, N. P. Brandon and S. J. Skinner, Chem. Soc. Rev., 2008, 37, 1568–1578 CAS.
- H. Shi, C. Su, R. Ran, J. Cao and Z. Shao, Prog. Nat. Sci.: Mater. Int., 2020, 30, 764–774 CrossRef CAS.
- P. Marmet, L. Holzer, T. Hocker, G. K. Boiger, H. Bausinger, A. Mai, M. Fingerle, S. Reeb, D. Michel and J. M. Brader, Characterization-app: Standardized microstructure characterization of SOC electrodes as a key element for Digital Materials Design, 2023 DOI:10.5281/zenodo.7741305.
- X. M. Ge, S. H. Chan, Q. L. Liu and Q. Sun, Adv. Energy Mater., 2012, 2, 1156–1181 CrossRef CAS.
- W. H. Kan and V. Thangadurai, Ionics, 2015, 21, 301–318 CrossRef CAS.
- M. C. Verbraeken, T. Ramos, K. Agersted, Q. Ma, C. D. Savaniu, B. R. Sudireddy, J. T. Irvine, P. Holtappels and F. Tietz, RSC Adv., 2015, 5, 1168–1180 RSC.
- F. S. da Silva and T. M. de Souza, Int. J. Hydrogen Energy, 2017, 42, 26020–26036 CrossRef CAS.
- A. Nenning, C. Bischof, M. Holzmann, M. Gerstl, J. Fleig, M. Bram and A. K. Opitz, 14th European SOFC & SOE Forum, EFCF, 2020, p. B0603 Search PubMed.
- C. Graves, L. Martinez and B. R. Sudireddy, ECS Trans., 2016, 72, 183–192 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00074a |
| This journal is © The Royal Society of Chemistry 2024 |