 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimal face-to-face coupling for fast self-folding kirigami†
Maks
Pecnik Bambic
 abc,
Nuno A. M.
Araújo
abc,
Nuno A. M.
Araújo
 de,
Benjamin J.
Walker
de,
Benjamin J.
Walker
 fg,
Duncan R.
Hewitt
fg,
Duncan R.
Hewitt
 gh,
Qing Xiang
Pei
gh,
Qing Xiang
Pei
 b,
Ran
Ni
b,
Ran
Ni
 c and
Giorgio
Volpe
c and
Giorgio
Volpe
 *a
*a
aDepartment of Chemistry, University College London, 20 Gordon Street, WC1H 0AJ London, UK. E-mail: g.volpe@ucl.ac.uk
bInstitute of High Performance Computing, A*STAR, Singapore
cSchool of Chemistry, Chemical Engineering and Biotechnology, Nanyang Technological University, 62 Nanyang Drive, 637459, Singapore
dDepartamento de Física, Faculdade de Ciências, Universidade de Lisboa, 1749-016 Lisboa, Portugal
eCentro de Física Teórica e Computacional, Faculdade de Ciências, Universidade de Lisboa, 1749-016 Lisboa, Portugal
fDepartment of Mathematical Sciences, University of Bath, Claverton Down, Bath, BA2 7AY, UK
gDepartment of Mathematics, University College London, Gordon Street, London, WC1H 0AY, UK
hDepartment of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, CB3 0WA, UK
First published on 9th January 2024
Abstract
Kirigami-inspired designs can enable self-folding three-dimensional materials from flat, two-dimensional sheets. Hierarchical designs of connected levels increase the diversity of possible target structures, yet they can lead to longer folding times in the presence of fluctuations. Here, we study the effect of rotational coupling between levels on the self-folding of two-level kirigami designs driven by thermal noise in a fluid. Naturally present due to hydrodynamic resistance, we find that this coupling parameter can significantly impact a structure's self-folding pathway, thus enabling us to assess the quality of a kirigami design and the possibility for its optimization in terms of its folding rate and yield.
Introduction
The art of kirigami, where three-dimensional shapes emerge from flat sheets (templates) through prescribed cuts and folds, is pursued as a route to design programmable materials that can self-fold into target structures across scales.1–3 Kirigami-inspired designs are promising due to the easiness of two-dimensional fabrication and for their potential for deployability and reconfigurability.1–3 Applications include morphable structures and sheets,4–8 mechanical actuators,9,10 nanocomposites,11,12 metamaterials13–15 and soft robots.16–20Due to the broad interest in kirigami designs, the quest to understand the geometrical, topological and mechanical principles behind their folding dynamics has driven a large body of research,21–24 which has also sought to define design rules to optimize them.25–28 At macroscopic scales, as folding is usually driven by stress relaxation,27–29 deterministic rules can be identified and relied upon directly.28,30–32 However, at microscopic scales, thermal noise can render the folding dynamics a stochastic process.33–38
Thermal fluctuations are critical to how microscopic systems explore their configuration space and converge to the desired target structures.25,36–38 Due to these fluctuations, the folding trajectories are stochastic and the final configuration might not coincide with the desired one. The trajectories depend on the initial template's choice,25 the materials properties,21 and the experimental conditions.36 Nonetheless, in some systems, if an undesired configuration is reached, the thermal energy provided by the surroundings might not be sufficient to reverse binding events, rendering them effectively irreversible, e.g. when liquid metal hinges fuse after folding driven by surface tension minimization25 or in DNA origami, where structures cannot come undone below the melting temperature of DNA.39 Folding yield (the proportion of templates that successfully fold into the target structure within a given time) has therefore been an important parameter to optimize.22,25 Beyond yield, folding time is an equally key parameter for real-life applications of microscopic kirigami designs, yet its optimization is much less understood. An accurate prediction of the folding time was possible for simple single level structures.37,38 However, kirigami designs often present multiple interdependent levels, whose folding could strongly depend on level-to-level correlations, e.g. due to materials or environmental properties.34,35,40,41
Here, we demonstrate how rotational coupling between levels emerges naturally in microscopic hierarchical kirigami templates folding in a fluid. We numerically show how the value of this coupling is key to enhance the folding rate and yield, thus defining a metric against which the quality of a kirigami template can be assessed. We rationalize the emergence of an optimal coupling parameter value by mapping our results into a first passage problem.
Results and discussion
As model target structures, we consider double pyramids with three sets of two hinged lateral faces of constant height h (Fig. 1a and b). The upper level's faces are hinged to the respective lower level's faces, which a second hinge tethers to the substrate. Two target angles define the structures' three-dimensional geometry (Fig. 1a): ϕl ∈ (0,π) and ϕu ∈ (−π,π), respectively defined with respect to the substrate and the plane containing the lower face. Based on the choice of angles, the target structures span from hourglass shapes to diamonds and their two-dimensional templates (Fig. 1b) are obtained by cutting and unfolding the edges of their lateral faces. Two time-dependent angles, θl(t) and θu(t), describe the motion of the two hinges during the folding process driven in the fluid by thermal fluctuations (here, in water at room temperature).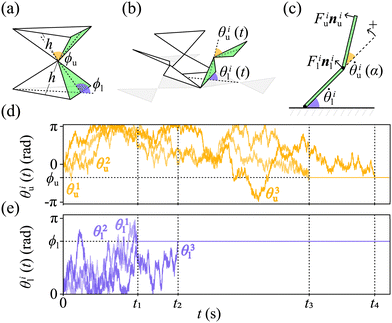 | ||
Fig. 1 Folding of a two-level kirigami. (a) Example of two-level kirigami target structure formed by three sets of two hinged flat sheets (faces) of constant height h. Two target angles, ϕl and ϕu, define the structure's lower and upper levels, respectively. Here, 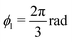 and and 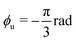 produce an hourglass shape. (b) Two-dimensional template (gray area) for the target structure in (a). The upper faces are hinged to the respective lower ones, which are hinged to the substrate. During folding, the motion of each set of connected faces (i = 1, 2, 3) is described by the angles of the lower and upper levels as a function of time, θil(t) and θiu(t), respectively defined with respect to the substrate and the plane of the lower face. (c) The folding dynamics can be modeled by considering the overdamped motion of each set i of faces ( produce an hourglass shape. (b) Two-dimensional template (gray area) for the target structure in (a). The upper faces are hinged to the respective lower ones, which are hinged to the substrate. During folding, the motion of each set of connected faces (i = 1, 2, 3) is described by the angles of the lower and upper levels as a function of time, θil(t) and θiu(t), respectively defined with respect to the substrate and the plane of the lower face. (c) The folding dynamics can be modeled by considering the overdamped motion of each set i of faces (![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) il and il and ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) iu) under driving forces Fil and Fiu (here, thermal noise), respectively acting on the lower and upper level.42 Both forces are directed along the unitary vectors normal to the faces (nil and niu), causing their rotation around the hinges. Counterclockwise rotations of the top level increase the upper angle towards positive values, with θiu(t) = 0 when the upper and lower levels are parallel. Due to the fluid's hydrodynamic resistance, the motion of the upper faces is naturally coupled to that of the respective lower faces with a dimensionless coupling constant α < 0 (here, α = αH = −5/2). (d) and (e) Sample trajectories of (d) upper and (e) lower faces. The horizontal dashed lines indicate the target angles ϕl and ϕu. The vertical dashed lines represent irreversible binding events between two faces of the lower (t1 and t2) or upper (t3 and t4) levels. iu) under driving forces Fil and Fiu (here, thermal noise), respectively acting on the lower and upper level.42 Both forces are directed along the unitary vectors normal to the faces (nil and niu), causing their rotation around the hinges. Counterclockwise rotations of the top level increase the upper angle towards positive values, with θiu(t) = 0 when the upper and lower levels are parallel. Due to the fluid's hydrodynamic resistance, the motion of the upper faces is naturally coupled to that of the respective lower faces with a dimensionless coupling constant α < 0 (here, α = αH = −5/2). (d) and (e) Sample trajectories of (d) upper and (e) lower faces. The horizontal dashed lines indicate the target angles ϕl and ϕu. The vertical dashed lines represent irreversible binding events between two faces of the lower (t1 and t2) or upper (t3 and t4) levels. | ||
A model for the coupled motion of two faces joined by a hinge can be derived using the approach of ‘resistive-force theory’.43,44 Under this approach, the hydrodynamic drag on each face combines with constraints of vanishing net torque and force (owing to the absence of inertia) to yield a coupled equation of motion, while secondary hydrodynamic interactions between the faces are neglected:42
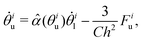 | (1a) |
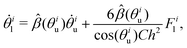 | (1b) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) < 0 and
< 0 and ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) < 0 provide negative feedbacks (i.e. contrary motions) between the faces.
< 0 provide negative feedbacks (i.e. contrary motions) between the faces.
Eqn (1) shows how the motion of the two hinged faces is thus naturally coupled due to the fluid's hydrodynamic resistance. In fact, for small upper angles θiu, the feedback terms in eqn (1) become roughly constant and are dominated by ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) (
(![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) = 15
= 15![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) in this limit). Indeed,
in this limit). Indeed, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) remains roughly an order of magnitude larger than
remains roughly an order of magnitude larger than ![[small beta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e114.gif) over a wide range of θiu (Fig. S2, ESI†),42i.e. the upper face is much more strongly affected by the motion of the lower than the lower is by the upper.
over a wide range of θiu (Fig. S2, ESI†),42i.e. the upper face is much more strongly affected by the motion of the lower than the lower is by the upper.
For microscopic structures such as those obtained by folding reconfigurable DNA patterns,45 the folding can be determined and driven by thermal fluctuations. As discussed previously for one-level structures,37 the driving forces (Fil and Fiu) change rapidly in similar cases, being well described by stochastic processes uncorrelated in space and time.46 The variance of this process, and hence the typical rotational diffusion coefficients Dθ for each face, can be derived assuming equipartition.42 For a hinged circular disc of radius 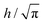 ,
, 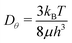 , where kB is the Boltzmann constant, T the thermostat temperature, and μ the fluid viscosity.42 For h being
, where kB is the Boltzmann constant, T the thermostat temperature, and μ the fluid viscosity.42 For h being ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (μm) to
(μm) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10 μm), Dθ varies from
(10 μm), Dθ varies from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10 rad2 s−1) to
(10 rad2 s−1) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−3 rad2 s−1).
(10−3 rad2 s−1).
To primarily explore the role of the dominant lower-to-upper coupling of the faces, and taking thermal fluctuations as the only drive, we consider the reduced model
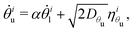 | (2a) |
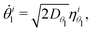 | (2b) |
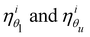 are independent white noise processes.46 Here, the weaker coupling is neglected and the dominant coupling is parameterized by a single dimensionless constant α; a reference value of α is obtained in the limit θiu → 0, which gives αH ≡
are independent white noise processes.46 Here, the weaker coupling is neglected and the dominant coupling is parameterized by a single dimensionless constant α; a reference value of α is obtained in the limit θiu → 0, which gives αH ≡ ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) (θiu → 0) = −5/2. This follows directly from the model in eqn (1) but, more generally, we leave α as a free parameter to assess the quality of a given kirigami template in terms of the maximum achievable folding rate and yield and to allow for this feedback to be engineered. Indeed, even within the modeling framework of eqn (1), it is possible to change the strength of coupling by allowing variability in the properties of the two faces and the hinge between them.42
(θiu → 0) = −5/2. This follows directly from the model in eqn (1) but, more generally, we leave α as a free parameter to assess the quality of a given kirigami template in terms of the maximum achievable folding rate and yield and to allow for this feedback to be engineered. Indeed, even within the modeling framework of eqn (1), it is possible to change the strength of coupling by allowing variability in the properties of the two faces and the hinge between them.42
For each set of coupled faces (Fig. 1), we solve these differential equations numerically with an example value of Dθl = Dθu = 0.64 rad2 s−1 (around the middle of the possible Dθ range) using the Euler integration scheme (timestep Δτ = 10 μs).46 We however note that our observations are qualitatively independent of the value of Dθ (Fig. S3, ESI†). We model the substrate as reflective boundary46 and detect and correct face collisions with the Gilbert–Johnson–Keerthi algorithm.47 We fix a cutoff time τcut = 2 × 108Δτ, when we consider misfolded any structure which is not folded completely. Fig. 1d and e shows sample trajectories for the faces of the upper and lower levels when α = αH, highlighting how the system converges to the target structure through a series of four binding events between faces of the lower level first followed by the upper level. Each event is defined by two faces being at their target angle (±π/180) concomitantly. We consider these events irreversible as in experiments with micro-polyhedra25 and DNA origami.39
Fig. 2 shows that varying the coupling by tuning the value – and sign – of the coupling parameter α can optimize the folding process. To avoid bias from long folding events, we define the folding rate, kα, as a function of α by taking the reciprocal of the folding time of each event before calculating the average for all successfully folded structures. The contribution of folding events that fold in a time t > τcut to the overall folding rate is therefore near zero and does not influence the numerical results significantly. Fig. 2a shows that, for the structure in Fig. 1 with an obtuse ϕl and a negative ϕu, the folding rate at negative α (α = −1) is enhanced by ≈1.3 and ≈1.1 times when compared to no coupling (α = 0) and the rate at αH. For the diamond with an acute ϕl and a positive ϕu instead (Fig. 2b), positive α values can enhance folding by up to ≈6 and ≈4.5 times when compared to the rates at αH and for no coupling, respectively. As mentioned earlier, these observations are qualitatively independent of the value of Dθ (Fig. S3, ESI†). Interestingly, for both structures, the α values that optimize the rate (αopt) and the yield (the percentage of fully folded structures within τcut) are closely related, with yields of ≈70% and ≈61% at αopt (against the highest yields of ≈74% and ≈62%) in Fig. 2a and b, respectively. A broad range of negative α values below α = −1 can be obtained in practice by modifying the relative lengths of the upper and lower faces in the kirigami template.42 Although this limits the experimentally attainable α values, our results allow one to assess the quality of a given kirigami design against its maximum attainable yield and folding rates as a function of the dominant coupling parameter α.
 | ||
| Fig. 2 Folding dependence on the coupling parameter. (a) and (b) Folding rate kα (circles) and yield (squares) as a function of coupling parameter α for two exemplary kirigami structures: (a) an hourglass (as in Fig. 1) and (b) a diamond (ϕl = 0.61 rad, ϕu = 1.92 rad). The rate is obtained by taking the reciprocal of the folding times of individual events then calculating the average across all successfully folded structures. Depending on the target geometry, (a) negative or (b) positive values of α can lead to optimal folding (αopt, filled circles). The vertical dashed lines show αH for reference. Folding rates are normalized to k0 (kα for α = 0). The shaded areas represent one standard error from 5000 folding events lasting up to the cutoff time τcut. | ||
Fig. 2 suggests that the value of the coupling between faces can optimize both folding rate and yield of a given kirigami structure at once. This observation can be generalized to a variety of structures (examples in Fig. 3a) with varying target angles ϕl and ϕu (Fig. 3 and Fig. S4, ESI†). To a first analysis, the value of ϕu is the decisive factor discerning whether a negative (for ϕu < 0) or positive α (for ϕu > 0) optimizes the folding rate (Fig. 3b). Structures with upper levels opening away from the center (e.g.Fig. 3bII, IV and VI) tend to benefit from a negative coupling to their respective lower levels, while structures whose upper levels point towards their centers (e.g.Fig. 3bI) tend to fold faster with a positive coupling. The absence of coupling instead tends to be optimal for structures (e.g.Fig. 3bIII and Fig. S4a, ESI†) where the lower and upper levels roughly lie on the same plane (ϕu ≈ 0). Indeed, the benefits in folding rate because of coupling between levels increases the farther a structure is from this condition, as kα ≈ k0 around ϕu ≈ 0 (Fig. 3c). These results further highlight the importance of choosing a kirigami template based on the optimal value of the coupling parameter, as the folding of target structures in the ranges of relatively smaller upper angles and positive upper angles tends to be comparatively inhibited by the sub-optimal coupling due to the natural hydrodynamic resistance of the hinged faces.42 The range of ϕu values where no coupling is advantageous broadens asymmetrically towards positive α values as ϕl increases towards π. In these situations, stronger coupling tends to push the upper level's faces against the substrate, thus delaying the convergence to the target structure. As in Fig. 2, the value of α that optimizes folding rate also roughly optimizes yield (Fig. S4b–d, ESI†), thus enabling one to assess the quality of a kirigami template in terms of these two quantities: for most structures, the ratio between the yield achieved at αopt and the maximum yield at any α (max(yield), Fig. S4b, ESI†) is close to one (Fig. S4c, ESI†), and the distance between these two α values is often close to zero (|αmax(yield) − αopt| ≈ 0, Fig. S4d, ESI†). Larger separations between these two values are possible but often coincide with regions where the yield is relatively insensitive to the exact α value (Fig. S4c, ESI†) or where advantages over no coupling are negligible (Fig. 3c).
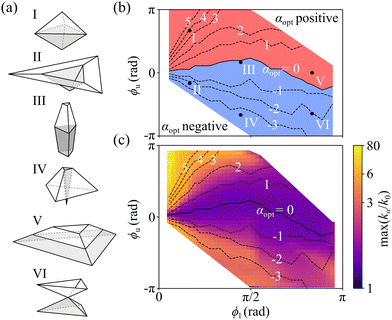 | ||
| Fig. 3 Optimal coupling for different target structures. (a) Examples of different kirigami target structures with varying target angles ϕl and ϕu (Fig. 1a). As ϕl increases from acute to obtuse, the lower levels (gray faces) transition from inverted pyramids (I, II and IV) as in Fig. 2b to regular pyramids (VI) as in Fig. 2avia truncated pyramids (III and V). For ϕu going from negative to positive values, the upper level goes from an umbrella shape, either convex (IV) or concave (VI), to a pyramid (I, III and V), truncated or not, through a flat plane (II). (b) Phase diagram of the optimal coupling parameter αopt for different structures: either a negative (blue) or positive (red) α is optimal (Fig. S4a, ESI†). (c) Highest folding rate max(kα) at any α for different structures. Folding rates are normalized to k0. In (b) and (c), the black isolines highlight structures whose folding is optimal at (dashed) a given α or (solid) in the absence of coupling (α = 0). Each data point is an average of 5000 folding events. | ||
To rationalize the emergence of an optimal coupling parameter α, we can map our results into a first passage problem to a target.42 This choice is justified as, for single-level pyramids with less than five faces, the folding time is dominated by the closing of the first pair of faces – event well described as a first passage problem in a two-dimensional random walk.37 Thus, the total folding time for single-level structures depends on the initial location of its faces.37 Similarly, for two-level structures, when the lower level folds much faster than the upper as observed here in simulations, the closing of the first pair of upper level's faces after the lower level has closed completely is the event dominating the folding of most structures. The optimal value of α should then be the one that leads to the distribution of angles in the upper level when the lower level has closed that minimizes the time for the first two faces of the upper level to reach their target angle ϕu. Starting from a location drawn from a one-dimensional Gaussian distribution ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (μ,σ) with varying mean μ(α) and fixed variance σ and reflected at the boundaries to ensure its proper normalization,42 the mean first passage time to a trap at location ϕ = (ϕu, ϕu) of a two-dimensional random walk on a lattice with reflective boundaries is calculated as48
(μ,σ) with varying mean μ(α) and fixed variance σ and reflected at the boundaries to ensure its proper normalization,42 the mean first passage time to a trap at location ϕ = (ϕu, ϕu) of a two-dimensional random walk on a lattice with reflective boundaries is calculated as48
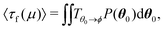 | (3) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (μ,σ)|θ01
(μ,σ)|θ01 ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (μ,σ)|θ02.42Fig. 4a shows that 〈τf(μ)〉 should be minimized when α is chosen so that μ(α) ≈ ϕu. Our numerical results confirm that, for a given α, the means of the distributions of the angles in the upper level after to lower has closed completely (exemplary distributions in Fig. S5, ESI†) as a function of the lower level target angle ϕl closely resemble the upper level target angles ϕu of the structures with the highest folding rate at that α (Fig. 4b and Fig. S6, ESI†). This observation provides an effective rule to assess the quality of a kirigami template to achieve a target geometry against its maximum attainable yield and folding rate as a function of the experimentally possible values of the coupling parameter α.42
(μ,σ)|θ02.42Fig. 4a shows that 〈τf(μ)〉 should be minimized when α is chosen so that μ(α) ≈ ϕu. Our numerical results confirm that, for a given α, the means of the distributions of the angles in the upper level after to lower has closed completely (exemplary distributions in Fig. S5, ESI†) as a function of the lower level target angle ϕl closely resemble the upper level target angles ϕu of the structures with the highest folding rate at that α (Fig. 4b and Fig. S6, ESI†). This observation provides an effective rule to assess the quality of a kirigami template to achieve a target geometry against its maximum attainable yield and folding rate as a function of the experimentally possible values of the coupling parameter α.42
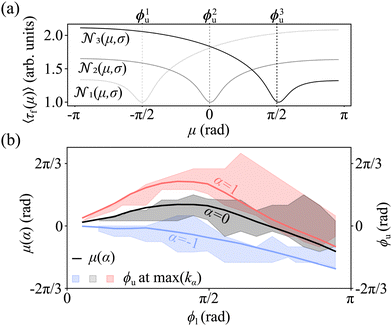 | ||
Fig. 4 Assessing optimal coupling as a first passage problem. (a) Expected mean first passage time 〈τf(μ)〉 of two upper level's faces to a target angle ϕnu (with n = 1, 2, 3) at the closing time of the lower level t2 as a function of the mean μ of the probability distribution of the faces' starting position.42 Here, the starting positions of each face are drawn from a one-dimensional Gaussian distribution ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) n(μ,σ) with varying mean μ, fixed variance σ and reflected at the boundaries of the possible range of angles.42 Three cases are shown: n(μ,σ) with varying mean μ, fixed variance σ and reflected at the boundaries of the possible range of angles.42 Three cases are shown: 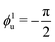 , ϕ2u = 0 and , ϕ2u = 0 and 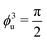 . The minimum value of 〈τf(μ)〉 occurs when μ ≈ ϕnu. (b) For a given α and lower level's target angle ϕl (see also Fig. S6, ESI†), the means of the probability distributions of the angles θiu of the upper level's faces when the lower level has closed (solid lines) are well captured by the range of possible structures with the highest folding rate at that α value (Fig. 3c) once the numerical uncertainty in determining the position of max(kα) is accounted for (shaded areas). This uncertainty is calculated taking the largest between the discretization step in α and the range of data points around the peak falling within the standard error. . The minimum value of 〈τf(μ)〉 occurs when μ ≈ ϕnu. (b) For a given α and lower level's target angle ϕl (see also Fig. S6, ESI†), the means of the probability distributions of the angles θiu of the upper level's faces when the lower level has closed (solid lines) are well captured by the range of possible structures with the highest folding rate at that α value (Fig. 3c) once the numerical uncertainty in determining the position of max(kα) is accounted for (shaded areas). This uncertainty is calculated taking the largest between the discretization step in α and the range of data points around the peak falling within the standard error. | ||
Conclusions
In conclusion, we have shown how the folding of microscopic hierarchical two-level kirigami structures in a fluid develops a natural degree of coupling between levels due to hydrodynamic resistance. This coupling is essential to understand the folding dynamics of similar structures as both folding rate and yield are impacted in its absence. Moreover, we show how rational design rules (e.g. based on solving a first passage time problem) can explain the emergence of an optimal coupling parameter for maximizing folding rates and yield as a function of the target geometry. Even within the reduced modeling framework of eqn (1), the coupling parameter α allows optimization of the folding process (in terms of folding rate and yield) in a broad range of negative values below α = −1 by tuning the relative lengths of the lower and upper faces in the kirigami template. Outside of the experimentally attainable α values, our results can be employed to assess and select optimal designs for a given three-dimensional target structure from a set of different two-dimensional templates based on the efficiency of the folding pathway against the maximum attainable folding rate and yield. Additionally, in these cases, further degrees of control could be introduced to optimize the folding pathway by, e.g., engineering the hydrodynamic resistance of the faces or exploiting active or driven hinges.42 We envisage that similar design rules could be adopted to engineer fast self-folding hierarchical multi-level kirigami structures for applications in, e.g., soft robotics, mechanical actuators and metamaterials.9,10,13–20Author contributions
Author contributions based on CRediT. Conceptualization: NAMA, GV. Data curation: MPB, NAMA, BJW, DRH, GV. Formal analysis: MPB, NAMA, BJW, DRH, GV. Funding acquisition: QXP, RN, GV. Investigation: MPB, NAMA, BJW, DRH, GV. Methodology: MPB, NAMA, BJW, DRH, GV. Project administration: QXP, RN, GV. Resources: QXP, RN, GV. Software: MPB. Supervision: NAMA, QXP, RN, GV. Validation: MPB, NAMA, GV. Visualization: MPB, BJW. Writing – original draft: MPB, NAMA, BJW, DRH, GV. Writing – review and editing: MPB, NAMA, BJW, DRH, QXP, RN, GV.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MPB, QXP and GV are grateful to the studentship funded by the A*STAR-UCL Research Attachment Programme through the EPSRC M3S CDT (EP/L015862/1). NAMA acknowledges financial support from the Portuguese Foundation for Science and Technology (FCT) under the contracts no. UIDB/00618/2020 and UIDP/00618/2020. BJW is supported by the Royal Commission for the Exhibition of 1851. NAMA and GV acknowledge support from the UCL MAPS Faculty Visiting Fellowship programme.Notes and references
- X. Ning, X. Wang, Y. Zhang, X. Yu, D. Choi, N. Zheng, D. S. Kim, Y. Huang, Y. Zhang and J. A. Rogers, Adv. Mater. Interfaces, 2018, 5, 1800284 CrossRef.
- X. Cheng and Y. Zhang, Adv. Mater., 2019, 31, e1901895 CrossRef PubMed.
- S. Chen, J. Chen, X. Zhang, Z.-Y. Li, J. Li and J. Li, Light: Sci. Appl., 2020, 9, 75 CrossRef CAS.
- K. Kuribayashi-Shigetomi, H. Onoe and S. Takeuchi, PLoS One, 2012, 7, e51085 CrossRef CAS.
- R. Fernandes and D. H. Gracias, Adv. Drug Delivery Rev., 2012, 64, 1579–1589 CrossRef CAS.
- W. Guo, M. Li and J. Zhou, Smart Mater. Struct., 2013, 22, 115028 CrossRef.
- H. Fu, K. Nan, W. Bai, W. Huang, K. Bai, L. Lu, C. Zhou, Y. Liu, F. Liu, J. Wang, M. Han, Z. Yan, H. Luan, Y. Zhang, Y. Zhang, J. Zhao, X. Cheng, M. Li, J. W. Lee, Y. Liu, D. Fang, X. Li, Y. Huang, Y. Zhang and J. A. Rogers, Nat. Mater., 2018, 17, 268–276 CrossRef CAS.
- J. D. Paulsen, Annu. Rev. Condens. Matter Phys., 2019, 10, 431–450 CrossRef CAS.
- K. Malachowski, M. Jamal, Q. Jin, B. Polat, C. J. Morris and D. H. Gracias, Nano Lett., 2014, 14, 4164–4170 CrossRef CAS.
- R. Niu, C. X. Du, E. Esposito, J. Ng, M. P. Brenner, P. L. McEuen and I. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24402–24407 CrossRef CAS.
- R. M. Erb, J. S. Sander, R. Grisch and A. R. Studart, Nat. Commun., 2013, 4, 1712 CrossRef PubMed.
- T. C. Shyu, P. F. Damasceno, P. M. Dodd, A. Lamoureux, L. Xu, M. Shlian, M. Shtein, S. C. Glotzer and N. A. Kotov, Nat. Mater., 2015, 14, 785 CrossRef CAS.
- K. Bertoldi, V. Vitelli, J. Christensen and M. Van Hecke, Nat. Rev. Mater., 2017, 2, 17066 CrossRef CAS.
- H. Fang, S. A. Chu, Y. Xia and K. Wang, Adv. Mater., 2018, 30, e1706311 CrossRef PubMed.
- H. Zhang and J. Paik, Adv. Functional Mater., 2022, 32, 2107401 CrossRef CAS.
- C. Wang, C. Wang, Z. Huang and S. Xu, Adv. Mater., 2018, 30, e1801368 CrossRef.
- D. Rus and M. T. Tolley, Nat. Rev. Mater., 2018, 3, 101–112 CrossRef.
- M. Z. Miskin, A. J. Cortese, K. Dorsey, E. P. Esposito, M. F. Reynolds, Q. Liu, M. Cao, D. A. Muller, P. L. McEuen and I. Cohen, Nature, 2020, 584, 557–561 CrossRef CAS.
- A. Bacchetti, P. Lloyd, S. Taccola, E. Fakhoury, S. Cochran, R. A. Harris, P. Valdastri and J. H. Chandler, Front. Robot. AI, 2022, 9, 1040984 CrossRef PubMed.
- Y. Dong, L. Wang, N. Xia, Z. Yang, C. Zhang, C. Pan, D. Jin, J. Zhang, C. Majidi and L. Zhang, Sci. Adv., 2022, 8, eabn8932 CrossRef CAS PubMed.
- M. Stern, V. Jayaram and A. Murugan, Nat. Commun., 2018, 9, 4303 CrossRef.
- N. Araújo, R. Da Costa, S. Dorogovtsev and J. Mendes, Phys. Rev. Lett., 2018, 120, 188001 CrossRef PubMed.
- C. D. Santangelo, Soft Matter, 2020, 16, 94–101 RSC.
- Y.-K. Lee, Z. Xi, Y.-J. Lee, Y.-H. Kim, Y. Hao, H. Choi, M.-G. Lee, Y.-C. Joo, C. Kim, J.-M. Lien and I.-S. Choi, Sci. Adv., 2020, 6, eaax6212 CrossRef CAS.
- S. Pandey, M. Ewing, A. Kunas, N. Nguyen, D. H. Gracias and G. Menon, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19885–19890 CrossRef CAS.
- T. Castle, Y. Cho, X. Gong, E. Jung, D. M. Sussman, S. Yang and R. D. Kamien, Phys. Rev. Lett., 2014, 113, 245502 CrossRef PubMed.
- L. H. Dudte, E. Vouga, T. Tachi and L. Mahadevan, Nat. Mater., 2016, 15, 583–588 CrossRef CAS PubMed.
- P. Dieleman, N. Vasmel, S. Waitukaitis and M. van Hecke, Nat. Phys., 2020, 16, 63–68 Search PubMed.
- C. D. Santangelo, Annu. Rev. Condens. Matter Phys., 2017, 8, 165–183 Search PubMed.
- Y. Zhang, Z. Yan, K. Nan, D. Xiao, Y. Liu, H. Luan, H. Fu, X. Wang, Q. Yang, J. Wang, W. Ren, H. Si, F. Liu, L. Yang, H. Li, J. Wang, X. Guo, H. Luo, L. Wang, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11757–11764 CrossRef CAS PubMed.
- G. P. T. Choi, L. H. Dudte and L. Mahadevan, Phys. Rev. Res., 2021, 3, 043030 CrossRef CAS.
- K. Xiao, Z. Liang, B. Zou, X. Zhou and J. Ju, Nat. Commun., 2022, 13, 7474 CrossRef CAS.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- T. G. Leong, P. A. Lester, T. L. Koh, E. K. Call and D. H. Gracias, Langmuir, 2007, 23, 8747–8751 CrossRef CAS PubMed.
- A. Azam, K. E. Laflin, M. Jamal, R. Fernandes and D. H. Gracias, Biomed. Microdevices, 2011, 13, 51–58 CrossRef CAS PubMed.
- P. M. Dodd, P. F. Damasceno and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6690–E6696 CAS.
- H. Melo, C. Dias and N. Araújo, Commun. Phys., 2020, 3, 154 CrossRef.
- T. S. A. N. Simões, H. P. M. Melo and N. A. M. Araújo, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 46 CrossRef PubMed.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- A. Azam, T. G. Leong, A. M. Zarafshar and D. H. Gracias, PLoS One, 2009, 4, e4451 CrossRef PubMed.
- N. Bao, Q. Liu, M. F. Reynolds, M. Figueras, E. Smith, W. Wang, M. C. Cao, D. A. Muller, M. Mavrikakis, I. Cohen, P. L. McEuen and N. L. Abbott, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2221740120 CrossRef CAS PubMed.
- ESI†.
- G. J. Hancock, Proc. R. Soc. A, 1953, 217, 96–121 Search PubMed.
- J. Gray and G. J. Hancock, J. Exp. Biol., 1955, 32, 802–814 CrossRef.
- M. Kim, C. Lee, K. Jeon, J. Y. Lee, Y.-J. Kim, J. G. Lee, H. Kim, M. Cho and D.-N. Kim, Nature, 2023, 619, 78–86 CrossRef CAS PubMed.
- G. Volpe and G. Volpe, Am. J. Phys., 2013, 81, 224–230 CrossRef CAS.
- E. Gilbert, D. Johnson and S. Keerthi, IEEE J. Robot. Autom., 1988, 4, 193–203 CrossRef.
- L. Giuggioli, Phys. Rev. X, 2020, 10, 021045 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01474f |
| This journal is © The Royal Society of Chemistry 2024 |
