Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Identifying key environmental objectives for integrated process and fuel design†
Simon
Voelker
 a,
Philipp
Ackermann
a,
Philipp
Ackermann
 b,
Marcel
Granderath
b,
Marcel
Granderath
 a,
Clemens
Kortmann
a,
Clemens
Kortmann
 b,
Joern
Viell
b,
Joern
Viell
 b,
Alexander
Mitsos
b,
Alexander
Mitsos
 bcd and
Niklas
von der Assen
bcd and
Niklas
von der Assen
 *ac
*ac
aInstitute of Technical Thermodynamics, RWTH Aachen University, Aachen 52062, Germany. E-mail: niklas.vonderassen@ltt.rwth-aachen.de
bProcess Systems Engineering, RWTH Aachen University, Aachen 52074, Germany
cJARA-ENERGY, 52056 Aachen, Germany
dEnergy Systems Engineering (IEK-10), Forschungszentrum Jülich, Jülich 52425, Germany
First published on 11th March 2024
Abstract
Integrated process and fuel design enables tailoring renewable fuels for optimal production while simultaneously fulfilling desired fuel specifications. In this work, we extend the integrated process and fuel design framework from [A. König et al., Comput. Chem. Eng., 2020, 134, 106712] towards multiple environmental impact categories of the life cycle assessment methodology as additional objectives to “production cost” and “global warming impact”. We then apply the technique of [G. Guillén-Gosálbez, Comput. Chem. Eng., 2011, 35(8), 1469] to reduce the high dimensionality of the objective vector while still covering the major trade-offs of the optimization problem. Commonly, the input data required for this technique are normalized. We analyze the influence of normalization variants on the identification of the key environmental objectives. For the specific case of designing advanced spark-ignition engine fuels, our findings suggest that “land use” and “resource use of minerals and metals” represent key environmental objectives in addition to “production cost”. These key objectives hold for both current and future technologies for feedstock and utility supply as well as different normalization variants. Our subsequent multi-objective optimization with these key objectives demonstrates that the obtained renewable bio-hybrid fuels, produced from biomass and renewable electricity, can balance the benefits and drawbacks of both biomass- and electricity-based fuels.
1. Introduction
Integrating renewable electricity and feedstocks into synthetic fuels is considered a key technology for sustainable mobility. With fuel design, new promising components or blends for synthetic fuels can be identified that exhibit a priori defined properties. These fuels often contain unconventional components. Most fuel design studies focus on screening molecules or mixtures that lie in a pre-defined range of physico-chemical and combustion-related properties with the aim of identifying a feasible fuel.1–8 Many of these studies target fuel properties that allow for increased engine efficiency,1e.g., through a high octane number,2,6–8 enthalpy of vaporization,6,8 laminar burning velocity,6,8 and compression ratio,3 which in turn can lead to a reduced global warming impact (GWI). In contrast, only a few studies consider the impact of fuel chemistry on emission formation1,4,5,8 or the eco-toxicity and human toxicity of the fuel.8–10Additionally, several studies focus solely on designing a fuel blend, neglecting other phases of the fuel's life cycle. For instance, designing blends with a minimal amount of fossil fuel and maximal amount of alternative fuel aims to reduce both fossil resource depletion and GWI.9–12 However, to estimate the environmental impact of a fuel over its whole life cycle, fuel production needs to be considered as well. Estimating the environmental impact of production processes for unconventional fuel components is challenging, since the processes typically have not been realized outside of laboratories. Identifying optimal synthetic fuels or blends thereof is thus a complex task that can be supported by mathematical optimization, e.g., with methods that combine process and product design in an integrated manner. To this end, Marvin et al. combined a reaction network generator with linear fuel property models to design a blend of biomass-based components with fossil gasoline that complies with ASTM standards, targeting different objectives such as energy loss, catalyst requirement and heat duty of reactions.13
Dahmen and Marquardt built on the method by Marvin et al. and combined mass-based screening by reaction network flux analysis (RNFA)14 with nonlinear fuel property models to design fuel blends for high efficiency engines with minimal resource consumption.15 RNFA uses experimental data like stoichiometry and yields for production processes and was further developed towards process network flux analysis (PNFA). PNFA also considers estimated energy demands of separation steps based on shortcut models by Bausa et al. for distillation columns.16–18 Combining PNFA with predictive fuel property models enabled the integrated early-stage design of production processes and fuels, minimizing the objectives production cost and GWI.19 The application of integrated process and fuel design in a case study for spark-ignition engine fuels with 47 fuel species identified a ketone-ester-alcohol-alkane (KEAA) blend. This KEAA blend represented a promising Pareto-optimal process and fuel design that compromises the conflicting objectives production cost and GWI.20,21
While a lot of studies address the environmental impacts of the fuel, so far, the approach of König et al. is the only design approach that considers the well-to-wheel life cycle of the fuel.19 It uses a bi-objective optimization, minimizing production cost and GWI as the only environmental impact category, which may overlook a potential burden shift to other currently neglected impact categories. Electricity-based fuels (e-fuels), for instance, can reduce GWI substantially compared to fossil fuels if produced from renewable electricity and carbon sources, at the cost of increases in other impact categories, e.g., resource use of minerals and metals.22,23 In contrast, biomass-based fuels (bio-fuels), e.g., ethanol, are known to increase agricultural land occupation substantially compared to their fossil-based counterparts.24 Therefore, a holistic design approach should cover a wide range of impact categories as additional objectives to quantify and avoid potential burden-shifting.25 With these additional objectives, the optimization formulation for integrated process and fuel design is a multi-objective optimization problem (MOP). However, MOPs are challenging for two reasons: the computational effort of approximating a well-resolved Pareto front increases exponentially with the number of objectives.26 Additionally, human decision-making is difficult as visualizing, interpreting, and weighing many different objectives is a complex and subjective task.
In MOPs, the number of actual trade-offs among all objectives is often fewer than expected a priori since at least some objectives are highly correlated.27 These correlated objectives may be less important or even redundant for optimization. According to Gal and Leberling, an objective is redundant if its removal does not change the original Pareto front.28 Consequently, both challenges of MOPs may be resolved by considering only those objectives as key objectives for optimization that are most conflicting and thus covering the major trade-offs of the original MOP. However, identifying the key objectives of an optimization problem is challenging.
In the literature, several methods have been proposed to identify a key objective subset that adequately represents the trade-offs of the original MOP; see the review article by Li et al. for an extensive overview.26 These methods are commonly referred to as dimensionality or objective reduction methods since they reduce the dimensionality of the objective space, i.e., the number of objectives.29,30 For the sake of brevity, we will use the term “objective reduction” whenever we refer to reducing the number of objectives in the objective space. Methods for objective reduction can be roughly categorized based on the timing of objective reduction and the expression of the key objective subset: objective reduction may take place during (online) or after (offline) the generation of a Pareto-optimal solution set,26 and the key objectives are either expressed as a subset (selection) or linear combination (extraction) of the full objective vector.31 Most of these methods are correlation-based or aim to preserve the original MOP's Pareto dominance structure.32 Note that some approaches are also based on feature similarity measures,33 the analytic hierarchy process,34 objective clustering,35,36 and representative and extreme criteria.37
Deb and Saxena developed correlation-based methods for both linear and nonlinear objective reduction, using principal component analysis (PCA) to evaluate the degree of correlation among objectives.31,38,39 PCA transforms a set of correlated objectives linearly into a smaller set of uncorrelated objectives, i.e., the so-called principal components, capturing the maximum variance in the underlying data.40 Correlation-based objective reduction with PCA has, however, two major drawbacks:41 transformed objectives can be difficult to interpret for decision makers since they no longer represent distinct objectives but linear combinations thereof. Additionally, existing PCA-based methods do not take the dominance relation among solutions into account. Thus, preserving the dominance structure cannot be guaranteed.
In contrast, the dominance-based method by Brockhoff and Zitzler evaluates changes in the Pareto dominance structure induced by objective reduction.42 These changes in the dominance structure are quantified by the so-called δ-error. The δ-error can be interpreted as the maximum distance between the Pareto fronts of the original and the reduced objective spaces. Following this approach, objectives are considered redundant if omitting them does not change the dominance structure, resulting in a δ-error of zero. Consequently, a minimum key objective subset without changes to the dominance structure is identified if omitting further objectives would increase the δ-error above zero. The approach also allows the number of objectives to be reduced even further, accepting changes in the dominance structure in favor of a smaller objective subset.
Guillén-Gosálbez et al. introduced a mixed-integer linear programming (MILP) formulation for this approach to minimize the error of omitting objectives with common branch and bound algorithms.43,44 The advantage of this dominance-based method is twofold: identified key objectives represent a true subset instead of transformations of the full objective space. Additionally, the Pareto dominance structure can be preserved, as reported by Guillén-Gosálbez et al.43,44 It should be noted though that identified key objective subsets are not guaranteed to preserve the Pareto dominance structure. The number of input datasets, the approach to generate them, e.g., heuristics, and their normalization may affect Pareto dominance preservation.
The aforementioned objective reduction methods have been already applied in several case studies with environmental objectives to identify key objective subsets (see Note S1†). So far, for integrated process and fuel design, key environmental objectives have not yet been identified. However, their identification is crucial to enable model-based fuel design with a justified selection of the most relevant environmental objectives. With these key environmental objectives identified, potential burden shifts in early-stage fuel design can be captured with manageable computational cost. An a priori selection of key environmental objectives without the use of optimization-based techniques is not feasible, due to the problem size of integrated process and fuel design.
In this work, we close this gap by identifying the key environmental objectives of integrated process and fuel design for a case study on spark-ignition engine fuels. For this purpose, we extend the existing design framework, which considers the objectives production cost and GWI, by all 16 environmental impact metrics recommended for life cycle assessment (LCA) by the European Commission. Next, the dominance-based MILP approach of Guillén-Gosálbez et al.43,44 is applied for objective reduction to identify those objectives that are key to cover the major trade-offs of the optimization problem. Key objectives are derived for two scenarios to consider potential changes in energy and feedstock supply in the next decades. With these key objectives, we generate Pareto-optimal process and fuel designs that we evaluate regarding a potential burden shift. Additionally, these designs are benchmarked against both the KEAA blend of previous studies and fossil gasoline.
The article is structured as follows. First, the problem statement is presented. Next, the methodology of life cycle assessment is explained, followed by an overview of the general solution procedure. Methods used in the solution procedure are presented subsequently: the integrated process and fuel design framework, the objective reduction algorithm, and correlation between variables. Then, the case study on spark-ignition engine fuels is briefly described. After that, the key objectives are identified and used to generate Pareto-optimal process and fuel designs. Lastly, conclusions and recommendations are drawn.
2. Problem statement
The problem we address within this study can be formally stated as follows. Given are the feedstock, electricity, heat, cooling, and refrigeration demands as well as the associated costs and environmental impacts of an array of possible fuel production pathways. Additionally, fuel requirements are given to ensure that targeted fuel standards are fulfilled. The goal of the analysis is to design fuel blends for spark-ignition engines that simultaneously minimize the production cost and environmental impacts. For this goal, we use the integrated process and fuel design framework by König et al.19 In this framework, decisions to be made comprise the mole fluxes of the fuel production network and the composition of the resulting fuel blend.3. Methods
The life cycle assessment methodology is described first. Second, the overall solution procedure is outlined to identify key objectives for integrated process and fuel design. The framework for integrated process and fuel design is presented afterwards. Next, normalization of solutions is explained, followed by the applied objective reduction method. Subsequently, correlation between variables is described.3.1. Life cycle assessment
Environmental impacts of production systems and products can be comprehensively evaluated along the entire life cycle by applying the methodology of life cycle assessment (LCA). Throughout the product system's life cycle, all material and energy flows that the product system exchanges with its environment are quantified. These exchanges are consumed natural resources, e.g., freshwater, and emitted pollutants, e.g., nitrous oxide, which are characterized according to their contribution to environmental impact categories such as water use and climate change. Owing to LCA's holistic approach, potential burden shifting between life cycle stages and impact categories can be identified and quantified. In the 1990s, LCA was standardized using the ISO 14040 and 14044 standards.45,46 According to these standards and recent guidelines for LCA practitioners, LCAs are commonly conducted in four phases that we describe briefly in the following sections.47| Abbreviation | Impact category | Unit | Level of recommendation |
|---|---|---|---|
| GWI | Climate change | kg CO2 eq. | I |
| OD | Ozone depletion | kg CFC-11 eq. | I |
| PM | Particulate matter | Disease incidence | I |
| A | Acidification | mol H+ eq. | II |
| Efw | Eutrophication, freshwater | kg P eq. | II |
| Em | Eutrophication, marine | kg N eq. | II |
| Et | Eutrophication, terrestrial | mol N eq. | II |
| IR | Ionizing radiation, human health | kBq U235 eq. | II |
| POF | Photochemical ozone formation | NMVOC eq. | II |
| ET | Ecotoxicity, freshwater | CTUe | III |
| HTc | Human toxicity, carcinogenic | CTUh | III |
| HTnc | Human toxicity, non-carcinogenic | CTUh | III |
| LU | Land use | Points | III |
| RUe | Resource use, energy carriers | MJ | III |
| RUm | Resource use, minerals and metals | kg Sb eq. | III |
| WU | Water use | m3 world eq. | III |
3.2. Solution procedure to identify key objectives
The applied solution procedure is based on the work of Guillén-Gosálbez et al.43,44 and divided into nine steps (Fig. 1). First, an initial Pareto-optimal solution set is generated by applying the integrated process and fuel design method in the full objective space F (step 1). To generate this solution set, we minimize each single objective separately and subsequently determine the range of each objective. With these ranges, we next apply bi-objective optimization on every combination of objective pairs, using the ε-constraint method with solely four partitions in favor of manageable computational effort.52,53 From the 17 objectives considered in this work, there are 136 possible objective pairs with four partitions per pair, resulting in 544 solutions Sinitial.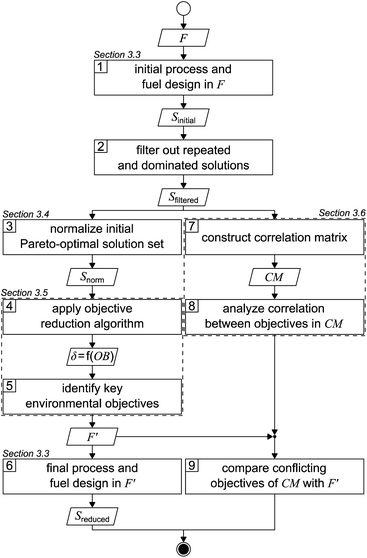 | ||
| Fig. 1 Flowsheet of the applied solution procedure based on the work of Guillén-Gosálbez et al.43,44F: full objective space, F′: reduced objective space, S: solution set, δ: delta-error, OB: number of omitted objectives, and CM: correlation matrix. | ||
After repeated and dominated solutions have been sorted out (step 2), we obtain the filtered solutions Sfiltered. Note that the aforementioned procedure represents a heuristic approach to limit the computational cost: the generated initial solutions are weakly Pareto-optimal since, by bi-objective optimization, we solely optimize two-dimensional projections of the 17-dimensional objective space. Thus, the remaining dimensions of the objective space are not optimized. The filtered solutions Sfiltered are used for the objective reduction algorithm and to construct a correlation matrix (left and right branches, Fig. 1).
In the left branch of Fig. 1, we proceed with normalizing the filtered solutions to obtain a normalized solution set Snorm (step 3). These normalized solutions are used as the input for the objective reduction method applied in step 4. By applying the objective reduction method, we calculate the δ-error, which quantifies the change in the Pareto dominance structure, as a function of the number of omitted objectives (OB). In step 5, we can identify the key objectives representing an acceptable compromise of omitted objectives and the induced δ-error. Lastly, in step 6, we generate a set of Pareto-optimal process and fuel designs Sreduced in a reduced objective space F′. We apply multi-objective optimization on all key objectives, again using the ε-constraint method.52,53 In contrast to the first step, we increase the number of partitions from four to 32 in favor of a higher resolution of the Pareto front. Additionally, we refrain from using heuristics to generate these Pareto-optimal solutions, accepting increased computational cost that is partly offset by the smaller number of objectives considered.
In the right branch of Fig. 1, we use the filtered solutions Sfiltered to construct a correlation matrix (CM) (step 7). Next, the degree of correlation among the objectives is analyzed to gain a first notion about redundancy and conflict (step 8). Lastly, in step 9, we compare the conflicting objectives from the correlation matrix with the key objectives identified by objective reduction. Based on this comparison, we derive conclusions about the suitability of correlation matrices to identify the key objectives covering an optimization problem's major trade-offs.
3.3. Integrated process and fuel design
Here, we concisely describe the integrated process and fuel design method by König et al.19 An in-depth description is given in the original work. Integrated process and fuel design combines a pathway model based on PNFA17,18 with the fuel property model of Dahmen and Marquardt.15 The most important characteristics of the pathway and fuel property models are described in the following section. Subsequently, the resulting optimization problem is explained.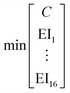 | (1) |
The production cost is evaluated by dividing the total annualized production cost Ctotal by a fixed annual fuel production of 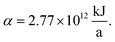 This annual fuel production is related to the energy content of 100
This annual fuel production is related to the energy content of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons of ethanol per year, in line with previous studies.17,19,20
000 tons of ethanol per year, in line with previous studies.17,19,20
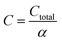 | (2) |
The total annualized production cost Ctotal is determined by summing up the annualized costs due to investments Cinvest, utilities Cutil, feedstocks Cfeedstock, and wastes Cwaste. The considered utilities are electricity, process heat, cooling, and refrigeration.
| Ctotal = Cinvest + Cutil + Cfeedstock + Cwaste | (3) |
The mth environmental impact per functional unit EIm is calculated by dividing the total environmental impact EItotal,m by the fixed annual fuel production α.
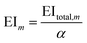 | (4) |
The total environmental impact EItotal,m comprises the impacts due to the supply of utilities EIutil,m and feedstocks EIfeedstock,m.
| EItotal,m = EIutil,m + EIfeedstock,m | (5) |
In this MOP, design variables are the resulting fuel composition and the mole fluxes of the reaction network. Trade-offs among objectives can be evaluated by using the ε-constraint method.52,53 See Note S2† and König et al. for more details regarding the economic and environmental objectives as well as the original optimization problem including all constraints.19,20
3.4. Normalization of solutions
There are good reasons to normalize solutions prior to objective reduction: the herein considered objectives differ regarding their physical units, e.g., GWI in kg CO2 eq. and water use in m3 eq. Thus, without normalization, the δ-error's unit would also differ depending on the omitted objective since the error is directly calculated from the objective function values (see eqn (10) and (11) below). Moreover, the scales among objectives can vary by several orders of magnitude, depending on the objectives' units. Therefore, without normalization, objectives with a small scale would be omitted preferentially, as the δ-error of omitting these objectives would be also small. However, solutions can be normalized in different ways, rendering the choice of the applied normalization variant arbitrary. We emphasize, therefore, that normalization is a critical step that induces ambiguity in the identification of key objective sets.54 In fact, the identified key objective subsets and the corresponding approximation errors might change if different normalization variants are used.Solutions are usually normalized with mathematical or environmental reference values. As mathematical reference values, the objective-specific minimum and maximum values of all solutions are commonly used to normalize the range of each objective. Environmental reference values are typically the environmental impacts of a reference system, e.g., a country's environmental impacts or planetary boundaries of the Earth. These environmental reference values can be optionally weighted, e.g., based on expert judgment, to rank the importance among objectives. Both mathematical and environmental reference values have advantages and drawbacks. While mathematical normalization attributes arbitrarily equal relevance to all objectives, mathematical reference values can be objectively calculated. In contrast, environmental normalization derives the relevance of objectives by comparison with the reference system. However, the reference system can be chosen arbitrarily and derived reference values are often uncertain, e.g., global environmental impacts or the Earth's planetary boundaries. Additionally, optional weighting based on expert judgements is highly subjective. For energy system optimization, Postels et al. analyzed the influence of normalization variants based on mathematical and environmental reference values on the identified key objective subset.55 The authors show that, in their case study, mathematical normalization variants lead to similar results while the identified key objective subsets differed substantially for the environmental reference values.
In this work, we focus on comparing four mathematical normalization variants regarding the key objective subsets identified by subsequent objective reduction. The variants (N1–N4) normalize each objective value OFs,i of solution s regarding objective i. For this purpose, the objective-specific minimum 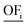 and maximum
and maximum 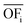 of all solutions are used as reference values, following Marler and Arora.56
of all solutions are used as reference values, following Marler and Arora.56
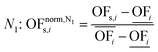 | (6) |
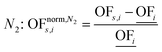 | (7) |
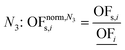 | (8) |
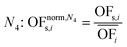 | (9) |
3.5. Objective reduction
To identify key objectives of integrated process and fuel design, we apply the dominance-based MILP approach for objective reduction by Guillén-Gosálbez et al.43,44 This approach reduces the number of objectives in the objective vector using mathematical optimization such that changes in the Pareto dominance structure are minimized, i.e., the major trade-offs of the original problem are covered. Before objective reduction is applied, it is required to normalize Pareto-optimal solutions used as the input for objective reduction (see Section 3.4). In the following section, we briefly explain the formulation of the optimization problem for objective reduction. See Note S3† for an exemplary minimization problem describing the underlying idea of this approach.Here, the optimization problem for objective reduction is briefly summarized for completeness. For a more extensive description of the MILP formulation, see the work of Guillén-Gosálbez et al.43,44 This MILP formulation is based on the problem of computing a “minimum objective subset of size k with minimum error” (k-EMOSS) by Brockhoff and Zitzler.42 For q objectives in the full objective space F, the optimization problem seeks to minimize the maximum δ-error induced by omitting objectives:
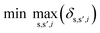 | (10) |
All solutions of the minimization problem must satisfy a set of constraints that are described in the following section. The δ-error is the difference between solution s and solution s′ regarding the ith objective (eqn (11)). Under this constraint, OFs,i represents the normalized value of the ith objective of Pareto solution s, whereas ZOi and ZDs,s′ are two binary variables. ZOi is 1 if the ith objective is omitted while ZDs,s′ is 1 if solution s dominates solution s′ in the reduced objective space.
| δs,s′,i = (OFs′,i − OFs,i)ZOiZDs,s′ ∀ s ≠ s′,i | (11) |
In eqn (12) and (13), ZDs,s′ is calculated using a third binary variable YPs′,s,i, which is 1 if solution s is better than solution s′ in the ith objective.
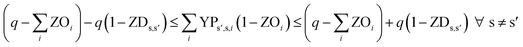 | (12) |
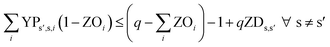 | (13) |
The following four equations are used to linearize the product of the binary variables ZOi and ZDs,s′ in eqn (11):
| (OFs′,i − OFs,i)ZODs,s′,i = δs,s′,i ∀ s ≠ s′,i | (14) |
| ZODs,s′,i ≤ ZOi ∀ s ≠ s′,i | (15) |
| ZODs,s′,i ≤ ZDs,s′ ∀ s ≠ s′,i | (16) |
| ZODs,s′,i ≥ ZOi + ZDs,s′ − 1 ∀ s ≠ s′,i | (17) |
Lastly, the number of objectives to be omitted (OB) is prescribed:
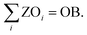 | (18) |
Note that alternative objective subsets may exist which exhibit equal δ-errors. To find those alternatives for a prescribed number of omitted objectives, we iteratively exclude previously found objective subsets from the solution space by adding integer cut constraints.
3.6. Correlation between two variables
Calculating the correlation coefficient is a common means to get a notion of the trade-off between variables. Often, the Pearson correlation coefficient is used to evaluate the degree of correlation between two variables for a given sample. Applied to our work, the variables are two objectives i and i′, e.g., production cost and GWI. The sample comprises n solutions of the integrated process and fuel design. Regarding the ith objective, OFs,i denotes the objective function value of the sth solution, whereas OFmi is the mean value of objective i. To calculate the degree of correlation between two objectives i and i′, the Pearson correlation coefficient ri,i′ is calculated as the ratio between the covariance of both objectives and the product of their standard deviations: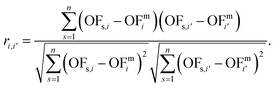 | (19) |
Noteworthily, the Pearson correlation coefficient ranges between −1 and 1: perfectly negative or positive correlation is implied by values of −1 or 1, whereas a value of zero implies that no linear correlation exists. For q objectives, a correlation matrix CM of size q × q can be constructed whose (i,i′) entry is
| CMi,i′ = ri,i′. | (20) |
In such a correlation matrix, all diagonal entries equal 1 since each objective is perfectly correlated with itself (i = i′). Negative or positive correlation indicates a conflicting or redundant pair of objectives, respectively.
4. Integrated process and fuel design for spark-ignition engine fuels
We apply the above described solution procedure in a case study on integrated process and fuel design for spark-ignition engine fuels by König et al.20 In the following, we briefly review the main features of this case study and describe which aspects we adapt in this work. The case study considers 47 pre-screened fuel species as suitable components for multi-component gasoline-type fuels to be used in spark-ignition engines (see Table S2†). For these fuel species, reaction routes for biomass and hydrogen conversion have been collected from the literature and the authors' previous studies for the pathway model. Energy demands for downstream processing have been calculated with thermodynamically sound intermediate-fidelity methods for distillation columns.16 As possible feedstocks, biomass, CO2, and renewable hydrogen are considered for fuel production. To distinguish the renewable fuels by feedstock type, we use the terms ‘bio-fuel’ if biomass is used, ‘e-fuel’ if CO2 and renewable hydrogen are used, and ‘bio-hybrid fuel’ if all three feedstocks are used.For the fuel property model, pure-component data have been incorporated for all fuel species from databases, the literature, and property prediction models. Fuel requirements for the so-called ultra-high efficiency engine (UHEE) fuels have been adapted from previous studies.19 These UHEE fuel requirements have been derived for highly boosted spark-ignition engines with a high compression ratio, targeting high engine efficiency and low combustion-induced pollutant emissions. The considered fuel properties are the research octane number, density, oxygen content, olefin and aromatic content, surface tension, kinematic viscosity, enthalpy of vaporization, bubble point pressure, and distillation curve.
4.1. Goal and scope definition
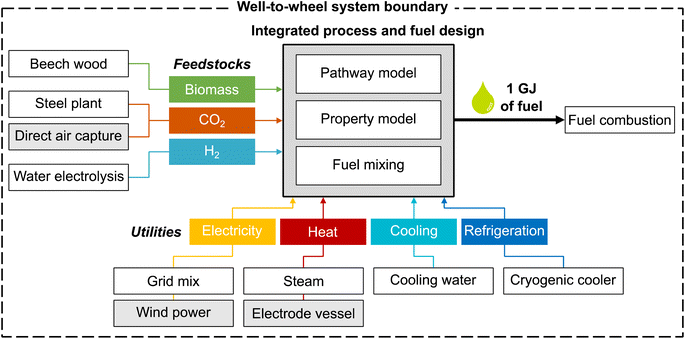
The overall aim of this case study is to identify those environmental metrics that are key for the integrated process and fuel design of renewable spark-ignition engine fuels. For this purpose, this LCA's goal is to analyze the environmental impacts of production-optimal fuels with tailor-made properties for spark-ignition engines within a German fuel production setting. These environmental impacts are benchmarked with fossil gasoline and the KEAA blend of previous studies.20,21 For a consistent comparison among different fuels, we define the functional unit as “the provision of 1 GJ of enthalpy of combustion”, as recommended by Müller et al.57 and by following previous work by König et al.20 The fuel production model comprises a well-to-wheel system boundary that considers the supply of feedstocks and utilities, the pathway model for fuel production, and fuel combustion with air (Fig. 2). In contrast to previous studies, we do not allow fossil gasoline as a blending component since our aim is to design fully renewable fuels.We characterize all material and energy flows exchanged with the environment according to the LCIA method EF 3.0, which is recommended by the Joint Research Centre of the European Commission.48 We, therefore, extend the objective space by 15 environmental impact categories of the EF 3.0 method, in addition to the objectives production cost and GWI considered in previous case studies.20,21 An overview of the included impact categories with the corresponding abbreviations, units, and recommendation levels is presented in Table 1. Consequently, the resulting objective vector contains in total one economic and 16 environmental objectives. Of these 16 environmental objectives, we subsequently identify those objectives that cover the key trade-offs of integrated process and fuel design by applying the objective reduction approach. Note that, in this work, solely environmental objectives can be omitted by objective reduction to keep the only economic objective, production cost, in the key objective subset.
4.2. Life cycle inventory
For the case study, we distinguish between a ‘today’ and a ‘future’ scenario to consider potential technology changes in feedstock and energy supply (Table 2). While the ‘today’ scenario represents incumbent technologies, the ‘future’ scenario portrays a likely, fully renewable energy system. As our ‘today’ scenario slightly adjusts LCA datasets and prices compared to the work of König et al.,19,20 we analyze the implications of these adjustments in Note S4.† Overall, our adjustments result in a similar Pareto front for GWI and production cost, with slight increases in GWI scores due to our changes regarding the modeled steam and refrigeration supply. In the following, we briefly describe the inventory data used for the LCA as well as assumed prices for each scenario. A detailed overview of the LCA datasets is presented in Note S5.†| Inputs | Scenario | |
|---|---|---|
| Today | Future | |
| a For water electrolysis, electricity from wind power is considered regardless of the scenario. | ||
| Feedstocks | ||
| Carbon dioxide | Steel plant | Direct air capture |
| Biomass | Beech wood | Beech wood |
| Hydrogen | Water electrolysisa | Water electrolysisa |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Utilities | ||
| Electricitya | Grid mix | Wind power |
| Process heat | Steam | Electrode vessel |
| Cooling | Cooling water | Cooling water |
| Refrigeration | Cryogenic cooler | Cryogenic cooler |
The feedstock CO2 is either supplied by carbon capture at a steel plant or direct air capture (DAC). Carbon capture at a steel plant requires 0.87 MJ of electricity and 0.95 MJ of process heat per kg of captured CO2, according to von der Assen et al.58 For DAC, we consider the predicted energy requirements of a temperature-swing adsorption system, following Deutz et al.59 Each kg of captured CO2via DAC requires 1.80 MJ of electricity and 5.40 MJ of process heat. The process heat for DAC is supplied by heat pumps with a modeled coefficient of performance of 3.28.60 Beech wood is assumed to be a representative lignocellulosic biomass, using process data from the LCA database ecoinvent.50 Note that no carbon credit, i.e., avoided burden, is given for CO2 that is removed from the atmosphere by either biomass growth or DAC since this CO2 is released again to the atmosphere at the fuel's end-of-life.20
Designing renewable fuels necessitates renewable hydrogen production in both scenarios. Therefore, hydrogen is assumed to be supplied renewably via polymer electrolyte membrane (PEM) water electrolysis in both scenarios, using electricity from wind power. Using electricity from wind power for electrolysis also in the ‘today’ scenario reflects a realistic scenario of importing renewable energy via hydrogen. Already today, so-called green hydrogen hubs are developed by several large ports, e.g., those of Antwerp-Bruges, Rotterdam and Hamburg, to import and produce green hydrogen. These green hydrogen hubs are scheduled to start operating by 2025 (“Shell Holland 1”, “HyoffWind”, and “Plugpower”) and 2026 (“Hamburg Green Hydrogen Hub”). The modelled PEM electrolysis requires 8.94 kg of water and 47.6 kW h of electricity from wind power per kg of hydrogen, using process data by Reuß et al.61
Regarding utilities, we consider the provision of electricity, process heat, cooling, and refrigeration. We assume that electricity for processes other than water electrolysis is mainly supplied by the German grid in the ‘today’ scenario and by clean electricity from wind power in the ‘future’ scenario, using process data from ecoinvent.50 Process heat is provided via steam or an electrode vessel with a power-to-heat efficiency of 95%.57 For cooling and refrigeration, the use of cooling water50 and cryogenic coolers is assumed, respectively. In this early-stage design, we assume a constant refrigeration temperature of −100 °C as a rough estimation and model cryogenic coolers with an energy efficiency ratio of 0.25, based on curve fit functions of Ladner et al.62
Use phase pollutants from non-ideal fuel combustion are not covered in integrated process and fuel design. Soot emissions for hydrocarbon fuels can be predicted using the particulate matter index by Aikawa et al.,63 which predicts engine-out emissions based on the fuel's volatility and its chemical tendency to form soot. As a measure for the latter, the number of double bonds is used. However, soot chemistry becomes more complicated for oxygenated hydrocarbons since different oxygen functionalities reduce the formation of soot precursors to different degrees.64 While this effect is captured by the yield sooting index by Das et al.,65 the yield sooting index does however not predict engine-out emissions. Further pollutant emissions like unburned hydrocarbons, carbon monoxide, and nitrogen oxides depend strongly on the engine operation and can therefore not be predicted at an early design stage. Additionally, engine efficiencies are disregarded for simplicity, i.e., it is assumed that different fuels could be used with equal efficiency in spark-ignition engines.20
For price estimations, we adopt prices from previous studies on integrated process and fuel design by König et al. where possible, maintaining comparability with preceding studies as much as possible.19,20 Due to the German scope of this study, the following prices are converted from United States dollar ($) to euro (€), using 2022's average exchange rate of 1.05 $ per €. These adopted prices comprise 7.5 $-ct per kW h of electricity from the grid,66 9.5 $ per ton of steam,66 6.5 $-ct per m3 of cooling water,66 5.78 $ per kg of hydrogen from water electrolysis using electricity from wind power,67 50 $ per ton of biomass,68 and 40 $ per ton of CO2 captured at a steel plant.69 We further assume prices of 6.0 $-ct per kW h of electricity from wind power,70 6.3 $-ct per kW h of process heat from electrode vessels using electricity from wind power with a power-to-heat efficiency of 95%, and 200 $ per ton of CO2 captured from ambient air.71,72 Cryogenic refrigeration costs are modeled for the assumed refrigeration temperature of −100 °C and a two-stage compression refrigeration system, according to Luyben:73 refrigeration costs result in 22.4 or 18.9 $-ct per kW h of refrigeration if electricity from the grid or wind power is used, respectively.
5. Results
Both the continuous NLP of integrated process and fuel design and the MILP of the objective reduction approach are implemented in GAMS v35.2.0 and solved on a computer with an Intel E5-1660 v4 3.2 GHz processor and 128 GB RAM. The continuous NLP is solved with the deterministic global solver BARON v21.1.13, using one thread, a branching priority of 20 on the molar fuel fraction, a time limit of 1000 seconds, and a relative optimality tolerance of 0.1% (single objective optimization) or 1% (bi- and multi-objective optimization). For the MILP, we use the solver CPLEX v20.1.0.1 and four parallel threads. Any other solver settings are left at default values. Similar to König et al.,20 some solutions of the continuous NLP are globally optimal while other runs do not converge to the specified optimality even though we increased the time limit drastically. Similar to previous work, the lower bound convergence stagnates for these runs, and we follow the assumption of König et al. that the found solutions are globally optimal.After filtering out the initial 544 solutions Sinitial, 156 and 158 unique solutions Stodayfiltered and Sfuturefiltered remain for the ‘today’ and ‘future’ scenario, respectively (see Tables S6 and S7†). With these unique Pareto-optimal solutions, we construct correlation matrices for both scenarios to gain a first notion about conflicting and redundant objective pairs (see Tables S10 and S11†). The correlation matrices indicate that the most conflicting objectives are land use in the ‘today’ scenario as well as land use and freshwater eutrophication in the ‘future’ scenario. Furthermore, weakly correlated objectives are production cost in both scenarios and freshwater eutrophication in the ‘today’ scenario. All other objective pairs show large coefficients in the correlation matrices, indicating redundancy among these objectives. We next normalize the scenario-specific filtered solutions with each normalization variant (see Section 3.4), yielding four normalized solution sets per scenario, e.g.,  and so on.
and so on.
5.1. Identifying key environmental objectives
After generating the normalized solution sets, we identify key environmental objectives and redundant ones for each scenario. To analyze how the problem's dominance structure may change if we omit redundant objectives, we apply the dominance-based objective reduction approach (see Section 3.5). Thus, we quantify this change, i.e., the δ-error, as function of the number of omitted objectives for each normalization variant (Fig. 3). Note that the normalization variants lead to different ranges of values regarding the normalized solutions and, consequently, resulting δ-errors. To enable comparability between δ-errors calculated with different normalization variants, we use the relative δ-error δrel introduced by Postels et al.:55 For each normalization variant, the δ-error is referenced to its maximum value that occurs if all but one, i.e., 16 out of 17, objectives are omitted. Additionally, we specify a threshold δ* of 0.1 to identify small key objective subsets with a still acceptable δ-error (Fig. 3, dotted horizontal line).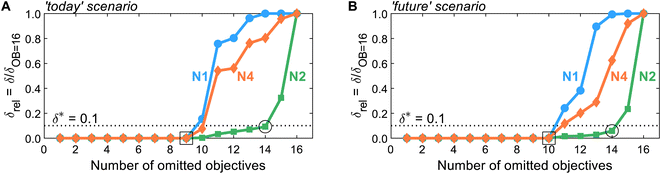 | ||
| Fig. 3 The δ-error δrel as a function of the number of omitted objectives for normalization variants N1, N2, and N4 in the (A) ‘today’ or (B) ‘future’ scenario. Note that normalization variant N3 is not shown since it yields identical results to N2, as both variants differ only by a constant offset of 1. A threshold δ* of 0.1 is introduced to identify small objective subsets with an acceptable δ-error. For numerical results and the corresponding identified objective subsets, see Tables S8 and S9.† | ||
Regarding the determined threshold δ* of 0.1, two numbers of omitted objectives are of greater interest: the maximum number of omitted objectives for which all (square, Fig. 3) or at least one (circle, Fig. 3) normalization variant is below the threshold. For both scenarios, many objectives can be omitted without inducing a δ-error, i.e., a change in the dominance structure of integrated process and fuel design. Without inducing a δ-error, up to nine and ten objectives can be omitted in the ‘today’ and ‘future’ scenario (square, Fig. 3), respectively. In the ‘today’ scenario, all normalization variants result in the same minimal reduced objective subset without a δ-error of FtodayOB=9 = (C, LU, RUm, RUe, WU, Efw, HTc, PM)T. In contrast, in the ‘future’ scenario, two minimal reduced objective subsets without δ-error are identified by all normalization variants: Ffuture,1OB=10 = (C, LU, RUm, RUe, WU, ET, HTnc)T and Ffuture,2OB=10 = (C, LU, RUm, RUe, WU, ET, IR)T. Hence, the objectives production cost (C), land use (LU), resource use of minerals and metals (RUm) and energy carriers (RUe), and water use (WU) are present in the reduced objective subsets without δ-error in both scenarios.
With normalization variant N2, further objectives can be omitted while still maintaining a δ-error below the threshold δ*. In both scenarios, up to 14 objectives can be omitted (circle, Fig. 3), resulting in equally reduced objective subsets of FOB=14N2,today = FN2,futureOB=14 = (C, LU, RUm)T with δ-errors of 0.09 and 0.06, respectively. Note that increasing the number of Pareto points generated as inputs for objective reduction has negligible effect on the δ-error while the identified reduced objective subset FN2,todayOB=14 is entirely unaffected (see Note S6†). The other normalization variants, N1 and N4, result in the same reduced objective subsets but with much greater δ-errors. In fact, normalization variant N1 reaches the maximal δ-error of one for 14 omitted objectives in the ‘today’ scenario, rendering the choice of the three objectives arbitrary. Notable, alternative objective subsets with equivalent approximation error and three objectives were not found. However, in near-optimal objective subsets, other sets of three objectives can be seen (e.g., land use (LU) and water use (WU)).
Overall, we find that the normalization variants considered herein do not affect the minimal reduced objective subsets without δ-error identified in both scenarios (square, Fig. 3). If even smaller reduced objective subsets are targeted, normalization affects, however, both the identified reduced objective subsets and the induced δ-error. Nonetheless, land use (LU) and resource use of minerals and metals (RUm) stand out against the other objectives since they are present in all reduced objective subsets for up to 14 objectives omitted, irrespective of the scenario and normalization variant (see Tables S8 and S9†). We, therefore, suggest using land use (LU) and resource use of minerals and metals (RUm) as key environmental objectives for integrated process and fuel design of spark-ignition engine fuels.
When we compare these findings with the constructed correlation matrices (see Note S7†), we find, as a priori expected, that correlation matrices alone provide insufficient information to select reduced objective subsets. Land use is the only objective that is conflicting with any other objective in the ‘today’ scenario while, in the ‘future’ scenario, land use and freshwater eutrophication are both in conflict with the other objectives. On the one hand, this degree of conflict matches our findings from objective reduction that land use is a key objective. On the other hand, the correlation matrices indicate that resource use of minerals and metals is correlated with the other objectives although it is also a key objective from objective reduction. Therefore, correlation matrices alone appear unsuitable for choosing key objectives since the error inherent to omitting objectives cannot be quantified.
5.2. Integrated process and fuel design with key environmental objectives
Based on our findings from objective reduction, we proceed with generating Pareto-optimal process and fuel designs for spark-ignition engine fuels in a reduced objective space (Fig. 4). It would be sensible to perform the integrated fuel design with the minimal objective subset that does not induce a δ-error irrespective of the normalization variant (see the square, Fig. 3). However, multi-objective optimization with eight objectives comes at the cost of high computational effort for a well-resolved Pareto front. Here, we thus choose the smaller reduced objective subset FN2,todayOB=14 = FN2,futureOB=14 = (C, LU, RUm)T containing both key environmental objectives land use (LU) and resource use of minerals and metals (RUm) to gain a well-resolved Pareto front with manageable computational effort. Note though that this reduced objective subset induces a δ-error that is small for normalization variant N2 but large for N1 and N4 (see Section 5.1). We obtain 43 and 46 unique Pareto-optimal solutions for the ‘today’ and the ‘future’ scenario, respectively (see Tables S12 and S13†). The majority of Pareto-optimal solutions are bio-hybrid fuels, followed by bio-fuels and only one e-fuel (Table 3). For contribution analyses of these solutions, see Note S9.†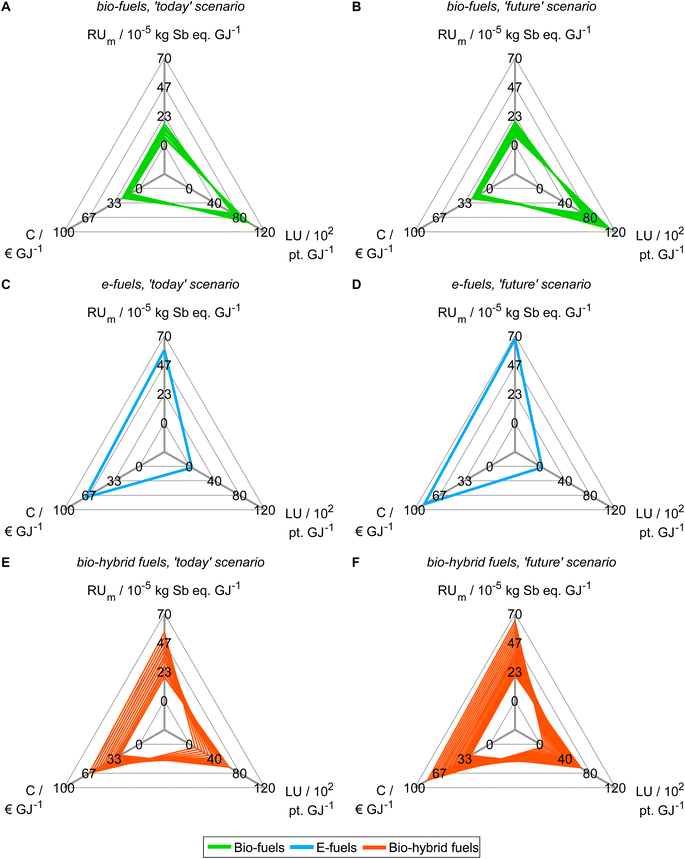 | ||
| Fig. 4 Pareto-optimal process and fuel designs of bio-, e-, and bio-hybrid fuels regarding the reduced objective space of the ‘today’ (A, C and E) and ‘future’ (B, D and F) scenarios. In Note S8,† we present an alternative figure that shows the single-objective minima of the Pareto-optimal solutions generated with the reduced objective subsets. For contribution analyses of these solutions, see Note S9.† | ||
| Scenario | ||
|---|---|---|
| Today | Future | |
| Total | 43 | 46 |
| Bio-fuels | 19 | 18 |
| E-fuels | 1 | 1 |
| Bio-hybrid fuels | 23 | 27 |
In both scenarios, the bio-fuels yield the lowest production cost (C) and resource use of minerals and metals (RUm) but the highest land use (LU) (Fig. 4A and B). In contrast, the e-fuel has minimal land use but the highest scores in both other objectives (Fig. 4C and D). Notably, in the ‘future’ scenario, e-fuels exhibit slightly higher production cost and resource use of minerals and metals: CO2 supply by DAC is expected to be much more expensive than CO2 capture from industrial point sources, e.g., capture at steel plants, resulting in increased production cost (see Fig. S6C and D†). Additionally, the demand for minerals and metals increases as electrification with renewable energy is increasing in all life cycle phases (see Fig. S7C and D†). The bio-hybrid fuels can balance all three objectives (Fig. 4E and F), leveling the advantages and drawbacks of bio- and e-fuels: lower land use scores than those of bio-fuels are possible but at the cost of increases in the other objectives and vice versa.
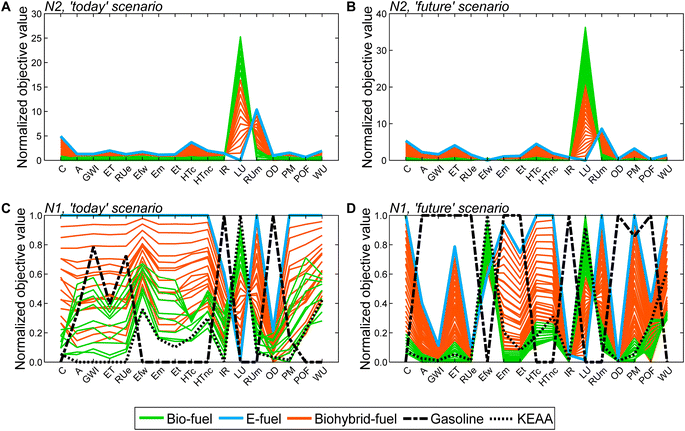
Based on the generated Pareto-optimal solutions, we next analyze trends in the full objective space and benchmark the generated solutions with gasoline and the KEAA blend, which was designed in a previous study considering only production cost and GWI.20 For the analysis of the generated solutions, we normalize the solutions with variant N2 (Fig. 5A and B). For the comparison with both benchmarks shown in Fig. 5C and D, we normalize with variant N1 instead. With variant N1, all objectives are scaled to the range [0,1], facilitating comparison especially for objectives with small variance among all generated solutions, e.g., acidification (A).
When we evaluate the Pareto-optimal solutions in the full objective space (Fig. 5A and B), we see that land use (LU) and resource use of minerals and metals (RUm) represent, as expected, the most apparent trade-off in both scenarios and for all fuels, i.e., the higher the land use the lower the resource use of minerals and metals and vice versa. Besides land use (LU) and resource use of minerals and metals (RUm), there is also larger variance among solutions regarding production cost (C) and human toxicity (HT) for the ‘today’ scenario as well as additionally ecotoxicity (ET) and particulate matter (PM) for the ‘future’ scenario. Overall, the e-fuel performs worst in all objectives except for land use in the ‘today’ scenario and additionally in freshwater eutrophication (Efw) in the ‘future’ scenario. Conversely, the bio-fuels rank worst for these objectives and best for all others. As already indicated by the results from the reduced objective space (see Fig. 4), bio-hybrid fuels level the impacts of bio- and e-fuels in most objectives.
Comparing the generated solutions with the benchmark gasoline reveals that the designed fuels can achieve better or at least similar scores compared to gasoline in many objectives (Fig. 5C and D). However, in both scenarios, gasoline has the lowest production cost (C), freshwater eutrophication (Efw), human toxicity (HT), land use (LU), resource use of minerals and metals (RUm), and water use (WU). For human toxicity (HT), electricity consumption is the main driver for the generated solutions (see Fig. S19 and S20†). Depending on whether electricity from wind power or the grid is consumed, the major contributors are the production of either metals or lignite and hard coal, respectively, and associated waste treatment processes. Conversely, gasoline performs worse, if not the worst, in ionizing radiation (IR) and ozone depletion (OD), acidification (A), GWI, ecotoxicity (ET), and resource use of fossil energy carriers (RUe).
Benchmarking the generated solutions with the KEAA blend from previous fuel design studies20,21 shows that the KEAA blend is still an exceptionally promising synthetic fuel, except for land use (LU). Apart from land use, the KEAA blend yields the lowest scores among all synthetic fuels for almost every objective in the ‘today’ scenario. Moreover, the KEAA blend is also among the best synthetic fuels in our ‘future’ scenario although the blend was originally designed for a scenario considering solely today's technologies.20,21 Nonetheless, we can identify bio-fuel designs among our generated solutions that yield better scores than the KEAA blend in all objectives for the ‘future’ scenario (see Fig. S5†).
6. Discussion
Our findings indicate that up to nine or ten of 17 objectives can be omitted in early-stage fuel design for our ‘today’ or ‘future’ scenario, respectively. For these objective subset sizes, no error is induced regarding the approximated Pareto front, irrespective of the applied normalization variant. If even smaller objective subsets are desired for fuel design, one has to weigh the benefit of a decreasing computational effort against the drawback of an increasing approximation error. Notably, the approximation error differs depending on the normalization variant applied. Normalization is thus a critical, arbitrary step since various normalization variants exist.By reducing the objective space even further, we find that “land use” and “resource use of minerals and metals” are present in all reduced objective subsets irrespective of the scenario, normalization variant, and objective subset size. In our view, these results underline the relevance of both objectives to cover the major trade-offs in the design of bio-, e-, and bio-hybrid fuels for spark-ignition engines. We, therefore, consider “land use” and “resource use of minerals and metals” as key environmental objectives and suggest the inclusion of both, in addition to “production cost,” for fuel design.
Our integrated process and fuel design with these key environmental objectives and “production cost” demonstrates that bio-fuels yield among the best scores in most objectives but shift burdens to large increases in land use due to biomass cultivation. Conversely, the e-fuel has the lowest land use but the highest scores regarding all other objectives. We show that the generated bio-hybrid fuels can step in as balanced fuel designs: by using both biomass and renewable electricity as feedstocks, they can balance the benefits and drawbacks of bio- and e-fuels. Compared to the KEAA blend of previous studies,20,21 most blend components of the generated bio-hybrid fuels have similar shares, e.g., ethanol and ethyl acetate (see Note S10†). However, some blend components differ to a larger extent: the bio-hybrid fuels contain more than twice as much methyl acetate (45%) as the KEAA blend, whereas methyl isopropyl ketone, one of KEAA's main components, is completely absent.
In the following, we discuss the generalizability of our findings towards a universal assessment of renewable fuels in terms of the considered scenario, the product, the production scale, data gaps in the process model, and the methodological maturity of the environmental impact categories. In general, it cannot be guaranteed that our findings hold generically if the scenarios are altered or other products are to be designed. Thus, we underline that the herein identified key environmental objectives are case-specific for both the considered scenarios and the design of advanced spark-ignition engine fuels. Similar findings are, however, likely if alternative utilities and feedstocks are considered whose costs and environmental impacts differ only marginally from those of the technologies considered herein.
Notably, our ‘future’ scenario does not reflect potential changes in the background system although grid decarbonization will progress and less carbon-intensive technologies, e.g., low-carbon steel, will become more established in the future. This influence of background system changes on environmental impacts was analyzed for a national energy system optimization by Reinert et al.74 The authors found that while accounting for changes does indeed reduce most environmental impacts, the general trends are adequately captured with a static background system as applied in our work. Overall, we therefore do not expect our findings to change substantially if changes in the background system would be considered.
Furthermore, we are confident that the key environmental objectives also hold for other liquid carbon-based energy carriers produced from renewable feedstocks, e.g., diesel-type fuels, since the involved processing steps are similar among different synthetic fuels. The two identified key environmental objectives “land use” and “resource use of minerals and metals” account for the fact that the production of renewable carbon-based energy carriers involves a step to chemically reduce CO2, which is present in the atmosphere. In the case of biomass, CO2 reduction through photosynthesis requires land for biomass cultivation. For e-based energy carriers, CO2 is reduced by hydrogen from renewable electricity via water electrolysis, which requires minerals and metals for the construction of wind parks and photovoltaic plants. These findings suggest that both key environmental objectives also cover the trade-offs of GWI, which is strongly interconnected with CO2.
The scale of fuel production modelled might change the identified subset of key environmental objectives. While we assume constant prices and environmental impacts of feedstocks and auxiliaries as input parameters for our model, these parameters can be expected to vary for different production scales. With increasing production scale, prices and environmental impacts of feedstocks and auxiliaries might change due to market effects such as the price elasticity of demand and land-use change emissions induced by the development of new land for biomass cultivation or wind parks. Although such scaling effects could be modeled, in principle, by incorporating integrated assessment models into our framework, solving these models would further increase computational cost drastically.
Regarding data gaps in the process model, our findings might change if more detailed models of transportation, production, and use phase are developed for the fuel design framework. Currently, the cost and environmental impacts of feedstock transportation are neglected. However, the supply of feedstocks, in particular renewable hydrogen, may require their production or cultivation in regions with high renewable energy potential and subsequent transportation around the globe. During fuel production, potential direct emissions are not covered since the fuel design framework was developed as an early-stage screening tool based on stoichiometry and yield data. In the use phase, combustion-induced pollutants, e.g., soot, nitrogen oxides, and carbon monoxide, are neglected since, so far, they cannot be predicted accurately at an early design stage.
Noteworthily, the environmental impact categories considered herein vary regarding their methodological maturity (Table 1), which might be an additional source of uncertainty for the identified key environmental objectives. Only three of 16 impact categories are classified as recommended and satisfactory. Although also recommended, the remaining 13 impact categories are still classified as in need of some improvement or to be applied with caution (see Section 3.1). For instance, human toxicity (HT) and the identified key environmental objectives land use (LU) and resource use of minerals and metals (RUm) are recommended but should be applied with caution. Regarding human toxicity, it is questionable whether gasoline is actually less toxic to humans over the entire life cycle than all renewable fuels generated herein (see Fig. 5C and D). This finding might hint at data gaps in the underlying LCIA methods because gasoline is well-known for its acute toxicity.
As a consequence, we recommend the verification our findings with the approach described herein if the case study is altered or another product or production scale is studied. Likewise, the identified key environmental objectives should be verified if the fuel design framework is enhanced, e.g., by a sophisticated engine model, or if environmental impact categories that are currently immature are improved.
7. Conclusions
This work suggests key environmental objectives for the integrated process and fuel design of spark-ignition engine fuels. For this goal, we add 16 common environmental impact metrics of the life cycle assessment methodology as additional objectives to the integrated process and fuel design framework. We analyze a ‘today’ and a ‘future’ scenario to consider technology changes in feedstock and utility supply. To identify a reduced objective subset covering the problem's key trade-offs, we use a dominance-based optimization approach to reduce the number of objectives in the objective vector with minimal changes to the problem's dominance structure. As it is required to normalize input data for this objective reduction approach, we evaluate the normalization's influence on the identified reduced objective subset and the induced change in the problem's dominance structure. Lastly, Pareto-optimal process and fuel designs are generated for the identified reduced objective subset.Overall, we consider “land use” as well as “resource use of minerals and metals” as key environmental objectives, covering the major trade-offs of integrated process and fuel design for advanced spark-ignition engine fuels. Therefore, we recommend the inclusion of both as additional objectives to production cost in future fuel design studies. As demonstrated herein, we suggest the evaluation of the identified key objectives regarding their robustness towards different normalization variants since normalization of input data for objective reduction is arbitrary. Using these three objectives for integrated process and fuel design, we show that the obtained bio-hybrid fuels for spark-ignition engines can balance the benefits and drawbacks of pure bio- and e-fuels.
As a complement to this study's objective reduction approach, future studies could assess the absolute sustainability of the Pareto-optimal process and fuel designs generated herein. This way, burden-shifting observed among the generated designs could be put into perspective by comparison with the Earth's planetary boundaries. However, LCA-based planetary boundaries would introduce a new source of uncertainty for two reasons.75 First, planetary boundaries are derived from complex ecological mechanisms that are difficult to quantify and to attribute to LCIA models. Second, downscaling of the so-called safe operating space would be required since synthetic fuels would account only for a fraction of all human activities. As different allocation principles could be applied for downscaling, this step is reported as subject to the greatest uncertainty when applying planetary boundaries.76
Lastly, we stress that our recommendations on key environmental objectives refer explicitly to early-stage process and fuel design. In this context, the emphasis is on using as few objectives as possible to reduce the computational effort without neglecting major trade-offs of the optimization problem. Therefore, our recommendations by no means imply that objectives identified as redundant for fuel design are negligible for overall decision-making. For instance, global warming impact is surprisingly not suggested as a key environmental objective for early-stage fuel design, indicating that its trade-offs with the other objectives can be adequately captured by the reduced objective subsets identified in this work. Nonetheless, global warming impact represents one of the most important metrics in decision-making to evaluate the climate change mitigation potential of new technologies.
Author contributions
Simon Voelker: conceptualization, methodology, software, investigation, visualization, writing – original draft, project administration. Philipp Ackermann: conceptualization, methodology, software, investigation, writing – review & editing. Marcel Granderath: software, investigation, visualization, writing – review & editing. Clemens Kortmann: software, investigation, writing – review & editing. Joern Viell: conceptualization, writing – review & editing. Alexander Mitsos: conceptualization, supervision, writing – review & editing, funding acquisition. Niklas von der Assen: conceptualization, supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed as part of the Cluster of Excellence EXC2186 “The Fuel Science Center,” which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy (ID 390919832).References
- M. Dahmen and W. Marquardt, Energy Fuels, 2016, 30(2), 1109 CrossRef CAS.
- R. L. McCormick, G. Fioroni, L. Fouts, E. Christensen, J. Yanowitz, E. Polikarpov, K. Albrecht, D. J. Gaspar, J. Gladden and A. George, SAE Int. J. Fuels Lubr., 2017, 10(2), 442 CrossRef.
- D. Gschwend, P. Soltic, A. Wokaun and F. Vogel, Energy Fuels, 2019, 33(3), 2186 CrossRef CAS.
- G. Fioroni, L. Fouts, J. Luecke, D. Vardon, N. Huq, E. Christensen, X. Huo, T. Alleman, R. McCormick, M. Kass, E. Polikarpov, G. Kukkadapu and R. A. Whitesides, SAE Int. J. Adv. Curr. Pract. Mobil., 2019, 1(3), 1117 CrossRef.
- X. Huo, N. A. Huq, J. Stunkel, N. S. Cleveland, A. K. Starace, A. E. Settle, A. M. York, R. S. Nelson, D. G. Brandner, L. Fouts, P. C. St. John, E. D. Christensen, J. Luecke, J. H. Mack, C. S. McEnally, P. A. Cherry, L. D. Pfefferle, T. J. Strathmann, D. Salvachúa, S. Kim, R. L. McCormick, G. T. Beckham and D. R. Vardon, Green Chem., 2019, 21(21), 5813 RSC.
- F. vom Lehn, L. Cai, R. Tripathi, R. Broda and H. Pitsch, Appl. Energy Combust. Sci., 2021, 5, 100018 Search PubMed.
- J. G. Rittig, M. Ritzert, A. M. Schweidtmann, S. Winkler, J. M. Weber, P. Morsch, K. A. Heufer, M. Grohe, A. Mitsos and M. Dahmen, AIChE J., 2023, 69(4), e17971 CrossRef CAS.
- L. Fleitmann, P. Ackermann, J. Schilling, J. Kleinekorte, J. G. Rittig, F. vom Lehn, A. M. Schweidtmann, H. Pitsch, K. Leonhard, A. Mitsos, A. Bardow and M. Dahmen, Energy Fuels, 2023, 37(3), 2213 CrossRef CAS.
- N. A. Yunus, K. V. Gernaey, J. M. Woodley and R. Gani, Comput. Chem. Eng., 2014, 66, 201 CrossRef CAS.
- L. Zhang, S. Kalakul, L. Liu, N. O. Elbashir, J. Du and R. Gani, Ind. Eng. Chem. Res., 2018, 57(20), 7008 CrossRef CAS.
- H. Hashim, M. Narayanasamy, N. A. Yunus, L. J. Shiun, Z. A. Muis and W. S. Ho, J. Cleaner Prod., 2017, 146(2), 208 CrossRef CAS.
- S. Kalakul, L. Zhang, Z. Fang, H. A. Choudhury, S. Intikhab, N. Elbashir, M. R. Eden and R. Gani, Comput. Chem. Eng., 2018, 116(1), 37 CrossRef CAS.
- W. A. Marvin, S. Rangarajan and P. Daoutidis, Energy Fuels, 2013, 27(6), 3585 CrossRef CAS.
- A. Voll and W. Marquardt, AIChE J., 2012, 58(6), 1788 CrossRef CAS.
- M. Dahmen and W. Marquardt, Energy Fuels, 2017, 31(4), 4096 CrossRef CAS.
- J. Bausa, R. v. Watzdorf and W. Marquardt, AIChE J., 1998, 44(10), 2181 CrossRef CAS.
- K. Ulonska, M. Skiborowski, A. Mitsos and J. Viell, AIChE J., 2016, 62(9), 3096 CrossRef CAS.
- A. König, K. Ulonska, A. Mitsos and J. Viell, Energy Fuels, 2019, 33(2), 1659 CrossRef.
- A. König, L. Neidhardt, J. Viell, A. Mitsos and M. Dahmen, Comput. Chem. Eng., 2020, 134, 106712 CrossRef.
- A. König, M. Siska, A. M. Schweidtmann, J. G. Rittig, J. Viell, A. Mitsos and M. Dahmen, Chem. Eng. Sci., 2021, 237, 116562 CrossRef.
- P. Ackermann, K. E. Braun, P. Burkardt, S. Heger, A. König, P. Morsch, B. Lehrheuer, M. Surger, S. Völker, L. M. Blank, M. Du, K. A. Heufer, M. Roß-Nickoll, J. Viell, N. von der Aßen, A. Mitsos, S. Pischinger and M. Dahmen, ChemSusChem, 2021, 14(23), 5254 CrossRef CAS PubMed.
- C. Hank, L. Lazar, F. K. Mantei, M. Ouda, R. J. White, T. Smolinka, A. Schaadt, C. Hebling and H.-M. Henning, Sustainable Energy Fuels, 2019, 3(11), 3219 RSC.
- J. D. Medrano-García, M. A. Charalambous and G. Guillén-Gosálbez, ACS Sustainable Chem. Eng., 2022, 987 Search PubMed.
- I. Muñoz, K. Flury, N. Jungbluth, G. Rigarlsford, L. M. i. Canals and H. King, Int. J. Life Cycle Assess., 2014, 19(1), 109 CrossRef.
- J. Kleinekorte, L. Fleitmann, M. Bachmann, A. Kätelhön, A. Barbosa-Póvoa, N. von der Assen and A. Bardow, Annu. Rev. Chem. Biomol. Eng., 2020, 11, 203 CrossRef PubMed.
- B. Li, J. Li, K. Tang and X. Yao, ACM Comput. Surv., 2015, 48(1), 1 CrossRef CAS.
- Z. J. N. Steinmann, A. M. Schipper, M. Hauck and M. A. J. Huijbregts, Environ. Sci. Technol., 2016, 50(7), 3913 CrossRef CAS PubMed.
- T. Gal and H. Leberling, Eur. J. Oper. Res., 1977, 1(3), 176 CrossRef.
- P. Vaskan, G. Guillén-Gosálbez, M. Turkay and L. Jiménez, Ind. Eng. Chem. Res., 2014, 53(50), 19559 CrossRef CAS.
- D. Vázquez, R. Ruiz-Femenia, L. Jiménez and J. A. Caballero, Ind. Eng. Chem. Res., 2018, 57(20), 6992 CrossRef.
- D. K. Saxena, J. A. Duro, A. Tiwari, K. Deb and Q. Zhang, IEEE Trans. Evol. Comput., 2013, 17(1), 77 Search PubMed.
- H. K. Singh, A. Isaacs and T. Ray, IEEE Trans. Evol. Comput., 2011, 15(4), 539 Search PubMed.
- A. López Jaimes, C. A. Coello Coello and D. Chakraborty, in Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, ed. C. Ryan, ACM, New York, NY, 2008, p. 673 Search PubMed.
- J. Wheeler, J. A. Caballero, R. Ruiz-Femenia, G. Guillén-Gosálbez and F. D. Mele, Comput. Chem. Eng., 2017, 102(4), 64 CrossRef CAS.
- M. Pal, S. Saha and S. Bandyopadhyay, Inf. Sci., 2018, 423(1), 200 CrossRef.
- D. G. Oliva, G. Guillén-Gosálbez, J. M. Mateo-Sanz and L. Jiménez-Esteller, Comput. Chem. Eng., 2013, 56, 202 CrossRef CAS.
- N. V. Thoai, J. Glob. Optim., 2012, 52(3), 499 CrossRef.
- K. Deb and D. K. Saxena, in Proceedings of the World Congress on Computational Intelligence (WCCI-2006), 2006, p. 3352 Search PubMed.
- D. K. Saxena and K. Deb, in Evolutionary Multi-Criterion Optimization: 4th International Conference, EMO 2007, Matsushima, Japan, March 5–8, 2007, Proceedings, ed. S. Obayashi, Springer Berlin/Heidelberg, Berlin, Heidelberg, 2007, p. 772 Search PubMed.
- K. Deb and D. K. Saxena, On Finding Pareto-Optimal Solutions Through Dimensionality Reduction for Certain Large-Dimensional Multi-Objective Optimization Problems, 2005, 1 Search PubMed.
- D. Brockhoff and E. Zitzler, Evol. Comput., 2009, 17(2), 135 CrossRef PubMed.
- D. Brockhoff and E. Zitzler, in Parallel Problem Solving from Nature – PPSN IX: 9th International Conference, Reykjavik, Iceland, September 9–13, 2006, Proceedings, ed. D. Hutchison, T. Kanade, J. Kittler, J. M. Kleinberg, F. Mattern, J. C. Mitchell, M. Naor, O. Nierstrasz, C. Pandu Rangan, B. Steffen, M. Sudan, D. Terzopoulos, D. Tygar, M. Y. Vardi, G. Weikum, T. P. Runarsson, H.-G. Beyer, E. Burke, J. J. Merelo-Guervós, L. D. Whitley, X. Yao and E. K. Burke, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, p. 533 Search PubMed.
- G. Guillén-Gosálbez, Comput. Chem. Eng., 2011, 35(8), 1469 CrossRef.
- A. Kostin, G. Guillén-Gosálbez, F. D. Mele and L. Jiménez, Ind. Eng. Chem. Res., 2012, 51(14), 5282 CrossRef CAS.
- ISO, ISO 14040: Environmental Management: Life Cycle Assessment: Principles and Framework, 2006 Search PubMed.
- ISO, ISO 14044: Environmental Management: Life Cycle Assessment: Requirements and Guidelines, 2006 Search PubMed.
- J. Sadhukhan, K. S. Ng and E. M. Hernandez, Biorefineries and Chemical Processes, Wiley, 2014 Search PubMed.
- European Commission, Supporting information to the Characterisation Factors of Recommended EF Life Cycle Impact Assessment Methods: Version 2, from ILCD to EF 3.0, 2018 Search PubMed.
- R. Frischknecht, Life Cycle Inventory Analysis for Decision-Making: Scope-dependent Inventory System Models and Context-specific Joint Product Allocation, PhD thesis, ETH Zurich, Zurich, 1998 Search PubMed.
- G. Wernet, C. Bauer, B. Steubing, J. Reinhard, E. Moreno-Ruiz and B. Weidema, Int. J. Life Cycle Assess., 2016, 21(9), 1218 CrossRef.
- European Commission, International Reference Life Cycle Data System (ILCD) Handbook: General Guide for Life Cycle Assessment: Provisions and Action Steps, Publications Office, Luxembourg, 2011 Search PubMed.
- Y. Y. Haimes, L. S. Lasdon and D. A. Wismer, IEEE Trans. Syst. Man. Cybern., 1971, SMC-1(3), 296 Search PubMed.
- G. Mavrotas, Appl. Math. Comput., 2009, 213(2), 455 CrossRef.
- D. Vázquez, M. J. Fernández-Torres, R. Ruiz-Femenia, L. Jiménez and J. A. Caballero, Comput. Chem. Eng., 2018, 108, 382 CrossRef.
- S. Postels, N. von der Assen, P. Voll and A. Bardow, in 28th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2015): Pau, France, 30 June-3 July 2015, Curran Associates Inc., Red Hook, NY, 2015, p. 787 Search PubMed.
- R. T. Marler and J. S. Arora, Struct. Multidiscip. Optim., 2004, 26(6), 369 CrossRef.
- L. J. Müller, A. Kätelhön, M. Bachmann, A. Zimmermann, A. Sternberg and A. Bardow, Front. Energy Res., 2020, 8, 1 CrossRef.
- N. von der Assen, L. J. Müller, A. Steingrube, P. Voll and A. Bardow, Environ. Sci. Technol., 2016, 50(3), 1093 CrossRef CAS PubMed.
- S. Deutz and A. Bardow, Nat. Energy, 2021, 6, 203 CrossRef CAS.
- A. David, B. V. Mathiesen, H. Averfalk, S. Werner and H. Lund, Energies, 2017, 10(4), 578 CrossRef.
- M. Reuß, T. Grube, M. Robinius, P. Preuster, P. Wasserscheid and D. Stolten, Appl. Energy, 2017, 200, 290 CrossRef.
- D. R. Ladner, in Cryocoolers 16: Proceedings of the 16th International Cryocooler Conference, ICC Press, 2011 Search PubMed.
- K. Aikawa, T. Sakurai and J. J. Jetter, SAE Int. J. Fuels Lubr., 2010, 3(2), 610 CrossRef CAS.
- C. K. Westbrook, W. J. Pitz and H. J. Curran, J. Phys. Chem. A, 2006, 110(21), 6912 CrossRef CAS PubMed.
- D. D. Das, P. C. St. John, C. S. McEnally, S. Kim and L. D. Pfefferle, Combust. Flame, 2018, 190, 349 CrossRef CAS.
- M. M. El-Halwagi, in Sustainable Design through Process Integration, Elsevier, 2012, p. 15 Search PubMed.
- T. Grube and B. Höhlein, in Wasserstoff und Brennstoffzelle: Technologien und Marktperspektiven, ed. J. Lehmann and J. Töpler, Springer Vieweg, Berlin, Heidelberg, 2014, p. 225 Search PubMed.
- M. Ruth, Hydrogen Production Cost Estimate Using Biomass Gasification: Independent Review: Technical Report DE-AC36-08GO28308, National Renewable Energy Laboratory (NREL), 2011 Search PubMed.
- M. A. Quader, S. Ahmed, R. A. Raja Ghazilla, S. Ahmed and M. Dahari, J. Cleaner Prod., 2016, 120(3), 207 CrossRef CAS.
- F. Ueckerdt, L. Hirth, G. Luderer and O. Edenhofer, Energy, 2013, 63(1), 61 CrossRef.
- F. Sabatino, A. Grimm, F. Gallucci, M. van Sint Annaland, G. J. Kramer and M. Gazzani, Joule, 2021, 5(8), 2047 CrossRef CAS.
- N. McQueen, K. V. Gomes, C. McCormick, K. Blumanthal, M. Pisciotta and J. Wilcox, Prog. Energy, 2021, 3(3), 32001 CrossRef.
- W. L. Luyben, Comput. Chem. Eng., 2017, 103, 144 CrossRef CAS.
- C. Reinert, S. Deutz, H. Minten, L. Dörpinghaus, S. von Pfingsten, N. Baumgärtner and A. Bardow, Comput. Chem. Eng., 2021, 153(2), 107406 CrossRef CAS.
- S. Sala, E. Crenna, M. Secchi and E. Sanyé-Mengual, J. Environ. Manage., 2020, 269, 110686 CrossRef PubMed.
- M. W. Ryberg, M. Owsianiak, J. Clavreul, C. Mueller, S. Sim, H. King and M. Z. Hauschild, Sci. Total Environ., 2018, 634, 1406 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3se01602a |
| This journal is © The Royal Society of Chemistry 2024 |