Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Early-stage performance change of gas diffusion electrodes for CO2 electroreduction to formate†
Verena
Theußl
 *ab,
Henning
Weinrich
*ab,
Henning
Weinrich
 a,
Fabrizio
Lisi
a,
Hermann
Tempel
a,
Fabrizio
Lisi
a,
Hermann
Tempel
 a and
Rüdiger-A.
Eichel
ab
a and
Rüdiger-A.
Eichel
ab
aInstitute of Energy and Climate Research – Fundamental Electrochemistry (IEK-9), Forschungszentrum Jülich, 52428 Jülich, Germany. E-mail: v.theussl@fz-juelich.de
bRWTH Aachen University, Institute of Physical Chemistry, Landoltweg 2, 52074 Aachen, Germany
First published on 14th February 2024
Abstract
The electroreduction of CO2 provides an intriguing technology for the sustainable production of value-added products from unavoidable exhaust gas emissions such as formate. Aiming at a suitable electrode architecture for the electroreduction of CO2 to formate, in this study for the effect of the catalyst loading on the GDE performance, an early-stage performance change was observed by a loss of GDE activity in terms of maximum current density at −1.15 VRHE. The loss of GDE activity was already apparent within the first hour of GDE use and points out the inadequacy of GDEs regarding the lifetime and stability in the field of electroreduction of CO2. Based on the results of the present study, the loss of activity can be explained by agglomeration of catalyst particles and the loss of hydrophobicity.
Introduction
With CO2 in the atmosphere being one of the major causes of climate change, strategies to mitigate the emission of CO2 need to be implemented to limit global warming to “well below” 2 °C.1 In this context, carbon capture and utilization (CCU) is of particular interest since CCU does not only reduce CO2 emissions but may also provide a carbon feedstock for industry. For example, using the electroreduction of CO2 as a power-to-X technology, the production of value added products such as formic acid is possible and enables its use as a green commodity in the chemical industry.2 Moreover, the formic acid produced via electroreduction of CO2 is an attractive liquid hydrogen storage carrier which can enable renewable electricity for use on demand, i.e. in the form of the direct formic acid fuel cell (DFAC).3Despite numerous advances and novel approaches in the last few decades, the electroreduction of CO2 remains a challenging process because of high overpotentials,4 low solubility of CO2 in aqueous electrolytes and electrode degradation processes.5 To overcome the problems concerning the solubility of CO2 in electrolytes and the accompanying mass-transfer limitations, gas-fed electrolysers are used, which require long-lasting gas diffusion electrodes (GDE). In general, GDEs consist of a porous carbon fibre structure bearing a catalyst layer in contact with the electrolyte. Moreover, an additional carbonaceous microporous layer may or may not be sandwiched in between them.6,7
Although the technology for GDEs is quite advanced, as its usage in several electrochemical processes such as chlorine electrolysis,8–10 water electrolysis11–14 and PEM fuel cells15–17 is mature, the GDEs for electroreduction of CO2 face severe problems concerning long-term stability and electrode degradation. The uniqueness of GDEs for the electroreduction of CO2 stems from their bifunctionality and makes it difficult to directly compare them to GDEs for other electrochemical processes. The comparison with water electrolysis illustrates the differences: in water electrolysis, the products are initially formed in the liquid phase, and depending on the local mass transfer situation and surface properties of the electrode, an oversaturation and bubble formation occur. In CO2 electroreduction, on the other hand, the gaseous reactant must first diffuse to the catalyst layer and directly bind to the catalyst at the triple-phase boundary, before the electrochemical conversion can take place.11,18 Furthermore, the nature of evolving products such as formic acid and ethanol alters surface wetting, which may lead to electrode flooding due to the enrichment of low-surface-tension liquid products.19 It is, therefore, all the more important to investigate the stability of GDEs, but until today, the focus mostly lay on catalyst design,20–23 the composition of the gas diffusion electrodes (GDEs)7,24–27 and process studies on a laboratory scale.28–30 Moreover, those publications that do consider GDE degradation31–33 mostly investigate electrode flooding19,34–36 and carbonate formation.37–39
In this publication, a study about the early-stage performance change of GDEs based on the influence of the catalyst loading on the electroreduction of CO2 to formate is reported. For the implementation of this study, custom-made GDEs are investigated in a static gas-fed batch electrolyzer. The used gas-fed batch electrolyzer is a commercial cell setup, which is specially designed for the reproducible study of GDEs and, therefore, particularly suitable but rarely reported for the targeted investigation.40 The centrepiece of this study is the observed mechanisms causing early stage GDE performance change alongside the investigation of the effect of the catalyst loading on the electroreduction of CO2 to formate. For the preparation of the GDEs, Freudenberg E20H carbon paper (former H23I2) is used as a gas diffusion layer (GDL). Freudenberg E20H is typically used in the field of PEM water electrolysis,12–14 and was selected for this study due to its superior performance in terms of average electrode potential and faradaic efficiency for formate (Fig. S1, all figure numbers preceded by an S can be found in the ESI†), despite a yet absent microporous layer (MPL).7
Experimental methods
Gas diffusion electrode preparation
The gas diffusion electrodes (GDEs) were prepared via manual spray coating with an airbrush (HG Trigger type 0.3 mm Double Action, Tamiya, Japan).7 In summary, a commercial gas diffusion layer (GDL, E20H (former H23I2), Freudenberg, Germany) with a size of 3 × 3 cm2 was applied as the catalyst support and coated with a catalyst ink. For the preparation of the catalyst ink, SnO2 nanoparticles (<100 nm, broad range of 10–80 nm,41 Sigma Aldrich, Germany) and Nafion resin solution (15 wt% in H2O/EtOH, IonPower, Germany), in a ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt%, were dispersed in isopropyl alcohol (3 ml, 99.5+%, Thermo Scientific, USA) in an ultrasonic bath for 30 min. Table 1 provides an overview of the investigated catalyst loadings and the corresponding weight of the applied catalyst and binder.
10 wt%, were dispersed in isopropyl alcohol (3 ml, 99.5+%, Thermo Scientific, USA) in an ultrasonic bath for 30 min. Table 1 provides an overview of the investigated catalyst loadings and the corresponding weight of the applied catalyst and binder.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 wt%)
10 wt%)
| Catalyst loading [mg cm−2] | Absolute amount [mg] | |
|---|---|---|
| SnO2 | Nafion | |
| 1.1 | 9.5 | 1.3 |
| 1.3 | 11.9 | 1.3 |
| 2.3 | 20.3 | 1.6 |
| 4.2 | 37.8 | 4.3 |
| 5.8 | 51.9 | 5.2 |
| 13.0 | 116.9 | 9.2 |
Electrochemical measurements
The electrochemical experiments were performed with the as-prepared GDEs in a gas-fed, three-electrode PTFE test cell (FlexCell® PTFE, Gaskatel, Germany).7 For the electrochemical investigations, a multi-channel potentiostat (VSP-300, BioLogic, France) was used. The whole measurement setup is shown in Fig. S2 and S3.† In this measurement set-up the GDEs were used as the working electrodes (WE), a Pt wire was used as the counter electrode (CE) and an Ag/AgCl electrode (RE, RE-1BP, ALS, Japan) was employed as the reference electrode. The active electrode area, i.e., the cathode area exposed to the electrolyte, was 2.81 cm2. 1 M KHCO3 (≥99.5%, AnalaR NORMAPUR, VWR, Germany) was used as both the catholyte and anolyte. The two compartments of the cell were separated by a Nafion 117 membrane (IonPower, Germany). During the electrochemical measurements, a continuous CO2 flow (4.5 N, Air Products GmbH, Germany) of 20 sccm was applied to the cell, controlled by a mass flow controller (EL-FLOW, 10 ml to 500 ml, Bronkhorst, The Netherlands). All measurements were conducted at room temperature.The electrochemical analysis was carried out according to a specific procedure, which is sketched in Fig. S4.† Each GDE was investigated at three different current densities (Run 1: −36 mA cm−2, Run 2: −71 mA cm−2 and Run 3: −107 mA cm−2) for 45 min per electrolysis run. Prior to each run a “before” measurement sequence was conducted, consisting of three repetitive linear sweep voltammetry (LSV-) scans, from OCV to −2.0 V vs. Ag/AgCl. The LSV – scans were repeated three times to ensure experimental stability. For the comparison between the different GDEs, only the last scan is used. Moreover, in between the electrolysis runs (Run 1–3), the electrolyte was exchanged and refreshed manually, providing comparable starting conditions for each run.
All potentials shown in this publication are reported with reference to the reversible hydrogen electrode (RHE). Therefore, the obtained electrode potentials are recalculated according to eqn (1), assuming a constant pH of the CO2 saturated electrolyte, 1 M KHCO3, of pH = 7.6.42
| E(RHE) = E(Ag/AgCl) + 0.059 V × pH + 0.210 V | (1) |
Furthermore, all potentials are iR drop corrected using the resistance of the whole measurement set-up (0.7 Ω), which was obtained from a reference experiment conducted using a silver plate at various electrode potentials as a working electrode (Fig. S5†).
Product analysis
The quantification of the evolving products was performed via online gas chromatography (GC, Trace 1310, Thermo Fisher Scientific, USA)) and offline ion exclusion chromatography (IC, S150, Sykam, Germany).The GC system was equipped with two channels using a sequence of a Haysep Q and a molecular sieve 5 Å packed column and a thermal conductivity detector, each. For the determination of H2 and CO, Ar (6 N, Linde, Germany) and He (6 N, AirProducts, Germany) were used as carrier gases, respectively. Sample acquisition took place every nine minutes: automatically via a transfer line for the gaseous products and manually, by the collection of a 0.5 ml sample of catholyte, for the determination of formate (without refill of fresh electrolyte).
For the quantification, both methods were calibrated using external standards. For the gas products H2 and CO, calibration measurements with certified calibration gases (Linde, Germany) were conducted (3 – point calibration with fixed amounts of H2 (1000 ppm, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ppm, and 99
700 ppm, and 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ppm) and CO (979 ppm, 19
700 ppm) and CO (979 ppm, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ppm, and 99
900 ppm, and 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 ppm)). The gas flow out of the cell was determined prior to every measurement with a gas counter (MGC–1 V3.4 PPMA, MilliGascounter, Ritter, Germany). The flow was determined three times, and the average was used for the calculation of the faradaic efficiency (FE).
900 ppm)). The gas flow out of the cell was determined prior to every measurement with a gas counter (MGC–1 V3.4 PPMA, MilliGascounter, Ritter, Germany). The flow was determined three times, and the average was used for the calculation of the faradaic efficiency (FE).
The faradaic efficiency for gaseous products i (=H2, CO) was calculated as a momentary value FE, using the following eqn (2):
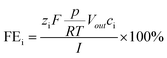 | (2) |
The ion exchange chromatography (IC) system was equipped with a SykroGel-Ex 450 SA-E01 column using an aqueous eluent solution composed of 7% acetonitrile (≥99.3%, HiPerSolv CHROMANORM®, VWR, USA) and 0.7 mmol perflourobutyric acid (99%, Thermo Scientific, USA). Prior to each analysis run of multiple samples, a calibration series for formate in the range from 3.3 × 10−4 mol l−1 to 2.2 × 10−2 mol l−1 was recorded.
Comparing the concentration of formate in the static catholyte of the cell at certain time intervals during the measurement, the faradaic efficiency (FE) for the electroreduction of CO2 to formate was calculated as an interval value FE, using the following eqn (3)–(5):
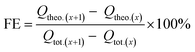 | (3) |
| Qtheo. = n × z × F × 0.277 | (4) |
| Qtot. = ∑ (I × t) | (5) |
Q theo denotes the theoretical charge, which was determined based on the produced amount of formate n during the time interval x (e.g. t min to t + y min). Qtot denotes the total charge consumed during the respective interval.
GDE-physical characterisation methods
For the study of the GDE surface topography and chemical composition, a scanning electron microscope (SEM, Quanta FEG 650 ESEM, FEI Europe, The Netherlands) coupled with an energy dispersive X-ray detector (EDX, Octane Super-A, Ametek, USA) was employed. The SEM was operated at 20 kV and the images were recorded at 100×, 250×, 400× and 550× magnifications. The Raman investigations (Senterra, Bruker, Germany) were carried out with a 532 nm laser with a spectral resolution of 9–18 cm−1. The sessile drop contact angles of 1 M KHCO3 in air were recorded on an optical contact angle goniometer (OCA100, DataPhysics Instruments, Germany). For the measurement, 2 μl droplets were dispensed onto three different locations of every sample, determining an average. To ensure comparable conditions for the GDEs before and after the electroreduction of CO2, each sample was thoroughly rinsed with deionised water and dried in air to remove residual electrolyte before the contact angle measurement. Moreover, thermogravimetric analyses were conducted using a thermogravimetric analyser (TGA, STA 449 F1 Jupiter, Netzsch, Germany) with a heating rate of 10 K min−1 in oxygen. The vapor sorption measurements were conducted with a dynamic vapor sorption system (DVS, Surface Measurement System Ltd, USA) to determine the bulk hydrophilicity of GDEs at different states of humidity (0–80%). Before the measurements, the samples were degassed at 100 °C for 2 h, and an additional vacuum of 10−6 mbar was applied. The measurements were conducted at 25 °C with a sample size between 10 and 30 mg.With respect to the reproducibility, the preparation, and the electrochemical analysis, one GDE was repeated three times. Based on the scattering of the individual results for these three measurements in terms of faradaic efficiency for formate, as well as the current density during LSV and the electrode potential during continuous electroreduction of CO2 to formate, the standard deviation was estimated conservatively. The estimated standard deviations are as follows and were added as error bars to the corresponding results:
• LSV current density: ±20% of the reported value.
• Faradaic efficiency – formate: ±10% of the reported value.
• Avr. electrode potential: ±0.05 VRHE of the reported value.
Results and discussion
General electrode performance
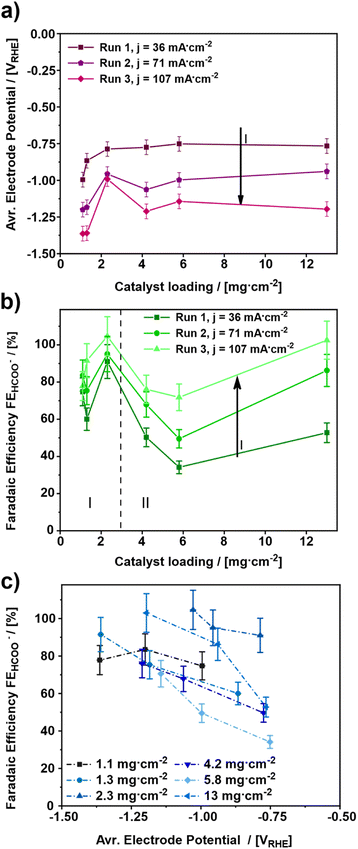
For elucidating the influence of the catalyst loading on the electroreduction of CO2 to formate, various gas diffusion electrodes (GDEs) were prepared and tested at increasing cathodic current densities (Fig. 1). In total, six different catalyst loadings ranging from 1.1 to 13 mg cm−2 (Table 1) were investigated.The influence of the catalyst loading on the average electrode potential, shown in Fig. 1a, can be divided into two regimes. Concerning the catalyst loadings ≤2.3 mg cm−2 the average electrode potential upon the electroreduction of CO2 becomes more positive with increasing catalyst loading (regime I). However, for the catalyst loadings >2.3 mg cm−2 the average electrode potential stays almost constant in the same range (regime II). This is particularly evident comparing the average electrode potentials of the 1.1 to 2.3 mg cm−2 GDE and the 4.2 to 13 mg cm−2 GDE at the applied current density of 36 mA cm−2. The lowest catalyst loading of 1.1 mg cm−2 leads to the most negative average electrode potential of −0.99 VRHE ± 0.05 VRHE at 36 mA cm−2, while 2.3 mg cm−2 leads to a 200 mV more positive average electrode potential of −0.79 VRHE ± 0.05 VRHE. On the other hand, the obtained average electrode potentials for the catalyst loadings of 4.2 and 13 mg cm−2 are −0.77 VRHE ± 0.05 VRHE for both, respectively. Thus, the lowest catalyst loading leads to the most negative electrode potential. In addition to the influence of the catalyst loading, the influence of the cathodic current density was investigated. For this, three different current densities 36, 71 and 107 mA cm−2 were applied. As a result, the electrode potentials become more negative with increasing cathodic current density. This behaviour can be ascribed to increased electrode polarization because of higher currents.43–45 An exception to this trend seems to be the GDE with a catalyst loading of 2.3 mg cm−2. Here, the obtained average electrode potential increases by 170 mV from –0.79 VRHE ± 0.05 VRHE to –0.96 VRHE ± 0.05 VRHE at the first step from 36 mA cm−2 to 71 mA cm−2 but remains constant at –0.97 VRHE ± 0.05 VRHE for an increase from 71 mA cm−2 and 107 mA cm−2. Thus, the most positive average electrode potentials are obtained for catalyst loadings ≥ 2.3 mg cm−2. Comparing the results shown in Fig. 1a with those from the literature, a similar trend regarding the effect of the catalyst loading on the electrode performance can be observed.46 There, thicker catalyst layers also showed lower electrode potentials for a given current density, which can be attributed to the increase in the active surface area.
Fig. 1b depicts the faradaic efficiency for formate obtained during the experiments shown in Fig. 1a. As a result, the obtained faradaic efficiency can again be divided into two regimes. For the catalyst loadings ≤2.3 mg cm−2 (regime I) the faradaic efficiency increases with increasing catalyst loading. Whereas, the faradaic efficiency for the catalyst loadings > 2.3 mg cm−2 (regime II) decreases with increasing catalyst loading. The GDE with a catalyst loading of 13 mg cm−2, however, is an exception. It shows a faradaic efficiency almost as high as the one for the 2.3 mg cm−2 GDE. Hence, the two catalyst loadings, 2.3 mg cm−2 and 13 mg cm−2 show the highest faradaic efficiencies for formate with 91% ± 9.1% to 100% ± 10.0% and 50% ± 5.0% up to 100% ± 10.0% from run 1 to run 3 for 2.3 mg cm−2 and 13 mg cm−2, respectively. Therefore, these two catalyst loadings appear to be the most suitable ones for the GDEs in the applied setup.
The result for the GDE with a catalyst loading of 13 mg cm−2 most probably arises from structural changes of the electrode, as a part of a run-in phase which will be discussed in detail towards the end of this publication. As of this moment, the structural changes become evident when comparing faradaic efficiencies for 4.2 and 13 mg cm−2 catalyst loading between run 1 and run 3, respectively. In run 1, both catalyst loadings allow the same faradaic efficiency for formate of 50% ± 5.0 and 53% ± 5.3, respectively. In run 3, the faradaic efficiency for 13 mg.cm−2 reaches up to 100% ± 10%, whereas for 4.2 mg cm−2 only 76% ± 7.6% is observed.
Similar to the observations above, in a previous investigation it was found that a change in the catalyst layer composition either influences the through-plane concentration gradient for CO2 or the pH within the catalyst layer as a function of distance from the GDL. In the case of increasing catalyst loading, a larger mean path of transportation of CO2 and HCO3− through the thicker catalyst layer is caused, which results in regions of high alkalinity and depletion of CO2. This on the other hand results in suppression of pH-sensitive products such as HCOO− and leads to an increase of CO release. Moreover, the variation of Nafion content showed similar results, but a high Nafion loading presented more of a barrier for the mass transportation of the reactant CO2 towards the catalytic sites than an increase in the mean path of transportation.47 Such impediment of the mass transport can be rationalized by a slower through-plane transport of reactants (CO2 and HCO3−) leading to a favoured HER. Both effects, the higher HER and the reduced mass transport, could also be observed in own experiments, which can be seen in Fig. S6.† However, for a dedicated explanation of the observed effects in Fig. 1b, further analysis will be discussed in the section GDE-physical characterisation methods towards the end of this publication.
Regarding the influence of the cathodic current density, it can be stated that a catalyst loading ≤2.3 mg cm−2 has no significant impact on the faradaic efficiency for formate. However, with a catalyst loading >2.3 mg cm−2 this effect can be observed very well. For both regimes (regime I and II), the highest faradaic efficiency is obtained for the highest cathodic current density; hence 107 mA cm−2 leads to the most favourable electrode potential investigated in this study. Similar effects have been observed in the literature, where at current densities up to 100 mA cm−2 an increase of faradaic efficiency was observed, followed by a decrease for higher current densities due to the favoured HER.48
Fig. 1c depicts the average electrode potential dependent faradaic efficiency towards formate. In this diagram, the faradaic efficiency for formate increases for an increasing electrode potential, except for the lowest catalyst loading of 1.1 mg cm−2. In fact, the 1.1 mg cm−2 GDE shows a maximum faradaic efficiency of 84% ± 8.4% at −1.20 VRHE ± 0.05 VRHE, while the other GDEs provide 70% ± 7.0% to 100% ± 10% faradaic Efficiency in the potential range from −1.10 VRHE ± 0.05 VRHE to −1.40 VRHE ± 0.05 VRHE Thus, an electrode potential at least between −1.10 VRHE ± 0.05 VRHE and −1.40 VRHE ± 0.05 VRHE appears to be most favourable for formate production. A similar trend was also observed in a previous study about SnO2 nanosheets as a catalyst for CO2 electroreduction to formate, where an optimum electrode potential between −1.0 VRHE and −1.2 VRHE was observed.49 Furthermore, a preferential electrode potential for certain products besides formate, is also known for the electroreduction of CO2 on Cu catalysts where the applied electrode potential determines which product range is obtained.50
In addition to the continuous electroreduction of CO2, three LSV scans were performed prior to each electrolysis run as a direct indicator for the GDE stability. Fig. 2a depicts the results of the third of three scans from OCV to −1.24 VRHE for the 13 mg cm−2 GDE. Furthermore, Fig. 2b shows the influence of the catalyst loading on the cathodic current density at −1.15 VRHE (blue line in Fig. 2a). Based on the course of the LSVs in Fig. 2a the influence of the repeated scanning can be described as shifting the CO2RR on-set to about −0.55 VRHE more negative potentials and decreasing the cathodic current density.
In Fig. 2b on the other hand, the cathodic current density obtained at −1.15 VRHE can be divided into two regimes according to the catalyst loading again. For the catalyst loadings ≤2.3 mg cm−2 an increase of cathodic current density occurs. Whereas for the catalyst loadings >2.3 mg cm−2 a rather constant cathodic current density is observed. This becomes evident in the comparison of the catalyst loadings for the GDEs with 1.1 to 2.3 mg cm−2 and 4.2 to 13 mg cm−2 at the first run. While for the lowest catalyst loading of 1.1 mg cm−2 the lowest cathodic current density of 55 mA cm−2 ± 11 mA cm−2 is obtained, 2.3 mg cm−2 leads to a three times higher cathodic current density of 165 mA cm−2 ± 33 mA cm−2. On the other hand, the cathodic current density for 4.2 and 13 mg cm−2 varies by only about 10 mA cm−2 from 137 mA cm−2 ± 27 mA cm−2 to 127 mA cm−2 ± 25 mA cm−2, respectively. This effect is also observable for the subsequent LSV scans before run 2 and run 3. In very good agreement with the results in Fig. 1 and in agreement with the literature, the results in Fig. 2b suggest that a high catalyst loading is not the decisive factor in reaching a high cathodic current density for the electroreduction of CO2 to formate.48,51
However, upon repeated use of the GDEs, a significant change of the cathodic current can be observed, which suggests a run-in phase for the catalyst during the electroreduction of CO2. The only exception here is the GDE with the lowest catalyst loading of 1.1 mg cm−2, where the cathodic current density stays constant at around –60 mA cm−2 ± 12 mA cm−2.
To further elucidate the observed effects during the current density screening, the two best performing electrodes in terms of observed faradaic efficiency were chosen, i.e. 2.3 and 13 mg cm−2, to undergo a second test cycle with the identical procedure behind the results in Fig. 1 and 2. The results of the corresponding experiments are shown in Fig. 3. Comparing the results of the LSV-scans of cycle 1 and cycle 2 at −1.15 VRHE in Fig. 3a, a drop in cathodic current density for both investigated catalyst loadings is shown. In the case of the 2.3 mg cm−2 GDE the decrease of the cathodic current density is around 25%, from 170 mA cm−2 ± 34 mA cm−2 to 120 mA cm−2 ± 24 mA cm−2. The 13 mg cm−2 GDE, however, shows an even higher decrease. Here a drop of 52% from 130 mA cm−2 ± 26 mA cm−2 to 70 mA cm−2 ± 14 mA cm−2 occurs. In the second cycle, on the other hand, the obtained cathodic current densities stay constant at slightly lower values for both catalyst loadings, i.e., 115 mA cm−2 ± 23 mA cm−2 for the 2.3 mg cm−2 and 70 mA cm−2 ± 14 mA cm−2 for the 13 mg cm−2 GDE. Thus, the decrease of cathodic current density does not continue and appears to be limited to the first cycle, supporting the previous assumption of a run-in phase occurring.
Evaluating the GDEs further, Fig. 3b shows the influence of the GDE change on the electrode performance upon repeated cycling by means of average electrode potential. Comparing the results for the GDE with a catalyst loading of 2.3 mg cm−2, Fig. 3b shows a drop of the electrode potential by 10% comparing the first runs of cycles 1 and 2. However, in the second and the third runs the electrode potentials are almost identical and constant with −0.95 VRHE ± 0.05 VRHE. In contrast to the 2.3 mg cm−2 GDE, a more severe drop of electrode potential is apparent between cycles 1 and 2 for the 13 mg cm−2 electrode. For this GDE, the average electrode potential in cycle 2 is always more negative than the electrode potential in cycle 1. For the runs at 36 mA cm−2 the electrode potential in the second cycle is 25% lower compared to cycle 1. For the runs at 71 mA cm−2 the electrode potential in the second cycle is decreased by 20% compared to cycle 1. And for run 3 at 107 mA cm−2 the electrode potential in cycle 2 is around 5% lower than in cycle 1. Referring to the faradaic efficiency towards formate, in Fig. 3c it can be observed that both GDEs show an increasing faradaic efficiency for an increasing applied current density in the first cycle. However, in the second cycle, the changes are inconsistent. For the GDE with 2.3 mg cm−2 catalyst loading, a continuous decrease of faradaic efficiency up to 15% occurs, from 91% ± 9.1% to 76% ± 7.6% at 36 mA cm−2, from 95% ± 9.5% to 90% ± 9.0% at 71 mA cm−2 and from 104% ± 10.4% to 89% ± 8.9% at 107 mA cm−2. On the other hand, for the GDE with 13 mg cm−2 catalyst loading first an increase of 50% is observed, followed by a stagnation in the second run and a decrease by −15% in the third run. Thus, in conjunction with Fig. 2c it can be stated that the performance of the GDEs in terms of faradaic efficiency decreases between cycle 1 and cycle 2 but appears to be constant within the second cycle regardless of the current density. This leads to the conclusion that a run-in phase of the GDEs occurs during the first cycle.
Physical reason for the run-in phase
To elucidate the physical reason for the run-in phase, the GDEs from Fig. 3 were further investigated by scanning electron microscopy (SEM), Raman spectroscopy, contact angle (CA) measurements, vapor sorption measurements and thermogravimetric analysis (TGA). Fig. 4a–f show the topography of the 2.3 mg cm−2 and the 13 mg cm−2 GDE before and after cycle 1 as well as after cycle 2. Comparing Fig. 4a and d it is evident that with an increasing catalyst loading a continuous catalyst coverage of the GDL is achieved. While at 2.3 mg cm−2 the original fibre structure of the GDL is still visible, large catalyst layer planes cover the carbon fibres already. However, at 13 mg cm−2 the substrate is completely covered by a continuous layer. Based on the SEM images in Fig. S7 and S8,† the increase in catalyst coverage can be described as continuous for catalyst loadings ≥4.2 mg cm−2, which is in very good agreement with the literature.48 Furthermore, besides the increasing coverage with SnO2, there are also some cracks in the catalyst layer at catalyst loadings ≥4.2 mg cm−2. These cracks are most probably a result of the drying process during the catalyst deposition.52 | ||
| Fig. 4 Exemplary SEM images of the investigated GDEs: (a) and (d) show the pristine GDEs, while (b) and (e) represent the topography after cycle 1. Images (c) and (f) show the GDE after cycle 2 of CO2 electroreduction to formate for two different catalyst loadings (2.3 mg cm−2 and 13 mg cm−2 (top/bottom)). Additional images for the other catalyst loadings are shown in Fig. S7 and S8.†). | ||
Further analysing the SEM images in Fig. 4b and e, catalyst agglomeration can be observed. However, while at 2.3 mg cm−2 the agglomeration is limited to small agglomerates with diameters under 10 μm, the agglomerates with increasing catalyst loading appear to get larger. The largest agglomerates of around 50 μm are found for the 13 mg cm−2 GDE. Due to the agglomeration of the catalyst layer, holes and indentations are observed, especially around the course of the carbon fibres for the 13 mg cm−2 GDE. Thus, the carbon fibres appear to act as initiators for changes in the catalyst layer since the applied current passes through the fibres and provides the impetus for the change. In comparison to the 1.1 mg cm−2 GDE (Fig. S7 and S8†) it becomes clear that agglomeration also occurs for the lowest catalyst loading, while the catalyst particles here appear to be centred in the interspace between the individual carbon fibres. Furthermore, considering the additional SEM cross-sections in Fig. S9† it can be stated that next to the catalyst agglomeration also catalyst migration into deeper GDL layers occurs for electrodes with a catalyst loading > 2.3 mg cm−2, leading to a loss of catalyst nanoparticles in contact with the electrolyte.7 Hence, the observed agglomeration and the catalyst migration lead to changes in the catalyst layer topography, which initiates a change in the available active surface area of the catalyst. This becomes especially evident in the results of Fig. 1b, where the influence of the catalyst loading on the faradaic efficiency is investigated. For catalyst loadings > 2.3 mg cm−2 a decrease of faradaic efficiency is observed, while the 13 mg cm−2 GDE, as an exception, allows similar results to the 2.3 mg cm−2 GDE because sufficient catalyst remains available in the first layer of the GDL. Due to the agglomeration and the catalyst migration, the amount of accessible active surface area decreases, which can be the reason for the decrease in faradaic efficiency for catalyst loadings >2.3 mg cm−2. In the case of the 2.3 and 13 mg cm−2 GDE, however, the amount of accessible active surface area seems to converge which leads to similar performances regarding the obtained faradaic efficiencies.
Fig. 4c and f show that the change in surface topography continues during cycle 2. For the catalyst loading of 2.3 mg cm−2 the change can be described as smoothing, which leads to even more visible carbon fibres. The smoothing is accompanied by an obvious decrease in the active catalyst surface area. However, at 13 mg cm−2 the opposite effect occurs. The reorganisation results in a much rougher surface, which may also explain the results in Fig. 3B. Here, decreasing performance was observed for the 2.3 mg cm−2 GDE while increasing performance was observed for the 13 mg cm−2 GDE.
In addition, based on the reorganisation of the GDE topography, the carbon fibres appear to get increasingly exposed to the electrolyte. This increasing exposure on the other hand could lead to increased HER and GDL dissolution upon further, use. Especially GDL dissolution triggered by surface-oxide formation in the presence of a liquid electrolyte32 can lead to severe GDE alteration. This can be in terms of a reduction of the hydrophobicity of the GDL46 and loss of carbon from the electrode due to the eventual conversion of the oxidized graphene particles into CO2.32 However, as for the presented state of the GDEs, GDL dissolution is not apparent.
To analyse whether there is also a change in the composition of the GDEs due to CO2 electroreduction, Raman spectroscopy measurements were performed for the 2.3 and the 13 mg cm−2 GDE. The corresponding results are depicted in Fig. 5a and b and show distinct differences for the pristine and the used GDEs, respectively. For the pristine GDEs, the Raman spectra are mostly governed by the response of the catalyst layer, i.e. the response of the catalyst and the binder, SnO2 and Nafion. The Raman spectrum of SnO2 typically consists of three bands at 470 cm−1 (Eg), 630 cm−1 (A1g) and 770 cm−1 (B2g), respectively, which are the classical modes of SnO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 and can be retrieved in Fig. 5a and b. In addition to the classical modes, also disordered activated surface modes can occur for SnO2 as broad peaks in the region from 475 to 775 cm−1 (S1, S2 and S3). The occurrence of these defect modes depends on the nanoparticle size and can be detected at 570 cm−1 (S1) in the pristine state for both GDEs.41 Besides this, the remaining bands in the Raman spectra can be attributed to Nafion, which shows four specific bands at 292 cm−1 (A1), 385 cm−1 (At), 731 cm−1 (A1) and 971 cm−1.54
53 and can be retrieved in Fig. 5a and b. In addition to the classical modes, also disordered activated surface modes can occur for SnO2 as broad peaks in the region from 475 to 775 cm−1 (S1, S2 and S3). The occurrence of these defect modes depends on the nanoparticle size and can be detected at 570 cm−1 (S1) in the pristine state for both GDEs.41 Besides this, the remaining bands in the Raman spectra can be attributed to Nafion, which shows four specific bands at 292 cm−1 (A1), 385 cm−1 (At), 731 cm−1 (A1) and 971 cm−1.54
Comparing the two Raman spectra for both GDEs to their individual counterparts after the electroreduction the SnO2 bands at 570 cm−1 (S1) and 630 cm−1 (A1g) change due to the experiments. The change can be ascribed to the reduction of SnO2 to metallic SnO but still prevalent SnIVO2.55 Furthermore, the broad peak arising at 570 cm−1 is probably a result of the formation of amorphous hydrous SnIVO2 and is a further indicator for the morphological changes observed in the SEM images after cycle 2.56
Besides the general evolution of the Raman spectra, two specific observations in Fig. 5 are that the Raman bands for Nafion vanish during the experiments, which could be a result of the binder loss. Furthermore, given the absence of corresponding peaks, the Raman spectra of the investigated GDEs after use do not show any indication of carbonate formation.37,38
Further elucidating the property changes of the investigated GDEs, Table 2 provides the contact angles of the pristine GDL, the GDEs with increasing catalyst loading before and after first-time use as well as after repeated cycling for the 2.3 and 13 mg cm−2 GDE.
| Catalyst loading/[mg cm−2] | GDE (before) [°] | GDE (after cycle 1) [°] | GDE (after cycle 2) [°] |
|---|---|---|---|
| 0 | 137.9 ± 5.0 | — | — |
| 1.1 | 119.9 ± 9.8 | 110.9 ± 13.3 | — |
| 1.3 | 125.8 ± 4.5 | 82.1 ± 7.3 | — |
| 2.3 | 126.7 ± 2.7 | 83.5 ± 9.7 | 41.9 ± 6.5 |
| 4.2 | 126.4 ± 2.5 | Absorbed | — |
| 5.8 | 115.9 ± 9.7 | Absorbed | — |
| 13 | 123.2 ± 1.6 | Absorbed | Absorbed |
The pristine GDL (loading: 0 mg cm−2, Table 2) shows a largely hydrophobic surface with a contact angle of 137.9° ± 5.0°. However, due to the catalyst deposition, the contact angle of the GDL is generally reduced by approximately 20°. An additional reference experiment without the catalyst showed that the deposition of Nafion alone also reduces the contact angle by about 4° ± 1.0° (Table S1†). Thus, in addition to the intrinsic hydrophilicity of SnO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 Nafion itself also appears to conceal the hydrophobicity of the GDL.7 Moreover, the electrochemical experiment further reduces it. In fact, due to the electroreduction of CO2, the contact angles for 1 M KHCO3 on most GDEs decrease significantly. The 1.3 and 2.3 mg cm−2 GDEs show a drop of 40°, while the other GDEs do not show hydrophobicity at all. For the latter, the test liquid is absorbed by the sample immediately. Furthermore, the decrease of hydrophobicity continues beyond cycle 1 as the contact angle for the 2.3 mg cm−2 GDE decreases further from 83.5° ± 9.7° to 41.9° ± 6.5°. Thus, the contact angle measurements clearly support the observation of an altered GDE surface, which could either include a loss or deterioration of Nafion.
57 Nafion itself also appears to conceal the hydrophobicity of the GDL.7 Moreover, the electrochemical experiment further reduces it. In fact, due to the electroreduction of CO2, the contact angles for 1 M KHCO3 on most GDEs decrease significantly. The 1.3 and 2.3 mg cm−2 GDEs show a drop of 40°, while the other GDEs do not show hydrophobicity at all. For the latter, the test liquid is absorbed by the sample immediately. Furthermore, the decrease of hydrophobicity continues beyond cycle 1 as the contact angle for the 2.3 mg cm−2 GDE decreases further from 83.5° ± 9.7° to 41.9° ± 6.5°. Thus, the contact angle measurements clearly support the observation of an altered GDE surface, which could either include a loss or deterioration of Nafion.
To obtain further information about the GDE surface and its influence on bulk hydrophilicity, vapor sorption measurements were conducted. Fig. 6 and S10† show the vapor adsorption isotherms for 2.3 and 13 mg cm−2 as well as for the other catalyst loadings at different states of the GDEs, respectively – pristine, after cycle 1 and after cycle 2.
For all investigated samples, the pristine state of the GDE adsorbs the least amount of water with a water uptake of up to 0.73 wt% with minor differences depending on the catalyst loading. The water uptake after the first cycle is up to twenty times higher as compared to the pristine samples. GDEs with a catalyst loading of 5.8 mg cm−2 exhibit the highest adsorption after the first cycle, increasing from 0.45 to 8.9 wt% at 80% humidity. After cycle 2 the increase in adsorbed water continues. At 13 mg cm−2, a 10-fold increase of water adsorption at 80% humidity is observed comparing the pristine and final state. With this, the present observations confirm the loss of hydrophobicity, due to the electrochemical measurements.
Furthermore, based on the vapor sorption data a correlation between surface wettability and bulk hydrophobicity can be established. For low catalyst loadings (≤2.3 mg cm−2), both the results of the contact angle measurements after cycle 1 as well as vapor sorption data suggest a remaining hydrophobicity, given the intermediate contact angle and comparatively low water uptake (up to 2% change in mass). For high catalyst loadings (>2.3 mg cm−2), the same correlation can be seen. After cycle 1, the contact angle measurements show a very hydrophilic electrode surface, and the vapor sorption measurements confirm this observation by a change in mass of up to 9%. The correlation between surface wettability and internal hydrophilicity is most probably caused by the open GDL structure. SEM cross-section experiments (Fig. S9†) show a migration of the catalyst into the deeper layers of the GDL and in addition to the loss or deterioration of Nafion, these may lead to a change in the internal wettability.57 The observed structural changes could also facilitate electrode flooding as previously indicated.
Aiming to determine the reason for the observations above and whether the catalyst material is lost along with the GDE alterations, TGA measurements were conducted. In the decomposition profiles of the pristine GDEs in Fig. 5c and d three decomposition steps can be identified at 400 °C, 500 °C and 600 °C. These can be allocated as follows. The first step at 400 °C represents the decomposition of Nafion (Fig. S11†).58 The second and the third steps at 500 °C and 600 °C correspond to the decomposition of the GDL (Fig. S11†), namely the decomposition of the hydrophobic treatment59 and the combustion of the carbon fibres. After the combustion only the white SnO2 remains and the total amount of catalyst on the GDE can easily be determined. For the two investigated samples, the amount of remaining catalyst amounts up to 14.9 and 47.2 wt% respectively, which agrees with the expected GDE composition (expected 15.7 and 50.1 wt% SnO2, Table 3).
| Relative weight | 2.3 mg cm−2 | 13 mg cm−2 | ||||
|---|---|---|---|---|---|---|
| Expected [%] | Pristine [%] | Used [%] | Expected [%] | Pristine [%] | Used [%] | |
| GDE | 100 | 100 | 99.8 | 100 | 99.6 | 100 |
| Nafion | 2.1 | 2.1 | 2.9 | 4.3 | 4.0 | 3.9 |
| GDL | 82.2 | 83.0 | 87.3 | 45.6 | 48.4 | 49.2 |
| SnO2 | 15.7 | 14.9 | 9.6 | 50.1 | 47.2 | 46.9 |
Comparing the decomposition profiles of the pristine and the GDEs after repeated cycling three additional weight loss steps at 150 °C, 300 °C and 900 °C for both GDEs can be observed. The two steps at 150 °C and 900 °C can be allocated to the decomposition of electrolyte residuals (KHCO3) and carbonate (K2CO3), with the latter being formed due to the decomposition of KHCO3.60
Moreover, for a better allocation of the decomposition steps in the temperature range from RT to 700 °C, magnified plots of Fig. 5c and d are shown in Fig. S12.† In these graphs it can be seen that the weight loss step of Nafion around 400 °C does not occur in the same way as in the pristine GDE anymore. Furthermore, the decomposition steps for both catalyst loadings start at 300 °C already, where the first part might be associated with the desulfonation of sulfonic side chains of Nafion.58 Thus, the appearance of the decomposition step of the sulfonic side chains in combination with the changed decomposition steps of Nafion at 400 °C most probably assumes a structural change within the Nafion occurring during the electroreduction of CO2.32
Furthermore, structural modifications in the Nafion may result in hydrophobicity changes in the catalyst layer. This effect can already be seen in the contact angle measurements of the GDL coated with Nafion (Table S1†), where Nafion alone already alters the hydrophobicity of the GDL. The loss of the GDE's hydrophobicity over the course of the electroreduction experiments (Table 2), as also observed in the vapor sorption measurements (Fig. 6) and missing Raman peaks, points out to the loss of Nafion due to structural changes. In addition, the decomposition step of the hydrophobic treatment of the carbon fibres is also less prominent in the GDEs after the electroreduction suggesting a complex decomposition of this material as well. Thus, the progressive loss of Nafion and loss of hydrophobicity of the carbon fibres over continuous usage of the GDEs can result in electrode failure due to GDE flooding.
In addition to the previous discussion, the TGA results also allow for the determination of catalyst losses along with the deterioration of Nafion. At the end of the TGA measurement 9.6% and 46.9% SnO2 remain for the investigated GDEs. In comparison to the remaining weights of the pristine GDEs (14.9% and 47.2%) it can be stated that the 2.3 mg cm−2 GDE already lost about 30% of its catalyst material during the electroreduction of CO2. On the other hand, the 13 mg cm−2 GDE shows only minor or no loss of catalyst material despite the observed catalyst agglomeration and the loss of Nafion. Thus, Nafion displays only limited stability under the applied electrochemical conditions, which is at least part if not the reason for the observed run-in effects of the investigated GDEs.
Conclusion
The present study investigated early-stage changes of GDE performance based on the influence of the catalyst loading on the electroreduction of CO2 to formate on custom-made gas diffusion electrodes (GDEs). The results shown demonstrate that the electrode performance in terms of electrode potential and faradaic efficiency are affected by at least two mechanisms occurring during the GDE use. The affecting mechanisms include catalyst agglomeration and the decline in hydrophobicity. The latter is most likely a consequence of Nafion loss used as a binder. These effects lead to a decrease of faradaic efficiency (−15%) for formate and the disappearance of the electrode's hydrophobicity, which could result in GDE flooding upon utilization. The progressive loss of binder, which is probably induced by structural changes of the side chains/and or sulfonic groups in the Nafion, suggests its unsuitability under the applied operating conditions. However, the catalyst agglomeration and binder deterioration did not yet lead to a significant loss of catalyst. Moreover, the catalyst loading appeared to have a characteristic effect on the change in the GDE performance. While the increase of catalyst loading only improved the electrode performance up to a certain point, it was quite surprising that the highest catalyst loading showed a good performance in terms of faradaic efficiency again due to changes in the accessible active surface area. Nevertheless, the best performance was observed for a medium catalyst loading of 2.3 mg cm−2.Author contributions
V. T.: writing, conceptualization, data curation, formal analysis, methodology, visualization, F. L.: data curation, H. W.: conceptualization, validation, formal analysis, visualization, editing, H. T.: supervision, methodology, editing, and R.-A. E.: funding acquisition, supervision, editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors kindly acknowledge the financial support from the German Federal Ministry of Education and Research within the project ‘iNEW2.0 – Inkubator Nachhaltige Elektrochemische Wertschöpfungsketten’ Project No. 03SF0627A. The authors thank Sebastian B. C. Lehmann for the graphical support and Ansgar Kretzschmar for the vapor sorption measurements.References
- A. M. Vicedo-Cabrera, Y. Guo, F. Sera, V. Huber, C. F. Schleussner, D. Mitchell, S. Tong, M. S. Z. S. de Coelho, P. H. N. Saldiva, E. Lavigne, P. M. Correa, N. V. Ortega, H. Kan, S. Osorio, J. Kyselý, A. Urban, J. J. K. Jaakkola, N. R. I. Ryti, M. Pascal, P. G. Goodman, A. Zeka, P. Michelozzi, M. Scortichini, M. Hashizume, Y. Honda, M. Hurtado-Diaz, J. Cruz, X. Seposo, H. Kim, A. Tobias, C. Íñiguez, B. Forsberg, D. O. Åström, M. S. Ragettli, M. Röösli, Y. L. Guo, C. fu Wu, A. Zanobetti, J. Schwartz, M. L. Bell, T. N. Dang, D. Do Van, C. Heaviside, S. Vardoulakis, S. Hajat, A. Haines, B. Armstrong, K. L. Ebi and A. Gasparrini, Clim. Change, 2018, 150, 391–402 CrossRef PubMed
.
- M. Rumayor, A. Dominguez-Ramos and A. Irabien, Appl. Sci., 2018, 8, 1–12 Search PubMed
.
- J. Eppinger and K. W. Huang, ACS Energy Lett., 2017, 2, 188–195 CrossRef CAS
.
- K. M. Vetter, C. Aring da Silva Ramos Mauro, D. Reinisch, T. Reichbauer, N. Martić, C. Jandl, O. Hinrichsen and G. Schmid, Electrochem. Sci. Adv., 2022, 2, 1–16 Search PubMed
.
- E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135 RSC
.
- S. Hernandez-Aldave and E. Andreoli, Catalysts, 2020, 10, 713 CrossRef CAS
.
- V. Theußl, H. Weinrich, C. Heume, K. Dzieciol, B. Schmid, H. Kungl, H. Tempel and R.-A. Eichel, ChemElectroChem, 2023, 13, 202300121 CrossRef
.
- S. Hernandez-Aldave and E. Andreoli, Catal. Sci. Technol., 2022, 12, 3412–3420 RSC
.
- R. Kuwertz, N. Aoun, T. Turek and U. Kunz, J. Electrochem. Soc., 2016, 163, F988–F997 CrossRef CAS
.
- R. Kuwertz, I. G. Martinez, T. Vidaković-Koch, K. Sundmacher, T. Turek and U. Kunz, Electrochem. commun., 2013, 34, 320–322 CrossRef CAS
.
- B. J. M. Etzold, U. Krewer, S. Thiele, A. Dreizler, E. Klemm and T. Turek, Chem. Eng. J., 2021, 424, 130501 CrossRef CAS
.
- F. Hegge, R. Moroni, P. Trinke, B. Bensmann, R. Hanke-Rauschenbach, S. Thiele and S. Vierrath, J. Power Sources, 2018, 393, 62–66 CrossRef CAS
.
- A. Martin, P. Trinke, B. Bensmann and R. Hanke-Rauschenbach, J. Electrochem. Soc., 2022, 169, 094507 CrossRef CAS
.
- M. Suermann, B. Bensmann and R. Hanke-Rauschenbach, J. Electrochem. Soc., 2019, 166, F645–F652 CrossRef
.
- S. Park, J. W. Lee and B. N. Popov, Int. J. Hydrogen Energy, 2012, 37, 5850–5865 CrossRef CAS
.
- F. Lapicque, M. Belhadj, C. Bonnet, J. Pauchet and Y. Thomas, J. Power Sources, 2016, 336, 40–53 CrossRef CAS
.
- Z. Lu, M. M. Daino, C. Rath and S. G. Kandlikar, Int. J. Hydrogen Energy, 2010, 35, 4222–4233 CrossRef CAS
.
- N. T. Nesbitt, T. Burdyny, H. Simonson, D. Salvatore, D. Bohra, R. Kas and W. A. Smith, ACS Catal., 2020, 10(23), 14093–14106 CrossRef CAS
.
- M. E. Leonard, M. J. Orella, N. Aiello, Y. Román-Leshkov, A. Forner-Cuenca and F. R. Brushett, J. Electrochem. Soc., 2020, 167, 124521 CrossRef CAS
.
- B. Bohlen, D. Wastl, J. Radomski, V. Sieber and L. Vieira, Electrochem. commun., 2020, 110, 106597 CrossRef CAS
.
- M. F. Philips, D. Pavesi, T. Wissink, M. C. Figueiredo, G.-J. M. Gruter, M. T. M. Koper and K. J. P. Schouten, ACS Appl. Energy Mater., 2022, 5, 1720–1730 CrossRef CAS
.
- R. Reske, H. Mistry, F. Behafarid, B. Roldan Cuenya and P. Strasser, J. Am. Chem. Soc., 2014, 136, 6978–6986 CrossRef CAS PubMed
.
- D. Bell, D. Rall, M. Großeheide, L. Marx, L. Hülsdünker and M. Wessling, Electrochem. commun., 2020, 111, 106645 CrossRef CAS
.
- K. Junge Puring, D. Siegmund, J. Timm, F. Möllenbruck, S. Schemme, R. Marschall and U. P. Apfel, Adv. Sustainable Syst., 2021, 5, 1–13 Search PubMed
.
- B. Kim, F. Hillman, M. Ariyoshi, S. Fujikawa and P. J. A. Kenis, J. Power Sources, 2016, 312, 192–198 CrossRef CAS
.
- M. Gebhard, M. Paulisch, A. Hilger, D. Franzen, B. Ellendorff, T. Turek, I. Manke and C. Roth, Materials, 2019, 12(8), 1275 CrossRef CAS PubMed
.
- N. Weber, J. Linkhorst, R. Keller and M. Wessling, Adv. Mater. Technol., 2023, 1–8, 2300720 CrossRef
.
- M. Quentmeier, B. Schmid, H. Tempel, H. Kungl and R. A. Eichel, ACS Sustain. Chem. Eng., 2023, 11, 679–688 CrossRef CAS
.
- G. Marcandalli, M. C. O. Monteiro, A. Goyal and M. T. M. Koper, Acc. Chem. Res., 2022, 55, 1900–1911 CrossRef CAS PubMed
.
- M. Ramdin, A. R. T. Morrison, M. De Groen, R. Van Haperen, R. De Kler, E. Irtem, A. T. Laitinen, L. J. P. Van Den Broeke, T. Breugelmans, J. P. M. Trusler, W. De Jong and T. J. H. Vlugt, Ind. Eng. Chem. Res., 2019, 58, 22718–22740 CrossRef CAS
.
- S. Popović, M. Smiljanić, P. Jovanovič, J. Vavra, R. Buonsanti and N. Hodnik, Angew. Chem., Int. Ed., 2020, 59, 14736–14746 CrossRef PubMed
.
- U. O. Nwabara, E. R. Cofell, S. Verma, E. Negro and P. J. A. Kenis, ChemSusChem, 2020, 13, 855–875 CrossRef CAS PubMed
.
- K. Van Daele, B. De Mot, M. Pupo, N. Daems, D. Pant, R. Kortlever and T. Breugelmans, ACS Energy Lett., 2021, 4317–4327 CrossRef CAS
.
- M. E. Leonard, L. E. Clarke, A. Forner-Cuenca, S. M. Brown and F. R. Brushett, ChemSusChem, 2020, 13, 400–411 CrossRef CAS PubMed
.
- A. M. Kalde, M. Grosseheide, S. Brosch, S. V. Pape, R. G. Keller, J. Linkhorst and M. Wessling, Small, 2022, 18(49), 2204012 CrossRef CAS PubMed
.
- F. Bienen, A. Löwe, J. Hildebrand, S. Hertle, D. Schonvogel, D. Kopljar, N. Wagner, E. Klemm and K. A. Friedrich, J. Energy Chem., 2021, 62, 367–376 CrossRef CAS
.
- U. O. Nwabara, A. D. Hernandez, D. A. Henckel, X. Chen, E. R. Cofell, M. P. De-Heer, S. Verma, A. A. Gewirth and P. J. A. Kenis, ACS Appl. Energy Mater., 2021, 4, 5175–5186 CrossRef CAS
.
- E. R. Cofell, U. O. Nwabara, S. S. Bhargava, D. E. Henckel and P. J. A. Kenis, ACS Appl. Mater. Interfaces, 2021, 13, 15132–15142 CrossRef CAS PubMed
.
- S. Verma, Y. Hamasaki, C. Kim, W. Huang, S. Lu, H. R. M. Jhong, A. A. Gewirth, T. Fujigaya, N. Nakashima and P. J. A. Kenis, ACS Energy Lett., 2018, 3, 193–198 CrossRef CAS
.
- F. Bienen, J. Hildebrand, D. Kopljar, N. Wagner, E. Klemm and K. A. Friedrich, Chem.-Ing.-Tech., 2021, 93, 1015–1019 CrossRef CAS
.
- H. Weinrich, B. Rutjens, S. Basak, B. Schmid, O. Camara, A. Kretzschmar, H. Kungl, H. Tempel and R. A. Eichel, Catalysts, 2023, 13, 17 CrossRef
.
- M. Schatz, S. Jovanovic, R. A. Eichel and J. Granwehr, Sci. Rep., 2022, 12, 1–9 CrossRef PubMed
.
- F. Li, L. Chen, G. P. Knowles, D. R. MacFarlane and J. Zhang, Angew. Chem., Int. Ed., 2017, 56, 505–509 CrossRef CAS PubMed
.
- Y. Wei, J. Liu, F. Cheng and J. Chen, J. Mater. Chem. A, 2019, 7, 19651–19656 RSC
.
- H. Xiang, H. A. Miller, M. Bellini, H. Christensen, K. Scott, S. Rasul and E. H. Yu, Sustainable Energy Fuels, 2019, 4, 277–284 RSC
.
- C. T. Dinh, T. Burdyny, G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. Pelayo García De Arquer, A. Kiani, J. P. Edwards, P. De Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787 CrossRef CAS PubMed
.
- T. Möller, T. Ngo Thanh, X. Wang, W. Ju, Z. Jovanov and P. Strasser, Energy Environ. Sci., 2021, 14, 5995–6006 RSC
.
- A. Del Castillo, M. Alvarez-Guerra, J. Solla-Gullón, A. Sáez, V. Montiel and A. Irabien, Appl. Energy, 2015, 157, 165–173 CrossRef CAS
.
- J. Li, J. Jiao, H. Zhang, P. Zhu, H. Ma, C. Chen, H. Xiao and Q. Lu, ACS Sustain. Chem. Eng., 2020, 8, 4975–4982 CrossRef CAS
.
-
Y. Hori, in Modern Aspects of Electrochemistry vol. 42, ed. C. G. Vayenas, R. E. White and M. E. Gamboa-Aldeco, Springer, New York, NY, 42nd edn, 2008, pp. 89–189 Search PubMed
.
- A. Löwe, M. Schmidt, F. Bienen, D. Kopljar, N. Wagner and E. Klemm, ACS Sustain. Chem. Eng., 2021, 9, 4213–4223 CrossRef
.
- D. S. Hwang, C. H. Park, S. C. Yi and Y. M. Lee, Int. J. Hydrogen Energy, 2011, 36, 9876–9885 CrossRef CAS
.
- A. Diéguez, A. Romano-Rodríguez, A. Vilà and J. R. Morante, J. Appl. Phys., 2001, 90, 1550–1557 CrossRef
.
- J. -L. Bribes, M. El Boukari and J. Maillols, J. Raman Spectrosc., 1991, 22, 275–279 CrossRef CAS
.
- A. Dutta, A. Kuzume, M. Rahaman, S. Vesztergom and P. Broekmann, ACS Catal., 2015, 5, 7498–7502 CrossRef CAS
.
- M. Ristić, M. Ivanda, S. Popović and S. Musić, J. Non-Cryst. Solids, 2002, 303, 270–280 CrossRef
.
- A. Kumar, A. Sanger, A. Kumar and R. Chandra, RSC Adv., 2016, 6, 47178–47184 RSC
.
- S. H. De Almeida and Y. Kawano, J. Therm. Anal. Calorim., 1999, 58, 569–577 CrossRef CAS
.
- V. Henri, E. Dantras, C. Lacabanne, A. Dieudonne and F. Koliatene, Polym. Degrad. Stab., 2020, 171, 109053 CrossRef CAS
.
- M. Hartman, K. Svoboda, B. Čech, M. Pohořelý and M. Šyc, Ind. Eng. Chem. Res., 2019, 58, 2868–2881 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3se01347b |
| This journal is © The Royal Society of Chemistry 2024 |