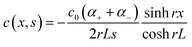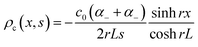Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recent advances in ionic thermoelectric systems and theoretical modelling
Nazish
Jabeen
a,
Muhammad
Muddasar
 b,
Nicolás
Menéndez
a,
Mohammad Ali
Nasiri
b,
Nicolás
Menéndez
a,
Mohammad Ali
Nasiri
 c,
Clara M.
Gómez
a,
Maurice N.
Collins
c,
Clara M.
Gómez
a,
Maurice N.
Collins
 b,
Rafael
Muñoz-Espí
b,
Rafael
Muñoz-Espí
 a,
Andrés
Cantarero
a,
Andrés
Cantarero
 c and
Mario
Culebras
c and
Mario
Culebras
 *a
*a
aInstitute of Materials Science (ICMUV), Universitat de València, PO Box 22085, E46071, Valencia, Spain. E-mail: Mario.Culebras@uv.es
bStokes Laboratories, School of Engineering, Bernal Institute, University of Limerick, Limerick, Ireland
cInstitute of Molecular Science (ICMol), Universitat de València, PO Box 22085, E46071, Valencia, Spain
First published on 20th August 2024
Abstract
Converting waste heat from solar radiation and industrial processes into useable electricity remains a challenge due to limitations of traditional thermoelectrics. Ionic thermoelectric (i-TE) materials offer a compelling alternative to traditional thermoelectrics due to their excellent ionic thermopower, low thermal conductivity, and abundant material options. This review categorizes i-TE materials into thermally diffusive and thermogalvanic types, with an emphasis on the former due to its superior thermopower. This review also highlights the i-TE materials for creating ionic thermoelectric supercapacitors (ITESCs) that can generate significantly higher voltages from low-grade heat sources compared to conventional technologies. Additionally, it explores thermogalvanic cells and combined devices, discussing key optimization parameters and theoretical modeling approaches for maximizing material and device performance. Future directions aim to enhance i-TE material performance and address low energy density challenges for flexible and wearable applications. Herein, the cutting-edge of i-TE materials are comprehensively outlined, empowering researchers to develop next-generation waste heat harvesting technologies for a more sustainable future.
1. Introduction
Driven by the depletion of fossil fuels and the increasing frequency of climate disasters, the 21st century faces an unprecedented energy crisis. This has sparked significant interest from both academia and industry in exploring techniques for converting renewable power sources into electrical energy.1 Several technologies have been developed to harness heat, including thermoelectric generators (TEGs), thermoosmotic energy conversion, and organic Rankine cycles. One key area of exploration within TEGs involves leveraging the Seebeck effect of inorganic semiconductors (Bi2Te3), making them particularly effective in harvesting low-grade heat.2–4 The evaluation of their thermoelectric (TE) performance is commonly based on the dimensionless figure of merit (ZT),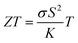 , where the incorporated factors are electrical conductivity (σ), the Seebeck coefficient (S), thermal conductivity (K), and absolute temperature (T).5,6
, where the incorporated factors are electrical conductivity (σ), the Seebeck coefficient (S), thermal conductivity (K), and absolute temperature (T).5,6
The literature reports the highest ZT at 3.1 at 783 K, and the highest ZT at room temperature at 1.3 approximately.7,8 However inorganic TE materials have drawbacks, including high costs, scarcity of elements, and limited mechanical flexibility. Efforts to enhance TEG performance are underway through nanostructuring existing materials, even though this approach comes with considerable production costs.9 On the other side, TEGs are gaining attention as a promising solution for powering wearable sensors and devices compared to heat engines. However, the mechanical stiffness of inorganic semiconductors and semimetals restricts their use in portable and wearable devices.10
Turning to electronic conducting polymers, their composition of abundant elements has sparked interest in recent studies for potentially lowering material costs.11 Despite substantial efforts and achievements in recent years, the optimized ZT of p-type organic thermoelectric materials still yields a relatively low Seebeck coefficient (maximum 70 μV K−1 for commonly produced polymers like PEDOT with a conductivity of 900 S cm−1). In contrast, the ratio of their electrical to thermal conductivities is already comparable to that of Bi2Te3 alloys.12,13 The interconnected material properties present a challenge in attaining a high ZT for electronic thermoelectric (e-TE) materials. Specifically, the Seebeck coefficient of e-TE is typically influenced by the transported excess energy or entropy to the Fermi level of charge carriers. Consequently, it tends to be considerably high in insulators characterized by large band gaps in their electronic band structures. However, the electrical conductivity is suppressed by such a wide bandgap. The e-TE materials with a Seebeck coefficient of ∼200 μV K−1 are typically optimized to achieve a high ZT or power factor, similar to the conventional Bi2Te3-based thermoelectric materials.14,15 Another difficulty in fabricating devices with such a low Seebeck coefficient is the large number of p- and n-type pairs required to achieve a reasonable voltage output, particularly in situations where there is a small temperature difference, as the case of harvesting thermal energy from the environment and the body to power small sensors. Consequently, there is a great need for new material classes and innovative ideas that can aid in resolving these issues.15
Recently, the discovery of “ionic thermpower” in electrolytes has introduced a novel phenomenon for heat-to-electricity conversion, which are hundreds of times larger than the electronic Seebeck coefficients found in conventional thermoelectric materials. It was established that the ionic Seebeck effect is the primary cause of the enormous thermopower, which can reach several mV K−1. An electrolyte that is subjected to a temperature gradient will undergo thermal diffusion of its internal ions until equilibrium is reached. The ions are finally reorganized, leading to the formation of an ion concentration gradient (also known as the Soret effect). This kind of ionic Seebeck effect can be found in gel electrolytes, inorganic solid electrolytes, ionic solids, and liquids.16 Among ionic thermoelectric (i-TE) materials, polymer-based electrolytes have gained attention due to their solid or gel states, facilitating easier device manufacturing. Additionally, i-TE materials possess excellent flexibility and stretchability, enhancing their potential for practical applications. These i-TE materials can be utilized in flexible TE devices to harness power from irregular heat sources.17 Two primary sources of ionic thermovoltage generation are Soret effect and thermogalvanic effect. Both effects involve an electrolyte for ion movement and electrodes for conducting currents and providing potential. The former effect is the thermodiffusion of ions that takes place in redox-free electrolytes. This phenomenon is primarily driven by the electric double layer (EDL), which forms as ions accumulate at the electrodes.18 However, the utilization of thermodiffusion among ionic charge carriers within an electrolyte has been implemented to convert heat into electrical energy, subsequently storing it in a supercapacitor.19,20 The later effect occurs in thermogalvanic cells based on thermogalvanic process. This effect arises from temperature-dependent entropy changes, originating from the electron transfer between redox molecules and the electrode.16
Recent research on i-TE materials has made significant progress over the past decade as illustrated in Fig. 1. Shu et al. reported the fabrication of high-performance, flexible, and thermally stable carbon-based TE materials with an impressive power factor (S2σ) of 38.7 μW m−1 K−2. A fabricated TE device achieved a maximum power density of 79.3 nW cm−2 under a temperature difference of 20 K and a cold-side temperature of 300 K, showcasing the potential for cost-effective, high-performance TE applications.21 In the last decade, a novel i-TE film composed of carbon-based materials, an ionic liquid (1-butyl-3-methylimidazolium chloride, BMIM:Cl), and a crosslinker (N,N′-methylenebisacrylamide, MBA) was developed. The film exhibited enhanced TE performance, characterized by a high Seebeck coefficient (−76.7 mV K−1), power factor (753.0 μW m−1 K−2), and dimensionless figure of merit (ZT) of 0.19 at 383 K. A flexible, 9-legged thermoelectric device measuring 25 × 25 mm2 was fabricated, achieving a maximum power density of 1.32 mW cm−2 under a 20 K temperature difference. This work presents a promising foundation for developing high-performance, flexible i-TE materials and devices.17
 | ||
| Fig. 1 Recent advances in strategic development and application of ionic thermoelectric materials and devices. | ||
Recent advancements in i-TE materials have shed light on their mechanisms and operational modes within ITESC materials by Zhao et al.12 2017. They underscore the application of i-TE materials in energy conversion devices. Conversely, Wu et al. 2021 studies centered only on ionic conductors with promising applications in thermoelectric converters.18 Agar and their colleagues explored thermogalvanic cells, which utilize temperature-dependent redox pairs in the electrolyte to enhance the system's thermoelectric efficiency.22 In 2023 Shuai et al.1 review examined insightful strategies for thermo-electrochemical systems and TE performance. These reviews collectively elucidate the current state of research in the emerging field of ionic thermoelectrics covering i-TE mechanisms, material characteristics, figure of merit and energy conversion application. However, these reviews fall short of adequately highlighting the i-TE materials in energy integrated devices and ionic thermogalvanic cells based on electrochemical energy conversion system. Additionally, they do not provide a discussion on the utilization of combined ionic thermoelectric devices, as well as the significant categorization of theoretical modeling.1,12,18,22
This review will begin with a historical overview of i-TE materials, then move on to the Soret effect (thermodiffusion effect) and thermogalvanic effect, which serve as the primary driving forces behind the state of the art regarding the combined effect of both ionic systems involved in i-TE materials. The optimization parameters and theoretical models for TEG (one and two dimensional case) are outlined and examined in the final section. Consequently, the present review aims to not only stimulate the development of novel i-TE materials but also foster collaboration between researchers specializing in energy storage devices, thermodiffusion, and thermogalvanic phenomena. By bridging these areas of expertise, we can significantly advance our understanding of temperature-dependent ion transport and unlock applications beyond the capabilities of traditional electronic materials in low-grade energy harvesting technologies.
2. Historical overview of ionic thermoelectric materials
The exploration of ionic thermoelectric materials commenced with the investigation into ion thermodiffusion conducted by Swiss physicist and chemist Charles Soret (September 23, 1854, to April 4, 1904). Soret conducted experiments in which sodium chloride and potassium nitrate were placed in a vertical tube measuring 30 cm in length and 2 cm in diameter. The tube top and bottom ends were maintained at temperatures of 80 °C and room temperature, respectively. He observed that the concentration of salt solutions in the tube did not remain uniform. Between 1879 and 1884, Soret published several papers (originally in French) documenting his thermodiffusion experiments. These papers were later summarized and briefly discussed in English by Platten and Costesèque.23 The migration of ions induced by a temperature gradient resulted in the generation of a potential difference known as ionic thermopower. This phenomenon bears similarity to the Seebeck effect observed in electronic conductors or semiconductors, but the underlying principle differs significantly. Ionic thermopower is primarily governed by the disparity in ion contributions to conductivity and the transport numbers of cations and anions. Consequently, when there is a substantial difference in the sizes of anions and cations, high values of ionic thermopower are expected. One of the earlies works was carried out by Toshio Ikeda in the 60s measuring the ionic thermopower of the combination of ionic solutions based on: Ag, AgNO3; Cu, CuSO4; Ag, AgNO3; Cu, CuSO4; Hg, HgO, LiOH or NaOH or KOH; Hg, Hg2SO4, Na2SO4 varying the concentration from 0.01 to 2.0 molal.24,25 Moreover, the first studies of polyelectrolytes in particular, polystyrene sulfonic acid, were considered for thermocells during that decade.26 In latest 70s, starting to appear the first works utilising molten salts for ionic thermoelectric applications, in particular, mixtures of LiNO3 + AgNO3 and NaNO3 + AgNO3.27 However, it was not until 2016 when ionic thermoelectric materials started to be used as ionic thermoelectric supercapacitors with the work of Crispin et al.28 reporting the thermoelectric properties of a polymeric electrolyte based on polyethyleneoxide treated by NaOH with an exceptionally high ionic thermopower up to 11.1 mV K−1. During the last decade, research on ionic thermoelectric materials has been focused on hydrogels combining different electrolytes and natural based polymer matrices in particular cellulose and lignin. Highlights the work reported by Li et al.29 with a very high ionic thermopower up to 24 mV K−1 obtained for oxidized cellulose membranes. For the case of lignin, several works published by our group have been demonstrated the enormous potential of lignin-based membranes and hydrogels in combination with KOH as electrolyte as ionic thermoelectric materials reaching very high iZT values (0.6–3.5).6,30 In addition, the combination of the ionic thermoelectric effect in thermogalvanic cells has recently opened avenues for maximising the thermoelectric performance. A good example of this is the work published in Science by Han et al.,31 where they developed wearable device consisting of 25 unipolar elements based on a gelatin matrix modulated with ion providers (KCl, NaCl, and KNO3) for thermodiffusion effect and a redox couple [Fe(CN)64−/Fe(CN)63−] for thermogalvanic effect. The device generated more than 2 volts and a peak power of 5 microwatts using body heat. In recent years, significant progress on thermoelectric fiber-based woven devices can be integrated with other functional components to create smart textiles. These components include moisture sensors, triboelectric generators, wearable current–voltage regulators, and energy storage units like tiny supercapacitors. Such integration of i-TE materials represents a valuable advancement for researchers working on flexible, wearable thermoelectric materials and devices, as well as their novel applications in customized thermal management and electronic skin.323. Ionic thermoelectric system
This section explores the essential principles underlying thermodiffusion and thermogalvanic systems, giving rise to the i-TE phenomenon. We explore several phenomenological models to understand how these effects result in the creation of an electric potential difference. The principles of heat transfer in i-TE materials are examined considering recent advancements.3.1 Basic mechanisms
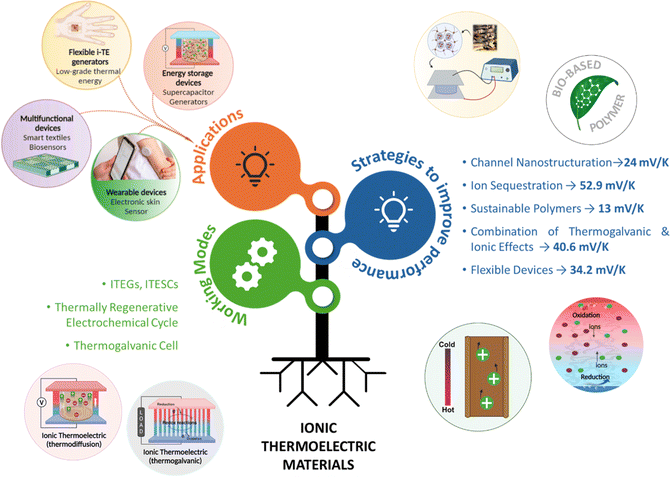
Electronic (e-TE) and ionic thermoelectric (i-TE) materials both offer pathways for converting heat into electricity, but their underlying mechanisms differ significantly. In e-TE materials (Fig. 2a), the Seebeck effect drives the process. Under a temperature gradient (ΔT), electrons (or holes) act as charge carriers, propelled by an electromotive force.34 Due to their negative charge, electrons migrate from the hot to cold side, generating an electric potential difference against the temperature gradient. i-TE materials, however, rely on two distinct sources for potential generation: thermodiffusion and the thermogalvanic effect. Thermodiffusion leads to ion concentration gradients within the material due to ΔT, creating an internal potential. Additionally, the thermogalvanic effect harnesses the temperature dependence of electrode/electrolyte interactions, resulting in another potential contribution, as depicted in Fig. 2b and c.1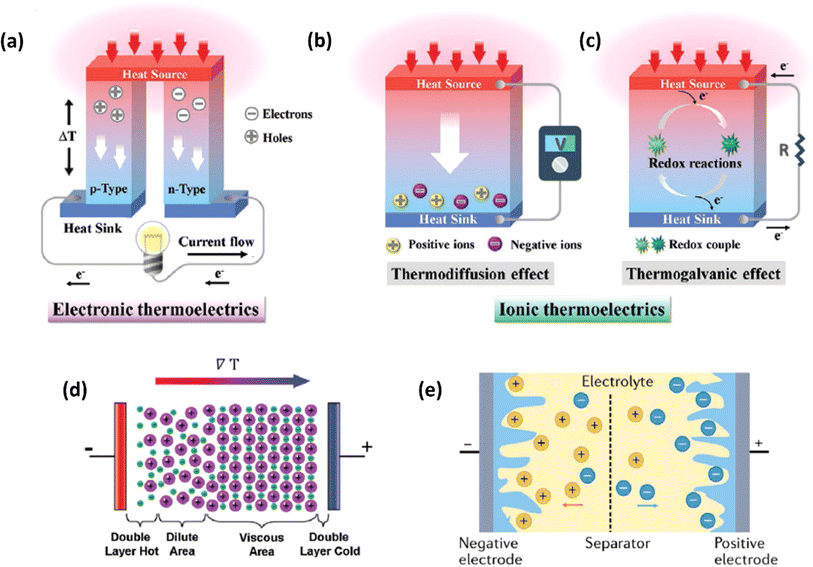 | ||
| Fig. 2 Representation of (a) diagram portraying a group of n-type and p-type e-TE materials, (b) thermodiffusive-based i-TE materials, (c) thermogalvanic-based i-TE material, (d) the internal structure of a thermodiffusive-based i-TE materials in its operational mode, reproduced with permission.1 Copyright 2023, Wiley-VCH. (e) Electric double-layer in supercapacitor, reproduced with permission.33 Copyright 2019, Elsevier. | ||
3.2 Thermodiffusion based system
The thermodiffusion-based system, originating from the Soret effect that was first discovered by Soret and Ludwig in the 19th century, plays a pivotal role in i-TE materials. Under a ΔT ions migrate from the hot to cold side, leading to concentration imbalances at the electrodes. To maintain electrical neutrality, both cations and anions participate in this process within the i-TE material. However, the distinctive migration speeds (diffusion rates) of these ions are influenced by variations in size, coulomb force and activation energy, resulting in different diffusion rates between cationic and anionic ions. This leads to an imbalance in the concentrations of each type of ion. As shown in Fig. 2d, a double-layer region containing a Helmholtz layer and a diffusion layer form close to the electrolyte/electrode interface following the Gouy–Chapman–Stern theory.35 The difference in ion concentration causes a dilute region to be near one electrode and a viscous region near the other, which results in different chemical potentials in each electrode's Helmholtz layer. Thus, an electric potential difference between the two electrodes is initiated by the chemical potential difference between the two Helmholtz layers.18A recent study on i-TE materials, inspired by Soret effect, draws a parallel intention with e-TE materials based on the Seebeck effect, as both exhibit the ability to generate thermovoltage associated with charge transfer enthalpy. However, some noteworthy differences are present. (i) Ions can have charges significantly higher than electrons, depending on their overall valence state. Electrons have a charge of one unit. (ii) Unlike ion transport, electron transport is confined within a particular energy window and follows the Fermi–Dirac statistical functional. (iii) Electrons are the only carriers that contribute to electrical conductance in e-TE materials, while cations and anions are also involved in i-TE materials. Importantly, (iv) electrons can traverse an external circuit, while ions accumulate at electrodes, leading to the formation of an electric double layer (EDL), as depicted in Fig. 2e. This process induces a transient thermoinduced current, illustrating the charge stored in the EDL capacitors. By utilizing high-capacitance electrode materials, this accumulated charge can be significantly increased, enabling the charging of a supercapacitor or a battery.1 This principle is employed in the design of ionic thermoelectric supercapacitors (ITESCs), which combine the functionalities of a thermoelectric generator and a supercapacitor. The establishment of an equivalent circuit, combining a TEG and a supercapacitor, is crucial for electronic material-based thermoelectric applications.36,37
3.3 Ionic thermoelectric generators
Ionic thermoelectric generators (ITEGs) are gaining recognition for their ability to efficiently recover low-grade waste heat. However, their practical application is hindered by low power and energy density. To address this, scientists have developed innovative ITEGs with enhanced power and energy density, enabling continuous charging of small devices. By synergistically combining electrode redox reactions with the thermodiffusion effect, these ITEGs demonstrate impressive thermoelectric conversion properties. This technology holds commercial promise for powering wearable electronics and sensors, opening new avenues for advanced ionic thermoelectric devices with improved heat-to-electricity conversion and storage capabilities.38 Li et al.29 introduced a generator mode where an i-TE cell is directly connected to a load resistance after voltage build-up. This study reported the three stages ITEG mode as illustrated in Fig. 3a. Voltage build-up: under a temperature difference (ΔT), a voltage is generated across the i-TE material due to the movement of ions from the hot to the cold side. Power output: once a sufficient voltage is built up, an external circuit can be connected to the i-TE device. This allows for the flow of ions and the generation of electrical power. Reactivation: to maintain consistent power output, the i-TE device needs to be reactivated. This involves removing the temperature difference (ΔT) to allow for the redistribution of ions within the material, preparing it for the next charging and discharging cycle.39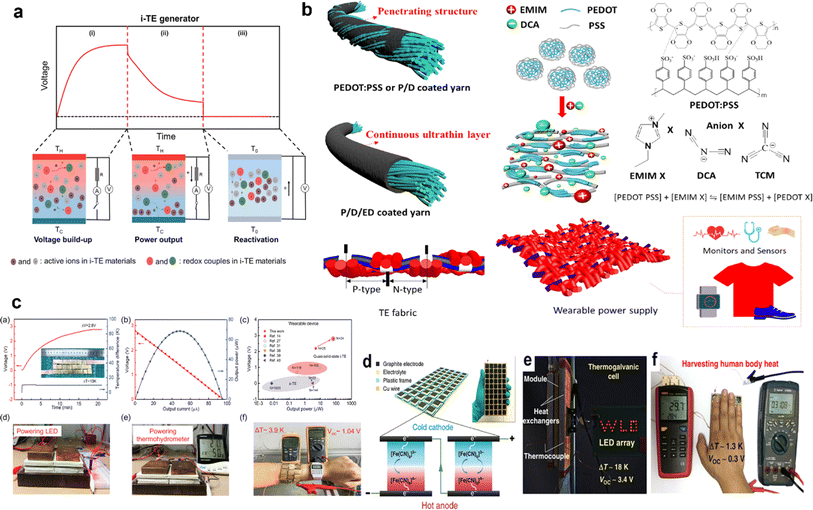 | ||
| Fig. 3 (a) Schematic representation of ITEGs, reproduced with permission.39 Copyright 2022, Wiley-VCH. (b) Chemical interactions between PEDOT:PSS and [EMIM:DCA], reproduced with permission.1 Copyright 2023, Wiley-VCH (c) voltage output of a wearable i-TE device, reproduced with permission.39 Copyright 2022, Wiley-VCH. (d–f) Photographs of the i-TE generators, reproduced with permission.1 Copyright 2023, Wiley-VCH. | ||
Fig. 3b demonstrate a i-TE generator fabricated by coating a fabric with a PEDOT/DMSO/[EMIM] solution.40 This process yielded a continuous, 8.78 μm-thick TE layer on the cotton yarn, contrasting with the discontinuous structure of pristine PEDOT-coated yarn. This enhancement is attributed to the PEDOT/DMSO/[EMIM] composite's higher viscosity and surface tension, preventing yarn penetration. The surface-coated yarn demonstrated significantly improved flexibility compared to its pristine counterpart. Moreover, the maximum power factor (S2σ) was optimized to 24.7 μW m−1 K−2, a substantial improvement over the pristine PEDOT value of 0.00684 μW m−1 K−2. Researchers have focused on practical application of long-term power generation of the gelatin–KCl–FeCN4−/3− i-TE cell by designing 3D hierarchical Au/Cu electrodes as shown in Fig. 3c. The optimized i-TE cell shows high output power and thermopower, making it a potential electricity source for sensors and wearable electronics. This watch-strap-styled device generates 2.8 V and 68 μW when worn on the arm, with a skin temperature of 30 °C and an environmental temperature of 20 °C, resulting in a ΔT of approximately 10 K. The high output voltage can drive sensors without additional DC–DC voltage boosters, as most sensors operate within a voltage range of 1.5–3.6 V. Compared to other i-TE and electronic thermoelectric (e-TE) devices, optimized devices demonstrated the output voltage and power are significantly 127% and 1360% respectively, and substantially higher than other reported devices. The device can directly power various electronics, including an LED bulb and a thermohydrometer. It also harvests heat from the body, generating a stable voltage of approximately 1.04 V under a small ΔT of approximately 3.9 K in an indoor summer environment, enough to drive a digital watch without voltage boosters.39 Additionally, a thermogalvanic i-TE module was developed using guanidine chloride (GdmCl) and urea-enhanced [Fe(CN)64−/Fe(CN)63−] electrolytes. A polyamide frame housed 50 individual units, each containing a graphite electrode sandwiching the electrolyte. This module generated an open-circuit voltage of 3.4 V and a short-circuit current of 1.2 mA under an 18 K temperature difference, capable of powering an LED array. Notably, the device effectively harvested human body heat, producing a stable voltage of over 0.3 V under a minimal temperature difference of 1.3 K41 (Fig. 3d–f).
3.4 Ionic thermoelectric supercapacitors
Over the last few years researchers reported that ionic thermoelectric supercapacitors (ITESCs) create a transient thermo-induced current by forming an EDL at the electrodes through the aggregation of thermally diffused ions. Supercapacitors or batteries can be charged by using high-capacitance electrode materials, which can greatly increase the accumulated charge.42 Zhao et al. explored the thermoelectric characteristics of the PEO-NaOH solution by injecting the liquid electrolyte contained within a 1 mm thick, 10 mm diameter cylindrical chamber. The planner surfaces of Au electrodes were deposited on each side, making direct contact with the polymer electrolyte (see Fig. 4a). Thermistors embedded beneath the electrodes monitored the temperature difference (DT). The open voltage induced by Soret under different ΔT conditions was explored while subjecting one side of the device to heating and the other side to cooling, as depicted in Fig. 4b. The investigation of thermovoltage was conducted within various ΔT conditions between 25 to 35 °C. Five minutes after stabilization at each ΔT, the voltage was recorded. The outcomes, showcased in Fig. 4c, reveal a linear variation of Vthermo with ΔT. From the linear fit, the researchers calculated an ionic Seebeck coefficient of +11.1 mV K−1 for the PEO-NaOH electrolyte. Using both CNT and Au electrodes yields similar saturation of Vthermovs. time (Fig. 4c) and the evolution of Vthermovs. ΔT (Fig. 4d). This suggests that electrodes nature does not influence the results, indicating that the thermovoltage is the inherent property of the polymer electrolyte.28 However, in recent years, researchers have found that the thermopower of ionic thermoelectric devices does not solely depend on the intrinsic properties of the materials but also includes a significant contribution from electrode polarization, necessitating careful consideration and correction in measurements.43 This can be expressed as ΔV = SΔT + ΔVelectrode, where ΔV is the total measured voltage difference, SΔT is the thermoelectric voltage, and ΔVelectrode is the voltage contribution from electrode polarization. When an inert metal is used as electrode, the term of ΔVelectrode could be negligible.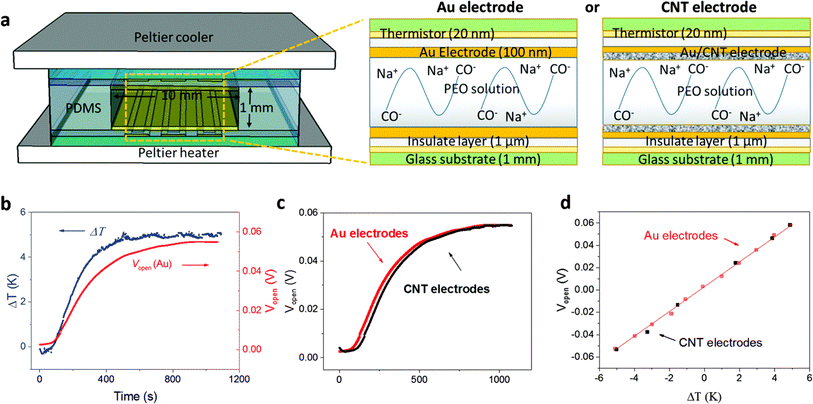 | ||
| Fig. 4 (a) Illustration of the ITESCs device (left) featuring two distinct electrodes (right, Au and CNT), along with the reaction occurring in the solution. (b) Recorded Vthermo and ΔT during the heating process using the Au electrode. (c) The observed Vthermo while heating with either CNT or Au electrodes. (d) Vthermo at various ΔT values using CNT electrodes (black solid squares) and Au electrodes (red open squares), reproduced with permission.28 Copyright 2016, Royal Society of Chemistry. | ||
3.5 Operational mechanism of ITESCs
Wang et al.44 reported the four distinct steps that comprise the comprehensive operational mechanism of ITESC in Fig. 5a, making it easier to extract energy from i-TE materials. The first step of the charging process described, setting up the device for a ΔT, which causes an open circuit to produce thermal voltage.45 The representation in Fig. 5a has a positive thermal voltage arise at the cold side, primarily due to dominant sodium cation thermodiffusion. Moving on to the second step, the EDLC is charged by connecting the electrodes, via a load or a short circuit. In this stage, an electric current flow from the electrodes with a higher electric potential to the one with a lower potential, all while maintaining the ΔT. The third step involves an equilibration period, involves removing the load and the ΔT from the circuit. Importantly, the charges that were stored at the electrode–electrolyte interface did not disappear even as the ions diffused back. Since there is no thermal voltage generated, stored charge at electrodes controls the ensuing open circuit voltage at ΔT = 0, which should be observed in this step with a sign opposite to initial thermal voltage in step I. Finally, the fourth step involved the loss of stored charge due to the EDLC discharging through an external circuit load resistance. Once the charging process is finished, the DT is no longer necessary and is only needed for stages I and II. After completing a full cycle, brings the ITESC back to its initial state.12,44 The repeated cycling yields highly reproducible charge–discharge current patterns, as illustrated in Fig. 5b. These observations underscore the stability of the device and suitability for harvesting energy from fluctuating heat sources. This characteristic also makes it possible to store and use energy without a constant heat source. Such a device is particularly well-suited for use with intermittent heat sources like solar energy, allowing capacitors to charge during the day and discharge during the night.28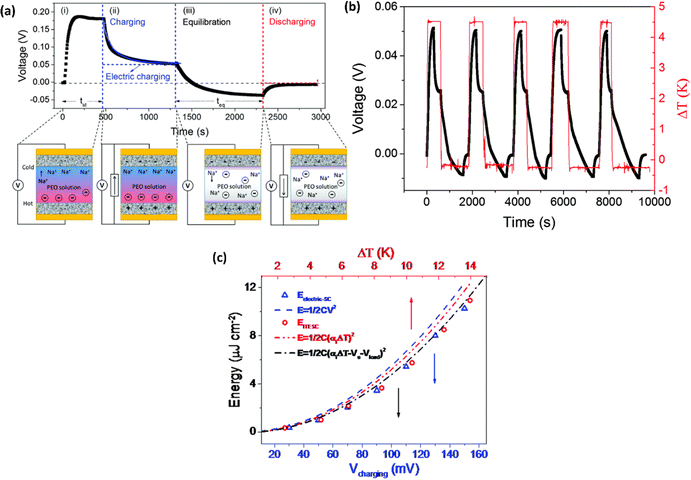 | ||
| Fig. 5 Operation principle of ITESC (a) schematic mechanism: (i) ΔT generates ionic thermal voltage, (ii) thermoelectric charging, (iii) ΔT removal for ion equilibrium, (iv) discharging. (b) Charging/discharging with periodic heating, reproduced with permission.44 Copyright 2017, Wiley-VCH. (c) Depicts the energy density of the ITESC compared to both ΔT and electric charging methods. The red open circles represent the data for the ITESC, while the blue open squares represent electric charging. The dashed lines show theoretical predictions based on thermal voltage (Vthermo, dashed red line), electric voltage (Velectric, dashed blue line), and effective voltage (Veffective, dashed and dotted black line), reproduced with permission.28 Copyright 2016, Royal Society of Chemistry. | ||
3.6 Stored charge and energy
To understand the charging mechanism of the ITESC, Dan Zhao et al. investigated the relationship between the stored electrical energy in the supercapacitor and the ionic thermopower, signifying the thermal voltage generated by the electrolyte. This involved charging and discharging the ITESC under different ΔT and subsequently calculating the energy stored in the supercapacitor by integrating the current over time across a load resistance.12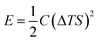 | (1) |
3.7 ITESCs for integrated energy conversion-storage
Drawing inspiration from the work of Xinyu Yang et al.,46 they proposed a model for understanding the charge–discharge behavior of an ITESC based on an equivalent circuit (as shown in Fig. 6a). Within this framework, the thermal voltage arising from the DT acts as the driving force. During stages i and ii, the absence of voltage signals points towards an equilibrium state within the device, with electrons and holes balanced at the positive and negative electrodes.47 It is crucial to note that a temperature gradient of 0 K would result in minimal redistribution of Na+ ions within the electrolyte interface. Additionally, without a counterbalancing charge attraction, electron and hole movement across the interface would not be expected. When the external circuit remained disconnected during stages i and ii, limited ion transport resulted in an inherent charge imbalance. This imbalance generated a potential difference across the positive and negative electrodes, measurable as the open-circuit voltage (Fig. 6b). Analysis revealed a linear relationship between this voltage and the applied DT, with the highest recorded voltage of 0.45 V achieved at ∼30 K DT. Further investigation conducted a series of calculations to evaluate the quantity of charge transferred during stage iii. The results presented in Fig. 6c illustrate a nearly linear correlation between the amount of charge and the loop, contingent on the DT. However, discharge capacity suffered a notable decline due to internal resistance contributing to a voltage drop. Xinyu Yang reported a more comprehensive understanding of the energy consumption dynamics during both charging and discharging processes, to assess the charge–discharge ratio in relation to ΔT and voltage. Fig. 6d showcases the remarkable consistency of the charge–discharge ratio across varying DT and initial voltage conditions. Notably, at 50 mV (T = 2 K), the ratio remains near 96%, highlighting the substantial charge storage capacity and exceptional stability of the ITESC. Further investigation explored the device's tensile stability by subjecting it to 20 cycles of 20% stretching. Subsequent charge–discharge analysis revealed a consistent linear relationship between voltage and the ratio across a 30–150 mV range, regardless of pre- or post-stretching conditions. This finding underscores the notable tensile stability of the integrated device. Xinyu Yang. et al. reported the practicality of integrated i-TE device into wearable electronics. As shown in Fig. 6e, a flexible and stretchable device was applied to the back of the hand, simulating real-world interactions with the human body. The device effectively harvested low-grade heat during palm bending, generating a voltage output of 90 mV at a temperature difference of 6 K (Fig. 6f). This finding highlights the applicability of such devices in powering wearable electronics.46,48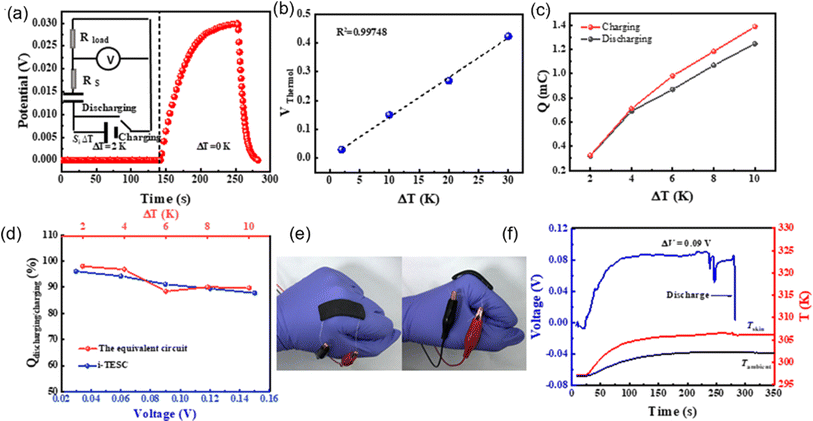 | ||
| Fig. 6 Representation of (a) equivalent circuit and charge–discharge characteristics of ITESCs. (b) Thermal voltage of ITESCs vs. ΔT. (c) Stored charge as a function of ΔT. (d) The charge–discharge ratio in relation to both ΔT and voltage. (e) Potential applications of ITESCs in wearable electronics. (f) Output voltage from a prototype stretchable ITESC worn on the back of a hand, reproduced with permission.46 Copyright 2022, Wiley. | ||
3.8 Ionic thermoelectric figure of merit
Over the past three years the researcher successfully explained that ionic figure of merit (iZT = σiSi2T/K), served as a key parameter for assessing the performance of i-TE materials, drawing parallels with their electronic counterparts. It is crucial to highlight that iZT for electrolytes does not exhibit the same correlation with heat to electron conversion efficiency as observed in traditional thermoelectric materials, mainly due to the limitations in utilizing ionic materials in conventional TEGs.12 Zhao and their colleagues described a comprehensive study into the figure of merit for ITESC.12 The assessment of charging performance involved determining the ratio between stored electric energy and absorbed heat during the charging process, with expression detailed in eqn (2). Using this equation,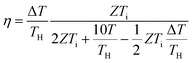 | (2) |
It is important to mention here that this formula is applicable only to ITESC. Currently, there is a lack of a universal ionic thermoelectric Z that can serve as a comprehensive figure of merit for all the ionic thermoelectric systems. A recent study by Ma et al. have introduced a new figure of merit for the thermodiffusion based i-TE materials (eqn (2a)).49
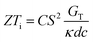 | (2a) |
Previous work introduced novel parameters to characterize thermodiffusion-based ionic thermoelectric (i-TE) devices, including capacitance (C), thermopower (S), and a factor (GT/(κdc)) representing the relaxation of temperature difference. This research offered valuable insights into device operation but overlooked the influence of ionic conductivity and the discharge process. Consequently, a more comprehensive figure of merit is necessary to fully understand i-TE device performance. Recent studies by X. Qian, R. G. Yang, and colleagues have addressed these limitations by incorporating ion transport dynamics and electrochemical reactions into the figure of merit (Z) for i-TE devices that leverage both thermodiffusion (TD) and thermogalvanic (TG) effects.50
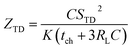 | (2b) |
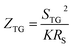 | (2c) |
They considered a critical parameter tch when i-TE devices work. However, combining these above two equations is still a big challenge. This gap in research hinders our ability to accurately compare and optimize various ionic thermoelectric systems, as current figures of merit often do not account for the unique interplay between thermogalvanic and thermodiffusion effects.
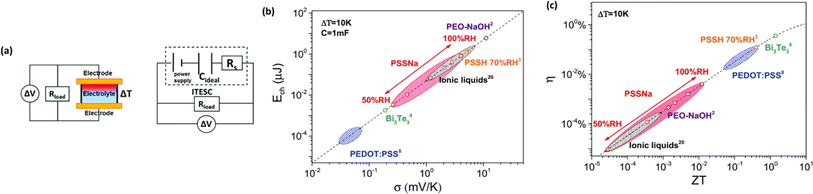
The investigation of research team described that effectiveness of an electrolyte, denoted by iZT, plays a potential role in determining the efficiency of an ITESC employing this specific material. A direct comparison between ionic and electronic thermoelectric materials proves challenging due to the distinct operational characteristics of a TEG and an ITESC. However, a meaningful comparison can be drawn by examining ionic materials within an ITESC featuring capacitance and electronic materials within a TEG coupled in series with SC of capacitance (C). This comparison is justified as they share analogous equivalent circuits, as shown in Fig. 7a. Consequently, a unified graph can depict the energy conversion efficiency of both electronic and i-TE materials by considering ITESCs as equivalent to series-connected TEG-SC circuit (as illustrated in Fig. 7b), this approach has limitation. In practical applications the efficiency of converting heat to stored electricity in an ITESC using electrolytes is still lower compared to Bi2Te3 in a TEG-SC circuit, mainly because of the significantly lower ionic conductivity. Conversely, as presented in Fig. 7c, electrolytes facilitate the storage of significantly larger electrical energy per leg/per ΔT. This phenomenon is attributed to the square of the ionic thermopower (as per eqn (1)), that is substantially higher for polymer electrolytes (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μV K−1) compared to Seebeck coefficient of Bi2Te3 alloys (∼200 μV K−1). Future research should focus on simultaneously improving ionic conductivity and maintaining a high ionic thermopower in materials designed for ITE applications. Interestingly, devices utilizing either a series circuit where a TEG charges a SC or a single ITESC system can offer pulsed electrical power through the discharge of the SC, addressing the limitation of continuous low power output encountered with TEGs alone.6 However, beyond material advances, unlocking the full potential of i-TE for practical applications introduces additional challenges related to device design. The continuous power generation capability of ionic thermoelectric devices encounters a fundamental challenge due to the necessity for discharging in the absence of a temperature difference. Ionic thermoelectric concepts demonstrate particular effectiveness in converting intermittent heating/cooling scenarios. Through deliberate design considerations, the charging duration of the supercapacitor can be synchronized with the source of heat fluctuation cycle. This presents opportunities for integrating with other steady-state power generation systems like TEGs and solar cells, both reliant on heating or illumination for operation. However, it is crucial to address the inherent limitation of low energy density in i-TE devices.51 However, this challenge is amenable to resolution through circuit manipulation. For example, harnessing the ITESC to charge capacitors directly provides a means to mitigate this concern. Additionally, adjusting the circuit configuration from parallel to series during energy utilization offers a pathway for enhancing energy density. This strategic manipulation of the circuit holds promise for overcoming the limitations associated with the energy devices of i-TE devices.44
000 μV K−1) compared to Seebeck coefficient of Bi2Te3 alloys (∼200 μV K−1). Future research should focus on simultaneously improving ionic conductivity and maintaining a high ionic thermopower in materials designed for ITE applications. Interestingly, devices utilizing either a series circuit where a TEG charges a SC or a single ITESC system can offer pulsed electrical power through the discharge of the SC, addressing the limitation of continuous low power output encountered with TEGs alone.6 However, beyond material advances, unlocking the full potential of i-TE for practical applications introduces additional challenges related to device design. The continuous power generation capability of ionic thermoelectric devices encounters a fundamental challenge due to the necessity for discharging in the absence of a temperature difference. Ionic thermoelectric concepts demonstrate particular effectiveness in converting intermittent heating/cooling scenarios. Through deliberate design considerations, the charging duration of the supercapacitor can be synchronized with the source of heat fluctuation cycle. This presents opportunities for integrating with other steady-state power generation systems like TEGs and solar cells, both reliant on heating or illumination for operation. However, it is crucial to address the inherent limitation of low energy density in i-TE devices.51 However, this challenge is amenable to resolution through circuit manipulation. For example, harnessing the ITESC to charge capacitors directly provides a means to mitigate this concern. Additionally, adjusting the circuit configuration from parallel to series during energy utilization offers a pathway for enhancing energy density. This strategic manipulation of the circuit holds promise for overcoming the limitations associated with the energy devices of i-TE devices.44
 | ||
| Fig. 7 A comparison is presented between ionic and electronic thermoelectric materials within an ITESC. (a) Displays the experimental setup for ITESC measurement (left) and the corresponding equivalent circuit, highlighting the setup for experimental measurements (right). (b) Efficiency comparisons are drawn between different materials within the ITESC based on their ZT. (c) The impact of material choice on the ITESCs stored energy capacity by varying ZT values, reproduced with permission.44 Copyright 2017, Wiley-VCH. | ||
3.9 Hydrogels in ITESC for thermoelectric energy systems
Hydrogel can boost thermal capacity, make TE material more flexible, and stop leakage of electrolyte.52 In order to enhance thermoelectric conversion, it can help electrodes or act as an electrolyte in ITECS. In the hydrogel ITESC principle, an active substance with capacitive characteristics serves as electrode, and a TE hydrogel based on the Soret effect behaves as electrolyte. A potential difference is created at each end of an ionic electrolyte because of concentration difference due to thermal diffusion of carriers in the presence of ΔT. Ions build up at the electrode surface transition as a result of the incapacity of ion transfer and electron between electrolyte and electrode. At this point, when both electrodes are activated, they create an induced current, as a result EDLC forms between electrolyte and electrode, and the electrode stores the converted electrical energy.53 When applied to the ITESC electrode, i-TE hydrogel offers numerous benefits. The rich and uniform porous structure facilitates ions movement from electrolyte to reach electrode surface as well as to increase the electrode material's specific surface area and contact area when the polymer is dispersed around the electrolyte and pores. The electrode surface can retain more charges for high specific surface area capacitance during the formation EDLC. Liu et al. in 2017 reported smart responsive hydrogels, such as poly(N-isopropylacrylamide) (PNIPAM), are uniformly and chemically dispersed on material of electrode (Fig. 8a).54 Elashnikov et al. in 2021 demonstrated that these hydrogels can be used for external transport and charge storage control, allowing ITESC's electrical capacity to be adjusted on-demand (Fig. 8b). They can also control the disruption or formation of the electrode material's conductive network by changes in light or temperature. The stability of ITESC can be affected by repeated charging and discharging of hydrogel materials, which are highly dependent on their water content. This can be mitigated by encapsulating the hydrogel with the use of cast stretchable polymer or impregnated coatings, or by weakening the interactions between the hydrogel and water by adding double network structures, hydrophobic linkages, ionic complexes, etc.55 On adding hydrogels to ITESC electrolytes, efficient ion-selective networks are formed by entangled molecular chains. In addition, good processability of electrolytes in hydrogel offers additional flexibility in ITESC process design, such as area, thickness etc., which facilitates the easy fabrication of ITESCs are reported by Horike et al.56 in 2020. However, at a specific ΔT, the migration of anions and cations in pure hydrogels is hindered by the electrostatic interactions produced by entangled chains. These interactions close the hydrophobic transition and ion-conducting channels on the surface of hydrogel, lowering electrical conductivity and influencing thermoelectric conversion as show in Fig. 8c.57 Additional approaches include building crosslinked networks with cation selectivity or increasing the concentration gradient between the cations and anions. When the hydrogel electrolyte is a low critical solution temperature responsive polymer, such as PNIPAM, methyl cellulose (MC) and pluronic[poly(ethylene oxide)-block-poly(propylene oxide)-block-poly(ethylene oxide) (PEO–PPO–PEO)], reversible thermal switching self-protection of ITESC is also possible. Zhang and colleagues, for instance, created poly(N-isopropylacrylamide-co-N-methylolacrylamide) (PNIPAM/NMAM) hydrogel polyelectrolytes. As demonstrated in Fig. 8d, a mechanism of self-protection was achieved in hydrophobic segment of PNIPAM through thermally induced switching. Though this is a feasible approach, there has not been much research done on ion-conductive hydrogel electrodes particularly for ITESC when both electrode and electrolyte materials are made up of hydrogel.53,58 | ||
| Fig. 8 (a) Preparation for a conductive composite hydrogel (GOaCNTpega-OPF-MTAC), reproduced with permission.54 Copyright 2017, American Chemical Society. (b) Reversible on-demand adjustment of ITESC capacity through light changes. (c) Synthesis of a cellulose-based ionic conductive hydrogel using entangled chain networks. (d) The schematic representation of PNIAPM-co-NMAM polyelectrolytes highlighting their self-protective and thermal-switching capabilities in energy storage devices, reproduced with permission.53 Copyright 2023, Elsevier. (e) Ionic thermoelectric properties of TcB9-2.5% lignin-based hydrogel infiltered with KOH electrolyte, reproduced with permission.6 Copyright 2024, Springer. | ||
To address these drawbacks, one of studies reported the synthesis of lignin-based hydrogels, with improved thermoelectric properties. This study demonstrates the effect of adjusting electrolyte concentration within the hydrogels. Notably, TcB9-2.5% hydrogels infiltrated with 6 M KOH electrolyte exhibit a compelling combination of properties for ITESC applications. As shown in Fig. 8e, these hydrogels achieve a high ionic conductivity 226.5 mS cm−1, a remarkably low thermal conductivity 0.29 W m−1 K−1, and an impressive ionic thermopower of 13 mV K−1, resulting in a superior 3.75 ionic figure of merit (iZT).6 These exceptional i-TE characteristics are further enhanced by the biocompatibility, environmental friendliness, and biodegradability of lignin-based hydrogels. This unique combination opens doors for their utilization in a wide range of high-value energy applications. Promising areas of implementation include environmental temperature sensors, healthcare-oriented biomedical sensors, and wearable electronics engineered for efficient and sustainable energy harvesting. This development not only represents a significant advancement in the field of ionic thermoelectricity but also holds immense potential for both promoting environmental sustainability and fostering technological progress.
4. Thermogalvanic cells
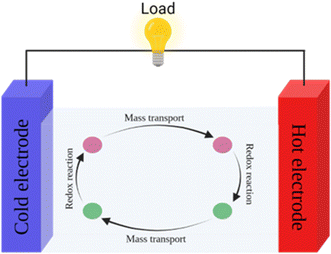
Thermogalvanic cells (TGCs) are a type of ionic thermoelectric materials consisting of electrodes surrounded by an electrolyte where the charge carriers are the ions contained in the electrolytes of the cells. TGCs exploit electrochemical processes within liquid, solid, or quasi-solid electrolytes to convert temperature differences into electrical potential.59 These systems offer similar advantages to other ionic thermoelectric materials when compared to traditional thermoelectric materials such as the higher thermopower and the compatibility with various temperature ranges, which positions them as promising avenues for energy harvesting.60 This section delves into the fundamental principles and recent advancements of thermogalvanic systems within the broader context of ionic thermoelectric materials. We will explore the underlying electrochemical mechanisms, the role of electrolytes, and key factors influencing the performance of these systems. Understanding the intricacies of thermogalvanic cells is essential for harnessing their full potential and realizing their role in the transition towards more efficient and sustainable energy conversion technologies. At the heart of thermogalvanic systems lies the principle of electrochemical conversion of thermal energy. As previously mentioned, these systems typically consist of two identical electrodes and an electrolyte; when exposed to a temperature gradient across the cell, electrochemical reactions occur at the electrode–electrolyte interfaces.61 The temperature difference induces unequal chemical equilibriums on either electrode, generating an electric potential difference which can be harnessed to produce electrical power through the flow of electrons along the outer circuit. A schematic representation of a TGCs working mechanism is illustrated in Fig. 9. Importantly, the key to efficient operation in thermogalvanic systems is the appropriate selection of electrode materials and electrolytes that enable optimal ion concentration, electrolyte diffusion, charge transfer resistance at the electrode/electrolyte interface, and electrical conductivity of the electrodes.62,63As has been described, TGCs operate in a similar manner than other ionic thermoelectric materials, and as such, have a ionic thermopower or ionic Seebeck coefficient, or thermopower, equivalent of their own which is defined in eqn (3) as:64
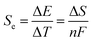 | (3) |
Another parameter of interest for TGCs is the Carnot-relative efficiency, which denotes the theoretical maximum of energy conversion efficiency that the TGC can achieve, shown in eqn (4):65,66
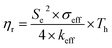 | (4) |
Solution based TGCs represent a category of thermogalvanic systems where the electrolyte matrix is in a liquid state, typically water-based and predominantly centered around the (Fe(CN)63−/Fe(CN)64−) redox couple.71 These cells leverage the dynamic properties of aqueous electrolytes to facilitate ion transport and electrochemical reactions, making them a versatile and practical choice for various applications. They present distinct advantages, such as high ionic conductivity, cost-effectiveness, and utilization of common elements. Their main disadvantage is their limited operational temperature range.64 Recently, research on this type of TGCs has focused on improving efficiency by introducing alternative electrode materials or altering the electrolyte matrix.41,69 This type of cell is ideal for scenarios where the use of other types of TGCs would be obstructed by cost or constraints related to their materials, such as for harnessing low-temperature heat sources. Aqueous state thermogalvanic cells, leveraging the advantages of water-based electrolytes, present a cheap and versatile solution for various energy conversion applications. Their high ionic conductivity, cost-effectiveness, and ease of handling make them well-suited for both industrial and smaller-scale scenarios with low-temperature heat sources.72 Solid-state thermogalvanic cells represent another subset of thermogalvanic systems that differ from their liquid-state counterparts by employing solid-state materials as their electrolyte matrix, these materials can be conductive ceramics, metals, polymers, or other solid compounds with high ionic conductivity, allowing for the transport of ions within the cell. Historically, solid-state thermogalvanic cells based on beta-alumina solid electrolytes garnered significant attention, particularly in aerospace applications.73 Despite their inherent advantages, such as heightened stability, enhanced design flexibility, and reduced maintenance demands, these cells have been hindered by their requirement for elevated operating temperatures, rendering them impractical for low-grade heat harvesting applications.74 However, recent research endeavors have aimed to address this limitation by exploring the development of solid-state thermogalvanic cells suitable for low-grade heat harvesting purposes.70 Similar to their liquid counterparts, solid-state thermogalvanic cells rely on the establishment of thermal gradients across the cell. When one side of the cell is exposed to a higher temperature than the other, the solid electrolyte allows charge transport to occur through ion migration, leading to an electric potential difference between the electrodes.74 Solid-state thermogalvanic cells present a viable option, particularly in environments where the use of liquid electrolytes is unfeasible, such as high-temperature conditions. Despite inherent limitations, they remain a significant avenue in the field of thermogalvanic systems, offering robust, efficient, and versatile solutions for diverse energy conversion applications. Quasi-solid thermogalvanic cells are a distinct and relatively new class of thermogalvanic systems that combines the characteristics of solid-state and liquid-state thermogalvanic cells. These cells use a hydrogel or gel-like electrolyte, often in combination with liquid components or ions, to enable efficient ion transport and electrochemical reactions, and have seen the most innovation and research in recent times in the field of TGCs.75,76 This hybrid design brings together the benefits of both solid and liquid systems, providing advantages in terms of performance, design flexibility, stability, and ease of fabrication. In these types of systems, the solid-state component of the electrolyte often acts as a scaffold for ion transport, while the liquid or gel-like component carries mobile ions and facilitates electrochemical reactions.77 The combination of solid and liquid/gel components in the electrolyte allows for efficient ion transport, which can improve the overall performance of the cell.78 Additionally, they offer a degree of flexibility in design, allowing for customization to match the specific requirements of different applications.39 Their quasi-solid state provides enhanced stability and resistance to thermal and mechanical stresses, while maintaining high ionic conductivity. This combination leads to greater overall stability in various operating conditions and high thermoelectric performance.79 The following Table 1 shows recently reported TGCs, showcasing that an abundant majority of reported TGCs in recent times are either liquid or quasi-solid.
| Electrolyte state | Matrix | Redox couple | Ionic thermopower (mV K−1) | Carnot-relative efficiency | P max (W m−2) | Reference |
|---|---|---|---|---|---|---|
| Liquid | Water/CsCl | Fe(CN)63−/Fe(CN)64− | −1.50 | — | 0.15 | 72 |
| Solid | Nafion®117 | H+/H2 | 0.53 | 0.04% | 0.2 | 70 |
| Quasi-solid | Sand/water | Cu/Cu2+ | 8.40 | 4% | 0.06 | 75 |
| Quasi-solid | Gelatin/KCl | Fe(CN)63−/Fe(CN)64− | 17.00 | — | 0.53 | 39 |
| Liquid | Water/CoO | Fe(CN)63−/Fe(CN)64− | — | 14.80% | 24.50 | 69 |
| Quasi-solid | PVA/GdmCl | Fe(CN)63−/Fe(CN)64− | 6.50 | 2.66% | 1.72 | 79 |
| Liquid | Water/GdmCl/urea | Fe(CN)63−/Fe(CN)64− | 4.20 | 0.79% | — | 41 |
| Quasi-solid | PAM/CMC | Fe(CN)63−/Fe(CN)64− | 1.26 | — | 0.02 | 77 |
| Quasi-solid | MC/KCl | I−/I3− | 9.62 | — | — | 78 |
| Quasi-solid | PVA/PEDOT:PSS | SO42−/SO32− | 1.63 | — | — | 76 |
5. Thermally regenerative electrochemical cycle
Ionic thermoelectric cycling mode or thermally regenerative electrochemical cycle (TREC) and thermogalvanic technologies are both employed for harvesting low-grade heat, but they operate on distinct principles. Thermogalvanic systems generate electrical energy directly from a temperature gradient across an electrolyte, utilizing the Seebeck effect to create a voltage difference between two electrodes immersed in the electrolyte. However, these systems face significant limitations due to the low ion conductivity of existing electrolytes, which restricts their efficiency to less than 0.5%.80,81 In contrast, TREC utilizes a cyclical process to convert thermal energy into electrical energy by exploiting the temperature-dependent voltage of electrodes in a thermodynamic cycle. The TREC approach also addresses some of the limitations of thermogalvanic methods by incorporating mechanisms to manage internal resistance and heat recuperation, making it a more versatile and efficient solution for low-grade heat harvesting.825.1 Working mechanism
This cycle involves four distinct steps: cooling, charging, heating, and discharging, where the voltage of the cell changes with temperature fluctuations (Fig. 10). In a TREC system, the process begins with a battery-like cell being heated from a low temperature (TL) to a high temperature (TH) in an open-circuit state, during which its open-circuit voltage (OCV) varies with temperature changes. The cell is then charged at TH, absorbing heat and increasing its entropy through electrochemical reactions. After charging, the cell cools back to TL, causing the OCV to rise. During discharge at TL, the cell releases heat into the environment, which lowers the voltage. The efficiency is determined by the voltage difference between charging and discharging phases, with key factors including the electrodes' temperature coefficients, their charge capacities, and the system heat capacity.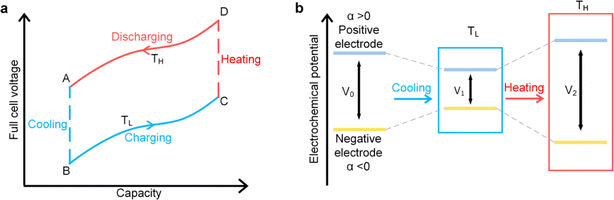 | ||
| Fig. 10 (a) Working mechanism of TREC system for thermal energy harvesting, (b) electrochemical potential change of the electrodes. Reproduced with permission.81 Copyright 2019, ACS Publications. | ||
One of the first research on TREC systems has revealed promising advancements in low-grade heat energy harvesting. Utilizing solid CuHCF and Cu electrodes, the study achieved a cycle efficiency of 3.7% between 10 and 60 °C without heat recuperation and up to 5.7% with 50% heat recuperation.83 These efficiencies are notable improvements over previous thermogalvanic cells, which typically had efficiencies below 0.5% at similar temperatures. Another study by Yang et al. have developed innovative TREC that efficiently converts low-grade heat into electricity without external electrical charging, enhancing practicality and cost-effectiveness.80 Utilizing a Fe(CN)63−/4− redox pair and a Prussian blue electrode, the system operates between 20 and 60 °C, achieving up to 2% heat-to-electricity conversion efficiency. This cycle discharges at both high and low temperatures with polarity reversal, making it ideal for remote and off-grid settings. Further research is needed to optimize efficiency, stability, and material compatibility. This technology holds promise for extracting low-grade heat from the environment, potentially opening doors for various applications.
In another study, a novel TREC for low-grade heat harvesting was developed using spinel lithium manganese oxide (LMO) and copper hexacyanoferrate (CuHCF) electrodes.81 This system operates in a hybrid aqueous electrolyte of lithium and potassium ions, offering a cost-effective and simplified approach compared to traditional methods that require complex ion-exchange membranes. LMO, known for its high positive thermopower of approximately 0.48 mV K−1, was successfully paired with CuHCF, which has a negative thermopower of about −0.44 mV K−1. The combination of these materials results in a full cell with an overall thermopower of 1.16 mV K−1. This system demonstrates a heat-to-electricity conversion efficiency of 1.8% when heat recuperation is not considered, and up to 2.6% with 50% heat recuperation efficiency. The stable electrochemical performance of LMO and CuHCF in the hybrid electrolyte and the high coulombic efficiency observed suggest significant potential for positive-thermopower materials in enhancing low-grade heat harvesting.
In a latest recent research, TREC systems incorporating a nickel hexacyanoferrate (NiHCF) cathode and a zinc anode achieved a notable thermopower of −1.575 mV K−1, along with a heat-to-electricity efficiency of 2.41% at a 30 °C temperature difference, equivalent to 25.15% of Carnot efficiency.82 This performance surpasses that of existing TREC systems. A key innovation in this work was the introduction of mixed membranes with mixed pH electrolytes, which boosted thermopower to a record-high value of −2.270 mV K−1. These advancements in TREC not only showcase significant improvements in converting low-grade heat to electricity but also highlight the potential for further refinement and application in diverse settings, potentially transforming energy harvesting and sustainability efforts.
6. Combined ionic thermoelectric devices
Both ionic thermoelectric systems (thermodiffusion-based and thermogalvanic-based) present promising characteristics, yet they have distinct limitations. Thermodiffusion-based systems have excellent mechanical properties and exhibit impressive thermopower, often in the range of several mV K−1. However, these systems rely on ion transport and exhibit characteristics analogous to capacitance behaviour. This results in a non-continuous operation mode that can be a disadvantage in applications requiring a constant and consistent energy supply, leading to potential interruptions in power generation or temperature regulation.84 Additionally, these devices experience rapid instantaneous power decay during the discharging stage, making long-term continuous operation challenging. This limitation leads to relatively low average power density and energy density, thereby severely limiting their practical applications.43On the other hand, thermogalvanic systems display significant ionic thermopower, surpassing those of traditional electronic thermoelectric materials. Additionally, thermogalvanic cells generate continuous electricity by utilizing temperature gradients, relying on spontaneous electrochemical redox reactions at electrode interfaces. However, conventional thermogalvanic cells due to the liquid nature of the electrolytes, pose encapsulation issues, often leading to leakage problems.85 Such vulnerabilities hinder their scalability and reliability, limiting their widespread adoption in practical devices. Developing materials that possess both high thermopowers for efficient energy conversion and mechanical resilience to withstand diverse environmental conditions is a significant hurdle. Additionally, ensuring long-term stability and compatibility with various operating environments is another pressing concern. The quest to overcome these limitations has driven researchers toward exploring the combined potential of thermodiffusion and thermogalvanic effects.48 By employing the combined strengths of these mechanisms, researchers aim to develop materials that not only exhibit superior thermopower but also boast enhanced mechanical properties, paving the way for versatile, durable, and efficient ionic thermoelectric materials.
The first such study that investigated the combined potential of both ionic thermoelectric mechanisms was published by Han et al. in 2020.31 The ionic thermoelectric material, derived from a gelatin matrix modified with ion providers (KCl, NaCl, and KNO3) for thermodiffusion and [Fe(CN)64−/Fe(CN)63−] redox couple for thermogalvanic effect, exhibited an outstanding ionic thermopower of 17 mV K−1. This achievement was attributed to the combined interplay between gelatin-KCl (6.7 mV K−1) and gelatin–FeCN4−/3− (4.8 mV K−1). The ionic concentration differences between K+ and Cl− (thermodiffusive ions) and K+ and FeCN4−/3− (redox couple) were also increased due to the negatively charged surface of the gelatin matrix. Consequently, the concentration difference between cations and anions accounted for 71.9% of the total thermopower. The maximum output power of 0.66 mW m−2 K−2 and harvested energy density of 12.8 J m−2 were obtained in the ionic thermoelectric gel gelatin–KCl–FeCN4−/3−. When wearing a device comprising 25 units (each measuring 5 × 5 × 1.8 mm) connected in series to harness human body heat, a voltage of 2.2 V and a maximum output power of 5 μW were attained. This foundational study highlighted the promising approach of exploiting the combined effects of thermogalvanic and thermodiffusion mechanisms to significantly enhance the ionic thermopower of quasi-solid electrolytes, paving the way for efficient and leakproof ionic thermoelectric devices.
6.1 Optimisation parameters
Over the last three years, there has been significant progress in the study of combined ionic thermoelectric materials. Researchers have been working to improve three crucial aspects: ionic thermopower (mV K−1), which relates to the material's ability to convert heat into electricity; output power density (W m−2), indicating how much power can be generated per unit area; and mechanical properties, ensuring the durability and stability of devices.86 To achieve these goals, scientists have explored various combinations of polymer matrices, thermodiffusive electrolytes, redox pairs, and electrode materials. The main aim of these studies is to find the most effective combination that enhances the ionic thermoelectric efficiency and durability of ionic thermoelectric materials. The findings from these studies, detailed in Table 2, provide valuable insights into the ongoing efforts to harness the potential of these materials.| Polymer | Electrolyte | Redox pair | Seebeck coefficient (mV K−1) | Ionic/electrical conductivity (mS cm−1) | Thermal conductivity (W m−1 K−1) | Specific power density (mW m−2 K−2) | Energy density (J m−2) | Ref. |
|---|---|---|---|---|---|---|---|---|
| Gelatin/glutaraldehyde | KCl | FeCN4−/3− | 24.7 | — | — | 9.6 | 198 | 87 |
| Gelatin | KCl | FeCN4−/3− | 17 | — | — | 8.9 | 80 | 39 |
| Acrylic acid-acrylamide/carboxymethyl cellulose | H2SO4 | Polyaniline | 40.60 | 30.2 | 0.4551 | 11.31 | 570 | 38 |
| Polyacrylamide/carboxymethyl cellulose | Li2SO4 | FeCN4−/3− | 11.58 | 18.4 | 0.47 | 32 mW m−2 | — | 2 |
| Polyvinyl alcohol/gelatin | NaCl | Fe2+/Fe3+ | −1.63 | 7 | 0.6 | 1.2 mW m−2 | — | 88 |
| Gelatin | KCl | FeCN4−/3− | 17 | 5 mS m−1 | 0.15 | 0.66 | 12.8 | 31 |
| Bacterial cellulose | LiBr | FeCN4−/3− | 1.21 | — | — | ≈0.03 | — | 85 |
| Polyvinyl alcohol | GdmCl | FeCN4−/3− | 6.5 | ≈15 | 0.473 | 1.96 | — | 79 |
| Polyvinyl alcohol | NaCl | Sn2+/Sn4+ | −1.62 | ≈9 | 2.08 | 2.8 mW m−2 | 160 mJ m−2 | 89 |
| Polyvinyl alcohol | NaCl | SO4/32− | 1.63 | 29.2 | 0.7 | 72 nW | — | 76 |
| Methylcellulose | KCl | I−/I3− | 9.62/−8.18 | 6 | — | 0.36/0.12 | — | 78 |
| Polyacrylamide/sodium alginate | GdmCl | FeCN4−/3− | 4.4 | 105 | ≈0.55 | 1.78 | — | 90 |
6.2 Selection of polymer matrices
The selection of a polymer matrix is one of the key parameters for enhancing the performance of ionic thermoelectric devices based on their surface functionalities. Polymers with suitable surface properties enhance ionic diffusion, a key factor in improving the material's thermoelectric performance.16 Additionally, selected polymers should exhibit excellent mechanical properties, ensuring the resulting ionic thermoelectric device stability and durability. The selection criteria for such polymers are rooted in their chemical composition. For instance, polyvinyl alcohol (PVA) is valued for its excellent ability to create a stable matrix and superior mechanical properties.91 Its chemical structure, featuring hydroxyl groups, provides numerous functional sites, facilitates strong hydrogen bonding, which enhances the mechanical integrity and flexibility of the resulting materials. This is crucial for ionic thermoelectric devices as it allows the matrix to accommodate ionic movement without structural degradation. Moreover, its hydrophilic nature supports the incorporation and uniform distribution of ionic species, enhancing ionic conductivity and thermoelectric performance. Li and team successfully prepared an organohydrogel electrolyte (OHE) using a straightforward freezing–thawing approach, incorporating PVA polymer, Sn2+/Sn4+ redox couple, and NaCl as a thermodiffusive ions electrolyte.89 This OHE exhibited exceptional flexibility and mechanical strength, attributed to the properties of the PVA polymer, enabling it to withstand diverse deformations (Fig. 11a–c). Remarkably, the OHE displayed anti-freezing and anti-drying characteristics, making it operatable effectively across a broad temperature range (−20 to 60 °C). Moreover, the OHE demonstrated outstanding ionic thermoelectric properties, including a remarkable ionic thermopower of −1.62 mV K−1, a high figure of merit (3.75), and an impressive maximum power density of 2.8 mW m−2 (Fig. 11d and e). These findings highlight the potential of PVA-based OHE's for practical applications, emphasizing its robust performance and adaptability in demanding environments.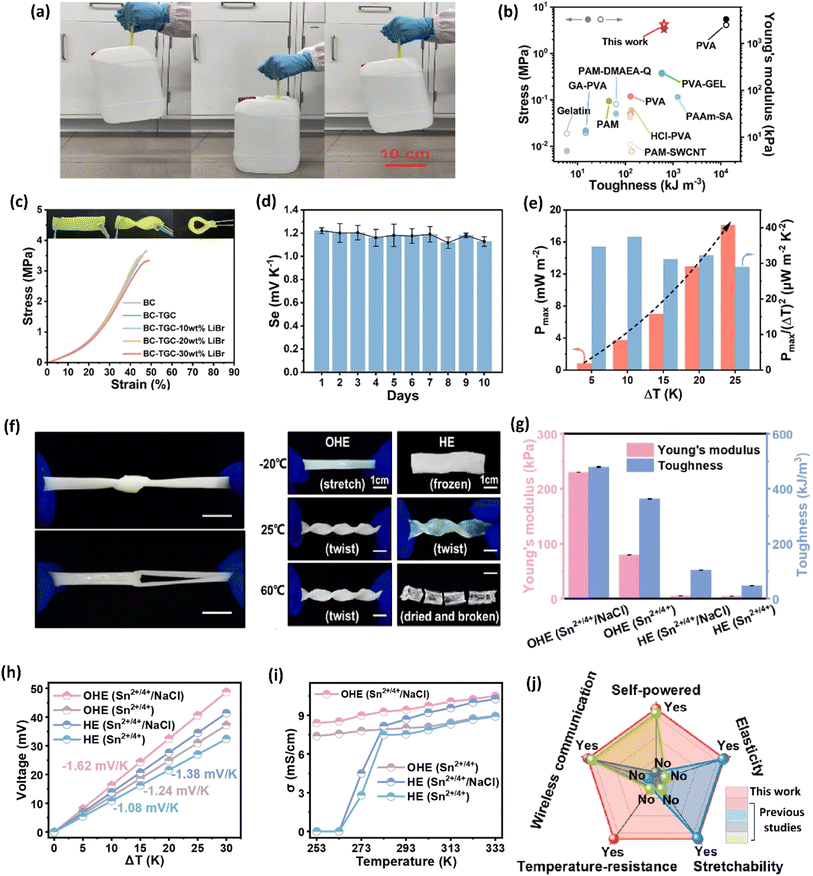 | ||
| Fig. 11 Bacterial cellulose–LiBr–FeCN4−/3− hydrogel: mechanical properties (a) hydrogel holding 5 kg water bottle, (b) toughness and Young's modulus, (c) stress–strain curves; ionic thermoelectric properties (d) ionic thermopower variations over the period of 10 days, (e) output power density vs. temperature difference, reproduced with permission.85 Copyright 2023, Elsevier; organohydrogel electrolyte: (f) mechanical properties of hydrogel in tensile deformation including knotting and crossing stretching, (g) photos of the OHE after 6 h at different temperatures, (h) thermovoltage response vs. temperature difference, (i) conductivity as a function of temperature, and (j) comparison of this study with previous studies, reproduced with permission.89 Copyright 2023, Elsevier. | ||
Gelatin, derived from collagen, possesses unique biopolymer characteristics, making it biocompatible and environmentally friendly.92 It possesses a triple-helix structure that provides good mechanical strength and flexibility. The ability of gelatin to form hydrogels with high water content improves ionic mobility, which is essential for efficient ionic thermoelectric conduction. The amphoteric nature of gelatin, containing both carboxyl and amino groups, allows for effective ionic exchange and interaction with various ionic species, thus enhancing the thermoelectric efficiency of the device.93 A quasi-solid-state ionic thermoelectric cell, fabricated by incorporating glutaraldehyde into a gelatin–KCl–FeCN4−/3− matrix, exhibited significantly enhanced thermoelectric properties.87 The resulting robust, porous structure increased the maximum temperature difference from 9 °C to 23 °C and boosted thermopower (24.7 mV K−1) due to expanded entropy between redox couples. This led to a record-high power density of 9.6 mW m−2 K−2 and a 2 hours energy density of 198 J m−2. Demonstrating excellent cycling stability and generating a high voltage of 3.6 V and 115 μW output in a wearable device, this cell showcases promising potential for practical applications.
Cellulose, composed of glucose units, offers high mechanical strength and chemical stability.94 The extensive hydrogen-bonding network within cellulose provides significant tensile strength and rigidity, which helps in maintaining the structural integrity of ionic thermoelectric devices under mechanical stress. Additionally, the hydrophilic nature of cellulose facilitates the absorption and transport of ionic species, which is critical for maintaining high ionic conductivity. The abundance of hydroxyl groups in cellulose also allows for functionalization, which can be tailored to improve specific ionic interactions and enhance thermoelectric properties.95 In a recent study conducted by Yin et al. in 2023, it was demonstrated that bacterial cellulose also has the potential to be utilized in creating quasi-solid ionic thermogalvanic cells.85 These cells exhibited impressive mechanical characteristics and thermoelectric properties, such as toughness, elasticity, flexibility, ionic conductivity, ionic thermopower, comparable to those found in PVA-based devices (Fig. 11f–j). They employed FeCN4−/3− redox couple along with LiBr hygroscopic salt to give superior anti-freezing and anti-drying properties to prepare thermogalvanic cells. The prepared cells exhibit an excellent ionic thermopower of 1.62 mV K−1, which remains at 1.06 mV K−1 after three months of air exposure, indicating their high stability (Fig. 11h).
Polyacrylamide (PAAM) is recognized for its ability to form hydrogels with high water content, significantly enhancing ionic mobility and overall ionic conductivity. The hydrophilic nature of PAAM allows it to absorb large amounts of water, creating a conducive environment for the movement of ions, which is critical for improving the thermoelectric performance of devices. In a notable study, Chen et al. successfully developed a water-resistant ionic thermoelectric gel by integrating the hydrophobic structure of PMMA with a hydrophobic ionic liquid (BMIM:PF6).96 This innovative combination resulted in an i-TE gel that achieved an impressive thermopower of 3.1 mV K−1. The incorporation of PMMA provided the necessary mechanical strength and stability, while the hydrophobic ionic liquid ensured efficient ionic transport and enhanced thermoelectric properties.
Agarose, a seaweed-derived linear polysaccharide, forms thermally stable gels, ideal for applications demanding consistent performance across temperature fluctuations. Its hydrophilic nature readily accommodates water molecules within its structure. Simple agarose based hydrogels proves not suitable for ionic thermoelectric devices.97 Recent research, however, has demonstrated the potential of agarose-based i-TE gels. By incorporating sodium dodecyl benzene sulfonate (DBS), a remarkable p-type thermopower of 41.8 mV K−1 was achieved.98 This significant enhancement stems from the formation of a unique porous structure through DBS micellization. The hydrophilic sulfonic group binds to the agarose gel, while the hydrophobic alkyl chain orients inward, immobilizing DBS-ions relative to sodium ions. This structural decoupling of thermodiffusion markedly improves i-TE performance.
Polyurethane (PU) can also be a useful polymer for ionic thermoelectric applications due to its excellent mechanical properties and structural diversity. A latest study developed a PU ionogel with self-healing, high thermoelectric performance, transparency, and stretchability, making it ideal for wearable thermoelectric generators.99 The ionogels, synthesized using PU prepolymer, a reversible borate bond crosslinker, and an ionic liquid (EMIM:DCA), showed high thermovoltage (up to 25.6 mV K−1) and significant stretchability (up to 635% strain at break). Self-healing restored 95% of tensile strength and 99% strain at break within 30 minutes. The ITESC fabricated a maximum energy output of 2.34 μW m−2 with an 8 kΩ load at a 0.4 K temperature difference, highlighting their potential for durable, efficient, and flexible wearable energy solutions.
Poly(vinylidene fluoride) (PVDF) is another non-aqueous polymer known for its high chemical resistance, thermal stability, and mechanical strength, making it suitable for ionic thermoelectric applications. A recent study demonstrates a significant improvement in the thermopower of PVDF-HFP ionogels by doping with sodium dicyanamide (Na:DCA).100 The ionogel doped with 0.5% in mol of Na+ relative to EMIM+ achieved a thermopower of 43.8 mV K−1, ionic conductivity of 19.4 mS cm−1, and thermal conductivity of 0.183 W m−1 K−1. These enhanced ionogels are promising for use in iTE capacitors for thermoelectric conversion.
Sodium alginate, extracted from brown algae, boasts excellent ion exchange capabilities due to its polysaccharide nature.101 The presence of carboxyl groups in its molecular structure enables strong ionic interactions and exchange, which are vital for ionic thermoelectric performance. This characteristic, combined with its good biocompatibility and mechanical flexibility, makes sodium alginate an ideal candidate for enhancing the ionic conductivity and overall thermoelectric efficiency of devices. These inherent chemical attributes make these polymers highly suitable for synthesizing quasi-solid ionic thermoelectric devices, meeting the criteria of both enhanced ionic diffusion and mechanical stability, thus ensuring the device's robustness and effectiveness in real-world applications.
These promising advances suggest that the future of this field will involve exploration of the possibility of combining two or more polymers in a single matrix. By integrating the unique properties of each polymer, scientists might create innovative quasi-solid matrices with enhanced flexibility, durability, superior mechanical strength, and remarkable ionic thermoelectric properties. This novel approach may open new horizons in the development of combined ionic thermoelectric devices for efficient energy harvesting applications.
6.3 Selection of thermodiffusive electrolytes
Another vital aspect for optimising the performance of combined ionic thermoelectric devices involves the selection of suitable inorganic/organic salts as thermodiffusive electrolytes. Salts like NaCl, KCl, LiBr, GdmCl, Li2SO4, and H2SO4 have been employed in recent years owing to their easy dissolution in solvents and high conductivity. Easy dissolution is crucial for the uniform mixing of salts within the polymer matrix, ensuring a consistent distribution of the electrolyte throughout the quasi-solid gels.102 The high conductivity of these salts enables efficient ion transport within the material, a fundamental requirement for enhancing ionic thermoelectric performance.8 The careful selection of these inorganic salts is therefore a cornerstone for advanced combined ionic thermoelectric devices to achieve exceptional levels of efficiency and practicality.Liu et al. 2023 fabricated a quasi-solid stretchable thermogalvanic thermocell using PVA as a polymer matrix, FeCN4−/3− as redox couple, and guanidinium chloride (GdmCl) as electrolyte.79 The use of PVA polymer conveyed excellent mechanical properties to the cells in terms of stretchability (1300%) and toughness (163.4 MJ m−3), as shown in Fig. 12c. The inclusion of GdmCl increased the entropy difference in the FeCN4−/3− redox couple due to Gdm+-induced crystallization of FeCN4− ions, resulting in superior thermogalvanic performance (Fig. 12a). The resulting system had a large thermopower of 6.5 mV K−1 and an excellent high specific output power density of 1969 μW m−2 K−2 (Fig. 12b). Another study published by Zhou et al. 2023 prepared a carboxymethyl cellulose-based quasi-solid gel composed of FeCN4−/3− redox couple and Li2SO4 salt as thermodiffusive electrolyte.2 Li+ ions have a smaller radius and exhibit a faster migration rate in the electrolyte resulting in better ionic diffusion, contributing to the overall performance of the device (Fig. 12d and e). By combining the principles of thermodiffusion and the thermogalvanic effect, the prepared devices demonstrated a superior ionic thermopower of 11.58 mV K−1 (Fig. 12f). Moreover, these devices exhibited a high ionic conductivity of 18.4 mS cm−1, indicating the rapid migration of Li+ ions through the electrolyte, leading to enhanced ionic diffusion. This unique combination resulted in a noteworthy thermoelectric figure of merit of 0.11 and a substantial power factor of 198.2 μW m−1 K−2 at room temperature, underscoring their exceptional overall performance.
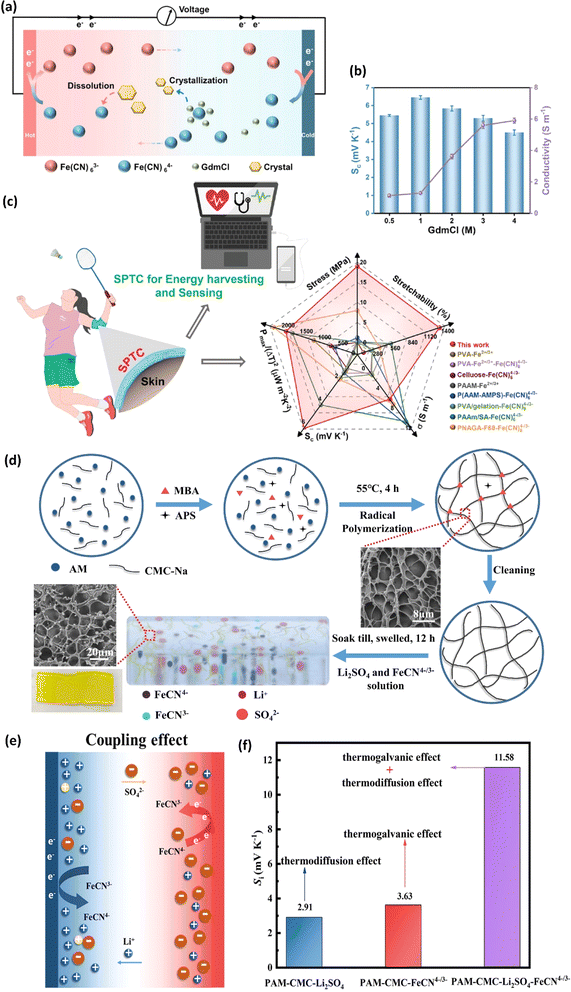 | ||
| Fig. 12 PVA–GdmCl–FeCN4−/3− based thermogalvanic hydrogel: (a) schematic illustration of the Gdm+ contribution to the thermogalvanic effect, (b) Seebeck and conductivity as function of electrolyte concentration, (c) schematic diagram of employing the device to power up the medical devices and the comprehensive comparison with previous quasi-solid stretchable thermogalvanic thermocells, reproduced with permission.79 Copyright 2023, Wiley-VCH; cellulose–Li2SO4–FeCN4−/3− based thermogalvanic hydrogel: schematic representation of (d) preparation process of hydrogel and its microstructure, (e) mechanism of coupling effect, and (f) ionic Seebeck before and after coupling, reproduced with permission.2 Copyright 2023, Elsevier. | ||
Future research directions in this domain are likely to focus on refining electrolyte selection to further enhance their efficiency and contribute towards their commercialisation. Investigating novel inorganic salts and their combinations could provide insights into improving ionic diffusion and thermoelectric performance. Moreover, the exploration of organic–inorganic hybrid electrolytes might offer a new avenue, potentially combining the advantages of both materials. Additionally, optimising the interplay between electrolyte composition, polymer matrix, and redox couples could lead to the development of advanced quasi-solid gels with superior homogeneity and stability, contributing to prolonged device lifespan. Ultimately, future research activities should explore innovative electrolytes, pushing the boundaries of combined ionic thermoelectric devices and opening avenues for sustainable energy harvesting technologies.
6.4 Selection of redox pairs
In the past few years, the exploration of a variety of redox couples and their interplay with the rest of the components has also been a focal point of researchers. Redox reactions, involving the transfer of electrons between matrix and electrodes, are associated with an increase in the entropy of the system that can result in efficient electron transfer.103 Therefore, researchers have examined diverse redox couples (FeCN4−/3−, Fe2+/Fe3+, Sn2+/Sn4+, SO4/32−, I−/I3−) to influence this increase in entropy. By understanding and manipulating this entropy change, scientists aim to identify optimal redox pairs that can efficiently facilitate electron transfer, thereby enhancing ionic thermoelectric efficiency.In a study by Han and colleagues in 2022, thermogalvanic cells were created using a substance called methylcellulose, a redox pair I−/I3−, and KCl as the electrolyte.78 Methylcellulose, which responds to temperature changes, resulted in a polarization switching from n-type to p-type above a transition temperature as shown in Fig. 13a and b. This change occurred due to a strong hydrophobic interaction between I3− ions and methylcellulose. As a result, the cells exhibited remarkably high thermoelectric voltages of 9.62 mV K−1 for p-type and −8.18 mV K−1 for n-type (Fig. 13c). These high thermopower values were attributed to the gelation effect of I3− ions with methylcellulose at a hot electrode resulting in an increased entropy change and differences in ion concentrations in the redox pair (Fig. 13d and e). The optimized p-type thermogalvanic cell achieved a normalized maximum power density of 0.36 mW m−2 K−2 (Fig. 13f). A recent study by Tian et al. 2023 reported a novel non-toxic redox couple (SO4/32−) in a PVA matrix along with NaCl electrolyte.76 The fabricated device had excellent mechanical properties including stretchability and flexibility because of PVA (Fig. 13g). Moreover, the novel redox pair at a concentration of 0.1 M, resulted in an excellent ionic thermopower value of 1.63 mV K−1 (Fig. 13h and i). The addition of thermodiffusive electrolytes led to an improved ionic conductivity of 29.2 mS cm−1 which overall enhanced the ionic thermoelectric performance of the devices.
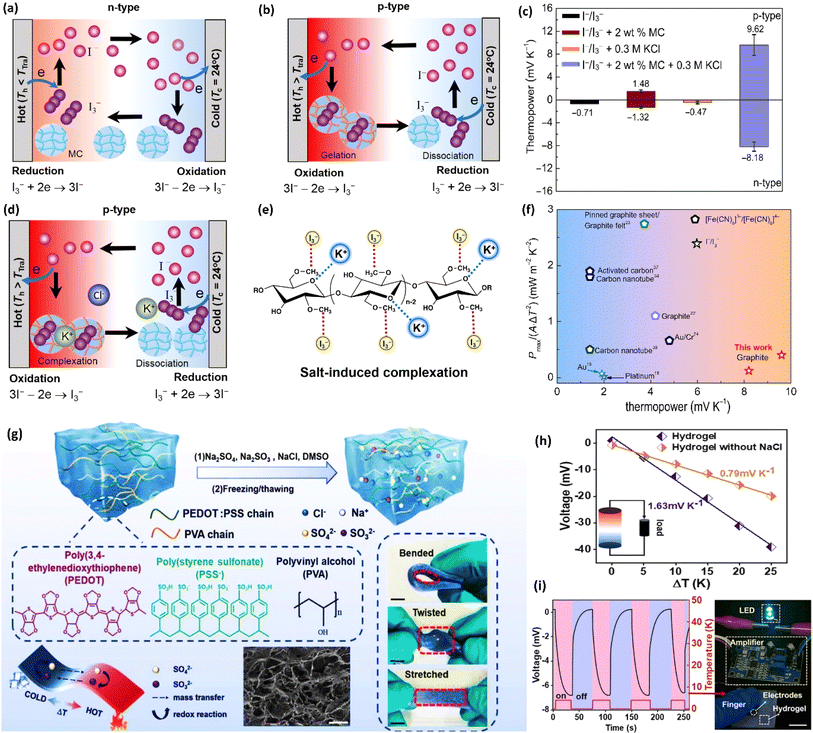 | ||
| Fig. 13 Methylcellulose–KCl–I−/I3− based thermogalvanic gel: schematics of the polarization switching from (a) n-type to (b) p-type, (c) comparison of the thermopowers, schematics of (d) a p-type TGC with the ternary electrolyte and (e) salt-induced complexation. K+ and I3− ions, (f) comparison of this study with previous studies, reproduced with permission.78 Copyright 2022, Science; PVA-NaCl-SO4/32− based hydrogel (g) schematic illustration of design, chemical structure, morphology, and mechanical properties, (h) thermal voltage response at different temperature differences, and (i) output voltage of the hydrogel under 4-repeated heating–cooling cycles for powering LED, reproduced with permission.76 Copyright 2023, Elsevier. | ||
Future research directions emphasize the strategic selection of redox couples. Exploring a broader spectrum of redox pairs beyond traditional ones holds the key to unlocking innovative avenues. Researchers should comprehensively investigate the synthesis and evaluation of novel redox couples, considering factors like electrochemical stability, entropy change, and efficiency in facilitating electron transfer. Furthermore, it would be noteworthy to explore organic-based redox couples and other environmentally benign materials, aiming to reduce the ecological footprint of ionic thermoelectric devices.
6.5 Selection of electrode materials
A recent advancement in enhancing the power and energy density of combined ionic thermoelectric devices involves the engineering of the device electrodes. In a study conducted by Li and colleagues in 2022, advancements were made in enhancing the power and energy density of combined ionic thermoelectric devices by focusing on electrode engineering.39 They employed a quasi-solid ionic thermoelectric device based on gelatin/KCl/FeCN4−/3− from their previous study and altered the electrodes.31 They developed three-dimensional hierarchical copper electrodes coated with gold (3D Au/Cu) using a specialized oxidization–etching–reduction technique (Fig. 14a). These electrodes exhibited a unique micro flower-like structure, comprising numerous porous and zigzagging petals (Fig. 14b and c). This structure significantly increased the electroactive surface area of the electrodes, providing more sites for thermogalvanic reactions and reducing the resistance at the interface for charge transfer. The modified device demonstrated a comparable ionic thermopower of 17 mV K−1 (Fig. 14d). Remarkably, it achieved an exceptional instantaneous output power density of 8.9 mW m−2 K−2 and an exceptionally high output energy density of 80 J m−2 under a temperature difference of 9 K (Fig. 14e). Over a week-long continuous operation, the device maintained an average energy density of 59.4 J per m2 per day. These findings represent a significant step forward in the development of efficient and wearable thermoelectric devices.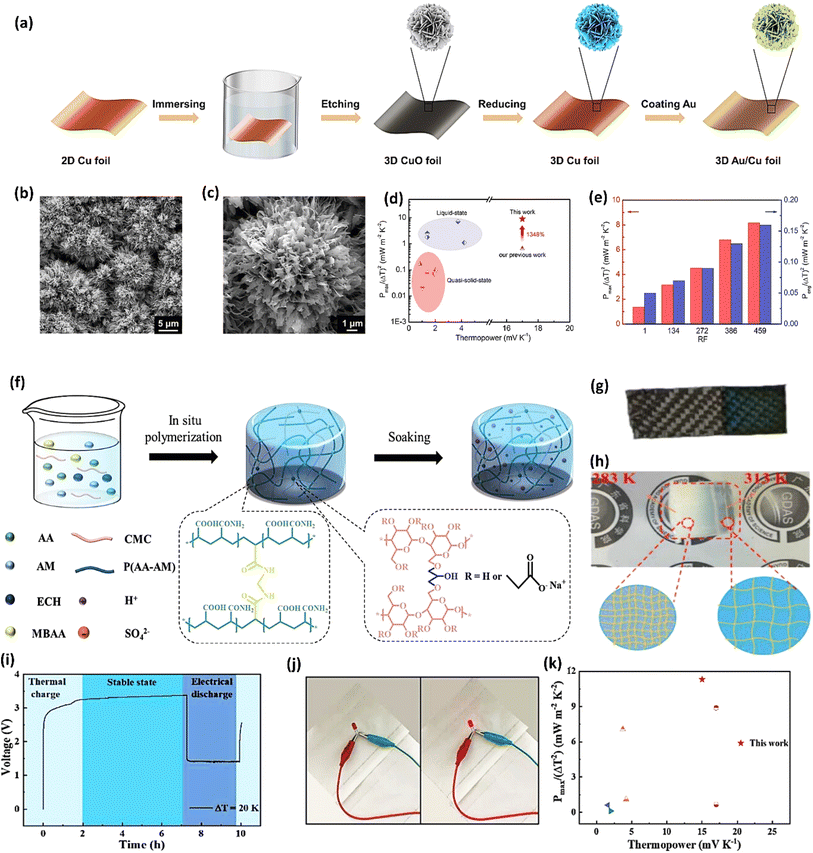 | ||
| Fig. 14 3D Au/Cu electrodes: (a) schematic illustration showing the preparation process of the 3D Au/Cu foil from 2D Cu foil, (b and c) SEM images of as-fabricated microflower CuO foil, (d) thermoelectric performance comparison of this work with previous studies, (e) output power density compared to RF values of electrodes, reproduced with permission.39 Copyright 2022, Wiley-VCH; PANI@CWF electrodes with cellulose–H2SO4 hydrogel: (f) schematic diagram of the preparation process and chemical structure of hydrogel, (g) digital image of PANI@CWF electrodes, (h) schematic diagram of hydrogel networks under ΔT, (i) thermal charging and electrical discharging process of the integrated generator, (j) LED light powered by the generator, and (k) comparison of this work with previous studies, reproduced with permission.38 Copyright 2023, Wiley-VCH. | ||
A recent research study introduced an innovative approach to ionic thermoelectric systems by employing polymer redox polyaniline (PANI) doped carbon weaved fabric electrodes (PANI@CWF) and an ionic gel based on carboxymethyl cellulose (Fig. 14f and g).38 This gel featured a distinct interpenetrating polymer network structure, infused with H2SO4 to enhance hydrogen bonds, thereby improving its mechanical properties and thermopower output (Fig. 14h). This unique system exhibited a remarkable Seebeck of 40.60 mV K−1 and achieved a maximum figure of merit value of 3.95 at a temperature difference of 5 K. The study also revealed a synergistic effect of the PANI@CWF electrode, enhancing current density through redox reactions on both electrodes. Consequently, this configuration yielded an output power density of 11.31 mW m−2 K−2 and an energy density of 570 J m−2, demonstrating its significant potential for practical energy harvesting applications (Fig. 14i–k).
7. Theoretical models conduction in electrolytes
7.1 Organic electronic, ionic and mixed conductors
In Fig. 15 we show a plot of the Seebeck coefficient as a function of the conductivity in a double logarithmic for several electronic, ionic and mixed materials. In most polymers the dependence is S ∝ σ1/4, typical of transport by hopping. However, in PEDOT the dependence is much lower, typical of a semiconductor. The electrical conductivity is σ = −enμn(epμp), i.e. is proportional to the mobility, which in most polymers is of the order of 10−4–10−5 cm2 V−1 s−1, while in PEDOT is much higher, of the order of 1 cm2 V−1 s−1, thus, the electron (or hole) concentration to have a given conductivity is much lower in PEDOT, giving a semiconducting behaviour. In ionic materials, the ionic thermopower increases with increasing ionic concentration. If in contrast, we have a p-type semiconductor, since the carriers diffuse from the hot region to the colder one, the thermopower will be positive. In the case of electronic conduction, the Seebeck conduction (this is an approximation for metals) can be written as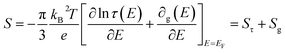 | (5) |
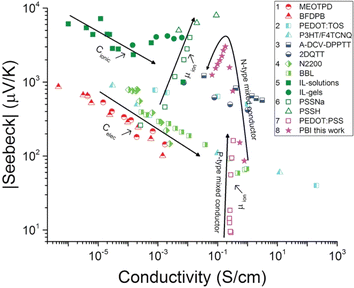 | ||
| Fig. 15 Seebeck coefficient as a function of the electrical conductivity, reproduced with permission.104 Copyright 2020, Wiley-VCH. | ||
The Seebeck coefficient has two contributions, one coming from the relaxation time or the mobility, and a second one coming from variations in the density of states. This second term is often suggested as the way to increase the Seebeck coefficient changing the density of states by nanostructuration. The change in the Seebeck coefficient due to the increase of the mobility can be related to the Nernst coefficient, which can be obtained applying a magnetic field perpendicular to the temperature gradient and measuring the voltage in the transversal direction, as shown in Fig. 16. Physically, the Peltier effect is the opposite to the Seebeck effect, if we supply a voltage difference in the two ends of the semiconductor we produce a temperature gradient.
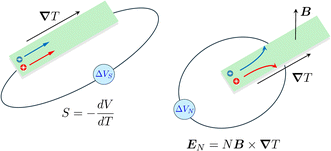 | ||
| Fig. 16 Seebeck and Nernst coefficients, reproduced with permission.105 Copyright 2021, American Physical Society. | ||
Qiao et al.106 proposed a linear scheme to solve numerically the Poisson–Nernst–Plank equations. It is based on gradient-flow formulation. They linearize the logarithm function. Fish107 examine the nanocomposite electrolyte through a theoretical model. A rigorous description of the space charge layer and its impact on conductivity insulating spheres dispersed in an ionic conducting material.
Fleharty et al.108 modelled small nanochannel with an electric double layer formed at the walls comparable to the channel width. They solve the Poisson–Boltzmann equation with charge regulation boundary conditions Moya et al.109 studied cylindrical nanopores filled with a ternary electrolyte solution as a function of the sign of the fixed charge on the pore wall. The Poisson–Boltzmann equation in cylindrical coordinates was solved by using the network simulation method. The velocity and conductivity were obtained using the modified Navier–Stokes equation and the Nernst–Planck flux equations. Koerver et al.110 used cobalt bipyridyl salts as active redox couple, they used cyclic voltammetry to determine the Seebeck coefficient. Jing et al.111 analyze the electro-viscous effect on the EDL, it seems that, at sufficiently high Z potential, the effect is negligible.
Luo et al.112 studied the electrophoresis and electric conduction in a salt-free suspension. They obtained analytical expressions for electrophoretic mobility and effective electrical conductivity. The scale z-potential, increases phoretic mobility and effective electric conductivity increases monotonically with the increase of the scale surface charge density. In addition, Varner113 studied the effect of dilution in ionic liquid supercapacitors. Huang114 studed the effect of hydrodynamic slippage on the power generation performance, indicating that velocity boundary conditions are relevant at the nanoscale. Levy et al.115 studied the variation of the dielectric response of the ionic liquid including the interaction of the ions with the dipoles present in the liquid. A closed form for the dielectric constant is obtained. Stout et al.116 have written the basic principles of ionic transport, the basic equations, etc. Qiao et al.106 developed a linear scheme for the solution of the Poisson–Nernst–Planck equations.
7.2 Basic formulation of the problem
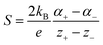 | (6) |
The basic problem is that of a channel ended in two electrodes as drawn in Fig. 17, with an electrolyte with anions and cations. In the upper panel of Fig. 17 we show the channel at equilibrium at a temperature T0 with a completely dissociated electrolyte solution. Let us call n+ the concentration of cations and n− that of anions. The lower panel shows the ion distribution when a temperature gradient (T0 → TH, TH being the temperature at the hot side) is applied through the electrolyte. We are supposed to have a long channel with a length of 2L. When compared with the lateral dimensions d (d ≪ L), but d is assumed to be wide enough to consider the problem as one dimensional. The mass and charge conservation are given by the continuity equation, which in the case of charged particles moving in a fluid is called the Nernst–Planck equation,
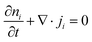 | (7) |
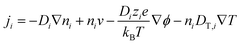 | (8) |
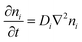 | (9) |
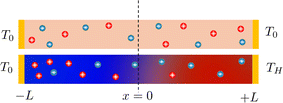 | ||
| Fig. 17 Upper panel: electrolyte with the ions in thermal equilibrium; lower panel: ion distribution when a temperature gradient exists through the electrolyte. | ||
D i can be written as Di = μikBT, the so called Einstein relation, μi being the ion drift mobility, the second term is the contribution of the fluid movement (advection), v(r, t) being the fluid velocity, the third term is the contribution to the ionic current due to the existence of an electric field E = −∇ϕ (electromigration), the fourth is the thermodiffusive flux, DT,i being the thermodiffusion coefficient. The Brownian diffusion coefficient is assumed to be the same for anions and cations and the thermodiffusion coefficient can be written in terms of the thermodiffusion factor αi, sometimes called Soret coefficient (actually α = STT, ST being the Soret coefficient51).
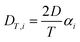 | (10) |
Thus, in the one-dimensional case, assuming that the fluid is at rest, the ionic fluxes become116,120
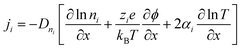 | (11) |
On the other hand, the electrostatic potential must satisfy the Poisson equation,
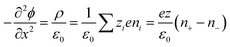 | (12) |
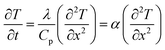 | (13) |
The thermovoltage can be calculated from
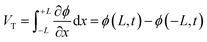 | (14) |
To proceed further some approximations are needed. We will assume that all transients have already ended, and the temperature gradient is small (ΔT = TH – T0 ≪ T0). Then, the ion concentration ni = ni,0 + δni, where ni,0 is the equilibrium ion density. If D/α ≪ 1 (D/α ≈ 100 for aqueous solutions of electrolytes116,121), we can neglect the temporal dependence (basically we can consider that the temperature changes instantaneously from the initial to the final value) and the solution of eqn (13) is
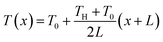 | (15) |
Then, the thermodiffusive contribution to the current has been reduced to a constant
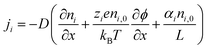 | (16) |
Introducing ji in the Nernst–Planck equation, Stout R. F. et al.116 analyze the dynamics of the ionic charges within the electrolyte under low temperature gradients using the Laplace transformation
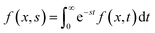 | (17) |
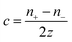 | (18) |
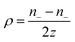 | (19) |
The charge density is divided by the elementary charge. Using the appropriate boundary conditions,116 the solution of these equations are
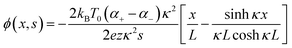 | (20) |
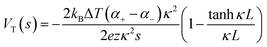 | (21) |
To obtain the time evolution of the neutral concentration, charge density and thermovoltage we have to Laplace transform the above equations, which can be done in the limit of long times. In particular, the thermovoltage takes the expression
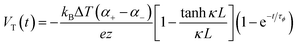 | (22) |
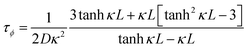 | (23) |
A similar treatment can be found in the work of Sehnem, A. L. et al.122 They study the time evolution of the thermopower when the temperature gradient is established and gradually changed. They also use the Laplace transform to find the solution of the Nernst–Planck, Poisson and heat equations. As in the previous case, the lateral dimensions d is small compared to 2L, the distance between the electrodes, thus the system is considered isothermal in the lateral direction. The temperature difference is assumed to be
| ΔT = ΔT∞h[1 − e−t/τap] | (24) |
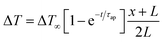 | (25) |
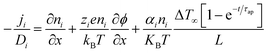 | (26) |
Then, they introduce the parameters ε = ΔT∞/T, where ΔT∞ is the temperature gradient in the final or stationary state, and n = Lκ, where L is the length of the channel and 1/κ the Debye length. With the approximations ε ≪ 1 (small temperature gradients) and n ≫ 1 (in their experiments n > 3.5 × 106) they found an analytical solution for the thermopower:
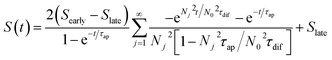 | (27) |
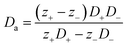 | (28) |
In Fig. 18 we can see the time evolution of the Seebeck coefficient with the parameters given in the caption. The Seebeck coefficient remains practically constant until t ∼ 10−2τdif, then it decreases to the stationary value at a time along the diffusion time. In the article, Sehnem A. L. et al.122 present also experimental results using different electrolytes. They obtain from the fitting with the theory the ambipolar diffusion coefficient and the time scale to which thermovoltage relax to equilibrium (steady state).
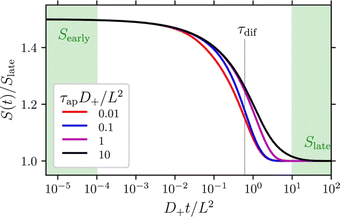 | ||
| Fig. 18 S(t)/Slate (eqn (27)) for several values of τapD+/L2 [0.01 (red), 0.1 (blue), 1 (magenta), and 10 (black)] with ξ ≡ D+/D− = 2, α+ = 0.5, α− = 0.1, z+ = −z− = 1, and max(j) = 500 throughout. For these parameters, Searly = (3/2)Slate. | ||
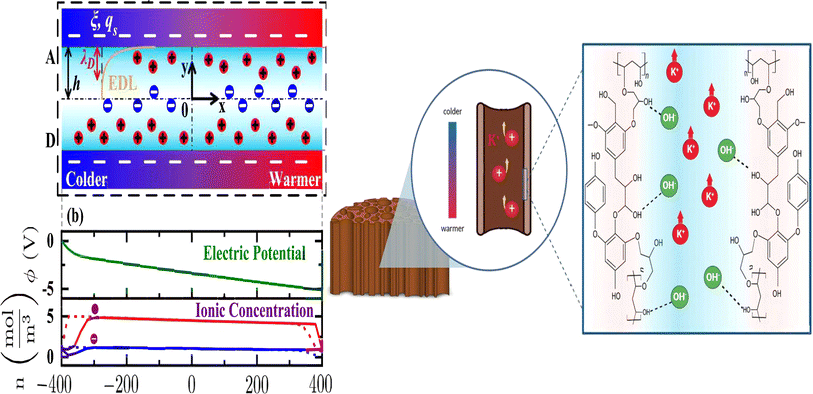 | ||
| Fig. 19 Left panel: The channel drawn in Fig. 14 (length 2L along x) has now a lateral dimension of width 2h (along the y-axis) confining the electrolyte. The positive ions moving towards the wall create charges in the Electric Double Layer (EDL). Right panel: cylindrical channel from lignin with an electrolyte and K+ and OH− ions. | ||
The physical problem of a layer and a capillary is equivalent, we will analyze here that of a capillary, which is mathematically a little bit more complex. The starting point is eqn (7), (11), (12) and (13), written in cylindrical coordinates. The problem has no φ-dependence, thus ni(r, z) and ϕ(r, z), but since the temperature gradient is established between the points z = −L and z = L, the temperature will depend only on z. In the stationary case ∂n/∂t = 0, thus ∇·j = 0, i.e.
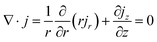 | (29) |
But the radial component of the current must be zero, the particle flux will be established along z. Thus, on one hand we have
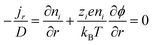 | (30) |
On the other hand,
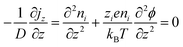 | (31) |
Let us call ψ = zieϕ/kBT, the two equations can be rewritten as
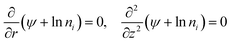 | (32) |
From the solution of the two equations, ψ + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ni = cz, c being a constant. The constant c must be zero, otherwise the concentration would increase exponentially along z. Thus
ni = cz, c being a constant. The constant c must be zero, otherwise the concentration would increase exponentially along z. Thus
| ni(r, z) = ni,0e−ψ | (33) |
8. Future direction for practical applications
Despite significant advancements in i-TE materials and devices over the past decade, the efficiency of i-TE devices still does not align with the performance of the materials used. High electrical and thermal contact resistances are primary reasons for the lower conversion efficiency at the device level. Enhancing both the flexibility and thermoelectric properties of i-TE materials to construct energy storage devices remains one of the biggest challenges.Extensive studies on device manufacturing and electrical and thermal contacts are required to improve the conversion efficiency of energy conversion and storage devices. Additionally, improved fabrication methods could enhance the performance and robustness of thermoelectric devices. The ultimate goal of improving the performance of i-TE materials is their practical application. We highlight the outlook for future high-performance i-TE materials and devices, as summarized in Fig. 20.
8.1 Reducing thermal conductivity
Research on i-TEs has primarily focused on enhancing ionic thermopower and ionic conductivity for efficient heat conversion. While i-TEs inherently exhibit low thermal conductivity, reducing it further by an order of magnitude could significantly improve device performance.8.2 Electrolyte interaction
The thermopower of thermally diffusive i-TEs is significantly higher than that of thermogalvanic i-TEs, suggesting promising and diverse potential applications. However, a major challenge is that ions struggle to pass through electrodes unless utilizing the ion-electron thermoelectric synergy (IETS) effect to directly power an external connection. This limitation currently restricts many of these materials to functioning as supercapacitors, with intermittent charging and discharging reducing current density and conversion efficiency. Addressing this challenge is urgent, and potential solutions could involve leveraging the combined effects of electrolyte interactions.8.3 Electrode interaction and design
Future exploration of i-TEs should consider the critical impact of electrodes. Innovative methods to tackle the issue of intermittent charging and discharging are anticipated. Since i-TEs, when used as electrolytes, inherently require electrodes, the choice of electrodes is crucial for influencing thermoelectric properties. Enhancing these properties can be further achieved through thoughtful electrode design that incorporates the thermoelectric effect.1248.4 Developing novel designs for i-TE devices
Despite advancements in i-TE device development, challenges persist in waste heat harvesting, efficient heat transfer, scalability, and durability. Utilizing ultrathin, flexible films with a modulus matching thermoelectric materials as substrates could facilitate the fabrication of high-performance TE devices capable of withstanding repeated bending. This approach may address critical issues such as high interfacial resistance between electrodes and TE legs, and overall mechanical durability in flexible devices.8.5 Commercialization of flexible i-TE devices
The compatibility of i-TE materials with polymer substrates makes 3D printing a feasible method for fabricating flexible i-TE devices. However, the field is still in its infancy, requiring further research to develop robust techniques for ink preparation and 3D printing that minimize morphological defects and maximize mechanical stability.488.6 Advanced 3D textiles
One promising research avenue is the development of revolutionary i-TE devices based on 3D textiles. The fabrication methods for 3D textile devices need improvement due to their superior breathability and flexibility. Computational methods, such as finite element numerical simulation, are expected to assist in the design of textile-based devices. Additionally, establishing evaluation standards is crucial for future commercial applications.8.7 Bio-based and waste recycling in i-TE
The current low thermoelectric performance and device efficiency necessitate the exploration of alternative resources. These include recycled carbon fiber, the development of biodegradable thermoelectric papers, and the extraction of useful elements from waste or recycled materials, such as spent modules.8.8 Multifunctional wearable design
Despite advancements in preventing device failure, the limited energy conversion efficiency of flexible i-TEGs remains a challenge. To maximize energy output for commercial applications, exploring multifunctional wearable devices integrating pyroelectric, triboelectric, piezoelectric, magnetoelectric, and photovoltaic functionalities is crucial.1259. Conclusion and perspective
In recent years, ionic thermoelectric materials (i-TEs) have emerged as a promising technology for waste heat harvesting. Unlike traditional electronic thermoelectric (e-TE) materials, i-TEs boast exceptionally high ionic thermopower, making them ideal for capturing and converting low-grade thermal energy. Additionally, i-TEs offer advantages in terms of flexibility, cost-effectiveness, and environmental friendliness. In this review, a unique feature of i-TE devices is their ability to function as both thermoelectric generators and thermal-powered capacitors. This review comprehensively allows them to generate electricity even from fluctuating heat sources. However, due to limitations in ion transport across electrodes, i-TE materials cannot be directly used in conventional thermoelectric generators (TEGs). Instead, i-TEs find application in ionic thermoelectric supercapacitors (ITESCs), which can harvest intermittent heat and exhibit transient voltage behavior. Thermogalvanic cells (TGC) represent another promising avenue for waste heat recovery using i-TE materials. These cells utilize an electrode–electrolyte pairing that maximizes reaction entropy and minimizes internal resistance, enabling continuous current flow. With their potential for cost-effective waste heat cogeneration, TGC hold significant promise for future applications, particularly where solid-state TEGs are economically impractical. The ferricyanide/ferrocyanide couple exemplifies a common choice for thermogalvanic cell electrodes due to its clean and reversible nature. Recent advancements further suggest that the performance of thermogalvanic generators can be significantly improved. This review also highlights the synergistic effect between the thermodiffusion phenomenon and electrode redox reactions, paving the way for the development of high-performance, thermochargeable devices suitable for commercialization. However, the theoretical models presented in this review require further refinement to accurately capture the complexities of ion diffusion, migration, and conduction within i-TE materials.Several key challenges remain in optimizing i-TE material performance.
• The discovery of novel n-type and p-type i-TE systems, finding a balance between thermoelectric and mechanical properties (flexibility, self-healing, etc.), and enhancing material stability. Notably, improving ionic conductivity (σ) is crucial for optimizing the thermoelectric behavior of i-TE materials.
• Furthermore, the integration of i-TE materials with other advanced TE components offers exciting possibilities for unlocking their full performance potential. While aqueous electrolytes offer an appealing approach, their limitations in heat and charge transport necessitate further exploration. Molten salt-based alternatives, while offering some improvement, may not justify the increased cost and complexity. Beyond their potential as capacitors, generators, and sensors, the high-efficiency operation of i-TE devices remains paramount.
• Future advancements will require a deeper understanding of high-performance devices, large-scale feasibility, and cost-effective material innovation. This includes exploring novel battery architectures, tailoring materials for specific applications, and developing biocompatible materials for wearable electronics. Additionally, minimizing contact resistance and optimizing electrode materials through targeted research efforts are crucial for unlocking the full potential of i-TE technology.
This review provides a comprehensive survey of advanced i-TE materials, equipping researchers to explore next-generation waste heat recovery technologies that contribute to a sustainable future. As the field of ionic thermoelectrics continues to emerge, this review serves as a valuable handbook, offering a foundational understanding of the current state-of-the-art and propelling advancements in low grade energy harvesting technologies.
Data availability
No primary research results, no new data were generated or analysed as part of this review.Author contributions
Nazish Jabeen: writing – original draft preparation, visualization, review & editing. Muhammad Muddasar, Nicolás Menéndez, & Mohammad Ali Nasiri: writing – original draft preparation. Clara M Gómez & Maurice N Collins: visualization, review & editing. Rafael Muñoz-Espí & Andrés Cantarero: review & editing. Mario Culebras: writing – original draft preparation, supervision, review & editing, funding acquisition.Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
This research was supported through the Grant PID2021-124845OA-I00 funded by MCIN/AEI/10.13039/501100011033 and by the “European UnionNextGenerationEU/PRTR”. NJ and MC acknowledge the Santiago Grisolia program CIGRIS/2022/132 funded by the Generalitat Valenciana. MM and MNC would like to acknowledge support from the Irish Government funding via the DAFM NXTGENWOOD research program 2019PROG704.References
- S. Sun, M. Li, X. L. Shi and Z. G. Chen, Advances in ionic thermoelectrics: from materials to devices, Adv. Energy Mater., 2023, 13(9), 2203692 CrossRef
.
- Z. Zhou, Y. Wan, J. Zi, G. Ye, T. Jin, X. Geng, W. Zhuang and P. Yang, Flexible hydrogel with a coupling enhanced thermoelectric effect for low-grade heat harvest, Mater. Today Sustain., 2023, 21, 100293 Search PubMed
.
- C. Gao, Y. Yin, L. Zheng, Y. Liu, S. Sim, Y. He, C. Zhu, Z. Liu, H. W. Lee and Q. Yuan, Engineering the electrochemical temperature coefficient for efficient low-grade heat harvesting, Adv. Funct. Mater., 2018, 28(35), 1803129 CrossRef
.
- M. Muddasar, M. Mushtaq, A. Beaucamp, T. Kennedy, M. Culebras and M. N. Collins, Synthesis of sustainable lignin precursors for hierarchical porous carbons and their efficient performance in energy storage applications, ACS Sustain. Chem. Eng., 2024, 12, 2352–2363 CrossRef PubMed
.
- J. Wei, L. Yang, Z. Ma, P. Song, M. Zhang, J. Ma, F. Yang and X. Wang, Review of current high-ZT thermoelectric materials, J. Mater. Sci., 2020, 55, 12642–12704 CrossRef
.
- M. Muddasar, N. Menéndez, Á. Quero, M. A. Nasiri, A. Cantarero, J. García-Cañadas, C. M. Gómez, M. N. Collins and M. Culebras, Highly-efficient sustainable ionic thermoelectric materials using lignin-derived hydrogels, Adv. Compos. Hybrid Mater., 2024, 7(2), 47 CrossRef
.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen and J. Y. Lee, Polycrystalline SnSe with a thermoelectric figure of merit greater than the single crystal, Nat. Mater., 2021, 20(10), 1378–1384 CrossRef
.
- H. Cheng, Q. Le, Z. Liu, Q. Qian, Y. Zhao and J. Ouyang, Ionic thermoelectrics: principles, materials and applications, J. Mater. Chem. C, 2022, 10(2), 433–450 RSC
.
- G. Chen, M. Dresselhaus, G. Dresselhaus, J.-P. Fleurial and T. Caillat, Recent developments in thermoelectric materials, Int. Mater. Rev., 2003, 48(1), 45–66 CrossRef
.
- J.-H. Bahk, H. Fang, K. Yazawa and A. Shakouri, Flexible thermoelectric materials and device optimization for wearable energy harvesting, J. Mater. Chem. C, 2015, 3(40), 10362–10374 RSC
.
- G.-H. Kim, L. Shao, K. Zhang and K. P. Pipe, Engineered doping of organic semiconductors for enhanced thermoelectric efficiency, Nat. Mater., 2013, 12(8), 719–723 CrossRef CAS PubMed
.
- D. Zhao, A. Würger and X. Crispin, Ionic thermoelectric materials and devices, J. Energy Chem., 2021, 61, 88–103 CrossRef CAS
.
- A. Weathers, Z. Ullah Khan, R. Brooke, D. Evans, M. T. Pettes, J. Wenzel Andreasen, X. Crispin and L. Shi, Significant electronic thermal transport in the conducting polymer poly (3, 4-ethylenedioxythiophene), Adv. Mater., 2015, 27(12), 2101–2106 CrossRef CAS PubMed
.
- J. Pei, B. Cai, H.-L. Zhuang and J.-F. Li, Bi2Te3-based applied thermoelectric materials: research advances and new challenges, Natl. Sci. Rev., 2020, 7(12), 1856–1858 CrossRef PubMed
.
- W. Liu, X. Qian, C.-G. Han, Q. Li and G. Chen, Ionic thermoelectric materials for near ambient temperature energy harvesting, Appl. Phys. Lett., 2021, 118(2), 020501 CrossRef CAS
.
- B. Lei, S. Bai, S. Ju, C. Yin, C. Chen and J. Zhang, Review on advances in thermoelectric conversion using ion-conducting polymers, Mater. Res. Express, 2021, 8(6), 062001 CrossRef CAS
.
- S. Sun, X. L. Shi, W. Lyu, M. Hong, W. Chen, M. Li, T. Cao, B. Hu, Q. Liu and Z. G. Chen, Stable, Self-Adhesive, and High-Performance Graphene-Oxide-Modified Flexible Ionogel Thermoelectric Films, Adv. Funct. Mater., 2024, 2402823 CrossRef
.
- X. Wu, N. Gao, H. Jia and Y. Wang, Thermoelectric converters based on ionic conductors, Chem.–Asian J., 2021, 16(2), 129–141 CrossRef
.
- T. H. Park, B. Kim, S. Yu, Y. Park, J. W. Oh, T. Kim, N. Kim, Y. Kim, D. Zhao and Z. U. Khan, Ionoelastomer electrolytes for stretchable ionic thermoelectric supercapacitors, Nano Energy, 2023, 114, 108643 CrossRef
.
- A. Beaucamp, M. Muddasar, T. Crawford, M. N. Collins and M. Culebras, Sustainable lignin precursors for tailored porous carbon-based supercapacitor electrodes, Int. J. Biol. Macromol., 2022, 221, 1142–1149 CrossRef
.
- S. Sun, X.-L. Shi, M. Li, T. Wu, L. Yin, D. Wang, Q. Liu and Z.-G. Chen, Ultrafast and cost-effective fabrication of high-performance carbon-based flexible thermoelectric hybrid films and their devices, ACS Appl. Mater. Interfaces, 2023, 15(21), 25650–25660 CrossRef PubMed
.
- J. Agar, Solutions of Electrolytes, Annu. Rev. Phys. Chem., 1964, 15(1), 469–488 CrossRef
.
- J. Platten and P. Costesèque, Charles S. A short biographya: On the occasion of the hundredth anniversary of his death, Eur. Phys. J. E, 2004, 15, 235–239 CrossRef
.
- T. Ikeda, Absolute Estimation of the Ionic Entropies of Transfer, Bull. Chem. Soc. Jpn., 1959, 32, 96–97 CrossRef
.
- T. Ikeda, Transported entropies and conventional eastman entropies of the transfer of some univalent ions in aqueous solutions at 25 c, Bull. Chem. Soc. Jpn., 1964, 37(10), 1485–1489 CrossRef CAS
.
- W. Breck and E. King, On the use of a polyelectrolyte in a thermocell, Can. J. Chem., 1969, 47(18), 3480–3482 CrossRef CAS
.
- R. Haase, U. Prüser and J. Richter, Evaluation of Measurements on Thermocells Containing Molten Salt Mixtures, Ber. Bunsenges. Phys. Chem., 1977, 81(6), 577–584 CrossRef CAS
.
- D. Zhao, H. Wang, Z. U. Khan, J. Chen, R. Gabrielsson, M. P. Jonsson, M. Berggren and X. Crispin, Ionic thermoelectric supercapacitors, Energy Environ. Sci., 2016, 9(4), 1450–1457 RSC
.
- T. Li, X. Zhang, S. D. Lacey, R. Mi, X. Zhao, F. Jiang, J. Song, Z. Liu, G. Chen and J. Dai, Cellulose ionic conductors with high differential thermal voltage for low-grade heat harvesting, Nat. Mater., 2019, 18(6), 608–613 CrossRef CAS
.
- M. Muddasar, M. A. Nasiri, A. Cantarero, C. Gómez, M. Culebras and M. N. Collins, Lignin-Derived Ionic Conducting Membranes for Low-Grade Thermal Energy Harvesting, Adv. Funct. Mater., 2024, 34(12), 2306427 CrossRef CAS
.
- C.-G. Han, X. Qian, Q. Li, B. Deng, Y. Zhu, Z. Han, W. Zhang, W. Wang, S.-P. Feng, G. Chen and W. Liu, Giant thermopower of ionic gelatin near room temperature, Science, 2020, 368(6495), 1091–1098 CrossRef CAS PubMed
.
- X.-L. Shi, S. Sun, T. Wu, J. Tu, Z. Zhou, Q. Liu and Z.-G. Chen, Weavable thermoelectrics: advances, controversies, and future developments, Mater. Futures, 2024, 3(1), 012103 CrossRef
.
- D. R. Lobato-Peralta, E. Duque-Brito, H. I. Villafan-Vidales, A. Longoria, P. Sebastian, A. K. Cuentas-Gallegos, C. A. Arancibia-Bulnes and P. U. Okoye, A review on trends in lignin extraction and valorization of lignocellulosic biomass for energy applications, J. Clean. Prod., 2021, 293, 126123 CrossRef CAS
.
- Y. Jia, Q. Jiang, H. Sun, P. Liu, D. Hu, Y. Pei, W. Liu, X. Crispin, S. Fabiano and Y. Ma, Wearable thermoelectric materials and devices for self-powered electronic systems, Adv. Mater., 2021, 33(42), 2102990 CrossRef CAS
.
- E. Laux, S. Uhl, T. Journot, J. Brossard, L. Jeandupeux and H. Keppner, Aspects of protonic ionic liquid as electrolyte in thermoelectric generators, J. Electron. Mater., 2016, 45, 3383–3389 CrossRef CAS
.
- H. Zhu, C. Xiao and Y. Xie, Design of highly efficient thermoelectric materials: tailoring reciprocal-space properties by real-space modification, Adv. Mater., 2018, 30(48), 1802000 CrossRef
.
- C. Cheng, Y. Dai, J. Yu, C. Liu, S. Wang, S. P. Feng and M. Ni, Review of liquid-based systems to recover low-grade waste heat for electrical energy generation, Energy Fuels, 2020, 35(1), 161–175 CrossRef
.
- K. Jiang, J. Jia, Y. Chen, L. Li, C. Wu, P. Zhao, D. Y. Zhu and W. Zeng, An Ionic Thermoelectric Generator with a Giant Output Power Density and High Energy Density Enabled by Synergy of Thermodiffusion Effect and Redox Reaction on Electrodes, Adv. Energy Mater., 2023, 13(21), 2204357 CrossRef CAS
.
- Y. Li, Q. Li, X. Zhang, B. Deng, C. Han and W. Liu, 3D Hierarchical Electrodes Boosting Ultrahigh Power Output for Gelatin-KCl-FeCN4−/3− Ionic Thermoelectric Cells, Adv. Energy Mater., 2022, 12(14), 2103666 CrossRef CAS
.
- M. Li, F. Zeng, M. Luo, X. Qing, W. Wang, Y. Lu, W. Zhong, L. Yang, Q. Liu and Y. Wang, Synergistically improving flexibility and thermoelectric performance of composite yarn by continuous ultrathin PEDOT: PSS/DMSO/ionic liquid coating, ACS Appl. Mater. Interfaces, 2021, 13(42), 50430–50440 CrossRef CAS
.
- J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest, Nat. Commun., 2018, 9(1), 5146 CrossRef
.
- B. Yang and G. Portale, Ionic thermoelectric materials for waste heat harvesting, Colloid Polym. Sci., 2021, 299, 465–479 CrossRef CAS
.
- Y. T. Malik, Z. A. Akbar, J. Y. Seo, S. Cho, S.-Y. Jang and J.-W. Jeon, Self-Healable Organic–Inorganic Hybrid Thermoelectric Materials with Excellent Ionic Thermoelectric Properties, Adv. Energy Mater., 2022, 12(6), 2103070 CrossRef CAS
.
- H. Wang, D. Zhao, Z. U. Khan, S. Puzinas, M. P. Jonsson, M. Berggren and X. Crispin, Ionic thermoelectric figure of merit for charging of supercapacitors, Adv. Electron. Mater., 2017, 3(4), 1700013 CrossRef
.
- M. Bonetti, S. Nakamae, B. T. Huang, T. J. Salez, C. Wiertel-Gasquet and M. Roger, Thermoelectric energy recovery at ionic-liquid/electrode interface, J. Chem. Phys., 2015, 142(24), 244708 CrossRef PubMed
.
- X. Yang, Y. Tian, B. Wu, W. Jia, C. Hou, Q. Zhang, Y. Li and H. Wang, High-performance ionic thermoelectric supercapacitor for integrated energy conversion-storage, Energy Environ. Mater., 2022, 5(3), 954–961 CrossRef CAS
.
- H. Cheng, X. He, Z. Fan and J. Ouyang, Flexible quasi-solid state ionogels with remarkable seebeck coefficient and high thermoelectric properties, Adv. Energy Mater., 2019, 9(32), 1901085 CrossRef
.
- Y. Tian, X. Yang, K. Li, Q. Zhang, Y. Li, H. Wang and C. Hou, High-performance ionic thermoelectric materials and emerging applications of ionic thermoelectric devices, Mater. Today Energy, 2023, 36, 101342 CrossRef CAS
.
- D. Song, C. Chi, M. An, Y. Du, W. Ma, K. Wang and X. Zhang, Ionic Seebeck coefficient and figure of merit in ionic thermoelectric materials, Cell Rep. Phys. Sci., 2022, 3(9), 101018 CrossRef CAS
.
- X. Qian, Z. Ma, Q. Huang, H. Jiang and R. Yang, Thermodynamics of Ionic Thermoelectrics for Low-Grade Heat Harvesting, ACS Energy Lett., 2024, 9(2), 679–706 CrossRef CAS
.
- M. Rahman and M. Saghir, Thermodiffusion or Soret effect: Historical review, Int. J. Heat Mass Transfer, 2014, 73, 693–705 CrossRef
.
- A. Al-zubaidi, X. Ji and J. Yu, Thermal charging of supercapacitors: a perspective, Sustain. Energy Fuels, 2017, 1(7), 1457–1474 RSC
.
- L. Kong, Z. Yuan, N. Sun, J. Ding, S. Liu, S. Zhang, Z. Lv, W. Xu, G. Liu and X. Liu, Advances in flexible hydrogels for light-thermal-electricity energy conversion and storage, J. Energy Storage, 2023, 60, 106618 CrossRef
.
- X. Liu, A. L. Miller, S. Park, B. E. Waletzki, Z. Zhou, A. Terzic and L. Lu, Functionalized carbon nanotube and graphene oxide embedded electrically conductive hydrogel synergistically stimulates nerve cell differentiation, ACS Appl. Mater. Interfaces, 2017, 9(17), 14677–14690 CrossRef CAS PubMed
.
- R. Elashnikov, A. Trelin, A. Tulupova, E. Miliutina, K. Zahorjanová, P. Ulbrich, D. Tomeček, P. e. Fitl, V. c. Švorčík and O. Lyutakov, Switchable PNIPAm/PPyNT hydrogel for smart supercapacitors: External control of capacitance for pulsed energy generation or prolongation of discharge time, ACS Appl. Mater. Interfaces, 2021, 13(40), 48030–48039 CrossRef CAS PubMed
.
- S. Horike, Q. Wei, K. Kirihara, M. Mukaida, T. Sasaki, Y. Koshiba, T. Fukushima and K. Ishida, Outstanding electrode-dependent Seebeck coefficients in ionic hydrogels for thermally chargeable supercapacitor near room temperature, ACS Appl. Mater. Interfaces, 2020, 12(39), 43674–43683 CrossRef CAS PubMed
.
- Y. Hu, M. Chen, C. Qin, J. Zhang and A. Lu, Cellulose ionic conductor with tunable Seebeck coefficient for low-grade heat harvesting, Carbohydr. Polym., 2022, 292, 119650 CrossRef CAS
.
- H. Zhang, P. Xue, J. Liu and X. Xu, Thermal-switching and repeatable self-protective hydrogel polyelectrolytes for energy storage applications of flexible electronics, ACS Appl. Energy Mater., 2021, 4(6), 6116–6124 CrossRef CAS
.
- Y. Liu, M. Cui, W. Ling, L. Cheng, H. Lei, W. Li and Y. Huang, Thermo-electrochemical cells for heat to electricity conversion: from mechanisms, materials, strategies to applications, Energy Environ. Sci., 2022, 15(9), 3670–3687 RSC
.
- M. A. Buckingham and L. Aldous, Thermogalvanic cells: A side-by-side comparison of measurement methods, J. Electroanal. Chem., 2020, 872, 114280 CrossRef CAS
.
- Y. Liu, Q. Zhang, G. O. Odunmbaku, Y. He, Y. Zheng, S. Chen, Y. Zhou, J. Li, M. Li and K. Sun, Solvent effect on the Seebeck coefficient of Fe2+/Fe3+ hydrogel thermogalvanic cells, J. Mater. Chem. A, 2022, 10(37), 19690–19698 RSC
.
- I. Burmistrov, N. Kovyneva, N. Gorshkov, A. Gorokhovsky, A. Durakov, D. Artyukhov and N. Kiselev, Development of new electrode materials for thermo-electrochemical cells for waste heat harvesting, Renew. Energy Focus, 2019, 29, 42–48 CrossRef
.
- M. A. Buckingham, K. Laws, E. Cross, A. J. Surman and L. Aldous, Developing iron-based anionic redox couples for thermogalvanic cells: towards the replacement of the ferricyanide/ferrocyanide redox couple, Green Chem., 2021, 23(22), 8901–8915 RSC
.
- T. I. Quickenden and Y. Mua, A Review of Power Generation in Aqueous Thermogalvanic Cells, J. Electrochem. Soc., 1995, 142(11), 3985 CrossRef CAS
.
- B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Zhuang, H. Wang, B. Qi, M. Xu, Z. L. Wang and J. Zhou, Thermosensitive crystallization–boosted liquid thermocells for low-grade heat harvesting, Science, 2020, 370(6514), 342–346 CrossRef CAS PubMed
.
- H. Im, T. Kim, H. Song, J. Choi, J. S. Park, R. Ovalle-Robles, H. D. Yang, K. D. Kihm, R. H. Baughman, H. H. Lee, T. J. Kang and Y. H. Kim, High-efficiency electrochemical thermal energy harvester using carbon nanotube aerogel sheet electrodes, Nat. Commun., 2016, 7(1), 10600 CrossRef
.
- B. Burrows, Discharge Behavior of Redox Thermogalvanic Cells, J. Electrochem. Soc., 1976, 123(2), 154 CrossRef CAS
.
- R. L. McCreery, Advanced Carbon Electrode Materials for Molecular Electrochemistry, Chem. Rev., 2008, 108(7), 2646–2687 CrossRef CAS
.
- X. Zhuang, H. Jin, S. Dai, X. Li, W. Guo, Y. Wang, J. Wu, L. Huang, J. Duan and J. Zhou, Self-Assembled Asymmetric Electrodes for High-Efficiency Thermogalvanic Cells, Adv. Energy Mater., 2023, 13(39), 2302011 CrossRef CAS
.
- L. Yang, H. Sun, S. Wang, L. Jiang and G. Sun, A solid state thermogalvanic cell harvesting low-grade thermal energy, Int. J. Hydrogen Energy, 2017, 42(41), 25877–25881 CrossRef CAS
.
- M. Al Maimani, J. J. Black and L. Aldous, Achieving pseudo-‘n-type p-type’ in-series and parallel liquid thermoelectrics using all-iron thermoelectrochemical cells with opposite Seebeck coefficients, Electrochem. Commun., 2016, 72, 181–185 CrossRef CAS
.
- M. A. Buckingham, S. Hammoud, H. Li, C. J. Beale, J. T. Sengel and L. Aldous, A fundamental study of the thermoelectrochemistry of ferricyanide/ferrocyanide: cation, concentration, ratio, and heterogeneous and homogeneous electrocatalysis effects in thermogalvanic cells, Sustain. Energy Fuels, 2020, 4(7), 3388–3399 RSC
.
- J.-M. Tournier and M. S. El-Genk, Performance analysis of Pluto/Express, multitube AMTEC cells, Energy Convers. Manage., 1999, 40(2), 139–173 CrossRef CAS
.
- T. Cole, Thermoelectric Energy Conversion with Solid Electrolytes, Science, 1983, 221(4614), 915–920 CrossRef CAS PubMed
.
- K. Han and L. Xie, A Quasisolid Electrolyte Thermogalvanic Cell by Using Sand Grains, Adv. Electron. Mater., 2023, 9(7), 2300089 CrossRef CAS
.
- C. Tian, C. Bai, T. Wang, Z. Yan, Z. Zhang, K. Zhuo and H. Zhang, Thermogalvanic hydrogel electrolyte for harvesting biothermal energy enabled by a novel redox couple of SO4/32- ions, Nano Energy, 2023, 106, 108077 CrossRef CAS
.
- J. Shen, Y. Ma, C. Yang, S. Liu, J. Li, Z. Chen, B. Tian and S. Li, Boosting solar-thermal-electric conversion of thermoelectrochemical cells by construction of a carboxymethylcellulose-interpenetrated polyacrylamide network, J. Mater. Chem. A, 2022, 10(14), 7785–7791 RSC
.
- Y. Han, J. Zhang, R. Hu and D. Xu, High-thermopower polarized electrolytes enabled by methylcellulose for low-grade heat harvesting, Sci. Adv., 2022, 8(7), eabl5318 CrossRef CAS
.
- L. Liu, D. Zhang, P. Bai, Y. Mao, Q. Li, J. Guo, Y. Fang and R. Ma, Strong Tough Thermogalvanic Hydrogel Thermocell With Extraordinarily High Thermoelectric Performance, Adv. Mater., 2023, 35(32), 2300696 CrossRef CAS
.
- Y. Yang, S. W. Lee, H. Ghasemi, J. Loomis, X. Li, D. Kraemer, G. Zheng, Y. Cui and G. Chen, Charging-free electrochemical system for harvesting low-grade thermal energy, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(48), 17011–17016 CrossRef CAS
.
- Y. Liu, C. Gao, S. Sim, M. Kim and S. W. Lee, Lithium Manganese Oxide in an Aqueous Electrochemical System for Low-Grade Thermal Energy Harvesting, Chem. Mater., 2019, 31(12), 4379–4384 CrossRef CAS
.
- C. Cheng, S. Wang, P. Tan, Y. Dai, J. Yu, R. Cheng, S.-P. Feng and M. Ni, Insights into the Thermopower of Thermally Regenerative Electrochemical Cycle for Low Grade Heat Harvesting, ACS Energy Lett., 2021, 6(2), 329–336 CrossRef CAS
.
- S. W. Lee, Y. Yang, H.-W. Lee, H. Ghasemi, D. Kraemer, G. Chen and Y. Cui, An electrochemical system for efficiently harvesting low-grade heat energy, Nat. Commun., 2014, 5(1), 3942 CrossRef CAS PubMed
.
-
Z. Jianwei, X. Ying, L. Bowei, L. Gengyuan and Z. Wenshu, Research Progress of Ionic Thermoelectric Materials for Energy Harvesting, in Thermoelectricity, ed. Q. Guangzhao, IntechOpen, Rijeka, 2022, ch. 4 Search PubMed
.
- P. Yin, Y. Geng, L. Zhao, Q. Meng, Z. Xin, L. Luo, B. Wang, Z. Mao, X. Sui, W. Wu and X. Feng, Robust and flexible bacterial cellulose-based thermogalvanic cells for low-grade heat harvesting in extreme environments, Chem. Eng. J., 2023, 457, 141274 CrossRef CAS
.
- L. Yang and C.-G. Han, Perspective and advances on ionic thermoelectric energy conversion, Mater. Lab., 2023, 230010 Search PubMed
.
- Y. Li, Q. Li, X. Zhang, J. Zhang, S. Wang, L. Lai, K. Zhu and W. Liu, Realizing record-high output power in flexible gelatin/GTA-KCl-FeCN4−/3− ionic thermoelectric cells enabled by extending the working temperature range, Energy Environ. Sci., 2022, 15(12), 5379–5390 RSC
.
- C. Bai, X. Li, X. Cui, X. Yang, X. Zhang, K. Yang, T. Wang and H. Zhang, Transparent stretchable thermogalvanic PVA/gelation hydrogel electrolyte for harnessing solar energy enabled by a binary solvent strategy, Nano Energy, 2022, 100, 107449 CrossRef CAS
.
- N. Li, S. A. Khan, K. Yang, K. Zhuo, Y. Zhang and H. Zhang, A self-powered thermogalvanic organohydrogel-based touch-to-speech Braille transmission interface with temperature resistance and stretchability, Compos. Sci. Technol., 2023, 239, 110077 CrossRef CAS
.
- D. Zhang, Y. Mao, F. Ye, Q. Li, P. Bai, W. He and R. Ma, Stretchable thermogalvanic hydrogel thermocell with record-high specific output power density
enabled by ion-induced crystallization, Energy Environ. Sci., 2022, 15(7), 2974–2982 RSC
.
- H. Adelnia, R. Ensandoost, S. Shebbrin Moonshi, J. N. Gavgani, E. I. Vasafi and H. T. Ta, Freeze/thawed polyvinyl alcohol hydrogels: Present, past and future, Eur. Polym. J., 2022, 164, 110974 CrossRef CAS
.
- F. Mushtaq, Z. A. Raza, S. R. Batool, M. Zahid, O. C. Onder, A. Rafique and M. A. Nazeer, Preparation, properties, and applications of gelatin-based hydrogels (GHs) in the environmental, technological, and biomedical sectors, Int. J. Biol. Macromol., 2022, 218, 601–633 CrossRef CAS
.
- J. A. Rather, N. Akhter, Q. S. Ashraf, S. A. Mir, H. A. Makroo, D. Majid, F. J. Barba, A. M. Khaneghah and B. N. Dar, A comprehensive review on gelatin: Understanding impact of the sources, extraction methods, and modifications on potential packaging applications, Food Packag. Shelf Life, 2022, 34, 100945 CrossRef CAS
.
- H. Tu, M. Zhu, B. Duan and L. Zhang, Recent Progress in High-Strength and Robust Regenerated Cellulose Materials, Adv. Mater., 2021, 33(28), 2000682 CrossRef CAS
.
- M. Muddasar, A. Beaucamp, M. Culebras and M. N. Collins, Cellulose: Characteristics and applications for rechargeable batteries, Int. J. Biol. Macromol., 2022, 219, 788–803 CrossRef CAS PubMed
.
- L. Li, H. Li, J. Wei, R. Li, J. Sun, C. Zhao and T. Chen, Water-Resistant Thermoelectric Ionogel Enables Underwater Heat Harvesting, Polymers, 2023, 15(7), 1746 CrossRef CAS
.
- M. Yu, H. Li, Y. Li, S. Wang, Q. Li, Y. Wang, B. Li, K. Zhu and W. Liu, Ionic thermoelectric gels and devices: Progress, opportunities, and challenges, EnergyChem, 2024, 6(3), 100123 CrossRef CAS
.
- Q. Li, D. Yu, S. Wang, X. Zhang, Y. Li, S.-P. Feng and W. Liu, High Thermopower of Agarose-Based Ionic Thermoelectric Gel Through Micellization Effect Decoupling the Cation/Anion Thermodiffusion, Adv. Funct. Mater., 2023, 33(49), 2305835 CrossRef CAS
.
- J. Xu, H. Wang, X. Du, X. Cheng, Z. Du and H. Wang, Highly Stretchable PU Ionogels with Self-Healing Capability for a Flexible Thermoelectric Generator, ACS Appl. Mater. Interfaces, 2021, 13(17), 20427–20434 CrossRef CAS
.
- Z. Liu, H. Cheng, Q. Le, R. Chen, J. Li and J. Ouyang, Giant Thermoelectric Properties of Ionogels with Cationic Doping, Adv. Energy Mater., 2022, 12(22), 2200858 CrossRef CAS
.
- S. Lomartire and A. M. M. Gonçalves, Algal Phycocolloids: Bioactivities and Pharmaceutical Applications, Mar. Drugs, 2023, 21(7), 384 CrossRef CAS PubMed
.
- J. Lu, P. Jaumaux, T. Wang, C. Wang and G. Wang, Recent progress in quasi-solid and solid polymer electrolytes for multivalent metal-ion batteries, J. Mater. Chem. A, 2021, 9(43), 24175–24194 RSC
.
- H. Tributsch and L. Pohlmann, Electron Transfer: Classical Approaches and New Frontiers, Science, 1998, 279(5358), 1891–1895 CrossRef CAS
.
- Q. Jiang, H. Sun, D. Zhao, F. Zhang, D. Hu, F. Jiao, L. Qin, V. Linseis, S. Fabiano and X. Crispin, High Thermoelectric Performance in n-Type Perylene Bisimide Induced by the Soret Effect, Adv. Mater., 2020, 32(45), 2002752 CrossRef CAS
.
- M. Zebarjadi, S. E. Rezaei, M. S. Akhanda and K. Esfarjani, Nernst coefficient within relaxation time approximation, Phys. Rev. B, 2021, 103(14), 144404 CrossRef CAS
.
- T. Qiao, Z. Qiao, S. Sun and S. Zhou, An unconditionally energy stable linear scheme for Poisson–Nernst–Planck equations, J. Comput. Appl. Math., 2024, 443, 115759 CrossRef
.
- J. S. Fish, C.-P. Li, J. D. Fehribach, C. A. Wolden, R. O'Hayre, A. L. Bunge and C. E. Goodyer, Poisson–Boltzmann model of space charge layer effects on conductivity in randomly distributed nanoionic composites, Electrochim. Acta, 2012, 83, 454–462 CrossRef CAS
.
- M. E. Fleharty, F. van Swol and D. N. Petsev, The effect of surface charge regulation on conductivity in fluidic nanochannels, J. Colloid Interface Sci., 2014, 416, 105–111 CrossRef CAS
.
- A. Moya and V. Nikonenko, A comparative theoretical study of potential distribution and conductivity in cation-and anion-exchange nanoporous membranes filled with ternary electrolytes, Electrochim. Acta, 2015, 180, 929–938 CrossRef CAS
.
- R. Koerver, D. R. MacFarlane and J. M. Pringle, Evaluation of electrochemical methods for determination of the Seebeck coefficient of redox electrolytes, Electrochim. Acta, 2015, 184, 186–192 CrossRef CAS
.
- D. Jing and B. Bhushan, Electroviscous effect on fluid drag in a microchannel with large zeta potential, Beilstein J. Nanotechnol., 2015, 6(1), 2207–2216 CrossRef CAS PubMed
.
- R. H. Luo and H. J. Keh, Electrophoresis and electric conduction in a salt-free suspension of charged particles, Electrophoresis, 2021, 42(21–22), 2134–2142 CrossRef CAS
.
- S. Varner and Z.-G. Wang, Effects of dilution in ionic liquid supercapacitors, Phys. Chem. Chem. Phys., 2022, 24(44), 27362–27374 RSC
.
- W.-H. Huang, C.-C. Chang and R.-J. Yang, Effect of hydrodynamic slip on thermoelectric response in negatively-charged nanofluidic channels, Int. J. Heat Mass Transfer, 2023, 214, 124454 CrossRef CAS
.
- A. Levy, D. Andelman and H. Orland, Dipolar Poisson-Boltzmann approach to ionic solutions: a mean field and loop expansion analysis, J. Chem. Phys., 2013, 139(16), 164909 CrossRef
.
- R. F. Stout and A. S. Khair, Diffuse charge dynamics in ionic thermoelectrochemical systems, Phys. Rev. E, 2017, 96(2), 022604 CrossRef
.
- E. D. Eastman, Thermodynamics of non-isothermal systems, J. Am. Chem. Soc., 1926, 48(6), 1482–1493 CrossRef CAS
.
- C. Wagner, Über die thermodynamische Behandlung stationärer Zustände in nicht isothermen Systemen, Ann. Phys., 1929, 395(5), 629–687 CrossRef
.
- D. Pu, A. Panahi, G. Natale and A. M. Benneker, A Mode-Coupling Model of Colloid Thermophoresis in Aqueous Systems: Temperature and Size Dependencies of the Soret Coefficient, Nano Lett., 2024, 24, 2798–2804 CrossRef CAS PubMed
.
- X. Qian, T.-H. Liu and R. Yang, Confinement effect on thermopower of electrolytes, Mater. Today Phys., 2022, 23, 100627 CrossRef CAS
.
-
I. D. Zaytsev and G. G. Aseyev, Properties of Aqueous Solutions of Electrolytes, CRC press, 1992 Search PubMed
.
- A. L. Sehnem and M. Janssen, On the time-dependent electrolyte Seebeck effect, J. Chem. Phys., 2021, 154(16), 164511 CrossRef CAS
.
- J. Zhong and C. Huang, Influence factors of thermal driven ion transport in nano-channel for thermoelectricity application, Int. J. Heat Mass Transfer, 2020, 152, 119501 CrossRef CAS
.
- S. Jia, W. Qian, P. Yu, K. Li, M. Li, J. Lan, Y.-H. Lin and X. Yang, Ionic thermoelectric materials: Innovations and challenges, Mater. Today Phys., 2024, 101375 CrossRef CAS
.
- L. Zhang, X.-L. Shi, Y.-L. Yang and Z.-G. Chen, Flexible thermoelectric materials and devices: From materials to applications, Mater. Today, 2021, 46, 62–108 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2024 |