Open Access Article
Open Access ArticlePrediction of the ground state for indenofluorene-type systems with Clar's π-sextet model†
Gibu
George
 a,
Anton J.
Stasyuk
a,
Anton J.
Stasyuk
 *abc and
Miquel
Solà
*abc and
Miquel
Solà
 *a
*a
aInstitut de Química Computacional i Catàlisi, Departament de Química, Universitat de Girona, C/Maria Aurèlia Capmany 69, 17003 Girona, Catalonia, Spain. E-mail: miquel.sola@udg.edu; antony.stasuk@gmail.com
bFaculty of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
cDepartament de Farmàcia i Tecnologia Farmacèutica, i Fisicoquímica, Facultat de Farmàcia i Ciències de l'Alimentació, Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona (UB), Av. Joan XXIII 27-31, Barcelona, Spain
First published on 24th July 2024
Abstract
This study introduces the Ground State Stability (GSS) rule that allows predicting the nature of the ground state of indenofluorene (IF)-type systems from the simple counting of the Clar's π-sextets in the closed- and open-shell configurations. The IF-type system exhibits a triplet ground state when acquiring double or more the number of Clar's π-sextets in the open-shell form relative to the closed-shell form; otherwise, it assumes an open-shell singlet ground state. Performed state-of-the-art DFT calculations and analysis of aromaticity for the systems of interest validate the effectiveness of the proposed rule. We demonstrate that aromaticity plays the most crucial role in determining the ground electronic state for such polycyclic hydrocarbons. The simplicity of the GSS rule makes it a robust strategy for identifying promising systems in the development of indenofluorene-type materials.
Introduction
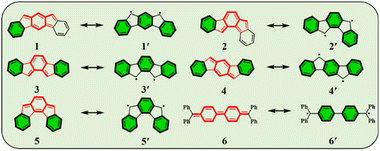
Conjugated polycyclic hydrocarbons (CPHs) have gained considerable interest due to their versatile applications in optoelectronic devices,1–4 organic spintronics5–8 and semiconductors,9 as well as energy storage devices.10,11 The unique photophysical properties of CPHs make them a promising solution not only in functional materials but also found to be fundamentally important for providing insights into chemical properties such as the open-shell radical character and aromaticity.12–15 Among such CPHs conjugated indenofluorenes (IFs) possess one of the most interesting topologies of delocalized π-electrons with different types of behavior (aromatic/antiaromatic) and ground state electronic structure (biradical/quinoidal).16,17 They exhibit a 6–5–6–5–6 ring architecture, which is obtained by a fusion of the indene unit to various positions of the fluorene unit. Since 2010 all five possible IF regioisomers have been intensively studied by Haley's18–20 and Tobe's21,22 group (structures 1–5 in, Fig. 1).In 1986, Montgomery and co-workers studied classical Chichibabin's hydrocarbon and demonstrated that diradical behavior of such a system can be explained by the regaining of two aromatic Clar's π-sextets23,24 at the expense of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond (6, 6′).25 More recently, Escayola et al.26 studied the dependence of the nature of the ground state (closed-shell (CS) quinoidal structure vs. open-shell (OS) aromatic structure) in Chichibabin's hydrocarbons as a function of the elongation of the π-system and the exocyclic substituents. Similarly to Chichibabin's hydrocarbon, the IFs have the potential to re-aromatize the quinoidal motif leading to an OS structure that is in resonance with the CS quinoidal structure. It has been shown that structures 1 and 2 depicted in Fig. 1 exhibit a greater y0 value (a measure of the diradical character, calculated by the Yamaguchi scheme,27 see computational details in ESI†) than 3, 4, and 5, and is mainly associated with the recovery of a larger number of the Clar's π-sextets in the OS form than the CS quinoid form.28 Moreover, the higher diradical character for structures 1 and 2 as compared to 3, 4, and 5 can be associated in part with the pro-aromatic quinodimethane framework. Both 1 and 2 have a meta-quinodimethane (m-QDM) subunit (highlighted with bold red lines in Fig. 1), in contrast to the 3 with ortho-quinodimethane (o-QDM) or 4 and 5 with para-quinodimethane (p-QDM) framework (Fig. 1).20
C double bond (6, 6′).25 More recently, Escayola et al.26 studied the dependence of the nature of the ground state (closed-shell (CS) quinoidal structure vs. open-shell (OS) aromatic structure) in Chichibabin's hydrocarbons as a function of the elongation of the π-system and the exocyclic substituents. Similarly to Chichibabin's hydrocarbon, the IFs have the potential to re-aromatize the quinoidal motif leading to an OS structure that is in resonance with the CS quinoidal structure. It has been shown that structures 1 and 2 depicted in Fig. 1 exhibit a greater y0 value (a measure of the diradical character, calculated by the Yamaguchi scheme,27 see computational details in ESI†) than 3, 4, and 5, and is mainly associated with the recovery of a larger number of the Clar's π-sextets in the OS form than the CS quinoid form.28 Moreover, the higher diradical character for structures 1 and 2 as compared to 3, 4, and 5 can be associated in part with the pro-aromatic quinodimethane framework. Both 1 and 2 have a meta-quinodimethane (m-QDM) subunit (highlighted with bold red lines in Fig. 1), in contrast to the 3 with ortho-quinodimethane (o-QDM) or 4 and 5 with para-quinodimethane (p-QDM) framework (Fig. 1).20
Diradical species in an open-shell form can exist in two forms, as either the OS singlet or a triplet state. Due to the dynamic spin polarization, π-diradicals29 usually exist as OS singlets in the electronic ground state and have low-lying triplet excited states.30IF's have been subjected to several structural modifications aiming to tune their optical and magnetic properties:31,32 (i) a longitudinal extension of the indacene π-conjugated core (by replacing the central benzene ring of IF to naphthalene or anthracene units producing fluorenofluorene (FF)33–35 and diindenoanthracene (DIAn)36) and (ii) lateral extension of the terminal benzene rings with other fused arenes.37 These techniques, used by the Haley and Tobe groups have been shown effective in tuning the OS character and aromaticity of IF-type scaffolds.38 However, despite all the achievements of recent years, there are significant difficulties in predicting the electronic nature of the ground state for such diradicals since it strongly depends on spatial separation and overlapping between unpaired electrons.30,39
In this work, we propose a simple Ground State Stability (GSS) rule to predict the electronic ground state for a given indenofluorene-type system based on the number of Clar's π-sextets40 it possesses in both CS and OS resonance forms. We carried out a detailed theoretical study of all the possible isomers of indenofluorene (IF), fluorenofluorene (FF), and diindenoanthracene (DIAn) to determine the stable ground state which allowed us to formulate and verify the GSS rule. Finally, several measures of aromaticity based on the electron density and magnetic criteria were employed to validate the proposed rule. Our concept, employing the straightforward and highly effective Clar's π-sextet model make possible the selective identification of IF-type systems based on their stable ground state without the need for performing advanced quantum-chemical calculations.
Computational details
Geometry optimizations for the CS isomers of the target systems were conducted using long-range corrected LC-ωPBE functional41 with empirical (D3BJ) Grimme dispersion correction42,43 and triple-ζ def2-TZVPP basis set.44,45 Long-range corrected functionals provide a better description of the delocalization in π-conjugated molecules,46–48 whereas the functionals with low percentage of HF exchange tends to exaggerate the electron delocalization.48,49 OS structures were optimized using broken-symmetry approximation with the spin-unrestricted ULC-ωPBE-D3BJ/def2-TZVPP level of theory, as implemented in Gaussian 16 (rev. A03).50 Normal mode vibrational frequencies were also calculated in each case to confirm the presence of local minimum, at the same level of theory. The singlet–triplet energy gap (ΔES–T) was estimated at the same level of theory.The contribution of aromatic OS structure with the quinoidal CS resonance form was analyzed using the biradical character index (y0) according to the Yamaguchi's scheme.51 In addition, we used the fractional occupation number weighted density (FOD) method52,53 to quantitatively describe the OS singlet biradical character. FOD analysis was performed with the default parameters as implemented in ORCA 4.1.2 (ref. 54) (TPSS/def2-TZVPP; Tel = 5000 K). Aromaticity analyses55 were carried out based on electronic (EDDB)56,57 and magnetic (NICS(0)iso and NICS(1)zz along with visualizing the 2D- and 3D-NICS isosurfaces)58–61 criteria using the same level of theory. The π-electron delocalization has been also examined by the multicenter index (MCI)62 (for details, see the ESI†).
Results and discussion
To get more insight into the electronic structure and stability of IF, FF, and DIAn biradicals, y0 values, the singlet–triplet energy gap (ΔES–T), and the FOD52 parameters were assessed. Fig. 2 demonstrates the set of the studied model compounds of IF, FF, and DIAn in their CS configuration with the indication of the Clar's π-sextets. To determine the extent of the multi-reference nature of the systems, the T1 diagnostic63 from DLPNO-CCSD(T)/cc-pVTZ single-point energy calculations64,65 were performed for the smallest IF systems. Calculation revealed that in all cases T1 values were smaller than 0.015 and 0.020 for singlet and triplet electronic states, respectively (Table S1, ESI†). Obtained number are lower than recommended T1 diagnostics values,63,66 therefore the systems of interest can be adequately treated using single-reference methods.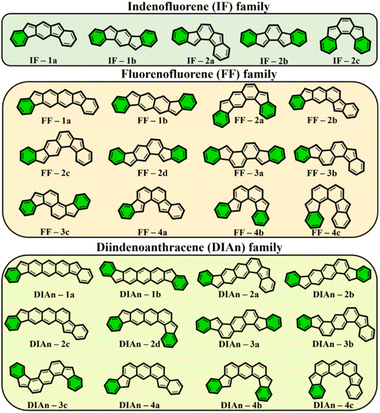 | ||
| Fig. 2 The whole set of regioisomers of IF, FF, and DIAn studied in this work with their corresponding Clar's π-sextet (highlighted in green) present in the CS resonance structure. | ||
Indenofluorene family and ground state stability rule
DFT calculations reveal that all the IF systems have an OS ground state. In particular, IF-1a and IF-2a possess a triplet ground state with a ΔES–T gap of 2.04 and 3.65 kcal mol−1, respectively (Table 1). Note that both structures belong to the m-QDM pro-aromatic network. The gain of two additional Clar's π-sextets in the OS form compared to the CS form that provides the extra stability for IF-1a and IF-2a to exist in the OS form. Previous calculations confirm that both these systems exhibit an OS ground state.20,67 Furthermore, the mesityl-substituted IF-1a was studied utilizing temperature-dependent 1H NMR and ESR spectroscopy, which validate the ground state to be an OS state.22| E (CS) | E (T) | E (OSS) | ΔES–Ta | y 0 | N FOD | R | |
|---|---|---|---|---|---|---|---|
| a ΔES–T = E (OSS) − E (T). b The ratio of number of Clar's π-sextets between the ground state OS and CS resonance structures. The number in parentheses represents the spin multiplicity of this ground OS electronic state. | |||||||
| IF-1a | 0.00 | −14.07 | −12.03 | 2.04 | 0.53 | 1.42 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
| IF-1b | 0.00 | 13.61 | −0.51 | −14.12 | 0.03 | 0.68 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| IF-2a | 0.00 | −16.19 | −12.54 | 3.65 | 1.00 | 2.03 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
| IF-2b | 0.00 | 8.78 | −1.22 | −10.00 | 0.07 | 0.94 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| IF-2c | 0.00 | 11.91 | −0.34 | −12.25 | 0.02 | 0.73 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
The obtained y0 value of 1.00 for IF-2a indicates that it would exhibit pure diradical character compared to the moderate y0 value of 0.53 for IF-1a (Table 1). In addition, the calculated NFOD values of >1.4 for both systems (Table 1) suggest a pronounced OS character. Good agreement of y0 and FOD values is observed since a linear relationship is often observed between them (Fig. S1, ESI†).52 The FOD plots in Fig. S2, ESI,† show the ρFOD density is greatest on the apical carbon atom of the five-membered rings correlating the location of the radical centers in the OS structure. The calculated spin density distribution of IFs confirms this, showing largest amplitudes at these apical carbon atoms (Fig. S3, ESI†).
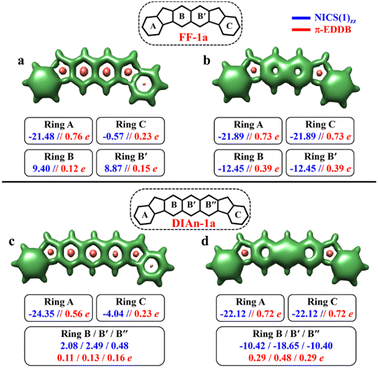
The aromaticity for the systems of interest was analyzed based on magnetic criteria using NICS(1)zz values for the CS and OS states respectively. In the CS singlet state of IF-1a, the aromatic character is prominently observed in ring A, as indicated by a NICS(1)zz value of −16.32 ppm, while rings B and C exhibit substantial positive values of 22.11 and 6.90 ppm, respectively, suggesting their antiaromatic nature (Fig. 3a). However, for the OS triplet state, rings A, B, and C display negative NICS(1)zz values, with ring A and C exhibiting relatively high negative values of −23.11 ppm, revealing the aromatic character for all three six-membered rings (Fig. 3b). In addition to the magnetic criteria, the aromaticity was analysed based on the electron density using EDDB measure of aromaticity. The calculated π-EDDB values for the OS triplet agrees well with the NICS(1)zz (Fig. 3), especially highlighting the aromatic character for the terminal benzene rings. This is clearly evident from the gauge-included magnetically induced currents68–72 (GIMIC) plots, which show a diatropic current (clockwise circuit) only for a terminal benzene ring in the CS form of IF-1a (Fig. 3i), in contrast to the diatropic ring current observed for all six-membered rings in the OS triplet state of IF-1a (Fig. 3j). For these molecules, 3D-NICSzz maps, NICS(1)zz values, and ring currents lead to the same conclusions, despite the well-known fact that the contribution of shieldings from adjacent rings in some cases provides unreliable NICS results in polycyclic molecules.72–74 The electronic and magnetic aromaticity descriptors are in good agreement with the depicted one Clar's π-sextet in the CS singlet and three Clar's π-sextets in the OS resonance structures for IF-1a. The same observation about the number of Clar's π-sextets can also be drawn for the IF-2a structure (Fig. S5, ESI†). This difference in the number of Clar's π-sextets is responsible for the relatively high stability of the OS forms for IF-1a and IF-2a structures. On the other hand, for these systems, the triplet and singlet OS species have similar energies, the triplet being slightly more stable as expected from Hund's rule.
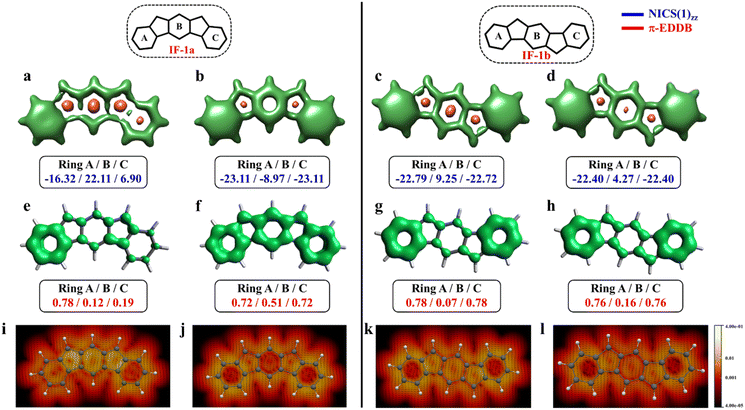 | ||
| Fig. 3 3D-NICSzz maps (isovalues: [−15.0, 20.0]) showing shielded (green) and deshielded (salmon) regions, with NICS(1)zz values (blue) of six-membered rings (in ppm) for CS (a)/(c), OS triplet (b), and singlet (d) states of IF-1a and IF-1b. Also shown are π-EDDB plots (e–h) (isovalue: 0.015 e) with normalized π-EDDB values (red) and GIMIC plots (i–l) (currents in the perpendicular plane with respect to the magnetic field located 2 bohr above the molecular plane. The intensity of current decreases going from light yellow (0.4 nA T−1 Å−2) to red and black (4 × 10−5 nA T−1 Å−2), and the black arrows indicate the direction of the current flow) for the same states (see Fig. S7† for enlarged GIMIC plots). | ||
For the other IF systems belonging to p-QDM (IF-1b and IF-2c) or o-QDM (IF-2b) networks, transition from CS to OS form is associated with an increase of only one Clar's π-sextet and thus only a modest gain in the stability observed. This, in turn, facilitates an easy return to the CS electronic state and results in a low diradical character28,75 with a y0 value smaller than 0.1 (Table 1), implying their categorization as nearly CS systems. Our conclusion is consistent with the previous experimental and theoretical studies,20,28 in which the calculations also shows a y0 value of less than 0.1 and also assigned them into a nearly CS systems.76 However, our electronic structure calculations show that the CS singlets of these systems are slightly higher in energy than the OS singlet by 0.34 and 1.22 kcal mol−1 for IF-2c and IF-2b, respectively. As we said before, the OS singlet has a very low diradical character, so its energy is not much influenced by this radical character, and, therefore, a similar energy to that of the CS singlet is expected. On the other hand, the triplet state is not favored because the loss of a π-bond is not compensated by the slight increase in aromaticity. The aromaticity descriptors indicate that the terminal six-membered rings in these systems are fully Clar's π-sextet in nature for all the resonance structures (CS and OS forms). While the central benzene ring in the OS singlet state exhibits a slight enhancement in the aromaticity compared to its CS one. For instance, in the case of IF-1b, we can see a modest gain in the aromaticity for ring B in the OS form compared to the CS state (Fig. 3c and d).
The NICS-XY scan is useful to explore different type of ring currents in flat π-conjugated systems, especially the global and semi-global ring currents.77,78 The NICS-XY scan (at 1.7 Å above the molecular plane) of CS state of IF-1b shows two diatropic rings (−17.86 ppm) at the terminal benzene rings, while the central 5–6–5 core can be considered non-aromatic. In contrast, the NICS-XY scan of the OS singlet state shows a semi-global weak diatropicity within the central 5–6–5 core with a value of −4.7 ppm (Fig. S6, ESI†). The 3D-NICSzz map distinctly illustrates the decrease in the deshielding region associated with the ring B in the OS state compared to the CS state. Although this increase in aromaticity cannot be attributed entirely to an additional gain of a full π-Clar's sextet ring in the OS form, it does support the presence of three aromatic rings in the OS form compared to two in the CS form. It is worth noting that the π-electron delocalization index (MCI), calculated for all IF systems, exhibits a similar trend to that observed with NICS and π-EDDB values (Fig. S8, ESI†). Consequently, for the analysis of aromaticity in subsequent larger systems, only NICS and EDDB criteria will be utilized. The calculated larger ΔES–T gap of −14.12 kcal mol−1 together with the smaller biradical character makes IF-1b behave nearly like a CS system. A detailed analysis of aromaticity for all the IFs is provided in the ESI (Fig. S4–S8, ESI†).
We utilized this difference in the number of Clar's π-sextets between the resonance structures in the CS and OS forms to determine the stability of ground state of IF-type systems. The proposed ground state stability (GSS) rule can be formulated as follows: “If the OS form gains double or more the number of Clar's π-sextets compared to the CS form, the ground state of that IF-type system will be a triplet; otherwise, it will be an OS singlet”.
Validation of the GSS rule for IFs with longitudinal core extension
To make sure that the formulated GSS rule is general and can be applied to systems other than indenofluorenes, we extended the study by modifying the conjugation pathway through the extension of the core units.We considered complete families of fluorenofluorenes (FF's) and diindenoanthracenes (DIAn's), in which the indene units are now linked by naphthalene and anthracene spacers respectively (Fig. 2). Similar to IF-1a, both FF-1a, and DIAn-1a gain more than double the number of Clar's π-sextets in the OS form compared to their corresponding CS form. In both FF-1a and DIAn-1a, the NICS(1)zz value for ring A in the CS form suggest an aromatic character with large negative values (−21.48 ppm for FF-1a and −24.35 ppm for DIAn-1a), whereas for ring C, they are weakly paratropic (Fig. 4a and c).
In the OS triplet form, rings A, B, and C have aromatic character, so there is a gain of two Clar's π-sextets in the OS form with respect to the CS resonance structure. In the case of FF-1a, the Clar's π-sextet of the OS form located in the naphthalene unit is a migrating Clar's π-sextet.40 This gain of two Clar's π-sextets is supported by the π-EDDB and 2D-NICS(1)zz plots of the OS form for FF-1a and DIAn-1a structures, as depicted in Fig. S9b and d, ESI.† Therefore according to the GSS rule, both systems should possess a triplet ground state. The electronic structure calculations confirm this, showing triplet ground state with very small ΔES–T gaps (2.04 and 3.05 kcal mol−1 for FF-1a and DIAn-1a respectively, as shown in Table 2).
| E (CS) | E (T) | E (OSS) | ΔES–Ta | y 0 | N FOD | R | |
|---|---|---|---|---|---|---|---|
| a ΔES–T = E (OSS) − E (T). b The ratio of number of Clar's π-sextets between the ground state OS and CS resonance structures. The number in parentheses represents the spin multiplicity of this ground OS electronic state. | |||||||
| FF-1a | 0.00 | −23.00 | −20.96 | 2.04 | 0.69 | 1.55 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
| FF-1b | 0.00 | 0.30 | −6.92 | −7.23 | 0.31 | 1.10 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| DIAn-1a | 0.00 | −30.74 | −27.70 | 3.05 | 0.81 | 1.74 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
| DIAn-1b | 0.00 | −8.13 | −13.62 | −5.49 | 0.51 | 1.40 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
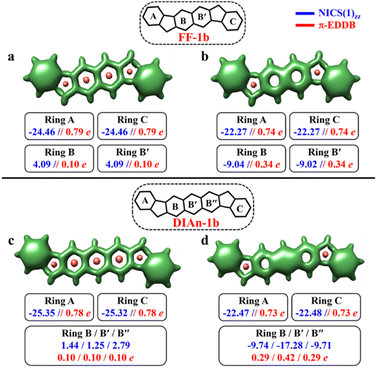
In contrast to the FF-1a and DIAn-1a, the analysis of the aromaticity for FF-1b and DIAn-1b isomers revealed that both their terminal rings exhibit pronounced aromatic character with a NICS(1)zz value of −24.46 and −25.35 ppm, respectively (Fig. 5). While the naphthalene spacer remains antiaromatic with a deshielded region within those rings. The transition from the CS to the OS structure induces substantial aromatization of the central ring B, while rings A and C retain almost the same level of aromaticity. The calculated π-EDDB values (Fig. 5) together with the 2D-NICS(1)zz scan lead to the same conclusion (Fig. S10, ESI†). The detailed analysis of aromaticity for all the FF and DIAn systems are provided in the ESI (Fig. S9–S14, ESI†). To compare the predictions made within the GSS rule, a series of DFT calculations for the CS and OS forms of FF-1b and DIAn-1b were performed. The obtained results are in perfect agreement with the GSS rule suggesting that both FF-1b and DIAn-1b have OS singlet as their ground state. Interestingly to note that the ΔES–T gap decreases as the π-conjugation core extends from benzene (IF-1b) to anthracene (DIAn-1b), reducing from −14.12 to −5.49 kcal mol−1, respectively. A notable increase in the diradical character y0, rising from 0.03 for IF-1b to 0.51 for DIAn-1b, is also observed (Table 2). Our observations aligns with the findings from other studied diradicaloids, where elongating the conjugation distance between radical centers results in increased diradical character.26,79 The rise in the y0 value and the decreasing in the ΔES–T gap are linked to the increased stability of the singlet diradical state. The greater stability of the singlet state with respect to the triplet state can be rationalized by an additive dynamic spin polarization phenomenon, which stabilizes the singlet state.29 We confirm the consistency of the GSS rule with the remaining isomers of FF and DIAn families outlined in Fig. 2. For all the examined systems, the results are in full accordance with the GSS rule: in every IF, FF, and DIAn isomers, if the systems acquire more than double the number of Clar's π-sextets in the OS form compared to the CS form, it adopts a triplet state; otherwise, it persists as an OS singlet state (Tables S2–S3 and Fig. S13–S14, ESI†).
Validation of the GSS rule for IFs with lateral core and outer arene ring extensions
From the previously obtained results, it is evident that longitudinal extension of the core unit from benzene (IF's) to anthracene (DIAn's) does not alter the applicability of the derived rule. Additionally, we explored lateral extension of the core unit in some IF-systems to further investigate the rule.As illustrated in Fig. 6, the different core extensions for the IF-2b behave similarly to the parent system concerning the GSS rule. Specifically, the number of Clar's π-sextets in the OS resonance form is less than double compared to the CS state, indicating an OS singlet ground state. In addition, we considered several possible extensions for selected fluorenofluorenes. In particular, the core-extension applied to FF-1a (Fig. 6), results in more than double the number of Clar's π-sextets in the OS form compared to the CS form suggesting a triplet ground state according to the GSS rule. In the literature we found an interesting example of the π-extended FF-1b system (FF-1b-ext), synthesized by Feng and co-workers80 (Fig. 6), which involving a lateral extension that fuses the core 6-membered ring with the terminal benzene ring. According to the GSS rule this compound is expected to be an OS singlet in the electronic ground state. Indeed, our DFT calculations confirm these expectations (Table 3). All details on the aromaticity for these systems are provided in the ESI (Fig. S15–S16†).
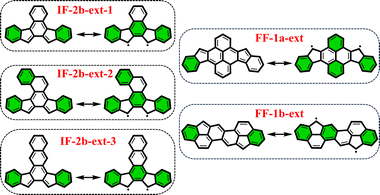 | ||
| Fig. 6 Clar's π-sextet (highlighted in green) representation of some of the core-extended systems in its closed and open-shell states. | ||
| E (CS) | E (T) | E (OSS) | ΔES–Ta | y 0 | N FOD | R | |
|---|---|---|---|---|---|---|---|
| a ΔES–T = E (OSS) − E (T). b The ratio of number of Clar's π-sextets between the ground state OS and CS resonance structures. The number in parentheses represents the spin multiplicity of this ground OS electronic state. | |||||||
| Core-extension | |||||||
| IF-2b-ext-1 | 0.00 | −3.31 | −9.56 | −6.25 | 0.44 | 1.64 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| IF-2b-ext-2 | 0.00 | 4.07 | −3.86 | −7.93 | 0.21 | 1.40 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| IF-2b-ext-3 | 0.00 | −11.33 | −18.20 | −6.87 | 0.68 | 2.08 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| FF-1a-ext | 0.00 | −44.73 | −40.20 | 4.53 | 0.99 | 2.36 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (3) 4 (3) |
| FF-1b-ext | 0.00 | 2.76 | −4.16 | −6.93 | 0.25 | 1.12 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Periphery-extension | |||||||
| IF-1a-NT | 0.00 | −25.98 | −21.86 | 4.12 | 0.79 | 1.89 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
| IF-1b-NT | 0.00 | 12.80 | −0.81 | −13.61 | 0.04 | 0.81 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
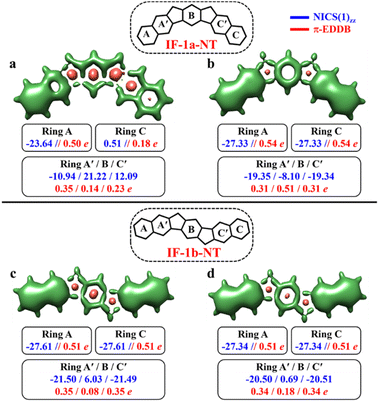
After successfully demonstrating the GSS rule applicability to a broad type of core-extended systems, we decided to test the periphery extension. The lateral extension of the terminal benzene rings of IF-1a and IF-1b systems with π-extended (naphthalene) extremities resulted in IF-1a-NT and IF-1b-NT with increased conjugation lengths (Fig. 7).
The CS resonance form of IF-1a-NT allows for the depiction of one Clar's π-sextet specifically ring A (Fig. 7a), with a corresponding NICS(1)zz value of −23.64 ppm. In contrast, the OS form, illustrated by the 3D-NICSzz maps in Fig. 7b, reveals the existence of three Clar's π-sextets – rings A, B, and C with significantly greater aromaticity for the terminal rings with a NICS(1)zz value of −27.33 ppm. At the same time, the behavior of the IF-1b-NT system is similar to the parental IF-1b – both the terminal six-membered rings in CS and OS state have a full Clar's π-sextet with a NICS(1)zz value of around −27.0 ppm. Most importantly in the case of ring B, NICS(1)zz values indicate an enhancement in the aromaticity for the OS state compared to the CS state, leading to a total of three aromatic rings in the OS form (Fig. 7d). The analysis of π-EDDB values and plots also corroborate this analysis (Fig. S17, ESI†).
As per the GSS rule, IF-1a-NT ground state should be a triplet, given the gain of more than double the number of Clar's π-sextet in its OS form. At the same time, IF-1b-NT ground state is expected to be an OS singlet, as it gains only one additional Clar's π-sextet in the OS form compared to the CS resonance form. Indeed, performed calculations confirm these predictions (Table 3). The calculations also showed a slight decrease in the ΔES–T gap for IF-1b-NT compared to the parent IF-1b by about 0.5 kcal mol−1, alongside an increase in the diradical character (NFOD value rising from 0.68 in IF-1b to 0.81 in IF-1b-NT).
Validation of GSS rule for IFs with massive extended and curved core
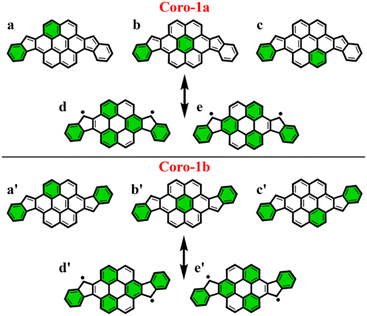
To make sure that the proposed GSS rule can be reliably used in the most sophisticated cases, involving massive core extension, we considered two systems with laterally extended anthracene spacer. Both Coro-1a and Coro-1b systems are π-extensions of DIAn-1a and DIAn-1b, respectively, and contain coronene as the core spacer (Fig. 8).According to Clar's model, Coro-1a can be depicted with two Clar's π-sextets for the CS form and five for the OS form. It is important to highlight that in both CS and OS forms, the Clar's model doesn't neatly align with a particular resonance structure. Instead, the valence structure of the coronene spacer is a superposition of equivalent structures and can be represented by a migrating π-sextet.81 This is especially pronounced in the OS form, where the actual structure can be considered as a combination of two resonance structures with π-sextets that can migrate to its adjacent rings82 (Fig. 8d and e). In accordance with the GSS rule, the ground state should be regarded as a triplet, given that transitioning from the CS to the OS form results in a gain of more than double the number of Clar's π-sextets in the CS form. Indeed, the results of quantum-chemical calculations fully support GSS rule, predicting triplet ground state with a ΔES–T gap of 3.73 kcal mol−1 (Table 4).
| E (CS) | E (T) | E (OSS) | ΔES–Ta | y 0 | N FOD | R | |
|---|---|---|---|---|---|---|---|
| a ΔES–T = E (OSS) − E (T). b The ratio of number of Clar's π-sextets between the ground state OS and CS resonance structures. The number in parentheses represents the spin multiplicity of this ground OS electronic state. | |||||||
| Coro-1a | 0.00 | −38.30 | −34.57 | 3.73 | 0.94 | 2.24 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (3) 5 (3) |
| Coro-1b | 0.00 | −17.89 | −21.69 | −3.80 | 0.75 | 2.04 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (1) 5 (1) |
| Cora-1a | 0.00 | −39.88 | −39.06 | 0.82 | 0.98 | 2.40 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (3) 4 (3) |
| Cora-1b | 0.00 | −28.80 | −27.30 | 1.51 | 0.94 | 2.26 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (3) 4 (3) |
Coro-1b in contrast to Coro-1a structure, in the CS form, could be represented by three aromatic π-sextets – two on the terminal benzene rings and a migrating π-sextet positioned on the coronene spacer (Fig. 8a′–c′). At the same time, OS forms for Coro-1a and Coro-1b systems are the same and can be depicted by five Clar's π-sextets. Thus, according to the GSS rule Coro-1b should exhibit an OS singlet ground state, since the number of Clar's π-sextets in the OS form is less than double the number of Clar's π-sextets in the CS form. The DFT calculations confirm that the ground state in Coro-1b is an OS singlet, with a ΔES–T gap of −3.80 kcal mol−1. It is worth noting that Coro-1a and Coro-1b, which have an OS singlet state of similar diradical character, have different states as their ground states.
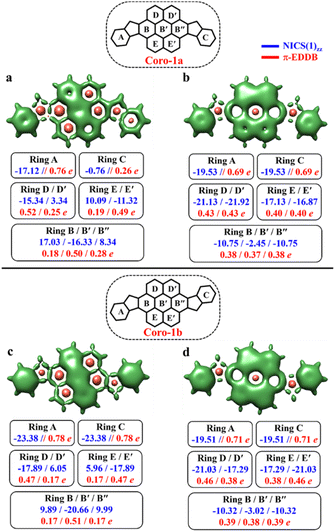
As seen in Fig. 9, the 3D-NICSzz map illustrates the difference in aromaticity for the terminal benzene rings between Coro-1a and Coro-1b in the CS state. As expected, the migrating Clar's π-sextet in the coronene spacer is evident from these plots (Fig. 9a and c), as well as from the provided NICS(1)zz values. Meanwhile, in the OS form, the NICS(1)zz values for the benzene rings in the coronene spacer exhibit very similar values for both Coro-1a and Coro-1b structures, indicating the delocalized nature of the spacer. This is supported by the aromaticity analysis using the electronic descriptor π-EDDB values (Fig. 9), 2D-NICS(1)zz, and π-EDDB plots (Fig. S18, ESI†).
It is worth mentioning that Kubo et al. demonstrated that in benzenoid CPHs with the same chemical composition, the molecule with more aromatic Clar's π-sextets in the diradical resonance forms has greater diradical character.83,84 While this rule is interesting, our study uses the ratio of Clar's π-sextets in CS and OS forms instead of the difference in their numbers. To explain this, we compared two sets of molecules: DIAn-1a/1b and Coro-1a/1b. The Coro-1a/1b systems gain more Clar's π-sextets when transitioning to OS states (3 and 2, respectively) compared to the DIAn-1a/1b systems (2 and 1, respectively). However, the increase in global aromaticity is smaller for Coro systems than for DIAn systems (Table S4, ESI†). This means that simply counting the gain in Clar's π-sextets is not a reliable way to predict the preferred electronic state. Instead, we found that the ratio of Clar's π-sextets between CS and OS states is a more consistent and reliable predictor across different systems, regardless of the size of the π-electron system.
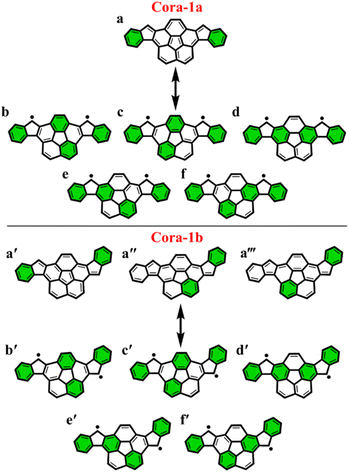
To further explore the applicability of the GSS rule we examined two, not just core-extended, but also bent systems. Both these regioisomers – Cora-1a and Cora-1b, that can be considered as IF-type systems with corannulene spacers, were synthesized and characterized by Cao and co-workers (Fig. 10).85
According to the Clar's model, both the Cora-1a and Cora-1b can be represented as having two Clar's π-sextets, comprising the terminal benzene rings in the CS form. Additionally, the CS form of Cora-1b can also be represented by two other resonance structures (Fig. 10a′′ and a′′′), where one Clar's π-sextet resides on the terminal benzene ring and the other within the corannulene spacer. However, in the case of the OS form, both Cora-1a and Cora-1b exhibit four Clar's π-sextets – two in the terminal benzene rings and the other two as migrating sextets within the corannulene spacer (Fig. 10). Therefore, in line with the GSS rule, with the doubling of the number of Clar's π-sextets in the OS form compared to the CS form, both systems should be in a triplet ground state. Indeed, our DFT calculations fully support this, predicting a triplet as the ground state with a small ΔES–T gap of 0.82 and 1.51 kcal mol−1 for Cora-1a and Cora-1b, respectively (Table 4). The calculated diradical character of more than 0.94 for both systems suggests they are nearly pure diradicals consistent with reported values.85
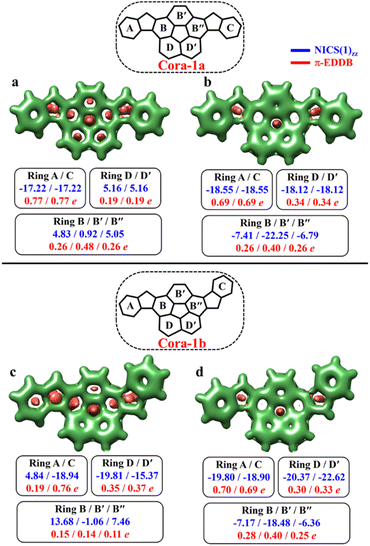
As depicted in Fig. 11, the NICS(0)iso values suggest the difference in aromaticity for the terminal benzene rings between Cora-1a and Cora-1b in the CS state. In Cora-1a, both terminal benzene rings, ring A and C provide a NICS(1)zz value of −17.22 ppm, whereas in Cora-1b, the most aromatic rings correspond to terminal ring C and ring D from the corannulene spacer, with a value exceeding −18.94 ppm. Consequently, resonance structure a′′′ (Fig. 10) corresponds to the CS form of Cora-1b according to the aromaticity analysis. Meanwhile in the OS form, there is an increase in aromaticity for both systems. Specifically, both Cora-1a and Cora-1b shows pronounced aromatic character in both terminal rings (with NICS(1)zz values ranging from −18.5 to −19.8 ppm) and two other rings from the corannulene spacer (values ranging from −18.1 to −22.6 ppm), suggesting a greater contribution from resonance structures b/c and b′/c′ (Fig. 10) for Cora-1a and Cora-1b, respectively. These trends are also evident in the π-EDDB values and plots (Fig. S19, ESI†). This result further validates the GSS rule with the presence of two and four Clar's π-sextets in the CS and OS forms of these systems.
Exploring the GSS rule beyond IF systems
In order to test the applicability of the proposed GSS rule to systems beyond the IF-type, several biradicaloids that are polycyclic arenes have been selected. Among the tested systems, we considered heptazethrene (HPZ1 and HPZ2)86,87 and octazethrene (OCZ)88 derivatives, benzo-extended bis-periazulene (BPaz),89,90 and azulene-embedded nanographene (Az-NG)91 (Fig. 12).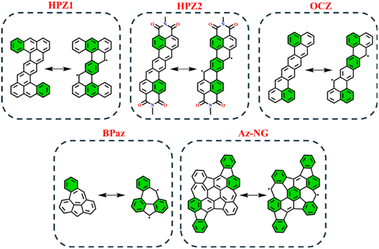 | ||
| Fig. 12 Graphical representation of non-indenofluorene-type biradicaloids in their closed and open-shell states. Clar's π-sextet is highlighted in green. | ||
As seen, the selected biradicaloids have different ratios of the Clar's π-sextets in their CS and OS states and thus, in accordance with the GSS rule, must appear either as OS singlets or as triplets. In the case of HPZ1, HPZ2, OCZ, and Az-NG, the ratio of Clar's π-sextets is less than two; thus, these systems are expected to be OS singlets in their ground state. For BPaz, the ratio is equal to three, and thus a triplet state must be the ground state. Performed quantum chemical calculations (see Table 5) fully confirmed the correctness of the predictions made within the GSS rule.
| E (CS) | E (T) | E (OSS) | ΔES−Ta | y 0 | N FOD | R | |
|---|---|---|---|---|---|---|---|
| a ΔES–T = E (OSS) − E (T). b The ratio of number of Clar's π-sextets between the ground state OS and CS resonance structures. The number in parentheses represents the spin multiplicity of this ground OS electronic state. | |||||||
| HPZ1 | 0.00 | −2.44 | −11.78 | −9.34 | 0.45 | 1.53 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| HPZ2 | 0.00 | −0.33 | −9.44 | −9.11 | 0.38 | 1.53 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| OCZ | 0.00 | −5.80 | −14.37 | −8.58 | 0.50 | 1.50 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (1) 3 (1) |
| Az-NG | 0.00 | −19.48 | −21.12 | −1.64 | 0.82 | 2.27 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (1) 7 (1) |
| BPaz | 0.00 | −13.16 | −7.65 | 5.51 | 0.65 | 1.54 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (3) 3 (3) |
As can be noticed, in the majority of considered cases, the difference in Clar's π-sextet numbers between the CS and the corresponding OS electronic state follows a certain pattern (see Table S5†). In particular, if there is a gain of more than one Clar's π-sextet in the OS form compared to the CS form, the ground state of that IF-type system will be a triplet; otherwise, it will be an OS singlet.92 Indeed, the rule formulated in this way works well for parental IF-, FF-, and DIAn-systems. Moreover, lateral core extension and outer arene ring extension do not lead to its violation. However, for massively core-extended systems like Coro-1b, the rule formulated in terms of the difference in Clar's π-sextets gives an incorrect prediction. Another system in which the ground state does not correspond to predictions made on the basis of the difference in the number of Clar's π-sextets is Az-NG. Note that in both mentioned cases, the difference between OS singlet and triplet states was found to be −3.80 and −1.64 kcal mol−1 for Coro-1b and Az-NG, respectively. These values are rather small and can potentially be rationalized by the non-accounting of a resonance term of the Clar's resonators81,92 (Fig. S20, ESI†). A comparison of the difference in Clar's π-sextet numbers and their ratio for all studied systems is provided in Table S5, ESI.† It is important to highlight that the proposed GSS rule, which uses the ratio of number of Clar's π-sextets between the CS and OS states instead of the difference in their exact numbers, accurately predicts the ground state for all the studied systems without any exceptions.
Overall, the excellent performance of the GSS rule in predicting the nature of the ground state not only in IF-type systems but also in other arene biradicals confirms that the proposed rule is reliable and robust and can be applied to a wide variety of organic systems. Finally, for all the studied system, the comparison of global aromaticity in both CS and corresponding OS electronic states shows that OS states (both triplet and singlet biradical) exhibit higher aromaticity compared to CS states (Table S4, ESI†). Notably, the increase in aromaticity is more pronounced in the triplet state than in the OS singlet state. This observation aligns with the increase in the number of Clar's π-sextets during the transition from CS to OS forms.
Conclusions
In this work, we formulate a simple rule to predict the ground state stability of a class of indenofluorene-type systems based on the number of Clar's π-sextets present in their closed-shell and open-shell resonance structures. The complete set of isomers, beginning from the indenofluorene (IF) featuring a single six-membered ring core, as well as their longitudinally π-extended version with naphthalene (FF) and anthracene (DIAn) between two indene units were considered for the proposed rule validation. Moreover, selected systems with π-extended terminal rings and laterally extended core spacers were also examined.In accordance with the proposed GSS rule, the electronic ground state of the IF-type system is triplet if there is a gain of double or more the number of Clar's π-sextets in the open-shell resonance form compared to the closed-shell form; otherwise, the ground state is an open-shell singlet. Performed quantum chemical calculations and analysis of the aromaticity of studied systems confirms the proposed rule and demonstrates that aromaticity plays the most crucial role in determining of the electronic ground state for such polycyclic hydrocarbons. The simplicity of the GSS rule together with the underlying Clar's π-sextet model makes the proposed rule a powerful and easy-to-use tool for selecting systems with desirable properties for building new IF-type materials.
Data availability
The detailed description of the supporting data included in the ESI,† which contains relative energies in different electronic states for all the studied systems and the detailed analysis of aromaticity for the same. The results of the DFT simulations for the systems of interest are available at https://doi.org/10.5281/zenodo.12532666.Author contributions
G. G. investigation, data curation, formal analysis, writing – original draft, writing – review & editing. A. J. S. investigation, supervision, writing – review & editing. M. S. supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Spanish Ministerio de Ciencia e Innovación (Network RED2018-102815-T, project PID2020-113711GB-I00/MCIN/AEI/10.13039/501100011033), and the Catalan Conselleria de Recerca i Universitats of the Generalitat de Catalunya (project 2021SGR623). G. G. is thankful for the contract 2020 FISDU 00345 from the Generalitat de Catalunya. A. J. S. gratefully acknowledges Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grant no. PLG/2022/015981 and PLG/2023/016841. Authors are grateful to Consorci de Serveis Universitaris de Catalunya (CSUC) for the computational time.References
- Z. Zeng, Y. M. Sung, N. Bao, D. Tan, R. Lee, J. L. Zafra, B. S. Lee, M. Ishida, J. Ding, J. T. López Navarrete, Y. Li, W. Zeng, D. Kim, K.-W. Huang, R. D. Webster, J. Casado and J. Wu, J. Am. Chem. Soc., 2012, 134, 14513–14525 CrossRef CAS.
- L. Zhang, Y. Cao, N. S. Colella, Y. Liang, J.-L. Brédas, K. N. Houk and A. L. Briseno, Acc. Chem. Res., 2015, 48, 500–509 CrossRef CAS PubMed.
- D. M. Guldi, B. M. Illescas, C. M. Atienza, M. Wielopolski and N. Martín, Chem. Soc. Rev., 2009, 38, 1587–1597 RSC.
- M. Hermann, D. Wassy and B. Esser, Angew. Chem., Int. Ed., 2021, 60, 15743–15766 CrossRef CAS PubMed.
- V. A. Dediu, L. E. Hueso, I. Bergenti and C. Taliani, Nat. Mater., 2009, 8, 707–716 CrossRef CAS PubMed.
- Y. Morita, S. Nishida, T. Murata, M. Moriguchi, A. Ueda, M. Satoh, K. Arifuku, K. Sato and T. Takui, Nat. Mater., 2011, 10, 947–951 CrossRef CAS PubMed.
- J. M. Fernández-García, P. J. Evans, S. Filippone, M. Á. Herranz and N. Martín, Acc. Chem. Res., 2019, 52, 1565–1574 CrossRef.
- S. Mishra, G. Catarina, F. Wu, R. Ortiz, D. Jacob, K. Eimre, J. Ma, C. A. Pignedoli, X. Feng, P. Ruffieux, J. Fernández-Rossier and R. Fasel, Nature, 2021, 598, 287–292 CrossRef CAS.
- C. Poriel and J. Rault-Berthelot, Chem. Soc. Rev., 2023, 52, 6754–6805 RSC.
- D. Kong, T. Cai, H. Fan, H. Hu, X. Wang, Y. Cui, D. Wang, Y. Wang, H. Hu, M. Wu, Q. Xue, Z. Yan, X. Li, L. Zhao and W. Xing, Angew. Chem., Int. Ed., 2022, 61, e202114681 CrossRef CAS PubMed.
- M. D. Hager, B. Esser, X. Feng, W. Schuhmann, P. Theato and U. S. Schubert, Adv. Mater., 2020, 32, 2000587 CrossRef CAS PubMed.
- P. Hu, S. Lee, T. S. Herng, N. Aratani, T. P. Gonçalves, Q. Qi, X. Shi, H. Yamada, K.-W. Huang, J. Ding, D. Kim and J. Wu, J. Am. Chem. Soc., 2016, 138, 1065–1077 CrossRef CAS PubMed.
- J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- Z. Majzik, N. Pavliček, M. Vilas-Varela, D. Pérez, N. Moll, E. Guitián, G. Meyer, D. Peña and L. Gross, Nat. Commun., 2018, 9, 1198 CrossRef PubMed.
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Chem. Sci., 2023, 14, 5569–5576 RSC.
- C. K. Frederickson, B. D. Rose and M. M. Haley, Acc. Chem. Res., 2017, 50, 977–987 CrossRef CAS PubMed.
- S. Mishra, M. Vilas-Varela, L.-A. Lieske, R. Ortiz, S. Fatayer, I. Rončević, F. Albrecht, T. Frederiksen, D. Peña and L. Gross, Nat. Chem., 2024, 16, 755–761 CrossRef CAS PubMed.
- D. T. Chase, B. D. Rose, S. P. McClintock, L. N. Zakharov and M. M. Haley, Angew. Chem., Int. Ed., 2011, 50, 1127–1130 CrossRef CAS PubMed.
- A. G. Fix, P. E. Deal, C. L. Vonnegut, B. D. Rose, L. N. Zakharov and M. M. Haley, Org. Lett., 2013, 15, 1362–1365 CrossRef CAS PubMed.
- J. J. Dressler, Z. Zhou, J. L. Marshall, R. Kishi, S. Takamuku, Z. Wei, S. N. Spisak, M. Nakano, M. A. Petrukhina and M. M. Haley, Angew. Chem., Int. Ed., 2017, 56, 15363 CrossRef CAS PubMed.
- A. Shimizu and Y. Tobe, Angew. Chem., Int. Ed., 2011, 50, 6906–6910 CrossRef CAS PubMed.
- A. Shimizu, R. Kishi, M. Nakano, D. Shiomi, K. Sato, T. Takui, I. Hisaki, M. Miyata and Y. Tobe, Angew. Chem., Int. Ed., 2013, 52, 6076–6079 CrossRef CAS PubMed.
- E. Clar and R. Schoental, Polycyclic hydrocarbons, Springer-Verlag, Berlin, 1964, vol. 2 Search PubMed.
- E. Clar, The Aromatic Sextet, New York, Wiley, 1972 Search PubMed.
- L. K. Montgomery, J. C. Huffman, E. A. Jurczak and M. P. Grendze, J. Am. Chem. Soc., 1986, 108, 6004–6011 CrossRef CAS PubMed.
- S. Escayola, M. Callís, A. Poater and M. Solà, ACS Omega, 2019, 4, 10845–10853 CrossRef CAS PubMed.
- K. Yamaguchi, Chem. Phys. Lett., 1975, 33, 330–335 CrossRef CAS.
- M. Di Giovannantonio, K. Eimre, A. V Yakutovich, Q. Chen, S. Mishra, J. I. Urgel, C. A. Pignedoli, P. Ruffieux, K. Müllen, A. Narita and R. Fasel, J. Am. Chem. Soc., 2019, 141, 12346–12354 CrossRef CAS PubMed.
- P. Karafiloglou, J. Chem. Educ., 1989, 66, 816 CrossRef CAS.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed.
- I. Badía-Domínguez, S. Canola, V. Hernández Jolín, J. T. López Navarrete, J. C. Sancho-García, F. Negri and M. C. Ruiz Delgado, J. Phys. Chem. Lett., 2022, 13, 6003–6010 CrossRef PubMed.
- C. A. Barboza, R. Bast, E. Barboza, D. MacLeod-Carey and R. Arratia-Perez, New J. Chem., 2018, 42, 15648–15654 RSC.
- B. D. Rose, C. L. Vonnegut, L. N. Zakharov and M. M. Haley, Org. Lett., 2012, 14, 2426–2429 CrossRef CAS PubMed.
- J. E. Barker, C. K. Frederickson, M. H. Jones, L. N. Zakharov and M. M. Haley, Org. Lett., 2017, 19, 5312–5315 CrossRef CAS PubMed.
- A. S. Hacker, M. Pavano, J. E. Wood, H. Hashimoto, K. M. D'Ambrosio, C. K. Frederickson, J. L. Zafra, C. J. Gómez-García, V. Postils, A. Ringer McDonald, D. Casanova, D. K. Frantz and J. Casado, Chem. Commun., 2019, 55, 14186–14189 RSC.
- G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. Ponce Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Nat. Chem., 2016, 8, 753–759 CrossRef CAS PubMed.
- J. J. Dressler and M. M. Haley, J. Phys. Org. Chem., 2020, 33, e4114 CrossRef CAS.
- J. Guo, X. Tian, Y. Wang and C. Dou, Chem. Res. Chin. Univ., 2023, 39, 161–169 CrossRef CAS.
- X. Xu, S. Takebayashi, H. Hanayama, S. Vasylevskyi, T. Onishi, T. Ohto, H. Tada and A. Narita, J. Am. Chem. Soc., 2023, 145, 3891–3896 CrossRef CAS PubMed.
- M. Solà, Front. Chem., 2013, 1, 22 Search PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- O. A. Vydrov, J. Heyd, A. V Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 74106 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. W. Szczepanik, M. Solà, M. Andrzejak, B. Pawełek, J. Dominikowska, M. Kukułka, K. Dyduch, T. M. Krygowski and H. Szatylowicz, J. Comput. Chem., 2017, 38, 1640–1654 CrossRef CAS PubMed.
- I. Casademont-Reig, T. Woller, J. Contreras-García, M. Alonso, M. Torrent-Sucarrat and E. Matito, Phys. Chem. Chem. Phys., 2018, 20, 2787–2796 RSC.
- L. J. Karas, S. Jalife, R. V Viesser, J. V Soares, M. M. Haley and J. I. Wu, Angew. Chem., Int. Ed., 2023, 62, e202307379 CrossRef CAS PubMed.
- R. A. King, T. D. Crawford, J. F. Stanton and H. F. Schaefer, J. Am. Chem. Soc., 1999, 121, 10788–10793 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, 2016 Search PubMed.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS.
- C. A. Bauer, A. Hansen and S. Grimme, Chem.–Eur. J., 2017, 23, 6150–6164 CrossRef CAS PubMed.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- M. Solà, A. I. Boldyrev, M. K. Cyrañski, T. M. Krygowski and G. Merino, Aromaticity and Antiaromaticity: Concepts and Applications, Wiley, Chichester, 2022 Search PubMed.
- D. W. Szczepanik, M. Andrzejak, K. Dyduch, E. Żak, M. Makowski, G. Mazur and J. Mrozek, Phys. Chem. Chem. Phys., 2014, 16, 20514–20523 RSC.
- D. W. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawełek, T. M. Krygowski, H. Szatylowicz and M. Solà, Phys. Chem. Chem. Phys., 2017, 19, 28970–28981 RSC.
- I. Fernández, Aromaticity: Modern Computational Methods and Applications, Elsevier, Dordretch, 2021 Search PubMed.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- R. Gershoni-Poranne and A. Stanger, Chem.–Eur. J., 2014, 20, 5673–5688 CrossRef CAS PubMed.
- E. Kleinpeter and A. Koch, Org. Biomol. Chem., 2024, 22, 3035–3044 RSC.
- P. Bultinck, R. Ponec and S. Van Damme, J. Phys. Org. Chem., 2005, 18, 706–718 CrossRef CAS.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207 CrossRef.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. Meana-Pañeda, X. Xu, H. Ma and D. G. Truhlar, J. Phys. Chem. A, 2017, 121, 1693–1707 CrossRef PubMed.
- J. E. Barker, J. J. Dressler, A. Cárdenas Valdivia, R. Kishi, E. T. Strand, L. N. Zakharov, S. N. MacMillan, C. J. Gómez-García, M. Nakano, J. Casado and M. M. Haley, J. Am. Chem. Soc., 2020, 142, 1548–1555 CrossRef CAS PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, R. J. F. Berger and H. Fliegl, Phys. Chem. Chem. Phys., 2016, 18, 15934–15942 RSC.
- M. Orozco-Ic and G. Merino, Chemistry, 2021, 3, 1381–1391 CrossRef CAS.
- E. Paenurk and R. Gershoni-Poranne, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644 RSC.
- M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, J. Phys. Chem. A, 2021, 125, 5753–5764 CrossRef CAS PubMed.
- D. Inostroza, V. García, O. Yañez, J. J. Torres-Vega, A. Vásquez-Espinal, R. Pino-Rios, R. Báez-Grez and W. Tiznado, New J. Chem., 2021, 45, 8345–8351 RSC.
- J. Poater, M. Solà, R. G. Viglione and R. Zanasi, J. Org. Chem., 2004, 69, 7537–7542 CrossRef CAS PubMed.
- S. Moles Quintero, M. M. Haley, M. Kertesz and J. Casado, Angew. Chem., Int. Ed., 2022, 61, e202209138 CrossRef CAS PubMed.
- K. Fukuda, T. Nagami, J. Fujiyoshi and M. Nakano, J. Phys. Chem. A, 2015, 119, 10620–10627 CrossRef CAS PubMed.
- A. Stanger, G. Monaco and R. Zanasi, ChemPhysChem, 2020, 21, 65–82 CrossRef CAS PubMed.
- J. L. Marshall, K. Uchida, C. K. Frederickson, C. Schütt, A. M. Zeidell, K. P. Goetz, T. W. Finn, K. Jarolimek, L. N. Zakharov, C. Risko, R. Herges, O. D. Jurchescu and M. M. Haley, Chem. Sci., 2016, 7, 5547–5558 RSC.
- P. Hu and J. Wu, Can. J. Chem., 2016, 95, 223–233 CrossRef.
- J. Liu, J. Ma, K. Zhang, P. Ravat, P. Machata, S. Avdoshenko, F. Hennersdorf, H. Komber, W. Pisula, J. J. Weigand, A. A. Popov, R. Berger, K. Müllen and X. Feng, J. Am. Chem. Soc., 2017, 139, 7513–7521 CrossRef CAS PubMed.
- Y. Wang, J. Phys. Chem. A, 2022, 126, 164–176 CrossRef CAS PubMed.
- A. Kumar, M. Duran and M. Solà, J. Comput. Chem., 2017, 38, 1606–1611 CrossRef CAS PubMed.
- S. Das and J. Wu, in Polycyclic Arenes and Heteroarenes, Wiley-VCH, Weinheim, 2015, pp. 1–36 Search PubMed.
- A. Konishi, Y. Hirao, M. Nakano, A. Shimizu, E. Botek, B. Champagne, D. Shiomi, K. Sato, T. Takui, K. Matsumoto, H. Kurata and T. Kubo, J. Am. Chem. Soc., 2010, 132, 11021–11023 CrossRef CAS PubMed.
- R.-Q. Lu, S. Wu, L.-L. Yang, W.-B. Gao, H. Qu, X.-Y. Wang, J.-B. Chen, C. Tang, H.-Y. Shi and X.-Y. Cao, Angew. Chem., Int. Ed., 2019, 58, 7600–7605 CrossRef CAS PubMed.
- Z. Sun, S. Lee, K. H. Park, X. Zhu, W. Zhang, B. Zheng, P. Hu, Z. Zeng, S. Das, Y. Li, C. Chi, R.-W. Li, K.-W. Huang, J. Ding, D. Kim and J. Wu, J. Am. Chem. Soc., 2013, 135, 18229–18236 CrossRef CAS PubMed.
- Z. Sun, K.-W. Huang and J. Wu, J. Am. Chem. Soc., 2011, 133, 11896–11899 CrossRef CAS PubMed.
- Y. Li, W.-K. Heng, B. S. Lee, N. Aratani, J. L. Zafra, N. Bao, R. Lee, Y. M. Sung, Z. Sun, K.-W. Huang, R. D. Webster, J. T. López Navarrete, D. Kim, A. Osuka, J. Casado, J. Ding and J. Wu, J. Am. Chem. Soc., 2012, 134, 14913–14922 CrossRef CAS PubMed.
- K. Horii, R. Kishi, M. Nakano, D. Shiomi, K. Sato, T. Takui, A. Konishi and M. Yasuda, J. Am. Chem. Soc., 2022, 144, 3370–3375 CrossRef CAS PubMed.
- F. Wu, J. Ma, F. Lombardi, Y. Fu, F. Liu, Z. Huang, R. Liu, H. Komber, D. I. Alexandropoulos, E. Dmitrieva, T. G. Lohr, N. Israel, A. A. Popov, J. Liu, L. Bogani and X. Feng, Angew. Chem., Int. Ed., 2022, 61, e202202170 CrossRef CAS PubMed.
- J. Liu, S. Mishra, C. A. Pignedoli, D. Passerone, J. I. Urgel, A. Fabrizio, T. G. Lohr, J. Ma, H. Komber, M. Baumgarten, C. Corminboeuf, R. Berger, P. Ruffieux, K. Müllen, R. Fasel and X. Feng, J. Am. Chem. Soc., 2019, 141, 12011–12020 CrossRef CAS PubMed.
- This alternative formulation was proposed by Reviewer 1.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03465a |
| This journal is © The Royal Society of Chemistry 2024 |