Open Access Article
Open Access ArticleMachine learning demonstrates the impact of proton transfer and solvent dynamics on CO2 capture in liquid ammonia†
Marcos F.
Calegari Andrade
 *,
Sichi
Li
*,
Sichi
Li
 *,
Tuan Anh
Pham
*,
Tuan Anh
Pham
 ,
Sneha A.
Akhade
,
Sneha A.
Akhade
 and
Simon H.
Pang
and
Simon H.
Pang
 *
*
Materials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA. E-mail: calegariandr1@llnl.gov; li77@llnl.gov; pang6@llnl.gov
First published on 9th July 2024
Abstract
Direct air capture of CO2 using supported amines provides a promising means to achieve the net-zero greenhouse gas emissions goal; however, many mechanistic details regarding the CO2 adsorption process in condensed phase amines remain poorly understood. This work combines machine learning potentials, enhanced sampling and grand-canonical Monte Carlo simulations to directly compute experimentally relevant quantities to elucidate the mechanism of CO2 chemisorption in liquid ammonia as a model system. Our simulations suggest that CO2 capture in the liquid occurs in a sequential fashion, with the formation of a metastable zwitterion intermediate. Furthermore, we identified the importance of solvent-mediated proton transfer and solvent dynamics, not only in the reaction pathway but also in the efficiency of CO2 chemisorption. Beyond liquid ammonia, the methodology presented here can be readily extended to simulate amines with more complex chemical structures under experimental conditions, paving the way to elucidate the structure–performance of amines for CO2 capture.
The growing anthropogenic CO2 emission into the atmosphere over the past few decades has raised a series of concerns over its environmental impacts,1 such as global warming2 and food security.3 Among the existing technologies to attack this problem, direct air capture (DAC) can effectively remove CO2 from the atmosphere and is especially suitable to remove distributed emission of CO2 (from transportation vehicles, for example) and compensate for residual emissions from difficult to decarbonize industries.4 This approach employs highly efficient sorbents to extract CO2 from ultradilute sources, which is then coupled with geological sequestration5 or conversion into value-added products.6 An increasingly popular class of DAC sorbents consists of amines supported on solid matrices. These amine composites offer several advantages, i.e., they can capture CO2 from air under ambient conditions; in addition, they are not adversely affected by water vapor and can be regenerated by relatively mild temperature swings.7–10
Although it is well known that amines are efficient for CO2 capture and their chemical structures can significantly influence the CO2 absorption capacity,11–15 a fundamental understanding of CO2 capture in these systems is largely lacking, and conflicting results have been reported on the mechanism of the process. Early kinetic experimental studies conclude that the reaction proceeds through the formation of a zwitterion intermediate.16,17 On the other hand, more recent studies suggest that CO2 capture follows a 3rd order reaction where proton transfer and N–C bond formation occur concertedly.18,19 Computational simulations – particularly those derived from first principles – are excellently suited for addressing this knowledge gap.20,21 However, existing studies often neglect the role of solvent, entropy, and thermal fluctuations, which are known to be critical to explaining CO2 solubility in liquid phases.22,23 This brief yet incomplete summary highlights that much is left to be understood regarding the CO2 capture process in amines.
In this contribution, we developed and applied an integrated simulation framework to investigate the reactive adsorption of CO2 into condensed phase amines. Rather than relying on conventional simulation methods grounded exclusively in first-principles density functional theory or classical force fields, we combine machine learning (ML) potentials with enhanced sampling methods and grand-canonical Monte Carlo (GCMC) simulations to explicitly account for the complexity of condensed phase amines. In particular, machine learning potentials allow for an accurate description of chemical reactions at more realistic scales with a significantly lower computational cost compared to first principles electronic structure methods.24,25 Our ML model was trained with active learning, exploring configurations of pure liquid ammonia, pure CO2 and reactive events of ammonia with CO2 in a condensed phase. In addition, GCMC simulations combined with enhanced sampling enables efficient calculation of the free energy of CO2 chemisorption and its temperature dependence; the latter can be directly compared to experiments to elucidate reaction mechanisms. By using liquid ammonia as a model system, we suggest that CO2 capture in the liquid proceeds in a sequential fashion, with the formation of a metastable zwitterion intermediate. Our simulations also point to the importance of solvent-mediated proton transfer on the energetics of CO2 chemisorption and of solvent dynamics on CO2 uptake, phenomena that have not been discussed in the literature.
We start by discussing the accuracy of our ML potentials. The model reproduces well quantities both derived directly from first principles molecular dynamics (FPMD) and experiments. As a first test, it is shown that the model well reproduces the FPMD structure of liquid ammonia. Here, FPMD simulations were 50 ps-long and sampled the NVT ensemble at 300 K. None of the configurations sampled by FPMD were included in the ML training data. The pair correlation functions reported in Fig. 1A support a good agreement between ML and DFT-SCAN on the structure of pure liquid ammonia (Fig. 1A, left) and chemically bound CO2 in liquid ammonia (Fig. 1A, right). Moreover, our ML potential also provides consistent results with experimental measurements. This is shown in Fig. 1B, where the N–N partial structure factor of liquid ammonia at 277 K and 5 bar obtained by X-ray diffraction26 is close to the one computed with ML simulations under the same thermodynamic conditions. Finally, ML simulations also predict the density (ρ) and the self-diffusion coefficient (D) of liquid deutero-ammonia at 277 K and 1 bar (ρ = 0.65 g mL−1, D = 8.0 × 10−5 cm2 s−1) close to the values (ρ = 0.636 g mL−1, D = 8.5 × 10−5 cm2 s−1) measured experimentally.27,28
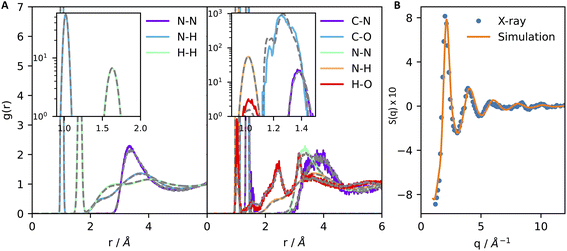 | ||
| Fig. 1 Machine learning simulations reproduce the first-principles structure of liquid ammonia (A, left) and of carbamate/carbamic acid dissolved in liquid ammonia (A, right). Type–type pair correlation functions of liquid ammonia and carbamate–carbamic acid dissolved in liquid ammonia are shown in panels (A) left and right, respectively. Continuous lines contain the results derived from machine learning, while dashed grey lines display the pair correlation functions obtained through first-principles molecular dynamics. Insets of both figures show an amplified region of the plot to better visualize the strong correlation arising from covalent bonds and intramolecular H–H pairs. (B) N–N partial structure factor of liquid ammonia at 277 K and 5 bar obtained by X-ray diffraction26 (points) and machine learning simulations (continuous line). | ||
The ML model developed in this work lacks the explicit inclusion of long-range interactions. The inclusion of long-range forces in ML models was key to properly model long-ranged charge separation in condensed phase systems.29,30 However, in this work, all charge separation remains restricted to atomic distances within the radius cutoff of the ML atomic descriptors and thus should be properly captured by our model. Additional validation of the ML potential is presented in the ESI†, confirming the accuracy of our ML model to describe the free energy surface of CO2 chemisorption, including the short-ranged charge separation occurring during this chemical reaction.
Given the physical description of liquid ammonia and chemically bound CO2 by the machine learning potential, we now explore the quantum accuracy and the computational efficiency of this ML potential to derive a first principles-quality free energy surface of CO2 chemisorption in a liquid amine. Free energy is computed in two steps. First, GCMC simulation evaluates the free energy to transfer CO2 from ambient air (at 400 ppm concentration) to the liquid ammonia phase with no chemical reaction. Second, we apply enhanced sampling techniques to compute the free energy needed to chemically react CO2 with ammonia. The sum of these steps provides the free energy to capture CO2 directly from air.
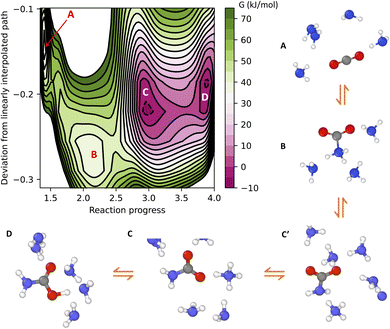
The free energy surface of CO2 binding in liquid ammonia under ambient conditions is given in Fig. 2. Here, the four separate wells of the colormap are associated with (A) physically dissolved CO2, (B) zwitterion (see charge analysis in the ESI†), (C) ammonium carbamate and (D) carbamic acid. Ammonium carbamate (C) and carbamic acid (D) compose the two most stable species of CO2 chemisorption. The formation of ammonium carbamate or carbamic acid reduces the free energy of the system by approximately 30 kJ mol−1 relative to the CO2 physically dissolved in liquid ammonia. On the other hand, the formation of the zwitterion increases the free energy by 5 kJ mol−1 relative to the unbound CO2 state. The zwitterion is the only CO2-bound species in ammonia not requiring proton transfer during CO2 adsorption, pointing to the decisive role of proton transfer to explain the high efficiency of amines in CO2 capture. Proton transfer not only allows the transition from zwitterion (B) to carbamate (C), but also a fast chemical equilibrium between carbamate (C) and carbamic acid (D). As shown in Fig. 2, species C and D have approximately the same free energy and are separated by a free energy barrier close to 10 kJ mol−1. These two species frequently interconvert into one another, forming a stable carboxylate–ammonium ion pair with proton hopping on the picosecond timescale. This chemical equilibrium cannot be captured by gas-phase simulations at 0 K, thus providing additional motivation to study CO2 chemisorption with atomistic simulations at finite temperatures.
Analysis of the minimum free energy path connecting species A–D reveals the reaction mechanism of CO2 chemisorption in liquid ammonia. The path is represented schematically in Fig. 2, in which only a few ammonia molecules are shown for clarity. Following the path A to D, the starting state is the free CO2 dissolved in liquid ammonia (A). CO2 binding first involves the formation of the zwitterion (B), followed by a proton transfer from the amino group of species B to a neighboring ammonia molecule. The carbamate (C′) just formed has an ammonium ion close to its amino (–NH2) group, but this is still not the most stable state for the carbamate in solution. A series of proton jumps further moves the ammonium ion closer to the carboxylate group of carbamate, thus forming the most stable carmabate–ammonium ion pair (C). Finally, this ion pair undergoes frequent proton exchange, leading to a fast chemical equilibrium between carbamate (C) and carbamic acid (D).
The mechanism of CO2 capture provided by machine learning simulations aligns with the early conclusions drawn from kinetic experiments16,17 and also offers additional insights. Our results indicate that CO2 capture in liquid ammonia occurs sequentially, with the formation of a metastable zwitterion intermediate. Our simulations also suggest that the mechanism that involves a direct transition from unbound CO2 to carbamate, as previously proposed by Crooks and Gutowski,18,19 is unlikely to proceed. This reaction pathway requires not only concerted C–N bond formation and proton transfer, but also additional solvent-mediated proton transfer to form the NH4+–carboxylate ion pair (transition from C′ to C in Fig. 2). This third-order reaction requires a fully H-bond connected path from the amino to the carboxylate group of carbamate, rendering such a reaction mechanism unlikely for systems with an even lower number of H-bonds than ammonia, such as aminopolymers. The mechanism of CO2 chemisorption observed in this work requires Grotthuss-like diffusion of the ammonium ion (species C′, Fig. 2) in order to form the most stable carbamate product (species C, Fig. 2), thus implying that CO2 chemisorption kinetics depends on the H-bond network of the condensed phase amine.
To better understand the impact of the solvation environment on the energetics of CO2 capture, we investigated the temperature-dependence of the reaction free energy. The variation of the reaction free energy with respect to temperature provides three thermodynamically relevant quantities: the adsorption enthalpy, the adsorption entropy, and the temperature of CO2 desorption. The reaction free energy corresponds to the free energy difference between CO2 chemically bound in liquid ammonia and gas phase CO2 at 0.4 mbar partial pressure. The adsorption enthalpy and entropy of −109 ± 4 kJ mol−1 and −340 ± 13 J (mol−1 K−1), respectively, were estimated based on the linear coefficients fitted to data in Fig. 3. The CO2 desorption temperature is defined as the temperature value whose free energy difference between gas phase CO2 and chemisorbed CO2 is zero, resulting in a desorption temperature of 320 ± 6 K. The computed adsorption of CO2 in the condensed phase exhibits lower exothermicity compared to the previously reported experimental formation enthalpy of ammonium carbamate from gaseous ammonia and CO2, which was measured at −159 kJ mol−1.31 In contrast, measurements of the heat of CO2 adsorption on primary and secondary amines supported on silica yield values within the range of 86 to 92 kJ mol−1,32 only slightly lower than the adsorption enthalpy observed in our simulations. These comparisons underscore the critical distinction between gas-phase and condensed-phase adsorption and emphasize the necessity of explicitly representing the condensed phase in modeling technologically relevant amine-based sorbents.
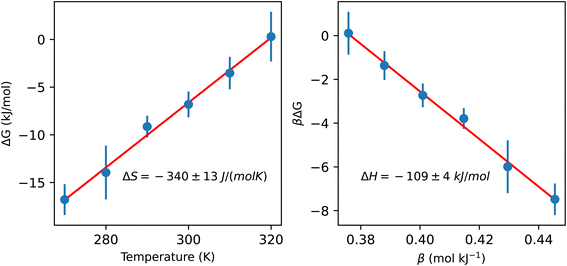 | ||
| Fig. 3 Temperature dependence of the free energy difference between CO2 chemically bound in liquid ammonia and gas phase CO2 at 0.4 mbar partial pressure. The entropy and enthalpy of the reaction are determined from the slope of the left and right plots, respectively (more details are given in the ESI†). The bound CO2 state includes the zwitterion, carbamate and carbamic acid (species B, C and D in Fig. 2, respectively). | ||
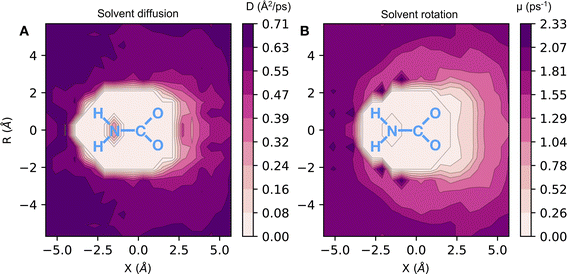
Here, we have found a substantial impact of the solvation environment on CO2 chemisorption. The solvent not only decreases the CO2 adsorption enthalpy relative to the gas phase reaction, but it also has a sizeable contribution to the entropy reduction in this chemical reaction. The transfer of CO2 from air at 0.4 mbar partial pressure to unbound CO2 in liquid ammonia accounts for an entropy loss of 120 J (mol−1 K−1), while the formation of chemically bound CO2 species reduces the entropy of the system by 220 J (mol−1 K−1). This additional loss of entropy arises both from the fewer degrees of freedom in NH3 and CO2 bound species (relative to the unbound ones) and from a reduction of the rotational and translational dynamics of the solvent environment around the carbamate/carbamic acid species. We find that the slowdown in solvent dynamics around carbamate and carbamic acid molecules extends beyond the 5 Å radial distance from the carboxylate group. This is evident from the 2D map of solvent dynamics (translation and rotation) around the carbamate species shown in Fig. 4. The carboxylate group of carbamate has the major contribution to the slowdown of solvent dynamics, while the –NH2 group perturbs little the solvent around it. Up to one order of magnitude reduction in rotational and translational dynamics is observed close to the solute's carboxylic group, resulting from the strong carboxylate–ammonium ion pair undergoing frequent proton exchange. Translation dynamics is quantified from the diffusion coefficient of N atoms, while rotational dynamics was computed from the frequency of N–H bond reorientation. The 3 dimensional distribution functions were projected into the molecular frame of carboxylate in cylindrical coordinates, with the axial direction X given as the O–C–O bisector and the C atom taken as the origin, whereas the R axis corresponds to the radial distance from the X axis.
The sluggish dynamics of amines upon CO2 chemisorption has important implications for the performance of the system. Our simulations suggest that the increase in CO2 loading in liquid amines creates a progressively more viscous liquid. Ultimately, this reduces the efficacy of the sorbent, imposing kinetic constraints on further CO2 chemisorption at high CO2 loading. We note that the viscosity increase upon CO2 loading aligns with the solvent slowdown shown in Fig. 4 given the linear correlation between solvent diffusion and viscosity given by the Stokes–Einstein formula.33 It is also worth emphasizing that our prediction of sluggish dynamics of amines upon CO2 chemisorption is also consistent with existing experimental measurements.19,34
Nuclear quantum effects (NQEs) may impact both the dynamics and statistics of atomic systems, with more significant effects on light atoms, such as hydrogen.35 Of particular relevance to this work is the known impact of NQEs on model proton transfer reactions in a condensed phase.36–39 For this reason, we have also included the NQE in the enhanced sampling simulations of CO2 chemisorption using path integral molecular dynamics and compared it with the results using classical ion dynamics (see Fig. 5). Our results corroborate previous findings that the NQE decreases the free energy barrier of proton transfer reactions, but we found only a minor influence on the free energy difference between the (meta)stable species (labeled A–D in Fig. 2). The only free energy barrier not impacted by the NQE is the formation of the zwitterion from physisorbed CO2, since this is the only reaction studied here not involving proton transfer.
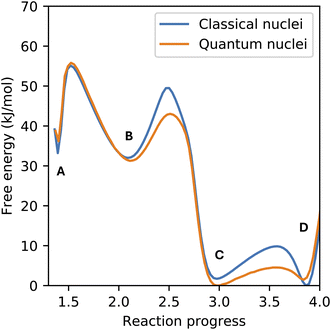 | ||
| Fig. 5 Comparison between the free energy surface of CO2 chemisorption obtained from classical and quantum statistics of the nuclei. Simulations were performed at 300 K and fixed at a density of 0.0229 Å−3. Labels A–D correspond to the same species shown in Fig. 2. | ||
In summary, we combined machine learning, enhanced sampling and grand-canonical Monte Carlo simulations to enable a direct parallel between simulations and CO2 adsorption experiments. While ML is key to accurately sample the CO2 chemisorption with sufficient statistics, the combination of enhanced sampling and GCMC simulations allows the derivation of free energy using CO2 in air as the reference state. The methodology developed in this paper provides experimentally accessible quantities, such as the free energy and enthalpy of CO2 adsorption. Moreover, the minimum free energy path from reactants to products evidenced the critical role of proton transfer (mediated by the solvation environment) in the formation of the most stable CO2-bound species: carbamate and carbamic acid. These CO2-bound species reduce solvent dynamics through conjugate acid-base and hydrogen bond interactions, which are expected to gradually increase solvent viscosity and hinder further CO2 uptake kinetics as CO2 loading increases. Although the present paper focused on CO2 adsorption in liquid ammonia, the proposed methodology should be equally applicable to study more complex systems (see discussion in the ESI†). The future introduction of more complex systems to the machine learning training data will allow an atomic-level understanding of the effect of chemical composition of amines on the CO2 adsorption efficiency of amine-based systems.
Methods
The potential energy surface of the systems was described with a deep neural network (DNN) potential trained on the density functional SCAN.40 The DNN potential was constructed based on the smooth version of the Deep Potential Molecular Dynamics (DPMD) method,41,42 and its training data include atomic configurations of liquid ammonia, liquid CO2 and ammonia–CO2 mixtures (including reactive events) explored through reinforcement learning.43 Well-Tempered Metadynamics44 (WTMetad) was used to compute the free energy surface of the reactive adsorption of CO2 in liquid ammonia. Free energy surfaces were averaged over 9 independent WTMetad simulations, each starting from a different initial condition. Each simulation accumulated 20 million WTMetad steps using a timestep of 1 fs. Deuterium replaces hydrogen atoms, allowing longer timesteps with no change to the free energy since the classical configurational partition function is independent of atomic mass. Grand-canonical Monte Carlo simulation was used to compute the free energy to transfer a CO2 molecule from air (at a concentration of 400 ppm) to the liquid ammonia phase. All of the values of the free energy difference reported in this manuscript thus refer to the free energy of a particular state relative to the free energy of the state of pure liquid ammonia and gas phase CO2 in air at 400 ppm concentration.First principles simulations
SCAN calculations were performed using periodic boundary conditions, as implemented in the Quantum-ESPRESSO package.45,46 Wavefunctions and electron density were plane–wave expanded with kinetic energy cutoffs of 200 and 800 Ry, respectively. Pseudopotentials of Troullier–Martins47 type replaced explicit core-valence electron interactions. The large wavefunction cutoff used in this work results from the known numerical instability of the SCAN functional. Future work might benefit from the usage of the r2SCAN,48,49 since this functional will retain the accuracy of the SCAN functional and decrease its numerical instability, thus allowing SCF calculations at lower wavefunction cutoff. Atomic charge analysis (ESI†) was performed through Hirshfeld charge partitioning.50Deep neural network potential
The deep neural network potential was trained using the DeepMD-Kit package.51 The DNN architecture was composed of a 3-layer-deep neural network with 120 neurons each. Within this training scheme, the DNN model is iteratively optimized with cycles composed of (1) extensive exploration of configurational space using DPMD simulation; (2) selection of a few configurations with large uncertainty of force prediction; and (3) fitting DNN models using new data. For item 1, liquid ammonia, liquid CO2 and ammonia–CO2 mixtures were explored. Enhanced sampling was also used to collect data of the chemical reactivity of CO2 with liquid ammonia. The uncertainty estimator employed the maximum deviation of atomic forces between 3 DNN models trained on the same data but with different random initializations of the DNN parameters. DNN models were iteratively optimized until the deviation of their atomic forces was below 0.2 eV Å−1.Molecular dynamics and enhanced sampling
All molecular dynamics (MD) simulations using DPMD were performed with the Lammps code52 interfaced with DeepMD-kit51 and Plumed.53 WTMetad was performed with a bias factor of 5, initial Gaussian height 1.0 and 0.1 spread. Temperature was controlled with a 3-bead Nosé–Hoover thermostat chain.54,55 Pressure was kept at 10 bar using the Parrinello–Rahman barostat.56 Simulations of CO2 in liquid NH3 were performed in a system containing 2051 atoms (512 NH3 and one CO2) periodically repeated in a cubic unit cell with 28.9 Å edge length. It is important to note that experimental measurements have determined the vapor phase of ammonia to be the most thermodynamically stable state at 10 bar external pressure and temperatures exceeding 300 K.27 Our simulations thus sample the metastable liquid phase of ammonia above 300 K and the absence of spontaneous phase transitions in our model results from the limited timescale accessed by our simulations.Collective variables
Fig. 2 presents the free energy as a function of two path collective variables (S and Z) suitable to describe complex chemical reactions in a condensed phase.57 The variables S and Z were labeled as “reaction progress” and “deviation from the linearly interpolated path”, respectively. The parametric forms of S and Z as a function of the configurational space vectors X are given in eqn (1) and (2). In this work, the components of vector X are: (1) the C–N coordination number, (2) O–H coordination number and (3) the N*–H coordination number, with N* the N closest to the CO2's C atom (see the definition below). The combination of these 3 variables uniquely defines the 4 chemical states of interest in this work, as shown by the 4 separate wells in Fig. 2.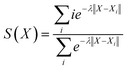 | (1) |
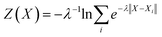 | (2) |
The collective variables (CVs) composing the vector X are smooth and all differentiable, allowing the derivation of bias forces needed for enhanced sampling. Smooth coordination numbers QAB (number of species B within radius distance Rc from species A) are computed using eqn (3), with RAB the distance between atoms A and B.
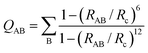 | (3) |
One of the CVs used in this work requires the N–H coordination number exclusively from the N atom closest to the C atom from CO2. The smooth version of this CV can be computed using eqn (4), with QNC a switching function approaching 1 when N is closest to the CO2 C atom and 0 instead. An upper harmonic potential V = k(QNC − 1)2 is added to prevent more than one N atom from binding to the CO2's C atom.
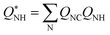 | (4) |
Structure factor
The structure factor was computed using the equation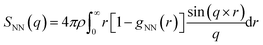 | (5) |
Path integral molecular dynamics
Path integral molecular dynamics (PIMD) simulations were performed using the generalized Langevin equation with colored-noise thermostat,58,59 as implemented using the i-PI code.60 The path integral was discretized with 8 beads, temperature was controlled at 300 K, volume was kept constant (N number density of ρ = 0.0229 Å−3) and the integration timestep was set to 0.25 fs. A total of 4 M WTMetaD steps were sampled using a total of 10 walkers.Data availability
All the data used to train the DNN model, as well as input scripts of DeepMD-Kit, Lammps and Plumed, are available at https://github.com/marcoscaa/amines_co2.Author contributions
M. C. A., S. L. and S. H. P. designed the research. M. C. A. performed the research. M. C. A., S. L., S. H. P., S. A. A. and T. A. P. analysed the data. M. C. A., S. L., S. H. P., S. A. A. and T. A. P. wrote the paper.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division (SCW1726). The work at the Lawrence Livermore National Laboratory was performed under the auspices of the U.S. Department of Energy under Contract DE-AC52-07NA27344. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP0023097.References
- O. Hoegh-Guldberg, et al., in Impacts of 1.5 °C Global Warming on Natural and Human Systems, ed. V., Masson-Delmotte, et al., IPCC Secretariat, 2018, pp 175–311 Search PubMed.
- J. Hansen, R. Ruedy, M. Sato and K. Lo, Global surface temperature change, Rev. Geophys., 2010, 48, 2010RG000345 CrossRef.
- T. Wheeler and J. von Braun, Climate Change Impacts on Global Food Security, Science, 2013, 341, 508–513 CrossRef CAS PubMed.
- E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Direct Capture of CO2 from Ambient Air, Chem. Rev., 2016, 116, 11840–11876 CrossRef PubMed.
- D. A. Voormeij and G. J. Simandl, Geological, Ocean, and Mineral CO 2 Sequestration Options: A Technical Review, Geosci. Can., 2004, 31, 11–22 Search PubMed.
- K. M. K. Yu, I. Curcic, J. Gabriel and S. C. E. Tsang, Recent advances in CO2 capture and utilization, ChemSusChem, 2008, 1, 893–899 CrossRef CAS PubMed.
- S. Choi, J. H. Drese and C. W. Jones, Adsorbent materials for carbon dioxide capture from large anthropogenic point sources, ChemSusChem, 2009, 2, 796–854 CrossRef CAS PubMed.
- S. Choi, J. H. Drese, P. M. Eisenberger and C. W. Jones, Application of amine-tethered solid sorbents for direct CO2 capture from the ambient air, Environ. Sci. Technol., 2011, 45, 2420–2427 CrossRef CAS PubMed.
- P. Priyadarshini, G. Rim, C. Rosu, M. Song and C. W. Jones, Direct Air Capture of CO2 Using Amine/Alumina Sorbents at Cold Temperature, ACS Environ. Au, 2023, 3, 295–307 CrossRef CAS PubMed.
- J. S. Carneiro, G. Innocenti, H. J. Moon, Y. Guta, L. Proaño, C. Sievers, M. A. Sakwa-Novak, E. W. Ping and C. W. Jones, Insights into the Oxidative Degradation Mechanism of Solid Amine Sorbents for CO2 Capture from Air: Roles of Atmospheric Water, Angew. Chem., Int. Ed., 2023, 62, e202302887 CrossRef CAS PubMed.
- C. J. Yoo, L. C. Lee and C. W. Jones, Probing Intramolecular versus Intermolecular CO2 Adsorption on Amine-Grafted SBA-15, Langmuir, 2015, 31, 13350–13360 CrossRef CAS PubMed.
- S. H. Pang, L. C. Lee, M. A. Sakwa-Novak, R. P. Lively and C. W. Jones, Design of Aminopolymer Structure to Enhance Performance and Stability of CO2 Sorbents: Poly(propylenimine) vs. Poly(ethylenimine), J. Am. Chem. Soc., 2017, 139, 3627–3630 CrossRef CAS PubMed.
- M. E. Potter, S. H. Pang and C. W. Jones, Adsorption Microcalorimetry of CO2 in Confined Aminopolymers, Langmuir, 2017, 33, 117–124 CrossRef CAS PubMed.
- A. R. Sujan, S. H. Pang, G. Zhu, C. W. Jones and R. P. Lively, Direct CO2 Capture from Air using Poly(ethylenimine)-Loaded Polymer/Silica Fiber Sorbents, ACS Sustainable Chem. Eng., 2019, 7, 5264–5273 CrossRef CAS.
- S. Li, M. F. C. Andrade, A. J. Varni, G. A. Russell-Parks, W. A. Braunecker, E. Hunter-Sellars, M. A. Marple and S. H. Pang, Enhanced hydrogen bonding via epoxide-functionalization restricts mobility in poly(ethylenimine) for CO2 capture, Chem. Commun., 2023, 59, 10737–10740 RSC.
- M. Caplow, Kinetics of Carbamate Formation and Breakdown, J. Am. Chem. Soc., 1968, 20, 6795–6803 CrossRef.
- P. V. Danckwerts, The Reaction of CO2 with Ethanolamines, Chem. Eng. Sci., 1979, 34, 443–446 CrossRef CAS.
- J. E. Crooks and J. P. Donnellan, Kinetics and Mechanism of the Reaction between Carbon Dioxide and Amines in Aqueous Solution, J. Chem. Soc., Perkin Trans., 1989, 2, 331–333 RSC.
- K. E. Gutowski and E. J. Maginn, Amine-functionalized task-specific ionic liquids: A mechanistic explanation for the dramatic increase in viscosity upon complexation with CO2 from molecular simulation, J. Am. Chem. Soc., 2008, 130, 14690–14704 CrossRef CAS PubMed.
- Z. R. Lee, L. J. Quinn, C. W. Jones, S. E. Hayes and D. A. Dixon, Predicting the Mechanism and Products of CO2 Capture by Amines in the Presence of H2O, J. Phys. Chem. A, 2021, 125, 9802–9818 CrossRef CAS PubMed.
- R. B. Said, J. M. Kolle, K. Essalah, B. Tangour and A. Sayari, A Unified Approach to CO2–Amine Reaction Mechanisms, ACS Omega, 2020, 5, 26125–26133 CrossRef CAS PubMed.
- J. M. P. Martirez and E. A. Carter, Solvent Dynamics Are Critical to Understanding Carbon Dioxide Dissolution and Hydration in Water, J. Am. Chem. Soc., 2023, 145, 12561–12575 CrossRef CAS PubMed.
- B. Yoon and G. A. Voth, Elucidating the Molecular Mechanism of CO2 Capture by Amino Acid Ionic Liquids, J. Am. Chem. Soc., 2023, 145, 15663–15667 CrossRef CAS PubMed.
- L. Li, M. F. C. Andrade, R. Car, A. Selloni and E. A. Carter, Characterizing Structure-Dependent TiS2/Water Interfaces Using Deep-Neural-Network-Assisted Molecular Dynamics, J. Phys. Chem. C, 2023, 127, 9750–9758 CrossRef CAS.
- M. Yang, L. Bonati, D. Polino and M. Parrinello, Using metadynamics to build neural network potentials for reactive events: the case of urea decomposition in water, Catal. Today, 2022, 387, 143–149 CrossRef CAS.
- A. H. Narten, Liquid ammonia: Molecular correlation functions from x-ray diffraction, J. Chem. Phys., 1976, 66, 3117–3120 CrossRef.
- K. Gao, J. Wu, I. H. Bell, A. H. Harvey and E. W. Lemmon, A Reference Equation of State with an Associating Term for the Thermodynamic Properties of Ammonia, J. Phys. Chem. Ref. Data, 2023, 52, 013102 CrossRef CAS.
- D. E. O’Reilly, E. M. Peterson and C. E. Scheie, Self-diffusion in liquid ammonia and deuteroammonia, J. Chem. Phys., 1973, 58, 4072–4075 CrossRef.
- M. C. Andrade, R. Car and A. Selloni, Probing the self-ionization of liquid water with ab initio deep potential molecular dynamics, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302468120 CrossRef CAS PubMed.
- C. Zhang, M. C. Andrade, Z. K. Goldsmith, A. S. Raman, Y. Li, P. Piaggi, X. Wu, R. Car and A. Selloni, Electrical double layer and capacitance of TiO2 electrolyte interfaces from first principles simulations, 2024 Search PubMed.
- K. G. Clark and H. C. Hbtherington, The heat of formation of ammonium carbamate from ammonia and carbon dioxide, J. Am. Chem. Soc., 1927, 49, 1909–1915 CrossRef CAS.
- M. A. Alkhabbaz, P. Bollini, G. S. Foo, C. Sievers and C. W. Jones, Important roles of enthalpic and entropic contributions to CO2 capture from simulated flue gas and ambient air using mesoporous silica grafted amines, J. Am. Chem. Soc., 2014, 136, 13170–13173 CrossRef CAS PubMed.
- R. Zwanzig, On the relation between self-diffusion and viscosity of liquids, J. Chem. Phys., 1983, 79, 4507–4508 CrossRef CAS.
- M. D. Soutullo, C. I. Odom, B. F. Wicker, C. N. Henderson, A. C. Stenson and J. H. Davis, Reversible CO2 capture by unexpected plastic-, resin-, and gel-like ionic soft materials discovered during the combi-click generation of a TSIL library, Chem. Mater., 2007, 19, 3581–3583 CrossRef CAS.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- R. Yuan, J. A. Napoli, C. Yan, O. Marsalek, T. E. Markland and M. D. Fayer, Tracking Aqueous Proton Transfer by Two-Dimensional Infrared Spectroscopy and ab Initio Molecular Dynamics Simulations, ACS Cent. Sci., 2019, 5, 1269–1277 CrossRef CAS PubMed.
- L. Lin, J. A. Morrone and R. Car, Correlated Tunneling in Hydrogen Bonds, J. Stat. Phys., 2011, 145, 365–384 CrossRef CAS.
- M. E. Tuckerman, D. Marx, M. L. Klein, M. Parrinello, M. E. Tuckerman, M. L. Klein, D. Marx and M. Parrinello, On the Quantum Nature of the Shared Proton in Hydrogen Bonds, Science, 1997, 275, 817–820 CrossRef CAS PubMed.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Nuclear quantum effects and hydrogen bond fluctuations in water, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, W. A. Saidi, R. Car and W. E, End-to-end Symmetry Preserving Inter-atomic Potential Energy Model for Finite and Extended Systems, 2018, pp , pp. 4436–4446 Search PubMed.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and W. E, Active learning of uniformly accurate interatomic potentials for materials simulation, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: A smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- P. Giannozzi, et al., Quantum ESPRESSO: a Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens.Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, et al., Advanced Capabilities for Materials Modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Efficient Pseudopotentials for Plane–Wave Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and Numerically Efficient r2SCAN Meta-Generalized Gradient Approximation, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J. M. Mewes, R2SCAN-3c: A “swiss army knife” composite electronic-structure method, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- P. Bultinck, C. V. Alsenoy, P. W. Ayers and R. Carbó-Dorca, Critical analysis and extension of the Hirshfeld atoms in molecules, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- H. Wang, L. Zhang, J. Han and W. E, DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- S. Nosé, A Molecular Dynamics Method for Simulations in the Canonical Ensemble, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, Crystal Structure and Pair Potentials: A Molecular Dynamics Study, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- D. Branduardi, F. L. Gervasio and M. Parrinello, From A to B in free energy space, J. Chem. Phys., 2007, 126, 054103 CrossRef PubMed.
- M. Ceriotti, D. E. Manolopoulos and M. Parrinello, Accelerating the convergence of path integral dynamics with a generalized Langevin equation, J. Chem. Phys., 2011, 134, 084104 CrossRef PubMed.
- M. Ceriotti and D. E. Manolopoulos, Efficient first-principles calculation of the quantum kinetic energy and momentum distribution of nuclei, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef PubMed.
- M. Ceriotti, J. More and D. E. Manolopoulos, I-PI: A Python interface for ab initio path integral molecular dynamics simulations, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc00105b |
| This journal is © The Royal Society of Chemistry 2024 |