Open Access Article
Open Access ArticleDigital Pareto-front mapping of homogeneous catalytic reactions†
Negin
Orouji
 ,
Jeffrey A.
Bennett
,
Sina
Sadeghi
and
Milad
Abolhasani
,
Jeffrey A.
Bennett
,
Sina
Sadeghi
and
Milad
Abolhasani
 *
*
Department of Chemical and Biomolecular Engineering, North Carolina State University, Raleigh, NC 27695, USA. E-mail: abolhasani@ncsu.edu; Web: https://www.abolhasanilab.com
First published on 11th March 2024
Abstract
We report a digital framework for accelerated exploration and optimization of transition metal-based homogeneous catalytic reactions through autonomous experimentation and Bayesian optimization (BO). Specifically, we utilize a machine learning model constructed with deep neural networks for a rhodium-catalyzed hydroformylation reaction to investigate the role of BO hyperparameters, including the acquisition function and sampling size, on the efficiency of reaction Pareto-front mapping.
Transition metal-based homogeneous catalytic reactions are crucial in industrial processes and fine chemical synthesis, driving technological advancements.1 These reactions employ metal complexes as catalysts, with the metal serving as a central hub to convert reactants into desired products efficiently and selectively under mild conditions. The choice of ligands is pivotal, influencing catalytic activity and the stereoselectivity of the reactant at the metal center in homogeneous catalytic reactions. The discovery of more active and tuneable catalysts can result in significant energy and chemical savings in the chemical industry. However, ligand identification in homogeneous catalysis is a laborious task that necessitates the simultaneous optimization of molecular structure and reaction conditions. Conventional catalyst/ligand screening and development strategies, including high-throughput screening or design of experiment response screening fail at revealing complete performance of a candidate ligand for a given homogeneous catalytic reaction. To efficiently and fully explore the performance capabilities of a particular ligand, a new framework for more comprehensive catalyst/ligand performance evaluation strategy that incorporates efficient experimentation is required.
Over the past decade, flow chemistry has been demonstrated as an ideal reactor of choice for studies of gas–liquid processes.2–14 Additionally, the facile integration of flow reactors with online characterization techniques makes them amenable to closed-loop autonomous operation.15 Closed-loop autonomous reaction exploration is a rapidly emerging field which promises to fast-track the discovery and development of materials and molecules by 10–100× compared to conventional manual experimental strategies.3,15–25 Autonomous reaction exploration enables rapid navigation of a vast parameter space with the ultimate goal of achieving a user-defined objective (single or multiple outputs) with intelligent (machine learning (ML)-assisted) decision-making (experiment-selection).15,17,21
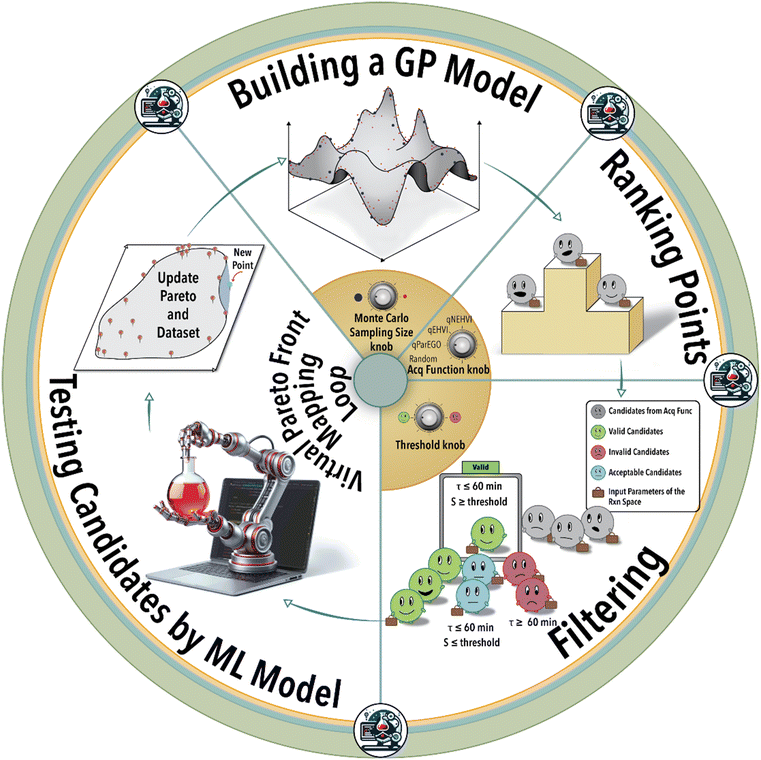
Autonomous homogeneous catalysis, incorporating Bayesian optimization (BO), leverages a continuously evolving understanding of the process of interest (e.g., homogeneous catalytic reaction) via ML modelling, and uncertainty quantification to accelerate the process of revealing the full performance map (Pareto-front) of each catalyst/ligand system. This closed-loop reaction space exploration strategy involves minimal to no human intervention and reduces the total experimental cost of mapping the full potential of a given catalyst/ligand system for a specific reaction of interest.26 Pareto optimization method is a decision-making approach utilized in complex systems characterized by multiple conflicting objectives.27 Its primary objective is the identification of non-dominated solutions, where no alternative solution exists that improves any objective without compromising another. The Pareto front is represented by the set of non-dominated optimal solutions (e.g., reaction yield vs. regioselectivity).23,28–33
The essence of autonomous experimentation lies in the loop of automated experiment, data generation (in situ or online reaction analysis), and selection of the next experiment or set of experiments guided by ML. In each BO-guided autonomous experimental campaign, the ML algorithm predicts system response and iteratively refines the next reaction conditions performed automatically until the desired objective is achieved or the experimental budget is reached. Optimization of hyperparameters, architecture of the ML model, and experiment-selection algorithms of autonomous experimentation platforms plays a critical role in defining the efficiency of navigating a massive reaction space. Utilizing the physical platform of an autonomous lab to study the role of ML model hyperparameters and Pareto mapping policy on the rate of achieving the defined scientific objective is time- and resource-intensive. In-house experimental data can be used to construct an ML model of the physical world of the autonomous lab using ML modelling techniques such as Gaussian process regression (GPR) or deep neural networks (DNNs). The constructed ML model for a given catalyst/ligand system and a specific transition metal-catalyzed reaction can then be utilized to query different reaction conditions, visualize reaction spaces, and investigate the impact of process parameters on catalytic performance.26
In this study, we utilized an autonomous flow reactor integrated with an online gas chromatography (GC) unit to create an in-house experimental dataset (Fig. S1†) for an exemplary homogeneous catalytic reaction,26 rhodium (Rh)-catalyzed hydroformylation of 1-octene (see ESI† S1). This study is aimed at the delineation of the catalysis Pareto-front associated with the reaction condition variables of a given catalyst/ligand system. In particular, we investigate the variations in reaction conditions such as flow rate, concentrations, temperature, and pressure for a given catalyst/ligand system (see ESI† S2–S4 for an additional details about the experimental setup).
Hydroformylation of 1-octene involves the addition of a formyl group to the carbon–carbon double bond to create aldehydes.1 The addition of the formyl group to the carbon–carbon double bond can occur on either carbon atom, resulting in a blend of products (Scheme S1†). In the past four decades, significant research in academic and industrial domains has focused on the development of specialized ligands to engineer the catalytic cycle of the Rh through metal–ligand and steric interactions towards producing the desired aldehyde product with increased regioselectivity.34–43
In the first step of this work, we create an ML model of the hydroformylation reaction, constituting an ensemble of DNNs (see ESI† S5). Subsequent to this step, fine-tuning the hyperparameters becomes essential to accurately simulate the reaction space within the virtual environment (see ESI† S6). Next, the trained and validated ML model is integrated into a virtual BO campaign as the ground truth of the reaction to systematically navigate the reaction space virtually. This virtual BO process aims to effectively map the ligand's capacity to attain the targeted regioselectivity and yield during the hydroformylation reaction.
As depicted in Fig. 1, the iterative BO process initiates with the construction of a surrogate model (GPR) utilizing four initial data points acquired from the experiment (in this case from the ground truth ML model). Subsequently, the surrogate model generates recommendations for additional reaction conditions to be investigated by the experimental platform (in the case from the ground truth ML model), guided by its designated acquisition function. BO involves a Monte Carlo (MC) sampling of reaction conditions and their outcomes via the current surrogate model during each iterative step. The sampled reaction conditions are subsequently assessed and integrated into the specific acquisition function. Determining the optimal size for MC sampling necessitates a nuanced analysis, taking into account factors such as computational resources, convergence speed, and striking a balance between exploration and exploitation. The selection of the acquisition function can be tailored according to the user's specific objective, either emphasizing exploration or exploitation within the solution space. Given the multifaceted nature of the catalysis optimization task at hand, this study incorporates four distinct acquisition functions: 1) parallel efficient global optimization (qParEGO), 2) expected hypervolume improvement (qEHVI), 3) noisy expected hypervolume improvements (qNEHVI), and 4) random sampling. The first three options offer diverse strategies for balancing the exploration and exploitation trade-offs, thereby enabling a comprehensive exploration of the solution space in the pursuit of a Pareto optimal solution.
The qParEGO method utilizes random augmented Chebyshev scalarization, a technique that combines multiple objectives into a single scalar objective using the Chebyshev norm, along with the qExpectedImprovement acquisition function.44 In situations where the parallel setting is enabled (where q, the number of the batches, is greater than 1), each potential solution undergoes sequential optimization using a distinct random scalarization method. This process is executed in a greedy fashion, ensuring that each candidate solution is thoroughly explored and optimized with respect to the multiple objectives at hand. For more comprehensive information on the intricacies of the method, please refer to ref. 44.
The qEHVI method relies on the concept of hypervolume, which measures the volume dominated by a set of solutions in the objective space.45qEHVI calculates the expected improvement of the multi-objective hypervolume metric analogous to the classical expected improvement metric in single-objective optimization.45 The qEHVI method aims to improve the hypervolume metric by enhancing its calculation and interpretation, thereby providing a more accurate assessment of the trade-offs and benefits associated with various solutions.
The qNEHVI acquisition function is built upon the foundational principles shared with qEHVI.44,45 However, qNEHVI incorporates a perturbation (noise) into the proposed solutions, accounting for the uncertainties arising from the model or experimental settings. This strategic inclusion of noise prevents the method from focusing on local extrema and facilitates a more comprehensive exploration of the solution space, thereby aiding in the identification of the global optimal solution.44
The random acquisition function was incorporated to establish a baseline metric for comparing the performance of the afore-mentioned Pareto-front mapping acquisition functions.
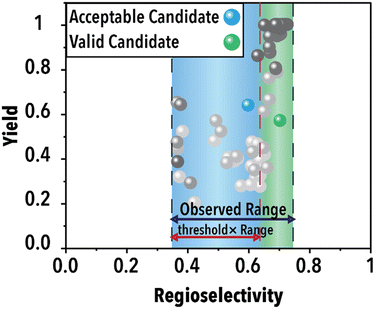
Following the acquisition function calculation step, the suggested experimental conditions by the ML model undergo a filtering process to ensure compliance with the operational limits of the experimental system (i.e., physical world of an autonomous lab). For instance, to maintain operational feasibility, any suggested experiment's residence (reaction) time must not exceed 60 min. Moreover, to facilitate a more effective exploration of the reaction space boundaries, we have implemented a criterion for the anticipated product regioselectivity. By establishing a threshold value, we can determine the significance of the product regioselectivity range. This threshold filter assesses the minimum and maximum product regioselectivity observed experimentally (in this case from the ground truth ML model) so far and compare it against the predicted product regioselectivity of the suggested future experimental conditions. The predicted product regioselectivity should exceed the threshold value multiplied by the observed range. For example, with a threshold of 0.7, the ML-suggested future experimental conditions must exhibit a predicted regioselectivity greater than 70% of the current observed range plus the minimum observed regioselectivity to pass to the next step (see Fig. 2). This relationship is expressed in eqn (1):
| Sx,valid ≥ threshold × (SMax − SMin) + SMin | (1) |
| Sbranched = 1 − Slinear | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) branched and branched
branched and branched![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) linear aldehyde regioselectivity, respectively. Separate campaigns for targeting linear and branched products have been conducted. During branched campaigns, our aim is to optimize the regioselectivity for branched products, mirroring our strategy in linear campaigns that focuses on enhancing the linear product's regioselectivity. It is imperative to note that our regioselectivity threshold rule is uniformly applied across both branched and linear campaign types. Nevertheless, the primary difference lies in the specific regioselectivity metric targeted: in branched campaigns, the rule is applied to the regioselectivity of the branched product, in contrast to its application to the linear product's regioselectivity during linear campaigns. Given that branched and linear campaigns are executed distinctly, the range of regioselectivity observed (max(S) − min(S)) is calculated separately for each product type, aligning with the specific focus of the campaign.
linear aldehyde regioselectivity, respectively. Separate campaigns for targeting linear and branched products have been conducted. During branched campaigns, our aim is to optimize the regioselectivity for branched products, mirroring our strategy in linear campaigns that focuses on enhancing the linear product's regioselectivity. It is imperative to note that our regioselectivity threshold rule is uniformly applied across both branched and linear campaign types. Nevertheless, the primary difference lies in the specific regioselectivity metric targeted: in branched campaigns, the rule is applied to the regioselectivity of the branched product, in contrast to its application to the linear product's regioselectivity during linear campaigns. Given that branched and linear campaigns are executed distinctly, the range of regioselectivity observed (max(S) − min(S)) is calculated separately for each product type, aligning with the specific focus of the campaign.
Finally, the recommended (highest ranked) experimental condition is passed to the ML model for evaluation, replicating the actual experimental conditions. This step allows us to ascertain the aldehyde yield and regioselectivity of the ML-suggested reaction conditions, subsequently incorporating them into the catalyst/ligand Pareto-front for comprehensive analysis. Subsequently, the iterative process recommences, wherein the surrogate model is retrained using the expanded dataset comprising the previous data points along with the newly added experimental result. This cyclic refinement process ensures that the surrogate model of the catalytic reaction continually incorporates the latest information to make more accurate suggestions for subsequent experimental conditions. In this context, the objective is to fine-tune the selection of the ‘best’ experiment iteratively at each step to maximize the aldehyde yield-regioselectivity Pareto-front area. In other words, the aim is to optimize the mapping of the reaction space in the most effective manner.
In the initial set of hydroformylation Pareto-front mapping studies, we studied the effect of threshold value, representing the extent to which we prioritize exploring the aldehyde regioselectivity. In industrial applications of transition metal-catalyzed reactions, the ability to control product regioselectivity on-demand is crucial. This product regioselectivity flexibility becomes particularly valuable when transitioning from one product configuration, such as linear to branched aldehyde, within the same catalyst system. By adjusting the threshold value, a broader regioselectivity range is systematically explored. Fig. 3 illustrates the hydroformylation Pareto-front for a cyclic fluorophosphite ligand, 12-(tert-butyl)-6-fluoro2,4,8,10-tetrakis(2-phenylpropan-2-yl)-12H-dibenzo[d,g][1,3,2], across threshold values ranging from 0.5 to 0.9. These results were obtained utilizing qNEHVI as the acquisition function. The selection of qNEHVI as the acquisition function was driven by the inherent nature of the problem, which involves optimizing two objectives. The results indicate a trade-off between achieving higher aldehyde yields and a broader regioselectivity range. A higher threshold value, intended to expand the aldehyde regioselectivity range, leads to a compromise in the aldehyde yield, as evident in Fig. 3D. Considering the industrial preference for aldehyde yields exceeding 70% in chemical production (Fig. 3C and D), we selected 0.75 as the optimal threshold value, striking a balance between maximizing aldehyde yield and maintaining a desirable range of regioselectivity. However If the objective is to maximize the regioselectivity range without imposing a relatively high aldehyde yield restriction (e.g., accepting a yield of 0.4 or higher), Fig. 3E suggests that setting higher threshold values would be more advantageous.
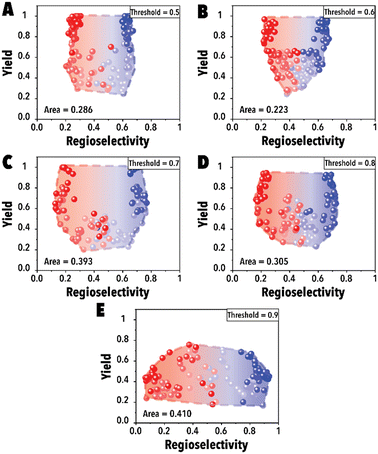 | ||
| Fig. 3 Pareto-front maps with threshold values of (A) 0.5, (B) 0.6, (C) 0.7, (D) 0.8, and (E) 0.9. The red and blue colors represent the branched and linear aldehyde product campaigns, respectively. | ||
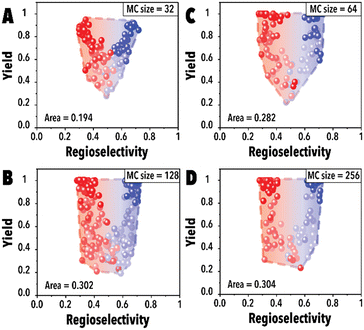
Next, the impact of the MC sampling size was investigated. In the BO framework, a designated number of reaction conditions are drawn at each iteration to be evaluated and introduced to the acquisition function to pick the top candidates. This process, built upon the sampled points, is employed to optimize complex, black-box functions. Increasing the number of samples may improve the probability of finding a better reaction condition candidate and improve the Pareto-front mapping, however, it may bias the Pareto-front by adding points with higher yields. Raising the number of MC samples could unintentionally promote reaction conditions that are more likely to achieve higher reaction yields in the hydroformylation reaction, even though these points may not substantially contribute to advancing the Pareto-front. In essence, as the probability of discovering optimal reaction conditions rises, there's also a potential for oversaturating the dataset with points that, while commendable, do not effectively expand the boundaries of the Pareto-front. This phenomenon is presented in Fig. 4A, the Pareto-front exhibits minimal evolution for smaller MC sampling values. However, with an increase in the number of samples, the Pareto-front expands substantially (Fig. 4C) before eventually reaching a plateau. It is worth noting that each experimental run was consistently conducted with an identical number of cycles (60 points for each linear and branched aldehyde campaign), totaling 120 points. The concentration of datapoints in the corners observed in Fig. 4D is attributed to the inherent characteristics of the hydroformylation reaction, where high reaction yields are more readily achievable than improved product regioselectivity. The increased probability of encountering high-yield data points with larger MC sampling sizes is highlighted, alongside the qNEHVI algorithm's tendency to favor these points, provided the improvement in their hypervolume by getting higher yields and an acceptable residence times. As a result, the Pareto front in panel D predominantly reflects yield improvements. Consequently, we selected 128 as the optimal MC sampling size where a balanced representation of the Pareto-front is achieved.
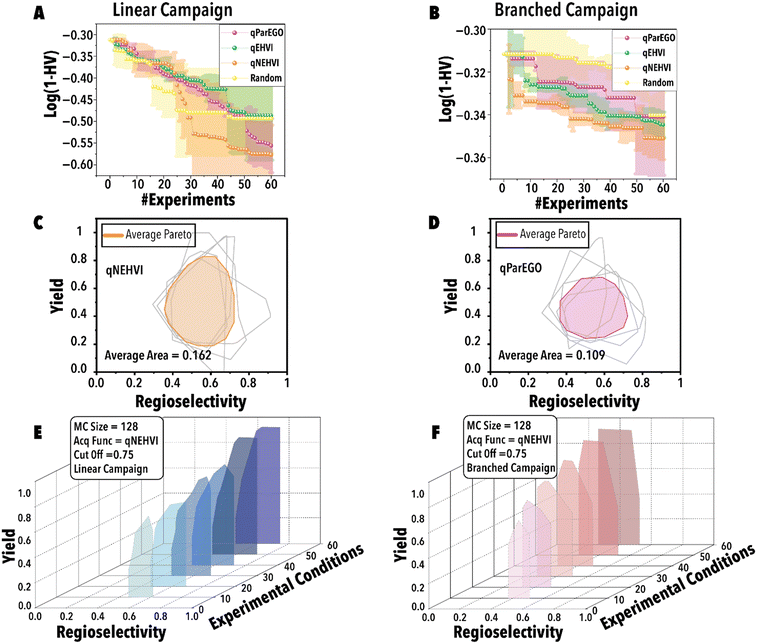
Next, utilizing the optimal threshold value and MC sampling size, we studied the impact of acquisition function on the Pareto-front mapping of Rh-catalyzed hydroformylation of 1-octene (Fig. 5). As discussed previously, each acquisition function plays a distinctive role in either exploring or exploiting the solution space. In order to benchmark the performance for different acquisition functions, we utilized a loss function to maximize the hypervolume attained at each BO step through the suggested reaction point (Fig. 5). The rate at which the loss function diminishes serves as an indicator of the thoroughness with which the reaction space has been explored for the linear (Fig. 5A) and branched (Fig. 5B) aldehydes. Fig. 5A and B reveal that both qParEGO and qNEHVI have outperformed random and qEHVI acquisition functions to minimize the Pareto-front mapping loss function within an experimental budget of 30 reactions for the linear and branch aldehyde campaigns. It is acknowledged that random search exhibits considerable variance, rendering it a less dependable method compared to other acquisition functions. These functions, in contrast, are recognized for their ability to progressively diminish the loss and enhance the mapping of the Pareto front after an ample series of experiments. In comparison, random search is characterized by a minimal slope in loss reduction, indicating its success as sporadic and lacking consistency. It is pertinent to note that the results presented, while reflective of general trends, are derived from a limited dataset (average outcomes of five runs). It is hypothesized that an increase in the number of trials beyond 120 would make the variability inherent in random search more pronounced. Concurrently, the superior and more consistent performance of other acquisition functions, in comparison to random search, is anticipated to become more evident. Considering the results shown in Fig. 5C vs. D, it is evident that qNEHVI has mapped the reaction space more efficiently than qParEGO, resulting in the identification of more desirable reaction conditions with high yields and a broader regioselectivity range. The area of the average Pareto front after five replicates was larger for qNEHVI than qParEGO showing a greater extent of exploration on average. This improved exploration arises from the added experimental noise and unbiased objective sampling of qNEHVI rather than the repeated random scalarization of qParEGO. Consequently, qNEHVI was found to be the best acquisition function, among the ones studied in this work, effectively mapping the reaction space for both the linear and branched aldehyde campaigns (refer to the ESI† for more information). Fig. 5E and F shows the Pareto-front evolution of Rh-catalyzed hydroformylation of 1-octene with the cyclic fluorophosphite ligand (L) using the fine-tuned BO framework.
In conclusion, this work presents a framework for the development of a virtual catalyst/ligand performance mapping using a fine-tuned BO technique. While this study represents a significant step towards autonomous experimentation methodologies, we acknowledge that the generalizability of our approach may require further refinement. Additionally, we recognize that the optimization surface, while informative, may not fully capture the intricacies of all reaction spaces, as it is a simplified model surface. Nevertheless, this research lays the foundation for future advancements in the field of autonomous catalysis and offers valuable insights into navigating complex chemical landscapes of homogeneous transition metal-catalyzed gas–liquid reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Eastman Chemical Company for funding this research and providing the cyclic fluorophosphite ligand.References
- M. Y. Ibrahim, J. A. Bennett, D. Mason, J. Rodgers and M. Abolhasani, J. Catal., 2022, 409, 105–117 CrossRef CAS.
- M. Brzozowski, M. O'Brien, S. V. Ley and A. Polyzos, Acc. Chem. Res., 2015, 48, 349–362 CrossRef CAS PubMed.
- B. Gutmann, D. Cantillo and C. O. Kappe, Angew. Chem., Int. Ed., 2015, 54, 6688–6728 CrossRef CAS PubMed.
- B. Pieber, S. T. Martinez, D. Cantillo and C. O. Kappe, Angew. Chem., 2013, 125, 10431–10434 CrossRef.
- V. Hessel, D. Kralisch, N. Kockmann, T. Noël and Q. Wang, ChemSusChem, 2013, 6, 746–789 CrossRef CAS PubMed.
- L. Buglioni, F. Raymenants, A. Slattery, S. D. Zondag and T. Noël, Chem. Rev., 2021, 122, 2752–2906 CrossRef PubMed.
- M. B. Plutschack, B. U. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893 CrossRef CAS PubMed.
- D. Dallinger, B. Gutmann and C. O. Kappe, Acc. Chem. Res., 2020, 53, 1330–1341 CrossRef CAS PubMed.
- M. O'Brien, N. Taylor, A. Polyzos, I. R. Baxendale and S. V. Ley, Chem. Sci., 2011, 2, 1250–1257 RSC.
- C. W. Coley, M. Abolhasani, H. Lin and K. F. Jensen, Angew. Chem., Int. Ed., 2017, 56, 9847–9850 CrossRef CAS PubMed.
- S. Han, M. Ramezani, P. TomHon, K. Abdel-Latif, R. W. Epps, T. Theis and M. Abolhasani, Green Chem., 2021, 23, 2900–2906 RSC.
- K. Raghuvanshi, C. Zhu, M. Ramezani, S. Menegatti, E. E. Santiso, D. Mason, J. Rodgers, M. E. Janka and M. Abolhasani, ACS Catal., 2020, 10, 7535–7542 CrossRef CAS.
- M. Ramezani, M. A. Kashfipour and M. Abolhasani, J. Flow Chem., 2020, 10, 93–101 CrossRef CAS.
- S. Han, M. Y. Ibrahim and M. Abolhasani, Chem. Commun., 2021, 57, 11310–11313 RSC.
- A. A. Volk and M. Abolhasani, Trends Chem., 2021, 3, 519–522 CrossRef CAS.
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3, 1337–1344 CrossRef CAS PubMed.
- R. W. Epps, M. S. Bowen, A. A. Volk, K. Abdel-Latif, S. Han, K. G. Reyes, A. Amassian and M. Abolhasani, Adv. Mater., 2020, 32, 2001626 CrossRef CAS PubMed.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 1–10 Search PubMed.
- J. A. Bennett and M. Abolhasani, Curr. Opin. Chem. Eng., 2022, 36, 100831 CrossRef.
- R. W. Epps, A. A. Volk, M. Y. Ibrahim and M. Abolhasani, Chem, 2021, 7, 2541–2545 CAS.
- J. M. Granda, L. Donina, V. Dragone, D.-L. Long and L. Cronin, Nature, 2018, 559, 377–381 CrossRef CAS PubMed.
- V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264 RSC.
- A. A. Volk and M. Abolhasani, Nat. Commun., 2024, 15, 1378 CrossRef CAS PubMed.
- D. Karan, G. Chen, N. Jose, J. Bai, P. McDaid and A. A. Lapkin, React. Chem. Eng., 2024, 9, 619–629 RSC.
- J. A. Bennett, N. Orouji, M. Khan, S. Sadeghi and M. Abolhasani, Nat. Chem. Eng., 2024, 1, 240–250 CrossRef.
- C. S. Tan, A. Gupta, Y.-S. Ong, M. Pratama, P. S. Tan and S. K. Lam, Sci. Rep., 2023, 13, 7842 CrossRef CAS PubMed.
- S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson and D. Angelone, Science, 2019, 363, eaav2211 CrossRef CAS PubMed.
- E. Bradford, A. M. Schweidtmann and A. Lapkin, J. Glob. Optim., 2018, 71, 407–438 CrossRef.
- C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger, G. Chessari, C. N. Johnson and A. A. Lapkin, ACS Cent. Sci., 2023, 9, 957–968 CrossRef CAS PubMed.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz and H. Tribukait, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- R. L. Hartman, J. P. McMullen and K. F. Jensen, Angew. Chem., Int. Ed., 2011, 50, 7502–7519 CrossRef CAS PubMed.
- M. Movsisyan, E. Delbeke, J. Berton, C. Battilocchio, S. Ley and C. Stevens, Chem. Soc. Rev., 2016, 45, 4892–4928 RSC.
- M. Vilches-Herrera, L. Domke and A. Börner, ACS Catal., 2014, 4, 1706–1724 CrossRef CAS.
- H. Klein, R. Jackstell, K. D. Wiese, C. Borgmann and M. Beller, Angew. Chem., Int. Ed., 2001, 40, 3408–3411 CrossRef CAS PubMed.
- A. Seayad, M. Ahmed, H. Klein, R. Jackstell, T. Gross and M. Beller, Science, 2002, 297, 1676–1678 CrossRef CAS PubMed.
- Y. Yan, X. Zhang and X. Zhang, J. Am. Chem. Soc., 2006, 128, 16058–16061 CrossRef CAS PubMed.
- B. Breit and W. Seiche, J. Am. Chem. Soc., 2003, 125, 6608–6609 CrossRef CAS PubMed.
- L. A. van der Veen, P. C. Kamer and P. W. van Leeuwen, Angew. Chem., Int. Ed., 1999, 38, 336–338 CrossRef CAS PubMed.
- Y. Jiao, M. S. Torne, J. Gracia, J. H. Niemantsverdriet and P. W. van Leeuwen, Catal. Sci. Technol., 2017, 7, 1404–1414 RSC.
- P. W. Van Leeuwen and C. Claver, Rhodium catalyzed hydroformylation, Springer Science & Business Media, 2002 Search PubMed.
- A. Van Rooy, J. N. de Bruijn, K. F. Roobeek, P. C. Kamer and P. W. Van Leeuwen, J. Organomet. Chem., 1996, 507, 69–73 CrossRef CAS.
- A. van Rooy, E. N. Orij, P. C. Kamer and P. W. van Leeuwen, Organometallics, 1995, 14, 34–43 CrossRef CAS.
- S. Daulton, M. Balandat and E. Bakshy, Adv. Neural Inf. Process. Syst., 2021, 34, 2187–2200 Search PubMed.
- S. Daulton, M. Balandat and E. Bakshy, Adv. Neural Inf. Process. Syst., 2020, 33, 9851–9864 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00673e |
| This journal is © The Royal Society of Chemistry 2024 |