Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exciton annihilation and diffusion length in disordered multichromophoric nanoparticles†
Amira Mounya
Gharbi
 a,
Deep Sekhar
Biswas
b,
Olivier
Crégut
a,
Pavel
Malý
a,
Deep Sekhar
Biswas
b,
Olivier
Crégut
a,
Pavel
Malý
 c,
Pascal
Didier
c,
Pascal
Didier
 b,
Andrey
Klymchenko
b,
Andrey
Klymchenko
 b and
Jérémie
Léonard
b and
Jérémie
Léonard
 *a
*a
aIPCMS, Université de Strasbourg – CNRS, Strasbourg, France. E-mail: jeremie.leonard@ipcms.unistra.fr
bLBP, Université de Strasbourg, Illkirch, France
cCharles University, Prague, Czech Republic
First published on 8th June 2024
Abstract
Efficient exciton transport is the essential property of natural and synthetic light-harvesting (LH) devices. Here we investigate exciton transport properties in LH organic polymer nanoparticles (ONPs) of 40 nm diameter. The ONPs are loaded with a rhodamine B dye derivative and bulky counterion, enabling dye loadings as high as 0.3 M, while preserving fluorescence quantum yields larger than 30%. We use time-resolved fluorescence spectroscopy to monitor exciton–exciton annihilation (EEA) kinetics within the ONPs dispersed in water. We demonstrate that unlike the common practice for photoluminescence investigations of EEA, the non-uniform intensity profile of the excitation light pulse must be taken into account to analyse reliably intensity-dependent population dynamics. Alternatively, a simple confocal detection scheme is demonstrated, which enables (i) retrieving the correct value for the bimolecular EEA rate which would otherwise be underestimated by a typical factor of three, and (ii) revealing minor EEA by-products otherwise unnoticed. Considering the ONPs as homogeneous rigid solutions of weakly interacting dyes, we postulate an incoherent exciton hoping mechanism to infer a diffusion constant exceeding 0.003 cm2 s−1 and a diffusion length as large as 70 nm. This work demonstrates the success of the present ONP design strategy at engineering efficient exciton transport in disordered multichromophoric systems.
Introduction
The transport of electronic excitation energy – excitons – is the function of so-called Light-Harvesting (LH) organic materials. In natural LH pigment-protein complexes, a subtle balance between structural organisation and disorder results in a partial delocalisation of electronic excitation over a few nearby pigments and a remarkably efficient exciton transport directed towards the photosynthetic reaction center.1–5 In synthetic organic materials, the efficiency of light energy conversion remains limited by exciton transport to a donor–acceptor interface, where electron–hole charge separation may occur.6–8 The recent use of non-fullerene acceptors enabling a larger exciton diffusion length – i.e. beyond the typical 5 to 10 nm range – was essential to improve significantly the efficiency of organic photovoltaic energy conversion9–12 or photocatalysis.13,14Much larger singlet exciton diffusion lengths – with diffusion constants approaching or exceeding 1 cm2 s−1 – have been reported in structurally well organized, molecular aggregates or crystals,15–19 possibly also enabling directed transport.20,21 In such systems, tight molecular packing and large dye interactions favor the quantum delocalisation of electronic excitation over multiple sites.22–24 As a limiting case of such a behavior, macroscopic exciton coherence, i.e. quantum delocalisation over the entire length (≃10 μm) of a highly-ordered single polymer chain was demonstrated at 10 K.25 Conversely, static or dynamic disorder promotes excitation energy localisation on individual sites. In the corresponding limiting case (e.g. weakly interacting dyes in solution), exciton transport results from the incoherent hopping of electronic excitation,26 where individual hopping events are described by the Förster model for Resonant Energy Transfer (FRET) from a dye in its first excited singlet (S1) state to a nearby dye in its ground (S0) state. Remarkable exciton transport properties have been reported at room temperature, e.g. along 1D supramolecular aggregates, and proposed to result from a “combined coherent–incoherent motion”,16 such as an incoherent hoping of excitons delocalised over few units,18,27 in line with the exciton transport mechanism described in natural LH complexes.28 In less ordered systems, transient exciton delocalisation is introduced as a mechanism to explain exciton transport outperforming the prediction of the incoherent hopping model.19,29,30
In this paper, we investigate fluorescent, dye-loaded polymer organic nanoparticles (ONPs), as a model for a disordered, weakly interacting multi-chromophoric system exhibiting remarkable exciton transport properties. Originally designed to produce high-brightness nanoprobes for bioimaging and biosensing applications,31,32 the polymer ONPs encapsulate cationic rhodamine B dye derivatives – see Fig. 1 – together with bulky counterions used to prevent dye aggregation and mitigate aggregation-caused fluorescence quenching (also called “self-quenching”).33,34 Depending on the polymer used, the ONPs exhibit various photophysical properties indicative of very efficient exciton transport, such as a collective fluorescence on/off switching,35 similar to that observed e.g. in molecular J-aggregates.36 Here, we use poly(methyl methacrylate-co-methacrylic acid) (PMMA–MA) as the polymer and the dyes are argued to be distributed homogeneously inside the ONP,37 like in a disordered, rigid solution. Still sub-ps electronic energy transfer between chromophores is observed, indicating a very efficient exciton transport held responsible for a “giant” antenna effect,38 with promising application to single (bio)molecule detection.39
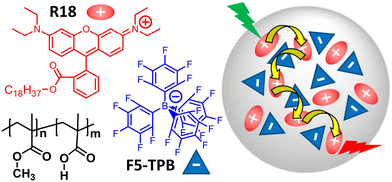 | ||
| Fig. 1 Chemical structures of dye (R18) with its bulky counter ion (F5-TPB) and polymer (PMMA–MA) constituting dye-loaded polymeric, light-harvesting nanoparticles sketched on the right-hand side. | ||
Among various methods to characterise exciton transport in organic materials,40,41 exciton–exciton annihilation (EEA) is a process controlled by exciton transport and exciton–exciton interactions, which results in an acceleration of the exciton population decay kinetics with increasing light excitation power. EEA has been investigated with a variety of experimental techniques including steady-state or time-resolved photoluminescence spectroscopy,40,42–46 photon antibunching,47–50 transient absorption spectroscopy,9,10,18,51–57 time-resolved fluorescence up-conversion,58,59 coherent multi-dimensional electronic spectroscopy60,61 and related “intensity cycling” transient absorption spectroscopy.62 Here we propose to investigate the exciton diffusion properties in these dye-loaded ONPs by monitoring EEA via time-resolved photoluminescence detection, as a function of excitation power.
The mechanism commonly described for EEA in organic materials is an energy transfer47–49 between two “colliding” excitons, producing one electronic ground state S0, and one higher-lying electronic state Sp, with p > 1. In general, Sp is very short-lived and decays back to S1via internal conversion (IC) on the sub-100 fs time scale. Therefore, the exciton population n(t) is modelled according to the following rate equation:40,42,54,57,63,64
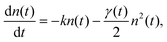 | (1) |
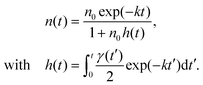 | (2) |
Because of the bimolecular term ∝n2(t) in eqn (1), the exciton population decay kinetics depends non-linearly on the initial exciton density n0, hence on the intensity of the excitation light pulse. Since the detected signal is integrated over the detection volume, the non-uniform transverse intensity profile of the excitation light pulse must be taken into account to enable a quantitative analysis of the observed population decay kinetics.64 In other words – and in contrast to the vast majority of the photoluminescence investigations of EEA reported in the literature – one may in general not expect eqn (2) to reproduce the observed decay kinetics unless special excitation (e.g. flat excitation profile) or detection schemes are implemented.
Here, after deriving the analytical expression for the fluorescence decay kinetics actually expected for an ensemble of ONPs in solution with a Gaussian excitation profile, we propose a simple confocal detection scheme in order to restrict the actual detection volume to the central part of the excitation volume where the initial exciton density is nearly uniform. Only then can we fit the data with eqn (2).65 We demonstrate that the decay kinetics recorded with and without the confocal detection scheme are indeed qualitatively different, while fits of either dataset with the appropriate function give the same result for the EEA rate, within experimental reproducibility. We also show that overlooking this experimental issue leads to a systematic underestimate of γ, by a factor of two to three typically, and possibly more depending on the excitation beam intensity profile.
In addition, in the ONPs loaded with the largest dye concentration, we observe a shortening of the exciton lifetime upon increasing the excitation power, with a threshold effect indicating a very non-linear power dependence. Importantly, this phenomenon remains unnoticed without the confocal detection scheme. The observed decay kinetics are nicely reproduced with a modified model where quenchers Q are formed with low yield as by-products of EEA, via a minor Sp decay channel competing with IC. The exciton decay rate k then increases with the quencher density due to S1 − Q collisional quenching, in perfect analogy with previous observations of exciton lifetime shortening due to singlet–triplet exciton annihilation in conjugated polymers.66
Eventually, all our data are nicely fitted with a time-independent γ coefficient, in line with the efficient exciton diffusion expected in these ONPs.38 In fact, we observe that excitation probabilities as low as 0.1% – meaning no more than few excitons on average per nanoparticle – are enough to observe the signature of EEA, demonstrating the effective diffusion of excitons within the entire nanoparticle on a time scale shorter than their natural lifetime.
Dimensional analysis reveals that γ is proportional to the product DRe of the exciton diffusion coefficient D and an effective distance Re, interpreted as the distance at which excitons should approach to annihilate.40,67 Measuring γ is therefore not enough to infer D: “additional information is required to separate motional (D) and interaction (Re) effects”.40 Recently, the independent measurements of D and γ revealed the coherent suppression of exciton–exciton interaction at low temperature in highly ordered molecular crystals.46,68 However, when knowing only γ, a model to describe EEA must be postulated in order to evaluate D. Here, we assume the validity of the FRET, and evaluate Re as a function of the Förster radius REEA associated with electronic excitation energy transfer between two excitons.69–71 We perform complementary transient absorption spectroscopy (TAS) to determine REEA from the overlap between the excitons (S1) absorption and emission spectra. Eventually we evaluate D = 300 nm2 ns−1 = 0.003 cm2 s−1, a value more than one order of magnitude larger than in previously reported dye-loaded PMMA films,57,72 thus validating the success of the present ONP design strategy to synthesize disordered multi-chromophoric systems acting as efficient LH materials.
Materials and methods
Nanoprecipitation is used to encapsulate rhodamine B octadecyl ester (R18) and its counterion tetrakis(pentafluorophenyl)borate (F5-TPB) in nanoparticles of poly(methyl methacrylate-co-methacrylic acid) (PMMA–MA) polymer, as described elsewhere.38 The average diameter of the organic nanoparticles (ONPs) is measured by transmission electron microscopy to be ≃40 nm, with a dispersion of ±20%. Nanoparticles labelled ONP30 and ONP100 are produced with dye concentrations of, respectively, 30 wt% and 100 wt%, expressed as the mass of dye and counterion (R18/F5-TPB) relative to the mass of the polymer. This corresponds to R18 dye molar concentrations of 0.17 M and 0.36 M, respectively. Two distinct batches A and B of each type of nanoparticle have been synthesized and investigated in distinct measurement campaigns, to demonstrate the reproducibility of the results below.Fig. 2 illustrates the experimental scheme for time-resolved fluorescence (TRF) spectroscopy. In short (see the details in the ESI†), a 300 fs laser pulse centered at 515 nm is used to excite the fluorescence of ONP30 and ONP100 dispersed in water to a typical absorption coefficient of 0.5 mm−1 or less at 515 nm. The laser system (Tangerine, by Amplitude) enables tuning the repetition rate from 100 kHz to 100 Hz when changing the excitation pulse energy from low to high, respectively. The solutions are circulated in a flow cell of thickness l = 0.2 or 0.5 mm. A streak camera is used to monitor the fluorescence decay kinetics with 10 ps time resolution (see Fig. S8(B)†). The transverse profile of the laser pulse is nearly Gaussian and carefully measured by imaging the fluorescence spot with a conventional CCD camera, under very low excitation power to avoid EEA and saturation of the fluorescence intensity. At higher excitation power where EEA takes place, more EEA and faster decay kinetics will occur for ONPs located in the center of the excitation volume – where the pulse intensity and excitation probability are higher – than in the periphery. The decay kinetics actually monitored results from the average over the entire excitation volume. Alternatively, we may collect the fluorescence emission using a confocal detection scheme which allows us to overlap a pinhole with an intermediate real optical image of the excitation volume in order to detect only the fluorescence emitted from the central part of the excitation volume.
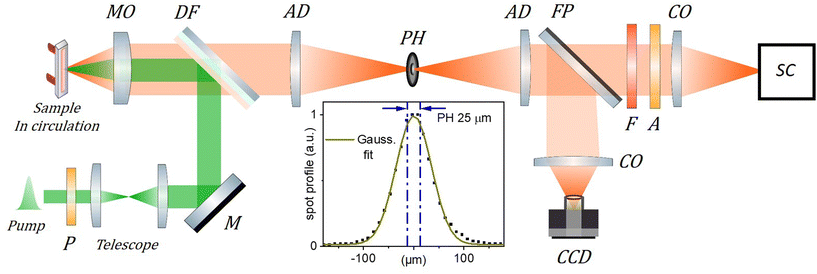 | ||
| Fig. 2 Scheme of the TRF setup. The 515 nm, 300 fs excitation (pump) beam is collimated and its diameter adjusted to 1.3 mm FWHM using a telescope. It is then reflected by a dichroic filter (DF) and focused by a microscope objective (MO, Mitutoyo Plan Apo 10X, f = 20 mm, NA = 0.28, pupill diameter = 11.2 mm ) in the circulated sample solution. The emitted fluorescence is collected by the same MO and transmitted through the DF to the “confocal setup” composed of two achromatic doublets (AD, f = 100 mm) and a 25 μm pinhole (PH) used to spatially filter the fluorescence signal. A streak camera (SC, Hamamatsu Streakscope C10627) working in single photon counting mode is used for detection under magic angle configuration (P: polarizer, A: analyzer; F: long pass filter; CO: camera objectives). In addition, a flip mirror (FP) and a CCD camera are used to monitor the fluorescence spot intensity profile in the PH plane as shown in the inset (dots; PH removed) together with its Gaussian fit (green curve), and the 25 μm central region over which the fluorescence signal is detected when the PH is in place (blue dash-dotted lines). The actual excitation spot size in the sample plane is 5 times smaller than in the PH plane and must be carefully calibrated (see details in the ESI†) to evaluate accurately the initial exciton density n0. | ||
For a quantitative analysis of the observed decay kinetics, we define the excitation pulse energy profile as: 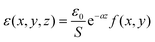 , where ε0 is the energy per pulse, f(x,y) the transverse energy profile with f(x = y = 0) = 1 and
, where ε0 is the energy per pulse, f(x,y) the transverse energy profile with f(x = y = 0) = 1 and 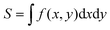 the pulse transverse section. The e−az factor accounts for the pulse absorption along its propagation direction z inside the sample, with a the absorption coefficient. The assumption that the transverse beam profile f(x,y) does not depend on z remains valid at the beam focus, provided that the Rayleigh length L exceeds the sample thickness l or light penetration depth. We typically have L > 0.6 mm > l (see ESI† for details). The fluorescence emission of an ONP located in
the pulse transverse section. The e−az factor accounts for the pulse absorption along its propagation direction z inside the sample, with a the absorption coefficient. The assumption that the transverse beam profile f(x,y) does not depend on z remains valid at the beam focus, provided that the Rayleigh length L exceeds the sample thickness l or light penetration depth. We typically have L > 0.6 mm > l (see ESI† for details). The fluorescence emission of an ONP located in  within the excitation volume is proportional to its exciton population
within the excitation volume is proportional to its exciton population 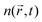 , which decays according to eqn (2), with an initial exciton density
, which decays according to eqn (2), with an initial exciton density 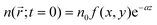 directly proportional to the energy pulse profile (see ESI†). The measured fluorescence decay kinetics is thus proportional to the integral F(t) of
directly proportional to the energy pulse profile (see ESI†). The measured fluorescence decay kinetics is thus proportional to the integral F(t) of 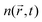 over the entire detection volume V:
over the entire detection volume V:
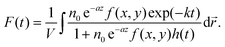 | (3) |
In the confocal detection scheme, the pinhole is used to restrict the detection volume V to only the central part of the excitation volume, i.e. x, y small enough that f(x, y) ≃ 1 inside V. In this case, the detected signal is, for a weakly absorbing sample (al < 1):
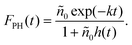 | (4) |
This is nothing but eqn (2), where n0 is replaced by 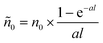 , the peak exciton density averaged along z over the sample thickness l, see ESI† for details. Hence, only for a flat excitation profile – or in the presence of a small-enough pinhole in the confocal detection scheme – do we expect to observe decay kinetics obeying eqn (2).
, the peak exciton density averaged along z over the sample thickness l, see ESI† for details. Hence, only for a flat excitation profile – or in the presence of a small-enough pinhole in the confocal detection scheme – do we expect to observe decay kinetics obeying eqn (2).
When removing the pinhole, the integration volume V extends to the entire excitation volume. For a Gaussian pulse profile, the integration can be written analytically (see ESI† for details), and for a weakly absorbing sample, the measured decay kinetics is expected to obey:
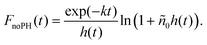 | (5) |
The light power dependence of the fluorescence decay kinetics predicted by eqn (4) or (5) are qualitatively different, and neglecting the effect of an inhomogeneous beam energy profile results in significant errors on the γ value, as illustrated in Fig. S4 in the ESI.† In the following, we report a series of fluorescence decay kinetics recorded as a function of excitation power on several ONP solutions produced from different synthetic batches. We compare the results obtained with and without the pinhole and fit the data with the functional forms given by eqn (4) or (5), respectively. As will be seen below, the exciton decay kinetics is nicely reproduced in all cases when postulating a time-independent γ value, meaning that h(t) = (1 − exp(−kt))/nA, where we define nA = 2k/γ the critical exciton density above which the exciton decay is dominated by EEA rather than natural S1 lifetime. The determination of reliable γ values requires accurate calibration of the initial exciton density n0, deduced from the R18 dye extinction coefficient – calibrated to εmax = 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1,73 at λmax = 560 nm – and from the dye number density ρ in the ONPs (see ESI† for details).
000 M−1 cm−1,73 at λmax = 560 nm – and from the dye number density ρ in the ONPs (see ESI† for details).
Results
Fig. 3(A) shows the absorption and emission spectra of ONPs with 0.5, 30 and 100 wt% dye-loading. We observe a slight increase in the intensity of the vibrational shoulder at 525 nm, indicating a relatively weak interaction between dyes despite the large dye concentration. The weak red shift of the fluorescence emission (by no more than 120 cm−1), may also be due to dye–dye interactions. However, since the single nanoparticle absorbance approaches 0.15 at λmax for the largest dye concentration, also reabsorption likely contributes to the observed fluorescence red-shift.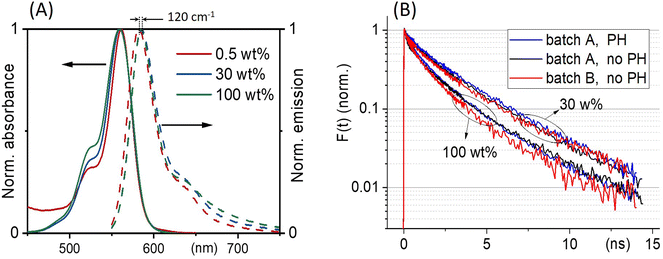 | ||
| Fig. 3 (A) ONPs steady-state absorption and emission spectra as a function of R18/F5-TPB loading. (B) Comparison of the fluorescence decay kinetics recorded with (PH) or without (no PH) pinhole, at low excitation power where no EEA occurs, for two batches A and B of nanoparticles ONP30 and ONP100. The results of the tri-exponential fits of all these curves are disclosed in Table 1. | ||
With low-enough excitation power where no EEA occurs, the exciton decay kinetics do not depend on the excitation power. Fig. 3(B) compares the fluorescence decay kinetics monitored at such low excitation powers on different samples. The decay kinetics are clearly not monoexponential, but correctly fitted with a sum of 3 exponential decay components (ki, i = 1 to 3) representative of a distribution of exciton decay rates, itself indicative of a distribution of exciton sub-populations possibly related to structural disorder among ONPs. The results of the fits are displayed in Table 1 and show that all decay kinetics exhibit a consistent 4.3 ns long-lived component with a significant relative weight. Noticeably, this lifetime is that of low-loading ONPs showing a 99% fluorescence quantum yield.38 We conclude, that even at much higher loadings, a significant sub-population of dyes (of 34% and 19% for ONP30 and ONP100, respectively) still keep a non-quenched fluorescence lifetime.
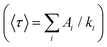 and quantum yields (QY), as a function of dye loading
and quantum yields (QY), as a function of dye loading
| Loading (wt%) | Triexp. fit amplitudesa (%) | 〈τ〉 (ns) | QY | ||
|---|---|---|---|---|---|
| 1/k1 (ns) 0.1 to 0.2 | 1/k2 (ns) 1.35 ± 0.15 | 1/k3 (ns) 4.3 ± 0.6 | |||
| a All decay kinetics displayed in Fig. 3 are fitted independently and reveal similar decay rates within the specified error bars. b Values taken from ref. 38. | |||||
| 0.5b | — | — | 100 | 4.2 | 0.99 |
| 30 | 17 ± 2 | 49 ± 2 | 34 ± 2 | 2.35 ± 0.15 | 0.44 ± 0.02 |
| 100 | 22 ± 2 | 57 ± 2 | 19 ± 2 | 1.6 ± 0.2 | 0.32 ± 0.04 |
Fig. 4 compares the decay kinetics observed with ONP30A when increasing the excitation power, in two distinct experiments performed in the absence or presence of the pinhole in the confocal detection scheme. The excitation power dependence of the decay kinetics is qualitatively different in both experiments. The quantitative analysis is done as follows. In line with the above tree-component analysis of the low-power decay kinetics indicating a distribution of ONPs (or a distribution of domains within ONPs), we postulate a 3-component fitting function KPH/noPH(t), with three exciton decay rates (the ki's evidenced above), but a common γ coefficient describing the exciton diffusion and interaction in all ONPs or domains:
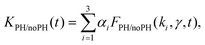 | (6) |
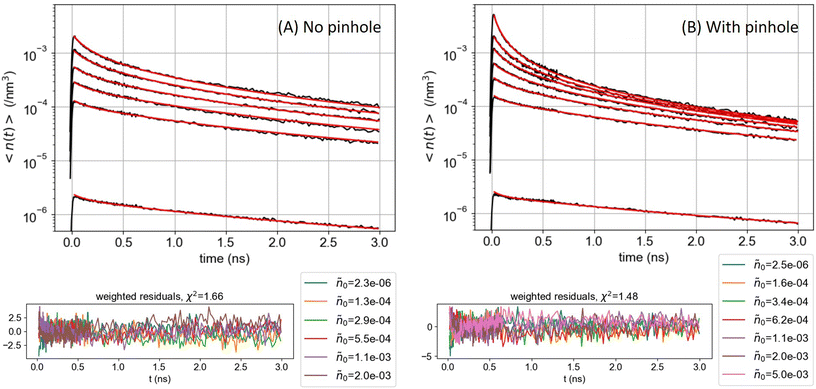 | ||
| Fig. 4 ONP30, batch A: comparison of the exciton density (in nm−3) decay kinetics averaged over the detection volume (A) without or (B) with the pinhole in the confocal detection scheme, for increasing excitation powers (see ESI† for the vertical axis calibration). The red lines are the result of the global fit of the decay kinetics with KnoPH(t) for panel (A) and KPH(t) for panel (B), see eqn (6), yielding γ = 6500 and 4700 nm3 ns−1, respectively, with the residuals displayed in the lower panels. | ||
With the 100 wt% dye-loaded ONPs, we observe a similar behavior up to intermediate excitation powers, but a shortening of the excitons lifetime for the highest excitation powers, as illustrated in Fig. 5. This observation is much more spectacular in the presence of the pinhole (compare Fig. 5A and C), as we collect the signal only from the center of the excitation volume, where the initial exciton density is the highest. To account for this observation, we need to modify the model proposed in eqn (1): we hypothesize the light-induced formation of long-lived quenchers Q at a density nQ(t) such that collisional quenching occurs with rate γQnQ(t) and shortens the lifetime of the mobile excitons. Such a model is described by the following rate equations:
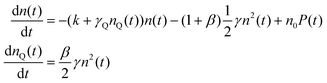 | (7) |
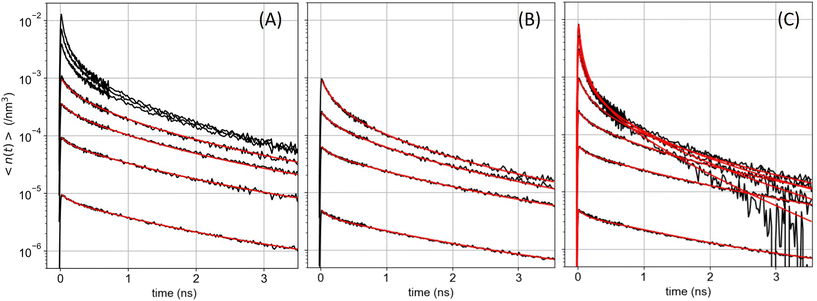 | ||
| Fig. 5 ONP100, batch B: exciton density (in nm−3) decay kinetics averaged over the detection volume (A) without or (B and C) with the pinhole in the confocal detection scheme, for increasing excitation powers. The red lines are the result of the global fit with three distinct models. In panel (A) the global fit is done with KnoPH(t) while disregarding the decay traces recorded with the highest three excitation powers. In panel (B) the data are the same as in panel (C) but we disregard the highest three excitation powers and the global fit is performed with KPH(t). In panel (C) all decay traces are analyzed globally based on the model described by eqn (7), with β = 0.024 as a result of the fit (see text). The three analyses yield γ = 7800, 8300, 8030 nm3 ns−1, for panel A, B, and C, respectively. | ||
The highly-excited singlet Sp state produced by EEA is very commonly assumed to decay quantitatively via IC to the S1 state, justifying the factor 1/2 in the EEA-induced population decay term in eqn (1). However, in various conjugated polymers, other decay channels have been reported, which compete with IC: highly-excited singlet states produced either by sequential two photon absorption from sub-ps pulses or by EEA were observed to decay into charge-separated states42,74–79 also referred to as molecular radical ions,78 or into triplet states – via ultrafast singlet fission.80,81 Single molecule spectroscopy of the rhodamine 6G fluorophore also evidenced photobleaching pathways from higher lying states (Sp > 1),82 as well as the photoproduction of both, long-lived triplet T1 and reduced radical states.83 For rhodamine B in ethanol, the T1 and radical states happen to absorb at wavelengths λmax = 560 nm and 550 nm, respectively – where the ground state S0 also absorbs – with an extinction coefficient εmax about 4 to 5 times weaker than that of the S0 state.84 The Förster radius RQ for the exciton energy transfer to these species is thus close to R0/51/6 ≃ 4 nm, where R0 is the Förster radius for homo-FRET evaluated from the spectral overlap of R18 emission and absorption spectra (see ESI† for the evaluation of R0). Hence, both the T1 and radical states qualify as good exciton quenchers in the OPNs.
The exciton quenching (γQ) and annihilation (γ) rates in eqn (7) are related, since they describe diffusion-limited excitation energy transfer to a fixed quencher (with Förster radius RQ) or to another diffusing exciton (with Förster radius REEA), respectively. Anticipating the Discussion section, we argue that γQ = γ/23/4 × (RQ/REEA)3/2. If we assume RQ = 4 nm and use the value derived below for REEA, we get γQ ≃ γ/3. Setting γQ = γ/3, and solving numerically the model described by eqn (7), yields fluorescence decay kinetics FQ(β,k,γ,t). In line with eqn (6) we again postulate a 3-component fitting function 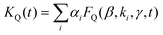 – with β and γ parameters common to all three sub-populations – to fit the data recorded in the presence of PH (where no additional averaging over the excitation volume is needed) as illustrated in Fig. 5C. The fitting procedure (see ref. 65) yields β = 0.024, and γ = 8030 nm3 ns−1.
– with β and γ parameters common to all three sub-populations – to fit the data recorded in the presence of PH (where no additional averaging over the excitation volume is needed) as illustrated in Fig. 5C. The fitting procedure (see ref. 65) yields β = 0.024, and γ = 8030 nm3 ns−1.
An alternative model, where the quencher Q would be produced as a secondary decay channel directly from S1 rather than from Sp does not reproduce the data so well (see ESI†). We conclude that a fraction of order 2% of the EEA events produce a byproduct Q, which is a good energy acceptor and reduces the exciton lifetime by collisional quenching. This result calls for scaling down by 2% the γ values obtained based on eqn (1) (where γ should be replaced by (1 + β)γ, even if no signature of Q is detectable). In the present case, this correction is anyway negligible compared to the experimental reproducibility. When performing the same experiments on ONP100 from the other synthetic batch (batch A, see Fig. S11†), we did not quite explore such high excitation densities and did not observe the shortening of the excitons lifetime. Still, we retrieved γ = 7000 ± 1100 m3 ns−1 (without or with PH), in reasonable agreement with the results obtained with batch B (Fig. 5).
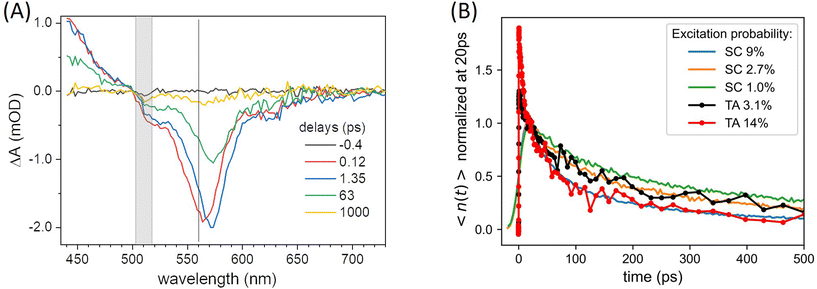
Complementary transient absorption (TA) experiments (see ESI† for details) are carried out to retrieve the excited state absorption (ESA) spectrum and its overlap with the fluorescence spectrum in order to evaluate the Förster radius RESA associated with the energy transfer between two S1 excited states. The TA data recorded with various excitation probabilities in the range 3% to 14%, are illustrated in Fig. 6. The negative contribution observed at wavelengths longer than 500 nm (Fig. 6(A)) is dominated by ground state bleach (GSB) and stimulated emission (SE), while excited state absorption (ESA) dominates the signal at shorter wavelengths. The negative band (GSB + SE) is observed to slightly deepen and red-shift by 1.35 ps. This is mostly attributed to the dynamic Stokes shift of the SE signal – also observed for rhodamine dyes in aqueous solution (not shown) – resulting from vibrational and solvent (here polymer) relaxation on this time scale in the excited state. In addition, inhomogeneous broadening of the ground state absorption band may contribute to a genuine red-shift of the GSB due to exciton transfer from higher-energy absorbing dyes to lower-energy absorbing dyes, already on the ps time scale in these ONPs. A significant GSB redshift was observed, although on a much slower time scale, in other dye-loaded PMMA films85 and attributed to inhomogeneous spectral broadening. Following this early spectral relaxation, the TA signal decays already very significantly by 60 ps, indicating rapid EEA. With a pump pulse focused in the sample to a diameter of ≃70 μm, approximately twice as large as the diameter of the probe pulse, the decay kinetics compare very well with the data recorded with the SC in the presence of a pinhole, as illustrated in Fig. 6(B). This good agreement is also a consistency check for our evaluations of the excitation probabilities in both experimental setups. Provided that the large majority of excitons decays via EEA in the TA experiments, the formation with a 2% yield of a quencher state Q characterized by an extinction coefficient 5 times weaker than the SE and GSB signals, would contribute a positive signal of ≃0.008 mOD at maximum – in the same spectral range as the corresponding ≃−0.04 mOD residual negative GSB. This remains undetectable in the present TA experiment characterized by a noise floor ≃0.04 mOD rms at 550 nm (evaluated at negative time delays, see e.g. the −0.4 ps signal in Fig. 6(A)), and further underlines the unparalleled sensitivity of the proposed confocal implementation of the photoluminescence experiment, as compared to a TA experiment.
The ESA spectrum can be extracted quantitatively from the TA signal observed on long times scales (i.e. after the early spectral relaxation) by subtracting the GSB and SE contributions. While the GSB is simply proportional to the opposite of the ground state absorption, the negative extinction coefficient for SE εSE(λ) can be computed (in units of M−1 cm−1) as (see ESI† for details):
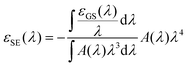 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1 falls within our error bar.
000 M−1 cm−1 falls within our error bar.
Discussion
In all kinetic traces reported in this work, the asymptotic decay corresponds to the 4.2 ns radiative lifetime of R18/F5-TPB in PMMA, except when the excitation power exceeds the threshold where EEA-induced byproducts start reducing the exciton lifetimes via collisional quenching (Fig. 5(C) and eqn (7)). We propose that also collisional quenching – itself boosted by large exciton diffusivity – is the mechanism for the onset of shorter-lived exciton sub-populations,87 as a function of dye concentration (Fig. 3(B)). Increasing dye-loading most likely enhances the population of molecular aggregates possibly also acting as quenchers available for exciton collisional quenching. However, the fact that even at 100 wt% dye loading, about 20% of the exciton population has an unquenched lifetime would then reveal the presence of nanoparticles or sub-domains inside nanoparticles, where no quenching occurs. Conversely, the population of shorter-lived excitons would reveal various degrees of quenching probabilities as a function of the (small, hence fluctuating) number of effective quenchers in ONPs. Together with the assumption of a homogeneous distribution of (R18/F5-TPB) inside ONPs, these considerations led us to define eqn (6) as a fitting function, where we postulate an average EEA rate γ, but a distribution of lifetimes, in fact revealing a distribution of quencher concentrations to collide with.With γ = 5600 nm3 ns−1 in ONP30 particles or domains where no quencher is present (i.e. k−1 = 4.2 ns), we find that the critical density above which EEA becomes significant is nA = 2k/γ = 8 × 10−5 nm−3. This corresponds to an average distance88 between excitons of 0.554/nA1/3 ∼ 13 nm > 2REEA, meaning that no “direct” EEA57 may occur at such low densities. Instead, EEA is rather a diffusion-limited process, justifying a posteriori the fact that γ is time-independent. To further test this statement, we performed a simultaneous global fit (not shown) of the entire dataset illustrated in Fig. 6(B) including the relatively noisier TA data (with time delays from 1 ps on) together with the SC data (with time delays from 30 ps on) at all excitation powers realized in both experiments. The fit function was KPH as given by eqn (6), and the fit quality was evaluated in terms of the reduced χ2 weighted with the data noise distribution on each kinetic trace. The fit quality was neither improved when assuming a time-dependent EEA rate γ(t) = a + b/√t as expected in case of direct energy transfer at very early time delays,57,67 nor significantly degraded when keeping a time-independent γ fitting parameter.
We also note that with a dye number density ρ = 0.1 nm−3 for ONP30 – i.e. ≃4000 dyes per nanoparticle – the exciton density nA corresponds to an excitation probability of 0.08%, i.e. no more than 3 to 4 excitons per nanoparticle. We conclude that exciton diffusion is efficient enough, that EEA occurs with significant probability with only few excitons inside a nanoparticle, provided no other quencher limits the excitons lifetime. Similarly, few energy acceptors or quenchers must be enough to cause collisional shortening of the exciton lifetime, as argued above, and in line with previous reports of a giant antenna effect enhancing the effective brightness of a single fluorescent acceptor in these ONPs,38 or a collective fluorescence quenching in closely related ONPs (R18/F5-TPB in poly(D,L-lactide-co-glycolide) – PLGA – polymer).35
For biosensing applications, single ONP fluorescence spectroscopy is performed under cw illumination with light intensities in the range of 1 W cm−2 or lower.32,38,89 Under such conditions (see ESI Section 8† for details), a 30 wt% loaded ONP absorbs photons with a rate in the MHz range, and we evaluate to ∼10 Hz the frequency of EEA events. Hence, about 1 EEA-induced quencher state Q is produced every 5 seconds. The rates of EEA events and Q state production are 5 times larger in ONP100.
We now discuss how to infer a diffusion coefficient D from the measured, time-independent γ parameter. As mentioned in the introduction, we need to postulate a model for the diffusion-limited EEA process. In the following, we will postulate the validity of the Förster model which describes an incoherent energy transfer due to a resonant dipole–dipole interaction, because (i) the disorder and weak interactions between the dyes are arguments in favor of the incoherent hoping assumption (i.e. we hypothesize, that there is no electronic excitation delocalisation among nearby chromophores), and (ii) the investigation of any other model is beyond the scope of this work. Unless numerical modeling is used, only two limiting cases can be discussed analytically: the low-diffusion limit, where direct energy transfer dominates, and the high-diffusion limit.40,52,67,70,71 Following the above discussion, we shall consider the latter case.
The high-diffusion limit is commonly discussed based on the Smoluchovsky model for coagulation in colloids, where Re is a contact radius introduced as a boundary condition in the diffusion equation.67,88 As such, Re defines a distance also called the radius of “dark sphere”, at which EEA occurs with probability one at first encounter.40,71 Very generally, Re is postulated to be equal to the inter-dye distance and arbitrarily chosen to be Re = 1 nm.9,10,40,42,45,66,90
An alternative approach to the dark sphere model describes the evolution of the exciton pair correlation function 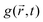 , with:52,69,70
, with:52,69,70
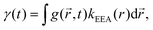 | (9) |
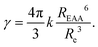 | (10) |
In contrast to the dark sphere model, we argue that when two excitons approach at a distance as low as the inter-dye or “hopping” distance, they still have a non vanishing probability to hop on another ground state chromophore also available within the same distance – and to continue their diffusive motion – rather than to annihilate at first encounter. Therefore Re may be defined as the inter-dye distance at which annihilation and further diffusion balance, by equating the typical times scales for exciton transport on distance Re and energy transfer between excitons separated by Re: Re2/(2D) = 1/kEEA(Re).52,71 As a result we get:
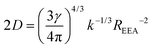 | (11) |
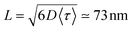 . For ONP100, γ ≃ 8000 nm2 ns−1 yields a larger D = 580 nm2 ns−1, but the same L = 75 nm due to the slightly reduced 〈τ〉 value.
. For ONP100, γ ≃ 8000 nm2 ns−1 yields a larger D = 580 nm2 ns−1, but the same L = 75 nm due to the slightly reduced 〈τ〉 value.
In a disordered solution of dyes interacting via resonant dipole interaction with Förster radius R0, incoherent exciton transport is predicted to become diffusive on a time scale shorter than the exciton lifetime k−1 provided the dimensionless concentration 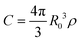 exceeds unity, with ρ the dye number density.26 For the 30 wt% dye-loaded ONPs, we have C ∼ 60 indicative of a fully diffusive transport. In such a case the diffusion coefficient is predicted to be:
exceeds unity, with ρ the dye number density.26 For the 30 wt% dye-loaded ONPs, we have C ∼ 60 indicative of a fully diffusive transport. In such a case the diffusion coefficient is predicted to be:
| Dth = ζ × kC4/3R02, | (12) |
While we provide an accurate measurement of the EEA rate and sensitive detection of EEA by-products acting as quenchers, complementary theoretical investigation is required to refine the present evaluation of the exciton diffusion length, and to conclude whether the proposed incoherent hoping mechanism holds, or whether (transient) electronic excitation delocalization operates – like argued in natural LH complexes – to further enhance exciton transport properties also in disordered, rigid dye solutions at such large concentrations.
Conclusion
We report on EEA kinetics in dye-loaded ONPs dispersed in water solution, by monitoring photoluminescence decay kinetics as a function of excitation pulse intensity. We demonstrate that the inhomogeneous intensity profile of the excitation pulse has a very significant influence on the observed decay kinetics. While this effect is most generally overlooked, we show that it induces a systematic underestimate – possibly exceeding a factor of 3 depending on the actual pulse intensity profile – of the retrieved EEA rate γ, which also erroneously appears to be intensity dependent. We propose two methods to solve this experimental issue. (i) We derive the functional form expected for the decay kinetics actually observed with a Gaussian excitation pulse profile and use it to fit the data. Alternatively, (ii) we implement a simple “confocal” experimental scheme (i.e. one pinhole in between two achromats). Only in the latter case can one use the expected eqn (2) to globally fit the observed decay kinetics and extract an unbiased γ value, independent of the pulse intensity. The confocal detection scheme also appears superior in detecting the EEA-induced formation of minor by-products inducing further exciton collisional quenching, a process which remains unnoticed when averaging the signal over the entire excitation volume.With the present PMMA–MA ONPs loaded with rhodamine B dye derivatives (R18) and bulky F5-TPB counterions, we observe efficient EEA already at excitation probabilities as low as 0.1% – i.e. few excitons per ONP – indicating efficient exciton transport within the ONPs, in perfect line with the outstanding LH properties previously reported for these ONPs. The quantitative evaluation of the exciton diffusion constant and diffusion length is conditioned to the modeling of both exciton transport and exciton interactions in the ONPs. Assuming here incoherent exciton hopping and FRET between colliding excitons, we infer an exciton diffusion length in the range of 70 nm, i.e. almost twice the ONP diameter. This is a remarkably high value for a disordered, rigid solution of dyes, which results from (i) a diffusion coefficient exceeding that of other dye loaded PMMA films by one order of magnitude, and (ii) a relatively large exciton lifetime. Both properties are due to the ONP design strategy using bulky counterions to mitigate aggregation-caused fluorescence quenching even at large dye concentration (up to 0.3 M). The ONP100 explores the limits of the present synthetic design, since the exciton diffusion length does not exceed that of ONP30. In contrast with the quest for structurally ordered molecular systems possibly enabling exciton delocalization and quantum transport, this work adopts an alternative design strategy, which results in outstanding exciton transport in disordered assemblies of weakly interacting dyes in ONPs with remarkable, functional LH properties.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We are grateful to Pascal Hébraud, Stefan Haacke, and Seogjoo Jang for fruitful discussions. We acknowledge support from the French ANR via the “LHnanoMat” project (ANR-19-CE09-0006-02), and from the Interdisciplinary Thematic Institute QMat as part of the ITI 2021-2028 program of the University of Strasbourg, CNRS and Inserm via the IdEx Unistra (ANR 10 IDEX 0002), SFRI STRAT'US (ANR 20 SFRI 0012), and Labex NIE (ANR-11-LABX-0058-NIE) projects of the French Investments for the Future Program. A. G. acknowledges support from the Region Grand-Est (contract #19-GE6-161).References
- R. Monshouwer, M. Abrahamsson, F. Van Mourik and R. Van Grondelle, Superradiance and exciton delocalization in bacterial photosynthetic light-harvesting systems, J. Phys. Chem. B, 1997, 101(37), 7241–7248 CrossRef CAS.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Lessons from nature about solar light harvesting, Nat. Chem., 2011, 3, 763–774 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Light Absorption and Energy Transfer in the Antenna Complexes of Photosynthetic Organisms, Chem. Rev., 2017, 117(2), 249–293 CrossRef CAS PubMed.
- J. Cao, R. J. Cogdell, D. F. Coker, H.-G. Duan, J. Hauer, U. Kleinekathöfer, T. L. C. Jansen, T. Mančal, R. J. D. Miller, J. P. Ogilvie, V. I. Prokhorenko, T. Renger, H.-S. Tan, R. Tempelaar, M. Thorwart, E. Thyrhaug, S. Westenhoff and D. Zigmantas, Quantum biology revisited, Sci. Adv., 2020, 6, eaaz4888 CrossRef CAS.
- A. Klinger, D. Lindorfer, F. Müh and T. Renger, Living on the edge: light-harvesting efficiency and photoprotection in the core of green sulfur bacteria, Phys. Chem. Chem. Phys., 2023, 25(28), 18698–18710 RSC.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Exciton diffusion in organic semiconductors, Energy Environ. Sci., 2015, 8(7), 1867–1888 RSC.
- Y. Tamai, H. Ohkita, H. Benten and S. Ito, Exciton Diffusion in Conjugated Polymers: From Fundamental Understanding to Improvement in Photovoltaic Conversion Efficiency, J. Phys. Chem. Lett., 2015, 6, 3417–3428 CrossRef CAS.
- S. M. Menke, W. A. Luhman and R. J. Holmes, Tailored exciton diffusion in organic photovoltaic cells for enhanced power conversion efficiency, Nat. Mater., 2013, 12, 152–157 CrossRef CAS.
- S. Chandrabose, K. Chen, A. J. Barker, J. J. Sutton, S. K. K. Prasad, J. Zhu, J. Zhou, K. C. Gordon, Z. Xie, X. Zhan and J. M. Hodgkiss, High Exciton Diffusion Coefficients in Fused Ring Electron Acceptor Films, J. Am. Chem. Soc., 2019, 141, 6922–6929 CrossRef CAS PubMed.
- Y. Firdaus, V. M. Le Corre, S. Karuthedath, W. Liu, A. Markina, W. Huang, S. Chattopadhyay, M. M. Nahid, M. I. Nugraha, Y. Lin, A. Seitkhan, A. Basu, W. Zhang, I. McCulloch, H. Ade, J. Labram, F. Laquai, D. Andrienko, L. J. A. Koster and T. D. Anthopoulos, Long-range exciton diffusion in molecular non-fullerene acceptors, Nat. Commun., 2020, 11, 5220 CrossRef CAS PubMed.
- P. A. Hume, W. Jiao and J. M. Hodgkiss, Long-range exciton diffusion in a non-fullerene acceptor: approaching the incoherent limit, J. Mater. Chem. C, 2021, 9(4), 1419–1428 RSC.
- Y. Cai, Q. Li, G. Lu, H. S. Ryu, Y. Li, H. Jin, Z. Chen, Z. Tang, G. Lu, X. Hao, H. Y. Woo, C. Zhang and Y. Sun, Vertically optimized phase separation with improved exciton diffusion enables efficient organic solar cells with thick active layers, Nat. Commun., 2022, 13, 2369 CrossRef CAS PubMed.
- H. Wang, S. Jin, X. Zhang and Y. Xie, Excitonic Effects in Polymeric Photocatalysts, Angew. Chem., Int. Ed., 2020, 59, 22828–22839 CrossRef CAS PubMed.
- Y. Zhu, Z. Zhang, W. Si, Q. Sun, G. Cai, Y. Li, Y. Jia, X. Lu, W. Xu, S. Zhang and Y. Lin, Organic Photovoltaic Catalyst with Extended Exciton Diffusion for High-Performance Solar Hydrogen Evolution, J. Am. Chem. Soc., 2022, 144, 12747–12755 CrossRef CAS PubMed.
- C. B. Winiger, S. Li, G. R. Kumar, S. M. Langenegger and R. Häner, Long-Distance Electronic Energy Transfer in Light-Harvesting Supramolecular Polymers, Angew. Chem., Int. Ed., 2014, 53, 13609–13613 CrossRef CAS PubMed.
- A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Köhler, H.-W. Schmidt and R. Hildner, Long-range energy transport in single supramolecular nanofibres at room temperature, Nature, 2015, 523, 196–199 CrossRef CAS.
- X.-H. Jin, M. B. Price, J. R. Finnegan, C. E. Boott, J. M. Richter, A. Rao, S. M. Menke, R. H. Friend, G. R. Whittell and I. Manners, Long-range exciton transport in conjugated polymer nanofibers prepared by seeded growth, Science, 2018, 360, 897–900 CrossRef CAS.
- C. Rehhagen, M. Stolte, S. Herbst, M. Hecht, S. Lochbrunner, F. Würthner and F. Fennel, Exciton Migration in Multistranded Perylene Bisimide J-Aggregates, J. Phys. Chem. Lett., 2020, 11(16), 6612–6617 CrossRef CAS.
- A. J. Sneyd, T. Fukui, D. Paleček, S. Prodhan, I. Wagner, Y. Zhang, J. Sung, S. M. Collins, T. J. A. Slater, Z. Andaji-Garmaroudi, L. R. MacFarlane, J. D. Garcia-Hernandez, L. Wang, G. R. Whittell, J. M. Hodgkiss, K. Chen, D. Beljonne, I. Manners, R. H. Friend and A. Rao, Efficient energy transport in an organic semiconductor mediated by transient exciton delocalization, Sci. Adv., 2021, 7, eabh4232 CrossRef CAS PubMed.
- S. Stäter, F. A. Wenzel, H. Welz, K. Kreger, J. Köhler, H.-W. Schmidt and R. Hildner, Directed Gradients in the Excited-State Energy Landscape of Poly(3-hexylthiophene) Nanofibers, J. Am. Chem. Soc., 2023, 145, 13780–13787 CrossRef PubMed.
- K. Müller, K. S. Schellhammer, N. Gräßler, B. Debnath, F. Liu, Y. Krupskaya, K. Leo, M. Knupfer and F. Ortmann, Directed exciton transport highways in organic semiconductors, Nat. Commun., 2023, 14, 5599 CrossRef PubMed.
- J. M. Moix, M. Khasin and J. Cao, Coherent quantum transport in disordered systems: I. The influence of dephasing on the transport properties and absorption spectra on one-dimensional systems, New J. Phys., 2013, 15, 085010 CrossRef CAS.
- T. Brixner, R. Hildner, J. Köhler, C. Lambert and F. Würthner, Exciton Transport in Molecular Aggregates – From Natural Antennas to Synthetic Chromophore Systems, Adv. Energy Mater., 2017, 7(16), 1700236 CrossRef.
- W. Popp, D. Brey, R. Binder and I. Burghardt, Quantum Dynamics of Exciton Transport and Dissociation in Multichromophoric Systems, Annu. Rev. Phys. Chem., 2021, 72, 591–616 CrossRef CAS.
- F. Dubin, R. Melet, T. Barisien, R. Grousson, L. Legrand, M. Schott and V. Voliotis, Macroscopic coherence of a single exciton state in an organic quantum wire, Nat. Phys., 2006, 2, 32–35 Search PubMed.
- C. R. Gochanour, H. C. Andersen and M. D. Fayer, Electronic excited state transport in solution, J. Chem. Phys., 1979, 70(9), 4254–4271 CrossRef CAS.
- B. Wittmann, F. A. Wenzel, S. Wiesneth, A. T. Haedler, M. Drechsler, K. Kreger, J. Köhler, E. W. Meijer, H.-W. Schmidt and R. Hildner, Enhancing Long-Range Energy Transport in Supramolecular Architectures by Tailoring Coherence Properties, J. Am. Chem. Soc., 2020, 142, 8323–8330 CrossRef CAS.
- V. I. Novoderezhkin and R. van Grondelle, Physical origins and models of energy transfer in photosynthetic light-harvesting, Phys. Chem. Chem. Phys., 2010, 12(27), 7352 RSC.
- S. Giannini, W.-T. Peng, L. Cupellini, D. Padula, A. Carof and J. Blumberger, Exciton transport in molecular organic semiconductors boosted by transient quantum delocalization, Nat. Commun., 2022, 13, 2755 CrossRef CAS PubMed.
- D. Balzer and I. Kassal, Mechanism of Delocalization-Enhanced Exciton Transport in Disordered Organic Semiconductors, J. Phys. Chem. Lett., 2023, 14, 2155–2162 CrossRef CAS PubMed.
- A. Reisch and A. S. Klymchenko, Fluorescent Polymer Nanoparticles Based on Dyes: Seeking Brighter Tools for Bioimaging, Small, 2016, 12, 1968–1992 CrossRef CAS PubMed.
- D. S. Biswas, P. Gaki, E. C. Da Silva, A. Combes, A. Reisch, P. Didier and A. S. Klymchenko, Long-range Energy Transfer Between Dye-loaded Nanoparticles: Observation and Amplified Detection of Nucleic Acids, Adv. Mater., 2023, 2301402 CrossRef CAS PubMed.
- I. Shulov, S. Oncul, A. Reisch, Y. Arntz, M. Collot, Y. Mely and A. S. Klymchenko, Fluorinated counterion-enhanced emission of rhodamine aggregates: ultrabright nanoparticles for bioimaging and light-harvesting, Nanoscale, 2015, 7(43), 18198–18210 RSC.
- A. H. Ashoka, I. O. Aparin, A. Reisch and A. S. Klymchenko, Brightness of fluorescent organic nanomaterials, Chem. Soc. Rev., 2023, 52(14), 4525–4548 RSC.
- A. Reisch, P. Didier, L. Richert, S. Oncul, Y. Arntz, Y. Mély and A. S. Klymchenko, Collective fluorescence switching of counterion-assembled dyes in polymer nanoparticles, Nat. Commun., 2014, 5, 4089 CrossRef CAS PubMed.
- H. Lin, R. Camacho, Y. Tian, T. E. Kaiser, F. Würthner and I. G. Scheblykin, Collective Fluorescence Blinking in Linear J-Aggregates Assisted by Long-Distance Exciton Migration, Nano Lett., 2010, 10(2), 620–626 CrossRef CAS PubMed.
- A. Reisch, K. Trofymchuk, A. Runser, G. Fleith, M. Rawiso and A. S. Klymchenko, Tailoring Fluorescence Brightness and Switching of Nanoparticles through Dye Organization in the Polymer Matrix, ACS Appl. Mater. Interfaces, 2017, 9(49), 43030–43042 CrossRef CAS PubMed.
- K. Trofymchuk, A. Reisch, P. Didier, F. Fras, P. Gilliot, Y. Mely and A. S. Klymchenko, Giant light-harvesting nanoantenna for single-molecule detection in ambient light, Nat. Photonics, 2017, 11, 657–663 CrossRef CAS PubMed.
- N. Melnychuk, S. Egloff, A. Runser, A. Reisch and A. S. Klymchenko, Light-Harvesting Nanoparticle Probes for FRET-Based Detection of Oligonucleotides with Single-Molecule Sensitivity, Angew. Chem., Int. Ed., 2020, 59(17), 6811–6818 CrossRef CAS PubMed.
- R. C. Powell and Z. G. Soos, Singlet exciton energy transfer in organic solids, J. Lumin., 1975, 11(1–2), 1–45 CrossRef CAS.
- J. D. A. Lin, O. V. Mikhnenko, J. Chen, Z. Masri, A. Ruseckas, A. Mikhailovsky, R. P. Raab, J. Liu, P. W. M. Blom, M. A. Loi, C. J. García-Cervera, I. D. W. Samuel and T.-Q. Nguyen, Systematic study of exciton diffusion length in organic semiconductors by six experimental methods, Mater. Horiz., 2014, 1(2), 280–285 RSC.
- M. A. Stevens, C. Silva, D. M. Russell and R. H. Friend, Exciton dissociation mechanisms in the polymeric semiconductors poly(9,9-dioctylfluorene) and poly(9,9-dioctylfluorene-co-benzothiadiazole), Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(16), 165213 CrossRef.
- A. Lewis, A. Ruseckas, O. Gaudin, G. Webster, P. Burn and I. Samuel, Singlet exciton diffusion in MEH-PPV films studied by exciton–exciton annihilation, Org. Electron., 2006, 7, 452–456 CrossRef CAS.
- P. E. Shaw, A. Ruseckas and I. D. W. Samuel, Exciton Diffusion Measurements in Poly(3-hexylthiophene), Adv. Mater., 2008, 20(18), 3516–3520 CrossRef CAS.
- S. Cook, H. Liyuan, A. Furube and R. Katoh, Singlet Annihilation in Films of Regioregular Poly(3-hexylthiophene): Estimates for Singlet Diffusion Lengths and the Correlation between Singlet Annihilation Rates and Spectral Relaxation, J. Phys. Chem. C, 2010, 114, 10962–10968 CrossRef CAS.
- S. Kumar, I. S. Dunn, S. Deng, T. Zhu, Q. Zhao, O. F. Williams, R. Tempelaar and L. Huang, Exciton annihilation in molecular aggregates suppressed through quantum interference, Nat. Chem., 2023, 15, 1118–1126 CrossRef CAS.
- C. G. Hübner, G. Zumofen, A. Renn, A. Herrmann, K. Müllen and T. Basché, Photon Antibunching and Collective Effects in the Fluorescence of Single Bichromophoric Molecules, Phys. Rev. Lett., 2003, 91(9), 093903 CrossRef.
- J. Hofkens, M. Cotlet, T. Vosch, P. Tinnefeld, K. D. Weston, C. Ego, A. Grimsdale, K. Mullen, D. Beljonne, J. L. Bredas, S. Jordens, G. Schweitzer, M. Sauer and F. De Schryver, Revealing competitive Forster-type resonance energy-transfer pathways in single bichromophoric molecules, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(23), 13146–13151 CrossRef CAS PubMed.
- D. Nettels, D. Haenni, S. Maillot, M. Gueye, A. Barth, V. Hirschfeld, C. G. Hubner, J. Léonard and B. Schuler, Excited-state annihilation reduces power dependence of single-molecule FRET experiments, Phys. Chem. Chem. Phys., 2015, 17(48), 32304–32315 RSC.
- G. J. Hedley, T. Schröder, F. Steiner, T. Eder, F. J. Hofmann, S. Bange, D. Laux, S. Höger, P. Tinnefeld, J. M. Lupton and J. Vogelsang, Picosecond time-resolved photon antibunching measures nanoscale exciton motion and the true number of chromophores, Nat. Commun., 2021, 12, 1327 CrossRef CAS.
- L. Valkunas, G. Trinkunas, V. Liuolia and R. Van Grondelle, Nonlinear annihilation of excitations in photosynthetic systems, Biophys. J., 1995, 69, 1117–1129 CrossRef CAS PubMed.
- V. Gulbinas, M. Chachisvilis, L. Valkunas and V. Sundström, Excited State Dynamics of Phthalocyanine Films, J. Phys. Chem., 1996, 100(6), 2213–2219 CrossRef CAS.
- G. Trinkunas, J. L. Herek, T. Polívka, V. Sundström and T. Pullerits, Exciton Delocalization Probed by Excitation Annihilation in the Light-Harvesting Antenna LH2, Phys. Rev. Lett., 2001, 86(18), 4167–4170 CrossRef CAS PubMed.
- E. Engel, K. Leo and M. Hoffmann, Ultrafast relaxation and exciton–exciton annihilation in PTCDA thin films at high excitation densities, Chem. Phys., 2006, 325(1), 170–177 CrossRef CAS.
- V. Gulbinas, I. Minevičiutė, D. Hertel, R. Wellander, A. Yartsev and V. Sundström, Exciton diffusion and relaxation in methyl-substituted polyparaphenylene polymer films, J. Chem. Phys., 2007, 127(14), 144907 CrossRef CAS PubMed.
- S. M. King, D. Dai, C. Rothe and A. P. Monkman, Exciton annihilation in a polyfluorene: Low threshold for singlet-singlet annihilation and the absence of singlet-triplet annihilation, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(8), 085204 CrossRef.
- F. Fennel and S. Lochbrunner, Exciton-exciton annihilation in a disordered molecular system by direct and multistep Förster transfer, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 140301 CrossRef.
- S. E. Bradforth, R. Jimenez, F. van Mourik, R. van Grondelle and G. R. Fleming, Excitation Transfer in the Core Light-Harvesting Complex (LH-1) of Rhodobacter sphaeroides: An Ultrafast Fluorescence Depolarization and Annihilation Study, J. Phys. Chem., 1995, 99(43), 16179–16191 CrossRef CAS.
- H. Wang, H.-Y. Wang, B.-R. Gao, L. Wang, Z.-Y. Yang, X.-B. Du, Q.-D. Chen, J.-F. Song and H.-B. Sun, Exciton diffusion and charge transfer dynamics in nano phase-separated P3HT/PCBM blend films, Nanoscale, 2011, 3(5), 2280 RSC.
- J. Dostál, F. Fennel, F. Koch, S. Herbst, F. Würthner and T. Brixner, Direct observation of exciton–exciton interactions, Nat. Commun., 2018, 9(1), 2466 CrossRef PubMed.
- P. Malý, J. Lüttig, A. Turkin, J. Dostál, C. Lambert and T. Brixner, From wavelike to sub-diffusive motion: exciton dynamics and interaction in squaraine copolymers of varying length, Chem. Sci., 2020, 11(2), 456–466 RSC.
- P. Malý, J. Lüttig, P. A. Rose, A. Turkin, C. Lambert, J. J. Krich and T. Brixner, Separating single- from multi-particle dynamics in nonlinear spectroscopy, Nature, 2023, 616(7956), 280–287 CrossRef PubMed.
- A. Dogariu, D. Vacar and A. J. Heeger, Picosecond time-resolved spectroscopy of the excited state in a soluble derivative of poly(phenylene vinylene): Origin of the bimolecular decay, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(16), 10218–10224 CrossRef CAS.
- M. Kirm, V. Nagirnyi, E. Feldbach, M. De Grazia, B. Carré, H. Merdji, S. Guizard, G. Geoffroy, J. Gaudin, N. Fedorov, P. Martin, A. Vasil'ev and A. Belsky, Exciton-exciton interactions in CdWO4 irradiated by intense femtosecond vacuum ultraviolet pulses, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(23), 233103 CrossRef.
- A. Gharbi and J. Léonard, EEA_Photolum, 2024, https://hal.archives-ouvertes.fr/hal-04561022 Search PubMed.
- Y. Zaushitsyn, K. G. Jespersen, L. Valkunas, V. Sundström and A. Yartsev, Ultrafast dynamics of singlet-singlet and singlet-triplet exciton annihilation in poly(3-2′-methoxy-5′-octylphenyl)thiophene films, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195201 CrossRef.
- U. Gösele, M. Hauser, U. Klein and R. Frey, Diffusion and long-range energy transfer, Chem. Phys. Lett., 1975, 34, 519–522 CrossRef.
- R. Tempelaar, T. L. C. Jansen and J. Knoester, Exciton–Exciton Annihilation Is Coherently Suppressed in H-Aggregates, but Not in J-Aggregates, J. Phys. Chem. Lett., 2017, 8, 6113–6117 CrossRef CAS PubMed.
- A. Suna, Kinematics of Exciton-Exciton Annihilation in Molecular Crystals, Phys. Rev. B: Solid State, 1970, 1(4), 1716–1739 CrossRef.
- S. Jang, K. J. Shin and S. Lee, Effects of excitation migration and translational diffusion in the luminescence quenching dynamics, J. Chem. Phys., 1995, 102, 815–827 CrossRef CAS.
- V. M. Agranovich and M. D. Galanin, Electronic Excitation Energy Transfer in Condensed Matter, North-Holland Publishing Company, 1982 Search PubMed.
- K. A. Colby, J. J. Burdett, R. F. Frisbee, L. Zhu, R. J. Dillon and C. J. Bardeen, Electronic Energy Migration on Different Time Scales: Concentration Dependence of the Time-Resolved Anisotropy and Fluorescence Quenching of Lumogen Red in Poly(methyl methacrylate), J. Phys. Chem. A, 2010, 114(10), 3471–3482 CrossRef CAS PubMed.
- R. P. Haugland, Handbook of fluorescent probes and research chemicals, Molecular Probes, Eugene, 1996, vol. 8 Search PubMed.
- V. Klimov, D. McBranch, N. Barashkov and J. Ferraris, Biexcitons in π-conjugated oligomers: Intensity-dependent femtosecond transient-absorption study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(12), 7654 CrossRef CAS.
- B. Kraabel, V. I. Klimov, R. Kohlman, S. Xu, H.-L. Wang and D. W. McBranch, Unified picture of the photoexcitations in phenylene-based conjugated polymers: Universal spectral and dynamical features in subpicosecond transient absorption, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8501–8515 CrossRef CAS.
- G. Denton, N. Tessler, M. Stevens and R. Friend, Optical response of conjugated polymers excited at high intensity, Synth. Met., 1999, 102, 1008–1009 CrossRef CAS.
- S. V. Frolov, Z. Bao, M. Wohlgenannt and Z. V. Vardeny, Ultrafast Spectroscopy of Even-Parity States in π-Conjugated Polymers, Phys. Rev. Lett., 2000, 85(10), 2196–2199 CrossRef CAS PubMed.
- C. Silva, A. S. Dhoot, D. M. Russell, M. A. Stevens, A. C. Arias, J. D. MacKenzie, N. C. Greenham, R. H. Friend, S. Setayesh and K. Müllen, Efficient exciton dissociation via two-step photoexcitation in polymeric semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125211 CrossRef.
- V. Gulbinas, Y. Zaushitsyn, H. Bässler, A. Yartsev and V. Sundström, Dynamics of charge pair generation in ladder-type poly(para-phenylene) at different excitation photon energies, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 035215 CrossRef.
- B. Kraabel, D. Hulin, C. Aslangul, C. Lapersonne-Meyer and M. Schott, Triplet exciton generation, transport and relaxation in isolated polydiacetylene chains: Subpicosecond pump-probe experiments, Chem. Phys., 1998, 227, 83–98 CrossRef CAS.
- M. Wohlgenannt, W. Graupner, G. Leising and Z. V. Vardeny, Photogeneration and recombination processes of neutral and charged excitations in films of a ladder-type poly(para-phenylene), Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 5321–5330 CrossRef CAS.
- C. Eggeling, A. Volkmer and C. A. M. Seidel, Molecular Photobleaching Kinetics of Rhodamine 6G by One- and Two-Photon Induced Confocal Fluorescence Microscopy, ChemPhysChem, 2005, 6, 791–804 CrossRef CAS PubMed.
- R. Zondervan, F. Kulzer, S. B. Orlinskii and M. Orrit, Photoblinking of Rhodamine 6G in Poly(vinyl alcohol): Radical Dark State Formed through the Triplet, J. Phys. Chem. A, 2003, 107(35), 6770–6776 CrossRef CAS.
- A. Dunne and M. F. Quinn, Triplet–triplet absorption spectra and the spectra of the photoreduced states of Rhodamine B and Rhodamine 110, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 1104 RSC.
- F. Fennel and S. Lochbrunner, Förster-mediated spectral diffusion in disordered organic materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(9), 094203 CrossRef.
- P. C. Beaumont, D. G. Johnson and B. J. Parsons, Excited state and free radical properties of rhodamine dyes in aqueous solution: A laser flash photolysis and pulse radiolysis study, J. Photochem. Photobiol., A, 1997, 107(1–3), 175–183 CrossRef CAS.
- G. Fanciullo, I. Conti, P. Didier, A. Klymchenko, J. Léonard, M. Garavelli and I. Rivalta, Modelling quenching mechanisms of disordered molecular systems in the presence of molecular aggregates, Phys. Chem. Chem. Phys., 2022, 24, 1787–1794 RSC.
- S. Chandrasekhar, Stochastic problems in physics and astronomy, Rev. Mod. Phys., 1943, 15(1), 1 CrossRef.
- A. Reisch, A. Runser, Y. Arntz, Y. Mély and A. S. Klymchenko, Charge-Controlled Nanoprecipitation as a Modular Approach to Ultrasmall Polymer Nanocarriers: Making Bright and Stable Nanoparticles, ACS Nano, 2015, 9(5), 5104–5116 CrossRef CAS PubMed.
- C. Rehhagen, S. Rafiq, K. N. Schwarz, G. D. Scholes and S. Lochbrunner, The effect of intermolecular electronic coupling on the exciton dynamics in perylene red nanoparticles, Phys. Chem. Chem. Phys., 2022, 24(15), 8695–8704 RSC.
- S. W. Haan and R. Zwanzig, Förster migration of electronic excitation between randomly distributed molecules, J. Chem. Phys., 1978, 68(4), 1879–1883 CrossRef CAS.
- M. Schlosser and S. Lochbrunner, Exciton Migration by Ultrafast Förster Transfer in Highly Doped Matrixes, J. Phys. Chem. B, 2006, 110(12), 6001–6009 CrossRef CAS PubMed.
- F. Fennel and S. Lochbrunner, Long distance energy transfer in a polymer matrix doped with a perylene dye, Phys. Chem. Chem. Phys., 2011, 13(8), 3527 RSC.
- K. A. Colby and C. J. Bardeen, Electronic Energy Migration in Solid versus Liquid Host Matrices for Concentrated Perylenediimide Dye Solutions, J. Phys. Chem. A, 2011, 115(26), 7574–7581 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr00325j |
| This journal is © The Royal Society of Chemistry 2024 |