Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A physics-inspired approach to the understanding of molecular representations and models
Luke
Dicks
 a,
David E.
Graff
a,
David E.
Graff
 bc,
Kirk E.
Jordan
bc,
Kirk E.
Jordan
 d,
Connor W.
Coley
d,
Connor W.
Coley
 ce and
Edward O.
Pyzer-Knapp
ce and
Edward O.
Pyzer-Knapp
 *a
*a
aIBM Research Europe, Hartree Centre, Daresbury, UK. E-mail: epyzerk3@uk.ibm.com
bDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02139, USA
cDepartment of Chemical Engineering, MIT, Cambridge, MA 02139, USA
dIBM Thomas J. Watson Research Center, Cambridge, MA 02142, USA
eDepartment of Electrical Engineering and Computer Science, MIT, Cambridge, MA 02139, USA
First published on 1st March 2024
Abstract
The story of machine learning in general, and its application to molecular design in particular, has been a tale of evolving representations of data. Understanding the implications of the use of a particular representation – including the existence of so-called ‘activity cliffs’ for cheminformatics models – is the key to their successful use for molecular discovery. In this work we present a physics-inspired methodology which exploits analogies between model response surfaces and energy landscapes to richly describe the relationship between the representation and the model. From these similarities, a metric emerges which is analogous to the commonly used frustration metric from the chemical physics community. This new property shows state-of-the-art prediction of model error, whilst belonging to a novel class of roughness measure that extends beyond the known data allowing the trivial identification of activity cliffs even in the absence of related training or evaluation data.
Design, System, ApplicationMachine learning has become deeply integrated within molecular design and optimization and a key component of their success has been the richness of generated molecular representations. When building systems which utilise machine-learning to accelerate molecular discovery, understanding the interplay between the representation and the model is key to its optimal configuration. Our new methodology allows, for the first time, the quantification of this interplay, even in regions in which data does not yet exist. Additionally, we are able to effortlessly locate activity cliffs which lie, often hidden, within a model and are a significant challenge to model-based molecular design. Whilst this paper primarily demonstrates the utility on datasets from the therapeutic design community, the underlying approach applies broadly to molecular design, and indeed also model-driven optimization approaches. |
1 Introduction
The ability to use chemical information to accelerate discovery tasks is underpinned by the existence of structure–property relationships.1–4 These relationships allow molecular space to be systematically explored to locate novel molecules with desirable properties. Recent advances in machine learning have enabled the identification of these relationships from ever-increasing sources of data through the construction of data-driven models.One important quantity for rationalising structure–property relationship accuracy is roughness. Rougher surfaces contain a greater number of large property differences between molecules close in space, which are known as activity cliffs.5,6 Such activity cliffs are challenging to replicate in regression models, leading to degradation in model performance, which can manifest in poor outcomes when used for discovery tasks. Consequently, the modellability of molecular datasets, and indeed the utility of derived representations, can be related to the roughness of a molecular property landscape.
The roughness of a property landscape depends upon the dataset, but also crucially on the molecular representation, which is key to determining the similarity between any given pair of molecules. Since smooth surfaces place molecules with similar property values and locally similar representations close in space, there is a direct link between the representation and the resulting smoothness. There are various common representations that have been used in structure–property relationships such as strings (SMILES7 and SELFIES8), binary fingerprints,9 physico-chemical descriptors, and recently latent space models based on variational autoencoders.10 A key aim of molecular representations is the production of smooth molecular landscapes, which allow the construction of accurate structure–property relationships.11–13
Due to its correlation with modellability there have been various attempts to quantify roughness. Popular metrics include the structure–activity landscape index (SALI),14 structure–activity relationship index (SARI)15 and the modellability index (MODI) as applicable to both classification16 and regression tasks.17 Recently, the roughness index (ROGI)18,19 was developed to measure dataset roughness with respect to machine learning predictive performance. This measure captures the roughness in a single scalar value that correlates strongly with the regression model performance for a wide range of molecular regression tasks.
Whilst current methods utilise information which is derived from surface topography, to date the topography itself has not been directly accessed. Direct exploration and analysis of topography, however, is routinely performed in the chemical physics community, in particular for the characterization of potential energy landscapes.20 Recently, this methodology has been extended by some of the authors to selected tasks in machine learning such as clustering,21 and hyperparameter tuning in Gaussian processes,22 for which we point interested readers to a recent tutorial review.23
In this contribution, we develop a novel roughness measure inspired by the similarities between model response surfaces and energy landscapes. We describe a method for representing discrete molecular datasets as a continuous surface and encoding the surface topography as a weighted graph. From the resulting graph we propose an adapted frustration metric as a roughness measure for structure–property relationships. Such a frustration metric directly accesses the topography across the full molecular space, unlike previous methods which are limited to the discrete data point evaluations. We illustrate its strong correlation with modellability for a wide range of structure–property relationships, and highlight that the metric can be decomposed to report on local roughness even outside of known data.
2 Methods
2.1 Topographical mapping
Surface topography was analysed using the energy landscape framework.24 This framework decomposes surfaces into their stationary points, which are separated into minima (only positive eigenvalues of the Hessian matrix) and transition states (a single negative eigenvalue of the Hessian matrix). Each transition state connects the two minima obtained by steepest-descent paths along the eigenvector corresponding to the negative eigenvalue, and is the maximum on the lowest-valued path between them.25 Therefore, transition states provide important information about intermediate regions of a surface between its local minima.All minima were enumerated using random initialisation and minimisation. Transition states were located between all known local minima using the nudged elastic band algorithm26 paired with hybrid-eigenvector following.27 We represent the resultant set of transition states and their connected minima as a weighted graph, where each minimum is a node and edges exist between any pair of minima directly connected by a transition state.28 Encoding of topography as a graph allows application of a suite of analysis tools to understand spatial properties, even for abstract cost function surfaces.29
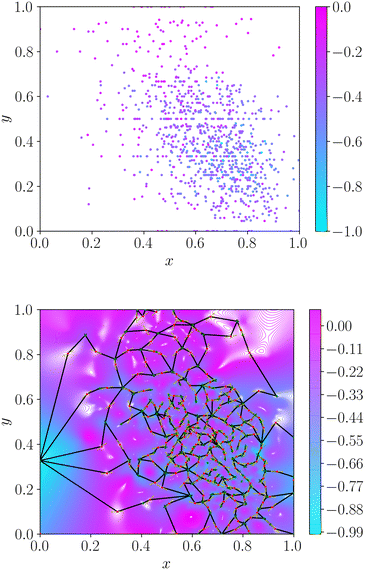
Application of the energy landscape framework requires a continuous surface. Therefore, we cannot estimate topography based only on the discrete property values associated with molecular datasets. We construct a continuous representation of the dataset via radial basis function interpolation30 with a thin-plate kernel. We specify the smoothness as 10−5 throughout to ensure a faithful description of the dataset. This choice of smoothness parameter forces an almost exact fit of the interpolating function to all known data, whilst alleviating fitting issues in datasets with severe activity cliffs. Interpolation produces a continuous smooth function, which can be queried at any point in molecular space. We construct the convex hull around the data via Deluanay triangulation and remove any minima outside this polygon to retain only the region of space in which we interpolate the dataset. We provide an illustration of the topographical encoding in Fig. 1.
2.2 Roughness measure
From the weighted graph we can compute many possible measures that probe different topographical features. Here, we compute the frustration metric,31 which is designed to capture topographical roughness in chemical physics applications, and adapt it to report on molecular property surface roughness. The modified metric has the functional form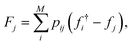 | (1) |
In chemical physics pij denotes the equilibrium population of a specified minimum i, which is related to both the energy and width of the minimum.32 The population simply provides an appropriate reweighting of the frustration contributions, and we replace it with a distance-based measure that reflects the proximity of local minima. The closer two separate minima are the more relevance they have for roughness so we specify the weighting by a radial basis function kernel
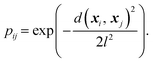 | (2) |
d(xi, xj) is the Euclidean distance between specified minima and l is the lengthscale that determines the range of influence of local minima. The lengthscale was specified as 0.8 in this work through calibration on representative functions, as described in the Results. An absolute value of the distance can be specified here due to normalisation of the feature space to lie in the range (0, 1).
In molecular science the reference minimum is almost always the global minimum, but in this application the roughness at high function values is equally as important for model error. Therefore, we compute the average frustration metric with each minimum in the network used as the reference
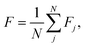 | (3) |
To estimate roughness for high-dimensional spaces we compute the frustration metric for each combination of feature pairs by extracting the data in the two specified dimensions, with the associated response values. Low-dimensional representations allow for more accurate interpolation models and limit the effect of monotonic dimensions. A single such dimension poses a significant challenge to this methodology by removing minima in all positions apart from the bounds, which leads to loss of information in higher dimensions. Therefore, the final roughness measure is the average over all feature pairs
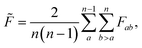 | (4) |
The frustration metric is one example of many such measures that can be derived from the weighted graph encoding of surface topography. All methods derived from these weighted graphs capture different information from existing roughness metrics. Current roughness measures depend only upon the dataset values, but these landscape-based methods report on the varying curvature of the function across all feature space.
2.3 Structure–property relationships
To demonstrate how this method can impact molecular design, we apply it to the analysis of machine learning models for therapeutic discovery. These models are built from molecular datasets extracted from the Guacamol33 and Therapeutics Data Commons (TDC)34 property databases. Datasets were generated by randomly sampling 500, 1000 or 2000 molecules from each database. The specific tasks chosen from these datasets are shown in Table 1. Both the property values and the training data were normalised throughout, and to avoid numerical problems associated with the interpolation we removed any data points within 10−4 of each other in feature space.| Task short name | Task source |
|---|---|
| Aripiprazole_Similarity | GM |
| CaCO2_Wang | TDC |
| Celecoxib_Rediscovery | GM |
| Clearance_Hepatocyte_AZ | TDC |
| Clearance_Microsome_AZ | TDC |
| Fexofenadine_MPO | GM |
| Half_Life_Obach | TDC |
| HydrationFreeEnergy_FreeSolv | TDC |
| LD50_Zhu | TDC |
| Lipophilicity_AstraZeneca | TDC |
| Median 1 | GM |
| Osimertinib_MPO | GM |
| PPBR_AZ | TDC |
| Ranolazine_MPO | GM |
| Scaffold hop | GM |
| Solubility_AqSolDB | TDC |
| VDss_Lombardo | TDC |
The molecular representation used throughout was the 14 physico-chemical descriptors selected in Aldeghi et al.18 These descriptors are molecular weight, fraction of sp3 centres, number of hydrogen bond donors and acceptors, number of NHOH and NO groups, number of aliphatic rings, number of aliphatic heterocycles, number of aromatic heterocycles, number of aromatic rings, number of rotatable bonds, polar surface area, quantitative estimate of druglikeness and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, all of which were computed given the SMILES string by RDKit.35 Several of the descriptors are discrete (e.g. fraction of sp3 centres), but we allow them to vary continuously within the interpolation model. The molecular description will exhibit varying modellability across the properties and is not intended to be a good representation for all given properties.
P, all of which were computed given the SMILES string by RDKit.35 Several of the descriptors are discrete (e.g. fraction of sp3 centres), but we allow them to vary continuously within the interpolation model. The molecular description will exhibit varying modellability across the properties and is not intended to be a good representation for all given properties.
We produced datasets for 17 different molecular properties with varying dataset size and dimensionality. Datasets with lower dimensionality were generated by randomly selecting subsets of the 14 original descriptors. For the complete 14 descriptors we extracted datasets composed of 1000 and 2000 molecules. For the feature subsets (6 or 10 descriptors) we sampled datasets of both 500 and 1000 data points. The dataset generation resulted in 102 distinct structure–property relationships, which we use to validate the roughness measure.
To maintain consistency with the current state of the art methods,18,19 we assess the strength of the structure–property relationships via a neural network regression model, as implemented in sklearn.36 The prediction error was computed as the average root mean squared error from five-fold cross validation, further averaged over four models generated by different random seeds. The model error can be considered a good surrogate for modellability in these applications, and the performance of one regression model can be largely correlated with the performance of others.18
3 Results
First, we analyse a wide range of two-dimensional surfaces to highlight the key features of the frustration metric. We calibrate the population lengthscale within the frustration computation for these range of topologies. After showing its utility across a range of low-dimensional examples we apply the methodology to a range of structure–property relationships and correlate the frustration metric with the regression model error to validate its use as a surrogate for dataset modellability.3.1 Two-dimensional surfaces
We initially computed the frustration metric for a diverse set of smooth two-dimensional functions. Application of the methodology to low-dimensional examples with a variety of topologies allows us to parameterise the frustration metric and evaluate its correlation with model error. Random functions were generated through summation of multiple individual Gaussians as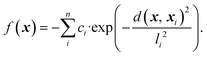 | (5) |
n is the number of Gaussians, each of which is given a random centre, xi, in the range (0, 1). Their width and depth are controlled by li and ci, respectively. Different combinations of these parameters can significantly modify the surface roughness, and we produced a range of datasets with all combinations of parameters: n ∈ (10, 20, 30, 40), l ∈ (0.05, 0.10, 0.15, 0.25) and c ∈ (0.25, 0.50, 75). Each individual ci and li took a random number distributed between 0 and c or l, respectively. We generated two datasets for each of these parameter sets with 500 or 1000 data points within the normalised feature space x, y ∈ (0, 1). We subsequently normalised the response to f ∈ (0, 1).
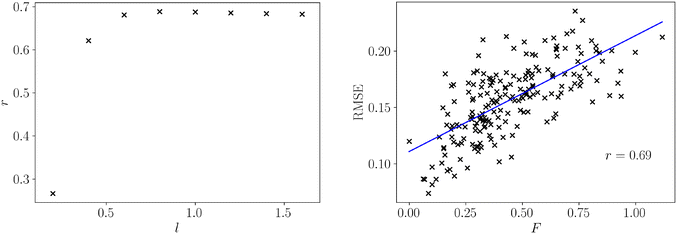
For all datasets we computed both the frustration metric and the neural network model error. An appropriate lengthscale for the population, pij, is not known so we computed the frustration at varying lengthscales, allowing the computation to consider progressively larger regions of feature space. We evaluated the quality of a linear fit between frustration and model error at each of these parameter choices in Fig. 2 to determine an appropriate lengthscale for use in structure–property relationships.
We observe that the correlation sharply increases with lengthscale before largely plateauing. The lengthscale that produces the strongest correlation between frustration and model error is 0.8, and after this value there is a small reduction in correlation. However, longer lengthscales do not significantly degrade correlation, indicating that additional curvature information from further across the feature space ceases to add relevant information for predicting model error. The optimal lengthscale itself is quite large relative to the normalised feature space xi ∈ (0, 1), which illustrates that large regions of curvature change remain relevant for model fitting. Given a normalised feature range and response, f ∈ (0, 1), we can specify the same lengthscale (l = 0.8) for all other normalised functions, such as structure–property relationships.
The relation between frustration and model error at l = 0.8 is shown in Fig. 2. There is a strong positive relationship between the frustration and the model error as evidenced by the Pearson correlation coefficient, r = 0.69. There remain significant fluctuations about the line of best fit, which is expected for such a wide range of surface topologies and dataset sizes. However, the presence of a strong correlation highlights this simple geometric representation of roughness contains much of the information needed to describe model error, and is applicable for datasets with a wide range of sizes and properties simultaneously.
3.2 Structure–property relationships
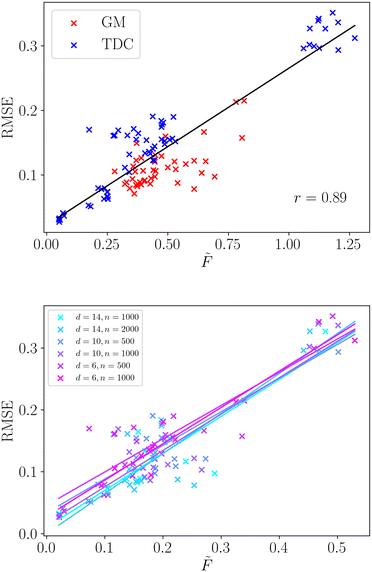
We apply the same methodology to a wide selection of structure–property relationships, the selection of which is described in sec. 2.3. We compute the averaged frustration metric,![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , for all molecular regression tasks and compare with the root mean squared error for the neural network model. The regression model performance is a key property for structure–property relationships, reflecting the accuracy with which the model makes predictions across the complete molecular space. We present the correlation of frustration with model performance in Fig. 3.
, for all molecular regression tasks and compare with the root mean squared error for the neural network model. The regression model performance is a key property for structure–property relationships, reflecting the accuracy with which the model makes predictions across the complete molecular space. We present the correlation of frustration with model performance in Fig. 3.
We observe that there is a very strong linear correlation (Pearson r = 0.89) between model performance and the frustration metric across this wide selection of structure–property relationships. Such a strong correlation shows that the modellability of datasets can be accurately decomposed in terms of the surface topography through the frustration metric. Furthermore, we observe that the correlation is significantly stronger than the simple two-dimensional example surfaces analysed in the previous section. The range of surface topographies exhibited by the structure–property relationships is likely less varied than those generated in the previous section, and averaging over two-dimensional cuts may better capture the roughness of a single surface.
We provide a direct comparison of common roughness measures for these selected structure–property relationships in Table 2. The frustration metric produces modellability predictions comparable with ROGI, and significantly better than MODI. Both the frustration metric and ROGI give very strong correlations for the datasets taken from the TDC database. The modellability of datasets taken from GuacaMol is more challenging to capture and both frustration and ROGI show a weaker correlation. However, both still show a strong positive linear correlation, with ROGI showing slightly better performance for these examples. It is worth noting that the outliers for the frustration metric are largely localised to two particular structure–property relationships (Osimertinib_MPO and PPBR). In the absence of these SPRs the Pearson correlation coefficient grows significantly to r = 0.95, and future work aims to identify the dataset features that pose a challenge to this methodology.
| Roughness measure | TDC | GuacaMol | Combined |
|---|---|---|---|
| Frustration | 0.95 | 0.64 | 0.89 |
| ROGI | 0.99 | 0.76 | 0.95 |
| RMODI | 0.69 | 0.34 | 0.58 |
Both ROGI and MODI, like all common roughness measures, explicitly use only known data points in the roughness computation. Instead, the frustration metric, after construction of the interpolated surfaces, does not explicitly use the known data in the roughness computation. The roughness is computed only from stationary points, across the full feature space, that will be unlikely to lie at any known data points (and may lie significantly outside). It is worth noting that, for this novel class of method, performance comparable with ROGI is even more impressive given the test data is only implicitly considered. Therefore, the frustration metric provides an alternative and complementary approach to estimating the modellability of a given molecular representation, and there are several reasons such a topographical metric provides additional advantages.
The global frustration metric can be decomposed into local contributions to the sum, from which we can easily locate features such as activity cliffs. Large barriers, (f†i − fj), over small distances correspond to activity cliffs, and this method directly identifies these features through large individual contributions to the frustration, pij(f†i − fj). Therefore, because the method directly maps topography, such features become trivial to locate and, importantly, these features can be predicted even in the absence of associated data. The ability to make predictions of activity cliffs within unexplored regions of feature space provides significant utility over existing methods. Moreover, we can associate roughness with a particular minimum, which reports on the model error within a given basin of attraction, or particular features, which can highlight how to improve molecular representations for a given task.
Furthermore, we observe that using this frustration measure all the varied datasets exhibit a single relationship with the model error. We do not need to distinguish the dimensionality, number of data points or data source, as shown in Fig. 3. The linear relationship is strongly conserved for the six different dataset properties, along with their individual Pearson correlation coefficients. Therefore, this method can faithfully compare datasets of different size and dimensionality, which provides significant utility in real-world examples where these properties can vary widely.
4 Conclusions
In this work we presented a novel method for computing the roughness of molecular property landscapes. This physics-inspired approach reduces the topography of the structure–property surface into a weighted graph. The graph representation reports on topographical information that was previously inaccessible and we propose a roughness measure that incorporates all this information. We exploited similarities between the energy landscape concept from chemical physics and response surfaces from machine learning to develop an analogous frustration metric, which we applied to this novel application by changing the functional form to report on modellability. We also present a parameterisation that allows application of this methodology to any other normalised surface.We demonstrated that this metric accurately captures the modellability of structure–property relationships through a strong correlation with regression performance; r = 0.89 with over 100 different regression tasks. The prediction of model error using the frustration metric is comparable to state-of-the-art methods, such as ROGI, allowing the appropriateness of a molecular representation to be evaluated before training a machine learning model. Our graph-based methodology, despite showing similar predictive ability, approaches roughness from a different perspective to existing methods by analysing the full feature space beyond the known data points. Whilst the inclusion of the full feature space results in a higher computational cost than methods such as ROGI and MODI, the computational cost is by no means prohibitive. We believe that the benefits of this approach - namely its unique ability to be applied beyond the original training data – justify the expense.
Such strong predictive ability shown by the frustration metric is very promising, especially as graph-based methods provide additional advantages. These methods can attribute roughness to particular features and local regions of feature space, allowing straightforward determination of activity cliffs from the frustration metric. Each edge in the graph represents a direction in which the surface increases to the specified transition state value, which are activity cliffs if they have a large barrier size and small distance. The ability to locate activity cliffs, even outside of the known data is very valuable for understanding modellability and has broad impact within the chemical informatics communities – especially materials and drug discovery. Furthermore, the frustration metric allows comparison between datasets of varying size and dimensionality, which further extends its applicability.
We propose that this novel class of topographical roughness metric can provide a valuable tool for analysing molecular dataset modellability. It provides comparable predictive ability to current state-of-the-art, whilst making its predictions from regions outside the known data. This topographical information was previously inaccessible and we highlight how it can be used to easily locate activity cliffs, even in the absence of data. There are many alternative roughness metrics that can be derived from the proposed topographical description and we believe that this work forms an enlightening route for further modellability research.
Data availability
The code used to generate the results presented in this work is freely available at https://github.com/IBM/topography-searcher. Illustrative examples for the roughness applications are given within the same repository. The molecular datasets analysed in this publication were generated from the publicly available notebook https://github.com/coleygroup/rogi-results/blob/main/regression.ipynb.Author contributions
EOP-K conceived and supervised the project, aided in the analysis and the writing of the paper. LD wrote the software, led the investigation and analysis, curated the data and led the writing of the paper CWC, KEJ and DEG aided in the investigation and the writing of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Hartree National Centre for Digital Innovation – a collaboration between Science and Technology Facilities Council and IBM – and the MIT-Watson AI Lab.Notes and references
- P. P. Meyer, C. Bonatti, T. Tancogne-Dejean and D. Mohr, Mater. Des., 2022, 223, 111175 CrossRef CAS.
- L. Bouarab-Chibane, V. Forquet, P. Lantéri, Y. Clément, L. Léonard-Akkari, N. Oulahal, P. Degraeve and C. Borders, Front. Microbiol., 2019, 10, 00829 CrossRef PubMed.
- Z. Cai, M. Zafferani, O. M. Akande and A. E. Hargrove, J. Med. Chem., 2022, 65, 7262–7277 CrossRef CAS PubMed.
- C. Suh, C. Fare, J. A. Warren and E. O. Pyzer-Knapp, Annu. Rev. Mater. Res., 2020, 50, 1–25 CrossRef CAS.
- D. Stumpfe, Y. Hu, D. Dimova and J. Bajorath, J. Med. Chem., 2014, 57, 18–28 CrossRef CAS PubMed.
- D. Stumpfe, Y. Hu and J. Bajorath, ACS Omega, 2019, 4, 14360–14368 CrossRef CAS PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- M. Krenn, F. Häsel, A. K. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2020, 1, 045024 Search PubMed.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- R. Goméz-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hérnandez-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- R. P. Sheridan, P. Karnachi, M. Tudor, Y. Xu, A. Liaw, F. Shah, A. C. Cheng, E. Joshi, M. Glick and J. Alvarez, J. Chem. Inf. Model., 2020, 60, 1969–1982 CrossRef CAS PubMed.
- D. van Tilborg, A. Alenicheva and F. Grisoni, J. Chem. Inf. Model., 2022, 62, 5938–5951 CrossRef CAS PubMed.
- S. Tamura, T. Miyao and J. Bajorath, J. Cheminf., 2023, 15, 4 Search PubMed.
- R. Guha and J. H. V. Drie, J. Chem. Inf. Model., 2008, 48, 646–658 CrossRef CAS PubMed.
- L. Peltason and J. Bajorath, J. Med. Chem., 2007, 50, 5571–5578 CrossRef CAS PubMed.
- A. Golbraikh, E. Muratov, D. Fourches and A. Tropsha, J. Chem. Inf. Model., 2014, 54, 1–4 CrossRef CAS PubMed.
- I. L. Ruiz and M. A. Gómez-Nieto, J. Chem. Inf. Model., 2018, 58, 2069–2084 CrossRef PubMed.
- M. Aldeghi, D. E. Graff, N. Frey, J. A. Morrone, E. O. Pyzer-Knapp, K. E. Jordan and C. W. Coley, J. Chem. Inf. Model., 2022, 62, 4660–4671 CrossRef CAS PubMed.
- D. E. Graff, E. O. Pyzer-Knapp, K. E. Jordan, E. I. Shakhnovich and C. W. Coley, Digital Discovery, 2023, 2, 1452 RSC.
- D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- L. Dicks and D. J. Wales, J. Chem. Phys., 2022, 156, 054109 CrossRef CAS PubMed.
- M. P. Niroomand, L. Dicks, E. O. Pyzer-Knapp and D. J. Wales, arXiv, 2023, preprint, arXiv:2305.10748, DOI:10.48550/arXiv.2305.10748.
- M. P. Niroomand, L. Dicks, E. O. Pyzer-Knapp and D. J. Wales, Digital Discovery, 2024 10.1039/D3DD00204G.
- D. J. Wales, Annu. Rev. Phys. Chem., 2017, 69, 401–425 CrossRef PubMed.
- J. N. Murrell and K. J. Laidler, Trans. Faraday Soc., 1968, 64, 371–377 RSC.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- L. J. Munro and D. J. Wales, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3969–3980 CrossRef CAS.
- F. Noé and S. Fischer, Curr. Opin. Struct. Biol., 2008, 18, 154–162 CrossRef PubMed.
- L. Dicks and D. J. Wales, arXiv, 2023, preprint, arXiv:2306.14346, DOI:10.48550/arXiv.2306.14346.
- R. Hardy, J. Geophys. Res., 1971, 76, 1905–1915 CrossRef.
- V. K. D. Souza, J. D. Stevenson, S. P. Niblett, J. D. Farrell and D. J. Wales, J. Chem. Phys., 2017, 146, 124103 CrossRef PubMed.
- D. J. Wales, Phys. Rev. E, 2017, 95, 030105 CrossRef PubMed.
- N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inf. Model., 2019, 59, 1096–1108 CrossRef CAS PubMed.
- K. Huang, T. Fu, W. Gao, Y. Zhao, Y. Roohani, J. Leskovec, C. W. Coley, C. Xiao and J. Sun, Nat. Chem. Biol., 2022, 18, 1033–1036 CrossRef CAS PubMed.
- G. Landrum, RDKit: Open-source cheminformatics, http://www.rdkit.org, 2023 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |