Open Access Article
Open Access ArticleIn silico approaches for the prediction of the breakthrough of organic contaminants in wastewater treatment plants†
Nicola
Chirico
 *a,
Michael S.
McLachlan
*a,
Michael S.
McLachlan
 b,
Zhe
Li
b,
Zhe
Li
 b and
Ester
Papa
b and
Ester
Papa
 a
a
aQSAR Research Unit in Environmental Chemistry and Ecotoxicology, Department of Theoretical and Applied Sciences, University of Insubria, via J. H. Dunant 3, 21100, Varese, Italy. E-mail: nicola.chirico@uninsubria.it
bDepartment of Environmental Science (ACES), Stockholm University, 106 91 Stockholm, Sweden
First published on 11th January 2024
Abstract
The removal efficiency (RE) of organic contaminants in wastewater treatment plants (WWTPs) is a major determinant of the environmental impact of chemicals which are discharged to wastewater. In a recent study, non-target screening analysis was applied to quantify the percentage removal efficiency (RE%) of more than 300 polar contaminants, by analyzing influent and effluent samples from a Swedish WWTP with direct injection UHPLC-Orbitrap-MS/MS. Based on subsets extracted from these data, we developed quantitative structure–property relationships (QSPRs) for the prediction of WWTP breakthrough (BT) to the effluent water. QSPRs were developed by means of multiple linear regression (MLR) and were selected after checking for overfitting and chance relationships by means of bootstrap and randomization procedures. A first model provided good fitting performance, showing that the proposed approach for the development of QSPRs for the prediction of BT is reasonable. By further populating the dataset with similar chemicals using a Tanimoto index approach based on substructure count fingerprints, a second QSPR indicated that the prediction of BT is also applicable to new chemicals sufficiently similar to the training set. Finally, a class-specific QSPR for PEGs and PPGs showed BT prediction trends consistent with known degradation pathways.
Environmental significanceBreakthrough of chemicals from wastewater treatment plants (WWTPs) can be a big risk for the environment and the human health. Time and cost-effective solutions to estimate the potential to break from WWTPs would help prioritizing chemicals before the application of more expensive experimental techniques. In this work we propose an in silico methodology for the development of new quantitative structure–property relationship (QSPR) models able to predict the breakthrough of chemicals from WWTPs from their molecular structure. These models are easily interpretable and checked for their robustness, both in terms of overfitting and chance relationships. Furthermore, we discuss strengths and weaknesses of the proposed modelling approach in relation to the use of experimental data from non-target analysis. |
1. Introduction
Wastewater treatment plants (WWTPs) are an important filter between the technosphere and the environment, preventing the export of many anthropogenic chemicals to aquatic systems. Ensuring high effectiveness of this filter is thus a central goal to safeguard the environment. Therefore, WWTP removal efficiency (RE) is a central parameter in chemical safety assessment. Measured values of RE are available for some existing chemicals, but not for new chemicals. When conducting risk assessments of new chemicals, other methods for estimating the removal efficiency of WWTPs are required. In silico approaches like quantitative structure–property relationship (QSPRs), which are both cost and time saving, could help fill this need.A major challenge in developing QSPRs is obtaining consistent datasets. WWTP RE varies between plants due to e.g., differences in treatment technology. It can also vary over time as a result of changes in the wastewater influent and the plant operating conditions. Furthermore, differences in sampling strategy and the quality of analytical techniques introduce between-study uncertainty. Consequently, it is difficult to construct a QSPR from data assembled from diverse literature sources.
Single studies providing RE data for a large number of chemicals are rare. Most studies focus on just a handful of chemicals. Often, they are focused on assessing the risk of a particular substance or on elucidating the behavior of a particular class of chemicals in WWTPs. Broader studies have usually relied on targeted analysis of a specific set of substances, which constrains the information obtained. However, analytical approaches using suspect screening and non-target screening are now being employed in assessing WWTP removal efficiency.1,2 These approaches have the potential to generate consistent datasets for large numbers of chemicals.
In a recent paper written by Li and colleagues,3 the RE in a Swedish municipal WWTP was measured by a high-throughput methodology, which allowed the detection of many organic chemicals (from now on referred to as “chemicals”) and quantification of their removal efficiency without requiring calibration. One of the conclusions of the study by Li and colleagues was that such methodology is suitable when “RE values for a large number of chemicals are needed”, and one of the possible future applications is “generating quantitative structure–property relationships (QSPRs) to predict RE from chemical structures…”, which is the focus of this work. Therefore, we are interested in developing QSPRs specifically addressing RE while considering the WWTP as a whole, even though, typically, existing QSPRs target only specific technologies/processes concerning the WWTPs like adsorption,4 oxidation,4 photolysis,4 coagulation,4 filtration4 and biological processes.5
In this work we make an initial attempt to develop QSPRs to predict the overall breakthrough (BT) of chemicals from a WWTP, which is directly related with the RE, using specifically tailored subsets of data from an internally consistent dataset of measured RE for 319 chemicals in a Swedish WWTP.
Our objective is to develop statistically valid QSPRs which can be used to predict BT at a screening level without making initial assumptions related to the complexity of the WWTP. The ability of these QSPRs to predict the BT of new chemicals is also assessed, where applicable, by means of bootstrapped estimations and external test sets, in order to support their possible application to new chemicals. Therefore, particular attention is also devoted to estimating the probability of incurring chance relationships, by means of randomization techniques,6 and in estimating the number of molecular descriptors able to minimize the overfitting7 of the QSPRs. This is important because QSPRs may be plagued by chance relationships and/or overfitting, which means that while they may seem good in fitting, chances are that they will fail in predicting the BT of new chemicals.
2. Material and methods
2.1 Retention efficiency dataset
The dataset was from a published study in which influent and effluent samples were collected flow proportionally over 24 h from a municipal WWTP in Stockholm (Sweden) which had mechanical, chemical and biological treatment and sand filtration as the final treatment step.3 These samples were analyzed by direct injection into an UHPLC-Orbitrap-MS/MS system following filtration. Chemical separation was achieved using a reversed phase column and a binary mobile phase gradient consisting of water and acetonitrile, both containing 0.1% formic acid. The mass spectrometer was operated at a mass resolution of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and data dependent acquisition was employed using both ESI positive mode and ESI negative mode. Isotope-labeled standards of 40 polar contaminants were used for target analysis of these contaminants and for quality control, while some of these and additional chemicals (319 in total) were identified via non-targeted suspect screening using the online database mzCloud. The response factors of the isotope-labeled standards showed that matrix effects were similar for influent and effluent for most chemicals. From this it was concluded that RE could be calculated using the peak areas in influent and effluent, which made it possible to estimate RE for all 319 chemicals. Of the chemicals for which a positive RE was determined, there were 22 for which matched isotope labelled standards showed similar matrix effects in influent and effluent. Further information about the dataset can be found in the publication.3 For our work, BT has been calculated from the original data as the ratio between effluent and influent peak areas. Calculated BT was modelled by QSPR (see Section 2.4).
000 and data dependent acquisition was employed using both ESI positive mode and ESI negative mode. Isotope-labeled standards of 40 polar contaminants were used for target analysis of these contaminants and for quality control, while some of these and additional chemicals (319 in total) were identified via non-targeted suspect screening using the online database mzCloud. The response factors of the isotope-labeled standards showed that matrix effects were similar for influent and effluent for most chemicals. From this it was concluded that RE could be calculated using the peak areas in influent and effluent, which made it possible to estimate RE for all 319 chemicals. Of the chemicals for which a positive RE was determined, there were 22 for which matched isotope labelled standards showed similar matrix effects in influent and effluent. Further information about the dataset can be found in the publication.3 For our work, BT has been calculated from the original data as the ratio between effluent and influent peak areas. Calculated BT was modelled by QSPR (see Section 2.4).
2.2 Chemicals selection
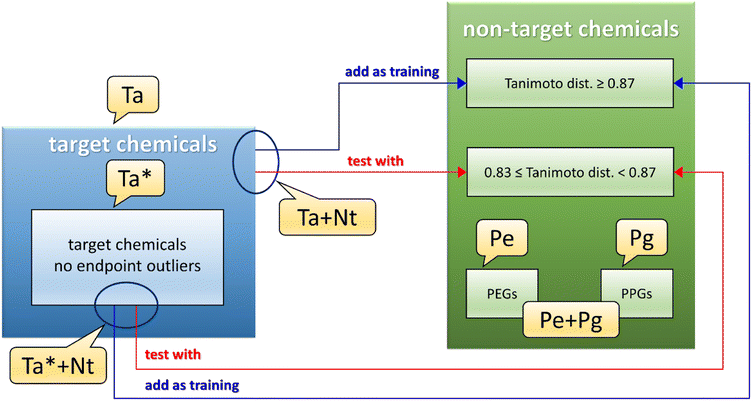
A dataset called Ta (see Fig. 1 and Table S3,† gray and dark gray rows) was developed using the 22 target chemicals having similar matrix effects in influent and effluent, as these data were deemed to be less uncertain. A second dataset, called Ta* (see Fig. 1 and also Table S3,† gray rows), was the same as Ta except for the removal of 2 endpoint outliers detected by the QSPR based on the Ta dataset (see Section 3.1).The next step was to pool the Ta dataset with the collected non-target data, to further populate the training set. However, the wide heterogeneity of the full dataset of non-target chemicals did not allow us to build a reasonable QSPR. To reduce the structural dissimilarities of the non-target (Nt) chemicals with the Ta dataset, Nt chemicals were filtered using the Tanimoto index (calculated using substructure count fingerprint8) as a measure of distance from Ta chemicals. The Tanimoto index measures the similarity between two chemicals structures, spanning from 1 (the chemical structures are identical) to 0 (no similarity is found between the chemical structures). In this work, the best compromise between the number of Nt chemicals (which should be the biggest possible) and the structural similarity to Ta chemicals, was found for values of the Tanimoto index between 1.0 and 0.87 (included). These values led to the pooled training set Ta + Nt (see Fig. 1 and Table S3,† orange and dark orange rows), composed of 70 chemicals (i.e., only Nt chemicals with a Tanimoto index ≥0.87 were included). Values of the Tanimoto index between 0.87 (excluded) and 0.83 were found optimal for the test set, since it was the best compromise between the number of chemicals and the structural dissimilarity from the Ta dataset; in fact, large dissimilarities would lead to an underestimation of the QSPR predictive power. The resulting test set consisted of 28 chemicals. The same procedure was applied to the Ta* dataset, ending in a dataset called Ta* + Nt (see Fig. 1 and Table S3,† dark orange rows) consisting of 56 training and 17 test chemicals.
PEGs and PPGs were selected separately and called respectively Pe and Pg datasets (see Fig. 1 and Table S3,† green rows for PEGs and dark green rows for PPGs), then they were pooled together as another dataset called Pe + Pg (see Fig. 1 and Table S3,† green and dark green rows).
The ranges of BT for the datasets used to develop the QSPRs are: dataset Ta/Ta* from 0.0012 to 0.95; dataset Ta/Ta* + Nt from 0.00031 to 0.96; dataset Pe + Pg from 0.0074 to 0.37; dataset Pg from 0.070 to 0.37.
2.3 Molecular descriptors
Mono and bidimensional descriptors were calculated from canonical Simplified Molecular-Input Line Entry System (SMILES) notations, desalted and converted in the canonical form using OpenBabel software version 2.4.1.9 The list of chemicals and SMILES is reported in Table S1.†PaDEL-Descriptor software version 2.21,10 configured for detecting aromaticity and standardizing nitro groups, was used to calculate descriptors and fingerprints (see Table S2†).
Problematic QSPRs may arise when the descriptors are highly inter-correlated, have zero or nearly zero variance, or have problematic ranges. For these reasons, descriptors were pre-filtered according to (1) pair-wise correlation above 0.95, (2) redundancy measured as the repetition of the same value in more than 80% of the chemicals and (3) span less than 2 orders of magnitude. The filtering by range was applied to avoid numerical instabilities that would impact the leave-one-out bootstrap procedure, see Section 2.4.
2.4 Development of QSPRs
The RE of a WWTP is measured as one minus the quotient of the concentration of the chemical in effluent and influent. This measure focuses on the treatment plant, while from an environmental standpoint a measure of the remaining chemical in water, here called breakthrough (BT), defined as the quotient of the chemical concentration between effluent and influent, was deemed more appropriate.In this work, multiple linear regression (MLR) by means of ordinary least squares (OLS) is used as the modeling tool. We restricted our analysis to linear model by design because we wanted to test one of the simplest approaches available to create QSPRs, which is more transparent and portable compared to other more complex solutions. Furthermore, due to their usually limited complexity in terms of number of descriptors, MLR models are easier to interpret than machine learning approaches based on tens or hundreds of molecular descriptors. Finally, even though MLR QSPRs may suffer from higher modeling bias in comparison to non-linear alternatives, they tend to have less modeling variance.
The log10 BT, called log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT for brevity, is used as the endpoint because the uncertainty of the logarithm of the measured BT is largely independent of the magnitude of BT (while this is not the case for either BT, RE or log
BT for brevity, is used as the endpoint because the uncertainty of the logarithm of the measured BT is largely independent of the magnitude of BT (while this is not the case for either BT, RE or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RE). This is due to the fact that the uncertainty of the logarithm of the concentration is independent of concentration itself. The independence of the uncertainty of the endpoint from its magnitude provides for homoscedasticity of the residuals, which is one of the requirements for applying MLR.
RE). This is due to the fact that the uncertainty of the logarithm of the concentration is independent of concentration itself. The independence of the uncertainty of the endpoint from its magnitude provides for homoscedasticity of the residuals, which is one of the requirements for applying MLR.
To reduce chances of overfitting the descriptors selection procedure7 (here the step-up procedure, see below), reiterated descriptors selections were performed from scratch using training sets generated by a leave-one-out bootstrap procedure,11 and the one standard error rule12 was then applied to select the most parsimonious QSPR. See Method S1 and S2† for further details.
The MAE (Mean Average Error) values, where 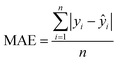 (yi and
(yi and 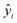 are respectively the measured and predicted log
are respectively the measured and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values), were calculated from the leave-one-out bootstrap procedure and provide a cross validation that includes the descriptors selection procedure. This is known to be more robust and less biased7,11 than cross validating the finally chosen model (i.e., after the descriptors' selection procedure) which gives overly optimistic results.
BT values), were calculated from the leave-one-out bootstrap procedure and provide a cross validation that includes the descriptors selection procedure. This is known to be more robust and less biased7,11 than cross validating the finally chosen model (i.e., after the descriptors' selection procedure) which gives overly optimistic results.
The selection of the descriptors was performed by the step-up procedure introduced by Rücker et al.,6 using R2 as the objective function. The step-up size of the population of QSPRs was set to 25, unless the number of available descriptors was smaller (in this case the population size equals the number of descriptors).
The probability of a coincidental relationship between the descriptors and the endpoint was calculated by applying the step-up procedure 100 times on randomized descriptors, as described in Rücker et al.,6 and by a customized randomization technique, see Method S3† for further details. QSPRs with probabilities above 5% using both approaches were dropped.
Once a candidate QSPR was selected, its performance was assessed by means of R2 and MAE for fitting, Q2 (leave-one-out) for stability and y-scramble (50 iterations) for chance correlation between the descriptors and the endpoint.
Where bootstrap was deemed applicable to the step-up procedure because the number of available chemicals was sufficient, the MAE for the corresponding QSPR size was reported. Where a test set was available, the corresponding MAE was also reported.
All procedures were performed by custom in-house developed R (version 4.2.1)13 scripts.
QQ charts (quantile–quantile charts) are used to evaluate the distribution of the residuals. It is here recalled that the more the residuals fall along a straight line, the closer they are to being normally distributed.
2.5 QSPR applicability domain
Chemicals with a leverage value exceeding three times the ratio between the number of descriptors + 1 and the number of chemicals (this is called h* threshold) were considered chemical structural outliers.14 The leverages are calculated as hii = xi(X′X)−1xiT (where X is the descriptor's matrix) and measure the distance between the descriptors values for the ith chemical point and the average of all chemicals descriptors.Chemicals with a standardized ordinary residual (calculated as 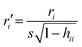 , where r is the residual) greater than 2.5 standard deviation units, were considered as endpoint outliers.14
, where r is the residual) greater than 2.5 standard deviation units, were considered as endpoint outliers.14
The charts plotting the leverages values vs. the standardized residuals are reported in the QSPRs ESI.† These charts also report the leverage threshold (h*) as a vertical line on the abscissa axis for the detection of the structural outliers, and the 2.5 standard deviation thresholds as horizontal lines for the detection of the endpoint outliers.
3. Results
3.1 Target chemical QSPR (Ta and Ta* datasets)
Starting from the Ta dataset (see for reference the Ta callout in Fig. 1), the bootstrap smallest average MAE value (see Bootstrap analysis S1,† middle chart) was found for a 1-descriptor QSPR at index 1 of the step-up population. The corresponding one standard error chart (see Bootstrap analysis S1,† lower chart) indicated that a QSPR with more than one descriptor would overfit, so the first 1-descriptor QSPR was finally chosen from the step-up population of candidate QSPRs (see Method S2† for details concerning the selection of the QSPR).The equation of the 1-descriptor Ta QSPR is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = −0.44*** (±0.11) − 6.2*** (±1.1)·MATS2m BT = −0.44*** (±0.11) − 6.2*** (±1.1)·MATS2m | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT is the logarithm of the breakthrough and MATS2m is the descriptor.
BT is the logarithm of the breakthrough and MATS2m is the descriptor.
The performance metrics for eqn (1) are reported in Table 1. According to the QQ chart (see Fig. S1†), the residuals are reasonably normally distributed, apart from the skewness due to aniline (ID 25) and acetaminophen (ID 29).
| QSPR | Training set items | Descriptors | Probability% of coincidental relationshipa | R 2 | R 2 y-scrb | Q 2 | MAE trainingd | MAE bootstrapd,e |
|---|---|---|---|---|---|---|---|---|
| a Calculated between descriptors and endpoint: upper = mode 1, lower = descriptor nature. b R 2 calculated using shuffled endpoints. c Leave-one-out cross validated R2. d MAE = mean absolute error. e Bootstrap ± standard error. f Target chemicals. g Target chemicals without endpoint outliers. | ||||||||
| Taf | 22 | 1 | 0.0083 | 0.61 | 0.047 | 0.48 | 0.34 | 0.68 ± 0.01 |
| 0.0060 | ||||||||
| Ta*g | 20 | 1 | <2.2 × 10−14 | 0.84 | 0.040 | 0.69 | 0.21 | 0.44 ± 0.01 |
| 2.2 × 10−14 | ||||||||
The leverage vs. standardized residuals chart (see Fig. S1†) spotted caffeine (ID 30) as a structural outlier, acetaminophen (ID 29) as an endpoint outlier, and aniline (ID 25) just within the residual endpoint threshold.
To check whether the removal of aniline (ID 25) and acetaminophen (ID 29) from the training set would lead to a better performing QSPR, the whole procedure was repeated without them (which led to a new dataset here called Ta*, see also the Ta* callout in Fig. 1). The bootstrap smallest average MAE value (see Bootstrap analysis S2,† middle chart) and the corresponding one standard error chart (see Bootstrap analysis S2,† lower chart) still indicated that a QSPR with more than one descriptor would overfit and, also in this case, the first 1-descriptor QSPR was finally chosen from the bootstrap step-up population.
The equation of the 1-descriptor Ta* QSPR is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = −0.31*** (±6.4 × 10−2) − 6.5*** (±0.67)·MATS2m BT = −0.31*** (±6.4 × 10−2) − 6.5*** (±0.67)·MATS2m | (2) |
The explanation of the equation is the same as eqn (1). The performance metrics for eqn (2) are reported in Table 1. According to the QQ chart (see Fig. S2†), the residuals are broadly normally distributed.
3.2 Target and non-target chemical QSPR (Ta + Nt and Ta* + Nt datasets)
Continuing with the Ta + Nt dataset, the bootstrap smallest average MAE value was obtained for the 2-descriptor QSPR at index 13 of the bootstrap step-up population (see Bootstrap analysis S3,† middle chart). However, many predictions of the corresponding candidate QSPR in the step-up population were identical (i.e., 19 training and 5 test chemicals had log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = −1.92) for almost the whole range of experimental values (see Bootstrap analysis S3,† lower left chart) because of the GGI7 descriptor being 0 and the PubchemFP443 descriptor being 1 simultaneously. For this reason, the next smallest average MAE from the bootstrap step-up population was looked for, and it resulted in a 3-descriptor QSPR located at the 24th step-up population index. The one standard error chart (see Bootstrap analysis S3,† lower right chart) indicated that a QSPR with more than three descriptors would overfit, while the 2-descriptor QSPR bootstrap average MAE misses (even though slightly) the one standard error of the 3-descriptor QSPR bootstrap average MAE, so the 3-descriptor QSPR was finally chosen from the step-up population of candidate QSPRs at index 24 (see Method S2† for details concerning the selection of the QSPR).
BT = −1.92) for almost the whole range of experimental values (see Bootstrap analysis S3,† lower left chart) because of the GGI7 descriptor being 0 and the PubchemFP443 descriptor being 1 simultaneously. For this reason, the next smallest average MAE from the bootstrap step-up population was looked for, and it resulted in a 3-descriptor QSPR located at the 24th step-up population index. The one standard error chart (see Bootstrap analysis S3,† lower right chart) indicated that a QSPR with more than three descriptors would overfit, while the 2-descriptor QSPR bootstrap average MAE misses (even though slightly) the one standard error of the 3-descriptor QSPR bootstrap average MAE, so the 3-descriptor QSPR was finally chosen from the step-up population of candidate QSPRs at index 24 (see Method S2† for details concerning the selection of the QSPR).
The equation of the 3-descriptor Ta + Nt QSPR is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = −1.2***(±0.24) − 1.0***(±0.18)·PubchemFP420 + 0.11***(±2.1 × 10−2)·VR3_Dzs − 0.63**(±0.19)·PubchemFP373 BT = −1.2***(±0.24) − 1.0***(±0.18)·PubchemFP420 + 0.11***(±2.1 × 10−2)·VR3_Dzs − 0.63**(±0.19)·PubchemFP373 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT is the logarithm of the breakthrough, and PubchemFP420, VR3Dzs, PubchemFP373 are the descriptors.
BT is the logarithm of the breakthrough, and PubchemFP420, VR3Dzs, PubchemFP373 are the descriptors.
The performance metrics for eqn (3) are reported in Table 2. The absolute pair correlation between the descriptors was below or equal to 0.20, and the QQ chart (see Fig. S3†) indicated reasonably normally distributed residuals.
| QSPR | Training set items | Test set items | Descriptors | Probability% of coincidental relationshipa | R 2 | R 2 y-scrb | Q 2 | MAE trainingd | MAE bootstrapd,e | MAE testd | MAE testd,f (16) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Calculated between descriptors and endpoint: upper = mode 1, lower = descriptor nature. b R 2 calculated using shuffled endpoints. c Leave-one-out cross validated R2. d MAE = mean absolute error. e Bootstrap ± standard error. f Test chemicals (16) in common between the Ta + Nt and Ta* + Nt QSPRs. g Target and non-target chemicals. h Target chemicals without endpoint outliers and non-target chemicals. | |||||||||||
| Ta + Ntg | 70 | 28 | 3 | 3.3 × 10−14 | 0.58 | 0.045 | 0.53 | 0.49 | 0.75 ± <0.01 | 0.69 | 0.62 |
| 8.9 × 10−14 | |||||||||||
| Ta* + Nth | 56 | 17 | 2 | 4.6 × 10−13 | 0.54 | 0.047 | 0.48 | 0.51 | 0.75 ± <0.01 | 0.58 | 0.59 |
| 1.0 × 10−12 | |||||||||||
The leverage vs. standardized residuals chart (see Fig. S3†) highlighted benzophenone (ID 76) and fexofenadine (ID 229) as training structural outliers, and 10-hydroxycarbazepine (ID 39) as a training endpoint outlier (even though it is just above the threshold). The same chart also highlighted acridine (ID 71) and epinephrine (ID 227) as test endpoint outliers.
In Section 3.1, the Ta* QSPR (eqn (2)) performed better than the Ta QSPR (eqn (1)) because of the removal of two outliers/problematic chemicals i.e., acetaminophen (ID 29) and aniline (ID 25). Therefore, a new dataset (called Ta* + Nt, see also Fig. 1), compiled starting from the Ta* dataset, could also lead to a better QSPR in comparison to the Ta + Nt QSPR (eqn (3)).
For the Ta* + Nt dataset, the bootstrap smallest average MAE was obtained for a 2-descriptor QSPR from the bootstrap step-up population at index 25 (see Bootstrap analysis S4,† middle chart). Indeed, the smallest value was obtained for a 1-descriptor QSPR, located at index 1 in the population, but the difference in terms of MAE, compared to the 2-descriptor QSPR at index 25, was negligible i.e., 0.7495 vs. 0.7499, and the corresponding QSPR was deemed not acceptable because it predicted only two values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT i.e., −2.0 and −0.6, because of the nT9HeteroRing descriptor. However, predictions of the corresponding candidate QSPR in the step-up population tended to cluster around log
BT i.e., −2.0 and −0.6, because of the nT9HeteroRing descriptor. However, predictions of the corresponding candidate QSPR in the step-up population tended to cluster around log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT −2.0 and log
BT −2.0 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT −0.5 (see Bootstrap analysis S4,† lower left chart). For this reason, the next smallest average MAE from the bootstrap step-up population was investigated, and it resulted in a 2-descriptors QSPR located at the index 12 in the step-up population. The one standard error chart (see Bootstrap analysis S4,† lower right chart) indicated that a QSPR with more than two descriptors would overfit, so the 12th 2-descriptor QSPR was finally chosen from the step-up population of candidate QSPRs (see Method S2† for details concerning the selection of the QSPR).
BT −0.5 (see Bootstrap analysis S4,† lower left chart). For this reason, the next smallest average MAE from the bootstrap step-up population was investigated, and it resulted in a 2-descriptors QSPR located at the index 12 in the step-up population. The one standard error chart (see Bootstrap analysis S4,† lower right chart) indicated that a QSPR with more than two descriptors would overfit, so the 12th 2-descriptor QSPR was finally chosen from the step-up population of candidate QSPRs (see Method S2† for details concerning the selection of the QSPR).
The equation of the chosen 2-descriptor QSPR for the Ta* + Nt dataset is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = 1.8**(±0.64) − 0.92***(±0.18)·AATS1s + 0.99***(±0.21)·ETA_Beta_ns_d BT = 1.8**(±0.64) − 0.92***(±0.18)·AATS1s + 0.99***(±0.21)·ETA_Beta_ns_d | (4) |
±, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT and asterisks meaning is the same as for eqn (3), while AATS1s, and ETA_Beta_ns_d are the descriptors.
BT and asterisks meaning is the same as for eqn (3), while AATS1s, and ETA_Beta_ns_d are the descriptors.
The performance metrics for eqn (4) are reported in Table 2. The absolute pair correlation between the descriptors was 0.21 and the QQ chart (see Fig. S4†) indicated broadly normally distributed residuals.
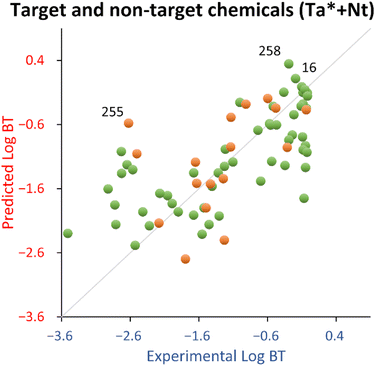
The leverage vs. standardized residuals chart (see Fig. S4†) spotted 4′-hydroxydiclofenac (ID 258) as a training structural outlier and 3-indoxyl sulphate (ID 255) as a test endpoint outlier.
3.3 PEG (polyethylene glycol) and PPG (polypropylene glycol) QSPRs (Pe + Pg, Pe and Pg datasets)
The bootstrap smallest average MAE value (see Bootstrap analysis S5,† middle chart) was obtained for a 1-descriptor QSPR, index 2 in the step-up population. The corresponding one standard error chart (see Bootstrap analysis S5,† lower chart) indicated that a QSPR with more than one descriptor would overfit, so the 1-descriptor QSPR, located at index 2, was chosen from the step-up population of candidate QSPRs (see Method S2† for details concerning the selection of the QSPR).The equation of the Pe + Pg QSPR is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = 18*** (±2.2) − 28*** (±3.1)·hmax BT = 18*** (±2.2) − 28*** (±3.1)·hmax | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT and ***asterisks meaning is the same as for eqn (3), and hmax is the descriptor.
BT and ***asterisks meaning is the same as for eqn (3), and hmax is the descriptor.
The performance metrics for eqn (5) are reported in Table 3. The QQ chart (see Fig. S5†) indicated broadly normally distributed residuals, but the sudden breaks between PPG n5 (ID 135) and PPG n10 (ID 179) suggests a possible bimodal character.
| QSPR | Training set items | Descriptors | Probability% of coincidental relationshipa | R 2 | R 2 y-scrb | Q 2 | MAE trainingd | MAE bootstrapd,e |
|---|---|---|---|---|---|---|---|---|
| a Calculated between descriptors and endpoint: upper = mode 1, lower = descriptor nature. b R 2 calculated using shuffled endpoints. c Leave-one-out cross validated R2. d MAE = mean absolute error. e Bootstrap ± standard error. f PEGs and PPGs. g PPGs. | ||||||||
| Pe + Pgf | 16 | 1 | <2.2 × 10−14 | 0.85 | 0.079 | 0.80 | 0.19 | 0.25 ± <0.01 |
| <2.2 × 10−14 | ||||||||
| Pgg | 6 | 1 | 2.2 | 0.93 | 0.19 | 0.77 | 0.059 | — |
| 2.0 | ||||||||
The leverage vs. standardized residual chart (see Fig. S5†) highlighted PPG n.4 (ID 134) as a relatively high leverage chemical.
Concerning PEGs, QSPRs were developed for one descriptor to avoid overfitting. The first QSPR in the step-up population was not acceptable because predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values were only −2.0 and −1.7 (see Fig. S6†). The next best performing QSPR showed insufficient fitting, was unstable, and the probability of chance correlated descriptors with the endpoint due to the variable selection procedure was too high (especially mode 1). For these reasons (see Fig. S6† and Statistics S6 for further information) the modelling of PEGs as an independent class was not further considered.
BT values were only −2.0 and −1.7 (see Fig. S6†). The next best performing QSPR showed insufficient fitting, was unstable, and the probability of chance correlated descriptors with the endpoint due to the variable selection procedure was too high (especially mode 1). For these reasons (see Fig. S6† and Statistics S6 for further information) the modelling of PEGs as an independent class was not further considered.
Concerning PPGs, also in this case only QSPRs of one descriptor could be developed to avoid overfitting.
The equation of the Pg QSPR is
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT = −7.4 × 10−2 (±9.2 × 10−2) + 0.71** (±0.10)·ATSC7s BT = −7.4 × 10−2 (±9.2 × 10−2) + 0.71** (±0.10)·ATSC7s | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT and ** asterisks meaning is the same as for eqn (3), while no asterisks means that the p-value is 0.1 < p ≤ 1, and ATSC7s is the descriptor.
BT and ** asterisks meaning is the same as for eqn (3), while no asterisks means that the p-value is 0.1 < p ≤ 1, and ATSC7s is the descriptor.
The performance indicators for eqn (6) are reported in Table 3. The QQ chart (see Fig. S7†) suggested normally distributed residuals.
The leverage vs. standardized residuals chart (see Fig. S7†) highlighted PPG n.10 (ID 179) as a relatively high structural leverage chemical.
4. Discussion
4.1 Target chemical QSPR (Ta and Ta* datasets)
The aim of this work was to evaluate the possibility to develop QSPRs, based on a simple approach, for the prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT. The BT values determined for target chemicals showing negligible matrix effects were deemed to be less uncertain than the BT values for the other target chemicals and the non-target chemicals, so we began our exploration of the feasibility of developing a QSPR using the target chemicals.
BT. The BT values determined for target chemicals showing negligible matrix effects were deemed to be less uncertain than the BT values for the other target chemicals and the non-target chemicals, so we began our exploration of the feasibility of developing a QSPR using the target chemicals.
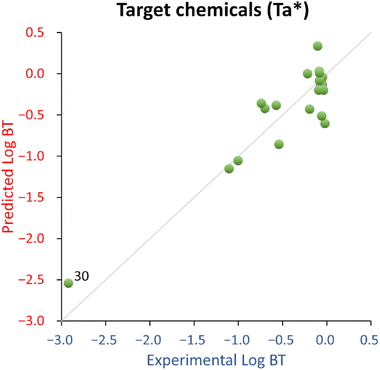
The QSPR developed using all the 22 chemicals (Ta dataset, eqn (1)) shows acceptable fitting performance (R2 = 0.61) but suffers some instability (Q2 = 0.48). However, it has an acceptable estimated prediction accuracy when applied to new chemicals (MAEbootstrap = 0.68 ± 0.01), and the probability of a coincidental relationship due to the descriptor selection procedure is low (<0.01%, see also Table 1). The removal from the training set of aniline (ID 25) and acetaminophen ID (29), because of their large deviation from the normality of the residual, substantially improved the performance of the QSPR (R2 = 0.84, Q2 = 0.69, MAEbootstrap = 0.44 ± 0.01, and negligible probability of a coincidental relationship due to the descriptor selection procedure), see also Table 1. For this reason, eqn (2) was deemed as a possible final candidate QSPR for target chemicals.
For this QSPR, caffeine (ID 30) was spotted as a structural outlier and is the only xanthine-like compound in the training set. The corresponding residual is not much different from most of the other compounds, so caffeine was deemed as a good high leverage chemical expanding the QSPR's structural and endpoint domain.
The chemical descriptor in eqn (2), MATS2s, reflects the local heterogeneity within the molecular structure in terms of atomic mass at lag 2 distance, and how this information is recursively distributed within the molecule (autocorrelation). The sign of the descriptor in the model suggests that large local atomic heterogeneity (detected for instance in caffeine and acesulfame), encoded by more positive values of MATS2s (above 0.1 in the studied training set) is related to low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values (below 10% in the studied training set). In contrast large log
BT values (below 10% in the studied training set). In contrast large log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values were detected in the studied dataset for chemicals with values of MATS2m close to zero, such as atenolol and metoprolol acid.
BT values were detected in the studied dataset for chemicals with values of MATS2m close to zero, such as atenolol and metoprolol acid.
Overall, the proposed QSPR has acceptable fitting properties (see Table 1 and Fig. 2) and suggests the role of molecular complexity as highly relevant to discriminate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT within the small training set used to develop eqn (2) (which is similar to eqn (1)). However, it is necessary to highlight that eqn (2) (and eqn (1)), is representative for a narrow structural and response domain. Therefore, it is encouraging that the proposed relationship encodes for about 80% of the information using only one descriptor, with a negligible probability of the relationship of being by chance. This is a good indication that QSPRs for the prediction of log
BT within the small training set used to develop eqn (2) (which is similar to eqn (1)). However, it is necessary to highlight that eqn (2) (and eqn (1)), is representative for a narrow structural and response domain. Therefore, it is encouraging that the proposed relationship encodes for about 80% of the information using only one descriptor, with a negligible probability of the relationship of being by chance. This is a good indication that QSPRs for the prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT can be developed. However, eqn (2) is too simplistic to be suggested as a predictive model applicable to a larger domain of chemicals.
BT can be developed. However, eqn (2) is too simplistic to be suggested as a predictive model applicable to a larger domain of chemicals.
4.2 Target and non-target chemical QSPR (Ta + Nt and Ta* + Nt datasets)
The target chemical training sets served as the basis to build more populated training sets which should, at least in principle, lead to more stable and generalizable QSPRs. Therefore, non-target analysis chemicals were added to both the Ta and Ta* datasets separately, on a structural similarity basis (see Section 2.2).Using the Ta + Nt dataset, a 3-descriptor QSPR (eqn (3)) was developed and showed acceptable fitting performance (R2 = 0.58), coherent stability (Q2 = 0.53) and negligible probability of a coincidental relationship due to the descriptor selection procedure (see Table 2 for further details). In addition, this QSPR also performed well when validated by an external test set (MAEtest = 0.69). This was further supported by the bootstrap estimation (MAEbootstrap = 0.75 ± 3.3 × 10−3) and highlighted the potential predictive ability of this QSPR when applied to new chemicals.
The eqn (3) QSPR contains three descriptors, which are discussed here on the basis of their standardized residual values (which indicates their influence on predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT), from the biggest to the smallest. The most influential descriptor, PubchemFP420, encodes for the presence of a C
BT), from the biggest to the smallest. The most influential descriptor, PubchemFP420, encodes for the presence of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragment, considering the bond order, type, and aromaticity. It is known from the literature (e.g., Papageorgiou et al.15) that the concentration of carbonyl compounds decrease during coagulation/flocculation, sand/activated carbon filtration and biofiltration (for biofiltration see e.g., Marron et al.16), therefore having an impact on the BT.
O fragment, considering the bond order, type, and aromaticity. It is known from the literature (e.g., Papageorgiou et al.15) that the concentration of carbonyl compounds decrease during coagulation/flocculation, sand/activated carbon filtration and biofiltration (for biofiltration see e.g., Marron et al.16), therefore having an impact on the BT.
VR3_Dzs is a descriptor based on the Barysz matrix, which accounts for the presence of multiple bonds and heteroatoms, and includes atomic weight. It reinforces the findings for PubchemFP420 because it provides a topological aspect. It also gives an additional discriminant for different atomic types.
Finally, even though PubchemFP373 is the descriptor in the QSPR with the least impact, it is interesting because it tests for the presence of N where bond aromaticity is significant, thus suggesting that aromatic N also plays a role in determining BT. Aromatic amines in general are known to be very susceptible to electrophilic aromatic substitution. We hypothesize that biodegradation of aromatic N may be a process influencing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT in the studied WWTP (see for example Pankaj17 and Masoom et al.18). The selection of these molecular descriptors, which have a negative sign in eqn (3) (i.e., their presence reduces BT), seems to be in line with known mechanisms of removal and degradation in WWTPs.
BT in the studied WWTP (see for example Pankaj17 and Masoom et al.18). The selection of these molecular descriptors, which have a negative sign in eqn (3) (i.e., their presence reduces BT), seems to be in line with known mechanisms of removal and degradation in WWTPs.
Considering the structural outliers in the eqn (3) QSPR, while benzophenone (ID 76) seems to be not particularly different from other chemicals in the training set, fexofenadine (ID 229) is different because of the three benzene rings and one N acyclic ring, thus playing a role as a good (low residual) structural outlier, extending the structural applicability domain of the QSPR.
Concerning the test set, no simple or evident explanation could be found for acridine (ID 71) and epinephrine (ID 227) as endpoint outliers. Therefore, the eqn (3) QSPR, based on only three descriptors, may simply lack sufficient structural information to correctly predict these two chemicals in comparison to the rest of the test set chemicals.
Looking for an improvement of this QSPR, recall that the removal of two problematic chemicals (detected using the eqn (1)) i.e., aniline (ID 25) and acetaminophen (ID 29), significantly improved the performance of the target chemical QSPR (see eqn (2)). Therefore, it was hypothesized that also the corresponding QSPR based on pooled target and non-target chemicals (here called Ta* + Nt) would benefit from the removal of these two chemicals. However, the removal of aniline (ID 25) and acetaminophen (ID 29) reduced the training set size from 70 to 56 items, which in turn led to the non-overfitting QSPR being based on two descriptors instead of three. Indeed, the fitting and cross validated (in terms of Q2) performance slightly decreased with respect to the Ta + Nt QSPR (from R2 = 0.58 to R2 = 0.54, and from Q2 = 0.53 to Q2 = 0.48), while the probability of coincidental relationships is basically the same. However, it is important to highlight that the performance on the test set, in terms of MAE, improved from 0.69 to 0.58. However, since this finding is based on test sets of different size (28 for the Ta + Nt QSPR and 17 for the Ta* + Nt QSPR), the performance was further evaluated using only the test set chemicals common to both datasets. In this case a small (but still noticeable) improvement from 0.62 to 0.59 (in terms of MAE) was obtained, thus supporting the previous finding. Furthermore, even though the performance of the two QSPRs, both in fitting and cross validation, and by considering the test set validation sharing the common chemicals, is similar (see also Table 2), it should be taken into account that the number of descriptors included in the Ta* + Nt QSPR is smaller than in the Ta + Nt QSPR, which may explain the poorer fitting of the training set by the Ta* + Nt QSPR.
Eqn (4) consists of two descriptors. The one with the biggest standardized coefficient, AATS1s, is a lag 1 averaged Broto-Moreau autocorrelation descriptor weighted by I-state, which takes into account the electronic and topological environment (lag 1) of atoms in a molecule, depending on their electronegativity values (Kier and Hall19). The second descriptor, ETA_Beta_ns_d, considers “size, shape, branching and functionality contributions of a molecular graph in addition to contributions of specific vertices or positions within common substructures of molecular graphs towards total functionality” (Roy and Ghosh20) and, according to the authors it “…may be taken as a relative measure of electron-richness (unsaturation) of the substructure (Roy and Gosh.21)”. In our study, it seems that, the higher the value of ETA_Beta_ns_d, the higher the breakthrough.
4′-Hydroxydiclofenac (ID 258) was highlighted as a relevant structural outlier (see Fig. S4†). However, since its experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT (−0.29) is comparable to that of diclofenac (−0.19, ID 16), it is expected to be a good (low residual) structural outlier, effectively extending the applicability domain of the QSPR.
BT (−0.29) is comparable to that of diclofenac (−0.19, ID 16), it is expected to be a good (low residual) structural outlier, effectively extending the applicability domain of the QSPR.
Concerning the test set, 3-indoxyl sulphate (ID 255) was a response outlier (see Fig. S4†). Indeed, there is a tendency of this QSPR to overestimate (on average 1.6 times) the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT of indoles belonging to the training set (see Table S3†).
BT of indoles belonging to the training set (see Table S3†).
For this explorative work, the proposed QSPR has acceptable fitting properties (see Table 2 and Fig. 3) and it is encouraging that the relationship uses only two descriptors, which makes it very parsimonious from a modeling standpoint, with negligible probability that this is due to chance. In addition, it should be noted that, in comparison to the training set, the test set chemicals were more dissimilar than for the target chemicals, because the latter were chosen using lower values of the Tanimoto index from the target chemicals (see Section 2.2). Therefore, the test set used for this QSPR is expected to give a more pessimistic view of its generalized performance (it should be noted that the estimation by the bootstrapped MAE, being 0.75 in comparison to 0.58 estimated by the test set, suggests that the approach used in this work is robust).
Therefore, this QSPR is expected to give predictions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT, when applied to new chemicals, with an expected average error between 0.58 and 0.75, for a WWTP and conditions like those reported in Section 5. This model could be reasonably used for an initial screening phase of the BT of new chemicals, within an applicability domain defined in terms of leverage distance.
BT, when applied to new chemicals, with an expected average error between 0.58 and 0.75, for a WWTP and conditions like those reported in Section 5. This model could be reasonably used for an initial screening phase of the BT of new chemicals, within an applicability domain defined in terms of leverage distance.
4.3 PEG (polyethylene glycol) and PPG (polypropylene glycol) QSPRs (Pe + Pg, Pe and Pg datasets)
Since the mechanisms influencing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT can be many and can differ among heterogeneous chemicals, questions arise whether structurally homogeneous chemicals, interacting by means of few or just one mechanism, would lead to better performing QSPRs. For this reason, PEGs and PPGs, for which mechanisms of degradation are known, were selected. PEGs are aerobically degraded by oxidation of the terminal alcohol groups followed by the terminal ether cleavage,22 thus the chemicals are shortened, while PPGs are oxidized to ketones and/or aldehydes,23 but the chemicals are not shortened.23,24
BT can be many and can differ among heterogeneous chemicals, questions arise whether structurally homogeneous chemicals, interacting by means of few or just one mechanism, would lead to better performing QSPRs. For this reason, PEGs and PPGs, for which mechanisms of degradation are known, were selected. PEGs are aerobically degraded by oxidation of the terminal alcohol groups followed by the terminal ether cleavage,22 thus the chemicals are shortened, while PPGs are oxidized to ketones and/or aldehydes,23 but the chemicals are not shortened.23,24
The QSPR developed for pooled PEGs and PPGs (Pe + Pg, eqn (5)) fits well (R2 = 0.85) and is stable (Q2 = 0.80), and the probability of a coincidental relationship between the descriptor and the endpoint due to the descriptor selection procedure is negligible.
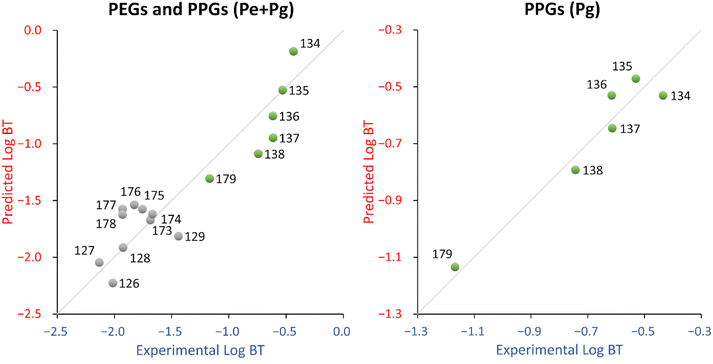
The descriptor for the QSPR equation, hmax, is the maximum hydrogen E-State (hydrogen electro-topological state index), which encodes electronic and topological information about the hydrogens. For PPGs, hmax increases as the chain length increases, while for PEGs, hmax decreases as the chain length increases up to 13, then hmax increases again. Since PEGs and PPGs relate in the opposite way with hmax, this suggests that they should not be modelled in the same QSPR. In fact, taking PPGs and PEGs separately, a regression of hmax vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT for PPGs correlates well (R2 = 0.75) while for PEGs it does not (R2 = 0.19). Indeed, while both the experimental and predicted log
BT for PPGs correlates well (R2 = 0.75) while for PEGs it does not (R2 = 0.19). Indeed, while both the experimental and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT of PPGs consistently decreases as the chain length increases, the same is not true of PEGs, as the experimental log
BT of PPGs consistently decreases as the chain length increases, the same is not true of PEGs, as the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values show no consistent relationship with chain length (see Fig. S5†). Also, the experimental vs. predicted log
BT values show no consistent relationship with chain length (see Fig. S5†). Also, the experimental vs. predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT chart (see Fig. 4, left panel) showed a clear distinction between PEGs and PPGs.
BT chart (see Fig. 4, left panel) showed a clear distinction between PEGs and PPGs.
As a consequence, the PEGs and PPGs were modeled separately.
Concerning PEGs (Pe dataset), no reasonable 1-descriptor QSPR was found (see Section 3.3). This could be due, at least in part, to the absence of a consistent chain-length dependence with the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT values.
BT values.
On the other hand, the PPGs QSPR (Pg dataset) fits well (R2 = 0.93) and has an acceptable stability (Q2 = 0.78). The probability that the relationship between the descriptor and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT is coincidental was reasonably low (around 2%, see Table 3). The descriptor in this QSPR, ATSC7s, is a lag 7 centered Broto-Moreau autocorrelation weighted by I-state. This descriptor is similar to the AATS1s descriptor in eqn (4), which is an auto-correlation descriptor taking into account the electronic and topological environment (lag 7) of atoms in a molecule, depending on their electronegativity values. From the fitting standpoint there is some improvement in the Pg QSPR in comparison to the Pe + Pg QSPR, especially in terms of training MAE (the improvement could be due, at least in part, to the coherence with the degradation pathways). The Pg QSPR shows a decrease in terms of stability and coincidental relationships, which is expected because of the smaller number of available chemicals (6 instead of 16).
BT is coincidental was reasonably low (around 2%, see Table 3). The descriptor in this QSPR, ATSC7s, is a lag 7 centered Broto-Moreau autocorrelation weighted by I-state. This descriptor is similar to the AATS1s descriptor in eqn (4), which is an auto-correlation descriptor taking into account the electronic and topological environment (lag 7) of atoms in a molecule, depending on their electronegativity values. From the fitting standpoint there is some improvement in the Pg QSPR in comparison to the Pe + Pg QSPR, especially in terms of training MAE (the improvement could be due, at least in part, to the coherence with the degradation pathways). The Pg QSPR shows a decrease in terms of stability and coincidental relationships, which is expected because of the smaller number of available chemicals (6 instead of 16).
Finally, it should be noted that while the molecular size decreases, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT increases. This seemed counter-intuitive, but the experimental results of Li et al.3 are supported by the literature, where PPG 425 proved to be less biodegradable than PPG 725 (which is longer).24
BT increases. This seemed counter-intuitive, but the experimental results of Li et al.3 are supported by the literature, where PPG 425 proved to be less biodegradable than PPG 725 (which is longer).24
As a side note, it should also be noted that in the paper of Li et al.3 PEG n8 to n15 and PPG n10 were severely out of the structural domain of the target chemicals when considering the second and third PCA axis, while the remaining PEGs and PPGs were scarcely represented. However, the relationship found for the PPGs suggested that the methodology for RE calculation described in Li et al.3 seems to also be reliable for chemicals outside the structural domain of the target chemicals.
5. Limitations of the approach
This work is based on removal efficiencies measured by target and non-target analysis from the Henriksdal municipal WWTP located in Stockholm (Sweden) which includes mechanical, chemical and biological treatments, with a final sand filtration step. Flow-proportional samples were collected for 24 hours, during dry weather, on June 15, 2016.3 Therefore, the proposed QSPRs and performances in predicting the BT should be considered applicable only for WWTPs under similar conditions. This specification is in addition to the need to verify the inclusion of new predictions within the structural applicability domain of the models, by checking the structural similarity to the training set of eqn (4) or by using the leverage approach.14The QSPRs have been developed treating the WWTP as a whole, not taking into consideration specific mechanisms which are responsible for the BT of the chemicals. While this approach simplifies the development of predictive QSPRs, it makes it difficult to relate the molecular descriptors to specific WWTPs processes, thus impacting the interpretability of the QSPRs. However, the thorough checking of chance correlation and overfitting adds confidence to the proposed QSPRs, even though a straightforward mechanistic interpretation of the descriptors is not always possible.
Finally, it is necessary to highlight, as also reported in Section 2.4, that MLR was used here for simplicity to develop QSPRs which are transparent and easily applicable as linear equations. These models are based on molecular descriptors which can be calculated for new chemicals using free software. However, relationships between molecular descriptors and the BT of heterogeneous chemicals are unlikely to be linear, which limits the accuracy of MLR QSPRs. On the other hand, it should be noted that linear regressions tend to be more robust (i.e., have less variance) than non-linear alternatives. Therefore, there is a tendency for linear QSPRs to be less overfitted than more complex approaches.
6. Conclusions
This work aimed to check whether the BT calculated as the ratio between effluent and influent peak areas of target and non-target chemicals from WWTPs can be predicted by in silico methodologies, specifically QSPRs. Even though the WWTP under scrutiny is a complex system, a simple approach was followed i.e., QSPRs were developed for direct relationships between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT and the structure of the chemicals under consideration.
BT and the structure of the chemicals under consideration.
Overall, there is evidence that reasonable QSPRs for the prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT, at least for a screening phase level, can be developed, by regressing the structural information of the chemical to the log
BT, at least for a screening phase level, can be developed, by regressing the structural information of the chemical to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT.
BT.
We want to highlight that, to the best of our knowledge, this work represents the first attempt reported in the literature to model BTs, using simple, but statistically robust, MLR equations and molecular descriptors derived from a freely distributed software. In particular, the QSPR developed merging target and non-target chemicals (eqn (4)) can be applied for an initial screening phase of the BT of new chemicals, at least for WWTPs with treatment steps and operating conditions similar to the one used here. Moreover, since the structural heterogeneity of the studied compounds was a fundamental factor in defining the dimension of the training and of the test set, we strongly recommend to apply the proposed QSPR strictly within the structural applicability domain defined by the leverage approach.14
Author contributions
Nicola Chirico: conceptualization, methodology, data curation, software, writing – original draft. Michael S. McLachlan: conceptualization, writing – review & editing, resources. Zhe Li: resources. Ester Papa: conceptualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.References
- E. Parry and T. M. Young, Water Res., 2016, 104, 72–81 CrossRef CAS PubMed.
- G. Nürenberg, U. Kunkel, A. Wick, P. Falås, A. Joss and T. A. Ternes, Water Res., 2019, 163, 114842 CrossRef PubMed.
- Z. Li, E. Undeman, E. Papa and M. S. McLachlan, Environ. Sci.: Processes Impacts, 2018, 20(3), 561–571 RSC.
- D. Awfa, M. Ateia, D. Mendoza and C. Yoshimura, ACS EST Water., 2021, 1(3), 498–517 CrossRef CAS.
- T. M. Nolte, G. C. Chen, C. S. van Schayk, K. Pinto-Gil, A. J. Hendriks, W. J. G. M. Peijnenburg and A. M. J. Ragas, Sci. Total Environ., 2020, 708, 133863 CrossRef CAS PubMed.
- C. Rucker, G. Rucker and M. Meringer, J. Chem. Inf. Model., 2007, 47(6), 2345–2357 CrossRef PubMed.
- G. C. Cawley and N. L. C. Talbot, J. Mach. Learn. Res., 2010, 11, 2079–2107 Search PubMed.
- D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 20 Search PubMed.
- Open Babel, The Open Source Chemistry Toolbox, https://openbabel.org/wiki/Main_Page, accessed 21-06-2023 Search PubMed.
- C. W. Yap, J. Comput. Chem., 2011, 32(7), 1466–1474 CrossRef CAS PubMed.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning. Data Mining, Inference, and Prediction, 2nd edn, Springer Series in Statistics, 2009 Search PubMed.
- L. Breiman, J. H. Friedman, R. Olshen and C. J. Stone, Classification and Regression Trees, Chapman & Hall, New York, 1984 Search PubMed.
- The Comprehensive R Archive Network, https://cran.r-project.org, accessed 21-06-2023 Search PubMed.
- A. Tropsha, P. Gramatica and V. K. Gombar, QSAR Comb. Sci., 2003, 22(1), 69–77 CrossRef CAS.
- A. Papageorgiou, D. Voutsa and N. Papadakis, Sci. Total Environ., 2014, 481, 392–400 CrossRef CAS PubMed.
- E. L. Marron, P. Carsten, J. V. Buren and D. L. Sedlak, Water Reuse Systems. Environ. Sci. Technol., 2020, 54, 10895–10903 CAS.
- K. A. Pankaj, Front. Microbiol., 2015, 6, 820 Search PubMed.
- F. Masoom, M. Saeed, M. Aslam, R. Wreland Lindström and R. Farooq, J. Microbiol. Methods, 2020, 174, 105941 CrossRef PubMed.
- L. B. Kier and L. H. Hall, Pharm. Res., 1990, 7, 801–807 CrossRef CAS PubMed.
- K. Roy and G. Ghosh, Internet Electron. J. Mol. Des., 2003, 2, 599–620 CAS.
- K. Roy and G. Ghosh, Chem. Inf. Comput. Sci., 2004, 44(2), 559–567 CrossRef CAS PubMed.
- F. Kaway, Appl. Microbial Biotechnol., 2002, 58(1), 30–38 CrossRef PubMed.
- A. Zgola-Grzeskowiak, T. Grzeskowiak, J. Zembrzuska, M. Franska, R. Franski, T. Kozik and Z. Lukaszewski, Chemosphere, 2007, 67(5), 928–933 CrossRef CAS PubMed.
- A. Zgola-Grzeskowiak, T. Grzeskowiak, J. Zembrzuska and Z. Lukaszewski, Chemosphere, 2006, 64(5), 803–809 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3em00267e |
| This journal is © The Royal Society of Chemistry 2024 |