Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capacity-prediction models for organic anode-active materials of lithium-ion batteries: advances in predictors using small data†
Haruka
Tobita
a,
Yuki
Namiuchi
b,
Takumi
Komura
a,
Hiroaki
Imai
 a,
Koki
Obinata
c,
Masato
Okada
a,
Koki
Obinata
c,
Masato
Okada
 c,
Yasuhiko
Igarashi
c,
Yasuhiko
Igarashi
 *b and
Yuya
Oaki
*b and
Yuya
Oaki
 *a
*a
aDepartment of Applied Chemistry, Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan. E-mail: oakiyuya@applc.keio.ac.jp
bFaculty of Engineering, Information and Systems, University of Tsukuba, 1-1-1 Tennodai, Tsukuba 305-8573, Japan. E-mail: igayasu1219@cs.tsukuba.ac.jp
cGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8561, Japan
First published on 17th May 2023
Abstract
Organic energy storage has attracted a lot of interest in enhancing performance and reducing the consumption of resources. If performance predictors are prepared, the exploration of new compounds can be accelerated without consumption of time, energy, and effort. In the present work, a new straightforward capacity predictor is constructed for the exploration of organic anode-active materials. Sparse modeling for small data (SpM-S) combining machine learning (ML) and our chemical insights was used to construct linear regression models of specific capacity. In our previous work, two predictors (models G1 and G2) were prepared using small datasets. However, the descriptors and prediction accuracy of these models were not validated. In the present work, a new improved model (model G3) has been constructed with the addition of new data. These three models were studied in terms of data science: namely, prediction accuracy, validity of the descriptors, amount of training data used, and effect of ML algorithms. The straightforward, generalizable, and interpretable model G3 can be applied to explore new organic anode-active materials. Moreover, these data-scientific approaches to model construction and validation can be used to explore new energy-related materials even with small data.
1. Introduction
Organic electrode-active materials are needed to achieve next-generation high-performance and resource-saving energy storage.1–9 One significant process is the exploration and discovery of new compounds for electrode-active materials. If a potential compound, e.g. a lead compound in the field of drug discovery, is found, we can design molecules, nanostructures, and electrodes to enhance performance. However, it is not easy to discover new compounds in a wide search space of organic compounds. Exploration based only on experience and intuition with trial and error encounters limitations. If predictors of electrochemical performance, such as reaction potential, capacity, and cyclability, are prepared, the efficient exploration of new compounds can be achieved. In the present work, a new capacity prediction model (model G3) was constructed to explore organic anode-active materials for lithium-ion batteries using SpM-S (Fig. 1), a data-driven method based on small data.10–14 The validity of model G3 was studied in a data-scientific manner and compared with that of the previous models G1 and G2.Organic anode-active materials exhibit high specific capacity compared with conventional graphite.1–9 In previous work, conductive polymers with redox reactions in the range of 2.0–0.5 V vs. Li/Li+ were studied as a classical organic anode-active material.15–18 Tarascon et al. reported a new scheme for the lithium alkoxylation of carbonyl groups in π-conjugated molecules.19 Sun et al. found the uptake of multiple lithium ions (Li+) in a π-conjugated framework,20i.e. superlithiation, drastically enhancing specific capacity.21–29 Although π-conjugated molecules have potential for superlithiation, not all such compounds show high specific capacity. In recent years, known compounds with high specific capacity were introduced into polymers and covalent organic frameworks to enhance performance.30–32 The exploration and discovery of new compounds depending only on professional experience encounter limitations. A more specific design strategy is required to discover new anode-active materials efficiently. If the correlations between molecular structure and capacity are elucidated, a predictor can be constructed to accelerate the exploration of new compounds. Redox potentials were calculated to design organic electrode-active materials by computational chemistry.33,34 The reactivity of organic anode-active materials with multiple lithium ions was studied by calculation.20,28 However, specific capacity is not easily predicted by computational chemistry alone because various factors, such as conductivity, size, and shape of the particles, are related to capacity. Therefore, we have focused on machine learning (ML) to extract the significant factors and construct the capacity predictors.
Data-driven approaches have been rapidly developed in recent materials science.35–40 ML has been used to predict the structures and functions of molecules and materials. In general, bigger training data is preferred to construct more accurate predictors. Big data sufficient for conventional ML algorithms is not easily prepared based on experimental studies in the laboratory. New ML schemes applicable to small data have been studied in recent years.10,41–43 In addition, automated, robotic, and combinatorial methods are used to obtain big training data efficiently.44–47 However, not all experiments including synthesis and characterization are integrated in an automated system. Although training data can be collected from the literature, the reported values include differences and errors depending on the experimental conditions of an individual research group. Experimental scientists need a new methodology to use ML for small data. Our group has developed SpM-S, a new scheme of ML for small data.10–14 Sparse modeling (SpM) is a general concept to describe whole high-dimensional data using a limited number of significant descriptors extracted by ML. In SpM-S, the extraction of the descriptors using ML is followed by further selection based on our chemical insight. Combination with our chemical insight contributes to avoiding overtraining caused by the small data and improving generalizability.10,14 Therefore, SpM-S provides straightforward, interpretable, and generalizable linear regression models using a limited number of descriptors. Our group constructed performance predictors for organic cathode-active and anode-active materials using SpM-S.48–50 Although two predictors (G1 and G2) for the specific capacity of an anode were prepared in our previous work (Fig. 1a–d),48,49 their prediction accuracy was not sufficient. Moreover, the validity of the predictors and extracted descriptors were not studied in terms of data science. In the present work, a new improved model G3 was prepared with the addition of new experimental data (Fig. 1c and d). The validity of the prediction models G1–G3 was studied in terms of prediction accuracy, extracted descriptors, amount of training data, and ML algorithm (Fig. 1e).
2. Results and discussion
The capacity predictors of organic anode-active materials were constructed using small data based on our own charge–discharge measurements (Fig. S1 in ESI†).48,49 Predictors G1 and G2 were prepared in our previous work (Fig. 2).48,49 In the present work, predictor G3 was constructed to improve the prediction accuracy with the addition of new data (Fig. 3). The objective variable (y) was the measured specific capacity of commercially available compounds 1–54, such as conjugated molecules and heteroaromatic compounds, at a current density of 10 mA g−1 for model G1 and 100 mA g−1 for models G2 and G3 (Table 1 and Scheme S1 in the ESI†).48,49 New data was added in the training data for the construction of model G3 (note # in Table 1 and Fig. S1 in the ESI†). | ||
| Fig. 2 Relationship between the estimated and measured capacity in the training (black) and test (red) data for models G1 (a) and G2 (b). | ||
| No. | Specific capacity/mA h g−1 | G1 | G2 | G3 | Ref. | No. | Specific capacity/mA h g−1 | G1 | G2 | G3 | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The molecular structures of 1–54 are displayed in Scheme S1 in the ESI. b The specific capacity refers to the training and test datasets in our previous work.48,49 c The specific capacity was measured in the present work (Fig. S1 in the ESI). d The differences in the specific capacity are caused by the differences in the current density. The former and latter values are the measured capacity in the datasets G1 and G2, respectively.48,49 | |||||||||||
| 1 | 0 | G1 | 48 | 28 | 490 | G2 | G3 | 49 | |||
| 2 | 0 | G1 | 48 | 29 | 6 | G2 | 49 | ||||
| 3 | 0 | G1 | 48 | 30 | 178 | G2 | G3 | 49 | |||
| 4 | 0 | G1 | 48 | 31 | 30 | G2 | G3 | 49 | |||
| 5 | 0 | G1 | 48 | 32 | 798 | G2 | G3 | 49 | |||
| 6 | 19 | G1 | 48 | 33 | 55 | G2 | 49 | ||||
| 7 | 732/0 | G1 | G2 | 48, 49 | 34 | 513 | G2 | G3 | 49 | ||
| 8 | 126/221 | G1 | G2 | G3 | 48, 49 | 35 | 109 | G2 | G3 | 49 | |
| 9 | 0 | G1 | 48 | 36 | 56 | G3 | # | ||||
| 10 | 478/28 | G1 | G2 | G3 | 48, 49 | 37 | 105 | G3 | # | ||
| 11 | 0 | G1 | 48 | 38 | 0 | G2 | 49 | ||||
| 12 | 0 | G1 | 48 | 39 | 277 | G2 | G3 | 49 | |||
| 13 | 84 | G1 | 48 | 40 | 0 | G2 | 49 | ||||
| 14 | 135/64 | G1 | G2 | G3 | 48, 49 | 41 | 201 | G3 | # | ||
| 15 | 178/1147 | G1 | G2 | G3 | 48, 49 | 42 | 277 | G2 | G3 | 49 | |
| 16 | 0 | G1 | 48 | 43 | 141 | G2 | G3 | 49 | |||
| 17 | 355 | G2 | G3 | 49 | 44 | 134 | G3 | 49 | |||
| 18 | 175 | G3 | 49 | 45 | 15 | G3 | 49 | ||||
| 19 | 24 | G3 | # | 46 | 267 | G3 | # | ||||
| 20 | 105 | G2 | G3 | 49 | 47 | 73 | G3 | 49 | |||
| 21 | 0 | G2 | 49 | 48 | 318 | G3 | 49 | ||||
| 22 | 142 | G2 | G3 | 49 | 49 | 63 | G3 | # | |||
| 23 | 405 | G3 | 49 | 50 | 229 | G3 | # | ||||
| 24 | 227 | G2 | G3 | 49 | 51 | 133 | G3 | 49 | |||
| 25 | 91 | G3 | # | 52 | 279 | G3 | 49 | ||||
| 26 | 310 | G2 | G3 | 49 | 53 | 23 | G3 | # | |||
| 27 | 0 | G2 | 49 | 54 | 273 | G3 | # | ||||
The explanatory variables (xn) were the potential descriptors related to capacity prepared based on our chemical insight (Table 2). The following parameters were used as xn (Table 2):48,49 the energy levels (E) of LUMO (x1: ELUMO0), four energy levels higher than the LUMO (x2–x5: ELUMOj, j = 1–4), the absolute values of the differences in the energy levels (x6–x15: ΔELUMOj–k: j, k = 0–4), molecular weight (x16), expected maximum (theoretical) capacity (x17), theoretical specific capacity for reaction with one Li+ (x18), the number of carboxy groups (x19), the number of carbonyl groups (x20), the number of conjugated carbons (x21), the number of occupied orbitals (Norb) lower than the work function of lithium and energy level (E) E = 0 (x22: Norb, ELUMO0 ≤ E < ΦLi, x23: Norb, ELUMO0 ≤ E < 0), the sum of absolute values of E for the orbitals in the range from ELUMO0 to E = 0 (Σ|E|, ELUMO0 ≤ E < 0, x24), Hansen solubility-(similarity-)parameter (HSP) distance between the target compound and electrolyte solution (x25), melting point (x26), the number of sulfur (S) atoms in the heteroaromatic rings (x27), dipole moment (x28), the minimum and maximum values of the partial charge density (x29, x30), HSP dispersion (δD), polarity (δP), and hydrogen-bonding (δH) terms (x31–33, respectively), the number of nitrogens and oxygens in the heteroaromatic rings (x34 and x35, respectively), the ratio of the number of heteroatoms (N, S, O) to the total number of carbon, N, S, and O (x36). In SpM-S, the significant descriptors were extracted by ML and then selected in combination with our experience and chemical insight. Linear regression models were constructed using the selected descriptors. After predictors G1 and G2 were introduced, the validity of predictor G3 and the advances in the processes of these predictors were studied in terms of data science.
| No. | Explanatory variable xn | Unit | G1c | G2c | G3c |
|---|---|---|---|---|---|
| a DFT calculation values. b HSP calculation values. c x n values shown in bold and italics were used as descriptors in models G1–G3 with positive and negative correlations, respectively. | |||||
| 1 | E LUMO0 | eV | G1 | G2 | G3 |
| 2 | E LUMO1 | eV | G1 | G2 | G3 |
| 3 | E LUMO2 | eV | G1 | G2 | G3 |
| 4 | E LUMO3 | eV | G1 | G2 | G3 |
| 5 | E LUMO4 | eV | G1 | G2 | G3 |
| 6 | E LUMO1-0 | eV | G1 | ||
| 7 | E LUMO2-0 | eV | G1 | ||
| 8 | E LUMO3-0 | eV | G1 | ||
| 9 | E LUMO4-0 | eV | G1 | ||
| 10 | E LUMO2-1 | eV | G1 | ||
| 11 | E LUMO3-2 | eV | G1 | ||
| 12 | E LUMO3-1 | eV | G1 | ||
| 13 | E LUMO4-3 | eV | G1 | ||
| 14 | E LUMO4-2 | eV | G1 | ||
| 15 | E LUMO4-1 | eV | G1 | ||
| 16 | Molecular weight | g mol−1 | G1 | G2 | G3 |
| 17 | Expected maximum capacity | mA h g−1 | G1 | ||
| 18 | Capacity reacted with 1 Li+ | mA h g−1 | G2 | ||
| 19 | Number of carboxy groups | — | G1 | G2 | |
| 20 | Number of carbonyl groups | — | G3 | ||
| 21 | Number of conjugated carbons | — | G1 | G2 | G3 |
| 22 | N orb, ELUMO0 ≤ E < ΦLi | — | G1 | G2 | |
| 23 | N orb, ELUMO0 ≤ E <0 | — | G1 | G2 | G3 |
| 24 | Σ|E|, ELUMO0 ≤ E <0 | eV | G1 | G2 | |
| 25 | HSP distance | — | G1 | G2 | G3 |
| 26 | Melting point | °C | G1 | G2 | |
| 27 | Number of S | — | G2 | ||
| 28 | Dipole moment | Debye | G2 | G3 | |
| 29 | Minimum of charge density | — | G2 | G3 | |
| 30 | Maximum of charge density | — | G3 | ||
| 31 | HSP-δD | — | G2 | G3 | |
| 32 | HSP-δP | — | G2 | G3 | |
| 33 | HSP-δH | — | G2 | G3 | |
| 34 | Number of N | — | G2 | ||
| 35 | Number of O | — | G2 | ||
| 36 | Ratio of heteroatoms | — | G2 | G3 | |
2.1. Prediction model G1
Model G1 was constructed using the training data (training dataset G1) containing 24 xn (n = 1–17, 19, 21–26, Table 2) and 16 y (compounds 1–16 in Table 1 and Scheme S1 in the ESI†) by SpM-S (Tables S1 and S2 in the ESI†).48 The descriptors were initially extracted using a minimax concave penalty and penalized linear unbiased selection algorithm (MCP) and then selected according to our chemical insight.48 The predicted y (y′) was described by (eqn (1)) using three xn with root mean square error (RMSE) of 162 mA h g−1 for the training data (black circles in Fig. 2a). Here the coefficients are converted to a normalized frequency distribution such that the mean is 0 and the standard deviation is 1. The coefficients of xn quantitatively represent the contribution to y′.48| y′ = 64.6x23 + 67.3x25 – 98.2x26 + 109.5 | (1) |
The test data including compounds A–M was prepared using literature values (Table 3 and Scheme S2 and Table S2 in the ESI†).21–29 As predictor G1 needs the melting point (x26) to calculate y′, only nine compounds (A, B, C, E, F, G, H, L, M) with melting point data were used for the test (test dataset G1, Table S2 in the ESI†). Predictor G1 had an RMSE of 629 mA h g−1 for the test data (red circles in Fig. 2a). The black and red plots are not in the diagonal line of the y–y′ plots representing the relationship between the predicted and measured values. A couple of new potential compounds, such as benzodithiophene, were successfully found using predictor G1 in a limited number of experiments.48 However, the predictor needs improvement for the following reasons. The measured capacity is higher than the estimated value, as indicated by the red arrow (Fig. 2a). This fact means that the capacity is underestimated by model G1. The underestimation is caused by the unbalanced small training data because nine of the 16 compounds had a specific capacity of 0 (Table 1). In addition, the melting point (x26) is not always available for unknown new compounds. Therefore, model G1 is not easily applied to the practical exploration of new compounds.
2.2. Prediction model G2
Model G2 was constructed using the training data (training dataset G2) containing 23 xn (n = 1–5, 16, 18, 19, 21–29, 31–36 in Table 2) and 25 y (compounds 7, 8, 10, 14, 15, 17, 20–22, 24, 26–35, 38–40, 42, 43 in Table 1, Scheme S1 in the ESI†) by SpM-S (Tables S3 and S4 in the ESI†).49 As the specific capacity was measured at a current density of 100 mA g−1 to accelerate the collecting of y for the construction of models G2 and G3 (Table 1), the capacity (y) of some compounds was different from that used for model G1. In addition, compounds with specific capacity 0 (1–5, 9, 11, 12, 16) were removed to adjust the balance of the training data. The descriptors were extracted using an exhaustive search with linear regression (ES-LiR) and then selected according to our chemical insight, as explained later (Section 2.3). Predictor G2 was described by (eqn (2)) using six xn with an RMSE of 217 mA h g−1 for the training data (black circles in Fig. 2b).49| y′ = 20.4x4 – 307.6x16 + 303.2 x22 – 9.13x23 + 12.4 x25 + 40.3x35 +218.9 | (2) |
The RMSE for the test data including 13 compounds A–M was 338 mA h g−1 (red circles in Fig. 2b and Table 3 and Scheme S2 and Table S4 (test dataset G2) in ESI†).21–29 The black and red plots approach the diagonal line of the y–y′ plots compared with those in model G1. A new potential active material with high specific capacity and cycle stability, namely 5-formylsarytilic acid, was found using predictor G2.49 However, predictor G2 still needs an improvement in accuracy.
2.3. Prediction model G3 and its data scientific validity
Model G3 was constructed using the training data (training dataset G3) containing 17 xn (n = 1–5, 16, 20, 21, 23, 25, 28–33, 36 in Table 2) and 36 y (compounds 8, 10, 14, 15, 17–20, 22–26, 28, 30–32, 34–37, 39, 41–54 in Table 1) by SpM-S (Tables S5 and S6 in the ESI†). The measured specific capacity of new compounds was added to dataset G3 (# in Table 1 and Fig. S1 in the ESI†). The descriptor was extracted from the weight diagram of ES-LiR and then considered based on our chemical insights (Fig. 3a). In ES-LiR, linear regression models are exhaustively prepared with all the possible combinations of xn (n = 1, 2, 3, …, n). Here a total of 217−1 (≈ 1.3 × 105) patterns of the regression models are available whether or not each xn (n = 1–17) is used as a descriptor. The coefficients of each model are visualized by the color in the weight diagram in ascending order of cross validation error (CVE) (Fig. 3a). In the weight diagram, xn with more densely colored bands are used as descriptors more frequently. A deeper color indicates a larger coefficient of the descriptor, implying a larger contribution. The warm and cool colors correspond to positive and negative correlations, respectively. The coefficients of 100 models with the smallest CVE (top 0.08% of a total of 1.3 × 105 models) are summarized in the weight diagram (Fig. 3a). In general, a full state search (2n–1 patterns) of the regression models is not performed to find a sparse regression model, because evaluating each model results in a computational explosion. Computational explosion is prevented by replacing the task with a relaxation scheme, such as L1 regularization, and its optimization.51,52 The methodology can end up with an exponential amount of computation with a realistic computation time of polynomial order. However, only a limited number of models are obtained by the optimization. In addition, the solution has no guarantee that it will be the optimal one for real data analysis. In recent years, all models with dozens of descriptors can be searched in a realistic amount of time through improved computing power, although ES-LiR needs an exponential amount of computation. Therefore, the search is exhaustively achieved for all possible models unlike optimization depending on relaxation problems.53 This method visualizes the contribution of each xn in the weight diagram, as shown in Fig. 3a.We visually extracted seven xn (n = 2, 16, 21, 25, 33, 36) from the weight diagram (the left-hand axis in Fig. 3a) and then studied their validity as descriptors. The positive correlation of x25 (HSP distance) and negative correlation of x33 (HSP-δH) imply that rigid molecular frameworks with low solubility to the electrolyte enable a stable redox reaction leading to high specific capacity. The positive correlation of x36 (ratio of the heteroatoms) implies that charge localization in the molecules promotes the introduction of Li+. These xn (n = 2, 25, 33, 36) are consistent with our chemical insight. Although the positive correlation of x2 (ELUMO1) is not directly explained, the positive correlation of the LUMO levels was used as the results of ML in model G2.49 In the present work, x2 is also adopted as a descriptor in model G3. Further studies including a calculation study are needed to elucidate the correlation between the LUMO level and capacity. The positive correlation of x16 (molecular weight) and the negative correlation of x21 (number of conjugated carbons) are not simply consistent with our chemical insight. In principle, the correlation of these descriptors is inverse. A higher specific capacity (mA h g−1) is achieved by compounds with a lower molecular weight. More conjugated carbons enhance superlithiation, leading to an increase in specific capacity. Therefore, these xn (n = 16, 21) are not selected for model G3. On the other hand, two xn (n = 20, 28) are added as descriptors according to our chemical insight. The positive correlation of x20 (the number of carbonyl groups) means an increase in the reactivity of Li+. In addition, carbonyl groups were reported to be reaction sites in previous work.3–6 The positive correlation of x28 (dipole moment) means charge localization of the molecule enhances the introduction of Li+. In this manner, six xn (n = 2, 20, 25, 28, 33, 36) were selected as descriptors in combination with ES-LiR and our chemical insights. Predictor G3 was described by (eqn (3)) using six xn with RMSE 144 mA h g−1 for the training data (black circles in Fig. 3b).
| y′ = 164.6x2 + 58.0x20 + 116.8x25 + 98.5x28 – 280.1x33 + 296.9x36 + 229.9 | (3) |
When five-fold cross validation was performed using (eqn (3)) in training dataset G3, the average RMSE values were 194 ± 12.6 mA h g−1 for the training and 218 ± 113 mA h g−1 for the test data. Model G3 showed an RMSE of 366 mA h g−1 for the test data, including compounds A–M (red circles in Fig. 3b, Table 3 and Scheme S2 in the ESI†). Although the RMSE value of model G3 is smaller than that of model G2 for the training dataset (the black circles in Fig. 2b and 3c), model G3 shows a larger RMSE value than model G2 for the test dataset (the red circles in Fig. 2b and 3c). The relationship between the estimated and measured capacity of model G3 more accurately represents the trend of high and low capacity compared with that of models G1 and G2 (Fig. 2b and 3b), because more plots are on the diagonal line in the true-error plots. The overall accuracy and generalizability of the prediction model are evaluated not only by the RMSE values but also by the true-error plots. These results imply that model G3 can be used for an exploration of new unknown compounds.
The validity of the extracted descriptors was studied in terms of data science. The averaged absolute values of the coefficients were calculated for each xn in 100 models with the smallest CVE values (Fig. 3c). The averages were larger than 35 for the visually extracted xn (n = 2, 16, 21, 25, 33, 36) from the weight diagram. The chart quantitatively supports the validity of the visually extracted xn from the weight diagram (Fig. 3a). However, the selected xn (n = 20, 28) based on our chemical insight were not supported by the chart (Fig. 3c). In addition, the chart indicates that xn (n = 16, 21) are potential descriptors. The validity of the six selected descriptors is not fully supported by ES-LiR alone. In general, ES-LiR has the following two problems which need to be solved. CVE is used to evaluate the prediction accuracy of the models. As this CVE-based model selection causes overfitting the training data, a true model is not always obtained.53 The other problem is the visual and qualitative extraction process of the descriptors from the weight diagram displaying the coefficients of the models in order of lowest CVE. The weight diagram represents not only a model with a specific CVE, such as the lowest one, but also multiple models with low CVE in the ranking. The visual effect of the weight diagram depends on the threshold of the CVE ranking defined by researcher. A more quantitative scheme including reliability is needed to extract the descriptors more appropriately.
Here reliability assessment and subsequent extraction of descriptors based on Bayesian model averaging (BMA) were carried out in the data.54 Bayesian inference was applied to a linear regression model in our previous work.55 In Bayesian inference,56 the likelihood of each linear regression model using various descriptors is expressed by a probability value, assuming that noise is added to each of the experimental data. This evaluation method based on probability value approaches a true model, avoiding overtraining in training data compared with that based on the CVE value.57 The model with the highest probability value can be selected to explain the experimental data. BMA is introduced in the selection process because the influence of the training data is significant. All possible models for each descriptor are integrated with weighting by the probability values explaining the experimental data. Then, the probability that each xn is a descriptor is calculated (Fig. 3d). This ES-BMA method provides more quantitative information in the extraction processes of the descriptors, whereas the descriptors are visually extracted from the weight diagram of ES-LiR (Fig. 2 and 3a–c). ES-BMA analysis indicates that the selected descriptors xn (n = 2, 20, 25, 28, 33, 36) have a probability higher than 0.8. Therefore, ES-BMA supports the validity of the descriptors in model G3.
In this manner, the appropriate descriptors were extracted and selected in model G3 by ES-LiR in combination with our chemical insight. The validity of the model and its descriptors is supported by ES-BMA. These results imply that a straightforward and interpretable linear predictor can be constructed in small data using ES-LiR and ES-BMA in combination with our chemical insight.
2.4. Dataset independence of model G3
Cross-validation by merging the training and test datasets was carried out to study whether the selected descriptors are not extracted only from the specific training data.14 The original training dataset G3 and test dataset G3 contained 36 y and 13 y, respectively. These datasets were mixed and then divided into ten segments. One segment and the remaining nine segments were assigned to test and training data, respectively. Validation was performed by changing the assignments of the test data in the total ten patterns. The average RMSE was 194 ± 12.6 mA h g−1 for the training dataset and 219 ± 114 mA h g−1 for the test datasets (Table S7 and Fig. S2 in the ESI†). The same ten-fold cross validation with merging of training and test data was performed for models G1 and G2. In model G1, the average RMSE was 280 ± 18.2 mA h g−1 for the training dataset and 303 ± 150 mA h g−1 for the test datasets (Table S7 and Fig. S3 in the ESI†). In model G2, the average RMSE was 240 ± 12.1 mA h g−1 for the training dataset and 261 ± 105 mA h g−1 for the test datasets (Table S7 and Fig. S4 in the ESI†). The smallest RMSE values for model G3 indicate that model G3 is constructed without dependence on the datasets compared with models G1 and G2.2.5. Effect of the data quantity on the extractability of the descriptors
The effect of data size on the validity and extractability of the descriptors in model G3 was studied with a reduction in the size of the datasets (Fig. 4). The reduced training datasets G1′ and G2′ including the same compounds (y) in training dataset G1 (16 y) and training dataset G2 (25 y) were prepared from training dataset G3, respectively (Tables S8 and S9 in the ESI†). ES-LiR and ES-BMA were performed on the reduced training datasets G1′ and G2′ to study whether the same six descriptors in model G3 (xn: n = 2, 20, 25, 28, 33, 36) are extractable or not (Fig. 4). The same xn in model G3 were not fully extracted from datasets G1′ and G2′ (Fig. 4).In training dataset G1′, six xn (n = 1, 21, 23, 25, 28, 36) were visualized and extractable based on the weight diagram of ES-LiR and a chart displaying the averaged absolute values of the coefficients in the 100 models with the smallest CVE (the left-hand axes in Fig. 4a and c). The probability from ES-BMA indicates the potential descriptors xn (n = 1, 23, 25, 28) (the left-hand axis in Fig. 4e). However, xn (n = 2, 20, 23) were not extractable by ES-LiR and/or ES-BMA in dataset G1′. In training dataset G2′, xn (n = 1, 2, 4, 16, 21, 28, 36) were extractable based on the weight diagram of ES-LiR and the averaged coefficients (the left-hand axis in Fig. 4b and d). The ES-BMA analysis indicates potential descriptors xn (n = 1, 2, 20, 28, 29) with a probability higher than 0.8 (Fig. 4f). However, xn (n = 25, 23) were not extractable by ES-LiR and/or ES-BMA in dataset G2′. These analyses imply that the data sizes in datasets G1 and G2 were insufficient to extract the descriptors.
The effect of the data was studied by another method (Table 4). Dataset G3 containing 36 y was reduced in six random patterns (Fig. S5–S9 in the ESI†). The weight diagrams were prepared by ES-LiR using the reduced datasets containing 35, 34, 33, 30, and 27 y to study the extractability of the descriptors. The number of extractable xn (Nx) in the six xn (n = 2, 20, 25, 28, 33, 36) of model G3 was counted in each weight diagram (Figs. S5–S9 in the ESI†). The average Nx (Nx,ave) of the six weight diagrams was calculated in the reduced datasets (Table 4). In addition, the numbers in the weight diagram (Nwd) satisfied with Nx = 6 and Nx ≥ 5 are summarized in Table 4. The extractability of xn distinctly decreases for y lower than 33 (Table 4). When the data size is y = 30 or 27, the extractable xn from the weight diagram depend on the datasets. The results support model G3 being constructed on a sufficient amount of training data y = 36.
| y in the reduced dataset | 35 | 34 | 33 | 30 | 27 |
|---|---|---|---|---|---|
| N ave | 1 | 2 | 0 | 0 | 0 |
| N wd|Nx = 6 | 3 | 4 | 3 | 2 | 0 |
| N wd|Nx ≥ 5 | 4.17 | 4.83 | 4.17 | 3.50 | 3.00 |
2.6. Construction of predictors using other ML algorithms
Other prediction models were constructed using training dataset G3 by different ML algorithms, namely least absolute shrinkage and selection operate (LASSO) and multiple linear regression without variable selection (ML-R). The constructed predictors were validated using the test dataset including compounds A–M (Table 3 and Scheme S2 in the ESI†). The accuracy was evaluated by the RMSE values for the training data (dataset G3) and test data. The reference models comprised 13 xn for LASSO and 17 xn for ML-R. The RMSE values of these reference models for the training data were smaller than that of model G3 (gray bars in Fig. 5). The lower RMSE values imply that the reference models have higher prediction accuracy than model G3. Although the number of descriptors used is limited to six, model G3 has sufficient prediction accuracy. The RMSE value of model G3 for the test data was the smallest compared with that of the reference models (red bars in Fig. 5). The large differences in the RMSE values between the training and test datasets imply overtraining. As the difference is smallest for model G3, overtraining is avoided compared with the other models. These results indicate that SpM-S provides a straightforward, generalizable, and interpretable model G3 even in a small dataset.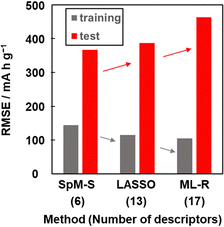 | ||
| Fig. 5 RMSE of the prediction models constructed with SpM-S, LASSO, and ML-R in the training (gray) and test (red) datasets. | ||
3. Conclusions
Capacity prediction models for organic anode-active materials (models G1–G3) were constructed by SpM-S combining ML and our chemical insight for small experimental data. Models G1–G3 have been developed with the addition of training data. In the present work, the validity of these models was studied in terms of data science. Whereas the previous models G1 and G2 needed improvements in prediction accuracy, model G3 had sufficient prediction accuracy. The extracted and selected descriptors in model G3 were supported by a combination of ES-LiR and ES-BMA. On the other hand, the same descriptors were not extracted from the datasets for models G1 and G2 even in combination with ES-LiR and ES-BMA. In other words, generalizable and appropriate descriptors were not extractable in the training datasets of models G1 and G2 for the exploration of new compounds because of the lack of training data. The required amount of data was studied using the weight diagrams of ES-LiR with a reduction in the size of the training data. Model G3 was constructed on a sufficient amount of training data compared with that of models G1 and G2. In addition, SpM-S provided generalizable model G3 compared with other ML algorithms. The straightforward, interpretable, and generalizable predictor G3 can be applied to the exploration of new organic anode-active materials in a wide search space. Our methods for model construction and validation, SpM-S combined with ES-LiR, ES-BMA, and our chemical insight, can be applied to other small-data-driven material exploration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by JST PRESTO (Y.O., JPMJPR16N2 and Y. I. JPMJPR17N2), JST CRESTO (M.O., JPMJCR1761, Y.I., JPMJCR21O1), Ogasawara Science and Technology Foundation (Y.O.), JSPS-KAKENHI (Y. O. JP22H04559 and M. O. JP23H00486).Notes and references
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652 CrossRef CAS PubMed.
- H. Nishide and K. Oyaizu, Science, 2008, 319, 737 CrossRef CAS PubMed.
- Z. Song and H. Zhou, Energy Environ. Sci., 2013, 6, 2280 RSC.
- B. Häupler, A. Wild and U. S. Schubert, Adv. Energy Mater., 2015, 5, 1402034 CrossRef.
- J. Kim, J. H. Kim and K. Ariga, Joule, 2017, 1, 739 CrossRef CAS.
- C. Friebe, A. Lex-Balducci and U. S. Schubert, ChemSusChem, 2019, 12, 4093 CrossRef CAS PubMed.
- S. Lee, J. Hong and K. Kang, Adv. Energy Mater., 2020, 10, 2001445 CrossRef CAS.
- J. J. Shea and C. Luo, ACS Appl. Mater. Interfaces, 2020, 12, 5361 CrossRef CAS PubMed.
- Y. Chen and C. Wang, Acc. Chem. Res., 2020, 53, 2636 CrossRef CAS PubMed.
- Y. Oaki and Y. Igarashi, Bull. Chem. Soc. Jpn., 2021, 94, 2410 CrossRef CAS.
- K. Noda, Y. Igarashi, H. Imai and Y. Oaki, Adv. Theory Simul., 2020, 3, 2000084 CrossRef CAS.
- R. Mizuguchi, Y. Igarashi, H. Imai and Y. Oaki, Nanoscale, 2021, 13, 3853 RSC.
- Y. Haraguchi, Y. Igarashi, H. Imai and Y. Oaki, Adv. Theory Simul., 2021, 4, 2100158 CrossRef CAS.
- Y. Haraguchi, Y. Igarashi, H. Imai and Y. Oaki, Digital Discovery, 2022, 1, 26 RSC.
- P. Novák, K. Müller, K. S. V. Santhanam and O. Hass, Chem. Rev., 1997, 97, 207 CrossRef PubMed.
- J. Ĉaja, R. B. Kaner and A. G. MacDiarmid, J. Electrochem. Soc., 1984, 131, 2744 CrossRef.
- G. C. Farrington and R. Huq, J. Power Sources, 1985, 14, 3 CrossRef CAS.
- A. Mahammadi, O. Inganäs and I. Lundström, J. Electrochem. Soc., 1986, 133, 947 CrossRef.
- M. Armand, S. Grugeon, H. Vezin, S. Laruelle, P. Ribière, P. Poizot and J.-M. Tarascon, Nat. Mater., 2009, 8, 120 CrossRef CAS PubMed.
- X. Han, G. Qing, J. Sun and T. Sun, Angew. Chem. Int. Ed., 2012, 51, 5147 CrossRef CAS PubMed.
- H. H. Lee, Y. Park, K.-H. Shin, K. T. Lee and S. Y. Houng, ACS Appl. Mater. Interfaces, 2014, 6, 19118 CrossRef CAS PubMed.
- W. Walker, S. Grugeon, O. Mentre, S. Laruelle, J.-M. Tarascon and F. Wudl, J. Am. Chem. Soc., 2010, 132, 6517 CrossRef CAS PubMed.
- S. Wang, L. Wang, K. Zhang, Z. Zhu, Z. Tao and J. Chen, Nano Lett., 2013, 13, 4404 CrossRef CAS PubMed.
- V. A. Mihali, S. Renault, L. Nyholm and D. Brandell, RSC Adv., 2014, 4, 38004 RSC.
- C. Wang, Y. Xu, Y. Fang, M. Zhou, L. Liang, S. Singh, H. Zhao, A. Schober and Y. Lei, J. Am. Chem. Soc., 2015, 137, 3124 CrossRef CAS PubMed.
- L. Fédèle, F. Sauvage, J. Bois, J.-M. Tarascon and M. Bécuwe, J. Electrochem. Soc., 2014, 161, A46 CrossRef.
- P. Yang, L. Ma, S. Bi, X. Xi, T. Huang, R. Liu, Y. Su and D. Wu, Chem. Eng. J., 2020, 294, 123924 Search PubMed.
- W. Hu, N. Chen, D. Chen and B. Tong, ChemElectroChem, 2022, 9, e202200026 CAS.
- F. M. Wang, K. W. Guji, A. Ramar, L. Merinda and W. C. Chien, ACS Sustainable Chem. Eng., 2021, 9, 12286 CrossRef CAS.
- X. Gao, Y. Dong, S. Li, J. Zhou, L. Wang and B. Wang, Electrochem. Energy Rev., 2020, 3, 81 CrossRef.
- D. Zhu, G. Xu, M. Barnes, Y. Li, C.-P. Tseng, Z. Zhang, J.-J. Zhang, Y. Zhu, S. Khalil, M. M. Rahman, R. Verduzco and P. M. Ajayan, Adv. Funct. Mater., 2021, 31, 2100505 CrossRef CAS.
- Y. Cao, M. Wang, H. Wang, C. Han, F. Pan and J. Sun, Adv. Energy Mater., 2022, 12, 2200057 CrossRef CAS.
- A. Kuhn, K. G. von Eschwege and J. Conradie, J. Phys. Org. Chem., 2012, 25, 58 CrossRef CAS.
- R. B. Araujo, A. Banerjee, P. Panigrahi, L. Yang, M. Strømme, M. Sjodin, C. M. Araujo and R. Ahuja, J. Mater. Chem. A, 2017, 5, 4439 RSC.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191 CrossRef CAS PubMed.
- K. Rajan, Annu. Rev. Mater. Res., 2015, 45, 153 CrossRef CAS.
- K. T. Butler, J. M. Frost, J. M. Skelton, K. L. Svanea and A. Walsh, Chem. Soc. Rev., 2016, 45, 6138 RSC.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360 CrossRef CAS PubMed.
- A. Agrawal and A. Choudhary, MRS Commun., 2019, 9, 779 CrossRef CAS.
- A. Aspuru-Guzik, Digital Discovery, 2022, 1, 6 RSC.
- A. D. Sendek, B. Ransom, E. D. Cubuk, L. A. Pellouchoud, J. Nanda and E. J. Reed, Adv. Energy Mater., 2022, 12, 2200553 CrossRef CAS.
- Y. Zhang and C. Ling, npj Comput. Mater., 2018, 4, 25 CrossRef.
- P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42 CrossRef.
- J. M. Granda, L. Donina, V. Dragone, D. L. Long and L. Cronin, Nature, 2018, 559, 377 CrossRef CAS PubMed.
- T. N. Nguyen, T. T. P. Nhat, K. Takimoto, A. Thakur, S. Nishimura, J. Ohyama, I. Miyazato, L. Takahashi, J. Fujima, K. Takahashi and T. Taniike, ACS Catal., 2020, 10, 921 CrossRef CAS.
- R. Shimizu, S. Kobayashi, Y. Watanabe, Y. Ando and T. Hitosugi, APL Mater., 2020, 8, 111110 CrossRef CAS.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237 CrossRef CAS PubMed.
- H. Numazawa, Y. Igarashi, K. Sato, H. Imai and Y. Oaki, Adv. Theory Simul., 2019, 2, 1900130 CrossRef CAS.
- T. Komura, K. Sakano, Y. Igarashi, H. Numazawa, H. Imai and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 8990 CrossRef CAS.
- K. Sakano, Y. Igarashi, H. Imai, S. Miyakawa, T. Saito, Y. Takayanagi, K. Nishiyama and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 2074 CrossRef CAS.
- C. H. Zhang, Ann. Stat., 2010, 38, 894 Search PubMed.
- R. Tibshirani, J. Royal Stat. Soc. Ser. B, 1996, 58, 267 Search PubMed.
- Y. Igarashi, H. Takenaka, Y. Nakanishi-Ohno, M. Uemura, S. Ikeda and M. Okada, J. Phys. Soc. Jpn., 2018, 87, 044802 CrossRef.
- A. E. Raftery, D. Madigan and J. A. Hoeting, J. Am. Stat. Assoc., 1997, 92, 179 CrossRef.
- K. Obinata, T. Nakayama, A. Ishikawa, K. Sodeyama, K. Nagata, Y. Igarashi and M. Okada, Sci. Technol. Adv. Mater. Methods, 2022, 2, 355 CAS.
- C. M. Bishop and N. M. Nasrabadi, Pattern recognition and machine learning, Springer, New York, 2006, vol. 4 Search PubMed.
- S. Watanabe, Mathematical theory of Bayesian statistics. CRC Press, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Methods, molecular structures, charge–discharge measurements, datasets, reference weight diagrams. See DOI: https://doi.org/10.1039/d3ya00161j |
| This journal is © The Royal Society of Chemistry 2023 |