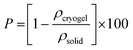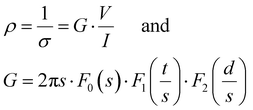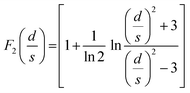Open Access Article
Open Access ArticleTailoring the 3D porous structure of conducting PEDOT:PSS gels via ice-templating†
Quentin
Weinbach
a,
Naoures
Hmili
a,
Emma
Gottis
a,
Guillaume
Fleith
a,
Jérôme
Combet
a,
Vasiliki
Papaefthimiou
 b,
Vincent
Malesys
b,
Vincent
Malesys
 c,
Emmanuel
Denys
c,
Laurent
Simon
c,
Marc
Schmutz
c,
Emmanuel
Denys
c,
Laurent
Simon
c,
Marc
Schmutz
 a,
Alain
Carvalho
a,
Doru
Constantin
a,
Alain
Carvalho
a,
Doru
Constantin
 a and
Laure
Biniek
a and
Laure
Biniek
 *a
*a
aUniversité de Strasbourg, CNRS, Institut Charles Sadron UPR22, F-67000 Strasbourg, France. E-mail: laure.biniek@ics-cnrs.unistra.fr
bInstitut de Chimie et Procédées pour l’Energie, l’Environnement et la Sante (ICPEES), Université De Strasbourg, CNRS UMR 7515, 25 rue Becquerel, F-67087 Strasbourg Cedex 2, France
cUniversité de Haute-Alsace, CNRS, Institut de Science des Matériaux de Mulhouse UMR 7361, 3Bis rue Alfred Werner, 68093 Mulhouse, France
First published on 23rd May 2023
Abstract
Poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) has been fascinating material scientists for more than 30 years, but still has structural features and new properties to reveal. Mostly developed in thin films, it has been recently processed as a bulk porous material for new electronic applications. However, the formation and control of the porous structure remain to be understood in depth. We used a combination of X-ray scattering, cryo-electron microscopy and X-ray photoelectron spectroscopy techniques to study the self-assembly mechanism of PEDOT:PSS in the dispersion, gel and dried states. We show that unique fibrils form a 3D fibrillar network upon acidification of the dispersion and that ice crystal growth modifies the structure into a honeycomb-like material. Control of the freezing rate (and freezing temperature) and directionality allowed us to produce anisotropic porous samples with tunable channel size (aligned in the longitudinal direction). Finally, the impacts of porosity on the electrical and thermal transport properties were studied at the macroscale (porous bulk samples). A highly porous templated cryogel with a very low thermal conductivity (37 mW m−1 K−1) and apparent electrical conductivity of a few S cm−1 was obtained. Preliminary measurements at the mesoscale (on a single pore wall) showed anisotropy of charge transport.
1. Introduction
In the research field of high-performance energy conversion devices, porous conducting polymers (PCPs) have attracted much attention these recent years.1,2 High porosity and surface area combined with favorable charge transport properties put them at the forefront of promising materials for many innovative applications such as supercapacitors,3 thermoelectrics,4 solar cells,5 solar steam generators6,7 or triboelectrics.8 Porous conducting polymers are made either by (i) covalent or coordination linkages connecting chemical building blocks in an extended 2- or 3D open framework, or by (ii) physical coupling of polymer objects (aggregates/fibers/colloids), forming a 3D network. In the former case, PCPs include hyper-crosslinked polymers (HPCs), conjugated microporous polymers (CMPs), polymers with intrinsic microporosity (PIMS) and covalent organic frameworks (COFs). The pore size engineering is mainly governed by the synthesis strategy at a molecular level, providing micro- (<2 nm) or meso-porosity (2 nm <pore size <50 nm). The latter case dominantly corresponds to polymer gels, which are mostly characterized by macropores (>50 nm). The porous structure is governed either by covalent bonds (e.g., crosslinking for chemical gels) or by co-operative bonds (hydrogen- bonds or van der Waals interactions for physical gels) between the objects.2Controlling the porous structure (i.e. the pore size, morphology and topology, pore directionality) is of prime importance for the targeted properties (thermal exchange, charge transport and diffusion, charge separation,…). As the commonly used chemical synthesis approach allows rational pore size engineering, we focus our attention on the macroporous conducting polymer gels for which there is less control over the porous structure.
The few reported studies are typically based on the widely known poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) conducting polymer. Commonly used in thin film technology because of its excellent printing properties,9 it is also one of the best candidates for 3D macroscopic porous materials because of its water processability and its ability to form conducting gels.10,11
Inducing and controlling porosity in PEDOT:PSS is not straightforward, and various methods have been reported. A first strategy consists in lyophilizing the PEDOT:PSS aqueous dispersion (freezing in liquid nitrogen and further sublimation of the ice).12,13 This simple method provides light but brittle samples containing pores with typical sizes of tens of micrometers. To overcome the brittleness limitation, plasticizers can be added to the dispersion prior to lyophilization. However, the additives can also affect the porous structure. As shown by Tang et al., the addition of a block copolymer based on ethylene glycol to the PEDOT:PSS dispersion provided an open-cell structure with a 3D fibrillary network that differed from the structure of the pure lyophilized PEDOT:PSS dispersion.12 A second strategy is to pre-form PEDOT:PSS gels before solvent drying. Different additives have been used as gelation agents, such as H2SO4,14 polar solvents,13 and metal salts.15 Hydrogels can also be obtained by rehydration of PEDOT:PSS thick films.16 Interestingly, after freeze-drying none of the gels showed the same porous structure (varying from a 3D interconnected network with a mean pore size of 80 μm14 to semi-closed cell walls of 40 to 100 μm size.15 Although the gelation mechanism has been discussed in the references cited above, the pore formation is seldom studied and controlled.
An interesting strategy to tailor the macroporous structure of polymers is the ice-templating method (also called “freeze-casting” in some reports). This process, derived from freeze-drying, depends on the controlled growth of ice crystals followed by their sublimation.17,18 The pores are more or less the inverse replica of the ice crystals formed during the freezing step. However, mastering the freezing of water is a complex process that depends on many variables; a constrained environment such as a gel network makes it even more complex. Water freezing can be separated into two steps: (i) nucleation and (ii) ice crystal growth. The very first instants of these two steps are of paramount importance, as they determine the shape and orientation of the final crystals (and thus of the pores). Matsumoto et al. showed that, when water is sufficiently cooled, water molecules tend to form clusters (i.e., nuclei) by hydrogen bonding in an arrangement similar to ice crystals.19 In impure or complex systems (such as PEDOT:PSS dispersions), nucleation can be considered heterogeneous because there are different energetically favorable sites for nucleus formation. Once the nuclei reach critical mass (by the diffusion of new atoms or molecules towards them), ice crystallization occurs throughout the system. The cooling conditions play a decisive role in the formation of the nuclei (and the crystals). Generally, the freezing rate is one of the key properties that control the number of nuclei formed, the rate of ice growth, and the size of ice crystals.20 A low freezing rate leads to a few large ice crystals. Conversely, the higher the freezing rate, the greater the number and the smaller the size of ice crystals (and thus of the pores). After freezing, the sample is placed in a pre-cooled tank at a temperature below the equilibrium freezing temperature of the material and solution (to prevent collapsing of the structure) and subjected to medium vacuum (to induce sublimation). The process can be completed by increasing the temperature above 0 °C to remove any remaining moisture, resulting in an ice-templated, dry porous sample. In the literature, the ice-templating method has been applied to a wide range of colloids18 or polymers (such as agarose21 or cellulose22). Ice-templating the PEDOT:PSS dispersion (but not to pre-formed gels), resulted in poorly defined pores of various shapes (lamellar or interconnected open pores) and orientations.23–26
Here, we applied this drying process to PEDOT:PSS hydrogels to form macroporous materials with ordered pores of tunable size. In this study, we focused on (i) better understanding the formation of the gel and the porous structure, (ii) tuning the porous structure by controlling key parameters during ice-templating, and (iii) revealing the correlations between the new structures and their electrical and thermal transport properties. A combination of X-Ray scattering and cryo-electron microscopy was used to follow the self-assembly of PEDOT:PSS from the dispersion state to the porous cryogel state. Unique structural features are revealed for the first time, such as the transformation from a fibrillar network to a honey-comb like structure. Finally, the electrical and thermal transports of the porous materials were measured and discussed in regards to their structure.
2. Experimental section
Materials
All materials were obtained from commercial suppliers and used as received unless otherwise stated. PEDOT:PSS (CleviosTM PH1000, 1.08 wt%, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 weight ratio PEDOT:PSS, batch number 9007391368) was purchased from Heraeus, sulfuric acid (≥95%) was purchased from Fisher Scientific, absolute ethanol and isopropanol from Carlo Erba, potassium bromide and poly(sodium 4-styrenesulfonate) (NaPSS, Mw = 1000
2.5 weight ratio PEDOT:PSS, batch number 9007391368) was purchased from Heraeus, sulfuric acid (≥95%) was purchased from Fisher Scientific, absolute ethanol and isopropanol from Carlo Erba, potassium bromide and poly(sodium 4-styrenesulfonate) (NaPSS, Mw = 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) from Sigma-Aldrich.
000 g mol−1) from Sigma-Aldrich.
Hydrogel fabrication
The PEDOT:PSS blend is composed of two charged polymers, whose chemical structures are shown in Fig. 1. PEDOT is a semi-conducting conjugated polymer that transports holes along its backbone when doped. Conversely, PSS is an electrical insulator. It does however play a major role in the blend as a dopant for PEDOT and also as a surfactant, allowing PEDOT to be dispersed in water. In this commercial dispersion, PSS is present in excess (for PH1000 commercial grade) to allow dispersion in water and favor wet processability. The PEDOT:PSS gelation process, illustrated in Fig. 1, was adapted from the work of Yao et al.14 The method is based on acidifying the dispersion with H2SO4 and can be described as follows: First, the PEDOT:PSS dispersion was vortexed for a few minutes and filtered through a PVDF 0.45 μm membrane, to ensure homogeneous dispersion. A given volume was then introduced in a flat bottom pyrex tube and treated with 3 mol L−1 of sulfuric acid to reach 0.1 mol L−1 H2SO4 in the dispersion. The mixture was immediately placed in a 90 °C oil bath for 3 to 30 hours, depending on the total volume of the dispersion (2 to 10 mL, respectively). During formation, the hydrogel kept the shape of the mold (in our case, flat bottom cylindrical tubes of 22 mm inner diameter gave rise to gel cylinders about 16 mm in diameter). The resulting sample was shrunk and floated in a transparent supernatant, suggesting expulsion of liquid from the gel, also known as the syneresis effect. The supernatant was removed after gelation and the gel was washed with fresh deionized water (with a volume equal to the volume of PEDOT:PSS used to form the gel (this step corresponds to the ‘rinsing water RW1’ in Fig. S4B, ESI†). The water was replaced again after 24 h (RW2) and left for another 24 h before replacement (RW3). The obtained hydrogels are shown in Fig. 1. Prior to freezing, about 0.5 mm was sliced off the top and bottom of the samples with a razor blade to flatten both surfaces.Cryogel formation via quenched freezing or ice templating
Two freeze-drying methods were used to get porous dried gels (or cryogels): the quenched freezing method induced rapid but isotropic freezing, while the ice-templating method allowed a controllable freezing rate and directionality, leading to anisotropic porous structure.As a comparison, the quenched freezing method was also applied to the dispersion (prior to gelation). The stock PH1000 dispersion was vortexed and filtered through a 0.45 μm PTFE filter. Then, the PEDOT:PSS dispersion was frozen in liquid nitrogen (N2L) for 10 min, and the ice was sublimated at −15 °C under vacuum for 48 h (as for the quenched cryogel). The resulting sample is light blue and takes the shape of the vial it was frozen in (in that case a cylindrical vial). The lyophilized dispersion (LD) is very brittle and can easily break when manipulated. The sample is very light, with very low density (∼ 0.02 g cm−3) and high porosity (∼ 98%), (see Fig. S1, ESI†).
The size and weight of the cryogels (dried gels) were measured immediately after drying, using an OTMT caliper and an analytical balance, respectively. Typically, cryogels are at least 1 cm thick and 1.5 cm in diameter. Only minimal shrinkage occurred between the gel and the cryogel states. The low cryogel density (ρcryogel = 0.03 ± 0.006 g cm−3) signals a very high porosity P (>95%), estimated using the following equation:
Characterization methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 weight ratio. Solid samples were ground with KBr powder, while the PH1000 dispersion was directly drop-casted onto KBr powder prior to drying at 90 °C for 30 min in an oven. Then, cylindrical pellets (of ∼1 mm thickness) were formed using a mechanical press at 5 MPa for 20 s.
100 weight ratio. Solid samples were ground with KBr powder, while the PH1000 dispersion was directly drop-casted onto KBr powder prior to drying at 90 °C for 30 min in an oven. Then, cylindrical pellets (of ∼1 mm thickness) were formed using a mechanical press at 5 MPa for 20 s.
Cryo-SEM. A small piece of hydrogel was sliced off with a razor blade, quickly dipped into liquid ethane (used as an efficient coolant to avoid the formation of crystalline ice to preserve the native structure of the hydrogel).27,28 Subsequently, the sample was transferred under high vacuum (10−6 mbar) and low temperature (−150 °C) into the Quorum PT 3010 chamber attached to the microscope. There, the frozen sample was fractured with an adapted razor blade and a slight sublimation of water at −90 °C was performed to reveal the details of the morphology. The sample was finally transferred into the FEG-cryo-SEM (Hitachi SU8010) and observed at 1 kV at −150 °C (under 10−6 mbar).
SEM. The cryogels were dipped into liquid nitrogen before cutting along or across the temperature gradient. The samples were observed at 1 kV at room temperature with the FEG-cryo-SEM (Hitachi SU8010).
The pore size of the cryogels was estimated from the SEM images with the ImageJ software. Several images in different areas of the sample were treated in order to estimate the pore size all over the material. Contrast was enhanced to obtain an optimized black and white image for thresholding with ImageJ. Then, ellipses were fitted to the pores and their mean dimensions were recorded (mean value between the major and the minor axes). Pore size was then determined by plotting at least 200 values and fitting a Gaussian curve as presented in the histogram, as in in Fig. 5F.
Cryo-TEM. Cryo-TEM allows visualizing the particles in their dispersion state by rapid vitrification in a thin layer of solvent (in this case, water). Although cryo-TEM requires complex sample preparation, it is the only technique able to image nanoparticles in their native form, without any drying effects. The diluted PEDOT:PSS dispersion was observed before and after acid treatment.
The PH1000 dispersion was vortexed for a few minutes, filtered through a PVDF 0.45 μm membrane and then diluted with deionized water height times (providing the reference dispersion sample). Cryo-TEM grids were also prepared from the stock dispersion (without filtration or dilution) and from another batch (number 9007086839, filtered and diluted) to confirm the reproducibility of the observation (see cryo-TEM images in Fig. S3A and B, ESI†). For the acidified sample, the PH1000 dispersion was vortexed for a few minutes, filtered through a PVDF 0.45 μm membrane and then diluted two times with deionized water. 8 μL of H2SO4 (3 mol L−1) was added to the diluted dispersion and then vortexed for 30 s. This acidified solution was further diluted 50 times (providing the acidified cryo-TEM sample). This high dilution rate was applied to the acidified sample in order to observe the unique fibers and to minimize the gelation process.
Five microliters of sample solution (as described above) were pipetted onto a 400 mesh Cu grid covered with a lacey carbon film that had been freshly glow discharged to render it hydrophilic (Elmo, Cordouan Technologies). The grid was rapidly plunged into a liquid ethane slush by using a homemade freezing machine with a controlled temperature chamber. The grid was then mounted onto a Gatan 626 cryoholder and observed under low dose conditions on a Tecnai G2 microscope (FEI) operating at 200 kV. The images were recorded with a slow scan CCD camera (Eagle 2k2k FEI).
Cryo-TEM images of stock and acidified dispersions shown in Fig. 1C and D were taken at a similar focus (considering that a high defocus has to be applied on the stock dispersion to reveal the fibers).
The scattered signal was recorded by an Eiger 4 M detector (Dectris Ltd, Switzerland) with pixel size 75 μm. Preliminary data treatment (angular averaging and normalization) was done using the software Foxtrot developed at the beamline, which yielded the intensity as a function of the scattering vector I(q) in absolute units. Subsequent data modeling was done in Igor Pro 7.0 using functions available in the NCNR SANS package29 (Cylinder PolyRadius and FlexCyl PolyRadius used to model the SAXS data in Fig. 2A and Fig. S2B, ESI†). The artefacts at very low q can be attributed to imperfect subtraction of the reference signal (solvent capillary).
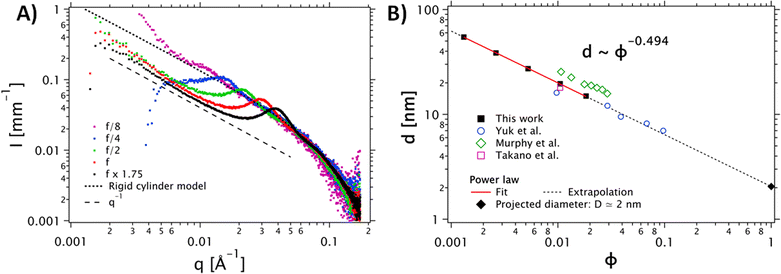 | ||
| Fig. 2 (A) Dependence of the SAXS intensity profiles as a function of the scattering vector I(q) for different concentrations of the PEDOT:PSS dispersion. The stock PEDOT:PSS dispersion, corresponding to f, is shown in red. Other data are normalized by their dilution factor with respect to the reference concentration. The grey dots correspond to the cylinder model (the diameter polydispersity is described by a Schulz distribution). (B) Dilution law of the structure factor peak. The data were fitted with a power law d(ϕ) = D ϕn, with n = −0.494. This fit confirms a scaling behavior of ϕ−1/2. The data extracted from Yuk et al.35 (open circles) Takano et al.34 (open square) ref and Murphy et al.33 (open diamonds) are in good agreement with our data. | ||
Several concentrations of the PEDOT:PSS dispersion were prepared, referenced to that of the stock dispersion (f in Fig. 2). First, the stock dispersion was vortexed for a few minutes and filtered through a PVDF 0.45 μm membrane. To prepare the more concentrated sample (i.e., f × 1.75), a vial containing 1 g of the PEDOT: PSS dispersion was left open under a constant argon flow to favor partial evaporation of the water. Then, the final mass was weighed and yielded its final concentration. To produce the less concentrated samples f/2, f/4, and f/8, water was added to the initial PEDOT: PSS dispersion to dilute it by the desired factor.
WAXS experiments on the ice templated cryogels were also performed at the DiffériX platform of the Institut Charles Sadron. The monochromatic beam with λ = 0.154 nm (8 keV) was obtained by projecting the primary beam from an X-ray generator (Rigaku, MicroMax 007HF) with Cu anode onto a confocal mirror with a multilayer coating (Confocal Max-FluxTM Optic, Rigaku). After pinhole collimation, the size of the beam at the sample position is about 800 μm. The hybrid photon-counting detector (Dectris Pilatus®3 R 300 K, pixel size 172 μm) was 7.7 cm downstream of the sample and covered a q-range of 2 Å−1 with a resolution of 0.003 Å−1.
To insure homogeneity of composition, XPS analyses were performed on different parts (bottom, middle and top) of the cryogel (not shown here).
At the macroscopic scale. A Keithley 2634B sourcemeter and a Lab Assistant Semiprobe station placed inside a Jacomex glovebox under N2 atmosphere (≈1 ppm O2, ≈1 ppm H2O) were used to determine the electrical conductivity of all samples. The electrical resistance was measured using a standard four probes collinear probes method with a probe space of 1.6 mm. The electrical resistivity and conductivity in the vertical direction were calculated using the equation of Yilmaz et al.30
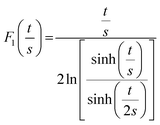
with:
| F0(s) = 2πs |
where ρ is the electrical resistivity, σ the electrical conductivity, V the voltage, I the current intensity, s the probe space, t the thickness of the sample and d the diameter. F0, F1 and F2 are geometric correction factors used when the sample is circular and t > s/2. When studying the pore size effect, all the measurements were performed on top of the samples, with the pores vertically oriented. The as-determined electrical conductivity corresponds to an apparent value, which reflects the high volume fraction porosity. As for comparison, dense PEDOT:PSS thin films treated with H2SO4 are known to reach a high electrical conductivity, above 2000 S cm−1.31,32 Comparison with similar works on porous PEDOT:PSS can be found in our previous works (ref. 2 and 4).
At the mesoscopic scale. Complementary resistivity measurements were done using a four-probe station equipped with IMINA® mibots nanomanipulators on a 600 K–77 K Kammrath®cryo-stage mounted in a FEG XL30 SEM.
The goal of this study was to determine at the scale of only one channel/tube of the templated N2L cryogel (visible in Fig. 8A), the conductivity and possible anisotropy of charge transport.
By using a conductive adhesive tape, we have transferred some pieces of tubes on the sample stage (Fig. S8, ESI†). We have performed four-probe measurements in the van der Pauw geometry. In this geometry the resistivity is given by:
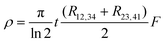 with:
with: 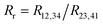 which satisfies the relation:
which satisfies the relation: 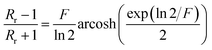 . With the linear V(I) curve, we found the ratio Rr = 2, (R12,34 + R23,41)/2 = 76 ± 3 Ω and F = 0.9.
. With the linear V(I) curve, we found the ratio Rr = 2, (R12,34 + R23,41)/2 = 76 ± 3 Ω and F = 0.9.
The collinear method has then been used to probe a possible anisotropy at the scale of the individual tube. These measurements were done on a self-standing tube as seen in Fig. 8.
The four probes, in collinear alignment, were put in contact with the tube via the high precision robots (with equal distance s between the probes) either along the tube (along the freezing direction) or perpendicular to the tube (perpendicular to the freezing direction). We have checked that the contact remained ohmic by measuring the I(V) characteristic between each pair of tips. For this, we applied 10 mV and detected a current in the range of a few tens of nA, which corresponds to a contact resistivity of 100 kΩ. Then we conducted standard four-probe collinear measurements.
As the wall thickness t (typically 500 nm) was much lower than the typical tip to tip distance s (5–100 μm), the resistivity is given by: ρ = G × Rsheet, with 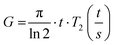
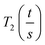 a geometric factor (
a geometric factor (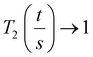 as
as 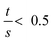 ). The wall thickness of the tube was measured by SEM.
). The wall thickness of the tube was measured by SEM.
The experiments were performed in ambient conditions and the input power and time duration were set at 5 mW and 10 s, respectively. The experiments were performed on batches of four cryogel samples and the measurements were repeated several times. The working principle of the TPS 1000 method does not allow probing the anisotropy of thermal transport in the aligned samples, since heat transfer from the probe is isotropic.
3. Results and discussion
The commercial PEDOT:PSS dispersion was transformed to a hydrogel (by acidification, see the experimental part) before solvent sublimation. Fig. 1 shows the stepwise process leading to PEDOT:PSS cryogels (via the quenched freezing method). In the following, we carefully analyze the structure of the material at each stage by a combination of multiscale spectroscopy, scattering and microscopy techniques.3.1. From the PEDOT:PSS dispersion to hydrogel formation
Fig. 1C reveals that the dispersion is mainly composed of fibrils with a mean diameter of 5 ± 2 nm and an approximate length of 150 ± 50 nm. These fibrils were not very contrasted. A strong defocus had to be applied to distinguish them. Only a very small proportion of spherical objects (of a few tens of nm in diameter) were observed. The presence of these cylinder-like objects was not an effect of the filtration, the dilution, or the batch (see Fig. S3, ESI†). Although nanofibrils were previously observed in thin films of PEDOT:PSS treated with acid,31 to the best of our knowledge, only one other cryo-TEM experiment on PEDOT:PSS dispersion (PH1000) also showed nanofibrils, but was not discussed further.35
To confirm the shape of the objects, we performed SAXS measurements on the PH1000 dispersion at different concentrations (see Fig. 2). A single peak was observed in the 0.01 Å−1 < q < 0.1 Å−1 range, at a position that varies with the concentration. Interestingly, in the low-q range, (q < 0.01 Å−1), the intensity follows a q−1 power law for all concentrations, indicating the presence of elongated objects. Moreover, comparison of the higher-q data (q > 0.01 Å−1) with a cylinder model (implemented by the NIST data analysis library29) yielded a mean fibril diameter D = 1.6 nm, with a relative polydispersity σD/D = 0.55. Visual comparison with a flexible cylinder model allows us to conclude that the objects are relatively stiff, with a persistence length above 75 nm (see Fig. S2B, ESI†).
To confirm the 1D nature of the objects, we also studied the evolution of the structure factor S(q), which describes the spatial correlation of particle positions (see Fig. S2A, ESI†). Assuming a regular arrangement of infinite parallel cylinders with a typical distance between neighbors d (corresponding to 2π/qmax), the volume fraction ϕ is proportional to π R2/d2 and the distance d varies like d ∼ ϕ−1/2. The plot in Fig. 2B shows the experimental evolution of d against the volume fraction ϕ, which does indeed follow a power law very close to ϕ−1/2. Extrapolation to ϕ = 1 (no more solvent, so the cylinders are in contact with each other), yields an estimate for the diameter: D ≈ d (ϕ = 1) = 2 nm (see Fig. 2B, squares and solid line). This extrapolated diameter is in good agreement with the fibril thickness estimated from the form factor. The SAXS data of Yuk and coworkers,35 who prepared PEDOT:PSS inks with various concentrations of PH1000 by lyophilization and redispersion, are also in excellent agreement with our analysis (Fig. 2B, open dots and dashed line). We also show the data of Murphy et al.33 and Takano et al.34 All these data are consistent with our findings and follow the same d ∼ ϕ−1/2 dependence.
The slight difference in diameter between cryo-TEM and SAXS could be due to the resolution limit in cryo-TEM (especially for such low contrast and such strong defocus), but might also originate in a non-homogeneous fibril structure, e.g. with a more concentrated PEDOT core and a 3–4 nm loose PSS shell.34
Although the presence of fibrils in the dispersion is a novel result, discussing the different structural models of the literature on the PEDOT:PSS dispersion is not the purpose of this work. However, our experimental data are consistent and support the formation mechanism of a fibrillar 3D network (see below).
The change of structure upon acidification of the PEDOT:PSS dispersion was followed by cryo-TEM. Fig. 1D shows the cryo-TEM image of the acidified dispersion (at a very low concentration <5. 10−3 mol L−1, to prevent the gelation) which is composed of very long fibrils (≫150 nm) of a mean diameter of 3 ± 1 nm. The fibrils, seen in Fig. 1D, differ from the ones seen in the stock dispersion (Fig. 1C). They exhibit a higher persistence length (>100 nm) than in the dispersion and appear somewhat more contrasted and longer. In some cases, we can observe two intertwined fibrils forming a fiber with a slightly larger diameter. The fibers tend to entangle very easily even at high dilution rate (100 times).
To reveal the inner structure of the final hydrogel, cryo-scanning electron microscopy (cryo-SEM) was performed by quickly dipping the hydrogel in liquid ethane. Fig. 1E depicts the fibrillar morphology of the hydrogel. This 3D network is composed of an entanglement of thick fibers (13 ± 4 nm, mean diameter and standard deviation) and voids (10–50 nm wide). The fiber-like structure of the hydrogel was also confirmed by SAXS analysis (displayed in Fig. S5, ESI†). In the low-q range, (q < 0.01 Å−1), the intensity follows a q−1 power law, typical of an elongated object. The quantitative fit with a cylinder model (as described above) yielded a mean fibril diameter D = 2 nm, with a relative polydispersity σD/D = 0.55. Therefore, we suggest that unique fibrils, 2 to 3 nm in diameter, formed in the acidified dispersion, associate into thicker ones due to the strong π–π interactions between the PEDOT chains (Fig. S3C, ESI†), resulting in a robust 3D network.
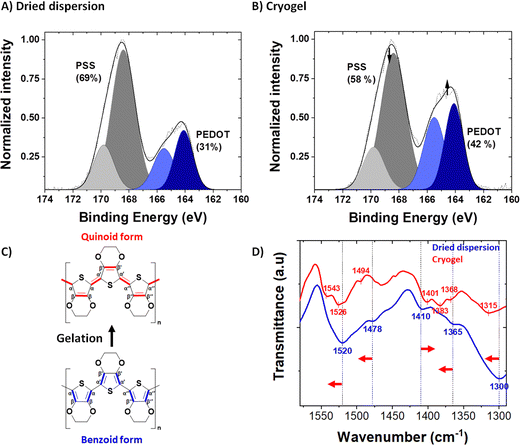
The syneresis discussed above implies a modification of the polymer chains packing (confirmed by microscopy) and/or a rearrangement between PEDOT and PSS upon acid treatment. The PEDOT to PSS ratio before and after acid treatment was followed by XPS spectroscopy, in the S 2p XPS spectra of the dried dispersion (Fig. 3A) and the dried gel (Fig. 3B). Both PEDOT and PSS contain one sulfur atom per repeat unit: within the thiophene ring for PEDOT and in the sulfonate moiety for PSS. Due to their different chemical environment, their binding energies are different, and it is possible to discriminate their XPS signature peaks: a spin-orbit doublet at 164.3 and 165.5 eV binding energy for the former and a spin-orbit doublet peak at 168.3 and 169.5 eV binding energy for the latter.36,37 The intensity ratio between the PSS and PEDOT signals gives the sulfonate/thiophene unit ratio (RS/T). This molar ratio dropped from 2.22, for PH1000 dispersion, to 1.38, for dried gels, indicating partial protonation and removal of PSS during gelation (i.e., acid treatment and rinsing processes as seen in Fig. S4, ESI†).
The composition of the aqueous supernatant of the gel was also investigated by UV-Visible spectroscopy. We observed a characteristic peak at 262 nm, attributed to the π–π* electron transition for the benzene ring of PSS38 (see Fig. S4, ESI†). The presence of PSS in the supernatant, correlated with the XPS measurements, suggests that an excess of unbound PSS was partly released from the PEDOT:PSS complex into the acidic medium.
In order to probe structural changes at a molecular scale, we followed the Fourier transform infra-red (FTIR) spectra of PEDOT:PSS before and after gelation (i.e., in the dried dispersion and the dried gel, blue and red spectra respectively, at 1600-1300 cm−1) in Fig. 2D. The entire FTIR spectrum is available in Fig. S6 (ESI†). In the dried dispersion, the band at 1300 cm−1 is due to the symmetric Cα–Cα′ stretching between the thiophene rings. After gelation, this vibrational band shifted to 1315 cm−1. Similarly, Cβ–Cβ′ stretching vibration band shifted from 1365 cm−1 to 1368 cm−1 (with a doublet appearing at 1383 cm−1). The Cα![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ asymmetric band (and its shoulder) is located at 1520 cm−1 (1478 cm−1 for the shoulder) for the PH1000 dispersion sample and shifted after gelation to higher wavenumber at 1526 cm−1 (1494 cm−1 for the shoulder). A new peak also appeared at 1543 cm−1. Conversely, the band corresponding to C
Cβ asymmetric band (and its shoulder) is located at 1520 cm−1 (1478 cm−1 for the shoulder) for the PH1000 dispersion sample and shifted after gelation to higher wavenumber at 1526 cm−1 (1494 cm−1 for the shoulder). A new peak also appeared at 1543 cm−1. Conversely, the band corresponding to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C symmetric stretching shifted to lower wavenumbers from 1410 cm−1 to 1401 cm−1. These findings correlated well with the conformational changes observed by Raman spectroscopy after acidification of the PH1000 dispersion14 and also with the variation of FTIR peaks of PEDOT:Tos with pH.39
C symmetric stretching shifted to lower wavenumbers from 1410 cm−1 to 1401 cm−1. These findings correlated well with the conformational changes observed by Raman spectroscopy after acidification of the PH1000 dispersion14 and also with the variation of FTIR peaks of PEDOT:Tos with pH.39
Splitting of the Cβ–Cβ stretching and Cα![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cβ asymmetric stretching vibrational bands after gelation suggest that the gels are not composed of a unique pure conformation, but of a mixture of both quinoid and benzoid forms. Hence, we suggest that during gelation the conformation of PEDOT changes from a dominant benzoid to a dominant quinoid structure.
Cβ asymmetric stretching vibrational bands after gelation suggest that the gels are not composed of a unique pure conformation, but of a mixture of both quinoid and benzoid forms. Hence, we suggest that during gelation the conformation of PEDOT changes from a dominant benzoid to a dominant quinoid structure.
Below, we attempt a description of the gelation mechanism of PEDOT:PSS on addition of sulfuric acid.
We demonstrated that gelation induces modifications of the PEDOT:PSS system at different scales. Starting from the thin fibrils present in the dispersion state, fibrils of higher persistence length and composed of more ordered PEDOT stacks distributed along PSS chains are formed upon acidification. The acidification during gelation participates in the partial removal of PSS (upon protonation and further solubilization of PSSH). The addition of sulfuric acid may lower the repulsive forces between the particles and destabilize the dispersion. Neutralizing a fraction of the PSS chains weakens their coulombic interactions with PEDOT, resulting in a conformation change of the freed PEDOT chains towards their quinoidal and more linear form. The attraction between fibrils, at close contact, becomes even stronger with higher potential π–π interactions. Thus, the objects assemble mainly through π-stacking and van der Waals interactions. The resulting fibrils tend to entangle into thicker ones and form a robust 3D fibrillar network.
3.2. From the hydrogel to the dried gel: controlling the porous structure by freeze-drying
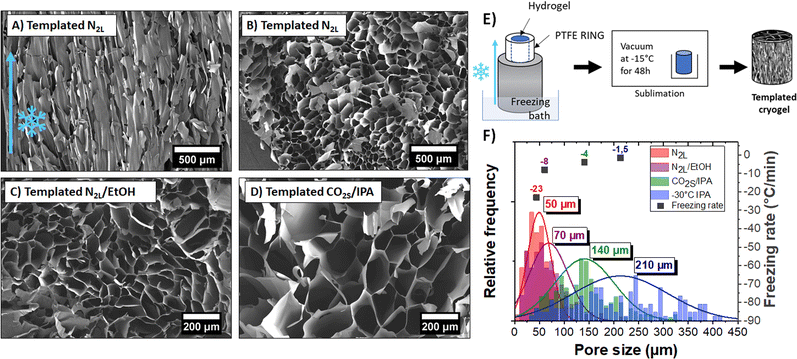
It is well known in the freeze-drying community that this process induces modifications of the initial gel structure. The solvent (retained in the gel) crystallizes during the freezing step, serving as a template for the 3D polymer network. The frozen solvent is then sublimated, leaving behind a cryogel.18 A cryo-SEM experiment allowed us to investigate the change of morphology induced by solvent crystal growth. The rapid freezing of the sample with liquid ethane allowed the formation of amorphous ice (as discussed above). However, if the sample is large enough (>1 mm2), a temperature gradient can occur, between the outer part (that is in direct contact with the liquid ethane) and the core of the sample. It is therefore possible to observe the network modified by different stages of ice crystallization on the same sample. The cryo-SEM images of the hydrogel dipped vertically into liquid ethane are shown in Fig. 4A. The outer part of the frozen hydrogel (in close contact with liquid ethane) is at the bottom of the image, whereas the core of the gel (at slightly higher temperature) is at the top of the image. The schematic in Fig. 4B illustrates how the sample was frozen.
Three distinct areas are clearly identified. Area 1 was the first in contact with liquid ethane. As the freezing rate was very high, water did not have enough time to crystallize and the native structure of the gel could be preserved, i.e., a mesoporous 3D network made of entangled PEDOT:PSS fibers (as discussed previously). As we go deeper inside the gel, the freezing rate decreases, allowing ice crystals to form. Area 2 (represented in purple on schematic Fig. 3B) shows the transition between two types of structures. At the bottom left of the SEM image, the fibrillar structure of the native gel is still present, whereas porous hexagons are clearly defined at the top right corner of the image. This second channel-like structure is due to the crystallization of ice into the confined space of the network. The morphology of the pores is templated by the ice crystals. In Area 3 (red part on the schematic Fig. 4B), a honeycomb-like macroporous structure starts to develop. It is clear from these observations that ice crystals serve as a template for the porous structure. The pore walls are composed of densely stacked fibers of the native gel structure (see Fig. 4D), pushed aside by the ice crystals during the freezing step, while the size and shape of the pores are defined by the ice crystals. Water crystals usually grow in a dendritic morphology.18 However, confinement due to the fibrillar network tends to constrain dendrite formation, resulting in this hexagonal columnar morphology.
The quenched cryogel (obtained by freezing the hydrogel in liquid nitrogen and further drying it under high vacuum) displayed a similar channel-like structure separated by dense walls. Even though the channels appear locally aligned, the sample is composed of multiple oriented grains (of a few mm3), as seen in Fig. 1F. These different orientations are due to the uncontrolled ice crystal growth as the tube is plunged quickly into liquid nitrogen and the cold source is isotropic. Due to the pyrex vial surrounding the sample, ice crystal formation initiates on multiple points in contact with the container walls, resulting in different pore orientations.
With this method, cm-thick macroporous PEDOT:PSS samples can be obtained but the pores are randomly aligned. However as compared with the directly lyophilized PEDOT:PSS dispersion structure (see Experimental part and Fig. S1, ESI†), freeze-drying the PEDOT:PSS hydrogel provides a more controlled porous structure with better defined pore shape and size. Our understanding of the formation mechanism of the macroporous structure from the gel phase allowed us to push further the control of pore size and pore alignment within the samples. In the following, we applied the ice-templating method to control the alignment of the pores within the samples.
Owing to the controlled nucleation and temperature gradient along the vertical direction, crystals grew from the bottom to the top of the gel, resulting in an anisotropic orientation of the pores throughout the sample. A SEM image of the vertically cut cryogel (shown in Fig. 5A) highlights the anisotropic orientation of the channels along the freezing direction. The pore length is challenging to measure, but the channels seem to extend along the full sample thickness (>1 cm). The SEM image of a horizontally cut cryogel (in Fig. 5B) shows a quite homogeneous honeycomb-like structure on a large scale. We can also note that the lateral sample surface is undistorted due to mechanical constraints from the PTFE cylinder.
Interestingly, the pores had a larger mean diameter (∼50 μm) than the ones obtained with the quenched freezing method described previously (24 μm). As mentioned above, the pore size depends on the size of the ice crystals and thus on the freezing rate (and freezing temperature). Here, as the sample is not directly in contact with liquid nitrogen (but on top of an aluminum rod), the freezing rate is slower (−23 °C min−1) than for quenched freezing (−54 °C min−1).
We demonstrated the possibility to control both the orientation and size of the pores by mastering nucleation and freezing rate. Different ice-templated cryogels with mean pore size varying between 50 to 210 μm were produced by only changing the temperature of the freezing bath. Horizontal cuts of those ice-templated PEDOT:PSS cryogel samples are shown in Fig. 5B–D. Fig. 5F represents a histogram of pore sizes obtained with the ice-templating method at different cooling temperatures. The colder the bath, the colder the freezing temperature and higher the freezing rate, and thus the smaller the pore size. Also, freezing above −50 °C (temperature of the bath) leads to a high dispersion of pore size (210 ± 100 μm).
The pore wall thickness also changed with the freezing rates (see Fig. S7, ESI†). At constant sample density, larger ice crystals push aside more PEDOT:PSS fibers, forming thicker pore walls (∼300 nm to 3 μm, depending on the freezing bath temperature).
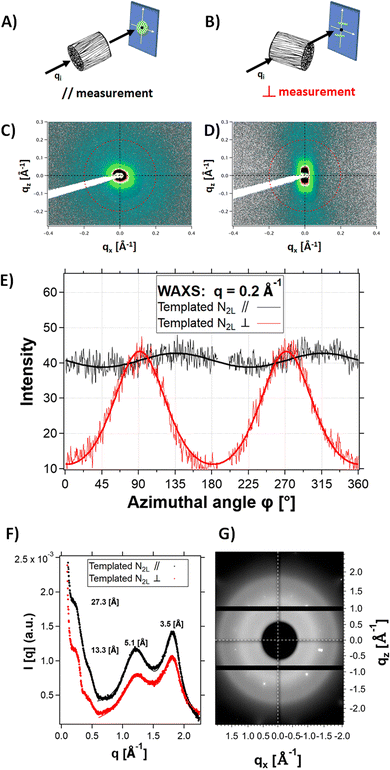
X-ray scattering experiments on N2L templated samples revealed strong structural anisotropy. Fig. 6 shows the 2D detector images of the sample in the mid-angle range, with the beam aligned parallel to the channels (Fig. 6A and C) or perpendicular to them (Fig. 6B and D). Fig. 6E shows the comparison of the intensity profiles for the parallel and perpendicular configurations, as a function of the azimuthal angle. In the perpendicular configuration, the signal scattered at q = 0.2 Å−1 (red line) was reinforced at ϕ = 90° and 270° (along the normal to the channels). In the parallel configuration, the modulation of the signal (black line) is negligible. This result highlights the orientation anisotropy along the channels (i.e. the freezing direction) at a q position corresponding to the fibril-fibril distance within the pore walls (q = 0.23 Å−1, i.e., a d spacing of 27.3 Å). We therefore suggest that polymer fibers tend to align preferentially parallel to the channels, along the freezing direction (with the unidirectional ice crystal growth). On the cm-scale sample thickness, the ice crystals growth is probably not homogeneous, leaving behind (after sublimation) channels (and thus pore walls) that are not uniformly aligned. This could explain the relatively broad angular dispersion (35° HWHM) of the peaks.
No anisotropy (see the 2D detector images of the sample in the wide-angle range, Fig. 6G) was observed at higher q-range (q > 1 Å−1) in the perpendicular configuration. In particular, the two scattering features at 1.23 Å−1 and 1.8 Å−1 are isotropic. Since they are attributed to ordering of the PSS and PEDOT π–π stacking,40 respectively, this suggests lack of alignment of the polymer chains within the fibers.
| Material | Density (g cm−3) | Porosity (%) | PEDOT: PSS ratio (%mol) | σ app (S cm−1) | K (mW m−1 K−1) |
|---|---|---|---|---|---|
| Lyophilized dispersion | 0.02 | 98 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 69 |
0.05 ± 0.01 | 59 ± 2 |
| Quenched cryogel | 0.03 | 97 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
2.0 ± 0.5 | 42 ± 1 |
| N2L templated | 0.03 | 97 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
1.3 ± 0.2 | 37 ± 2 |
| N2L/EtOH templated | 0.03 | 97 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
1.2 ± 0.1 | 41 ± 1 |
| CO2s/IPA templated | 0.03 | 97 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
1.0 ± 0.2 | 47± 2 |
| −30 °C IPA | 0.03 | 97 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
0.8 ± 0.2 | 46 ± 2 |
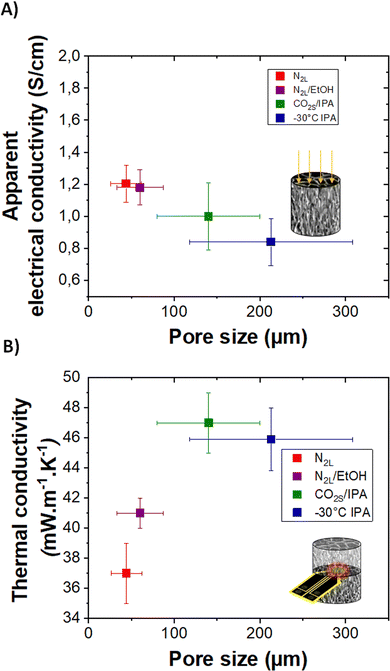 | ||
| Fig. 7 (A) and (B) Apparent electrical conductivity and thermal conductivity of templated cryogels with different pore sizes, respectively. | ||
Although highly porous (>0.97 volume fraction porosity) and cm-thick, all cryogels are electrically conducting. The highest value of 2 ± 0.5 S cm−1 is obtained for the quenched N2L cryogels while the lowest one, 0.8 ± 0.2 S cm−1, corresponds to the templated −30 °C IPA cryogel. The electrical conductivity values measured on the cryogels, appearing low as compared to our reference PEDOT:PSS values in thick film (see ESI†), correspond to apparent electrical conductivity since they take into account the porosity of the samples.
The apparent electrical conductivity decreases slightly with the increase in pore size (and in pore wall thickness, see Fig. S7, ESI†). This evolution is difficult to explain. One hypothesis is that at lower freezing rate (cooling bath temperature closer to the melting temperature of ice), the nucleation and ice crystal growth are less homogeneous. The fibers pushed aside the pore walls are likely more disordered for the −30 °C IPA than for the N2L cryogels. In addition, at higher freezing rate, the pores are smaller and there are more wall intersections leading to a better percolation between the channels.
As preliminary results, we have also measured the mesoscopic conductivity at the level of an individual tube (i.e. at the scale of a single pore wall). These measurements were done in a SEM chamber using a four-probe station equipped with high precision robots (see experimental part and ESI†). Considering a pore wall average thickness of 500 nm, the conductivity of the pore wall was estimated at 62 ± 3 S cm−1 (in the van der Pauw geometry). This value was obviously highly dependent on the wall thickness, which appeared to vary by a factor of two to three across the tube.
Further nanoprobing measurements are needed to conclude on the mean value of conductivity of the pore walls. Nevertheless, these preliminary results strongly suggest that the cryogel formation (ice-templating) preserves the electrical characteristics of the PEDOT:PSS material and that the low apparent electrical conductivity of the cryogel (measured in the macroscopic state) is indeed mainly due the porous morphology.
Using these unique nanoprobing measurements, in a four-probe collinear set-up, we also looked for possible anisotropy of electrical charge transport at the scale of a single tube (as seen in Fig. 8). (The macroscopic measurements along the longitudinal or the radial axes of the templated cryogels, not shown here, did not reveal a clear trend in terms of anisotropy of the electrical transport within the 3D network). The four probes were placed on a tube wall, in a collinear arrangement, either parallel or perpendicular to the axis of the tube (along or perpendicular to the freezing direction). Typical V(I) curves and linear fits (Fig. 8D and E) yielded the following average sheet resistances Rsheet,par = 19 ± 2 Ω and Rsheet,perp = 153 ± 102 Ω for the parallel and the perpendicular orientations respectively. Thus, charge transport appears to be much higher along the tube axis (i.e. the freezing direction) than in the perpendicular direction. Further analysis is needed to conclude on the correlation between structural anisotropy (the PEDOT:PSS fibers tend to align preferentially parallel to the channels, vide infra) and charge transport anisotropy.
Thermal transport was also investigated. The high porosity gives cryogels very good thermal insulation properties. The thermal conductivity (determined by the transient plane source method, see the experimental part) ranges between 37 and 47 mW m−1 K−1. These values are almost eight times lower than the one reported in the literature for dense PEDOT:PSS (300 mW m−1 K−1),41 and three to four time lower than the calculated lattice thermal conductivity value of PEDOT.42 The thermal conductivity of the cryogels is lower than that of the lyophilized dispersion (59 mW m−1 K−1), probably due to a reduction in lattice contribution owing to better pore structuration and sharper solid/gas interfaces. Interestingly, the pore sizes, although in the macroporous range, impact the thermal properties. The thermal conductivity increases with the pore size from 50 to 140 μm and then seems to reach a plateau. In the porous materials produced herein, the lattice contribution to the thermal conductivity should mainly be due to heat conduction through the gas and the solid (convection and radiation phenomenon can be neglected at room temperature for cm-size samples). For pore sizes above the mean free path of air molecules (70 nm), the gas conduction should not be affected (value very close to the thermal conductivity of air ∼25 mW m−1 K−1).43,44
For electrically conducting samples, according to Wiedemann–Franz law, there should also be an electronic contribution to the thermal conductivity. Considering the low apparent electrical conductivity of the samples and its very modest variation with pore size, the electronic contribution is almost negligible compared to the lattice contribution. Therefore, the variation of thermal conductivity with pore size could be mainly related to scattering effects due to texturing of pore walls (composed of fibers) as also discussed for ice-templated cellulose-based macroporous materials.22 Thicker pore walls and random orientation of the polymer fibers composing the walls may result in a smaller thermal resistance, increasing the thermal conductivity. Further studies are needed to fully understand all the mechanisms involved in the reduction of thermal conductivity down to 37 mW m−1 K−1. As a comparison, a PEDOT:PSS aerogel with a mesoporous fibrillar structure (obtained by gelation followed by supercritical drying) showed much higher thermal conductivity (65 mW m−1 K−1).4 Finally, following the study on heat transport properties of anisotropic cellulose foams,22 anisotropic thermal conductivity could be expected in the templated cryogels. We are currently working on obtaining a reliable radial thermal diffusivity value on our oriented samples which is needed to measure the thermal conductivity in the anisotropic mode.
Conclusion
The self-assembly mechanism of PEDOT:PSS from the dispersion state to a controlled macroporous structure has been studied. A combination of SAXS and cryo-TEM revealed that the PEDOT:PSS commercial dispersion contains fibrils that intertwine and self-assemble upon the addition of sulfuric acid to form a robust 3D fibrillar hydrogel. Cryo-SEM conclusively showed how the growth of ice crystals pushes apart the fibers to form a honeycomb-like structure. Controlling the direction of freezing, and thus the growth of the crystals, provided anisotropic porous samples on a cm-scale. The cooling rate influenced the growth of the crystals, and thus the size of the pores. Unique mesoscopic electrical transport properties at the scale of a pore wall revealed that the formation of the cryogels (by ice-templating) preserves the electrical characteristics of the PEDOT:PSS material. The low macroscopic (apparent) electrical conductivity measured on the bulk samples reflects their porous structure. Preliminary results showed anisotropic electrical conductivity within the pore wall. Altogether, we devised a well-controlled process to produce electrically conducting and thermally insulating PEDOT:PSS samples with a well-defined macroporous structure on cm scale. These hierarchically controlled and multifunctional materials open the door for different applications such as thermoelectrics, solar steam generators, or ion diffusion membranes. Such oriented macroporous scaffolds are also promising candidate for 3D cell culture and tissue engineering.Author contributions
Q.W. fabricated most of the samples and characterized their electrical and thermal transport properties, analyzed the data and provided a first draft of the manuscript. N.H. and E.G., during their master thesis, optimized the ice-templating method and provided the gels with tunable pore sizes. G.F. performed the X-ray scattering measurements on DiffériX facility. D.C. performed X- ray scattering measurements at the synchrotron. J.C. and D.C. analyzed the X-ray scattering data. V.P. performed the XPS measurements and helped in their analyses. A.C. performed the cryo-SEM measurements, trained and provided technical support on SEM measurements and image analyses to Q.W., N.H. and E.G. M.S. performed (cryo-)TEM experiments and corresponding analysis. E.D., V.M. and L.S. performed the mesoscopic transport measurements and corresponding analysis. L.B. conceived the original idea and supervised the project, aided in interpreting the results and finalized the manuscript with the input of D.C. All authors discussed the results and commented on the final manuscript.Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
Financial support by ANR JCJC 2019 (BODYTEG), the Région Grand Est 2020 and the French Microscopy Society (SFμ) are gratefully acknowledged. E. D., V. M. and L. S. acknowledge the National Research Agency (ANR) under the program “Investissements d’avenir”-Mat-Light 4.0 (Grant No. ANR-21-EXES-0012), the Région Grand Est and European fund FEDER through the “NanoteraHertz” Project. The CarMac platform, PLAMICS microscopy facility and DiffériX x-ray facility of the ICS are acknowledged for technical support and the use of their equipment. The Institute Carnot MICA is also thanked for the purchase of the Dectris Pilatus 3R detector. We acknowledge SOLEIL for the provision of synchrotron radiation facilities and we thank Thomas Bizien for assistance in using beamline SWING for the SAXS and WAXS experiments. Martin Brinkmann and C3-Fab platform (ICube) are acknowledged for providing access to the collinear four-probe setups. Patrick Allgayer, Christophe Lambour, Laurent Hermann and Jean-Philippe Lamps are thanked for technical support. Sylvain Deville's fascination with freezing has inspired this work.References
- W. He and X. Zhang, in Conducting Polymer Aerogels, Conducting Polymers, ed. F. Yilmaz, InTech, 2016, pp. 49–72 Search PubMed.
- Q. Weinbach, C. B. Nielsen and L. Biniek, Multi length scale porosity as a playground for organic thermoelectric applications, J. Mater. Chem. C, 2021, 9, 10173 RSC.
- Y. Liao, H. Wang, M. Zhu and A. Thomas, Efficient Supercapacitor Energy Storage Using Conjugated Microporous Polymer Networks Synthesized from Buchwald–Hartwig Coupling, Adv. Mater., 2018, 30, 1705710 CrossRef PubMed.
- Q. Weinbach, S. V. Thakkar, A. Carvalho, G. Chaplais, J. Combet, D. Constantin, N. Stein, D. Collin and L. Biniek, Efficient Control of a Mesoporous Fibrillar PEDOT:PSS Aerogel Structure for Promising Thermoelectric Applications, Front. Electron. Mater., 2022, 2, 875856 CrossRef.
- H. Bildirir, V. G. Gregoriou, A. Avgeropoulos, U. Scherf and C. L. Chochos, Porous organic polymers as emerging new materials for organic photovoltaic applications: Current status and future challenges, Mater. Horiz., 2017, 4, 546 RSC.
- P. Mu, W. Bai, Z. Zhang, J. He, H. Sun, Z. Zhu, W. Liang and A. Li, Robust aerogels based on conjugated microporous polymer nanotubes with exceptional mechanical strength for efficient solar steam generation, J. Mater. Chem. A, 2018, 6, 18183–18190 RSC.
- S. Han, T. P. Ruoko, J. Gladisch, J. Erlandsson, L. Wågberg, X. Crispin and S. Fabiano, Cellulose-Conducting Polymer Aerogels for Efficient Solar Steam Generation, Adv. Sustainable Syst., 2020, 4, 2000004 CrossRef CAS.
- Z. Saadatnia, S. G. Mosanenzadeh, E. Esmailzadeh and H. E. Naguib, A High Performance Triboelectric Nanogenerator Using Porous Polyimide Aerogel Film, Sci. Rep., 2019, 9, 1370 CrossRef PubMed.
- K. Sun, S. Zhang, P. Li, Y. Xia, X. Zhang, D. Du, F. H. Isikgor and J. Ouyang, Review on application of PEDOTs and PEDOT:PSS in energy conversion and storage devices, J. Mater. Sci.: Mater. Electron., 2015, 26, 4438–4462 CrossRef CAS.
- B. Lu, H. Yuk, S. Lin, N. Jian, K. Qu, J. Xu and X. Zhaao, Pure PEDOT:PSS hydrogels, Nat. Commun., 2019, 10, 1043 CrossRef PubMed.
- R. Maeda, Y. Shinohara, H. Kawakami, Y. Isoda, I. Kanazawa and M. Mitsuishi, The Conducting Fibrillar Networks of a PEDOT:PSS Hydrogel and an Organogel Prepared by the Gel-film Formation Process, Nanotechnology, 2020, 32, 135403 CrossRef.
- S. Tang, X. Zhang, J. Fan, B. Li, Z. Li, C. Wang, H. Li, P. Zhang and J. Zhou, Fibrillation of well-formed conductive aerogel for soft conductors, Appl. Mater. Today, 2022, 26, 101399 CrossRef.
- X. Wang, P. Liu, Q. Jiang, W. Zhou, J. Xu, J. Liu, Y. Jia, X. Duan, Y. Liu, Y. Du and F. Jiang, Efficient DMSO-Vapor Annealing for Enhancing Thermoelectric Performance of PEDOT:PSS-Based Aerogel, ACS Appl. Mater. Interfaces, 2019, 11, 2408–2417 CrossRef CAS PubMed.
- B. Yao, H. Wang, Q. Zhou, M. Wu, M. Zhang and C. Li, Ultrahigh-Conductivity Polymer Hydrogels with Arbitrary Structures, Adv. Mater., 2017, 29, 1700974 CrossRef PubMed.
- G. Chen, R. Rastak, Y. Wang, H. Yan, V. Feig, Y. Liu, Y. Jiang, S. Chen, F. Lian, F. Molina-Lopez, L. Jin, K. Cui, J. W. Chung, E. Pop, C. Linder and Z. Bao, Strain- and Strain-Rate-Invariant Conductance in a Stretchable and Compressible 3D Conducting Polymer Foam, Matter, 2019, 1, 205 CrossRef.
- M. P. Gordon, E. W. Zaia, P. Zhou, B. Russ, N. E. Coates, A. Sahu and J. J. Urban, Soft PEDOT:PSS aerogel architectures for thermoelectric applications, J. Appl. Polym. Sci., 2017, 134, 44070 CrossRef.
- M. A. Shahbazi, M. Ghalkhani and H. Maleki, Directional Freeze-Casting: A Bioinspired Method to Assemble Multifunctional Aligned Porous Structures for Advanced Applications, Adv. Eng. Mater., 2020, 22, 2000033 CrossRef CAS.
- S. Deville, Freezing Colloids: Observations, Principles, Control, and Use, ed. B. Derby, Springer International Publishing, Cham, 2017 Search PubMed.
- M. Matsumoto, S. Saito and I. Ohmine, Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing, Nature, 2002, 416, 409 CrossRef CAS.
- R. Geidobler and G. Winter, Controlled ice nucleation in the field of freeze-drying: Fundamentals and technology review, Eur. J. Pharm. Biopharm., 2013, 85, 214 CrossRef CAS PubMed.
- S. Stokols and M. H. Tuszynski, Freeze-dried agarose scaffolds with uniaxial channels stimulate and guide linear axonal growth following spinal cord injury, Biomaterials, 2006, 27, 443–451 CrossRef CAS PubMed.
- V. Apostolopoulou-Kalkavoura, P. Munier, L. Dlugozima, V.-L. Heuthe and L. Bergström, Effect of density, phonon scattering and nanoporosity on the thermal conductivity of anisotropic cellulose nanocrystal foams, Sci. Rep., 2021, 11, 18685 CrossRef CAS PubMed.
- X. Zhang, C. Li and Y. Luo, Aligned/unaligned conducting polymer cryogels with three-dimensional macroporous architectures from ice-segregation-induced self-assembly of PEDOT-PSS, Langmuir, 2011, 27, 1915 CrossRef CAS PubMed.
- A. M. D. Wan, S. Inal, T. Williams, K. Wang, P. Leleux, L. Estevez, E. P. Giannelis, C. Fischbach, G. G. Malliaras and D. Gourdon, 3D conducting polymer platforms for electrical control of protein conformation and cellular functions, J. Mater. Chem. B, 2015, 3, 5040 RSC.
- J. Zhang, X. Fan, X. Meng, J. Zhou, M. Wang, S. Chen, C. W. Bielawski and J. Geng, Ice-Templated Large-Scale Preparation of Two-Dimensional Sheets of Conjugated Polymers: Thickness-Independent Flexible Supercapacitance, ACS Nano, 2021, 15, 8870 CrossRef CAS PubMed.
- A. G. Guex, J. L. Puetzer, A. Armgarth, E. Littmann, E. Stavrinidou, E. P. Giannelis, G. G. Malliaras and M. M. Stevens, Highly porous scaffolds of PEDOT:PSS for bone tissue engineering, Acta Biomater., 2017, 62, 91–101 CrossRef CAS PubMed.
- J. Dubochet, M. Adrian, J.-J. Chang, J.-C. Homo, J. Lepault, A. McDowall and P. Schultz, Cryo-electron microscopy of vitrified specimens, Q. Rev. Biophys., 1988, 21, 129–228 CrossRef CAS PubMed.
- C. Efthymiou, M. A. K. Williams and K. M. McGrath, Revealing the structure of high-water content biopolymer networks: Diminishing freezing artefacts in cryo-SEM images, Food Hydrocolloids, 2017, 73, 203 CrossRef CAS.
- S. R. Kline, Reduction and analysis of SANS and USANS data using IGOR Pro, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- S. Yilmaz, The geometric resistivity correction factor for several geometrical samples, J. Semicond., 2015, 36, 082001 CrossRef.
- N. Kim, S. Kee, S. H. Lee, B. H. Lee, Y. H. Kahng, Y. R. Jo, B.-J. Kil and K. Lee, Highly conductive PEDOT:PSS nanofibrils induced by solution-processed crystallization, Adv. Mater., 2014, 26, 2268 CrossRef CAS PubMed.
- Y. Xia, K. Sun and J. Ouyang, Solution-processed metallic conducting polymer films as transparent electrode of optoelectronic devices, Adv. Mater., 2012, 24, 2436 CrossRef CAS PubMed.
- R. J. Murphy, K. M. Weigandt, D. Uhrig, A. Alsayed, C. Badre, L. Hough and M. Muthukumar, Scattering Studies on Poly(3,4-ethylenedioxythiophene)-Polystyrenesulfonate in the Presence of Ionic Liquids, Macromolecules, 2015, 48, 8989 CrossRef CAS.
- T. Takano, H. Masunaga, A. Fujiwara, H. Okuzaki and T. Sasaki, PEDOT nanocrystal in highly conductive PEDOT:PSS polymer films, Macromolecules, 2012, 45, 3859 CrossRef CAS.
- H. Yuk, B. Lu, S. Lin, K. Qu, J. Xu, J. Luo and X. Zhao, 3D printing of conducting polymers, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- X. Crispin, S. Marciniak, W. Osikowicz, G. Zotti, A. W. Denier Van Der Gon, F. Louwet, L. Groenendaal, F. De Schryver and W. R. Salaneck, Stability of Poly (3, 4-ethylene dioxythiophene)– Poly (styrene sulfonate): A Photoelectron Spectroscopy Study, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2561–2583 CrossRef CAS.
- G. Zotti, S. Zecchin, G. Schiavon, F. Louwet, L. Groenendaal, X. Crispin, W. Osikowicz, W. Salaneck and M. Fahlman, Electrochemical and XPS studies toward the role of monomeric and polymeric sulfonate counterions in the synthesis, composition, and properties of poly(3,4-ethylenedioxythiophene), Macromolecules, 2003, 36, 3337 CrossRef CAS.
- N. Su, H. Li, Y. Huang and X. Zhang, Synthesis of Salt Responsive Spherical Polymer Brushes, J. Nanomater., 2015, 2015, 1–7 Search PubMed.
- Z. U. Khan, O. Bubnova, M. J. Jafari, R. Brooke, X. Liu, R. Gabrielsson, T. Ederth, D. R. Evans, J. W. Andreasen, M. Fahlman and X. Crispin, Acido-basic control of the thermoelectric properties of poly(3,4-ethylenedioxythiophene)tosylate (PEDOT-Tos) thin films, J. Mater. Chem. C, 2015, 3, 10616 RSC.
- E. Hosseini, V. O. Vinayaraj Ozhukil Kollath and K. Karan, The key mechanism of conductivity in PEDOT:PSS thin films exposed by anomalous conduction behaviour upon solvent-doping and sulfuric acid post-treatment, J. Mater. Chem. C, 2020, 8, 3982 RSC.
- J. Liu, X. Wang, D. Li, N. E. Coates, R. A. Segalman and D. G. Cahill, Thermal conductivity and elastic constants of PEDOT:PSS with high electrical conductivity, Macromolecules, 2015, 48, 585–591 CrossRef CAS.
- P. S. Floris, C. Melis and R. Rurali, Interplay Between Doping, Morphology, and Lattice Thermal Conductivity in PEDOT:PSS, Adv. Funct. Mater., 2023, 2215125, 1–11 Search PubMed.
- M. Noroozi, M. Panahi-Sarmad, M. Abrisham, A. Amirkiai, N. Asghari, H. Golbaten-Mofrad, N. Karimpour-Motlagh, V. Goodarzi, A. R. Bahramian and B. Zahiri, Nanostructure of Aerogels and Their Applications in Thermal Energy Insulation, ACS Appl. Energy Mater., 2019, 2, 5319–5349 CrossRef CAS.
- V. Apostolopoulou-Kalkavoura, P. Munier and L. Bergström, Thermally Insulating Nanocellulose-Based Materials, Adv. Mater., 2020, 2001839, 1–17 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Direct lyophilization of the PH1000 dispersion; SAXS and cryo-TEM data on the PH1000 dispersion; UV-Visible spectroscopy analysis of the gel supernatant; SAXS data on the hydrogel, IR spectra of the dried dispersion and dried gel; Pore walls thickness measurements; Discussion on electrical conductivity measurements (reference thick film, two contact resistance and van der Pauw measurements). See DOI: https://doi.org/10.1039/d3tc01110k |
| This journal is © The Royal Society of Chemistry 2023 |