Distinct anharmonic characteristics of phonon-driven lattice thermal conductivity and thermal expansion in bulk MoSe2 and WSe2†
Mayanak K.
Gupta
 *ab,
Sajan
Kumar
ab,
Ranjan
Mittal
*ab,
Sajan
Kumar
ab,
Ranjan
Mittal
 *ab,
Sanjay K.
Mishra
ab,
Stephane
Rols
c,
Olivier
Delaire
*ab,
Sanjay K.
Mishra
ab,
Stephane
Rols
c,
Olivier
Delaire
 d,
Arumugum
Thamizhavel
e,
P. U.
Sastry
ab and
Samrath L.
Chaplot
d,
Arumugum
Thamizhavel
e,
P. U.
Sastry
ab and
Samrath L.
Chaplot
 ab
ab
aSolid State Physics Division, Bhabha Atomic Research Centre, Trombay, Mumbai 400085, India. E-mail: mayankg@barc.gov.in; rmittal@barc.gov.in
bHomi Bhabha National Institute, Anushaktinagar, Mumbai 400094, India
cInstitut Laue-Langevin, BP 156, 38042 Grenoble Cedex 9, France
dDepartment of Mechanical Engineering and Materials Science, Duke University, NC 27708, USA
eTata Institute of Fundamental Research, Homi Bhabha Road, Colaba, Mumbai 400005, India
First published on 19th September 2023
Abstract
Using inelastic neutron scattering and X-ray diffraction measurements, together with ab initio and machine-learning molecular dynamics simulations, we bring out the distinct nature of anharmonicity in the phonon spectra of MoSe2 and WSe2 relevant to thermal transport and thermal expansion behaviour. We show that the perturbation method, including 4th-order force constants, is insufficient to capture the temperature-dependent explicit anharmonicity. The Green–Kubo method captures the explicit anharmonicity and reproduces the thermal conductivity (κl) with high fidelity. Our mode-resolved calculation reveals that the major contribution (∼90%) to κl is attributed to a small explicit anharmonicity of low-energy phonons. In contrast, these modes exhibit large positive Grüneisen parameters (implicit anharmonicity), causing the large thermal expansion of the material.
Introduction
Low dimensional materials such as transition-metal dichalcogenides (TMDCs) are known to exhibit interesting electronic, optical and thermodynamic properties and are promising materials for applications across thermoelectrics, transistors, optoelectronics, topological materials, solid lubrication, electrode materials for Mg and Zn batteries, energy storage and photovoltaic devices.1–16 Many TMDCs, such as WSe2, WS2, MoSe2 and MoS2, are considered promising candidates for thermoelectric applications, and comprehensive studies have investigated their electronic, optical and transport properties.2–6,17,18 In particular, WSe2 has been found to exhibit ultralow thermal conductivity in single-layer form.19 These 2D materials are also promising candidates for flexible electronic devices and nano-electromechanical systems due to their ultralow weight, flexibility and high tensile strength.7,8,20–22Limited experimental and theoretical studies exist on the thermal conductivity of TMDCs, and they show discrepancies between different measurements and simulations.10,23–26 P. Jiang et al. measured the anisotropic thermal conductivity of MX2 (M = Mo, W and X = S, Se) using the time-domain thermoreflectance technique, from which they obtained in-plane (out-of-plane) conductivities ∼35 W m−1 K−1 (2.5 W m−1 K−1) and 40 W m−1 K−1 (2.2 W m−1 K−1), in MoSe2 and WSe2, respectively, at room temperature.23 S. Kumar et al. used first-principles calculations and found that the three lowest optical modes for bulk MoSe2 and WSe2 contribute to the lattice thermal conductivity almost as much as the acoustic modes.10 The authors reported in-plane (out-of-plane) thermal conductivity values at a room temperature of ∼57 W m−1 K−1 (∼6 W m−1 K−1) and ∼48 W m−1 K−1 (∼6 W m−1 K−1), for MoSe2 and WSe2, respectively.10 Another theoretical investigation of thermal conductivity by Lindroth et al. on WSe2 and MoSe2 found in-plane and out-of-plane conductivities ∼33 W m−1 K−1 and 4 W m−1 K−1, respectively, for both compounds.24 These calculations were performed with boundary scattering contribution considering a sample size of ∼1 μm. There are many other TMDCs, for which thermal conductivity measurements and simulations show significant variance in their values.23,25–30 Hence, a comprehensive theoretical study exploring different techniques is informative to clarify the underlying physics of the thermal conductivity in these TMDCs and the possible source of error/variance.
Besides the specifics of TMDCs, a microscopic understanding of thermal properties is generally important to design materials for applications. The anharmonic characteristics of phonons are crucial in both thermal transport and thermal expansion behaviour.31,32 For instance, Grüneisen parameters, which estimate phonon energy shifts due to anharmonicity upon expanding volume, are needed to account for thermal expansivity, while the phonon lifetimes, reflecting anharmonic phonon interactions control thermal conductivity.33 Hence, predicting these quantities accurately and rationalizing their microscopic origins can help design materials with tailored properties. Several methods are widely used to compute the lattice thermal conductivity of solids: solving the phonon Boltzmann transport equation (BTE) within perturbation theory,34–36 computing the heat-flux auto-correlation function with equilibrium molecular dynamics,37 or computing the thermal gradient or heat flow using non-equilibrium molecular dynamics,38–40 homogeneous non-equilibrium molecular dynamics,41,42 atomic green function methods,43,44etc. While the perturbation and Green–Kubo methods are among the most popular approaches, all these techniques have certain limitations and advantages.
The lowest-order perturbation theory of the linearized phonon BTE uses the second and third-order force-constants computed around an equilibrium configuration (at T = 0 K) and treats finite temperatures by considering the respective phonon occupation numbers. An extension of this method consists in using renormalized second and third-order force-constants at finite temperature, as obtained from ab initio molecular dynamics (AIMD) simulations, which can extend accuracy to a broader temperature range. However, even at low-T, these methods do not perform well for strongly anharmonic solids where high-order interactions are sizeable. Classical molecular dynamics simulations intrinsically capture all orders of anharmonicity in the interatomic potential, but do not capture the quantum effect at low temperatures. Hence, this approach tends to work best in moderate and high-temperature regimes.
In this manuscript, we calculated the thermal conductivity of MoSe2 and WSe2 by different techniques. We find that the perturbation methods are not satisfactory, and the machine-learning molecular dynamics (MLMD) simulations quantitatively well capture the higher-order anharmonicity. In addition, we measured the temperature dependence of the phonon density of states (DOS) from 313 K to 1098 K using inelastic neutron scattering (INS), which is used to benchmark our simulations and assess the strength of the anharmonicity. Furthermore, we also measured the thermal expansion by X-ray diffraction (XRD) and calculated the same within the quasi-harmonic approximation (QHA). By combining the experiments and simulations, we found that the contribution of the low-energy (low-E) phonons dominates the heat transport as well as the thermal expansion. These low-E phonons show the right magnitude of the phonon lifetimes and the Gruneisen parameters, which quantitatively reproduce the experimental thermal properties. The details about the sample synthesis, INS and XRD measurements, and state-of-the-art computational techniques of the temperature-dependent effective potential (TDEP) and MLMD are given in the ESI.†45
Experimental
A polycrystalline MoSe2 sample has been prepared from a stoichiometric ratio of high purity Mo (in powder form) and Se in small shots. To start with, the Mo powders and selenium shots were thoroughly ground in an agate mortar. The mixed powders were then cold-pressed into pellets. The pellets were then sealed under 10−6 mbar vacuum in a quartz ampoule. The quartz ampoule was then loaded into a resistive heating box-type furnace. The temperature of the furnace was gradually raised at a rate of 15 °C h−1 up to 900 °C and kept at this temperature for about 48 h. Then, the furnace was cooled at a rate of about 20 °C h−1 down to room temperature. We purchased the WSe2 polycrystalline sample from Sigma Aldrich. Powder XRD was performed to characterize the samples and their phase purity. Temperature-dependent X-ray diffraction studies were carried out using an 18 kW rotating Cu anode-based powder diffractometer operating in the Bragg–Brentano focusing geometry with a curved crystal monochromator. Data were collected in the continuous scan mode at a scan speed of 1° per minute and step interval of 0.02°.The inelastic neutron scattering measurements were carried out using a high-flux time-of-flight (IN4C) spectrometer at the Institut Laue Langevin (ILL), France, covering a wide range of scattering angles from 10° to 110°. Thermal neutrons of wavelength 2.4 Å (14.2 meV) were used for the measurements. The orientation-averaged scattering function, S(Q,E), was measured in the neutron energy gain mode with momentum transfer, Q, extending up to 7 Å−1. The polycrystalline samples were loaded into a cylindrical niobium sample holder and mounted in a furnace. INS data were collected with samples heated to 313 K, 498 K, 673 K and 898 K. The neutron-weighted phonon DOS, g(n)(E) was extracted from the measured S(Q, E) using the incoherent one-phonon approximation as follows:
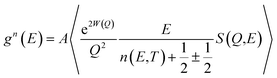 | (1) |
In simulations, one can also compute g(n)(E) from the calculated partial phonon DOS, gk(E), as follows:
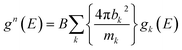 | (2) |
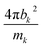 for W, Mo, and Se are 0.025, 0.060, and 0.105 in units of barns per amu, respectively. The neutron scattering lengths for various atoms can be found in ref. 47.
for W, Mo, and Se are 0.025, 0.060, and 0.105 in units of barns per amu, respectively. The neutron scattering lengths for various atoms can be found in ref. 47.
Computational details
Ab initio molecular dynamics
Ab initio molecular dynamics simulations were performed within the density functional theory (DFT) framework implemented in the Vienna Ab initio Simulation Package (VASP).48,49 The simulations used the projector-augmented wave formalism50 and the generalized gradient approximation exchange–correlation functional parameterization by Perdew, Burke, and Ernzerhof.51,52 The DFT-D3 method with the Becke–Johnson damping function was used to account for the van der Waals dispersive interactions between WSe2/MoSe2 layers along the c-axis.53,54 Under ambient conditions, WSe2 and MoSe2 crystallize in a hexagonal structure (space group no. 194, P63/mmc) that contains six atoms in the unit-cell (2 metal atoms and 4 Se) (Fig. S1†45). A 4 × 4 × 1 supercell (96 atoms) was used for AIMD simulations. For DFT calculations, we used a 2 × 2 × 2 k-point mesh generated using the Monkhorst–Pack method55 and a plane-wave energy cut-off of 800 eV. Before AIMD simulations, we fully relaxed the crystal structure with an energy and Hellmann–Feynman force convergence thresholds of 10−8 eV and 10−6 eV Å−1, respectively, and obtained the optimized lattice constants a and c shown in Table S1.†45 The total energy convergence criteria were set to 10−6 eV. The simulations were performed from 100 K to 1000 K in intervals of 100 K within the NVT framework, and the temperatures were controlled using a Nose–Hoover thermostat.55 All the simulations were run for 10–15 ps with a time step of 2 fs.Machine learning molecular dynamics (MLMD)
The DEEP-MD code was used to generate a machine-learning surrogate force field based on a neural network representation.56 Subsequent MLMD simulations were performed with this DEEP-MD potential using LAMMPS.57 The generated force field was tested against several quantities also computed from AIMD (see Fig. S2†45). The phonon spectral energy density (SED) was computed based on MLMD on a 20 × 20 × 10 supercell (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) up to 100 ps, which provides a Q- and E-resolution of 0.05 rlu and 0.05 meV, respectively.
000 atoms) up to 100 ps, which provides a Q- and E-resolution of 0.05 rlu and 0.05 meV, respectively.
Lattice thermal conductivity from MLMD
To compute the thermal conductivity within the Green–Kubo formalism, we performed MLMD simulations on a 24 × 24 × 5 supercell (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280) up to 2 ns with 1 fs time steps at 100 K, 300 K, 500 K and 700 K for both WSe2 and MoSe2. The heat-flux vector, J(t) is given by:
280) up to 2 ns with 1 fs time steps at 100 K, 300 K, 500 K and 700 K for both WSe2 and MoSe2. The heat-flux vector, J(t) is given by: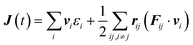 | (3) |
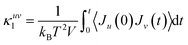 | (4) |
Lattice thermal conductivity simulation from perturbation theory
The lattice thermal conductivity (κl) using the perturbation method was calculated using 2nd, 3rd and 4th order force constants using ShengBTE. These force-constants were evaluated at 0 K. To investigate the effect of temperature on force-constants and subsequently on κl, we have computed κl using 2nd and 3rd-order renormalized force constants (FCs) at 300 K implemented in TDEP.58,59The thermal conductivity, κl is expressed as:
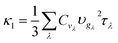 | (5) |
The Cvλ and υgλ can be determined from harmonic phonons, while τλ can be determined by calculating the phonon scattering rate due to three or higher order phonon–phonon scattering as well as from other scattering processes. Here, we only consider the phonon–phonon scattering. The harmonic interatomic force constants (IFCs) are calculated using a 4 × 4 × 1 supercell and a 2 × 2 × 2 Monkhorst–Pack grid within a finite displacement scheme, as implemented in the open-source software package Phonopy.60 The third and fourth-order IFCs were calculated through third order and fourth order packages of ShengBTE, considering up to the third-nearest neighbours. The same supercell size and k-point mesh were used to calculate the third and fourth IFCs by the finite difference method. With these IFCs, the phonon frequencies and velocities are then obtained by diagonalizing the dynamical matrix, and the three-phonon scattering rates are calculated from the iterative solution of the BTE, while four-phonon scatterings were calculated within the relaxation time approximation. The thermal conductivity is solved on a 24 × 24 × 5 q-mesh, sufficient to integrate the BZ (Fig. S3†45). The expressions for all involved scattering rates are described in ref. 34 and 36.
Spectral energy density (SED)
The phonon SED at wavevector![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0071_20d1.gif) and energy E were obtained from MLMD trajectories using the following formalism:61
and energy E were obtained from MLMD trajectories using the following formalism:61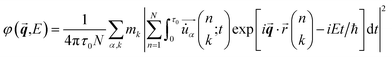 | (6) |
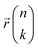 are the mass of the kth atom and its equilibrium position in the nth unit cell, and
are the mass of the kth atom and its equilibrium position in the nth unit cell, and 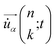 is the velocity of the kth atom in the nth unit cell at time t.
is the velocity of the kth atom in the nth unit cell at time t.
Results and discussion
X-ray diffraction, inelastic neutron scattering and phonon dynamics
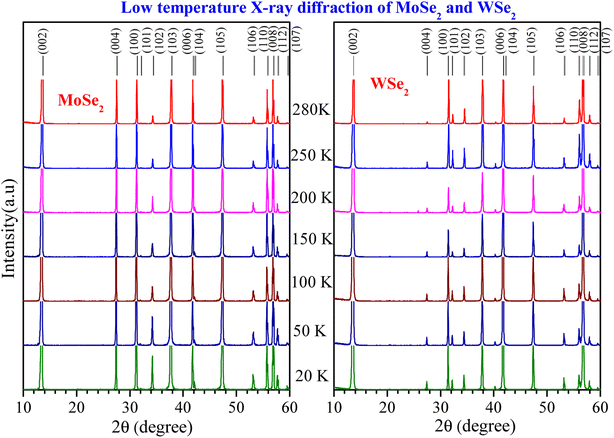
We have performed the temperature-dependent X-ray diffraction measurements on polycrystalline samples of MoSe2 and WSe2 from 20 K to 280 K, as shown in Fig. 1. There are no impurity peaks in the XRD pattern, confirming the single-phase nature of the sample. The XRD peaks are indexed as per the data reported in Powder Diffraction File ICDD JCPDS-PDF 04-004-8782 and 00-038-1388 for hexagonal (space group P63/mmc) MoSe2 and WSe2, respectively.The INS measurements were carried out at five temperatures: 313 K, 498 K, 673 K, 898 K, and 1098 K (Fig. 2 and S4†45). The phonon spectra of MoSe2 and WSe2 extend up to 45 and 40 meV, respectively. The temperature-dependent spectra show several peaks at around 5, 14, 16, 19, 22, 26, and 36 meV in MoSe2 and 5, 13, 15, 24, 27 and 32 meV in WSe2. From our partial DOS calculations, we found that the entire spectral range (0–45 meV) is contributed by both Mo/W and Se dynamics. Interestingly, even at 1098 K, the low-E (<10 meV) phonon spectra do not show any significant change, while above 10 meV, the phonon peaks clearly soften. The low-E portion of the spectra is largely attributed to phonons from acoustic branches and the three lowest optical branches. The softening and broadening of phonon modes are attributed to lattice expansion (implicit anharmonicity) and phonon–phonon interactions (explicit anharmonicity). The implicit anharmonic shifts largely contribute to the thermal expansion, while the explicit anharmonicity dominates thermal transport. Hence, we have computed both anharmonic components in the entire BZ to identify the modes relevant to thermal expansion and lattice thermal conductivity.
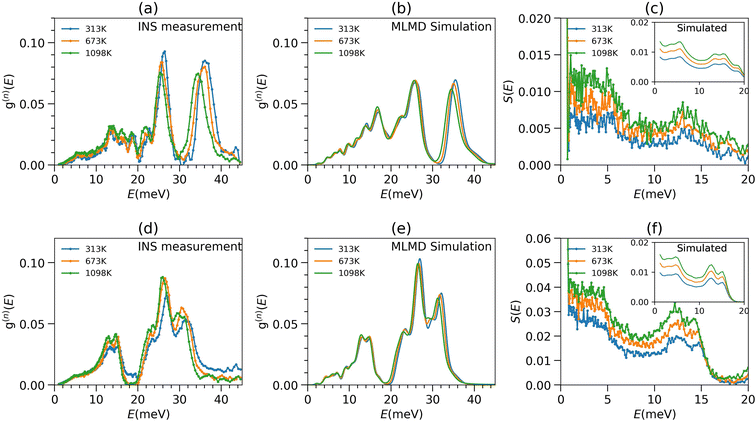
We performed NVT-MLMD simulation to explicitly probe the temperature evolution of the neutron-weighted phonon spectra (Fig. 2(b) and (e)). We observe that the simulated low-E modes do not show significant change with temperature, while the high energy modes slightly soften at elevated temperatures as experimentally observed, although less in magnitude than in the measured spectra. The AIMD simulated phonon DOS as a function of temperatures are also shown in Fig. S7.†
To further probe the temperature behaviour of low-E modes, we plot the measured Q-integrated dynamical structure factor, S(E) (1.0 Å−1 < Q < 4.0 Å−1) in Fig. 2(c) and (f). This plot clearly shows that the modes barely shift upon warming but visibly broaden. We expect the explicit anharmonicity due to the phonon–phonon interactions and increased phonon amplitudes and the implicit anharmonicity due to the volume changes. Our detailed calculations show that the negligible shift of the low-E modes occurs due to a cancellation of the hardening due to the fourth and higher order explicit anharmonicity and the softening due to the implicit anharmonicity of these modes.
To investigate the effect of third-order and higher-order anharmonicity on phonon spectra, we computed the phonon spectral energy density (SED) along various high-symmetry directions in the Brillouin zone (BZ) using two different approaches. The first approach is based on the TDEP method, which computes the phonon SED using third-order force-constants only (referred to here as TDEP-SED), and the second approach is based on molecular dynamics trajectories (NVT-MLMD)61 and referred to here as MLMD-SED. The latter approach includes third and higher-order anharmonicity to phonon SED. Hence, comparing the phonon SED from the two methods helps us identify the region in the BZ dominated by fourth or higher-order anharmonicity. In Fig. 3, we plot TDEP-SED and MLMD-SED at 100 K and 500 K. TDEP-SED at 100 K shows sharp features in intensity profiles and does not change significantly at 500 K in both compounds. However, while MLMD-SED also shows sharp phonon peaks at 100 K, these become significantly broader at 500 K, making MLMD-SED look more diffuse compared to TDEP-SED.
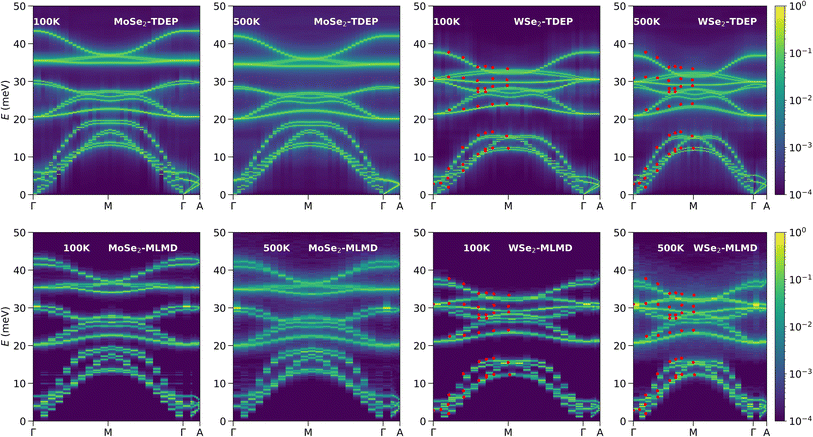 | ||
| Fig. 3 (Top panel) The TDEP-calculated phonon SED (including up to third-order anharmonicity) at 100 K and 500 K of MoSe2 and WSe2. (Bottom-panel) The MLMD-calculated phonon SED (including all orders of anharmonicity) at 100 K and 500 K of MoSe2 and WSe2. The red markers in WSe2 SED are the phonon energies measured at 300 K by Cai et al.80 | ||
Lattice thermal conductivity and anharmonic phonons
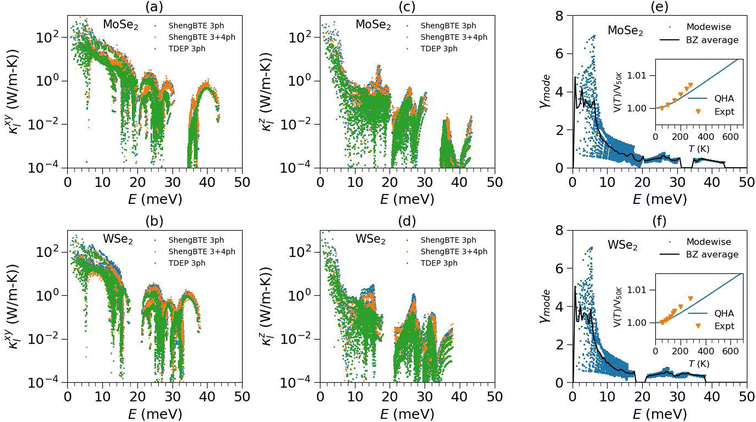
In the harmonic picture of lattice dynamics, the phonons are non-interacting and infinitely long-lived quasiparticles and hence the infinite lattice thermal conductivity. However, phonons in real systems get scattered by other phonons (intrinsic scattering processes), leading to a finite lifetime of phonons. Crystal defects and a finite sample size further reduce the phonon lifetimes, and the shortened mean free paths limit the phononic thermal conductivity (extrinsic scattering processes). In ideal single-crystals, the finite lattice thermal conductivity results from intrinsic phonon scattering processes, namely Umklapp and normal processes. Generally, normal processes do not directly contribute to the thermal resistance. Umklapp processes are the leading phonon scattering processes in heat conduction at high temperatures. Furthermore, intrinsic phonon scattering processes may involve three or more phonons. Three-phonon scattering processes include two phonons annihilating and creating a new phonon or one phonon splitting into two phonons. This is generally the dominant scattering channel in crystalline materials and leads to a 1/T dependence of κl. However, some materials such as BAs, perovskites, Heusler alloys and others62–70 show limited scattering space for three-phonon processes and significantly higher scattering phase space for four-phonon processes, and as a result do not exhibit the typical 1/T dependence of κl, with a lower conductivity than three-phonon processes alone.From INS measurements and MLMD simulations, we find that the phonons in both compounds do not change significantly at elevated temperatures; hence phase space and group velocity would not show any significant change. However, phonons substantially broaden on heating, corresponding to decreased lifetimes. The temperature dependence of thermal conductivity in these compounds is therefore primarily governed by phonon lifetimes. We first calculated the lattice thermal conductivity using third-order force constants at 0 K using ShengBTE (κSheng3). In this approach, the phonon lifetime is only contributed by three-phonon scattering processes. In Fig. 4(a), (b) and S5,† we have shown the three-phonon scattering rates, life times and group velocities of MoSe2 and WSe2 at 300 K. The lattice thermal conductivity of MoSe2 and WSe2 was measured by Puqing Jiang et al.23 using a time-domain thermoreflectance approach and found large anisotropy between the in-plane and out-of-plane lattice thermal conductivity. In Fig. 4(c)–(f), we have shown the calculated thermal conductivity from three-phonon processes in the ab-plane and along the c-axis and also shown the experimental values.23 However, three-phonon scattering has shown a significant overestimation of thermal conductivity compared to experimental values (κexpt). Including the four-phonon scattering rates improves this discrepancy, and we examined their impact on the thermal conductivity and phonon lifetimes using ShengBTE (κSheng4). Here also, the fourth-order force constants were evaluated at 0 K. We found that four-phonon scattering resistance significantly reduces the thermal conductivities and phonon lifetimes but is still overestimated compared to experimental values (Fig. 4). This suggests that either higher-order processes dominate and/or that the third and fourth-order force constants at 0 K are insufficient. To further probe these aspects, we also used the renormalized second and third-order force constants to compute the thermal conductivity at respective temperatures using TDEP (κTDEP). Surprisingly, we find that the κTDEP at low-T shows lower thermal conductivity values than κSheng4; however, they are nearly the same at higher temperatures (Fig. 4). This indicates that the 0 K anharmonic force constants cannot explain the measured thermal conductivity, and one also needs to consider the temperature dependence of higher-order force-constants. However, it is currently not feasible to evaluate the temperature dependence of fourth-order force constants and their effect on thermal conductivity due to TDEP limitations.
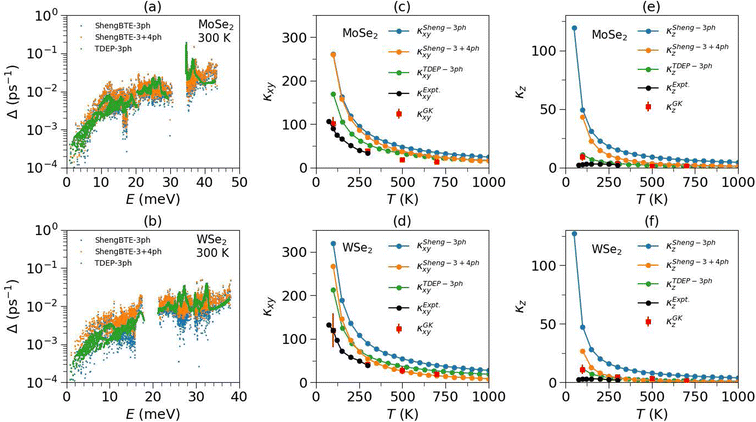 | ||
| Fig. 4 (a and b) Calculated mode-resolved phonon scattering rates on a (24 × 24 × 7) q-point grid in the BZ in MoSe2 and WSe2 at 300 K using 3-phonon scattering, calculated from 2nd and 3rd-order force-constants at 0 K (ShengBTE-3ph), and renormalized 2nd and 3rd-order force-constants at 300 K (TDEP-3ph). The scattering rates are also calculated using 3- and 4-phonon scattering processes using 0 K 3rd and 4th order force-constants (ShengBTE 3ph + 4ph). (c and d) The calculated in-plane lattice thermal conductivity (κxy) and (e and f) out-of-plane lattice thermal conductivity (κz), using 3-phonon scattering from ShengBTE-3ph, TDEP-3ph and ShengBTE 3ph + 4ph methods and the Green–Kubo method based on equilibrium molecular dynamics simulation, includes all orders of anharmonicity. The calculated quantities are compared with available experimental measurements.23 The numerical values of thermal conductivity from different methods (contribution of 4th and higher order interactions) are given in Table S3.† | ||
To further analyze the full impact of anharmonicity on κ, we performed MLMD simulations and evaluated the thermal conductivity within the Green–Kubo formalism, κGK. Strikingly, the κGK from MLMD reproduces the measured in-plane thermal conductivity (κexptxy) very well and over a wide range of temperatures. However, the out-of-plane component (κexptz) is somewhat overestimated. It is important to note that these TMDCs have a weak interplanar interaction and are governed by van der Waals forces. In the DFT framework, precisely capturing the van der Waals interactions is difficult and may lead to an overestimated thermal conductivity along the c-axis. Hence, the extensive simulation based on the perturbation method and MLMD Green–Kubo approach indicates that the importance of the temperature effect on higher-order force-constants is critical in understanding and predicting the thermal conductivity. To determine which phonon modes are most critical in heat transport in the ab-plane and along the c-axis, we computed the mode-resolved in-plane and out-of-plane lattice thermal conductivity as a function of phonon energy at 300 K (Fig. 5). Interestingly, more than 90% of lattice thermal conductivity is attributed to modes below 20 meV. By comparing the different methods, it appears that the higher-order scattering processes and temperature-renormalised force constants are critical for precisely evaluating these low-E phonon lifetimes and, hence, the thermal conductivity of TMDCs. The effect of higher-ordered scattering processes and their temperature dependence was also observed in strongly anharmonic superionics and 2-d materials, including WS2 and graphene, where the impact of higher-order anharmonicity on thermal conductivity is found to be significant.71–79
Lattice thermal expansion behaviour and phonon anharmonicity
Thermal expansion is also associated with anharmonicity on the potential energy surface. By knowing the phonon frequency shifts with temperature and volume, one can estimate how the material would behave at a given temperature. The phonon frequency shifts due to changes in the vibrational amplitudes with temperature are usually much smaller than the frequency shifts due to the change in volume with temperature.32 We have calculated the phonon frequencies at different volumes using lattice dynamics within the quasi-harmonic approximation (QHA).In the quasi-harmonic approximation, the volume thermal expansion coefficient42 of a crystalline material is given by the following relation: 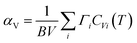 . Here,
. Here, 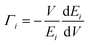 is the mode Grüneisen parameter, which is a measure of the pressure response of the phonon energy to determine the nature of the expansion behaviour. For instance, the phonon modes with negative values of Γ tend to contract the lattice, while the positive ones would expand the lattice. CVi(T) is the specific heat contribution of the ith phonon mode (of energy Ei) at temperature T, while B and V stand for the bulk modulus and volume of the compound, respectively. The calculated elastic constants and bulk modulus are given in Table S2.†45 The pressure dependence of the phonon spectra within QHA has been calculated in the entire Brillouin zone to allow for the calculation of the energy dependence of the Grüneisen parameter Γ(E) and further processed to obtain the thermal expansion coefficient αV(T).
is the mode Grüneisen parameter, which is a measure of the pressure response of the phonon energy to determine the nature of the expansion behaviour. For instance, the phonon modes with negative values of Γ tend to contract the lattice, while the positive ones would expand the lattice. CVi(T) is the specific heat contribution of the ith phonon mode (of energy Ei) at temperature T, while B and V stand for the bulk modulus and volume of the compound, respectively. The calculated elastic constants and bulk modulus are given in Table S2.†45 The pressure dependence of the phonon spectra within QHA has been calculated in the entire Brillouin zone to allow for the calculation of the energy dependence of the Grüneisen parameter Γ(E) and further processed to obtain the thermal expansion coefficient αV(T).
The volume dependence of the phonon spectra within the QHA has been calculated in the entire Brillouin zone to allow for the calculation of the mode-wise Grüneisen parameter Γ(qj,E) (Fig. 4(e) and (f)) and to obtain the thermal expansion coefficient αV(T). We have calculated the mode-wise thermal expansion contribution on a 20 × 20 × 10 q-point grid in the BZ at 300 K, as shown in Fig. S6.†45 It is evident that the most significant contribution to thermal expansion comes from low-E modes. We have performed temperature-dependent X-ray diffraction measurements on MoSe2 and WSe2 from 50 K to 300 K. The temperature dependence of fractional change in volume with respect to 50 K is shown in Fig. 5(e) and (f), which exhibits positive expansion. The large implicit anharmonicity of the low-E modes leads to large thermal expansion. It is interesting to note that the same low-E modes exhibit rather small explicit anharmonicity and contribute most to thermal conductivity.
Conclusions
We combined inelastic neutron scattering measurements and ab initio and machine-learning molecular dynamics simulations to unravel the phonon anharmonicity and their role in thermal transport and thermal expansion in MoSe2 and WSe2. We find that low-energy phonons play a crucial role in determining both the thermal-expansion behaviour and heat transport in these materials. Conventional perturbation methods are insufficient to capture the temperature-dependent anharmonicity of these phonon modes, particularly the low-E modes in strongly anharmonic systems. Machine-learning molecular dynamics simulations pave the way to completely treat the anharmonicity of phonons by performing temperature-dependent large-scale molecular dynamics simulations. These results establish the importance of anharmonic low-energy modes in TMDCs, which drive the thermal and transport properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The use of the ANUPAM super-computing facility at BARC is acknowledged. SLC acknowledges the financial support of the Indian National Science Academy for the INSA Senior Scientist position. OD acknowledges funding from the U.S. Department of Energy (DOE) BES MSED, under Award No. DE-SC0019978.References
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033 CrossRef CAS.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- X. Hong, J. Kim, S.-F. Shi, Y. Zhang, C. Jin, Y. Sun, S. Tongay, J. Wu, Y. Zhang and F. Wang, Nat. Nanotechnol., 2014, 9, 682–686 CrossRef CAS PubMed.
- M. Massicotte, P. Schmidt, F. Vialla, K. G. Schädler, A. Reserbat-Plantey, K. Watanabe, T. Taniguchi, K. J. Tielrooij and F. H. L. Koppens, Nat. Nanotechnol., 2016, 11, 42–46 CrossRef CAS PubMed.
- H. Liang, Z. Cao, F. Ming, W. Zhang, D. H. Anjum, Y. Cui, L. Cavallo and H. N. Alshareef, Nano Lett., 2019, 19, 3199–3206 CrossRef CAS PubMed.
- K. Nassiri Nazif, A. Daus, J. Hong, N. Lee, S. Vaziri, A. Kumar, F. Nitta, M. E. Chen, S. Kananian, R. Islam, K.-H. Kim, J.-H. Park, A. S. Y. Poon, M. L. Brongersma, E. Pop and K. C. Saraswat, Nat. Commun., 2021, 12, 7034 CrossRef CAS PubMed.
- D. B. Velusamy, R. H. Kim, S. Cha, J. Huh, R. Khazaeinezhad, S. H. Kassani, G. Song, S. M. Cho, S. H. Cho, I. Hwang, J. Lee, K. Oh, H. Choi and C. Park, Nat. Commun., 2015, 6, 8063 CrossRef PubMed.
- W. Huang, H. Da and G. Liang, J. Appl. Phys., 2013, 113, 104304 CrossRef.
- S. Kumar and U. Schwingenschlögl, Chem. Mater., 2015, 27, 1278–1284 CrossRef CAS.
- H.-P. Komsa, J. Kotakoski, S. Kurasch, O. Lehtinen, U. Kaiser and A. V. Krasheninnikov, Phys. Rev. Lett., 2012, 109, 035503 CrossRef.
- G. Wang, C. Robert, M. M. Glazov, F. Cadiz, E. Courtade, T. Amand, D. Lagarde, T. Taniguchi, K. Watanabe, B. Urbaszek and X. Marie, Phys. Rev. Lett., 2017, 119, 047401 CrossRef CAS PubMed.
- F. Wu, T. Lovorn, E. Tutuc, I. Martin and A. H. MacDonald, Phys. Rev. Lett., 2019, 122, 086402 CrossRef CAS PubMed.
- D. Li, H. Shan, C. Rupprecht, H. Knopf, K. Watanabe, T. Taniguchi, Y. Qin, S. Tongay, M. Nuß, S. Schröder, F. Eilenberger, S. Höfling, C. Schneider and T. Brixner, Phys. Rev. Lett., 2022, 128, 087401 CrossRef CAS PubMed.
- Z. Lin, Y. Liu, Z. Wang, S. Xu, S. Chen, W. Duan and B. Monserrat, Phys. Rev. Lett., 2022, 129, 027401 CrossRef CAS PubMed.
- Y.-M. Wu, Z. Wu and H. Yao, Phys. Rev. Lett., 2023, 130, 126001 CrossRef CAS PubMed.
- H. Guo, T. Yang, P. Tao, Y. Wang and Z. Zhang, J. Appl. Phys., 2013, 113, 013709 CrossRef.
- D. Sarkar, W. Liu, X. Xie, A. C. Anselmo, S. Mitragotri and K. Banerjee, ACS Nano, 2014, 8, 3992–4003 CrossRef CAS PubMed.
- C. Chiritescu, D. G. Cahill, N. Nguyen, D. Johnson, A. Bodapati, P. Keblinski and P. Zschack, Science, 2007, 315, 351–353 CrossRef CAS PubMed.
- S. Manzeli, D. Dumcenco, G. Migliato Marega and A. Kis, Nat. Commun., 2019, 10, 4831 CrossRef PubMed.
- L. Gao, Small, 2017, 13, 1603994 CrossRef PubMed.
- W. Choi, N. Choudhary, G. H. Han, J. Park, D. Akinwande and Y. H. Lee, Mater. Today, 2017, 20, 116–130 CrossRef CAS.
- P. Jiang, X. Qian, X. Gu and R. Yang, Adv. Mater., 2017, 29, 1701068 CrossRef PubMed.
- D. O. Lindroth and P. Erhart, Phys. Rev. B, 2016, 94, 115205 CrossRef.
- J. J. Bae, H. Y. Jeong, G. H. Han, J. Kim, H. Kim, M. S. Kim, B. H. Moon, S. C. Lim and Y. H. Lee, Nanoscale, 2017, 9, 2541–2547 RSC.
- X. Gu, B. Li and R. Yang, J. Appl. Phys., 2016, 119, 085106 CrossRef.
- R. Yan, J. R. Simpson, S. Bertolazzi, J. Brivio, M. Watson, X. Wu, A. Kis, T. Luo, A. R. Hight Walker and H. G. Xing, ACS Nano, 2014, 8, 986–993 CrossRef CAS PubMed.
- J. Judek, A. P. Gertych, M. Świniarski, A. Łapińska, A. Dużyńska and M. Zdrojek, Sci. Rep., 2015, 5, 12422 CrossRef CAS PubMed.
- X. Zhang, D. Sun, Y. Li, G.-H. Lee, X. Cui, D. Chenet, Y. You, T. F. Heinz and J. C. Hone, ACS Appl. Mater. Interfaces, 2015, 7, 25923–25929 CrossRef CAS.
- I. Jo, M. T. Pettes, E. Ou, W. Wu and L. Shi, Appl. Phys. Lett., 2014, 104, 201902 CrossRef.
- V. A. Drebushchak, J. Therm. Anal. Calorim., 2020, 142, 1097–1113 CrossRef CAS.
- R. Mittal, M. K. Gupta and S. L. Chaplot, Prog. Mater. Sci., 2018, 92, 360–445 CrossRef CAS.
- X. Qian, J. Zhou and G. Chen, Nat. Mater., 2021, 20, 1188–1202 CrossRef CAS PubMed.
- Z. Han, X. Yang, W. Li, T. Feng and X. Ruan, Comput. Phys. Commun., 2022, 270, 108179 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- A. J. McGaughey and M. Kaviany, Adv. Heat Transfer, 2006, 39, 169–255 CAS.
- M. S. Green, J. Chem. Phys., 1954, 22, 398–413 CrossRef CAS.
- R. Kubo, Rep. Prog. Phys., 1966, 29, 255 CrossRef CAS.
- R. Kubo, M. Yokota and S. Nakajima, J. Phys. Soc. Jpn., 1957, 12, 1203–1211 CrossRef.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- Z. Fan, H. Dong, A. Harju and T. Ala-Nissila, Phys. Rev. B, 2019, 99, 064308 CrossRef CAS.
- J.-S. Wang, J. Wang and N. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 033408 CrossRef.
- N. Mingo and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245406 CrossRef.
- See the ESI† for force-field validation, sample preparation, numerical data of thermal conductivities, phonon DOS, group velocity and lifetime calculations.
- A. Sjolander, Ark. Fys., 1958, 14, 315 Search PubMed.
- Neutron Scattering, ed. D. Price and K. Skold, Academic Press, Orlando, 1986, vol. 35 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104111 CrossRef.
- O. Hellman and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144301 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. A. Thomas, J. E. Turney, R. M. Iutzi, C. H. Amon and A. J. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081411 CrossRef.
- T. Yue, Y. Zhao, J. Ni, S. Meng and Z. Dai, npj Comput. Mater., 2023, 9, 17 CrossRef CAS.
- Y. Xiao, Y. Zhao, J. Ni, S. Meng and Z. Dai, Mater. Today Commun., 2023, 35, 105450 CrossRef CAS.
- X. Song, J. Wang, Y. Zhao, J. Ni, S. Meng and Z. Dai, Phys. Lett. A, 2022, 456, 128550 CrossRef CAS.
- Y. Zhao, S. Zeng, G. Li, C. Lian, Z. Dai, S. Meng and J. Ni, Phys. Rev. B, 2021, 104, 224304 CrossRef CAS.
- C. Zhang, J. Sun, Y. Shen, W. Kang and Q. Wang, J. Phys. Chem. Lett., 2022, 13, 5734–5741 CrossRef CAS PubMed.
- T. Feng, L. Lindsay and X. Ruan, Phys. Rev. B, 2017, 96, 161201 CrossRef.
- K.-C. Zhang, C. Shen, H.-B. Zhang, Y.-F. Li and Y. Liu, Phys. Rev. B, 2022, 106, 235202 CrossRef CAS.
- N. K. Ravichandran and D. Broido, Phys. Rev. X, 2020, 10, 021063 CAS.
- F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou, T.-H. Liu, M. Goni, Z. Ding, J. Sun, G. A. G. Udalamatta Gamage, H. Sun, H. Ziyaee, S. Huyan, L. Deng, J. Zhou, A. J. Schmidt, S. Chen, C.-W. Chu, P. Y. Huang, D. Broido, L. Shi, G. Chen and Z. Ren, Science, 2018, 361, 582–585 CrossRef CAS PubMed.
- A. She, Y. Zhao, J. Ni, S. Meng and Z. Dai, Int. J. Heat Mass Transfer, 2023, 209, 124132 CrossRef CAS.
- G. Sun, J. Ma, C. Liu, Z. Xiang, D. Xu, T.-H. Liu and X. Luo, Int. J. Heat Mass Transfer, 2023, 215, 124475 CrossRef.
- G.-H. Liu, Z.-X. Xie, P.-Z. Jia, X.-J. Wu and X.-K. Chen, Diamond Relat. Mater., 2023, 137, 110116 CrossRef CAS.
- G. Zhang, S. Dong, C. Yang, D. Han, G. Xin and X. Wang, Appl. Phys. Lett., 2023, 123, 052205 CrossRef CAS.
- J. Tang, G. Li, Q. Wang, J. Zheng, L. Cheng and R. Guo, Int. J. Heat Mass Transfer, 2023, 207, 124011 CrossRef CAS.
- J. Han, Q. Zeng, K. Chen, X. Yu and J. Dai, Nanomaterials, 2023, 13, 1576 CrossRef CAS PubMed.
- Q. Ren, M. K. Gupta, M. Jin, J. Ding, J. Wu, Z. Chen, S. Lin, O. Fabelo, J. A. Rodríguez-Velamazán, M. Kofu, K. Nakajima, M. Wolf, F. Zhu, J. Wang, Z. Cheng, G. Wang, X. Tong, Y. Pei, O. Delaire and J. Ma, Nat. Mater., 2023, 22, 999–1006 CrossRef CAS PubMed.
- M. K. Gupta, J. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Adv. Energy Mater., 2022, 12, 2200596 CrossRef CAS.
- M. K. Gupta, J. Ding, N. C. Osti, D. L. Abernathy, W. Arnold, H. Wang, Z. Hood and O. Delaire, Energy Environ. Sci., 2021, 14, 6554–6563 RSC.
- Q. Cai, B. Wei, Q. Sun, A. H. Said and C. Li, Mater. Today Phys., 2022, 28, 100856 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta03830k |
| This journal is © The Royal Society of Chemistry 2023 |