Open Access Article
Open Access ArticleQuantum chemical calculations for reaction prediction in the development of synthetic methodologies
Hiroki
Hayashi
 *ab,
Satoshi
Maeda
*ab,
Satoshi
Maeda
 abc and
Tsuyoshi
Mita
abc and
Tsuyoshi
Mita
 *ab
*ab
aInstitute for Chemical Reaction Design and Discovery (WPI-ICReDD), Hokkaido University, Kita 21, Nishi 10, Kita-ku, Sapporo, Hokkaido 001-0021, Japan. E-mail: hhayashi@icredd.hokudai.ac.jp; tmita@icredd.hokudai.ac.jp
bJST-ERATO, Maeda Artificial Intelligence in Chemical Reaction Design and Discovery Project, Kita 10, Nishi 8, Kita-ku, Sapporo, Hokkaido 060-0810, Japan
cDepartment of Chemistry, Faculty of Science, Hokkaido University, Kita 10, Nishi 8, Kita-ku, Sapporo, Hokkaido 060-0810, Japan
First published on 30th September 2023
Abstract
Quantum chemical calculations have been used in the development of synthetic methodologies to analyze the reaction mechanisms of the developed reactions. Their ability to estimate chemical reaction pathways, including transition state energies and connected equilibria, has led researchers to embrace their use in predicting unknown reactions. This perspective highlights strategies that leverage quantum chemical calculations for the prediction of reactions in the discovery of new methodologies. Selected examples demonstrate how computation has driven the development of unknown reactions, catalyst design, and the exploration of synthetic routes to complex molecules prior to often laborious, costly, and time-consuming experimental investigations.
1. Introduction
The discovery of chemical reactions is a primary research area that can provide new synthetic methods to create molecules in organic chemistry. Based on the developed methods, synthetic plans can be constructed for the preparation of complex molecules such as drug candidates or functional materials.1–3 However, the development of synthetic methodologies usually requires a number of experiments, mainly because the process relies on trial and error as well as on the intuition of organic chemists, which generates unwanted waste and inflates costs. Moreover, unexpected reactions are also often found during the research campaign, which may change the direction of the research project and are recognized as serendipitous findings that depend both on the researchers' intuition and on luck.4,5 Therefore, an efficient and systematic process without unnecessary experiments has long been desired, in line with the recent trends of research automation and digitalization.6For this purpose, extensive investigations into the application of experimental or informatic technologies for methodology development have been conducted. For example, high-throughput experimentation (HTE), a technique widely used in medicinal chemistry for drug discovery7 that performs multiple experiments in parallel and thus accelerates the screening process, has been applied to investigate chemical reactions. This technique enables the combinatorial screening of reaction parameters, including reagents, catalysts, or additives, leading to conditions that provide better yields or selectivities in known chemical reactions.8 Although HTE has been proven to be effective in discovering certain unknown chemical reactions, it still requires a large number of experiments (typically >1000).9–11 For the systematic development of chemical reactions, data-driven approaches have also made significant progress with the advancement of chemoinformatic techniques, in which the experimental results are correlated to reaction parameters in order to create models that capture data trends,12 understanding of mechanistic insights, and prediction of reaction outcomes. This approach has evolved from the Brønsted catalysis law,13 a pioneering study in organic chemistry that established a quantitative relationship between acidity and reaction rate, to the data-driven optimization of reaction parameters that include not only conventionally effective factors such as the solvent and temperature, but also the substrate or catalyst structures, to improve the yield or selectivity.14–16 Despite the significant progress in modeling chemical reactions, applications for discovering unknown reactions still remain underdeveloped, and the models developed in reported studies are currently limited to predicting the optimal conditions for known reactions.
Quantum chemical calculations have also been used to investigate the properties of molecules and reaction mechanisms.17 Since the 1960s, significant advances in computational chemistry, such as the launch of the Gaussian program18 and the development of density functional theory (DFT),19 have made the use of quantum chemical calculations more common in organic chemistry. The technology and its accuracy continue to improve, enabling calculations that reveal detailed reaction processes, ranging from entire catalytic cycles to biological reaction pathways involving enzymatic catalysis. Consequently, quantum chemical calculations are at present primarily employed to gain mechanistic insight into known chemical reactions.
Due to the ability of quantum chemical calculations to be performed on even unknown reaction processes, their application in the prediction of reactions holds significant potential for methodology development. In biochemistry, analogous studies are often conducted to simulate protein–protein interactions or docking simulations between small molecules and target protein binding pockets using computational methods such as molecular dynamics, molecular mechanics, or their hybrid methods.20 Unlike such simulations, which primarily focus on a single chemical process, the prediction of chemical reactions requires consideration of potential competitive reaction pathways; this encompasses the calculation of the relative energies of potential transition states and the resulting products using quantum-chemical calculations. It should be noted some such processes, e.g., those involving dynamical bifurcations, cannot be predicted accurately based solely on these parameters.21–23
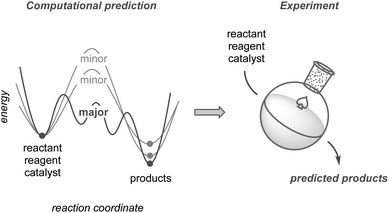
This perspective highlights the development of synthetic methodologies based on computational predictions using quantum chemical calculations (Fig. 1). While other reviews on this topic have mainly focused on improving yields or selectivities based on existing results,24–30 this perspective places greater emphasis on research in which prediction has significantly contributed to the discovery of new methodologies, including unexplored selectivity, catalyst design, and new synthetic routes toward complex molecules. We also compare the current calculation methods used to explore chemical reaction pathways, which are critical for predicting reactions, and discuss the potential of modern methods to guide computation-based methodology development. Although such predictive strategies have not yet reached a mature level of practical use, they promise substantial potential to evolve into a next-generation tool. Finally, this perspective discusses the hurdles that remain to be overcome, along with an outlook for the future.
2. Approaches for estimating chemical reaction pathways using quantum chemical calculations
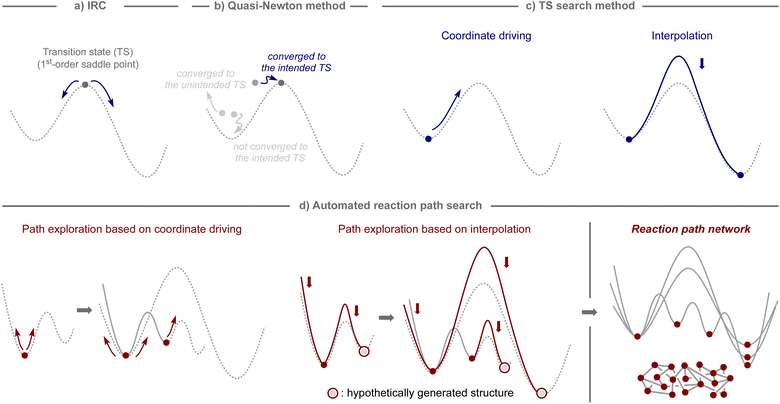
In computational studies, reaction pathways have traditionally been traced starting from the structure of the transition state, which serves as the first-order saddle point on the potential-energy surface, using intrinsic reaction coordinate (IRC) calculations (Fig. 2a).31,32 Therefore, computational methods to obtain a transition state for a desired chemical transformation have been the focus of development in the field of quantum chemistry.33,34 The most common tool is the quasi-Newton method,35–38 which can find the transition state closest to the initial structure, as illustrated in Fig. 2b.However, the quasi-Newton method does not converge or converges to a transition state of an unintended transformation if the assumed structures are not sufficiently close to those of the transition state of focus. To avoid such shortcomings, several approaches have been developed, which can be broadly classified into two subcategories: coordinate driving and interpolation (Fig. 2c).33,34 The coordinate driving approach maximizes the energy along a selected variable, such as a bond length or a normal mode, while minimizing the energy for all other variables.35,39–44 This procedure provides the approximate pathway for a chemical transformation driven by a change in the selected variable, and the maximum energy point on the pathway provides an appropriate estimate for the transition state that can serve as an input in further calculations using the quasi-Newton method. The relaxed scan and eigenvector following techniques are well-established and available in many standard quantum chemistry software packages.35,39 The interpolation approach minimizes a set of structures that represent a pathway between two equilibrium states while ensuring that the structures are properly distributed along the pathway.45–51 This procedure generates a minimum energy pathway by iteratively minimizing the energy until a predefined convergence is reached. Additionally, the quasi-Newton method is used to optimize the maximum energy point on the pathway, either after or in parallel with path optimization. The nudged elastic band (NEB) and string methods are widely employed as interpolation techniques, and can be found in various computational programs.48,49
By harnessing the aforementioned approaches, automated procedures have been devised to capture theoretically conceivable reaction pathways, enabling their effective application for the elucidation of reaction mechanisms and the prediction of reactions (Fig. 2d).32,52,53 For example, through iterative application of the coordinate driving method using different variables selected from an equilibrium structure, pathways to the other equilibrium structures can be obtained, and by continuing this process with the generated equilibrium structures, a network of reaction pathways can be established. Likewise, analogous networks can be obtained by generating hypothetical molecular graphs and applying an interpolation method iteratively to all of them or to systematically selected pairs. The practical effectiveness of these algorithms depends on the level of thoroughness inherent in the selected path finding method. Although sufficiently exhaustive methods for exploring all the important reaction pathways are still limited,54,55 and bi- or multimolecular processes involving molecules that are not included in calculations cannot be considered, these algorithms are potentially suitable not only for mechanistic investigations of known reaction processes, but also for the estimation of unknown reaction modes, ultimately leading to the development of new synthetic methods.
This perspective is divided into two parts based on the calculation approach. The first part describes examples of prediction-based reaction developments, in which the original reaction candidates are primarily provided by researchers. The second part presents a distinct example in which an automated reaction path search algorithm provided the original idea for the development of chemical reactions.
3. Reaction development using computational predictions of researcher-guided reaction pathways
3.1 Pericyclic reactions
In 1987, the predictive capability of quantum chemical calculations based on transition states was first reported by Houk and co-workers in the field of synthetic organic chemistry with the successful prediction and subsequent experimental validation of the conrotatory electrocyclic ring-opening of 3-formylcyclobutene (Fig. 3).26,56 During their study on the ring-opening of substituted cyclobutenes, the authors found that the reaction of C3-substituted cyclobutenes such as 3-methyl-, 3-chloro-, 3-acetoxy-, and 3-ethoxycyclobutene exhibited a preference for the outward rotation of the substituent, resulting in the selective formation of the E-alkene.57,58 The authors also investigated the analogous reaction of 3-formylcyclobutene using quantum chemical calculations, which indicated that this substrate can be expected to selectively undergo inward rotation (ΔΔG‡ = −4.6 kcal mol−1) due to the participation of the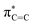 orbital in the stabilization of the HOMO σC–C orbital of the inward transition state, which stands in contrast to the selectivity of the aforementioned example. This counterintuitive prediction was subsequently validated experimentally. These findings prompted further investigations to understand the reaction mode.59–63 This study demonstrated that computations could provide predictions that are contrary to human intuition.
orbital in the stabilization of the HOMO σC–C orbital of the inward transition state, which stands in contrast to the selectivity of the aforementioned example. This counterintuitive prediction was subsequently validated experimentally. These findings prompted further investigations to understand the reaction mode.59–63 This study demonstrated that computations could provide predictions that are contrary to human intuition.
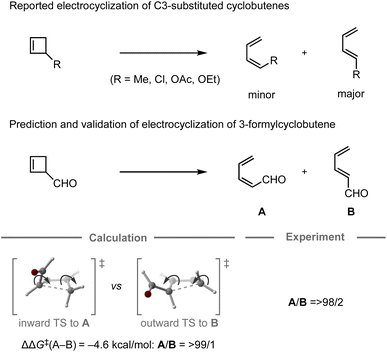 | ||
| Fig. 3 Computational prediction of the ring-opening of 3-formylcyclobutene; calculations were performed at the HF/6-31G(d)//HF/3-21G level. | ||
3.2 Computational design of organocatalysts
The computational design of catalysts is the holy grail in organic chemistry, as conventional catalyst development traditionally relies on a trial-and-error approach based on empiricism. This approach often requires a large number of experiments including the preparation of catalyst candidates and the evaluation of their catalytic activity. To transition from an intuitive approach to a systematic design, studies using computational methods have emerged as one of the most promising and prominent topics in this research field. In particular, catalytic enantioselective reactions have attracted the attention of many researchers due to their utility in producing optically active molecules and their relatively simple principle for achieving selectivity, in which enantiomeric excess is typically determined by the energy difference between the transition states leading to each enantiomer.29 Recently, chemoinformatic approaches, in which models are generated using the experimental results and parameters of each target reaction, have been studied extensively for the prediction of the performance of chiral catalysts.17–19 Some studies have successfully developed models capable of predicting enantioselectivity, even in extrapolation spaces, allowing for the identification of catalysts that provide higher enantiomeric excess compared to others in the model.Likewise, the application of quantum chemical calculations in the design of catalysts for controlling enantioselective processes is undeniably attractive, as it offers a rational strategy for the development of catalyst scaffolds. Conventionally, quantum chemical calculations have often been used to elucidate the structure of the transition states in known enantioselective reactions, as well as to identify the factors that contribute to the induction of the observed selectivities. These abilities have prompted chemists to use them for enantioselectivity predictions, whereby most studies have hitherto focused on the modification of substituents on catalysts to improve known selectivities.24–30 In contrast, Houk, Tanaka, Barbas, and co-workers have jointly reported a remarkable design achievement in the field of enantioselective organocatalysis (Fig. 4).64 Typically, proline-catalyzed Mannich reactions provide an enantioenriched product with syn-selectivity, in which the catalyst dictates the conformation of the chair-like transition state, assisted by the hydrogen-bonding interaction between the imine substrate and the carboxylic acid moiety of proline.65 In their computational study, a catalyst bearing a methyl group at the C2 position and a carboxylic acid at the C4 position on pyrrolidine was expected to favor the transition state leading to the formation of the anti-product, which was successfully validated experimentally with high enantiomeric excess and anti-selectivity (70% yield, >99% ee, anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) syn = 94
syn = 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6). While the general approach for designing proline catalysts involves introducing a bulky substituent at the C2 position to enhance their enantiodiscrimination ability,66 this work presents a different strategy (using a small substituent) guided by quantum chemical calculations, highlighting the potential of computational approaches for catalyst design in the development of new methodologies.
6). While the general approach for designing proline catalysts involves introducing a bulky substituent at the C2 position to enhance their enantiodiscrimination ability,66 this work presents a different strategy (using a small substituent) guided by quantum chemical calculations, highlighting the potential of computational approaches for catalyst design in the development of new methodologies.
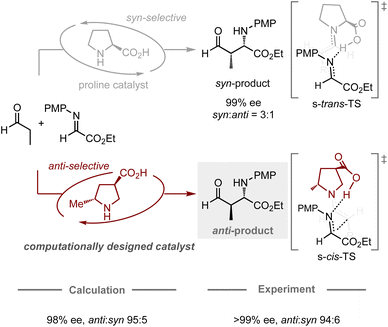 | ||
| Fig. 4 Computational design of organocatalysts for enantio- and anti-selective Mannich reactions; calculations were performed at the HF/6-31G* level. | ||
In addition to designing catalysts for superior catalytic activity, computational methods can also facilitate the simplification of catalyst structures. In this context, Paton, Dixon, and co-workers have reported the enantioselective desymmetrization of a prochiral cyclohexanone catalyzed by thiourea-based organocatalysts (Fig. 5).67 Initially, they conducted experimental catalyst screening trials to enhance the enantioselectivity in the target reaction, leading to a thiourea catalyst68,69 bearing both tert-leucine and trans-1,2-cyclohexanediamine units that furnished the product in 84% yield with 96% ee, and >98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dr. In the mechanistic study, calculations indicated that the tert-leucine moiety on the thiourea catalyst no longer contributes to controlling the selectivity at the stereo-determining proton transfer step after the enantioselective intramolecular Michael addition. Accordingly, replacing this unit with a methyl group resulted in a structurally significantly simpler catalyst with similar catalytic activity (83% yield, 97% ee, and >98
2 dr. In the mechanistic study, calculations indicated that the tert-leucine moiety on the thiourea catalyst no longer contributes to controlling the selectivity at the stereo-determining proton transfer step after the enantioselective intramolecular Michael addition. Accordingly, replacing this unit with a methyl group resulted in a structurally significantly simpler catalyst with similar catalytic activity (83% yield, 97% ee, and >98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 dr).
2 dr).
 | ||
| Fig. 5 Computational truncation of a thiourea catalyst for the asymmetric desymmetrization of cyclohexanes; calculations were performed at the M06-2X/6-311+G(d,p)/CPCM(CH2Cl2) level. | ||
3.3 Computational design of transition–metal complexes
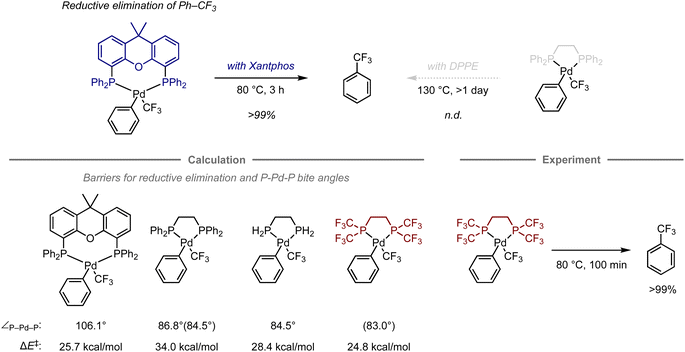
Transition-metal complexes have been studied extensively in the development of synthetic methodologies because they exhibit unique abilities that cannot be achieved using organic compounds alone, which has led to the discovery of new elementary processes and catalytic reactions that serve as valuable synthetic tools in organic synthesis.70 Given that the reactivity and selectivity of metal complexes are significantly affected by the constituent ligands, the design of ligand structures and their complexes with metals is critical for the development of transition-metal-mediated or -catalyzed reactions. In this context, computational chemistry has been used to investigate the properties of complexes and elucidate the structures of intermediates or transition states in mechanistic studies.71–74 However, predicting their reactivity or selectivity poses a considerable challenge due to many factors beyond the cost of calculations. Altering the structure of metal complexes not only affects their reactivity and selectivity, but also other properties, such as catalyst stability and solubility, which are difficult to estimate via calculations. In addition, reactions are often influenced by solvents or additives, making it virtually unfeasible to fully understand their role using quantum chemical calculations due to the vast number of possible mechanisms. Charge and spin multiplicity must also be considered, and the involvement of counterions makes the prediction even more challenging. Even when calculations are performed to account for the factors mentioned above, the estimation of energy is significantly affected by the calculation method, and the appropriate calculation level for each reaction is not yet well understood. For example, calculations of the dispersion effect are highly dependent on the choice of functional.75 Due to the aforementioned considerations, predicting transition-metal-mediated or -catalyzed reactions is significantly more complicated than predicting organic reactions.Despite these challenges, in certain cases, computational predictions can effectively aid in the development of organometallic reactions. For example, Schoenebeck and co-workers have reported an approach that uses computational methods for ligand design in the reductive elimination of benzotrifluoride from palladium complexes (Fig. 6).76 Previously, this reaction had been studied experimentally using bidentate phosphine ligands. The palladium complex with Xantphos is able to effectively promote this step at 80 °C, while the complex with 1,2-bis(diphenylphosphino)ethane (DPPE) does not furnish the desired elimination product, not even at 130 °C.77–79 This result suggests that the large bite angle of the bidentate phosphine ligand plays a crucial role in the acceleration of reductive elimination.80
Later, the authors also investigated the energy barriers for these reductive eliminations using DFT calculations.81 The computations revealed that the reaction with Xantphos had a much lower energy barrier compared to that with DPPE (barrier of electronic energy, ΔE‡ = 25.7 kcal mol−1vs. 34.0 kcal mol−1; bite angle ∠P–Pd–P = 106.1° vs. 86.8°). In contrast, an analogous ligand with two hydrogen atoms on the phosphine atoms on DPPE instead of phenyl groups exhibited a significant reduction of these values (ΔE‡ = 28.4 kcal mol−1, ∠P–Pd–P = 84.5°), suggesting that an appropriate substituent on the phosphine atom might accelerate this step even when using an ethylene-bridged scaffold, beyond the effect of the bite angle. Accordingly, replacing the phenyl groups in DPPE with trifluoromethyl groups resulted in a reduced barrier that was even lower than that with DPPE or Xantphos (ΔE‡ = 24.8 kcal mol−1, ∠P–Pd–P = 83.0).76 This observation was further validated experimentally, resulting in a quantitative conversion to provide benzotrifluoride at 80 °C. The acceleration in this case can be attributed to two factors, i.e., the destabilization of the complex caused by electrostatic repulsion between the trifluoromethyl groups of one of the phosphine ligands and the ligand bound to palladium, and the reduced electron density of the metal center, which often facilitates the reductive elimination step in other organometallic reactions.82
Reactive metal complexes often cause decomposition or side reactions that can be problematic in catalytic reactions.83–85 Therefore, a balance between the reactivity and stability of metal complexes species is critical for reaction efficiency. In this context, Buchwald and co-workers reported the computational design of copper complexes with sufficient reactivity and stability to act as catalysts in the C–N cross-coupling of aryl bromides and amines (Fig. 7).86 The copper complexes comprise copper(I) species and an anionic N1,N2-diarylbenzene-1,2-diamine ligand designed to accelerate the oxidative addition step of aryl electrophiles, which is conventionally problematic in copper-catalyzed cross-coupling reactions.87–89 Initially, the reaction of 4-bromoanisole and morpholine using a copper complex with an anionic N1,N2-diphenylbenzene-1,2-diamine ligand was investigated, albeit the desired amination product was not obtained, presumably due to the instability of the naked anionic copper species. To this end, a computational analysis was conducted, which revealed that the introduction of two phenyl groups onto the ligand stabilizes the complex through copper–π interactions (ΔG = 13.6 kcal mol−1), while maintaining sufficient reactivity for the oxidative addition of 4-bromoanisole (ΔG‡ = 8.4 kcal mol−1). The reaction with this ligand proceeds at room temperature and provides the amination product in quantitative yield. While this work successfully demonstrates a predictive strategy for the development of catalytic reactions by focusing mainly on one elementary step, the prediction of entire catalytic cycles requires considering all individual steps in the catalytic cycle as well as the turnover for their catalytic efficiency.90
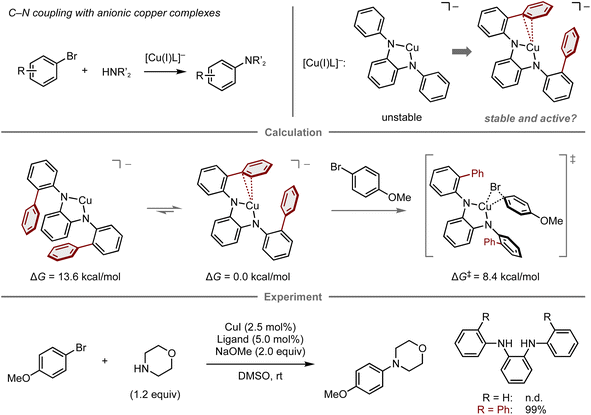 | ||
| Fig. 7 Computational design of diamine ligands for the copper-catalyzed amination of aryl bromides; calculations were performed at the B3LYP-D3/LACV3P/cc-pVTZ(-f)//B3LYP-D3/LACVP/6-31G(d,p) level. | ||
3.4 Computational prediction of the key step in complex natural product syntheses
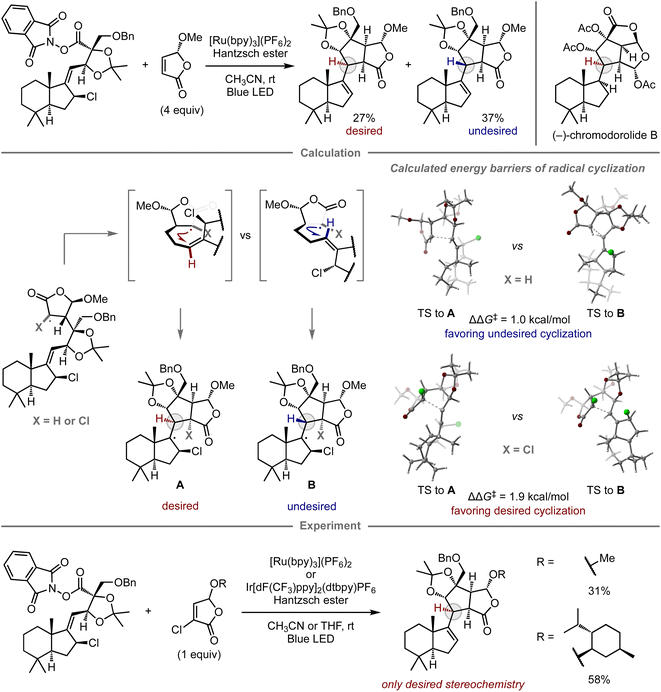
The computational prediction of chemical reactions is also potentially useful for retrosynthetic analysis, a concept used to devise synthetic routes toward complex molecules from readily available starting materials by converting a target compound to synthetic precursors and applying this process to each precursor, especially in the field of natural product synthesis. Since Corey's report on computational retrosynthetic analysis,91 this approach has received considerable attention, leading to studies using advanced chemoinformatics methods and databases that contain experimental data pertaining to molecular synthesis. These studies enable innovative computational synthetic planning for the synthesis of complex molecules,17–19 which has been verified experimentally.92–98Given that complex natural product synthesis often involves key synthetic steps, a considerable number of experimental investigations are often required to identify suitable substrates and reaction conditions. Ultimately, unsuccessful results force modifications onto the original synthetic route. To avoid such dead ends and detours, quantum chemical calculations have been used for the prediction of key steps and prospective substrates, thus enhancing the reliability of the retrosynthetic plan.99 In this context, Overman and co-workers reported the total synthesis of (−)-chromodorolide B, demonstrating the utility of computational predictions in a key step to achieve the desired stereoselectivity (Fig. 8).100 In their first report, one of the key steps was a radical cascade reaction involving an intermolecular C–C bond formation and subsequent stereoselective 5-exo-trig cyclization.101 Although their developed conditions afforded the product, the yield and stereoselectivity were low, i.e., the major product consisted of the undesired stereoisomer. To gain insight into the structure of the transition state and improve the selectivity, they performed DFT calculations for the radical cyclization step. While the alkyl radical derived from the original substrate exhibited the undesired preference (ΔΔG‡ = 1.0 kcal mol−1, favoring the undesired stereochemistry B), consistent with the observed selectivity in the experiment, the cyclization of the chlorinated variant exhibited inverse selectivity, resulting in the desired stereoselectivity (ΔΔG‡ = 1.9 kcal mol−1, favoring the desired stereochemistry A). These distinct selectivities were rationalized in terms of the steric interactions between the substituent at the α-position of the γ-butyrolactone and the alkene moiety at the transition states of 5-exo-trig cyclization. In the case of chlorinated substrates, the steric effects govern the olefin geometry of the transition state towards the desired diastereomer. Based on this notion, the reaction was performed using chlorinated substrates bearing either a methyl or a menthyl group, which resulted in selective cyclization and provided the desired product without the undesired diastereomer. The introduced chlorine atom was removed under the applied reaction conditions. With this improved key step, the authors ultimately completed the synthesis of (−)-chromodorolide B with a higher overall yield compared to that of the first-generation route.
Quantum chemical calculations have also been applied for selecting prospective substrates even prior to experimental investigations. Newhouse and co-workers reported the total synthesis of paspaline A and emindole PB using computation-directed substrate selection (Fig. 9).102 In that study, the authors aimed to synthesize both compounds from the same precursor in a divergent fashion.103 To this end, calculations were conducted to assess the energy barriers of the Friedel–Crafts type cyclization and the 1,2-methyl shift leading to each key scaffold, in which these pathways were explored from a carbocation intermediate bearing various substituents distant from the reaction site. Calculations revealed that among carbocations a–c, the reaction of carbocation c has the highest preference for forming the hexacyclic motif in paspaline A. Inspired by these theoretical results, the synthesis commenced with the preparation of the computationally proposed precursor for carbocation c bearing a hydroxy group as a leaving group. However, when subjected to the reaction in the presence of a stoichiometric amount of aluminum chloride as a Lewis acid additive to promote the elimination of the hydroxy group, both products were obtained via cyclization and methyl shift in 44% combined yield with the inverse selectivity ratio (A/B = 1/3). The observed mismatched selectivity might be attributed to the involvement of a concerted elimination/1,2-methyl shift, a process that was not considered in the calculations. From isolated A, the synthesis of paspaline A was accomplished in 9 overall steps, which is shorter than the previously reported synthetic route. The first total synthesis of emindole PB was also achieved from B. Although this computational strategy was unable to accurately predict the experimental ratio, it guided the selection of substrates that ultimately led to the development of a shorter synthetic route and the achievement of the first total synthesis in a divergent manner.
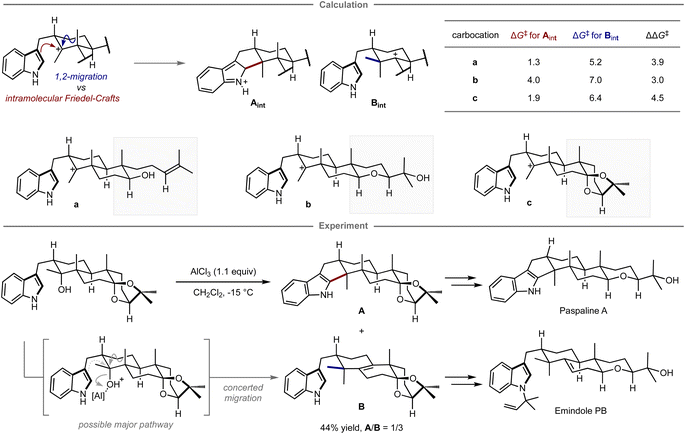 | ||
| Fig. 9 Computational substrate design for the divergent synthesis of paspaline A and emindole PB. The calculations were performed at the mPW1PW91/6-31+G(d,p)//B3LYP/6-31G(d) level. | ||
4. Reaction development with automated reaction path search methods
4.1 Automated reaction path search methods for reaction development
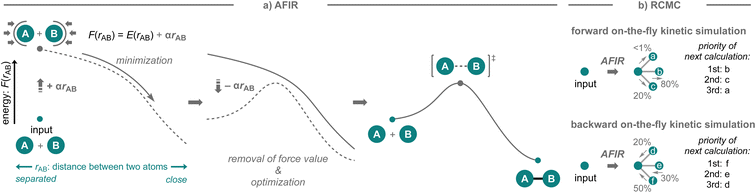
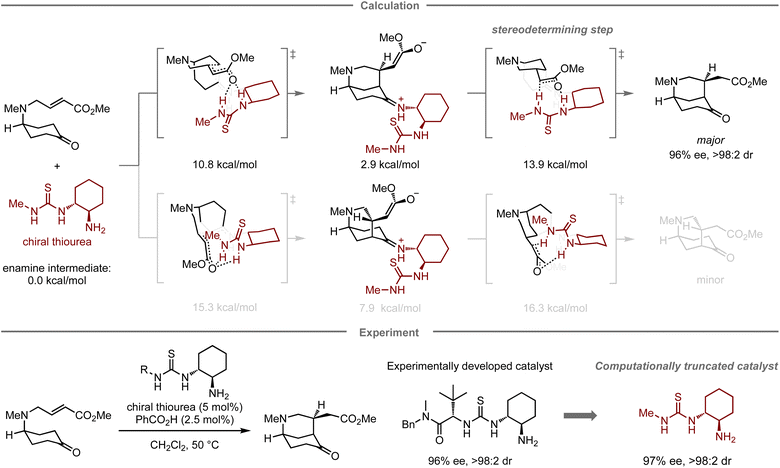
The strategies presented above successfully showcase the possibility to develop new synthetic methodologies based on computational prediction in which researchers select the target reactions and competitive side reactions. While this is without a doubt very impressive, the success of these strategies still largely depends on the researchers' knowledge of organic chemistry and computational skills. In particular, when competitive side reactions that are preferred over the target reaction are overlooked, the computational prediction becomes less reliable. In this context, an automated reaction path search algorithm that can explore conceivable reaction pathways may be highly beneficial (Fig. 2d). Such algorithms offer distinct advantages, as they are not solely reliant on human knowledge and often user-friendly, requiring minimal computational skills, and a variety of algorithms for exploring reaction pathways have been developed over the years.32,52,53 Given the recent continuous advances in computing power as well as automated workflows (for examples since 2021, see: QChASM,104 autodE,105 ChemDyME,106 YARP,107 AutoMeKin2021,108 CARNOT,109 ChemTraYzer-TAD,110 and Chemoton 2.0 (ref. 111)), these methods have been able to realize the transition from applications in mechanistic studies to comprehensive reaction prediction. While the developed algorithms have been used effectively for these purposes, little effort has been devoted to the experimental validation of the discovered reactions or mechanisms in the context of synthetic methodology development.A highly comprehensive exploration of chemical reaction pathways, integrated with deterministic kinetic simulations that possess numerical stability, is crucial for predicting all potential reaction products along with their yields. The artificial force induced reaction (AFIR) method,32,44,112–115 which uses a virtual force in quantum chemical calculations to find reaction pathways from an equilibrium structure, has been developed for this purpose (Fig. 10a). It has been shown to be sufficiently comprehensive for certain reaction classes including their conformational space.116 This method explores chemical reaction pathways by applying an arbitrary force to the input molecular structure to forcibly induce structural deformation. The force is applied to an automatically defined fragment pair in mutually approaching or diverging directions. The approximate reaction pathway estimated by minimizing the force-modified energy based on ab initio or semi-empirical calculations is optimized to obtain the actual reaction pathway or the IRC pathway. By applying the force to all conceivable fragment pairs, not only in the initial structure but also in the generated equilibrium structures, an exhaustive reaction path search can be performed to construct a network of chemical reaction pathways. To realize on-the-fly kinetic simulations,117 this method has been further combined with the deterministic and numerically stable kinetic simulation technique, termed rate constant matrix contraction (RCMC), which employs kinetics-based graph clustering to efficiently analyze complex reaction path networks that comprise thousands or more elementary reaction steps (Fig. 10b).118,119 By leveraging the integrated AFIR and RCMC methods, the forward on-the-fly kinetic simulation can be performed to estimate potential products together with their computational yields, starting from the input reaction components; moreover, the backward on-the-fly kinetic simulation can also be performed to provide potential reactant species that could generate the input chemical structure as the reaction product in high yield.117 The detailed algorithms of the AFIR and RCMC methods have already been discussed in other reviews and are beyond the scope of this perspective;116,117 instead, the application of these methods in the context of reaction prediction and experimental validation is discussed. In the next section, the application of the AFIR method for reaction prediction will be described.
4.2 Computational retrosynthetic analysis for a new synthetic route to difluoroglycine derivatives
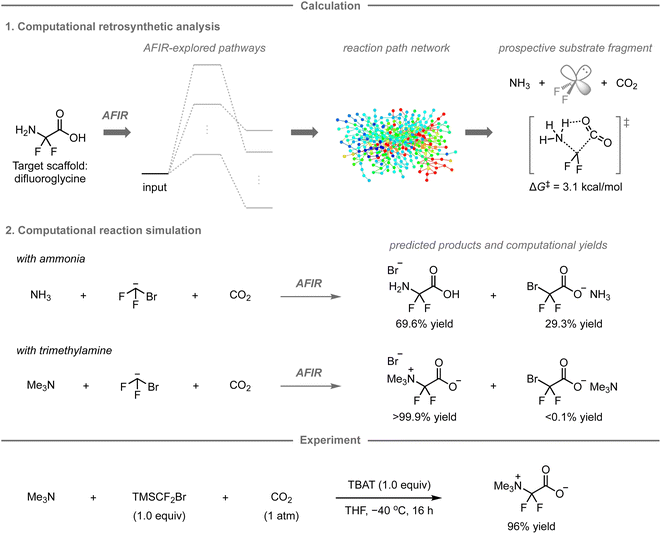
While the AFIR and RCMC methods have mainly been used for mechanistic investigations of established reactions or researcher-predicted reactions,120–130 our research group has embarked on exploring their potential as computational tools for predicting unexplored synthetic routes or reactions. In 2020, our research group reported a new synthetic route to difluoroglycine derivatives based on calculations using the AFIR/RCMC methods (Fig. 11).131 Due to limited synthetic routes toward this fluorinated motif, its promising applications have hitherto remained unexplored. To explore the potential synthetic route, the AFIR method was leveraged in computational retrosynthetic analysis, in which possible synthons were investigated by searching for equilibrium structures connected to difluoroglycine through reaction pathways. Among the 76 equilibrium structures generated as substrate candidates, the combination of ammonia, difluoroglycine, and carbon dioxide (CO2) had prospects for experimental implementation due to the facile assembly of these three components (ΔG‡ = 3.1 kcal mol−1) as well as their availability. Further calculations were conducted to explore the possible reaction pathways from ammonia, the bromodifluoromethyl anion as a difluorocarbene precursor, and CO2 using the AFIR method, after which the computational yields of possible products were estimated based on the obtained rate constant at the designated temperature and time using the RCMC method. Accordingly, difluoroglycine was expected to be formed in 69.6% yield, together with side products such as bromodifluoroacetic acid in 29.3% yield. To further explore other potential substrate candidates that could provide the glycine scaffold in better yield, analogous calculations were performed with trimethylamine instead of ammonia, resulting in a theoretically quantitative conversion to trimethyldifluoroglycine, while effectively suppressing the formation of any side products.Based on these promising computational predictions, the experimental realization of the reaction with the proposed substrates was investigated. Ultimately, the reaction was experimentally realized using commercially available trimethylamine, CO2, and (bromodifluoromethyl)trimethylsilane (TMSCF2Br) as the precursor for the generation of difluorocarbene in the presence of tetrabutylammonium difluorotriphenylsilicate (TBAT), furnishing the desired product in 96% yield. The developed three-component reaction can proceed with a wide range of tert-alkylamines and N-heteroaromatic compounds.132 However, the reaction with ammonia, one of the reactions originally predicted in this study, did not provide difluoroglycine experimentally, but ammonium fluoride instead. This is presumably due to the in situ formation of ammonium carbamate from ammonia and CO2, which was not estimated in the calculations due to the involvement of two molecules of ammonia; additional calculations and experiments indicated that this undesired pathway leads to the formation of ammonium fluoride.
4.3 In silico reaction screening with difluorocarbene for the development of three-component reactions
As the AFIR/RCMC method successfully guided the development of a new synthetic route to difluoroglycine derivatives, our group envisioned that these methods would also be effective in computational reaction screening toward the development of unexplored chemical reactions.133 To demonstrate this, difluorocarbene was used as a component in a calculation using the AFIR method due to its synthetic utility in incorporating difluoromethylene groups into organic molecules and its small size, which can reduce calculation costs for the quantum chemical calculations (Fig. 12). Computational reaction simulations were conducted to explore the three-component reaction of difluorocarbene and two components bearing unsaturated bonds (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C
O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
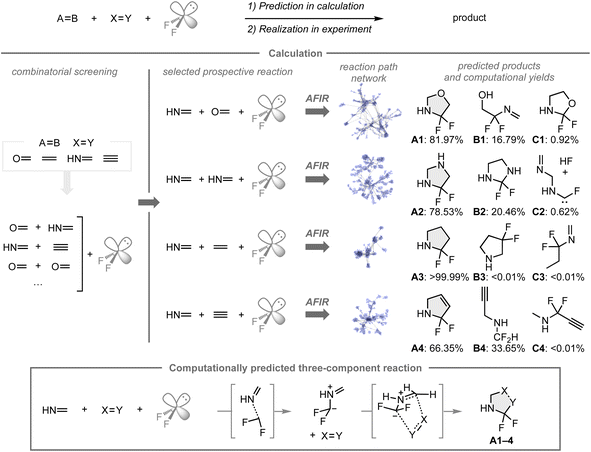
C, and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bonds), in which formaldehyde, methanimine, ethylene, and acetylene were chosen due to their low computational costs and the inherent reactivity associated with unsaturated bonds. Based on the combinatorial screening using the AFIR/RCMC method for all combinations to create the reaction path network that encompasses the possible intermediates, transition states, or products with their computational yields, four reactions with methanimine, difluorocarbene, and a series of unsaturated bonds were expected to provide the α,α-difluorinated N-heterocyclic compounds A1–4 as major products rather than other potential products such as B1–4 and C1–4. In these reactions, A1–4 were formed through 1,3-dipolar cycloadditions of the fluorinated azomethine ylide and the other coupling partners. While N-heterocyclic skeletons fluorinated β- or γ-positions relative to the nitrogen atom have been studied in medicinal chemistry, analogues that contain fluorine at the α-position are underexplored, presumably due to a lack of synthetic methods to construct such structures. Based on the results of the computational screening, the predicted reaction mode was investigated experimentally.
C bonds), in which formaldehyde, methanimine, ethylene, and acetylene were chosen due to their low computational costs and the inherent reactivity associated with unsaturated bonds. Based on the combinatorial screening using the AFIR/RCMC method for all combinations to create the reaction path network that encompasses the possible intermediates, transition states, or products with their computational yields, four reactions with methanimine, difluorocarbene, and a series of unsaturated bonds were expected to provide the α,α-difluorinated N-heterocyclic compounds A1–4 as major products rather than other potential products such as B1–4 and C1–4. In these reactions, A1–4 were formed through 1,3-dipolar cycloadditions of the fluorinated azomethine ylide and the other coupling partners. While N-heterocyclic skeletons fluorinated β- or γ-positions relative to the nitrogen atom have been studied in medicinal chemistry, analogues that contain fluorine at the α-position are underexplored, presumably due to a lack of synthetic methods to construct such structures. Based on the results of the computational screening, the predicted reaction mode was investigated experimentally.
To realize a three-component assembly of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, a C
N bond, a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, and difluorocarbene as the model reaction, available organic substrates were investigated instead of the unsaturated compounds used in the computational screening due to their gaseous and polymerizable characteristics, which made it difficult to control their amounts precisely in the experiments (Fig. 13a). Accordingly, the reactions were conducted with N-Boc (where Boc is tert-butyl carbamate) or N-phenyl imine derived from benzaldehyde, which have been widely used in organic synthesis, and benzaldehyde as the sources of the C
O bond, and difluorocarbene as the model reaction, available organic substrates were investigated instead of the unsaturated compounds used in the computational screening due to their gaseous and polymerizable characteristics, which made it difficult to control their amounts precisely in the experiments (Fig. 13a). Accordingly, the reactions were conducted with N-Boc (where Boc is tert-butyl carbamate) or N-phenyl imine derived from benzaldehyde, which have been widely used in organic synthesis, and benzaldehyde as the sources of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
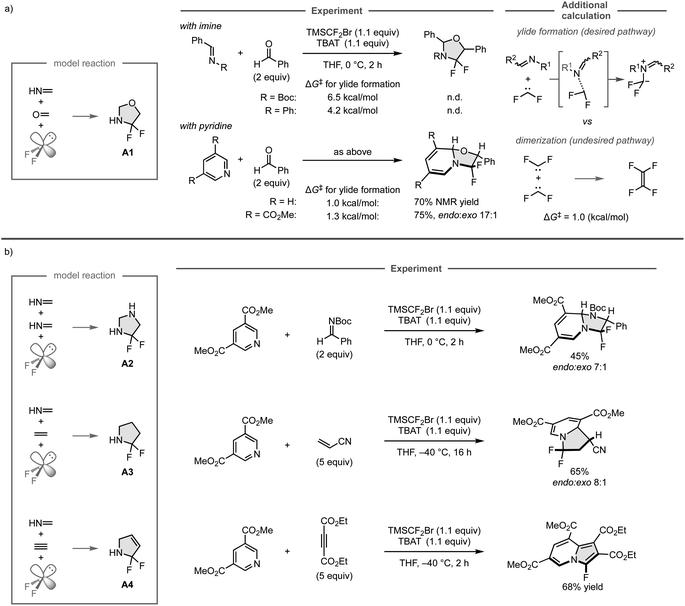
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, respectively, using TMSCF2Br and TBAT to generate difluorocarbene in situ. However, the reaction did not provide the desired products because the undesired dimerization of difluorocarbene (ΔG‡ = 1.0 kcal mol−1) has a lower barrier than that of the formation of iminium ylide (ΔG‡ = 6.5 kcal mol−1 or 4.2 kcal mol−1), and thus would proceed preferentially, as was indicated in additional DFT calculations. Further calculations also showed that the ylide formation barriers for pyridine and its derivative bearing an electron-withdrawing ester group are comparable to that of the undesired reaction (ΔG‡ = 1.0 kcal mol−1 and 1.3 kcal mol−1, respectively). Accordingly, the three-component reaction of pyridine and benzaldehyde leads to the formation of the desired cyclic compound involving the dearomatization of the pyridine ring. However, the product could not be isolated due to its instability, whereas the reaction with the pyridine derivative bearing the electron-withdrawing ester group provided the isolable product in 75% yield.
O bonds, respectively, using TMSCF2Br and TBAT to generate difluorocarbene in situ. However, the reaction did not provide the desired products because the undesired dimerization of difluorocarbene (ΔG‡ = 1.0 kcal mol−1) has a lower barrier than that of the formation of iminium ylide (ΔG‡ = 6.5 kcal mol−1 or 4.2 kcal mol−1), and thus would proceed preferentially, as was indicated in additional DFT calculations. Further calculations also showed that the ylide formation barriers for pyridine and its derivative bearing an electron-withdrawing ester group are comparable to that of the undesired reaction (ΔG‡ = 1.0 kcal mol−1 and 1.3 kcal mol−1, respectively). Accordingly, the three-component reaction of pyridine and benzaldehyde leads to the formation of the desired cyclic compound involving the dearomatization of the pyridine ring. However, the product could not be isolated due to its instability, whereas the reaction with the pyridine derivative bearing the electron-withdrawing ester group provided the isolable product in 75% yield.
The other computationally predicted reactions were also investigated experimentally (Fig. 13b). For the predicted reactions of two molecules of methanimine and difluorocarbene to form A2, the reaction with the pyridine derivative and N-Boc imine successfully proceeded to give the fluorinated imidazolidine derivatives in 45% yield. Similarly, the predicted reactions of methanimine, ethylene, and difluorocarbene to form A3 could also be realized by employing the pyridine derivative and acrylonitrile, furnishing the fluorinated indolizine products in 65% yield. On the other hand, while the three-component reaction of methanimine, acetylene, and difluorocarbene was expected to provide A4 based on the computational screening, the reaction of the pyridine derivative and diethyl acetylenedicarboxylate furnished the fluorinated cyclic product in aromatic form, which was presumably obtained through the elimination of hydrogen fluoride driven by aromatization after the predicted 1,3-dipolar cycloaddition. The developed three-component reaction can employ a wide range of coupling partners including aldehydes, ketones, alkenes, and alkynes, as well as pyridines that bear a variety of functional groups. This study showcases the power of computational screening and the automated reaction path search method for the development of new chemical reactions.
5. Challenges
The studies discussed in this perspective highlight the utility of quantum chemical calculations for the prediction of new reactions in the field of synthetic methodology development, which goes beyond the conventional use of such calculations in mechanistic studies of established reactions. However, challenges remain especially with respect to accurately predicting reactions and ensuring consistency between calculated results and experimental observations (vide infra).(a) In mechanistic studies, the choice of calculation level can be guided by experimental results, which may significantly influence the computational outcome. However, for the prediction of unknown reactions, there is currently no universal method to determine the appropriate calculation level. This becomes particularly problematic when predicting reaction selectivity, especially when there are small energy differences among competing reaction pathways, such as in stereoselective reactions with chiral catalysts or site-selective reactions with multiple reactive sites. This challenge may be addressed by further developing computational methods that can estimate reaction pathways with sufficient accuracy within a reasonable calculation time.
(b) Quantum chemical calculations hardly consider physical properties such as solubility or stability of the calculated molecules in the reaction medium. Even when calculations propose new reactions or catalysts, these factors may prevent their experimental success. Currently, empiricism still plays a pivotal role in addressing these concerns, while the emerging chemoinformatics techniques may offer promising avenues to effectively overcome this challenge.134
(c) The selection of the solvent is often critical to reaction outcomes, albeit the details of the solvent effects are not comprehensively understood. In particular, the participation of solvent molecules in the reaction mechanism poses challenges for computational modeling, as it raises questions regarding the optimal number and location of solvent molecules for the accurate prediction of reactions. Advancements in computing power and computational methods may provide appropriate solutions to this problem.
(d) While the algorithm for the automated reaction path search is effective in exploring potential chemical reaction pathways and predicting reaction outcomes by considering competitive pathways, it does not account for certain reactions that involve molecules that are excluded from the calculations. For example, the dimerization or polymerization of reactive species such as carbenes or radicals is not considered unless two or more identical structures are included in the initial components. Additionally, a calculation may miss a pathway involving a hidden catalyst that is not stoichiometrically involved in a reaction equation unless it is explicitly considered. A simple example is keto–enol tautomerisation, where the intramolecular 1,3-hydrogen shift is a thermally forbidden process, resulting in unreasonable barriers unless a molecule involved in proton transfer is explicitly considered.135 It is important to keep these aspects in mind when analysing the results of the calculations.
6. Conclusions and outlook
Quantum chemical calculations have become an indispensable tool to carry out research in organic chemistry. Currently, their primary role is to serve in mechanistic studies of established reaction processes. However, as shown in this perspective, quantum chemical calculations have considerable potential to further guide research directions, which would allow a more systematic experimentation and thus accelerate research and diminish associated costs. Although addressing the aforementioned issues is essential for future progress, it is obvious that the evolution of computers and computational methods is remarkably rapid, and can be expected to greatly expand the use of computational reaction prediction in the future. Furthermore, the field of chemistry is currently witnessing the integration of machine learning and artificial intelligence technology, in which data-driven strategies for the prediction of reaction performance have been extensively explored using quantum chemical calculations as well. Consequently, the continued use of quantum chemical calculations as a predictive tool will undoubtedly contribute to the development of future synthetic methodologies.Author contributions
H. H. compiled the reference list and drafted the manuscript. T. M. and S. M. supported the preparation of the final version.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors gratefully acknowledge JST-ERATO (grant no. JPMJER1903) and JSPS-WPI. H. H. gratefully acknowledges a Grant-in-Aid for Young Scientists (grant no. 23K13737). T. M. gratefully acknowledges grants for Challenging Research (Exploratory) (grant no. 21K18945), Scientific Research (B) (grant no. 22H02069), and Transformative Research Areas (A) (Digitalization-driven Transformative Organic Synthesis (Digi-TOS)) (grant no. 22H05330).Notes and references
- J. Wencel-Delord and F. Glorius, Nat. Chem., 2013, 5, 369 CrossRef CAS PubMed.
- D. G. Brown and J. Boström, J. Med. Chem., 2016, 59, 4443 CrossRef CAS PubMed.
- D. C. Blakemore, L. Castro, I. Churcher, D. C. Rees, A. W. Thomas, D. M. Wilson and A. Wood, Nat. Chem., 2018, 10, 383 CrossRef CAS PubMed.
- H. S. Eleuterio, J. Mol. Catal., 1991, 65, 55 CrossRef CAS.
- K. Fischer, K. Jonas, P. Misbach, R. Stabba and G. Wilke, Angew. Chem., Int. Ed. Engl., 1973, 12, 943 CrossRef.
- I. W. Davies, Nature, 2019, 570, 175 CrossRef CAS PubMed.
- R. Macarron, M. N. Banks, D. Bojanic, D. J. Burns, D. A. Cirovic, T. Garyantes, D. V. S. Green, R. P. Hertzberg, W. P. Janzen, J. W. Paslay, U. Schopfer and G. S. Sittampalam, Nat. Rev. Drug Discovery, 2011, 10, 188 CrossRef CAS PubMed.
- K. D. Collins, T. Gensch and F. Glorius, Nat. Chem., 2014, 6, 859 CrossRef CAS PubMed.
- A. McNally, C. K. Prier and D. W. C. MacMillan, Science, 2011, 334, 1114 CrossRef CAS PubMed.
- D. W. Robbins and J. F. Hartwig, Science, 2011, 333, 1423 CrossRef CAS PubMed.
- K. Troshin and J. F. Hartwig, Science, 2017, 357, 175 CrossRef CAS PubMed.
- W. L. Williams, L. Zeng, T. Gensch, M. S. Sigman, A. G. Doyle and E. V. Anslyn, ACS Cent. Sci., 2021, 7, 1622 CrossRef CAS PubMed.
- J. N. Brønsted and K. Pedersen, Phys. Chem., 1924, 108U, 185 Search PubMed.
- A. F. Zahrt, S. V. Athavale and S. E. Denmark, Chem. Rev., 2020, 120, 1620 CrossRef CAS PubMed.
- A. Nandy, C. Duan, M. G. Taylor, F. Liu, A. H. Steeves and H. J. Kulik, Chem. Rev., 2021, 121, 9927 CrossRef CAS PubMed.
- C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089 CrossRef CAS PubMed.
- K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539 CrossRef CAS PubMed.
- W. J. Hehre, W. A. Lathan, R. Ditchfield, M. D. Newton and J. A. Pople, Gaussian 70 Quantum Chemistry Program Exchange, Program, 1970, No. 237 Search PubMed.
- W. Kohn, Rev. Mod. Phys., 1999, 71, 1253 CrossRef CAS.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334 CrossRef PubMed.
- D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592 CrossRef CAS PubMed.
- S. Lee and J. M. Goodman, Org. Biomol. Chem., 2021, 19, 3940 RSC.
- P. Bharadwaz, M. Maldonado-Domínguez and M. Srnec, Chem. Sci., 2021, 12, 12682 RSC.
- J. E. Eksterowicz and K. N. Houk, Chem. Rev., 1993, 93, 2439 CrossRef CAS.
- K. B. Lipkowitz and M. A. Peterson, Chem. Rev., 1993, 93, 2463 CrossRef CAS.
- K. N. Houk and P. H.-Y. Cheong, Nature, 2008, 455, 309 CrossRef CAS PubMed.
- Y.-H. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750 CrossRef CAS PubMed.
- Q. Peng and R. S. Paton, Acc. Chem. Res., 2016, 49, 1042 CrossRef CAS PubMed.
- Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093 RSC.
- J. P. Reid and M. S. Sigman, Nat. Rev. Chem, 2018, 2, 290 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS.
- S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258 CrossRef CAS.
- H. B. Schlegel, J. Comput. Chem., 2003, 24, 1514 CrossRef CAS PubMed.
- H. B. Schlegel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 790 CAS.
- C. J. Cerjan and W. H. Miller, J. Chem. Phys., 1981, 75, 2800 CrossRef CAS.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214 CrossRef CAS.
- A. Banerjee, N. Adams, J. Simons and R. Shepard, J. Phys. Chem., 1985, 89, 52 CrossRef CAS.
- P. Culot, G. Dive, V. H. Nguyen and J. M. Ghuysen, Theor. Chim. Acta, 1992, 82, 189 CrossRef CAS.
- R. L. Jaffe, D. M. Hayes and K. Morokuma, J. Chem. Phys., 1974, 60, 5108 CrossRef CAS.
- J.-Q. Sun and K. Ruedenberg, J. Chem. Phys., 1993, 98, 9707 CrossRef CAS.
- Y. Abashkin and N. Russo, J. Chem. Phys., 1994, 100, 4477 CrossRef CAS.
- K. K. Irikura and R. D. Johnson, III., J. Phys. Chem. A, 2000, 104, 2191 CrossRef CAS.
- K. Ohno and S. Maeda, Chem. Phys. Lett., 2004, 384, 277 CrossRef CAS.
- S. Maeda and K. Morokuma, J. Chem. Phys., 2010, 132, 241102 CrossRef PubMed.
- R. Elber and M. A. Karplus, Chem. Phys. Lett., 1987, 139, 375 CrossRef CAS.
- C. Choi and R. Elber, J. Chem. Phys., 1991, 94, 751 CrossRef CAS.
- P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1997, 107, 375 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- W. E, W. Ren and E. Vanden-Eijnden, Phys. Rev. B, 2002, 66, 052301 CrossRef.
- B. Peters, A. Heyden, A. T. Bell and A. Chakraborty, J. Chem. Phys., 2004, 120, 7877 CrossRef CAS PubMed.
- A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2011, 135, 224108 CrossRef PubMed.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- G. N. Simm, A. C. Vaucher and M. Reiher, J. Phys. Chem. A, 2019, 123, 385 CrossRef CAS PubMed.
- C. A. Grambow, A. Jamal, Y.-P. Li, W. H. Green, J. Zádor and Y. V. Suleimanov, J. Am. Chem. Soc., 2018, 140, 1035 CrossRef CAS PubMed.
- S. Maeda and Y. Harabuchi, J. Chem. Theory Comput., 2019, 15, 2111 CrossRef CAS PubMed.
- K. Rudolf, D. C. Spellmeyer and K. N. Houk, J. Org. Chem., 1987, 52, 3708 CrossRef CAS.
- W. Kirmse, N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1984, 106, 7989 CrossRef CAS.
- N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1985, 107, 2099 CrossRef CAS.
- M. Murakami, T. Miyamoto and Y. Ito, Angew. Chem., Int. Ed., 2001, 40, 189 CrossRef CAS PubMed.
- P. S. Lee, X. Zhang and K. N. Houk, J. Am. Chem. Soc., 2003, 125, 5072 CrossRef CAS PubMed.
- M. Murakami, M. Hasegawa and H. Igawa, J. Org. Chem., 2004, 69, 587 CrossRef CAS PubMed.
- K. Aikawa, N. Shimizu, K. Honda, Y. Hioki and K. Mikami, Chem. Sci., 2014, 5, 410 RSC.
- K. Honda, S. A. Lopez, K. N. Houk and K. Mikami, J. Org. Chem., 2015, 80, 11768 CrossRef CAS PubMed.
- S. Mitsumori, H. Zhang, P. H.-Y. Cheong, K. N. Houk, F. Tanaka and C. F. Barbas, III, J. Am. Chem. Soc., 2006, 128, 1040 CrossRef CAS PubMed.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042 CrossRef CAS PubMed.
- S. Mukherjee, J. W. Yang, S. Hoffmann and B. List, Chem. Rev., 2007, 107, 5471 CrossRef CAS PubMed.
- A. D. G. Yamagata, S. Datta, K. E. Jackson, L. Stegbauer, R. S. Paton and D. J. Dixon, Angew. Chem., Int. Ed., 2015, 54, 4899 CrossRef PubMed.
- A. G. Doyle and E. N. Jacobsen, Chem. Rev., 2007, 12, 5713 CrossRef PubMed.
- T. Parvin, R. Yadav and L. H. Choudhury, Org. Biomol. Chem., 2020, 18, 5513 RSC.
- R. Noyori, Angew. Chem., Int. Ed., 2002, 41, 2008 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532 CrossRef CAS PubMed.
- S. Santoro, M. Kalek, G. Huang and F. Himo, Acc. Chem. Res., 2016, 49, 1006 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453 CrossRef CAS PubMed.
- E. Lyngvi, I. A. Sanhueza and F. Schoenebeck, Organometallics, 2015, 34, 805 CrossRef CAS.
- M. C. Nielsen, K. J. Bonney and F. Schoenebeck, Angew. Chem., Int. Ed., 2014, 53, 5903 CrossRef CAS PubMed.
- D. A. Culkin and J. F. Hartwig, Organometallics, 2004, 23, 3398 CrossRef CAS.
- V. V. Grushin and W. J. Marshall, J. Am. Chem. Soc., 2006, 128, 4632 CrossRef CAS PubMed.
- V. V. Grushin and W. J. Marshall, J. Am. Chem. Soc., 2006, 128, 12644 CrossRef CAS PubMed.
- P. C. J. Kamer, P. W. N. M. Van Leeuwen and J. N. H. Reek, Acc. Chem. Res., 2001, 34, 895 CrossRef CAS PubMed.
- P. Anstaett and F. Schoenebeck, Chem. - Eur. J., 2011, 17, 12340 CrossRef CAS PubMed.
- J. F. Hartwig, Inorg. Chem., 2007, 46, 1936 CrossRef CAS PubMed.
- P. E. Garrou, Chem. Rev., 1985, 85, 171 CrossRef CAS.
- P. W. N. M. van Leeuwen, Appl. Catal., A, 2001, 212, 61 CrossRef CAS.
- R. H. Crabtree, J. Organomet. Chem., 2014, 751, 174 CrossRef CAS.
- S.-T. Kim, M. J. Strauss, A. Cabré and S. L. Buchwald, J. Am. Chem. Soc., 2023, 145, 6966 CrossRef CAS PubMed.
- G. O. Jones, P. Liu, K. N. Houk and S. L. Buchwald, J. Am. Chem. Soc., 2010, 132, 6205 CrossRef CAS PubMed.
- H.-Z. Yu, Y.-Y. Jiang, Y. Fu and L. Liu, J. Am. Chem. Soc., 2010, 132, 18078 CrossRef CAS PubMed.
- R. Giri, A. Brusoe, K. Troshin, J. Y. Wang, M. Font and J. F. Hartwig, J. Am. Chem. Soc., 2018, 140, 793 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101 CrossRef CAS PubMed.
- E. J. Corey and W. T. Wipke, Computer-Assisted Design of Complex Organic Syntheses, Science, 1969, 166, 178 CrossRef CAS PubMed.
- T. Klucznik, B. Mikulak-Klucznik, M. P. McCormack, H. Lima, S. Szymkuć, M. Bhowmick, K. Molga, Y. Zhou, L. Rickershauser, E. P. Gajewska, A. Toutchkine, P. Dittwald, M. P. Startek, G. J. Kirkovits, R. Roszak, A. Adamski, B. Sieredzinska, M. Mrksich, S. L. J. Trice and B. A. Grzybowski, Chem, 2018, 4, 522 CAS.
- C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. J. Hart, T. F. Jamison and K. F. Jensen, Science, 2019, 365, eaax1566 CrossRef CAS PubMed.
- Y. Lin, Z. Zhang, B. Mahjour, D. Wang, R. Zhang, E. Shim, A. McGrath, Y. Shen, N. Brugger, R. Turnbull, S. Trice, S. Jasty and T. Cernak, Nat. Commun., 2021, 12, 7327 CrossRef CAS PubMed.
- B. Mikulak-Klucznik, P. Gołębiowska, A. A. Bayly, O. Popik, T. Klucznik, S. Szymkuć, E. P. Gajewska, P. Dittwald, O. Staszewska-Krajewska, W. Beker, T. Badowski, K. A. Scheidt, K. Molga, J. Mlynarski, M. Mrksich and B. A. Grzybowski, Nature, 2020, 588, 83 CrossRef CAS PubMed.
- A. Wołos, D. Koszelewski, R. Roszak, S. Szymkuć, M. Moskal, R. Ostaszewski, B. T. Herrera, J. M. Maier, G. Brezicki, J. Samuel, J. A. M. Lummiss, D. T. McQuade, L. Rogers and B. A. Grzybowski, Nature, 2022, 604, 668 CrossRef PubMed.
- Y. Lin, R. Zhang, D. Wang and T. Cernak, Science, 2023, 379, 453 CrossRef CAS PubMed.
- P. Zhang, J. Eun, M. Elkin, Y. Zhao, R. L. Cantrell and T. R. Newhouse, Nat. Synth., 2023, 2, 527 CrossRef.
- M. Elkin and T. R. Newhouse, Chem. Soc. Rev., 2018, 47, 7830 RSC.
- D. J. Tao, Y. Slutskyy, M. Muuronen, A. Le, P. Kohler and L. E. Overman, J. Am. Chem. Soc., 2018, 140, 3091 CrossRef CAS PubMed.
- D. J. Tao, Y. Slutskyy and L. E. Overman, J. Am. Chem. Soc., 2016, 138, 2186 CrossRef CAS PubMed.
- D. E. Kim, J. E. Zweig and T. R. Newhouse, J. Am. Chem. Soc., 2019, 141, 1479 CrossRef CAS PubMed.
- L. Li, Z. Chen, X. Zhang and Y. Jia, Chem. Rev., 2018, 118, 3752 CrossRef CAS PubMed.
- V. M. Ingman, A. J. Schaefer, L. R. Andreola and S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1510 CAS.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, Angew. Chem., Int. Ed., 2021, 60, 4266 CrossRef CAS PubMed.
- R. J. Shannon, E. Martínez-Núñez, D. V. Shalashilin and D. R. Glowacki, J. Chem. Theory Comput., 2021, 17, 4901 CrossRef CAS PubMed.
- Q. Zhao and B. M. Savoie, Nat. Comput. Sci., 2021, 1, 479 CrossRef.
- E. Martínez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodríguez, R. Rodríguez-Fernández, R. J. Shannon, J. J. P. Stewart, P. G. Tahoces and S. A. Vazquez, J. Comput. Chem., 2021, 42, 2036 CrossRef PubMed.
- X. Chen, M. Liu and J. Gao, J. Chem. Theory Comput., 2022, 18, 1297 CrossRef CAS PubMed.
- L. Krep, I. S. Roy, W. Kopp, F. Schmalz, C. Huang and K. Leonhard, J. Chem. Inf. Model., 2022, 62, 890 CrossRef CAS PubMed.
- J. P. Unsleber, S. A. Grimmel and M. Reiher, J. Chem. Theory Comput., 2022, 18, 5393 CrossRef CAS PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683 RSC.
- W. M. C. Sameera, S. Maeda and K. Morokuma, Acc. Chem. Res., 2016, 49, 763 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, J. Comput. Chem., 2018, 39, 233 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, T. Hasegawa, K. Suzuki and T. Mita, AsiaChem, 2021, vol. 2, p. 56 Search PubMed.
- S. Maeda and Y. Harabuchi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1538 CAS.
- S. Maeda, Y. Harabuchi, H. Hayashi and T. Mita, Annu. Rev. Phys. Chem., 2023, 74, 287 CrossRef PubMed.
- Y. Sumiya and S. Maeda, Chem. Lett., 2020, 49, 553 CrossRef CAS.
- Y. Sumiya, Y. Harabuchi, Y. Nagata and S. Maeda, JACS Au, 2022, 2, 1181 CrossRef CAS PubMed.
- S. Maeda, S. Komagawa, M. Uchiyama and K. Morokuma, Angew. Chem., Int. Ed., 2011, 50, 644 CrossRef CAS PubMed.
- W. Kanna, Y. Harabuchi, H. Takano, H. Hayashi, S. Maeda and T. Mita, Chem. - Asian J., 2021, 16, 4072 CrossRef CAS PubMed.
- H. Takano, Y. You, H. Hayashi, Y. Harabuchi, S. Maeda and T. Mita, ACS Omega, 2021, 6, 33846 CrossRef CAS PubMed.
- Y. Kamei, Y. Seino, Y. Yamaguchi, T. Yoshino, S. Maeda, M. Kojima and S. Matsunaga, Nat. Commun., 2021, 12, 966 CrossRef CAS PubMed.
- Y. You, W. Kanna, H. Takano, H. Hayashi, S. Maeda and T. Mita, J. Am. Chem. Soc., 2022, 144, 3685 CrossRef CAS PubMed.
- W. Matsuoka, Y. Harabuchi and S. Maeda, ACS Catal., 2022, 12, 3752 CrossRef CAS.
- H. Takano, H. Katsuyama, H. Hayashi, W. Kanna, Y. Harabuchi, S. Maeda and T. Mita, Nat. Commun., 2022, 13, 7034 CrossRef CAS PubMed.
- T. Mita, H. Takano, H. Hayashi, W. Kanna, Y. Harabuchi, K. N. Houk and S. Maeda, J. Am. Chem. Soc., 2022, 144, 22985 CrossRef CAS PubMed.
- S. R. Mangaonkar, H. Hayashi, H. Takano, W. Kanna, S. Maeda and T. Mita, ACS Catal., 2023, 13, 2482 CrossRef CAS.
- Y. Harabuchi, H. Hayashi, H. Takano, T. Mita and S. Maeda, Angew. Chem., Int. Ed., 2023, 62, 202211936 CrossRef PubMed.
- W. Matsuoka, Y. Harabuchi, Y. Nagata and S. Maeda, Org. Biomol. Chem., 2023, 21, 3132 RSC.
- T. Mita, Y. Harabuchi and S. Maeda, Chem. Sci., 2020, 11, 7569 RSC.
- H. Hayashi, H. Takano, H. Katsuyama, Y. Harabuchi, S. Maeda and T. Mita, Chem. - Eur. J., 2021, 27, 10040 CrossRef CAS PubMed.
- H. Hayashi, H. Katsuyama, H. Takano, Y. Harabuchi, S. Maeda and T. Mita, Nat. Synth., 2022, 1, 804 CrossRef.
- S. Boobier, D. R. J. Hose, A. J. Blacker and B. N. Ngun, Nat. Commun., 2020, 11, 5753 CrossRef CAS PubMed.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed., 1969, 8, 781 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |