Open Access Article
Open Access ArticlePlanar pentacoordinate s-block metals†
Meng-hui
Wang‡
a,
Amlan J.
Kalita‡
 b,
Mesías
Orozco-Ic‡
b,
Mesías
Orozco-Ic‡
 c,
Gai-ru
Yan
a,
Chen
Chen
a,
Bing
Yan
c,
Gai-ru
Yan
a,
Chen
Chen
a,
Bing
Yan
 a,
Gabriela
Castillo-Toraya
d,
William
Tiznado
a,
Gabriela
Castillo-Toraya
d,
William
Tiznado
 *e,
Ankur K.
Guha
*e,
Ankur K.
Guha
 *b,
Sudip
Pan
*b,
Sudip
Pan
 *a,
Gabriel
Merino
*a,
Gabriel
Merino
 *d and
Zhong-hua
Cui
*d and
Zhong-hua
Cui
 *af
*af
aInstitute of Atomic and Molecular Physics, Jilin University, Changchun 130023, China. E-mail: zcui@jlu.edu.cn; sudip@jlu.edu.cn
bAdvanced Computational Chemistry Centre, Department of Chemistry, Cotton University, Panbazar, Guwahati, Assam 781001, India. E-mail: ankurkantiguha@gmail.com
cDonostia International Physics Center (DIPC), 20018 Donostia, Euskadi, Spain
dDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Unidad Mérida. Km 6 Antigua Carretera a Progreso. Apdo. Postal 73, Cordemex, 97310, Mérida, Yucatan, Mexico. E-mail: gmerino@cinvestav.mx
eCentro de Química Teórica & Computacional (CQT&C), Departamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello, Avenida República 275, Santiago, Chile. E-mail: wtiznado@unab.cl
fKey Laboratory of Physics and Technology for Advanced Batteries (Ministry of Education), Jilin University, Changchun 130023, China
First published on 14th July 2023
Abstract
The presence of a delocalized π-bond is often considered an essential criterion for achieving planar hypercoordination. Herein, we show that σ-delocalization could be sufficient to make the planar configuration the most stable isomer in a series of planar pentacoordinate s-block metals. High-level ab initio computations reveal that the global minimum of a series of interalkali and interalkali-alkaline earth clusters (LiNa5, Li5Mg+, Na5Mg+, K5Ca+, CaRb5+, Rb5Sr+, and SrCs5+) adopts a singlet D5h structure with a planar pentacoordinate lithium or alkaline earth metal (AE = Mg, Ca, Sr). These clusters are unusual combinations to stabilize a planar pentacoordinate atom, as all their constituents are electropositive. Despite the absence of π-electrons, Hückel's rule is fulfilled by the six σ-electrons. Furthermore, the systems exhibit a diatropic ring current in response to an external magnetic field and a strong magnetic shielding, so they might be classified as σ-aromatic. Therefore, multicenter σ-bonds and the resulting σ-delocalization stabilize these clusters, even though they lack π-aromaticity.
Introduction
Planar tetracoordinate carbons (ptCs) defy the standard paradigm of organic chemistry, yet they have been theoretically predicted, and experimentally isolated and characterized.1,2 The story of these exotic molecules began with the report of a ptC transition state for methane in the stereomutation process of a tetrahedral carbon by Monkhorst.3 Subsequently, in a seminal paper, Hoffmann and co-workers analyzed bonding in planar methane and concluded that multicenter bond formation and lone pair delocalization on the central carbon atom are the key factors for the stability of ptC.4 Collins et al. followed these ideas to predict some ptC systems that are energetically more stable than their tetrahedral counterpart.5 This field has developed over time and now includes compounds containing planar tetra-, penta-, and even hexacoordinate carbon atoms.6–23 In fact, planar hypercoordination is not restricted to carbon only,24–38 other p-block elements have the ability to form these peculiar structures. However, as the electronegativity increases, stabilization of a planar hypercoordinate atom becomes more difficult since π-electrons would not be effectively delocalized. Although their number is relatively low, some planar hypercoordinate nitrogen and oxygen systems have been reported.39–43 Merino and co-workers have recently designed one of the challenging systems, (quasi) planar tetracoordinate fluorine (ptF) in FIn4+, FTl4+, FGaIn3+, FIn2Tl2+, FIn3Tl+, and FInTl3+.44 Being the most electronegative element, the interactions of fluorine with the peripheral atoms are electrostatic in nature, affecting electron delocalization. So, the fluorine in these odd structures does not act as a σ-acceptor, restraining any back-donation.So, a common feature of all these systems is that the hypercoordinate center is a p-block element. What about the s-block elements? Recently, some of us reported an intriguing set of systems with a planar pentacoordinate beryllium (ppBe) atom, BeM5+ (M = Cu, Ag, Au), where three delocalized σ-orbitals support the bonding between Be and M5 unit.45 Beryllium is unique among the s-block elements because of its relatively large electronegativity and small radius. It has the highest capability to form covalent bonds between elements of the same block. Therefore, the σ-bonds in these ppBe clusters seem strong enough to prevent isomerization into a non-planar form. Is it plausible to obtain candidates having a planar pentacoordinate alkali metal or an alkaline earth metal?
Herein, we attempt to extend the list of compounds with planar pentacoordinate alkali (ppA) and alkaline-earth (ppAE) metals. LiNa5 has a planar pentacoordinate lithium (ppLi) atom as the most stable isomer. Although this structure has previously been detected in the gas phase, its unusual form and way of stabilization were ignored. Gratifyingly, we found new planar pentacoordinate magnesium (Li5Mg+ and Na5Mg+), calcium (K5Ca+ and CaRb5+), and strontium (Rb5Sr+ and SrCs5+) atoms. To understand their stability, we have analyzed the nature of bonding and possible electron delocalization.
Computational details
The potential energy surfaces were systematically explored using the CALYPSO (Crystal structure Analysis by Particle Swarm Optimization) code.46 Initial screening of both singlet and triplet configurations was performed at the PBE0-D3/def2-SVP level.47 The resulting structures were re-minimized and characterized at the PBE0-D3/def2-QZVPP level. The final energies were refined at the CCSD(T)48/def2-QZVPP level of theory. Therefore, the further discussion is based on the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP results.The multireference complete-active space self-consistent field (CASSCF)49 computations were performed using MOLPRO.50 The single-point computations of CASSCF and its second-order multireference perturbation theory (CASPT2)51 were conducted using the def2-QZVPP basis set on the PBE0-D3/def2-QZVPP geometries. For the active space, six orbitals (three occupied and three unoccupied) and six electrons were considered. Additionally, the geometries of the first three low-lying isomers were optimized using the CASPT2/def2-TZVPP level.
Electron delocalization was analyzed by computing the magnetic response to a unit external magnetic field (1.0 T). The magnetically induced current density52 (Jind) and the induced magnetic field53–55 (Bind) were calculated using the GIMIC52 and Aromagnetic56 programs, respectively. The external magnetic field was oriented parallel to the z-axis, perpendicular to the molecular plane. Under these conditions, the z-component of Bind (Bindz) is equivalent to the NICSzz index. Since the BHandHLYP functional57 best matches the magnetic properties calculated at the CCSD(T) level, the magnetic response calculations were carried out using that functional together with the all-electron TZP-DKH58 basis set, which includes scalar relativistic corrections. To quantify the degree of delocalization in the seven clusters, the ring current strengths (Iind) were computed. These values are derived by integrating Jind along a plane that begins at the center of the molecule, intersects a bond, and ends where Jind vanishes. The contributions of the core electrons to the magnetic response were calculated using the RVE method, i.e., for highly charged molecules whose valence electrons have been removed but without relaxing the molecular structure. Therefore, the magnetic response of a system without its valence electrons is equivalent to the magnetic response of the core electrons.59
Chemical bonding analyses were performed using the natural bonding orbitals (NBO) program.60 To investigate the multicenter bonding feature, adaptive natural density partitioning (AdNDP)61 analysis was performed using the Multiwfn program code.62 The nature of the chemical bonding is further analyzed with interactive quantum atom analysis (IQA).63–65 IQA was performed at the PBE-D3/TZ2P level using the ADF 2020 package.66,67 All other calculations were performed with the Gaussian 16 package.68
Planar pentacoordinate alkali metals
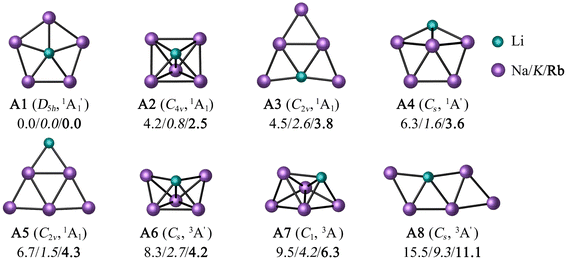
To minimize the computational cost, only the potential energy surfaces (PESs) of those combinations satisfying two conditions were explored: the first condition is that a perfect pentagon with a planar pentacoordinate alkali (ppA) at the center is a minimum. The second is that the ppA isomer is energetically more stable than the corresponding planar tetracoordinate alkali metal (ptA) form. Only three (LiNa5, LiK5, and LiRb5) of the 25 possibilities satisfy both criteria at the CCSD(T)/def2-QZVPP//PBE0-D3/def2-QZVPP level (see Table S1 and Fig. S1†).For these three combinations, the eight low-lying energy isomers are depicted in Fig. 1. According to global minimization, the most energetically stable configuration is a ppLi (A1). A C4v square pyramid (A2) is the closest form in energy (4.2, 0.8, and 2.5 kcal mol−1 for M = Na, K, and Rb, respectively), followed by a ptLi isomer (A3). Systems A4 and A5 contain a tricoordinate and dicoordinate A atom, respectively. Note that while the previous five isomers are in a singlet electronic state, the next three are triplets.
The T1-diagnostic was done to check the reliability of mono-determinantal methodologies in these systems. It is apparent from Table S2† that the LiK5 clusters have somewhat higher T1 values than LiNa5 analogues. Particularly, the triplet states have very high T1 values (0.08–0.15), which motivated us to perform CASPT2(6,6)/def2-QZVPP//PBE0-D3/def2-QZVPP computations. At the CASPT2 level, the ppLi isomer for LiNa5 remains the lowest energy structure, unequivocally confirming its genuine candidacy in the flat world (see Fig. S2†). In contrast, the square pyramid becomes the lowest energy structure for LiK5 and LiRb5, 2.8 and 2.1 kcal mol−1 more stable than the ppLi isomer, respectively (Fig. S2†). In fact, ptLi is 1.3 kcal mol−1 more stable for the latter system than ppLi at the CASPT2 level. The first three low-lying isomers were optimized at the CASPT2/def2-TZVPP level to confirm if the energy trend of the isomers matches the results of the CASPT2//PBE0-D3 level. As shown in Table S3,† the difference in relative energies between these two levels ranged from 0.2 to 2.5 kcal mol−1. However, the global minimum isomer remained the same in both cases. These findings suggest that the ppLi form is preferred for LiNa5 due to both electronic and geometric factors, but for its heavier analogues, the larger ring size weakens the interaction between Li and peripheral atoms, resulting in others less symmetric structures being more stable than ppLi isomer.
In previous studies, pure and inter-alkali metal clusters with different combinations and sizes, including LiM5, were detected in the gas phase by mass spectroscopy.69a LiNa5 has been identified experimentally and even Silva et al.69b found that the ppLi arrangement is the most stable at the MP2 level. So, strictly speaking, we only confirm what has already been reported up to this point using multireference level.
Planar pentacoordinate alkali-earth metals
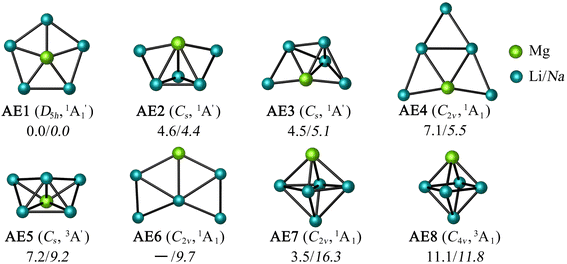
Let us expand this search to systems that contain a ppAE metal. Only six combinations (Li5Mg+, Na5Mg+, K5Ca+, CaRb5+, Rb5Sr+, and SrCs5+) satisfy both constraints following the same protocol established in the previous section (see Table S4†). Gratifyingly, the D5h ppMg form, with an electronic state, is the most stable isomer for both Li5Mg+ and Na5Mg+ (AE1, see Fig. 2). The nearest energy isomer has a Cs three-dimensional configuration (AE2), being 4.6 (Li) and 4.4 (Na) kcal mol−1 higher in energy than the global minimum. The ptMg isomer (AE4) lies 7.1 (Li) and 5.5 (Na) kcal mol−1 above the ppMg. The closest triplet has a three-dimensional structure with a relative energy of 7.2 (Li) and 9.2 (Na) kcal mol−1 with respect to the ppMg cluster. There is no significant difference in relative energy between CCSD(T) and CASPT2 levels (see Table S5 for T1-diagnostics, and Table S3 and Fig. S3† for relative energies). The trend is same for CaM5+ (M = K, Rb) and SrM5+ (M = Rb, Cs) clusters (see Fig. S4–S7†). The ppAE form (AE = Ca, Sr) in all four cases is the most stable isomer at the CCSD(T) and CASPT2 levels. The relative energies with the closest three-dimensional isomer and the ptAE isomer are gradually reduced from Mg to Sr.
electronic state, is the most stable isomer for both Li5Mg+ and Na5Mg+ (AE1, see Fig. 2). The nearest energy isomer has a Cs three-dimensional configuration (AE2), being 4.6 (Li) and 4.4 (Na) kcal mol−1 higher in energy than the global minimum. The ptMg isomer (AE4) lies 7.1 (Li) and 5.5 (Na) kcal mol−1 above the ppMg. The closest triplet has a three-dimensional structure with a relative energy of 7.2 (Li) and 9.2 (Na) kcal mol−1 with respect to the ppMg cluster. There is no significant difference in relative energy between CCSD(T) and CASPT2 levels (see Table S5 for T1-diagnostics, and Table S3 and Fig. S3† for relative energies). The trend is same for CaM5+ (M = K, Rb) and SrM5+ (M = Rb, Cs) clusters (see Fig. S4–S7†). The ppAE form (AE = Ca, Sr) in all four cases is the most stable isomer at the CCSD(T) and CASPT2 levels. The relative energies with the closest three-dimensional isomer and the ptAE isomer are gradually reduced from Mg to Sr.
Structure and bonding
One of the most evident geometrical features is that the Li–M and AE–M bond lengths in LiM5 (M = Na, K) and AEM5+ are significantly longer (between 0.17 and 0.59 Å, see Table 1) than the typical covalent bond lengths proposed by Pyykkö and Atsumi,70 which is typical for atoms bonded through multicenter bonds. The WBI values for Li–M and AE–M bonds range from 0.26 (Li–K) to 0.33 (Li–Mg), while they are smaller for M–M bonds (0.10–0.21). Since Na and K are more electropositive than Li, Li gets a negative CM5 charge of −0.18e in LiNa5 and −0.17e in LiK5. For the same reason, the natural charge on AE in the cationic clusters is also slightly negative (ranging between −0.13e and −0.18e).| q A/AE | q M | r A/AE–M | r M–M | WBIA/AE–M | WBIM–M | |
|---|---|---|---|---|---|---|
| LiNa5 | −0.18 | +0.04 | 3.111 | 3.657 | 0.28 | 0.21 |
| LiK5 | −0.17 | +0.03 | 3.797 | 4.464 | 0.26 | 0.19 |
| Li5Mg+ | −0.13 | +0.23 | 2.888 | 3.395 | 0.33 | 0.12 |
| Na5Mg+ | −0.17 | +0.23 | 3.234 | 3.802 | 0.31 | 0.10 |
| K5Ca+ | −0.16 | +0.23 | 4.123 | 4.847 | 0.32 | 0.11 |
| CaRb5+ | −0.15 | +0.23 | 4.337 | 5.098 | 0.31 | 0.10 |
| Rb5Sr+ | −0.13 | +0.22 | 4.490 | 5.278 | 0.28 | 0.11 |
| SrCs5+ | −0.17 | +0.23 | 4.764 | 5.600 | 0.29 | 0.10 |
To understand a little more about how atoms are bonded in these clusters, we performed an interacting quantum atom (IQA) analysis. Table 2 summarizes the values of the interatomic interaction energy (Vtotal) and their electrostatic (Vionic) and exchange (Vcoval) components. For Li/AE–M contacts, both ionic and covalent contributions are attractive, with the former being more dominant than the latter. Now, if we compare the values for ppLi with the corresponding ones in ppAE, both ionic and covalent interactions are improved in the latter cases. Note that the ionic attraction of AE–M bonds gradually decreases from Mg to Sr. On the other hand, for ppLi, there is a tiny electrostatic repulsion between the M–M bonds, which is compensated by the attractive covalent interaction. But for ppAE cases, a combination of enhanced ionic repulsion and weak covalent attraction makes the M–M contacts repulsive in nature.
| LiNa5 | LiK5 | Li5Mg+ | Na5Mg+ | K5Ca+ | CaRb5+ | Rb5Sr+ | SrCs5+ | |
|---|---|---|---|---|---|---|---|---|
| V total (Li/AE–M) | −30.0 | −35.9 | −268.1 | −116.1 | −77.9 | −65.9 | −57.2 | −58.6 |
| V ionic (Li/AE–M) | −22.7 | −10.6 | −241.0 | −80.7 | −47.4 | −37.1 | −28.7 | −31.9 |
| V coval (Li/AE–M) | −7.3 | −25.3 | −27.1 | −35.3 | −30.6 | −28.8 | −28.5 | −26.8 |
| V total (M–M) | −23.7 | −8.8 | 58.1 | 20.3 | 10.9 | 7.9 | 5.6 | 6.4 |
| V ionic (M–M) | 4.2 | 2.2 | 58.9 | 23.6 | 14.5 | 11.8 | 9.8 | 10.3 |
| V coval (M–M) | −27.8 | −11.0 | −0.8 | −3.4 | −3.6 | −4.0 | −4.2 | −3.9 |
Aromaticity
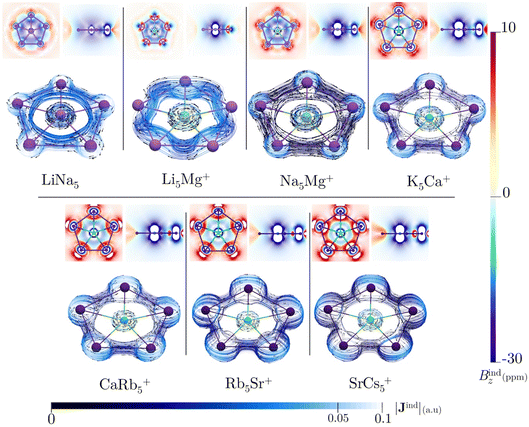
All of the ppA systems in this study have six valence electrons distributed in multicenter σ-orbitals, which include a degenerate HOMO and HOMO-1, as shown in Fig. S8† and AdNDP orbitals in Fig. S9†. Therefore, Hückel's rule is fulfilled by these σ-electrons. In previous studies, σ-aromaticity has been recognized as a crucial factor in stabilizing planar hypercoordination.44,45,71 However, this phenomenon is usually accompanied by the delocalization of p orbitals or the presence of d orbitals in the ligands. In the present cases, the clusters only possess weak s-bonding, particularly for LiNa5. This raises an intriguing question: can the limited σ-delocalization in these systems induce a diatropic ring current and a shielding cone when an external magnetic field is applied?All these systems exhibit a diamagnetic magnetic response (negative Bindz values) and the formation of a shielding cone below and above the ring (Fig. 3), which is characteristic of an aromatic system. But, the Bindz values are strongly affected by the core electron magnetic response, mainly because heavy nuclei produce strong local shielding cones. So, to quantify the degree of delocalization in the seven clusters, the ring current strengths (Iind) were computed. Since the integration domain covers the local atomic current of the central atom, the Iind values for the seven planar pentacoordinate s-block metals systems (ranging from 17.94 to 88.04 nA T−1) are relatively high compared to the benzene value of 12 nA T−1, particularly for those with heavier elements (see Table 3). It is well-known that the effect of the core electron on ring-current strengths in organic molecules is typically negligible59 but may be relevant for our molecules with heavy atoms,72–74 even more so if the integration plane crosses a nucleus. This is also evident in the Jind plots (Fig. 3), where the current–density pathways are distorted near the nuclei due to local atomic currents in the heaviest clusters. We also estimated the core-electron contribution of Iind using the removing valence electrons (RVE) approach75 to separate the influence of the core and valence electrons on these strengths. Consequently, the Iind values derived exclusively from the σ-electrons range between 8.53 and 21.34 nA T−1. So, we may claim that MgLi5+ is the least aromatic while SrCs5+ sustains the strongest ring current. These values are higher than those determined for benzene (a π-delocalized system) but lower than those obtained for Al42− or CAl42− (both (σ + π)-delocalized clusters).76,77 So, these results emphasize the significance of σ-aromaticity in determining the stability and preferred geometry of the cluster.78,79
| I ind | LiNa5 | Li5Mg+ | Na5Mg+ | K5Ca+ | CaRb5+ | Rb5Sr+ | SrCs5+ |
|---|---|---|---|---|---|---|---|
| Total | 17.94 | 27.79 | 33.22 | 50.50 | 50.59 | 81.95 | 88.04 |
| Core | 4.18 | 19.26 | 19.26 | 34.26 | 34.23 | 66.70 | 66.70 |
| Valence (σ) | 13.76 | 8.53 | 13.96 | 16.24 | 16.36 | 15.25 | 21.34 |
Conclusions
Is it plausible to obtain candidates with a planar pentacoordinate metal of the s-block? Yes, it is feasible. We have identified seven clusters with a planar pentacoordinate s-block metal as their global minimum by systematically exploring the potential energy surfaces of various combinations. Despite the electropositive nature of all their components, these clusters sustain a strong diatropic ring current and significant shielding, supporting their fully σ-delocalized character. So, multicentric σ-bonds and the resulting σ-delocalization stabilize these clusters, even in the absence of π-orbitals. These clusters push the covalent bonding tendency of alkali and alkaline earth metals to the limit and provide a basis for the design of rule-breaking planar hypercoordinate structures.Data availability
Computational details, extra data, and the Cartesian coordinates for all compounds are provided in the ESI† accompanying this paper.Author contributions
WT, AKG, SP, GM, and ZC designed the works and concepts, analyzed the data, wrote the draft, and finalized it. MW, AJK and MO-I performed the global minima search and aromaticity analysis. GY, CC and GC-T performed NBO and IQA. YB and MW performed CASPT2 calculations. All authors took part in the discussions and approved the final version. GM and SP wrote the final version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Natural Science Foundation of China (Grant no. 11922405, 11874178, 91961204) and was supported by the Fundamental Research Funds for the Central Universities. This work was funded in Mexico by Conacyt (Proyecto FORDECYT-PRONACES/1561802/2020). The partial calculations in this work are supported by the High Performance Computing Center of Jilin University, China. AKG acknowledges the financial support received from DST-SERB, INDIA (ECR/2016/001466). GCT thanks Conacyt for her PhD fellowship. M. O.-I. acknowledges the financial support from the Magnus Ehrnrooth Foundation. WT acknowledges the financial support of the National Agency for Research and Development (ANID) through FONDECYT projects 1211128.References
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114 CrossRef CAS.
- L. M. Yang, E. Ganz, Z. F. Chen, Z. X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed. Engl., 2015, 54, 9468–9501 CrossRef CAS PubMed.
- H. J. Monkhorst, Chem. Commun., 1968, 1111–1112 RSC.
- R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4492–4493 CrossRef.
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427 CrossRef CAS.
- G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS PubMed.
- R. Keese, Chem. Rev., 2006, 106, 4787–4808 CrossRef CAS PubMed.
- W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371 RSC.
- D. R. Rasmussen and L. Radom, Angew. Chem., Int. Ed. Engl., 1999, 38, 2876–2878 CrossRef CAS.
- Z. X. Wang and P. v. R. Schleyer, Science, 2001, 292, 2465–2469 CrossRef CAS PubMed.
- Y. Pei, W. An, K. Ito, P. V. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400 CrossRef CAS PubMed.
- O. Yanez, R. Baez-Grez, J. Garza, S. Pan, J. Barroso, A. Vasquez-Espinal, G. Merino and W. Tiznado, Chemphyschem, 2020, 21, 145–148 CrossRef CAS PubMed.
- M. H. Wang, X. Dong, Y. H. Ding and Z. H. Cui, Chem. Commun., 2020, 56, 7285–7288 RSC.
- J. C. Guo, L. Y. Feng, J. Barroso, G. Merino and H. J. Zhai, Chem. Commun., 2020, 56, 8305–8308 RSC.
- S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355 RSC.
- Z. H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y. H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141 RSC.
- J. C. Guo, W. J. Tian, Y. J. Wang, X. F. Zhao, Y. B. Wu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2016, 144, 244303 CrossRef PubMed.
- Y. B. Wu, Y. Duan, H. G. Lu and S. D. Li, J. Phys. Chem. A, 2012, 116, 3290–3294 CrossRef CAS PubMed.
- J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778 RSC.
- R. Sun, B. Jin, B. Huo, C. X. Yuan, H. J. Zhai and Y. B. Wu, Chem. Commun., 2022, 58, 2552–2555 RSC.
- K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- Y. B. Wu, Y. Duan, G. Lu, H. G. Lu, P. Yang, P. V. Schleyer, G. Merino, R. Islas and Z. X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 14760–14763 RSC.
- L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2020, 133, 8782–8786 CrossRef.
- E.-U. Würthwein and P. V. R. Schleyer, Angew. Chem., Int. Ed. Engl., 1979, 18, 553–554 CrossRef.
- F. L. Gu, X. M. Yang, A. C. Tang, H. J. Jiao and P. v. R. Schleyer, J. Comput. Chem., 1998, 19, 203–214 CrossRef CAS.
- H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed. Engl., 2003, 42, 6004–6008 CrossRef CAS PubMed.
- S.-D. Li, G.-M. Ren, C.-Q. Miao and H.-J. Zhai, Angew. Chem., Int. Ed. Engl., 2004, 43, 1371–1373 CrossRef CAS PubMed.
- A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed. Engl., 2000, 39, 3307–3310 CrossRef CAS PubMed.
- M.-h. Wang, X. Dong, Z.-h. Cui, M. a. Orozco-Ic, Y.-h. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775 RSC.
- M. Garcon, C. Bakewell, G. A. Sackman, A. J. P. White, R. I. Cooper, A. J. Edwards and M. R. Crimmin, Nature, 2019, 574, 390–393 CrossRef CAS PubMed.
- W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168 CrossRef CAS PubMed.
- T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed. Engl., 2012, 51, 2101–2105 CrossRef CAS PubMed.
- F. Ebner and L. Greb, J. Am. Chem. Soc., 2018, 140, 17409–17412 CrossRef CAS PubMed.
- F. Ebner and L. Greb, Chem, 2021, 7, 2151–2159 CAS.
- P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432 CrossRef CAS PubMed.
- F. Ebner, H. Wadepohl and L. Greb, J. Am. Chem. Soc., 2019, 141, 18009–18012 CrossRef CAS PubMed.
- M. H. Wang, C. Chen, S. Pan and Z. H. Cui, Chem. Sci., 2021, 12, 15067–15076 RSC.
- C. B. Shao and Y. H. Ding, Phys. Chem. Chem. Phys., 2010, 12, 13153–13157 RSC.
- Z. H. Cui and Y. H. Ding, Phys. Chem. Chem. Phys., 2011, 13, 5960–5966 RSC.
- X. M. Zhang, J. Lv, F. Ji, H. S. Wu, H. J. Jiao and P. V. R. Schleyer, J. Am. Chem. Soc., 2011, 133, 4788–4790 CrossRef CAS PubMed.
- Z. C. Liu, J. Y. Lei, M. Frasconi, X. H. Li, D. Cao, Z. X. Zhu, S. T. Schneebeli, G. C. Schatz and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 2014, 53, 9193–9197 CrossRef CAS PubMed.
- A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah, I. Baruah and A. K. Guha, Inorg. Chem., 2020, 59, 17880–17883 CrossRef CAS PubMed.
- G. Castillo-Toraya, M. Orozco-Ic, E. Dzib, X. Zarate, F. Ortiz-Chi, Z. H. Cui, J. Barroso and G. Merino, Chem. Sci., 2021, 12, 6699–6704 RSC.
- C. Chen, Y. Q. Liu and Z. H. Cui, Inorg. Chem., 2021, 60, 16053–16058 CrossRef CAS PubMed.
- J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- (a) M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (c) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS; (b) R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinsk, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- F. James, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef.
- (a) J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed; (b) H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC; (c) D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev., 2016, 6, 639–678 CAS.
- G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309 CrossRef CAS PubMed.
- R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228 CrossRef CAS PubMed.
- M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav- Mérida, México, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- F. E. Jorge, A. C. Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108 CrossRef CAS PubMed.
- M. Orozco-Ic, N. D. Charistos, A. Munoz-Castro, R. Islas, D. Sundholm and G. Merino, Phys. Chem. Chem. Phys., 2022, 24, 12158–12166 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. M. Pendas, M. A. Blanco and E. Francisco, J. Chem. Phys., 2004, 120, 4581–4592 CrossRef CAS PubMed.
- A. M. Pendas, E. Francisco and M. A. Blanco, J. Comput. Chem., 2005, 26, 344–351 CrossRef CAS PubMed.
- M. A. Blanco, A. M. Pendas and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- ADF2020, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com/ Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- (a) M. M. Kappes, Chem. Rev., 1988, 88, 369–389 CrossRef CAS; (b) F. T. Silva, A. Rocha-Santos, C. L. Firme, L. A. De Souza, I. C. Anjos and J. C. Belchior, J. Mol. Model., 2020, 26, 317–326 CrossRef CAS PubMed.
- P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197 CrossRef PubMed.
- (a) H. Tanaka, S. Neukermans, E. Janssens, R. E. Silverans and P. Lievens, J. Am. Chem. Soc., 2003, 125, 2862–2863 CrossRef CAS PubMed; (b) M. Kulichenko, W.-J. Chen, Y.-Y. Zhang, C.-Q. Xu, J. Li and L.-S. Wang, J. Phys. Chem. A, 2021, 125, 4606–4613 CrossRef CAS PubMed; (c) A. J. Kalita, I. Baruah, K. Sarmah, R. R. Borah, F. Yashmin and A. K. Guha, Inorg. Chem., 2022, 61, 1259–1263 CrossRef CAS PubMed; (d) A. J. Kalita, K. Sarmah, F. Yashmin, R. R. Borah, I. Baruah, R. P. Deka and A. K. Guha, Sci. Rep., 2022, 12, 10041 CrossRef CAS PubMed; (e) E. Ravell, S. Jalife, J. Barroso, M. Orozco-Ic, G. Hernández-Juárez, F. Ortiz-Chi, S. Pan, J. L. Cabellos and G. Merino, Chem. – Asian J., 2018, 13, 1467–1473 CrossRef CAS PubMed; (f) H. T. Pham, L. Q. Ngo, M. P. Pham-Ho and M. T. Nguyen, J. Phys. Chem. A, 2016, 120, 7964–7972 CrossRef CAS PubMed.
- C. Foroutan-Nejad, J. Vicha and A. Ghosh, Phys. Chem. Chem. Phys., 2020, 22, 10863–10869 RSC.
- Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789–4796 CrossRef CAS PubMed.
- G. Periyasamy, N. A. Burton, I. H. Hillier and J. M. H. Thomas, J. Phys. Chem. A, 2008, 112, 5960–5972 CrossRef CAS PubMed.
- M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Munoz-Castro and G. Merino, Chem.–Eur. J., 2020, 26, 326–330 CrossRef CAS PubMed.
- C.-G. Zhan, F. Zheng and D. A. Dixon, J. Am. Chem. Soc., 2002, 124, 14795–14803 CrossRef CAS PubMed.
- X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed. Engl., 2000, 39, 3630–3633 CrossRef CAS PubMed.
- S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304 RSC.
- (a) L.-M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed; (b) L.-M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551 RSC; (c) I. A. Popov, F.-X. Pan, X.-R. You, L.-J. Li, E. Matito, C. Liu, H.-J. Zhai, Z.-M. Sun and A. I. Boldyrev, Angew. Chem., Int. Ed., 2016, 55, 15344–15346 CrossRef CAS PubMed; (d) I. A. Popov, A. A. Starikova, D. V. Steglenko and A. I. Boldyrev, Chem. –Eur. J., 2018, 24, 292–305 CrossRef CAS PubMed; (e) H.-L. Xu, I. Popov, N. Tkachenko, Z.-C. Wang, A. Munoz-Castro, A. I. Boldyrev and Z.-M. Sun, Angew. Chem., Int. Ed., 2020, 59, 17286–17290 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05939h |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2023 |