Open Access Article
Open Access ArticleBond clusters control rupture force limit in shear loaded histidine-Ni2+ metal-coordinated proteins†
Eesha
Khare
 ab,
Darshdeep S.
Grewal
ab,
Darshdeep S.
Grewal
 ab and
Markus J.
Buehler
ab and
Markus J.
Buehler
 *b
*b
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
bLaboratory for Atomistic and Molecular Mechanics, Massachusetts Institute of Technology, 33 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: mbuehler@mit.edu
First published on 14th April 2023
Abstract
Dynamic noncovalent interactions are pivotal to the structure and function of biological proteins and have been used in bioinspired materials for similar roles. Metal-coordination bonds, in particular, are especially tunable and enable control over static and dynamic properties when incorporated into synthetic materials. Despite growing efforts to engineer metal-coordination bonds to produce strong, tough, and self-healing materials, the systematic characterization of the exact contribution of these bonds towards mechanical strength and the effect of geometric arrangements is missing, limiting the full design potential of these bonds. In this work, we engineer the cooperative rupture of metal-coordination bonds to increase the rupture strength of metal-coordinated peptide dimers. Utilizing all-atom steered molecular dynamics simulations on idealized bidentate histidine-Ni2+ coordinated peptides, we show that histidine-Ni2+ bonds can rupture cooperatively in groups of two to three bonds. We find that there is a strength limit, where adding additional coordination bonds does not contribute to the additional increase in the protein rupture strength, likely due to the highly heterogeneous rupture behavior exhibited by the coordination bonds. Further, we show that this coordination bond limit is also found natural metal-coordinated biological proteins. Using these insights, we quantitatively suggest how other proteins can be rationally designed with dynamic noncovalent interactions to exhibit cooperative bond breaking behavior. Altogether, this work provides a quantitative analysis of the cooperativity and intrinsic strength limit for metal-coordination bonds with the aim of advancing clear guiding molecular principles for the mechanical design of metal-coordinated materials.
Introduction
Biological organisms take advantage of dynamic noncovalent interactions to form structures with specific mechanical properties such as strength and toughness.1–3 Metal-coordination bonds, in particular, offer a larger range of tunability over bond energy and timescales compared to most dynamic noncovalent interactions. Simply changing the metal ion present in the system enables tunable control over static and dynamic properties.4,5 These bonds contribute to the remarkable strength, toughness, hardness, and extensibility of several natural protein materials.1,4 The marine worm jaw Nereis virens and its constitutive proteins, for example, feature as high as 8–12 wt% of metal ion and up to 25 mol% of histidine, an amino acid with an especially strong propensity towards metal ion binding.6 The worm jaw has the same hardness as the human cortical bone, despite only using metal-coordination bonds instead of mineralized regions. Mussel byssal threads, as another example, utilize metal-coordination for simultaneous self-healing and high toughness.1,7 Other histidine-rich proteins also exhibit binding interactions with several metal ions.8,9Inspired by these biological materials, research efforts using metal-coordination bonds have dramatically increased.4,10 Recent studies have incorporated coordination bonds in materials to engineer strength, self-healing, and energy absorbing properties.11–14 Despite these significant advances, both an understanding of the mechanical role of metal ions in metal-rich proteins and an extrapolation beyond biological proteins into synthetic materials is missing. This is in large part due to the smaller number of resolved structures of proteins with several metal ion binding sites,15 unlike the well-known structural resolution for hydrogen-bonded alpha helixes or beta-sheets. This lack of structural resolution, coupled with additional challenges such as polymorphic binding states and speciation,16 results in an unclear understanding of why natural materials have incorporated metal-coordination bonds or how to optimize their use in biologically-inspired materials for mechanical function.
The goal of this current work is to uncover critical structural-mechanical principles for metal-coordination bonds. We investigate whether mechanical cooperativity can be engineered in metal-coordination bonds. Additionally, we seek the extent to which strength and rupture mechanics can be modeled, understood, and predicted from fundamental interatomic and chemical principles. While most of the understanding of the cooperativity of such metal-coordination bonds has been in the context of structure or thermodynamic stability,17–19 with extensive literature discussing the effects of multivalent binding,20–22 few systematic studies exist on the cooperative contribution of multiple metal-coordination bonds to the mechanical properties of proteins, and broadly bio-inspired materials engineering.23–25 Developing such a systematic understanding would enable the rational design of mechanically robust metal-coordinated proteins and polymers, complementing the growing experimental work in incorporating multiple metal-coordination interactions in bio-inspired proteins or polymers.26–28
To examine the role of multiple metal-coordination bonds on the mechanical properties of proteins, we design de novo histidine-rich peptides that coordinate to Ni2+ metal ions in an ideal manner and test their mechanical strength using all-atom steered molecular dynamics (SMD) simulations. By analyzing the rupture force of the different metal-coordinated peptides, we find that multiple rupture pathways exist for these coordinated systems and that a maximum of three bonds can rupture at one time. This results in a maximum force limit where adding further metal-coordination bonds does not increase the strength of the peptide. The number of histidine-Ni2+ metal-coordination bonds at which this force limit occurs is equal to the most probable number of coordination bonds observed in proteins with excess metal ions. Given this, we extrapolate our findings to demonstrate how proteins might be tuned with dynamic noncovalent bonds more broadly to achieve alternate cooperative bond breaking behavior.
Results and discussion
De novo peptides (ESI File 1†) were designed to test whether metal-coordination bonds could behave cooperatively to increase to the mechanical strength of a metal-coordinated peptide dimer. To probe this question, the transient bond chemistry, number of coordination bonds, and peptide backbone architecture were specifically engineered. Histidine-Ni2+ bonds were selected as the coordination bond because they possess a strong binding chemistry and have been widely used and characterized in both biological and non-biological polymer contexts (such as the his-tag) using both experimental and computational methods.18,29–32 Ni2+ also has appropriate parameters for molecular dynamics modeling.33–35To inform the number of metal-coordination bonds that should be placed along the peptide backbone, we applied an earlier model36,37 that predicts the number of hydrogen bonds that break simultaneously (denoted as Ncr) to our transient histidine-Ni2+ peptides. The equation is rooted in the application of energetic arguments originally proposed in the Griffith fracture theory, which dictates that the release of energy during the fracture process (G) is counterbalanced by the energy penalty required to create new surfaces (γs).38 The Griffith fracture theory applies to a crack in a plate under tensile loading, which mimics the tensile pulling conditions in our simulations.
Key insights from the earlier model36,37 are briefly summarized here for clarity. The free energy release rate (G) is calculated from the Marko–Siggia worm-like chain model,39 and the release rate is dependent on α, the ratio between the end-to-end length of the free protein chain to its contour length.
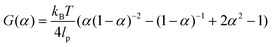 | (1) |
The critical free energy release (Gcr) is equal to the energy penalty required to create new surfaces (γs):
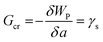 | (2) |
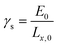 | (3) |
The critical αcr ratio is when (1) is set equal to (3). The corresponding critical rupture force of a system based on the WLC model is then:
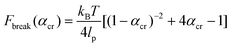 | (4) |
To calculate Ncr, the Bell model is used, and it is assumed that the energy barrier increases Ncr-fold when Ncr bonds break simultaneously, such that the resulting rupture force of the system is:
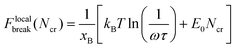 | (5) |
Setting Flocalbreak(Ncr) = Fbreak results in the critical number of bonds that ruptures simultaneously:
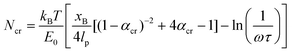 | (6) |
The following parameters are used to determine the Ncr prediction for the histidine-Ni2+ bonds: characteristic time scale of τ = 0.06 s (ref. 40) (for reference, τ ∼ 0.1 s for a 4PEG-His3 polymer in TRIS buffer which likely forms only 1 coordination bond),24 applied pulling distance at the moment of rupture xB of 2 Å, persistence length lp of 0.4 nm,41–43 and a bond energy E0 of ∼11 kcal mol−1 based on the SMD studies done in this work on the (histidine)2-Ni2+ complex (Fig. 1a). These inputs result in an Ncr prediction of 2–3 bonds, given a coordination bond spacing distance (Lx,0) of 4–7 Å (Fig. 1b). kB is the Boltzmann constant, and ω is the natural frequency of bond vibration 1 × 1013 s−1. For comparison, the Ncr of 5–6 bonds is predicted if other bond energies suggested in literature are also shown.23,44
 | ||
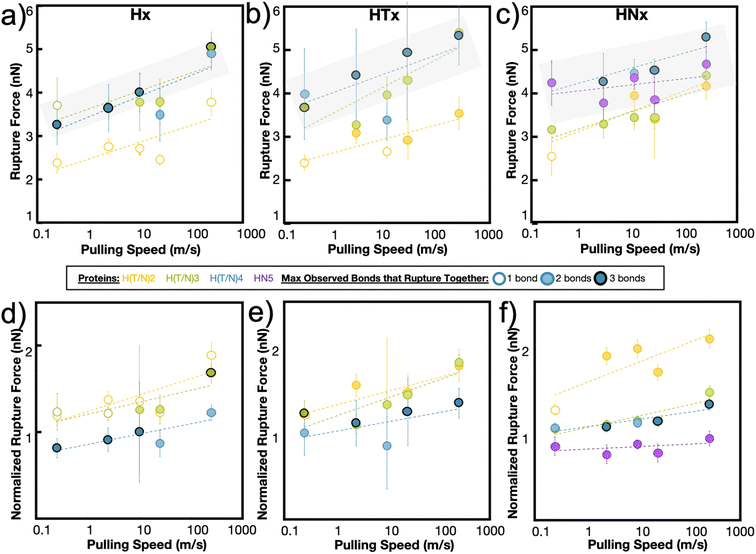
| Fig. 1 A set of de novo model peptides are designed to test metal-coordination cooperative rupture behavior under mechanical loading. (a) SMD on a (histidine)2-Ni2+ complex (shown in inset) at varying pulling rates shows that the rupture force decreases as the pulling rate decreases. (b) The Griffith fracture theory, modified to predict the fracture of hydrogen bonds,36 predicts an Ncr for histidine-Ni2+ bonds to be 2–3 bonds based on the SMD Bell Model energy of the (histidine)2-Ni2+ complex shown in (a), and 5–6 bonds for a lower bond energy calculated in literature. (c) Three peptide systems are designed for study—a purely histidine system (Hx), and a histidine (H) system with a threonine (T) or asparagine (N) as a spacer residue between the histidine residues. Side chains of each amino acid are shown in the inset, Ni2+ atoms are in green, and coordinating nitrogens on the histidines are shown as spheres. Explicit water molecules are not shown for clarity. | ||
To most closely mimic prior research efforts on the cooperativity in hydrogen bonds in beta-sheets,36,45 and to isolate the mechanical contributions of the metal-coordination bonds from the unwinding of the protein backbone,46 we designed peptides with a secondary structure of a beta-sheet-like linear protein. Histidine has a neutral propensity towards beta-sheet formation, so two molecules were designed with spacer amino acids (H-)x using threonine (T) and asparagine (N), which have both shown to have a high propensity for producing a flat beta-sheet when in solvent-exposed conditions (Fig. 1c).47–49 Further, though the polarity of threonine and asparagine are required to aid in solvent-exposed beta-sheet formation, they exhibit a significantly lower propensity for metal-coordination interactions with Ni2+ compared to histidine, which indicates that histidine-Ni2+ interactions should dominate the coordination binding modes.50,51 The resulting sequences are CGG-(HT)x or CGG-(HN)x. In addition, the peptides were designed such that metal-coordination bonds would have a dominating effect on the mechanical properties, as opposed to other secondary structure elements such as interchain hydrogen bonds (Fig. S1†).
In addition to the de novo beta-sheet-like (H-)x proteins, we also tested derivatives of the canonical his-tag system with regards to their cooperative behavior (Fig. 1c). The his-tag is typically composed of 6 histidines and it exhibits a high affinity to Ni2+ in a Ni-NTA column that has enabled the his-tag to be widely used in protein purification.52 His-tags have been studied with AFM-SMFS53 and significant work has also elucidated the structural stability of the his-tag given histidyl mutations.18 Given these prior research efforts, we also test varying numbers of histidine-only Hx peptides (CGG-Hx) under applied mechanical force.31
The maximum rupture force (RF) values for the various de novo peptide dimers are reported in Fig. 2 as a function of pulling speed. Consistent with other experimental and computational studies, the RF values increase as the pulling speed increases for Hx, HTx, and HNx. Further, the RF values observed in the simulation are in a reasonable force range and are twice as strong as hydrogen bonds.36 This increase in strength is unsurprising because the histidine-Ni2+ coordination bond is stronger than hydrogen bonds along the protein backbone based on our SMD calculations for histidine-Ni2+ (Fig. 1a) versus the SMD calculations in ref. 36. Interestingly, all peptides (Hx, HTx, HNx) achieve roughly similar RF values even though HTx and HNx have twice the number of amino acids as Hx for the same number of coordination bonds. This indicates that the strength of the peptides originates from the coordination bonds themselves.
Generally, we find that increasing the number of coordination bonds in the peptide increases the observed RF values to a certain extent. For example, RFH3 > RFH2 and RFHN4 > RFHN3, which suggests that adding additional coordination bonds increases peptide strength. An alternative interpretation is that having more coordination bonds along a backbone increases the possible opportunities for cooperative binding. However, this increase in strength of the peptide is not infinite. All three peptide systems exhibit a rupture force limit, indicated by the gray transparent box in Fig. 2, where increasing the number of coordination bonds does not increase the RF of the peptide dimer. This limit occurs around H3/H4 for the Hx system, HT3/HT4 for the HTx system, and HN4/HN5 for the HNx system. The location of the RF limit with respect to the number of coordination bonds on the peptide indicates that roughly three to four bonds work together to rupture in these peptide systems. Having the fourth coordination bond in the case of Hx or HTx, as an example, does not increase the RF value of the peptide, implying that three coordination bonds would be enough to reach the strength. The value of three to four bonds aligns with the Ncr prediction for Fig. 1b. Note that the canonical his-tag (H6) in a bidentate trans configuration was unstable during equilibration after several attempts to ensure binding and was therefore not simulated using SMD.
The RF data is normalized to the number of coordination bonds in the system and is plotted in Fig. 2d–f to demonstrate the diminishing-returns effect of adding additional coordination bonds to the peptide. This figure is one way to visualize how each coordination bond contributes to the rupture of the system, assuming all coordination bonds equally contribute to the strength of the dimer. From this normalized figure, we made two observations. First, H2/H3, HT2/HT3, and HN3/HN4 overlap in their normalized RF contribution. These normalized threshold values are 1 bond unit below the RF bond threshold values from Fig. 2a–c. Second, each additional bond contributes less to the strength of the peptide. If each metal-coordination bond in an (H)x system was to contribute to the mechanics of the peptide in the same strength as (H)x−1, we would expect the normalized peptide rupture forces in Fig. 2d–f to be superimposed. This implies that there is an optimum value of metal-coordination bonds that achieves maximum strength without wasting additional resources in the form of extra coordination bonds.
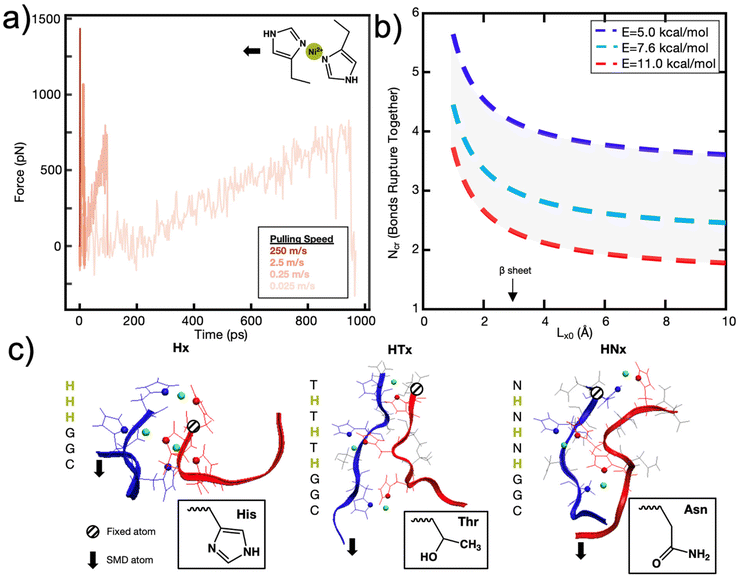
To explore this further, and to seek empirical evidence from naturally evolved protein structures, we conducted a search of representative metal-coordination sites of biological metals using the MetalPDB database.15 We examined representative protein structures with 5 to 10 metal sites and analyzed how many proteins had consecutively arranged metal ions (Fig. 3a), where consecutive is defined as separated by a distance of 3 Å but not necessarily on the same protein chain (Fig. 3b and c, ESI File 2†). We only analyzed proteins with 5 to 10 metal ions to characterize how metal ions were arranged when there is an “excess” of metal ions above the ∼3–4 cooperative bond threshold discussed above. We found that for this set of 143 representative metal sites, the most likely number of consecutive bonds observed was three for the biological metal ions. This finding seems to support that in most of the cases (63% for biological metal ions) we analyzed, metal ions are organized with 1, 2 or 3 bonds consecutively. This preliminary analysis can be further expanded by analyzing proteins with 2–4 metal ions to understand the spatial distribution of metal ions. Further, we note that MetalPDB mostly includes proteins of catalytic functions, but not structural functions. A more refined analysis beyond the scope of this study would include proteins with mechanical functions once their structures have been resolved and dimeric structures such as those analyzed in this investigation. Nonetheless, these biological proteins seem to confirm the existence of an optimum number of metal-coordination bonds to maximize properties.
 | ||
| Fig. 3 Biological metals from MetalPDB15 follow trend where structures are more likely to have 1–3 metal ions consecutively arranged than 4–8. (a) Percent of structures with x number of consecutive metal ions within the 143 structures analyzed. Gaussian fit with a peak at ∼2.6 bonds is also drawn. (b) Metal Site ID 2eul_6 with 3 of the 6 Zn2+ ions consecutively arranged. (c) Metal Site ID 3th4_1 with 6 metal ions (5 Ca2+, 1 Mg2+) consecutively arranged. | ||
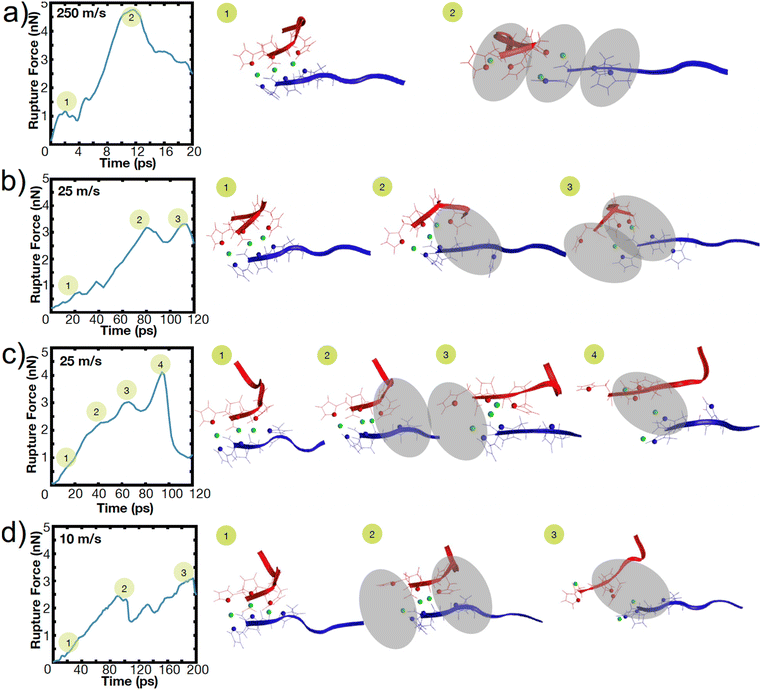
In our simulations, this optimum number manifests itself as the maximum number of coordination bonds that rupture together. Throughout all peptide systems, only a maximum of three bonds are observed to rupture at once, even when more coordination bonds are present in the system (Fig. 2). The shading of the circle (1, 2, or 3 bonds) indicates the maximum observed bonds that rupture together across all simulation repetitions in a specific peptide at a specific speed. These rupture events are highly heterogeneous, where different combinations of bond breaking clusters occur depending on the initial conditions or velocities.
To illustrate this heterogeneity in breaking events, Fig. 4 shows the heterogeneous breaking that independent simulations of the H3 peptide dimer undergo at various pulling rates. In Fig. 4a, for example, three bonds rupture together, but in Fig. 4c, one bond ruptures at a time. Further, even for the same pulling speed, Fig. 4b and c depict different breaking pathways, with two bonds breaking in Fig. 4b or sequential rupture in Fig. 4c. This surprising heterogeneity can be rationalized; the metal-coordination bonds here do not have the well-defined binding pocket or geometry that hydrogen bonds have in beta-sheets, enabling several mechanisms of rupture. Additional contributions to heterogeneity may also arise from other polymorphic binding states, even though only one binding state in a bidentate trans configuration is explored here.
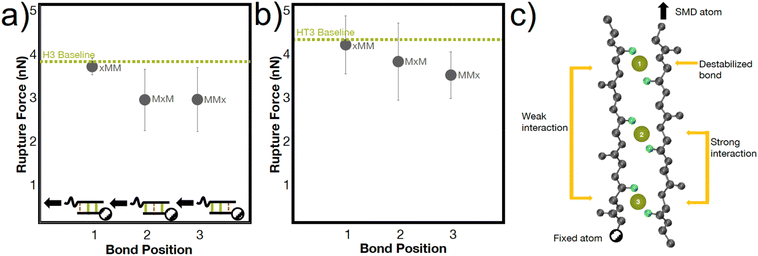
The heterogenous breaking patterns occur with the simultaneous breaking of bonds directly next to each other, spaced one bond apart, or spaced two bonds apart. To better understand how these different positions of bonds may affect the mechanical strength of the peptide, we conducted simulations in the H3 and HT3 peptides where the coordination bonds are placed in different positions (Fig. 5). In almost every simulation (66% for H3, 77% for HT3), the bond closer to the SMD pulling atom ruptures first. However, the resulting rupture forces are only weakly dependent on the position of the bond. The “xMM” systems have moderately higher RF values (p value ∼0.15 for H3, ∼0.25 for HT3) compared to the other geometric arrangements because the two coordination bonds are directly next to each other and away from the SMD pulling atom (Fig. 5a inset). These two coordination bonds can directly influence each other's breaking, and as a result, strengthen the peptide system. Surprisingly, the “MxM” system with a coordination bond in the first and third site and the “MMx” system with two coordination bonds closer to the SMD pulling atom have similar RF values. For “MxM”, the coordination bonds may be too far apart to influence each other without the presence of the coordination bond in the second site. For the “MMx” system, the force felt by the first coordination bond near the SMD pulling atom is likely directly felt by the second coordination bond in its proximity. The schematic in Fig. 5c illustrates these molecular learnings. The amino acids that are more closely spaced together have a greater effect on each other's conformations. This mechanism, while at a geometrically larger scale, may have similar energetic underpinnings as the trans/gauche conformations in polymers that are caused by short-range steric interactions.54
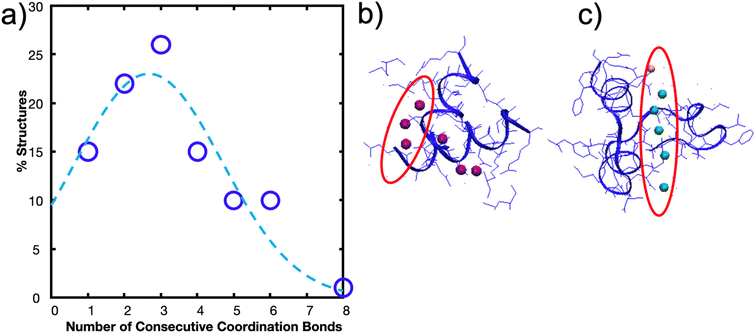
These mechanistic breaking pathways, the observation of an increase in RF followed by a plateau, and the comparison to biological metal-coordinated proteins suggest the presence of a critical number of metal-coordination bonds in these peptide systems. Given that this critical number for histidine-Ni2+ generally follows the predictions from the Ncr in Fig. 1b for our specific idealizing binding arrangement, we further parameterize the Ncr prediction to characterize how changing protein parameters can affect the cooperative strength or number of bonds that simultaneously rupture in other transient systems where the Griffith fracture theory is also applicable. As in hydrogen bonded beta-sheets,36 only a cluster of transient bonds break at once along a linear peptide, even if more bonds are present in the system (Fig. 6a). This may be why several biological materials have evolved to feature noncovalent interaction size effects,55 enabling an optimization of properties with limited mass or weight.
 | ||
| Fig. 6 N cr can be tuned by changing several design parameters with a major influence of energy of the bond (E) and Lx,0, and a minor influence from lp, xb, τ. (a) Adapted from ref. 36, the schematic illustration depicts that only Ncr bonds break in a structure, even if more transient bonds are present. To increase the force at rupture, Ncr bonds should be placed in parallel. In Fig. 1b, we show that Ncr is most sensitive to the values of E, the energy of the bond and Lx,0, or the distance between bonds. Here we characterize other variables that affect the Ncr to show how design parameters such as polymer backbone or bond relaxation time can be tuned to change the Ncr. (b) Ncr increases as a function of τ, the characteristic time scale of bond rupture. This dependence is plotted across multiple values of bond energy, which specific E values highlighted as: (i) 2.83 kcal mol−1 for hydrogen bonds,36 (ii) ∼11 kcal mol−1 for the metal-coordination bonds in this study, (iii) 25 kcal mol−1 for Zn2+(N-methylacetamide)4-(N-methylacetamide),72 (iv) 64 kcal mol−1 for HS–SH,73 and (v) 100 kcal mol−1 for C–H.74 (c) Ncr as a function of persistence length (lp) demonstrates that as the lp increases, Ncr decreases. We plot this dependence for various xb, or the applied pulling distance at the moment of rupture and include the inset to show how Lx,0 and xb are conceptually related. Vertical lines are drawn at critical lp values discussed in literature at (i) 0.13 nm for myosin fragments,56 (ii) 0.4 nm for elastin-like polypeptides or other proteins,36,41,42 (iii) 2 nm for a single disrupted amino acid chain,58 (iv) 45 nm for 1000 base pair DNA,57 and (v) 100 nm for an alpha helix or worm-like fibrils.59,60 Changing the strength of the van der Waals potential of the Ni2+ metal ion, equivalent to changing the energy of the bond (E), decreases the Ncr and rupture force of H4 (d) and (HT)4 (e and f). A multiple of 1 is the original van der Waals parameter for Ni2+ used throughout the paper. | ||
Fig. 1b shows that the spacing of the bonds along the backbone (Lx,0) and energy of the bond (E0) have the largest effects on the resulting Ncr. Decreasing the spacing helps the bonds more effectively mechanically “communicate” with each other, such that local steric interactions are directly affected by neighboring residues. Further, decreasing the energy of the bond allows the force to be distributed amongst the bonds of the backbone such that high stress or strain is not concentrated at the first bond that the force encounters. This is likely why the predicted Ncr value in our work, where the E0 of coordination bonds is ∼3× greater than for hydrogen bonds, is less than the Ncr of ∼3–4 bonds observed for hydrogen bonded systems.36 Increasing the τ, the characteristic time scale of bond rupture, also increases Ncr and various values are plotted in Fig. 6c. This increase is likely due to the idea that increasing τ increases the residence time of the coordination bonds in an area, which would increase their likelihood of rupturing together. The Ncr can also be tuned by changing the persistence length (lp), where an increased protein backbone rigidity (lp), causes a decrease in Ncr (Fig. 6b). This may be because the energy required to compensate the change in a rigid backbone (higher lp) upon additional metal-coordination binding penalty is too high, similar to the binding affinity decreases observed in Hebel et al.22 Various vertical lines on Fig. 6b show critical lp values discussed in literature56–60 to suggest possible backbones that could be used in further experimental or computational studies. Further, the effect of lp is shown with varying xB, or the applied pulling distance at the moment of rupture.
To demonstrate one aspect of this Ncr tunability, we changed the van der Waals interaction strength (epsilon) of the Ni2+ ions to directly simulate how the energy of the bond (E0) affects Ncr and RF. We tested the H4 and (HT)4 systems, as these proteins demonstrated the most opportunities for cooperative rupture. Our simulations show that as expected, increasing E decreases Ncr in both H4 (Fig. 6d) and (HT)4 (Fig. 6e). Interestingly, the trend of Ncrversus the strength of the interaction potential follows a pseudo-parabolic shape. Our simulations showed that this is because the low interaction potentials are too weak to keep the bonds intact, resulting in natural dissociation of the bonds before they can be pulled for cooperative rupture. These Ncr trends result in a similar parabolic shape in the rupture force (Fig. 6f). The decrease in RF even at high interaction potentials which should require large forces to rupture is surprising, but confirms that the RF is highly dependent on the number of bonds that rupture together. Together, these parameters suggest how de novo proteins may be designed with other protein backbones or dynamic noncovalent interactions to tune the cooperative rupture of bond clusters.
Conclusions
In this study, we sought to engineer the cooperative rupture of metal-coordination bonds to increase the strength of coordinated protein structures. Selecting de novo linear histidine-Ni2+ coordinated peptides as a model system, we have shown simultaneous rupture and how the rupture strength of the peptides can be tuned by adjusting the number of metal-coordination bonds in the protein. We designed idealized linear de novo Hx, HTx, and HNx peptide dimers in trans bidentate coordination geometries and showed that by increasing the amount of metal-coordination in the peptides, we could increase the rupture force of the peptides. We found that there was a strength limit in these peptides, at around three to four bonds for all three systems, where increasing the number of coordination bonds beyond this value did not contribute to increased strength of the system. To corroborate this finding, we used mechanistic insight into the metal-coordination breaking mechanisms found in simulation to show that only a maximum three bonds are observed to rupture in each system, even if there are more coordination bonds present in the system. These mechanisms revealed that a heterogenous breaking pattern emerged for the metal-coordinated peptides, where even under the same pulling conditions, different numbers or combinations bonds may break.These findings indicate important design insights into the use of metal-coordination bonds in natural and synthetic systems. There is a balance between achieving high strength and optimizing the resources, such as the number of coordination bonds used, in a protein structure. Despite the fact that the cooperative rupture limit in our work is dependent on protein structure and microenvironment, similar principles have been found for hydrogen bonded structures, where the most effective use of hydrogen bonds towards mechanical strength is when the bonds are clustered in groups of three to four to enable cooperative deformation.36,61,62 Further, this optimization results in several design principles, some of which are demonstrated here through the Griffith fracture theory if applicable to the system of interest, to influence mechanical strength. As such, the mechanistic insights gained here have a much larger relevance to the rational design of metal-coordinated or dynamic noncovalent material mechanics.
Perhaps most importantly, we find that metal-coordination bonds show extremely heterogeneous breaking mechanisms and that designing well-defined binding pockets could force specific rupture pathways. Future studies could design alternative protein backbones to program these rupture pathways, such as alpha helices where cooperativity has been observed in hydrogen bonds.63 Further, the simulations presented here were an idealized hydrogen-bonded beta-sheet-like configuration, and additional research should be tested on real metal-coordinated proteins systems once structures are characterized. Researchers can also apply methodologies similar to the one shown here to predict the cooperative rupture of other specific protein structures or bond chemistries. Such selectively engineered proteins can later be used to build hydrogels or polymer networks with high strength, toughness, and fast recovery for applications in recyclable polymers, self-healing polymers, artificial muscle actuators or electronic skin, as shown in early examples in literature with such bonds.23,26,64 Additional improvements in metal-ion force fields can also help improve these predictions.65
Altogether, this work contributes clear and fundamental molecular design principles for utilizing multiple metal-coordination bonds for increasing the strength a metal-coordinated protein dimer. These principles help contextualize the structural role of metal ions both within the context of natural systems, as well as in bioinspired synthetic proteins and polymers. Broadly, the systematic understanding from this work contributes to the rational design of cooperativity in metal-coordinated proteins and polymers with mechanical function and expands insights into other dynamic noncovalent interactions.
Methods
The initial structures of the de novo peptide dimers (Fig. 1, ESI File 1†) in a parallel orientation were first predicted using AlphaFold v2.0.66,67 Three additional amino acids (CGG) were attached on either side of the peptide to mimic the cysteine that is often used for immobilization in AFM-SMFS experiments and to ensure that the histidine-Ni2+ bonds were not directly being pulled. Ni2+ ions were added to the system, such that the histidine nitrogen atoms coordinate in a bidentate or tetradentate geometry to the Ni2+ ion. Histidine amino acids were modeled in the correct protonation state to match physiological pH and experiments where the histidine-Ni2+ dissociation time of τ = 0.06 s (ref. 40) has been measured. Simulations were implemented with Nanoscale Molecular Dynamics (NAMD) and all simulations utilized the CHARMM22 force field68 with Ni2+ parameters from Babu et al.33 and a 2 fs timestep. The Ni2+ ions were balanced with Cl− ions for charge neutrality and the peptide dimer was solvated with TIP3P water molecules with a 15 Å skin. Periodic boundary conditions are used with the Particle Mesh Ewald full system electrostatics method. After careful energy minimization using the conjugate gradient algorithm in NAMD, the simulations are equilibrated for 50 ns under NPT (1 atm, Nose–Hoover Langevin piston pressure control), followed by 50 ns in NVT (Langevin dynamics).Independent simulations under this procedure were carried out for subsequent SMD tests. The TIP3P water molecule box was extended by 60 Å to account for deformation in the pulling direction. The Cα atom on the N-terminus near the cysteine residue was selected as the SMD pulling atom, and the Cα atom on the opposite strand C-terminus was selected as the fixed atom. The structure was energy minimized for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Then SMD data were collected every picosecond with pulling rates from 0.25 m s−1 to 250 m s−1 under an NVT ensemble and 2 fs timestep. The simulation was run until the parallel proteins were fully separated and all intermolecular metal-coordination bonds fully ruptured. The rupture of a metal-coordinate bond was defined as a distance of 3 Å or more between the coordinating nitrogen of histidine and the Ni2+ ion. The time, distance, force, and type of bond rupture was recorded for each rupture event in each simulation. Simultaneous rupture was defined as multiple bond breaking events within 1 ps of each other in the visual file with the rupture force peaks that were indistinguishable from each other.
000 steps. Then SMD data were collected every picosecond with pulling rates from 0.25 m s−1 to 250 m s−1 under an NVT ensemble and 2 fs timestep. The simulation was run until the parallel proteins were fully separated and all intermolecular metal-coordination bonds fully ruptured. The rupture of a metal-coordinate bond was defined as a distance of 3 Å or more between the coordinating nitrogen of histidine and the Ni2+ ion. The time, distance, force, and type of bond rupture was recorded for each rupture event in each simulation. Simultaneous rupture was defined as multiple bond breaking events within 1 ps of each other in the visual file with the rupture force peaks that were indistinguishable from each other.
We found that tetradentate structures were not stable during the initial equilibration, and the metal-coordination binding sites would quickly dissociate into tridentate, bidentate, or monodentate structures during the equilibration process. As a result, we continued SMD tests with only bidentate coordination. While this lack of tetradentate stability may be due to challenges with the force field modeling for metal ions, speciation models predict a dominance of bidentate coordination stoichiometry in aqueous conditions between histidine and Ni2+.40,69,70 Further, though the short peptides are equilibrated for a significant amount of time, we note that the peptide structures used in this paper are not necessarily the equilibrium binding state of the peptide with the metal ion, because the peptide may be trapped in a local minima. We also enforce a trans bidentate binding configurations on the metal ions to most closely replicate the hydrogen-bonded beta-sheets. Despite these limitations, we proceed with our simulations because the goal of this paper is to determine whether cooperativity can exist in these bonds under “ideal” conditions, where “ideal” conditions represent the closest geometry to hydrogen bonds due to the cooperativity seen in beta-sheets with trans coordination along the backbone. Further, preliminary simulations of a single peptide (H4, (HT)4, and (HN)4) show that internal metal-coordination bonds are improbable (Fig. S2†), likely due to an entropic penalty of loop formation.71
Author contributions
E. K., M. J. B. conceptualized and designed the research. E. K. and D. S. G. performed the research and conducted the analysis. E. K., D. S. G., and M. J. B. wrote the paper.Data availability
Materials and data are included as ESI,† and/or are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. K. would like to acknowledge the NSF Graduate Research Fellowship Program and the MIT Office of Graduate Education. The authors acknowledge support from NIH (U01EB014976, 1R01AR07779), USDA (2021-69012-35978), ARO (W911NF2220213), DOD/DOE-SERDP (WP22-3475), and ONR (N00014-19-1-2375 and N00014-20-1-2189). The authors acknowledge Bo Ni for support with the Alpha Fold implementations at LAMM, and helpful discussions.References
- E. Degtyar, M. J. Harrington, Y. Politi and P. Fratzl, Angew. Chem., Int. Ed., 2014, 53, 12026–12044 CrossRef CAS PubMed.
- P. Zheng, Y. Cao, T. Bu, S. K. Straus and H. Li, Biophys. J., 2011, 100, 1534–1541 CrossRef CAS PubMed.
- M. Carrion-Vazquez, A. F. Oberhauser, T. E. Fisher, P. E. Marszalek, H. Li and J. M. Fernandez, Prog. Biophys. Mol. Biol., 2000, 74, 63–91 CrossRef CAS PubMed.
- E. Khare, N. Holten-Andersen and M. J. Buehler, Nat. Rev. Mater., 2021, 1–16 Search PubMed.
- D. E. Fullenkamp, L. He, D. G. Barrett, W. R. Burghardt and P. B. Messersmith, Macromolecules, 2013, 46, 1167–1174 CrossRef CAS PubMed.
- H. C. Lichtenegger, T. Schöberl, J. T. Ruokolainen, J. O. Cross, S. M. Heald, H. Birkedal, J. H. Waite and G. D. Stucky, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 9144–9149 CrossRef CAS PubMed.
- M. J. Harrington, A. Masic, N. Holten-Andersen, J. H. Waite and P. Fratzl, Science, 2010, 328, 216–220 CrossRef CAS PubMed.
- R. Ge, Y. Zhang, X. Sun, R. M. Watt, Q. Y. He, J. D. Huang, D. E. Wilcox and H. Sun, J. Am. Chem. Soc., 2006, 128, 11330–11331 CrossRef CAS PubMed.
- Y. B. Zeng, N. Yang and H. Sun, Chem. – Eur. J., 2011, 17, 5852–5860 CrossRef CAS PubMed.
- X. Xu, V. V. Jerca and R. Hoogenboom, Mater. Horiz., 2021, 8, 1173–1188 RSC.
- J. C. Lai, X. Y. Jia, D. P. Wang, Y. B. Deng, P. Zheng, C. H. Li, J. L. Zuo and Z. Bao, Nat. Commun., 2019, 10, 1164 CrossRef PubMed.
- S. A. Cazzell, B. Duncan, R. Kingsborough and N. Holten-Andersen, Adv. Funct. Mater., 2021, 31, 2009118 CrossRef CAS.
- H. Fu, B. Wang, J. Li, J. Xu, J. Li, J. Zeng, W. Gao and K. Chen, Mater. Horiz., 2022, 9, 1412–1421 RSC.
- X. Fan, Y. Fang, W. Zhou, L. Yan, Y. Xu, H. Zhu and H. Liu, Mater. Horiz., 2021, 8, 997–1007 RSC.
- C. Andreini, G. Cavallaro, S. Lorenzini and A. Rosato, Nucleic Acids Res., 2013, 41, D312–D319 CrossRef CAS PubMed.
- J. Watly, E. Simonovsky, N. Barbosa, M. Spodzieja, R. Wieczorek, S. Rodziewicz-Motowidlo, Y. Miller and H. Kozlowski, Inorg. Chem., 2015, 54, 7692–7702 CrossRef CAS PubMed.
- J. Wątły, A. Hecel, M. Rowińska-Żyrek and H. Kozłowski, Inorg. Chim. Acta, 2018, 472, 119–126 CrossRef.
- D. Brasili, J. Watly, E. Simonovsky, R. Guerrini, N. A. Barbosa, R. Wieczorek, M. Remelli, H. Kozlowski and Y. Miller, Dalton Trans., 2016, 45, 5629–5639 RSC.
- J. Qian and C. Berkland, iScience, 2019, 21, 124–134 CrossRef CAS PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 2754–2794 CrossRef.
- E. Zumbro, J. Witten and A. Alexander-Katz, Biophys. J., 2019, 117, 892–902 CrossRef CAS PubMed.
- M. Hebel, A. Riegger, M. M. Zegota, G. Kizilsavas, J. Gačanin, M. Pieszka, T. Lückerath, J. A. S. Coelho, M. Wagner, P. M. P. Gois, D. Y. W. Ng and T. Weil, J. Am. Chem. Soc., 2019, 141, 14026–14031 CrossRef CAS PubMed.
- W. Sun, B. Xue, Q. Fan, R. Tao, C. Wang, X. Wang, Y. Li, M. Qin, W. Wang, B. Chen and Y. Cao, Sci. Adv., 2020, 6, eaaz9531 CrossRef CAS PubMed.
- Q. Tang, D. Zhao, Q. Zhou, H. Yang, K. Peng and X. Zhang, Macromol. Rapid Commun., 2018, 39, 1800109 CrossRef PubMed.
- I. Mahmad Rasid, C. Do, N. Holten-Andersen and B. D. Olsen, Soft Matter, 2021, 17, 8960–8972 RSC.
- Z. Jiang, A. Bhaskaran, H. M. Aitken, I. C. G. Shackleford and L. A. Connal, Macromol. Rapid Commun., 2019, 40, 1900038 CrossRef PubMed.
- S. Tang, A. Habicht, S. Li, S. Seiffert and B. D. Olsen, Macromolecules, 2016, 49, 5599–5608 CrossRef CAS.
- K. Breul, S. Kissel and S. Seiffert, Macromolecules, 2021, 54, 8407–8422 CrossRef CAS.
- S. Zechel, M. Hager, T. Priemel and M. J. Harrington, Biomimetics, 2019, 4, 20 CrossRef CAS PubMed.
- S. Sjöberg, Pure Appl. Chem., 1997, 69, 1549–1570 CrossRef.
- S. Knecht, D. Ricklin, A. N. Eberle and B. Ernst, J. Mol. Recognit., 2009, 22, 270–279 CrossRef CAS PubMed.
- J. Nomata, M. Kitashima, K. Inoue and Y. Fujita, FEBS Lett., 2006, 580, 6151–6154 CrossRef CAS PubMed.
- C. S. Babu and C. Lim, J. Phys. Chem. A, 2006, 110, 691–699 CrossRef CAS PubMed.
- Y. Won, J. Phys. Chem. A, 2012, 116, 11763–11767 CrossRef CAS PubMed.
- P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2015, 119, 883–895 CrossRef CAS PubMed.
- S. Keten and M. J. Buehler, Nano Letters, American Chemical Society, 2008, vol. 1061, pp. 743–748 Search PubMed.
- M. J. Buehler and H. Gao, Nature, 2006, 439, 307–310 CrossRef CAS PubMed.
- A. A. Griffith, Philos. Trans. R. Soc., A, 1921, 221, 163–198 Search PubMed.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- E. Khare, S. A. Cazzell, J. Song, N. Holten-Andersen and M. J. Buehler, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2213160120 CrossRef CAS PubMed.
- W. Ott, M. A. Jobst, M. S. Bauer, E. Durner, L. F. Milles, M. A. Nash and H. E. Gaub, ACS Nano, 2017, 11, 6346–6354 CrossRef CAS PubMed.
- G. Stirnemann, D. Giganti, J. M. Fernandez and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3847–3852 CrossRef CAS PubMed.
- S. Fluegel, K. Fischer, J. R. McDaniel, A. Chilkoti and M. Schmidt, Biomacromolecules, 2010, 11, 3216–3218 CrossRef CAS PubMed.
- J. Song, E. Khare, L. Rao, M. J. Buehler and N. Holten-Andersen, chemRxiv, 2022 Search PubMed.
- Z. Qin and M. J. Buehler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061906 CrossRef PubMed.
- R. Rohs, C. Etchebest and R. Lavery, Biophys. J., 1999, 76, 2760–2768 CrossRef CAS PubMed.
- K. Fujiwara, H. Toda and M. Ikeguchi, BMC Struct. Biol., 2012, 12, 18 CrossRef CAS PubMed.
- C. K. Smith, L. Regan and J. M. Withka, Biochemistry, 1994, 33, 5510–5517 CrossRef CAS PubMed.
- N. Bhattacharjee and P. Biswas, BMC Struct. Biol., 2010, 10, 29 CrossRef PubMed.
- H. Zheng, M. Chruszcz, P. Lasota, L. Lebioda and W. Minor, J. Inorg. Biochem., 2008, 102, 1765–1776 CrossRef CAS PubMed.
- S. Barber-Zucker, B. Shaanan and R. Zarivach, Sci. Rep., 2017, 7, 16381 CrossRef PubMed.
- J. Crowe, B. S. Masone and J. Ribbe, Methods Mol. Biol., 1996, 58, 491–510 CAS.
- F. Kienberger, G. Kada, H. J. Gruber, V. P. Pastushenko, C. Riener, M. Trieb, H. G. Knaus, H. Schindler and P. Hinterdorfer, Single Mol., 2000, 1, 59–65 CrossRef CAS.
- R. J. Young and P. A. Lovell, Introduction to Polymers, Taylor & Francis Group, Boca Raton, 3rd edn, 2011 Search PubMed.
- H. D. Espinosa, J. E. Rim, F. Barthelat, M. J. Buehler and H. D. Espinosa, Prog. Mater. Sci., 2009, 54, 1059–1100 CrossRef CAS.
- D. D. Root, V. K. Yadavalli, J. G. Forbes and K. Wang, Biophys. J., 2006, 90, 2852–2866 CrossRef CAS PubMed.
- J. Van Noort, T. Van der Heijden, M. De Jager, C. Wyman, R. Kanaar and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7581–7586 CrossRef CAS PubMed.
- M. S. Z. Kellermayer, S. B. Smith, H. L. Granzier and C. Bustamante, Science, 1997, 276, 1112–1116 CrossRef CAS PubMed.
- S. Choe and S. X. Sun, J. Chem. Phys., 2005, 122, 244912 CrossRef PubMed.
- C. C. Vandenakker, M. F. M. Engel, K. P. Velikov, M. Bonn and G. H. Koenderink, J. Am. Chem. Soc., 2011, 133, 18030–18033 CrossRef CAS PubMed.
- S. Keten, Size-Dependent Mechanical Properties of Beta-Structures in Protein Materials, MIT, 2010 Search PubMed.
- T. Ackbarow, X. Chen, S. Keten and M. J. Buehler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16410–16415 CrossRef CAS PubMed.
- R. Wieczorek and J. J. Dannenberg, J. Am. Chem. Soc., 2003, 125, 8124–8129 CrossRef CAS PubMed.
- C. H. Li, C. Wang, C. Keplinger, J. L. Zuo, L. Jin, Y. Sun, P. Zheng, Y. Cao, F. Lissel, C. Linder, X. Z. You and Z. Bao, Nat. Chem., 2016, 8, 618–624 CrossRef CAS PubMed.
- P. Li and K. M. Merz, Chem. Rev., 2017, 117, 1564–1686 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- R. Evans, M. O'Neill, A. Pritzel, N. Antropova, A. Senior, T. Green, A. Žídek, R. Bates, S. Blackwell, J. Yim, O. Ronneberger, S. Bodenstein, M. Zielinski, A. Bridgland, A. Potapenko, A. Cowie, K. Tunyasuvunakool, R. Jain, E. Clancy, P. Kohli, J. Jumper and D. Hassabis, bioRxiv, 2021 DOI:10.1101/2021.10.04.463034.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- S. C. Grindy and N. Holten-Andersen, Soft Matter, 2017, 13, 4057–4065 RSC.
- L. E. Valenti, C. P. De Pauli and C. E. Giacomelli, J. Inorg. Biochem., 2006, 100, 192–200 CrossRef CAS PubMed.
- E. Zumbro and A. Alexander-Katz, ACS Omega, 2020, 5, 10774–10781 CrossRef CAS PubMed.
- Y. R. Luo, Comprehensive handbook of chemical bond energies, CRC Press, 2007 Search PubMed.
- L. F. Zou, Y. Fu, K. Shen and Q. X. Guo, J. Mol. Struct.: THEOCHEM, 2007, 807, 87–92 CrossRef CAS.
- F. H. Seubold, J. Chem. Phys., 1954, 22, 945–946 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr01287e |
| This journal is © The Royal Society of Chemistry 2023 |