Discovering layered lead-free perovskite solar absorbers via cation transmutation

Abstract

For the exploration of stable lead-free perovskites for solar cell applications, we propose a series of Dion–Jacobson (DJ) double perovskites with the formula BDA₂M_IM_IIIX₈ (BDA = 1,4-butanediamine) by substituting two Pb²⁺ in BDAPbI₄ with an M_I⁺ (Na⁺, K⁺, Rb⁺, Cu⁺, Ag⁺, and Au⁺) and M_III³⁺ (Bi³⁺, In³⁺, and Sb³⁺) pair. First-principles calculations demonstrated the thermal stabilities of all the proposed BDA₂M_IM_IIIX₈ perovskites. The electronic properties of BDA₂M_IM_IIIX₈ depend strongly on the choice of M_I⁺ + M_III³⁺ and the structural archetype, and three out of 54 candidates with suitable solar band gaps and superior optoelectronic properties were selected for photovoltaic application. A highest theoretical maximal efficiency of over 31.6% is predicted for BDA₂AuBiI₈. The DJ-structure-induced interlayer interaction of apical I–I atoms is found to play a crucial role in promoting the optoelectronic performance of the selected candidates. This study provides a new concept for designing lead-free perovskites for efficient solar cells.

---

New concepts

Double perovskites have the benefits of being environmentally friendly and stable. However, the majority of the synthesized bulk double perovskites have large indirect bandgaps, large carrier effective masses, and parity-forbidden transitions, which make them unsuitable for photovoltaic applications. Previous studies have demonstrated that indirect-to-direct bandgap transitions are induced by dimensionality reduction, as demonstrated in Cs₂AgBiBr₆ and BA₄AgBiBr₈, because of the avoidance of hybridization of Ag and Bi frontier orbitals. However, the large spacer cation results in suppressed carrier transportation along the interlayer direction. In this work, we construct Dion–Jacobson (DJ) double perovskites BDA₂M_IM_IIIX₈ (BDA = 1,4-butanediamine; M_I⁺ = monovalent cation; M_III³⁺ = trivalent cation). Unlike the transition mechanism in BA₄AgBiBr₈, the indirect-to-direct bandgap transition in selected BDA₂(Cu/Ag/Au)BiI₈ is mainly due to interlayer apical I–I-interaction-induced band broadening, as the smaller spacer divalent cation BDA²⁺ is used. This band broadening can induce further-reduced bandgaps and more-dispersive band edges along the interlayer direction, which is beneficial for carrier transportation. High absorption coefficients and transition probabilities are also established in BDA₂(Cu/Ag/Au)BiI₈. This work indicates that the combination of a DJ archetype and double substitution provide a new approach for designing stable lead-free perovskites for high-performance solar cells.

Hybrid lead-halide perovskites have rapidly developed as the most promising star materials for next-generation photovoltaic and optoelectronic devices because of their tunable bandgaps, balanced carrier effective masses, high absorption onset, small exciton binding energies, long carrier diffusion length, and high defect tolerance factor.^1–7 However, stability issues and the toxicity of lead have hindered their commercialization.^8–12 A effective way to improve the stability of metal-halide perovskites is through cation engineering, which can result in the formation of low-dimensional perovskites with intrinsically improved stability. Layered Dion–Jacobson (DJ) perovskites have attracted substantial attention because of their enhanced stability and improved carrier transportation along the interlayer direction induced by effective interlayer interaction.^13–16

One effective way to solve the toxicity issue of lead-halide perovskites is through cation transmutation, in which two Pb²⁺ cations are replaced by one M⁺ cation (e.g., Na⁺, K⁺, Cu⁺, Ag⁺, Au⁺) and one M³⁺ cation (e.g., Y³⁺, Gd³⁺, Au³⁺, In³⁺, Tl³⁺, Sb³⁺, Bi³⁺) to form double-perovskite structures.^17–24 However, the majority of the synthesized bulk double perovskites are chloride and bromide perovskites, normally with large indirect band gaps (> 1.9 eV) and large carrier effective masses because of the mismatch in angular momentum of the frontier atomic orbitals.¹⁹ Moreover, many reported double perovskites with direct band gaps have been proven to show inversion-symmetry-induced parity-forbidden transitions.¹⁷ These characteristics of most halide double perovskites make them unsuitable for photovoltaic applications. To date, Cs₂AgBiBr₆ has been widely investigated for solar cell application, and the record efficiency has only reached 6.37% because of the relatively large band gap of 2.19 eV.^25–27

Early studies have shown that reduction of dimensionality can lead to enhanced stability of double perovskites and indirect-to-direct band gap transition because of the avoidance of frontier orbital hybridization.^28–32 Additionally, the influence of interlayer coupling on the band gap feature in layered double perovskites has also been mentioned.³⁰ Particularly, the synthesized perovskites (C₆H₁₆N₂)₂AgBiI₈ and (C₆H₁₆N₂)₂CuBiI₈ have measured optical band gaps of 1.93 eV and 1.68 eV, and the CuBiI system shows promising use in photovoltaic applications. Therefore, in order to obtain stable lead-free perovskites with suitable band gaps and good optical properties for solar cell applications, the use of DJ double perovskites may be an efficient strategy.

In this communication, we theoretically studied the stability and optoelectronic properties of a series of environmentally friendly DJ double perovskites proposed through the cation transmutation strategy. Potential solar cell absorber candidates with good stability, a suitable band gap, superior carrier transport properties, and good optical properties are selected for photovoltaic application, and the influences of the cation pair and structural archetype on their optoelectronic properties are thoroughly explored. Among the selected candidates, a theoretical maximum efficiency comparable with that of CH₃NH₃PbI₃ is obtained for BDA₂AuBiI₈. The calculation details are given in the ESI.†

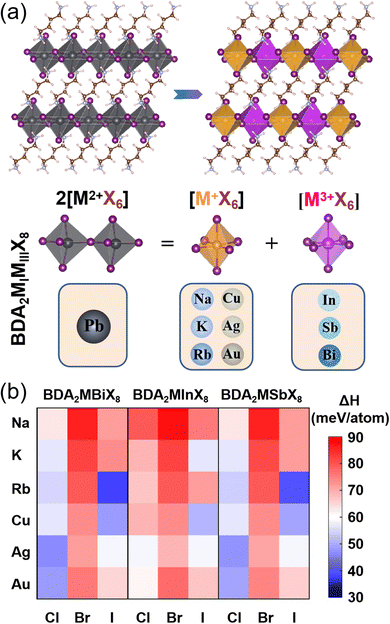
The basic concept of the proposed lead-free layered double perovskites is the replacement of two Pb²⁺ cations in the DJ perovskite APbX₄ with a monovalent M_I⁺ and trivalent M_III³⁺ cation to give the double DJ perovskite A₂M_IM_IIIX₈, as shown in Fig. 1a. Here, the A²⁺ cation is 1,4-butanediamine (BDA²⁺). The optimized structural parameters of 54 BDA₂M_IM_IIIX₈ (M_I⁺ = Na⁺, K⁺, Rb⁺, Cu⁺, Ag⁺, and Au⁺; M_III³⁺ = In³⁺, Sb³⁺, and Bi³⁺; X⁻ = Cl⁻, Br⁻, and I⁻) compounds are shown in Tables S1–S3 (ESI†), and all possess a triclinic symmetry. The doubly protonated cation BDA²⁺ is inserted between inorganic octahedron layers along the [001] direction, and the –NH₃⁺ ends intrude deep into the cavity formed by the apical I atoms and can interact with the bridging I atoms through hydrogen bonds. The interlayer distance is much reduced compared to that of the RP counterpart, which could induce effective interlayer coupling and promote charge transfer between the inorganic layers.³³

Fig. 1 (a) Structural configurations of the 2D perovskites BDAPbI₄ and 2D double perovskites BDA₂M_IM_IIIX₈, and illustration of the cation transmutation strategy to design Pb-free halide 2D double perovskites. (b) Decomposition enthalpies (ΔH) of 2D double BDA₂M_IM_IIIX₈ perovskites.

To evaluate the thermodynamic stability of the BDA₂M_IM_IIIX₈ compounds, their decomposition energies with respect to possible decomposition pathways were considered. Since no ternary option is available, the most possible decomposition path of BDA₂M_IM_IIIX₈ is into the corresponding common binary compounds (BDA₂M_IM_IIIX₈ → 2BDAX₂ + M_IX + M_IIIX₃), and the perovskites can be synthesized via the inverse reaction. The decomposition enthalpy (ΔH_d), which is defined via the free energy difference after and before the above decomposition path, is calculated as follows:

ΔH_d = (2E[BDAX₂] + E[M_IX] + E[M_IIIX₃] − E[BDA₂M_IM_IIIX₈])/N_tot

The calculated values of ΔH_d for all compounds are positive, as shown in Fig. 1b. Here, positive values of ΔH_d mean the decomposition process is endothermic, resulting in suppressed decomposition of BDA₂M_IM_IIIX₈, demonstrating that all the BDA₂M_IM_IIIX₈ have good thermodynamic stability. This enhanced stability can be ascribed to the above-mentioned hydrogen bonds normally found in DJ perovskites.^33,34 As an example, the case of BDAAgBiI₈ is considered. The closest H and bridging I atoms have separation distances of 2.53 and 2.55 Å and an interaction integrated crystal orbital Hamilton population (iCOHP) value of 0.53 eV and 0.51 eV, and the nearest H and apical I atoms have a distance of 2.52 Å and an interaction iCOHP value of 0.58 eV, validating the strong hydrogen bonding between NH₃⁺ and I atoms. These extra hydrogen bonds can promote the rigidity of the structure. Moreover, the divalent organic cation can induce fewer degrees of freedom in the structures because of the elimination of van der Waals gap.³⁵

The band gaps of the 54 compounds calculated using the generalized gradient approximation (GGA)-Perdew–Burke–Ernzerhof (PBE) method are listed in Tables S1–S3 (ESI†). However, due to the strong relativistic effect in heavy elements, the spin–orbit coupling (SOC) effect cannot be neglected. A severe band gap reduction in Bi-based compounds is induced with the inclusion of the SOC effect because of the splitting of the Bi-6p-derived conduction bands. Detailed analysis of the band edges indicates that the locations of the valence band maximum (VBM) and conduction band minimum (CBM) of many compounds are altered when the SOC effect is considered. A comparison of band structures calculated using the PBE and PBE + SOC schemes for several representative compounds is given in Fig. S1 (ESI†) for illustration. Additionally, we also performed band structure calculations using the hybrid HSE + SOC functional, which can provide more precise band gap estimation for most semiconductors.

The variations in the band gaps for different compositions calculated using the HSE + SOC method are shown in Fig. 2. The band gaps for BDA₂M_IBi/In/SbX₈ are found to decrease with decreasing halogen electronegativity. Furthermore, the band gaps are also closely connected with the M_I cation. The band gaps of alkali compounds are larger than those of noble metal compounds with the same halide because of their strong ionic characteristics. The alkali compounds all show indirect characteristics except for BDA₂RbInI₈ and BDA₂KSbBr₈. The projected band structures in Fig. S2–S4 (ESI†) indicate that the alkali elements have negligible contributions to the VBM and CBM, which are instead dominated by the halide p-states and In 5s/Bi 6p/Sb 5p–halide p-hybridization states in BDA₂MIn/Bi/SbX₈, respectively. The projected density of states (PDOS) and COHP analysis of BDA₂KInBr₈ and BDA₂KBiBr₈ in Fig. S5 and S6 (ESI†), as representatives of the alkali BDA₂MInX₈ and BDA₂MBiX₈/BDA₂MSbX₈ compounds, indicate that the VBMs and CBMs mainly originate from the antibonding coupling of interlayer Br 4p–Br 4p states on the K sites and the antibonding coupling of In 5s/Bi 6p–Br 4p states, respectively. The decomposed charge densities of the VBMs and CBMs of BDA₂KInBr₈ and BDA₂KBiBr₈ in Fig. S7 (ESI†) indicate that the VBMs mainly originate from the antibonding coupling of interlayer Br 4p–Br 4p states on the K sites, and have negligible contribution from in-plane interactions. These features of the alkali compounds are also reasons for the less-dispersive band edges and large band gaps in these structures, which are very undesirable for solar cell applications.

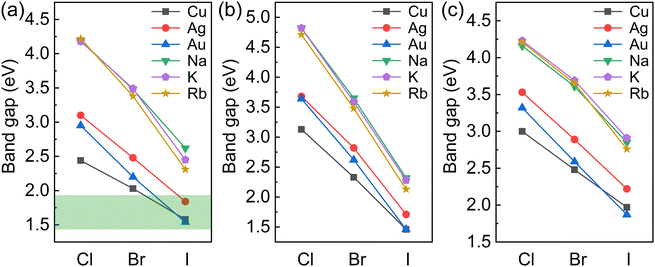Fig. 2 Variation in the band gaps for (a) BDA₂M_IBiX₈, (b) BDA₂M_IInX₈, and (c) BDA₂M_ISbX₈ (M_I = Cu, Ag, Au, Na, K, and Rb; X = Cl, Br, and I)

For the noble-metal BDA₂MInX₆ perovskites, the projected band structures of BDA₂MInX₈ in Fig. S8–S10 (ESI†) all show indirect band gaps. Therefore, despite the fact that BDA₂(Cu/Ag/Au)InI₈ have band gaps suitable for solar cells, their indirect band gap feature makes them unsuitable for thin-film solar cell application. The PDOS and CHOP analysis of BDA₂AgInBr₈ in Fig. S11 (ESI†), as a representative of the noble-metal BDA₂MInX₈ compounds, indicates that the VBM and CBM of BDA₂AgInBr₈ mainly originate from the antibonding coupling of Ag 4d–Br 4p states and In 5s–Br 4p states, respectively. The decomposed charge densities of the VBM and CBM are shown in Fig. S12 (ESI†) for intuitive illustration of the bonding characteristics. This bonding behavior is also the reason for the indirect band gaps of the BDA₂M_IInX₆ compounds.

For the noble-metal perovskites BDA₂MBiX₈ and BDA₂MSbX₈, the projected band structures in Fig. S8–S10 (ESI†) all exhibit direct band gaps, except for those of BDA₂AgSbI₈ and BDA₂AuSbI₈. The projected band structures indicate that the VBMs and CBMs are dominated by the hybridization between metal d–halide p states and Bi 6p/Sb 5p–halide p hybridization states in the BDA₂MBiX₈/BDA₂MSbX₈ perovskites, respectively. Among these structures, BDA₂(Cu/Ag/Au)BiI₈ possess suitable band gaps for solar photovoltaic application. The PDOS and COHP analysis of BDA₂(Cu/Ag/Au)BiI₈ in Fig. S13 and S14–S16 (ESI†), as representatives of the noble-metal BDA₂MBiX₈ and BDA₂MSbX₈ compounds, indicates that the hybridization of Bi 6p–I 5p states and interlayer I 5p–I 5p states on Bi sites near the CBM has mainly antibonding and bonding characteristics, respectively. In contrast, the VBM is dominated by antibonding Cu 3d/Ag 4d/Au 5d–I 5p states, along with weak interlayer antibonding I 5p–I 5p states on the noble metal sites. The coupling strength between apical I–I atoms is mainly determined by their distance. It is found the apical I–I distances in BDA₂AgBiI₈ are smaller than those in BDA₂(Cu/Au)BiI₈; this is mainly because of the stronger coupling of Cu/Au–I bonds than that of Ag–I bonds, as discussed in the next paragraph. Therefore, the COHP of apical I–I near the VBM in BDA₂CuBiI₈ and BDA₂AuBiI₈ are almost negligible, while a stronger apical I–I COHP is observed in BDA₂AgBiI₈. The antibonding characteristics ensure relatively small and balanced in-plane carrier effective masses in BDA₂(Cu/Ag/Au)BiI₈. The charge density distributions of BDA₂AuBiI₈ at the VBM and CBM points in Fig. S17 (ESI†) show good consistency with the PDOS and COHP analysis. To further demonstrate the thermodynamic stability of BDA₂(Cu/Ag/Au)BiI₈, the formation energies and phonon band structures of BDA₂(Cu/Ag/Au)BiI₈ are calculated. Here, the formation energies of BDA₂(Cu/Ag/Au)BiI₈ are calculated as E_f = (E[BDA₂M_IM_IIIX₈] − N_BDAμ_BDA − N_MIμ_MI − N_MIIIμ_MIII − N_Xμ_X)/N_tot, where μ_i is the chemical potential of the constituent element referred to its most stable phase. The calculated values for BDA₂(Cu/Ag/Au)BiI₈ are −0.320/−0.327/−0.317 eV/atom, respectively, indicating their thermodynamic stability. The phonon band structures of BDA₂(Cu/Ag/Au)BiI₈ are shown in Fig. S18 (ESI†) with no imaginary branches, indicating their dynamic stability.

Since the energy level of the Au 5d orbital is higher than that of the Ag 4d orbital because of the relativistic-effect-induced expansion of 5d states in Au, the Au 5d–I 5p antibonding coupling is stronger than the Ag 4d–I 5p antibonding coupling, resulting in a higher VBM in BDA₂AuBiI₈. Therefore, the band gap of BDA₂AuBiI₈ is smaller than that of BDA₂AgBiI₈. Because the energy level of Cu 3d orbital is located closer to the Au 5d orbital, BDA₂CuBiI₈ has a band gap almost equivalent to that of BDA₂AuBiI₈. The stronger couplings of the Au 5d–I 5p and Cu 3d–I 5p interactions than of Ag 4d–I 5p interactions were also verified by COHP analysis, as shown in Fig. S14–S16 (ESI†). Based on the above bonding analysis, an estimated molecular orbital bonding diagram of BDA₂(Cu/Ag/Au)BiI₈ is given in Fig. S19 (ESI†), which provides an intuitive way to understand the unique electronic properties of BDA₂(Cu/Ag/Au)BiI₈.

Notably, previous studies have demonstrated that the primitive cell of the bulk double perovskites Cs₂M_I(Cu, Ag, Au)M_III(Sb, Bi)X₆ possess indirect band gaps.¹⁸ However, indirect-to-direct band gap transition can be induced by dimensionality reduction, as demonstrated in BA₄AgBiBr₈.²⁸ The large spacer cation also results in a strong quantum confinement effect and thereby induces nearly flat band edges along the Γ-Z direction. Unlike the transition mechanism in BA₄AgBiBr₈, the direct band gaps in BDA₂(Cu/Ag/Au)BiI₈ are mainly due to the interlayer I–I-interaction-induced band-broadening as the smaller spacer divalent cation BDA²⁺ is used, which would induce a further-reduced band gap and more-dispersive band edges along the Γ-Z direction. This indicates that the construction of the structure archetype is also an effective way to tune the band gap type.

The effective masses of all structures were estimated by quadratic fitting of the PBE + SOC-calculated band edges, and are displayed in Tables S4–S6 (ESI†). The effective masses of BDA₂(Cu/Ag/Au)BiI₈ were also examined using the HSE + SOC functional, as shown in Fig. 3a. Slight differences can be noticed between the PBE + SOC and HSE + SOC functionals. Balanced electron and hole effective masses along the in-plane directions were obtained for three candidates due to the antibonding characteristic near the CBM and VBM. Low effective electron masses of 0.32–0.68 m₀ and effective hole masses of 0.27–0.48 m₀, which are comparable to the values for MAPbI₃, ensure superior carrier transport properties in these candidates. Much heavier electron and hole effective masses are obtained along the out-of-plane direction owing to the quantum confinement effect. Despite the relatively large effective masses along the out-of-plane direction, they are still much improved compared to those of RP perovskites due to the more dispersive edges along the Γ-Z direction.³⁴ As shown in Tables S4–S6 (ESI†), the carrier properties of the candidates are superior to those of others. Next, the Wannier–Mott exciton binding energies (E_b) were estimated using a modified hydrogen-atom-like Bohr model of E_b = μe⁴/2ħ²ε², where ε, μ, and e are the high-frequency-limit dielectric constant, reduced effective mass, and charge of an electron, respectively. The results for BDA₂(Cu/Ag/Au)BiI₈ are displayed in Fig. 3b. E_b values as low as ∼70 meV were estimated for BDA₂CuBiI₈ and BDA₂AuBiI₈ for the in-plane directions, which are comparable with that of MAPbI₃. The relatively small E_b values further establish their superior carrier transport properties. These carrier features ensure good photovoltaic performance of the selected candidates.

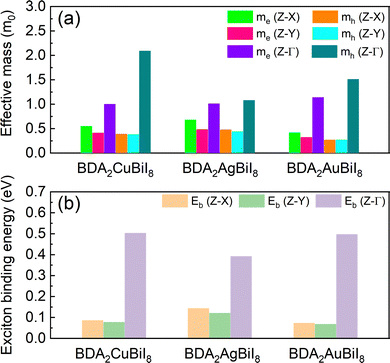Fig. 3 Calculated (a) effective masses of the electron (m_e*) and holes (m_h*), and (b) exciton binding energies, E_b (meV), of BDA₂Cu/Ag/AuBiI₈ in different directions.

In order to evaluate the photovoltaic performance of the selected absorber candidates, their absorption spectra are also calculated, along with that of MAPbI₃ for comparison. Fig. 4a shows that BDA₂(Cu/Ag/Au)BiI₈ possess relatively high absorption edges, which are mainly contributed by the optical transition channels from the Cu 3d/Ag 4d/Au 5d–I 5p orbitals to the Bi 6p–I 5p orbitals. In addition, inversion-symmetry-induced parity-forbidden transitions in bulk double perovskites are not observed in these layered structures, as shown in Fig. S13 (ESI†). High transition probabilities are found at the Z point. Therefore, BDA₂(Cu/Ag/Au)BiI₈ are suitable candidates for solar cells with favorable optical absorption. Their “spectroscopic limited maximum efficiency (SLME)” was then calculated to evaluate their theoretical maximum efficiency. Fig. 4b shows the calculated SLMEs of BDA₂(Cu/Ag/Au)BiI₈, along with that of MAPbI₃ for comparison. For the first 200 nm of film thickness, the SLME of MAPbI₃ is higher than that of BDA₂(Cu/Ag/Au)BiI₈ because of its higher absorption intensity near the absorption edge. At a film thickness of 200 nm, the SLMEs of BDA₂AuBiI₈, BDA₂CuBiI₈, and MAPbI₃ are almost equivalent and can reach a value of ∼23%. The SLME values of BDA₂(Cu/Ag)BiI₈ reach their theoretical limit value of about 30.8%/27.0% at a film thickness of ∼1 μm. The SLME of BDA₂AuBiI₈ is higher than even that of MAPbI₃ from 200 nm to 1 μm, and achieved its limit value of 31.6% at ∼1 μm. Hence, it is believed that BDA₂AuBiI₈ and BDA₂CuBiI₈ may be promising as good solar absorbers that can obtain high efficiency using a low film thickness. The absorption spectra and SLMEs of BDA₂(Cu/Ag/Au)InI₈, which have proper indirect solar band gaps, were also calculated for comparison, as shown in Fig. S20 (ESI†). Much weaker absorption intensities are observed compared to that of BDA₂(Cu/Ag/Au)BiI₈. Therefore, slow increase in the SLMEs with film thickness and lower theoretical limits are obtained for BDA₂(Cu/Ag/Au)InI₈, indicating a much thicker film is needed for achieving suitable efficiencies.

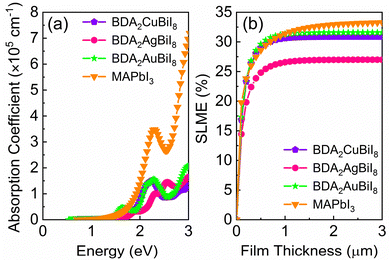Fig. 4 (a) Calculated absorption spectra of BDA₂Cu/Ag/AuBiI₈ and MAPbI₃; (b) simulated spectroscopic limited maximum efficiency (SLME) of BDA₂Cu/Ag/AuBiI₈ and MAPbI₃.

In summary, DJ-type double perovskite BDA₂M_IM_IIIX₈ solar cell absorber candidates were selected and showed good stability, suitable band gaps, superior carrier transport properties, and good optical properties. Improved interlayer carrier transportation in BDA₂Cu/Ag/AuBiI₈ is observed because of the DJ-structure-induced interlayer I–I interaction. The crucial role of the structure archetype in their superior optoelectronic properties is revealed. Finally, theoretical maximal efficiencies of about 30.8%/27.0%/31.6% were predicted for BDA₂Cu/Ag/AuBiI₈. This work indicates that the combination of a DJ archetype and double substitution represents a new approach for designing stable lead-free perovskites for high-performance solar cells.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (62005148/12004235), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA17040506), the DNL Cooperation Fund CAS (DNL180311), and the 111 Project (B14041).

References

1. M. He, J. Liang, Z. Zhang, Y. Qiu, Z. Deng, H. Xu, J. Wang, Y. Yang, Z. Chen and C.-C. Chen, J. Mater. Chem. A, 2020, 8, 25831–25841.
2. H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636–642.
3. S.-T. Ha, C. Shen, J. Zhang and Q. Xiong, Nat. Photonics, 2016, 10, 115–121.
4. S. Park, W. J. Chang, C. Lee, S. Park, H.-Y. Ahn and K. T. Nam, Nat. Energy, 2016, 2, 16185.
5. X. Li, W. Zhang, X. Guo, C. Lu, J. Wei and J. Fang, Science, 2022, 375, 434–437.
6. W. Chen, Y. Zhu, J. Xiu, G. Chen, H. Liang, S. Liu, H. Xue, E. Birgersson, J. W. Ho, X. Qin, J. Lin, R. Ma, T. Liu, Y. He, A. M.-C. Ng, X. Guo, Z. He, H. Yan, A. B. Djurišić and Y. Hou, Nat. Energy, 2022, 7, 229–237.
7. M. Jeong, I. W. Choi, K. Yim, S. Jeong, M. Kim, S. J. Choi, Y. Cho, J.-H. An, H.-B. Kim, Y. Jo, S.-H. Kang, J.-H. Bae, C.-W. Lee, D. S. Kim and C. Yang, Nat. Photonics, 2022, 16, 119–125.
8. B. Vargas, G. Rodríguez-López and D. Solis-Ibarra, ACS Energy Lett., 2020, 5, 3591–3608.
9. W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965.
10. S. Chatterjee and A. J. Pal, J. Mater. Chem. A, 2018, 6, 3793–3823.
11. D. Bryant, N. Aristidou, S. Pont, I. Sánchez-Molina, T. Chotchunangatchaval, S. Wheeler, J. R. Durrant and S. A. Haque, Energy Environ. Sci., 2016, 9, 1655–1660.
12. S. Chatterjee and A. J. Pal, J. Mater. Chem. A, 2018, 6, 3793–3823.
13. L. Mao, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 1171–1190.
14. G. Grancini and M. K. Nazeeruddin, Nat. Rev. Mater., 2019, 4, 4–22.
15. X. Xiao, J. Dai, Y. Fang, J. Zhao, X. Zheng, S. Tang, P. Rudd, Z. Cheng and J. Huang, ACS Energy Lett., 2018, 3, 684–688.
16. I. Spanopoulos, I. Hadar, W. Ke, Q. Tu, M. Chen, H. Tsai, Y. He, G. Shekhawat, V. P. Dravid, M. R. Wasielewski, A. D. Mohite, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 5518–5534.
17. W. Meng, X. Wang, Z. Xiao, J. Wang, D. B. Mitzi and Y. Yan, J. Phys. Chem. Lett., 2017, 8, 2999–3007.
18. G. Volonakis, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 1254–1259.
19. Z. Deng, F. Wei, S. Sun, G. Kieslich, A. K. Cheetham and P. D. Bristowe, J. Mater. Chem. A, 2016, 4, 12025–12029.
20. E. McClure, M. Ball, W. Windl and P. Woodward, Chem. Mater., 2016, 28, 1348–1354.
21. M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579–2585.
22. C. Savory, A. Walsh and D. Scanlon, ACS Energy Lett., 2016, 1, 949–955.
23. X.-G. Zhao, D. Yang, Y. Sun, T. Li, L. Zhang, L. Yu and A. Zunger, J. Am. Chem. Soc., 2017, 139, 6718–6725.
24. X. Cai, Y. Zhang, Z. Shi, Y. Chen, Y. Xia, A. Yu, Y. Xu, F. Xie, H. Shao, H. Zhu, D. Fu, Y. Zhan and H. Zhang, Adv. Sci., 2022, 9, 2103648.
25. B. Wang, N. Li, L. Yang, C. Dall’Agnese, A. K. Jena, S.-I. Sasaki, T. Miyasaka, H. Tamiaki and X.-F. Wang, J. Am. Chem. Soc., 2021, 143, 2207–2211.
26. Z. Li, P. Wang, C. Ma, F. Igbari, Y. Kang, K.-L. Wang, W. Song, C. Dong, Y. Li, J. Yao, D. Meng, Z.-K. Wang and Y. Yang, J. Am. Chem. Soc., 2021, 143, 2593–2600.
27. Z. Zhang, Q. Sun, Y. Lu, F. Lu, X. Mu, S.-H. Wei and M. Sui, Nat. Commun., 2022, 13, 3397.
28. B. A. Connor, L. Leppert, M. D. Smith, J. B. Neaton and H. I. Karunadasa, J. Am. Chem. Soc., 2018, 140, 5235–5240.
29. M. K. Jana, S. M. Janke, D. J. Dirkes, S. Dovletgeldi, C. Liu, X. Qin, K. Gundogdu, W. You, V. Blum and D. B. Mitzi, J. Am. Chem. Soc., 2019, 141, 7955–7964.
30. L. Mao, S. M. L. Teicher, C. C. Stoumpos, R. M. Kennard, R. A. DeCrescent, G. Wu, J. A. Schuller, M. L. Chabinyc, A. K. Cheetham and R. Seshadri, J. Am. Chem. Soc., 2019, 141, 19099–19109.
31. L.-Y. Bi, Y.-Q. Hu, M.-Q. Li, T.-L. Hu, H.-L. Zhang, X.-T. Yin, W.-X. Que, M. S. Lassoued and Y.-Z. Zheng, J. Mater. Chem. A, 2019, 7, 19662–19667.
32. L.-Y. Bi, T.-L. Hu, M.-Q. Li, B.-K. Ling, M. S. Lassoued, Y.-Q. Hu, Z. Wu, G. Zhou and Y.-Z. Zheng, J. Mater. Chem. A, 2020, 8, 7288–7296.
33. Y. Zhang, Y. Liu, Z. Xu, Z. Yang and S. Liu, Small, 2020, 16, 2003145.
34. Z. Xu, M. Chen and S. Liu, J. Phys. Chem. Lett., 2019, 10, 3670–3675.
35. L. Mao, W. Ke, L. Pedesseau, Y. Wu, C. Katan, J. Even, M. R. Wasielewski, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 3775–3783.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00499b

---