Open Access Article
Open Access ArticleOptimization of thermoelectric properties of carbon nanotube veils by defect engineering†
Chongyang
Zeng
 ab,
Pietro
Stenier
ab,
Pietro
Stenier
 cd,
Kan
Chen
cd,
Kan
Chen
 b,
Kening
Wan
b,
Kening
Wan
 b,
Ming
Dong
b,
Ming
Dong
 e,
Suwei
Li
b,
Coskun
Kocabas
cdf,
Michael J.
Reece
b,
Dimitrios G.
Papageorgiou
e,
Suwei
Li
b,
Coskun
Kocabas
cdf,
Michael J.
Reece
b,
Dimitrios G.
Papageorgiou
 b,
Alexey N.
Volkov
b,
Alexey N.
Volkov
 g,
Han
Zhang
g,
Han
Zhang
 b and
Emiliano
Bilotti
*a
b and
Emiliano
Bilotti
*a
aDepartment of Aeronautics, Imperial College London, Exhibition Road, London, SW7 2AZ, UK. E-mail: e.bilotti@imperial.ac.uk
bSchool of Engineering and Materials Science, Queen Mary University of London, London, E1 4NS, UK
cDepartment of Materials, University of Manchester, Manchester, M13 9PL, UK
dNational Graphene Institute, University of Manchester, M13 9PL, UK
eSchool of Physical and Chemical Sciences, Queen Mary University of London, London, E1 4NS, UK
fHenry Royce Institute for Advanced Materials, University of Manchester, Manchester, M13 9PL, UK
gDepartment of Mechanical Engineering, University of Alabama, 7th Avenue, Tuscaloosa, AL 35487, USA
First published on 16th June 2023
Abstract
Carbon nanotubes (CNTs), with their combination of excellent electrical conductivity, Seebeck coefficient, mechanical robustness and environmental stability are highly desired as thermoelectric (TE) materials for a wide range of fields including Internet of Things, health monitoring and environmental remediation solutions. However, their high thermal conductivity (κ) is an obstacle to practical TE applications. Herein, we present a novel method to reduce the κ of CNT veils, by introducing defects, while preserving their Seebeck coefficient and electrical conductivity. Solid-state drawing of a CNT veil embedded within two polycarbonate films generates CNT veil fragments of reducing size with increasing draw ratio. A successive heat treatment, at above the polycarbonate glass-to-rubber transition temperature, spontaneously reconnects the CNT veils fragments electrically but not thermally. Stretching to a draw ratio of 1.5 and heat repairing at 170 °C leads to a dramatic 3.5-fold decrease in κ (from 46 to 13 W m−1 K−1), in contrast with a decrease in electrical conductivity of only 26% and an increase in Seebeck coefficient of 10%. To clarify the mechanism of reduction in thermal conductivity, a large-scale mesoscopic simulation of CNT veils under uniaxial stretching has also been used. This work shows that defect engineering can be a valuable strategy to optimize TE properties of CNT veils and, potentially, other thermoelectric materials.
New conceptsWe propose a new concept for optimizing the thermoelectric performance of carbon nanotube veils by reducing their thermal conductivity while preserving their high Seebeck coefficient and electrical conductivity. This is achieved by solid-state drawing of CNT veils, embedded between two polymer films, to generate CNT veil fragments (in a process reminiscent of fibre fragmentation in continuous fibre-reinforced composites), which are then spontaneously reconnected by the shape-memory effect of the oriented polymer matrix. This defect-engineering method achieved: (i) a 3.5-fold reduction in thermal conductivity of CNT veils (from 46 to 13 W m−1 K−1), combined with an increase in Seebeck coefficient of 10% and a decrease in electrical conductivity of only 26%; (ii) an increase of the ZT figure-of-merit from 5.6 × 10−4 (virgin CNT veil) to 2.7 × 10−2 (stretched and heat-treated PC/CNT/PC multilayer composite). A large-scale mesoscopic simulation of CNT veils under uniaxial stretching was used to provide an insight in the mechanism of reduction in thermal conductivity, which is attributed to the reduction of CNT network connectivity in the low-density gaps. This work shows that defect engineering can be a valuable strategy to optimize TE properties of CNT veils and, potentially, other thermoelectric materials. |
Thermoelectric (TE) materials can provide a promising route to harvest ubiquitous waste heat, directly converting thermal gradients into electrical power,1–6 benefiting applications like aerospace,7 industrial waste heat recovery,8 energy harvesting,9–11 self-powered sensors,12–15 electromagnetic wave shielding and absorption,16 touch sensing,17 health monitoring and personal temperature regulation. Generally, the TE performance of a material can be evaluated by a dimensionless figure of merit (ZT), which scales with the electrical conductivity (σ), the square of the Seebeck coefficient (S), the inverse of thermal conductivity (κ) and the material temperature T (ZT = TS2σ/κ). Unfortunately, optimizing ZT often requires frustrating compromises, as σ, S and κ are interlinked physical properties.3,18–23 Traditional TE materials are heavily doped inorganic semiconductors with high S and σ, like PbTe, Bi2Te3 and SnSe.24–27 However, their wider use is restricted by the toxicity, scarcity and high cost of some of the constituent elements, as well as their poor mechanical toughness and manufacturability. Compared to the inorganic counterpart, organic TE materials and their (nano) composites have recently gained visibility thanks to the low toxicity and wide availability of constituent elements, potentially high toughness and ease of manufacturing as well as intrinsically low κ.28 Nevertheless, the generally low σ and S pose a significant limit to the TE performance of conducting polymers.
Nanocomposites based on carbon nanotubes (CNTs) have seen the highest TE properties among all organic materials. For example, a power factor (PF = S2σ) of up to 2000 μW m−1 K−2 at room temperature has been reported for polyaniline (PANI)/CNT/graphene multilayer films.29 The presence of a polymer matrix is desirable to decrease thermal conductivity while increasing toughness and processability. Meng et al. demonstrated that the formation of a thin uniform coating of PANI, by in situ chemical polymerization, decreased the thermal conductivity of CNT networks to about 0.5 W m−1 K−1, with a σ of 60 S cm−1 and a S of 28 μV K−1, when the PANI content was 15.8 wt%.30 Zhang et al. reported a relatively stretchable carboxylic surface-modified single-walled carbon nanotube (SWCNT)-based TE fibre, prepared by a wet spinning method. The Seebeck coefficient S of the annealed SWCNT-based TE fibre remained stable at 44 μV K−1, even under a tensile strain of ∼20%, while the electrical resistance was increased by only 11%.31 However, the greatest majority of CNT-based films reported so far have been prepared from CNT powders, which requires good dispersions of CNTs in a suitable solvent or polymer matrix, often being an important limiting factor for property enhancement, reproducibility and practical applications. In addition, the intertube junctions, which dominate the ultimate properties of the CNT network, are difficult to control due to the weak interactions and the presence of insulating surfactant residues.32 Recently, CNT veils fabricated by floating catalyst chemical vapour deposition (FCCVD) method, with high σ and relatively high S,33–35 have attracted considerable attention. This kind of free-standing CNT films, constituted by a continuous network of exceptionally long CNTs – unlike CNT films prepared from filtration or deposition of liquid suspensions of CNT powders (also referred to as buckypapers) – can be directly employed as a TE material into devices without the need of an intermediate (solution) process. These materials also possess advantages such as easy processing in lightweight and flexible TE devices at large scale, thanks to the mechanical robustness imbued by the continuous reticulate structure.36,37 Zhou et al. developed flexible n-type SWCNT films with a PF value as high as 1500 μW m−1 K−2 and outstanding long-term stability in ambient conditions (less than 5% variation in electrical conductivity and Seebeck coefficient, over 3 months).38 Choi et al. fabricated a wearable thermoelectric generator (TEG) based on highly aligned CNT veils. Here, the CNT veils were used as continuous TEG materials, without metal electrodes between TE ‘legs’, providing a significant reduction in internal contact resistance compared to traditional TEGs. N- and p-types legs were created by doping the CNT veils with 8 mM polyethyleneimine (PEI) and 2 mM ferric chloride (FeCl3) ethanol solutions, respectively. A TEG prototype with 9 p–n pairs yielded a maximum output power of 8 μW under a temperature difference of 50 K.39
In free-standing CNT veils, the in-plane oriented continuous network structure predetermines the superior electrical (σ of 432–5020 S cm−1, depending on orientation) and mechanical properties (Young's modulus of about 55.2–58.9 GPa, maximum tensile stress of 2.7–2.9 GPa, maximum elongation at break of 5–8% and good toughness),40 which is unfortunately linked to high thermal conductivity (κ of 26–700 W m−1 K−1, depending on the orientation),40 substantially reducing the ZT value and restricting potential TE applications.
The thermal conductivity of CNT materials is constrained from above by the conductivity of individual nanotubes (kT). Both experiments and simulations predict values of kT for single walled carbon nanotubes (SWCNTs) and multiwalled carbon nanotubes (MWCNTs) on the order of 1000 W m−1 K−1,41,42 which makes CNTs one of the best heat conductors in nature. The thermal conductivity of CNT films, of different types, spans a remarkably broad range from ∼0.1 W m−1 K−1 to ∼800 W m−1 K−1,42 with the upper boundary of this range corresponding to super aligned high-density CNT arrays.43 At moderate material densities, for CNT films with entangled networks of nanotubes bundles, the measured thermal conductivity varies in a range from ∼2 W m−1 K−1 to ∼200 W m−1 K−1.42 For instance, Wang et al. prepared aligned CNT films (26 μm in thickness), from aligned CNT arrays, by using a “domino pushing” method, with κ reaching 153 W m−1 K−1.44 The variability of thermal conductivity of CNT materials is supported by theoretical studies,45 which predict the strong effects of material density, nanotube length, connectivity and structural parameters of the CNT network, as well as presence of impurities and defects. This variability paves the way for improving the TE properties of CNT materials through reducing the thermal conductivity by engineering nanotube networks.
Herein, we present a new method to decrease the thermal conductivity of CNT veils, without significantly affecting the values of S and σ, inspired by fibre fragmentation in traditional fibre-reinforced composites materials.46–48 Specifically, a CNT veil, sandwiched between thermoplastic polymer films, is subjected to a solid-state drawing process, which fragments the CNT veil and progressively introduces defects, responsible for reducing the lattice thermal conductivity. A thermal treatment process can then reverse the fragment separation process, driven by the elastic entropic response of the oriented thermoplastic polymer films, hence partially restoring the electrical conductivity, without affecting the Seebeck coefficient. Polycarbonate (PC) is chosen to be the polymer matrix due to its amorphous microstructure and optical transparency.
In this work, the TE properties (σ, S and κ) of CNT veils and their composites are systematically tuned and investigated by the defect engineering method mentioned above. The results of the experimental study are supplemented by large-scale mesoscopic simulations, which confirm that the strongly reduced thermal conductivity of non-homogeneously stretched CNT films can be explained by the reduced connectivity of the CNT veil network. The results can provide a valuable strategy to optimize TE performance of CNT-based materials and organic thermoelectrics.
Results and discussion
Mechanical properties of PC/CNT/PC composites
Composites of CNT veils partially embedded within two polycarbonate (PC) films (herein called PC/CNT/PC) were fabricated by compression moulding (Fig. 1(a)). Solid-state drawing was then used to stretch PC films, CNT veils and PC/CNT/PC composites. For pure PC films (ESI,† Fig. S1), the maximum draw ratio (DR, defined as the ratio of the final length by the original length) was about 3.2 at a drawing speed of 10% min−1 and a temperature of 160 °C. When the speed increased to 50% min11 and 100% min−1, both the maximum stress and strain of PC films increased, and the DR reached 11. Due to strain hardening, the drawing behaviour became more stable at higher drawing speeds, leading to an increase in the maximum DR.49 Therefore, the speed of 100% min−1 was chosen for all tensile tests and stretching experiments. At the same strain rate, the tensile strain and stress at break of pure CNT veils were 40% and 37.2 MPa, respectively (ESI,† Fig. S2e). Raman tests (ESI,† Fig. S3) indicated a random (in-plane) arrangement of CNT bundles within the CNT veils, which is in accordance with the surface morphological investigation (ESI,† Fig. S2a–d). For PC/CNT/PC composites, the results showed a maximum tensile stress of about 2.5 MPa and a maximum strain at break of approximately 200% (DR = 3) (ESI,† Fig. S4). Compared to the pure PC films (1000% and 1.17 MPa, Fig. S1), the tensile strain at break of PC/CNT/PC was far lower (200%), while the maximum tensile stress was higher (2.5 MPa), showing a typical composite reinforcement mechanism. In analogy with fibre-reinforced polymer composites (and their fibre fragmentation behaviour),46 the CNT veil can be regarded as a brittle continuous reinforcing phase while the PC film acts as the more ductile matrix phase.Stretching and heat repairing of PC/CNT/PC composites
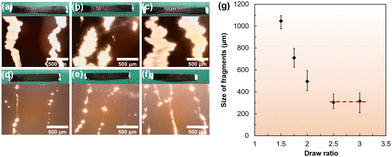
To explore the effect of DR on TE performance of heat-repaired PC/CNT/PC composites, the corresponding composite films were stretched to different extend (ESI,† Fig. S5 and S6). CNT veils fragments were produced by the solid-state drawing process and reconnected via the thermal treatment (i.e. heat-repaired). During the stretching process, the PC matrix transmitted the load to the CNT veil until reaching its failure point (at a strain of about 30%; ESI,† Fig. S2e), after which CNT fragments were created. When the stretched composites films were then subjected to a temperature above the PC glass-to-rubber transition, they spontaneously recovered their initial unstretched dimensions, exhibiting the shape memory effect due to entropic elasticity, which reconnected the CNT veils fragments. During the fragmentation process, cracks can be observed with an optical microscope (bright areas in Fig. 2(a)–(c)). It can be seen that cracks become progressively wider with the increase of DR, while suddenly closing during thermal treatment at 170 °C (Fig. 2(d)–(f)). The fragments decreased from an average width of 1046 μm to 496 μm, in correspondence of a DR of 1.5 and 2, respectively, and reached a minimum of around 300 μm at DR 2.5. Further increasing the DR from 2.5 to 3 did not result in any significant change in CNT veil fragment width (Fig. 2(g)). This phenomenon is analogous to the critical fibre length in fibre-reinforced composites, which can be described by the Kelly–Tyson model.50 Such a model was used (detailed in Note S1, ESI†) to estimate the interfacial shear stress between PC and CNT veil of 0.43 MPa, which indicates a relatively good interaction.51 Here, we have prepared stretched PC/CNT/PC composites up to DR 3, but we were only able to measure TE properties for DR up to 2. Therefore, only DR of 1, 1.5, 1.75 and 2 are investigated further within this study.Thermoelectric performance
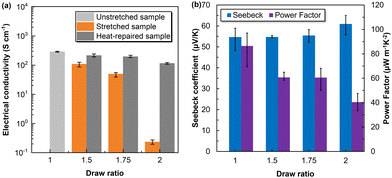
The TE performance of PC/CNT/PC composites were investigated by testing their Seebeck coefficient (S), electrical conductivity (σ) and thermal conductivity (κ). Upon increase in draw ratio, the value of S remained approximately unchanged at 55 μV K−1, increasing slightly to 61 μV K−1 only when reaching a draw ratio of 2 (Fig. 3). This suggests that S is relatively insensitive to the structure variation of the CNT veil in PC matrix after solid state drawing and heat-repairing (the Seebeck coefficient as a function of temperature, the carrier mobility and carrier concentration of the CNT veil are reported in Fig. S7 and Table S1, ESI† for reference). The electrical conductivity of the PC/CNT/PC composite after stretching and heat-repairing is presented in Fig. 3(a). Upon increase in draw ratio, σ decreased from 289 S cm−1 (unstretched PC/CNT/PC) to 109 S cm−1, at DR = 1.5, 49 S cm−1, at DR = 1.75, and 0.23 S cm−1, at DR = 2. The thermal treatment allowed a partial recovery of the electrical conductivity of stretched PC/CNT/PC composites. For instance, the electrical conductivity increased from 109 S cm−1 to 214 S cm−1, at DR = 1.5, from 49 S cm−1 to 196 S cm−1, at DR = 1.75, and from 0.23 S cm−1 to 115 S cm−1, at DR = 2, after heat-repairing. The reduction of σ for stretched PC/CNT/PC samples was caused by the progressive fragmentation of the CNT veil and the separation of the fragments with increasing draw ratio, which resulted in a decreased carrier mobility and hence electrical conductivity. Conversely, the thermal treatment reconnected the CNT veil fragments and promoted the formation of a more robust electrically conductive network.This is consistent with the morphological investigation presented in Fig. 4. In the heat-repaired samples, only a few small cracks are evident. However, it is interesting to notice the presence of individual CNTs or small bundles of CNTs, characterised by a relatively low network density, bridging the crack edges. Away from the crack, a more dense and compact network structure appears, very similar to the unstretched CNT veil. Such a morphology demonstrates the continuous electrical conductive network formed in the heat repaired PC/CNT/PC composites.
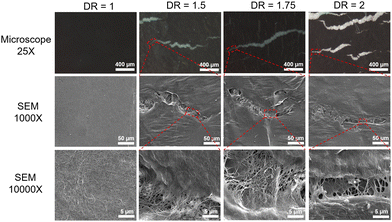 | ||
| Fig. 4 Optical microscope and SEM images of heat-repaired CNT veils after stretching at different draw ratios DR. The scale bars are 400 μm, 50 μm and 5 μm, respectively, from top to bottom row. | ||
Returning to the TE performance of CNT veils and composites, it is useful to discuss it in terms of parameters like power factor (PF) and figure of merit (ZT), since, as mentioned earlier, thermoelectricity is often a compromise between mutually interlinked properties. As expected, the values of PF, presented in Fig. 3(b), followed a similar trend as the electrical conductivity, decreasing from 86 μW m−1 K−2, for un-stretched samples, to 61 μW m−1 K−2, for sample that are stretched (at a DR of 1.5 or 1.75) and then thermally repaired. The PF decreased to 40 μW m−1 K−2, for samples stretched to a DR of 2 and heat-repaired, in which the increase in S (61 μV K−1) – even if expressed as a square power in the calculation of the PF – did not compensate the 50% decrease in σ.
The other important TE parameter is the figure of merit ZT, directly proportional to the power factor and inversely proportional to the thermal conductivity. Fig. 5(a) presents the IR images of unstretched CNT veils and CNT veils after stretching to DR = 1.5 and heat-repaired, used to calculate values of effective in-plane thermal diffusivity and thermal conductivity, κ. According to the Angstrom method,52 the κ of unstretched and stretched (DR = 1.5) and heat repaired CNT veils are about 46 W m−1 K−1 and 13 W m−1 K−1, respectively. Hence, the thermal conductivity κ decreases 3.5 times, which leads to a more than two folds increase in ZT (Fig. 5(b)). Such a large decrease in thermal conductivity could be caused either by the presence of an insulating polymer layer between CNTs and/or by the defects introduced into the CNT veil during fragmentation. To eliminate the first hypothesis, the tests presented in Fig. 5 were actually carried out on samples in which the polymer was removed by dissolution in dichloromethane, as demonstrated by FTIR and TGA results (ESI,† Fig. S8 and S9). It is reminded that κ has two contributions, κ = κe + κl, where κe is the electronic contribution and κl is lattice contribution. The introduction of cracks affects the lattice contribution, κl, which is of critical importance since thermal conductivity of CNT is dominated by phonons transport (detailed in Note S2, ESI†).53,54 The thermal conductivity of PC/CNT/PC composites is difficult to calculate with the same experimental method. Herein the composite thermal conductivity is estimated by using the equations for the parallel and the series model, as the upper and lower bound prediction, respectively:55
| κcomposite = Φpκp + (1 − Φp)κ | (1) |
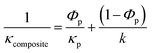 | (2) |
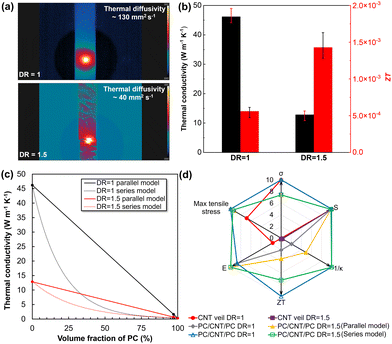 | ||
| Fig. 5 (a) IR images of unstretched CNT veils and CNT veils after stretching to a DR of 1.5 and heat repairing, for thermal diffusivity tests. (b) Results of thermal conductivity and ZT value of CNT veil. (c) Estimation of composites thermal conductivities based on a series or parallel model. (d) Comparison of a set of six important TE and mechanical properties of CNT veil and PC/CNT/PC composites. A number in the range of 0 to 10 is used for evaluating each property. The maximum value at each property was defined as 10, other values relative to the maximum value to get the normalized value (Table S2, ESI†). | ||
Mesoscopic simulations of thermal conductivity of stretched CNT films
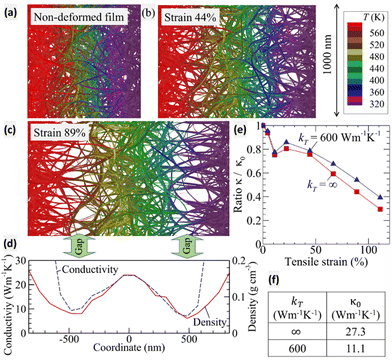
To better understand the mechanism of reduction in thermal conductivity in our system, we performed simulations of the effect of stretching of the thermal conductivity a thin CNT film with a continuous network of entangles bundles of nanotubes.56–59In the simulations, a CNT film with a thickness of 100 nm composed of 15395 400 nm-long (10,10) CNTs at a material density of 0.2 g cm−3 was used (Fig. 6(a)). The continuous network of nanotubes in the in silico generated sample was obtained with an approach based on dynamic spontaneous self-assembly of nanotubes.60,61 This sample is then subjected to tension at a constant deformation speed of 20 m s−1. Under this deformation speed, the film is stretched non-homogeneously with the formation of two low-density gaps and preservation of a zone with relatively high density between gaps in the central part of the film (Fig. 6(b) and (c)). The gaps are formed due to finite-strain-rate effects, since the maximum deformation speed, corresponding to a quasi-static tension for the considered sample, is expected to be smaller than 10 m s−1.61 This relatively high deformation speed is chosen intentionally to mimic in simulations the formation of cracks in the experimental samples of CNT veils. At a strain of 89%, the density in the gaps is about 3 times smaller than that in the central part of the film (Fig. 6(d)).
For films obtained at various degrees of stretching, a temperature gradient in the direction of deformation was applied to calculate the steady temperature fields, as shown in Fig. 6(a)–(c). These temperature fields are used to calculate the distribution of the average temperature, heat flux, and the local (Fig. 6(d)) and average (for the whole sample; Fig. 6(e)) thermal conductivities κ, based on the Fourier law.56,57
For a non-deformed film, the thermal conductivity κ0 varies depending on the adopted value of thermal conductivity of individual CNTs kT, from 27.3 W m−1 K−1 for CNTs with infinite kT to 11.1 W m−1 K−1 for kT = 600 W m−1 K−1. These values are in line with the measured values of thermal conductivity 9 W m−1 K−1 –19 W m−1 K−1 of CNT films, at a comparable nanotube volume fraction of 10%.62 The strong effect of finite conductivity of individual CNTs on the average material conductivity agrees with the previous mesoscopic simulations.56 Theoretical studies show that the effect of kT on the CNT material conductivity depends on the average number of thermal contacts per nanotube in the network, and, thus, can be affected by the material density, CNT length, and degree of connectivity of the CNT network.45 The calculated values of the film thermal conductivity κ0 are from 2 (at infinite kT) to 4 (at kT = 600 W m−1 K−1) times different from the experimentally measured conductivity of CNT veils with no stretch (Fig. 5(b)). This difference, however, is expected, since the experimental CNT veils and in silico generated CNT film are different from each other by the type of nanotubes, CNT length, material density, and structural parameters of the CNT networks.
The local thermal conductivity in the stretched samples is distributed non homogeneously and follows the distribution of local material density. At a strain of 89%, the local conductivity in gaps is about three times smaller than the conductivity of a non-deformed film (Fig. 6(d)). The ratio of the average conductivity of the deformed film κ to the conductivity of the non-deformed film κ0 demonstrates a linear decay with increasing strain when the strain is greater than ∼40% (Fig. 6(e)). The average conductivity exhibits three-fold decrease at a strain of 110–130% when the minimum local density in the gaps drops to ∼15% of κ0. This decrease in the average conductivity is explained by poor network connectivity in the low-density gaps. These results suggest that the reduced connectivity in the gaps or cracks is the primary factor that explains the drop in thermal conductivity of non-homogeneously stretched CNT veils.
Experimental section
Materials
Carbon nanotube (CNT) veils, fabricated by floating catalyst chemical vapor deposition method, were purchased from Suzhou Creative Nano Carbon Co., Ltd. The veils are composed of multiwalled carbon nanotube (MWCNT) of diameter of ∼5–20 nm and show an apparent density of about 0.5 g cm−3. Polycarbonate (PC) films (Lexan 8010MC, 500 μm) with density of 1.2 g cm−3 and specific heat capacity of 1.3 J g−1 K−1 were purchased from Cadillac Plastic Limited (U.K.). The chemical reagents used without further purifications are acetone (99.5%), ethanol (96%, v/v) and dichloromethane (DCM, ≥99%), purchased respectively from Thermo Scientific, Honeywell and Fisher Chemical.Preparation of PC/CNT/PC composites
Polymer/CNT veil composites sandwich structures were fabricated by compression moulding. First, a CNT veil (80 mm × 60 mm) was embedded in two PC films (90 mm × 90 mm). Temperature and pressure of a hot press (Dr Collin P300E, Germany) were set at 290 °C and 40 bar. The stack PC/CNT/PC was introduced into the chamber of the hot press, pre-heated for 10 min and then pressed for 3 min, before water-cooling down to room temperature under pressure.Preparation of stretched and heat-repaired PC/CNT/PC composites
Stretched and heat-repaired samples were made by using a universal tensile tester (Instron 5900R84, UK) equipped with an environmental chamber. PC/CNT/PC composites were cut into strips of 40 mm × 5 mm, followed by uniaxially drawing at 160 °C and 100% min−1 drawing speed, until reaching different draw ratios. Heat-repaired samples were obtained by heating stretched PC/CNT/PC composites at 170 °C for 10 min. Oriented PC spontaneously recovered to the initial state when exposed to temperatures above the PC glass-to-rubber transition (about 147 °C).Characterization
The thickness of CNT veils was measured by using a profilometer (Bruker Dektak Vision 64). FEI Inspect F Scanning Electron Microscope (SEM) and an optical microscope (40×-2500× Digital LED Trinocular Compound Microscope, VWR and Axio Vert.A1 Inverted Transmitted Light Microscope, ZEISS) were used to observe the morphology of CNT veils and the PC/CNT/PC composites, before and after stretching and annealing. Mechanical tests were performed by using a quasi-static tensile tester (Instron 5900R84) with a load cell of 100 N and different strain rates (from 10% min−1 to 100% min−1). The carrier mobility and concentration of the CNT veil were obtained by a Hall measurement system (Cryogenic, UK). A two-probe method was used to calculate the electrical conductivity of PC/CNT/PC, by measuring the electrical resistance with a Keithley 2000 multimeter. The length and width of the sample were 40 mm × 5 mm. At least three specimens per sample were tested and average values and standard deviation reported. Raman tests were carried out by an inVia Qontor confocal Raman spectrometer coupled with a microscope with a 633 nm laser source, to estimate the orientation of CNT veils (The VV (vertical/vertical) polarization, where the incident and scattered polarization were the same, was employed). The Seebeck coefficient was characterized at 300 K under nitrogen atmosphere, using a Seebeck testing system (MMR, SB100 digital Seebeck controller and K20 digital temperature controller). The effective thermal diffusivities (λ) of the specimens were measured by using a custom-built setup consisting of a pulsed (1 Hz) tunable laser beam to excite heat waves that propagate periodically into the sample and by using as detector a high-resolution infrared camera (FLIR T660). The camera was mounted with an IR microlens (pixel size 50 × 50). Thermal diffusivity is then calculated following the Angstrom method.52 Then the thermal conductivity can be calculated by the following equation.| κ = λcpρ | (3) |
Computational method
Dynamic mesoscopic model of CNT network materials
In the mesoscopic model, each nanotube is represented by a chain of stretchable cylindrical mesoscopic elements, connected with each other in mesoscopic nodes. The force field in the equations of motion for mesoscopic nodes accounts for stretching and bending of nanotubes,59 bending buckling,64 and van-der Waals interaction between nanotubes.58In silico generation of CNT films with a continuous network of nanotubes
To generate in silico an initial film sample with a continuous network of nanotubes, the straight and dispersed (10,10) 400 nm long CNTs were randomly distributed in a volume with a size of 103 nm × 103 nm × 102 nm at a material density of 0.2 g cm−3. Then the dynamics mesoscopic model was used to simulate the self-assembly of CNTs into bundles at an elevated mesoscopic temperature and fixed volume and with the periodic boundary conditions in the plane of the film. Finally, the film sample was relaxed at a mesoscopic temperature of 300 K to obtain a steady-state quasi-equilibrium CNT network shown in Fig. 6(a). Further details of the procedures used for the generation of the initial film can be found in ref. 59.Stretching of CNT film
To stretch the CNT film, the parts of CNTs belonging to the “clip” layers of 50 nm thickness were moved in the opposite directions with a constant deformation velocity of 20 m s−1. Further details of the procedure used for the CNT film stretching can be found in ref. 59.Calculation of thermal conductivity
The average thermal conductivity was calculated using a computational model.56,57 The model of thermal transport processes accounts for finite intrinsic conductivity of individual CNTs and the inter-tube contact heat transfer. The temperature distribution in each individual nanotubes is calculated by solving one-dimensional heat conduction equation with distributed source terms describing the inter-tube heat transfer.56 The model of inter-tube contact heat transfer57 was parameterised assuming a contact conductivity of 5 × 10−11 W K−1 for crossed (10,10) CNTs at equilibrium gaps between them.65 The thermal conductivity kT of individuals CNTs is known to be dependent on the CNT length.42,66 To quantify this effect, the simulations were performed for kT = 600 W m−1 K−1 (here kT is traditionally defined for a reference area of 2πRδ, where R is the SWCNT radius and δ = 3.4 Å is an equilibrium gap between graphene layers), which is a conservative estimate for relatively short 400 nm long CNTs considered in this study, and additionally for CNTs with infinite kT. In the latter case, each nanotube has a constant temperature that can be found from the condition of zero total contact heat flux.45 For calculations of thermal conductivity, the opposing sides of the film sample are attached to two heat baths at temperatures of 300 K and 600 K and then the steady-state distribution of temperature in all CNTs is calculated. Once the steady-state temperatures of CNTs are determined, the heat flux q through the whole sample and distribution of average temperature along the applied temperature gradient T(x) are calculated. The average thermal conductivity is calculated from the Fourier law as k = |q(x2 − x1)/(T(x2) − T(x1))/A|, where coordinates x1 and x2 correspond to the boundaries of the central part of the sample, where the temperature distribution T(x) is not affected by the vicinity of the heat baths (for a homogeneous sample, the distribution of T(x) is linear at x1 < x < x2),45 and A is the maximum cross-sectional area of the sample. The local thermal conductivity of the film is calculated based on the local gradient ∂T/∂x of the average temperature as κ(x) = |q/∂T/∂x|/A.Conclusions
A novel method to introduce defects into CNT veils to reduce their thermal conductivity, without significantly affecting Seebeck coefficient and electrical conductivity, has been demonstrated. Solid-state drawing of CNT veils embedded between two polycarbonate films generated fragments in the CNT veil of reducing size with increasing draw ratio, in a process reminiscent of fibre fragmentation in continuous fibre-reinforced composites. Fitting the Kelly–Tyson model, an interfacial shear stress between PC and CNT veil of 0.43 MPa could be estimated, indicating a relatively good interaction. A successive heat treatment at above the PC glass-to-rubber transition temperature spontaneously reconnected the CNT veils fragments electrically but not thermally.The defect-engineered CNT veils experienced a decrease in thermal conductivity from 46 (virgin) to 13 W m−1 K−1 (stretched to DR = 1.5 and heat-treated), while the Seebeck coefficient and electrical conductivity went from 51 to 61 μV K−1 and 289 to 214 S cm−1, respectively. A large-scale mesoscopic simulation indicates that the experimentally-observed reduction in CNT veils thermal conductivity can be explained by a weakened connectivity of the CNT network upon stretching. The ZT figure-of-merit is estimated to increase from 5.6 × 10−4 (virgin CNT veil) to 2.7 × 10−2 (stretched and heat-treated PC/CNT/PC) when the insulating polymer layer is accounted for. The above results show that defect engineering can be a valuable strategy to optimize TE properties of CNT veils and, potentially, other organic thermoelectric materials.
Author contributions
E. Bilotti designed the initial experiments. C. Zeng performed most of the experimental works on PC/CNT/PC composites fabrication, characterization, and data analysis under the primary supervision of E. Bilotti and the co-supervision of H. Zhang and D. Papageorgiou. P. Steiner tested the thermal conductivity, under the supervision of C. Kocabas. K. Chen helped with electrical conductivity, Seebeck coefficient measurements and data analysis. K. N. Wan supported the Seebeck coefficient measurement. M. Dong performed the Raman tests and analyzed the related data. S.W. Li performed the Hall measurement, under the supervision of M. J. Reece. A. N. Volkov performed mesoscopic simulations of thermal conductivity of stretched CNT films.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. Zeng acknowledges the China Scholarship Council for the scholarship support. A. N. V. acknowledges the support from the U.S. National Science Foundation (award CMMI-1554589).References
- Y. Jia, Q. Jiang, H. Sun, P. Liu, D. Hu, Y. Pei, W. Liu, X. Crispin, S. Fabiano, Y. Ma and Y. Cao, Adv. Mater., 2021, 42, 2102990 CrossRef PubMed.
- K. Yusupov and A. Vomiero, Adv. Funct. Mater., 2020, 30, 2002015 CrossRef CAS.
- L. Wei, H. F. Huang, C. M. Gao, D. Q. Liu and L. Wang, Mater. Horiz., 2021, 8, 1207–1215 RSC.
- J. L. Blackburn, A. J. Ferguson, C. Cho and J. C. Grunlan, Adv. Mater., 2018, 30, 1704386 CrossRef PubMed.
- L. Zhang, B. J. Xia, X. L. Shi, W. D. Liu, Y. L. Yang, X. J. Hou, X. H. Ye, G. Q. Suo and Z. G. Chen, Carbon, 2022, 196, 718–726 CrossRef CAS.
- J. Choi, Y. Jung, S. J. Yang, J. Y. Oh, J. Oh, K. Jo, J. G. Son, S. E. Moon, C. R. Park and H. Kim, ACS Nano, 2017, 11, 7608–7614 CrossRef CAS PubMed.
- A. Sarris, B. Bhatti and F. Ciampa, J. Intell. Mater. Syst. Struct., 2022, 33, 1602–1612 CrossRef.
- Fitriani, R. Ovik, B. D. Long, M. C. Barma, M. Riaz, M. F. M. Sabri, S. M. Said and R. Saidur, Renewable Sustainable Energy Rev., 2016, 64, 635–659 CrossRef CAS.
- F. Suarez, A. Nozariasbmarz, D. Vashaee and M. C. Ozturk, Energy Environ. Sci., 2016, 9, 2099–2113 RSC.
- V. Karthikeyan, J. U. Surjadi, J. C. K. Wong, V. Kannan, K. H. Lam, X. F. Chen, Y. Lu and V. A. L. Roy, J. Power Sources, 2020, 455, 227983 CrossRef CAS.
- T. Lee, J. W. Lee, K. T. Park, J. S. Kim, C. R. Park and H. Kim, ACS Nano, 2021, 15, 13118–13128 CrossRef CAS PubMed.
- P. J. Taroni, G. Santagiuliana, K. N. Wan, P. Calado, M. Qiu, H. Zhang, N. M. Pugno, M. Palma, N. Stingelin-Stutzman, M. Heeney, O. Fenwick, M. Baxendale and E. Bilotti, Adv. Funct. Mater., 2018, 28, 1704285 CrossRef.
- K. N. Wan, P. J. Taroni, Z. Liu, Y. Liu, Y. Tu, G. Santagiuliana, I. C. Hsia, H. Zhang, O. Fenwick, S. Krause, M. Baxendale, B. C. Schroeder and E. Bilotti, Adv. Electron. Mater., 2019, 5, 1900582 CrossRef CAS.
- J. Lee, S. Hwang, N. Hong, J. Kwak, J. E. Jang, S. Chung and H. Kang, Mater. Horiz., 2023, 10, 160–170 RSC.
- K. N. Wan, Y. Liu, G. Santagiuliana, G. Barandun, P. Taroni, F. Guder, C. W. M. Bastiaansen, M. Baxendale, O. Fenwick, D. G. Papageorgiou, S. Krause, H. Zhang and E. Bilotti, Mater. Horiz., 2021, 8, 2513–2519 RSC.
- S. J. Wu, H. L. Hou and X. Xue, Carbon, 2022, 196, 163–175 CrossRef CAS.
- T. Ding, K. H. Chan, Y. Zhou, X. Q. Wang, Y. Cheng, T. Li and G. W. Ho, Nat. Commun., 2020, 11, 6006 CrossRef CAS PubMed.
- H. Zhou, Z. Zhang, C. Sun, H. Deng and Q. Fu, ACS Appl. Mater. Interfaces, 2020, 12, 51506–51516 CrossRef CAS PubMed.
- S. Park, J. H. Mo, S. Kim, H. Hwang and K. S. Jang, ACS Appl. Mater. Interfaces, 2020, 12, 19415–19422 CrossRef CAS PubMed.
- C. Jiang, Y. Ding, K. Cai, L. Tong, Y. Lu, W. Zhao and P. Wei, ACS Appl. Mater. Interfaces, 2020, 12, 9646–9655 CrossRef CAS PubMed.
- I. Petsagkourakis, N. Kim, K. Tybrandt, I. Zozoulenko and X. Crispin, Adv. Electron. Mater., 2019, 5, 1800918 CrossRef CAS.
- Y. Ding, Y. Qiu, K. Cai, Q. Yao, S. Chen, L. Chen and J. He, Nat. Commun., 2019, 10, 841 CrossRef PubMed.
- X. Hu, G. Chen and X. Wang, Compos. Sci. Technol., 2017, 144, 43–50 CrossRef CAS.
- L. D. Zhao, S. H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- J. Male, M. T. Agne, A. Goyal, S. Anand, I. T. Witting, V. Stevanovic and G. J. Snyder, Mater. Horiz., 2019, 6, 1444–1453 RSC.
- Z. J. Chen, H. C. Lv, Q. C. Zhang, H. F. Wang and G. M. Chen, Carbon Energy, 2022, 4, 115–128 CrossRef CAS.
- Y. Zhao, Y. Li, J. X. Qiao, S. Jiang, P. Y. Mao, J. H. Qiu, S. Q. Kang, J. Tan, K. P. Tai and C. Liu, Carbon, 2020, 170, 191–198 CrossRef CAS.
- O. Bubnova, M. Berggren and X. Crispin, J. Am. Chem. Soc., 2012, 134, 16456–16459 CrossRef CAS PubMed.
- C. Cho, B. Stevens, J. H. Hsu, R. Bureau, D. A. Hagen, O. Regev, C. Yu and J. C. Grunlan, Adv. Mater., 2015, 27, 2996–3001 CrossRef CAS PubMed.
- C. Z. Meng, C. H. Liu and S. S. Fan, Adv. Mater., 2010, 22, 535–539 CrossRef CAS PubMed.
- C. Y. Zhang, Q. Zhang, D. Zhang, M. Y. Wang, Y. W. Bo, X. Q. Fan, F. C. Li, J. J. Liang, Y. Huang, R. J. Ma and Y. S. Chen, Nano Lett., 2021, 21, 1047–1055 CrossRef CAS PubMed.
- C. H. Yu, A. Murali, K. W. Choi and Y. Ryu, Energy Environ. Sci., 2012, 5, 9481–9486 RSC.
- K. Chatterjee, A. Negi, K. Kim, J. Liu and T. K. Ghosh, ACS Appl. Energy Mater., 2020, 3, 6929–6936 CrossRef CAS.
- X. Sun, Y. Wang, K. Li, J. Wang, X. Dai, D. Chong, J. Yan and H. Wang, Adv. Funct. Mater., 2022, 32, 2203080 CrossRef CAS.
- B. Wu, Y. Guo, C. Hou, Q. Zhang, Y. Li and H. Wang, Nano Energy, 2021, 89, 106487 CrossRef CAS.
- D. Li, C. Luo, Y. Chen, D. Feng, Y. Gong, C. Pan and J. He, ACS Appl. Energy Mater., 2019, 2, 2427–2434 CrossRef CAS.
- Z. Niu, H. Dong, B. Zhu, J. Li, H. H. Hng, W. Zhou, X. Chen and S. Xie, Adv. Mater., 2013, 25, 1058–1064 CrossRef CAS PubMed.
- W. Zhou, Q. Fan, Q. Zhang, L. Cai, K. Li, X. Gu, F. Yang, N. Zhang, Y. Wang, H. Liu, W. Zhou and S. Xie, Nat. Commun., 2017, 8, 14886 CrossRef CAS PubMed.
- J. Choi, Y. Jung, C. Dun, K. T. Park, M. P. Gordon, K. Haas, P. Yuan, H. Kim, C. R. Park and J. J. Urban, ACS Appl. Energy Mater., 2020, 3, 1199–1206 CrossRef CAS.
- H. Zhan, Y. W. Chen, Q. Q. Shi, Y. Zhang, R. W. Mo and J. N. Wang, Carbon, 2022, 186, 205–214 CrossRef CAS.
- A. A. Balandin, Nat. Mater., 2011, 10, 569–581 CrossRef CAS PubMed.
- A. M. Marconnet, M. A. Panzer and K. E. Goodson, Rev. Mod. Phys., 2013, 85, 1295–1326 CrossRef CAS.
- L. Zhang, G. Zhang, C. H. Liu and S. S. Fan, Nano Lett., 2012, 12, 4848–4852 CrossRef CAS PubMed.
- D. Wang, P. C. Song, C. H. Liu, W. Wu and S. S. Fan, Nanotechnology, 2008, 19, 075609 CrossRef PubMed.
- A. N. Volkov and L. V. Zhigilei, J. Appl. Phys., 2020, 127, 065102 CrossRef CAS.
- S. Shabahang, G. Tao, J. J. Kaufman, Y. Qiao, L. Wei, T. Bouchenot, A. P. Gordon, Y. Fink, Y. Bai, R. S. Hoy and A. F. Abouraddy, Nature, 2016, 534, 529–533 CrossRef CAS PubMed.
- M. Chen, Z. Wang, X. Ge, Z. Wang, K. Fujisawa, J. Xia, Q. Zeng, K. Li, T. Zhang, Q. Zhang, M. Chen, N. Zhang, T. Wu, S. Ma, G. Gu, Z. Shen, L. Liu, Z. Liu, M. Terrones and L. Wei, Matter, 2020, 2, 666–679 CrossRef.
- J. Zhou, X. Z. Xu, Y. Y. Xin and G. Lubineau, Adv. Funct. Mater., 2018, 28, 1705591 CrossRef.
- Y. Y. Lin, R. Patel, J. Can, W. Tu, H. Zhang, E. Bilotti, C. W. M. Bastiaansen and T. Peijs, Polymer, 2019, 171, 180–191 CrossRef CAS.
- L. Aliotta and A. Lazzeri, Compos. Sci. Technol., 2020, 186, 107920 CrossRef CAS.
- R. J. Young, L. Deng, T. Z. Wafy and I. A. Kinloch, J. Mater. Sci., 2016, 51, 344–352 CrossRef CAS.
- X. Wu, P. Steiner, T. Raine, G. Pinter, A. Kretinin, C. Kocabas, M. Bissett and P. Cataldi, Adv. Electron. Mater., 2020, 6, 2000232 CrossRef CAS.
- A. D. Avery, B. H. Zhou, J. Lee, E. S. Lee, E. M. Miller, R. Ihly, D. Wesenberg, K. S. Mistry, S. L. Guillot, B. L. Zink, Y. H. Kim, J. L. Blackburn and A. J. Ferguson, Nat. Energy, 2016, 4, 1–9 Search PubMed.
- W. B. Zhou, Q. X. Fan, Q. Zhang, L. Cai, K. W. Li, X. G. Gu, F. Yang, N. Zhang, Y. C. Wang, H. P. Liu, W. Y. Zhou and S. S. Xie, Nat. Commun., 2017, 8, 14886 CrossRef CAS PubMed.
- Y. Choongho, K. Choi, Y. Liang and C. G. Jaime, ACS Nano, 2011, 5, 7885–7892 CrossRef PubMed.
- A. N. Volkov and L. V. Zhigilei, Appl. Phys. Lett., 2012, 101, 043113 CrossRef.
- A. N. Volkov and L. V. Zhigilei, Phys. Rev. Lett., 2010, 104, 215902 CrossRef PubMed.
- A. N. Volkov and L. V. Zhigilei, J. Phys. Chem. C, 2010, 114, 5513–5531 CrossRef CAS.
- L. V. Zhigilei, C. Wei and D. Srivastava, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165417 CrossRef.
- A. N. Volkov, K. R. Simiov and L. V. Zhigilei, In Proceedings of the 47th AIAA Aerospace Sciences Meeting, 2009, 1544.
- K. W. Kayang, A. Banna and A. N. Volkov, Langmuir, 2022, 38, 1977–1994 CrossRef CAS PubMed.
- Y. J. Heo, C. H. Yun, W. N. Kim and H. S. Lee, Curr. Appl. Phys., 2011, 11, 1144–1148 CrossRef.
- H. Zhan, Y. W. Chen, Q. Q. Shi, Y. Zhang, R. W. Mo and J. N. Wang, Carbon, 2022, 186, 205–214 CrossRef CAS.
- A. N. Volkov and L. V. Zhigilei, ACS Nano, 2010, 4, 6187–6195 CrossRef CAS PubMed.
- R. S. Prasher, X. J. Hu, Y. Chalopin, N. Mingo, K. Lofgreen, S. Volz, F. Cleri and P. Keblinski, Phys. Rev. Lett., 2009, 102, 105901 CrossRef PubMed.
- L. V. Zhigilei, R. N. Salaway, B. K. Wittmaack and A. N. Volkov, inCarbon Nanotubes for Interconnects: Process, Design and Applications, ed. A. Todri-Sanial, J. Dijon and A. Maffucci, Springer, 2017, pp.129–161 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00525a |
| This journal is © The Royal Society of Chemistry 2023 |