Fluorinated linkers enable the synthesis of flexible MOFs with 1D alkaline earth SBUs and a temperature-induced phase transition

Abstract

Fluorination as a functionalization of organic linkers in MOFs has shown surprising effects both on the structure of the linker itself as well as on the topology and properties of the resulting framework materials. 4,4′,4′′-Benzene-1,3,5-triyl-tris-(benzoate), typically abbreviated to BTB, is a well-known linker in the construction of MOFs. It is expected to be planar due to a complete sp² hybridisation of its carbon atoms. However, some flexibility is frequently observed by twists of the outer carboxylate groups as well as by the benzoate rings. The latter is mainly influenced by substituents of the inner benzene ring. Herein, we present two novel alkaline earth metal based MOFs [EA(II)₅(3F-BTB)₃OAc(DMF)₅] (EA(II) = Ca, Sr) utilizing a fluorinated derivative of the BTB-linker (perfluorination of the inner benzene ring) with a unique topology, crystalline sponge behaviour and a low temperature induced phase transition.

---

Introduction

Metal–organic frameworks (MOFs) are an extensively studied class of porous materials with a broad field of possible applications in gas sorption and separation,¹ sensing,² or catalysis³ to name a few. MOFs consist of inorganic building blocks and organic linkers, where both components can be functionalized or modified to improve the properties of the resulting materials.⁴ Fluorine as a substituent of the organic linker has attracted the attention of many research groups due to improved properties in the fields of gas-storage and separation,^5–8 when compared to the non-fluorinated MOF counterparts. Generalizing trends, of how fluorine substituents influence the interactions of the host framework with guest molecules, is made difficult due to the relatively sparse list of isostructural framework materials with different degrees of fluorination.^9–11 Thus, a separation of the influence of fluorine substituents and structural effects is in most cases difficult or even impossible, which leads to sometimes inconsistent results in gas sorption measurements^7,12,13 or thermal analyses.¹¹

Typically, fluorine substituents alter the geometry of aromatic carboxylate-based linkers. Especially fluorine substituents in α-position to carboxylate groups lead to increased interplanar angles between the –COO⁻ group and the phenyl ring due to repulsive interactions. Furthermore, the electron-withdrawing nature of the fluorine atoms results in a reduced aromatic character of the C(phenyl)–C(carboxylate) bond and thus, a lower rotation barrier. This was shown for coordination polymers (CPs) and MOFs with isophthalate,^14,15 terephthalate,^15–17 and trimesate¹¹ linkers. The altered geometry of the linker typically leads to MOFs and CPs with entirely different framework structures compared to their non-fluorinated analogues.^18,19 Similar results were obtained for complexes with the 2,4,6-trifluorobenzoate ligand and for 2,4,6-trifluorobenzoic acid and its non-fluorinated congener in quantum chemical calculations.²⁰

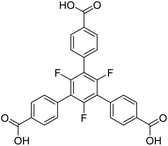
Another linker frequently used in the construction of large pore MOFs is 4,4′,4′′-benzene-1,3,5-triyl-tris-(benzoate) (BTB). Due to a complete conjugation (sp² hybridisation) of the carbon backbone, it is expected to be planar. In the pure acid (H₃BTB), which crystallizes in two distinct polymorphs with space groups I2 and P1,²¹ the interplanar angles between the inner benzene ring and the outer benzoate rings range from 23.7° to 41.2° for the P1 polymorph (mean: 33.8°) and from 28.1° to 40.1° for the I2 polymorph (mean: 34.8°). The respective angles between the benzoate rings and its carboxylate groups are significantly smaller: they range from 2.4° to 8.1° (P1, mean: 6.0°) and from 4.9° to 6.1° (I2, mean: 5.4°). These interplanar angles are, at a first sight, surprising and contradictory to the expected planarity, but plausible taking the repulsive (spatial) interactions between neighbouring benzoate rings into account. When introducing three methyl groups in the inner ring (H₃-Me₃-BTB), the interplanar angles between the inner phenyl and the outer benzoate rings increase significantly (mean: 83.8°), whereas the respective angles between the benzoate rings and its carboxylate groups remain small (mean: 4.7°).²²

Similar results were obtained for three MOFs based on UO₂²⁺ nodes and BTB linkers with different substituents in the inner ring. In [(CH₃)₂NH₂][UO₂(BTB)]·DMF·6.5H₂O with an unsubstituted BTB linker, interplanar angles between the inner phenyl and the outer benzoate rings range from 22.3° to 26.7°, which leads to a layered, slightly corrugated anionic coordination polymer with the layers stacked along [001] (space group P3₁21).²³ Using a Me₃-BTB linker, the interplanar angles between the inner and the benzoate rings increase to almost 90° (“out of plane”) resulting in a giant 3D-MOF (NU-1301) with an unprecedented complexity (V = 5 201 096 ų; 816 uranium nodes and linkers per unit cell).²⁴ UoC-3 (UoC: University of Cologne), recently published by our group, utilizes a 3F-BTB linker, which is perfluorinated in the inner benzene ring (Fig. 1).²⁵ The resulting interplanar angles between the inner and the benzoate rings are in-between the two other MOFs mentioned above, ranging from 40.3° to 63.9°. This also leads to a MOF with a 3D structure, but with a much lower complexity compared to NU-1301. Obviously, substituents in the inner ring of BTB linkers can be used to direct the synthesis of MOFs to structures with new topologies compared to those obtained with unsubstituted BTB. The general influence of subtle changes of the molecular structure of the linkers used for the construction of MOFs on their topologies has been reviewed recently.²⁶

Fig. 1 Lewis structure of 1,3,5-trifluoro-2,4,6-tris(4-carboxy-phenyl)benzene (H₃-3F-BTB).

In our ongoing research, we seek to follow the structure-directing aspects of substituted BTB linkers. We have synthesized two new isostructural calcium and strontium MOFs utilizing the 3F-BTB linker, which will be presented in the following and compared to known Ca- and Sr-MOFs based on the unsubstituted BTB linker.^27–30

Cations of the alkaline earth elements have so far played only a minor role for the synthesis of MOFs and coordination polymers. Particularly for calcium, this is surprising due to its low cost, high availability as well as its nontoxicity. We found that among the more than 100 000 entries of the MOF subset³¹ of the Cambridge Structural Database (CSD)³² only less than 1.1% contain Ca²⁺ cations compared to e.g. 14.7% of the entries containing Zn²⁺ cations. The limited use of Ca²⁺ might be due to the high ionic character of the coordinative bonds and thus, an increased instability with respect to hydrolysis. However, this has also been observed for many Zn²⁺ containing compounds, which are still an important subclass of MOF materials.

Results and discussion

The herein described fluorinated derivative of the BTB-linker, 1,3,5-trifluoro-2,4,6-tris(4-carboxy-phenyl)benzene (H₃-3F-BTB) (Fig. 1), was synthesized over three steps via the procedure published by Christoffels et al. starting from 1,3,5-trifluorobenzene.²⁵ The synthesis of the linker was tracked and confirmed via NMR-spectroscopy. Further details may be found in the Experimental section. Colourless crystals of the new MOFs (Fig. S1†), which will be referred to as UoC-9(Ca) and UoC-9(Sr) (UoC: University of Cologne), were obtained by heating an excess of the respective EA(NO₃)₂·xH₂O (EA = Ca: x = 4; EA = Sr: x = 0) with H₃-3F-BTB in DMF in the presence of acetic acid. All reactions were carried out in closed glass vials below the boiling point of the solvent. The purity of UoC-9(Ca) was assessed via PXRD (Fig. S2†). UoC-9(Sr) was not obtained as a single-phase material (vide infra).

Both MOFs of composition [EA₅(3F-BTB)₃OAc(DMF)₅] are isostructural and crystallize in the acentric orthorhombic space group Ima2 (no. 46) with four formula units per unit cell at room temperature. The asymmetric unit (Fig. S3 and S4†) contains three EA(II) cations (Wyckoff positions 4b, 8c and 8c), one and a half 3F-BTB and one half acetate anions as well as three and a half DMF molecules. Of the latter, two and a half DMF molecules coordinate to an EA(II) cation, while the last one is non-coordinating and located inside the voids of the MOF. The oxygen atoms of the 3F-BTB and acetate anions as well as the DMF molecules coordinate to the EA(II) cations via a variety of (bridging) binding motives. Due to the high complexity of the compounds, this will not be discussed in detail. Instead, we would like to refer to Fig. S5–S7 in the ESI.† The Ca–O (Ca1: 2.287(3)–2.602(4) Å, CN = 7; Ca2: 2.292(3)–2.700(2) Å, CN = 7; Ca3: 2.323(2)–2.561(2) Å, CN = 7) and Sr–O distances (Sr1: 2.481(4)–2.719(6) Å, CN = 7; Sr2: 2.437(5)–2.807(5) Å, CN = 7; Sr3: 2.455(5)–2.672(4) Å, CN = 7) are in the expected range found in comparable compounds.^27–30 The EA(II)O_x polyhedra are interconnected by bridging carboxylate groups to form corrugated 1D-strands (Fig. S6 and S7†) parallel to the crystallographic a-axis. The remaining coordination sites of the EA(II) cations are filled by the oxygen atoms of the DMF molecules. The strands are interconnected by 3F-BTB linkers to form a porous coordination network. Each linker bridges three of these strands (Fig. 2). As can be seen in Fig. 2, a benzoate ring of one 3F-BTB linker is disordered over two positions. Furthermore, one coordinating DMF molecule is so highly disordered that only its coordinating oxygen atom could be found and refined in both UoC-9(Ca) and UoC-9(Sr) at room temperature. However, in the low-temperature modification (vide infra) it can be verified that this oxygen atom belongs to a DMF molecule.

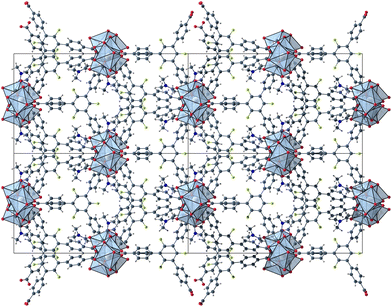Fig. 2 2 × 2 unit cells of UoC-9(Ca) viewed along the crystallographic a-axis with unit cell edges and coordination polyhedra around the Ca cations.

The void space of UoC-9(Ca) and UoC-9(Sr) accounts for 43.1% and 44.3% of the complete unit cell volume as calculated using the SQUEEZE³³ routine of PLATON.³⁴ It should be noted that due the disorder of some linker anions and DMF molecules these numbers have to be viewed with some caution. The shape of the void space is not trivially described (Fig. S8†). It meanders between the Ca/SrO_x-strands with its largest extent located between three strands close to the acetate anions as shown in Fig. 3. The pores are filled with DMF molecules, one of these can be found and refined from the room temperature single crystal data. Thermal analysis (TGA/DSC) of UoC-9(Ca) indicates a mass loss of approx. 38% up to ∼380 °C attributable to guest molecules released by the host material (Fig. S9†). This corresponds to approx. 58 DMF molecules per unit cell (2320 electrons per unit cell). Using the SQUEEZE³³ routine we obtained 1662 electrons in the solvent accessible voids of the unit cell (6590 ų). Taking into account that some DMF molecules were located and refined and are thus not included in this SQUEEZE calculation, the agreement between TGA and SQUEEZE data is reasonable. From low temperature single-crystal diffraction data (vide infra) approx. 34 non-coordinating DMF molecules per unit cell can be estimated (refined DMF molecules and electron density calculated from SQUEEZE:³³ 254 electrons in the solvent accessible voids of 2326 ų per unit cell). Together with the 20 coordinating DMF molecules per unit cell, this sums up to 54 DMF molecules, which is close to the 58 DMF molecules estimated from the TGA data (vide supra). These considerations suggest that also the DMF molecules coordinating to the alkaline earth centres are released upon heating.

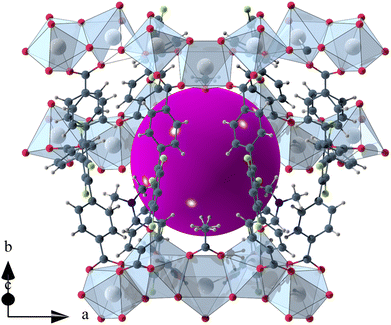Fig. 3 Isolated pore in the crystal structure of UoC-9(Ca). The void space is filled with a purple sphere.

UoC-9(Ca) and UoC-9(Sr) crystallize in the non-centrosymmetric space group Ima2 (no. 46) at room temperature. The acentricity of the structure may be rationalized by the orientation of the acetate anions, which are aligned along [001] with all anions pointing in the same direction.

Comparing the unit cells of UoC-9(Ca) and UoC-9(Sr) an increase of the unit cell volume by approx. 5% is found for the structure with the larger Sr(II) cations. The largest contribution for this increase stems from the elongation of the crystallographic a-axis from 32.0050(9) Å to 33.367(3) Å, which is the direction of the Ca/SrO_x-strands.

The influence of fluorinated linkers on the crystal structures of the resulting CPs/MOFs becomes apparent, when comparing them to similar CPs/MOFs based on non-fluorinated BTB-linkers. Noh et al. have reported the synthesis and crystal structure of [Ca₅(BTB)₂(HBTB)₂(H₂O)₆], a Ca(II)-based MOF with a 1D-SBU similar to that found in UoC-9.²⁷ In UoC-9 each 3F-BTB linker connects three inorganic SBUs. The linkers are oriented more or less perpendicular to the direction of the strands. In the structure of [Ca₅(BTB)₂(HBTB)₂(H₂O)₆] however, a connectivity of one BTB linker to only two 1D-SBUs is observed. This can be rationalized by comparing the average interplanar angles between the inner phenyl and the outer benzoate moieties of the BTB and 3F-BTB linkers summarized in Fig. 4. Generally, the unfluorinated BTB linker exhibits lower interplanar angles between the inner and the outer rings, when compared to its fluorinated derivative. This has already been pointed out in the introduction for two uranyl-based MOFs.^23,25Fig. 4 shows that this finding is confirmed by the analysis of the interplanar angles of the UoC-9 MOFs of this work compared with Ca/Sr-MOFs utilizing the non-fluorinated BTB linker.^27–30 Therein, non-fluorinated BTB exhibits an average interplanar angle between the inner and the outer phenyl rings of approx. 35°, whereas in UoC-9 this angle is increased to approx. 57°. This increase is even more evident, when considering the interplanar angle between the central phenyl ring and the outer carboxylate function. Here, an increase of the averaged interplanar angles from ∼38° (BTB) to ∼73° (3F-BTB) is observed (Fig S10†).

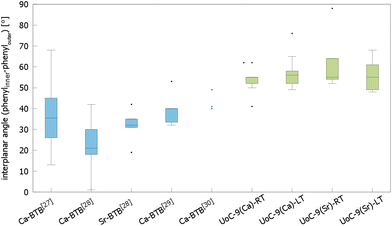Fig. 4 Comparison of the interplanar angles between the inner phenyl and the outer benzoate rings (box plot) in the crystal structures of (from left to right) [Ca₅(BTB)₂(HBTB)₂(H₂O)₆]·(THF)₁₂(H₂O)₂,²⁷ [H₂N(CH₃)₂][Ca₇(BTB)₅(H₂O)₈(DMF)₄]·4H₂O,²⁸ [H₂N(CH₃)₂][Sr₅(H₂O)₆(BTB)₄],²⁸ [Ca₃(BTB)₂(DMF)₃]·7DMF,²⁹ [Ca₃(BTB)₂(NMP)₂(H₂O)₂](NMP)(H₂O)₄,³⁰ and both polymorphs of UoC-9(Ca) and UoC-9(Sr).^{this work}

Single crystal X-ray diffraction data of UoC-9(Ca) and UoC-9(Sr) collected at 100 K reveals that both compounds undergo a phase transition from space group Ima2 to its orthorhombic subgroup Pna2₁. The low temperature polymorphs contain five EA(II) cations, three 3F-BTB and one acetate anions in their asymmetric unit (Fig. S11 and S12†). Furthermore, thirteen DMF molecules are localized in the asymmetric unit of UoC-9(Ca), five of which are coordinating to the Ca(II) cations. In UoC-9(Sr) ten DMF molecules are localized, six of them coordinate to the Sr(II) cations. In both low temperature polymorphs all atoms occupy positions with the Wyckoff symbol 4a. The framework structure, as described earlier, remains intact in both compounds, the EA(II) atoms and the organic anions/molecules merely shift/relax into more favourable positions. E.g. the acetate anions shift away from their exact alignment along the [001] direction in the Ima2 structure and are now tilted by 17.6(2)° for UoC-9(Ca) and by 6.7(6)° for UoC-9(Sr) with respect to [001].

In UoC-9(Ca) the transition can be rationalized chemically by examining the Ca(II)–oxygen bonds within the 1D-SBU. Above the transition temperature, all Ca²⁺ ions are coordinated by seven O-atoms (CN = 7), while all CaO₇–polyhedra connect to their neighbouring polyhedra via common edges. Below the transition temperature, one Ca–O bond is broken and two new Ca–O bonds are formed (Fig. 5). The acetate anion twists, such that the distance between O12_4 (in the low temperature modification) and Ca1 increases from 2.6024(4) Å to 3.0323(4) Å. Instead, two oxygen atoms O161_1 and O262_2 of the 3F-BTB linker shift along the strand to enter the coordination spheres of Ca5 and Ca4, respectively creating two new bonds with Ca–O bond distances of 2.615(3) Å and 2.685(3) Å (Fig. 5). This shifting of oxygen positions also results in a contraction of the entire SBU along the a-axis, which is visible in the unit cell parameters, as a is significantly reduced from 32.0050(9) Å in the room temperature modification to 31.6172(8) Å in the low temperature modification at 100 K.

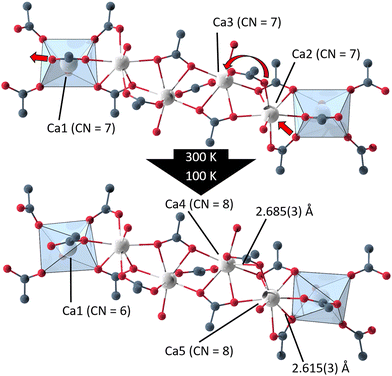Fig. 5 Excerpts from the 1D-SBU of UoC-9(Ca) highlighting the two new bonds formed in the phase transition from the high (Ima2) to the low temperature modification (Pna2₁).

In UoC-9(Sr) a mainly similar behaviour is found, but the description is more complex due to the disorder of a benzoate group of one 3F-BTB linker (Fig. S7†). Notably, the a-axis increases from 33.367(3) Å (RT) to 33.398(2) Å (100 K). This is due to the fact that the coordination sphere around Sr1 in the low temperature modification is expanded by the oxygen atom of a DMF molecule, which is not coordinating in the room temperature modification (Fig. S7†). This molecule most likely stems from within the pore and can coordinate to Sr1 due to the larger opening between the surrounding oxygen atoms in UoC-9(Sr).

To analyse the phase transition of UoC-9(Ca) in more detail, we collected X-ray single-crystal diffraction data from 250 K to 100 K in steps of 25 K (Table S1†). This data clearly indicates that the transition temperature lies between 225 K and 200 K. In Fig. 6 digitally generated precession images of the single crystal X-ray diffraction data of UoC-9(Ca) recorded at 225.15 K (above the transition temperature) and at 200.15 K (below the transition temperature) are presented. Additional reflections in the diffraction data recorded at lower temperatures clearly indicate the transition from a body centred to a primitive lattice. Heating the crystal back to room temperature gave the original body centred lattice.

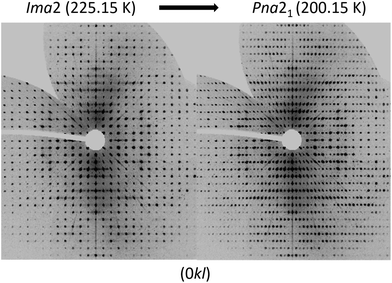Fig. 6 Digitally generated precession images of the (0kl) plane of UoC-9(Ca) from single crystal X-ray diffraction data (Mo-Kα) recorded at 225.15 K (left) and 200.15 K (right).

The group–subgroup relationship between Ima2 and Pna2₁ (the latter is a klassengleiche subgroup of index 2 of the former) suggests that this phase transition is a 2^nd order phase transition according to Landau.³⁵ 2^nd order phase transitions are continuous transitions so they should show no discontinuity of e.g. the unit cell volume at the transition temperature. In Fig. S13† the unit cell volume as obtained from single crystal X-ray diffraction data (Table S1†) is plotted against the temperature. This plot suggests that no discontinuity of the unit cell volume at the transition temperature occurs. To analyse the phase transition of UoC-9(Ca) in more detail we recorded powder X-ray diffraction data at low temperatures. However, even with well-resolved synchrotron powder diffraction data (DELTA, Dortmund/Germany, beamline BL9), we were not able to extract more information about the phase transition. Simulations show that the changes of the powder diffraction patterns of these very complex crystal structures with large unit cells are too subtle to be followed by this method.

In order to investigate if UoC-9 materials are MOFs with a permanent porosity as suggested from Fig. 3, we attempted to activate UoC-9(Ca) in vacuum upon heating. However, no significant N₂ gas uptake was measured after this procedure. Exchanging the embedded solvent with acetone, ethanol, or chloroform, prior to the measurement did not improve the activation. We assume that the crystal structure of UoC-9 collapses under these conditions after the release of solvent molecules from its pores. Therefore, we also tested to activate UoC-9(Ca) with supercritical (sc) CO₂, which is known to be a very mild activation method.³⁶ But again, it was not possible to record an adsorption isotherm indicating a successful N₂ gas uptake. The porosity of UoC-9 can, however, be confirmed by loading of small guest molecules in the liquid phase. When suspended in a liquid such as chloroform, UoC-9(Ca) initially floats on the surface of the liquid. By slow exchange of DMF molecules (ρ = 0.944 g cm⁻³, M = 73.09 g mol⁻¹) within the pores with denser CHCl₃ molecules (ρ = 1.49 g cm⁻³, M = 119.38 g mol⁻¹), the density of the whole guest@UoC-9 MOF increases and the crystals sink to the bottom of the solvent (Fig. 7). Obviously, the pores of UoC-9(Ca) are indeed accessible and the MOF may be thought of as a crystal sponge. To confirm this behaviour, we recorded DSC/TGA data of DMF and CHCl₃ loaded UoC-9(Ca) under similar conditions, i.e. due to the high volatility of CHCl₃ the sample container was closed with a lid in both measurements. The results are given in the ESI (Fig. S14†). As quantization of the data was still difficult, the 1^st derivative of the mass loss against time is shown. This plot shows nicely that CHCl₃ is released before DMF as expected from the different boiling points. After the solvent release, the framework seems to be still intact as indicated by the almost perfect overlap of the decomposition peaks.

Fig. 7 Crystals of UoC-9(Ca) immediately after the addition to chloroform (left) and after 3 days (right).

UoC-9(Ca) as well as UoC-9(Sr) exhibit this crystal-sponge-like behaviour. Both MOFs become amorphous, when the solvent diffuses out of the pores. Time-resolved PXRD measurements of UoC-9(Ca) in an open system reveal more details about this process (Fig. 8). Within the first 30 min, the reflection positions of the DMF-filled MOF remain constant. Then, for about 20 min, the reflection positions shift to higher angles, indicating decreasing lattice constants due to release of DMF molecules from the pores of UoC-9(Ca). Within the next hours the intensities of all reflections decrease gradually, which indicates an amorphization of the material. After ∼24 hours only two strong reflections at ∼6.1° and 10.6° (2θ) are still visible (Fig. S15†). Remarkably, adding DMF to this amorphous material results in a recrystallization as confirmed by PXRD of the solid in sealed capillaries (Fig. S16†). These findings seem to indicate that the framework itself is too flexible to retain a crystalline lattice structure without the presence of guest molecules. The connectivity however, remains intact in the amorphous material.³⁷ This was verified by IR spectra of as synthesized UoC-9(Ca), dried UoC-9(Ca) and the pristine linker H₃-3F-BTB (Fig. S17†). Whereas the frequencies of the C(aryl)-F vibrations at ∼1380 and ∼1040 cm⁻¹ remain mainly unchanged in all three compounds, the C–O(H) stretching vibration is only visible in the pristine acid at ∼1280 cm⁻¹. Broad features at ∼2820 cm⁻¹ and ∼2530 cm⁻¹ indicate OH groups in the latter. Signals at 2970 cm⁻¹ in as synthesized UoC-9(Ca) can be assigned to methyl groups of DMF guests, which are shifted to 2930 cm⁻¹ in dried UoC-9(Ca). No such signals are found for the pristine linker. The C=O carbonyl vibrations appear between 1660 and 1690 cm⁻¹ being weaker in the as synthesized MOF and stronger in the dried MOF. The signal is significantly shifted to higher frequencies in the pristine linker. We interpret this as a clear indication that the Ca–O coordination in dried UoC-9(Ca) is still intact, but different to the as synthesized material leading to different intensities of the signals. While the material can be handled under standard atmosphere for drying and “recrystallization”, it dissolves readily in water so that it is affected by moisture, if stored in air for prolonged periods.

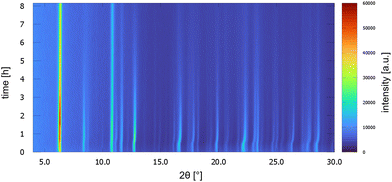Fig. 8 PXRD patterns of UoC-9(Ca) as a function of time over 8 h. Patterns were measured every 10 min with Cu-Kα radiation in a Bragg–Brentano geometry (Rigaku MiniFlex 600-C).

The crystal structure of the low temperature modification of UoC-9(Ca) may serve as an interesting case study for interactions of guest molecules with fluorinated frameworks, as there are eight unique guest molecule positions within the ASU of the structure that exhibit local energetic minima of DMF molecules within the pores. The nature of these interactions between guests and the host framework may be inferred from their Hirshfeld-isosurfaces. Most importantly, the main interaction of DMF molecules with the host can be derived from the orientation of their dipole moments (Fig. 9). The shortest contacts (seen as sharp spikes in the fingerprint plots, Fig. 9 below) are those between the oxygen atoms of DMF molecules with electropositive sites of the framework, i.e. C–H moieties of the benzoate rings or adjacent DMF molecules.

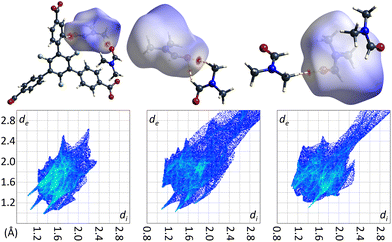Fig. 9 DMF molecules DMF_11, DMF_14 and DMF_15 (left to right) in the low temperature modification of UoC-9(Ca) shown with their calculated Hirshfeld-isosurfaces (d_norm-mapping)³⁸ and contacting moieties. The full fingerprint plots are shown below.

Remarkably, there are no indications for interactions of the C–F moieties of the 3F-BTB linker with DMF guest molecules. Unlike reported/postulated for many other F-MOFs,^5–8 direct fluorine contacts to guest molecules seem to play only a negligible role in UoC-9 materials. The Hirshfeld-isosurfaces of the 3F-BTB linkers (Fig. S18 and S19†) reveal that fluorine contributes to only 10.9%–11.6% (UoC-9(Ca)) and 10.7%–12.5% (UoC-9(Sr)) to the external contacts and no significant interactions below the sum of the respective VdW-radii are observed. All the herein presented structures, room and low temperature modifications alike, have in common that there is at least one DMF molecule in the asymmetric unit that does not coordinate to a metal centre. In all cases, this DMF is located between the central rings of two 3F-BTB linkers (Fig. 10). This may be described as a form of amide-π-stacking, a phenomenon that has been reported in protein crystallography. Theoretical investigations of this stacking by Harder et al. suggest that the interaction becomes more favourable with decreasing π-electron density.³⁹ Thus, this kind of interaction seems to be very likely for fluoro-substituted linkers. Based on ab initio calculations it was shown that three fluorine substituents on a benzene ring are the threshold, where the quadrupolar momentum is inverted,⁴⁰ further suggesting an attractive interaction of 3F-BTB with electron rich systems such as amides like DMF.

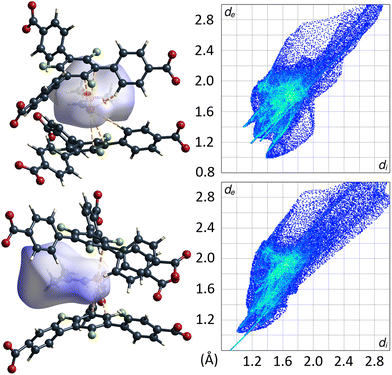Fig. 10 DMF molecule shown with its calculated Hirshfeld-isosurface (d_norm-mapping)³⁸ stacked between two 3F-BTB linkers in the framework of UoC-9(Ca) (top left) and UoC-9(Sr) (bottom left). Full fingerprint plots of the respective Hirshfeld-isosurfaces are shown to the right.

The distances between the C–N bonds of DMF and the centres of the central π-systems of the 3F-BTB linker are in agreement with the distances found in the geometries calculated by Harder et al.³⁹ With 3.4072(1)–3.6254(1) Å for UoC-9(Ca) and 3.5473(2)–3.5332(2) Å for UoC-9(Sr) they are in the range of the shortest distances, i.e. lowest energies reported in the literature (3.61 Å for 1,2,5-oxadiazole).³⁹ The observation that this DMF molecule is also ordered in the room temperature polymorphs of UoC-9(Ca) and UoC-9(Sr) supports the assumption of a strong attractive guest–host interaction. Whether this amide-π-sandwich plays a significant structure-directing role in the formation of the MOF due to a preformation in the reaction mixture or whether the space in-between the 3F-BTB linkers is occupied after crystallization of the framework, is speculative at this point and needs further investigation. It does however become apparent from the herein presented findings, that secondary effects of fluorine substituents, such as their inductive influence on π-systems, play a greater role in host–guest-interactions than simple R–F⋯guest contacts as suggested for many other FMOFs.^5–8

Experimental

Synthetic procedures

H₃-3F-BTB. The linker was synthesized following the procedure of Christoffels et al.²⁵ starting from 1,3,5-trifluorobenzene over three steps.

The syntheses of UoC-9(Ca) and UoC-9(Sr) were carried out in 15 mL screw-cap glass vials, which were closed prior to heating.

UoC-9(Ca). 10.0 mg of H₃-3F-BTB (0.02 mmol) and 30.0 mg Ca(NO₃)₂·4H₂O (0.13 mmol) were dissolved in a mixture of 4 mL DMF and 0.2 mL acetic acid. The mixture was heated for 48–72 h at 100 °C yielding colourless crystals of sufficient size for SCXRD.

UoC-9(Sr). 10.0 mg of H₃-3F-BTB (0.02 mmol) and 30.0 mg Sr(NO₃)₂ (0.14 mmol) were dissolved in a mixture of 4 mL DMF and 0.2 mL acetic acid. The mixture was heated for 48–72 h at 100 °C yielding colourless crystals. Crystals of sufficient size for SCXRD were obtained by adding seeding crystals of prior syntheses to the mixture and lowering the reaction temperature to 80 °C, keeping all other parameters the same. UoC-9(Sr) is not obtained as a pure substance; at least one other solid phase is present in the product, which is currently under investigation.

Analytical methods

Single crystal X-ray diffraction (SCXRD). Single crystal diffraction data was collected on a Bruker APEX-II CCD diffractometer (Cu-Kα radiation, mirror-monochromator, λ = 1.54187 Å) or on a Bruker D8 venture diffractometer (Mo-Kα radiation, mirror-monochromator, λ = 0.71075 Å / Ag-Kα radiation, mirror-monochromator, λ = 0.56089 Å). Suitable crystals were selected under a microscope and quickly mounted under a N₂ stream on the diffractometer, as the crystals lose some of their guest molecules very easily. An Oxford Cryostream 800 system with N₂ was used to control the temperature during XRD measurements. For the measurement of the phase transition, a single crystal of UoC-9(Ca) was mounted on the diffractometer and cooled to the measurement temperature with a rate of 1 K min⁻¹. The crystal was kept at this temperature for 15 min prior to the collection of diffraction data. The same procedure was used for all reported temperatures.

Powder X-ray diffraction (PXRD). Powder diffraction data was collected at room temperature on a Rigaku MiniFlex 600-C diffractometer (Cu-Kα radiation, Ni-filter, λ = 1.54187 Å, D/teX Ultra detector) in Bragg–Brentano Geometry or on a Huber G-670 (Cu-Kα₁ radiation, Ge-monochromator, λ = 1.54059 Å, Guinier-Camera). Measured data was processed employing the WinXPow software package.

Thermoanalytical measurements (DSC/TGA). Differential scanning calorimetry (DSC) and thermogravimetric analyses (TGA) were performed with a Mettler Toledo STAR^e TGA/DSC 1 system in an argon stream (30 mL min⁻¹). Samples were heated with a heating rate of 10 °C min⁻¹.

Hirshfeld-surface analysis. To calculate the Hirshfeld-surfaces, the CrystalExplorer 21.2^38,41 program-package was used. All hydrogen bond lengths were set to normalized values (1.083 Å for C–H) by the program prior to the calculation. The electron densities for each atom type were taken from the basis sets calculated by Koga et al.⁴² and the surfaces were generated on the very high setting for the number of grid points.

Sorption measurements. N₂ sorption measurements were attempted with an AUTOSORB-1-MP instrument (Quantachrome) at 77 K. Activation temperatures between 100 and 160 °C and activation times of 24 hours (vacuum: 1 × 10⁻⁷ mbar) did not lead to any significant N₂ uptake so that no gas sorption isotherm could be recorded. Attempts to activate UoC-9(Ca) with supercritical CO₂ also failed.

FTIR spectroscopy. All samples were measured on a PerkinElmer Spectrum Two spectrometer. The neat powders were pressed onto the ATR-crystal by a pressure device. The spectra were recorded from 450 cm⁻¹ to 4000 cm⁻¹ with a resolution of 1 cm⁻¹ in eight scans. The background corrections were applied with a measurement of the vacant ATR-crystal prior to the data collection.

Conclusions

In conclusion, we have synthesized and characterized two novel alkaline earth metal based MOFs [EA(II)₅(3F-BTB)₃OAc(DMF)₅] (EA(II) = Ca, Sr), named UoC-9(Ca) and UoC-9(Sr), utilizing a derivative of the BTB-linker (4,4′,4′′-benzene-1,3,5-triyl-tris-(benzoate)) with a perfluorination of the inner phenyl ring. This results in two isostructural MOFs (Ima2, Z = 4, RT) with a new topology, which is traced back to increased interplanar angles between the inner phenyl and the outer benzoate rings due to the fluorination. Upon cooling, both compounds undergo a 2^nd order phase transition (Pna2₁, Z = 4). Although crystal structure analysis reveals large pores within both MOFs, the recording of N₂ sorption isotherms did not lead to a significant gas uptake, as the MOFs obviously collapse upon heating in vacuum or activation with supercritical CO₂. Upon loss of DMF molecules, UoC-9 amorphisizes, but, remarkably, regains its crystallinity, when exposed to DMF again. Furthermore, an exchange of solvent molecules within the pores is possible.

The low temperature modifications of UoC-9(Ca/Sr) are ideal candidates to analyse guest–host interactions in MOFs with fluoro-substituted linkers. Analyses of Hirshfeld-isosurfaces reveal that the fluorine atoms of the inner phenyl ring of the 3F-BTB linker are not involved in any direct interaction with DMF guest molecules. Instead, DMF molecules are sandwiched between the inner phenyl rings of two 3F-BTB linkers forming an amide-π-stacking interaction. Its strength is increased by the electron-withdrawing nature of the fluorine atoms. Surprisingly, the fluoro-substituents have only a secondary effect on the guest–host interactions in these UoC-9 MOFs.

In our ongoing work in this field, we are aiming at finding more MOFs with fluorinated BTB and other linkers to shed more light on the specific interactions in these interesting FMOFs, which are assumed to be promising candidates for gas storage and separation.^5–7

Author contributions

S. S. S. undertook the investigation of UoC-9(Ca) and formal analysis of all crystal structures, supervised F. P. D. during his work, wrote parts of the original draft and visualized the herein presented results. F. P. D. prepared the first sample of UoC-9(Sr). U. R. supervised S. S. S. and F. P. D. during their work, was in charge of administration and funding for the project and wrote parts of the original draft. All authors reviewed and approved the final form of the submitted manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Lisa Körtgen, Christian Tobeck and Susanna Wenzel for the DSC/TGA measurements and the German Science Foundation (DFG) for financial support (Project No. RU 546/12-1).

References

1. J. Li, P. M. Bhatt, J. Li, M. Eddaoudi and Y. Liu, Adv. Mater., 2020, 32, 2002563.
2. M. Huangfu, M. Wang, C. Lin, J. Wang and P. Wu, Dalton Trans., 2021, 50, 3429–3449.
3. A. Dhakshinamoorthy, A. M. Asiri and H. Garcia, ChemCatChem, 2020, 12, 4732–4753.
4. Z. Ji, H. Wang, S. Canossa, S. Wuttke and O. M. Yaghi, Adv. Funct. Mater., 2020, 30, 2000238.
5. A. E. Amooghin, H. Sanaeepur, R. Luque, H. Garcia and B. Chen, Chem. Soc. Rev., 2022, 51, 7427–7508.
6. S. Kumar, B. Mohan, C. Fu, V. Gupta and P. Ren, Coord. Chem. Rev., 2023, 476, 214876.
7. C. Yang, X. Wang and M. A. Omary, J. Am. Chem. Soc., 2007, 129, 15454–15455.
8. R. A. Fischer and C. Wöll, Angew. Chem., Int. Ed., 2008, 47, 8164–8168.
9. P. Pachfule, Y. Chen, S. C. Sahoo, J. Jiang and R. Banerjee, Chem. Mater., 2011, 23, 2908–2916.
10. K. Peikert, F. Hoffmann and M. Fröba, CrystEngComm, 2015, 17, 353–360.
11. J. Krautwurst, D. Smets, R. Lamann and U. Ruschewitz, Inorg. Chem., 2019, 58, 8622–8632.
12. Z. Hulvey, D. A. Sava, J. Eckert and A. K. Cheetham, Inorg. Chem., 2011, 50, 403–405.
13. P. Pachfule, Y. Chen, J. Jiang and R. Banerjee, Chem. – Eur. J., 2012, 18, 688–694.
14. Z. Wang, V. C. Kravtsov, R. B. Walsh and M. J. Zaworotko, Cryst. Growth Des., 2007, 7, 1154–1162.
15. Z. Hulvey, J. D. Furman, S. A. Turner, M. Tang and A. K. Cheetham, Cryst. Growth Des., 2010, 10, 2041–2043.
16. C. Seidel, R. Ahlers and U. Ruschewitz, Cryst. Growth Des., 2011, 11, 5053–5063.
17. L.-M. Yang, G.-Y. Fang, J. Ma, R. Pushpa and E. Ganz, Phys. Chem. Chem. Phys., 2016, 18, 32319–32330.
18. T. Chen, I. Popov, W. Kaveevivitchai, Y.-C. Chuang, Y. Chen, A. J. Jacobson and O. Š. Miljanić, Angew. Chem., Int. Ed., 2015, 54, 13902–13906.
19. D. Smets and U. Ruschewitz, Z. Anorg. Allg. Chem., 2020, 646, 1157–1167.
20. R. Lamann, M. Hülsen, M. Dolg and U. Ruschewitz, Z. Anorg. Allg. Chem., 2012, 638, 1424–1431.
21. C. A. Zentner, H. W. H. Lai, J. T. Greenfield, R. A. Wiscons, M. Zeller, C. F. Campana, O. Talu, S. A. FitzGerald and J. L. C. Rowsell, Chem. Commun., 2015, 51, 11642–11645.
22. W. Yang, W. Zhou and B. Chen, Cryst. Growth Des., 2019, 19, 5184–5188.
23. Y. Wang, Z. Liu, Y. Li, Z. Bai, W. Liu, Y. Wang, X. Xu, C. Xiao, D. Sheng, J. Diwu, J. Su, Z. Chai, T. E. Albrecht-Schmitt and S. Wang, J. Am. Chem. Soc., 2015, 137, 6144–6147.
24. P. Li, N. A. Vermeulen, C. D. Malliakas, D. A. Gómez-Gualdrón, A. J. Howarth, B. L. Mehdi, A. Dohnalkova, N. D. Browning, M. O'Keeffe and O. K. Farha, Science, 2017, 356, 624–627.
25. R. Christoffels, C. Breitenbach, J. P. Weber, L. Körtgen, C. Tobeck, M. Wilhelm, S. Mathur, J. M. Neudörfl, M. S. Z. Farid, M. Maslo, E. Strub and U. Ruschewitz, Cryst. Growth Des., 2022, 22, 681–692.
26. V. Guillerm and D. Maspoch, J. Am. Chem. Soc., 2019, 141, 16517–16538.
27. K. Noh, N. Ko, H. J. Park, S. Park and J. Kim, CrystEngComm, 2014, 16, 8664–8668.
28. K. S. Asha, M. Makkitaya, A. Sirohi, L. Yadav, G. Sheet and S. Mandal, CrystEngComm, 2016, 18, 1046–1053.
29. D. Briones, P. Leo, J. Cepeda, G. Orcajo, G. Calleja, R. Sanz, A. Rodríguez-Diéguez and F. Martínez, CrystEngComm, 2018, 20, 4793–4803.
30. J. Liang, W. Yue, Z. Sun and A. Tong, J. Struct. Chem., 2019, 60, 1842–1849.
31. A. Li, R. Bueno-Perez, S. Wiggin and D. Fairen-Jimenez, CrystEngComm, 2020, 22, 7152–7161.
32. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
33. A. L. Spek, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 9–18.
34. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
35. L. D. Landau, Zh. Eksp. Teor. Fiz., 1937, 7, 19–32.
36. A. P. Nelson, O. K. Farha, K. L. Mulfort and J. T. Hupp, J. Am. Chem. Soc., 2009, 131, 458–460.
37. T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562.
38. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
39. M. Harder, B. Kuhn and F. Diederich, ChemMedChem, 2013, 8, 397–404.
40. J. Hernández-Trujillo and A. Vela, J. Phys. Chem., 1996, 100, 6524–6530.
41. P. Spackman, M. Turner, J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
42. T. Koga, K. Kanayama, T. Watanabe, T. Imai and A. J. Thakkar, Theor. Chem. Acc., 2000, 104, 411–413.

---

Footnote

† Electronic supplementary information (ESI) available: Containing additional figures and tables. CCDC 2240876 (UoC-9(Ca), RT), 2240878 (UoC-9(Ca), LT), 2240875 (UoC-9(Sr), RT), and 2240877 (UoC-9(Sr), LT). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00422h

---