Open Access Article
Open Access ArticleOn the accuracy of orbital based multi-level approaches for closed-shell transition metal chemistry†
Zohreh
Amanollahi‡
a,
Lukas
Lampe‡
b,
Moritz
Bensberg
 c,
Johannes
Neugebauer
c,
Johannes
Neugebauer
 b and
Milica
Feldt
b and
Milica
Feldt
 *a
*a
aLeibniz Institute for Catalysis (LIKAT), Albert-Einstein-Str. 29A, 18059 Rostock, Germany. E-mail: milica.feldt@catalysis.de
bTheoretische Organische Chemie, Organisch-Chemisches Institut and Center for Multiscale Theory and Computation, Westfälische Wilhelms-Universität Münster, Corrensstraße 36, 48149 Münster, Germany
cETH Zürich, Laboratorium für Physikalische Chemie, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland
First published on 9th January 2023
Abstract
In this work, we investigate the accuracy of the local molecular orbital molecular orbital (LMOMO) scheme and projection-based wave function-in-density functional theory (WF-in-DFT) embedding for the prediction of reaction energies and barriers of typical reactions involving transition metals. To analyze the dependence of the accuracy on the system partitioning, we apply a manual orbital selection for LMOMO as well as the so-called direct orbital selection (DOS) for both approaches. We benchmark these methods on 30 closed shell reactions involving 16 different transition metals. This allows us to devise guidelines for the manual selection as well as settings for the DOS that provide accurate results within an error of 2 kcal mol−1 compared to local coupled cluster. To reach this accuracy, on average 55% of the occupied orbitals have to be correlated with coupled cluster for the current test set. Furthermore, we find that LMOMO gives more reliable relative energies for small embedded regions than WF-in-DFT embedding.
1 Introduction
One main challenge of modern quantum chemistry is the calculation of accurate relative electronic energies (e.g., reaction energies and reaction barriers) for chemical reactions because they are fundamental for understanding and predicting their mechanisms and kinetics. An accuracy of about 1.0 kcal mol−1 in the free energies and hence in the underlying electronic energies is required to predict useful reaction kinetics. Such a high accuracy typically requires computationally expensive wave function-based methods such as coupled cluster with singles, doubles, and perturbative triples excitations [CCSD(T)].1,2 However, canonical CCSD(T) scales as N7, where N is a measure of the system size, which restricts its application to small molecular systems. Even though linear scaling approximations to CCSD(T) have been developed,3–9 practical applications on, e.g., transition metal complex catalyzed reactions remain computationally costly.One possible approach to reduce the computational effort for calculating accurate electronic energies is to employ a multi-level or embedding ansatz.10–17 Embedding approaches exploit the fact that an accurate description of the total system may not be required. For instance, it may be sufficient to describe only the transition metal center, for which the electron correlation is challenging, or the reaction center with an accurate wave function (WF) method and everything else (environment) with a computationally more efficient but less reliable method [e.g., density functional theory (DFT),18–22 second order Møller–Plesset perturbation theory (MP2)23–25 or approximate local coupled cluster26–28].
Multi-level local correlation approaches are a natural and straightforward extension of the original local correlation method because these already include prescreening and truncation schemes similar to a multi-level approach. For example, in the so-called local molecular orbital molecular orbital (LMOMO) approach,23 only orbital pairs localized in the so-called active region of the molecule are correlated with accurate local CCSD(T). All other orbital pairs are correlated with local MP2 only. Partitioning of the orbital pairs for the correlation treatment is, in fact, native to the local CCSD(T) ansatz6 because it describes orbital pairs at lower accuracy that contribute only little to the total correlation energy. The LMOMO ansatz was already extended to open-shell systems29 and applied to investigate the reaction kinetics of two enzyme models of sulfite oxidase and dimethyl sulfoxide reductase30,31 and aurophilic interaction in gold dimer complexes.32
DFT-based approaches are attractive because they promise high computational efficiency and can be formulated to be exact within the framework of Kohn–Sham DFT.16 Especially projection-based DFT embedding18 is computationally robust and numerically exact for DFT-in-DFT embedding of the same DFT methods. Furthermore, it has seen extensive algorithmic developments in recent years that aim at increasing its efficiency for WF-in-DFT embedding through basis-set adaptation33–36 and reliable strategies for the system partitioning.21,22,37–40 Additionally, it was extended to relativistic multi-component wave functions,41 analytical expressions for the nuclear gradients were formulated,42 and different formulations of the projection-operator21,43,44 were proposed. It was applied previously to study the kinetics of enzyme models,45–48 transition metal catalysts,22,49 and the oxidation potential of battery solvents.33
While there is an extensive range of multi-level approaches that all promise high computational efficiency and accuracy for relative energies, systematic comparisons of these strategies are rare. This is surprising since approaches such as projection-based embedding and LMOMO both partition the system in terms of their occupied orbital spaces which facilitates comparison of both schemes. Furthermore, we reported recently that projection-based domain-based local pair natural orbital- (DLPNO-)CCSD(T0)-in-DFT embedding shows significant errors in potential energy curves for chromium hexacarbonyl and a small active region even if the DFT potential energy curve is in very good agreement with the reference DLPNO-CCSD(T0) curve.50 The embedding ansatz essentially worsens the description of relative energies. We traced these errors to an inconsistent description of the electron correlation between the environment and the active region, which could be partially corrected by employing double hybrid exchange–correlation functionals for the interaction between subsystems, similar to earlier work employing a MP2-based correction for the exchange–correlation functional.51 In general, there is little data on the accuracy of DFT-based embedding or LMOMO for realistic examples of transition metal catalysts that require an accurate description of the electron correlation and are routinely investigated in mechanistic studies. Therefore, a precise characterization of the accuracy of these embedding approaches is required for any practical application that aims at accurate relative energies.
In addition, it is not clear for projection-based embedding or LMOMO how the active region should be selected to recover full coupled cluster results for such characteristic transition metal centered reactions. One could focus exclusively on the transition metal center and its immediate surroundings or extend this selection to other parts of the molecule. Partitioning the orbitals such that the active region includes the changing orbitals along the reaction path can be automatized through the so-called direct orbital selection22,37 (DOS) approach. The accuracy of the DOS approach was demonstrated previously for DLPNO-CCSD(T0)-in-DFT embedding,22 DFT-in-DFT embedding,37 and multi-level DLPNO-CCSD(T0).27,28 However, such an automatically selected orbital space may be unnecessarily larger and therefore computationally more expensive than focusing only on the electron correlation challenge, as is evident from recent work by some of us on orbital-pair selection criteria.28
In this work, we will compare Huzinaga-type21,44 projection-based DLPNO-CCSD(T0)-in-DFT embedding with LMOMO while focusing on the active region selection for both embedding approaches and the exchange–correlation functional selection for the DFT-embedding approach. For this comparison, we will use the DOS approach for the selection of the active region in both schemes. Furthermore, for LMOMO we will also apply the manual atom-based selection employed in previous studies23,29–32 to investigate the influence of the orbital selection. We intend to be predictive for systems that may be commonly encountered when investigating reaction mechanisms of transition metal species. Therefore, we selected a range of closed-shell systems from the MOBH3552 and MOR4153 test sets focusing on the variability of the transition metal center, and selected the complete WCCR1054,55 test to include examples with up 174 atoms. Furthermore, we do not restrict our investigation to systems that only show structural changes localized on a small part of the molecule. One example for such a system is the intramolecular proton-transfer reaction of a cobalt complex studied in ref. 49. While such systems are prime candidates for embedding calculations, they are rare in practical reaction mechanism investigations. However, so far projection-based WF-in-DFT embedding addressing transition metal systems has been mostly applied to systems of this type.22,49,56
This work is structured as follows: in Section 2 we introduce the multi-level LCCSD(T0):LMP2 and the DLPNO-CCSD(T0)-in-DFT embedding approaches, in Section 3 we discuss the technical settings we chose for the study, and in Section 4 we present error statistics for relative energies calculated with the embedding approaches and compare multi-level LCCSD(T0):LMP2 to DLPNO-CCSD(T0)-in-DFT embedding. We conclude from our results in Section 5.
2 Method
2.1 Local molecular orbital molecular orbital scheme
In the LMOMO scheme, the system is separated into an active part and an environment in terms of their occupied orbitals. Initially, Hartree–Fock (HF) orbitals are calculated for the full system. The occupied orbitals are then localized and projected out of the atomic orbitals space to generate projected atomic orbitals (PAOs). After localization, the occupied orbitals are assigned to orbital domains ([i]) which are atomic centers assigned to each orbital based on natural population analysis.57,58 The domains for pairs and triples are constructed as the union of orbital domains. If the atoms specification is used for the region selection, all localized molecular orbitals which contain at least one of the specified atoms in their domain list are included in the region. In the next step pair energies are calculated using different methods (LCCSD or LMP2) or neglected (HF) depending on the distance between the orbitals. In the case of LMOMO, this separation occurs due to the assignment of orbitals to different regions depending on the absolute position of the orbital and not anymore on the distance between orbitals. Only pairs which have both orbitals in the active region will be calculated at the high level (HL), while all other pairs will be calculated at the low level (LL). In the case that one orbital is in the active region and the other one is in the environment, the pair energy will be computed at the low level but it can be specified to easily compute those pairs at the high level, by including them as close pairs. However, we have not done this in the current study. Furthermore, all calculations involving the active region will include the effect of the amplitudes computed for the environment. At the end, the triples energies are calculated only for triples domains which belong to HL. This leads to the correlation energy: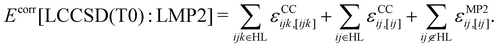 | (1) |
In practical LMOMO calculations, the active region and the environment are defined in terms of atoms. Occupied orbitals are then assigned to the subsystems through their natural orbital population on these subsystem atoms. Changes in the orbital domains along the reaction path can lead to inconsistent numbers of orbitals in the HL region for different states. To overcome this problem, one should manually include extra orbitals to the high level region or change certain orbital domains so that they are the same along the reaction path.30
2.2 Projection-based DLPNO-CCSD(T0)-in-DFT embedding
In top-down projection-based DFT embedding,18 the supersystem DFT orbitals are calculated, localized, and partitioned into an active subset and an environment subset. The description of the active orbital subset is then switched to Hartree–Fock (HF) and the orbitals are relaxed in the presence of the environment orbitals again. The interaction between both sets is described with DFT. Furthermore, the sets are constrained to be mutually orthogonal. The working equation for the active orbitals ψAi with eigenvalues εAi is given by(![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) AHF + vemb(ri) + Ô)ψAi = εAiψAi, AHF + vemb(ri) + Ô)ψAi = εAiψAi, | (2) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) AHF is the Fock operator of the active orbitals, vemb(ri) is the embedding potential from the DFT environment (see ref. 16, eqn (27) for more details, excluding any non-additive kinetic energy contributions), and Ô is a projection operator ensuring orthogonality between the orbital sets. We employ a shifted variant of the Huzinaga projection operator as proposed in ref. 44 because of its numerical stability in combination with DLPNO-CCSD(T0).50 The operator is given as
AHF is the Fock operator of the active orbitals, vemb(ri) is the embedding potential from the DFT environment (see ref. 16, eqn (27) for more details, excluding any non-additive kinetic energy contributions), and Ô is a projection operator ensuring orthogonality between the orbital sets. We employ a shifted variant of the Huzinaga projection operator as proposed in ref. 44 because of its numerical stability in combination with DLPNO-CCSD(T0).50 The operator is given asÔ = −![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ( (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) Aemb − εshift) − ( Aemb − εshift) − (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) Aemb − εshift) Aemb − εshift)![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) , , | (3) |
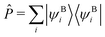 is a projection operator onto the environment orbitals,
is a projection operator onto the environment orbitals, ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) Aemb =
Aemb = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) AHF + vemb(ri) is the embedded Fock operator, and εshift is a constant shift. The operator Ô effectively shifts the eigenvalues εBi of the environment orbitals by − 2(εBi−εshift). Therefore, εshift ensures that all environment orbitals with eigenvalues smaller than εshift are shifted to high energies, preventing them from becoming occupied during the self consistent evaluation of eqn (2).
AHF + vemb(ri) is the embedded Fock operator, and εshift is a constant shift. The operator Ô effectively shifts the eigenvalues εBi of the environment orbitals by − 2(εBi−εshift). Therefore, εshift ensures that all environment orbitals with eigenvalues smaller than εshift are shifted to high energies, preventing them from becoming occupied during the self consistent evaluation of eqn (2).
After relaxation, the DLPNO-CCSD(T0) correction is calculated for the active orbitals and the final energy is evaluated as
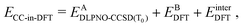 | (4) |
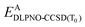 is the DLPNO-CCSD(T0) energy of the active orbitals, EBDFT is the DFT energy of the environment, and EinterDFT is the interaction energy between environment and active orbitals. The interaction energy EinterDFT is defined as
is the DLPNO-CCSD(T0) energy of the active orbitals, EBDFT is the DFT energy of the environment, and EinterDFT is the interaction energy between environment and active orbitals. The interaction energy EinterDFT is defined as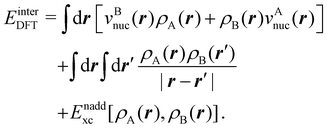 | (5) |
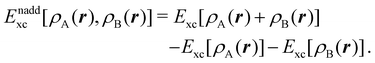 | (6) |
3 Computational details
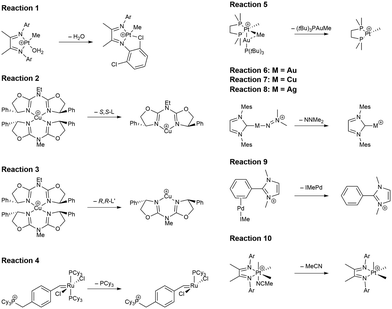
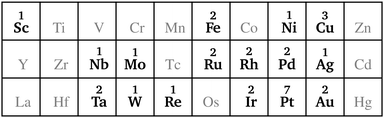
In this study, we investigated a selection of 30 closed-shell organometallic reactions from the reaction sets MOBH35,52 MOR4153 and WCCR10.54 As in previous studies on multi-level QM/QM approaches,27,28 we employed the WCCR10 test set of transition-metal complexes as a core set of benchmark reactions for our present study. This core set was expanded to a more diverse collection by including a hand-picked selection of reactions from the MOBH35 and MOR41 sets. The selection was guided by the following criteria: (i) the total number of additional reactions was limited to 20, thus keeping the size of the entire benchmark set manageable in the present study; (ii) open-shell reactions included in the MOBH35 set were excluded, since our WF-in-DFT implementation is currently restricted to closed-shell cases; (iii) since multi-level approaches obviously target large systems, reactions involving complexes with many atoms were prioritized. Based on theses guidelines, we selected the reactions 1, 6, 7, 11, 14, 21, 22, 24, 29, 30, 31, 34, and 35 from the MOBH35 set and the reactions 7, 9, 14, 16, 21, 22, and 36 from the MOR41 set. One may argue that additional and/or other reactions could have diversified our test even further. However, we want to emphasize that this selection defines one of the broadest organometallic reaction benchmark sets for the comparison of different QM/QM multi-level approaches so far.The structures were reoptimized with a consistent method. The optimizations were performed with Turbomole59 using Tao, Perdew, Staroverov, and Scuseria's exchange–correlation functional TPSS60 with Grimme's D3 dispersion correction61 and Becke-Johnson damping,62 and the def2-SVP63 basis set. The Lewis structures for all reactions are shown in Fig. 1–3. The coordinate files for reactants, transition states and products of all three reaction sets are given in the ESI.† As seen in Table 1, the test set involves 7 reactions containing 3d elements (Sc, Fe, Ni, Cu), 9 reactions containing 4d elements (Nb, Mo, Ru, Rh, Pd, Ag), and 14 reactions containing 5d elements (Ta, W, Re, Ir, Pt, Au). The transition metal compounds undergo various types of reactions, e.g., σ-donative and π-acceptor complexation, oxidative additions, ligand exchange reactions, ligand dissociations, and σ-bond metathesis. In most cases the reaction occurs directly at the transition metal center. The size of the transition metal compounds varies from 29 atoms (reaction 36 from MOR41) up to 174 atoms (reaction 4 from WCCR10). For the MOBH35 set, we calculated reaction barriers (tsn) and reaction energies (pn), while in the case of MOR41 and WCCR10 only the reaction energies (pn) were calculated.
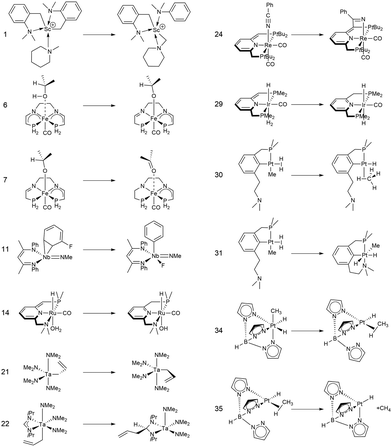 | ||
| Fig. 1 Lewis structures for the MOBH35 reactions used in this study. The reaction numbering is adopted from ref. 52. | ||
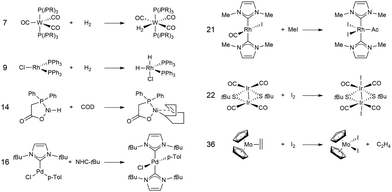 | ||
| Fig. 2 Lewis structures for the MOR41 reactions used in this study. The reaction numbering is adopted from ref. 53. | ||
Throughout this study, all reaction energies and reaction barriers were calculated with the def2-TZVP63 basis set and the corresponding effective core potentials (ECPs) for the core electrons of elements with an atomic number higher than 36 as published in ref. 64. For the calculations in Molpro which included iodine the refined ECP parameters for iodine published in ref. 65 were employed. Furthermore, in all local correlation calculations, outer core orbitals (3s3p for 3d TM, 4s4p for 4d TM and 5s5p for 5d TM) were correlated. We have chosen this basis set since it is commonly used in application studies of transition metal complexes and we did not try to get the most accurate results which could be achieved by using complete basis set extrapolation schemes. Accurate DLPNO-CCSD(T) results for these complexes already exist in the literature52,53,55,66 and agree relatively well with our DLPNO-CCSD(T0)/def2-TZVP results. In most cases the difference is below 5 kcal mol−1 with only a couple of them with differences up to 10 kcal mol−1 (see Tables S4–S6 in ESI†). One should point out that this difference does not come only from the basis set, but also from the TightPNO settings, the (T1) approximation, and slightly different structures used in the previous studies. In all local correlation calculations, the occupied orbitals were localized with the intrinsic bond orbital (IBO) scheme.67 In the case of LCCSD(T0) and LCCSD(T0):LMP2 calculations, the domains were determined according to the natural population analysis (NPA) criterion with TNPA = 0.03e. The LMP2, LCCSD(T0), and LCCSD(T0):LMP2 calculations were performed with the quantum chemistry program Molpro,68 employing density fitting approximations throughout.69–71
Using the LCCSD(T0):LMP2 method three region selections (R1 to R3) were considered. In the first one (R1), only the transition metal (TM) was included in the active region, in the second one (R2), the TM and all directly bonded atoms were assigned to the active region, and in the third (R3) selection, the region R2 was expanded to include also all atoms involved in the reaction if that was not already the case. The region R3 was constructed for reactions 6, 7, 11, 14, 22, 24 and 29 from the MOBH35 set and for reactions 14, 21 and 36 from the MOR41 set (for reaction 36 see below). Fig. 4 shows an example of the region selection for the reaction 22 from the MOBH35 set. We will refer to this selection as manual selection. In some cases, we had also to specify extra orbitals to ensure a consistent orbital selection along the reaction path. For example, for each orbital in the active region of the reactant a corresponding orbital has to be also included in the active region of all the other states and vice versa. The only exception for this selection criteria was reaction 36 in the MOR41 set. In this case for the R2 selection we have only included the TM, I and the carbon atoms of C2H4, while we have omitted the carbon atoms from the cyclopentadienyl ligands, because of the small system size. By including also the carbon atoms from the cyclopentadienyl ligands one treats the full system at the coupled cluster level which is done in selection R3.
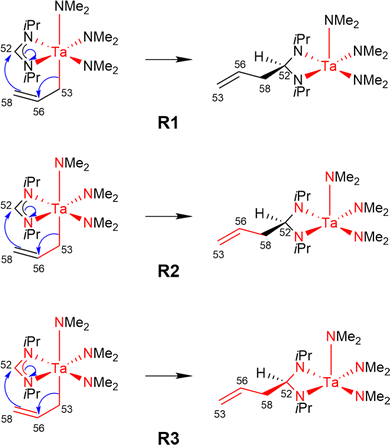 | ||
| Fig. 4 Manual region selection for LCCSD(T0):LMP2 calculations on the example of reaction 22 from the MOBH35 set. | ||
For LCCSD(T0):LMP2 calculations combined with the DOS, the localized orbitals were loaded in Serenity72–74 and partitioned into the active region and environment according to the DOS scheme37 using different values for the selection threshold for the orbital kinetic energies and the shell-wise intrinsic atomic orbital charges: 5 × 10−2 (RT1), 3 × 10−2 (RT2), 1 × 10−2 (RT3) and 8 × 10−3 (RT4).
The DLPNO-CCSD(T0) and DLPNO-CCSD(T0)-in-DFT reaction energies and reaction barriers were calculated with a development version of the quantum chemistry program Serenity.72–74 The new features included in this version will be part of an upcoming release. The frozen-core approximation and NormalPNO DLPNO-thresholds27,75 were applied for all DLPNO-CCSD(T0) and DLPNO-MP2 calculations. The latter were required for the evaluation of double-hybrid exchange–correlation functionals, as described in ref. 50. The DLPNO-CCSD(T0)-in-DFT calculations were performed using top-down projection-based embedding. The exchange–correlation functional was approximated with the BLYP functional by Lee, Yang, and Parr,76,77 the hybrid functional B3LYP78 and the double-hybrid functional DSDBLYP.79 The KS-DFT orbitals were calculated in the first step. Then we localized the reactant orbitals with the IBO scheme, aligned22 the orbitals of transition state and product before localizing them with the IBO scheme. The localized orbitals are then partitioned into active and environment orbitals with the DOS scheme using the four different selections introduced above (RT1 to RT4). We relaxed the selected active orbitals embedded in the frozen density of the KS-DFT environment using the shifted Huzinaga equation44 with a constant shift of 1Eh up to 103Eh [see eqn (3)] to obtain the embedded HF reference. In most cases, a shift of 1Eh was sufficient to achieve convergence. However, for very small active systems, we observed that a shift of 1Eh is insufficient to prevent occupation of occupied environment orbitals, leading to a failure of the embedded self-consistent field calculation. Specifically, for the systems 6 and 31 from MOBH35, 7, 9 and 14 from MOR41, and 2, 3, 4, 5 and 10 from WCCR10 in combination with RT1 and/or RT2, the shift had to be increased. A shift of 103Eh was only necessary for BLYP-D3 embedding for system 10 of the WCCR10 set with RT1. The non-additive exchange–correlation energy was approximated with the same exchange–correlation functional, including Grimme's D3 dispersion correction with Becke–Johnson damping,62 as used for the KS-DFT environment. Additionally, we combined the DSDBLYP functional for the non-additive exchange–correlation energy with the BLYP functional for the exchange–correlation energy of the environment, as described in ref. 50. Finally, the DLPNO-CCSD(T0) correction was calculated for the active system.
4 Results and discussion
In all our multi-level approaches, we will compare the results to the corresponding coupled cluster approach. Differences in relative energies between the two local coupled cluster versions (DLPNO-CCSD(T0) in Serenity and LCCSD(T0) in Molpro) are in most case on the order of a few kcal mol−1. The only exception are the reactions 22 and 36 in the MOR41 set, where the difference is very large (20 kcal mol−1). To investigate which approach is more accurate, we also ran PNO-CCSD(T)-F128 as implemented in Molpro on the system 36. These results are in agreement with DLPNO-CCSD(T0) (see Table S1 in the ESI†). Since in the LCCSD(T0) approach, errors can arise due to domain and pair approximations, we first ran LCCSD(T0) calculations with different thresholds for the distance criteria (different rclose and rweak values, see Table S1 in ESI†) which can reveal errors due to the pair approximation. However, this did not improve the results, suggesting that the problem is not caused by the pair approximation. Furthermore, we performed LCCSD(T0) calculations with the Pipek–Mezey localization80 instead of the IBO localization. The Pipek–Mezey localization aims to minimize the number of atomic centers over which an orbital extents by maximizing the orbital partial charges (either Mulliken or Löwdin partial charges are used). A similar procedure is also applied in the case of the IBO localization, where first a minimal basis of intrinsic atomic orbitals is created which is used to define partial charges for the subsequent localization. The advantage of the IBO localization is that it is basis set insensitive, while the Pipek–Mezey localization can encounter artifacts when using large basis sets or basis sets with diffuse functions. These two localization approaches can lead to different orbital domains in some cases. The LCCSD(T0) relative energies obtained using the Pipek–Mezey localization are in agreement with the energies from the DLPNO-CCSD(T0) and PNO-CCSD(T)-F12 calculations. We found that the orbital domains selected after the Pipek–Mezey and IBO localization are different for the reactant complex, leading to the difference in the LCCSD(T0) energy. The largest difference for reaction 36 is in the representation of the aromatic moieties where the orbital domains after the IBO localization spanned three carbon atoms and Molybdenum, while in the case of the Pipek–Mezey localization four carbon atoms and Molybdenum represented the orbital domains (see Table S2, ESI†). However, in the further discussion we will keep the results with the IBO localization for consistency.We will start by comparing the LMP2 and DFT energies to the LCCSD(T0) and DLPNO-CCSD(T0) energies first for the MOBH35 set and then for the other two sets to estimate how accurate LMP2 and the different DFT functionals (BLYP-D3, B3LYP-D3 and DSDBLYP-D3) perform for these systems. The relative energy errors for the MOBH35 set are shown in Fig. 5 and 6. The reaction barriers and reaction energies are given in the ESI† (Tables S4–S6), together with the figures for the MOR41 and WCCR10 sets (see Fig. S2 and S3, ESI†). Furthermore, mean absolute errors (MAE) and maximum absolute errors (MAX) are shown in the Table 2 for all sets. The smallest MAE (0.99 kcal mol−1) was observed for the MOBH35 set for the DSDBLYP-D3 functional followed by LMP2 (MAE = 2.09 kcal mol−1) for the same set. The MAX errors for these two approaches are 3.57 kcal mol−1 and 6.94 kcal mol−1 for DSDBLYP-D3 and LMP2, respectively. For the other two reaction sets, DSDBLYP-D3 was again the most accurate method with MAEs of 2.76 kcal mol−1 and 3.00 kcal mol−1 for MOR41 and WCCR10, respectively. Furthermore, the maximum absolute error of DSDBLYP-D3 was 5.24 kcal mol−1 for the reaction 3 of the WCCR10 set. LMP2 has a MAE of 4.50 kcal mol−1 and 3.94 kcal mol−1 for the sets MOR41 and WCCR10 set, respectively, and performs worse for these reactions than B3LYP-D3. The MAX for LMP2 are 13.93 kcal mol−1 for the reaction 22 in MOR41 and 10.93 kcal mol−1 for the reaction 9 in WCCR10. We want to note that these large differences between LMP2 and LCCSD(T0) for some of the reactions are beneficial to show the advantages of the multi-level LCCSD(T0):LMP2 scheme.
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . All errors are calculated with respect to the full relative energy from the full DLPNO-CCSD(T0) calculations for the DLPNO-CCSD(T0) embedding and with respect to the relative energies from the full LCCSD(T0) calculation for the multi-level LCCSD(T0):LMP2 results
. All errors are calculated with respect to the full relative energy from the full DLPNO-CCSD(T0) calculations for the DLPNO-CCSD(T0) embedding and with respect to the relative energies from the full LCCSD(T0) calculation for the multi-level LCCSD(T0):LMP2 results
| RT1 | RT2 | RT3 | RT4 | R1 | R2 | R3 | |||
|---|---|---|---|---|---|---|---|---|---|
| BLYP-D3 | DLPNO-CCSD(T0)-in-BLYP-D3 | ||||||||
| MAE | MOBH35 | 3.34 | 3.96 | 2.54 | 0.95 | 0.83 | |||
| MOR41 | 4.16 | 13.57 | 10.16 | 5.94 | 5.11 | ||||
| WCCR10 | 3.85 | 8.77 | 4.27 | 4.81 | 3.32 | ||||
| MAX | MOBH35 | 8.01 | 19.94 | 7.40 | 5.41 | 2.99 | |||
| MOR41 | 8.80 | 34.26 | 22.62 | 9.45 | 10.06 | ||||
| WCCR10 | 9.62 | 22.41 | 13.26 | 12.84 | 13.75 | ||||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
MOBH35 | 0.0 | 0.36 | 0.45 | 0.75 | 0.80 | |||
| MOR41 | 0.0 | 0.28 | 0.37 | 0.66 | 0.72 | ||||
| WCCR10 | 0.0 | 0.20 | 0.28 | 0.57 | 0.64 | ||||
| B3LYP-D3 | DLPNO-CCSD(T0)-in-B3LYP-D3 | ||||||||
| MAE | MOBH35 | 2.31 | 3.35 | 1.82 | 0.92 | 0.68 | |||
| MOR41 | 4.40 | 10.64 | 7.71 | 5.72 | 4.22 | ||||
| WCCR10 | 2.87 | 8.17 | 4.61 | 3.96 | 3.61 | ||||
| MAX | MOBH35 | 6.96 | 16.59 | 3.42 | 4.55 | 2.22 | |||
| MOR41 | 10.95 | 27.08 | 18.78 | 12.32 | 10.28 | ||||
| WCCR10 | 5.69 | 17.41 | 11.16 | 11.59 | 12.39 | ||||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
MOBH35 | 0.0 | 0.36 | 0.45 | 0.73 | 0.79 | |||
| MOR41 | 0.0 | 0.31 | 0.37 | 0.67 | 0.73 | ||||
| WCCR10 | 0.0 | 0.19 | 0.28 | 0.57 | 0.64 | ||||
| DSDBLYP-D3 | DLPNO-CCSD(T0)-in-DSDBLYP-D3 | ||||||||
| MAE | MOBH35 | 0.99 | 1.57 | 1.00 | 0.57 | 0.36 | |||
| MOR41 | 2.76 | 10.15 | 5.52 | 3.46 | 4.84 | ||||
| WCCR10 | 2.95 | 4.24 | 2.88 | 2.66 | 2.20 | ||||
| MAX | MOBH35 | 3.57 | 7.31 | 2.37 | 1.66 | 1.36 | |||
| MOR41 | 4.72 | 29.11 | 9.51 | 7.28 | 18.85 | ||||
| WCCR10 | 5.24 | 11.64 | 6.41 | 5.70 | 5.47 | ||||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
MOBH35 | 0.0 | 0.36 | 0.45 | 0.74 | 0.80 | |||
| MOR41 | 0.0 | 0.28 | 0.37 | 0.67 | 0.72 | ||||
| WCCR10 | 0.0 | 0.19 | 0.27 | 0.57 | 0.63 | ||||
| BLYP-D3 | DLPNO-CCSD(T0)-in-BLYP-D3 with DSDBLYP-D3-int | ||||||||
| MAE | MOBH35 | 3.34 | 2.46 | 1.90 | 0.49 | 0.55 | |||
| MOR41 | 4.16 | 9.00 | 4.91 | 7.36 | 3.00 | ||||
| WCCR10 | 3.85 | 5.73 | 4.14 | 3.43 | 2.30 | ||||
| MAX | MOBH35 | 8.01 | 6.24 | 6.62 | 2.93 | 2.34 | |||
| MOR41 | 8.80 | 27.15 | 10.21 | 30.92 | 4.38 | ||||
| WCCR10 | 9.62 | 11.63 | 11.78 | 6.81 | 6.54 | ||||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
MOBH35 | 0.0 | 0.36 | 0.45 | 0.75 | 0.80 | |||
| MOR41 | 0.0 | 0.28 | 0.37 | 0.66 | 0.72 | ||||
| WCCR10 | 0.0 | 0.20 | 0.28 | 0.57 | 0.64 | ||||
| LMP2 | LCCSD(T0):LMP2 | ||||||||
| MAE | MOBH35 | 2.09 | 2.41 | 1.99 | 1.57 | 0.19 | 2.15 | 1.11 | 0.39 |
| MOR41 | 4.50 | 8.32 | 1.92 | 0.71 | 0.55 | 4.56 | 0.98 | 0.60 | |
| WCCR10 | 3.94 | 2.44 | 1.27 | 0.59 | 0.44 | 2.40 | 0.93 | ||
| MAX | MOBH35 | 6.94 | 25.86 | 17.29 | 18.24 | 0.48 | 7.34 | 4.16 | 1.28 |
| MOR41 | 13.93 | 29.08 | 4.68 | 1.78 | 1.63 | 8.29 | 2.59 | 1.15 | |
| WCCR10 | 10.93 | 4.86 | 3.23 | 1.86 | 1.41 | 6.19 | 2.08 | ||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
MOBH35 | 0.0 | 0.35 | 0.43 | 0.73 | 0.79 | 0.23 | 0.47 | 0.56 |
| MOR41 | 0.0 | 0.32 | 0.39 | 0.64 | 0.70 | 0.18 | 0.49 | 0.52 | |
| WCCR10 | 0.0 | 0.20 | 0.26 | 0.54 | 0.61 | 0.14 | 0.29 | ||
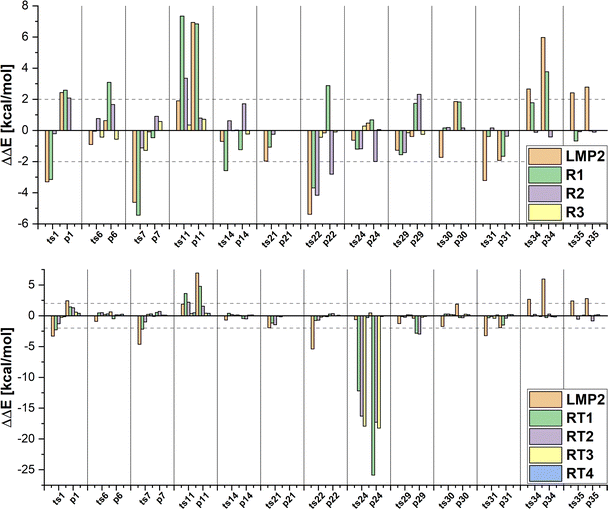
In the first set of hybrid LCCSD(T0):LMP2 calculations, we included only the transition metal in the active region (R1). In this selection around 23% of valence orbitals are treated at the LCCSD(T0) level of theory for the MOBH35 reactions set. The MAE values show that there is no increase in accuracy compared to the LMP2 results. However, if we consider the individual results presented in Fig. 5 for the MOBH35 set one can see that in many cases the errors are larger than those from the LMP2 calculations with the largest one being 7.34 kcal mol−1 for the reaction barrier of reaction 11. This can happen if the correlation energy is recovered inconsistently for different structures along the reaction path, suggesting that in some of the structures other orbitals than those included in the active region are important. For example, for the reactant complex of reaction 11 with selection R1, 95.48% of the LCCSD(T0) correlation energy is recovered, while for the transition state only 95.28% is recovered, which leads to the large error of 7.34 kcal mol−1. On the other hand, in the reaction 35 the difference of the recovered LCCSD(T0) correlation energy is only 0.01% between reactant and product thus leading to an error of only − 0.03 kcal mol−1. While for most reactions this selection of the active region was proven not to be suitable, the barriers of the reactions 6, 30, 31 and 35 are very close to the reference energies with a difference of less than 1 kcal mol−1.
In the next step, we enlarge our active region by including also the first neighbours of the TM (R2) correlating in average around 50% of the occupied orbitals at the LCCSD(T0) level for MOBH35. The errors given in Table 2 show that the accuracy is improved compared to LMP2 and the R1 selection. Furthermore, Fig. 5 illustrates that the error is around 2 kcal mol−1 or even smaller for most cases. For instance, the reactions of the platinum complexes (30, 31, 34 and 35) show the smallest errors in R2 (less than 0.2 kcal mol−1). The only two outliers with larger errors are ts11 and ts22 with absolute errors of 3.35 kcal mol−1 and 4.11 kcal mol−1. The reason for this is that we have not included all atoms involved in the reaction in the active region because they are not the next neighbors of TM.
Thus, we expanded our active region to include all atoms involved in the bond breaking/formation (R3), increasing the number of orbitals in the active region to an average of 55%. Enlargement of the active region from R2 to R3 applies only to those systems in which the reaction involves other atoms than the TM and directly bonded atoms. In MOBH35, these include the reactions 6, 7, 11, 14, 22, 24 and 29. The results show a clear improvement with the largest error in the reaction energy of reaction 7 of around 1.3 kcal mol−1. One interesting reaction is the carbon–fluorine bond cleavage of a fluoroarene in reaction 11. In this case the fluoroarene in the reactant is coordinated to the TM which disturbs the aromatic systems. The aromaticity is restored during the reaction and the consequence is that one has to include all atoms of the aromatic system in the active region since it is directly involved in the reaction. This leads to an error of 0.35 kcal mol−1 for the reaction barrier, while in the case of the R2 selection, in which only a part of the cycle and the fluorine atom were included in the active region, the error is 3.35 kcal mol−1.
Now we would like to see if these observations also hold for the reactions from the MOR41 and WCCR10 sets (see Fig. S1 and Table 2, ESI†). If one looks at the MAE values the same trends are observed for MOR41 as for MOBH35: the R1 selection has a similar MAE value as in the case of LMP2, and the MAE is already reduced to less than 1 kcal mol−1 for the R2 selection. In the case of the WCCR10 reactions, the MAE is already reduced for the smallest R1 selection and below 1 kcal mol−1 for R2. Furthermore, there are still individual cases where R1 has a larger error compared to LMP2. In the case of the R2 selection, the error is always smaller than the LMP2 error. The largest error is 2.59 kcal mol−1 in the case of reaction 36 in the MOR41 set. The system contains only 29 atoms, including two cyclopentadienyl ligands and does not allow for a meaningful selection without including all atoms of the complex in the active region.
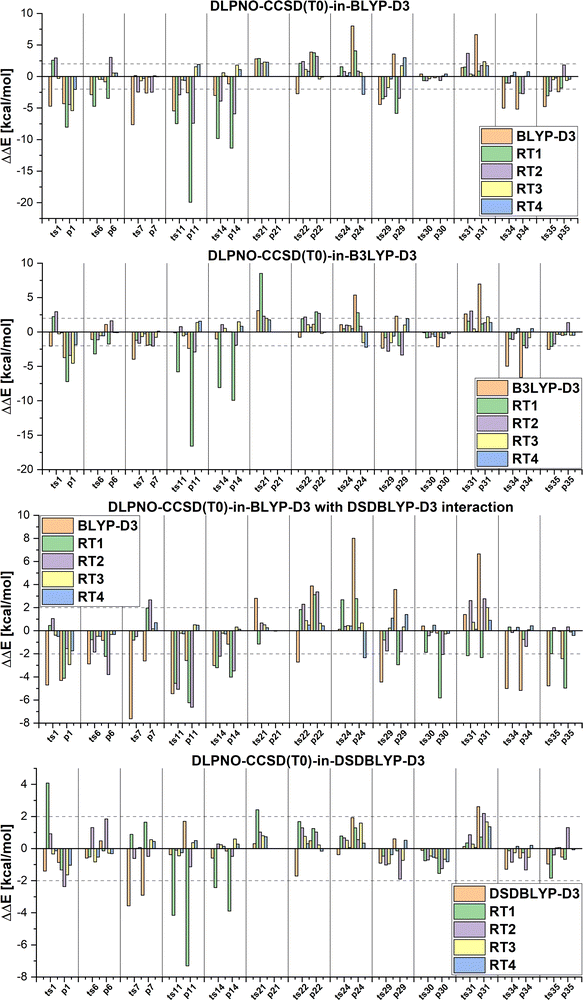
Next we will discuss the DLPNO-CCSD(T0)-in-DFT embedding and multi-level LCCSD(T0):LMP2 results calculated with the automatically selected orbital sets (RTX, X = 1, 2, …). The mean absolute errors and maximum errors in the relative energies are given in Table 2. The errors are calculated with respect to the relative energies of DLPNO-CCSD(T0) or LCCSD(T0) for the DFT-based embedding and LMP2 multi-level calculation, respectively. The MAEs are smaller for the reactions from the MOBH35 set than for the reactions from the MOR41 and WCCR10 set independently of the multi-level method. This is due to a higher ratio of active to environment orbitals for the same selection threshold and a better performance of the corresponding DFT functionals as well as LMP2 for the MOBH35 reactions. Additionally, the DOS selection performs better if a transition state is available since orbitals are mapped between three structures rather than two.
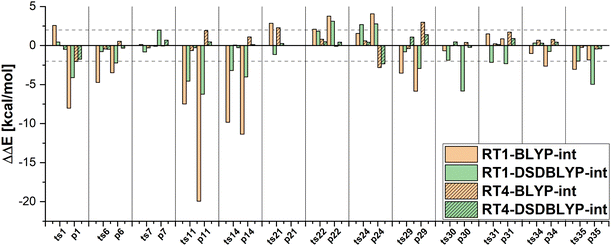
Furthermore, DFT-based embedding with small active orbital spaces (e.g., RT1) leads to less accurate relative energies than only the full DFT calculation. This agrees with the findings from ref. 50 for chromium hexacarbonyl. The DLPNO-CCSD(T0) description of the active region leads to a loss of beneficial error cancellation between relative energy errors in the active subsystem and the interaction with the environment. This effect is clearly visible for the errors in the relative energies for the reactions from the MOBH35, as shown in Fig. 6 (the error diagrams for the MOR41 and WCCR10 set of reactions are given in the ESI†). The errors for the first selection (RT1, green) are often higher than the errors of the pure DFT description (orange). Naturally, the errors in the relative energies eventually converge to zero upon increasing the size of the active region. However, this does not hold for the reactions 7 and 31 in MOBH35, reactions 14 and 16 in MOR41 and reaction 2 and 3 in WCCR10 in the case of DLPNO-CCSD(T0)-in-BLYP-D3 embedding, where the errors increase with the enlargement of the active region for the employed selection thresholds. This behavior is also present for the other functionals used in this study. One of the most pronounced examples is the reaction 16 in the MOR41 set where the absolute error of DLPNO-CCSD(T0)-in-BLYP-D3 goes from −1.28 kcal mol−1 for RT1 to 10.06 kcal mol−1 for RT4. In this case, very tight thresholds were required to achieve convergence, i.e. a threshold of 5 × 10−3 still has an error of 3.08 kcal mol−1, whereas the threshold 1 × 10−3 reduces the error to −0.34 kcal mol−1. Furthermore, in reaction 22 non-systematic behaviour is observed in the case of DLPNO-CCSD(T0)-in-BLYP-D3 with DSDBLYP-D3 for the interaction where one has a large error (−27.15 kcal mol−1) for RT1 selection, which is then reduced to −9.56 kcal mol−1 for RT2 but increases again to 30.92 kcal mol−1 for the RT3 selection. In the case of DLPNO-CCSD(T0)-in-DSDBLYP-D3 embedding, this is not so pronounced, however, for reaction 21 in the MOR41 set, the error increases from around 1.85 kcal mol−1 for RT1, RT2 and RT3 to 18.85 kcal mol−1 for RT4. These observations are in agreement with previous work (see ref. 22) where in some reactions the error only converges for very tight thresholds (e.g., 1 × 10−3) while oscillations due to error cancellation effects appear before. Therefore, the threshold RT4 (8 × 10−3) is too loose for DFT-based embedding, especially for investigating reactions like those in the MOR41 and WCCR10 sets. Since more than 90% of valence orbitals are included in the active region for the threshold 1 × 10−3, we have not included these results.
The MAEs in Table 2 show that this error is reduced significantly if double hybrid functionals describe the interaction between subsystems. We demonstrate this in Fig. 7 in which the relative energy errors for the MOBH35 set and the RT1 and RT4 selections with BLYP-D3-based embedding and DSDBLYP-D3 for the interaction are compared. The errors are lower in nearly all cases if the interaction between subsystems is described with DSDBLYP-D3 instead of BLYP-D3. This improvement is in particular significant for the reactions with the largest errors (e.g., reactions 11 and 14) suggesting that in these cases the environment orbitals contribute significantly to the relative energy through their changing interaction with the active system. This interaction is better described with a double hybrid functional. The WCCR10 and MOR41 sets show similar error trends. For instance, the MAE for BLYP-D3 embedding, the WCCR10 set, and the selection RT1 is 8.77 kcal mol−1. If the interaction between subsystems is described with DSDBLYP-D3, this error is reduced to 5.73 kcal mol−1. If also the environment is described through DSDBLYP-D3, the MAE is further reduced to 4.24 kcal mol−1. By contrast, describing the environment and interaction between subsystems with B3LYP-D3, leaves the MAE essentially unchanged at 8.17 kcal mol−1.
The LCCSD(T0):LMP2 multi-level ansatz gives slightly lower MAEs and maximum errors as the DSDBLYP-D3 embedding, although DSDBLYP-D3 is more accurate than LMP2 for all reaction sets. This highlights the loss of beneficial error cancellation of DFT-based embedding with respect to the full DFT calculation that is not present for LCCSD(T0):LMP2. Furthermore, for the selection RT1, we find no significant increase in accuracy compared to the LMP2 relative energies. For instance, only for the WCCR10 set of reactions, the MAE is lowered from 3.94 kcal mol−1 for LMP2 to 2.24 kcal mol−1 for LCCSD(T0):LMP2. For the MOBH35 and MOR41, the MAEs are increased from 2.09 kcal mol−1 and 4.50 kcal mol−1 to 2.41 kcal mol−1 and 8.32 kcal mol−1, respectively.
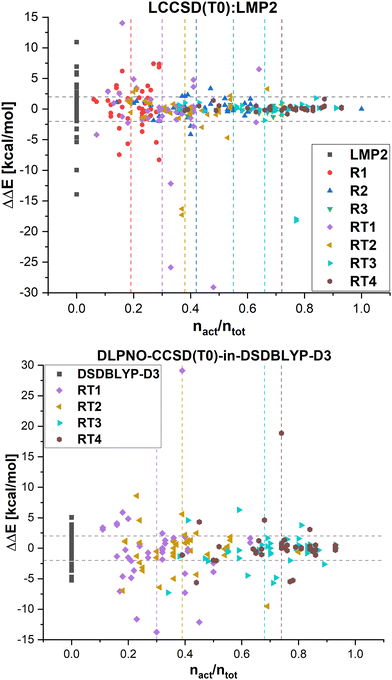
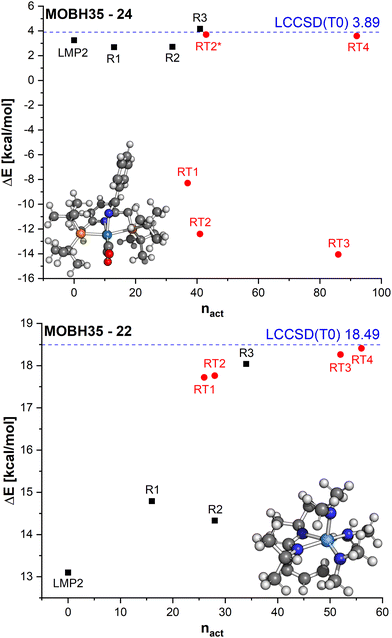
In Fig. 8, the errors in the relative energies for all LCCSD(T0):LMP2 and DLPNO-CCSD(T0)-in-DSDBLYP-D3 embedding calculations with respect to LCCSD(T0) and DLPNO-CCSD(T0), respectively, are plotted against the ratio of orbitals correlated with coupled cluster to the total number of valence orbitals for all the reactions. On average, the errors tend to converge to zero with a higher ratio of correlated electrons. However, several outliers can be observed, mostly for automatically selected active orbitals, e.g., the reaction barrier for reaction 24 from MOBH35 calculated with LCCSD(T0):LMP2 using RT3 has an error of −17.94 kcal mol−1 with 77% of all valence orbitals correlated. In the case of DLPNO-CCSD(T0)-in-DSDBLYP-D3 embedding, the largest error is 18.85 kcal mol−1 for reaction 21 in the MOR41 set with 74% of orbitals correlated at the coupled cluster level. Furthermore, it should be pointed out that in the case of RT4 selection, there are still some cases with errors larger than 2 kcal mol−1 even though around 74% of orbitals are correlated at the coupled cluster level, while this was not the case for LCCSD(T0):LMP2.
In reaction 24 from MOBH35 an enamido-rhenium complex is formed. The LMP2 reaction barrier is already close to the LCCSD(T0) barrier with a difference of only 0.6 kcal mol−1. The manual orbital selections show that the error increases slightly for R1 and R2, but it does not exceed 1.5 kcal mol−1. In the case of the R3 selection, it is lowered to only 0.3 kcal mol−1. On the other hand, the errors with the DOS selection are substantially larger and amount to more than 10 kcal mol−1 for the three selections RT1, RT2 and RT3. The only case where the error becomes significantly smaller is in the case of RT4 (−0.3 kcal mol−1). To understand the reason for such large errors we compared the orbitals which were included in the active region for the R3 and RT2 selections, since they had the same number of orbitals in the active region. The main difference was that in the case of the RT2 selection, two orbitals localized on the TM were not included in the active region (see Table S3 in ESI†). By including them in RT2 the error is significantly reduced to only −0.2 kcal mol−1 (see RT2* in Fig. 9).
 | ||
| Fig. 9 Relative energies ΔE calculated with LCCSD(T0):LMP2 for different region selections on the example of MOBH35 reactions 24 and 22 for the reaction barrier. | ||
Finally, we will discuss the reaction 22 from MOBH35 in which the allyl group is transferred to the formamidinate ligand via a metallo-Claisen rearrangement. In this case, LMP2 has an error of ∼5.5 kcal mol−1. This error is reduced with the manual region selection R1. However, increasing the region to R2 does not increase the accuracy, because not all atoms involved in the reaction are included in the active region. Increasing the active region to R3 to include all relevant atoms improves the results significantly and the remaining error is only ∼0.5 kcal mol−1. On the other hand, by doing the DOS selection, the difference is less than 1 kcal mol−1 already for the smallest threshold (RT1). This is because already for the very loose threshold, the orbitals involved in the reaction are included in the active region. For example, the selections R2 and RT2 both have 28 orbitals, but the RT2 result is much more accurate.
5 Conclusions
We systematically investigated the accuracy of DLPNO-CCSD(T0)-in-DFT embedding and multi-level LCCSD(T0):LMP2 for realistic example reactions all involving transition metals in their reaction center. Our results demonstrate that for small active system selections (R1 and RT1), the accuracy of neither LCCSD(T0):LMP2 nor DLPNO-CCSD(T0)-in-DFT embedding is increased compared to the full calculation with LMP2 or DFT, respectively. Especially for DFT-based embedding, the errors in the relative energies are increased significantly. Furthermore, we found that the accuracy of hybrid functional-based embedding is comparable to that of generalized gradient approximation-based embedding which highlights that the dominating error source in DFT-based embedding is the description of the electron correlation between subsystems compared to the DLPNO-CCSD(T0) reference. The accuracy of the embedding is increased significantly through double hybrid functionals for the description of the interaction. For meaningful DFT-based embedding calculations, the system selection RT3 or larger is required combined with a double hybrid functional. The effect of MP2-like energy contributions and double-hybrid functions on the accuracy of WF-in-DFT embedding was investigated in smaller case studies before.50,51 Both times, it was found that such orbital-dependent energy contributions describe the subsystem correlation interaction more accurately, thus, increasing the accuracy of the WF-in-DFT embedding. We confirm that these findings are transferable to a wide range of systems.Multi-level LCCSD(T0):LMP2 converges faster to the reference result with the extension of the active region than DFT-based embedding. LCCSD(T0):LMP2 with the selection RT3 provides highly accurate results without any manual selection of the active region. If a manual selection of the active region is desired, the transition metal and the first neighbours as well as all atoms involved in the reaction should be included in the active region. The advantage of the manual selection over the DOS is that it provided on average more converged results, i.e. smaller MAE, for a smaller average number of orbitals (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ) in the active region. In this study, in average we needed to correlated around 35 valence orbitals with the manual selection which corresponds to about 55% of the valence orbitals. It should be noted that the required number of orbitals in the active region would not increase with the system size for similar reactions.
) in the active region. In this study, in average we needed to correlated around 35 valence orbitals with the manual selection which corresponds to about 55% of the valence orbitals. It should be noted that the required number of orbitals in the active region would not increase with the system size for similar reactions.
We found that the DOS algorithm significantly facilitates LCCSD(T0):LMP2 calculations similar to DFT-based embedding22,37 and multi-level DLPNO-CCSD(T0).27 However, the large errors we found for the interaction between fragments suggests that the DOS-based selection could be enhanced by considering not only which orbitals change along the reaction path but also for which relatively unchanged environment orbitals the interaction with the active region is changed significantly, essentially transferring the idea of orbital pair selection28 from multi-level DLPNO-CCSD(T0) to DFT-based embedding or multi-level LCCSD(T0):LMP2.
Author contributions
Z. A.: investigation, writing – original draft, visualisation; L. L.: investigation, writing – original draft, software; M. B.: conceptualization, software, writing, supervision; J. N.: conceptualization, funding acquisition, writing – review and editing, supervision; M. F.: conceptualization, writing, supervision, funding acquisition, visualisation, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Z. A. and M. F. were supported by the Leibniz Association through the Leibniz Competition. L. L. and J. N. gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through IRTG 2678 Münster-Nagoya (Grant No. GRK 2678-437785492).References
- J. F. Stanton and J. Gauss, in A Discussion of Some Problems Associated with the Quantum Mechanical Treatment of Open-Shell Molecules, Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley & Sons, Inc., 2003, pp. 101–146 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- W. Li, Z. Ni and S. Li, Mol. Phys., 2016, 114, 1447–1460 CrossRef CAS.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- H.-J. Werner and M. Schütz, J. Chem. Phys., 2011, 135, 144116 CrossRef PubMed.
- J. Yang, G. K.-L. Chan, F. R. Manby, M. Schütz and H.-J. Werner, J. Chem. Phys., 2012, 136, 144105 CrossRef PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2018, 14, 198–215 CrossRef CAS PubMed.
- L. Gyevi-Nagy, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2021, 17, 860–878 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- J. M. Herbert, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1519 CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- L. O. Jones, M. A. Mosquera, G. C. Schatz and M. A. Ratner, J. Am. Chem. Soc., 2020, 142, 3281–3295 CrossRef CAS PubMed.
- H.-Z. Ye, H. K. Tran and T. V. Voorhis, J. Chem. Theory Comput., 2020, 16, 5035–5046 CrossRef CAS PubMed.
- G. Knizia and G. K.-L. Chan, J. Chem. Theory Comput., 2013, 9, 1429–1432 Search PubMed.
- C. R. Jacob and J. Neugebauer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 325–362 CAS.
- A. Goez and J. Neugebauer, in Frontiers of Quantum Chemistry, ed. M. J. Wójcik, Springer, 2018, ch. 7, pp. 139–180 Search PubMed.
- F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, J. Chem. Theory Comput., 2012, 8, 2564–2568 CrossRef CAS PubMed.
- S. J. R. Lee, M. Welborn, F. R. Manby and T. F. Miller, Acc. Chem. Res., 2019, 52, 1359–1368 CrossRef CAS PubMed.
- F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775 CrossRef CAS PubMed.
- B. Hégely, P. R. Nagy, G. G. Ferenczy and M. Kállay, J. Chem. Phys., 2016, 145, 064107 CrossRef.
- M. Bensberg and J. Neugebauer, J. Chem. Theory Comput., 2020, 16, 3607–3619 CrossRef CAS PubMed.
- R. A. Mata, H.-J. Werner and M. Schütz, J. Chem. Phys., 2008, 128, 144106 CrossRef PubMed.
- W. Li and P. Piecuch, J. Phys. Chem. A, 2010, 114, 6721–6727 CrossRef CAS PubMed.
- Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 CrossRef PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, J. Chem. Theory Comput., 2017, 13, 3198–3207 CrossRef CAS PubMed.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2021, 155, 224102 CrossRef CAS PubMed.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2022, 157, 064102 CrossRef CAS PubMed.
- M. Feldt and R. A. Mata, J. Chem. Theory Comput., 2018, 14, 5192–5202 CrossRef CAS PubMed.
- M. Andrejić and R. A. Mata, J. Chem. Theory Comput., 2014, 10, 5397–5404 CrossRef PubMed.
- J. Li, M. Andrejić, R. A. Mata and U. Ryde, Eur. J. Inorg. Chem., 2015, 3580–3589 CrossRef CAS.
- M. Andrejić and R. A. Mata, Phys. Chem. Chem. Phys., 2013, 15, 18115–18122 RSC.
- T. A. Barnes, J. D. Goodpaster, F. R. Manby and T. F. Miller, J. Chem. Phys., 2013, 139, 024103 CrossRef PubMed.
- S. J. Bennie, M. Stella, T. F. Miller and F. R. Manby, J. Chem. Phys., 2015, 143, 024105 CrossRef PubMed.
- B. Hégely, P. R. Nagy and M. Kállay, J. Chem. Theory Comput., 2018, 14, 4600–4615 CrossRef PubMed.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2019, 150, 184104 CrossRef PubMed.
- M. Bensberg and J. Neugebauer, J. Chem. Phys., 2019, 150, 214106 CrossRef PubMed.
- D. Claudino and N. J. Mayhall, J. Chem. Theory Comput., 2019, 15, 1053–1064 CrossRef CAS PubMed.
- D. Claudino and N. J. Mayhall, J. Chem. Theory Comput., 2019, 15, 6085–6096 CrossRef CAS PubMed.
- M. Welborn, F. R. Manby and T. F. Miller, J. Chem. Phys., 2018, 149, 144101 CrossRef PubMed.
- C. E. Hoyer and X. Li, J. Chem. Phys., 2020, 153, 094113 CrossRef CAS PubMed.
- S. J. R. Lee, F. Ding, F. R. Manby and T. F. Miller, J. Chem. Phys., 2019, 151, 064112 CrossRef.
- P. K. Tamukong, Y. G. Khait and M. R. Hoffmann, J. Phys. Chem. A, 2014, 118, 9182–9200 CrossRef CAS PubMed.
- D. V. Chulhai and J. D. Goodpaster, J. Chem. Theory Comput., 2018, 14, 1928–1942 CrossRef CAS PubMed.
- S. J. Bennie, M. W. van der Kamp, R. C. R. Pennifold, M. Stella, F. R. Manby and A. J. Mulholland, J. Chem. Theory Comput., 2016, 12, 2689–2697 CrossRef CAS PubMed.
- K. E. Ranaghan, D. Shchepnovska, S. J. Bennie, N. Lawan, S. J. Macrae, J. Zurek, F. R. Manby and A. J. Mulholland, J. Chem. Inf. Model., 2019, 59, 2063–2078 CrossRef CAS PubMed.
- X. Zhang, S. J. Bennie, M. W. van der Kamp, D. R. Glowacki, F. R. Manby and A. J. Mulholland, R. Soc. Open Sci., 2018, 5, 171390 CrossRef PubMed.
- O. A. Douglas-Gallardo, I. Shepherd, S. J. Bennie, K. E. Ranaghan, A. J. Mulholland and E. Vöhringer-Martinez, J. Comput. Chem., 2020, 41, 2151–2157 CrossRef CAS PubMed.
- P. Huo, C. Uyeda, J. D. Goodpaster, J. C. Peters and T. F. Miller, ACS Catal., 2016, 6, 6114–6123 CrossRef CAS.
- M. Bensberg and J. Neugebauer, Phys. Chem. Chem. Phys., 2020, 22, 26093–26103 RSC.
- J. D. Goodpaster, T. A. Barnes, F. R. Manby and T. F. Miller, J. Chem. Phys., 2014, 140, 18A507 CrossRef PubMed.
- M. A. Iron and T. Janes, J. Phys. Chem. A, 2019, 123, 3761–3781 CrossRef CAS PubMed.
- S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596–2608 CrossRef CAS PubMed.
- T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103 CrossRef CAS PubMed.
- T. Husch, L. Freitag and M. Reiher, J. Chem. Theory Comput., 2018, 14, 2456–2468 CrossRef CAS PubMed.
- D. S. Graham, X. Wen, D. V. Chulhai and J. D. Goodpaster, J. Chem. Theory Comput., 2020, 16, 2284–2295 CrossRef CAS PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, The Journal of Chemical Physics, 1985, 83, 735–746 CrossRef CAS.
- R. A. Mata and H.-J. Werner, Mol. Phys., 2007, 105, 2753–2761 CrossRef CAS.
- TURBOMOLE V7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preu, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- E. Semidalas and J. M. Martin, J. Chem. Theory Comput., 2022, 18, 883–898 CrossRef CAS PubMed.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net Search PubMed.
- H.-J. Werner, F. R. Manby and P. J. Knowles, J. Chem. Phys., 2003, 118, 8149–8160 CrossRef CAS.
- M. Schütz, H.-J. Werner, R. Lindh and F. R. Manby, J. Chem. Phys., 2004, 121, 737–750 CrossRef PubMed.
- R. Polly, H.-J. Werner, F. R. Manby and P. J. Knowles, Mol. Phys., 2004, 102, 2311–2321 CrossRef CAS.
- J. P. Unsleber, T. Dresselhaus, K. Klahr, D. Schnieders, M. Böckers, D. Barton and J. Neugebauer, J. Comput. Chem., 2018, 39, 788–798 CrossRef CAS PubMed.
- N. Niemeyer, P. Eschenbach, M. Bensberg, J. Tölle, L. Hellmann, L. Lampe, A. Massolle, A. Rikus, D. Schnieders, J. P. Unsleber and J. Neugebauer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1647 Search PubMed.
- Latest Release of Serenity is available from https://github.com/qcserenity/serenity.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Different flavours of local coupled cluster for reaction 36 in the MOR41 set, as well as a comparison of orbital domains obtained after IBO and Pipek–Mezey localization in the reactant complex; comparison of domains for the reaction 22 in the MOBH35 set; summary of all DFT, LMP2 and local coupled cluster relative energies, as well as DLPNO-CCSD(T) values from the literature; summary of all reaction barriers and reaction energies calculated with LCCSD(T0):LMP2 and DLPNO-CCSD(T0)-in-DFT (DFT = BLYP, B3LYP and DSDBLYP) for different selections of active regions; errors of LMP2 and LCCSD(T0):LMP2 as well as DFT and DLPNO-CCSD(T0)-in-DFT (DFT = BLYP, B3LYP and DSDBLYP) with different selections of active regions for the MOR41 and WCCR10 sets. Coordinates are included separately as a .zip file. See DOI: https://doi.org/10.1039/d2cp05056k |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2023 |