The application of food/agro-waste and spent household products for the environmentally benign separation of thorium
Received
11th April 2022
, Accepted 15th August 2022
First published on 15th August 2022
Abstract
The cost-effective and environmentally benign separation of thorium from an aqueous acidic medium using spent food/agro-byproducts has been demonstrated utilizing used tea leaves, coffee powder, and coconut leaves. The presence of carbonyl functionalities, hydroxyl moieties, and amine moieties was found to be responsible for coordinating with Th4+ ions, while rough sorbent surfaces provide more surface area for Th4+ ions to interact with. The Langmuir isotherm model was found to be applicable, involving monolayer sorption, without any neighboring-group participation, and chemisorption. Pseudo-second-order rate kinetics were revealed, with rate constants for thorium sorption of 3.4 × 10−6 mg g−1 min−1, 2.7 × 10−5 mg g−1 min−1, and 1.9 × 10−5 mg g−1 min−1 for coconut leaves, tea leaves, and coffee powder, respectively. The sorption process was thermodynamically favourable, having ΔG0 values of −5.91 kJ mol−1, −8.60 kJ mol−1, and −7.22 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The sorption processes were endothermic in nature (ΔHcoconu0t leaf = 3.30 kJ mol−1, ΔH0tea leaf = 6.33 kJ mol−1, and ΔH0coffee powder = 3.70 kJ mol−1). The overall enhancement in entropy (ΔS0coconut leaf = 0.03 kJ mol−1 K−1, ΔS0tea leaf = 0.04 kJ mol−1 K−1, and ΔS0coffee powder = 0.04 kJ mol−1 K−1) showed the spontaneity of the process. Upon exposure to 100 kGy gamma radiation, the Kd values for thorium were reduced to ∼49.9% of the original values for coconut leaves and tea leaves, while Kd was reduced to 40.4% of the original value for coffee powder.
Environmental significance
This manuscript demonstrates the highly efficient, cost-effective, and green separation of thorium from aqueous acidic streams using food-based agro- and household waste. Actinides are associated with the continuous emission of radiotoxicity into the environment; therefore, there is a need to separate such radiotoxic actinides from aqueous streams. Moreover, using liquid–liquid extraction to achieve the above purpose can generate radiotoxic organic waste, which is difficult to manage, and volatile organic compounds are of serious environmental concern. The ligands used in those cases are not completely biodegradable or incinerable, and hence they are not environmentally benign. These food-based agro- and household waste substances are not only cheap but they are also completely biodegradable. Hence using such waste materials to remove radiotoxicity is cost-effective and environmentally benign.
|
Introduction
Nuclear energy is a viable energy resource which can drastically reduce the greenhouse effect and other environmental issues associated with conventional energy sources like coal, hydrothermal, etc.1–4 However, the success of nuclear energy highly depends on the efficient and selective separation of fissile materials for fuel fabrication and the management of the highly radiotoxic waste generated during different stages of the fuel cycle, mainly pertaining to spent fuel.5–8 The environmental impact associated with radiotoxic waste is of high concern. Thorium is one of the potential resources for the third stage of the nuclear fuel cycle in India.9–12 Thorium is an abundant material with large deposits along the south coast of India, and it can be utilized for the generation of fission isotopes.13–16 However, the success of the chosen nuclear fuel cycle highly depends on the efficient and selective separation of fissile and fertile materials.13–15 Thorium, as a tetravalent actinide, is prone to coordinate with several functional groups. Phosphate, phosphonate, and phosphine oxides have been widely used in liquid–liquid separation for the efficient removal of Th4+.16–19 Phosphate-based ligands lead to environmental concerns (CHON principle), as they are not completely biodegradable or incinerable.20 Liquid–liquid extraction, a highly explored separation technique, leads to the generation of a large amount of radiotoxic organic liquid waste, which is difficult to manage due to the mobility of the liquid phase and container compatibility. Therefore, solid-phase extraction might be a potential alternative to avoid liquid waste storage problems.21,22
Novel acrylic acid and acrylamide grafted carbon nanotubes (CNTs) have been utilized for phenol removal.23,24 Polyethylene grafted CNTs have also been reported for the removal of phenol from industrial wastewater.25 The grafting of poly(trimesoyl, m-phenylenediamine) on CNTs enhanced the removal of phenol.26 Saleh reported safe, clean, and environmentally benign technologies for sulphur removal from petroleum.27 A comprehensive review has also been reported in the literature assessing nanomaterials as environmental contaminants.28 Carbon nanotubes, graphene oxides, and other novel materials showed high sorption efficiencies for tetravalent actinides from aqueous acidic waste.29–31 In addition, the selectivity can be enhanced via augmenting functional groups to such technologically important materials. Amide, amine, amidoamine, diamide, and glycolamide moieties are some of the functionalities that have been widely explored in the literature.32–36 It must be noted that the laboratory-scale preparation of such advanced sorbents and ligands is cumbersome, requiring multistage synthesis schemes with high material synthesis difficulty. The commercial-scale utilization of such materials may not be viable. In light of this, a strategy has been adopted in the present investigation where spent household and food/agro-waste can be utilized for the sequestration of highly radiotoxic actinides.37 This would certainly reduce the overall environmental burden in a cost-effective way. Spent tea leaves and coffee powder are some very common household items and are some of the major components of municipal waste. On the other hand, coconut leaves are very common waste from food/agro-industries. It is believed that the utilization of such waste for actinide removal would be an environmentally benign and commercially adoptable option for actinide sequestration. Due to the importance of Th in the nuclear industry and the requirement for cost-effective, biodegradable, and environmentally benign solid-phase separation, the present investigation was carried out. Some efforts have been documented in the literature to achieve the efficient separation of thorium using a carbon-nanofiber-modified polymer, a bentonite–gum–arabic composite, nanomaterials, and green materials.38–41 In order to understand the mechanism of sorption, different isotherm models have been employed to fit the experimental data. The sorption kinetics and related thermodynamic parameters, including changes in energy, have been monitored. The elution of thorium from the loaded materials and radiation-induced performance modification have also been studied to understand the overall feasibility of these sorbent materials.
Experimental
Sorbent preparation
5 g of coconut leaves was collected, shredded into pieces, and soaked in 5 L of distilled water (DI) for 72 h. This removed dust and other micro-pollutants. Then, this was washed three to four times with DI water (500 mL each time) until the material became free from any dirt or colour. Subsequently, it was dried at room temperature for 48 h, followed by incineration at 60 °C inside an oven for 5 h. Finally, the material was ground well in a pestle and mortar for 0.5 h to obtain a biosorbent with a uniform size distribution (within 10 μm). The tea leaves used in the present investigation were used and not fresh. Spent tea (5 g) leaves were washed with DI water (500 mL each time) 3–4 times until the supernatant became colourless. Then, they were dried for 12 h at room temperature. 2.5 g of this material was added to 250 mL of 1 M H2SO4 under continuous stirring. The stirring was continued for 6 h. Subsequently, the solution was filtered, and the material was collected and washed with DI water until the material was acid-free (5 times, each time with 500 mL of DI water). Then, it was dried at 60 °C for 12 h. Finally, the product was obtained. The biosorbent coffee powder used in the present investigation was prepared from spent coffee powder. 15 g of spent coffee powder was washed thoroughly with DI water (4 times with 500 mL of DI water each time) and dried overnight at room temperature (60 °C for 12 h). Subsequently, 10.2 g of this coffee powder was taken in a beaker containing 250 mL of 0.1 M HCl, and the mixture was stirred well for 6 h at room temperature (300 K). Then, the material was filtered, washed with DI water until it was acid-free, and dried overnight (at 60 °C for 12 h) for subsequent investigations.
Instrumentation
The detection and estimation of thorium were carried out via energy-dispersive X-ray fluorescence (EDXRF) spectroscopy using 5 mL of the aqueous phase in a Teflon container with a transparent bottom window made of Mylar film. After excitation and other subsequent photophysical phenomena, the resulting X-rays were measured using the detector. The spectrometer was procured from Jordan Valley, EX 3600, Israel. The spectrometer has a 12.5 mm Be window, a Rh source, and a Si–Li detector with a resolution of 139 eV for the Mn-Kα peak. It can cover an energy range up to 40 keV. The optimized instrumental and experimental parameters have been summarized elsewhere.42–44 Sorption experiments were carried out in a water bath with a thermostat, which was procured from Lab Enterprise, Mumbai, India. The shaker had a capacity of 108 L with outer dimensions of 700 mm × 500 mm × 900 mm. The working temperature range was from ambient temperature to 90 °C, with precision of 0.1 °C. The centrifuge machine used for complete phase separation was also procured from Lab Enterprise, Mumbai India. The maximum RPM achievable was 5200 RPM, the capacity was 16 × 15 mL, and a rotor head with a low AC induction motor (ELTEK MODEL: TC-650F+ TC 657) was included. FTIR spectroscopic analysis was carried out using a BRUKER Alpha T Module spectrometer with spectral resolution of 2 cm−1 and a spectral range of 6000–500 cm−1 with ZnSe optics. The signal-to-noise ratio is 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. FTIR spectra from solid samples were taken in ATR mode, i.e., total attenuated reflection mode. 5 mg of sample was placed on the diamond window and spectra were recorded from 25 scans. Scanning electron microscopy (SEM) images were taken using a Philips XL30 ESEM spectrometer operating with an accelerating voltage of 30 kV.
1. FTIR spectra from solid samples were taken in ATR mode, i.e., total attenuated reflection mode. 5 mg of sample was placed on the diamond window and spectra were recorded from 25 scans. Scanning electron microscopy (SEM) images were taken using a Philips XL30 ESEM spectrometer operating with an accelerating voltage of 30 kV.
Methods
Sorption
The biosorbent sorption efficiency for thorium was investigated based on the partition coefficient Kd45,46 using the formula:| | 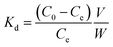 | (1) |
where C0 and Ce are the initial concentration and concentration after equilibrium of Th4+, V is the aqueous phase volume, and W is the weight of sorbent material. The Kd values were monitored as a function of the nitric acid concentration in the aqueous phase. The aqueous feed acidity was varied from 0.01 M HNO3 to 6 M HNO3. 20 mg of sorbent was allowed to equilibrate with the aqueous phase with different levels of feed acidity (a volume of 1.5 mL with an initial thorium concentration of 2 mg mL−1). Then, the biphasic system was allowed to equilibrate for 4 h at 303 K. After that, centrifugation was carried out for 2 min to achieve phase separation. Suitable aliquots (1 mL) of the aqueous phase were collected and analyzed via EDXRF for thorium. 1 mg of Th(NO3)4 dissolved in 4 M HNO3 was taken as the initial stock solution for thorium. In the next set of sorption experiments, the amount of biosorbent was varied from 10 mg to 50 mg. The nitric acid concentration in the aqueous phase was kept at 3 M, and 1.5 mL of aqueous phase containing 10 mg mL−1 thorium was allowed to equilibrate for 4 h at 200 rpm, followed by 2 min of centrifugation. Suitable aliquots (1 mL) were collected for thorium estimation via EDXRF. The experimental data thus obtained were fitted to linear regression equations from different isotherm models. To study the kinetics of sorption, the equilibration time was varied from 5 min to 4 h, keeping the other experimental parameters constant. The feed acidity was kept at 3 M HNO3. The sorbent amount was 20 mg. The temperature was kept at 303 K. The thorium concentration was kept at 10 mg mL−1. 2 min of centrifugation was carried out for complete phase separation. Finally, suitable aliquots (1 mL) were used for Th estimation via EDXRF. In order to calculate the thermodynamics of the sorption process, the temperature of phase mixing was varied from 303 K to 333 K. The sorbent amount was kept at 20 mg, the initial Th concentration was kept at 10 mg mL−1, and the time of equilibration was kept at 4 h, with a further 2 min of centrifugation. To understand the radiation-induced performance deterioration of the biosorbent, the materials were exposed inside the gamma chamber at BARC to different doses, from 25 kGy to 100 kGy. Using these irradiated sorbents, the Kd values for thorium were calculated and compared with those obtained using unirradiated materials. The volume of the aqueous phase was kept at 1.5 mL, with 3 M HNO3 and 10 mg mL−1 Th. The sorbent amount was 20 mg, the equilibration time was 4 h, and there was an additional 2 min of centrifugation. Experiments were carried out at ambient temperature. For stripping studies, two consecutive experiments were performed. The first step was the extraction of thorium and the second step was elution from the loaded solid phase. Extraction was performed using 3 M HNO3, 20 mg of sorbent, 10 mg mL−1 Th, and 4 h of equilibration. In the subsequent step, 1.5 mL of 0.5 M of oxalic acid and 0.5 M Na2CO3 were employed for elution with an equilibration time of 30 min using the loaded sorbent materials (20 mg). After phase disintegration, the aqueous phase was analyzed for thorium and the stripping percentage was calculated. For reporting data from sorption experiments, triplicate measurements were carried out, and the average of these triplicate measurements was reported. The error associated with the data was calculated based on three times the standard deviation, i.e., a 99.7% confidence limit. The relative standard deviations of the triplicate measurements were well below 10%.
Results and discussion
Surface characterization
The surface functionalization of the biosorbents was monitored via FTIR spectroscopy [Fig. 1(a)]. The FTIR spectra of the tea leaves and coffee powder were found to be very similar, while that of the coconut leaves was found to differ. In all the spectra, a prominent and broad peak was observed in the range of 3300 cm−1 to 3600 cm−1, which was attributed to hydroxyl groups at the surface of the sorbents.47 In the case of coffee powder, the peak at 3340 cm−1 was ascribed to C–H stretching from CH3 groups. The peak at 3100 cm−1 was attributed to aromatic –CH stretching. The peak at 2850 cm−1 corresponds to –CH stretching. The peak at 1701 cm−1 was attributed to carbonyl stretching.48 The peaks at 1639 and 1484 cm−1 were ascribed to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–C stretching, respectively. The peaks at 1547 cm−1 and below 1484 cm−1 were attributed to C–N stretching.49 In the case of tea leaves, the peaks at 2920 cm−1 and 2851 cm−1 were ascribed to C–H and CH2 vibrations pertaining to aliphatic hydrocarbons. The peaks at 1609 cm−1, 1515 cm−1, and 1450 cm−1 corresponded to aromatic ring stretching. The peak at 1036 cm−1 was attributed to C–O stretching. The presence of carbonyl and hydroxyl functional groups might be useful for coordinating with thorium ions from aqueous acidic waste solution.
C and C–C stretching, respectively. The peaks at 1547 cm−1 and below 1484 cm−1 were attributed to C–N stretching.49 In the case of tea leaves, the peaks at 2920 cm−1 and 2851 cm−1 were ascribed to C–H and CH2 vibrations pertaining to aliphatic hydrocarbons. The peaks at 1609 cm−1, 1515 cm−1, and 1450 cm−1 corresponded to aromatic ring stretching. The peak at 1036 cm−1 was attributed to C–O stretching. The presence of carbonyl and hydroxyl functional groups might be useful for coordinating with thorium ions from aqueous acidic waste solution.
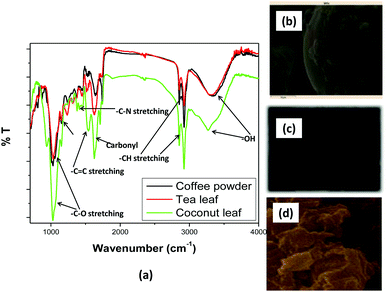 |
| | Fig. 1 (a) FTIR spectra of the biosorbents and SEM images of (b) coffee powder, (c) tea leaves, and (d) coconut leaves. | |
The surface morphology of a sorbent material is important when evaluating the sorption properties of the material. The rougher the surface, the higher the effective surface area. This increases the chances of interaction with metal ions and, hence, the separation efficiency will be higher.
Fig. 1(b)–(d) shows SEM images of coffee powder, tea leaves, and coconut leaves, respectively. The SEM image of the coffee powder showed a very smooth surface with a spheroidal nature, although some bulges were also seen on the spheroids. In the case of the tea leaves, the SEM image showed an oval-shaped material with a rougher surface compared to coffee powder. For coconut leaves, many particles with different geometrical shapes were observed. In fact, the SEM image showed an irregularly shaped rough surface. Based on the SEM images, it can be inferred that coconut leaves and tea leaves would provide a more effective surface area for interactions with thorium compared to coffee powder. Silica combined with 2% multiwalled carbon nanotubes was utilized for the sorption of Hg2+. The researchers confirmed the incorporation of SiO2 on CNTs based on the appearance of a peak at 700 cm−1 in the FTIR spectrum, which was attributed to Si–O–Si moieties.50 Saleh et al. reported a shift in the carbonyl peak from 1710 cm−1 to 1630 cm−1 between oxidized nanotubes and a nanocomposite, revealing bond formation between alumina and CNTs.51 The oxidation of multiwalled carbon nanotubes (MWCNTs) using mixtures of HNO3 and H2SO4–HNO3 was qualitatively characterized based on the appearance of a carbonyl peak in FTIR spectrum, which became more prominent at higher temperatures.52 To achieve high efficiency in the hydrodesulphurization of thiophene, CNTs were introduced to the catalyst. SEM imaging was utilized to evidence the modification.53,54
Extraction characteristics
Fig. 2(a) shows the variations in the Kd values for thorium as a function of the nitric acid concentration in the aqueous phase, keeping a fixed equilibration time of 4 h, while Fig. 2(b) shows the variations in the extent of extraction as a function of the equilibration time. In 0.01 M HNO3, the Kd values for thorium using coconut leaves, tea leaves, and coffee powder were found to be 1.31 × 104, 5.75 × 104, and 1.29 × 104, respectively. Upon increasing the acid concentration, the Kd values for coconut leaves were enhanced up to 1 M HNO3, with a maximum value of 2.07 × 104. From 1 M HNO3 to 6 M HNO3, the Kd values were constantly reduced, and at 6 M HNO3, Kd was 1.04 × 104. For tea leaves, the Kd values also were enhanced up to 1 M HNO3, with a maximum value of 8.37 × 104, followed by a reduction up to 6 M HNO3, with a value of 1.76 × 104. In the case of coffee powder, the enhancement in the Kd values was seen up to 2 M HNO3, with a value of 2.54 × 104, while beyond that, a reduction in Kd values was noticed up to 6 M HNO3, with a value of 1.24 × 104. In the case of tea leaves, the major constituent was tannin or tannin-derived products. At higher nitric acid concentrations, the carboxylic acid groups in tannin moieties can become protonated and hence their coordination with thorium ions can be hampered. Several phenolic groups can also be responsible for binding with thorium ions, resulting in very high Kd values. The coffee powder contained caffeine as a major ingredient along with other derived compounds. This material generally exhibited imidazole-derived heterocyclic aromatic moieties that were slightly basic in nature. Thorium extraction took place either through cation–pi interactions or via the coordination of carbonyl groups with metal ions. Similar to tea leaves, higher acidity also led to competition between H+ ions and Th4+ for coffee powder, hence reducing the extraction efficiency. The coconut leaves contained 90% saturated fatty acids and 10% unsaturated fatty acids. The protonation/deprotonation equilibrium of these acids was responsible for the higher thorium extraction at lower feed acidity. The study clearly indicated that maximum sorption took place in the acidity range of 0.1 M HNO3 to 2.5 M HNO3. Based on Fig. 2(b), the extent of Th sorption was found to increase for all the sorbents with an initial increase in the equilibration time. Although more than 98% mass transfer was achieved within 1 h, a plateau was found to appear in the f (mass transfer fraction) vs. equilibration time curves beyond 1 h for tea leaves, 2 h for coffee powder, and 4 h for coconut leaves. Hence, these times were considered as the times taken to achieve equilibrium.
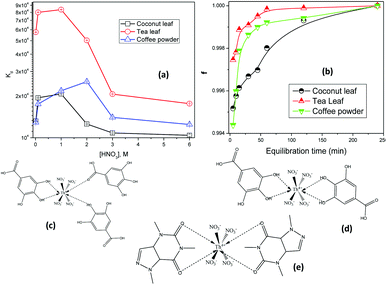 |
| | Fig. 2 (a) The variations in the Kd values of thorium as a function of the nitric acid concentration in the aqueous phase; sorbent amount: 20 mg, aqueous phase volume: 1.5 mL, initial Th concentration: 2 mg mL−1, equilibration time: 4 h, centrifugation time: 2 min, temperature: 303 K. (b) The variations in the extent of the sorption of thorium as a function of the equilibration time; sorbent amount: 20 mg, aqueous phase volume: 1.5 mL, Th initial concentration: 2 mg mL−1, aqueous phase acidity: 3 M HNO3, time of centrifugation: 2 min, temperature: 303 K. (c) The probable coordination of tannin with Th4+ in ML3 fashion. (d) The probable coordination of tannin with Th4+ in ML2 fashion. (e) The probable coordination of caffeine with Th4+. | |
3 M HNO3 is not where the maximum Kd values are achieved, as clearly seen in the curves in Fig. 2. However, above 3 M HNO3, the Kd values were only slightly reduced for all the biosorbents. Since the peaks of the Kdvs. [HNO3] plots are at different acidity levels for different biosorbents, we believed it might be confusing to use different acidity levels for different biosorbents when studying the subsequent kinetics, isotherms, and thermodynamics of the sorption processes. Hence, to use the same experimental parameters for all the biosorbents, 3 M HNO3 has been chosen for subsequent investigations (not for obtaining maximum Kd values). In addition, to calculate Kd values, the initial Th concentration in the aqueous phase and the final Th concentration in the aqueous phase after extraction were analyzed using EDXRF.
In the case of very high Kd values, the Th counts in the aqueous raffinate after extraction would be very small. Hence, there would be large error in estimating Th in the aqueous raffinate after extraction. Due to the above facts, 3 M HNO3 was chosen for subsequent sorption investigations.
Fig. 2(c)–(e) shows the probable coordination of tannin and caffeine with Th4+. Th4+ generally exhibits a coordination number of eight or higher. With the species being neutral, four nitrate ions are likely to coordinate with Th4+, maintaining charge neutrality. They can be coordinated in monodentate fashion. Consequently, for coordination saturation, four or more monodentate sites are required from the ligand moieties. Four tannin, phenolic –OH, or benzoic acid groups can coordinate with Th4+. Under acidic conditions, the formation of phenolate or benzoate ions is very much unlikely. Therefore, the lone pair of electrons of phenolic –OH groups or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(OH) groups can directly coordinate with Th4+. This coordination can occur in two different ways. The first case might show the involvement of three tannin molecules. One tannin molecule utilizes its two adjacent –OH groups, forming a five-membered ring. The other two tannin molecules can coordinate with Th4+ through –OH or –COOH groups [Fig. 2(c)]. This would achieve a coordination of eight for Th4+. The latter two tannin molecules may coordinate in a multi-dentate way. Since several water molecules are present in the system, water coordination may also be involved. However, the enhancement in entropy, as seen from thermodynamic analysis, points towards the release of water molecules during complexation. Hence, water coordination has not been shown. In the second case, two tannin molecules may be involved. Both of them utilize their ortho phenolic –OH groups for coordination with Th4+, forming two five-membered chelate rings [Fig. 2(d)]. The formation of ML4 and other higher stoichiometric complexes may be less probable from steric and thermodynamic points of view.
O(OH) groups can directly coordinate with Th4+. This coordination can occur in two different ways. The first case might show the involvement of three tannin molecules. One tannin molecule utilizes its two adjacent –OH groups, forming a five-membered ring. The other two tannin molecules can coordinate with Th4+ through –OH or –COOH groups [Fig. 2(c)]. This would achieve a coordination of eight for Th4+. The latter two tannin molecules may coordinate in a multi-dentate way. Since several water molecules are present in the system, water coordination may also be involved. However, the enhancement in entropy, as seen from thermodynamic analysis, points towards the release of water molecules during complexation. Hence, water coordination has not been shown. In the second case, two tannin molecules may be involved. Both of them utilize their ortho phenolic –OH groups for coordination with Th4+, forming two five-membered chelate rings [Fig. 2(d)]. The formation of ML4 and other higher stoichiometric complexes may be less probable from steric and thermodynamic points of view.
Fig. 2(e) depicts the coordination of caffeine with Th4+. The coordination of four nitrate ions in a monodentate way satisfies the electrical neutrality of the system. Caffeine has two carbonyl groups. The lone pair of electrons present on O can be utilized for coordination towards Th4+. The simplest form of coordination is the formation of an ML2-type complex, wherein each caffeine molecule provides two carbonyl oxygen atoms for coordination with Th4+ (a total coordination number of four is obtained with two caffeine molecules). Two six-membered chelate rings are formed. In this case, also, water molecules can coordinate. However, as discussed earlier, water coordination has not been shown when considering the formation of an inner-sphere complex upon the release of water molecules from the primary coordination sphere of Th4+. Although nitrate is a weakly coordinating anion, it is preferred over water molecules with Th4+ for maintaining charge neutrality. Such complexes have been widely reported in the literature.19,35,36,55–57 This structure elucidation is purely speculative in nature. Evidencing the same is beyond the scope of this manuscript.
Sorption mechanism
In order to understand the nature of sorption and the mechanism responsible for mass transfer, different isotherm models were employed. The experimental results were fitted to the linear equations of different isotherm models, namely the Langmuir isotherm, Freundlich isotherm, Dubinin–Radushkevich (D–R) isotherm, and Temkin isotherm. Based on regression analysis, it was revealed which isotherm model best represented the sorption behavior. The Langmuir isotherm is based on ideal sorption behavior, i.e., that sorption proceeds via monolayer coverage. There is no influence from neighbouring functional sites on actual sites during sorption. Practically, this situation occurs only in the case when the sorbent has a very low surface density of active sites. The linear equation for the Langmuir isotherm is as follows:56| | 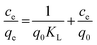 | (2) |
where Ce is the equilibrium concentration of thorium ions, qe is the amount of thorium adsorbed on the sorbent material at equilibrium, and q0 is the capacity of sorption. The higher the KL value, the higher the qe value. As seen from Table 1, in 3 M HNO3, the Kd values for Th followed the trend: tea leaves > coffee powder > coconut leaves. A similar trend is also seen for the q0 values obtained from Langmuir isotherm analysis. This isotherm only represents the ideal sorption behaviour. Moreover, monolayer sorption results in a drastic reduction in the entropy of the molecular system, bringing the 2nd law of thermodynamics into play. The surface roughness and inhomogeneity are not accounted for using this isotherm model. In view of this, the Freundlich isotherm model was also employed to explain the nature of sorption. This empirical model attributes changes in the equilibrium constant during the binding process to the heterogeneity of the surface and variations in the heat of adsorption. The linear equation for the Freundlich isotherm model can be expressed as follows:57| | 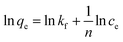 | (3) |
where kf is the Freundlich isotherm constant and ‘n’ is the sorption intensity. If n is evaluated as being equal to 1, sorption is independent of the Th4+ concentration. When n is evaluated as being more than 1, then sorption is ideal in nature. In the case of n being estimated as being lower than 1, then sorption proceeds through a cooperative mechanism. The Dubinin–Radushkevich (D–R) isotherm model is represented by three types: H-, L-, and S-shaped curves. The model can be expressed using the following expression:58| | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xm + βε2 xm + βε2 | (4) |
where xm signifies the sorption capacity of a D–R monolayer, ε is the Dubinin–Radushkevich isotherm constant, and β is associated with the sorption energy as follows:| | 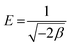 | (5) |
Table 1 Analysis of the Langmuir, Freundlich, D–R, and Temkin isotherm models (triplicate measurements with less than 10% RSD)
| Biosorbent |
Langmuir |
Freundlich |
D–R |
Temkin |
|
q
0 (mg g−1) |
K
L (L mol−1) |
n
|
K
f (mg g−1) |
E (kJ mol−1) |
X
m (mg g−1) |
b (L mg −1) |
A
T (L mg −1) |
| Coconut leaves |
303.5 |
3.1 |
11.0 |
282.7 |
8.6 |
323.3 |
88.9 |
11.9 |
| Tea leaves |
324.7 |
4.5 |
22.0 |
317.8 |
17.1 |
500.3 |
115.2 |
18.2 |
| Coffee powder |
308.5 |
3.6 |
15.0 |
296.5 |
9.9 |
414.6 |
96.7 |
15.6 |
The D–R isotherm is based on a pore filling mechanism, and it is a semi-empirical formula best fitted to physical adsorption. ε is the Polyani potential and it can be estimated as follows:
| | 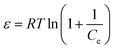 | (6) |
The Temkin isotherm model is associated with the assumption that the adsorption heat of all thorium ions decreases linearly with an enhancement in the coverage of the biosorbent surface. Adsorption is characterized based on a uniform distribution of binding energy. The Temkin isotherm model can be given as follows:59
| | 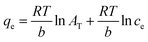 | (7) |
where
AT and
b are constants pertaining to the Temkin isotherm model.
B is related to the heat of sorption. Using these isotherm models, experimental data were plotted as follows: Langmuir isotherm,
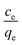 vs. Ce
vs. Ce; Freundlich isotherm, ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs.
qevs. ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce; D–R isotherm, ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. ε2
qevs. ε2; and Temkin isotherm,
qevs. ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce. The data were subjected to linear regression analysis, and the predominance of an isotherm model was determined based on the regression coefficients.
Fig. 3 shows the linear fitting of the experimental parameters to the different isotherm models. The fitting parameters indicated that Langmuir, Temkin, and Freundlich isotherms were rather equally possible, and no preference could be proposed. However, for the Langmuir model, the regression coefficients were closer to 1; hence, the Langmuir model might be favoured over the other models.
Table 1 summarizes the results from the linear regression analysis of the different isotherm models.
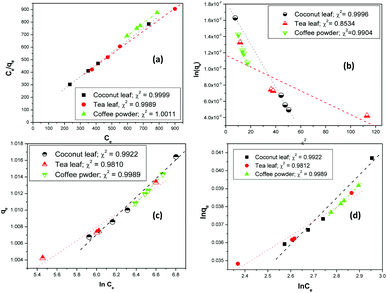 |
| | Fig. 3 The linear fitting of experimental data to (a) Langmuir, (b) D–R, (c) Temkin, and (d) Freundlich isotherm models; aqueous phase volume: 1.5 mL, initial Th concentration: 2 mg mL−1, equilibration time: 4 h, centrifugation time: 2 min, temperature: 303 K, aqueous phase acidity: 3 M HNO3. | |
The estimated thorium sorption capacity values were 303.5 mg g−1, 324.7 mg g−1, and 308.5 mg g−1 for coconut leaves, tea leaves, and coffee powder, respectively, with the Langmuir isotherm model. The experimentally obtained sorption capacities were found to be 300.2 mg g−1, 329.4 mg g−1, and 310.9 mg g−1 for coconut leaves, tea leaves, and coffee powder, respectively. The constant b is the Langmuir isotherm constant and it signifies the affinity of binding sites. The b values for the sorption processes indicated that Th4+ has the strongest affinity towards the binding sites of tea leaves, followed by coffee powder, while the lowest binding affinity was toward coconut leaves. In the case of tannin (a major constituent of tea leaves), three phenolic –OH groups and one carboxylic group provided a more suitable electron cloud for coordination with Th4+ compared with the two carbonyl oxygen atoms present in caffeine (a major constituent of coffee powder). However, in the case of coconut leaves, there were no coordination sites that were specific to Th4+. The predominance of the Langmuir isotherm model indicated the sorption processes to involve chemisorption, which was further confirmed by the sorption energy values obtained from D–R isotherm analysis. The maximum sorption energy was obtained for Th sorption onto tea leaves (17.1 kJ mol−1), whereas the values for coconut leaves and coffee powder were 8.6 kJ mol−1 and 9.9 kJ mol−1, respectively. Since the sorption energy values were well above 8 kJ mol−1, which is equivalent to typical bond energy, chemical interaction was involved during the sorption and mass transfer of thorium onto these biosorbents. The Xm values from the D–R isotherm model, which are also a measure of the sorption capacity, followed a similar trend to those obtained using the Langmuir isotherm model; however, the maximum sorption capacity values were found to be overestimated compared to both the experimentally obtained capacities and those calculated using the Langmuir isotherm model. The n values calculated via the Freundlich isotherm model were found to be more than 1, indicating normal sorption and an ideal nature, agreeing well with the predominance of the Langmuir isotherm. The values of b from the Temkin isotherm model indicated that the Th4+ heat of sorption values followed the trend: tea leaves > coffee powder > coconut leaves, which was similar to the trend obtained for the Kd values and sorption capacity values.
Fig. 4 depicts the fitting of the experimental data to the non-linear Langmuir equation for all biosorbents. The regression coefficients for fitting were found to be 0.9989, 0.9993, and 0.9962 for coconut leaves, tea leaves, and coffee powder, respectively. The estimated q0 values (q0,coconut leaf = 305 mg g−1, q0,tea leaf = 330 mg g−1, and q0,coffee powder = 312 mg g−1) were comparable to those obtained via linear regression analysis and to the experimentally obtained values. The b values followed a similar trend: bcoconut leaf (3.3 l mol−1) < bcoffee powder (3.9 l mol−1) < btea leaf (4.9 l mol−1).
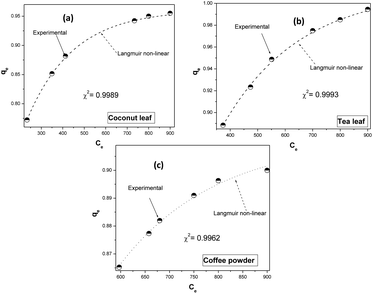 |
| | Fig. 4 Non-linear fitting of the experimental data to the Langmuir isotherm model: (a) coconut leaves, (b) tea leaves, and (c) coffee powder. | |
Sorption kinetics
The time required to attain equilibrium, or the rate of mass transfer, is a very important aspect pertaining to the sorption process. As discussed above, complete mass transfer of thorium could be achieved within 4 h of equilibration and, hence, kinetics experiments were done up to 4 h. Three different kinetics models were considered in the present case, and linear regression analysis was performed on the experimental data upon fitting to these models to identify the nature of the kinetics of sorption. According to Lagergren pseudo-first-order rate kinetics, the rate of change of thorium sorption with time is directly proportional to the difference between the saturation concentration and the amount of thorium adsorbed over time. Generally, the initial stage of an adsorption process matches this assumption. The linear rate equation can be expressed as follows:60| | 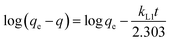 | (8) |
where kL1 is the rate constant for Lagergren pseudo-first-order kinetics. Since there is a large number of active sites compared to the concentration of thorium ions, the rate of sorption is only dependent on the concentration of one of the components, i.e., the amount of sorbent.
Webber and Morris proposed an intraparticle diffusion model, which has also been applied to explain the experimentally obtained kinetics data. Based on this, the rate equation can be formulated as follows:61
where
kIPD is the intraparticle diffusion rate constant. According to this, thorium sorption on biomaterials consists of the following small steps: (i) the diffusion of Th
4+ from bulk solution to a liquid film on the adsorbent surface; (ii) the diffusion of Th
4+ across the liquid film on the adsorbent surface; (iii) the adsorption of Th
4+ on active sites on the surface; and (iv) the diffusion of Th
4+ through pores of different sizes in the biosorbent material. The experimental data were also fitted to pseudo-second-order rate kinetics with the following linear expression:
62| | 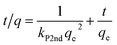 | (10) |
where
kP2nd is the rate constant for the pseudo-second-order reaction. The regression coefficients were estimated for plots of log(
qe −
q)
vs. t, and they were found to be 0.9916, 0.9299, and 0.8579 for coconut leaves, tea leaves, and coffee powder, respectively. Plots of
t/
q vs. t provided regression coefficients of 1.0011, 0.9984, and 0.9999 for coconut leaves, tea leaves, and coffee powder, respectively. Based on the analysis, sorption was found to proceed
via pseudo-second-order rate kinetics. The rate constants for sorption were estimated to be 3.4 × 10
−6, 2.7 × 10
−5, and 1.9 × 10
−5 for coconut leaves, tea leaves, and coffee powder, respectively. The rate constants followed the trend expected from the results obtained for the time required to reach equilibrium.
Table 2 summarizes the results obtained from analysis of the kinetics models, while
Fig. 5 shows the linear fitting.
Table 2 Analysis of the kinetics of the sorption processes using Lagergren first-order and pseudo-second-order kinetics models (triplicate measurements with less than 10% RSD)
| Biosorbent |
Lagergren first-order model |
Pseudo-second-order model |
|
k
L1 (min−1) |
q
e (mg g−1) |
K
P2nd (mg g−1 min−1) |
q
e (mg g−1) |
| Coconut leaves |
0.01 |
1.80 |
3.4 × 10−6 |
244.41 |
| Tea leaves |
0.02 |
9.90 |
2.7 × 10−5 |
515.30 |
| Coffee powder |
0.02 |
3.71 |
1.9 × 10−5 |
325.92 |
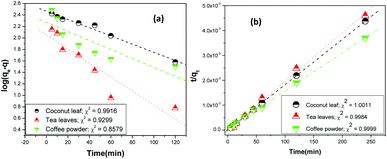 |
| | Fig. 5 Linear regression analysis of the kinetics data using (a) Lagergren first-order kinetics and (b) pseudo-second-order rate kinetics; sorbent amount: 20 mg, aqueous phase volume: 1.5 mL, initial Th concentration: 2 mg mL−1, centrifugation time: 2 min; temperature: 303 K, aqueous phase acidity: 3 M HNO3. | |
Fig. 6 shows the fitting of the experimental kinetics data to the Weber–Morris intraparticle diffusion model.63,64 The overall thorium sorption process on coconut leaves could be divided into two steps, while for tea leaves and coffee powder it could be divided into three steps. Based on work by Fierro et al.,65 the first step for Th sorption on coconut powder was assigned to mass transfer, whereas the subsequent step was attributed to intraparticle diffusion. In the initial 2 h, mass-transfer kinetics played a significant role in the overall kinetics of sorption, while beyond 2 h, the rate was governed by a diffusion process, which was slower than the former process. The rate constants for these two steps were 280 mg g−1 min−1 (χ2 = 0.9974) and 222 mg g−1 min−1 (χ2 = 0.9999), respectively. In the case of tea leaves and coffee powder, the first step was in the initial 15 min and was attributed to the effects of a boundary layer. Th4+ ions diffused towards the binding sites of the biosorbent (tannin and caffeine) and adsorbed readily. The second step was in the time range of 15 to 60 min, where the kinetics became slower. This phase was assigned to the diffusion of Th4+ ions towards the internal binding sites of the biosorbents. After 1 h, equilibrium was reached, and intraparticle diffusion further slowed down. This was attributed to the unavailability of active sites to bind to Th4+ ions. The rate constants for the three steps of Th4+ sorption on tea leaves were estimated to be 595.3 mg g−1 min−1 (χ2 = 0.9856), 571.8 mg g−1 min−1 (χ2 = 0.9962), and 553.3 mg g−1 min−1 (χ2 = 0.9958), respectively, while the values for coffee powder were 382.6 mg g−1 min−1 (χ2 = 0.9915), 349.9 mg g−1 min−1 (χ2 = 0.9854), and 321.4 mg g−1 min−1 (χ2 = 0.9846), respectively.
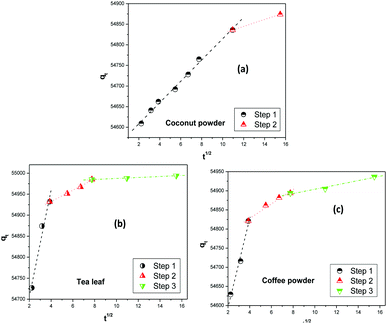 |
| | Fig. 6 The Weber–Morris intraparticle diffusion model for the adsorption of Th4+ on biosorbents: (a) coconut leaves, (b) tea leaves, and (c) coffee powder. | |
Sorption thermodynamics
The energetics involved in the sorption of thorium onto these biosorbents have been investigated in accordance with the Van't Hoff equation:66,67| | 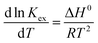 | (11) |
| | 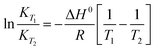 | (12) |
The change in Gibb's energy was found to be related to the equilibrium constant as follows:
| | ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kex Kex | (13) |
The changes in Gibb's energy and enthalpy are associated with the change in entropy as follows:
Fig. 7 shows the variations in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kex as a function of the reciprocal of the temperature. The linear curves revealed that the equilibrium constant increases with an increase in temperature. In other words, the temperature favours the equilibrium moving in the forward direction, i.e., toward sorption. This revealed that the sorption processes were endothermic in nature. From the slopes of the straight lines, the ΔH0 values were estimated to be 3.3 kJ mol−1, 6.3 kJ mol−1, and 3.7 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The positive signs signify the endothermicity of sorption. The Gibb's energy changes for all the systems were found to be negative, revealing the spontaneous nature of sorption. The ΔG0 values followed the trend: tea leaves > coffee powder > coconut leaves [Table 3]. This trend was in accordance with the KD values for thorium on the biosorbents. The entropy changes were found to be positive, i.e., sorption increased the entropy of the systems. This revealed that the sorption processes were entropically driven. Sorption might progress through inner-sphere complexation. The overall sorption of Th4+ can be broadly divided into several steps: the dehydration of Th4+ at the solid–liquid interphase, coordination between active sites of the biosorbent and Th4+, and, ultimately, Th4+ loading onto the sorbent through chemical interactions. During the dehydration of Th4+, lots of water molecules become detached and return to the bulk liquid phase, hence enhancing the entropy of the system. The dehydration of active sites of the biosorbent might also contribute towards the overall enhancement in the entropy of the systems.
Kex as a function of the reciprocal of the temperature. The linear curves revealed that the equilibrium constant increases with an increase in temperature. In other words, the temperature favours the equilibrium moving in the forward direction, i.e., toward sorption. This revealed that the sorption processes were endothermic in nature. From the slopes of the straight lines, the ΔH0 values were estimated to be 3.3 kJ mol−1, 6.3 kJ mol−1, and 3.7 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The positive signs signify the endothermicity of sorption. The Gibb's energy changes for all the systems were found to be negative, revealing the spontaneous nature of sorption. The ΔG0 values followed the trend: tea leaves > coffee powder > coconut leaves [Table 3]. This trend was in accordance with the KD values for thorium on the biosorbents. The entropy changes were found to be positive, i.e., sorption increased the entropy of the systems. This revealed that the sorption processes were entropically driven. Sorption might progress through inner-sphere complexation. The overall sorption of Th4+ can be broadly divided into several steps: the dehydration of Th4+ at the solid–liquid interphase, coordination between active sites of the biosorbent and Th4+, and, ultimately, Th4+ loading onto the sorbent through chemical interactions. During the dehydration of Th4+, lots of water molecules become detached and return to the bulk liquid phase, hence enhancing the entropy of the system. The dehydration of active sites of the biosorbent might also contribute towards the overall enhancement in the entropy of the systems.
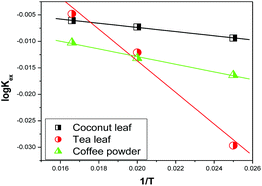 |
| | Fig. 7 The variation in equilibrium sorption constants as a function of the reciprocal of the temperature (1/T, K); sorbent amount: 20 mg, aqueous phase volume: 1.5 mL, initial Th concentration: 2 mg mL−1, equilibration time: 4 h, centrifugation time: 2 min, aqueous phase acidity: 3 M HNO3. | |
Table 3 The thermodynamic parameters for the sorption of thorium on coconut leaves, tea leaves, and coffee powder (triplicate measurements with less than 10% RSD)
| Biosorbent |
ΔG0 (kJ mol−1) |
ΔH0 (kJ mol−1) |
ΔS0 (kJ mol−1 K−1) |
| Coconut leaves |
–5.91 |
3.30 |
0.03 |
| Tea leaves |
–8.60 |
6.33 |
0.04 |
| Coffee powder |
–7.22 |
3.70 |
0.04 |
Radiation-induced performance deterioration
During the processing of radiotoxic elements, there can be the continuous emission of high-energy particles, like alpha and beta particles, and high-energy gamma radiation, depending on the nature of the isotopes present in the system. This can ultimately deposit huge amounts of energy into the system. This energy might lead to the breaking of chemical bonds of lower energy. In due course, this might affect the active sites of the biosorbent that are responsible for binding with Th4+ ions. Hence, this can lead to radiation-induced deterioration in the performance of these materials. For coconut leaves, the unirradiated material exhibited a Th4+Kd value of 2.03 × 104, and this was reduced to 1.57 × 104 following 25 kGy irradiation. This value was further reduced in response to gamma irradiation and finally became 1.01 × 104 following 100 kGy gamma exposure. Hence the kd value was reduced to around 50% of its initial value. For tea leaves, the original Kd value for Th4+ was 8.4 × 104 using unirradiated material; this gradually decreased with an increase in gamma exposure and ultimately became 4.2 × 104 following 100 kGy irradiation. Here, the sorption efficiency was also reduced to around 50% of the initial value in response to 100 kGy irradiation. For coffee powder, the situation was even worse. The Kd value of 2.1 × 104 for Th4+ became 8.7 × 103 after exposure to 100 kGy irradiation. The radiolytic stability of these biosorbents was only moderate, and the least stable was coffee powder. Fig. 8 depicts the radiation-induced performance deterioration of these biosorbents for thorium sorption.
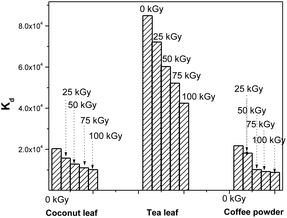 |
| | Fig. 8 The radiation-induced performance deterioration of coconut leaves, tea leaves, and coffee powder for thorium; sorbent amount: 20 mg, irradiated at different doses, aqueous phase volume: 1.5 mL, initial Th concentration: 2 mg mL−1, equilibration time: 4 h, centrifugation time: 2 min, temperature: 303 K, aqueous phase acidity: 1 M HNO3. | |
Conclusions
The used household items and agro-products of coconut leaves, tea leaves, and coffee powder have been used for the efficient separation of thorium ions from aqueous acidic solution. The DTh values from 3 M HNO3 were evaluated to be 1.2 × 104 for coconut leaves, 1.45 × 104 for coffee powder, and 2.1 × 104 for tea leaves, whereas the times required to reach equilibrium were 4 h, 2 h, and 1 h for coconut leaves, coffee powder, and tea leaves, respectively. Although it is very difficult to determine the predominance of a particular isotherm model, the regression coefficients for the Langmuir isotherm were found to be closer to 1; hence, the Langmuir isotherm model might be favoured over the other isotherm models. The sorption capacities were 220 mg g−1, 644 mg g−1, and 310 mg g−1 for coconut leaves, tea leaves, and coffee powder, respectively. Pseudo-second-order rate kinetics were predominantly followed, with rate constants of 3.4 × 10−6 mg g−1 min−1, 2.7 × 10−5 mg g−1 min−1, and 1.9 × 10−5 mg g−1 min−1 for coconut leaves, tea leaves, and coffee powder, respectively. The spontaneity of the sorption processes was quantitatively determined based on the negative ΔG values of −5.91 kJ mol−1, −8.60 kJ mol−1, and −7.22 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The processes were found to take heat energy (ΔHcoconut leaf = 3.30 kJ mol−1, ΔHtea leaf = 6.33 kJ mol−1, and ΔHcoffee powder = 3.70 kJ mol−1) from the surroundings. Hence, the conditional extraction constants were higher at higher temperatures. Radiation-induced performance deterioration was evidenced for these sorbents. Upon exposure to 25 kGy gamma irradiation, KDTh reductions of 22%, 15%, and 16% were observed for coconut leaves, tea leaves, and coffee powder. Upon exposure to 50 kGy gamma irradiation, the values were reduced by 36%, 29%, and 53%, respectively. However, after 100 kGy exposure, the values decreased by 50% of the original value for coconut powder and tea leaves and by 59% of the original value for coffee powder.
Author contributions
G. Salunkhe: experiments and data acquisition; Rohit Singh Chauhan: review of manuscript; Arijit Sengupta: conceptualization and manuscript writing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors wish to acknowledge Dr S. Kannan, Director, RC & I Group, and Dr P.K. Mohapatra, Head, Radiochemistry Division, Bhabha Atomic Research Centre, Mumbai, India.
References
- B. W. Brook, A. Alonso, D. A. Meneley, J. Misak, T. Bleese and J. B. vanErp, Why nuclear energy is sustainable and has to be part of the energy mix, Sustainable Mater. Technol., 2014,(1–2), 8–16 CrossRef.
- J. E. Zafrilla, M.-Á. Cadarso, F. Monsalve and C. de la Rúa, How Carbon-Friendly Is Nuclear Energy? A Hybrid MRIO-LCA Model of a Spanish Facility, Environ. Sci. Technol., 2014, 48(24), 14103–14111 CrossRef CAS PubMed.
- S. A. Sarkodie and S. Adams, Renewable energy, nuclear energy, and environmental pollution: accounting for political institutional quality in South Africa, Sci. Total Environ., 2018, 643, 1590–1601 CrossRef CAS PubMed.
- A. Bandyopadhyay and S. Rej, Can nuclear energy fuel an environmentally sustainable economic growth? Revisiting the EKC hypothesis for India, Environ. Sci. Pollut. Res., 2021, 28, 63065–63086 CrossRef PubMed.
- R. Lidskog and G. Sundqvist, On the right track? Technology, geology and society in Swedish nuclear waste management, J. Risk Res., 2004, 7(2), 251–268 CrossRef.
- R. C. Ewing and F. N. von Hippel, Nuclear Waste Management in the United States—Starting Over, Science, 2009, 325(5937), 151–152 CrossRef CAS PubMed.
- M. Salvatores and G. Palmiotti, Radioactive waste partitioning and transmutation within advanced fuel cycles: achievements and challenges, Prog. Part. Nucl. Phys., 2011, 66(1), 144–166 CrossRef CAS.
- M. Salvatores, Nuclear fuel cycle strategies including Partitioning and Transmutation, Nucl. Eng. Des., 2005, 235(7), 805–816 CrossRef CAS.
- MichelLung11OttoGremm, Perspectives of the thorium fuel cycle, Nucl. Eng. Des., 1998, 180(2), 133–146 CrossRef.
- K. Anantharaman, V. Shivakumar and D. Saha, Utilisation of thorium in reactors, J. Nucl. Mater., 2008, 383(1–2), 119–121 CrossRef CAS.
- U. E. Humphrey and M. U. Khandaker, Viability of thorium-based nuclear fuel cycle for the next generation nuclear reactor: Issues and prospects, Renew. Sustain. Energy Rev., 2018, 97, 259–275 CrossRef CAS.
- T. Ünak, What is the potential use of thorium in the future energy production technology?, Prog. Nucl. Energy, 2000, 37(1–4), 137–144 CrossRef.
- M. E. Nasab, A. Sama and S. A. Milani, Determination of optimum process conditions for the separation of thorium and rare earth elements by solvent extraction, Hydrometallurgy, 2011, 106(3–4), 141–147 CrossRef CAS.
- Y. Lu, H. Wei, Z. Zhang, Y. Li, G. Wu and W. Liao, Selective extraction and separation of thorium from rare earths by a phosphorodiamidate extractant, Hydrometallurgy, 2016, 163, 192–197 CrossRef CAS.
- M. Tan, C. Huang, S. Ding, F. Li, Q. Li, L. Zhang, C. Liu and S. Li, Highly efficient extraction separation of uranium(VI) and thorium(IV) from nitric acid solution with di(1-methyl-heptyl) methyl phosphonate, Sep. Purif. Technol., 2015, 146(26), 192–198 CrossRef CAS.
- M. E. Nasab, Solvent extraction separation of uranium(VI) and thorium(IV) with neutral organophosphorus and amine ligands, Fuel, 2014, 116, 595–600 CrossRef.
- E. P. Wildman, G. Balázs, A. J. Wooles, M. Scheer and S. T. Liddle, Thorium–phosphorus triamidoamine complexes containing Th–P single- and multiple-bond interactions, Nat. Commun., 2016, 7, 12884 CrossRef CAS PubMed.
- S. Priya, A. Sengupta, S. Jayabun and V. C. Adya, Piperidinium based ionic liquid in combination with sulphoxides: highly efficient solvent systems for the extraction of thorium, Hydromet, 2016, 164, 111–117 CrossRef CAS.
- D. Das, S. Hashmi, A. Sengupta, S. Kannan and C. P. Kaushik, Understanding the extraction behavior of UO22+ and Th4+ using novel picolinamide/N-oxo picolinamide in ionic liquid: a comparative evaluation with molecular diluent, J. Mol. Liq., 2021, 332, 115773 CrossRef CAS.
- M. Weigl, A. Geist, K. Gompper and J.-I. Kim, kinetics of lanthanide/actinide co-extraction with
N,N′-dimethyl-n,n′-dibutyltetradecylmalonic diamide (DMDBTDMA), Solv. Extr. Ion Exch., 2001, 19(2), 215–229 CrossRef CAS.
- C. S. Kesav and R. M. S. Subramanian, Sequential separation of lanthanides, thorium and uranium using novel solid phase extraction method from high acidic nuclear wastes, J. Hazard. Mater., 2007, 145(1–2), 315–322 Search PubMed.
- Q. He, X. Chang, Q. Wu, X. Huang, Z. Hu and Y. Zhai, Synthesis and applications of surface-grafted Th(IV)-imprinted polymers for selective solid-phase extraction of thorium(IV), Anal. Chim. Acta, 2007, 605(2), 192–197 CrossRef CAS PubMed.
- T. A. Saleha, A. M. Elsharif, S. A Abdul-Rashid, I. Mohammed and H. Dafalla, Synthesis of carbon nanotubes grafted with copolymer of acrylic acid and acrylamide for phenol removal, Environ. Nanotechnol. Monit. Manag., 2020, 14, 100302 Search PubMed.
- O. A. B-Dahman and T. A. Saleh, Synthesis of carbon nanotubes grafted with PEG and its efficiency for the removal of phenol from industrial wastewater, Environ. Nanotechnol. Monit. Manag., 2020, 13, 100286 Search PubMed.
- T. A. Saleh, A. Sarı and M. Tuzen, Carbon nanotubes grafted with poly(trimesoyl, m-phenylenediamine) for enhanced removal of phenol, J. Environ. Manag., 2019, 252(15), 109660 CrossRef CAS PubMed.
- G. Fadillah, T. A. Saleh and S. Wahyuningsih, Enhanced electrochemical degradation of 4-nitrophenol molecules using novel Ti/TiO2-NiO electrodes, J. Mol. Liq., 2019, 289, 111108 CrossRef CAS.
- T. A. Saleh, Characterization, determination and elimination technologies for sulfur from petroleum: toward cleaner fuel and a safe environment, Trends Environ. Anal. Chem., 2020, 25, e00080 CrossRef CAS.
- T. A. Saleh, Trends in the sample preparation and analysis of nanomaterials as environmental contaminants, Trends Environ. Anal. Chem., 2020, 28, e00101 CrossRef CAS.
- T. Xiu, Z. Li, Y. Wang, P. Wu, Y. Du and Z. Cai, Thorium adsorption on graphene oxide nanoribbons/manganese dioxide composite material, J. Radioanal. Nucl. Chem., 2019, 319, 1059–1067 CrossRef CAS.
- N. Pan, J. Deng, D. Guan, Y. Jin and C. Xi, Adsorption characteristics of Th(IV) ions on reduced graphene oxide from aqueous solutions, Appl. Surf. Sci., 2013, 287(15), 478–483 CrossRef CAS.
- C. Endes, Y. Mahmoud, A. A. Aslani and C. K. Aslani, Removal of thorium by modified multi-walled carbon nanotubes: optimization, thermodynamic, kinetic, and molecular dynamic viewpoint, Prog. Nucl. Energy, 2020, 127, 103445 CrossRef.
- Y. Wang, X. Chen, X. Hu, P. Wu, T. Lan, Y. Li, H. Tu, Y. Liu, D. Yuan, Z. Wu, Z. Liu and J. W. Chew, Synthesis and characterization of poly(TRIM/VPA) functionalized graphene oxide nanoribbons aerogel for highly efficient capture of thorium(IV) from aqueous solutions, Appl. Surf. Sci., 2021, 536, 147829 CrossRef CAS.
- F. Li, Z. Yang, H. Weng, G. Chen, M. Lin and C. Zhao, High efficient separation of U(VI) and Th(IV) from rare earth elements in strong acidic solution by selective sorption on phenanthroline diamide functionalized graphene oxide, Chem. Eng. J., 2018, 332, 340–350 CrossRef CAS.
- S. Li, L. Wang, J. Peng, M. Zhai and W. Shi, Efficient thorium(IV) removal by two-dimensional Ti2CTx MXene from aqueous solution, Chem. Eng. J., 2019, 366, 192–199 CrossRef CAS.
- A. Sengupta, S. Jayabun, A. Boda and S. M. Ali, An amide functionalized task specific carbon nanotube for the sorption of tetra and hexa valent actinides: experimental and theoretical insight, RSC Adv., 2016, 6, 39553–39562 RSC.
- A. Sengupta and N. K. Gupta, MWCNTs based sorbents for nuclear waste management: A review, J. Environ. Chem. Eng., 2017, 5(5), 5099–5114 CrossRef CAS.
- S. Hashmi, A. Sengupta and R. Singh Chauhan, Cost effective separation of uranium ion using exhausted household products and natural bio-sorbent, J. Radioanal. Nucl. Chem., 2021, 329, 1361–1373 CrossRef CAS.
- M. Tuzen, A. Sarı and T. A. Saleh, Synthesis, characterization and evaluation of carbon nanofiber modified-polymer for ultra-removal of thorium ions from aquatic media, Chem. Eng. Res. Des., 2020, 163, 76–84 CrossRef CAS.
- T. A. Saleh, A. Sarı and M. Tuzen, Development and characterization of bentonite-gum arabic composite as novel highly-efficient adsorbent to remove thorium ions from aqueous media, Cellulose, 2021, 28, 10321–10333 CrossRef CAS.
- T. A. Saleh, Protocols for synthesis of nanomaterials, polymers, and green materials as adsorbents for water treatment technologies, Environ. Technol. Innovat., 2021, 24, 101821 CrossRef CAS.
- T. A. Saleh and M. K. Mustaqeem, Water treatment technologies in removing heavy metal ions from wastewater: a review, Environ. Nanotechnol. Monit. Manag., 2022, 17, 100617 Search PubMed.
- Sk. Jayabun, S. Pathak and A. Sengupta, A comprehensive investigation alongwith the statistical evaluation for the characterization of ilmenite mineral by X-ray fluorescence spectrometry and Optical emission Spectrometry, ChemistrySelect, 2021, 6, 1911–1919 CrossRef.
- Sk. Jayabun, S. Pathak and A. Sengupta, Characterization & Categorization of Garnet samples for Major and Minor Constituents by Energy Dispersive X-ray Fluorescence Spectroscopy, Nucl. Instrum. Methods Phys. Res., Sect. A, 2021, 1019, 165854 CrossRef CAS.
- Sk. Jayabun, S. Pathak and A. Sengupta, Determination of major, minor and trace metallic constituents in sillimanite: comparative evaluation of EDXRF and D. C. Arc carrier distillation AES, At. Spectrosc., 2020, 41(4), 162–168 CrossRef CAS.
- J. M. A. E. Fraga, Some physical and chemical features of the variability of kd distribution coefficients for radionuclides, J. Environ. Radioact., 1996, 30(3), 253–270 CrossRef.
- F. Chauvin, P.-E. Dufils, D. Gigmes, Y. Guillaneuf, S. R. A. Marque, P. Tordo and D. Bertin, Nitroxide-Mediated Polymerization: The Pivotal Role of the kd Value of the Initiating Alkoxyamine and the Importance of the Experimental Conditions, Macromol, 2006, 39(16), 5238–5250 CrossRef CAS.
- K. Yoshinag, H. Yoshid, Y. Yamamoto, K. Takakura and M. Komatsu, A convenient determination of surface hydroxyl group on silica gel by conversion of silanol hydrogen to dimethylsilyl group with diffuse reflectance FTIR spectroscopy, J. Colloid Interface Sci., 1992, 153(1), 207–211 CrossRef.
- B. M. Carter, A. Sengupta, X. Qian, M. Ulbricht and S. R. Wickramasinghe, Tuning surface modification of ultrafiltration membranes external versus internal pore surface: a new approach to surface-initiated AGET-ATRP, J. Membr. Sci., 2018, 554, 109–116 CrossRef CAS.
- M. M. Paradkar and J. Irudayaraj, A Rapid FTIR Spectroscopic Method for Estimation of Caffeine in Soft Drinks and Total Methylxanthines in Tea and Coffee, J. Food Sci., 2006, 67, 2507–2511 CrossRef.
- T. A. Saleh, Isotherm, kinetic, and thermodynamic studies on Hg(II) adsorption from aqueous solution by silica- multiwall carbon nanotubes, Environ. Sci. Pollut. Res., 2015, 22, 16721–16731 CrossRef CAS PubMed.
- T. A. Saleh and V. K. Gupta, Characterization of the Chemical Bonding between Al2O3 and Nanotube in MWCNT/Al2O3 Nanocomposite, Curr. Nanosci., 2012, 8(5), 739–743 CrossRef CAS.
- T. A. Saleh, The influence of treatment temperature on the acidity of MWCNT oxidized by HNO3 or a mixture of HNO3/H2SO4, Appl. Surf. Sci., 2011, 257(17), 7746–7751 CrossRef CAS.
- T. A. Saleh, Simultaneous adsorptive desulfurization of diesel fuel over bimetallic nanoparticles loaded on activated carbon, J. Clean. Prod., 2018, 172, 2123–2132 CrossRef CAS.
- T. A. Saleh, Carbon nanotube-incorporated alumina as a support for MoNi catalysts for the efficient hydrodesulfurization of thiophenes, Chem. Eng. J., 2021, 404, 126987 CrossRef CAS.
- P. Patil, S. Pathak, M. Sharathbabu, A. Sengupta and R. M. Kadam, Understanding the sorption behaviour of Pu/U on zirconium phosphosilicate prepared by gelation route, Radiochim. Acta, 2020, 108, 433–441 CrossRef CAS.
- S. Pahan, A. Sengupta, A. K. Yadav, S. N. Jha, D. Bhattacharyya, S. Musharaf Ali, P. N. Khan, A. K. Debnath, D. Banerjee, T. Vincent, S. Manohar and C. P. Kaushik, Exploring Functionalized Titania for Task Specific Application on Efficient Separation of Trivalent f-block Elements, New J. Chem., 2020, 44(16), 6151–6162 RSC.
- H. Viltresa, Y. C. Lópeza, N. K. Gupta, C. Leyv, R. Paza, A. Gupta and A. Sengupta, Functional metal-organic frameworks for metal removal from aqueous solutions, Sep. Purif. Rev., 2020, 51, 78–99 CrossRef.
- N. K. Gupta, H. Viltres, Y. C. Lópezc, G. Salunkhe and A. Sengupta, Magnetic CoFe2O4/Graphene oxide nanocomposite for highly efficient separation of f-block elements, Surf. Interfaces, 2021, 23, 100916 CrossRef CAS.
- G. Salunkhe, A. Sengupta, A. Boda, R. Paz, N. K. Gupta, C. Leyva, R. S. Chauhan and Sk. M. Ali, Application of hybrid MOF composite in extraction of f-block elements: experimental and computational investigation, Chemosphere, 2022, 287, 132232 CrossRef CAS PubMed.
- S. Pahan, A. Sengupta, Sk. M. Ali, A. K. Debnath, D. Banerjee, T. Vincent, G. Sugilal and C. P. Kaushik, Dipicolinamide functionalized titania for highly efficient sorption of tetra and hexavalent actinide, Sep. Purif. Technol., 2021, 279, 119703 CrossRef CAS.
- A. Singha Deb, K. Dasgupta, V. C. Adya and M. Ali Sheikh, Diglycolamic acid functionalized multiwalled carbon nanotube highly efficient sorbent for f-block elements: experimental and theoretical investigation, New J. Chem., 2017, 41, 4531–4545 RSC.
- N. K. Gupta and A. Sengupta, Understanding the sorption behavior of trivalent lanthanides on amide functionalized multi walled carbon nanotubes, Hydrometallurgy, 2017, 171, 8–15 CrossRef CAS.
- M. Belhachemia, Z. Belala, D. Lahcene and F. Addoun, Adsorption of phenol and dye from aqueous solution using chemically modified date pits activated carbons, Desalination Water Treat., 2009, 7, 182–190 CrossRef.
- N. F. Campos and C. M. B. M. Barbosa, Removal of naphthenic acids using activated charcoal: kinetic and equilibrium studies, Adsorpt. Sci. Technol., 2018, 36, 1405–1421 CrossRef CAS.
- V. Fierro, V. Torné-Fernández, D. Montané and A. Celzard, Microporous Mesoporous Mater., 2008, 111, 276–284 CrossRef CAS.
- P. M. Mathias and J. P. O'Connell, The Gibbs–Helmholtz Equation and the Thermodynamic Consistency of Chemical Absorption Data, Ind. Eng. Chem. Res., 2012, 51(13), 5090–5097 CrossRef CAS.
- P. M. Mathias, The Gibbs–Helmholtz Equation in Chemical Process Technology, Ind. Eng. Chem. Res., 2016, 55(4), 1076–1087 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
 Open Access Article
Open Access Article a and
Arijit
Sengupta
a and
Arijit
Sengupta
 *bc
*bc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. FTIR spectra from solid samples were taken in ATR mode, i.e., total attenuated reflection mode. 5 mg of sample was placed on the diamond window and spectra were recorded from 25 scans. Scanning electron microscopy (SEM) images were taken using a Philips XL30 ESEM spectrometer operating with an accelerating voltage of 30 kV.
1. FTIR spectra from solid samples were taken in ATR mode, i.e., total attenuated reflection mode. 5 mg of sample was placed on the diamond window and spectra were recorded from 25 scans. Scanning electron microscopy (SEM) images were taken using a Philips XL30 ESEM spectrometer operating with an accelerating voltage of 30 kV.
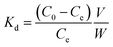
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–C stretching, respectively. The peaks at 1547 cm−1 and below 1484 cm−1 were attributed to C–N stretching.49 In the case of tea leaves, the peaks at 2920 cm−1 and 2851 cm−1 were ascribed to C–H and CH2 vibrations pertaining to aliphatic hydrocarbons. The peaks at 1609 cm−1, 1515 cm−1, and 1450 cm−1 corresponded to aromatic ring stretching. The peak at 1036 cm−1 was attributed to C–O stretching. The presence of carbonyl and hydroxyl functional groups might be useful for coordinating with thorium ions from aqueous acidic waste solution.
C and C–C stretching, respectively. The peaks at 1547 cm−1 and below 1484 cm−1 were attributed to C–N stretching.49 In the case of tea leaves, the peaks at 2920 cm−1 and 2851 cm−1 were ascribed to C–H and CH2 vibrations pertaining to aliphatic hydrocarbons. The peaks at 1609 cm−1, 1515 cm−1, and 1450 cm−1 corresponded to aromatic ring stretching. The peak at 1036 cm−1 was attributed to C–O stretching. The presence of carbonyl and hydroxyl functional groups might be useful for coordinating with thorium ions from aqueous acidic waste solution.

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(OH) groups can directly coordinate with Th4+. This coordination can occur in two different ways. The first case might show the involvement of three tannin molecules. One tannin molecule utilizes its two adjacent –OH groups, forming a five-membered ring. The other two tannin molecules can coordinate with Th4+ through –OH or –COOH groups [Fig. 2(c)]. This would achieve a coordination of eight for Th4+. The latter two tannin molecules may coordinate in a multi-dentate way. Since several water molecules are present in the system, water coordination may also be involved. However, the enhancement in entropy, as seen from thermodynamic analysis, points towards the release of water molecules during complexation. Hence, water coordination has not been shown. In the second case, two tannin molecules may be involved. Both of them utilize their ortho phenolic –OH groups for coordination with Th4+, forming two five-membered chelate rings [Fig. 2(d)]. The formation of ML4 and other higher stoichiometric complexes may be less probable from steric and thermodynamic points of view.
O(OH) groups can directly coordinate with Th4+. This coordination can occur in two different ways. The first case might show the involvement of three tannin molecules. One tannin molecule utilizes its two adjacent –OH groups, forming a five-membered ring. The other two tannin molecules can coordinate with Th4+ through –OH or –COOH groups [Fig. 2(c)]. This would achieve a coordination of eight for Th4+. The latter two tannin molecules may coordinate in a multi-dentate way. Since several water molecules are present in the system, water coordination may also be involved. However, the enhancement in entropy, as seen from thermodynamic analysis, points towards the release of water molecules during complexation. Hence, water coordination has not been shown. In the second case, two tannin molecules may be involved. Both of them utilize their ortho phenolic –OH groups for coordination with Th4+, forming two five-membered chelate rings [Fig. 2(d)]. The formation of ML4 and other higher stoichiometric complexes may be less probable from steric and thermodynamic points of view.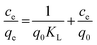
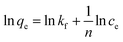
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln
qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xm + βε2
xm + βε2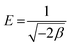
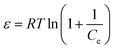
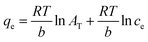
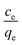 vs. Ce; Freundlich isotherm, ln
vs. Ce; Freundlich isotherm, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. ln
qevs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce; D–R isotherm, ln
Ce; D–R isotherm, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qevs. ε2; and Temkin isotherm, qevs. ln
qevs. ε2; and Temkin isotherm, qevs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce. The data were subjected to linear regression analysis, and the predominance of an isotherm model was determined based on the regression coefficients. Fig. 3 shows the linear fitting of the experimental parameters to the different isotherm models. The fitting parameters indicated that Langmuir, Temkin, and Freundlich isotherms were rather equally possible, and no preference could be proposed. However, for the Langmuir model, the regression coefficients were closer to 1; hence, the Langmuir model might be favoured over the other models. Table 1 summarizes the results from the linear regression analysis of the different isotherm models.
Ce. The data were subjected to linear regression analysis, and the predominance of an isotherm model was determined based on the regression coefficients. Fig. 3 shows the linear fitting of the experimental parameters to the different isotherm models. The fitting parameters indicated that Langmuir, Temkin, and Freundlich isotherms were rather equally possible, and no preference could be proposed. However, for the Langmuir model, the regression coefficients were closer to 1; hence, the Langmuir model might be favoured over the other models. Table 1 summarizes the results from the linear regression analysis of the different isotherm models.

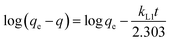
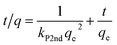

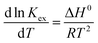
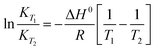
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kex
Kex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kex as a function of the reciprocal of the temperature. The linear curves revealed that the equilibrium constant increases with an increase in temperature. In other words, the temperature favours the equilibrium moving in the forward direction, i.e., toward sorption. This revealed that the sorption processes were endothermic in nature. From the slopes of the straight lines, the ΔH0 values were estimated to be 3.3 kJ mol−1, 6.3 kJ mol−1, and 3.7 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The positive signs signify the endothermicity of sorption. The Gibb's energy changes for all the systems were found to be negative, revealing the spontaneous nature of sorption. The ΔG0 values followed the trend: tea leaves > coffee powder > coconut leaves [Table 3]. This trend was in accordance with the KD values for thorium on the biosorbents. The entropy changes were found to be positive, i.e., sorption increased the entropy of the systems. This revealed that the sorption processes were entropically driven. Sorption might progress through inner-sphere complexation. The overall sorption of Th4+ can be broadly divided into several steps: the dehydration of Th4+ at the solid–liquid interphase, coordination between active sites of the biosorbent and Th4+, and, ultimately, Th4+ loading onto the sorbent through chemical interactions. During the dehydration of Th4+, lots of water molecules become detached and return to the bulk liquid phase, hence enhancing the entropy of the system. The dehydration of active sites of the biosorbent might also contribute towards the overall enhancement in the entropy of the systems.
Kex as a function of the reciprocal of the temperature. The linear curves revealed that the equilibrium constant increases with an increase in temperature. In other words, the temperature favours the equilibrium moving in the forward direction, i.e., toward sorption. This revealed that the sorption processes were endothermic in nature. From the slopes of the straight lines, the ΔH0 values were estimated to be 3.3 kJ mol−1, 6.3 kJ mol−1, and 3.7 kJ mol−1 for coconut leaves, tea leaves, and coffee powder, respectively. The positive signs signify the endothermicity of sorption. The Gibb's energy changes for all the systems were found to be negative, revealing the spontaneous nature of sorption. The ΔG0 values followed the trend: tea leaves > coffee powder > coconut leaves [Table 3]. This trend was in accordance with the KD values for thorium on the biosorbents. The entropy changes were found to be positive, i.e., sorption increased the entropy of the systems. This revealed that the sorption processes were entropically driven. Sorption might progress through inner-sphere complexation. The overall sorption of Th4+ can be broadly divided into several steps: the dehydration of Th4+ at the solid–liquid interphase, coordination between active sites of the biosorbent and Th4+, and, ultimately, Th4+ loading onto the sorbent through chemical interactions. During the dehydration of Th4+, lots of water molecules become detached and return to the bulk liquid phase, hence enhancing the entropy of the system. The dehydration of active sites of the biosorbent might also contribute towards the overall enhancement in the entropy of the systems.




