Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How to calibrate luminescent crossover thermometers: a note on “quasi”-Boltzmann systems†
Benedikt
Bendel
and
Markus
Suta
 *
*
Inorganic Photoactive Materials, Institute of Inorganic and Structural Chemistry, Heinrich Heine University Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany. E-mail: markus.suta@hhu.de
First published on 26th April 2022
Abstract
Luminescent thermometers are potential material candidates for remote and non-invasive temperature sensing by means of a temperature-dependent optical signal. A particularly well-known class of luminescent thermometers are Boltzmann thermometers that rely on thermal coupling between two excited levels from the same configuration. Their thermal coupling kinetics is then governed by multiphonon transitions. A substantial part of potential luminescent thermometers does, however, rely on an interconfigurational crossover between two excited state potentials with differing equilibrium metal-ligand distances such as Cr3+ or Pr3+. These thermometers are often characterized by much higher intrinsic non-radiative coupling rates that allow exploiting a much higher energy gap for high relative sensitivities at appreciably low temperatures. For this class of luminescent thermometers, fitting models are often merely effective and no clear guidelines on how to tune them or how to verify the physical reliability of the fit are available. In this work, we derive a generalized fitting model for luminescent crossover thermometers and demonstrate that they generally follow a “quasi”-Boltzmann law. We explicitly demonstrate the concepts on the established phosphor SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+. In this compound, Sm2+ can be efficiently excited with blue light and shows intense red 5D0 → 7FJ (J = 0…6) luminescence above 680 nm and broad-banded 4f55d1 → 4f6-related luminescence peaking at 585 nm. By additional time-resolved measurements, it is possible to independently assess the expected order of magnitude of the fitting parameters and thus, judge the physical content of the calibration model of a luminescent crossover thermometer. It is finally shown that crossover thermometers are characterized by high relative sensitivities and low-temperature measurement uncertainty at elevated temperatures but their liability toward thermal quenching poses a serious limitation to the dynamic working range of this class of thermometers.
0.5% Sm2+. In this compound, Sm2+ can be efficiently excited with blue light and shows intense red 5D0 → 7FJ (J = 0…6) luminescence above 680 nm and broad-banded 4f55d1 → 4f6-related luminescence peaking at 585 nm. By additional time-resolved measurements, it is possible to independently assess the expected order of magnitude of the fitting parameters and thus, judge the physical content of the calibration model of a luminescent crossover thermometer. It is finally shown that crossover thermometers are characterized by high relative sensitivities and low-temperature measurement uncertainty at elevated temperatures but their liability toward thermal quenching poses a serious limitation to the dynamic working range of this class of thermometers.
1. Introduction
Luminescence thermometry has emerged as a promising alternative for non-invasive, remote temperature sensing and relies on the temperature dependence of the optical signals of luminescent compounds.1–3 Its potential as a local non-invasive temperature probe has been shown in several niche applications ranging from catalysis4,5 over biological processes6 to heat transport phenomena at the micro-and nanoscale.7–9Various readout options exist such as the intensity of a signal, the luminescence decay time, width, or position of an emission band. Among the different methodological concepts,10–12 especially the ratiometric intensity approach exploiting the emission from two thermally coupled excited levels has become popular due to its simplicity and possibility for the fast readout (by the usage of sensitive CCD cameras for example). If the two emission bands of interest arise from two thermally coupled excited levels of the same configuration, the luminescence intensity ratio expectedly follows Boltzmann's law and can be linearized if plotted in the correct way.13 This is particularly appealing for applications as linear calibration laws allow simple identification of systematic biases that are simple, and Boltzmann's law offers the possibility to readily verify the fitting parameter for its physical content.
Boltzmann-type thermalization between two excited levels and thus, the working concept of a ratiometric Boltzmann thermometer requires that the non-radiative transition rate responsible for the coupling of the two excited levels is larger than any radiative or non-radiative depopulation rate of the lower excited level.13,14 Otherwise, the excited levels decouple, and thermometry with them is not possible anymore. Non-radiative transitions in crystalline solids rely on the thermal occupation of phonon modes and become faster with increasing temperature. However, the low-temperature onset for thermal coupling of the two excited levels depends on the ratio between the intrinsic non-radiative transition rate and radiative depopulation rate of the lower excited level. This ratio determines the dynamic working range of a luminescent Boltzmann thermometer.13
The lanthanoid ions with their rich spin–orbit energy-level structure arising from the 4fn (n = 2–12) open-shell configuration are among the primary candidates for Boltzmann-based luminescence thermometry.1 Their emission is characterized by high quenching temperatures and narrow linewidths due to the intraconfigurational character of the optical transitions, which offers an intrinsically high resolution of peaks from thermally coupled excited levels. Among the most significant limitations of Boltzmann thermometers are, however, their typically small non-radiative coupling rates that only allow use of energy gaps in the order of the thermal energies of interest (ΔE21 ∺ kBT).
There are several luminescent thermometers that rely on thermalization between excited states with different equilibrium metal-ligand distances, which happens to enhance the non-radiative coupling strength between the thermalized states. One important class is dual-center energy transfer thermometers. Although very flexible, the temperature dependence of the luminescence intensity ratio is typically non-linear and requires more sophisticated (although physically still transparent!) modelling approaches.15–18 Another related class with similar properties to the excited states are so-called ratiometric luminescent crossover thermometers. Examples include Cr3+ with its thermally coupled 2E(g) and 4T2(g) states in octahedral coordination,19–21 or Pr3+22–24 with the excited 4f15d1- and 4f2(3P0)-based emission. However, also organic emitters with so-called thermally activated delayed fluorescence based on thermally coupled singlet and triplet states have come into the focus of this potential application.25–30 For these single-center luminescent thermometers, it is often simply assumed that the calibration of the luminescence intensity ratio from the thermally coupled emissions can be also fitted with Boltzmann's law. However, very often, deviations at low temperatures are observed, or physically non-meaningful fitting parameters are obtained. A critical re-evaluation of the foundations of the calibration model for this type of luminescent thermometer is, however, relevant for an appropriate judgement of their performance and reliability. Moreover, the derivation of a generalized, physically meaningful calibration model would help establish design principles or guidelines for luminescent crossover thermometers and how their properties could be tuned into a desirable range.
It was our goal within this work to establish a generalized model for luminescent crossover thermometers and experimental tests that on the representative example of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+. It is well-known that this tetraborate stabilizes several lanthanoid dopants in their divalent oxidation state even in the air. Sm2+ has a 4f6 configuration and can be efficiently excited with blue light into the 4f55d1 configuration. This configuration is energetically close to the excited 5DJ (J = 1, 2) spin–orbit levels,31,32 in contrast to its isoelectronic trivalent analogue Eu3+, in which the excited 4f55d1 electronic configuration is located in the vacuum UV range.33 This can be chemically intuitively understood by the much smaller absolute value of the reduction potential of Sm3+/Sm2+ (E0 = −1.55 V) compared to Eu4+/Eu3+ (E0 = +6.20 V).34 The energetic proximity of the 4f55d1 configuration and the radiatively emitting excited 5D0 level offers the desired conditions for a configurational crossover and gives rise to a temperature-dependent change in the appearance of the luminescence spectra of Sm2+ in SrB4O7.31,32 We show that our proposed generalized fitting model for luminescent crossover thermometers is physically reasonable, and the parameters can be related to independent time-resolved studies. Based on the calibration model, it is possible to evaluate the performance of the luminescent thermometer and compare it to that obtained on the conventional Boltzmann thermometers.
0.5% Sm2+. It is well-known that this tetraborate stabilizes several lanthanoid dopants in their divalent oxidation state even in the air. Sm2+ has a 4f6 configuration and can be efficiently excited with blue light into the 4f55d1 configuration. This configuration is energetically close to the excited 5DJ (J = 1, 2) spin–orbit levels,31,32 in contrast to its isoelectronic trivalent analogue Eu3+, in which the excited 4f55d1 electronic configuration is located in the vacuum UV range.33 This can be chemically intuitively understood by the much smaller absolute value of the reduction potential of Sm3+/Sm2+ (E0 = −1.55 V) compared to Eu4+/Eu3+ (E0 = +6.20 V).34 The energetic proximity of the 4f55d1 configuration and the radiatively emitting excited 5D0 level offers the desired conditions for a configurational crossover and gives rise to a temperature-dependent change in the appearance of the luminescence spectra of Sm2+ in SrB4O7.31,32 We show that our proposed generalized fitting model for luminescent crossover thermometers is physically reasonable, and the parameters can be related to independent time-resolved studies. Based on the calibration model, it is possible to evaluate the performance of the luminescent thermometer and compare it to that obtained on the conventional Boltzmann thermometers.
2. Experimental section
2.1. Synthesis
Microcrystalline powder of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ was prepared by a conventional solid-state method as reported earlier.35 In detail, SrCO3 (Aldrich, ≥99.9%), H3BO3 (ChemSolute, ≥99.5%), and the appropriate fraction of Sm2O3 (abcr Chemicals, 99.999%) were intimately mixed in an agate mortar and preheated at 550 °C for 5 h with a ramp of 150 °C h−1 in a corundum crucible. After natural cooling to room temperature, the sintered powder was again intimately ground for 10 min and finally treated at 850 °C with the same heating ramp overnight. This heating step was repeated two more times with intermediate grinding steps. A reducing atmosphere was generated by placing the corundum crucibles on a bed of active charcoal in the heating steps at 850 °C. The obtained powder was colourless and showed slight red luminescence upon excitation with a 365 nm UV lamp (10 W).
0.5% Sm2+ was prepared by a conventional solid-state method as reported earlier.35 In detail, SrCO3 (Aldrich, ≥99.9%), H3BO3 (ChemSolute, ≥99.5%), and the appropriate fraction of Sm2O3 (abcr Chemicals, 99.999%) were intimately mixed in an agate mortar and preheated at 550 °C for 5 h with a ramp of 150 °C h−1 in a corundum crucible. After natural cooling to room temperature, the sintered powder was again intimately ground for 10 min and finally treated at 850 °C with the same heating ramp overnight. This heating step was repeated two more times with intermediate grinding steps. A reducing atmosphere was generated by placing the corundum crucibles on a bed of active charcoal in the heating steps at 850 °C. The obtained powder was colourless and showed slight red luminescence upon excitation with a 365 nm UV lamp (10 W).
2.2. Characterization and methods
The purity of all microcrystalline samples was verified by powder X-ray diffraction in Debye-Scherrer/transmission geometry (Stoe & Cie STADI P, Cu Kα1 radiation filtered by a focussing Ge(111) monochromator, λ = 1.5406 Å; see Fig. S1 in the ESI†).Optical measurements were performed on an FLS1000 photoluminescence spectrometer from Edinburgh Instruments equipped with a 450 W Xe arc lamp as an excitation source, double excitation and emission monochromators in Czerny-Turner configuration and a thermoelectrically cooled (−20 °C) photomultiplier tube PMT-980. The emission spectra were corrected with respect to the grating efficiency and PMT sensitivity, while excitation spectra were additionally corrected with respect to the lamp intensity. The decay traces of the intense 5D0 → 7F0-based emission of Sm2+ were measured with a laser diode VPL-420 (Edinburgh Instruments, 70 mW average incident peak power, λ = 423.2 nm) with adjustable temporal pulse width (0.1 μs…1 ms) and variable trigger frequency (0.1 Hz…5 MHz) as the pulsed excitation source. The laser could also be used in a continuous wave excitation mode. The detection mode for the time-resolved measurements was single-photon multi-channel scaling.
Temperature-dependent measurements were performed with a Linkam Scientific THMS600 temperature cell with temperature accuracy of ± 0.1 °C in the regarded temperature range between room temperature and 300 °C. The temperature intervals were 25 °C.
3. Results and discussion
3.1. High-resolution luminescence spectra of Sm2+ in SrB4O7
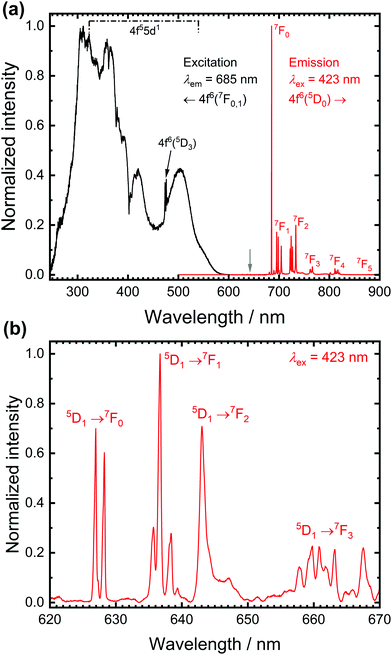
Fig. 1 depicts high-resolution photoluminescence excitation and emission spectra of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ at room temperature. While the excitation spectra are dominated by broad bands due to electric dipole allowed interconfigurational 4f6 → 4f55d1 transitions, the emission spectra at room temperature are dominated by the very narrow line emission due to the intraconfigurational 4f6(5D0) → 4f6(7FJ) transitions.36,37 The most intense line at 685 nm stems from the actually strongly forbidden 5D0 → 7F0 transition. The strong intensity is in stark contrast to most known cases of Eu3+-activated phosphors, in which that transition is only very weak (a known exception is, however, LaOBr:Eu3+38). This transition has also been considered a potential alternative for optical pressure sensing of the narrow R emission lines of Cr3+ in ruby (Al2O3:Cr3+).36,39
0.5% Sm2+ at room temperature. While the excitation spectra are dominated by broad bands due to electric dipole allowed interconfigurational 4f6 → 4f55d1 transitions, the emission spectra at room temperature are dominated by the very narrow line emission due to the intraconfigurational 4f6(5D0) → 4f6(7FJ) transitions.36,37 The most intense line at 685 nm stems from the actually strongly forbidden 5D0 → 7F0 transition. The strong intensity is in stark contrast to most known cases of Eu3+-activated phosphors, in which that transition is only very weak (a known exception is, however, LaOBr:Eu3+38). This transition has also been considered a potential alternative for optical pressure sensing of the narrow R emission lines of Cr3+ in ruby (Al2O3:Cr3+).36,39
The high intensity of the 5D0 → 7F0 transition of Sm2+ is not readily explicable within the framework of Judd-Ofelt intensity theory of the 4fn-4fn transitions but can be well-understood with the Wybourne-Downer mechanism instead.40–43 It is attributed to the high intensity of the induced electric dipole character to the 5D0 → 7F0 transition mediated by a spin–orbit interaction between the 4f6 and 4f55d1 levels of Sm2+, which is a third-order perturbative effect only. Since the 4f55d1 configuration is, however, energetically much closer to the 5D0 level in the case of Sm2+ in most inorganic host compounds, the Wybourne-Downer mechanism has a significant contribution. The strong 5D0 → 7F0-related line is accompanied by small peaks with an average separation of 90 cm−1 that can be assigned to vibronic sidebands.31 Their presence, together with the very narrow linewidth of the 4f6–4f6 transitions of Sm2+ indicates very weak vibronic coupling of the 4f6 levels, which is a characteristic feature of all 4fn–4fn emissions of divalent and trivalent middle lanthanoid ions.44,45
A closer inspection of the luminescence spectra also reveals the presence of weak emission peaks from the higher energetic 5D1 spin–orbit level of Sm2+ in the range between 620 nm and 650 nm (see Fig. 1(b)). The luminescence spectra allow the determination of a 5D1–5D0 separation of ΔE10 = 1330 cm−1, in excellent agreement with literature-reported values.31,32,46 The presence of the three resolved lines for the 5D1 → 7F0 and 5D0 → 7F1 transition, respectively, is compatible with the local CS symmetry at the Sr sites in SrB4O7.
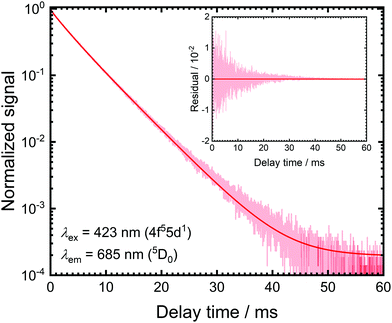
The luminescence decay traces upon excitation with 423 nm and monitoring the emission from the 5D1 and 5D0 levels are depicted in Fig. 2. Both show purely single exponential decay at room temperature. The energy separation between the 5D0 and lower energetic 7F6 levels is around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and the cut-off phonon energy of SrB4O7 is around 1300 cm−1. In addition, no 4f55d1 → 4f6 broad-band luminescence is detectable at room temperature. Thus, decay from the 5D0 = |1〉 level can be assumed to be purely radiative at 298 K with a radiative decay rate of k1r = (0.193 ± 0.001) ms−1, which agrees perfectly well with previously reported rates.31,32,46
000 cm−1 and the cut-off phonon energy of SrB4O7 is around 1300 cm−1. In addition, no 4f55d1 → 4f6 broad-band luminescence is detectable at room temperature. Thus, decay from the 5D0 = |1〉 level can be assumed to be purely radiative at 298 K with a radiative decay rate of k1r = (0.193 ± 0.001) ms−1, which agrees perfectly well with previously reported rates.31,32,46
3.2. Model for configurational crossover thermometers over a wide temperature range
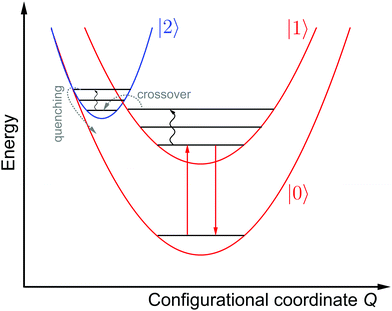
Fig. 3 schematically depicts the potential energy curves of the excited 5D0 and 4f55d1-related electronic levels of Sm2+ projected in configurational coordinate space, which are relevant for a thermal configurational crossover. It has been convincingly shown both theoretically47–50 and experimentally35,51–55 that upon excitation into the lowest energetic states of a 4fn5d1 configuration (n = 1, 5, 6, 12, 13), the lanthanoid-ligand distance decreases slightly. However, it should be noted that also a parabola with higher equilibrium distances would not change the following discussion. This is relevant for e.g. organic luminophors displaying thermally activated delayed fluorescence (TADF).Thus, the potential energy curves of the lowest excited 4f55d1 and 4f6(5D0) levels will necessarily cross. Moreover, the nature of the chemical metal-ligand bond in both states differs, translating into different curvatures of the potential energy curves. This case has been thoroughly treated theoretically by Struck and Fonger assuming harmonic potentials, which is a reasonable approximation in crystalline solids.56 They could show that for the two excited levels |2〉 and |1〉 with ΔE21 ≥ 103 cm−1 and non-negligible configurational coordinate offset, the non-radiative absorption rate can be described by Mott's formula,
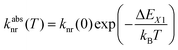 | (1) |
In most typical cases, the activation barrier ΔE2X from the vibrational ground level of the higher excited electronic state to the configurational crossover point is much lower, typically even ΔE2X ≪ kBT. Consequently, the corresponding non-radiative emission rate from the higher excited to the lower excited level is usually dominated by the intrinsic coupling rate knr(0) and has a weak to negligible temperature dependence.
The steady-state population density ratio of the two excited levels can be generally derived as13,14
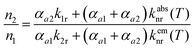 | (2) |
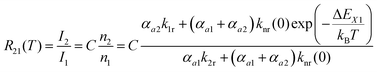 | (3) |
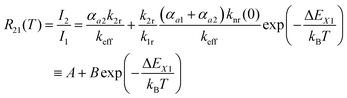 | (4) |
Thus, the LIR simply follows an effective or “quasi”-Boltzmann-type law with constant offset at low temperatures, which was also experimentally found earlier already but was lacking theoretical justification so far.32,57
The relative sensitivity, Sr(T), is often considered a figure-of-merit for luminescent thermometers. For the case of a configurational crossover thermometer with the LIR obeying eqn (4), Sr is given by
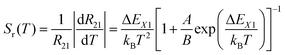 | (5) |
Unlike the relative sensitivity of a conventional Boltzmann thermometer 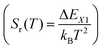 , the relative sensitivity of a crossover thermometer goes through a maximum at a specific temperature Topt (in this case Topt ∼ 400 K) dependent on the relative size of the different radiative and non-radiative rates encoded in the ratio A/B. Only at high temperatures (kBT ≳ ΔEX1) and small ratios of A/B does the relative sensitivity of a crossover thermometer agree with that of a conventional Boltzmann thermometer. It should be noted, however, that it is the interplay between the relative sensitivity and high signal-to-noise ratio that defines the practically actually relevant quantity of statistical precision of a luminescent thermometer.13,58,59 The statistically expected relative temperature uncertainty is given by
, the relative sensitivity of a crossover thermometer goes through a maximum at a specific temperature Topt (in this case Topt ∼ 400 K) dependent on the relative size of the different radiative and non-radiative rates encoded in the ratio A/B. Only at high temperatures (kBT ≳ ΔEX1) and small ratios of A/B does the relative sensitivity of a crossover thermometer agree with that of a conventional Boltzmann thermometer. It should be noted, however, that it is the interplay between the relative sensitivity and high signal-to-noise ratio that defines the practically actually relevant quantity of statistical precision of a luminescent thermometer.13,58,59 The statistically expected relative temperature uncertainty is given by
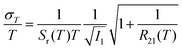 | (6) |
3.2. Case study: configurational crossover thermometry with Sm2+ (4f6)
We demonstrate the concept of a configurational crossover thermometer on SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+. Fig. 4(a) depicts the temperature-dependent steady-state luminescence spectra (normalized to the intensity of the most intense 5D0 → 7F0 transition) of SrB4O7
0.5% Sm2+. Fig. 4(a) depicts the temperature-dependent steady-state luminescence spectra (normalized to the intensity of the most intense 5D0 → 7F0 transition) of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+. At higher temperatures, a broad band due to the 4f55d1 → 4f6 transition is clearly visible, in good agreement with earlier findings. The evolution of the LIR with temperature is shown in Fig. 4(b) and can be fitted very accurately by the model (4). An energy gap of (3810 ± 90) cm−1 between the 5D0 level and crossover point of the 4f55d1-related level is obtained. This appears reasonable as it is assumed that the zero-phonon energy of the broad-banded 4f55d1 → 4f6-related emission (E0–0 ≈ 17
0.5% Sm2+. At higher temperatures, a broad band due to the 4f55d1 → 4f6 transition is clearly visible, in good agreement with earlier findings. The evolution of the LIR with temperature is shown in Fig. 4(b) and can be fitted very accurately by the model (4). An energy gap of (3810 ± 90) cm−1 between the 5D0 level and crossover point of the 4f55d1-related level is obtained. This appears reasonable as it is assumed that the zero-phonon energy of the broad-banded 4f55d1 → 4f6-related emission (E0–0 ≈ 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 according to the crossing point between emission and excitation spectrum) should be at the slightly lower energies than the actual crossover point (EX ≈ 18
700 cm−1 according to the crossing point between emission and excitation spectrum) should be at the slightly lower energies than the actual crossover point (EX ≈ 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1).
400 cm−1).
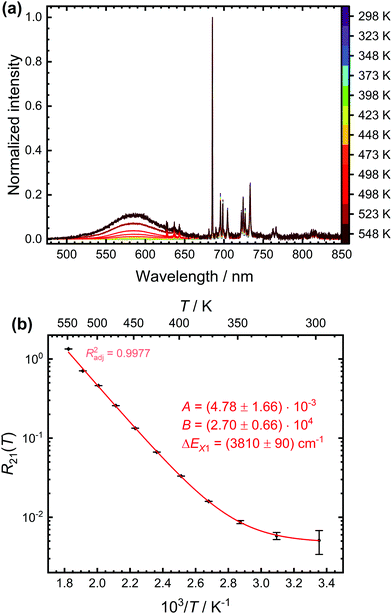 | ||
Fig. 4 (a) Temperature-dependent emission spectra of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ (λex = 423 nm) normalized to the intensity of the most intense 5D0 → 7F0 transition. The peaks on the top of the broad 4f55d1 → 4f6-based emission band stem from the 5D1 → 7FJ (J = 0, 1, 2)-related emission. (b) Data (black points) and least-squares fit (red line) according to eqn (4) of the temperature-dependent luminescence intensity ratio between the 4f55d1 → 4f6- and 5D0 → 7FJ-based emission. The fitting parameters and the adjusted (squared) correlation coefficient indicating the quality of the fit is given as well. 0.5% Sm2+ (λex = 423 nm) normalized to the intensity of the most intense 5D0 → 7F0 transition. The peaks on the top of the broad 4f55d1 → 4f6-based emission band stem from the 5D1 → 7FJ (J = 0, 1, 2)-related emission. (b) Data (black points) and least-squares fit (red line) according to eqn (4) of the temperature-dependent luminescence intensity ratio between the 4f55d1 → 4f6- and 5D0 → 7FJ-based emission. The fitting parameters and the adjusted (squared) correlation coefficient indicating the quality of the fit is given as well. | ||
The fitting parameters A and B can also be evaluated in terms of their physical context. According to eqn (4), A basically represents the ratio between the radiative rate of the higher excited level and an effective overall rate containing both the radiative and intrinsic non-radiative crossover transition rate. In a crossover thermometer, it is usually knr(0) ≫ k2r, as estimated from the temperature dependence of the 5D0 related decay time (see Fig. S2 in the ESI†) or reported for other Sm2+-activated compounds such as the matlockite-type fluoridochlorides MFCl (M = Ca, Sr, Ba).60 Thus, A is expectedly to be very small (A ≪ 1). This is also found from the fit of the temperature-dependent luminescence data in SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+, for which A = (4.78 ± 1.66) × 10−3. The parameter B consists of two factors according to eqn (4). On the one hand, it contains the ratio of the radiative rates of the two excited levels coupled with the crossover process. While k1r = (0.193 ± 0.001) ms−1, the radiative rate of the 4f55d1 → 4f6-based emission could not be reliably determined with our equipment as it only gains appreciable intensity at higher temperatures and the overall decay is dominated by the non-radiative relaxation rate then. However, it is known for most Sm2+-doped phosphors that the radiative rate of a 4f55d1 → 4f6 transition is in the order of 1–10 μs−1.61–63 Thus, the order of magnitude of the factor
0.5% Sm2+, for which A = (4.78 ± 1.66) × 10−3. The parameter B consists of two factors according to eqn (4). On the one hand, it contains the ratio of the radiative rates of the two excited levels coupled with the crossover process. While k1r = (0.193 ± 0.001) ms−1, the radiative rate of the 4f55d1 → 4f6-based emission could not be reliably determined with our equipment as it only gains appreciable intensity at higher temperatures and the overall decay is dominated by the non-radiative relaxation rate then. However, it is known for most Sm2+-doped phosphors that the radiative rate of a 4f55d1 → 4f6 transition is in the order of 1–10 μs−1.61–63 Thus, the order of magnitude of the factor 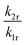 is expectedly 103–104. The second factor contained in B relates the intrinsic non-radiative crossover coupling rate knr(0) to the effective total relaxation rate of the 4f55d1 level also dominated by knr(0). This factor should be expected to be of the order of 1. Thus, B is overall expected to be in the order of 103–104. From the least-squares fit of the model (4) to the temperature-dependent LIR, a value of B = (2.70 ± 0.66)·104 is derived, which perfectly agrees with the previous estimates. The presented calibration model for crossover thermometers allows the physical interpretation that can be independently verified by time-resolved measurements and thus, in principle, simulated independently from the experiment.
is expectedly 103–104. The second factor contained in B relates the intrinsic non-radiative crossover coupling rate knr(0) to the effective total relaxation rate of the 4f55d1 level also dominated by knr(0). This factor should be expected to be of the order of 1. Thus, B is overall expected to be in the order of 103–104. From the least-squares fit of the model (4) to the temperature-dependent LIR, a value of B = (2.70 ± 0.66)·104 is derived, which perfectly agrees with the previous estimates. The presented calibration model for crossover thermometers allows the physical interpretation that can be independently verified by time-resolved measurements and thus, in principle, simulated independently from the experiment.
The expected relative sensitivity and relative temperature uncertainty of the luminescent crossover thermometer SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ are depicted in Fig. 5. The relative sensitivity of the tetraborate shows a maximum at around 400 K with a value of 2.98% K−1, similar to earlier reports.32 Both the temperature and the value of the relative sensitivity depend on the interplay between ΔEX1 and the ratio A/B and thus, basically intrinsic electronic properties of the emitting luminescent centre. The practically more relevant quantity of a (relative) temperature measurement uncertainty can be particularly controlled by the emission intensity I1 of the lower excited level.13,58,59 Since Sm2+ is a very bright emitter in SrB4O7 that can be even efficiently excited due to the electric-dipole allowed nature of the 4f6 → 4f55d1 transition, the statistically expected relative temperature uncertainty is typically below 0.1% even for integrated intensities of the 5D0 → 7FJ-based emission as low as 106 counts (see Fig. 5(b)). Due to the efficient thermal coupling between the two excited levels, crossover thermometers are therefore a very promising class of effective luminescent thermometers since high energy gaps can be exploited at rather low temperatures (here > 400 K) in contrast to e.g. Boltzmann thermometers. At lower temperatures, the vanishing intensity of the broad 4f55d1 → 4f6 emission band leads to a strong increase in the statistical relative measurement uncertainty above 1%.
0.5% Sm2+ are depicted in Fig. 5. The relative sensitivity of the tetraborate shows a maximum at around 400 K with a value of 2.98% K−1, similar to earlier reports.32 Both the temperature and the value of the relative sensitivity depend on the interplay between ΔEX1 and the ratio A/B and thus, basically intrinsic electronic properties of the emitting luminescent centre. The practically more relevant quantity of a (relative) temperature measurement uncertainty can be particularly controlled by the emission intensity I1 of the lower excited level.13,58,59 Since Sm2+ is a very bright emitter in SrB4O7 that can be even efficiently excited due to the electric-dipole allowed nature of the 4f6 → 4f55d1 transition, the statistically expected relative temperature uncertainty is typically below 0.1% even for integrated intensities of the 5D0 → 7FJ-based emission as low as 106 counts (see Fig. 5(b)). Due to the efficient thermal coupling between the two excited levels, crossover thermometers are therefore a very promising class of effective luminescent thermometers since high energy gaps can be exploited at rather low temperatures (here > 400 K) in contrast to e.g. Boltzmann thermometers. At lower temperatures, the vanishing intensity of the broad 4f55d1 → 4f6 emission band leads to a strong increase in the statistical relative measurement uncertainty above 1%.
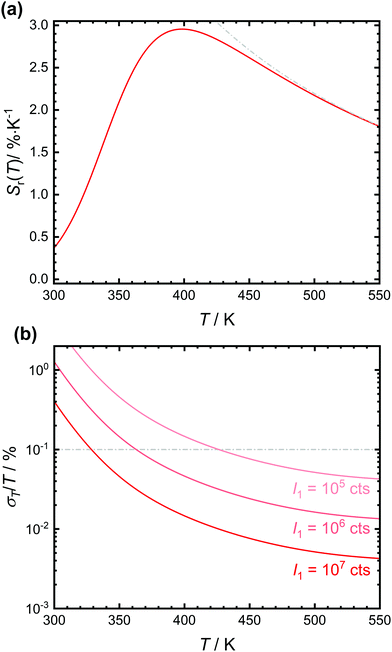 | ||
Fig. 5 (a) Plot of the relative sensitivity, Sr(T), of the anticipated luminescent crossover thermometer SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ using the fitting values from the plot in Fig. 4(b). The expected relative sensitivity of a purely Boltzmann-based luminescent thermometer with energy gap ΔEX1 = 3810 cm−1 is also indicated in grey colour. (b) Expected relative statistical temperature uncertainties of SrB4O7 0.5% Sm2+ using the fitting values from the plot in Fig. 4(b). The expected relative sensitivity of a purely Boltzmann-based luminescent thermometer with energy gap ΔEX1 = 3810 cm−1 is also indicated in grey colour. (b) Expected relative statistical temperature uncertainties of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ with different integrated intensities of the 5D0 → 7FJ transitions. 0.5% Sm2+ with different integrated intensities of the 5D0 → 7FJ transitions. | ||
It should not be misinterpreted, however, that crossover thermometers can be readily used for wide ranges. Due to the configurational coordinate shift of one of the excited state potentials, not only a crossover to an excited level of interest but also to the ground-level potential is possible. Given the high non-radiative coupling rates knr(0) between the 4f55d1- and 4f6-based levels, thermal quenching of the luminescence is a serious problem at high temperatures (see also Fig. 3), as was already demonstrated several times for transition metal ions by the Marciniak group64,65 or in dual-centre luminescent thermometers by e.g. Kaczmarek et al.66 Thus, despite the promising relative sensitivities and high measurement precision, crossover thermometers are usually reasonably applicable in a limited temperature range only. This is different from conventional luminescent Boltzmann thermometers based on two excited levels thermally coupled by multiphonon transitions. This type of thermometer does not usually suffer from high-temperature quenching, but the slower thermal coupling processes limit the low-temperature threshold above which thermometry with a Boltzmann-type thermometer would be possible. In that regard, luminescent crossover thermometers offer a practical alternative to classical Boltzmann-type luminescent thermometers.
Conclusions
In this work, we discussed the class of ratiometric luminescent crossover thermometers and derived a physically-interpretable calibration model for them. We showed that the luminescence intensity ratio of such a thermometer generally follows a “quasi”-Boltzmann-type behaviour with constant offset at low temperatures and how to physically interpret the different fitting parameters. Such verifiability is important for critically judging the quality and physical content of a thermometric calibration model.The concepts were explicitly demonstrated on experimental data of synthesized microcrystalline SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+. Sm2+ (4f6) has a low energetic excited 4f55d1 configuration that allows a configurational crossover from the excited 5D0 level of the 4f6 configuration. While the luminescence of SrB4O7
0.5% Sm2+. Sm2+ (4f6) has a low energetic excited 4f55d1 configuration that allows a configurational crossover from the excited 5D0 level of the 4f6 configuration. While the luminescence of SrB4O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5% Sm2+ at room temperature is dominated by narrow line emission due to the 5D0 → 7FJ (J = 0–6) transitions of Sm2+ with a particularly strong 5D0 → 7F0-based emission line at 685 nm, a broad-banded 4f65d1 → 4f7-based emission with a maximum at 585 nm emerges at temperatures above 400 K. The temperature-dependent luminescence intensity ratio defined by the integrated intensities of the 4f65d1 → 4f7- and 5D0 → 7FJ-based emission can be fitted very well with the presented model and the fitting parameters related to the excited state kinetic data. A maximum relative sensitivity of almost 3%K-1 at around 400 K was derived. Together with the high luminescence intensity of the 5D0 → 7FJ-based emission of Sm2+ in SrB4O7, relative statistical temperature measurement uncertainty below 0.1% can be retained above 400 K. However, despite the promising performance values, crossover thermometers suffer from severe thermal quenching of the luminescence at high temperatures (T > 548 K), which poses an upper threshold to the dynamic working range of this type of luminescent thermometers. This is different from classic Boltzmann thermometers, which usually do not suffer from this limitation but are rather insensitive and thus, less precise at high temperatures. Nonetheless, the presented calibration model with the possibility of explicit verification of the physical content offers a way to design luminescent thermometers with desirable performance properties.
0.5% Sm2+ at room temperature is dominated by narrow line emission due to the 5D0 → 7FJ (J = 0–6) transitions of Sm2+ with a particularly strong 5D0 → 7F0-based emission line at 685 nm, a broad-banded 4f65d1 → 4f7-based emission with a maximum at 585 nm emerges at temperatures above 400 K. The temperature-dependent luminescence intensity ratio defined by the integrated intensities of the 4f65d1 → 4f7- and 5D0 → 7FJ-based emission can be fitted very well with the presented model and the fitting parameters related to the excited state kinetic data. A maximum relative sensitivity of almost 3%K-1 at around 400 K was derived. Together with the high luminescence intensity of the 5D0 → 7FJ-based emission of Sm2+ in SrB4O7, relative statistical temperature measurement uncertainty below 0.1% can be retained above 400 K. However, despite the promising performance values, crossover thermometers suffer from severe thermal quenching of the luminescence at high temperatures (T > 548 K), which poses an upper threshold to the dynamic working range of this type of luminescent thermometers. This is different from classic Boltzmann thermometers, which usually do not suffer from this limitation but are rather insensitive and thus, less precise at high temperatures. Nonetheless, the presented calibration model with the possibility of explicit verification of the physical content offers a way to design luminescent thermometers with desirable performance properties.
Author contributions
B. B. performed the synthesis, characterization, and optical measurements. M. S. supervised the project, analysed the data, and wrote the manuscript. All authors agreed on the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. Dr W. Frank and Dr G. Kreiner at the Heinrich Heine University for the possibility of and assistance in the usage of the powder X-ray diffraction facilities at their institute.References
- C. D.-S. Brites, S. Balabhadra and L. D. Carlos, Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- M. D. Dramićanin, Trends in Luminescence Thermometry, J. Appl. Phys., 2020, 128, 40902 CrossRef.
- A. Bednarkiewicz, J. Drabik, K. Trejgis, D. Jaque, E. Ximendes and L. Marciniak, Luminescence based temperature bio-imaging: Status, challenges, and perspectives, Appl. Phys. Rev., 2021, 8, 11317 CAS.
- T. Hartman, R. G. Geitenbeek, G. T. Whiting and B. M. Weckhuysen, Operando monitoring of temperature and active species at the single catalyst particle level, Nat. Catal., 2019, 2, 986–996 CrossRef CAS.
- T. P. van Swieten, T. van Omme, D. J. van den Heuvel, S. J.-W. Vonk, R. G. Spruit, F. Meirer, H. H.-P. Garza, B. M. Weckhuysen, A. Meijerink, F. T. Rabouw and R. G. Geitenbeek, Mapping Elevated Temperatures with a Micrometer Resolution Using the Luminescence of Chemically Stable Upconversion Nanoparticles, ACS Appl. Nano Mater., 2021, 4, 4208–4215 CrossRef CAS PubMed.
- A. Skripka, D. Méndez González, R. Marin, E. Ximendes, B. del Rosal, D. Jaque Garcia, P. Rodriguez Sevilla, D. Mendez-Gonzalez, D. Jaque and P. Rodríguez-Sevilla, Near infrared bioimaging and biosensing with semiconductor and rare-earth nanoparticles: recent developments in multifunctional nanomaterials, Nanoscale Adv., 2021, 3, 6310–6329 RSC.
- C. D.-S. Brites, X. Xie, M. L. Debasu, X. Qin, R. Chen, W. Huang, J. Rocha, X. Liu and L. D. Carlos, Instantaneous ballistic velocity of suspended Brownian nanocrystals measured by upconversion nanothermometry, Nat. Nanotechnol., 2016, 11, 851–856 CrossRef CAS PubMed.
- A. R.-N. Bastos, C. D.-S. Brites, P. A. Rojas-Gutierrez, C. DeWolf, R. A.-S. Ferreira, J. A. Capobianco and L. D. Carlos, Thermal Properties of Lipid Bilayers Determined Using Upconversion Nanothermometry, Adv. Funct. Mater., 2019, 29, 1905474 CrossRef CAS.
- A. R.-N. Bastos, C. D.-S. Brites, P. A. Rojas-Gutierrez, R. A.-S. Ferreira, R. L. Longo, C. DeWolf, J. A. Capobianco and L. D. Carlos, Thermal properties of lipid bilayers derived from the transient heating regime of upconverting nanoparticles, Nanoscale, 2020, 12, 24169–24176 RSC.
- A. Ćirić, Ł. Marciniak and M. D. Dramićanin, Luminescence intensity ratio squared—A new luminescence thermometry method for enhanced sensitivity, J. Appl. Phys., 2022, 131, 114501 CrossRef.
- J. Drabik and L. Marciniak, Excited State Absorption for Ratiometric Thermal Imaging, ACS Appl. Mater. Interfaces, 2021, 13, 1261–1269 CrossRef CAS PubMed.
- A. Paściak, A. Pilch-Wróbel, Ł. Marciniak, P. J. Schuck and A. Bednarkiewicz, Standardization of Methodology of Light-to-Heat Conversion Efficiency Determination for Colloidal Nanoheaters, ACS Appl. Mater. Interfaces, 2021, 13, 44556–44567 CrossRef PubMed.
- M. Suta and A. Meijerink, A theoretical framework for ratiometric single ion luminescent thermometers - Thermodynamic and kinetic guidelines for optimized performance, Adv. Theory Simul., 2020, 3, 2000176 CrossRef CAS.
- R. G. Geitenbeek, H. W. de Wijn and A. Meijerink, Non-Boltzmann Luminescence in NaYF4:Eu3+: Implications for Luminescence Thermometry, Phys. Rev. Appl., 2018, 10, 64006 CrossRef CAS.
- R. Piñol, J. Zeler, C. D.-S. Brites, Y. Gu, P. Téllez, A. N. Carneiro Neto, T. E. da Silva, R. Moreno-Loshuertos, P. Fernandez-Silva, A. I. Gallego, L. Martinez-Lostao, A. Martínez, L. D. Carlos and A. Millán, Real-Time Intracellular Temperature Imaging Using Lanthanide-Bearing Polymeric Micelles, Nano Lett., 2020, 20, 6466–6472 CrossRef PubMed.
- T. P. van Swieten, D. Yu, T. Yu, S. J.-W. Vonk, M. Suta, Q. Zhang, A. Meijerink and F. T. Rabouw, A Ho3+-Based Luminescent Thermometer for Sensitive Sensing over a Wide Temperature Range, Adv. Opt. Mater., 2021, 9, 2001518 CrossRef CAS.
- A. N. Carneiro Neto, E. Mamontova, A. M.-P. Botas, C. D.-S. Brites, R. A.-S. Ferreira, J. Rouquette, Y. Guari, J. Larionova, J. Long and L. D. Carlos, Rationalizing the Thermal Response of Dual-Center Molecular Thermometers: The Example of an Eu/Tb Coordination Complex, Adv. Opt. Mater., 2022, 10, 2101870 CrossRef CAS.
- V. Trannoy, A. N. Carneiro Neto, C. D.-S. Brites, L. D. Carlos and H. Serier-Brault, Engineering of Mixed Eu3+/Tb3+ Metal–Organic Frameworks Luminescent Thermometers with Tunable Sensitivity, Adv. Opt. Mater., 2021, 9, 2001938 CrossRef CAS.
- S. Otto, N. Scholz, T. Behnke, U. Resch-Genger and K. Heinze, Thermo-Chromium: A Contactless Optical Molecular Thermometer, Chem. – Eur. J., 2017, 23, 12131–12135 CrossRef CAS PubMed.
- M. Back, J. Ueda, M. G. Brik and S. Tanabe, Pushing the Limit of Boltzmann Distribution in Cr3+-Doped CaHfO3 for Cryogenic Thermometry, ACS Appl. Mater. Interfaces, 2020, 12, 38325–38332 CrossRef CAS PubMed.
- M. Back, J. Ueda, H. Nambu, M. Fujita, A. Yamamoto, H. Yoshida, H. Tanaka, M. G. Brik and S. Tanabe, Boltzmann Thermometry in Cr3+-Doped Ga2O3 Polymorphs: The Structure Matters!, Adv. Opt. Mater., 2021, 9, 2100033 CrossRef CAS.
- C. D.-S. Brites, K. Fiaczyk, J. F.-C. B. Ramalho, M. Sójka, L. D. Carlos and E. Zych, Widening the Temperature Range of Luminescent Thermometers through the Intra- and Interconfigurational Transitions of Pr3+, Adv. Opt. Mater., 2018, 6, 1701318 CrossRef.
- M. Sójka, J. F.-C. B. Ramalho, C. D.-S. Brites, K. Fiaczyk, L. D. Carlos and E. Zych, Bandgap Engineering and Excitation Energy Alteration to Manage Luminescence Thermometer Performance. The Case of Sr2(Ge,Si)O4:Pr3+, Adv. Opt. Mater., 2019, 7, 1901102 CrossRef.
- M. Sójka, C. D.-S. Brites, L. A.-D. Carlos and E. Zych, Exploiting Bandgap Engineering to Fine Control Dual-mode Lu2(Ge,Si)O5:Pr3+ Luminescent Thermometers, J. Mater. Chem. C, 2020, 8, 10086–10097 RSC.
- J. C. Fister, D. Rank and J. M. Harris, Delayed Fluorescence Optical Thermometry, Anal. Chem., 1995, 67, 4269–4275 CrossRef CAS.
- C. Baleizão, S. Nagl, S. M. Borisov, M. Schäferling, O. S. Wolfbeis and M. N. Berberan-Santos, An optical thermometer based on the delayed fluorescence of C70, Chem. – Eur. J., 2007, 13, 3643–3651 CrossRef PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- A. Steinegger, I. Klimant and S. M. Borisov, Purely Organic Dyes with Thermally Activated Delayed Fluorescence–A Versatile Class of Indicators for Optical Temperature Sensing, Adv. Opt. Mater., 2017, 5, 1700372 CrossRef.
- M. Y. Wong and E. Zysman-Colman, Purely Organic Thermally Activated Delayed Fluorescence Materials for Organic Light-Emitting Diodes, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- A. Steinegger and S. M. Borisov, Zn(II) Schiff Bases: Bright TADF Emitters for Self-referenced Decay Time-Based Optical Temperature Sensing, ACS Omega, 2020, 5, 7729–7737 CrossRef CAS PubMed.
- S. Sakirzanovas, A. Katelnikovas, D. Dutczak, A. Kareiva and T. Jüstel, Concentration influence on temperature-dependent luminescence properties of samarium substituted strontium tetraborate, J. Lumin., 2012, 132, 141–146 CrossRef CAS.
- Z. Cao, X. Wei, L. Zhao, Y. Chen and M. Yin, Investigation of SrB4O7:Sm2+ as a Multimode Temperature Sensor with High Sensitivity, ACS Appl. Mater. Interfaces, 2016, 8, 34546–34551 CrossRef CAS PubMed.
- L. van Pieterson, M. F. Reid, R. T. Wegh, S. Soverna and A. Meijerink, 4fn → 4fn−15d transitions of the light lanthanides: Experiment and theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 45113 CrossRef.
- L. R. Morss, Thermochemical properties of Yttrium, Lanthanum, and the Lanthanide Elements and Ions, Chem. Rev., 1976, 76, 827–841 CrossRef CAS.
- A. Meijerink, J. Nuyten and G. Blasse, Luminescence and energy migration in (Sr,Eu)B4O7, a system with a 4f7-4f65d crossover in the excited state, J. Lumin., 1989, 44, 19–31 CrossRef CAS.
- A. Lacam and C. Château, High-pressure measurements at moderate temperatures in a diamond anvil cell with a new optical sensor: SrB4O7:Sm2+, J. Appl. Phys., 1989, 66, 366–372 CrossRef CAS.
- M. Suta and C. Wickleder, Synthesis, spectroscopic properties and applications of divalent lanthanides apart from Eu2+, J. Lumin., 2019, 210, 210–238 CrossRef CAS.
- J. Hölsä and P. Porcher, Crystal field effects in REOBr:Eu3+, J. Chem. Phys., 1982, 76, 2790–2797 CrossRef.
- T. Zheng, M. Sójka, M. Runowski, P. Woźny, S. Lis and E. Zych, Tm2+ Activated SrB4O7 Bifunctional Sensor of Temperature and Pressure—Highly Sensitive, Multi-Parameter Luminescence Thermometry and Manometry, Adv. Opt. Mater., 2021, 9, 2101507 CrossRef CAS.
- G. W. Burdick, M. C. Downer and D. K. Sardar, A new contribution to spin–forbidden rare earth optical transition intensities: Analysis of all trivalent lanthanides, J. Chem. Phys., 1989, 91, 1511–1520 CrossRef CAS.
- M. Tanaka and T. Kushida, Interference between Judd-Ofelt and Wybourne-Downer mechanisms in the 5D0–7FJ (J = 2,4) transitions of Sm2+ in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 588–593 CrossRef CAS PubMed.
- M. Tanaka and T. Kushida, Optical transition mechanisms of Sm2+ and Eu3+ in solids, J. Lumin., 1997, 72-74, 141–143 CrossRef CAS.
- O. L. Malta, W. M. Azevedo, E. A. Gouveia and G. F. de Sá, On the 5D0 → 7F0 transition of the Eu3+ ion in the {(C4H9)4N}3Y(NCS)6 host, J. Lumin., 1982, 26, 337–343 CrossRef CAS.
- K.-H. Hellwege, Über die Fluoreszenz und die Kopplung zwischen Elektronentermen und Kristallgitter bei den wasserhaltigen Salzen der Seltenen Erden, Ann. Phys., 1941, 432, 529–542 CrossRef.
- A. Ellens, H. Andres, M. L.-H. ter Heerdt, R. T. Wegh, A. Meijerink and G. Blasse, Spectral-line-broadening study of the trivalent lanthanide-ion series. II. The variation of the electron-phonon coupling strength through the series, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 180–186 CrossRef CAS.
- P. Solarz, M. Karbowiak, M. Głowacki, M. Berkowski, R. Diduszko and W. Ryba-Romanowski, Optical spectra and crystal field calculation for SrB4O7:Sm2+, J. Alloys Compd., 2016, 661, 419–427 CrossRef CAS.
- Z. Barandiarán and L. Seijo, Quantum chemical analysis of the bond lengths in fn and fn−1d1 states of Ce3+, Pr3+, Pa4+, and U4+ defects in chloride hosts, J. Chem. Phys., 2003, 119, 3785–3790 CrossRef.
- J. L. Pascual, Z. Barandiarán and L. Seijo, Relation between high-pressure spectroscopy and fn−1d1 excited-state geometry: A comparison between theoretical and experimental results in SrF2:Sm2+, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 104109 CrossRef.
- M. de Jong, A. Meijerink, L. Seijo and Z. Barandiarán, Energy Level Structure and Multiple 4f125d1 Emission Bands for Tm2+ in Halide Perovskites: Theory and Experiment, J. Phys. Chem. C, 2017, 121, 10095–10101 CrossRef CAS.
- J. J. Joos, P. F. Smet, L. Seijo and Z. Barandiarán, Insights into the complexity of the excited states of Eu-doped luminescent materials, Inorg. Chem. Front., 2020, 7, 871–888 RSC.
- R. Valiente, F. Rodríguez, J. González, H. U. Güdel, R. Martín-Rodríguez, L. Nataf, M. N. Sanz-Ortiz and K. Krämer, High pressure optical spectroscopy of Ce3+-doped Cs2NaLuCl6, Chem. Phys. Lett., 2009, 481, 149–151 CrossRef CAS.
- S. Mahlik, K. Wiśniewski, M. Grinberg and R. S. Meltzer, Temperature and pressure dependence of the luminescence of Eu2+-doped fluoride crystals BaxSr1−xF2 (x = 0, 0.3, 0.5 and 1): experiment and model, J. Phys.: Condens. Matter, 2009, 21, 245601 CrossRef CAS PubMed.
- S. Mahlik, M. Grinberg, L. Shi and H. J. Seo, Pressure evolution of LiBaF3:Eu2+ luminescence, J. Phys.: Condens. Matter, 2009, 21, 235603 CrossRef CAS PubMed.
- S. Mahlik, A. Lazarowska, M. Grinberg, J.-P. R. Wells and M. F. Reid, Pressure dependence of the emission in CaF2:Yb2+, J. Phys.: Condens. Matter, 2015, 27, 305501 CrossRef CAS PubMed.
- M. de Jong, D. Biner, K. W. Krämer, Z. Barandiarán, L. Seijo and A. Meijerink, New Insights in 4f125d1 Excited States of Tm2+ through Excited State Excitation Spectroscopy, J. Phys. Chem. Lett., 2016, 7, 2730–2734 CrossRef CAS PubMed.
- C. W. Struck and W. H. Fonger, Unified model of the temperature quenching of narrow-line and broad-band emissions, J. Lumin., 1975, 10, 1–30 CrossRef CAS.
- A. Ćirić, S. Stojadinović, Z. Ristić, I. Zeković, S. Kuzman, Ž. Antić and M. D. Dramićanin, Supersensitive Sm2+-Activated Al2O3 Thermometric Coatings for High-Resolution Multiple Temperature Read-Outs from Luminescence, Adv. Mater. Technol., 2021, 6, 2001201 CrossRef.
- C. Abram, I. Wilson Panjikkaran, S. N. Ogugua and B. Fond, ScVO4:Bi3+ thermographic phosphor particles for fluid temperature imaging with sub-°C precision, Opt. Lett., 2020, 45, 3893–3896 CrossRef PubMed.
- T. P. van Swieten, A. Meijerink and F. T. Rabouw, Impact of Noise and Background on Measurement Uncertainties in Luminescence Thermometry, ACS Photonics, 2022, 9, 1366–1374 CrossRef CAS PubMed.
- Y. Shen and K. L. Bray, Effect of pressure and temperature on 4f–4f luminescence properties of Sm2+ ions in MFCl crystals (M = Ba, Sr, and Ca), Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11944–11958 CrossRef CAS.
- L. C. Dixie, A. Edgar and M. F. Reid, Sm2+ fluorescence and absorption in cubic BaCl2: Strong thermal crossover of fluorescence between 4f6 and 4f55d1 configurations, J. Lumin., 2012, 132, 2775–2782 CrossRef CAS.
- M. Karbowiak, P. Solarz, R. Lisiecki and W. Ryba-Romanowski, Optical spectra and excited state relaxation dynamics of Sm2+ ions in SrCl2, SrBr2 and SrI2 crystals, J. Lumin., 2018, 195, 159–165 CrossRef CAS.
- M. Karbowiak and C. Rudowicz, Trends in Hamiltonian parameters determined by systematic analysis of f-d absorption spectra of divalent lanthanides in alkali-halides hosts: II. CaCl2:Ln2+ (Ln = Sm, Eu, Tm, and Yb), J. Lumin., 2018, 197, 66–75 CrossRef CAS.
- K. Kniec, W. Piotrowski, K. Ledwa, L. D. Carlos and L. Marciniak, Spectral and thermometric properties altering through crystal field strength modification and host material composition in luminescence thermometers based on Fe3+ doped AB2O4 type nanocrystals (A = Mg, Ca; B = Al, Ga), J. Mater. Chem. C, 2021, 9, 517–527 RSC.
- K. Kniec, W. Piotrowski, K. Ledwa, M. Suta, L. D. Carlos and L. Marciniak, From quencher to potent activator – Multimodal luminescence thermometry with Fe3+ in the oxides MAl4O7 (M = Ca, Sr, Ba), J. Mater. Chem. C, 2021, 9, 6268–6276 RSC.
- A. M. Kaczmarek, H. S. Jena, C. Krishnaraj, H. Rijckaert, S. K. P. Veerapandian, A. Meijerink and P. Van der Voort, Luminescent ratiometric thermometers based on a 4f–3d grafted covalent organic framework to locally measure temperature gradients during catalytic reactions, Angew. Chem., Int. Ed., 2021, 60(7), 3727–3736 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Powder X-ray diffraction pattern of synthesised SrB4O7:Sm2+ and temperature-dependent time-resolved luminescence measurements. See DOI: https://doi.org/10.1039/d2tc01152b |
| This journal is © The Royal Society of Chemistry 2022 |