Chemical lattice strain in nonstoichiometric oxides: an overview†
Dmitry S.
Tsvetkov
 *ab,
Vladimir V.
Sereda
*ab,
Vladimir V.
Sereda
 ab,
Dmitry A.
Malyshkin
ab,
Dmitry A.
Malyshkin
 ab,
Ivan L.
Ivanov
ab,
Ivan L.
Ivanov
 ab and
Andrey Yu.
Zuev
a
ab and
Andrey Yu.
Zuev
a
aInstitute of Natural Sciences and Mathematics, Ural Federal University, 620002, 19 Mira St., Yekaterinburg, Russia. E-mail: dmitry.tsvetkov@urfu.ru
bLaboratory of Hydrogen Energy, Ural Federal University, 620002, 19 Mira St., Ekaterinburg, Russia
First published on 14th February 2022
Abstract
Strong coupling between the chemical composition and crystal lattice dimensions resulting in the contraction or expansion of a material upon change of its chemical composition is known as chemical expansion or chemical strain. This phenomenon significantly influences the performance of oxide materials in different energy conversion and storage devices. In many such applications, e.g., in oxygen-permeating membranes or solid oxide fuel cells (SOFCs), the materials are subject to significant in situ variation of their chemical composition, which is accompanied by large volume changes. This may often be detrimental to the operation of the electrochemical device. Not only is chemo-mechanical coupling crucial for various practical applications, but also, when measured accurately and discussed appropriately, the chemical strain of an oxide material allows better understanding of its local electronic and defect structure. Chemical strain is also strongly correlated with diffusion phenomena in high-temperature electrochemical devices – the subject that for many years has been of particular scientific interest for John Kilner and where he holds a lot of pioneering achievements. This article reviews the state of the art in the field of chemical strain of various oxide materials, primarily those intended to operate at elevated temperatures, and aims at summarizing the available experimental, theoretical and computational insights into its origins, factors impacting its magnitude, and the available means for its a priori quantitative estimation.
1. Introduction
Oxides with fluorite- and perovskite-type structures are the state-of-the-art materials for various electrochemical devices, such as solid oxide fuel cells (SOFCs),1,2 dense oxygen-conducting membranes3 and catalysts for various processes including those important from the ecological viewpoint, for example, oxidation of CO.4 These oxides possess unique combinations of electrical, magnetic and catalytic properties, which can be substantially altered by engineering the chemical composition and morphology. While enhancing electro-chemical performance (e.g. reaction rates in SOFCs) has largely been the focus in developing such energy related materials, the challenges provided by mechano-chemical and mechano-electrical coupling are becoming increasingly important for further progress in developing devices for energy conversion and storage.5 As a result, a recently emerging field of Mechano-Electro-Chemical (MEC) coupling examining the relationships between a material's physico-electro-chemical state and its processing, structure and properties has received great attention in the last decade.5 Mechano-chemical coupling as an important part of MEC coupling plays a crucial role, since energy-related oxide materials are commonly operated at elevated temperatures in both oxidizing and reducing environments and, upon heating, undergo not only thermal expansion, but also the one caused by a change in their oxygen content or hydration degree6 (in case of proton-conducting oxides) or, in other words, in the concentration of point defects in them. Even the materials designed to work at low temperatures, for example, LiMO2 (M = Ni, Co, Mn) based cathodes for lithium ion batteries, when subject to relatively mild thermal stresses develop inter- and intragranular cracks due to oxygen release and oxygen vacancy formation.7–9 Therefore, understanding the origin and the microscopic mechanisms of chemical lattice strain is crucial for identifying the ways to avoid its detrimental effect on the mechanical integrity of a particular device. Moreover, chemical expansion itself, provided that its nature is well understood, may be an important source of information on the processes in solids since it is influenced by the particularities of crystal structure,10 point defect interactions,11–13 diffusion,14–16 magnetic properties,17–20etc. For example, chemical expansion relaxation has been established as one of the methods for measuring diffusion and surface exchange coefficients14–16 in oxides – topics that John Kilner has been involved in for years and where he holds a lot of pioneering achievements. It is also gratifying that he was among those pioneers who showed the importance of the relationship between the host cation radius and oxygen vacancy formation for understanding the nature of chemical strain in oxides.21 Thanks to these efforts not only chemical expansion but also oxide ion conductivity became more understandable too.Thus, this work is aimed at giving an overview of a very important field of mechano-chemical coupling in oxide materials for energy conversion and storage taking into account various historical aspects, the state-of-the-art achievements and existing trends, inconsistencies and challenges. The review is organized as follows. First, some definitions and a selection of units for chemical expansion will be discussed. Then the current level of understanding of chemical expansion in oxides and available modeling approaches will be summarized, and some features and trends in chemical expansion of oxides of various structural types will be identified. Finally, the negative consequences and recently reported possible practical applications of chemical strain will be outlined.
The scope of any review, and this one is no exception, of course, is somehow restricted. First of all, the review is more focused on the results obtained by various experimental or computational techniques rather than on these techniques themselves. The measurement and calculation techniques will be only briefly mentioned without their thorough discussion. That is because the range of experimental and computational methods used to measure and evaluate chemical lattice strain comprises essentially all the modern techniques for investigating the composition of oxides and their dimensions on the macro-, micro- and nanoscale. The latter is not an exaggeration: in the studies of chemical expansivity, detectable changes in linear dimensions of as small as 5 pm were reported.22 However fascinating the ever-increasing magnification of modern analytical methods, more “conventional” ones, such as thermogravimetric analysis, dilatometry, and X-ray and neutron diffraction, despite having been with us for many decades, are still indispensable when it comes to the properties of bulk materials.23 Imaging techniques such as scanning electron microscopy24,25 or even X-ray tomography7 are useful for assessment of the consequences of chemical expansion, e.g., the damage caused to electrochemical devices. In turn, the more complex, in terms of the experimental setups and the interpretation of the results, and more recently developed methods—transmission electron microscopy,26 scanning probe microscopy,27,28 X-ray absorption fine structure (EXAFS),29etc.—are well-suited for studying thin films and interfaces.10 Various original combinations of methods, e.g., Raman spectroscopy coupled with electrochemical titration30 and time-resolved XRD coupled with potential step chronoamperometry,31 regularly emerge, allowing previously inaccessible insights into chemical strain to be obtained. State-of-the-art computational approaches commonly employed in chemical expansion calculations are based on molecular dynamics12,21,32 and ab initio density functional theory.32–34 As seen, the great multitude of experimental and computational methods does not allow them to be reviewed in this work in detail.
Some more applied aspects of chemical expansion, such as the modeling of chemically induced stresses in membranes35–42 and SOFCs,43,44 were thought to be beyond the scope of this rather more fundamentally oriented review. However, our leaving them out does not mean that they are somehow unrelated – on the contrary, high quality experimental data on defect equilibria and chemical expansion of materials figure among the necessary parameters of these models.35,36,38,43 We would also like to draw the attention of interested readers to other existing reviews10,23,45,46 which may provide additional information on the topic.
As our review was intended for publication in the special issue in honour of Prof. John Kilner's 75th birthday, we focused it to a large extent on materials that are closer to his scientific interests – the oxides for higher-temperature applications, and there were quite a lot of those to cover. Fortunately, those important aspects of chemical strain in lithium ion conductors for low-temperature electrochemical devices that are left out of the scope of this review can be found in other recent reports.47–52
2. Definitions, historical aspects and choice of units
Chemical expansion is introduced by analogy with, perhaps, the most familiar type of solid body expansion – thermal expansion,53 and these two phenomena quite often occur simultaneously. Therefore, the definitions and origins of thermal expansion should be discussed first. Indeed, it is well known that thermal expansion is a fundamental property of materials originating from asymmetry of the resulting interaction potential of site species in the crystal lattice, which leads to anharmonicity of atomic vibrations and, consequently, to an increase in the average interatomic distances with temperature. This phenomenon can be quantified using the volumetric (αV) or linear (αL) thermal expansion coefficients (TECs)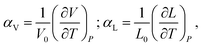 | (1) |
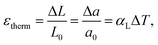 | (2) |
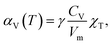 | (3) |
However, the Grüneisen parameter, in the first approximation, can be treated as a temperature-independent constant for a given substance, especially at T ≫ ΘD, where ΘD is the Debye temperature.54 The values of χT and Vm for solids are also known to depend on temperature only weakly. Thus, the change in TEC with temperature is governed mainly by the temperature dependence of the specific heat. The latter is rather flat at high temperatures and therefore, αV(T) tends to be a constant.53 Therefore, if thermal expansion mostly contributes to strain then the latter can be treated as a linear function of temperature with a constant TEC.
Nevertheless, Strelkow55 was the first who reported a significant positive deviation from the linear trend of ε with temperature for several solid halides such as NaCl, AgCl, and AgBr in the vicinity of their melting points. He called this phenomenon “abnormal expansion”. Later Mott and Gurney56 as well as Seitz57 proposed that this anomaly in expansion should be attributed to point defects arising in the crystal lattice at elevated temperatures. Indeed, Lawson58 compared the activation heat for abnormal expansion to that determined earlier for ionic conductivity of silver halides, found good agreement between both values, and concluded that the “abnormal expansion” is caused by the increasing concentration of lattice defects responsible for the ionic conductivity. Using ionic radii Lawson58 also first calculated the volume expansion caused by Schottky defect formation and found the calculated values to be completely consistent with those reported by Strelkow.55
Thus, “abnormal expansion” of the crystal lattice originates from the points defect formation therein and depends on the concentration of defects. Hence, such expansion can be observed at a constant temperature – for example, when the content of the volatile component in the gas phase changes. For this reason, it is also called “isothermal,” “defect-induced,” or “chemical” expansion, to emphasize the difference between its nature and the usual thermal expansion.
Surprisingly, the first evidence that oxides can exhibit chemical expansion appeared prior to Strelkow's pioneering work. Back in 1933, the volume of the unit cell of wustite, Fe1–yO, was found59 to depend on the content of iron vacancies, which can indicate the change of iron cation radius upon its reduction or oxidation. Nevertheless, extensive study of the isothermal expansion of oxides began only in the 90s of the 20th century because of their wide application as energy-related materials. To date, a lot of evidence has been reported in the literature to demonstrate that the phenomenon of chemical expansion is inherent in many such complex oxide materials.10
In broad terms, chemical strain or chemical expansion of solids can be defined as the change in their dimensions following any change in their composition. Even the host/dopant cation concentration ratio, which is set during the synthesis and then remains fixed, can play the role of the composition parameter. Then, electrochemical processes can be used to change the cationic composition of oxides. Lithiation/delithiation occurring in Li-ion battery cathodes is, perhaps, among the most prominent examples of this.52,60 Finally, if a material is redox active or hydratable, its chemical composition may, of course, vary in situ at sufficiently high temperature upon equilibration with the surrounding atmosphere.
Fig. 1 outlines a few reasons behind the chemical lattice strain of oxides—substitution, redox processes and hydration—on which this review is focused. While Fig. 1 provides a useful visual metaphor, the real physical processes underlying chemical expansion can be much more complex. For instance, in Fig. 1 the sample preserves its phase state during the chemical composition change. Marrocchelli et al.61 suggested to call this type of chemical expansion “stoichiometric” in contrast to “phase change expansion” when the sample's phase state is changing as well. The former represents the main subject of the current review.
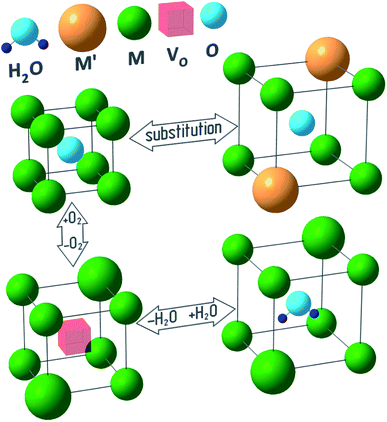 | ||
| Fig. 1 Possible causes of chemical expansion of oxide materials, represented for a hypothetical M1−xM′xO1−y(H2O)z oxide. | ||
The use of TEC only is, therefore, insufficient for a full definition of solid oxides' expansion when substantial amounts of defects form at elevated temperatures. For example, in the case of the oxygen-nonstoichiometric oxide, the overall lattice strain can be quantified in terms of both usual volumetric TEC (αV) and volumetric chemical expansivity (αVC) induced by oxygen vacancy formation as suggested by Adler62
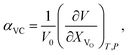 | (4) |
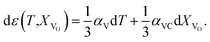 | (5) |
Eqn (5), valid for isotropic materials, enables simultaneous determination of both thermal and chemical constituents of the uniaxial isotropic strain, for instance, of cubic oxides measured at a given oxygen partial pressure (pO2) depending on temperature. However, such a thermodynamic approach, firstly, is not applicable for layered oxides exhibiting anisotropic chemical strain and, secondly, it does not allow the origin of chemical strain itself to be understood.
Eqn (4) describes only one possible definition of chemical expansivity.61 Depending on how the concentration of the defects responsible for chemical strain is defined, at least three possibilities exist:
(1) the concentration may be defined as a molar fraction of defects in the corresponding sublattice, i.e.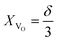 in the case of ABO3–δ oxide. This is similar to eqn (4). Hence, the uniaxial expansivity is
in the case of ABO3–δ oxide. This is similar to eqn (4). Hence, the uniaxial expansivity is
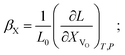 | (6) |
(2) if the concentration is defined in cm−3, then the chemical expansion coefficient is
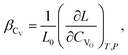 | (7) |
(3) if the concentration is defined in moles per mole of oxide (for example, ABO3–δ), then the chemical expansivity is
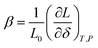 | (8) |
Although it may be argued61 that βX and βCV should be preferred for the comparison among different structural types, it is the β-coefficient which is the most used in current practice for convenience reasons. This way of expressing chemical expansivity will be used throughout this review.
In the case of proton conducting oxides exhibiting chemical expansion upon hydration,6 a similar definition of expansivity will be employed. In addition, the amount of water, x, per mole of hydrated oxide, ABO3–δ–x·xH2O, is used as a composition variable34,63,64 instead of the concentration of protons in the crystal structure employed in ref. 65–70 so that β would reflect the expansion per mole of hydrated oxygen vacancies:
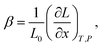 | (9) |
3. Various models and approaches to understand the chemical expansion
3.1. Fluorites
The pioneering targeted studies of chemical expansion in oxide materials concerned primarily the oxides with a fluorite-like structure. These studies were aimed at finding the compositional dependences of unit cell dimensions for MO2–R2O3 and MO2–ZO (M = Hf, Zr, Ce, Th, U; R = Y, Gd, Yb, Zr, Sc, La, Sm, Eu; Z = Ca, Mg, Sr) solid solutions. Cubic symmetry, typical of the fluorite crystal structure, was found to be retained upon MO2–R2O3 and MO2–ZO substitutions for all solid solutions up to the respective solubility limits.71Based on the geometrical considerations an expression for the unit cell parameter can be derived:72
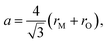 | (10) |
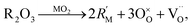 | (11) |
To take this into account Glushkova et al.73 suggested modifying the ionic radii in eqn (10), replacing rM with a weighted mean ionic radius, xr(R3+) + (1 − x)r(M4+), and rO with an “effective” oxygen ion radius, reff. In this approach, the oxygen vacancy is thought to occupy no space. Hence, the effective oxygen ion volume is equal to 4/3·πrO3·(1 − x/4), and reff = rO(1 − x/4)1/k, where k = 3 for noninteracting vacancies and k > 3 for cases when oxygen vacancies form clusters.73 In the original work, the value of k = 3.6 was used for calculating the unit cell parameter a.
Ingel and Lewis,74 applying the model suggested by Aleksandrov et al.75 for calculating the unit cell parameters of yttrium-stabilized zirconia (YSZ) as a function of Y content, arrived at the following equation:
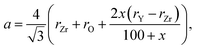 | (12) |
The aforementioned models work well for those solid solutions for which they were initially derived, and when applied to different materials give significant discrepancies between the calculated and experimental data.76,77 The later efforts were directed at finding more general models.
According to the empirical Vegard's rule,78 the relationship between the unit cell parameters and concentrations of the solid solution components should be linear. We should mention here that, being simple as well as very general, Vegard's rule plays an important role in the analysis of chemical strain in some cases, e.g., in thin films of Li ion conductors. Therein, terms such as “Vegard strain” or “Vegard coefficient” are sometimes used to describe chemical strain that linearly depends on the concentration of ions or the slope of such dependence.79,80 However, chemical expansion as a bulk property of highly nonstoichiometric oxides often deviates from a simple linear compositional dependence predicted with Vegard's rule.
Assuming that oxides MO2 (M = Hf, Zr, Ce, Th, U) with a fluorite structure conform to Vegard's rule, Kim76 developed a model that is also, by its nature, empirical. For example, an expression for the unit cell parameter a of the substituted ceria in Kim's model framework is
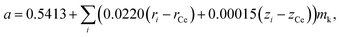 | (13) |
Discussing the fact that the oxygen vacancy located near M4+ in MO2–x can effectively lower the coordination number of the cation, Hong and Virkar72 suggested a model for calculating a of variously substituted ceria and zirconia. In place of variable CN, they introduced another parameter – oxygen vacancy radius rV, independent of the concentration and nature of the dopant. As a result, the value of a can be obtained by replacing rM and rO in eqn (10) with the weighted mean cation and anion radii, respectively:
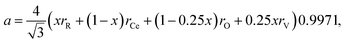 | (14) |
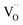 radii, respectively. The 0.9971 multiplier is added to make the calculated a parameter of undoped CeO2 equal to the experimental one (5.411 Å).
radii, respectively. The 0.9971 multiplier is added to make the calculated a parameter of undoped CeO2 equal to the experimental one (5.411 Å).
The values of rV were found using the experimental ∂a/∂x = f(rR) plots. From them, the critical cation radii 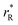 were determined, which are hypothetical rR at which substituting R for Ce in CeO2 (or Zr in ZrO2) does not change a, i.e.
were determined, which are hypothetical rR at which substituting R for Ce in CeO2 (or Zr in ZrO2) does not change a, i.e.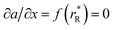 . Next, substituting
. Next, substituting 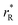 into ∂a/∂x = 0 with a as per eqn (14) yielded the following expression:
into ∂a/∂x = 0 with a as per eqn (14) yielded the following expression:
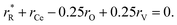 | (15) |
The as-calculated rV was found to be 1.164 Å for RO1.5–CeO2 and 0.993 Å for RO1.5–ZrO2, as compared with the ionic radius of O2− (1.38 Å).
Thus, as follows from eqn (14) and (15), the total chemical expansion observed upon changing the composition of fluorite-type oxides is due to the simultaneous unit cell expansion, caused by the cation size increase, and contraction, caused by the formation of oxygen vacancies that are smaller than oxygen ions. For example, the experimentally determined chemical expansion of CeO2–δ, which can be thought of as a solid solution of Ce2O3 in CeO2, is Δa/a0 ≈ 10% per mole of oxygen vacancies, which in the framework of the model of Hong and Virkar72 is a result of ≈15% “cationic” expansion and ≈5% oxygen-vacancy-induced contraction.45
Similarly to eqn (14), Marrocchelli et al.12 expressed an equation for the relative elongation of RxM1–xO2–x/2 (M = Zr, Ce; R = Y, Yb, Ho, Er, Dy, Gd, Nd, Sm, Tb, La, Pr, Ce):
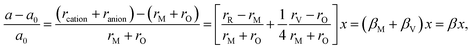 | (16) |
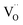 , and βM = (rR − rM)/(rM + rO) and βV = (rV − rO)/4(rM + rO) are the “partial” chemical expansion coefficients, reflecting the magnitude of expansion arising from the cation radius change and vacancy formation, respectively. As βM + βV = β, the oxygen vacancy radius is equal to:
, and βM = (rR − rM)/(rM + rO) and βV = (rV − rO)/4(rM + rO) are the “partial” chemical expansion coefficients, reflecting the magnitude of expansion arising from the cation radius change and vacancy formation, respectively. As βM + βV = β, the oxygen vacancy radius is equal to:| rV = 4(rM + rO)(β − βM) + rO, | (17) |
It has to be noted that rV should not be considered as the real size of oxygen vacancies. The so-called vacancy radius is rather a certain effective value reflecting the local crystal lattice size changes following the 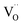 formation.71
formation.71
The aforementioned a(M1−xRxO2−δ) = f(ri, x,…) model dependences were derived primarily using the room-temperature XRD data for different series of solid solutions where both oxygen nonstoichiometry and cationic composition varied. However, the chemical expansion occurring at elevated temperatures for oxides with varying oxygen nonstoichiometry (upon pO2 changes) is no less important. This is evidenced by a number of studies devoted to this phenomenon for doped and undoped ceria.11,12,21,82–91
As mentioned above, partially reduced CeO2–δ can be seen as a solution of Ce2O3 in CeO2,82 which allows models such as Kim's76 or Hong and Virkar's72 to be applied to this oxide expansion. Being based on Vegard's rule, these models assume by definition that chemical strain vs. nonstoichiometry dependences are linear. The actual εchem = f(δ) dependences, however, are nonlinear for CeO2–δ (ref. 82 and 92) and Ce1–xGdxO2–δ,84,93,94 especially at large deviations from stoichiometry (δ > 0.06 (ref. 94) for Ce0.9Gd0.1O2–δ and δ > 0.1 for CeO2–δ (ref. 92)).
One likely hypothesis explaining the nonlinearity of εchem(δ) considered it to be caused by formation of electrostatic clusters, such as 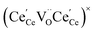 ,84,94–96 and oxygen vacancy ordering at high δ.11,94 This was made use of by Bishop et al.84,94 who suggested a defect chemistry based approach to discussing the chemical expansion of doped ceria. Indeed, the defect structure modeling results showed that one oxygen exchange reaction,
,84,94–96 and oxygen vacancy ordering at high δ.11,94 This was made use of by Bishop et al.84,94 who suggested a defect chemistry based approach to discussing the chemical expansion of doped ceria. Indeed, the defect structure modeling results showed that one oxygen exchange reaction,
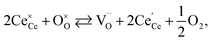 | (18) |
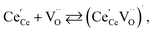 | (19) |
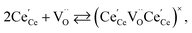 | (20) |
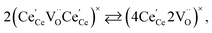 | (21) |
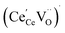 concentration was found to be low,84 it was assumed that oxygen vacancies form clusters predominantly in accordance with eqn (20) and eqn (21),83,84,94 the latter process describing the experimentally determined
concentration was found to be low,84 it was assumed that oxygen vacancies form clusters predominantly in accordance with eqn (20) and eqn (21),83,84,94 the latter process describing the experimentally determined 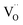 ordering along the 〈111〉 directions in the crystal lattice of ceria at high δ.11 Supposing the size of
ordering along the 〈111〉 directions in the crystal lattice of ceria at high δ.11 Supposing the size of 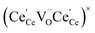 or
or 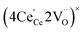 to be different from the sum of the individual point defect sizes, Bishop et al.84,94 concluded that these clusters' contributions to chemical expansion should also be different, which can be expressed as
to be different from the sum of the individual point defect sizes, Bishop et al.84,94 concluded that these clusters' contributions to chemical expansion should also be different, which can be expressed as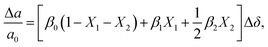 | (22) |
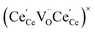 and
and 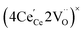 , and β0, β1, and β2 are the chemical expansion coefficients due to
, and β0, β1, and β2 are the chemical expansion coefficients due to 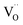 ,
, 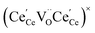 and
and 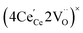 formation, respectively. For calculating X1 and X2, defect structure models based on eqn (18) and (20) for CeO2–δ (X2 was taken as 0)84 and eqn (18), (20) and (21) for Ce0.9Gd0.1O2–δ (ref. 94) were used. The β0, β1, and β2 coefficients were determined by fitting.
formation, respectively. For calculating X1 and X2, defect structure models based on eqn (18) and (20) for CeO2–δ (X2 was taken as 0)84 and eqn (18), (20) and (21) for Ce0.9Gd0.1O2–δ (ref. 94) were used. The β0, β1, and β2 coefficients were determined by fitting.
Fig. 2 shows the experimental data and model functions for chemical strain of CeO2–δ and Ce0.9Gd0.1O2–δ.84,92,94
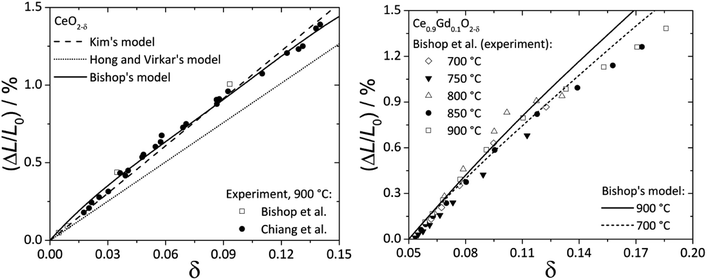 | ||
| Fig. 2 Chemical expansion of CeO2–δ (ref. 84 and 92) (left) and Ce0.9Gd0.1O2–δ (ref. 94) (right): points – experiment, lines – calculations according to Kim's,76 Bishop's84 or Hong and Virkar's72 model. | ||
It is seen that Kim's76 and Bishop's84 models (eqn (13) and (22), respectively) agree much better with experimental data for CeO2–δ, while for Ce0.9Gd0.1O2–δ even eqn (22) where oxygen vacancy ordering is taken into account does not describe the experimental εchem within the whole nonstoichiometry range.
In this respect it should be noted that the real microscopic picture of ceria solid solutions on the local scale may be much more complex than that assumed by Bishop et al.84 in his analysis as shown recently in the excellent studies of Artini et al.97–104 They found that the clusterization of a rare-earth dopant with oxygen vacancies leads to the formation of microheterogeneity which at some point results in crystallization of the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) cubic C-phase, typical of sesquioxides of the rare earths from Gd to Lu, where the latter are six-coordinated by oxygen. For larger rare-earth dopant-cations formation of a hybrid H-phase intermediate between the fluorite (F) and C phases was observed, where the F-based solid solution mainly hosts randomly dispersed C clusters. These C-type microdomains are so intimately mixed with the matrix F-phase that diffraction peaks common to the F and C phases are perfectly superimposed, and the C cell size is exactly doubled with respect to that of the F-phase. Importantly, local probes such as Raman spectroscopy, selected area electron diffraction (SAED), transmission electron microscopy (TEM), extended X-ray absorption fine structure (EXAFS) and some others unambiguously show that a certain number of C-based nano- or microdomains remain stable within the F-matrix even within the fluorite stability region irrespective of the nature of rare-earth dopant cations. What is more, the real distribution of dopant between F and C phases remains unknown. All these circumstances cast doubt on the results of geometrical interpretations of chemical lattice strain described above, and the problem should be reexamined taking into account the new data on the local structure of ceria solid solutions.97–104
cubic C-phase, typical of sesquioxides of the rare earths from Gd to Lu, where the latter are six-coordinated by oxygen. For larger rare-earth dopant-cations formation of a hybrid H-phase intermediate between the fluorite (F) and C phases was observed, where the F-based solid solution mainly hosts randomly dispersed C clusters. These C-type microdomains are so intimately mixed with the matrix F-phase that diffraction peaks common to the F and C phases are perfectly superimposed, and the C cell size is exactly doubled with respect to that of the F-phase. Importantly, local probes such as Raman spectroscopy, selected area electron diffraction (SAED), transmission electron microscopy (TEM), extended X-ray absorption fine structure (EXAFS) and some others unambiguously show that a certain number of C-based nano- or microdomains remain stable within the F-matrix even within the fluorite stability region irrespective of the nature of rare-earth dopant cations. What is more, the real distribution of dopant between F and C phases remains unknown. All these circumstances cast doubt on the results of geometrical interpretations of chemical lattice strain described above, and the problem should be reexamined taking into account the new data on the local structure of ceria solid solutions.97–104
3.2. Perovskites
The unit cell parameter a of an ideal cubic perovskite, ABO3, may be expressed as
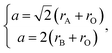 | (23) |
 of the pseudocubic lattice.
of the pseudocubic lattice.
A number of chemical expansion models for fluorites are based on eqn (10). Likewise, one of the geometric models relating the ionic radii with chemical expansion32,111,112 was inspired by the empirical approach to perovskite unit cell parameter calculations113 based on eqn (23). In this model, first applied to substituted lanthanum gallates,32,111 parameters A, B and C are introduced,
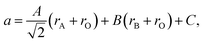 | (24) |
Change of the oxygen nonstoichiometry of a perovskite that occurs simultaneously with cation reduction/oxidation can be written as a transition from some initial state A0B0O03−δ to the final one, A01−xA1xB01−yB1yO13−δ. For example, for lanthanum gallate La1−xSrxGa1−zNizO3−δ the final state is written in the A01−xA1xB01−yB1yO13−δ form as
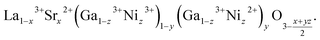 | (25) |
The indices x, y, and z from eqn (25) are used for deriving the expression for chemical deformation of oxides:
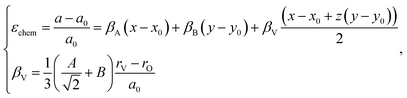 | (26) |
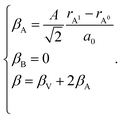 | (27) |
In case of B-sublattice cation change (as a result of substitution or redox processes), A0 = A1 and B0 ≠ B1, and
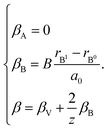 | (28) |
The detailed derivation of eqn (27) and (28) from eqn (26) is given in ref. 32. Among the several parameters in this model, A, B and C coefficients are pre-determined, βA and βB are calculated using Shannon ionic radii,81 and β can be found experimentally, so the only unknown parameter left is the oxygen vacancy radius rV. Interestingly, for a number of different oxides (La1–xSrxGa1–yMgyO3–δ, La1–xSrxAlO3–δ, SrTi1–xGaxO3–δ, La0.9Sr0.1Ga1–xNixO3–δ, and SrTi0.65Fe0.35O3–δ) the rV parameter calculated using both experimental and computational expansion data and eqn (26)–(28) was in the range of 1.24–1.57 Å,32,112 which is much closer to rO than rV in fluorites computed using similar geometric models.12,72 However, no apparent relationship was found between rV and the perovskite-like complex oxide composition,32 which severely limits the predictive power of such a model. This is, in principle, a common drawback of all the models based solely on the geometrical considerations and containing a number of variable coefficients to be determined by fitting and at the same time lacking the connection to the defect chemistry of oxides.
A similar approach, based on eqn (23), was developed for describing the chemical expansion of La1–xSrxGa1–yMgyO3–δ by Chatzichristodoulou et al.71 Its major differences from the one described above are two, instead of three in eqn (24), empirical fitting parameters, p1 and p2:
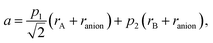 | (29) |
Another geometry-based approach to chemical expansion modeling is also built upon the concept of ionic radii. However, in this case an attempt is made to account for the defect chemistry of an oxide. Therein, no intermediate calculations of unit cell parameters are attempted, and the radii are used in a more straightforward way. For instance, Miyoshi et al.116 suggested that, as chemical expansion of LaMnO3–δ should be due to Mn ions changing their size with their oxidation state, a following equation could be used for calculating the chemical strain:
 | (30) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) Mn are the unit cell parameter of stoichiometric LaMnO3 and the difference between the mean weighted radius of Mnn+ and Mn3+, respectively. The point defect concentrations,
Mn are the unit cell parameter of stoichiometric LaMnO3 and the difference between the mean weighted radius of Mnn+ and Mn3+, respectively. The point defect concentrations, 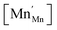 ,
, 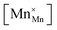 and
and 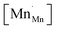 , were found using the corresponding defect structure model.117 Similar to the expression in eqn (30), an equation
, were found using the corresponding defect structure model.117 Similar to the expression in eqn (30), an equation 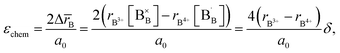 | (31) |
Zuev et al.119 and Hilpert et al.120 pointed out a similar behavior of εchem = ΔL/L0 and ΔrB/r0B, which is the relative change of the mean weighted radius of the B cation in ABO3, with both pO2 and δ for a number of promising SOFC interconnect materials – lanthanum chromite perovskites: La1–xCaxCrO3–δ (x = 0.1, 0.2), La0.8Sr0.2CrO3–δ, La0.8Sr0.2Cr0.97V0.03O3–δ, La0.95Ca0.05Cr0.84Al0.16O3–δ, LaCr0.79Co0.05Al0.16O3–δ, and LaCr0.79Mg0.05Al0.16O3–δ. Examples of such dependences are shown in Fig. 3 and 4. The appropriate defect structure models119,120 were used to calculate the B-site point defect concentrations under the different conditions needed to evaluate ΔrB.
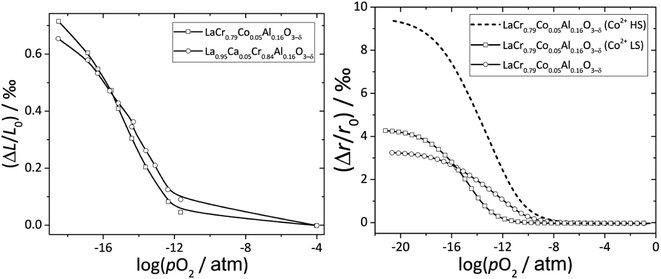 | ||
Fig. 3 ΔL/L0 = f(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) and ΔrB/r0B = f(log pO2) and ΔrB/r0B = f(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) dependences for La0.95Ca0.05Cr0.84Al0.16O3–δ and LaCr0.79Co0.05Al0.16O3–δ.120 pO2) dependences for La0.95Ca0.05Cr0.84Al0.16O3–δ and LaCr0.79Co0.05Al0.16O3–δ.120 | ||
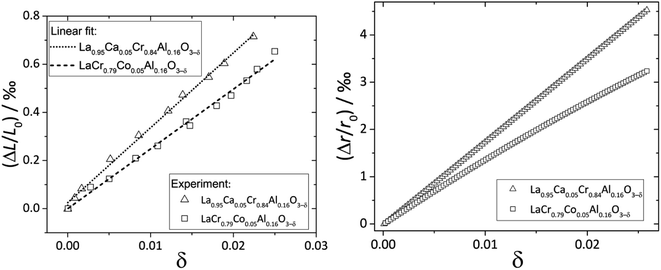 | ||
| Fig. 4 ΔL/L0 = f(δ) and ΔrB/r0B = f(δ) dependences for La0.95Ca0.05Cr0.84Al0.16O3–δ and LaCr0.79Co0.05Al0.16O3–δ.120 | ||
In principle, Co2+ ions can exist in low- (LS) and high-spin (HS) states. Among two possible ΔrB/r0B(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) dependences for LaCr0.79Co0.05Al0.16O3–δ, the one calculated assuming Co2+ (LS) resembles ΔL/L0(log
pO2) dependences for LaCr0.79Co0.05Al0.16O3–δ, the one calculated assuming Co2+ (LS) resembles ΔL/L0(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) better to the point that even the intersection of ΔrB/r0B(log
pO2) better to the point that even the intersection of ΔrB/r0B(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) and ΔL/L0(log
pO2) and ΔL/L0(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2) for La0.95Ca0.05Cr0.84Al0.16O3–δ and LaCr0.79Co0.05Al0.16O3–δ is at the same log
pO2) for La0.95Ca0.05Cr0.84Al0.16O3–δ and LaCr0.79Co0.05Al0.16O3–δ is at the same log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pO2 (see Fig. 3). Thus, it was assumed that the low-spin state is the most likely one for Co2+ in LaCr0.79Co0.05Al0.16O3–δ.120
pO2 (see Fig. 3). Thus, it was assumed that the low-spin state is the most likely one for Co2+ in LaCr0.79Co0.05Al0.16O3–δ.120
Later on, these promising, though only qualitative, observations119,120 were developed into a quantitative chemical expansion model.121,122 In its framework, the isotropic chemical strain of an oxide is approximated by that of a hypothetical crystal lattice formed by close-packed rigid spherical ions. It can be shown (see, for example, Tsvetkov et al.123) that the relative linear expansion of either the unit cell or the bulk of such a lattice is equal to the relative change in weighted mean ionic radius:
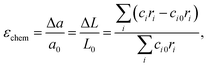 | (32) |
Among the initial explicitly made assumptions, or simplifications, in this model (eqn (32)) were the equality of oxygen ion and vacancy radii, rV = rO, and nonstoichiometry-independent coordination numbers of ions. One tricky implicit assumption which, however, is characteristic of all the models employing the ionic radii concept, deserves to be mentioned as well. It is a supposition that the values, or at least the ratios, of ionic radii derived from the room-temperature structural studies81 are more or less valid at higher temperatures where in situ chemical expansion is usually observed and measured.
In contrast to the models of Miyoshi et al.116 and Chen et al.118 (see eqn (30) and (31)), all ions are taken into account in eqn (32) and not only those that are actually changing their oxidation state. In addition, both the numerator and denominator in eqn (32) are calculated in a similar fashion – via the ionic radii and not the experimentally determined values such as unit cell parameters. As a result, the model based on eqn (32) was first shown to describe well the chemical strain dependences for LaCoO3–δ,121 La1–xMxCrO3–δ (M = Ca, Sr) and oxygen-deficient LaMnO3±δ (ref. 122) (εchem of which the DFT calculations124 severely overestimated).
As different spin states – high-spin (HS), low-spin (LS) or intermediate-spin (IS) – are characteristic of both Co2+ and Co3+ ions, and the ion size depends on the spin state,81 it becomes an important factor influencing unit cell volume of Co-containing oxides. For example, Shafeie et al.125 correlated the TEC change in a series of La2Co1+z(Ti1–xMgx)1–zO6 perovskites with the change in the LS/HS Co3+ content. Gradual transition of Co3+ from LS through IS to HS with temperature is also known to occur in LaCoO3–δ (ref. 126–128) and La1–xSrxCoO3–δ (ref. 129) oxides; such transition impacts TEC130,131 and is one of the reasons for the larger, as compared with LaFeO3–δ and LaNiO3–δ, TEC of LaCoO3–δ.132
In most cases, especially at high temperatures, spin states are unknown, so to define ri in eqn (32) the spin states of Co ions should be somehow assumed. While for LaCoO3–δ it was enough to suppose Co2+ (LS) and Co3+ (HS)121 for the model to coincide with the experimental data, such an approach did not work for some other cobaltites. Thus, presuming some IS state, where Con+ in different spin states coexisted within one oxide, rCon+ in eqn (32) was replaced by
| rCon+ = rCon+(HS)x + rCon+(LS)(1 − x), | (33) |
All Fen+ ions were assumed to be in the HS state in the chemical expansion model of Sr1–xLaxFeO3–δ (x = 0, 0.6).13 The model yielded similar chemical expansion coefficients for La0.6Sr0.4FeO3–δ and SrFeO3–δ, β ≈ 0.0197, and the calculated εchem(δ) dependences coincided with the experimental data136–140 for both oxides up to δ ≈ 0.2.13 At the same time, Bae et al.19,20 demonstrated recently that chemical expansion of Sr1–xLaxFeO3–δ (x = 0.2, 0.5) is less than that predicted by the model based on eqn (32) assuming high-spin-only Fen+ ions, and can be described with this model only if some Fen+ ions are in the LS state.
Among Sr1–xLaxFeO3–δ, only for SrFeO3–δ at δ > 0.3 did the in situ high-temperature XRD and dilatometric data show much higher chemical strain, with β ≈ 0.0574.13 Such disagreement between the model and the measurement results was explained by oxygen vacancy ordering, typical of highly nonstoichiometric SrFeO3–δ (ref. 13) as well as similar oxides such as SrFe1–xTixO3–δ,141,142 impacting εchem values. This conclusion is qualitatively supported by the DFT simulation results, showing increasing oxygen vacancy polaron size with increasing δ in Sr1–xLaxFeO3–δ due to the vacancy ordering.143
Some tetragonal double perovskite oxides – both A-site-ordered such as RBaCo2O6–δ (R = rare-earth metal, sp. gr. P4/mmm) and B-site-ordered such as Sr2FeMoO6–δ (sp. gr. I4/m) – are known to exhibit anisotropic chemical strain with expansion and contraction along the a and c axes, respectively, resulting in very small volumetric expansion.18,144,145 The chemical strain of these oxides, calculated with eqn (32), was shown to agree well with experimentally determined expansion along the a axis, εchem(a).123,145–147 Moreover, for Sr2FeMoO6–δ, εchem of the cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) polymorph is almost equal to that calculated with the model (eqn (32)) as well as to εchem(a) of its tetragonal polymorph.123,146 This indicates a similar nature of expansion of tetragonal ordered and cubic disordered perovskites along the a axis.146 Indeed, Cox-Galhotra et al.148,149 based on the neutron diffraction results supposed that the primary reason for expansion of RBaCo2O6–δ (R = Nd, Pr) within the ab plane is the same as in the simple perovskite cobaltites, i.e. the increase of cobalt ion radii upon reduction.
m) polymorph is almost equal to that calculated with the model (eqn (32)) as well as to εchem(a) of its tetragonal polymorph.123,146 This indicates a similar nature of expansion of tetragonal ordered and cubic disordered perovskites along the a axis.146 Indeed, Cox-Galhotra et al.148,149 based on the neutron diffraction results supposed that the primary reason for expansion of RBaCo2O6–δ (R = Nd, Pr) within the ab plane is the same as in the simple perovskite cobaltites, i.e. the increase of cobalt ion radii upon reduction.
In order to calculate the contraction of materials exhibiting anisotropic chemical strain, Tsvetkov et al.123,146 introduced the so-called anisotropic ratio of chemical expansion, βAR = εchem(c)/εchem(a), where εchem(c) = Δc/c0 and εchem(a) = Δa/a0 are the normalized changes of the corresponding unit cell parameters. This coefficient βAR is similar to Poisson's ratio, which characterizes the anisotropy of elastic properties of materials. The value of βAR should depend largely on the crystal structure and also to some extent may vary with the oxide composition.123 It was demonstrated that for tetragonal Sr2FeMoO6−δ and GdBaCo2O6−δ an assumption that βAR = −1 allowed estimating εchem(c) values in close agreement with the experimental ones.123,145,146
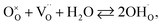 | (34) |
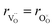 hypothesized, direct application of eqn (32) yields negative chemical expansion, contradicting the experimental data.6,65,67–69,150–161 Instead of making
hypothesized, direct application of eqn (32) yields negative chemical expansion, contradicting the experimental data.6,65,67–69,150–161 Instead of making 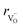 within the model smaller than
within the model smaller than 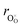 , the authors6 adopted another approach – it was assumed that the formation of oxygen vacancy decreases the coordination numbers of neighboring cations. Basically, taking
, the authors6 adopted another approach – it was assumed that the formation of oxygen vacancy decreases the coordination numbers of neighboring cations. Basically, taking 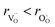 and assuming the CN of cations to be nonstoichiometry-dependent are two somewhat equivalent72 ways of describing the same phenomenon – the crystal lattice relaxation around the oxygen vacancy. However, the latter way was regarded as beneficial because it contains no arbitrary parameters such as
and assuming the CN of cations to be nonstoichiometry-dependent are two somewhat equivalent72 ways of describing the same phenomenon – the crystal lattice relaxation around the oxygen vacancy. However, the latter way was regarded as beneficial because it contains no arbitrary parameters such as 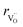 .
.
Within the framework of the modified model,6 the cation coordination numbers in ABO3–δ perovskites depend on oxygen nonstoichiometry as
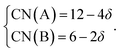 | (35) |
If, as a first approximation, the cation radii decrease linearly with CN, then
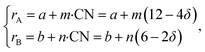 | (36) |
4. Atomistic insights
Modern computational methods such as molecular dynamics (MD) or density functional theory approach (DFT) allow the unit cell parameters that are more or less close to the experimental ones to be calculated, at least for CeO2.88,162 However, the magnitude of chemical strain has proven to be trickier to calculate accurately. But, most importantly, these methods allow semiquantitative insights into the mechanisms of this phenomenon, which is usually hard to acquire from the empirical knowledge only.To simulate the chemical expansion with MD, some oxygen ions should be removed and the required number of cations (e.g., Ce4+) replaced by those with a lower oxidation state (e.g., Ce3+). While in real experiments these events, accompanied by the cation radius change, occur simultaneously and cannot be decoupled, it is possible to do so in MD simulations. By varying the short range repulsion terms of interatomic potential so as to make the Ce3+ size equal to that of Ce4+, Marrocchelli et al.12 calculated the effects of creating oxygen vacancies in such “equal-radii” supercells. The removal of the oxygen ion eliminates the electrostatic screening, causing the relaxation of cations away from the vacancy and more prominent shifting of anions towards it, resulting in net crystal lattice contraction. In other words, an effective oxygen vacancy size in ceria is less than that of an oxygen ion. Similar results were obtained for substituted ceria and zirconia12 as well as for some other fluorite oxides,21 for which, in addition, a nonmonotonic dependence of rV on the host cation radius, rhost, with a maximum at rhost ≅ rCe4+ was found.21 Thus, MD results confirmed the chemical expansion mechanism that follows from the purely empirical Hong and Virkar's model.72
Ab initio DFT and equal-radii MD computations of Marrocchelli et al.32 as well as DFT results of Jedvik et al.70 paint the same picture of lattice relaxation around the oxygen vacancy as described above for another structural type of oxide – perovskites. Aidhy et al.33 using the DFT approach demonstrated that charged oxygen vacancies cause lattice expansion for oxides with pyrochlore and rock-salt structures as well. However, in case of different structures even the qualitative results seem to be less unanimous than for the fluorites: for some perovskites (SrTi1–xGaxO3 and La1–xSrxGa0.8Mg0.2O3–δ) DFT predicted rV ≥ rO – expansion upon anion vacancy formation.32 In addition, by computing the defect-induced strain tensors, several studies found the oxygen vacancy in perovskites to be anisotropic, its shape being more correctly described by an ellipsoid.70,163 Nonetheless, while the DFT method showed lattice contraction when 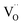 in BaZrO3 is created,64,70 atomistic simulations of BaZrO3 and SrTiO3 using shell-potential models revealed that, when averaged over all possible orientations of the defect within the crystal, the total volumetric effect from the
in BaZrO3 is created,64,70 atomistic simulations of BaZrO3 and SrTiO3 using shell-potential models revealed that, when averaged over all possible orientations of the defect within the crystal, the total volumetric effect from the 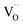 creation is negligible, i.e. βV ≈ 0.70,163,164
creation is negligible, i.e. βV ≈ 0.70,163,164
As for the quantitative results, different models and sets of interatomic potentials used in MD calculate different total chemical expansion coefficients. For example, for undoped ceria, the dipole polarizable ion model (DIPPIM)12,165 yielded β = 0.061 at 1000 °C, very close to the β = 0.061 experimentally determined by Hull et al.11 However, larger β values can be obtained from the experimental data of others: from 0.073 (δ = 0.12–0.18 in CeO2–δ)92 to 0.092 (δ = 0.02–0.20)82 and 0.101 (δ = 0.12–0.18),92 depending on the nonstoichiometry range. These β values are much closer to those computed with the shell model: 0.075, 0.081 or 0.091 for different potential sets.162 Different methods are also known to yield different results: for A- and B-site substituted LaGaO3, MD visibly underestimates and DFT overestimates the experimentally measured relative expansion.32 Marrocchelli et al.32 believe it to be due to the small magnitude of the chemical strain value, calculated from the difference between the computed unit cell parameters, as the absolute crystal lattice parameters themselves exhibited much better agreement with the measurement results.32 In this respect, an ab initio approach to calculating the chemical expansion coefficient via elastic dipole tensors, omitting the need for optimizing the lattice constants at each defect concentration, may be beneficial.88,91
Empirical models indicate that in order for chemical expansion to take place due to cation radius change, the charge carriers should be localized. The same conclusion can be reached using ab initio methods. As standard DFT functionals do not describe adequately the localized nature of f-electrons for Ce cations, the DFT + U approach is used to overcome this deficiency.12,66,166 By varying the Hubbard term U, Marrocchelli et al.166 demonstrated the strong dependence of β on the U value (or the degree of localization), while for the computed β to approach the experimental values, a very high degree of electron localization was required for both fluorites and perovskites (CeO2–δ and BaCeO3–δ, respectively). Based on such conclusions, Perry et al.111 explained the lower-than-expected chemical expansion of La0.9Sr0.1Ga1–xNixO3–δ by increased charge delocalization. In a similar way, the magnitude of chemical expansion of barium oxyhydride, BaTiO3–xHx, was found to be more consistent with the delocalized electron model, which was also supported by the electrical conductivity and inelastic neutron scattering results.167
However, the influence of charge localization on chemical expansion of perovskites seems to be rather more complex. As was demonstrated recently by Marthinsen et al.,168 depending on the electrostatic screening of oxygen vacancies, determined by the nature of B-site cations, chemical expansion in some perovskites may even be reduced by an increase in the Hubbard U term.
The importance of the defect charge was also highlighted by Aschauer and Spaldin,169 whose DFT calculations allowed them to conclude that altering the defect charge state could be used purposefully to control the thin film geometry via chemical expansion by using the field effect, selectively adding or removing the charge carriers. This is an alternative to the more “obvious” chemo-mechanical actuation through defect concentration control by, for example, direct electrochemical oxygen pumping.170
Computational methods have been actively employed to elucidate the possible magnitude and nature of defect-induced stresses in thin films and at surfaces.171–176 For example, the recent ab initio calculations showed that tensile or compressive strain stabilizes oxygen vacancies at complex oxide interfaces.171 This was explained by the chemical expansion due to the defect formation relieving the stress,172 and is closely related to the anisotropic – in directions parallel and normal to the interface – chemical strain observed with in situ TEM, scanning transmission electron microscopy (STEM), electron energy loss spectroscopy (EELS) and optical strain measurements in Ce1–xPrxO2–δ thin films on a YSZ substrate.172,173 The anisotropic character of chemical expansion was also found in perovskite-based epitaxial thin films using XRD.174 Both experimental and computational studies175,176 showed that the nature of the substrate determines the presence of compressive or tensile in-plane strain in perovskite La1–xSrxCoO3−δ films, which impacts the oxygen vacancy concentration therein, influencing such properties as the oxygen evolution reaction (OER) activity,175 oxygen surface exchange and diffusion.176
Due to the promise of higher efficiency of proton-conducting SOFCs, hydration-induced expansion became the focus of multiple studies, including the computational ones.34,64,66,70 Similar to the oxide expansion upon oxygen loss that resulted from the crystal lattice shrinkage due to 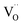 creation and expansion due to the cation reduction, two factors cause the chemical strain upon hydration. In the water sorption process, eqn (34), the decrease in size
creation and expansion due to the cation reduction, two factors cause the chemical strain upon hydration. In the water sorption process, eqn (34), the decrease in size 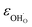 occurs when
occurs when 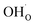 defects replace
defects replace 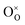 , and the more pronounced increase,
, and the more pronounced increase, 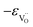 , follows from
, follows from 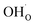 in place of
in place of 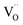 :34,64,70
:34,64,70
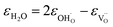 | (37) |
As was pointed out in our previous work,6 DFT-evaluated chemical expansion coefficient values for cerates and zirconates (Ba,Sr)(Zr,Ce)1–y(Y,In,Sc,Ga)yO3–δ tend to vary significantly even within one study depending on calculation conditions – the size of the supercell,70 proton defect trapping,70 relative positions of dopant ions and defects inside the supercell66,177 or temperature.34 Note that the importance of the point defect placement for correct DFT + U simulation of mixed-valence materials had been pointed out earlier using reduced ceria as an example.89 The temperature factor was investigated in detail by Løken et al.,34 who found that not only do both individual contributions from 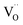 or
or 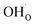 to the chemical expansion and the total chemical strain depend on temperature, but also that the thermal expansion coefficient depends on the presence of defects. This computational evidence34 in favor of cross-influences of thermal and chemical expansion is in line with the results of modulated temperature dilatometric measurements,178 showing that a lower TEC is characteristic of a more defect-rich crystal lattice of SrTiO3 or SrZrO3. However, in another dilatometric study an opposite trend was found for the TEC of SrFe0.35Sn0.65O3–δ,179 which indicates the strong dependence of TEC vs. defect concentration behavior on the oxide composition or crystal structure, or possibly both.
to the chemical expansion and the total chemical strain depend on temperature, but also that the thermal expansion coefficient depends on the presence of defects. This computational evidence34 in favor of cross-influences of thermal and chemical expansion is in line with the results of modulated temperature dilatometric measurements,178 showing that a lower TEC is characteristic of a more defect-rich crystal lattice of SrTiO3 or SrZrO3. However, in another dilatometric study an opposite trend was found for the TEC of SrFe0.35Sn0.65O3–δ,179 which indicates the strong dependence of TEC vs. defect concentration behavior on the oxide composition or crystal structure, or possibly both.
5. Some peculiarities and trends in the chemical expansion of oxides
5.1. Fluorites
Unfortunately, while the experimental εchem(δ) data are available in the literature for a number of (Pr, Tb, Y, Sm, Zr)-substituted ceria, their description and analysis are often much less thorough than those performed for CexGd1–xO2–δ as described above. However, let us briefly summarize the main observations available in the current literature. The values of chemical expansion coefficients for some undoped and doped ceria are presented in the ESI (Table S1†).Due to the higher reducibility of Pr4+ ions as compared with Ce4+, chemical expansion of Pr-substituted CeO2, Ce1–xPrxO2–δ and Ce0.8PrxTb0.2–xO2–δ can be observed at high T even at ambient oxygen partial pressure (0.21 atm)85,90,180 in contrast to pure ceria which requires a strongly reducing atmosphere.82,84 Similar behavior is also typical of fluorite oxides substituted with redox active 3d-metal cations, e.g., Mn-substituted YSZ.181 For Ce1–xPrxO2–δ no vacancy clustering was detected, and their defect structure can be adequately described by an oxygen exchange reaction
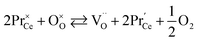 | (38) |
Chemical expansion of Ce1–xRxO2–δ (R = Y, Sm; x = 0.1–0.2) is almost temperature-independent at 700–1000 °C,182 and, in addition, is nearly linear within the wide δ ranges. The chemical expansion coefficient, β, is almost independent of the concentration of Sm in Ce1–xSmxO2–δ and decreases with x for Ce1–xYxO2–δ, while the β values of Ce0.9Y0.1O2–δ and Ce0.9Sm0.1O2–δ are almost equal.182,183
Substitution of Zr for Ce decreases the reduction enthalpy of Ce1–xZrxO2–δ leading to more facile oxygen exchange at higher pO2.184 Because Zr4+ ions are smaller than Ce4+, it is believed that they distort the crystal lattice so as to make the formation of smaller oxygen vacancies near Zr sites, which lowers the effective CN of Zr4+, energetically favorable.86 Unlike most substituted ceria, Ce0.8Zr0.2O2–δ possesses β that increases with δ and exhibits nonlinear temperature dependence.87 The chemical expansion coefficient of ceria with high Zr concentrations (Ce0.5Zr0.5O2–δ and Ce0.5Zr0.4Pr0.1O2–δ) is almost twice as low as that of Ce0.9Gd0.1O2–δ and Ce0.9Pr0.1O2–δ and does not depend on T or δ.
5.2. Cubic or ‘quasicubic’ (distorted) perovskites
The usage of substituted lanthanum chromites as SOFC interconnect materials led to their chemical expansion being investigated.114,115 Armstrong et al.114 suggested that both Coulomb repulsion between Cr cations and ≈13% growth in Cr ion size contributed to the chemical expansion upon reduction, the latter having a major effect. The average chromium oxidation state strongly influences the unit cell parameters of the chromites, which is why introducing an acceptor dopant (Sr or Ca) into La1–x(Sr,Ca)xCrO3–δ leads to a linear unit cell volume decrease.114,115 The increase in x in La1–xMxCrO3–δ (M = Sr, Ca) increases the chemical expansion of these oxides because of the growth in the fraction of “reducible” Cr4+ ions (see ESI Table S2†).114,115,185,186 Likewise, some B-site dopants affect the chemical strain of La1–xMxCrO3–δ (M = Sr, Ca) in accordance with their oxidation numbers: isovalent dopants (e.g. Al3+) hardly change it while those with higher valences (e.g. Ti4+) tend to decrease it.114,115 Cerium ions, being substituted for La in La1–xCaxCrO3–δ, cause εchem to be temperature-dependent because of the shifting Ce3+ + Cr4+ ⇄ Ce4+ + Cr3+ equilibrium.185 Somehow counterintuitively, despite having to increase the Cr4+ fraction, introducing Mg into LaCr1–xMgxO3–δ decreases εchem = Δa/a0, which is thought to be due to the large size of Mg2+ expanding the unit cell, i.e. increasing the value of a0.115Substituted lanthanum chromites exhibit oxygen exchange only at sufficiently low pO2 (pO2 < 10−8 atm at 1000 °C).114,119,120 In contrast, La1–xSrxMnO3±δ where oxygen excess (3 ± δ > 3) in the crystal lattice can be realized tend to release or take up O2 at higher pO2 as well, having plateaus on δ(log(pO2)) dependences between oxygen-excess and oxygen-deficient regions.117,122,187–189 These two regions differ significantly in the defect chemistry: the oxygen adsorbed by the oxide fills the oxygen vacancies at 3 ± δ < 3,
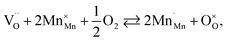 | (39) |
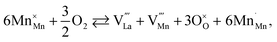 | (40) |
For LaMnO3±δ with 3 ± δ > 3, despite prolonged relaxation times and noticeable creep, dilatometric experiments showed visible sample expansion,188 but XRD showed unit cell volume contraction189 with increasing pO2. As shown in Fig. 5, the value of β for the oxygen-excess LaMnO3±δ (0.0476–0.056 (ref. 189)) is almost twice as high as that for the oxygen-deficient one (0.024 (ref. 116)). Similar observations were made for strontium-substituted manganites La1–xSrxMnO3±δ.109 The seeming contradiction between dilatometric and XRD results188,189 could be explained by the expansion of the crystal lattice due to the Schottky reaction (eqn (40)) being stronger than its contraction due to the Mn3+ oxidation. In other words, the expansion of the oxide bulk due to eqn (40) as measured by dilatometry should be greater than the average unit cell parameter increase detected by XRD.
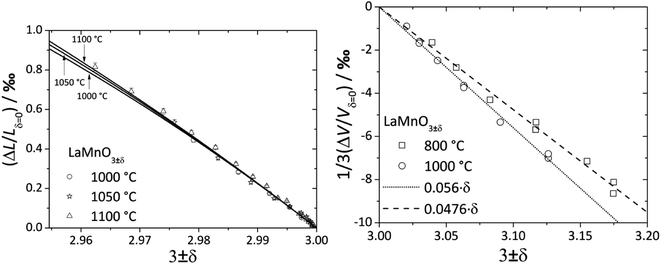 | ||
| Fig. 5 Chemical expansion of LaMnO3±δ with 3 ± δ < 3 (ref. 122) and 3 ± δ > 3:189 solid lines – model calculations,122 dashed lines – linear fit. | ||
The discrepancies between the defect structure models used for La1–xSrxM1–yByO3–δ (M = Co, Ni, Fe; B = Co, Ni, Fe; M ≠ B) are primarily related to the issue of charge localization. In some models, such as the “itinerant electron” or Lankhorst model,191–194 it is supposed that most electrons are located within the conduction band. While these models typically describe experimental δ = f(pO2) dependences as well as those with localized charge carriers,195–197 for chemical expansion to occur, cation reduction ought to take place,10,32,118 so most, if not all, electrons and holes should be localized. Thus, the models where the oxygen release from the crystal lattice of La1–xSrxM1–yByO3–δ is represented by the following process
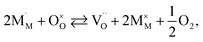 | (41) |
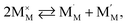 | (42) |
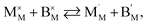 | (43) |
 and
and  are localized holes and electrons, respectively, received more attention in papers dealing with chemical expansion.94,108,121,195–201 If two different cations that are able to change their oxidation state, e.g. Cr, Mn, Fe, Co, or Ni, occupy the B-sublattice of La1–xSrxM1–yByO3–δ, and the fraction of one of them is significantly greater, eqn (42) can be used in the defect structure model along with either fixing the oxidation state of the other one200 or assuming M and B ions to be indistinguishable within the model's framework.134,199 In case the M and B concentrations are close, the model usually incorporates eqn (43) taking into account the respective electronegativities of B and M, e.g. M = Co if B = Ni or M = Fe if B = Co, because χFe = 1.64, χCo = 1.70 and χNi = 1.75.195,202
are localized holes and electrons, respectively, received more attention in papers dealing with chemical expansion.94,108,121,195–201 If two different cations that are able to change their oxidation state, e.g. Cr, Mn, Fe, Co, or Ni, occupy the B-sublattice of La1–xSrxM1–yByO3–δ, and the fraction of one of them is significantly greater, eqn (42) can be used in the defect structure model along with either fixing the oxidation state of the other one200 or assuming M and B ions to be indistinguishable within the model's framework.134,199 In case the M and B concentrations are close, the model usually incorporates eqn (43) taking into account the respective electronegativities of B and M, e.g. M = Co if B = Ni or M = Fe if B = Co, because χFe = 1.64, χCo = 1.70 and χNi = 1.75.195,202
Many of La1–xSrxM1–yByO3–δ and Ba1–xSrxCo1–yFeyO3–δ oxides release oxygen upon heating even at high oxygen partial pressures, e.g. in air. Therefore, characteristic chemical-expansion-related deviations from near linear trends are observed in high-temperature regions of dilatometric curves ε = f(T) of these oxides.118,203–208 An assumption that both thermal and chemical expansion coefficients are temperature-independent, ε(T,δ) = εchem(δ) + εtherm(T) = αΔT + βΔδ, allows β to be estimated from total expansion, i.e. the dilatometric ε(T,δ) curves. The value of α can be determined from the low-temperature ε(T,δ) region where no oxygen exchange occurs, and δ(T) can be measured with thermogravimetric analysis (TGA).23,118,203,209
The nonlinearity of εchem(δ) for (La1–xSrx)0.99Co1–yNiyO3–δ and La1–xSrxCoO3–δ, which was described118,203 by the equation β = β1 + β2δ, is quite small and can be neglected within a relatively narrow δ range, e.g. when εchem at one temperature is considered. In contrast, the temperature dependences of β for these oxides, shown in Fig. 6, are more pronounced. A gradual increase in the fraction of HS Co3+ with temperature was assumed to be the likely reason behind such dependences.17,18,133,134 An increase in β with T was also observed for La0.5Sr0.5Fe0.5Co0.5O3–δ,206 La0.1Sr0.9Fe0.2Co0.8O3–δ (ref. 134) and some ferrites, such as La0.3Sr0.7Fe0.6Ga0.4O3–δ,204 La0.3Sr0.7FeO3–δ,204 SrTi0.65Fe0.35O3–δ,112 and La0.2Sr0.8Fe0.55Ti0.45O3–δ.201 Some evidence exists for the possibility of Fe3+(LS) → Fe3+(HS) transition in perovskites at elevated temperatures,210 so this,112,135 along with some degree of charge delocalization, changes in B-site coordination and subtle crystal symmetry changes112 might also be responsible for the temperature-dependent chemical expansion of iron-containing perovskites. Interestingly, inverse trends – lower β at higher T – were reported for Ba0.5Sr0.5Co0.8Fe0.2O3–δ (ref. 205, 207, 211 and 212) and SrCo0.8Fe0.2O3−δ,212 and the reason behind this is yet unclear.
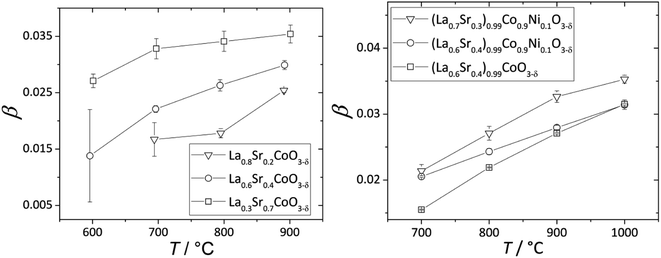 | ||
| Fig. 6 Temperature dependences of β for La1–xSrxCoO3–δ (ref. 118) and (La1–xSrx)0.99Co1–yNiyO3–δ.203 | ||
Some other trends in β of La1–xSrxCo1–yFeyO3–δ and La1–xSrxCo1–yNiyO3–δ can be tentatively established (see also Table S3 in the ESI†). For instance, substituting Sr for La increases β of La1–xSrxCoO3–δ,118,121 La1–xSrxFe0.2Co0.8O3–δ (ref. 134, 198 and 199) and (La1–xSrx)0.99Co1–yNiyO3–δ (ref. 203) (see Fig. 6). The slight A-sublattice substoichiometry and up to 10% substitution of Ni for Co in the B sublattice hardly change β.118,203 At the same time, for La0.6Sr0.4Fe1–xCoxO3–δ oxides no obvious relationship between the B-sublattice composition and chemical expansion coefficient can be observed.198,213,214 This may be because the temperature dependence of β, which may be strong and also composition-dependent for these oxides, was not taken into account in the respective studies.198,213,214
For some La1–xSrxFeO3–δ, existing chemical expansion data are contradictory: for example, β reported for La0.5Sr0.5FeO3–δ (ref. 20 and 215) and La0.6Sr0.4FeO3–δ (ref. 198 and 216) in separate papers differs almost by a factor of two. Nonetheless, it can be said that, similarly to La1–xSrxCoO3–δ,118 the chemical expansion coefficient of La1–xSrxFeO3–δ tends to increase with Sr content.13,19,20,198,204,215,216 In fact, alkaline earth metal ferrites such as SrFeO3–δ (ref. 13) (and also Ba0.95La0.05FeO3–δ (ref. 217)) demonstrate chemical expansion that is among the highest for all perovskite-like oxides (see ESI Tables S2 and S3†). As was noted above, such high εchem may be caused by the oxygen vacancy ordering in these highly nonstoichiometric oxides.13,19,20,108,143 In addition, and in support of the assertion that it is high nonstoichiometry that causes elevated chemical expansion, visibly nonlinear εchem with β increasing at higher δ was observed on both isotropic and anisotropic εchem(δ) dependences for La1–xSrxFeO3–δ (x = 0.2–0.5).19,20,108
B-site substitution with ions that do not change their oxidation state, such as Al or Ga, causes different chemical expansion changes in different ferrite perovskites. For example, β of La0.8Sr0.2Fe0.7Ga0.3O3–δ is greater than that of La0.8Sr0.2FeO3–δ,19,218 while replacing Fe in SrFeO3–δ with Al (or Ti) leads to the opposite effect of decreasing β;13,112,219 in both cases the high-temperature crystal lattice symmetry after the substitution remained practically unchanged.13,112,215,218,219 Though they have lower chemical expansion than SrFeO3–δ, SrFe1–xTixO3–δ oxides, which have been extensively studied lately as promising cobalt-free mixed ion–electron conductors (MIECs),220 still possess fairly high β, above that of most La1–xSrxCo1–yFeyO3–δ.112,201 As compared with SrFe0.35Ti0.65O3–δ, SrFe0.35Sn0.65O3–δ is characterized by lower chemical expansion coefficient values, and the opposite trends in both TEC and β: the TEC of SrFe0.35Sn0.65O3–δ decreases with δ, and β decreases with temperature.112,179 This is believed to be due to the asymmetric (close to tetragonal) crystal structure of SrFe0.35Sn0.65O3–δ as compared with the almost cubic SrFe0.35Ti0.65O3–δ.179
Based on the TG and dilatometric studies into Nd1−xSrxFe0.7Co0.3O3−δ (ref. 221) and Nd1−xSrxFeO3–δ,222 similarly to La0.6Sr0.4Fe1–xCoxO3–δ,114,130,131 no apparent influence of Co substitution on β can be stated. It can also be concluded that, on average, β of Nd1−xSrxFe0.7Co0.3O3−δ (ref. 221) and Nd1−xSrxFeO3–δ (ref. 222) is greater than that of their La-containing analogs. However, the data on chemical expansion of R1–xSrxCo1–yFeyO3–δ where R is a rare-earth metal other than La are rather scarce, so the influence of the nature of the A-site rare earth ion on εchem remains largely speculative.
5.3. Double perovskites
In contrast to simple perovskites, for which the deviations from cubic symmetry are caused by slight twists and distortions of the oxygen octahedra,223,224 the tetragonal (and orthorhombic) symmetry of double perovskites is due to cation ordering.225 For that reason, strong anisotropy of chemical expansion is typical of many double perovskites. Among the A-site ordered layered double perovskites, chemical expansion studies were primarily focused on RBaM2O6–δ (M = Co, Fe).31,123,144,148,149,226–238 Although the literature data are mostly rather scattered (see Table S4 in the ESI†), some common trends can nevertheless be established.As mentioned in Section 3.2.1, tetragonal RBaM2O6–δ (M = Co, Fe) oxides tend to expand along the a axis (or in the ab plane) with the decrease in δ, which is most probably because of the increase in 3d metal cation radii upon their reduction.148,149 Along the c axis, both the chemical strain εchem(c) and chemical expansion coefficient βc are negative. It is known that oxygen vacancies in these double perovskites form predominantly at O3 sites, i.e. within the rare-earth layers.239–242 Hence, simultaneous contraction of the unit cell along the c axis, in the direction normal to the R3+ and Ba2+ cation layers, can be qualitatively explained by the shifting of nearby ions (Co1 or Fe1 and O2) in the direction of RO planes.148,149 This may also be responsible for the composition-dependent βc observed for RBaFe2O6–δ (R = Pr, Nd, Sm, Eu, Gd), shown in Fig. 7. A decrease in the R3+ effective radius should lower the electrostatic repulsion, allowing the nearby ions to shift farther towards the RO layers when they are filled with oxygen vacancies, thus making βc higher for RBaFe2O6–δ with smaller R.226–232 At the same time, βa coefficients for all RBaFe2O6–δ (R = Pr, Nd, Sm, Eu, Gd) are much closer to each other than βc, only slightly growing with the R3+ radius (see ESI Table S4†).
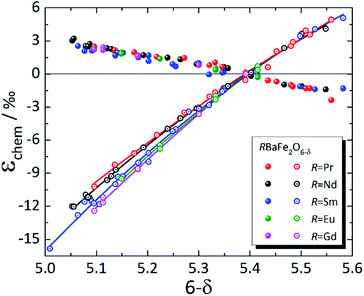 | ||
| Fig. 7 Chemical strain of RBaFe2O6–δ (R = Pr,226 Nd,227,228 Sm,228–230 Eu,231 Gd232), measured at T up to 47 °C. Filled symbols – εchem(a); empty symbols – εchem(c); lines are given to guide the eye only. | ||
On average, chemical expansion of the unit cell parameter a for both layered double cobaltites31,123,144,148,149,233–235 and ferrites226–232 RBaM2O6–δ (M = Co, Fe) is quite similar, which is somehow expected due to the equal difference between the “reducible” ion radii (at least in their HS states): r(Co3+) − r(Co2+) = r(Fe3+) − r(Fe2+).81 One clear exception is LaBaCo2O6–δ,236–238 for which both expansion of a and contraction of c are higher than for the other RBaCo2O6–δ (R = Pr, Nd, Gd).31,123,144,148,149,233–235 Bernuy-Lopez et al.236 even claimed the expansion of LaBaCo2O6–δ along the c axis, but their data are inconsistent across the plots presented in the article, and neither their nonstoichiometry values nor crystallographic data are supported by other studies.243–245
The values of βc, however, are several times greater (by absolute value) for RBaFe2O6–δ (ref. 226–232) than for RBaCo2O6–δ (see Table S4 in the ESI†).31,123,144,148,149,233–238 However, in contrast to RBaCo2O6–δ, where the expansion data were mostly collected at high temperatures,31,123,144,148,149,233–238 the chemical expansion of RBaFe2O6–δ (ref. 226–232) (see Fig. 7) refers to the quenched samples and was measured near room temperature. Under these conditions strongly anisotropic magnetic ordering is known to arise in RBaFe2O6–δ: for example, iron in its mixed-valent state in TbBaFe2O5 exhibits antiferromagnetic superexchange coupling through oxygen ion and ferromagnetic coupling – through oxygen vacancies across the Tb layer, while the bulk of the material remains antiferromagnetic.246 In addition, mixed-valent iron is known to have a smaller volume than the corresponding average of the HS Fe2+ and Fe3+.232,247 This and the nonstoichiometry-dependent magnetic interactions along the c axis of these layered ferrites246 may be responsible for the large contraction of their unit cells in that direction.
As seen in Fig. 8, where the measurement results at similar temperatures are presented for RBaCo2O6–δ (R = Pr, Nd, Gd), βa ≈ −βc for these double perovskite cobaltites, and their chemical expansion is close, taking into account the scatter in the data.123,148,149 However, when all available experimental data for each of these oxides are considered,31,123,144,148,149,233–235 it is immediately seen (Fig. S1–S3 in the ESI†) that the εchem(δ) values do not often coincide well except for GdBaCo2O6–δ, for which the results of Mogni et al.,233 Tsvetkov et al.123 and Chatterjee et al.31 agree with each other in the overlapping δ ranges. The smaller βc of GdBaCo2O6–δ at δ < 0.5 (ref. 31) (see ESI Fig. S1†) is likely, at least in part, because in this range the oxygen loss leads predominantly to Co4+ → Co3+ reduction causing a smaller ionic radius change as compared to Co3+ → Co2+ at δ > 0.5.81 A similar change in the slope of εchem(δ) at δ ≈ 0.5 is seen in Fig. 7 as slight nonlinearities on the respective dependences for RBaFe2O6–δ (R = Pr, Nd, Sm, Eu, Gd).226–232
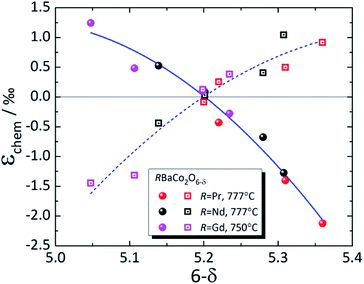 | ||
| Fig. 8 Chemical strain of RBaCo2O6–δ (R = Pr,149 Nd,148 Gd123). Filled symbols – εchem(a); empty symbols – εchem(c); lines are given to guide the eye only. | ||
The strong discrepancies between εchem(δ) of RBaCo2O6–δ (R = Pr, Nd) reported by Cox-Galhotra et al.148 and Szpunar et al.234 are probably due to several reasons. First of all, in the work of Szpunar et al.234 RBaCo2O6–δ (R = Pr, Nd) are orthorhombic in wide δ ranges (Δδ ≈ 0.5), which is in contrast to previous studies where orthorhombic symmetry, which is due to oxygen vacancy ordering, was found to be present only at δ close to 0.5.239 Then, the εchem(δ) therein234 was determined not from the isothermal experiment results, as in ref. 148 and 149, but from the temperature dependences of unit cell parameters by subtracting the low-temperature linear trend from the total ε values assuming temperature-independent TEC. In this respect, the volumetric chemical expansion of NdBaCo2O6–δ determined in a similar manner by Cherepanov et al.248 from the dilatometric experiments coincides with that measured by Szpunar et al.,234 but is visibly greater than that found by Cox-Galhotra et al.148 (see Fig. S4 in the ESI†). This may be accounted for by supposing that the TEC of NdBaCo2O6–δ actually increases with temperature, neglecting which would cause the calculated chemical expansion to be overestimated by the value of this increase.234,248
As opposed to RBaFe2O6–δ,226–232 both βa and βc of RBaFeCuO6–δ (R = Lu, Yb, Y, Eu, Sm, Nd, Pr) oxides are negligible (see also ESI Fig. S5†).249–251 The oxidation state of Cu2+ forces iron in RBaFeCuO6–δ to assume higher oxidation states at δ > 0.5 than in RBaFe2O6–δ. Hence, the oxygen release from RBaFeCuO6–δ is accompanied by Fe4+ → Fe3+ reduction, causing much lower ionic radius changes and much lower expansion.249,250 The absence of contraction of the unit cell parameter c with δ in RBaFeCuO6–δ (ref. 251) might be related to the crystal structure of these oxides, where corner-sharing strongly elongated CoO5 and already squashed FeO5 pyramids252 have little opportunity to shift towards oxygen-depleted rare-earth layers.
Kudyakova et al.147 reported that substituting Mn for Fe in PrBaFe2O6–δ results in a pronounced decrease in βc measured at room temperature, down to almost zero for PrBaMn2O6–δ, while βa of both PrBaFeMnO6–δ and PrBaMn2O6–δ are almost equal and more than two times greater than that of PrBaFe2O6–δ (see ESI Fig. S5 and Table S4†). Tomkiewicz et al.,253 on the other hand, found with in situ neutron diffraction that both a and c parameters of PrBaMn2O6–δ increase upon reduction; unfortunately, there is not yet enough data to speculate whether such discrepancy between two studies147,253 is caused by different temperature and nonstoichiometry ranges (see Table S4 in the ESI†) or something else.
5.4. Oxides with a Ruddlesden–Popper structure
The crystal structure of layered Ruddlesden–Popper oxides An+1BnO3n+1 may be represented as alteration of n successive perovskite ABO3 layers with one rock-salt AO layer. The most well-studied compounds in this family of oxides are those with n = 1 possessing a K2NiF4 structure (space group I4/mmm). These oxides can accumulate interstitial oxygen in the rock-salt layers254 and oxygen vacancies – in the perovskite ones,255 attaining oxygen excess (4 + δ) or deficiency (4 − δ), respectively.The oxygen-excess La2–xSrxNiO4+δ,256–258 La2(Ni0.9M0.1)O4+δ (M = Fe, Co, Cu)254,258 and Nd2–xSrxNiO4+δ (ref. 259) expand in the ab plane upon oxygen loss because of the nickel cation reduction. This is accompanied by a significant decrease of the unit cell parameter c, which may be related to the weakening of electrostatic repulsion between ions as interstitial oxygen leaves the crystal lattice.256 As a result, as for many double perovskites,31,123,144,148,149,226–235 the volumetric chemical expansion of Ruddlesden–Popper oxides is almost zero or even negative:10,254,256,257,259 for example, for La2NiO4+δ, βa = −0.028, βc = 0.076, and β = 0.002.10,256 Substitution of small amounts of Fe, Co or Cu for Ni in La2NiO4+δ increases, by an absolute value, its chemical strain along the a axis, while βc remains almost unchanged.254
Similar to that of substituted La2NiO4+δ (ref. 254 and 256–258) chemical strain behavior – expansion of a and contraction of c unit cell parameters upon reduction – was also found in Sr3Fe2O7–δ and Sr3Fe1.9Mo0.1O7–δ;255,260 the molybdenum-doped sample was characterized by lower thermal and chemical expansion.255
In contrast to Sr3Fe2O7–δ, both a and c parameters of Sr3FeCoO7–δ increased with δ (βc > βa > 0), which was believed260 to be due to the charge delocalization in Sr3FeCoO7–δ that decreased the electrostatic interactions, potentially responsible for the contraction along the c axis. Oxygen-deficient (R2–xSrx)0.98(Fe0.8Co0.2)1–yMgyO4–δ (R = La, Pr) also exhibit expansion upon reduction along the a and c axes;261 in this case, the fact that βc > βa was explained by the nearby rock-salt layers effectively limiting the ability of the perovskite layers to expand within the ab plane.261 The volumetric chemical expansion of these (R2–xSrx)0.98(Fe0.8Co0.2)1–yMgyO4–δ is much lower than that of the simple perovskites with similar composition, such as La0.6Sr0.4Fe0.8Co0.2O3−δ.262
6. Some consequences of chemical expansion and its possible practical applications
The most straightforward consequence of excessive chemical strain, similar to unwanted thermal expansion, is the mechanical failure of ceramic materials and devices. Various examples of this, some of which are quite graphic, can be readily found in the literature.9,24,47,49,263–266 For example, Fig. 9a and b show the microcracks occurring in lithium-ion battery cathodes,25 and Fig. 9c demonstrates the pinhole and crack formation in the ceria-based SOFC electrolyte, caused by the reduction-induced chemical expansion of ceria.24 In the latter case, dynamic load conditions, resulting in varying oxygen partial pressure gradients, were found to exacerbate the SOFC degradation.24 | ||
| Fig. 9 Failure of electrochemical devices due to chemical expansion. (a and b) Cross-sectional SEM images of the Li1−δ[Ni0.6Co0.2Mn0.2]O2 (a) and Li1−δ[Ni0.8Co0.1Mn0.1]O2 (b) cathodes in the fully charged state; reprinted with permission from H.-H. Ryu, K.-J. Park, C. S. Yoon and Y.-K. Sun, Chem. Mater., 2018, 30, 1155–1163. © 2018 American Chemical Society.25 (c) Post-mortem analysis of the SOFC (NiO–Nd0.1Ce0.9O2−δ composite anode, Nd0.1Ce0.9O2−δ electrolyte, NdBa0.5Sr0.5Co1.5Fe0.5O5+δ cathode) under constant current (0.2 A cm−2) and load cycle (0.2–0.12 A cm−2) conditions at 650 °C; reprinted from Y.-D. Kim, J. Yang, J.-I. Lee, M. Saqib, J.-S. Shin, K. Park, M. Jo, S.-J. Song and J.-Y. Park, Degradation studies of ceria-based solid oxide fuel cells at intermediate temperature under various load conditions, J. Power Sources, 452, 227758, © 2020, with permission from Elsevier.24 | ||
The fact that chemical strain can lead to mechanical failure is particularly well known in the field of solid-state battery development, since many widely employed Li-ion conducting materials experience large chemical expansion—up to several percents—upon lithiation/delithiation.47,49,60,265,267–269 This is also superimposed on the complex phase behavior of Li-conductors depending on lithium concentration,60,265,267,268,270 formation of dendrites,47,49,271etc. Therefore, to minimize the unwanted chemical stress effects, the components and microstructure of solid-state batteries need to be optimized with respect to chemical expansion.47,60,263,272 To achieve the necessary degree of optimization, several important aspects should be taken into account, among which are the compressibility of the battery components, the extent of pore filling due to volume changes, the morphology of the electrodes, etc.48,60,263 A very good example of this kind of optimization was shown by Koerver et al.60 where the authors combined two compounds with negative and positive chemical expansion to obtain an active electrode material with almost no chemical strain.
Unfortunately, this elegant method of avoiding chemical strain seems to be completely inapplicable in case of oxide materials for SOFCs since oxygen release, i.e. reduction, never leads to significant volume contraction, at least for the known oxide materials. However, as discussed above, oxides with an anisotropic (for example, layered) crystal structure may possess negative chemical lattice strain along some selected crystallographic directions.31,123,144,148,149,226–235,256–258 This decreases the overall volume chemical expansion compared to similar isotropic oxide materials. Therefore, it is logical to assume that in some materials with an appropriately selected crystal structure and chemical composition, ideal compensation of chemical expansion and contraction, occurring simultaneously in different crystallographic directions, can be achieved. Kharton et al.255 reported that this may indeed be observed, at least in the particular range of temperatures and oxygen partial pressures, in the case of Sr3Fe2−xMoxO7−δ oxides showing almost zero volumetric chemical expansion. Hence, controlling the lattice anisotropy through variation of an oxide's chemical composition and crystal structure can be viewed as an effective way of engineering chemical expansion. In this respect, layered oxides belonging to Ruddlesden–Popper, Dion–Jacobson and other homologous series, relatively unexplored from the viewpoint of chemical expansion, offer great structural and defect chemical flexibility and seem to be good model objects for further study of chemical strain phenomena.
Although, as mentioned above, chemical expansion is usually considered as a drawback leading to many problems when designing solid state electrochemical devices, in some cases, it can be beneficial. For example, many perovskite-like SOFC materials are known to suffer from alkaline earth metal (Sr or Ba) segregation on their surface, which negatively impacts their electrochemical performance. Both experimental and computational data indicate that at least for some of them introducing additional tensile strain suppresses the detrimental segregation.273 While applying external strain to a solid oxide electrochemical cell is impracticable, an effective internal strain can be created either at the synthesis stage, e.g., by isovalent B-site doping or A-site substoichiometry, or using operando techniques, by applying a cathodic bias (i.e. lowering the pO2). The latter increases the oxygen nonstoichiometry, which simultaneously shifts the respective equilibria away from the SrO segregation and causes chemical strain that works to the same effect.273,274 This opens the possibility of enhancing the stability of materials' interfaces by intentionally providing additional chemical-expansion-induced internal strain, while the undesirable side effects of chemical expansion, such as mechanical cracking, could be mitigated by other means, e.g., by creating composite materials.
While the abovementioned example of how materials could benefit from chemical strain can be viewed as a fortunate side effect, a few ways of using chemical expansivity directly for analytical and engineering purposes have been discovered recently (see Fig. 10). For instance, Swallow et al.170 demonstrated a proof of concept, shown in Fig. 10a, of how a “mechanical” part of mechano-electro-chemical coupling in nonstoichiometric oxides can be utilized. By applying bias voltages lower than 0.1 V (much less than would be necessary for similar piezoelectric actuators) to a Ce0.9Pr0.1O2−δ thin film grown on a YSZ substrate, i.e. by electrochemically pumping oxygen into or out of the film, they achieved nanometer-scale displacement (>0.1% strain) at 650 °C.173 Further developments of this approach275 resulted in a MEC actuator prototype capable of micrometer-scale displacement at room temperature.276 This actuator was made of a 150 nm thick Ce0.8Gd0.2O1.9 electrolyte membrane sandwiched between two 100 nm thick composite Ti/Ce0.8Gd0.2O1.9 electrodes, or working bodies, which provided mechanical action via their oxidation or reduction under the voltage applied.276
 | ||
| Fig. 10 (a) Illustration of the working principles of a thin film dynamic chemical expansion actuator: PCO – Ce0.9Pr0.1O2−δ, YSZ – yttria-stabilized zirconia. Adapted with permission from Springer Nature, J. G. Swallow, J. J. Kim, J. M. Maloney, D. Chen, J. F. Smith, S. R. Bishop, H. L. Tuller and K. J. Van Vliet, Dynamic chemical expansion of thin-film non-stoichiometric oxides at extreme temperatures, Nat. Mater., 2017, 16, 749–754, © 2017.170 (b) A prototype of the mechanical energy harvester: (left) schematic view of the device design. The compressed region is illustrated in red while the tensile region is illustrated in blue. Lithium ions migrating from the compressed plate to the tensile plate are shown with arrows. The electrolyte soaked separator is drawn in yellow. (right) An image of the actual device with a bending unit. Both scale bars indicate 1 cm. Reprinted from S. Kim, S. J. Choi, K. Zhao, H. Yang, G. Gobbi, S. Zhang and J. Li, Nat. Commun., 2016, 7, 10146.279 (c) Experimental apparatus for load-induced oxygen absorption measurements: 1 – oxide sample, 2 – sample holder, 3 – pushrod, 4 – YSZ electrolyte, 5 – Pt electrodes, 6 – typical pO2 signal before (τ < τ1) and after (τ1 < τ < τ2) applying the load, and after releasing the load (τ > τ2).280 (d) Electromechanical response of a battery material due to the correlation between Li-ion concentration and molar volume. (left) The scanning probe microscope tip is in contact with the sample surface (shown in layered LiCoO2 as an example). (right) Locally applied electrical fields result in Li-ion redistribution in the probed volume, which leads to surface displacements. PSD – position sensitive detector. Reproduced from S. V. Kalinin and N. Balke, Adv. Mater., 2010, 22, E193–E209, with permission from John Wiley and Sons, © 2010.28 (e) Overlay of electrochemical activity on the topography of the nanoparticles revealing the enhancement of activity along the triple-phase boundaries (TPB). ESM – electrochemical strain microscopy. This surface segment is around 270 × 270 nm in size. Reprinted with permission from Springer Nature, A. Kumar, F. Ciucci, A. N. Morozovska, S. V. Kalinin and S. Jesse, Measuring oxygen reduction/evolution reactions on the nanoscale, Nat. Chem., 2011, 3, 707–713, © 2011.291 | ||
A somewhat different example of room-temperature strain engineering was reported by Manca et al.,277 who adjusted the resonant frequency of WO3 microresonators by hydrogen gas intercalation into the WO3 crystal lattice. Thus, nonstoichiometric oxides with hydrogen- or oxygen-exchange-driven chemical strain capabilities could make a significant contribution to the emerging field of “straintronics”.278
Another interesting feature of materials prone to chemical lattice strain stems from its reversibility and reciprocity: whereas the change in chemical composition can cause mechanical strain, the reverse is also true, i.e. variation of chemical composition itself can be caused by applying external mechanical strain. Based on this phenomenon, Kim et al.279 developed a device for mechano-electro-chemical energy harvesting, shown in Fig. 10b. The device consists of an electrolyte layer placed between two identical electrodes. The EMF between them, driving Li+ ions from the compressed to the tensed electrode, is caused by the asymmetric stress applied to the device.279 Though, in fact, Li-alloyed Si electrodes were used in the original work,279 the working principle would be the same for oxide-based Li-conducting ones.
Likewise, the application of external mechanical strain to an oxide shifts its oxygen chemical potential and results in the readjustment of its equilibrium oxygen content. Some illustrative experiments in this respect were reported by Gerbshtein et al.,280 who applied the load to a bulk YBa2Cu3O6+δ sample under different external conditions (T, pO2). Fig. 10c shows a sketch of the setup as well as a typical pO2 sensor response curve. As seen, compression leads to a pO2 decrease due to the oxygen absorption by the sample, while the release of the load results in oxygen desorption, returning the whole system to the initial (mechanically unloaded) equilibrium state. The change of oxygen chemical potential per unit load as a function of oxygen content in YBa2Cu3O6+δ, obtained by Gerbshtein et al.,280 was found to correlate well with the thermodynamics of oxygen exchange and existence of phase transitions in this oxide, making this method an interesting, though somewhat exotic, analytical technique.
In thin films, misfit epitaxial strain may also play the role of an external mechanical load and, hence, can be employed to modify the oxygen content and related properties of the film. For example, Petrie et al.281 showed that controlling epitaxial strain in SrCoO3−δ thin films allows oxygen deficiencies in the cobaltite to be tailored from δ ≤ 0.1 to δ ∼ 0.25 in aqueous, highly oxidizing environments. These shifts in the oxygen content occur through modest amounts of tensile strain, around 1–4%, resulting in anion concentrations unattainable in the unstrained bulk material. In turn, the additional oxygen vacancies created through tensile strain enhance the catalytic activity of SrCoO3−δ toward the oxygen evolution reaction by over an order of magnitude, equaling that of precious-metal catalysts such as IrO2.281
The reverse is also true, i.e. chemical deformation due to targeted change of the oxygen content in the strained film can serve as a strain mediation mechanism.168,282–284 However, in case of thin films as compared to bulk samples the situation is complicated by anisotropic lattice distortions around oxygen vacancies inherent to many ABO3 perovskites.173,174 Elastic interactions of vacancy dipoles with an epitaxial misfit strain lead to preferential location of oxygen vacancies in a definite type of atomic plane and, as a result, may cause vacancy ordering, formation of new phases, or phase coexistence/separation.174 In turn, this may alter the charge transfer properties and cause many other side effects.173,174,285 To control them, the microscopic nature and elastic behavior of oxygen vacancies in epitaxial films should be thoroughly studied by both experimental and computational techniques.
On the nanoscale, chemical strain is used as a working principle of some modern microscopic techniques such as, for example, electrochemical strain microscopy (ESM).27,286–288 This is a scanning probe microscopy (SPM) related method, which is based on the detection of electrochemical strain associated with ionic movement during a local redox process induced by electrochemical polarization of the cantilever's tip. Fig. 10d demonstrates how such an electromechanical response originates.28 This allows direct study of redox reactions on the nanometer scale providing insights into both their kinetics and thermodynamics.286,289 The ESM technique was widely employed for investigation of both Li-ion28,286,290 and oxide-ion289,291 conducting materials. Fig. 10e shows, as an example, the results of mapping electrochemical activity near a triple-phase boundary on the platinum-nanoparticle-coated YSZ surface.291
7. Conclusions
Energy-related oxide materials are operated commonly at elevated temperatures in both oxidizing and reducing environments and undergo upon heating not only thermal expansion, but also chemical strain caused by a change in their oxygen content or by their hydration. This strain can be detrimental to the practical application of such materials; therefore, its understanding is a challenge critically affecting further progress in the development of energy conversion and storage devices. It explains why so many efforts regarding both experimental and theoretical studies of the chemical strain in the oxides were undertaken in the last few decades. Despite the great attention it has attracted, chemical strain remains far from being fully understood even for relatively simple – with respect to their crystal structure – fluorites and pseudocubic perovskites.To date, approaches available to explain the phenomenon of chemical strain are either based on computationally expensive methods with multiple arbitrarily variable parameters or limited to qualitative reasoning and empirical expressions. The latter are mostly evaluated on the basis of geometric assumptions and are, therefore, associated mainly with the crystal but not with the defect structure of oxides. Such a disregard for the defect structure when discussing chemical expansion leads to the empirical models being applicable only for a limited number of oxide materials. As a result, these models rarely allow the reasonably accurate values of chemical deformation to be predicted without carrying out the experimental measurements of chemical expansion itself. Furthermore, the relationship between the nature of the host and dopant cations and the effective radius of the oxygen vacancy has long been considered of importance for understanding the nature of chemical strain in oxides. However, to date, neither extensive computations nor empirical model analysis has led to any definite agreement regarding the size and shape of the oxygen vacancy and their variability across oxides with different structures and compositions. Meanwhile, an alternative approach to chemical strain modeling – using the oxygen nonstoichiometry dependence of cation coordination number instead of estimating the oxygen vacancy radius – remains underdeveloped.
Some other challenges may be summarized as follows. First of all, there is a strong need to understand the influence of the particularities of the oxide local structure on the chemical expansion. This includes the variation of coordination environments of ionic species, formation of defect clusters, nanodomains embedded in the matrix of the main phase, etc. For example, recent studies of ceria solid solutions97–104 show that all these aspects may significantly affect the behavior of the material including, of course, its chemical expansion. In this regard, it is clear that chemical strain should be reanalyzed with the emphasis on the real spatial arrangement of the constituent ionic species and not only on the idealized fluorite structure as was done in the past. This should be true for perovskite-type oxides as well.
The magnetic contribution to the chemical expansion mentioned above for some double perovskites226–232,246 is another emerging field of study which may hold answers for some still unexplained chemical strain related phenomena. This is also true for anisotropic chemical expansion of layered oxide materials, which have not yet been studied extensively in this respect, but the existing body of knowledge10,31,123,144,148,149,226–235,254,256,257,259 indicates that controlling the degree of anisotropy may be an important route to controlling the chemical expansion of oxides.
All in all, the field of chemical expansion as it develops will definitely have a profound impact on both our fundamental understanding of solid state materials and on our ability to design new oxide materials for their application in various energy-related devices.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
Dmitry Malyshkin acknowledges the project MK-800.2020.3 supported by the Council on grants of the President of the Russian Federation. The authors are grateful for the financial aid of the Ministry of Science and Higher Education of the Russian Federation (State Assignment No. 075-03-2021-051/5).References
- T. Ishihara, Perovskite Oxide for Solid Oxide Fuel Cells, Springer, US, Boston, MA, 2009 Search PubMed.
- J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
- J. Sunarso, S. Baumann, J. M. Serra, W. A. Meulenberg, S. Liu, Y. S. Lin and J. C. Diniz da Costa, J. Membr. Sci., 2008, 320, 13–41 CrossRef CAS.
- M. Misono, in Studies in Surface Science and Catalysis, ed. M. Misono, Elsevier, 2013, vol. 176, pp. 67–95 Search PubMed.
- J. D. Nicholas, Y. Qi, S. R. Bishop and P. P. Mukherjee, J. Electrochem. Soc., 2014, 161, Y11–Y12 CrossRef CAS.
- V. V. Sereda, D. S. Tsvetkov, D. A. Malyshkin, I. L. Ivanov, A. L. Sednev-Lugovets and A. Y. Zuev, Solid State Ionics, 2020, 358, 115516 CrossRef CAS.
- W. Zhang, D. Schröder, T. Arlt, I. Manke, R. Koerver, R. Pinedo, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, J. Mater. Chem. A, 2017, 5, 9929–9936 RSC.
- L. Mu, R. Lin, R. Xu, L. Han, S. Xia, D. Sokaras, J. D. Steiner, T.-C. Weng, D. Nordlund, M. M. Doeff, Y. Liu, K. Zhao, H. L. Xin and F. Lin, Nano Lett., 2018, 18, 3241–3249 CrossRef CAS PubMed.
- K.-J. Park, J.-Y. Hwang, H.-H. Ryu, F. Maglia, S.-J. Kim, P. Lamp, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2019, 4, 1394–1400 CrossRef CAS.
- S. R. Bishop, D. Marrocchelli, C. Chatzichristodoulou, N. H. Perry, M. B. Mogensen, H. L. Tuller and E. D. Wachsman, Annu. Rev. Mater. Res., 2014, 44, 205–239 CrossRef CAS.
- S. Hull, S. T. Norberg, I. Ahmed, S. G. Eriksson, D. Marrocchelli and P. A. Madden, J. Solid State Chem., 2009, 182, 2815–2821 CrossRef CAS.
- D. Marrocchelli, S. R. Bishop, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2012, 22, 1958–1965 CrossRef CAS.
- V. V. Sereda, D. S. Tsvetkov, I. L. Ivanov and A. Y. Zuev, Acta Mater., 2019, 162, 33–45 CrossRef CAS.
- M. B. Choi, S. Y. Jeon, H. S. Yang, J. Y. Park and S. J. Song, J. Electrochem. Soc., 2011, 158, B189 CrossRef CAS.
- M. B. Choi, D. K. Lim, E. D. Wachsman and S. J. Song, Solid State Ionics, 2012, 221, 22–27 CrossRef CAS.
- H. Im, S. Jeon, M. Choi, J. Park and S. Song, J. Ceram. Process. Res., 2012, 13, 579–585 Search PubMed.
- A. Y. Zuev, V. Sereda and D. Tsvetkov, Int. J. Hydrogen Energy, 2014, 39, 21553–21560 CrossRef CAS.
- A. Y. Zuev, V. Sereda and D. Tsvetkov, J. Electrochem. Soc., 2014, 161, F3032–F3038 CrossRef CAS.
- H. Bae, B. Singh, I.-H. Kim, H.-N. Im and S.-J. Song, J. Electrochem. Soc., 2018, 165, F641–F651 CrossRef CAS.
- H. Bae, J. Hong, B. Singh, A. K. Srivastava, J. H. Joo and S.-J. Song, J. Electrochem. Soc., 2019, 166, F180–F189 CrossRef CAS.
- D. Marrocchelli, S. R. Bishop and J. Kilner, J. Mater. Chem. A, 2013, 1, 7673–7680 RSC.
- H. Wulfmeier, D. Kohlmann, T. Defferriere, C. Steiner, R. Moos, H. L. Tuller and H. Fritze, Z. Phys. Chem., 2021 DOI:10.1515/zpch-2021-3125.
- A. Y. Zuev and D. S. Tsvetkov, in Electro-Chemo-Mechanics of Solids, ed. S. R. Bishop, N. H. Perry, D. Marrocchelli and B. W. Sheldon, Springer International Publishing, Cham, 2017, pp. 5–33, DOI:10.1007/978-3-319-51407-9_2.
- Y.-D. Kim, J. Yang, J.-I. Lee, M. Saqib, J.-S. Shin, K. Park, M. Jo, S.-J. Song and J.-Y. Park, J. Power Sources, 2020, 452, 227758 CrossRef CAS.
- H.-H. Ryu, K.-J. Park, C. S. Yoon and Y.-K. Sun, Chem. Mater., 2018, 30, 1155–1163 CrossRef CAS.
- J. H. Jang, Y.-M. Kim, Q. He, R. Mishra, L. Qiao, M. D. Biegalski, A. R. Lupini, S. T. Pantelides, S. J. Pennycook, S. V. Kalinin and A. Y. Borisevich, ACS Nano, 2017, 11, 6942–6949 CrossRef CAS PubMed.
- N. Balke, S. Jesse, Y. Kim, L. Adamczyk, I. N. Ivanov, N. J. Dudney and S. V. Kalinin, ACS Nano, 2010, 4, 7349–7357 CrossRef CAS PubMed.
- S. V. Kalinin and N. Balke, Adv. Mater., 2010, 22, E193–E209 CrossRef CAS PubMed.
- J. Li, Y. Li, P. K. Routh, E. Makagon, I. Lubomirsky and A. I. Frenkel, J. Synchrotron Radiat., 2021, 28, 1511–1517 CrossRef CAS PubMed.
- E. Sediva, T. Defferriere, N. H. Perry, H. L. Tuller and J. L. M. Rupp, Adv. Mater., 2019, 31, 1902493 CrossRef PubMed.
- A. Chatterjee, J. M. Caicedo, B. Ballesteros and J. Santiso, J. Mater. Chem. A, 2018, 6, 12430–12439 RSC.
- D. Marrocchelli, N. H. Perry and S. R. Bishop, Phys. Chem. Chem. Phys., 2015, 17, 10028–10039 RSC.
- D. S. Aidhy, B. Liu, Y. Zhang and W. J. Weber, Comput. Mater. Sci., 2015, 99, 298–305 CrossRef CAS.
- A. Løken, R. Haugsrud and T. S. Bjørheim, Phys. Chem. Chem. Phys., 2016, 18, 31296–31303 RSC.
- B. Euser, J. R. Berger, H. Zhu and R. J. Kee, J. Electrochem. Soc., 2016, 163, F1294–F1301 CrossRef CAS.
- B. Euser, J. R. Berger, H. Zhu and R. J. Kee, J. Electrochem. Soc., 2016, 163, F264–F271 CrossRef CAS.
- N. Nagendra, S. Biswas, T. Nithyanantham and S. Bandopadhyay, Mater. Res. Bull., 2013, 48, 2034–2039 CrossRef CAS.
- A. Atkinson and T. M. G. M. Ramos, Solid State Ionics, 2000, 129, 259–269 CrossRef CAS.
- K. Kwok, H. L. Frandsen, M. Søgaard and P. V. Hendriksen, J. Membr. Sci., 2014, 470, 80–89 CrossRef CAS.
- B. Euser, H. Zhu, J. R. Berger, C. A. Lewinsohn and R. J. Kee, J. Electrochem. Soc., 2017, 164, F732–F739 CrossRef CAS.
- E. Blond and N. Richet, J. Eur. Ceram. Soc., 2008, 28, 793–801 CrossRef CAS.
- K. Taghikhani, A. Dubois, J. R. Berger, S. Ricote, H. Zhu and R. J. Kee, Membranes, 2021, 11, 378 CrossRef CAS PubMed.
- X. Jin and X. Xue, RSC Adv., 2014, 4, 15782–15796 RSC.
- Y. Wu, X. Xu, Z. Yan and Z. Zhong, J. Electrochem. Soc., 2021, 168, 044511 CrossRef CAS.
- S. R. Bishop, Acta Mech. Sin., 2013, 29, 312–317 CrossRef CAS.
- A. Løken, S. Ricote and S. Wachowski, Crystals, 2018, 8, 365 CrossRef.
- P. Wang, W. Qu, W.-L. Song, H. Chen, R. Chen and D. Fang, Adv. Funct. Mater., 2019, 29, 1900950 CrossRef.
- Y. Ren and K. B. Hatzell, J. Mater. Chem. A, 2021, 9, 13804–13821 RSC.
- J. A. Lewis, J. Tippens, F. J. Q. Cortes and M. T. McDowell, Trends Chem., 2019, 1, 845–857 CrossRef CAS.
- Y. Wang, J. Liu, T. Chen, W. Lin and J. Zheng, Phys. Chem. Chem. Phys., 2022, 24, 2167–2175 RSC.
- D. Bistri, A. Afshar and C. V. Di Leo, Meccanica, 2021, 56, 1523–1554 CrossRef.
- Z. Xu, M. M. Rahman, L. Mu, Y. Liu and F. Lin, J. Mater. Chem. A, 2018, 6, 21859–21884 RSC.
- Y. S. Touloukian, R. K. Kirby, E. R. Taylor and T. Y. R. Lee, Thermophysical Properties of Matter - The TPRC Data Series. Volume 13. Thermal Expansion - Nonmetallic Solids, IFI/Plenum Data Company, New York, 1977 Search PubMed.
- R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal Expansion of Crystals, Pergamon Press, Oxford, 1979 Search PubMed.
- P. G. Strelkow, Phys. Z. Sowjetunion, 1937, 12, 77–82 Search PubMed.
- N. F. Mott and R. W. Gurney, Electronic Processes in Ionic Crystals, Clarendon Press, Oxford, 1948 Search PubMed.
- F. Seitz, Phys. Rev., 1939, 56, 1063–1064 CrossRef CAS.
- A. W. Lawson, Phys. Rev., 1950, 78, 185 CrossRef CAS.
- E. R. Jette and F. Foote, J. Chem. Phys., 1933, 1, 29–36 CrossRef CAS.
- R. Koerver, W. Zhang, L. de Biasi, S. Schweidler, A. O. Kondrakov, S. Kolling, T. Brezesinski, P. Hartmann, W. G. Zeier and J. Janek, Energy Environ. Sci., 2018, 11, 2142–2158 RSC.
- D. Marrocchelli, C. Chatzichristodoulou and S. R. Bishop, Phys. Chem. Chem. Phys., 2014, 16, 9229–9232 RSC.
- S. B. Adler, J. Am. Ceram. Soc., 2001, 84, 2117–2119 CrossRef CAS.
- A. Løken, S. Ricote and S. Wachowski, Crystals, 2018, 8 Search PubMed.
- T. S. Bjørheim, A. Løken and R. Haugsrud, J. Mater. Chem. A, 2016, 4, 5917–5924 RSC.
- V. Tsidilkovski, A. Kuzmin, L. Putilov and V. Balakireva, Solid State Ionics, 2017, 301, 170–175 CrossRef CAS.
- T. Fujisaki, A. T. Staykov, Y. Jing, K. Leonard, N. R. Aluru and H. Matsumoto, Solid State Ionics, 2019, 333, 1–8 CrossRef CAS.
- A. K. E. Andersson, S. M. Selbach, C. S. Knee and T. Grande, J. Am. Ceram. Soc., 2014, 97, 2654–2661 CrossRef CAS.
- D. Han, N. Hatada and T. Uda, J. Am. Ceram. Soc., 2016, 99, 3745–3753 CrossRef CAS.
- R. Sažinas, M.-A. Einarsrud and T. Grande, J. Mater. Chem. A, 2017, 5, 5846–5857 RSC.
- E. Jedvik, A. Lindman, M. Þ. Benediktsson and G. Wahnström, Solid State Ionics, 2015, 275, 2–8 CrossRef CAS.
- C. Chatzichristodoulou, P. Norby, P. V. Hendriksen and M. B. Mogensen, J. Electroceram., 2015, 34, 100–107 CrossRef CAS.
- S. J. Hong and A. V. Virkar, J. Am. Ceram. Soc., 1995, 78, 433–439 CrossRef CAS.
- V. B. Glushkova, F. Hanic and L. V. Sazonova, Ceramurg. Int., 1978, 4, 176–178 CrossRef CAS.
- R. P. Ingel and D. Lewis, J. Am. Ceram. Soc., 1986, 69, 325–332 CrossRef CAS.
- V. I. Aleksandrov, G. E. Val’yano, B. V. Lukin, V. V. Osiko, A. E. Rautbort, V. M. Tatarintsev and V. N. Filatova, 1976, 12, 273–277.
- D.-J. Kim, J. Am. Ceram. Soc., 1989, 72, 1415–1421 CrossRef CAS.
- S. Omar and J. C. Nino, Acta Mater., 2013, 61, 5406–5413 CrossRef CAS.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- A. N. Morozovska, E. A. Eliseev, G. S. Svechnikov and S. V. Kalinin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045402 CrossRef.
- N. Balke, S. Jesse, A. N. Morozovska, E. Eliseev, D. W. Chung, Y. Kim, L. Adamczyk, R. E. García, N. Dudney and S. V. Kalinin, Nat. Nanotechnol., 2010, 5, 749–754 CrossRef CAS PubMed.
- R. Shannon, Acta Crystallogr. A, 1976, 32, 751–767 CrossRef.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef CAS.
- T. Otake, H. Yugami, K. Yashiro, Y. Nigara, T. Kawada and J. Mizusaki, Solid State Ionics, 2003, 161, 181–186 CrossRef CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Electrochim. Acta, 2009, 54, 1436–1443 CrossRef CAS.
- S. R. Bishop, H. L. Tuller, Y. Kuru and B. Yildiz, J. Eur. Ceram. Soc., 2011, 31, 2351–2356 CrossRef CAS.
- S. R. Bishop, D. Marrocchelli, W. Fang, K. Amezawa, K. Yashiro and G. W. Watson, Energy Environ. Sci., 2013, 6, 1142–1146 RSC.
- S. R. Bishop, T. Nakamura and K. Amezawa, Solid State Ionics, 2014, 261, 1–4 CrossRef CAS.
- D. Er, J. Li, M. Cargnello, P. Fornasiero, R. J. Gorte and V. B. Shenoy, J. Electrochem. Soc., 2014, 161, F3060–F3064 CrossRef CAS.
- B. Wang, X. Xi and A. N. Cormack, Chem. Mater., 2014, 26, 3687–3692 CrossRef CAS.
- M. Heidenreich, C. Kaps, A. Simon, F. Schulze-Küppers and S. Baumann, Solid State Ionics, 2015, 283, 56–67 CrossRef CAS.
- T. Das, J. D. Nicholas, B. W. Sheldon and Y. Qi, Phys. Chem. Chem. Phys., 2018, 20, 15293–15299 RSC.
- H.-W. Chiang, R. N. Blumenthal and R. A. Fournelle, Solid State Ionics, 1993, 66, 85–95 CrossRef CAS.
- S. Wang, M. Katsuki, T. Hashimoto and M. Dokiya, J. Electrochem. Soc., 2003, 150, A952 CrossRef CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Acta Mater., 2009, 57, 3596–3605 CrossRef CAS.
- A. Nakamura, Solid State Ionics, 2010, 181, 1543–1564 CrossRef CAS.
- A. Nakamura, Solid State Ionics, 2010, 181, 1631–1653 CrossRef CAS.
- C. Artini, M. Pani, M. M. Carnasciali, M. T. Buscaglia, J. R. Plaisier and G. A. Costa, Inorg. Chem., 2015, 54, 4126–4137 CrossRef CAS PubMed.
- C. Artini, M. Pani, M. M. Carnasciali, J. R. Plaisier and G. A. Costa, Inorg. Chem., 2016, 55, 10567–10579 CrossRef CAS PubMed.
- C. Artini, Inorg. Chem., 2018, 57, 13047–13062 CrossRef CAS PubMed.
- C. Artini, M. M. Carnasciali, M. Viviani, S. Presto, J. R. Plaisier, G. A. Costa and M. Pani, Solid State Ionics, 2018, 315, 85–91 CrossRef CAS.
- C. Artini, S. Presto, S. Massardo, M. Pani, M. M. Carnasciali and M. Viviani, Energies, 2019, 12, 4148 CrossRef CAS.
- C. Artini, S. Massardo, M. M. Carnasciali, B. Joseph and M. Pani, Inorg. Chem., 2021, 60, 7306–7314 CrossRef CAS PubMed.
- C. Artini, S. Presto, M. Viviani, S. Massardo, M. M. Carnasciali, L. Gigli and M. Pani, J. Energy Chem., 2021, 60, 494–502 CrossRef.
- S. Massardo, A. Cingolani and C. Artini, Coatings, 2021, 11, 724 CrossRef CAS.
- M. Johnsson and P. Lemmens, in Handbook of Magnetism and Advanced Magnetic Materials, Wiley, Hoboken, 2007, pp. 2034–2042, DOI:10.1002/9780470022184.hmm411.
- V. L. Miller and S. C. Tidrow, Integr. Ferroelectr., 2013, 148, 1–16 CrossRef CAS.
- X. Chen and T. Grande, Chem. Mater., 2013, 25, 927–934 CrossRef CAS.
- X. Chen and T. Grande, Chem. Mater., 2013, 25, 3296–3306 CrossRef CAS.
- T. Grande, J. R. Tolchard and S. M. Selbach, Chem. Mater., 2012, 24, 338–345 CrossRef CAS.
- S. M. Selbach, A. Nordli Løvik, K. Bergum, J. R. Tolchard, M.-A. Einarsrud and T. Grande, J. Solid State Chem., 2012, 196, 528–535 CrossRef CAS.
- N. H. Perry, S. R. Bishop and H. L. Tuller, J. Mater. Chem. A, 2014, 2, 18906–18916 RSC.
- N. H. Perry, J. J. Kim, S. R. Bishop and H. L. Tuller, J. Mater. Chem. A, 2015, 3, 3602–3611 RSC.
- L. Q. Jiang, J. K. Guo, H. B. Liu, M. Zhu, X. Zhou, P. Wu and C. H. Li, J. Phys. Chem. Solids, 2006, 67, 1531–1536 CrossRef CAS.
- T. R. Armstrong, J. W. Stevenson, L. R. Pederson and P. E. Raney, J. Electrochem. Soc., 1996, 143, 2919–2925 CrossRef CAS.
- P. H. Larsen, P. V. Hendriksen and M. Mogensen, J. Therm. Anal., 1997, 49, 1263–1275 CrossRef CAS.
- S. Miyoshi, J.-O. Hong, K. Yashiro, A. Kaimai, Y. Nigara, K. Kawamura, T. Kawada and J. Mizusaki, Solid State Ionics, 2003, 161, 209–217 CrossRef CAS.
- J. Mizusaki, N. Mori, H. Takai, Y. Yonemura, H. Minamiue, H. Tagawa, M. Dokiya, H. Inaba, K. Naraya, T. Sasamoto and T. Hashimoto, Solid State Ionics, 2000, 129, 163–177 CrossRef CAS.
- Yu Chen and S. B. Adler, Chem. Mater., 2005, 17, 4537–4546 CrossRef.
- A. Zuev, L. Singheiser and K. Hilpert, Solid State Ionics, 2002, 147, 1–11 CrossRef CAS.
- K. Hilpert, R. W. Steinbrech, F. Boroomand, E. Wessel, F. Meschke, A. Zuev, O. Teller, H. Nickel and L. Singheiser, J. Eur. Ceram. Soc., 2003, 23, 3009–3020 CrossRef CAS.
- A. Y. Zuev, A. I. Vylkov, A. N. Petrov and D. S. Tsvetkov, Solid State Ionics, 2008, 179, 1876–1879 CrossRef CAS.
- A. Y. Zuev and D. S. Tsvetkov, Solid State Ionics, 2010, 181, 557–563 CrossRef CAS.
- D. S. Tsvetkov, I. L. Ivanov, D. Malyshkin, V. V. Sereda and A. Y. Zuev, ECS Trans., 2016, 72, 21–35 CrossRef CAS.
- Y.-L. Lee and D. Morgan, Phys. Chem. Chem. Phys., 2012, 14, 290–302 RSC.
- S. Shafeie, J. Grins, S. Y. Istomin, A. A. Gippius, L. Karvonen, S. Populoh, A. Weidenkaff, J. Köhler and G. Svensson, J. Mater. Chem., 2012, 22, 16269–16276 RSC.
- P. M. Raccah and J. B. Goodenough, Phys. Rev., 1967, 155, 932–943 CrossRef CAS.
- M. A. Señarís-Rodríguez and J. B. Goodenough, J. Solid State Chem., 1995, 116, 224–231 CrossRef.
- M. W. Haverkort, Z. Hu, J. C. Cezar, T. Burnus, H. Hartmann, M. Reuther, C. Zobel, T. Lorenz, A. Tanaka, N. B. Brookes, H. H. Hsieh, H. J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2006, 97, 176405 CrossRef CAS PubMed.
- M. A. Señarís-Rodríguez and J. B. Goodenough, J. Solid State Chem., 1995, 118, 323–336 CrossRef.
- C. Zobel, M. Kriener, D. Bruns, J. Baier, M. Grüninger, T. Lorenz, P. Reutler and A. Revcolevschi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 020402 CrossRef.
- X. Wang, Y. Han, X. Song, W. Liu, Y. Jin, W. Liu and H. Cui, Phys. Chem. Chem. Phys., 2018, 20, 17781–17789 RSC.
- S. Y. Istomin and E. V. Antipov, Russ. Chem. Rev., 2013, 82, 686–700 CrossRef.
- A. Y. Zuev, V. V. Sereda and D. S. Tsvetkov, J. Electrochem. Soc., 2012, 159, F594–F599 CrossRef CAS.
- M.-B. Choi, S.-Y. Jeon, B. Singh, Y.-S. Yoo, J.-H. Hwang and S.-J. Song, Acta Mater., 2014, 65, 373–382 CrossRef CAS.
- V. V. Sereda, D. S. Tsvetkov, I. L. Ivanov and A. Y. Zuev, J. Mater. Chem. A, 2015, 3, 6028–6037 RSC.
- Y. Takeda, K. Kanno, T. Takada, O. Yamamoto, M. Takano, N. Nakayama and Y. Bando, J. Solid State Chem., 1986, 63, 237–249 CrossRef CAS.
- T. C. Gibb, J. Mater. Chem., 1994, 4, 1445–1449 RSC.
- J. P. Hodges, S. Short, J. D. Jorgensen, X. Xiong, B. Dabrowski, S. M. Mini and C. W. Kimball, J. Solid State Chem., 2000, 151, 190–209 CrossRef CAS.
- M. Schmidt and S. J. Campbell, J. Solid State Chem., 2001, 156, 292–304 CrossRef CAS.
- J. Blasco, J. Stankiewicz and J. García, J. Solid State Chem., 2006, 179, 898–908 CrossRef CAS.
- N. Kim, N. H. Perry and E. Ertekin, Chem. Mater., 2019, 31, 233–243 CrossRef CAS.
- B. Ouyang, T. Chakraborty, N. Kim, N. H. Perry, T. Mueller, N. R. Aluru and E. Ertekin, Chem. Mater., 2019, 31, 3144–3153 CrossRef CAS.
- T. Das, J. D. Nicholas and Y. Qi, J. Mater. Chem. A, 2017, 5, 25031–25043 RSC.
- D. S. Tsvetkov, I. L. Ivanov, D. A. Malyshkin and A. Y. Zuev, Dalton Trans., 2014, 43, 11862–11866 RSC.
- D. S. Tsvetkov, I. L. Ivanov, D. A. Malyshkin, A. L. Sednev, V. V. Sereda and A. Y. Zuev, Pure Appl. Chem., 2019, 91, 923–940 CrossRef CAS.
- D. S. Tsvetkov, I. L. Ivanov, D. A. Malyshkin, A. S. Steparuk and A. Y. Zuev, Dalton Trans., 2016, 45, 12906–12913 RSC.
- V. S. Kudyakova, A. M. Shalamova, B. V. Politov and A. Y. Suntsov, J. Alloys Compd., 2021, 886, 161133 CrossRef CAS.
- R. A. Cox-Galhotra, A. Huq, J. P. Hodges, J.-H. Kim, C. Yu, X. Wang, A. J. Jacobson and S. McIntosh, J. Mater. Chem. A, 2013, 1, 3091–3100 RSC.
- R. A. Cox-Galhotra, A. Huq, J. P. Hodges, C. Yu, X. Wang, W. Gong, A. J. Jacobson and S. McIntosh, Solid State Ionics, 2013, 249–250, 34–40 CrossRef CAS.
- K. Papathanassopoulos, H. Wenzl and T. Schober, J. Am. Ceram. Soc., 1997, 80, 3278–3280 CrossRef CAS.
- T. Schober, J. Friedrich, D. Triefenbach and F. Tietz, Solid State Ionics, 1997, 100, 173–181 CrossRef CAS.
- T. Mono and T. Schober, Solid State Ionics, 1996, 91, 155–159 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- E. Makagon, R. Merkle, J. Maier and I. Lubomirsky, Solid State Ionics, 2020, 344, 115130 CrossRef CAS.
- D. Han, K. Shinoda, S. Sato, M. Majima and T. Uda, J. Mater. Chem. A, 2015, 3, 1243–1250 RSC.
- I. Ahmed, M. Karlsson, S.-G. Eriksson, E. Ahlberg, C. S. Knee, K. Larsson, A. K. Azad, A. Matic and L. Börjesson, J. Am. Ceram. Soc., 2008, 91, 3039–3044 CrossRef CAS.
- I. Oikawa and H. Takamura, Chem. Mater., 2015, 27, 6660–6667 CrossRef CAS.
- J. Hyodo, K. Kitabayashi, K. Hoshino, Y. Okuyama and Y. Yamazaki, Adv. Energy Mater., 2020, 10, 2000213 CrossRef CAS.
- A. V. Kasyanova, L. R. Tarutina, A. O. Rudenko, J. G. Lyagaeva and D. A. Medvedev, Russ. Chem. Rev., 2020, 89, 667–692 CrossRef CAS.
- D. Han, M. Majima and T. Uda, J. Solid State Chem., 2013, 205, 122–128 CrossRef CAS.
- A. V. Kuz’min, A. Y. Stroeva, V. P. Gorelov and A. A. Pankratov, Russ. J. Electrochem., 2018, 54, 43–48 CrossRef.
- H. Xu, R. K. Behera, Y. Wang, F. Ebrahimi, S. B. Sinnott, E. D. Wachsman and S. R. Phillpot, Solid State Ionics, 2010, 181, 551–556 CrossRef CAS.
- D. A. Freedman, D. Roundy and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064108 CrossRef.
- S. J. Stokes and M. S. Islam, J. Mater. Chem., 2010, 20, 6258–6264 RSC.
- M. Burbano, D. Marrocchelli, B. Yildiz, H. L. Tuller, S. T. Norberg, S. Hull, P. A. Madden and G. W. Watson, J. Phys.: Condens. Matter, 2011, 23, 255402 CrossRef PubMed.
- D. Marrocchelli, S. R. Bishop, H. L. Tuller, G. W. Watson and B. Yildiz, Phys. Chem. Chem. Phys., 2012, 14, 12070–12074 RSC.
- E. J. Granhed, A. Lindman, C. Eklöf-Österberg, M. Karlsson, S. F. Parker and G. Wahnström, J. Mater. Chem. A, 2019, 7, 16211–16221 RSC.
- A. Marthinsen, T. Grande and S. M. Selbach, J. Phys. Chem. C, 2020, 124, 12922–12932 CrossRef CAS.
- U. Aschauer and N. A. Spaldin, Appl. Phys. Lett., 2016, 109, 031901 CrossRef.
- J. G. Swallow, J. J. Kim, J. M. Maloney, D. Chen, J. F. Smith, S. R. Bishop, H. L. Tuller and K. J. Van Vliet, Nat. Mater., 2017, 16, 749–754 CrossRef CAS PubMed.
- D. S. Aidhy and K. Rawat, J. Appl. Phys., 2021, 129, 171102 CrossRef CAS.
- J. Sheth, D. Chen, J. J. Kim, W. J. Bowman, P. A. Crozier, H. L. Tuller, S. T. Misture, S. Zdzieszynski, B. W. Sheldon and S. R. Bishop, Nanoscale, 2016, 8, 16499–16510 RSC.
- J. G. Swallow, J. K. Lee, T. Defferriere, G. M. Hughes, S. N. Raja, H. L. Tuller, J. H. Warner and K. J. Van Vliet, ACS Nano, 2018, 12, 1359–1372 CrossRef CAS PubMed.
- M. Tyunina, O. Pacherova, T. Kocourek and A. Dejneka, Sci. Rep., 2021, 11, 15247 CrossRef CAS PubMed.
- X. Liu, L. Zhang, Y. Zheng, Z. Guo, Y. Zhu, H. Chen, F. Li, P. Liu, B. Yu, X. Wang, J. Liu, Y. Chen and M. Liu, Adv. Sci., 2019, 6, 1801898 CrossRef PubMed.
- M. Kubicek, Z. Cai, W. Ma, B. Yildiz, H. Hutter and J. Fleig, ACS Nano, 2013, 7, 3276–3286 CrossRef CAS PubMed.
- M. F. Hoedl, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2020, 124, 11780–11789 CrossRef CAS.
- M. Ram and Y. Tsur, J. Electroceram., 2009, 22, 120–124 CrossRef CAS.
- C. S. Kim, N. H. Perry, S. R. Bishop and H. L. Tuller, J. Electroceram., 2018, 40, 332–337 CrossRef CAS.
- C. Chatzichristodoulou, P. V. Hendriksen and A. Hagen, J. Electrochem. Soc., 2010, 157, B299 CrossRef CAS.
- A. Natoli, B. I. Arias-Serrano, E. Rodríguez-Castellón, A. Żurawska, J. R. Frade and A. A. Yaremchenko, Materials, 2021, 14, 641 CrossRef CAS PubMed.
- S. Wang, E. Oikawa and T. Hashimoto, J. Electrochem. Soc., 2004, 151, E46 CrossRef CAS.
- Y. Li, E. R. Maxey, J. W. Richardson Jr, B. Ma, T. H. Lee and S.-J. Song, J. Am. Ceram. Soc., 2007, 90, 1208–1214 CrossRef CAS.
- M. Kuhn, S. R. Bishop, J. L. M. Rupp and H. L. Tuller, Acta Mater., 2013, 61, 4277–4288 CrossRef CAS.
- T. R. Armstrong, J. W. Stevenson, K. Hasinska and D. E. McCready, J. Electrochem. Soc., 1998, 145, 4282–4289 CrossRef CAS.
- F. Boroomand, E. Wessel, H. Bausinger and K. Hilpert, Solid State Ionics, 2000, 129, 251–258 CrossRef CAS.
- J. H. Kuo, H. U. Anderson and D. M. Sparlin, J. Solid State Chem., 1989, 83, 52–60 CrossRef CAS.
- S. Miyoshi, J.-O. Hong, K. Yashiro, A. Kaimai, Y. Nigara, K. Kawamura, T. Kawada and J. Mizusaki, Solid State Ionics, 2002, 154–155, 257–263 CrossRef CAS.
- S. Miyoshi, A. Kaimai, H. Matsumoto, K. Yashiro, Y. Nigara, T. Kawada and J. Mizusaki, Solid State Ionics, 2004, 175, 383–386 CrossRef CAS.
- J. A. M. Van Roosmalen, E. H. P. Cordfunke, R. B. Helmholdt and H. W. Zandbergen, J. Solid State Chem., 1994, 110, 100–105 CrossRef CAS.
- M. H. R. Lankhorst and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 1268–1273 CrossRef CAS.
- M. H. R. Lankhorst, H. J. M. Bouwmeester and H. Verweij, J. Solid State Chem., 1997, 133, 555–567 CrossRef CAS.
- M. H. R. Lankhorst, H. J. M. Bouwmeester and H. Verweij, Solid State Ionics, 1997, 96, 21–27 CrossRef CAS.
- M. H. R. Lankhorst and J. E. ten Elshof, J. Solid State Chem., 1997, 130, 302–310 CrossRef CAS.
- V. Cherepanov, T. Aksenova, E. Kiselev and L. Gavrilova, Solid State Sci., 2008, 10, 438–443 CrossRef CAS.
- A. N. Petrov, V. A. Cherepanov and A. Y. Zuev, J. Solid State Electrochem., 2006, 10, 517–537 CrossRef CAS.
- A. Y. Zuev, A. N. Petrov, A. I. Vylkov and D. S. Tsvetkov, J. Mater. Sci., 2007, 42, 1901–1908 CrossRef CAS.
- M. Kuhn, S. Hashimoto, K. Sato, K. Yashiro and J. Mizusaki, Solid State Ionics, 2011, 195, 7–15 CrossRef CAS.
- S. Wang, M. Katsuki, M. Dokiya and T. Hashimoto, Solid State Ionics, 2003, 159, 71–78 CrossRef CAS.
- L. W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Solid State Ionics, 1995, 76, 273–283 CrossRef CAS.
- C. Y. Park and A. J. Jacobson, Solid State Ionics, 2005, 176, 2671–2676 CrossRef CAS.
- A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264–268 CrossRef CAS.
- P. Hjalmarsson, M. Søgaard and M. Mogensen, J. Solid State Chem., 2010, 183, 1853–1862 CrossRef CAS.
- V. V. Kharton, A. A. Yaremchenko, M. V. Patrakeev, E. N. Naumovich and F. M. B. Marques, J. Eur. Ceram. Soc., 2003, 23, 1417–1426 CrossRef CAS.
- R. Kriegel, R. Kircheisen and J. Töpfer, Solid State Ionics, 2010, 181, 64–70 CrossRef CAS.
- H. L. Lein, K. Wiik and T. Grande, Solid State Ionics, 2006, 177, 1795–1798 CrossRef CAS.
- S. McIntosh, J. F. Vente, W. G. Haije, D. H. A. Blank and H. J. M. Bouwmeester, Chem. Mater., 2006, 18, 2187–2193 CrossRef CAS.
- X. Dong, Z. Xu, X. Chang, C. Zhang and W. Jin, J. Am. Ceram. Soc., 2007, 90, 3923–3929 CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, J. Am. Ceram. Soc., 2010, 93, 4115–4121 CrossRef CAS.
- A. Feldhoff, J. Martynczuk, M. Arnold, M. Myndyk, I. Bergmann, V. Šepelák, W. Gruner, U. Vogt, A. Hähnel and J. Woltersdorf, J. Solid State Chem., 2009, 182, 2961–2971 CrossRef CAS.
- M. G. Sahini, J. R. Tolchard, K. Wiik and T. Grande, Dalton Trans., 2015, 44, 10875–10881 RSC.
- A. A. Yaremchenko, S. M. Mikhalev, E. S. Kravchenko and J. R. Frade, J. Eur. Ceram. Soc., 2014, 34, 703–715 CrossRef CAS.
- M. Kuhn, S. Hashimoto, K. Sato, K. Yashiro and J. Mizusaki, Solid State Ionics, 2013, 241, 12–16 CrossRef CAS.
- S.-i. Hashimoto, Y. Fukuda, M. Kuhn, K. Sato, K. Yashiro and J. Mizusaki, Solid State Ionics, 2011, 186, 37–43 CrossRef CAS.
- A. Fossdal, M. Menon, I. Wærnhus, K. Wiik, M.-A. Einarsrud and T. Grande, J. Am. Ceram. Soc., 2004, 87, 1952–1958 CrossRef CAS.
- C. de Leeuwe, W. Hu, D. Neagu, E. I. Papaioannou, S. Pramana, B. Ray, J. S. O. Evans and I. S. Metcalfe, J. Solid State Chem., 2021, 293, 121838 CrossRef CAS.
- H. Bae, B. Singh, L. Mathur, J. H. Joo and S.-J. Song, J. Electrochem. Soc., 2021, 168, 034511 CrossRef CAS.
- O. Valentin, F. Millot, É. Blond, N. Richet, A. Julian, E. Véron and S. Ory, Solid State Ionics, 2011, 193, 23–31 CrossRef CAS.
- A. A. Yaremchenko, E. V. Tsipis, A. V. Kovalevsky, J. C. Waerenborgh and V. V. Kharton, Solid State Ionics, 2011, 192, 259–268 CrossRef CAS.
- Y. Liu, S. Baumann, F. Schulze-Küppers, D. N. Mueller and O. Guillon, J. Eur. Ceram. Soc., 2018, 38, 5058–5066 CrossRef CAS.
- S. I. Elkalashy, T. V. Aksenova, A. S. Urusova and V. A. Cherepanov, Solid State Ionics, 2016, 295, 96–103 CrossRef CAS.
- T. V. Aksenova, A. E. Vakhromeeva, S. I. Elkalashy, A. S. Urusova and V. A. Cherepanov, J. Solid State Chem., 2017, 251, 70–78 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr. B, 1972, 28, 3384–3392 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr. A, 1975, 31, 756–762 CrossRef.
- G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796 RSC.
- P. Karen, J. Solid State Chem., 2021, 299, 122147 CrossRef CAS.
- P. Karen and P. M. Woodward, J. Mater. Chem., 1999, 9, 789–797 RSC.
- P. Karen, P. M. Woodward, P. N. Santhosh, T. Vogt, P. W. Stephens and S. Pagola, J. Solid State Chem., 2002, 167, 480–493 CrossRef CAS.
- J. Lindén, P. Karen, A. Kjekshus, J. Miettinen, T. Pietari and M. Karppinen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 15251–15260 CrossRef.
- J. Nakamura, J. Lindén, H. Yamauchi and M. Karppinen, Solid State Commun., 2002, 121, 269–274 CrossRef CAS.
- P. Karen, K. Gustafsson and J. Lindén, J. Solid State Chem., 2007, 180, 148–157 CrossRef CAS.
- P. Karen, J. Solid State Chem., 2003, 170, 9–23 CrossRef CAS.
- L. Mogni, F. Prado, C. Jiménez and A. Caneiro, Solid State Ionics, 2013, 240, 19–28 CrossRef CAS.
- I. Szpunar, R. Strandbakke, M. H. Sørby, S. L. Wachowski, M. Balaguer, M. Tarach, J. M. Serra, A. Witkowska, E. Dzik, T. Norby, M. Gazda and A. Mielewczyk-Gryń, Materials, 2020, 13, 4044 CrossRef CAS PubMed.
- A. L. Sednev-Lugovets, V. V. Sereda, D. A. Malyshkin, D. S. Tsvetkov, I. L. Ivanov, A. Y. Zuev and A. Maignan, J. Chem. Therm., 2021, 161, 106523 CrossRef CAS.
- C. Bernuy-Lopez, K. Høydalsvik, M.-A. Einarsrud and T. Grande, Materials154-151&ndash, 2016, 9, 154–118 Search PubMed.
- D. A. Malyshkin, A. Y. Novikov, V. V. Sereda, I. L. Ivanov, D. S. Tsvetkov and A. Y. Zuev, Inorg. Chem., 2018, 57, 12409–12416 CrossRef CAS PubMed.
- D. Malyshkin, A. Novikov, D. Tsvetkov and A. Zuev, Mater. Lett., 2018, 229, 324–326 CrossRef CAS.
- D. S. Tsvetkov, I. L. Ivanov, D. A. Malyshkin, A. L. Sednev, V. V. Sereda and A. Y. Zuev, Pure Appl. Chem., 2019, 91, 923–940 CrossRef CAS.
- S. García-Martín, K. Manabe, E. Urones-Garrote, D. Ávila-Brande, N. Ichikawa and Y. Shimakawa, Inorg. Chem., 2017, 56, 1412–1417 CrossRef PubMed.
- D. Ávila-Brande, G. King, E. Urones-Garrote, Subakti, A. Llobet and S. García-Martín, Adv. Funct. Mater., 2014, 24, 2510–2517 CrossRef.
- A. Maignan, C. Martin, D. Pelloquin, N. Nguyen and B. Raveau, J. Solid State Chem., 1999, 142, 247–260 CrossRef CAS.
- D. Garcés, C. F. Setevich, A. Caneiro, G. J. Cuello and L. Mogni, J. Appl. Crystallogr., 2014, 47, 325–334 CrossRef.
- T. Nakajima, M. Ichihara and Y. Ueda, J. Phys. Soc. Jpn., 2005, 74, 1572–1577 CrossRef CAS.
- E.-L. Rautama, P. Boullay, A. K. Kundu, V. Caignaert, V. Pralong, M. Karppinen and B. Raveau, Chem. Mater., 2008, 20, 2742–2750 CrossRef CAS.
- P. Karen, P. M. Woodward, J. Lindén, T. Vogt, A. Studer and P. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 214405 CrossRef.
- J. B. Goodenough, J. Alloys Compd., 1997, 262–263, 1–9 CrossRef CAS.
- V. A. Cherepanov, T. V. Aksenova, L. Y. Gavrilova and K. N. Mikhaleva, Solid State Ionics, 2011, 188, 53–57 CrossRef CAS.
- J. Lindén, M. Kochi, K. Lehmus, T. Pietari, M. Karppinen and H. Yamauchi, J. Solid State Chem., 2002, 166, 118–127 CrossRef.
- A. I. Klyndyuk, Phys. Solid State, 2008, 50, 609 CrossRef CAS.
- J. Nakamura, J. Lindén, H. Suematsu, M. Karppinen and H. Yamauchi, Phys. C Supercond., 2000, 338, 121–125 CrossRef CAS.
- A. W. Mombru, C. Christides, A. Lappas, K. Prassides, M. Pissas, C. Mitros and D. Niarchos, Inorg. Chem., 1994, 33, 1255–1258 CrossRef CAS.
- A. C. Tomkiewicz, M. A. Tamimi, A. Huq and S. McIntosh, J. Power Sources, 2016, 330, 240–245 CrossRef CAS.
- T. Nakamura, Y. Ling and K. Amezawa, J. Mater. Chem. A, 2015, 3, 10471–10479 RSC.
- V. V. Kharton, M. V. Patrakeev, E. V. Tsipis, M. Avdeev, E. N. Naumovich, P. V. Anikina and J. C. Waerenborgh, Solid State Ionics, 2010, 181, 1052–1063 CrossRef CAS.
- V. V. Kharton, A. V. Kovalevsky, M. Avdeev, E. V. Tsipis, M. V. Patrakeev, A. A. Yaremchenko, E. N. Naumovich and J. R. Frade, Chem. Mater., 2007, 19, 2027–2033 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2010, 181, 292–299 CrossRef CAS.
- T. Nakamura and K. Amezawa, 2016 IEEE 16th International Conference on Nanotechnology (IEEE-NANO), Chemically-induced structural deformation of layered perovskite oxides, 2016, pp. 429–430, DOI:10.1109/NANO.2016.7751481.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2010, 181, 402–411 CrossRef CAS.
- L. V. Mogni, F. D. Prado, G. J. Cuello and A. Caneiro, Chem. Mater., 2009, 21, 2614–2623 CrossRef CAS.
- C. Chatzichristodoulou, B. C. Hauback and P. V. Hendriksen, J. Solid State Chem., 2013, 201, 164–171 CrossRef CAS.
- C. Chatzichristodoulou, C. Schönbeck, A. Hagen and P. V. Hendriksen, Solid State Ionics, 2013, 232, 68–79 CrossRef CAS.
- G. Conforto, R. Ruess, D. Schröder, E. Trevisanello, R. Fantin, F. H. Richter and J. Janek, J. Electrochem. Soc., 2021, 168, 070546 CrossRef CAS.
- 2019 .
- P. Li, Y. Zhao, Y. Shen and S.-H. Bo, Journal of Physics: Energy, 2020, 2, 022002 CAS.
- S. P. S. Badwal, D. Fini, F. T. Ciacchi, C. Munnings, J. A. Kimpton and J. Drennan, J. Mater. Chem. A, 2013, 1, 10768–10782 RSC.
- D. Clerici, F. Mocera and A. Somà, Energies, 2021, 14, 6281 CrossRef CAS.
- H. Li, N. Zhang, J. Li and J. R. Dahn, J. Electrochem. Soc., 2018, 165, A2985–A2993 CrossRef CAS.
- V. Malavé, J. R. Berger and P. A. Martin, J. Appl. Mech., 2014, 81 Search PubMed.
- C. Xu, K. Märker, J. Lee, A. Mahadevegowda, P. J. Reeves, S. J. Day, M. F. Groh, S. P. Emge, C. Ducati, B. Layla Mehdi, C. C. Tang and C. P. Grey, Nat. Mater., 2021, 20, 84–92 CrossRef CAS PubMed.
- M. T. McDowell, MRS Bull., 2020, 45, 889–890 CrossRef.
- W. H. Woodford, W. C. Carter and Y.-M. Chiang, Energy Environ. Sci., 2012, 5, 8014–8024 RSC.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS.
- B. Koo, H. Kwon, Y. Kim, H. G. Seo, J. W. Han and W. Jung, Energy Environ. Sci., 2018, 11, 71–77 RSC.
- E. Mishuk, A. Ushakov, E. Makagon, S. R. Cohen, E. Wachtel, T. Paul, Y. Tsur, V. Y. Shur, A. Kholkin and I. Lubomirsky, Adv. Mater. Interfac., 2019, 6, 1801592 CrossRef.
- E. Makagon, E. Wachtel, L. Houben, S. R. Cohen, Y. Li, J. Li, A. I. Frenkel and I. Lubomirsky, Adv. Funct. Mater., 2021, 31, 2006712 CrossRef CAS.
- N. Manca, G. Mattoni, M. Pelassa, W. J. Venstra, H. S. J. van der Zant and A. D. Caviglia, ACS Appl. Mater. Interfaces, 2019, 11, 44438–44443 CrossRef CAS PubMed.
- A. A. Bukharaev, A. K. Zvezdin, A. P. Pyatakov and Y. K. Fetisov, Phys. Usp., 2018, 61, 1175–1212 CrossRef CAS.
- S. Kim, S. J. Choi, K. Zhao, H. Yang, G. Gobbi, S. Zhang and J. Li, Nat. Commun., 2016, 7, 10146 CrossRef CAS PubMed.
- Y. M. Gerbshtein, N. E. Timoshchenko, A. D. Muradov and A. Z. Rakhimbekov, Phys. Solid State, 1997, 39, 521–527 CrossRef.
- J. R. Petrie, H. Jeen, S. C. Barron, T. L. Meyer and H. N. Lee, J. Am. Chem. Soc., 2016, 138, 7252–7255 CrossRef CAS PubMed.
- U. Aschauer, R. Pfenninger, S. M. Selbach, T. Grande and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054111 CrossRef.
- A. Marthinsen, C. Faber, U. Aschauer, N. A. Spaldin and S. M. Selbach, MRS Commun., 2016, 6, 182–191 CrossRef CAS.
- R. U. Chandrasena, W. Yang, Q. Lei, M. U. Delgado-Jaime, K. D. Wijesekara, M. Golalikhani, B. A. Davidson, E. Arenholz, K. Kobayashi, M. Kobata, F. M. F. de Groot, U. Aschauer, N. A. Spaldin, X. Xi and A. X. Gray, Nano Lett., 2017, 17, 794–799 CrossRef CAS PubMed.
- K. Wen, W. Lv and W. He, J. Mater. Chem. A, 2015, 3, 20031–20050 RSC.
- A. N. Morozovska, E. A. Eliseev and S. V. Kalinin, Appl. Phys. Lett., 2010, 96, 222906 CrossRef.
- E. Strelcov, S. M. Yang, S. Jesse, N. Balke, R. K. Vasudevan and S. V. Kalinin, Nanoscale, 2016, 8, 13838–13858 RSC.
- S. Kalinin, N. Balke, S. Jesse, A. Tselev, A. Kumar, T. M. Arruda, S. Guo and R. Proksch, Mater. Today, 2011, 14, 548–558 CrossRef CAS.
- S. Doria, N. Yang, A. Kumar, S. Jesse, A. Tebano, C. Aruta, E. Di Bartolomeo, T. M. Arruda, S. V. Kalinin, S. Licoccia and G. Balestrino, Appl. Phys. Lett., 2013, 103, 171605 CrossRef.
- D. O. Alikin, A. V. Ievlev, S. Y. Luchkin, A. P. Turygin, V. Y. Shur, S. V. Kalinin and A. L. Kholkin, Appl. Phys. Lett., 2016, 108, 113106 CrossRef.
- A. Kumar, F. Ciucci, A. N. Morozovska, S. V. Kalinin and S. Jesse, Nat. Chem., 2011, 3, 707–713 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta08407k |
| This journal is © The Royal Society of Chemistry 2022 |
