Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling the fluorescence quantum yields of benzothiazole-difluoroborates by optimal substitution†
Patryk
Rybczyński‡
a,
Manon H. E.
Bousquet‡
b,
Anna
Kaczmarek-Kędziera
a,
Beata
Jędrzejewska
 c,
Denis
Jacquemin
c,
Denis
Jacquemin
 *bd and
Borys
Ośmiałowski
*bd and
Borys
Ośmiałowski
 *a
*a
aFaculty of Chemistry, Nicolaus Copernicus University in Toruń, Gagarina Street 7, 87-100 Toruń, Poland. E-mail: borys.osmialowski@umk.pl
bNantes Université, CNRS, CEISAM UMR 6230, F-44000 Nantes, France. E-mail: Denis.Jacquemin@univ-nantes.fr
cBydgoszcz University of Science and Technology, Faculty of Chemical Technology and Engineering, Seminaryjna 3, 85-326 Bydgoszcz, Poland
dInstitut Universitaire de France (IUF), Paris, FR-75005, France
First published on 24th October 2022
Abstract
Precise tuning of the fluorescence quantum yield, vital for countless applications of fluorophores, remains exceptionally challenging due to numerous factors affecting energy dissipation phenomena often leading to its counterintuitive behavior. In contrast to the absorption and emission wavelength which can be precisely shifted to the desired range by simple structural changes, no general strategy exists for controllable modification of the fluorescence quantum yield. The rigidification of the molecular skeleton is known to usually enhance the emission and can be practically realized via the limiting molecular vibrations by aggregation. However, the subtle balance between the abundant possible radiative and non-radiative decay pathways makes the final picture exceptionally sophisticated. In the present study, a series of nine fluorophores obtained by peripheral substitution with two relatively mild electron donating and electron withdrawing groups are reported. The obtained fluorescence quantum yields range from dark to ultra-bright and the extreme values are obtained for the isomeric molecules. These severe changes in emission efficiency have been shown to arise from the complex relationship between the Franck–Condon excited state and conical intersection position. The experimental findings are rationalized by the advanced quantum chemical calculations delivering good correlation between the measured emission parameters and theoretical radiative and internal conversion rate constants. Therefore, the described substituent exchange provides a method to rigorously adjust the properties of molecular probes structurally similar to thioflavin T.
1 Introduction
The fine-tuning of light emission of organic dyes is a subject of intensive research due to the rapid development of myriads of fluorescence- and phosphorescence-based technologies. Efforts are focused on optimizing the synthetic methods, improving the purification processes, and, of course, performing structural modifications allowing tailoring the dyes to meet the market demands. Starting from a known emissive core, such an optimization can be achieved through various structural changes including the introduction of side substituent(s), the elongation of the π-conjugation path, atom exchange in the emitter, doubling the acceptor core, etc.1–4 Among the available fluorescent cores, the BODIPY family, that contains a BF2 group providing both improved rigidity and electron-withdrawing character, is clearly one of the most popular platforms.5,6 This stems from the high fluorescence quantum yield of the parent BODIPY molecule (close to 100%), and the many synthetic approaches that have been developed for modifying BODIPYs. It is therefore not surprising that BODIPY derivatives are now used in countless areas such as chemosensing,7,8 bioimaging,9,10 photodynamic therapy,11,12 and redox batteries.13 For BODIPYs, like for other dyes, it is generally rather straightforward to predict the impact of chemical modifications on the absorption and emission wavelengths. For instance, longer π-conjugation paths typically redshift the fluorescence,14,15 while the same may be realized for absorption and emission peaks by introducing an intramolecular charge-transfer (ICT) state caused by an electron acceptor (A) and electron donor (D) attached at two extremities of a dye. In contrast, intuitively predicting the variations of the fluorescence quantum yield (ϕf) remains very challenging. For instance, it is known that more rigid molecules exhibit higher ϕf and that redshifting the emission, for instance through a D–A strategy, typically yields a smaller ϕf (the so-called “energy-gap law”), yet these rules-of-thumb remain qualitative, often fail, and are typically not very helpful for practical design. This is because ϕf depends on all non-radiative pathways and their balance,16 so that subtle chemical changes might open (or close) some specific routes or, more often, tilt the radiative/non-radiative balance in an unexpected direction. In this framework, it is interesting to stress that first-principles calculations face exactly the same challenges as chemical intuition: whilst emission energies and band shapes can typically be predicted with sufficient reliability for dye design,17 accurate ab initio predictions of ϕf are in their infancy.18–26 Likewise, one might wish to turn towards machine learning approaches, but yet again, they suffer from the same bias: reliable predictions can be obtained for wavelengths, much less so for ϕf.27,28Among the ICT dyes, thioflavin T (TT) attracted attention as a dye used for investigating amyloid β (Aβ) aggregation29–31 but its usage is not limited to amyloids.32 TT is fluorescent but with a low quantum yield in water,33 while its brightness significantly improves after aggregation with amyloids, with a ϕf reaching ca. 45%.34 The aggregation induced emission (AIE) mechanism35,36 responsible for this behavior is related to the restriction of molecular motions that inhibit the emission in solution.37 Indeed, the non-radiative processes in TT are driven not only by solute–solvent interactions but also by the rotation around a single bond present in its structure,38,39 and this rotation is hampered in the aggregated state (see below). From the structural point of view the common feature of many molecules used in studies of Aβ and its aggregation is the presence of a benzothiazole core.40–42 This applies to TT that contains a positively charged benzothiazole moiety coupled to a strong electron donating group, namely the N,N-dimethylamino moiety. In several other series of benzothiazole-based fluorophores a specific twisting mode controls (and often limits) the ϕf.43 In TT, and in many other compounds, the introduction of the strong electron-donating NMe2 moiety advantageously maximizes the ICT and redshifts the emission bands, but unfortunately also reduces ϕf in most solvents,33 in part due to the enhanced molecular motions. In contrast, weaker donors might not deliver the desired absorption and emission in the red part of the spectrum. In the same vein, it is also known that most compounds containing the strong electron-accepting NO2 group fluoresce weakly,44 besides few exceptions.45 Therefore, the elimination of the strongest D/A groups from the fluorophore together with the use of multiple substitutions could a priori be a smart strategy to bathochromically shift the emission while maintaining a relatively large ϕf. Yet again, such “deduction” remains of qualitative nature only.
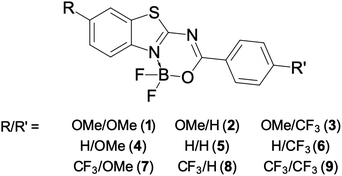
The current investigation tackles the impact of double substitution (Fig. 1) on a structural core greatly inspired by TT. The BF2 group was introduced to rigidify the skeleton, delivering a core structure combining the advantages of both the BODIPY core and TT. Still, one “twistable” single bond is present in these molecules, which might allow significant relaxation in the excited-state.
Our global target is to understand how the photophysical properties can be controlled by substitution with a rather mild donor (OMe, which is much weaker than NMe2) and an inductive acceptor (CF3, which is also much less potent than NO2; CF3 has typically a trifling impact on absorption and emission wavelengths). In more detail, our main goals are: (i) to determine to what extent extremely strong donors or acceptors are mandatory for tuning the photophysical properties of dyes; (ii) to check if the substitution pattern in isomeric molecules significantly impacts their emissive properties; and (iii) to test the molecules topologically similar to TT for their use in various environments. The OMe and CF3 groups are introduced systematically in the two substitution points (R and R′ in Fig. 1), namely the benzothiazole fragment (R) and the para position of the phenyl ring (R′). The simple exchange of the selected groups between R and R′ in Fig. 1 provides a set of nine compounds exhibiting, as we detail below, non-intuitive patterns in terms of photophysical properties.
2 Results and discussion
2.1 Experimental
The synthesis of all derivatives is described in the Experimental details section. The key photophysical properties of all dyes measured in chloroform are collected in Table 1. The corresponding absorption (black, solid), emission (red) and the mirrored emission spectra (black, dashed) are shown in Fig. 2.| Compound (R/R′) | λ absmax | ε | λ emmax | Δ SS | ϕ f | FWHMabs | FWHMem | Topology |
|---|---|---|---|---|---|---|---|---|
| 1 (OMe/OMe) | 368.0 | 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
454.5 | 5172 | 13.1 | 4246 | 4519 | DAD |
| 2 (OMe/H) | 361.0 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
458.5 | 5891 | 0.9 | 4691 | 4586 | DA– |
| 3 (OMe/CF3) | 367.0 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
491.5 | 6902 | 0.4 | 5046 | 4229 | DAA |
| 4 (H/OMe) | 364.0 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
419.5 | 3635 | 75.6 | 3722 | 4253 | –AD |
| 5 (H/H) | 343.0 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
439.5 | 6401 | 6.9 | 4269 | 5245 | –A– |
| 6 (H/CF3) | 345.0 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
447.0 | 6614 | 0.4 | 4602 | 5130 | –AA |
| 7 (CF3/OMe) | 362.5 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
412.0 | 3314 | 98.0 | 3465 | 3622 | AAD |
| 8 (CF3/H) | 339.5 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
406.0 | 4825 | 28.0 | 4159 | 4972 | AA– |
| 9 (CF3/CF3) | 341.0 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
434.5 | 6311 | 4.7 | 4361 | 5347 | AAA |
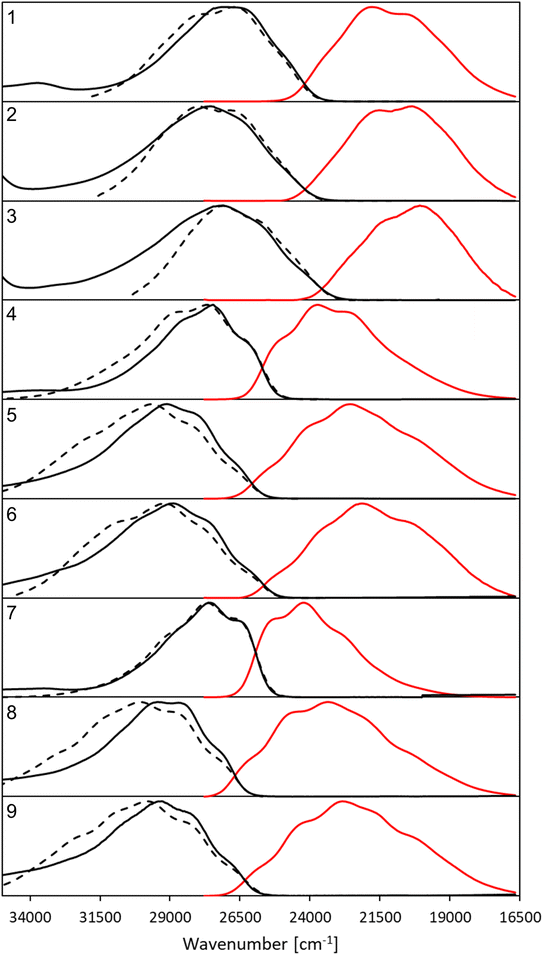 | ||
| Fig. 2 Normalized, corrected absorption (solid black line), fluorescence (solid red line) and mirror-image of fluorescence spectra (dashed black line) shifted to match the 0–0 point in CHCl3. | ||
All compounds exhibit a main absorption band between 340 and 370 nm. It is noteworthy that the H-to-CF3 substitution has always a very mild impact on both the absorption position and the band shape, whereas the use of the donating OMe group induces noticeable changes, as it tends to bathochromically move the absorption by ca. 20–30 nm (Fig. 2). Interestingly, dye 1, that has a DAD quadrupolar topology, presents the most redshifted absorption band, the traditional push–pull strategy represented by compounds 3 and 7 being slightly less effective. This confirms that the BF2-substituted benzothiazole is a strongly electron-withdrawing moiety. Notably the intensity of the absorption, as given by ε, can be maximized by plugging a methoxy group on the phenyl side (at R′) irrespective of the group substituting the benzothiazole. Nevertheless the ε always remains in the 30–80 × 103 M−1 cm−1 regime, values that are typical of conjugated organic dyes. The substitution of OMe by H and then by CF3 in the sub-series (1–3, 4–6, 7–9, see Table 1) always delivers broader absorption bands.
Let us now turn to emission. While, in general, λemmax values are more variable across the series than their absorption counterparts, the changes in fluorescence spectra remain rather mild for the nine compounds studied herein (Fig. 2). As for the absorption, the influence of the CF3 group is weak, whereas OMe has a more clearly detectable (bathochromic) effect, especially when added to the benzothiazole side (R). The presence of the methoxy also partially washes out the vibronic progression. It is 3 that delivers the largest λemmax. Nevertheless, one should be cautious in interpreting directly the λemmax listed in Table 1. Indeed, as can be seen in Fig. 2, the relative heights of the various vibronic peaks may differ from one compound to another, indicating that the λemmax, related to the most intense vibronic transition, could significantly change, while the actual energy shift between the electronic states (the bands) is mild. In any case, Fig. 2 indicates that the emission and absorption bands are close to mirror-shape hinting that the geometry of the emissive state should not (too) strongly differ from its absorption counterpart. We note that this mirror-shape trend is especially close to perfection for 7 that also displays a notably smaller Stokes shift than the other derivatives. On the other hand, the largest value of the Stokes shift is noted for 3, the only molecule that shows a broader absorption spectrum than the emission. For all dyes, and for both absorption and emission, the full width at half maximum (FWHM) values are in the 3500–5500 cm−1 range, which is quite typical of such systems.
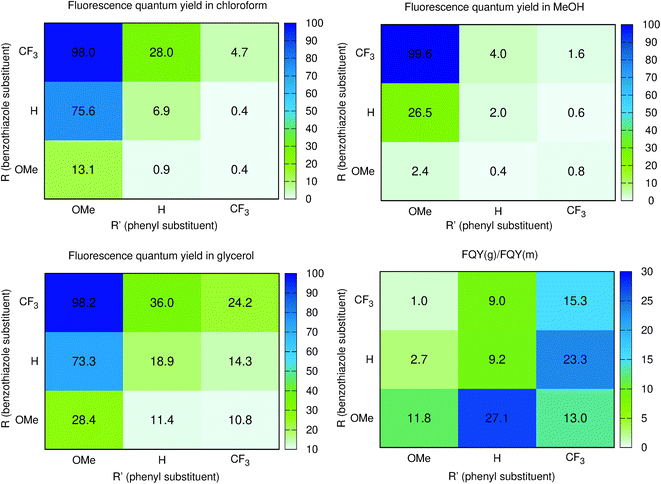
Until now, we have not unravelled any specific trends departing from “chemical expectations”, as one could clinically summarize the above findings by stating that all nine dyes share similar absorption and emission features but for slight/significant bathochromic/hyperchromic shifts induced by the methoxy donor. The picture is however much more blurred when investigating the fluorescence quantum yields listed in Table 1. Indeed ϕf is almost 100% for one of the push–pull dyes, 7, but close to zero for 3, presenting inverted R/R′ groups. From the data of Table 1, one can deduce that adding a methoxy substituent at R′ is beneficial in terms of brightness, irrespective of the group at R, whereas, in contrast, CF3 group at R position increases the ϕf. It is however not easy to interpret such a trend. A first explanation could be that the methoxy group favours a more quinoidal form on the side phenyl group in which the single bond separating the phenyl and benzothiazole moieties gains a double character, what, in turn decreases deleterious excited-state motions. Such changes of bonding pattern would however need to be quite drastic to explain the extreme changes of ϕf noted in the series. In such a scenario, one would also expect the FWHMs, which are roughly related to structural differences between the ground and excited states to significantly change, an unseen outcome. Indeed, the linear determination coefficient (R2) between ϕf and FWHMem is 0.50 only. Likewise, the “energy-gap law” is not very effective here, since the R2 obtained by a ϕf to λemmax relationship attains 0.44. The only experimental parameter nicely correlating with ϕf seems to be the Stokes shift (R2 = 0.88), but, as stated above, one should consider the λemmax with caution.
To obtain more insights into the relationship between the ϕf and molecular motions, changing the viscosity of the solution is a rather straightforward experimental approach. We therefore report in Fig. 3 and Table 2 a comparison between the ϕf measured in methanol and glycerol. We have used mixtures of methanol and glycerol to obtain media of controllable viscosity. This pair of solvents was selected as both are able to form hydrogen bonds due to their OH groups, allowing a smooth evolution of the solvents' physicochemical signatures. It is easy to notice that an increased viscosity positively influences the emission properties. Indeed as can be seen in Fig. S2†ϕf increases with the growing viscosity, giving good linear correlation coefficients for the doubly logarithmic plot of ϕf = f(η) except for 7, which exhibits practically a constant (close to 100%) fluorescence quantum yield irrespective of the medium. The observed relationships are in agreement with the ones of known viscosity-sensitive probes, in which the slope of the linear function is defined as a response factor of the probe.46 We therefore underline that, for the current series, the largest slopes are logically obtained for the weakest emitters in non-viscous solvents, i.e., 2 and 6. In contrast, as stated above, 7 enjoys a fluorescence dependent neither upon the modification of the hydrogen bonding nature of the solvent (CHCl3 to MeOH) nor upon the medium viscosity (MeOH vs. glycerol). This clearly suggests that several non-radiative mechanisms are at play in the series.
| Compound (R/R′) | ϕ f (m) | FWHMem (m) | FWHMem (g) | Log(ϕf) = f(log(η)) (slope) | |
|---|---|---|---|---|---|
| 1 (OMe/OMe) | 2.4 | 11.8 | 5320 | 5022 | 0.350 |
| 2 (OMe/H) | 0.4 | 27.1 | 5732 | 5202 | 0.441 |
| 3 (OMe/CF3) | 0.8 | 13.0 | 5394 | 5149 | 0.376 |
| 4 (H/OMe) | 26.5 | 2.7 | 5093 | 4570 | 0.148 |
| 5 (H/H) | 2.0 | 9.2 | 6735 | 5502 | 0.350 |
| 6 (H/CF3) | 0.6 | 23.3 | 6391 | 5559 | 0.463 |
| 7 (CF3/OMe) | 99.8 | 1.0 | 3585 | 3445 | 0.000 |
| 8 (CF3/H) | 4.0 | 9.0 | 6303 | 5364 | 0.306 |
| 9 (CF3/CF3) | 1.6 | 15.3 | 6631 | 5533 | 0.392 |
From the points of view of the photophysical properties of the dyes, we note that ϕf is very similar in chloroform (non-viscous, weakly hydrogen-bonding solvent) and glycerol (very viscous and strong hydrogen bonding solvent) for 4, 7, and 8. In contrast, a very low ϕf is recorded for 2, 3, and 6 in both chloroform and methanol but a reasonable increase is noticed in glycerol for these systems. The structural features for those compounds clearly differ from those of 4, 7, and 8, with a donor on the benzothiazole and an electron acceptor on the phenyl or both. This means that reversing the substitution of the acceptor and donor allows going from normal compounds to structures behaving like molecular rotors sensitive to viscosity. Finally, the remaining 1, 5, and 9 are fluorescent in chloroform, very weakly emissive in methanol and their emission is much higher in glycerol. They are simultaneously sensitive to the hydrogen bonding/polar environment and viscosity (see Fig. S1†).
2.2 Theory
We have used ab initio calculations to probe the excited state (ES) features of all nine compounds. We have decided to consider CHCl3 as the medium for these simulations as the theoretical protocol relies on a continuum model for the environmental effects (see Experimental details section for technical specification). The careful inspection of the geometry of the investigated systems in the two electronic states confirms that the excitation promotes the p-quinoid form of the terminal phenyl ring. This can be deduced from the respective shortenings and elongations of the alternate C–C bonds to form the![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(–CH
C(–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–)2C
CH–)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) moiety. These changes are similar to those found previously in NMe2-substituted benzothiazole derivatives.47 Since one of the envisaged deactivation pathways involves the rotation of the phenyl ring, (TD-)DFT calculations have been performed to quantify the related rotation barrier. Full DFT geometry optimizations of the transition state for the rotation around the C–C bond (C15–C17 in Fig. S52†) provide a ground-state picture consistent with chemical intuition. Indeed, as can be seen in Fig. 4, increasing the electron-donating character of the substituent at R′ causes increase of the rotation barrier by ca. 2 kcal mol−1, irrespective of the group at R, which fits with the quinoidal picture leading to a strengthening of the inter-ring bond upon addition of a mesomeric donor at R′. We also note that increasing the electron-accepting character of the substituent at the benzothiazole moiety induces a slight increase of the barrier, but the effect (ca. 0.5 kcal mol−1) is insignificant for a DFT calculation. The largest ground-state barrier, 10.4 kcal mol−1, is observed for 7, the lowest one for 3, 7.68 kcal mol−1. If such a pattern seems to fit the observed ϕf ranking (larger barriers, larger emission yields), one has to remember that these values are valid for the ground electronic state, i.e., they are not representative of the structures of the emissive species.
moiety. These changes are similar to those found previously in NMe2-substituted benzothiazole derivatives.47 Since one of the envisaged deactivation pathways involves the rotation of the phenyl ring, (TD-)DFT calculations have been performed to quantify the related rotation barrier. Full DFT geometry optimizations of the transition state for the rotation around the C–C bond (C15–C17 in Fig. S52†) provide a ground-state picture consistent with chemical intuition. Indeed, as can be seen in Fig. 4, increasing the electron-donating character of the substituent at R′ causes increase of the rotation barrier by ca. 2 kcal mol−1, irrespective of the group at R, which fits with the quinoidal picture leading to a strengthening of the inter-ring bond upon addition of a mesomeric donor at R′. We also note that increasing the electron-accepting character of the substituent at the benzothiazole moiety induces a slight increase of the barrier, but the effect (ca. 0.5 kcal mol−1) is insignificant for a DFT calculation. The largest ground-state barrier, 10.4 kcal mol−1, is observed for 7, the lowest one for 3, 7.68 kcal mol−1. If such a pattern seems to fit the observed ϕf ranking (larger barriers, larger emission yields), one has to remember that these values are valid for the ground electronic state, i.e., they are not representative of the structures of the emissive species.
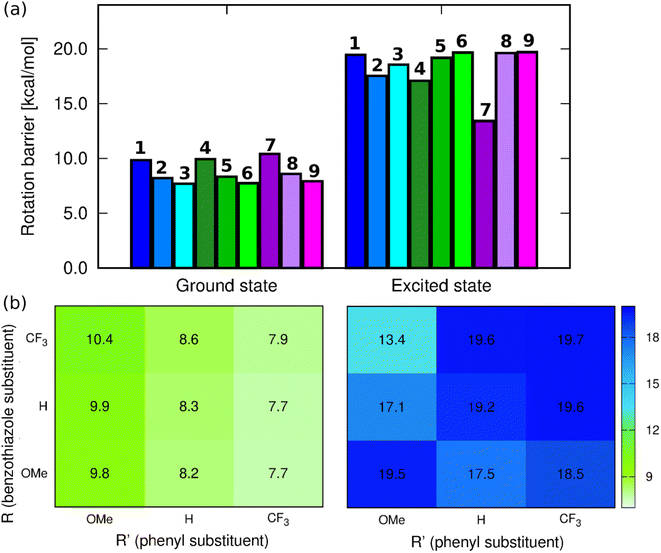 | ||
| Fig. 4 (a) Barriers for rotation around the C15–C17 bond computed at the PCM(CHCl3)-(TD-)MN15/6-311++G(d,p)) level for the ground and excited state geometries, (b) corresponding heatmaps. | ||
In contrast, the ES picture does not follow a clear systematic order nor correlates with the experimental ϕf (see Fig. 4). Interestingly, the ES rotation barriers are significantly higher than in the ground state, 8-out-of-9 exceeding 17 kcal mol−1, 7 being the only compound presenting a rather low ES barrier (13.4 kcal mol−1). If this smaller change of bond strength between the ground and excited states for 7 is consistent with the trends in the measured Stokes shift and almost perfect mirror symmetry of absorption and emission spectra, it is clearly not intuitive that the dye showing, by far, the lowest excited-state rotation barrier also displays the largest ϕf. We note that the increase of barriers after photon absorption is consistent with chemical intuition (π–π* excitation decreasing the bond length alternation) and also with the Wiberg bond indexes being larger by 0.1 to 0.2 in the excited than in the ground state, a statement holding for all molecules (see Table S4†).
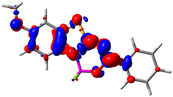
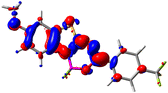
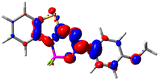
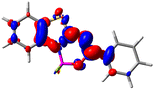
Let us now turn towards the charge transfer properties, i.e., the transferred charge, qCT, the distance between the barycenters of density gain and depletion, dCT, and the variation of the dipole moment between the states, Δμ. Table 3 reports these parameters together with density difference plots. The gain of density is always localized on the fluoroborate ring, whereas the loss of density varies from one compound to another, the role of the OMe group being clear. This is confirmed by the positions of the barycenters (see the ESI†): R+ remains almost unaffected by the variation of the substituents whereas R− depends on the considered dye. Among the analyzed fluorophores, the strongest photoinduced charge transfer appears for 3 which undergoes an 8.7 D dipole increase in the ES, corresponding to a displacement of 0.65e over 3.2 Å, quite large values in Le Bahers' model.49 There is a weak positive correlation between dCT and λemmax with an R2 of 0.61. Nevertheless, as for the barriers above, the CT parameters do not provide reasonable insights into the emission yields. Indeed, the R2 between the measured ϕf and dCT, qCT, and Δμ are all tiny: 0.12, 0.03, and 0.04, respectively. In other words, the magnitude of the charge-transfer does not control the fluorescence efficiency.
Given the above rather unfruitful attempts to rationalize the measured ϕf, we decided to search for the most accessible pathways allowing to directly go back from the excited to the ground electronic state through non-radiative decay. First, given the presence of a sulfur atom, we evaluated the possibility of intersystem crossing (ISC), by evaluating the singlet–triplet gap and the spin–orbit coupling (SOC) at the relaxed excited state geometry. The results are listed in Table 4. Only one triplet is below S1, and as can be seen in that table the gaps are typically quite large (at least 0.24 eV) while the SOC matrix elements are truly trifling (<0.05 cm−1). This strongly hints that ISC is not a major pathway for the considered systems.
| Compound (R/R′) | ΔES1–T1 | SOC | k r | k ic | k MECP | ϕ no-MECPf | ϕ MECPf | |
|---|---|---|---|---|---|---|---|---|
| a Computed considering only the radiative and internal conversion rates. b Considering the radiative, internal and MECP pathways. c SOC calculation did not converge. | ||||||||
| 1 (OMe/OMe) | 0.46 | 0.04 | 0.06 | 3.09 | 0.83 | 5060 | 79 | 0.0 |
| 2 (OMe/H) | 0.66 | 0.03 | −0.14 | 2.18 | 7.87 | ∞ | 22 | 0.0 |
| 3 (OMe/CF3) | 0.73 | 0.04 | −0.27 | 2.02 | 2.16 | ∞ | 48 | 0.0 |
| 4 (H/OMe) | 0.28 | 0.03 | 0.47 | 4.76 | 0.36 | 0.00 | 93 | 93 |
| 5 (H/H) | 0.44 | 0.03 | 0.12 | 3.21 | 0.57 | 682 | 85 | 0.1 |
| 6 (H/CF3) | 0.52 | 0.03 | −0.07 | 2.70 | 1.50 | ∞ | 64 | 0.0 |
| 7 (CF3/OMe) | 0.24 | 0.04 | 0.86 | 5.61 | 0.26 | 0.00 | 96 | 96 |
| 8 (CF3/H) | 0.36 | 0.56 | 3.92 | 0.28 | 0.00 | 93 | 93 | |
| 9 (CF3/CF3) | 0.44 | 0.04 | 0.10 | 2.78 | 2.14 | 1250 | 56 | 0.0 |
Next, we used spin-flip (SF) TD-DFT to locate the most accessible minimum energy crossing point (MECP) between the ground and excited states for all dyes. Indeed, several previous studies have demonstrated a direct relationship between the measured emission yield and the relative energy of the lowest MECP.18,21,50,51 Using the procedure described in the Experimental section, we found that this most accessible MECP corresponds, in all cases, to a strongly deformed geometry with an almost 90° kink between the two parts of the molecule (see Fig. 5). The relative SF-TD-DFT energies of this MECP and the S1 FC point are given in Table 4. Despite several attempts, we could not locate a proper transition state corresponding to the path to this MECP, likely indicating that the path is smooth and that these relative energies are indicators of the accessibility of this MECP. Interestingly, we note that the three dyes having an MECP more stable than the FC point are 2, 3, and 6, that is, the three experimentally “dark” compounds, i.e., compounds showing ϕf smaller than 1% (see Table 1). This is consistent with a downhill path to the MECP. Likewise, the three compounds for which reaching the MECP implies an energetic penalty larger than 0.3 eV, namely, 4, 8, and 7 are the only three showing rather large (>25%) ϕf in the experiment. We note that this is the first clear correlation between theoretical estimates and experimental ϕf found in this work. It is worth noting that the R2 = 0.81 for the correlation between these energies and the measured ϕf (in glycerol); a very similar value (R2 = 0.78) is obtained in chloroform which was used in measurements and calculations. The slightly higher value for glycerol may be due to the higher rigidity of the molecules in that solvent, a feature of well-defined geometry as in calculations limiting additional dynamic effects associated with energy dissipation.
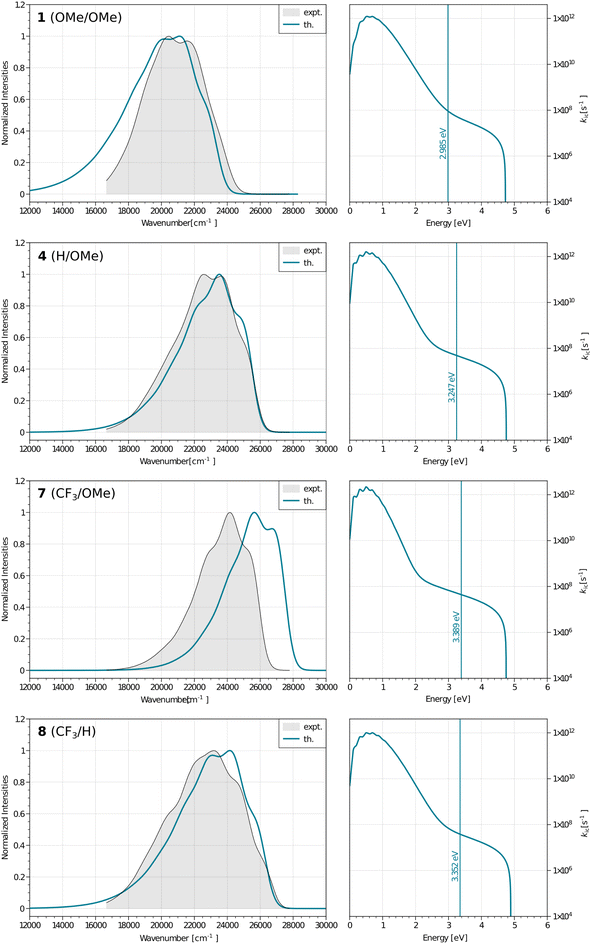
To go further, we have used Peng and Shuai's TVCF formalism to model both the radiative and internal conversion rates of all dyes on an equal footing (again see the Experimental section for details).52,53 Such calculations involve the calculations of vibronic couplings on the basis of harmonic vibrational frequencies, as well as the selection of models for the coupling between the potential energy surfaces, the coordinates, etc. After some tests, we have chosen the most refined model (so-called adiabatic Hessian), in a time-dependent framework and selected Cartesian coordinates – the computed rates are listed in Table 4. In Fig. 6, one can find comparisons between the theoretical and experimental emission lineshapes for the four brightest derivatives and the agreement gives confidence that theory correctly describes the vibronic couplings for the present class of derivatives. The ab initio radiative rates are in the 108 s−1 range, which fits the experimental trends (see the ESI†), the largest value being computed for 7, 5.61 × 108 s−1, a result perfectly consistent with the measurement, 5.93 × 108 s−1. The R2 between experiment and theory for the kr attains a very satisfying 0.87 value. We note nevertheless that the absolute magnitudes of the theoretical radiative rates significantly overestimate their experimental counterparts for the poorly emissive dyes, but for these almost dark compounds the experimental error bar becomes (much) larger, so it is not so straightforward to pinpoint if theory or experiment is faulty in that case. The internal conversion rates, kic, measure the non-radiative deactivation through non-adiabatic couplings between the excited and ground states. The computed values are in the 2 × 107 to 8 × 108 s−1 range (see Table 4), i.e., cover a quite broad panel of values, yet these kic have in general no direct experimental counterparts. In addition, we wish to stress the inherent limits of theory in evaluation of this rate, as it is rather common that kic strongly depends on the selected broadening, in contrast to kr.22 In the ESI Tables S6 and S7,† we provide comparisons between IC rates computed with different vibronic models, and one notices that the IC rate varies significantly depending on the selected model, but those changes do not impact the relatively poor correlation with experimental data.
By computing the ϕf on the basis of radiative and internal conversion rates only, one can estimate the emission yield if no other non-radiative processes take place, meaning, in the present case, that the MECPs would always be inaccessible. In this way, too large ϕf values are obtained but one notices that a value of 96%, consistent with the measurements, is determined for 7 which also presents the least accessible MECP (see above). Finally, it is possible to compute the non-radiative rate constant related to the MECP simply using
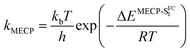 | (1) |
3 Conclusions and outlook
The series of benzothiazoles considered here shows that the fluorescence quantum yield may be tuned systematically and strongly by exchanging two (relatively mild) groups located on the periphery of the structures only. From the intuitive point of view this seems to be realised by modifying the height of the rotation barrier around the only single bond in the structure, as a viscous environment is beneficial for the brightness of the synthesized dyes, indicating the presence of significant detrimental motions. However, theoretical calculations indicate that these motions correspond to the kinking of the structure around the single bond, rather than a rotation. Indeed, the difference of excited state energy between the FC point and the minimum energy crossing point between ground and excited states strongly correlates with experimental fluorescence quantum yield. This correlation is even higher in viscous environments. We conclude that simple substituent exchange by no means induces an intuitive effect though such an approach delivers significant changes in the emission. The current series undoubtedly shows that substituents being not particularly potent ones in light of their electronic effects may be applied to cover the full range of emission quantum yields. This feature may be further adapted in the design of rotor-based/conical intersection-tuned emitters capable of sensing the viscosity and aggregation, and thus in molecular probes for a variety of needs including biochemistry-oriented ones.4 Experimental details
4.1 Synthesis and structure confirmation
All substrates for the synthesis (amines and benzoyl chlorides) and solvents were obtained from commercial sources. The studied series of compounds was obtained by a two-step synthesis. The amide: to a solution of 2-aminobenzothiazole (1 eq.) and triethylamine (2 eq.) in dry THF (20 ml, −78 °C, under an inert gas) the respective benzoyl chloride (1 eq.) was added dropwise (in dry THF). The mixture was allowed to warm to room temperature and stirred overnight. The solvent was evaporated and the residue extracted using DCM/NaHCO3 water solution. After evaporation of the organic layer the compound was purified by column chromatography (eluent hexane/ethyl acetate). In the second step, the appropriate amide was complexed with BF3·OEt2. The etherate was added dropwise to a mixture of amide (1 eq.) and diisopropylethylamine (3 eq.) in DCM (20 ml, room temperature). The reaction mixture was stirred overnight and then the DCM was evaporated. The compound was purified by column chromatography (SiO2, eluent DCM).The structure of the synthesized compounds was confirmed by NMR and MS techniques. All of the NMR spectra were recorded at 400 MHz or 700 MHz on a Bruker spectrometer at room temperature in CDCl3. HRMS data were obtained with a Waters spectrometer in the EI mode. The melting points were measured using a Stuart SMP50 Digital Melting Point Instrument.
4.2 Optical measurements
UV-vis absorption spectra of ca. 10−5 M solutions of dyes were recorded in quartz cells (1 cm) using a Shimadzu UV-1900 spectrometer. Fluorescence spectra of ca. 10−6 M solutions of complexes were recorded in quartz cells (1 cm) using an FS5 fluorimeter (Edinburgh Instruments). Fluorescence quantum yield measurements were carried out on the same equipment with the use of an integrating sphere. Time-correlated single-photon counting measurements were performed with an Edinburgh Analytical Instruments F920P spectrometer. Samples were excited at 373 nm using a laser diode. The emission intensity was recorded at fluorescence maximum wavelength. A solution of colloidal silica was used to obtain the instrument response function (IRF). Fluorescence lifetimes were calculated using the FAST software.4.3 Calculations
Geometry optimizations of the ground and excited state have been performed within the (TD-)MN15 (ref. 54) approach known to deliver especially accurate energies for compounds of the family investigated here55 using either the 6-311++G(d,p) or 6-311+G(d,p) basis sets, the former being applied for CT parameters and rotational barrier, the (more compact) latter for (the more expensive) vibronic calculations. The solvent was modelled through the well-known Polarizable Continuum Mode (PCM),56 selecting chloroform. The character of the stationary points on the potential energy surface has been confirmed with the harmonic vibrational analysis. The rotation barriers have been estimated by the optimization of the geometry of the transition state for the phenyl ring rotation around the C15–C17 bond (for atom numbering see Fig. S52†). All these calculations have been carried out with Gaussian16.57 The SOC matrix elements were determined at the M06-2X/def2-TZVP level58 using ORCA.5.0.1 (ref. 59) with CHCl3 as the solvent as modelled with the SMD solvation model. The RIJCOSX method was used to accelerate the calculation, and DefGrid3 and TightSCF settings were applied, whereas TDA was turned off. The S–T gaps were evaluated using SCS-CC2/aug-cc-pVTZ (in the gas phase)60,61 because this method performs especially well for these gaps.62 These SCS-CC2 calculations were performed with Turbomole 7.3.63 Given that ISC typically occurs after geometry relaxation in organic dyes (free of heavy elements), these calculations have been performed on the ES minima. For the MECP search, we used the Q-Chem 5.4 code,64 applying the same level of theory as above, that is PCM-MN15/6-311+G(d,p), using the spin-flip approach. We considered four roots, applied the branching plane approach to locate the MECP, and searched for the MECP between the two lowest singlet states, defined with a spin-contamination threshold of 1.2. Default Q-Chem parameters were otherwise applied. In practice the MECP search was first performed with the non-substituted 5, exploring a large number of possible deformations as the starting point (kinked structures twisting various moieties, hydrogen atoms moved out of plane, elongated bonds, etc.). It is indeed our experience that starting from the FC geometry does not necessarily yield the lowest MECP, especially for quasiplanar systems. This allowed the determination of the most accessible MECP. Starting from there, the MECPs of all other compounds were searched for. The energy difference between the MECP and the excited-state minimum was determined through PCM-SF-TD-MN15/6-311+G(d,p) single point calculations performed on the optimal excited-state structure found by conventional TD-DFT (see above) and on the SF-TD-DFT optimized MECP. All the vibronic calculations have been carried out using FCClasses 3 (v3-0.1-216-g29ba701).65 Both the adiabatic and vertical Hessian PES approximations (AH and VH, respectively) have been originally used along with the Time-Dependent (TD)66 and Time-Independent (TI)67,68 formalisms (see also below). Considering the large oscillator strength values (f > 0.5, typically ca. 0.8–1.2), the Herzberg–Teller effects were neglected. We used geometries, gradients, and Hessians computed at the PCM-MN15/6-311+G(d,p) level, and further corrected the energies and transition dipole moment using gas-phase CC2/aug-cc-pVTZ results. These CC2 calculations were performed in an effort to improve the accuracy and were made with Turbomole. Regarding the pre-screening parameters of FCClasses we used Cmax1 = 30, Cmax2 = 25 for the maximum number of integrals in both C1 and C2 classes and we set the threshold to select the thermally excited initial states to 0.8. The number of maximum integrals was set to 106 for the routine TI calculation. All the emission spectra were convoluted with a Gaussian broadening of 450 cm−1 to ensure matching with experimental data. The Internal Conversion (IC) spectra use a 10 cm−1 Lorentzian broadening, a typical choice.69 In order to select the appropriate vibronic model we carried out some tests on 4, H/OMe (the corresponding spectra shown in the ESI†). Since a better convergence of the TI spectra was obtained within the AH approximation, as well as the expected shape of the kICversus energy plot, we pursued the work using TD AH|FC formalism, which we report in the body of the text.Data availability
Additional computational data are available upon request to DJ while experimental ones from BO.Author contributions
PR: investigation, formal analysis, validation, visualization, writing – original draft preparation; MHEB: investigation, formal analysis, validation, visualization, writing – original draft preparation; AKK: investigation, visualization, writing – original draft preparation; BJ: investigation, formal analysis, writing – review & editing; DJ: conceptualization, methodology, resources, writing – original draft preparation, supervision; BO: conceptualization, project administration, methodology, resources, writing – original draft preparation, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MHEB and DJ are indebted to Dr R. Zaleśny (Wrocław) for fruitful discussions on the convergence of vibronic calculations and to Dr F. Santoro and J. Cerezo for making their great code available to them. We are very indebted for the financial support of research from the National Science Centre (project no. 2021/43/B/ST5/00753). Wrocław Centre for Networking and Supercomputing and Nantes' Glicid/CCIPL computational centers are gratefully acknowledged for the generous allotment of computational resources.Notes and references
- B. Jędrzejewska, A. Skotnicka, A. D. Laurent, M. Pietrzak, D. Jacquemin and B. Ośmiałowski, J. Org. Chem., 2018, 83, 7779–7788 CrossRef PubMed.
- R. Hu, E. Lager, A. Aguilar-Aguilar, J. Liu, J. W. Y. Lam, H. H. Y. Sung, I. D. Williams, Y. Zhong, K. S. Wong, E. Peña-Cabrera and B. Z. Tang, J. Phys. Chem. C, 2009, 113, 15845–15853 CrossRef CAS.
- Y. Kage, S. Kang, S. Mori, M. Mamada, C. Adachi, D. Kim, H. Furuta and S. Shimizu, Chem.–Eur. J., 2021, 27, 5259–5267 CrossRef CAS PubMed.
- Z. Shi, X. Han, W. Hu, H. Bai, B. Peng, L. Ji, Q. Fan, L. Li and W. Huang, Chem. Soc. Rev., 2020, 49, 7533–7567 RSC.
- R. Ziessel, G. Ulrich and A. Harriman, New J. Chem., 2007, 31, 496–501 RSC.
- A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS PubMed.
- P. Kaur and K. Singh, J. Mater. Chem. C, 2019, 7, 11361–11405 RSC.
- Q. Li, Y. Guo and S. Shao, Sens. Actuators, B, 2012, 171–172, 872–877 CrossRef CAS.
- Z. Shi, X. Han, W. Hu, H. Bai, B. Peng, L. Ji, Q. Fan, L. Li and W. Huang, Chem. Soc. Rev., 2020, 49, 7533–7567 RSC.
- S. Kolemen and E. U. Akkaya, Coord. Chem. Rev., 2018, 354, 121–134 CrossRef CAS.
- J. Zou, Z. Yin, K. Ding, Q. Tang, J. Li, W. Si, J. Shao, Q. Zhang, W. Huang and X. Dong, ACS Appl. Mater. Interfaces, 2017, 9, 32475–32481 CrossRef CAS PubMed.
- A. Kamkaew, S. H. Lim, H. B. Lee, L. V. Kiew, L. Y. Chung and K. Burgess, Chem. Soc. Rev., 2013, 42, 77–88 RSC.
- A. M. Kosswattaarachchi, A. E. Friedman and T. R. Cook, ChemSusChem, 2016, 9, 3317–3323 CrossRef CAS PubMed.
- E. Deniz, G. C. Isbasar, Ö. A. Bozdemir, L. T. Yildirim, A. Siemiarczuk and E. U. Akkaya, Org. Lett., 2008, 10, 3401–3403 CrossRef CAS PubMed.
- P. Verwilst, H.-R. Kim, J. Seo, N.-W. Sohn, S.-Y. Cha, Y. Kim, S. Maeng, J.-W. Shin, J. H. Kwak, C. Kang and J. S. Kim, J. Am. Chem. Soc., 2017, 139, 13393–13403 CrossRef CAS PubMed.
- B. Valeur, Molecular Fluorescence: Principles and Applications, Wiley-VCH, Weinheim, 2002 Search PubMed.
- F. Santoro and D. Jacquemin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 460–486 CAS.
- A. Prlj, A. Fabrizio and C. Corminboeuf, Phys. Chem. Chem. Phys., 2016, 18, 32668–32672 RSC.
- A. Prlj, L. Vannay and C. Corminboeuf, Helv. Chim. Acta, 2017, 100, e1700093 CrossRef.
- Z. Lin, A. W. Kohn and T. Van Voorhis, J. Phys. Chem. C, 2020, 124, 3925–3938 CrossRef CAS.
- Q. Ou, Q. Peng and Z. Shuai, J. Phys. Chem. Lett., 2020, 11, 7790–7797 CrossRef CAS PubMed.
- A. Humeniuk, M. Bužančić, J. Hoche, J. Cerezo, R. Mitrić, F. Santoro and V. Bonačić-Koutecký, J. Chem. Phys., 2020, 152, 054107 CrossRef CAS PubMed.
- K. Veys and D. Escudero, J. Phys. Chem. A, 2020, 124, 7228–7237 CrossRef CAS PubMed.
- J. S. A. Badaro, B. Koszarna, M. H. E. Bousquet, E. T. Ouellette, D. Jacquemin and D. T. Gryko, Org. Chem. Front., 2022, 9, 1861–1874 RSC.
- K. V. Vygranenko, Y. M. Poronik, M. H. E. Bousquet, O. Vakuliuk, D. Jacquemin and D. T. Gryko, Chem. Commun., 2022, 58, 1542–1545 RSC.
- M. Krzeszewski, S. Modrzycka, M. H. E. Bousquet, D. Jacquemin, M. Drąg and D. T. Gryko, Org. Lett., 2022, 24, 5602–5607 CrossRef CAS PubMed.
- C.-W. Ju, H. Bai, B. Li and R. Liu, J. Chem. Inf. Model., 2021, 61, 1053–1065 CrossRef CAS PubMed.
- J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427–438 CrossRef CAS PubMed.
- H. Levine III, Protein Sci., 1993, 2, 404–410 CrossRef PubMed.
- M. Biancalana and S. Koide, Biochim. Biophys. Acta, 2010, 1804, 1405–1412 CrossRef CAS PubMed.
- H. Levine III, Arch. Biochem. Biophys., 1997, 342, 306–316 CrossRef PubMed.
- S. Verma, V. Ravichandiran and N. Ranjan, Biochimie, 2021, 190, 111–123 CrossRef CAS PubMed.
- N. Amdursky, Y. Erez and D. Huppert, Acc. Chem. Res., 2012, 45, 1548–1557 CrossRef CAS PubMed.
- A. I. Sulatskaya, A. A. Maskevich, I. M. Kuznetsova, V. N. Uversky and K. K. Turoverov, PLoS One, 2010, 5, 1–7 CrossRef PubMed.
- G. R. Suman, M. Pandey and A. S. J. Chakravarthy, Mater. Chem. Front., 2021, 5, 1541–1584 RSC.
- J. Mei, N. L. C. Leung, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Chem. Rev., 2015, 115, 11718–11940 CrossRef CAS PubMed.
- L. S. Wolfe, M. F. Calabrese, A. Nath, D. V. Blaho, A. D. Miranker and Y. Xiong, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16863–16868 CrossRef CAS PubMed.
- V. I. Stsiapura, A. A. Maskevich, S. A. Tikhomirov and O. V. Buganov, J. Phys. Chem. A, 2010, 114, 8345–8350 CrossRef CAS PubMed.
- V. I. Stsiapura, A. A. Maskevich, V. A. Kuzmitsky, V. N. Uversky, I. M. Kuznetsova and K. K. Turoverov, J. Phys. Chem. B, 2008, 112, 15893–15902 CrossRef CAS PubMed.
- H. F. Kung, ACS Med. Chem. Lett., 2012, 3, 265–267 CrossRef CAS PubMed.
- N. S. Mason, C. A. Mathis and W. E. Klunk, J. Labelled Compd. Radiopharm., 2013, 56, 89–95 CrossRef CAS PubMed.
- S. Noël, S. Cadet, E. Gras and C. Hureau, Chem. Soc. Rev., 2013, 42, 7747–7762 RSC.
- S. Gao, Y. Ma and W. Lin, Anal. Methods, 2019, 11, 2626–2629 RSC.
- M.-C. Chen, D.-G. Chen and P.-T. Chou, ChemPlusChem, 2021, 86, 11–27 CrossRef CAS PubMed.
- K. Skonieczny, I. Papadopoulos, D. Thiel, K. Gutkowski, P. Haines, P. M. McCosker, A. D. Laurent, P. A. Keller, T. Clark, D. Jacquemin, D. M. Guldi and D. T. Gryko, Angew. Chem., Int. Ed., 2020, 59, 16104–16113 CrossRef CAS PubMed.
- S. Ye, H. Zhang, J. Fei, C. H. Wolstenholme and X. Zhang, Angew. Chem., Int. Ed., 2021, 60, 1339–1346 CrossRef CAS PubMed.
- A. M. Grabarz, B. Jędrzejewska, A. Skotnicka, N. A. Murugan, F. Patalas, W. Bartkowiak, D. Jacquemin and B. Ośmiałowski, Dyes Pigm., 2019, 170, 107481 CrossRef CAS.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
- I. Ciofini, T. Le Bahers, C. Adamo, F. Odobel and D. Jacquemin, J. Phys. Chem. C, 2012, 116, 11946–11955 CrossRef CAS.
- Y. Harabuchi, T. Taketsugu and S. Maeda, Phys. Chem. Chem. Phys., 2015, 17, 22561–22565 RSC.
- J. Shi, M. A. Izquierdo, S. Oh, S. Y. Park, B. Milián-Medina, D. Roca-Sanjuán and J. Gierschner, Org. Chem. Front., 2019, 6, 1948–1954 RSC.
- Q. Peng, Y. Niu, C. Deng and Z. Shuai, Chem. Phys., 2010, 370, 215–222 CrossRef CAS.
- Z. Shuai, Chin. J. Chem., 2020, 38, 1223–1232 CrossRef CAS.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- A. M. Grabarz and B. Ośmiałowski, Molecules, 2021, 26, 7434 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127 RSC.
- A. Pershin, D. Hall, V. Lemaur, J.-C. Sancho-Garcia, L. Muccioli, E. Zysman-Colman, D. Beljonne and Y. Olivier, Nat. Commun., 2019, 10, 597 CrossRef CAS PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. H. Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- F. Santoro and J. Cerezo, FCclasses3, a code for vibronic calculations. Version 1.0 (v3-0.1-177-g4b1514a), August 2021, visit, http://www.pi.iccom.cnr.it/fcclasse Search PubMed.
- F. J. Avila Ferrer, J. Cerezo, J. Soto, R. Improta and F. Santoro, Comput. Theor. Chem., 2014, 1040–1041, 328–337 CrossRef CAS.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 169903 CrossRef.
- A. Humeniuk, M. Bužančić, J. Hoche, J. Cerezo, R. Mitrić, F. Santoro and V. Bonačić-Koutecký, J. Chem. Phys., 2020, 152, 054107 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fluorescence quantum yield in various media, fluorescence lifetime, experimental radiative and non-radiative rate constants, fluorescence spectra in glycerol–methanol mixtures, NMR and mass spectra, barycenters for charge transfer, Wiberg bond indexes, dipole moments in the ground and excited states, comparison of various vibronic scheme approaches, Cartesian coordinates of the S0 and S1 minima. See DOI: https://doi.org/10.1039/d2sc05044g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |