 Open Access Article
Open Access ArticleOrientational self-sorting in cuboctahedral Pd cages†
Ru-Jin
Li
a,
Andrew
Tarzia
 b,
Victor
Posligua
b,
Victor
Posligua
 b,
Kim E.
Jelfs
b,
Kim E.
Jelfs
 b,
Nicolas
Sanchez
c,
Adam
Marcus
c,
Ananya
Baksi
d,
Guido H.
Clever
b,
Nicolas
Sanchez
c,
Adam
Marcus
c,
Ananya
Baksi
d,
Guido H.
Clever
 d,
Farzaneh
Fadaei-Tirani
d,
Farzaneh
Fadaei-Tirani
 a and
Kay
Severin
a and
Kay
Severin
 *a
*a
aInstitut of Chemical Sciences and Engineering, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne 1015, Switzerland. E-mail: kay.severin@epfl.ch
bDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, 82 Wood Lane, London, W12 0BZ, UK
cInstitut of Mathematics, EPFL, Lausanne 1015, Switzerland
dFakultät für Chemie und Chemische Biologie, Technische Universität Dortmund, Universität Dortmund, Dortmund 44227, Germany
First published on 30th September 2022
Abstract
Cuboctahedral coordination cages of the general formula [Pd12L24]24+ (L = low-symmetry ligand) were analyzed theoretically and experimentally. With 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 potential isomers, the structural space of these assemblies is vast. Orientational self-sorting refers to the preferential formation of particular isomers within the pool of potential structures. Geometric and computational analyses predict the preferred formation of cages with a cis arrangement at the metal centers. This prediction was corroborated experimentally by synthesizing a [Pd12L24]24+ cage with a bridging 3-(4-(pyridin-4-yl)phenyl)pyridine ligand. A crystallographic analysis of this assembly showed exclusive cis coordination of the 3- and the 4-pyridyl donor groups at the Pd2+ ions.
696 potential isomers, the structural space of these assemblies is vast. Orientational self-sorting refers to the preferential formation of particular isomers within the pool of potential structures. Geometric and computational analyses predict the preferred formation of cages with a cis arrangement at the metal centers. This prediction was corroborated experimentally by synthesizing a [Pd12L24]24+ cage with a bridging 3-(4-(pyridin-4-yl)phenyl)pyridine ligand. A crystallographic analysis of this assembly showed exclusive cis coordination of the 3- and the 4-pyridyl donor groups at the Pd2+ ions.
Introduction
Reactions of ditopic N-donor ligands L with Pd2+ ions can give molecularly defined nanostructures of the general formula [PdnL2n]2n+.1 The structural diversity of these assemblies is remarkable, ranging from simple dinuclear [Pd2L4]4+ complexes1c to interlocked [Pd4L8]8+ cages2 and giant [Pd30L60]60+ and [Pd48L96]96+ spheres.3 The geometry of the ligand is a decisive factor for the assembly process, with the ligand bend angle (the relative orientation of the coordinate vectors) being of special importance.1,4 Other factors such as ligand–ligand interactions5 or template effects6,7 can also influence the self-assembly process.In terms of applications, different directions have been explored, including the use of [PdnL2n]2n+ complexes as receptors for ions and drugs,8,9 as components of novel materials,10 as reactors for chemical transformations,11 and as links for nanoparticles.12
For future advances, it is desirable to extend the library of available [PdnL2n]2n+ nanostructures.13 Given the importance of the ligand in the self-assembly process, it is clear that ligand design is key for generating new [PdnL2n]2n+ complexes. Most homoleptic [PdnL2n]2n+ complexes are based on ligands with identical N-donor groups, and these ligands typically display C2v symmetry.1
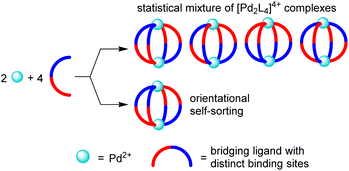
The utilization of low-symmetry ligands with two distinct donor groups represents an attractive strategy to access new [PdnL2n]2n+ structures.13,14 A potential problem of this approach is the formation of isomers. For [Pd2L4]4+-type assemblies, the use of a low-symmetry ligand can give rise to four different isomers, which differ in the relative orientation of the ligands (Fig. 1).
Experimental studies have shown that the selective formation of one isomer with a particular relative orientation of the ligands is possible (‘orientational self-sorting’).15 However, the energy difference between the isomers is sometimes not sufficient for providing a good selectivity.15b,c
For [PdnL2n]2n+ assemblies based on low-symmetry ligands, the number of potential isomers quickly increases with n. Macrocyclic [Pd3L6]6+ assemblies can form 9 isomers, pseudo-tetrahedral [Pd4L8]8+ complexes can form 35 isomers, and octahedral [Pd6L12]12+ complexes can form 112 different isomers.16,17 These numbers increase to 16, 68, and 186 if enantiomers are included.
Despite the vast number of potential isomers, orientational self-sorting is possible for high-nuclearity [PdnL2n]2n+ assemblies, as demonstrated by a recent experimental study from our group.16 The utilization of a thiophenylene-spaced ligand with 3- and 4-pyridyl donor groups gave rise to a structurally defined [Pd6L12]12+ complex.
Below, we analyze the structures and the potential isomers of cuboctahedral [Pd12L24]24+ complexes (n = 12). Geometric and computational analyses predict the preferred formation of cages with exclusive cis coordination at the metal centers. This prediction was corroborated experimentally by synthesis and structural analysis of a [Pd12L24]24+ cage with a bridging 3-(4-(pyridin-4-yl)phenyl)pyridine ligand.
Results and discussion
In order to determine the number of potential isomers for M12L24 structures based on low-symmetry ligands, we have used a standard mathematical counting argument related to the Orbit-Stabilizer Theorem.18 Our algorithm uses the cycle decomposition of the hyperoctahedral group19 to generate the collection of configurations with non-trivial symmetries and then uses the Orbit-Stabilizer Theorem18 to obtain a relationship between the number of distinct configurations and the number of symmetries each configuration has. As the set we generate is substantially smaller than the set of all possible configurations, we are able to apply this method of counting to M12L24 whose number of ligands proves too large for previous (exhaustive) methods.16 A more detailed description of the procedure is given in the (ESI, Section 4†).Our analysis revealed that M12L24 cages can form 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 potential isomers if the bridging ligands display distinct donor groups (Fig. 2). The vast majority of these isomers are chiral (99.8%). If enantiomers are taken into account, the total number of isomers increases to 700
696 potential isomers if the bridging ligands display distinct donor groups (Fig. 2). The vast majority of these isomers are chiral (99.8%). If enantiomers are taken into account, the total number of isomers increases to 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688. The calculations show that the structural space of MnL2n-type assemblies increases dramatically when going from n = 6 (octahedral cages, 112 isomers) to n = 12 (cuboctahedral cages, 350
688. The calculations show that the structural space of MnL2n-type assemblies increases dramatically when going from n = 6 (octahedral cages, 112 isomers) to n = 12 (cuboctahedral cages, 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 isomers).
696 isomers).
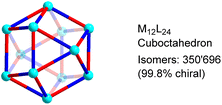 | ||
| Fig. 2 Potential isomers for M12L24 cages with low-symmetry bridging ligands. The graphic shows only one of the possible isomers. | ||
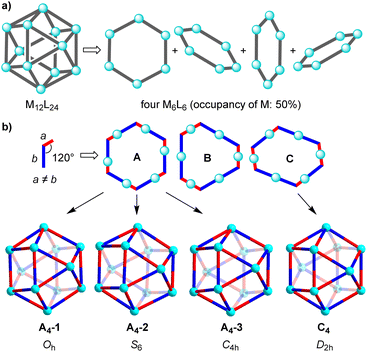
Cuboctahedral complexes of type M12L24 can be deconstructed into four M6L6 hexagons, with the metal centers having an occupancy of 50% (Fig. 5a). Let's consider the case, which is schematically depicted in Fig. 3b. The assemblies are based on ditopic ligands having the following general characteristics: the ligand is perfectly rigid, the donor groups are chemically distinct (red/blue), the coordinate vectors form an angle of 120°, and the distance between the donor atoms and the intersection of the coordinate vectors is not equal (a ≠ b). When combined with metal ions which act as linear connectors, three different hexagons can be formed (A–C, Fig. 3b). There are three ways to build an M12L24 assembly from A, and the resulting complexes have Oh, S6, and C4h symmetry. Hexagons of type B show two types of metal centers: three M are connected to the red parts of the ligand, and three M′ are connected to the blue parts of the ligand. The three M′ are positioned closer to the center of the hexagon B than the three M. The alternation of M and M′ in hexagon B makes it impossible to combine them into an M12L24-type assembly. The symmetry of the hexagon C, on the other hand, allows for the construction of a distorted cuboctahedron with D2h symmetry.
The analysis suggests that for ligands with a fixed bend angle of 120° and a pronounced difference between the distances a and b, orientational self-sorting should occur. The four preferred M12L24 isomers are shown in Fig. 3b. Obviously, the geometric analysis is based on perfectly rigid systems, and it does not account for the conformational flexibility of real molecular systems (e.g. variable coordinate vectors).
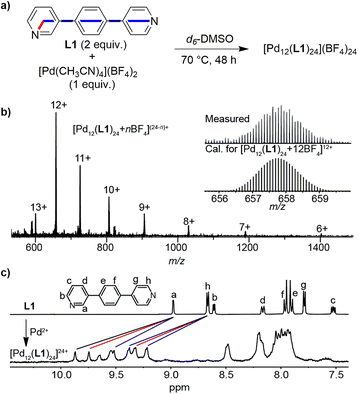
To investigate whether orientational self-sorting can be observed in [Pd12L24]24+-type assemblies, we have examined the reaction between [Pd(CH3CN)4](BF4)2 (a convenient source of Pd2+) and ligand L1 (Fig. 4a). This ligand was chosen because it displays a fixed bend angle of 120° (rotations around the C–C single bonds do not change the bend angle), and a pronounced difference between the distances of the N-donor atoms and the intersection of the coordinate vectors.
A mixture of [Pd(CH3CN)4](BF4)2 (1 equiv.) and L1 (2 equiv.) in d6-DMSO was tempered for 48 h at 70 °C. Subsequently, the resulting solution was analyzed by high-resolution ESI mass spectrometry and by NMR spectroscopy. The MS data confirmed the expected formation of a dodecanuclear assembly (Fig. 4b). The 1H NMR spectrum showed broad peaks (Fig. 4c), which is expected for assemblies of this size.1 A detailed analysis by 1H–1H COSY and NOESY correlation spectroscopy revealed three sets of signals for the protons of ligands L1 (see the ESI, Fig. S9 and S10†). The three sets of signals have equal intensity, and the DOSY NMR spectrum (Fig. S11†) showed that they all belong to a species with the same diffusion constant. Overall, the NMR data suggested that the self-assembly process had resulted in the formation of one main species, rather than a complex mixture of isomers.
It is interesting to compare the NMR data with the results of the geometric analysis. The latter had predicted a preference for four isomers. Only two of the isomers have a ligand multiplicity of three, namely the C4h symmetric isomer A4-3, and the D2h symmetric isomer C4 (ESI, Fig. S25†).
Expanding on the geometrical analysis depicted in Fig. 3, a computational study was performed in order to evaluate the relative stabilities of the four isomers A4-1, A4-2, A4-3, and C4 of complex [Pd12(L1)24]24+. Using an approach similar to recent work on Pd2L4 structures formed from low-symmetry ligands,20 models of the four cages were constructed with the help of our Python framework, stk.21,22 The geometry was optimized using a sequence of methods of increasing computational cost (see the ESI, Section 5†). Structures were optimized using UFF4MOF in GULP,23 the semiempirical tight-binding method GFN2-xTB,24 and, finally, density functional theory (DFT) geometry optimizations using hybrid and screened-hybrid functionals, PBE0-D3BJ25 and HSE06,26 respectively, with the Def2-SVP27 basis set. Fig. 5 shows the relative energy of the isomers at the HSE06 level of theory, with A4-3 being the most stable isomer. However, the energy differences between the three A4 isomers are very small. In fact, the relative energy of the A4 isomers changes depending on the level of theory (see the ESI, Table S3†). Therefore, the calculations do not provide a significant distinction between the A4 isomers. However, the preference for A4 over C4 is apparent with an energy difference larger than 150 kJ mol−1. This difference is significant, even if the limitations of our method (no solvent, no anions) are taken into account.
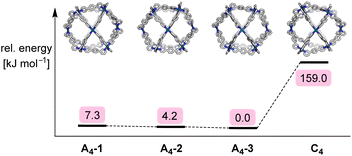 | ||
| Fig. 5 Schematic of the relative energy differences of the four isomers A4-1, A4-2, A4-3, and C4 of complex [Pd12(L1)24]24+, along with graphics of the HSE06/Def2-SVP-optimized structures. | ||
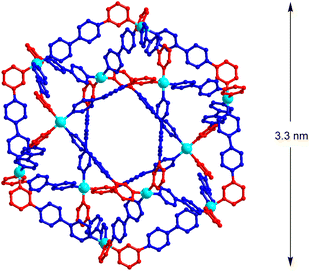
To determine the structure of cage [Pd12(L1)24]24+, a crystallographic analysis was needed. Obtaining good-quality diffraction data turned out to be challenging, but we finally succeeded in using single crystals obtained by vapor diffusion of THF/Et2O into a solution of the cage in DMSO.28 Co-crystallized solvent molecules could not be located, and the solvent-mask procedure from Olex2 (ref. 29) was used to account for residual electron density. The structure of the polycationic cage could clearly be established (Fig. 6). The 12 Pd2+ all show a cis configuration, and the cage displays an approximate C4h symmetry. Consequently, it is one of the four structures, which were predicted by the geometric analysis (A4-3, Fig. 3b). The observed symmetry matches the signal multiplicity in the 1H NMR spectrum (3 sets of signals), suggesting that the main structure in solution is the same as the one observed crystallographically. The presence of small amounts of other isomers cannot be excluded.
Cuboctahedral cages of the formula [Pd12L24]24+ are typically observed for ligands with a bend angle of around 120°.1,30 Further straightening of the ligand to bend angles between 134° and 149° can give rhombicuboctahedral [Pd24L48]48+ cages.1,4,31 [Pd24L48]48+ cages can form up to 5.86 trillion isomers if low-symmetry ligands are employed (ESI, Section 4†). A geometric analysis suggests that there is again a geometric preference for cages with cis-coordination at the metal centers (ESI, Section 3.3†). Preliminary attempts were made to examine orientational self-sorting in rhombicuboctahedral [Pd24L48]48+ cages, but the available analytical data did not provide information about the selectivity of the assembly process. The interested reader can find more information in the ESI (Fig. S19–S21†).
Conclusions
Cuboctahedral coordination cages of the general formula [Pd12L24]24+ (L = low-symmetry ligand) can potentially form 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 isomers, which differ in the relative orientation of the ligands. A geometric analysis combined with a computational study suggested the preferential formation of cages with cis coordination at the metal centers. Experimentally, we observed indeed the formation of a cage with cis-coordinated metal centers when Pd2+ salts were combined with 3-(4-(pyridin-4-yl)phenyl)pyridine.
696 isomers, which differ in the relative orientation of the ligands. A geometric analysis combined with a computational study suggested the preferential formation of cages with cis coordination at the metal centers. Experimentally, we observed indeed the formation of a cage with cis-coordinated metal centers when Pd2+ salts were combined with 3-(4-(pyridin-4-yl)phenyl)pyridine.
The preference for cis coordination mirrors what we had observed for octahedral assemblies of type [Pd6L12]12+ (L = low-symmetry ligand).16 In fact, a geometrical analysis analogous to that shown in Fig. 3 predicts that cis coordination should be favored for [Pd6L12]12+ cages (ESI, Section 3.2†).
Overall, our results substantiate that it is possible to obtain structurally defined [PdnL2n]2n+ cages of high nuclearity with low-symmetry ligands. A prerequisite for orientational self-sorting is the geometry of the ligand, which should display distinct distances between the donor atoms and the intersection of the coordinate vectors. Ligands of this kind will favor the formation of cages with a cis arrangement at the metal centers. We expect that the results of our analysis can be transferred to other types of coordination cages, given that donor groups of the ligands are coordinated in a square planar fashion to the metal centers.32
Data availability
The computational data is freely available at: https://github.com/andrewtarzia/citable_data/tree/master/li_2022Author contributions
R.-J. L. and K. S. initiated the study, R.-J. L. performed the experiments and analyzed the data, A. T., V. P. and K. E. J. performed a computational analysis of the stability of [Pd12(L1)24]24+ cages, N. S. and A. M. computed the potential isomers, A. B. and G. H. C were responsible for the MS measurements of cage [Pd24(L1)48](BF4)48, F. F.-T. collected and processed the X-ray data, and R.-J. L. and K. S. co-wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the Swiss National Science Foundation, and by the École Polytechnique Fédérale de Lausanne (EPFL). KEJ thanks the Royal Society for a University Research Fellowship and the European Research Council through Agreement No. 758370 (ERC-StG-PE5-CoMMaD).References
- (a) T. Tateishi, M. Yoshimura, S. Tokuda, F. Matsuda, D. Fujita and S. Furukawa, Coord. Chem. Rev., 2022, 467, 214612 CrossRef CAS; (b) N. B. Debata, D. Tripathy and H. S. Sahoo, Coord. Chem. Rev., 2019, 387, 273–298 CrossRef CAS; (c) S. Saha, I. Regeni and G. H. Clever, Coord. Chem. Rev., 2018, 374, 1–14 CrossRef CAS; (d) M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860 RSC; (e) K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49, 6703–6712 RSC.
- M. Frank, M. D. Johnstone and G. H. Clever, Chem.–Eur. J., 2016, 22, 14104–14125 CrossRef CAS PubMed.
- (a) D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101 CrossRef CAS; (b) D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Nature, 2016, 540, 563–566 CrossRef CAS PubMed.
- Q.-F. Sun, J. Iwasa, D. Ogawa, Y. Ishido, S. Sato, T. Ozeki, Y. Sei, K. Yamaguchi and M. Fujita, Science, 2010, 328, 1144–1147 CrossRef CAS.
- For examples, see: (a) J. Tessarolo, H. Lee, E. Sakuda, K. Umakoshi and G. H. Clever, J. Am. Chem. Soc., 2021, 143, 6339–6344 CrossRef CAS; (b) B. Chen, J. J. Holstein, S. Horiuchi, W. G. Hiller and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 8907–8913 CrossRef CAS; (c) B. Chen, S. Horiuchi, J. J. Holstein, J. Tessarolo and G. H. Clever, Chem.–Eur. J., 2019, 65, 14921–14927 CrossRef PubMed; (d) R. Zhu, W. M. Bloch, J. J. Holstein, S. Mandal, L. V. Schäfer and G. H. Clever, Chem.–Eur. J., 2018, 24, 12976–12982 CrossRef CAS PubMed; (e) S. M. Jansze, G. Cecot, M. D. Wise, K. O. Zhurov, T. K. Ronson, A. M. Castilla, A. Finelli, P. Pattison, E. Solari, R. Scopelliti, G. E. Zelinskii, A. V. Vologzhanina, Y. Z. Voloshin, J. R. Nitschke and K. Severin, J. Am. Chem. Soc., 2016, 138, 2046–2054 CrossRef CAS PubMed; (f) D. Preston, J. E. Barnsley, K. C. Gordon and J. D. Crowley, J. Am. Chem. Soc., 2016, 138, 10578–10585 CrossRef CAS PubMed; (g) M. D. Wise, J. J. Holstein, P. Pattison, C. Besnard, E. Solari, R. Scopelliti, G. Bricogne and K. Severin, Chem. Sci., 2015, 6, 1004–1010 RSC.
- E. G. Percástegui, Eur. J. Inorg. Chem., 2021, 4425–4438 CrossRef.
- For examples, see: (a) S. Sudan, F. Fadaei-Tirani, K. E. Ebbert, G. H. Clever and K. Severin, Angew. Chem., Int. Ed., 2022, e202201823 CAS; (b) T. Tsutsui, L. Catti, K. Yoza and M. Yoshizawa, Chem. Sci., 2020, 11, 8145–8150 RSC; (c) T. Zhang, L.-P. Zhou, X.-Q. Guo, L.-X. Cai and Q.-F. Sun, Nat. Commun., 2017, 8, 15898 CrossRef CAS PubMed; (d) R. Zhu, J. Lübben, B. Dittrich and G. H. Clever, Angew. Chem., Int. Ed., 2015, 54, 2796–2800 CrossRef CAS; (e) S. Freye, R. Michel, D. Stalke, M. Pawliczek, H. Frauendorf and G. H. Clever, J. Am. Chem. Soc., 2013, 135, 8476–8479 CrossRef CAS; (f) R. Sekiya, M. Fukuda and R. Kuroda, J. Am. Chem. Soc., 2012, 134, 10987–10997 CrossRef CAS PubMed.
- (a) G. H. Clever and P. Punt, Acc. Chem. Res., 2017, 50, 2233–2243 CrossRef CAS PubMed; (b) A. Casini, B. Woods and M. Wenzel, Inorg. Chem., 2017, 56, 14715–14729 CrossRef CAS PubMed.
- For examples of drug encapsulation, see: (a) B. Woods, R. D. M. Silva, C. Schmidt, D. Wragg, M. Cavaco, V. Neves, V. F. C. Ferreira, L. Gano, T. S. Morais, F. Mendes, J. D. G. Correira and A. Casini, Bioconjugate Chem., 2021, 32, 1399–1408 CrossRef CAS; (b) R. A. S. Vasdev, L. F. Gaudin, D. Preston, J. P. Jogy, G. I. Giles and J. D. Crowley, Front. Chem., 2018, 6, 563 CrossRef CAS; (c) F. Kaiser, A. Schmidt, W. Heydenreuter, P. J. Altmann, A. Casini, S. A. Sieber and F. E. Kühn, Eur. J. Inorg. Chem., 2016, 5189–5196 CrossRef CAS; (d) A. Schmidt, V. Molano, M. Hollering, A. Pöthig, A. Casini and F. E. Kühn, Chem.–Eur. J., 2016, 22, 2253–2256 CrossRef CAS PubMed; (e) J. E. M. Lewis, E. L. Gavey, S. A. Cameron and J. D. Crowley, Chem. Sci., 2012, 3, 778–784 RSC.
- (a) R.-J. Li, C. Pezzato, C. Berton and K. Severin, Chem. Sci., 2021, 12, 4981–4984 RSC; (b) S.-Q. Deng, D.-M. Li, X.-J. Mo, Y.-L. Miao, S.-L. Cai, J. Fan, W.-G. Zhang and S.-R. Zheng, ChemPlusChem, 2021, 86, 709–715 CrossRef CAS PubMed; (c) Y. Gao, S.-Q. Deng, X. Jin, S.-L. Cai and S.-R. Zheng, Chem. Eng. J., 2019, 357, 129–139 CrossRef CAS; (d) L. Zeng, Y. Xiao, J. Jiang, H. Fang, Z. Ke, L. Chen and J. Zhang, Inorg. Chem., 2019, 58, 10019–10027 CrossRef CAS; (e) S. Saha, B. Holzapfel, Y.-T. Chen, K. Terlinden, P. Lill, C. Gatsogiannis, H. Rehage and G. H. Clever, J. Am. Chem. Soc., 2018, 140, 17384–17388 CrossRef CAS PubMed; (f) Y. Gu, E. A. Alt, H. Wang, X. Li, A. P. Willard and J. A. Johnson, Nature, 2018, 560, 65–69 CrossRef CAS PubMed; (g) J. Uchida, M. Yoshio, S. Sato, H. Yokoyama, M. Fujita and T. Kato, Angew. Chem., Int. Ed., 2017, 56, 14085–14089 CrossRef CAS PubMed; (h) Y. Wang, Y. Gu, E. G. Keeler, J. V. Park, R. G. Griffin and J. A. Johnson, Angew. Chem., Int. Ed., 2017, 56, 188–192 CrossRef CAS PubMed; (i) A. V. Zhukhovitskiy, M. Zhong, E. G. Keeler, V. K. Michaelis, J. E. P. Sun, M. J. A. Hore, D. J. Pochan, R. G. Griffin, A. P. Willard and J. A. Johnson, Nat. Chem., 2016, 8, 33–41 CrossRef CAS; (j) A. V. Zhukhovitskiy, J. Zhao, M. Zhong, E. G. Keeler, E. A. Alt, P. Teichen, R. G. Griffin, M. J. A. Hore, A. P. Willard and J. A. Johnson, Macromolecules, 2016, 49, 6896–6902 CrossRef CAS.
- (a) R. Saha, B. Mondal and P. S. Mukherjee, Chem. Rev., 2022, 122, 12244–12307 CrossRef CAS PubMed; (b) P. Howlander and M. Schmittel, Beilstein J. Org. Chem., 2022, 18, 597–630 CrossRef; (c) Y. Xue, X. Hang, J. Ding, B. Li, R. Zhu, H. Pang and Q. Xu, Coord. Chem. Rev., 2021, 430, 213656 CrossRef CAS; (d) A. B. Grommet, M. Feller and R. Klajn, Nat. Nanotechnol., 2020, 15, 256–271 CrossRef CAS; (e) A. C. H. Jans, X. Caumes and J. N. H. Reek, ChemCatChem, 2019, 11, 287–297 CrossRef CAS; (f) L. J. Jongkind, X. Caumes, A. P. T. Hartendorp and J. N. H. Reek, Acc. Chem. Res., 2018, 51, 2115–2128 CrossRef CAS; (g) I. Sinha and P. S. Mukherjee, Inorg. Chem., 2018, 57, 4205–4221 CrossRef CAS.
- L. Tian, C. Wang, H. Zhao, F. Sun, H. Dong, K. Feng, P. Wang, G. He and G. Li, J. Am. Chem. Soc., 2021, 143, 8631–8638 CrossRef CAS PubMed.
- S. Pullen, J. Tessarolo and G. H. Clever, Chem. Sci., 2021, 12, 7269–7293 RSC.
- (a) C. T. McTernan, J. A. Davies and J. R. Nitschke, Chem. Rev., 2022, 122, 10393–10437 CrossRef CAS PubMed; (b) J. E. M. Lewis and J. D. Crowley, ChemPlusChem, 2020, 85, 815–827 CrossRef CAS.
- (a) S. S. Mishra and D. K. Chand, Dalton Trans., 2022, 51, 11650–11657, 10.1039/d2dt01571d; (b) R. A. S. Vasdev, D. Preston, C. A. Casey-Stevens, V. Martí-Centelles, P. J. Lusby, A. L. Garden and J. D. Crowley, Inorg. Chem., 2022 DOI:10.1021/acs.inorgchem.2c00937; (c) A. Tarzia, J. E. M. Lewis and K. E. Jelfs, Angew. Chem., Int. Ed., 2021, 60, 20879–20887 CrossRef CAS PubMed; (d) J. E. M. Lewis, Chem.–Eur. J., 2021, 27, 4454–4460 CrossRef CAS; (e) H. Yu, J. Li, C. Shan, T. Lu, X. Jiang, J. Shi, L. Wojtas, H. Zhang and M. Wang, Angew. Chem., Int. Ed., 2021, 60, 26523–26527 CrossRef CAS; (f) J. E. M. Lewis, A. Tarzia, A. J. P. White and K. E. Jelfs, Chem. Sci., 2020, 11, 677–683 RSC; (g) S. S. Mishra, S. V. K. Kompella, S. Krishnaswamy, S. Balasubramanian and D. K. Chand, Inorg. Chem., 2020, 59, 12884–12894 CrossRef CAS; (h) S. Samantray, S. Krishnaswarmy and D. K. Chand, Nat. Commun., 2020, 11, 880 CrossRef CAS; (i) S. K. Sen and R. Natarajan, Inorg. Chem., 2019, 58, 7180–7188 CrossRef CAS PubMed; (j) D. Ogata and J. Yuasa, Angew. Chem., Int. Ed., 2019, 58, 18424–18428 CrossRef CAS PubMed.
- R.-J. Li, A. Marcus, F. Fadaei-Tirani and K. Severin, Chem. Commun., 2021, 57, 10023–10026 RSC.
- B. Kandasamy, E. Lee, D.-L. Long, N. Bell and L. Cronin, Inorg. Chem., 2021, 60, 14772–14778 CrossRef CAS.
- D. S. Dummit and R. M. Foote, Abstract Algebra, 3rd edn, Wiley-VCH, 2003 Search PubMed.
- W. Y. C. Chen, SIAM J. Discret. Math., 1993, 6, 353–362 CrossRef.
- A. Tarzia, J. E. M. Lewis and K. E. Kelfs, Angew. Chem., Int. Ed., 2021, 60, 20879–20887 CrossRef CAS PubMed.
- L. Turcani, A. Tarzia, F. T. Szczypiński and K. E. Kelfs, J. Chem. Phys., 2021, 154, 214102 CrossRef CAS PubMed.
- (a) https://github.com/lukasturcani/stk, version2022.1.26.0; (b) The Python code for the computational model generation is open-source at, https://github.com/andrewtarzia/big_unsymm Search PubMed.
- (a) D. E. Coupry, M. A. Addicoat and T. Heine, J. Chem. Theory Comput., 2016, 12, 5215–5225 CrossRef CAS PubMed; (b) M. A. Addicoat, N. Vankova, I. F. Aktera and T. Heine, J. Chem. Theory Comput., 2014, 10, 880–891 CrossRef CAS PubMed; (c) J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS; (d) J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC; (e) A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- (a) C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wires Comput. Mol. Sci., 2021, 11, e1493 CAS; (b) C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- (a) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed; (b) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- (a) J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef; (b) J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- The crystallographic analysis suggests the presence of chloride instead of nitrate counter ions. The origin of the chloride anions is not clear. Potentially, anion exchange with the glassware had occurred over the very long crystallization period (several months), or small amounts of chloride were present in the Pd(NO3)2 salt. For a related discussion, see: E. O. Bobylev, B. De Bruin and J. N. H. Reek, Inorg. Chem., 2021, 60, 12498–12505 CrossRef CAS.
- O. V. Dolomanov, J. L. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- For examples, see: (a) R. Zaffaroni, E. O. Bobylev, R. Plessius, J. I. van der Vlugt and R. N. H. Reek, J. Am. Chem. Soc., 2020, 142, 8837–8847 CrossRef; (b) C.-L. Liu, E. O. Bobylev, Y. Fu, D. A. Poole III, K. Robeyns, C.-A. Fustin, Y. Garcia, J. N. H. Reek and M. L. Singleton, Chem.–Eur. J., 2020, 26, 11960–11965 CrossRef CAS; (c) S. Gonell, X. Caumes, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Chem. Sci., 2019, 10, 1316–1321 RSC; (d) S. Sato, M. Ikemi, T. Kikuchi, S. Matsumura, K. Shiba and M. Fujita, J. Am. Chem. Soc., 2015, 137, 12890–12896 CrossRef CAS; (e) C. J. Bruns, D. Fujita, M. Hoshino, S. Sato, J. F. Stoddart and M. Fujita, J. Am. Chem. Soc., 2014, 136, 12027–12034 CrossRef CAS PubMed; (f) C. Gütz, R. Hovorka, C. Klein, Q.-Q. Jiang, C. Bannwarth, M. Engeser, C. Schmuck, W. Assenmacher, W. Mader, F. Topíc, K. Rissanen, S. Grimme and A. Lützen, Angew. Chem., Int. Ed., 2014, 53, 1693–1698 CrossRef; (g) F. Jiang, N. Wang, Z. Du, J. Wang, Z. Lan and R. Yang, Chem.–Asian J., 2012, 7, 2230–2234 CrossRef CAS; (h) K. Suzuki, M. Kawano, S. Sato and M. Fujita, J. Am. Chem. Soc., 2007, 129, 10652–10653 CrossRef CAS PubMed; (i) T. Murase, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2007, 46, 1083–1085 CrossRef CAS; (j) S. Sato, J. Iida, K. Suzuki, M. Kawano, T. Ozeki and M. Fujita, Science, 2006, 313, 1273–1276 CrossRef CAS PubMed; (k) M. Tominaga, K. Suzuki, T. Murase and M. Fujita, J. Am. Chem. Soc., 2005, 127, 11950–11951 CrossRef CAS; (l) M. Tominaga, K. Suzuki, M. Kawano, T. Kusukawa, T. Ozeki, S. Sakamoto, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2004, 43, 5621–5625 CrossRef CAS PubMed.
- (a) M. Han, Y. Luo, B. Damaschke, L. Gómez, X. Ribas, A. Jose, P. Peretzki, M. Seibt and G. H. Clever, Angew. Chem., Int. Ed., 2016, 55, 445–449 CrossRef CAS; (b) H. Yokoyama, Y. Ueda, D. Fujita, S. Sato and M. Fujita, Chem.–Asian J., 2015, 10, 2292–2295 CrossRef CAS; (c) J. Bunzen, J. Iwasa, P. Bonakdarzadeh, E. Numata, K. Rissanen, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2012, 51, 3161–3163 CrossRef CAS.
- The crystallographic analysis of a [Cu6L12]12+ cage with bridging 3-pyridinyl-triazole ligands showed also exclusive cis coordination at the six metal centers: Y. Wang, P. Cheng, Y. Song, D.-Z. Liao and S.-P. Yan, Chem.–Eur. J., 2007, 13, 8131–8138 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Containing synthetic procedures and experimental details. CCDC 2161290. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc03856k |
| This journal is © The Royal Society of Chemistry 2022 |