Open Access Article
Open Access ArticlePerpetuating enzymatically induced spatiotemporal pH and catalytic heterogeneity of a hydrogel by nanoparticles†
Rishi Ram
Mahato
,
Priyanka
,
Ekta
Shandilya
and
Subhabrata
Maiti
 *
*
Department of Chemical Sciences, Indian Institute of Science Education and Research (IISER) Mohali, Knowledge City, Manauli, 140306, India. E-mail: smaiti@iisermohali.ac.in
First published on 23rd June 2022
Abstract
The attainment of spatiotemporally inhomogeneous chemical and physical properties within a system is gaining attention across disciplines due to the resemblance to environmental and biological heterogeneity. Notably, the origin of natural pH gradients and how they have been incorporated in cellular systems is one of the most important questions in understanding the prebiotic origin of life. Herein, we have demonstrated a spatiotemporal pH gradient formation pattern on a hydrogel surface by employing two different enzymatic reactions, namely, the reactions of glucose oxidase (pH decreasing) and urease (pH increasing). We found here a generic pattern of spatiotemporal change in pH and proton transfer catalytic activity that was completely altered in a cationic gold nanoparticle containing hydrogel. In the absence of nanoparticles, the gradually generated macroscopic pH gradient slowly diminished with time, whereas the presence of nanoparticles helped to perpetuate the generated gradient effect. This behavior is due to the differential responsiveness of the interface of the cationic nanoparticle in temporally changing surroundings with increasing or decreasing pH or ionic contents. Moreover, the catalytic proton transfer ability of the nanoparticle showed a concerted kinetic response following the spatiotemporal pH dynamics in the gel matrix. Notably, this nanoparticle-driven spatiotemporally resolved gel matrix will find applicability in the area of the membrane-free generation and control of spatially segregated chemistry at the macroscopic scale.
Introduction
The maintenance and regulation of chemical gradients across both space and time is one of the fundamental energy harnessing resources in aiding the functionality of living systems.1,2 Intriguingly, the natural proton gradients (of around four pH units) across deep-sea porous hydrothermal vents (alkaline) to seawater (acidic) have been considered to play a key role in the context of origin of life.3 In fact, proton-gradient-driven machineries are omnipresent in cellular processes, for instance, mitochondrial respiration, photosynthesis, ATPase-driven bacterial flagellar motility, etc.4,5 To this end, finding the basis for the preservation of pH heterogeneity in a spatiotemporal manner via mechanisms other than catalytically active processes will be of benefit not only in rationalizing possible scenarios for the generation of gradients relevant to prebiotic Earth, but also in designing macroscale spatially segregated chemistry.6–8In the last few decades, the question of how information can travel across gradients to instigate spatiotemporal communication and motile behavior among chemically interactive (bio)colloidal entities has been a hot research topic among various scientific communities.9–19 To this end, recent reports in the literature have highlighted many interesting dynamic modulations of solution pH using light or enzymes. Undoubtedly, this has led to the development of materials with adaptive and spatiotemporally controlled properties.20–31 However, to date, no systematic study exists describing how the interfacial pH of a cationic nanoparticle, along with the surrounding pH, are influenced in a dynamically changing environment as a function of both space and time. It is worth mentioning that positively charged surfaces play an important role in the in situ autotrophic growth of metabolites, such as anionic phosphates and coenzymes, and that this is one of the nascent stages of chemical evolution according to the famous surface metabolism theory of Wächtershäuser.32
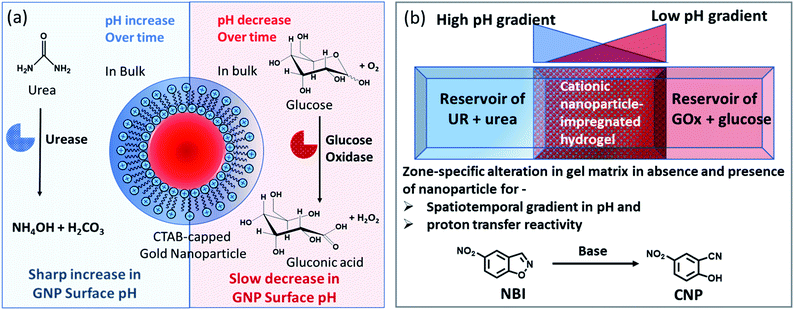
Herein, we have used the enzymes glucose oxidase (GOx) and urease (UR) to achieve a spatiotemporal pH gradient generating mode, as these enzymes can change the bulk pH towards acidic and basic pH, respectively. Firstly, we probed the response of the interfacial pH of a cationic gold nanoparticle (GNP), as well as its catalytic ability towards a proton transfer reaction, in these dynamically changing surroundings (Fig. 1a). A more accelerated increase in the interfacial pH coupled with a greater increase in the proton transfer reaction rate on the cationic GNP surface was observed due to UR activity. Furthermore, when an acidic and a basic environment were generated over time from opposite ends of the hydrogel, we demonstrated a kinetically trapped prolonged spatiotemporal pH gradient (synchronized with the proton transfer reactivity) in a hydrogel matrix in the presence of cationic GNPs in comparison to that of the system in the absence of GNPs (Fig. 1b shows the experimental setup for this scenario).
Results and discussion
Notably, physical properties, such as pH and polarity, in the microenvironment of the micellar interface are different than those in bulk solution; and this property is also preserved in surfactant-layer-anchored nanoparticle surfaces.33–35 Recently, we have shown that the catalytic ability of a cetyltrimethylammonium bromide (CTAB)-functionalized cationic gold nanoparticle (GNP) can be up- and downregulated by exploiting multivalent interactions between GNPs and adenosine-based nucleotides.35 The alteration of the local surface pH of the GNPs due to the assembly of these differently charged nucleotides was the key reason for this modulatory catalytic behavior. In the present work, we have also synthesized and characterized CTAB-capped GNPs with a diameter of 20 ± 3 nm and a positive surface zeta potential of 85 ± 5 mV (Fig. S1, ESI†). Throughout the work, we used 150 pM of GNPs, which contained ∼100 μM of CTAB; this concentration was almost 10 times lower than the critical micellar concentration (CMC) of CTAB itself. This property of miceller organization below CMC arises due to the self-assembled organic layer forming ability of the inorganic particle surface, which is in fact considered to be the most primitive assembly of organic molecules.36,37We first measured the surface pH of the GNPs in milliQ (mQ) water (pH of mQ water = 5.9 ± 0.05; in this case, the lower pH of the water was presumably due to the absorption of CO2 from air) using a micellar surface pH-monitoring probe, bromothymol blue (BTB). BTB is known to strongly bind to the cationic GNP surface owing to the presence of an anionic sulphonate group with an aromatic moiety and has been previously used to determine the interfacial pH of cationic micelles and nanoparticles.35,38 We started by calibrating the change in the UV absorbance of BTB at different pH values using buffered solutions (Fig. S2, ESI†). We found that the pH of the GNP interface was 6.0 ± 0.1, suggesting that the interfacial pH of the GNPs was not altered in the presence of water alone. We also measured the changes in the pH values in the presence of ammonium carbonate ((NH4)2CO3) and bicarbonate (NH4HCO3), as these molecules are supposed to form due to the UR reaction (Table S1, ESI†). In the presence of the carbonate and bicarbonate salt, the pH of the mQ water increased to 9.1 and 8, respectively, when measured using a pH meter in mQ water without GNPs.
Before proceeding to the pH measurements in the presence of GNPs in detail, we also investigated the stability of the CTAB headgroups on the GNP surface in the presence of BTB along with UR and GOx via an ultracentrifugation experiment as described in the ESI (Fig. S3 and S4, ESI†). We were pleased to observe that neither BTB nor CTAB were detached from the GNP surface even during the enzymatic reaction, suggesting the stability of the overall system for reproducible measurement. Next, we investigated the change in the pH of the system dynamically with time; for this, we employed the enzymatic reactions of GOx and UR in the presence of 100 mM of glucose or 15 mM urea, respectively. It was expected that the pH of the system would gradually become acidic due to the action of GOx on glucose (100 mM), as it forms gluconic acid, and basic due to the activity of UR toward urea (15 mM), as it forms ammonium carbonate in the solution. Indeed, upon monitoring the pH of the mQ water with time, we observed similar phenomena. For mQ water, the change in the solution pH was fast; starting from pH = 5.9, it reached pH = 9.15 ± 0.1 in ∼15 min in the UR case and pH = 4 ± 0.05 for GOx in ∼60 min. The pH study suggests that in the case of UR, ammonium carbonate is formed due to the hydrolysis of urea, as the maximum pH that can be reached by the (NH4)2CO3 solution in mQ water is 9.1 (see Table S1, ESI†). Interestingly, when the UR and GOx reactions were carried out in mQ water in the presence of GNPs, the interfacial pH of the GNPs reached 11.5 ± 0.3 within 6 min for UR and only decreased to 5.5 ± 0.1 even after 100 min for GOx (Fig. 2a and b). The presence of dense cationic charge results in the accumulation of a higher effective molarity of counterions, (here, anionic carbonate) in the vicinity of the interface than in the bulk (see also ESI† for theoretical calculations). Thus, the interfacial pH of the GNPs increased at a faster rate and also exhibited a pH two units higher than that of the bulk at the end. In contrast, in a gradually acidifying environment, the interfacial counter-anions bound on the positively charged surface held strongly and resisted the decrease in the pH in the environment surrounding the nanoparticles.
 | ||
| Fig. 2 pH change as a function of time due to the enzymatic action of (a) urease and (b) glucose oxidase on urea and glucose, respectively. Conditions: [urea] = 15 mM, [glucose] = 100 mM, [GNP] = 150 pM, [urease] = 10 nM, [glucose oxidase] = 100 nM. In the cases with GNP, BTB (20 μM) was used to determine the interfacial pH of the GNPs (filled square points in the graph), which were calculated from the calibration graph shown in Fig. S2 in the ESI.† | ||
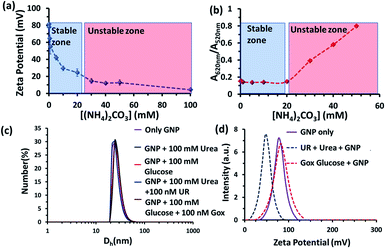
We also investigated the stability of the nanoparticles under our experimental conditions (Fig. 3 and S3–S6, ESI†). First, we performed zeta potential measurements of the nanoparticles by titrating ammonium carbonate in the system and found that the zeta potential of the nanoparticles decreased gradually, indicating the binding of the carbonate ions to the nanoparticle surface (Fig. 3a). After adding 30 mM of ammonium carbonate, the zeta potential decreased below +15 mV, which is considered to be the colloidal instability zone for charged particles. Next, we performed UV-vis spectra with the GNP solution and investigated the ratio of absorbance at 620 and 520 nm (A620/A520); increase in this ratio is a well-known indicator of GNP aggregation (Fig. 3b and S6, ESI†)).20,21 In fact, we also found in this experiment that the value only started to increase after the addition of more than 20 mM ammonium carbonate. All these data prompted us to choose a urea concentration of 15 mM for our reaction conditions, at which the nanoparticles will be stable. This concentration was also below the surface saturation concentration of carbonate. Thus, it also avoids any possible displacement of the small amount (0.02 mM) of BTB from the GNP surface, resulting in the coexistence of both BTB and carbonate on the GNP surface (Fig. S4, ESI†). Additionally, a dynamic light scattering study (DLS) did not show any aggregation of the nanoparticles in the presence of the enzyme and substrates (Fig. 3c). The zeta potential value of the GNPs in the presence of the reaction of urea and UR gradually decreased with time and finally settled at around 40 ± 5 mV, which also suggested the formation of ammonium carbonate ions and their binding to the nanoparticle surface (Fig. 3d and S5, ESI†). Interestingly, no destabilization of the GNPs was observed in the presence of the reaction of GOx and glucose, and the zeta potential value, instead of decreasing, remained almost constant at 90 ± 10 mV. Expectedly, the unchanged GNP zeta potential value in the presence of GOx and glucose suggested that no strong anionic species that could bind to the GNP surface were formed (Fig. S5, ESI†). All these experiments confirmed the stability of the nanoparticles under our experimental conditions and also the binding of carbonate to the GNP surface, which eventually increased the interfacial pH of the GNPs by almost two units.
Next, we also conducted an experiment to investigate the pH state of the bulk; centrifugation dialysis with 10 kDa filters was used to remove all the nanoparticles, and the dialysate was utilized for pH measurement (Fig. S7, ESI†). We first dialysed the aqueous GNP solution with urea and the enzyme UR after 15 min, and observed that the pH of the dialysate was 7.7 ± 0.2, whereas in the control experiment without GNPs under similar experimental conditions, the observed value was 9.2 ± 0.3. Here, it is worth mentioning that the measured surface pH of the GNPs was 11.2 ± 0.2 after 15 min in the presence of UR, whereas the bulk pH was 3.5 units lower. This again clearly suggests that most of the carbonate ions were bound to the GNP surface. In a similar way, when the dialysis experiment was performed with GOx and glucose, the bulk pH was found to decrease to 3.7 ± 0.2 in the presence of GNPs, and in a control experiment without GNPs the pH was nearly identical with a value of 4.05 ± 0.2. Notably, under this condition, the measured surface pH of the GNPs was 5.6 ± 0.1. Overall, these experiments confirmed that the enzymatic reactions occurred, as the bulk pH also changed in the presence of the enzymes as desired. The results also indicate a higher rate of increase in the local pH of the GNP surface in comparison to the bulk pH in the presence of UR.
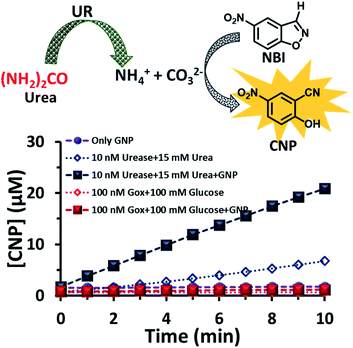
After exploring the surface pH of the GNPs, we were interested in determining the catalytic ability of the nanoparticles towards a proton transfer reaction, also known as the Kemp Elimination (KE) reaction. We have recently demonstrated that CTAB-capped GNPs can enhance the proton transfer rate by almost three orders of magnitude in the presence of anionic phosphate compared to the uncatalyzed reaction in the absence of GNPs. In the present work, we expected that the KE reaction could also be catalyzed on the GNP surface due to the formation and binding of anionic carbonate (hydrolyzed product of the urea and UR reaction).40,41 We used 5-nitrobenzisoxazole (NBI) as the substrate; the product, 2-cyanonitrophenol (CNP), is formed via base-catalyzed concerted E2 elimination and kinetics of the product formation can be monitored at 380 nm by temporal monitoring of UV-vis spectral change (Fig. S8 and S9, ESI†). It should be noted here that the KE reaction has been used as a model for understanding the mechanistic pathways of biotransformation and also for supramolecular cage catalysis.41–44 First, we measured the catalytic activity in the absence of GNP, but in the presence of UR (10 nM) at a fixed concentration of urea (15 mM) in mQ water (Fig. 4). We observed from the time-dependent catalytic profile that GNP alone in aqueous solution has no significant catalytic ability. However, in the presence of UR and urea, even in mQ water alone, around 5 μM of the product was formed after 10 min. This was due to the generation of basic carbonate ions, which eventually helped in the proton transfer. Interestingly, in the presence of GNP, the catalytic rate became faster, and around 20 μM of the KE catalytic product formed after 10 min in the presence of 10 nM of UR under similar experimental conditions, showing a four-fold enhanced catalytic rate. This enhanced activity in the presence of CTAB-capped GNPs is primarily due to (i) the higher substrate solubility in the hydrophobic domain of the surfactant layer and (ii) the much higher concentration of catalytic carbonate anions near the stern layer of the charged surface, among other factors such as the lower dielectric constant in the stern layer of the cationic CTAB interface. We also investigated the activity in the presence of the CTAB surfactant alone (100 μM) in the absence of the nanoparticles; however, the catalytic activity was found to be almost two times lower (∼11 μM CNP formed after 10 min), suggesting the ability of the nanoparticle in assembling a surfactant layer around its core (Fig. S10, ESI†). Overall, this data indicates that that the synergistic presence of GNPs and anionic carbonate is crucial for enhanced KE catalysis. Additionally, we also performed KE catalysis in the presence of GOx; however, a decrease in the activity rate was observed, as in this case, the pH decreases with time and no rate-enhancing anions are formed (Fig. 4).
Additionally, we also verified the binding and electric double layer formation propensity of the anions on the cationic charged surface theoretically using the software COMSOL Multiphysics (version 5.6) (please see also Fig. S11† and related discussion in the ESI†). Here, we considered an electrode of 100 nm having a positive potential of +100 mV (comparable to the positively charged nanoparticles used in this study).45 Next, we investigated the distribution of two salts at a concentration of 10 mM, namely, AX (with a singly charged cation (A+) and anion (X−)) and A2X (with a singly charged cation (A+) and doubly charged anion (X2−)). Unsurprisingly, in both cases, we observed that the concentration of anions was much higher near the positively charged electrode. Interestingly, we also found that the concentration of the divalent anion X2− near the electrode started at almost 15 M (more than three orders of magnitude higher than in the bulk) and for monovalent X−, it started at 0.5 M (50 times higher than in the bulk). Additionally, the diffused Debye layer only expands to ∼30 nm in the case of X2−, in comparison to ∼300 nm for X−. This suggests that divalent anions like carbonate have much higher binding ability to the positively charged surface than monovalent anions, and are densely concentrated near the surface. Thus, the increased charge density of anions like carbonate led much more efficiently to an increase in the pH at the cationic nanoparticle surface, as observed in our experimental data.
Next, we theoretically investigated the separation of ions in a unidirectional flow system in which one of the walls is positively charged and the other one is neutral using COMSOL (see Fig. S12, ESI†). Herein, we simply used a salt system with a monovalent cation (A+) and anion (X−), both having a 10 mM concentration in the inlet. We then used laminar electrophoretic transport through the channel.46 Here, we found that anions were slowly accumulated near the charged surface as they travelled through the channel and cations were accumulated at the uncharged surface. In the end, near the outlet the concentrations of anions were around 18 and 2 mM near the positively charged and uncharged surface, respectively, generating a concentration gradient. Thus, this result also suggests that the presence of a charged surface can generate and stabilize an anionic concentration gradient and thereby a possible spatiotemporal pH gradient. Overall, this theoretical result encouraged us to experimentally investigate the effect of a charged GNP surface in generating or stabilizing a pH gradient in space with time.
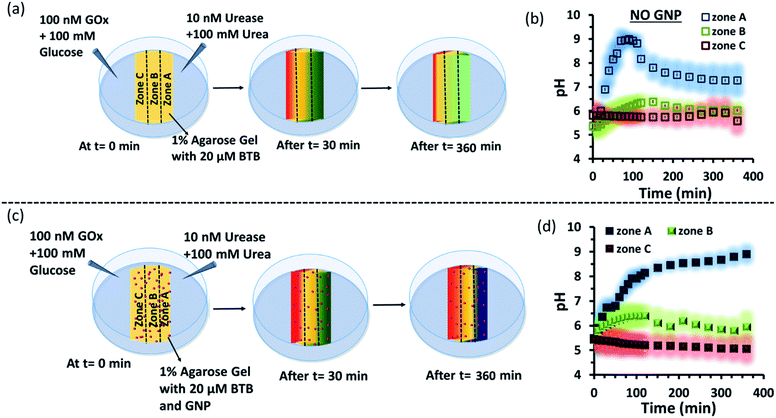
Subsequently, we started to explore how this effect could be observed spatiotemporally in experiments. For this, we designed the experiment shown in Fig. S13 in the ESI.† Here, we took a Petri dish with a 6 cm diameter and cast an agarose gel (1 wt% in water) in the middle part (2.2 cm width and 0.5 cm height), while the two opposite sides were kept empty. In one empty part of the Petri dish, we added 1.6 ml aqueous solution containing UR enzyme (10 nM) and urea (100 mM), and in the opposite side, a similar volume containing GOx enzyme (100 nM) and glucose (100 mM) were added. This experimental setup ensured that at one side of the gel, a basic pH gradient due to UR reactivity, and on the other side, an acidic pH due to GOx activity were generated. First, we investigated the spatiotemporal change in the pH of the gel both in the absence and presence of GNPs in the gel. For this, we measured the pH of the gel in three different locations: zone A (near the UR + urea solution), zone B (at the center) and zone C (near the GOx + glucose solution) as depicted in Fig. 5a–d, S13b and c, ESI.† For measuring the pH of the gel in the absence and presence of GNPs, we again used the probe BTB. Before proceeding, we first measured the change in the absorbance of BTB at 620 nm in our experimental setup when the agarose gel was made with different pH solutions along with BTB. The pH vs. absorbance calibration was done by placing the Petri dish containing agarose gel in a UV plate reader in a manner exactly identical to that in our real experimental setup (Fig. S14, ESI†). In the pH gradient experiment in the gel, as we expected, we observed that the pH of zone A started to increase at a rapid rate (increase of 2.1 ± 0.2 pH units in the first hour), whereas the pH of zone C started to decrease (0.2 pH unit in 1 h) and that of zone B also started to increase, but at a very slow rate (increase of only 0.3 ± 0.1 pH unit in 1 h) (Fig. 3b). Interestingly, after 120 min, the enhancement of the pH in zone A started to decrease at a slow rate, and the pH of zone A and B tended to converge. We were able to continue this experiment for up to 6 h, as beyond this time point the agarose gel started to shrink, specifically at the ends (zone A and C), due to drying, and after 7–8 h the absorbance data were inconsistent and irreproducible. The shrinking of the gel after 10 h in our experimental setup was very prominent and even clearly visible to the naked eye (Fig. S13d, ESI†). In this setup, the initial increase and subsequent decrease in the pH in zone A (near UR + urea) is due to the fast formation of (NH4)2CO3, which started to diffuse across the gel as these ions are small. Thus, after a certain time, the generated gradient tended to merge, and the pH difference among zones started to decrease; this was also due to the formation and diffusion of acidic-pH substances through the other side. We then performed the experiment in the presence of agarose gel impregnated with CTAB-capped cationic GNPs, which were dispersed uniformly throughout the gel, as the gel was made with the GNP solution (see ESI† for details). In this experiment, we observed that the pH of zone A started to increase at a faster rate, whereas the pH of zone B remained unaltered and that of zone C decreased. Intriguingly, in this case, the pH of zone A continually increased, and even after 5 h, it did not decrease, but instead increased at a slower rate. Surprisingly, the pH of zone B did not change substantially over time, and the pH of zone C decreased at a slower rate. Thus, in the case of the GNP-embedded agarose gel, the pH gradient continually increased, and the effect remained over a long period of time (under our experimental conditions, the perpetuated pH gradient effect was observed for the full experimental duration of 6 h (as our experimental conditions permitted observation only up to this time)), and a difference of almost four pH units was observed between zones A and C. Herein, we use the word ‘perpetuate’ to symbolize the maintenance or continuation of the event for a longer time period without showing any sign of fading. We believe that this effect is due to the binding of carbonate ions to the GNP surface and thus remains localized at zone A. In other words, the presence of GNPs inhibits the diffusion of the ions across the gel and helped to maintain the pH gradient across a centimeter-length distance. We also investigated whether any GNPs, BTB or NBI leaked from the gel into the aqueous solution. For this, after 4 h, we measured the absorbance spectra of the aqueous solutions from the sides containing UR and GOx separately (Fig. S15, ESI†). We were happy to observe no leakage of BTB, NBI or GNPs from the gel to the enzyme solution, as no corresponding absorbance peaks of these components were observed in either case. We believe that this is because in our experiment, concentrations of only 20 μM of BTB or 0.2 mM NBI were used in the gel; whereas much higher concentrations of reagents were used on both sides (urea and glucose 100 mM), and thus, those reagents will instead diffuse into the gel over time.
Next, as a control experiment, we also measured the zone-specific pH values of the hydrogel when only the UR and urea reaction took place at one side of the gel without having the GOx + glucose reaction on the other side (Fig. S16a and b, ESI†). Instead of GOx and glucose, only mQ water was present on that side. Thus, only a gradient of carbonate ions will be formed in the hydrogel in the absence and presence of GNPs. We then monitored the time-dependent change in the pH of the gel in different zones. We again observed that the pH of zone A near the UR reaction started to increase at a rapid rate initially, but then began to decrease with time, and the pH of all the zones converged after 4 h. In this case, we chose to monitor the absorbance for up to 4 h, as within this time interval the pH gradient almost disappeared for the hydrogel system without GNPs. However, in the presence of GNPs in the hydrogel, the pH of zone A started to increase from the beginning, continued to increase at a slower rate and did not decrease over time (Fig. S16c and d, ESI†). However, after some time, the pH of zone B and C also started to increase, but at a much slower rate. However, after 4 h, the difference between the pH values of zone A and C remained around two units, unlike in the case of our first system, in which the difference between the pH values of zone A and C was around four units (due to the presence of the GOx + glucose reaction). Overall, this experiment also suggested that the presence of cationic GNPs restricts the mobility of carbonate through the gel and thus helped in maintaining the pH gradient in our experimental setup.
We also investigated how proton transfer catalysis was affected in different zones of our experimental setup, which is important in setting up complex spatially distinctive chemistry. For this, we used the substrate NBI instead of the pH probe BTB. As mentioned earlier, this base-catalyzed E1CB reaction can be followed by monitoring the formation of CNP. We also calibrated the UV absorbance by adding only CNP to the gel and obtained a linear calibration curve by plotting the CNP concentration and absorbance (Fig. S17, ESI†). We again followed the formation of the product CNP in three different zones at different time intervals as shown in Fig. 6a and b; NBI (0.2 mM) was equally distributed throughout the gel. The amount of product formed in the absence of GNP was much higher in zone A (high pH zone), whereas for zone B, the rate of increase in product formation was much lower, and in zone C almost no product was formed even after 4 h. In this case, after 4 h, the amount of CNP in zone A was only ∼15 μM. However, we were pleased to observe that the amount of product was even higher in zone A when GNPs were embedded in the agarose gel. It has already been mentioned that GNPs can catalyze the reaction; this effect was also maintained in the gel matrix. The amount of product formed over time in zone A was ∼105 μM, which was ∼7-fold higher than that formed in the case of only agarose gel. Interestingly, the formed product in zone A did not decrease over time, presumably due to the anionic nature of the product at high pH, which might result in binding of the CNP to the GNP surface. In the presence of GNPs in the gel, the amount of product in zone B is also higher (∼45 μM) than that in the system without GNPs, indicating the catalytic ability of the CTAB-capped nanoparticle surface for this kind of proton transfer reaction, as mentioned previously. However, in zone C, no such enhanced product formation was observed, as only ∼15 μM of CNP was found. Overall, we demonstrated that the presence of GNPs in the gel was not only able to maintain the pH gradient across a hydrogel surface, but also helped to produce zone-specific catalytic reaction. The base-catalyzed proton transfer rate enhancement in zone A also indirectly demonstrates the higher pH of zone A, and more precisely, a spatiotemporal change in the pH and catalytic ability at different zones across a gel surface.
Next, we performed proton transfer catalytic experiments in gels in the absence and presence of GNPs, using only UR + urea solution on one side and only mQ water on the other side of the gel, instead of GOx + glucose (Fig. S18, ESI†). Unsurprisingly, in this case, the amount of CNP in zone A, in both the absence and presence of GNPs, was similar to that observed when both the enzymes (GOx and UR) were present on opposite sides of the gel. Specifically, we observed a similar catalytic rate in zone A, and the amount of product found after 4 h in the gel was around 20 and 100 μM in the absence and presence of GNPs in the gel matrix, respectively. However, in this case the amounts of product found in both zones B and C were much higher than those in the previous case described in Fig. 6. In fact, in the absence of GNPs, the amount of CNP in zone B and C started to increase at a higher rate after 100 and 150 min, respectively, and reached around 18 and 14 μM after 4 h. In the presence of GNPs in the gel matrix, the CNP concentrations in both zone B and C were around 50 μM after 4 h. In zone C, a sharp increase in the CNP accumulation rate was observed after 1 h. Overall, we also found more than two-fold product formed in zone A due to its higher pH, compared to zone B and C; suggesting manifestation of zone-specific kinetics in single system. In the case with both the UR + urea and Gox + glucose gradients the difference in product distribution was sharp, whereas in the case of only UR + urea, the gradient was lower, like the pH distribution in the different zones.
Conclusion
In conclusion, we first probed the nanoparticle surface pH behavior in a dynamically changing bulk environment with temporal variation in the pH. We found that the surface pH decreased slowly in a gradually changing acidic environment (in which gluconic acid was formed due to the reactivity of GOx with glucose) and quickly turned more basic in response to a small increase in the pH (due to the formation of ammonium carbonate by the reaction of UR and urea) of the surroundings. Furthermore, we have shown how the pH of an agarose gel surface changes when two different enzymatic products, one with a pH-increasing and the other with a pH-decreasing effect, are generated on two opposite ends. Encouragingly, we found that the pH gradient effect can be perpetuated or prolonged in the presence of cationic GNPs in the gel. It is worth mentioning that previous pioneering works demonstrated pH gradients in gel systems using light and a photoacid generator simultaneously, giving access to the generation of photopatterned multidomain, self-sorted materials.28,29,47,48 In this manuscript, we have shown that it is indeed possible to generate two distinct pH zones by restricting the mobility of the ions using anion-binding nanoparticles in a hydrogel system. In fact, it is also possible to catalyze a proton transfer reaction specifically in one distinct zone (the carbonate-rich zone) of the macroscopic gel. It has been hypothesized in literature reports that in addition to inorganic surfaces, hydrogel systems might have some importance in the context of the prebiotic origin of life due to their superior ability to perform energy-requiring tasks, such as cell division, transcription, metabolism, assembly of pre-cells, etc.32,49–52 In this context, we showed that the amalgamation of both hydrogel and hybrid inorganic–organic surfaces can maintain a pH gradient in a macroscale environment for a substantial time period. Herein, we did not observe any sign of the disappearance of the gradient for up to 6 h (as our experimental conditions permit up to 6 h of monitoring) in the presence of the nanoparticles, in contrast to ∼2 h in the absence of the nanoparticles. Maintenance of this pH gradient in the absence of a membrane and membrane-bound proton-pump-based complicated enzymes can be achieved inside a gel-like system, simply due to the carbonate ion trapping ability of the cationic-surfactant-containing gold nanoparticles.39,53–56 Additionally, this work shows a new route for autonomously harnessing energy as a pH gradient in a macroscale environment for performing spatially segregated chemical processes in a membrane-free environment for the generation of more complex multi-dimensional reaction-diffusion systems.57–62Experimental section
Materials and methods
All commercially available reagents were used exactly as received, with no further purification. Sodium borohydride (NaBH4), bromothymol blue, cetyltrimethylammonium bromide (CTAB), ascorbic acid, sodium hydroxide pellets, hydrochloric acid (HCl), glucose, glucose oxidase (GOx), urea and urease (UR) were purchased from Sisco Research Laboratory (SRL), India. 1,2-Benzisoxazole and gold(III) chloride trihydrate (HAuCl4·3H2O) were purchased from Sigma-Aldrich. Milli-Q water was used throughout the experiment. Polyethersulfone (PES) membrane (10k MWCO) was purchased from Sartorius.The substrates 5-nitrobenzisoxazole (NBI) and 2-cyanophenol (CNP) for Kemp elimination were synthesized and characterized as reported in the literature.41
Perylene-3,4,9,10-tetracarboxylic acid (PTCA) was synthesized following the reported protocol in the literature.63
A Varian Cary 60 (Agilent Technologies) spectrophotometer was used for performing UV-Vis studies. During the Kemp elimination reaction, the formation of the product was monitored by following the absorbance at 380 nm. pH studies were carried out by following the absorbance at 620 nm using the pH-sensitive probe bromothymol blue (BTB).
A JEOL JEM-F200 microscope was used to obtain transmission electron microscopy images of the gold nanoparticles (GNP).
A Horiba Scientific NanoParticle Observer (SZ-100V2) was used to measure the hydrodynamic diameter (Dh) of the nanoparticles.
A Merilyzer EIAQuant plate reader was used for performing UV-Vis studies. During the Kemp elimination reaction, the formation of the product was monitored by following the absorbance at 405 nm. pH studies were carried out by following the absorbance at 630 nm using the pH-sensitive probe bromothymol blue (BTB).
Fluorescence measurements were performed using a Cary Eclipse fluorescence spectrofluorometer.
Synthesis and characterization of gold nanoparticles (GNP)
The seed-growth method was used to synthesize the gold nanoparticles (GNP), as described in the literature.35 Firstly, a seed solution was prepared by mixing 0.052 ml of HAuCl4·3H2O (24 mM) and 3.75 ml of CTAB (100 mM) solution, followed by the reduction of gold using 1.2 ml of freshly prepared ice-cold NaBH4 (25 mM), resulting in a brown-colored solution indicating the formation of gold seeds. Then, a growth solution was prepared by mixing 10 ml of CTAB (100 mM) solution with 6.25 ml of HAuCl4·3H2O (4 mM) followed by the addition of 7.5 ml of L-ascorbic acid (100 mM) with gentle shaking, which resulted in a colorless solution. Finally, the addition of 56.5 μl of the seed solution to the growth solution with vigorous stirring resulted in the appearance of a red color, which indicated the formation of gold nanoparticles. The formed solution was kept undisturbed at 25 °C for 24 h.Before further study, the as-formed nanoparticles were purified by passing them through a Sephadex G-25 column, and the concentration of gold nanoparticles was measured using UV-vis spectroscopy, as reported in the literature.64
The DLS, zeta potential, TEM Images, and UV-Vis spectra are shown in ESI Fig. S1.†
Protocol for agarose gel preparation in the absence and presence of GNPs
For the preparation of the gel, 50 mg of agarose was heated in 5 ml milliQ water at 110 °C in a heating block. The agarose solution was then poured in the middle of a Petri dish (diameter 6.0 cm) using two rectangular-shaped pieces of cardboard, as shown in Fig. S10a,† and then it was allowed to polymerize. For the preparation of the gel containing GNP, GNP solution was added to the agarose solution before pouring it into the Petri dish. Gels containing GNP + BTB, GNP + NBI, NBI and BTB only were prepared in a similar way. The overall concentrations of the GNP solution, BTB, and NBI in the gel were 150 pM, 20 μM, and 200 μM respectively.Representative gel images are shown in ESI Fig. S11.†
Data availability
See ESI† for gel images, additional DLS, zeta potential, centrifugation experiment, catalysis data, and TEM images.Author contributions
RRM performed most of the experiments and synthesis. Priyanka did part of the experiments and most of the data plotting and fitting. ES did theoretical work related to COMSOL studies. SM conceived the idea, supervised the work and wrote the manuscript where RRM, Priyanka and ES made comments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. M. thanks the Science and Engineering Research Board (SERB), New Delhi (for Start-up research grant, File No. SRG/2019/000365) for financial support. RRM and Priyanka thank IISER Mohali for PhD fellowships. E. S. acknowledges CSIR, India (09/947(0109)/2019-EMR-I) for a doctoral research grant. We also thank the I-STEM facility (Govt. of India) for providing us access to COMSOL Multiphysics 5.6.Notes and references
- N. Lane and W. F. Martin, Cell, 2012, 151, 1406–1416 CrossRef CAS PubMed.
- N. Lane, Bioessays, 2017, 39, 1600217 CrossRef PubMed.
- W. Martin and M. J. Russell, Philos. Trans. R. Soc., B, 2003, 358, 59–83 CrossRef CAS PubMed.
- M. Meister, G. Lowe and H. C. Berg, Cell, 1987, 49, 643–650 CrossRef CAS PubMed.
- J. Santo-Domingo and N. Demaurex, J. Gen. Physiol., 2012, 139, 415–423 CrossRef CAS PubMed.
- C.-J. Guo, W.-W. Sun, K. S. Bruno, B. R. Oakley, N. P. Keller and C. C. C. Wang, Chem. Sci., 2015, 6, 5913–5921 RSC.
- Y. Liu, R. Zeng, R. Wang, Y. Weng, R. Wang, P. Zou and P. R. Chen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2025299118 CrossRef CAS PubMed.
- J. Zhou, X. Du, C. Berciu, H. He, J. Shi, D. Nicastro and B. Xu, Chem, 2016, 1, 246–263 CAS.
- H. H. Mattingly, K. Kamino, B. B. Machta and T. Emonet, Nat. Phys., 2021, 17, 1426–1431 Search PubMed.
- V. E. Deneke and S. Di Talia, J. Cell Biol., 2018, 217, 1193–1204 CrossRef CAS PubMed.
- A. Somasundar, S. Ghosh, F. Mohajerani, L. N. Massenburg, T. Yang, P. S. Cremer, D. Velegol and A. Sen, Nat. Nanotechnol., 2019, 14, 1129–1134 CrossRef CAS PubMed.
- M. Feng and M. K. Gilson, Annu. Rev. Biophys., 2020, 49, 87–105 CrossRef CAS PubMed.
- L. Tian, M. Li, J. Liu, A. J. Patil, B. W. Drinkwater and S. Mann, ACS Cent. Sci., 2018, 4, 1551–1558 CrossRef CAS PubMed.
- P. A. Korevaar, C. N. Kaplan, A. Grinthal, R. M. Rust and J. Aizenberg, Nat. Commun., 2020, 11, 386 CrossRef CAS PubMed.
- A. van der Weijden, M. Winkens, S. M. C. Schoenmakers, W. T. S. Huck and P. A. Korevaar, Nat. Commun., 2020, 11, 4800 CrossRef CAS PubMed.
- A.-D. C. Nguindjel and P. A. Korevaar, ChemSystemsChem, 2021, 3, e2100021 CAS.
- T. B. H. Schroeder and J. Aizenberg, Nat. Commun., 2022, 13, 259 CrossRef CAS.
- I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 1198–1199 CrossRef CAS PubMed.
- A. Paikar, A. I. Novichkov, A. I. Hanopolskyi, V. A. Smaliak, X. Sui, N. Kampf, E. V. Skorb and S. N. Semenov, Adv. Mater., 2022, 34, e2106816 CrossRef PubMed.
- M. Grzelczak, L. M. Liz-Marzán and R. Klajn, Chem. Soc. Rev., 2019, 48, 1342–1361 RSC.
- P. K. Kundu, D. Samanta, R. Leizrowice, B. Margulis, H. Zhao, M. Börner, T. Udayabhaskararao, D. Manna and R. Klajn, Nat. Chem., 2015, 7, 646–652 CrossRef CAS PubMed.
- R. Chen, K. Das, M. A. Cardona, L. Gabrielli and L. J. Prins, J. Am. Chem. Soc., 2022, 144, 2010–2018 CrossRef CAS PubMed.
- R. Chen, S. Neri and L. J. Prins, Nat. Nanotechnol., 2020, 15, 868–874 CrossRef CAS PubMed.
- F. della Sala, S. Neri, S. Maiti, J. L.-Y. Chen and L. J. Prins, Curr. Opin. Biotechnol., 2017, 46, 27–33 CrossRef CAS PubMed.
- K. P. Sonu, S. Vinikumar, S. Dhiman, S. J. George and M. Eswaramoorthy, Nanoscale Adv., 2019, 1, 1847–1852 RSC.
- X. Yang, H. Lu, Y. Tao, L. Zhou and H. Wang, Angew. Chem., Int. Ed., 2021, 60, 23797–23804 CrossRef CAS PubMed.
- H. S. Cooke, L. Schlichter, C. C. Piras and D. K. Smith, Chem. Sci., 2021, 12, 12156–12164 RSC.
- L. Schlichter, C. C. Piras and D. K. Smith, Chem. Sci., 2021, 12, 4162–4172 RSC.
- A. Q. Mai, T. Bánsági Jr, A. F. Taylor and J. A. Pojman Sr, Commun. Chem., 2021, 4, 101 CrossRef CAS.
- Y. Miele, S. J. Jones, F. Rossi, P. A. Beales and A. F. Taylor, J. Phys. Chem. Lett., 2022, 13, 1979–1984 CrossRef CAS PubMed.
- S. O. Krabbenborg, J. Veerbeek and J. Huskens, Chem.–Eur. J., 2015, 21, 9638–9644 CrossRef CAS PubMed.
- G. Wächtershäuser, Microbiol. Rev., 1988, 52, 452–484 CrossRef PubMed.
- C. D. Lacerda, M. F. C. Andrade, P. de S. Pessoa, F. M. Prado, P. A. R. Pires, M. F. Pinatto-Botelho, F. Wodtke, A. A. Dos Santos, L. G. Dias, F. da S. Lima, H. Chaimovich and I. M. Cuccovia, Colloids Surf., A, 2021, 611, 125770 CrossRef CAS.
- P. Mukerjee and K. Banerjee, J. Phys. Chem., 1964, 68, 3567–3574 CrossRef CAS.
- R. R. Mahato, E. Shandilya, B. Dasgupta and S. Maiti, ACS Catal., 2021, 11, 8504–8509 CrossRef CAS.
- L. J. Prins, Acc. Chem. Res., 2015, 48, 1920–1928 CrossRef CAS PubMed.
- D. Di Iorio and J. Huskens, ChemistryOpen, 2020, 9, 53–66 CrossRef CAS PubMed.
- D. Zaramella, P. Scrimin and L. J. Prins, J. Am. Chem. Soc., 2012, 134, 8396–8399 CrossRef CAS.
- C. Pezzato, P. Scrimin and L. J. Prins, Angew. Chem., Int. Ed., 2014, 53, 2104–2109 CrossRef CAS PubMed.
- E. Shandilya, B. Dasgupta and S. Maiti, Chem.–Eur. J., 2021, 27, 7831–7836 CrossRef CAS PubMed.
- S. Rani, B. Dasgupta, G. K. Bhati, K. Tomar, S. Rakshit and S. Maiti, ChemBioChem, 2021, 22, 1285–1291 CrossRef CAS PubMed.
- W. Cullen, M. C. Misuraca, C. A. Hunter, N. H. Williams and M. D. Ward, Nat. Chem., 2016, 8, 231–236 CrossRef CAS PubMed.
- A. Li, B. Wang, A. Ilie, K. D. Dubey, G. Bange, I. V. Korendovych, S. Shaik and M. T. Reetz, Nat. Commun., 2017, 8, 14876 CrossRef CAS PubMed.
- S. Martí, I. Tuñón, V. Moliner and J. Bertran, ACS Catal., 2020, 10, 11110–11119 CrossRef.
- J. Newman and K. E. Thomas-Alyea, Structure of the Electrical Double Layer, in Electrochemical Systems, Wiley-Interscience, 2004, ch. 7 Search PubMed.
- A. Contractor, A. Balasubramanian and G. Hughes, Multiphysics simulation of isoelectric point separation of proteins using non-gel microfluidic system, Proceedings of the COMSOL Conference, Boston, 2009 Search PubMed.
- D. J. Cornwell, O. J. Daubney and D. K. Smith, J. Am. Chem. Soc., 2015, 137, 15486–15492 CrossRef CAS PubMed.
- L. Thomson, R. Schweins, E. R. Draper and D. J. Adams, Macromol. Rapid Commun., 2020, 41, 2000093 CrossRef CAS PubMed.
- J. T. Trevors and G. H. Pollack, Prog. Biophys. Mol. Biol., 2005, 89, 1 CrossRef CAS PubMed.
- D. Yang, S. Peng, M. R. Hartman, T. Gupton-Campolongo, E. J. Rice, A. K. Chang, Z. Gu, G. Q. Lu and D. Luo, Sci. Rep., 2013, 3, 3165 CrossRef PubMed.
- N. Kitadai and S. Maruyama, Geosci. Front., 2018, 9, 1117–1153 CrossRef CAS.
- P. Reeves, M. Y. Yoshinaga, P. P. Nadine, I. Goldenstein, J. Peplies, A. Meyerdierks, R. Amann, W. Bach and K. –U. Hinrichs, Environ. Microbiol., 2014, 16, 3515–3532 CrossRef PubMed.
- L. Malacrida, P. N. Hedde, B. Torrado and E. Gratton, Biophysicist, 2020, 1, 9 CrossRef PubMed.
- A. Deshwal and S. Maiti, Langmuir, 2021, 37, 7273–7284 CrossRef CAS PubMed.
- E. Gouaux and R. Mackinnon, Science, 2005, 310, 1461–1465 CrossRef CAS PubMed.
- L. M. R. Keil, F. M. Möller, M. Kieß, P. W. Kudella and C. B. Mast, Nat. Commun., 2017, 8, 1897 CrossRef PubMed.
- B. A. Grzybowski and W. T. S. Huck, Nat. Nanotechnol., 2016, 11, 585–592 CrossRef CAS PubMed.
- Priyanka, E. Shandilya, S. K. Brar, R. R. Mahato and S. Maiti, Chem. Sci., 2021, 13, 274–282 RSC.
- A. S. Y. Wong and W. T. S. Huck, Beilstein J. Org. Chem., 2017, 13, 1486–1497 CrossRef CAS PubMed.
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
- D. Kroiss, G. Ashkenasy, A. B. Braunschweig, T. Tuttle and R. V. Ulijn, Chem, 2019, 5, 1917–1920 CAS.
- S. M. M. Reddy, E. Raßlenberg, S. Sloan-Dennison, T. Hesketh, O. Silberbush, T. Tuttle, E. Smith, D. Graham, K. Faulds, R. V. Ulijn, N. Ashkenasy and A. Lampel, Adv. Mater., 2020, 32, e2003511 CrossRef PubMed.
- D. Tai and J. Liu, Luminescence, 2015, 30, 358–361 CrossRef CAS PubMed.
- W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02317b |
| This journal is © The Royal Society of Chemistry 2022 |