A recurrent neural network model for biomass gasification chemistry†
Krishna Gopal
Sharma
a,
Niket S.
Kaisare
 b and
Himanshu
Goyal
b and
Himanshu
Goyal
 *b
*b
aDepartment of Computer Science and Engineering, Indian Institute of Technology Madras, Chennai, Tamil Nadu 600036, India
bDepartment of Chemical Engineering, Indian Institute of Technology Madras, Chennai, Tamil Nadu 600036, India. E-mail: goyal@iitm.ac.in
First published on 17th November 2021
Abstract
Detailed chemical kinetic models involving hundreds of species and thousands of reactions have recently been developed for biomass thermochemical conversion. The high computational cost of these kinetic models makes them impractical even for simple reactor geometries. In this work, we develop a recurrent neural network (RNN) model for the secondary gas-phase reactions of biomass gasification in an inert environment in the temperature range of 800–1000 °C. A gated recurrent unit (GRU) based RNN architecture is used to ensure accurate predictions over the entire range of time in the reactor. A compact kinetic model reduced from a detailed kinetic scheme using an automated reduction algorithm is employed as the reference kinetic scheme for the gas-phase reactions. A comprehensive range of biomass compositions and reactor conditions are used to generate the training data ensuring a wide range of the model applicability. The developed GRU-based RNN model can predict the temporal evolution of important reactants and products during biomass gasification in the freeboard region of a fluidized bed reactor. The model reduces the computational cost associated with the reference kinetic scheme by four orders of magnitude.
1 Introduction
Biomass is a crucial renewable source of carbon. Large-scale biomass conversion into fuels and chemicals is imperative in reducing our reliance on fossil fuels and tackling global warming. Thermochemical conversion, involving fast pyrolysis and gasification in fluidized bed reactors, is a robust technique to convert a wide variety of non-food sources of biomass into gaseous and liquid products. At present, this conversion technique is facing several challenges. For example, the lack of control over the yield and composition of tars produced during biomass gasification causes process interruptions and requires expensive cleanup.1,2 Experiments alone fail to provide detailed insights due to the harsh reactor conditions, opaque solid phase, and coupling of the reactor hydrodynamics with the chemical conversion process. Comprehensive models are required to predict reactor performance and allow reactor design and optimization.Models for the biomass thermochemical conversion range from detailed but computationally expensive computational fluid dynamics (CFD) simulations3 to computationally fast ideal reactors.4 The CFD simulations are necessary to understand the coupling between the reactor flow dynamics and chemical processes. However, CFD simulations become too expensive for large-scale applications, and ideal reactor models are preferred.4 In ideal reactor models, limits of transport processes are assumed, for example, complete mixing in a continuously stirred tank reactor (CSTR) and no-axial mixing in a plug flow reactor (PFR). In some cases, insights gained from CFD simulations are combined with ideal reactors.5 An adequate level of modeling is selected depending on the application and details required.
Biomass gasification takes place at higher temperatures (∼800–1000 °C), where the solid biomass produces intermediate or primary products, which are then converted to gases (e.g., CO and H2) and tar species (e.g., phenol and naphthalene). For biomass gasification modeling, a common assumption is to model the bubbling bed and freeboard regions of the fluidized bed as the CSTR and PFR, respectively.4–7 The accuracy of these models relies on adequately representing the conversion chemistry involving the volatile release from biomass (primary reactions) and the subsequent gas-phase evolution (secondary reactions). Recently developed detailed kinetic schemes,8–10 consisting of hundreds of species and thousands of reactions, allow the possibility of a comprehensive investigation of reactor operating conditions in biomass conversion. However, their usage is limited by the high computational cost and difficulty in solving the associated system of stiff ordinary differential equations (ODEs). For this reason, modeling studies in the literature utilize global kinetic schemes consisting of a few lumped species and reactions; however, these models cannot predict the product composition.11–13 In a few studies,8,14 automatic reduction algorithms, such as the directed relation graph (DRG)15 and the DRG with error propagation (DRGEP),16 are used to reduce the detailed kinetic models. Reduced kinetic models require less computational resources than detailed models, but they are still computationally expensive and need stiff ODE solvers.8 Nonetheless, high variability in biomass feedstock and the heterogeneous structure of biomass particles make the chemistry modeling a daunting task.9,17
The challenge of the high computational cost and complexity of using detailed or reduced kinetic models can partially be resolved using machine learning algorithms, which have recently found applications in numerous areas, including reaction engineering. Examples include reaction screening,18 reaction condition optimization,19 modeling fuel chemistry,20 and kinetic Monte Carlo models.21 Machine learning models require most of the computational effort a priori during the development stage and are computationally fast during their application. This aspect makes machine learning attractive in the context of biomass thermochemical conversion. Several investigations have focused on building machine learning models for biomass thermochemical conversion using experimental22–29 and simulation data.30 These investigations primarily employed artificial neural networks (ANN), decision tree, random forest, and support vector regression. Two significant limitations of these works are the inability to predict the temporal evolution of the product yield and composition and the applicability in a narrow range of parameters, especially for models based on experimental data. Machine learning models able to predict temporal variations in the reactant and product compositions under realistic reaction conditions are missing in the literature.
This work tackles the challenges mentioned above by combining DRGEP,16 an automatic reduction algorithm, with a recurrent neural network (RNN) to build a model for predicting the secondary gas-phase reactions of biomass devolatilization (primary) products in the freeboard region of a fluidized bed reactor. Since the freeboard region is modeled as a PFR, an RNN is employed due to its ability to store information in a sequence. The developed RNN model can predict the composition of 27 target species, consisting of major gaseous and tar products, in a PFR. These target species, the reactor temperature (between 800–1000 °C), and the residence time or length of the PFR constitute the model input. Our work demonstrates the efficacy of the combined application of automatic reduction algorithms and machine learning tools to develop computationally fast models for complex reaction systems, such as biomass gasification.
2 Methodology
The objective of developing an RNN model is to predict the reactant and product compositions during biomass gasification (under inert conditions) in fluidized bed reactors where the freeboard region can be modeled as an isothermal PFR. Fig. 1 shows a schematic of the biomass gasification process and where the RNN model fits. As shown in the figure, biomass is converted to primary products in the bubbling bed region, which are subsequently converted to secondary products in the freeboard region. The development of the RNN model for the freeboard region involves four essential steps: identification of input–output variables, generation of the training data representative of the target application, selection of the RNN structure, and training and testing of the developed model. These steps are detailed in the following subsections.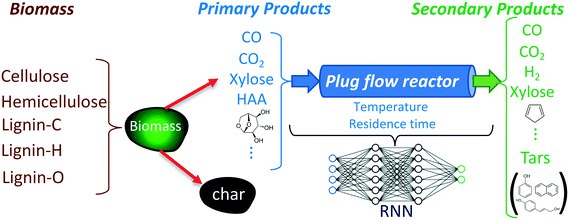 | ||
| Fig. 1 Schematic of the biomass gasification process and the RNN model. The RNN models the dynamics of the freeboard region of the fluidized bed gasifier. The input to the RNN model consists of the reactor temperature and the mass fractions of 27 species provided in Table 1. | ||
2.1 Input–output variables
Biomass gasification consists of two major sequential steps: devolatilization of solid biomass in the bubbling bed region and the secondary gas phase reactions of the devolatilization products in the freeboard region. The biomass devolatilization products, called the primary products, are the reactants for the secondary reactions. We use the kinetic model31 of the CRECK modeling group to describe biomass devolatilization. The solid-phase reactants, representing the biomass composition, include cellulose, hemicellulose and three types of lignin. Table S1 in the ESI† summarizes the compositions of these five components and ash in various biomass considered in this work. The model for devolatilization consists of 24 irreversible reactions involving the five solid-phase reactants and twenty gas-phase products. This kinetic scheme has been validated against experiments in a wide range of operating conditions and feedstock.31–33 For the secondary reactions, we use a compact kinetic model8 (39 species and 118 reactions) developed by reducing a detailed kinetic model (396 species and 3210 reactions) with the DRGEP,16 an automatic chemical mechanism reduction tool. The error between the predictions of the compact and detailed kinetic models is less than 10% for most of the species.8 The kinetic model takes the twenty primary products of the devolatilization chemistry31 as input and predicts the composition of major constituents of permanent gases and tar species. A total of 27 species (including the twenty primary products) were identified as the target species8 for the DRGEP. The reduced kinetic model8 is the reference model in this work that the RNN model is expected to reproduce.The input to the RNN model consists of the reactor temperature and the mass fractions of the 27 chemical species, provided in Table 1, that are part of the reference kinetic scheme. The temporal evolution of these 27 species in a PFR is the output of the RNN model. For this work, the temperature range is 800–1000 °C, and the maximum residence time is five seconds, representative of biomass gasification conditions.
2.2 Training, validation and test data
The applicability and accuracy of a machine learning model rely on the training and testing data. The complexity of biomass gasification makes this task challenging. There is considerable heterogeneity in the biomass composition and properties, which must be considered while generating the training data. To this end, we generate the training data in two steps. In the first step, biomass devolatilization is simulated employing a spherically symmetric one-dimensional intraparticle model34 coupled with the kinetic scheme31 of the CRECK modeling group for widely varying biomass properties and reactor conditions, as shown in Table 2. The first step provides 810 composition sets of primary products.| Parameter | Value |
|---|---|
| Reactor temperature | 800, 850, 900, 950, 1000 °C |
| Heat transfer coefficient | 300, 1000, 3000 W m−2 K−1 |
| Biomass particle diameters | 300 μm, 1 mm, 3 mm |
| Moisture content | 0, 10, 20 kg water per kg dry biomass |
| Solid heat capacity | 2300 J kg−1 K−1 |
| Biomass bulk density | 650 kg m−3 |
| Pressure | 1 atm |
| Biomass composition | List31 provided in Table S1 in the ESI† |
In the second step, the primary products obtained in the first step undergo secondary gas-phase reactions to form light gases and tar species. These reactions are represented by the reference kinetic scheme8 and simulated in a PFR configuration at five temperatures in the range of 800–1000 °C. A time resolution of 50 ms is used to resolve the evolution of chemical species adequately. Thus, for a 5 s residence time in the PFR, we generate data at 100 time points, for each of the 27 species. The resulting data consists of about 11 million species compositions (∼0.4 million data points for each of the 27 species). The mass fractions of the 27 target species are normalized to a standard normal distribution using StandardScaler class of scikit-learn,35 ensuring that the data for all species has the same order of magnitude and is zero-mean. The data is divided into training, validation, and test sets in the ratio of 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2
0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2. Normalization is performed on the training data, and the associated parameters (mean and standard deviation) are then used to normalize the validation and test sets. With the input–output variables being identified and training data being available, the next step is selecting an appropriate RNN structure.
0.2. Normalization is performed on the training data, and the associated parameters (mean and standard deviation) are then used to normalize the validation and test sets. With the input–output variables being identified and training data being available, the next step is selecting an appropriate RNN structure.
2.3 Structure of the RNN model
RNN is a subclass of neural network architectures commonly used for solving sequence-based problems. RNN can handle data with variable sequence lengths, and their parameter sharing properties make them ideal for solving tasks such as sentence classification, image captioning, and language translation.36–40 A brief description of the basic principles of the RNN model is provided here.We define an input sequence of length T as X = x1, x2⋯, xt, xt+1,⋯, xT for any general t ∈ {1,⋯, T}. The corresponding output at time t is represented as yt. Mathematically, a simple RNN model can be represented as:
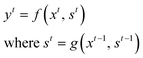 | (1) |
RNNs can be trained using the same backpropagation technique used in artificial neural networks and deep learning. The different steps in a sequence represent the residence timesteps in the PFR, along which the data for the 27 species is available. The technique called backpropagation through time41 (BPTT) involves backpropagation through these timesteps in a sequence while finding gradients of the parameters. It is similar to the usual backpropagation technique for finding gradients, apart from the fact that the gradient of the current timestep is calculated with respect to the previous timestep as well.
This work aims to predict the species concentrations along the length (residence time) of the reactor, starting from a given initial concentration. In general, an RNN model is adequate for sequences of short length; training an RNN model for long sequences is challenging. While backpropagating through time in long sequences, the training suffers from problems of exploding or vanishing gradients.42 In both situations, an RNN model fails to learn the model accurately. Commonly employed gradient descent is prone to fail to train an RNN model to learn long term dependencies in a long sequence. In this regard, long short term memory43 (LSTM) and gated recurrent units44 (GRU) are robust RNN architectures that handle some of the limitations of a feed forward RNN architecture and provide a way to address long term dependencies. LSTM and GRU use states to encode the sequence to handle the long term dependencies as valuable information is already saved in the states. Both GRU and LSTM based RNN models have comparable performance, but a GRU cell uses fewer parameters, requiring less memory and shorter training and execution time.45 We use GRU based RNN models in this work.
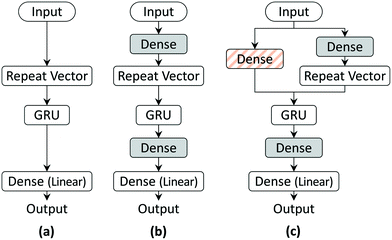 | ||
| Fig. 2 The three RNN architectures used in this work: (a) model 1, (b) model 2, and (c) model 3. Dense layers with ReLU activation (shaded and hatched boxes) are added to improve model prediction. | ||
RNNs use unique embedding layers to encode the input more efficiently for tasks such as machine translation and speech recognition. We add a fully connected dense layer after the input layer (grey-shaded box in Fig. 2(b)) in the architecture to mimic such an embedding layer. The output space of the GRU layer is limited as the gates use tanh or sigmoid activation. Since the output layer with linear activation of model 1 might not decode the output efficiently, we add another fully connected layer before the output layer with ReLU activation to introduce non-linearity. The improved RNN model architecture (model 2) is schematically depicted in Fig. 2(b).
Training and testing of the model architecture will be discussed in the next section. As shall be discussed subsequently, we observed that both of these models showed larger errors, especially at the initial time-points. One of the reasons for this could be the lack of variability in the initial state of GRU. The model architectures model 1 and model 2 initialize the GRU state to a zero vector for all model inputs. To address this issue, we add a fully connected layer (orange-hatched dense layer of Fig. 2(c)) into the model, which is taken as the input layer and uses its output as the initial state for the GRU. Including the initial state training in the model architecture considerably improved the results for the first few milliseconds. The model architecture (model 3) with the initial state training is shown in Fig. 2(c).
We end this discussion on model architecture by noting that an important distinction from the traditional RNN architectures is using a repeat vector layer to pass the input layer (model 1) or the output of the dense layer used to encode it (models 2 and 3) to the GRU cell at each time step during training and testing. In the traditional RNN structure, the output at time step t − 1 is used to predict the output at time step t. For example, in machine translation tasks, the output of the RNN model is the probability distribution over the vocabulary of the target language, and the prediction is accurate so long as the output word with the maximum probability distribution matches the reference word. In contrast, since any deviation of the output value from the reference value is an error, we employ the RNN architecture as a regression model using the initial concentration to predict future time steps. Another key distinction with tasks such as machine translation is that Teacher forcing46 is used in training such RNN models so that the model learns the correlation xt+1real = f(xtreal, st), where f is the function learned by the RNN. However, in tasks such as prediction of reactor concentrations in future, the model will be trained for xt+1pred = f(xtreal, st), whereas only the x0pred = x0real is known exactly and the error in prediction of future output, i.e., xt+1pred = f(xtpred, st), gets carried forward and compounded. Thus, in both training and testing stages, we provide only the initial concentration x0 as the RNN model input and let the state of GRU handle the time progression.
 | (2) |
| Hyperparameter | List of values |
|---|---|
| Dense layer neurons | {64, 128, 512, 1024} |
| GRU units | {64, 128, 512, 1024} |
| Initial learning rate | {0.01, 0.001, 0.0001} |
| Learning rate decay rate | {0.9, 0.99} |
| Learning rate decay steps | {25, 50, 100} |
The selected model architectures are trained on a NVIDIA GeForce GTX 1050Ti GPU with a batch size of 64 for 1500 epochs. The python packages – Keras48 and TensorFlow49 – are used to build and train the neural networks. The training took around one second for each epoch.
3 Results and discussion
3.1 Comparison of the three model architectures
The three different GRU-based RNN model architectures (Fig. 2) are trained as described in the previous section. We performed a random search over a range of the hyperparameter values, listed in Table 3, to determine the optimal hyperparameters for the model using the weight and bias tool.50 In order to test the performance of the fitted models, the mean absolute error (MAE) is calculated for the normalized variables in the validation and test set data. The hyperparameter values with the lowest MAE values on the validation data are shown in Table 4. The model architectures with these corresponding hyperparameter values are selected for further training and testing.| Layer | Activation | Output shape |
|---|---|---|
| Model 1 | ||
| Input | — | (None, 28) |
| Repeat vector | — | (None, 100, 128) |
| GRU | tanh | (None, 100, 128) |
| Dense (output) | Linear | (None, 100, 27) |
| Total parameters: | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 155 |
|
| Model 2 | ||
|---|---|---|
| Input | — | (None, 28) |
| Dense1 | ReLU | (None, 128) |
| Repeat vector | — | (None, 100, 128) |
| GRU | tanh | (None, 100, 128) |
| Dense2 | ReLU | (None, 100, 128) |
| Dense3 (output) | Linear | (None, 100, 27) |
| Total parameters: | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779 779 |
|
| Model 3 | ||
|---|---|---|
| Input | — | (None, 28) |
| Dense1 | ReLU | (None, 128) |
| Dense2 | ReLU | (None, 128) |
| Repeat vector | — | (None, 100, 128) |
| GRU | tanh | (None, 100, 128) |
| Dense3 | ReLU | (None, 100, 128) |
| Dense4 (output) | Linear | (None, 100, 27) |
| Total parameters: | 126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 491 |
|
The predictive ability of the trained RNN architectures is assessed by comparing their predictions with the test set. Note that the test set data is never used during the development of the RNN models, including the hyperparameter tuning. We compare the three model architectures for the accuracy in predicting the species concentrations and training and prediction computational time. The latter is also compared with that of solving the system of stiff ODEs associated with the reference kinetic scheme.8
A total of 100 cases are randomly selected from the test set and given as input to the RNN and compared with the reference kinetic model to predict the species evolution for five seconds in the PFR. The reference kinetic model is solved using the stiff ODE solver, DVODE, which required an average prediction time of around 252 s. Table 5 provides the training time, prediction time, coefficient of determination (R2), and MAE for the three RNN architectures described in section 2.3.1. The training time increases with the number of RNN model parameters, whereas the execution time is comparable for all the models. A reduction of four orders of magnitude in the execution time is achieved using the RNN model compared to the reference kinetic model. Note that we are using a reduced kinetic model developed from a detailed chemical mechanism. For the detailed mechanism as the reference kinetic scheme, the reduction in the execution time is expected to be much higher. For all the models, the R2 value is greater than 0.99, demonstrating the ability of even the simplest RNN model to capture the temporal species evolution. An increase in the model complexity also results in a smaller MAE.
| Model architecture | Training time (min) | Average model prediction time (s) | R 2 | MAE |
|---|---|---|---|---|
| Model 1 | 40 | 2.65 × 10−2 | 0.9985 | 15.16 × 10−3 |
| Model 2 | 55 | 2.87 × 10−2 | 0.9997 | 11.14 × 10−3 |
| Model 3 | 58 | 2.88 × 10−2 | 0.9998 | 9.10 × 10−3 |
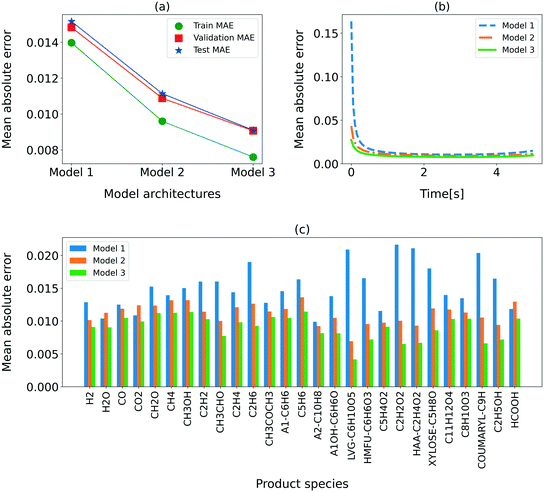
For further analysis of the performance of the three RNN models, the MAE for the training, validation, and test sets, varying residence time, and the individual chemical species is shown in Fig. 3. Also evident from Table 5, the MAE is the lowest for model 3. Fig. 3(a) shows that the MAEs for the training, validation, and test sets are comparable, confirming that the models are not overfitted. The MAE reported in this section corresponds to the normalized data to present a comparison across all species. The overall MAE for model 3 is below 1%. We also show the MAE at each time in Fig. 3(b). Clearly, the MAE is higher for the initial time (<0.5 s) than the rest of the residence time. This behavior is attributed to the low resolution (50 ms) of the training data during the initial phase of the secondary reactions (<0.5 s) at higher reactor temperatures. Model 3 provides the minimum MAE in the entire residence time range, though the performance improvement is especially significant in the first 0.5 s. Fig. 3(c) shows the MAEs for all the input–output species. As expected, model 3 provides the lowest MAE for all the species.
3.2 Model analysis and prediction
We select model 3 to keep the MAE around 1% or less for every input–output species. The discussion in the rest of this section is based on the utilization of model 3. Fig. 4 shows the parity plots between the RNN (model 3) predictions and the training, validation, and test set values of major gas and tar species mass fractions at all the timesteps. The parity plots for all the individual species are provided in Fig. S1–S3 in the ESI† and show excellent agreement between the model predictions and the generated data sets. These results demonstrate the accuracy of the RNN model.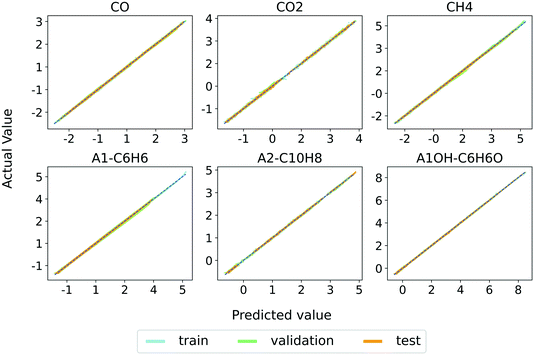 | ||
| Fig. 4 Parity plots of major light gases and tar species for training, validation, and test sets and predictions of model 3. | ||
As an application of the developed RNN model, we predict the temporal evolution of the major reactant and product species in the PFR. Only the species concentrations under the initial conditions, reactor temperature, and residence time are input to the RNN model. Fig. 5 shows the comparison of the RNN predictions and the test set data for a few randomly selected examples from the test set. The performance at three different temperatures is shown with the data converted back to mass fraction units. These results confirm the ability of the RNN model to predict the temporal evolution of species concentrations for the considered temperature (800–1000 °C) and residence time (5 s). With the excellent match for test data, we also tested the RNN model for future predictions of five more seconds (Fig. S4 in ESI†) to understand the function learned by the RNN model. Note that all the original data using the reference kinetic model is generated until five seconds (hence, the lines end at 5 s). Still, we make model predictions using the RNN for ten seconds. Interestingly the model is qualitatively performing as expected even for future predictions pointing to the suitability of the RNN algorithm for time series data. We will explore this aspect of the RNN models in our future studies.
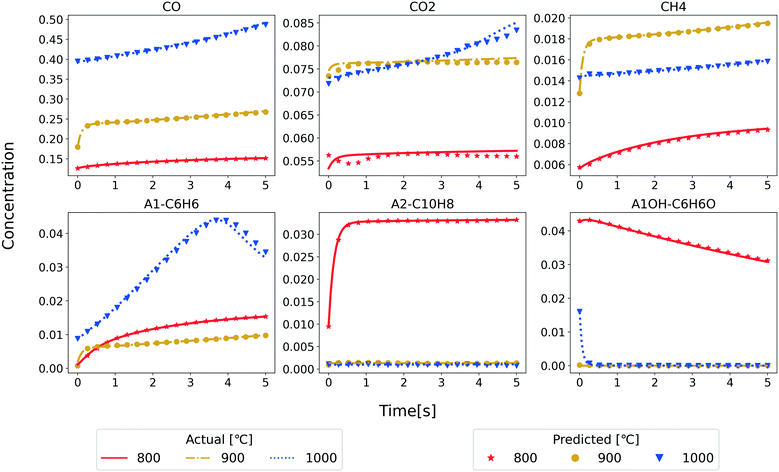 | ||
| Fig. 5 Comparison of the mass fraction profiles of the major product species obtained from model 3 (symbols) and test set (lines) at different temperatures. | ||
Finally, we analyze the effect of the training data since the availability of the training data plays a significant role in the predictive ability of the RNN model for unseen data. For this purpose, model 3 is trained separately for 500 epochs with different fractions of the entire training set. Fig. 6 shows the variation in the MAE for the RNN model 3 trained with different fractions of the training set while ignoring the remaining data from the training set. The validation and test sets remain identical for a fair comparison. The MAE decreases continuously with the amount of training data available, implying an increasing model accuracy. Moreover, the validation and test set MAE is comparable to the training set MAE in the entire range of the training data considered. This observation illustrates that the RNN model is not overfitted even for a smaller fraction of the training data and is thus also suitable when less training data is available. Note that even at 20%, the training data points are more than twice the number of parameters for the model 3 architecture.
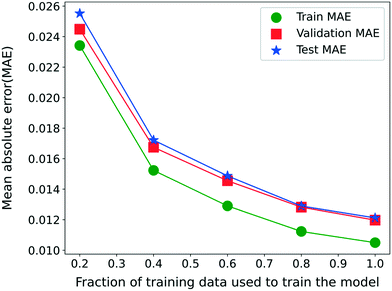 | ||
| Fig. 6 MAE on training, validation, and test sets when model 3 is trained with different fractions of training data. | ||
4 Conclusion
We demonstrate that the recurrent neural network (RNN) algorithm is suitable for reducing the computational cost and complexity of utilizing detailed chemistry in an ideal reactor configuration. We focused on biomass gasification in the freeboard region of a fluidized bed reactor as the target application. The developed gated recurrent unit (GRU) based RNN model can predict the temporal evolution of major reactant and product species in a wide range of biomass gasification conditions. To this end, we employ a kinetic scheme reduced from a detailed kinetic model using an automated reduction algorithm – DRGEP. Combining the existing automatic reduction algorithms with RNN becomes a powerful technique to develop high fidelity and computationally fast design tools that can predict and optimize complex conversion processes like biomass gasification. Predicting the transient behavior of chemical species during biomass gasification is a significant achievement of this work. The developed technique could be used for other reaction engineering problems where detailed chemistry models are too expensive to use.This work is a step towards reducing the current gap between data science and realistic reaction engineering problems. Future investigations can focus on integrating detailed chemistry with non-ideal reactor models.
Code availability
The RNN model developed for temporal evolution of species during biomass gasification and example data set are available for download at GitHub at the following link: https://github.com/CARE-IITM/RNN_biomass_gasification.Conflicts of interest
The authors have no known conflicting financial interests that could potentially influence this work.Acknowledgements
This work was supported by the National Supercomputing Mission (NSM; project number SP20211026CHNSMX008954). We acknowledge the National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Shivay’ the at Indian Institute of Technology (BHU), Varanasi, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and the Department of Science and Technology (DST), Government of India.References
- C. F. Palma, Modelling of tar formation and evolution for biomass gasification: a review, Appl. Energy, 2013, 111, 129–141 CrossRef.
- S. Van Paasen, J. Kiel and H. Veringa, Tar formation in a fluidised bed gasifier, 2004 Search PubMed.
- H. Goyal, O. Desjardins, P. Pepiot and J. Capecelatro, A computational study of the effects of multiphase dynamics in catalytic upgrading of biomass pyrolysis vapor, AIChE J., 2018, 64, 3341–3353 CrossRef CAS.
- A. K. Stark, R. B. Bates, Z. Zhao and A. F. Ghoniem, Prediction and validation of major gas and tar species from a reactor network model of air-blown fluidized bed biomass gasification, Energy Fuels, 2015, 29, 2437–2452 CrossRef CAS.
- A. K. Stark, C. Altantzis, R. B. Bates and A. F. Ghoniem, Towards an advanced reactor network modeling framework for fluidized bed biomass gasification: incorporating information from detailed CFD simulations, Chem. Eng. J., 2016, 303, 409–424 CrossRef CAS.
- B. Das, A. Bhattacharya and A. Datta, Kinetic modeling of biomass gasification and tar formation in a fluidized bed gasifier using equivalent reactor network (ERN), Fuel, 2020, 280, 118582 CrossRef CAS.
- R. Radmanesh, J. Chaouki and C. Guy, Biomass gasification in a bubbling fluidized bed reactor: experiments and modeling, AIChE J., 2006, 52, 4258–4272 CrossRef CAS.
- H. Goyal and P. Pepiot, A compact kinetic model for biomass pyrolysis at gasification conditions, Energy Fuels, 2017, 31, 12120–12132 CrossRef CAS.
- P. E. A. Debiagi, G. Gentile, M. Pelucchi, A. Frassoldati, A. Cuoci, T. Faravelli and E. Ranzi, Detailed kinetic mechanism of gas-phase reactions of volatiles released from biomass pyrolysis, Biomass Bioenergy, 2016, 93, 60–71 CrossRef CAS.
- K. Norinaga, T. Shoji, S. Kudo and J.-I. Hayashi, Detailed chemical kinetic modelling of vapour-phase cracking of multi-component molecular mixtures derived from the fast pyrolysis of cellulose, Fuel, 2013, 103, 141–150 CrossRef CAS.
- X. Ku, T. Li and T. Løvås, CFD–DEM simulation of biomass gasification with steam in a fluidized bed reactor, Chem. Eng. Sci., 2015, 122, 270–283 CrossRef CAS.
- Q. Xiong, S.-C. Kong and A. Passalacqua, Development of a generalized numerical framework for simulating biomass fast pyrolysis in fluidized-bed reactors, Chem. Eng. Sci., 2013, 99, 305–313 CrossRef CAS.
- Q. Xue, D. Dalluge, T. Heindel, R. Fox and R. Brown, Experimental validation and CFD modeling study of biomass fast pyrolysis in fluidized-bed reactors, Fuel, 2012, 97, 757–769 CrossRef CAS.
- T. Løvås, E. Houshfar, M. Bugge and Ø. Skreiberg, Automatic generation of kinetic skeletal mechanisms for biomass combustion, Energy Fuels, 2013, 27, 6979–6991 CrossRef.
- T. Lu and C. K. Law, A directed relation graph method for mechanism reduction, Proc. Combust. Inst., 2005, 30, 1333–1341 CrossRef.
- P. Pepiot-Desjardins and H. Pitsch, An efficient error-propagation-based reduction method for large chemical kinetic mechanisms, Combust. Flame, 2008, 154, 67–81 CrossRef CAS.
- A. Gómez-Barea and B. Leckner, Modeling of biomass gasification in fluidized bed, Prog. Energy Combust. Sci., 2010, 36, 444–509 CrossRef.
- N. S. Eyke, W. H. Green and K. F. Jensen, Iterative experimental design based on active machine learning reduces the experimental burden associated with reaction screening, React. Chem. Eng., 2020, 5, 1963–1972 RSC.
- H. W. Kim, S. W. Lee, G. S. Na, S. J. Han, S. K. Kim, J. H. Shin, H. Chang and Y. T. Kim, Reaction condition optimization for non-oxidative conversion of methane using artificial intelligence, React. Chem. Eng., 2021, 6, 235–243 RSC.
- S. Alqahtani and T. Echekki, A data-based hybrid model for complex fuel chemistry acceleration at high temperatures, Combust. Flame, 2021, 223, 142–152 CrossRef CAS.
- M. Bracconi and M. Maestri, Training set design for machine learning techniques applied to the approximation of computationally intensive first-principles kinetic models, Chem. Eng. J., 2020, 400, 125469 CrossRef CAS.
- F. Elmaz, Ö. Yücel and A. Y. Mutlu, Predictive modeling of biomass gasification with machine learning-based regression methods, Energy, 2020, 191, 116541 CrossRef CAS.
- A. Y. Mutlu and O. Yucel, An artificial intelligence based approach to predicting syngas composition for downdraft biomass gasification, Energy, 2018, 165, 895–901 CrossRef CAS.
- J. Xing, K. Luo, H. Wang, Z. Gao and J. Fan, A comprehensive study on estimating higher heating value of biomass from proximate and ultimate analysis with machine learning approaches, Energy, 2019, 188, 116077 CrossRef.
- E. E. Ozbas, D. Aksu, A. Ongen, M. A. Aydin and H. K. Ozcan, Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms, Int. J. Hydrogen Energy, 2019, 44, 17260–17268 CrossRef CAS.
- Y. Sun, L. Liu, Q. Wang, X. Yang and X. Tu, Pyrolysis products from industrial waste biomass based on a neural network model, J. Anal. Appl. Pyrolysis, 2016, 120, 94–102 CrossRef CAS.
- X. Zhu, Y. Li and X. Wang, Machine learning prediction of biochar yield and carbon contents in biochar based on biomass characteristics and pyrolysis conditions, Bioresour. Technol., 2019, 288, 121527 CrossRef CAS PubMed.
- Q. Tang, Y. Chen, H. Yang, M. Liu, H. Xiao, Z. Wu, H. Chen and S. R. Naqvi, Prediction of bio-oil yield and hydrogen contents based on machine learning method: effect of biomass compositions and pyrolysis conditions, Energy Fuels, 2020, 34, 11050–11060 CrossRef CAS.
- T. Onsree and N. Tippayawong, Machine learning application to predict yields of solid products from biomass torrefaction, Renewable Energy, 2021, 167, 425–432 CrossRef CAS.
- B. R. Hough, D. A. Beck, D. T. Schwartz and J. Pfaendtner, Application of machine learning to pyrolysis reaction networks: Reducing model solution time to enable process optimization, Comput. Chem. Eng., 2017, 104, 56–63 CrossRef CAS.
- M. Corbetta, A. Frassoldati, H. Bennadji, K. Smith, M. J. Serapiglia, G. Gauthier, T. Melkior, E. Ranzi and E. M. Fisher, Pyrolysis of centimeter-scale woody biomass particles: kinetic modeling and experimental validation, Energy Fuels, 2014, 28, 3884–3898 CrossRef CAS.
- E. Ranzi, A. Cuoci, T. Faravelli, A. Frassoldati, G. Migliavacca, S. Pierucci and S. Sommariva, Chemical kinetics of biomass pyrolysis, Energy Fuels, 2008, 22, 4292–4300 CrossRef CAS.
- M. Calonaci, R. Grana, E. Barker Hemings, G. Bozzano, M. Dente and E. Ranzi, Comprehensive kinetic modeling study of bio-oil formation from fast pyrolysis of biomass, Energy Fuels, 2010, 24, 5727–5734 CrossRef CAS.
- H. Goyal and P. Pepiot, On the validation of a one-dimensional biomass pyrolysis model using uncertainty quantification, ACS Sustainable Chem. Eng., 2018, 6, 12153–12165 CrossRef CAS.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- K. Cho, B. van Merrienboer, D. Bahdanau and Y. Bengio, On the Properties of Neural Machine Translation: Encoder-Decoder Approaches, CoRR, 2014, abs/1409.1259 Search PubMed.
- P. Liu, X. Qiu and X. Huang, Recurrent Neural Network for Text Classification with Multi-Task Learning, CoRR, 2016, abs/1605.05101 Search PubMed.
- D. Tang, B. Qin and T. Liu, Document Modeling with Gated Recurrent Neural Network for Sentiment Classification, Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 2015, pp. 1422–1432 Search PubMed.
- X. Chen and C. L. Zitnick, Learning a Recurrent Visual Representation for Image Caption Generation, CoRR, 2014, abs/1411.5654 Search PubMed.
- K. Cho, B. van Merrienboer, Ç. Gülçehre, F. Bougares, H. Schwenk and Y. Bengio, Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation, CoRR, 2014, abs/1406.1078 Search PubMed.
- P. Werbos, Backpropagation through time: what it does and how to do it, Proc. IEEE, 1990, 78, 1550–1560 CrossRef.
- S. Hochreiter, Untersuchungen zu dynamischen neuronalen Netzen, Diploma thesis, Institut für Informatik, Lehrstuhl Prof. Brauer, Technische Universität München, 1991 Search PubMed.
- S. Hochreiter and J. Schmidhuber, Long short-term memory, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS PubMed.
- F. Gers, J. Schmidhuber and F. Cummins, Learning to forget: continual prediction with LSTM, 1999 Ninth International Conference on Artificial Neural Networks ICANN 99. (Conf. Publ. No. 470), 1999, vol. 2, pp. 850–855 Search PubMed.
- J. Chung, Ç. Gülçehre, K. Cho and Y. Bengio, Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling, CoRR, 2014, abs/1412.3555 Search PubMed.
- R. J. Williams and D. Zipser, A Learning Algorithm for Continually Running Fully Recurrent Neural Networks, 1989 Search PubMed.
- D. P. Kingma and J. Ba, Adam: A method for stochastic optimization, 2014, arXiv preprint arXiv:1412.6980 Search PubMed.
- F. Chollet, et al., Keras, https://keras.io, 2015 Search PubMed.
- M. Abadi, et al., TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/, Software available from tensorflow.org Search PubMed.
- L. Biewald, Experiment Tracking with Weights and Biases, 2020, https://www.wandb.com/, Software available from wandb.com Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1re00409c |
| This journal is © The Royal Society of Chemistry 2022 |