Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Carbon cage isomers and magnetic Dy⋯Dy interactions in Dy2O@C88 and Dy2C2@C88 metallofullerenes†
Wei
Yang‡
ab,
Georgios
Velkos‡
a,
Svetlana
Sudarkova
a,
Bernd
Büchner
a,
Stanislav M.
Avdoshenko
*a,
Fupin
Liu
 *a,
Alexey A.
Popov
*a,
Alexey A.
Popov
 *a and
Ning
Chen
*a and
Ning
Chen
 *b
*b
aLeibniz Institute for Solid State and Materials Research (IFW Dresden), Helmholtzstrasse 20, 01069 Dresden, Germany. E-mail: f.liu@ifw-dresden.de; s.avdoshenko@ifw-dresden.de; a.popov@ifw-dresden.de
bCollege of Chemistry, Chemical Engineering and Materials Science, Soochow University, Suzhou, Jiangsu 215123, P. R. China. E-mail: chenning@suda.edu.cn
First published on 26th September 2022
Abstract
Three isomers of Dy2O@C88 and two isomers of Dy2C2@C88 were synthesized and structurally characterized by single-crystal X-ray diffraction, vibrational spectroscopy, and DFT calculations. Both types of clusterfullerenes feature 4-fold electron transfer to the carbon cage, thus resulting in the same carbon cage isomers identified as C1(26), Cs(32), and D2(35). The studies of Dy⋯Dy superexchange interactions in Dy2O and Dy2C2 clusters revealed that the O2− bridge favors antiferromagnetic coupling whereas the acetylide group C22− supports ferromagnetic coupling of Dy magnetic moments. The strength of the coupling showed a considerable variability in different cage isomers. All metallofullerenes exhibited slow relaxation of magnetization and magnetic hysteresis. In Dy2O@C88 isomers the hysteresis remained open up to 7–9 K, while in Dy2C2@C88 the hysteresis loops were closed already at 2.5 K. This study demonstrated that both the endohedral bridge between metal atoms and the fullerene cage play an important role in magnetic interactions and relaxation of magnetization.
Introduction
Endohedral metallofullerenes (EMFs) feature fascinating structural diversity, defined by a broad variability of endohedral species with 1–4 metal ions, which are encapsulated in carbon cages of various shape and size ranging from C66 to C108 and beyond.1–5 In clusterfullerenes, endohedral species also include some non-metal atoms, which acquire a negative charge and serve as bridges between metals.6,7 The non-metal then defines the names of clusterfullerenes, such as endohedral oxygen in oxide clusterfullerenes8,9 or endohedral carbon in carbide clusterfullerenes.10,11The exploration of oxide clusterfullerenes started with a discovery of Sc4O2,3@C80 by Stevenson et al.12,13 and then continued with a series of Sc2O@C2n EMFs with cage sizes from C70 to C82.14–20 More recently, the focus was shifted to lanthanides, resulting in several M2O@C2n EMFs with Ho (C2n = C74,21 C84,22 4 isomers of C90,23 and 2 isomers of C92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24), Dy (C2n = C72,25 C74,25 C80,26 three isomers of C82
24), Dy (C2n = C72,25 C74,25 C80,26 three isomers of C82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27), and two isomers of Lu2O@C80.28 In M2O@C2n clusterfullerenes, two rare-earth metal ions (M3+) are bridged by the μ2-O2− ion; the whole M2O cluster has a formal charge of +4 and is encapsulated in fullerene cages preferring the C2n4− state.
27), and two isomers of Lu2O@C80.28 In M2O@C2n clusterfullerenes, two rare-earth metal ions (M3+) are bridged by the μ2-O2− ion; the whole M2O cluster has a formal charge of +4 and is encapsulated in fullerene cages preferring the C2n4− state.
A special interest in Dy-EMFs is motivated by their magnetic properties.29 In lanthanide clusterfullerenes, the non-metal ions bear a large negative charge, which imposes a strong axial ligand field and large magnetic anisotropy of nearby lanthanide ions. At the same time, isolation of endohedral species inside the carbon cage enables rather uncommon and yet simple atomic arrangements, thus creating a platform for the study of magnetic interactions and relaxation phenomena, especially well established for Dy-EMFs. But the carbon cage is not just an inert container for encapsulated clusters. A size and shape of a fullerene and topology of its π-system not only determine the electronic properties of the host but also affect the properties of the guests. An intriguingly strong variation of the magnetic properties found for Dy2O@C2n clusterfullerenes with C72–C82 cages25–27 calls for a systematic study of this factor, and in this work we focus on the larger fullerene cage, C88, for which we isolate three isomers of Dy2O@C88, determine their molecular structures and analyze magnetic properties.
While oxide clusterfullerenes based on C88 were not reported yet, this cage is known for other EMFs with 4-fold electron transfer, such as dimetallofullerenes Sm2@C88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 and Lu2@C88,31 and carbide clusterfullerenes M2C2@C88 (M = Sc,32 Y,33 Er,34 and Lu;31,35 see Table 1). The structural studies revealed four cage isomers of C88 in those EMFs, including three classical fullerenes C1(26), Cs(32), and D2(35), and one heptagon-containing isomer with Cs symmetry (labeled as Cs(hept)). As both feature 4-fold electron transfer to the fullerene, it is reasonable to expect similarity of the cage structure of oxide and carbide clusterfullerenes, and we anticipated to find these cage isomers for Dy2O@C88 as well. But this structural similarity also allows a different question to be addressed – how the bridge between two Dy ions affects magnetic properties and in particular Dy⋯Dy coupling. This problem requires a study of different types of clusterfullerenes sharing the same fullerene cages, and therefore we also decided to synthesize Dy2C2@C88 isomers for comparison with Dy2O@C88 counterparts. Furthermore, magnetic properties of Dy2C2 clusterfullerenes remain poorly explored, except for a single study of Dy2C2@Cs(6)-C82, and thus analysis of the role of acetylide group in Dy2C2@C2n EMFs with different cages is an important task on its own.
30 and Lu2@C88,31 and carbide clusterfullerenes M2C2@C88 (M = Sc,32 Y,33 Er,34 and Lu;31,35 see Table 1). The structural studies revealed four cage isomers of C88 in those EMFs, including three classical fullerenes C1(26), Cs(32), and D2(35), and one heptagon-containing isomer with Cs symmetry (labeled as Cs(hept)). As both feature 4-fold electron transfer to the fullerene, it is reasonable to expect similarity of the cage structure of oxide and carbide clusterfullerenes, and we anticipated to find these cage isomers for Dy2O@C88 as well. But this structural similarity also allows a different question to be addressed – how the bridge between two Dy ions affects magnetic properties and in particular Dy⋯Dy coupling. This problem requires a study of different types of clusterfullerenes sharing the same fullerene cages, and therefore we also decided to synthesize Dy2C2@C88 isomers for comparison with Dy2O@C88 counterparts. Furthermore, magnetic properties of Dy2C2 clusterfullerenes remain poorly explored, except for a single study of Dy2C2@Cs(6)-C82, and thus analysis of the role of acetylide group in Dy2C2@C2n EMFs with different cages is an important task on its own.
| Isomer | C884− | Y2O@C88 | Y2C2@C88 | Known structures | This work | |||
|---|---|---|---|---|---|---|---|---|
| ΔE (kJ mol−1) | Gap (eV) | ΔE (kJ mol−1) | Gap (eV) | ΔE (kJ mol−1) | Gap (eV) | |||
| D 2(35) | 0.0 | 0.59 | 0.0 | 0.75 | 0.0 | 0.75 | Sm2,30 Lu2C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 31 |
Dy2O, Dy2C2 |
| C s(32) | 30.2 | 0.46 | 16.5 | 0.69 | 13.2 | 0.69 | Er2C2,34 Lu2C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 31 |
Dy2O, Dy2C2 |
| C 1(26) | 28.6 | 0.69 | 21.1 | 0.87 | 38.5 | 0.84 | Y2C2,33 Lu2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 31 |
Dy2O |
| C 1(30) | 47.7 | 0.40 | 36.2 | 0.59 | 30.0 | 0.63 | ||
| C s(hept) | 67.0 | 0.64 | 54.0 | 0.77 | 57.7 | 0.79 | Sc2C2,32 Lu2C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 35 |
|
Synthesis and separation
For the synthesis of Dy2O-clusterfullerenes, core-drilled graphite rods filled with Dy2O3/graphite powder mixture were evaporated in arc-discharge under He/CO2 (270/27 mbar) atmosphere. The soot was collected and extracted by carbon disulfide (CS2) under an argon atmosphere for 12 h. The crude extract, containing mainly empty fullerenes, Dy-monometallofullerenes, and Dy2O-oxide clusterfullerenes, was treated with TiCl4 following the method proposed by Shinohara et al.36,37 While empty fullerenes did not react with TiCl4, Dy-EMFs formed an insoluble complex and could be separated by filtration and then released by breaking the complex with water (Fig. S1†). Three isomers of Dy2O@C88 were then isolated from the recovered EMF mixture after several steps of linear and recycling HPLC (Fig. S2†) and characterized by LDI-TOF mass-spectrometry as described in ESI (Fig. S3†). The isomers are denoted as Dy2O-I, Dy2O-II, and Dy2O-III, where the Roman number corresponds to the retention time of a given isomer during HPLC separation.Dy2C2-clusterfullerenes were synthesized by a similar arc-discharge process, but using He atmosphere with the addition of N2 (180/10 mbar). The CS2 extract of the soot in this case contained mainly empty fullerenes, Dy-monometallofullerenes, Dy3N-nitride clusterfullerenes, and Dy2C2-carbide clusterfullerenes. Following the SAFA approach developed by Stevenson et al.,38–40 the extract was re-dissolved in toluene and reacted with dried diamino silica gel (DASG). Empty fullerenes, Dy-monometallofullerenes, and Dy2C2-clusterfullerenes reacted with amino groups and were trapped by DASG, whereas less reactive Dy3N@C2n clusterfullerenes mainly remained in solution. The DASG with immobilized fullerenes was then filtered and washed with CS2, which resulted in the release of Dy2C2@C2n, whereas Dy-monometallofullerenes and main part of empty fullerenes remained trapped (Fig. S4†). Two isomers of Dy2C2@C88 denoted as Dy2C2-I and Dy2C2-II (the Roman numbers correspond to the retention time), were then isolated by HPLC (Fig. S5†) and characterized by LDI-TOF mass-spectrometry as described in ESI† (Fig. S6).
Molecular structures
Single-crystal X-ray diffraction
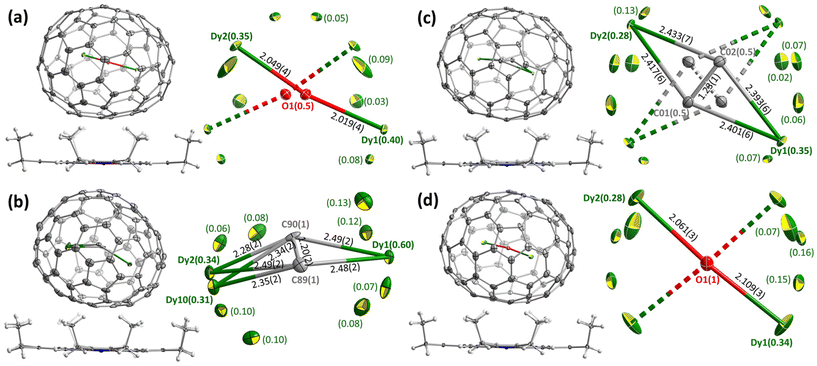
Molecular structures of Dy2O-I, Dy2C2-I, Dy2C2-II, and Dy2O-III were established by single-crystal X-ray diffraction (SC-XRD). The crystals were obtained by layering fullerene solutions in CS2 (for Dy2C2-I) or toluene (other EMFs) with a benzene solution of nickel octaethylporphyrin (NiOEP) in glass tubes. After slow diffusion of solutions during 3–4 weeks, fullerene·NiOEP co-crystals were obtained as black blocks on the tube walls. X-ray diffraction data collection was carried out at 100 K using synchrotron irradiation at the BESSY storage ring (BL14.2, Berlin-Adlershof, Germany).41 XDSAPP2.0 suite was employed for data processing.42,43 The structures were solved by direct methods and refined by SHELXL-2018.44 Hydrogen atoms were added geometrically and refined with a riding model. In each structure, the fullerene molecule is supported by one NiOEP molecule, which is the typical packing character of fullerene·NiOEP co-crystals.45–47 The endohedral units showed a considerable disorder as is common in EMF crystallography. However, in all crystals we could identify one major site with enhanced occupancy, which allowed discussion of the cluster shape and internal position inside the fullerene if not precise geometry parameters. Additional crystal data can be found in ESI† (Table S1 and Fig. S7, S8).Positions of endohedral clusters inside the fullerene are also very similar in the two structures. Dy atoms are disordered, but show enhanced occupancies of 0.28/0.34 (out of 0.50) for the main metal sites, which are located on one of the two-fold axes of the D2-symmetric fullerene cage. In Dy2C2@D2(35)-C88, the C2 unit has the bond length of 1.23(1) Å, and the main site of the Dy2C2 cluster has a slightly bent butterfly shape, with Dy–C bond lengths of 2.401(6), 2.393(6), 2.417(6), and 2.433(7) Å, the angle between Dy1-C2 and Dy2-C2 planes of 161.4(4)°, and Dy1⋯Dy2 distance of 4.602(2) Å. In Dy2O@D2(35)-C88, Dy–O bond lengths in the main site are 2.061(3) and 2.109(3) Å, the Dy1–O–Dy2 angle is 173.9(2)°, and Dy1⋯Dy2 distance is 4.164(2) Å.
DFT calculations
Crystallographic studies were augmented by extensive DFT calculations of Y2O@C88 and Y2C2@C88 for the four lowest-energy C884− isomers, including D2(35), Cs(32), C1(26), and C1(30), and also for Cs(hept), which was earlier found in some C88-based EMFs.32,35 For each cage isomer, we first used Fibonacci sampling to generate 120 starting structures with different orientations of the Y2O endohedral cluster27,48 and then performed their complete optimization, which gave several unique conformers (Fig. S9†). For Y2C2@C88, the reduced set of starting coordinates based on Y2O@C88 conformers was used, in which oxygen atom was replaced by the acetylide group. Relative energies of the most stable conformers for each cage isomer are listed in Table 1, more detailed data can be found in ESI.† The conformers of Y2O@C88 and Y2C2@C88 were then re-optimized with Dy replacing Y (Fig. 2). Since Y3+ and Dy3+ have similar ionic radii, the structure and relative energies are very similar, and the following discussion is based on Y analogs.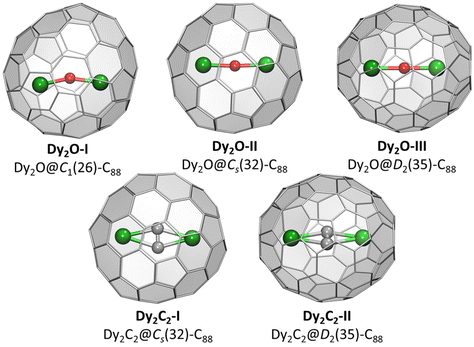 | ||
| Fig. 2 DFT-optimized molecular structure of Dy-EMFs (the lowest-energy conformers). Dy – green, O – red, C – gray. | ||
The most stable isomers of C884−, Y2O@C88, and Y2C2@C88 all have the D2(35)-C88 cage. For Y2O@C88, the calculations revealed only four unique conformers, of which two are 34 kJ mol−1 higher in energy than the two most stable ones. The structure of the lowest-energy conformer corresponds to the main site in SC-XRD structures of Dy2O-D2(35) and Dy2C2-D2(35) with the metal atoms aligned along the C2 axis of the cage. The Y2O cluster in this conformer is linear, but attains the Y–O–Y angles of 166° and 155° in higher-energy conformers. Likewise, the Y2C2 cluster is planar in the most stable conformer of Y2C2@D2(35)-C88. Interestingly, the optimized Y⋯Y distance in Y2O@C88 is 0.436 Å shorter than in Y2C2@C88 (4.206 Å versus 4.642 Å; compare to experimental values of 4.164(2) Å and 4.602(2) Å in Dy analogs), which leads to the shorter distance between the metal and the coordinated hexagon in Y2C2@C88 (2.015 Å) than in Y2O@C88 (2.167 Å) and makes the fullerene cage in Y2C2@C88 longer by 0.133 Å (8.673 Å versus 8.540 Å measured as the distance between centroids of Y-coordinated hexagons). A considerable variation of the fullerene size depending on the endohedral species was observed earlier in La2@D5(450)-C100 compared to La2C2@D5(450)-C100, but in that case it was the carbide clusterfullerene which had the shorter length, whereas the La-C6 distance was identical in both structures, and the whole effect could be explained by a stronger Coulomb repulsion between La ions when not mediated by the acetylide group.49
The next in the stability row are Y2O@C88 and Y2C2@C88 isomers based on the Cs(32)-C88 cage. The conformer survey of Y2O@Cs(32)-C88 gave 6 unique structures, of them three are almost isoenergetic within 4 kJ mol−1 and separated from other conformers by a gap of 25 kJ mol−1. The Y2O/Dy2O cluster in all of them is nearly linear with the M–O–M angle of 174–179°. For Y2C2@Cs(32)-C88, the lowest-energy conformer has the same position of metal atoms as in the most stable conformer of Y2O@C88 and corresponds to the main site in the SC-XRD structure of Dy2C2-Cs(32) and Lu2C2@Cs(32)-C88.31 The cluster is planar and is located on the symmetry plane of the fullerene cage.
Y2O@C1(26)-C88 is found to be the third most stable isomer of Y2O@C88. The endohedral cluster is located rather freely, with 9 unique conformers spread in the energy range of 57 kJ mol−1, of which six fall into the window of 15 kJ mol−1. The major site in the SC-XRD structure of Dy2O-C1(26) corresponds to the second conformer with the relative energy of 1.1 kJ mol−1. The Y–O–Y angle in this structure is 157°, but the Y2O cluster appears to be rather flexible with the angle varying strongly between conformers.
To summarize, the cage structures identified in this work for Dy2O@C88 and Dy2C2@C88 by SC-XRD correspond to the most stable cage isomers, whereas locations of the endohedral cluster, at least in their major crystallographic sites, correspond to the lowest-energy conformers. The disorder in the crystal structures may be partially caused by the conformational freedom as DFT predicts several structures with close energies. The relative energies of C1(30) and Cs(hept) isomers are not prohibitively high, and their formation should be considered as plausible, although they were not found in this work. A deeper study of other cage isomers and their thermodynamic functions may be required to fully disclose the stability row, but this exercise goes beyond the scope of this work.
Spectroscopic properties
While the SC-XRD is the golden standard of the molecular structure determination, a disorder may pose a serious problem for the structure elucidation and even reduce the reliability of the fullerene isomer assignment of EMFs. The high structural sensitivity of UV-Vis-NIR absorption spectra makes them a convenient complimentary technique, which can help resolving questionable structural assignments. If endohedral clusters are not contributing to the frontier orbitals, the absorption spectra of EMFs are dominated by π → π* excitations of the carbon cage. As a result, the spectra of EMFs with different metals or even different types of endohedral clusters may be very similar when they have the same fullerene isomer in the same formal charge state. In particular, close similarity of the spectra can be expected for the same isomers of carbide and oxide clusterfullerenes, as well as of dimetallofullerenes with divalent metals, as they all share the formal fullerene charge of 4−. The exact similarity, however, is expected only if the cluster is not involved at all, which is often not the case. Thus, different positions of the endohedral metal atoms (i.e. different conformers) may also contribute to the distinctions between the spectra.
Fig. 3 compares UV-Vis-NIR absorption spectra of Dy-EMFs isolated in this work. The spectrum of Dy2O-C1(26) with C1(26)-C88 cage resembles the spectra reported for Y2C2@C1(26)-C88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and Lu2@C1(26)-C88,31 but also that of Er2C2@Cs(32)-C88 from ref. 34. Given that the latter is also different from the spectra of other EMFs with Cs(32)-C88 cage, we suggest that the Er2C2@C88 identified as the Cs(32) isomer in ref. 34 requires reassignment to C1(26).
33 and Lu2@C1(26)-C88,31 but also that of Er2C2@Cs(32)-C88 from ref. 34. Given that the latter is also different from the spectra of other EMFs with Cs(32)-C88 cage, we suggest that the Er2C2@C88 identified as the Cs(32) isomer in ref. 34 requires reassignment to C1(26).
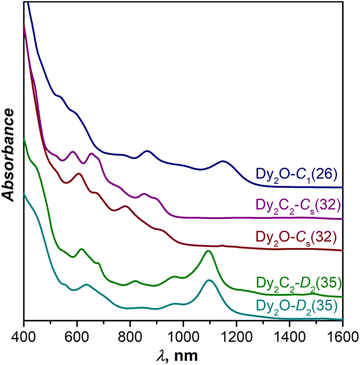 | ||
| Fig. 3 Vis-NIR absorption spectra of Dy2O@C88 and Dy2C2@C88 isomers measured in toluene solution at room temperature. | ||
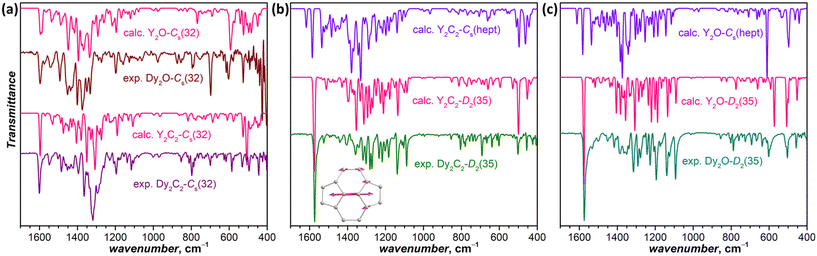
The spectrum of Dy2C2-Cs(32) is virtually identical to that of Lu2C2@Cs(32)-C88 from ref. 31, in agreement with the same fullerene cage determined by SC-XRD for both structures. It also shows a certain similarity to the spectrum of Dy2O-II, the only compound for which we did not succeed with the SC-XRD structure elucidation. We thus tentatively assign Cs(32) isomer to Dy2O-II, and further confirm this assignment by IR spectroscopy as discussed below.
In line with the same cage isomerism and metal positions determined by SC-XRD, Dy2C2-D2(35) and Dy2O-D2(35) have almost identical absorption spectra. Comparison to the literature data gave rather puzzling results. Our spectra are similar to that of Sm2@C88-D2(35)30 with the same fullerene cage as determined in this work, but also show a close resemblance with the spectra of Sc2C2@Cs(hept)-C88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 and Lu2C2@Cs(hept)-C88.35 We thus decided to look for further spectroscopic verification of the fullerene cage structure.
32 and Lu2C2@Cs(hept)-C88.35 We thus decided to look for further spectroscopic verification of the fullerene cage structure.
IR spectra are also very sensitive to the molecular structure of the fullerene cage. Besides, they can be predicted by DFT with high accuracy. This good agreement between experiment and theory was used earlier for the correct determination of some EMF structures when SC-XRD data were not available yet.50–52Fig. 4a compares experimental and calculated spectra of Dy2C2-Cs(32) and Dy2O-Cs(32) (note that calculations were performed for Y analogs, which does not affect the results of comparison because metal-based modes occur at much lower frequencies). For Dy2C2-Cs(32), the theory gives very good agreement with the experiment, especially in the range of tangential fullerene modes above 1000 cm−1. For Dy2O-Cs(32), we averaged the spectra of three low-energy conformers, as their spectra were found to be rather different. After the averaging, reasonable agreement with experimental data was obtained. Note that the spectra of Dy2C2-Cs(32) and Dy2O-Cs(32) with the same fullerene cage are still considerably different, which shows that the internal cluster and position of metal atoms do affect the IR spectra. Earlier we have already seen similar differences in the spectra of EMFs with Ih-C80 fullerene cage and different endohedral units.53
For Dy2C2-D2(35) (Fig. 4b) and Dy2O-D2(35) (Fig. 4c), the calculated spectra of D2(35) isomers show strikingly good agreement with the experimental data, whereas those of Cs(hept) isomers are substantially different. Thus, the IR spectroscopy confirms the cage isomer assignment of Dy2C2-D2(35) and Dy2O-D2(35). Both EMFs have a very characteristic absorption band at 1574 cm−1 with a particularly strong intensity considerably exceeding that of all other absorption features. DFT calculations ascribe this band to the stretching vibration of the shortest C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in the molecule (1.384 Å) located between pentagons in four pyracylene fragments.
C bonds in the molecule (1.384 Å) located between pentagons in four pyracylene fragments.
Magnetic properties
The isolation of three isomers of Dy2O@C88 and two isomers of Dy2C2@C88 allows us to analyze how the structural peculiarities of endohedral clusters and fullerene cages can affect the magnetic properties of Dy EMFs. The first effect may be addressed by comparing isostructural Dy2O and Dy2C2 compounds, whereas the second one can be considered by comparing different cage isomers with the same endohedral cluster. The role of the non-metal units, such as O2− and C22−, in the magnetism of EMFs is two-fold: they have a strong influence on the single-ion magnetic anisotropy of Dy ions by providing the main contribution to the ligand field,54–58 and they play a role of bridges between two Dy ions thus determining the strength of superexchange interactions.25,27,57,59–61Ab initio calculations
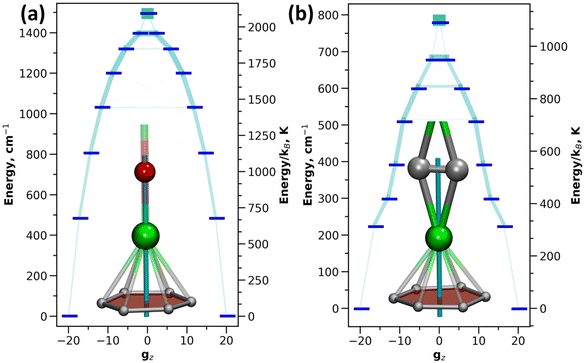
The single-ion anisotropy can be analyzed straightforwardly through multiconfigurational ab initio methods, such as the CASSCF/RASSI approach in Molcas employed in this work.62,63 We use Dy2O-D2(35) and Dy2C2-D2(35) as representative examples as they have the same fullerene cage isomer and identical η6-coordination of Dy ion to the carbon cage, and hence the difference between them can be directly ascribed to the different influence of O2− and C22− units. Fig. 5 shows the calculated ligand field splitting and orientation of magnetic moments for Dy ions in Dy2O-D2(35) and Dy2C2-D2(35). Both O2− and C22− impose an axial ligand field on Dy ions, yielding the ground state Kramers doublet (KD) with Jz = ±15/2. The orientation of the quantization axis is also similar in both clusters as it coincides with Dy–O bond in Dy2O and passes through the center of the acetylide group in Dy2C2. However, the ligand-field splitting and the degree of axiality imposed by O2− and C22− are very different. On average, the splitting in Dy2O is twice higher than in Dy2C2 (481 cm−1versus 224 cm−1 for the first excited KD and 1494 cm−1versus 780 cm−1 for the whole LF splitting in the ground-state 6H15/2 multiplet). Already for the ground-state KD, the gx and gy components of the pseudospin g-tensor in Dy2C2@C88 are 50 times larger than in Dy2O@C88. This indicates that Dy magnetic moments in Dy2C2 are more susceptible to perturbations of the magnetic field and hence can relax faster. A purity of the KD states when presented in |mJ〉 basis is also considerably higher in Dy2O than in Dy2C2. In the latter, only the first KD is relatively pure with 99.8% of the |15/2〉 term, whereas already in the second KD the contribution of the leading |13/2〉 term is only 86.5%, and the mixing is further increased in higher-energy KDs. In Dy2O@C88, the leading term contributions in the four lowest-energy KDs are 100.0% |15/2〉, 99.9% |13/2〉, 97.7% |11/2〉, and 94.3% |9/2〉, and only in the fifth KD the weight decreases below 90%, to 89.2% for |7/2〉. Thus, the Dy2O cluster with the negative charge localized on the single oxide ion features much stronger axiality than the Dy2C2 cluster, in which the negative charge is spread over two carbons.SQUID magnetometry
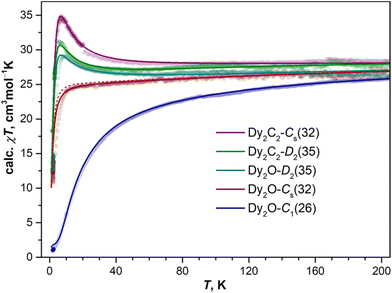
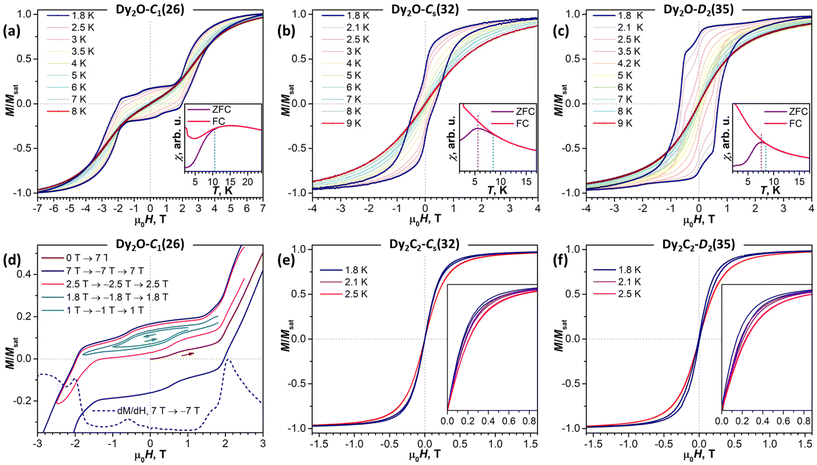
As follows from the results of ab initio calculations, magnetic ground state of Dy ions in all the studied EMFs is the Ising state with Jz = ± 15/2. It means that the differences in the static low-temperature magnetic behavior of the compounds should be caused by variation in the Dy⋯Dy interactions. The latter can be conveniently addressed by measurements of the temperature dependence of the magnetic susceptibility χ as the shape of the χT product curve exhibits characteristic signatures of interactions between magnetic moments. For two non-interacting moments, the curve should be almost flat with a steep decrease at the lowest temperatures. This is the behavior we observe for Dy2O-Cs(32) (Fig. 6). For the antiferromagnetic (AFM) coupling, the decrease of χT starts at higher temperatures and is smoother, which corresponds to the behavior found for Dy2O-C1(26). Finally, for the ferromagnetically-coupled (FM) moments, the χT curve develops a peak at low temperatures, which matches the behavior of Dy2O-D2(35). Thus, from the χT measurements, we infer that the isomers of Dy2O@C88 represent three different situations of magnetic Dy⋯Dy interactions. For the Dy2C2@C88 isomers the situation is different – both Dy2C2-Cs(32) and Dy2C2-D2(35) show clear signatures of FM coupling, which is stronger in Dy2C2-Cs(32). For all the compounds, the shapes of experimental χT curves are well reproduced by simulations with interaction parameters determined from the fit of magnetization curves as described below.Further details are obtained from isothermal magnetization curves plotted in Fig. 7. All three Dy2O@C88 isomers show magnetic hysteresis with a closing temperature of around 8–9 K at a sweep rate of 2.9 mT s−1. The hysteresis closing temperature matches the bifurcation temperatures of χ curves measured in zero-field cooled sample (ZFC) and during the in-field cooling (FC) and listed in Table 2 (see also insets in Fig. 7).
| ΔEAFM–FM | j | α (°) | T B | T irrev | T hyst | T B100 | |
|---|---|---|---|---|---|---|---|
| a ΔEAFM–FM (cm−1), j (cm−1), and α (°) are determined from the fits of magnetization curves. b T B is defined as the peak temperature in χZFC, Tirrev is the bifurcation point between χZFC and χFC curves (both measured with the sweep rate 5 K min−1), Thyst is the highest temperature at which the hysteresis loop is still open (sweep rate 2.9 mT s−1), and TB100 is the temperature, at which magnetization relaxation time is 100 s; all temperatures are in K. | |||||||
| Dy2O-C1(26) | −16.5 | −0.080 | 23 ± 1 | 10.5 | 8 | 6.0 | |
| Dy2O-Cs(32) | −0.4 | −0.002 | 23 ± 11 | 5.5 | 8.5 | 8 | 4.6 (0.2 T) |
| Dy2O-D2(35) | 3.6 | 0.022 | 43 ± 2 | 7.5 | 8.5 | 8 | 3.9 |
| Dy2C2-Cs(32) | 6.3 | 0.029 | 11 ± 3 | 2.1 | |||
| Dy2C2-D2(35) | 3.3 | 0.015 | 0 ± 5 | 2.1 | |||
The shapes of hysteresis are quite different between the isomers and reflect the nature of Dy⋯Dy interactions deduced from χT measurements. The most distinctive are the curves measured for Dy2O-C1(26). At 1.8 K the hysteresis is open in the whole measurement range from −7 T to +7 T and clearly shows two regimes with a small and large magnetic moment. The low-field regime corresponds to the dominant AFM alignment of the magnetic moments. But when the magnetic field exceeds 2 T, the state with the FM alignment gains lower energy and starts to increase its population, hence causing an increase of the magnetization. This hysteresis shape resembles that found in some other dinuclear Dy complexes with antiferromagnetic coupling,27,64–71 but the transition between the two states in Dy2O-C1(26) occurs at a considerably higher field, pointing to a much stronger Dy⋯Dy coupling in the fullerene.
To obtain the numerical parameters of the coupling, we fitted magnetization curves measured at different temperatures using the effective spin Hamiltonian (1):
| Ĥspin = ĤLF1 + ĤLF2 − 2j12Ĵ1·Ĵ2 + ĤZEE | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α), where the coefficient 225 appears because of the use of the full Dy3+ momentum in the Hamiltonian (1) and the single-ion ground state with Jz = ±15/2 (see ESI† for more details). In the fitting with PHI code,72j12 and α were treated as free parameters, and computed curves were powder-averaged to be compatible with experimental magnetization curves measured for powder samples. Finally, only experimental points in the field range where hysteresis is very narrow or completely closed were used as the Hamiltonian (1) does not include relaxation processes and hence cannot be used to model magnetic hysteresis. Experimental and fitted magnetization curves are compared in ESI.† Although different conformers of EMF molecules may have somewhat different single-ion LF parameters and LF splitting, our calculations in this work as well as earlier studies25–27,57 showed that the ground state KD of Dy ions in such EMFs are very close to the pure mJ = ±15/2 state irrespective of the Dy-cage coordination. Furthermore, the energy gap to the first excited KD is so high that only the ground-state KD will have significant population at low temperatures. Thus, it is not expected that the results of simulations with eqn (1) will be noticeably affected by the coexistence of different orientations of endohedral clusters or by accuracy limitations of the ab initio modelling of the LF splitting.
cos(α), where the coefficient 225 appears because of the use of the full Dy3+ momentum in the Hamiltonian (1) and the single-ion ground state with Jz = ±15/2 (see ESI† for more details). In the fitting with PHI code,72j12 and α were treated as free parameters, and computed curves were powder-averaged to be compatible with experimental magnetization curves measured for powder samples. Finally, only experimental points in the field range where hysteresis is very narrow or completely closed were used as the Hamiltonian (1) does not include relaxation processes and hence cannot be used to model magnetic hysteresis. Experimental and fitted magnetization curves are compared in ESI.† Although different conformers of EMF molecules may have somewhat different single-ion LF parameters and LF splitting, our calculations in this work as well as earlier studies25–27,57 showed that the ground state KD of Dy ions in such EMFs are very close to the pure mJ = ±15/2 state irrespective of the Dy-cage coordination. Furthermore, the energy gap to the first excited KD is so high that only the ground-state KD will have significant population at low temperatures. Thus, it is not expected that the results of simulations with eqn (1) will be noticeably affected by the coexistence of different orientations of endohedral clusters or by accuracy limitations of the ab initio modelling of the LF splitting.
For Dy2O-C1(26), the fitting procedure gave α of 23 ± 1° and j12 of −0.08 cm−1, yielding the ΔEAFM–FM value of −16.5 cm−1, one of the largest interaction energies between Dy magnetic moments in dinuclear {Dy2} compounds (see ref. 27 for a recent survey). Note that since Dy3+ magnetic moments in the Dy2O-C1(26) molecule are not collinear, the magnetic moment of the ground AFM state is not zero but amounts to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α/2) = 4μB. The fitted parameters and Hamiltonian (1) were then used to simulate χT curve, which gave good agreement to the experimental data (Fig. 6), thus confirming the reliable determination of the interaction parameters.
sin(α/2) = 4μB. The fitted parameters and Hamiltonian (1) were then used to simulate χT curve, which gave good agreement to the experimental data (Fig. 6), thus confirming the reliable determination of the interaction parameters.
In Dy2O-Cs(32), the hysteresis shape features a considerable decrease of the magnetization near zero field, which is consistent with the weak Dy⋯Dy interactions. When the coupling is negligible, an additional magnetization relaxation channel via zero-field quantum tunneling of magnetization is open, which results in a drastically reduced remanence. This hysteretic behavior is similar to the recently studied Dy2O@C74,25 although the QTM signatures in the hysteresis curve of Dy2O-Cs(32) are less pronounced than in the latter. The fitting of the magnetization curves with Hamiltonian (1) gave the angle of 23 ± 11° and a very small constant j12 of −0.002 cm−1. Note that when the coupling is weak, the dependence of the curves on the angle between magnetic moment is also reduced, thus resulting in a larger uncertainty. The small ΔEAFM–FM value of only −0.4 cm−1 is in line with the shape of χT curve, which is also well reproduced by simulations.
The shape of the magnetic hysteresis in Dy2O-D2(35) resembled that observed for some other dinuclear lanthanide fullerenes with FM coupling, such as Dy2ScN@C80,73 Tb2ScN@C80,74 and Dy2S@C82.61 After the sample is saturated at 7 T, ramping the field down produces only a small decrease of magnetization until reaching zero field. On crossing zero field, a certain decrease of magnetization occurs, which is likely due to the zero-field QTM. But the latter implies simultaneous flip of magnetic moments of both Dy3+ ions, and is not very efficient in a strongly coupled system. At a further negative ramping, another kink in the curve is seen at −0.48 T, after which the magnetization drops abruptly. Following earlier studies,61,74,75 this feature is assigned to the level crossing between the FM and AFM states, which promotes the efficient relaxation of magnetization via the QTM mechanism. Fitting the magnetization curves of Dy2O-D2(35) resulted in j12 of 0.022 cm−1, α of 43 ± 2°, and ΔEAFM–FM of 3.6 cm−1. The angle is unexpectedly large, given that SC-XRD and DFT results agree on the linear shape of the Dy2O cluster. Yet these parameters also give a good match between simulated and experimental χT curves. The AFM–FM energy difference can be also estimated from the magnetic field of the QTM kink (HQTM) in the hysteresis curve as ΔEAFM–FM = 0.935HQTM[T]μDy[μB] (ref. 61), which gives 4.4 cm−1.
In both isomers of Dy2C2@C88, only a very narrow opening of the hysteresis is observed at 1.8 K and 2.1 K, and the loop is completely closed by 2.5 K. Fitting of the magnetization curves gives the FM coupling with ΔEAFM–FM of 6.3 cm−1 in Dy2C2-Cs(32) and 3.3 cm−1 in Dy2C2-D2(35). The angle between magnetic moments is only 11 ± 3° in Dy2C2-Cs(32) and is nearly 0° in Dy2C2-D2(35) within the uncertainty limit of ±5°.
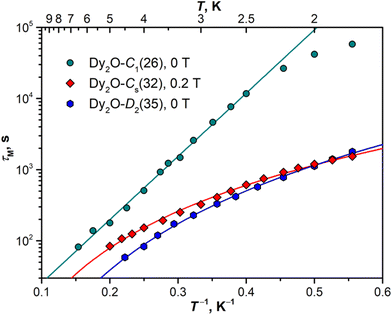
Magnetization relaxation times
The open magnetic hysteresis indicates that the studied Dy-EMFs are single-molecule magnets,76–80 and their magnetodynamics was further characterized by measuring the relaxation times τM at different temperatures. As the sample amount was not sufficient for AC measurements, only DC technique was employed. The samples were first magnetized at the field of 7 T, then the field was ramped down to zero as fast as possible, and the decay of magnetization was then followed and fitted with a stretched exponential function. The values determined for Dy2O@C88 isomers are plotted in Arrhenius coordinates in Fig. 8. The DC technique is reliable only for relaxation times longer than 50–100 s, which limits the accessible temperature range to that below TB.For Dy2O-C1(26), the increase of the relaxation time with cooling takes a linear form down to 2.5 K, with the sign of a leveling off at lower temperatures. The linear dependence is a characteristic feature of the Orbach relaxation mechanism with an effective barrier Ueff corresponding to an excited spin state:
τM−1(T) = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/T). exp(−Ueff/T). | (2) |
Fitting of the experimental data with eqn (2) gives Ueff of 20.5 ± 0.3 K (14.2 cm−1) and the attempt time τ0 of 3.3 ± 0.3 s. The barrier is much smaller than the energies of excited LF states but is close to the ΔEAFM–FM value determined from the fit of magnetization curves, which suggests that the magnetization reversal in the AFM ground state of Dy2O-C1(26) proceeds via sequential flips of individual Dy magnetic moments, including a formation of the FM state after the first flip. The levelling off below 2.5 K may indicate the switch to the simultaneous flip of two Dy moments through a temperature-independent QTM such as observed in Dy2S@C82 at sub-K temperatures.61
In Dy2O-Cs(32), the measurement at zero field showed coexistence of the fast relaxation (presumably a QTM) with a slower thermal process, which makes a determination of τM rather ambiguous. As the zero-field QTM can be suppressed by application of a finite magnetic field, the measurements were then performed in the field of 0.2 T. For Dy2O-D2(35), the measurements were performed in zero field. Dy2O-Cs(32) and Dy2O-D2(35) show a different temperature dependence of τM than Dy2O-C1(26), which can be described by a power-law function, τM−1(T) = CTn, characteristic for the Raman relaxation mechanism. The fit gives similar parameters for two isomers, C = (1.13 ± 0.05) × 10−4 s−1 K−n and n = 2.93 ± 0.04 in Dy2O-Cs(32) and C = (0.67 ± 0.03) × 10−4 s−1 K−n and n = 3.70 ± 0.04 in Dy2O-D2(35). The n values are much smaller than the classical expectation of n = 9 for the Raman process but are consistent with the behaviour of many other Dy-SMM, including Dy-EMFs, also showing smaller exponents in the Raman regime associated with the influence of optical phonons.81
For both Dy2C2@C88 isomers, the relaxation times appeared too short for their reliable determination by DC magnetometry. Since an open magnetic hysteresis requires τM of at least a few seconds, a conservative estimation would be 5–10 seconds at 1.8 K. Much faster relaxation of magnetization in Dy2C2@C88 when compared to Dy2O@C88 is in line with the ab initio calculations suggesting a substantially lower axiality in Dy2C2 clusters.
Discussion
With the study of Dy2O@C88 in this work, Dy-oxide clusterfullerenes Dy2O@C2n become the most diverse class of Dy-based EMF-SMMs both in terms of the cage size (ranging from C72 to C88) and isomeric composition (C82 and C88 are represented by three isomers each). Table 3 lists the energetic characteristics of Dy⋯Dy interactions and blocking temperatures of magnetization in the Dy2O@C2n series and compares the values to other dinuclear Dy-clusterfullerenes.| ΔEtotAFM–FM | ΔEdipAFM–FM | ΔEexchAFM–FM | U effexch | T B | T irrev | T B100 | Ref. | |
|---|---|---|---|---|---|---|---|---|
| a ΔEexchAFM–FM is the difference of ΔEtotAFM–FM and ΔEdipAFM–FM; Ueffexch is the energy barrier of the low-temperature Orbach process assigned to the relaxation via the exchange excitation; ΔEAFM–FM and Ueffexch values in cm−1, temperature in Kelvin. b ΔEtotAFM–FM is determined from the fit of magnetization curves. c ΔEtotAFM–FM is determined as the exchange barrier Ueffexch. d ΔEtotAFM–FM is determined from the QTM features in hysteresis curves. e Tw - this work. | ||||||||
Dy2O@Cs(10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528)-C72 528)-C72 |
1.5b | 3.0 | −1.5 | — | 4.0 | 8 | 3.4 | 25 |
Dy2O@C2(13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333)-C74 333)-C74 |
∼0.1b | 2.6 | −2.5 | — | 6.7 | 14 | 5.0 (0.2 T) | 25 |
| Dy2O@C2v(5)-C80 | −18.5b | 2.7 | −21.2 | 18.0 | 5.0 | 11 | 3.2 | 26 |
| Dy2O@Cs(6)-C82 | −7.5c | 3.0 | −10.5 | 7.5 | 4.4 | 10 | 2.8 | 27 |
| Dy2O@C3v(8)-C82 | −5.4c | 2.5 | −7.8 | 5.4 | 7.4 | 9 | 5.9 | 27 |
| Dy2O@C2v(9)-C82 | −12.9c | 2.6 | −15.6 | 12.9 | 5.8 | 8 | 3.7 | 27 |
| Dy2O@C1(26)-C88 | −16.5b | 2.5 | −19.0 | 14.2 | 10.5 | 6.0 | Twe | |
| Dy2O@Cs(32)-C88 | −0.4b | 2.3 | −2.7 | — | 5.5 | 8.5 | 4.6 (0.2 T) | Tw |
| Dy2O@D2(35)-C88 | 3.6b/4.4d | 2.2 | 1.4/2.2 | — | 7.5 | 8.5 | 3.9 | Tw |
| Dy2C2@Cs(6)-C82 | 12.1c | 2.6 | 9.5 | 12.1 | ∼2 | — | 57 | |
| Dy2C2@Cs(32)-C88 | 6.3b | 1.7 | 4.6 | — | ∼2 | — | Tw | |
| Dy2C2@D2(35)-C88 | 3.3b | 1.7 | 1.6 | — | ∼2 | — | Tw | |
| Dy2S@Cs(6)-C82 | 11.0b/10.7d | 2.2 | 8.5 | 12.4 | ∼2 | — | 57 and 61 | |
| Dy2S@C3v(8)-C82 | 6.4b/5.1d | 2.3 | 2.8 | 4.2 | 4.0 | 2.0 | 57 and 61 | |
| Dy2TiC@Ih(7)-C80 | 8.5b | 3.4 | 5.1 | 6.6 | ∼2 | 1.7 | 59 and 82 | |
| Dy2ScN@Ih(7)-C80 | 5.6c | 3.3 | 2.3 | 5.6 | 7.9 | 8 | 5.0 | 56 |
| Dy2LuN@Ih(7)-C80 | 3.0c | 3.3 | −0.3 | 3.0 | 7.9 | 10 | 5.2 | 60 |
Our new results demonstrate that that the O2− bridge in Dy2O cluster can support not only AFM interactions between Dy magnetic moments as in previously studied Dy2O@C2n EMFs, but also the FM coupling. It is different from Dy2-clusterfullerenes with S2−, C22−, C4−, and N3− bridges, which all favor the FM coupled ground state. Quite unusual is the magnitude of the variation of the Dy⋯Dy interaction energy found in seemingly similar Dy2O@C88 isomers. Estimation of dipolar contribution to ΔEAFM–FM shows that ΔEdipAFM–FM is positive in all EMFs and falls into the energy range of 1.5–3 cm−1. Thus, the exchange contribution to Dy⋯Dy coupling appears to be responsible for the strong variation of ΔEAFM–FM. Among the studied Dy2O@C2n compounds, only one, Dy2O@D2(35)-C88, has moderately positive ΔEexchAFM–FM value of 1.4–2.2 cm−1, whereas other 8 feature negative exchange term spanning from the modest −1.5 cm−1 in Dy2O@C72 to very large −21.2 cm−1 in Dy2O@C80 and −19.0 cm−1 in Dy2O@C1(26)-C88, by far the strongest Dy⋯Dy interactions in all Dy2-complexes. The data does not present any clear correlation between the structural parameters and the strength of the exchange coupling. The fullerene cage definitively plays an important role, as can be deduced from the considerable variation of the values within the isomeric series, especially for isomers of Dy2O@C88. However, it is hard to conclude at this moment if this strong influence is caused by the variation of the Dy2O cluster shape and size in different cages, by indirect interactions via the fullerene π-system, or because different Dy-fullerene coordination sites alter the metal orbital composition and hence modify the superexchange interactions via the O2− bridge. A combined influence of all these factors is likely to play a role.
Comparison of different clusters within one fullerene cage can be used to distinguish the cage and the bridge effects. However, this also appears to be rather ambiguous. For instance, Dy2C2@D2(35)-C88 and Dy2O@D2(35)-C88 have very close ΔEAFM–FM values, but at the same time Dy2C2@C88 and Dy2O@C88 isomers with the Cs(32) cage have different size and the sign of ΔEAFM–FM. The comparison of Dy2O@C82, Dy2C2@C82, and Dy2S@C82 with Cs(6) cage isomer shows that the strength and the sign of Dy⋯Dy coupling in Dy2S and Dy2C2 are similar, while Dy2O counterpart has the opposite sign of ΔEAFM–FM (Table 3). Finally, in isostructural and isoelectronic Dy2TiC and Dy2ScN clusters within the Ih(7)-C80 cage, the superexchange through C4− is almost twice stronger than through N3−.59 Overall, we can conclude that the bridge is certainly crucial in determining the Dy⋯Dy coupling, but not in a very deterministic way as the influence of other factors may be of a comparable magnitude.
The SMM performance of Dy2-clusterfullerenes does not show an obvious correlation with the Dy⋯Dy coupling strength but is clearly affected by the single-ion magnetic anisotropy. Thus, the blocking and hysteresis closing temperature in dinuclear systems reduces in the following row of the bridge units: O2− ≥ N3− > C4− ≥ S2− ≥ C22−, which corresponds to the decrease of the average ligand-field splitting in these types of clusterfullerenes as predicted by ab initio calculations.54,55,57,59,83 Counterintuitively, this conclusion is not directly transferable to analogous mono-nuclear Dy-EMFs. The hysteresis closing temperature in DySc2N@C80,45,84 DyLu2N@C80,60 DyY2N@C80,85 DyScS@C82,86 and DyYTiC@C80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 is near 7–8 K irrespective of their non-metal units. The synthesis and studies of mixed-metal oxide and carbide clusterfullerenes with single Dy atom, such as DyScO@C82 and DyScC2@C82, and the studies of mono-nuclear Dy-SMMs with different cage sizes will be required to fully disclose this phenomenon. However, it can be pointed out that the highest hysteresis closing temperature among Dy2-clusterfullerenes, 14 K, is found for Dy2O@C74, in which the Dy⋯Dy coupling is so weak that the compound shows butterfly-shaped hysteresis with pronounced zero-field QTM typical for single-ion SMMs.25
58 is near 7–8 K irrespective of their non-metal units. The synthesis and studies of mixed-metal oxide and carbide clusterfullerenes with single Dy atom, such as DyScO@C82 and DyScC2@C82, and the studies of mono-nuclear Dy-SMMs with different cage sizes will be required to fully disclose this phenomenon. However, it can be pointed out that the highest hysteresis closing temperature among Dy2-clusterfullerenes, 14 K, is found for Dy2O@C74, in which the Dy⋯Dy coupling is so weak that the compound shows butterfly-shaped hysteresis with pronounced zero-field QTM typical for single-ion SMMs.25
Although the Dy⋯Dy coupling does not seem to correlate with the blocking temperature in Dy2-clusterfullerenes, it does affect the low-temperature relaxation. The distinct Orbach relaxation mechanism involving the exchange excitation (either FM → AFM or AFM → FM) is observed only in Dy2-clusterfullerenes with |ΔEAFM–FM| values exceeding a threshold of 5 cm−1 (e.g., Dy2O@C1(26)-C88). For compounds with weaker coupling, the relaxation is better described by the Raman mechanism (as Dy2O@Cs(32)-C88 and Dy2O@D2(35)-C88, Fig. 8).
Conclusions
In this work, we report on the synthesis, isolation and systematic structural studies of endohedral metallofullerenes with Dy2O and Dy2C2 clusters encapsulated within C88 cages. As both clusters transfer four electrons to the fullerene host, they tend to feature the same cage isomers, which were identified by single-crystal X-ray diffraction as C1(26), Cs(32), and D2(35) and further supported by spectroscopic studies. These cage isomers correspond to the most stable C884− isomers according to DFT calculations.The availability of isomeric and isostructural Dy2O@C88 and Dy2C2@C88 EMFs allowed the study of magnetic Dy⋯Dy interactions as a function of the fullerene cage and the bridging unit. We showed that the oxide ion O2− tends to prefer an antiferromagnetic coupling of Dy magnetic moments, whereas the acetylide group C22− favors their ferromagnetic coupling. The strength of the interaction is found to vary strongly with the fullerene cage isomerism. All metallofullerenes exhibited single-molecule magnetism with an open magnetic hysteresis but with a considerably different blocking temperature of magnetization. Dy2C2@C88 isomers are weak SMMs with hysteresis closing already at 2.5 K, whereas in Dy2O@C88 isomers the hysteresis remained open up to 7–9 K. This difference in relaxation behavior agrees with the much stronger single-ion magnetic anisotropy in Dy2O@C88 than in Dy2C2@C88 predicted by ab initio calculations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support by Deutsche Forschungsgemeinschaft (grants PO 1602/7-1, LI 3055/3-1, and AV 169/3-1) and the National Science Foundation China (NSFC 91961109 to N. C.). Diffraction data have been collected on BL14.2 at the BESSY II electron storage ring operated by the Helmholtz-Zentrum Berlin; we would particularly like to acknowledge the help and support of Manfred Weiss and his group members during the experiments at BESSY II. Computational resources were provided by the Center for High Performance Computing at the TU Dresden. We appreciate the technical support with computational resources in IFW Dresden by Ulrike Nitzsche. Sandra Schiemenz is acknowledged for the help with spectroscopic measurements, and Dr Anja Wolter-Giraud and Sebastian Gaß are acknowledged for the help with magnetic measurements in IFW Dresden.References
- A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113(8), 5989–6113 CrossRef CAS PubMed.
- A. Rodriguez-Fortea, A. L. Balch and J. M. Poblet, Endohedral metallofullerenes: a unique host-guest association, Chem. Soc. Rev., 2011, 40, 3551–3563 RSC.
- X. Lu, W. Shen and S. Hu, Endohedral Metallofullerenes: New Structures and Unseen Phenomena, Chem. – Eur. J., 2020, 26(26), 5748–5757 CrossRef.
- W. Li, C.-R. Wang and T. Wang, Molecular Structures and Magnetic Properties of Endohedral Metallofullerenes, Chem. Commun., 2021, 57, 10317–10326 RSC.
- W. Cai, C.-H. Chen, N. Chen and L. Echegoyen, Fullerenes as Nanocontainers That Stabilize Unique Actinide Species Inside: Structures, Formation, and Reactivity, Acc. Chem. Res., 2019, 52(7), 1824–1833 CrossRef CAS PubMed.
- S. Yang, T. Wei and F. Jin, When metal clusters meet carbon cages: endohedral clusterfullerenes, Chem. Soc. Rev., 2017, 46(16), 5005–5058 RSC.
- S. Yang, F. Liu, C. Chen, M. Jiao and T. Wei, Fullerenes encaging metal clusters-clusterfullerenes, Chem. Commun., 2011, 47(43), 11822–11839 RSC.
- L. Abella, Y. Wang, A. Rodríguez-Fortea, N. Chen and J. M. Poblet, Current status of oxide clusterfullerenes, Inorg. Chim. Acta, 2017, 468, 91–104 CrossRef CAS.
- L. Feng, Y. Hao, A. Liu and Z. Slanina, Trapping Metallic Oxide Clusters inside Fullerene Cages, Acc. Chem. Res., 2019, 52(7), 1802–1811 CrossRef CAS PubMed.
- X. Lu, T. Akasaka and S. Nagase, Carbide Cluster Metallofullerenes: Structure, Properties, and Possible Origin, Acc. Chem. Res., 2013, 46(7), 1627–1635 CrossRef CAS PubMed.
- P. Jin, C. Tang and Z. Chen, Carbon Atoms Trapped in Cages: Metal Carbide Clusterfullerenes, Coord. Chem. Rev., 2014, 270–271, 89–111 CrossRef CAS.
- B. Q. Mercado, M. M. Olmstead, C. M. Beavers, M. L. Easterling, S. Stevenson, M. A. Mackey, C. E. Coumbe, J. D. Phillips, J. P. Phillips, J. M. Poblet and A. L. Balch, A seven atom cluster in a carbon cage, the crystallographically determined structure of Sc4(μ3-O)3@Ih-C80, Chem. Commun., 2010, 46, 279–281 RSC.
- S. Stevenson, M. A. Mackey, M. A. Stuart, J. P. Phillips, M. L. Easterling, C. J. Chancellor, M. M. Olmstead and A. L. Balch, A Distorted Tetrahedral Metal Oxide Cluster inside an Icosahedral Carbon Cage. Synthesis, Isolation, and Structural Characterization of Sc4(μ3-O)2@Ih-C80, J. Am. Chem. Soc., 2008, 130(36), 11844–11845 CrossRef CAS PubMed.
- B. Q. Mercado, M. A. Stuart, M. A. Mackey, J. E. Pickens, B. S. Confait, S. Stevenson, M. L. Easterling, R. Valencia, A. Rodriguez-Fortea, J. M. Poblet, M. M. Olmstead and A. L. Balch, Sc2(μ2-O) Trapped in a Fullerene Cage: The Isolation and Structural Characterization of Sc2(μ2-O)@Cs(6)-C82 and the Relevance of the Thermal and Entropic Effects in Fullerene Isomer Selection, J. Am. Chem. Soc., 2010, 132, 12098–12105 CrossRef CAS.
- Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Sc2O@C3v(8)-C82: A Missing Isomer of Sc2O@C82, Inorg. Chem., 2016, 55(4), 1926–1933 CrossRef CAS PubMed.
- L. Feng, M. Zhang, Y. Hao, Q. Tang, N. Chen, Z. Slanina and F. Uhlik, Endohedrally Stabilized C70 Isomer with Fused Pentagons Characterized by Crystallography, Dalton Trans., 2016, 45, 8142–8148 RSC.
- Y. Hao, Q. Tang, X. Li, M. Zhang, Y. Wan, L. Feng, N. Chen, Z. Slanina, L. Adamowicz and F. Uhlík, Isomeric Sc2O@C78 Related by a Single-Step Stone–Wales Transformation: Key Links in an Unprecedented Fullerene Formation Pathway, Inorg. Chem., 2016, 55(21), 11354–11361 CrossRef CAS PubMed.
- T. Yang, Y. Hao, L. Abella, Q. Tang, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Sc2O@Td(19151)-C76: Hindered Cluster Motion inside a Tetrahedral Carbon Cage Probed by Crystallographic and Computational Studies, Chem. – Eur. J., 2015, 21(31), 11110–11117 CrossRef CAS PubMed.
- Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Sc2O@C2v(5)-C80: Dimetallic Oxide Cluster Inside a C80 Fullerene Cage, Inorg. Chem., 2015, 54(20), 9845–9852 CrossRef CAS PubMed.
- M. Zhang, Y. Hao, X. Li, L. Feng, T. Yang, Y. Wan, N. Chen, Z. Slanina, F. Uhlik and H. Cong, Facile Synthesis of an Extensive Family of Sc2O@C2n (n = 35-47) and Chemical Insight into the Smallest Member of Sc2O@C2(7892)-C70, J. Phys. Chem. C, 2014, 118(49), 28883–28889 CrossRef CAS.
- A. Liu, M. Nie, Y. Hao, Y. Yang, T. Wang, Z. Slanina, H. Cong, L. Feng, C. Wang and F. Uhlik, Ho2O@C74: Ho2O Cluster Expands within a Small Non-IPR Fullerene Cage of C2(13333)-C74, Inorg. Chem., 2019, 58(8), 4774–4781 CrossRef CAS PubMed.
- H. Cong, A. Liu, Y. Hao, L. Feng, Z. Slanina and F. Uhlik, Ho2O@C84: Crystallographic Evidence Showing Linear Metallic Oxide Cluster Encapsulated in IPR Fullerene Cage of D2d(51591)-C84, Inorg. Chem., 2019, 58(16), 10905–10911 CrossRef CAS PubMed.
- W. Dong, Y. Yu, B. Dong and Y. Lian, Isolation and Electrochemical Property of Ho2O@C90 Isomers, J. Electrochem. Soc., 2022, 169(2), 026512 CrossRef.
- Y. Yu, Z. Slanina, F. Wang, Y. Yang, Y. Lian, F. Uhlik, B. Xin and L. Feng, Ho2O@D3(85)-C92: Highly Stretched Cluster Dictated by a Giant Cage and Unexplored Isomerization, Inorg. Chem., 2020, 59(15), 11020–11027 CrossRef CAS PubMed.
- G. Velkos, W. Yang, Y.-R. Yao, S. M. Sudarkova, X. Liu, B. Büchner, S. M. Avdoshenko, N. Chen and A. A. Popov, Shape-adaptive single-molecule magnetism and hysteresis up to 14 K in oxide clusterfullerenes Dy2O@C72 and Dy2O@C74 with fused pentagon pairs and flexible Dy–(μ2-O)–Dy angle, Chem. Sci., 2020, 11, 4766–4772 RSC.
- G. Velkos, W. Yang, Y.-R. Yao, S. M. Sudarkova, F. Liu, S. Avdoshenko, N. Chen and A. A. Popov, Metallofullerene single-molecule magnet Dy2O@C2v(5)-C80 with a strong antiferromagnetic Dy⋯Dy coupling, Chem. Commun., 2022, 58, 7164–7167 RSC.
- W. Yang, G. Velkos, F. Liu, S. M. Sudarkova, Y. Wang, J. Zhuang, H. Zhang, X. Li, X. Zhang, B. Büchner, S. M. Avdoshenko, A. A. Popov and N. Chen, Single Molecule Magnetism with Strong Magnetic Anisotropy and Enhanced Dy⋯Dy Coupling in Three Isomers of Dy-Oxide Clusterfullerene Dy2O@C82, Adv. Sci., 2019, 6(20), 1901352 CrossRef CAS PubMed.
- L. Bao, P. Yu, M.-Y. Li, W. Shen, S. Hu, P. Yu, X. Tian, X. Zhao and X. Lu, An unprecedented C80 cage that violates the isolated pentagon rule, Inorg. Chem. Front., 2022, 9, 2264–2270 RSC.
- L. Spree and A. A. Popov, Recent advances in single molecule magnetism of dysprosium-metallofullerenes, Dalton Trans., 2019, 48(9), 2861–2871 RSC.
- H. Yang, H. Jin, B. Hong, Z. Liu, C. M. Beavers, H. Zhen, Z. Wang, B. Q. Mercado, M. M. Olmstead and A. L. Balch, Large Endohedral Fullerenes Containing Two Metal Ions, Sm2@D2(35)-C88, Sm2@C1(21)-C90, and Sm2@D3(85)-C92, and Their Relationship to Endohedral Fullerenes Containing Two Gadolinium Ions, J. Am. Chem. Soc., 2011, 133(42), 16911–16919 CrossRef CAS PubMed.
- W. Shen, L. Bao, S. Hu, L. Yang, P. Jin, Y. Xie, T. Akasaka and X. Lu, Crystallographic characterization of Lu2C2n (2n = 76–90): cluster selection by cage size, Chem. Sci., 2019, 10(3), 829–836 RSC.
- C.-H. Chen, L. Abella, M. R. Cerón, M. A. Guerrero-Ayala, A. Rodríguez-Fortea, M. M. Olmstead, X. B. Powers, A. L. Balch, J. M. Poblet and L. Echegoyen, Zigzag Sc2C2 Carbide Cluster inside a [88]Fullerene Cage with One Heptagon, Sc2C2@Cs(hept)-C88: A Kinetically Trapped Fullerene Formed by C2 Insertion?, J. Am. Chem. Soc., 2016, 138(39), 13030–13037 CrossRef CAS PubMed.
- C. Pan, W. Shen, L. Yang, L. Bao, Z. Wei, P. Jin, H. Fang, Y.-P. Xie, T. Akasaka and X. Lu, Crystallographic Characterization of Y2C2n (2n = 82, 88-94): Direct Y-Y Bonding and Cage-Dependent Cluster Evolution, Chem. Sci., 2019, 10, 4707–4713 RSC.
- S. Hu, P. Zhao, W. Shen, M. Ehara, Y. Xie, T. Akasaka and X. Lu, Crystallographic Characterization of Er2C2@C80–88: Cluster Stretching with Cage Elongation, Inorg. Chem., 2020, 59(3), 1940–1946 CrossRef CAS PubMed.
- W. Shen, L. Bao, P. Yu, L. Yang, B. Li, P. Yu, P. Jin and X. Lu, Isolation and crystallographic characterization of Lu2C2@C2n (2n = 88–92): Internal cluster stretching upon outer cage expansion, Carbon, 2020, 164, 157–163 CrossRef CAS.
- K. Akiyama, T. Hamano, Y. Nakanishi, E. Takeuchi, S. Noda, Z. Wang, S. Kubuki and H. Shinohara, Non-HPLC Rapid Separation of Metallofullerenes and Empty Cages with TiCl4 Lewis Acid, J. Am. Chem. Soc., 2012, 134(23), 9762–9767 CrossRef CAS.
- Z. Wang, Y. Nakanishi, S. Noda, K. Akiyama and H. Shinohara, The Origin and Mechanism of Non-HPLC Purification of Metallofullerenes with TiCl4, J. Phys. Chem. C, 2012, 116(48), 25563–25567 CrossRef CAS.
- S. Stevenson, C. B. Rose, A. A. Robson, D. T. Heaps and J. P. Buchanan, Effect of Water and Solvent Selection on the SAFA Purification Times for Metallic Nitride Fullerenes, Fullerenes, Nanotubes, Carbon Nanostruct., 2014, 22(1–3), 182–189 CrossRef CAS.
- S. Stevenson, K. A. Rottinger and J. S. Field, Fractionation of rare-earth metallofullerenes via reversible uptake and release from reactive silica, Dalton Trans., 2014, 43(20), 7435–7441 RSC.
- S. Stevenson, K. Harich, H. Yu, R. R. Stephen, D. Heaps, C. Coumbe and J. P. Phillips, Nonchromatographic “stir and filter approach” (SAFA) for isolating Sc3N@C80 metallofullerenes, J. Am. Chem. Soc., 2006, 128(27), 8829–8835 CrossRef CAS PubMed.
- U. Mueller, R. Förster, M. Hellmig, F. U. Huschmann, A. Kastner, P. Malecki, S. Pühringer, M. Röwer, K. Sparta, M. Steffien, M. Ühlein, P. Wilk and M. S. Weiss, The macromolecular crystallography beamlines at BESSY II of the Helmholtz-Zentrum Berlin: Current status and perspectives, Eur. Phys. J. Plus, 2015, 130(7), 141 CrossRef.
- W. Kabsch, XDS, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66(2), 125–132 CrossRef CAS PubMed.
- K. M. Sparta, M. Krug, U. Heinemann, U. Mueller and M. S. Weiss, XDSAPP2.0, J. Appl. Crystallogr., 2016, 49(3), 1085–1092 CrossRef.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71(1), 3–8 Search PubMed.
- D. S. Krylov, F. Liu, A. Brandenburg, L. Spree, V. Bon, S. Kaskel, A. U. B. Wolter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Magnetization relaxation in the single-ion magnet DySc2N@C80: quantum tunneling, magnetic dilution, and unconventional temperature dependence, Phys. Chem. Chem. Phys., 2018, 20(17), 11656–11672 RSC.
- M. M. Olmstead, T. Zuo, H. C. Dorn, T. Li and A. L. Balch, Metal ion size and the pyramidalization of trimetallic nitride units inside a fullerene cage: Comparisons of the crystal structures of M3N@Ih-C80 (M = Gd, Tb, Dy, Ho, Er, Tm, Lu, and Sc) and some mixed metal counterparts, Inorg. Chim. Acta, 2017, 468, 321–326 CrossRef CAS.
- M. M. Olmstead, D. A. Costa, K. Maitra, B. C. Noll, S. L. Phillips, P. M. Van Calcar and A. L. Balch, Interaction of curved and flat molecular surfaces. The structures of crystalline compounds composed of fullerene (C60, C60O, C70, and C120O) and metal octaethylporphyrin units, J. Am. Chem. Soc., 1999, 121(30), 7090–7097 CrossRef CAS.
- V. Dubrovin, L.-H. Gan, B. Büchner, A. A. Popov and S. M. Avdoshenko, Endohedral metal-nitride cluster ordering in metallofullerene–NiII(OEP) complexes and crystals: a theoretical study, Phys. Chem. Chem. Phys., 2019, 21, 8197–8200 RSC.
- W. Cai, L. Bao, S. Zhao, Y. Xie, T. Akasaka and X. Lu, Anomalous Compression of D5(450)-C100 by Encapsulating La2C2 Cluster instead of La2, J. Am. Chem. Soc., 2015, 137(32), 10292–10296 CrossRef CAS.
- S. F. Yang, A. A. Popov and L. Dunsch, Violating the Isolated Pentagon Rule (IPR): The endohedral Non-IPR cage of Sc3N@C70, Angew. Chem., Int. Ed., 2007, 46(8), 1256–1259 CrossRef CAS PubMed.
- A. A. Popov, M. Krause, S. F. Yang, J. Wong and L. Dunsch, C78 cage isomerism defined by trimetallic nitride cluster size: A computational and vibrational spectroscopic study, J. Phys. Chem. B, 2007, 111(13), 3363–3369 CrossRef CAS PubMed.
- S. Yang, A. A. Popov and L. Dunsch, The role of an asymmetric nitride cluster on a fullerene cage: The Non-IPR endohedral DySc2N@C76, J. Phys. Chem. B, 2007, 111(49), 13659–13663 CrossRef CAS.
- A. A. Popov, C. Kästner, M. Krause and L. Dunsch, Carbon Cage Vibrations of M@C82 and M2@C2n (M = La, Ce; 2n = 72, 78, 80): The Role of the Metal Atoms, Fullerenes, Nanotubes, Carbon Nanostruct., 2014, 22(1–3), 202–214 CrossRef CAS.
- V. Vieru, L. Ungur and L. F. Chibotaru, Key Role of Frustration in Suppression of Magnetization Blocking in Single-Molecule Magnets, J. Phys. Chem. Lett., 2013, 4(21), 3565–3569 CrossRef CAS.
- M. K. Singh and G. Rajaraman, Acquiring a record barrier height for magnetization reversal in lanthanide encapsulated fullerene molecules using DFT and ab initio calculations, Chem. Commun., 2016, 52(97), 14047–14050 RSC.
- D. S. Krylov, F. Liu, S. M. Avdoshenko, L. Spree, B. Weise, A. Waske, A. U. B. Wolter, B. Büchner and A. A. Popov, Record-high thermal barrier of the relaxation of magnetization in the nitride clusterfullerene Dy2ScN@C80-Ih, Chem. Commun., 2017, 53, 7901–7904 RSC.
- C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter and A. A. Popov, Selective arc-discharge synthesis of Dy2S-clusterfullerenes and their isomer-dependent single molecule magnetism, Chem. Sci., 2017, 8(9), 6451–6465 RSC.
- A. Brandenburg, D. S. Krylov, A. Beger, A. U. B. Wolter, B. Büchner and A. A. Popov, Carbide clusterfullerene DyYTiC@C80 featuring three different metals in the endohedral cluster and its single-ion magnetism, Chem. Commun., 2018, 54(76), 10683–10686 RSC.
- R. Westerström, V. Dubrovin, K. Junghans, C. Schlesier, B. Büchner, S. M. Avdoshenko, A. A. Popov, A. Kostanyan, J. Dreiser and T. Greber, Precise measurement of angles between two magnetic moments and their configurational stability in single-molecule magnets, Phys. Rev. B, 2021, 104(22), 224401 CrossRef.
- L. Spree, C. Schlesier, A. Kostanyan, R. Westerström, T. Greber, B. Büchner, S. Avdoshenko and A. A. Popov, Single molecule magnets DyM2N@C80 and Dy2MN@C80 (M = Sc, Lu): The impact of diamagnetic metals on the Dy3+ magnetic anisotropy, Dy⋯Dy coupling, and mixing of molecular and lattice vibrations, Chem. – Eur. J., 2020, 26(11), 2436–2449 CrossRef CAS PubMed.
- D. Krylov, G. Velkos, C.-H. Chen, B. Büchner, A. Kostanyan, T. Greber, S. Avdoshenko and A. A. Popov, Magnetic hysteresis and strong ferromagnetic coupling of sulfur-bridged Dy ions in clusterfullerene Dy2S@C82, Inorg. Chem. Front., 2020, 7, 3521–3532 RSC.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. D. Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, Modern quantum chemistry with [Open]Molcas, J. Chem. Phys., 2020, 152(21), 214117 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137(6), 064112 CrossRef CAS.
- X. Yi, K. Bernot, F. Pointillart, G. Poneti, G. Calvez, C. Daiguebonne, O. Guillou and R. Sessoli, A Luminescent and Sublimable DyIII-Based Single-Molecule Magnet, Chem. – Eur. J., 2012, 18(36), 11379–11387 CrossRef CAS PubMed.
- J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, Single-Molecule Magnet Behavior for an Antiferromagnetically Superexchange-Coupled Dinuclear Dysprosium(III) Complex, J. Am. Chem. Soc., 2011, 133(14), 5319–5328 CrossRef CAS PubMed.
- S. A. Sulway, R. A. Layfield, F. Tuna, W. Wernsdorfer and R. E. P. Winpenny, Single-molecule magnetism in cyclopentadienyl-dysprosium chlorides, Chem. Commun., 2012, 48(10), 1508–1510 RSC.
- S. Xue, Y.-N. Guo, L. Ungur, J. Tang and L. F. Chibotaru, Tuning the Magnetic Interactions and Relaxation Dynamics of Dy2 Single-Molecule Magnets, Chem. – Eur. J., 2015, 21(40), 14099–14106 CrossRef CAS PubMed.
- C. Y. Chow, H. Bolvin, V. E. Campbell, R. Guillot, J. W. Kampf, W. Wernsdorfer, F. Gendron, J. Autschbach, V. L. Pecoraro and T. Mallah, Assessing the exchange coupling in binuclear lanthanide(III) complexes and the slow relaxation of the magnetization in the antiferromagnetically coupled Dy2 derivative, Chem. Sci., 2015, 6(7), 4148–4159 RSC.
- J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Hydroxide-bridged five-coordinate DyIII single-molecule magnet exhibiting the record thermal relaxation barrier of magnetization among lanthanide-only dimers, Chem. Sci., 2017, 8(2), 1288–1294 RSC.
- G. Huang, X. Yi, J. Jung, O. Guillou, O. Cador, F. Pointillart, B. Le Guennic and K. Bernot, Optimization of Magnetic Relaxation and Isotopic Enrichment in Dimeric DyIII Single-Molecule Magnets, Eur. J. Inorg. Chem., 2018, 2018, 326–332 CrossRef CAS.
- P.-B. Jin, Q.-C. Luo, Y.-Q. Zhai, Y.-D. Wang, Y. Ma, L. Tian, X. Zhang, C. Ke, X.-F. Zhang, Y. Lv and Y.-Z. Zheng, A study of cation-dependent inverse hydrogen bonds and magnetic exchange-couplings in lanthanacarborane complexes, iScience, 2021, 24(7), 102760 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34(13), 1164–1175 CrossRef CAS PubMed.
- R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Tunneling, remanence, and frustration in dysprosium-based endohedral single-molecule magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(6), 060406 CrossRef.
- A. Kostanyan, R. Westerström, D. Kunhardt, B. Büchner, A. A. Popov and T. Greber, Sub-Kelvin hysteresis of the dilanthanide single-molecule magnet Tb2ScN@C80, Phys. Rev. B, 2020, 101(13), 134429 CrossRef CAS.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, Strong Axiality and Ising Exchange Interaction Suppress Zero-Field Tunneling of Magnetization of an Asymmetric Dy2 Single-Molecule Magnet, J. Am. Chem. Soc., 2011, 133(31), 11948–11951 CrossRef CAS PubMed.
- T. G. Ashebr, H. Li, X. Ying, X.-L. Li, C. Zhao, S. Liu and J. Tang, Emerging Trends on Designing High-Performance Dysprosium(III) Single-Molecule Magnets, ACS Mater. Lett., 2022, 4, 307–319 CrossRef CAS.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- D. Shao and X.-Y. Wang, Development of Single-Molecule Magnets, Chin. J. Chem., 2020, 38, 1005–1018 CrossRef CAS.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- K. L. M. Harriman, D. Errulat and M. Murugesu, Magnetic Axiality: Design Principles from Molecules to Materials, Trends Chem., 2019, 1(4), 425–439 CrossRef CAS.
- A. Singh and K. N. Shrivastava, Optical-acoustic two-phonon relaxation in spin systems, Phys. Status Solidi B, 1979, 95(1), 273–277 CrossRef CAS.
- K. Junghans, C. Schlesier, A. Kostanyan, N. A. Samoylova, Q. Deng, M. Rosenkranz, S. Schiemenz, R. Westerström, T. Greber, B. Büchner and A. A. Popov, Methane as a Selectivity Booster in the Arc-Discharge Synthesis of Endohedral Fullerenes: Selective Synthesis of the Single-Molecule Magnet Dy2TiC@C80 and Its Congener Dy2TiC2@C80, Angew. Chem., Int. Ed., 2015, 54(45), 13411–13415 CrossRef CAS PubMed.
- F. Cimpoesu, N. Dragoe, H. Ramanantoanina, W. Urland and C. Daul, The Theoretical Account of the Ligand Field Bonding Regime and Magnetic Anisotropy in the DySc2N@C80 Single Ion Magnet Endohedral Fullerene, Phys. Chem. Chem. Phys., 2014, 16, 11337–11348 RSC.
- R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, An Endohedral Single-Molecule Magnet with Long Relaxation Times: DySc2N@C80, J. Am. Chem. Soc., 2012, 134(24), 9840–9843 CrossRef PubMed.
- M. Nie, J. Liang, C. Zhao, Y. Lu, J. Zhang, W. Li, C. Wang and T. Wang, Single-Molecule Magnet with Thermally Activated Delayed Fluorescence Based on a Metallofullerene Integrated by Dysprosium and Yttrium Ions, ACS Nano, 2021, 15(12), 19080–19088 CrossRef CAS PubMed.
- W. Cai, J. D. Bocarsly, A. Gomez, R. J. Letona Lee, A. Metta-Magaña, R. Seshadri and L. Echegoyen, High blocking temperatures for DyScS endohedral fullerene single-molecule magnets, Chem. Sci., 2020, 11, 13129–13136 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2175825–2175828. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi01796b |
| ‡ These authors contributed equally. |
| This journal is © the Partner Organisations 2022 |