Real-time imaging of metallic supraparticle assembly during nanoparticle synthesis†
Mei
Wang
a,
Chiwoo
Park
b and
Taylor J.
Woehl
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD, USA. E-mail: tjwoehl@umd.edu
bDepartment of Industrial and Manufacturing Engineering, Florida State University, Tallahassee, FL, USA
First published on 13th December 2021
Abstract
Observations of nanoparticle superlattice formation over minutes during colloidal nanoparticle synthesis elude description by conventional understanding of self-assembly, which theorizes superlattices require extended formation times to allow for diffusively driven annealing of packing defects. It remains unclear how nanoparticle position annealing occurs on such short time scales despite the rapid superlattice growth kinetics. Here we utilize liquid phase transmission electron microscopy to directly image the self-assembly of platinum nanoparticles into close packed supraparticles over tens of seconds during nanoparticle synthesis. Electron-beam induced reduction of an aqueous platinum precursor formed monodisperse 2–3 nm platinum nanoparticles that simultaneously self-assembled over tens of seconds into 3D supraparticles, some of which showed crystalline ordered domains. Experimentally varying the interparticle interactions (e.g., electrostatic, steric interactions) by changing precursor chemistry revealed that supraparticle formation was driven by weak attractive van der Waals forces balanced by short ranged repulsive steric interactions. Growth kinetic measurements and an interparticle interaction model demonstrated that nanoparticle surface diffusion rates on the supraparticles were orders of magnitude faster than nanoparticle attachment, enabling nanoparticles to find high coordination binding sites unimpeded by incoming particles. These results reconcile rapid self-assembly of supraparticles with the conventional self-assembly paradigm in which nanocrystal position annealing by surface diffusion occurs on a significantly shorter time scale than nanocrystal attachment.
Colloidal self-assembly integrates nanocrystals into ordered microscopic and macroscopic structures, such as 1D chains,1 2D superlattices,2–4 and 3D supraparticles,5 that have emergent functional properties not shown in individual particles.6 Self-assembled structures of nanocrystals possess unique optical,7,8 electronic,9,10 magnetic,11,12 mechanical,13,14 and catalytic properties15–17 due to physical and electronic interparticle coupling. For instance, collective dipole–dipole interactions arising from close interparticle spacing between nanocrystals modifies the excitonic and plasmonic properties of self-assembled structures compared to single nanocrystals.18–20 Nanoconfinement of chemical reactants between nanocrystals in self-assembled structures can affect heterogeneous catalytic reactions, improving the overall catalytic activity and modifying selectivity.15,21–24
Rational control of individual nanocrystal ordering in self-assembled structures is challenging due to the required delicate balance between attractive and repulsive interparticle forces and slow kinetics required for self-assembly.25–28 If the attractive forces (e.g., van der Waals) are too strong or assembly kinetics too rapid, kinetically trapped and disordered fractal aggregates form. Self-assembly therefore requires weak interparticle attraction on the order of thermal forces or less.29 Conventionally, self-assembly is carried out with monodisperse organic ligand coated nanoparticles prepared by colloidal synthesis. Solvent evaporation, antisolvent addition, or temperature changes slowly increase attractive interparticle interactions over time,30–32 allowing particles sufficient time to anneal into crystalline arrangements.6,28 Controlled evaporation of the solvent creates a supersaturated solution of nanoparticles where weak capillary drag and van der Waals forces drive self-assembly into ordered superlattices.33,34 However, evaporative nanocrystal self-assembly can require days, while temperature induced assembly of DNA coated nanoparticles requires thermal annealing for extended periods. Recent research has demonstrated rapid (minutes) self-assembly of colloidal nanocrystals into 3D superlattices during nanocrystal synthesis,35,36 in response to solvent temperature changes,31 or under electric field stimulus.37–39 Rapid assembly kinetics are at odds with the classical picture of self-assembly because conventional colloidal aggregation theory predicts formation of fractal aggregates.40 Prior observations of superlattice formation during nanoparticle synthesis have been explained by progressively increasing attractive van der Waals interactions as nanoparticles grow larger.35,36 However, these prior reports utilized ensemble in situ small angle X-ray scattering measurements so it was not possible to reconcile the kinetics of nanocrystal attachment to superlattices with interparticle interactions and annealing mechanisms. Direct real time visualization of nanoparticle self-assembly at the nanometer spatial scale would enable delineating self-assembly kinetics, nanoparticle (surface) diffusion, and interparticle interactions enabling self-assembly of nanoparticle superstructures over second to minute time scales.
Here we utilize liquid phase transmission electron microscopy (LP-TEM) to visualize self-assembly of 2–3 nm spherical platinum nanoparticles into 3D supraparticles over tens of seconds. Prior LP-TEM research has examined nanoparticle self-assembly, but has focused primarily on larger preformed nanoparticles (>10 nm) stabilized by organic ligands.41–49 In this study, electron beam reduction of an aqueous platinum salt forms 2–3 nm Pt nanocrystals, i.e., primary particles, in bulk solution that immediately assemble into 3D supraparticles over seconds. In contrast to prior LP-TEM studies where nanoparticles formed by heterogeneous nucleation,49 the primary nanocrystals formed by homogeneous nucleation and were nearly monodisperse. Unlike prior reports,35,36 the primary nanocrystals stopped growing after assembly, leaving ∼1 nm interparticle gaps within the supraparticle. While prior LP-TEM work has shown nanoparticle self-assembly via non-classical mechanisms such as amorphous nanoparticle condensates,46 nanoparticle chain intermediates,44 and reaction limited aggregation,41 our observations demonstrate rapid self-assembly during nanoparticle synthesis occurs by the classical route where nanoparticles attached at a rate defined by the diffusion limit and then annealed their position by rapid surface diffusion.29 The observations reconcile the rapid formation of close packed supraparticles with the conventional picture of self-assembly.
LP-TEM imaging experiments were performed in a silicon nitride microfluidic cell with the microscope operating in scanning transmission electron microscopy (STEM) mode.50 Nanoparticles were synthesized by continuously imaging aqueous precursor solutions containing 0.15 mM K2PtCl4 with or without 1 M tert-butanol (TBA) and 1 mM sodium citrate (SC). The electron beam creates reducing radical species, aqueous electrons (eaq−) and hydrogen radicals (H˙), which reduce the platinum precursors to metal atoms.51 TBA was added as a radical scavenger to consume hydroxyl radicals (OH˙) created by the electron beam, which can oxidize metal ions and atoms,52,53 while SC is a common negatively charged capping ligand for metal nanoparticles. Real time movies of nanoparticle formation showed that the morphology of the platinum nanoparticles changed as a function of the precursor chemistry. LP-TEM time lapsed images showed that 30–100 nm spherical nanoparticles formed in 0.15 mM K2PtCl4 with 1 M TBA over a time scale of ∼90 s (Fig. 1a, ESI video 1†). Nanoparticles were immobile during formation because they nucleated on the silicon nitride membrane,49 and grew by monomer attachment. Some neighboring particles were observed to undergo coalescence. Platinum nanoparticles with rough surfaces of similar size formed in 0.15 mM K2PtCl4 without TBA by a self-growth mechanism under the same electron beam conditions (Fig. 1b, ESI video 2†). In the presence of 1 mM SC and 1 M TBA, we noticed that no supraparticles formed on the silicon nitride membrane under the same beam current and magnification as the other precursor chemistries. However, a higher dose rate experimental condition showed that ∼10 nm nanoparticles appeared in the first ∼10 s of imaging and then detached from the membrane surface and rapidly diffused away, denoted by streaks in the image (Fig. 1c, ESI video 3†).
High resolution TEM (HRTEM) imaging after disassembling and drying the liquid cell membranes showed the nanoparticles were supraparticles consisting of close packed 3D assemblies of 2–3 nm primary platinum nanocrystals. Comparing the sizes and shapes of the particles in HRTEM to those observed with LPTEM indicates that drying the sample did not significantly alter packing of primary particles within the supraparticles. In the presence of TBA, the supraparticles were either nearly spherical or faceted with rounded corners (Fig. 2a–c). Primary nanoparticles were separated by ∼1 nm within the supraparticles. While most supraparticles contained random close packed primary particles, some supraparticles displayed crystalline packing as indicated by fast Fourier transforms (FFTs) showing spots with center-to-center particle separations of ∼3.3 nm (inset Fig. 2a and b). The ordered domains could not be put onto zone axis due to tilt limitations of the sample holder and the small number of available crystalline domains (<5% of supraparticles). In the absence of TBA, disordered Pt supraparticles with rough surfaces formed from non-spherical, polydisperse primary particles that were fused together to form a continuous network of platinum (Fig. 2d). It was not possible to obtain HRTEM images of the particles formed in the presence of SC because they did not adsorb to the silicon nitride membrane.
The discrete structure of the supraparticles, which consisted of distinct primary particles separated from each other, suggested they formed by homogeneous nucleation of primary particles followed by self-assembly on the silicon nitride. However, the STEM electron probe rasters across the image area too slowly to capture the motion of the rapidly diffusing primary nanoparticles.54 Instead, we observed diffusing nanoparticles as horizontal streaks in the STEM images because their fast motion created image blur (Fig. 3a, ESI video 4†), which supports the assertion that supraparticles formed by primary particle self-assembly. The supraparticles were not observed to move during the experiments (ESI video 4†), indicating the image streaks were from primary particles. While we cannot accurately quantify the diffusion coefficients (D) of the particles based on the horizontal streaks, a simple scaling analysis 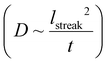 showed that the streak length yielded an effective particle diffusion coefficient close to that expected for Brownian motion in the bulk liquid. The streaks had a characteristic length on the order of lstreak ∼ 100 nm and the particles traversed the streaks in t ∼ 0.5 ms based on the known STEM beam pixel dwell time. This yields an approximate diffusion coefficient of 1 × 10−11 m2 s−1, which is within an order of magnitude of the Stokes–Einstein diffusion coefficient for a 2 nm diameter particle. Similar horizontal streaks were observed in the presence of 1 mM SC, but were observed to be due to motion of larger particles out of the image area (Fig. 3b, ESI video 3†). HRTEM images of the supraparticles after removing from the liquid cell and drying showed discrete 2–3 nm platinum particles attached to the silicon nitride near some supraparticles, providing further evidence that the supraparticles formed by assembly of primary particles (Fig. 3c). Taken together, the streak images and the HRTEM images of discrete primary particles provide strong evidence that the supraparticles formed by assembly of primary particles.
showed that the streak length yielded an effective particle diffusion coefficient close to that expected for Brownian motion in the bulk liquid. The streaks had a characteristic length on the order of lstreak ∼ 100 nm and the particles traversed the streaks in t ∼ 0.5 ms based on the known STEM beam pixel dwell time. This yields an approximate diffusion coefficient of 1 × 10−11 m2 s−1, which is within an order of magnitude of the Stokes–Einstein diffusion coefficient for a 2 nm diameter particle. Similar horizontal streaks were observed in the presence of 1 mM SC, but were observed to be due to motion of larger particles out of the image area (Fig. 3b, ESI video 3†). HRTEM images of the supraparticles after removing from the liquid cell and drying showed discrete 2–3 nm platinum particles attached to the silicon nitride near some supraparticles, providing further evidence that the supraparticles formed by assembly of primary particles (Fig. 3c). Taken together, the streak images and the HRTEM images of discrete primary particles provide strong evidence that the supraparticles formed by assembly of primary particles.
Fig. 4a shows the results of quantitative image analysis of supraparticle nucleation time (red stars) and time dependent supraparticle size (black lines). The supraparticle radius (rsupra) followed a power law increase with time of
| t = krsupra3 + t0. | (1) |
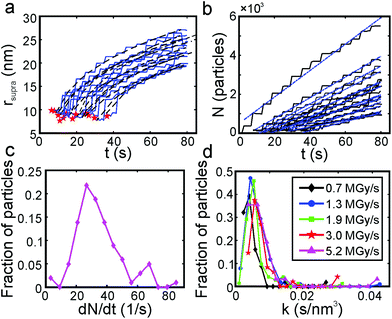 | ||
| Fig. 4 Supraparticle assembly kinetics were diffusion limited. (a) Platinum supraparticle radius as a function of time (solid blue lines) and non-linear least squares fits of eqn (1) (black dashed lines). Experimental nucleation times are shown as red stars. (b) Estimated number of platinum primary nanocrystals in each supraparticle as a function of time. Blue dashed lines are linear least squares best fits of eqn (2). (c) Histogram of the primary nanoparticle attachment rate distribution. The experimental conditions for the growth rate data in (a)–(c): beam current of 31 pA, magnification of 100 kx, and dose rate of 1.3 MGy s−1. (d) Distribution of growth coefficients, k, of platinum supraparticles at different dose rates. | ||
Here k is a constant related to the primary particle concentration, diffusion coefficient, and surface energy of the supraparticle, t is time, and t0 is the nucleation time.36 The cubic power law provided the best fit to the supraparticle growth traces when compared to a reaction limited growth law (quadratic scaling) and a mixed reaction and diffusion growth law (mixed quadratic and cubic; see ESI† for additional details on fitting and comparison to other models). Cubic scaling indicates that the growth of platinum supraparticles over the time scale of the experiments was a diffusion limited growth process, limited by the diffusion rate of primary particles to the supraparticle surface.55 The observed diffusion limited growth kinetics agree with prior small angle X-ray scattering (SAXS) measurements of nanoparticle superlattice growth kinetics.36 The attachment rate of primary nanocrystals to supraparticles was estimated by assuming the primary nanoparticles and supraparticles were spherical and the primary nanoparticles were randomly close packed with a packing density of Φ = 0.64. The number of primary particles in a supraparticle as a function of time (N(t)) was calculated by
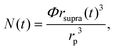 | (2) |
| dN/dt = 8πDprpn0, | (3) |
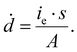 | (4) |
Here s = 2.798 × 105 eV m2 kg−1 is the stopping power of 200 keV electrons in water, A is the image area, and ie is the beam current. Prior work has established that the reduction rate of metal precursor and growth rate of nanoparticles increases as a function of the dose rate.57 The growth rate coefficient distribution was nearly the same for each dose rate, which is expected for diffusion limited growth where the growth kinetics are limited by the diffusional nanoparticle flux to the supraparticle as opposed to nanoparticle attachment kinetics. While the above growth kinetic modeling is a simple approximation, it captures the salient experimental observations, including the observed linear increase in number of particles, the primary particle concentration, and the dose rate independent growth rate coefficient.
Prior work by Wu et al. showing formation of nanoparticle superlattices during nanoparticle synthesis found that primary nanocrystals continued to grow after assembly.35 In contrast, here primary nanocrystals stopped growing after assembly as indicated by clear interparticle gaps in the HRTEM images (cf.Fig. 2a–c). Several factors could contribute to this phenomenon. Prior research showed that radiolysis near a solid–liquid interface locally increased radical concentrations due to enhanced secondary electron generation in the solid.58 Likewise, confinement of reactants within interparticle gaps in assembled structures can significantly impact reactant concentrations and rates.15 A locally higher oxidation rate near the supraparticle surface resulting from the latter two effects could limit the reduction of platinum precursor and halt growth of primary nanoparticles. Depletion of negatively charged platinum complexes near the negatively charged silicon nitride membrane could further reduce the local platinum precursor reduction rate. Lastly, TBA or its oxidized products formed by radiolysis could act as capping ligands that limit primary nanoparticle growth. TBA is a known hydrotrope due to it amphiphilic nature and has a size of ∼0.5 nm,59 so adsorbed layers of TBA on the primary particles could account for the ∼1 nm interparticle spacing in the supraparticles. Likewise, radical polymerization of TBA by OH˙ can form polymers that bind to primary particles. Gamma irradiation of TBA forms isobutylene oxide,60 which can polymerize into poly(isobutylene oxide) via ring opening polymerization.61 It is unclear which of the above factors limit the growth of primary particles following assembly because they cannot be directly probed experimentally; however, the observed ∼1 nm interparticle separation within the supraparticles is consistent with TBA or radical polymerized TBA forming an organic capping ligand layer. A scaling estimate based on reaction kinetics suggests TBA is the dominant capping ligand due to its larger concentration relative to polymerized TBA. Assuming mass action kinetics, the reaction rate for the polymerization of isobutylene oxide (IBO) molecules containing radical sites created by the electron beam is R = kPc2IBO. Prior kinetic measurements for polymer irradiated with electrons showed the bimolecular recombination rate constant is on the order of kp ∼ 107 M−1 s−1.62 Prior work in our lab has shown the steady state concentration of radical site containing organic monomers is limited by the hydroxyl radical concentration to 1–10 μM, giving a rate of reaction ranging from R = 10−4–10−3 M s−1.50,53 Assuming no diffusion, the maximum steady state concentration of polymer expected to form by radiolysis in the 80 s synthesis time is ∼0.08 M, more than 10 times less than the initial TBA concentration. Diffusion of polymer is expected to significantly lower the expected polymer concentration relative to the TBA concentration. Electron energy loss spectroscopy (EELS) measurements detected amorphous carbon within the supraparticles, but not on the silicon nitride membrane (Fig. S2†). However, HRTEM images showed no polymeric layer on the primary particle surface (cf.Fig. 2c), suggesting TBA is the ligand as opposed to a polymer, as TBA cannot be visualized with TEM. Taken together, the reaction kinetics argument, the EELS measurements, and the HRTEM images suggest TBA is the dominant ligand species, with polymerized TBA perhaps occupying a minor fraction of the particle surfaces. More direct measurements of the surface chemistry with infrared or mass spectrometry was not possible due to the small amount of supraparticles present in each sample, making them unsuitable for ensemble characterization.
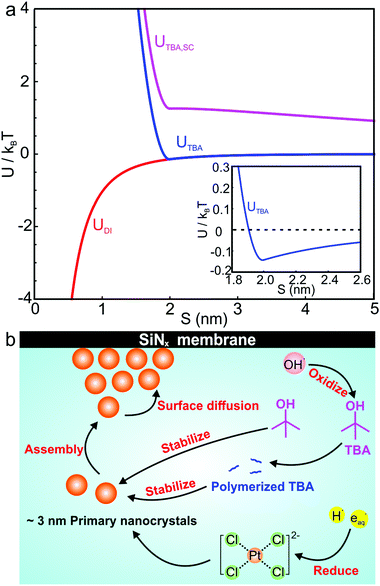
Several interparticle interactions between primary nanoparticles contribute to the self-assembly of supraparticles, including attractive van der Waals, repulsive electrostatic, and repulsive steric interactions. We calculated the pairwise interparticle interaction energy (U) between primary nanocrystals in DI water (UDI), 1 M TBA (UTBA), and 1 M TBA with 1 mM SC (UTBA, SC). In this model, primary nanoparticles interacted by attractive van der Waals interactions in DI water, by van der Waals and steric interactions between capping ligands in 1 M TBA, and by van der Waals, steric, and repulsive electrostatic interactions in 1 M TBA and 1 mM SC. The pairwise interparticle interaction energies as a function of surface-to-surface separation, S, for each synthesis condition are plotted in Fig. 5a (see calculation details in ESI†). In the absence of TBA, a purely attractive van der Waals interaction >1kBT (kBT ≡ room temperature thermal energy) at interparticle separations <1 nm (Fig. 5a, red curve) was computed, consistent with irreversible adhesion and aggregation of nanoparticles upon attachment. In this case, primary nanoparticles attached irreversibly with bond energies >kBT, preventing positional annealing by surface diffusion and forming disordered supraparticles (cf.Fig. 2d). With TBA present, binding of capping ligands to the primary particles created short ranged steric repulsive interactions that prevented irreversible aggregation and facilitated formation of close packed and sometimes crystalline structures. The balance of steric and van der Waals interactions created a shallow potential well of about 0.2kBT at a separation of ∼2 nm (Fig. 5a, inset). The calculated attractive energy is in the expected range for self-assembly of nanoparticle superlattices.29 The van der Waals attraction is balanced by short ranged repulsion due to steric interactions between adsorbed capping ligand, enabling nanoparticles to remain mobile after attaching to the supraparticle.31 Short ranged weak attraction balanced by steric repulsion enabled attaching nanocrystals to move by thermally activated surface diffusion or undergo multiple attachments and detachments to find high coordination binding positions.29 Adding SC to the solution created a long ranged (∼10 nm) electrostatic repulsion that prevented nanocrystals from closely approaching each other, leading to stable colloidal nanoparticles (Fig. 5a, magenta curve).
Fig. 5b summarizes the proposed formation mechanism of densely packed platinum supraparticles during nanoparticle synthesis in the presence of TBA. Primary nanocrystals nucleated homogeneously and grew to 2–3 nm after which they were capped by TBA and its radiolysis products. Supraparticles nucleated on the silicon nitride membrane and grew to sizes of 30–100 nm by primary particle attachment following a diffusion limited growth mechanism. The arrival period, i.e. the inverse of the attachment rate, of primary nanoparticles to the supraparticles ranged from 10–100 ms per particle (Fig. 4c). Primary particles weakly bound to the supraparticle surface by sub-kBT-scale attractive forces, allowing them to undergo rapid surface diffusion to search for and bind to high coordination positions.29 Prior estimates of surface diffusion coefficients for silicon nanocrystals with similar size and interparticle interaction energies as shown in Fig. 5a were estimated to be on the order of Dsurface ∼ 10−10 m2 s−1.29 A scaling estimate of the diffusive time scale for nanocrystal surface diffusion across a 50 nm supraparticle yields 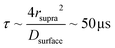 , significantly shorter than the 10–100 ms arrival period of nanocrystals to the supraparticle surface. This scaling analysis indicates that each primary nanocrystal rapidly traversed the supraparticle surface many times prior to arrival of the next nanocrystal, enabling unimpeded discovery of high coordination bonding sites. In the context of prior observations of rapid superlattice formation, the large nanocrystal surface diffusion rate compared to the primary particle attachment rate demonstrates that a classical thermal diffusion annealing process enabled close packing of primary particles. Further, the spherical and faceted shapes of the supraparticles suggests surface energy minimization by primary particle surface diffusion occurred during self-assembly. A key take away here is that while the growth rate of the supraparticles was large and diffusion limited, the surface diffusion rate was several orders of magnitude larger, enabling formation of close packed supraparticles.
, significantly shorter than the 10–100 ms arrival period of nanocrystals to the supraparticle surface. This scaling analysis indicates that each primary nanocrystal rapidly traversed the supraparticle surface many times prior to arrival of the next nanocrystal, enabling unimpeded discovery of high coordination bonding sites. In the context of prior observations of rapid superlattice formation, the large nanocrystal surface diffusion rate compared to the primary particle attachment rate demonstrates that a classical thermal diffusion annealing process enabled close packing of primary particles. Further, the spherical and faceted shapes of the supraparticles suggests surface energy minimization by primary particle surface diffusion occurred during self-assembly. A key take away here is that while the growth rate of the supraparticles was large and diffusion limited, the surface diffusion rate was several orders of magnitude larger, enabling formation of close packed supraparticles.
To conclude, we investigated the rapid assembly of small platinum nanocrystals into supraparticles during their synthesis utilizing LP-TEM. Aqueous platinum complexes were reduced by the electron beam and 2–3 nm primary nanocrystals homogeneously nucleated in solution, followed by their self-assembly into 3D supraparticles over tens of seconds. Primary nanocrystals stopped growing after assembly due to various factors, including but not limited to capping by TBA and its radiolysis products. Measurements of single supraparticle growth kinetics showed the growth was limited by diffusion of primary particles to the supraparticle surface. An interparticle interaction model revealed that van der Waals attraction was balanced by repulsive steric interactions, which resulted in weak interparticle attraction that allowed nanoparticle position annealing by rapid primary nanocrystal surface diffusion. This indicates the balance between nanocrystal surface diffusion and growth kinetics is a key factor to be considered in the rational design of rapid superlattice and supraparticle fabrication methods.
Author contributions
T. J. W. conceived and supervised the study. M. W. carried out all LP-TEM and HRTEM experiments, data analysis, and prepared all graphics. C. P. performed image analysis of the LP-TEM movies. T. J. W. and M. W. wrote the manuscript. All authors contributed to revising the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. P. acknowledges partial funding from Air Force Office of Scientific Research (Grant FA9550-18-1-0144). This material is based upon work supported by the National Science Foundation under Grant No. 2045258.References
- C. Yi, Y. Yang and Z. Nie, J. Am. Chem. Soc., 2019, 141, 7917–7925 CrossRef CAS PubMed.
- M. A. Boles and D. V. Talapin, ACS Nano, 2019, 13, 5375–5384 CrossRef CAS PubMed.
- H. Zhu, Z. Fan, L. Yu, M. A. Wilson, Y. Nagaoka, D. Eggert, C. Cao, Y. Liu, Z. Wei, X. Wang, J. He, J. Zhao, R. Li, Z. Wang, M. Grünwald and O. Chen, J. Am. Chem. Soc., 2019, 141, 6013–6021 CrossRef CAS PubMed.
- J. C. Ondry, J. P. Philbin, M. Lostica, E. Rabani and A. P. Alivisatos, ACS Nano, 2019, 13, 12322–12344 CrossRef CAS PubMed.
- P.-P. Wang, Q. Qiao, Y. Zhu and M. Ouyang, J. Am. Chem. Soc., 2018, 140, 9095–9098 CrossRef CAS PubMed.
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed.
- S. Vignolini, N. A. Yufa, P. S. Cunha, S. Guldin, I. Rushkin, M. Stefik, K. Hur, U. Wiesner, J. J. Baumberg and U. Steiner, Adv. Mater., 2012, 24, OP23–OP27 CrossRef CAS PubMed.
- X. Ye, J. Chen, B. T. Diroll and C. B. Murray, Nano Lett., 2013, 13, 1291–1297 CrossRef CAS PubMed.
- M. Cargnello, A. C. Johnston-Peck, B. T. Diroll, E. Wong, B. Datta, D. Damodhar, V. V. T. Doan-Nguyen, A. A. Herzing, C. R. Kagan and C. B. Murray, Nature, 2015, 524, 450–453 CrossRef CAS PubMed.
- J. Yan, W. Feng, J.-Y. Kim, J. Lu, P. Kumar, Z. Mu, X. Wu, X. Mao and N. A. Kotov, Chem. Mater., 2020, 32, 476–488 CrossRef CAS.
- A. Dong, J. Chen, X. Ye, J. M. Kikkawa and C. B. Murray, J. Am. Chem. Soc., 2011, 133, 13296–13299 CrossRef CAS PubMed.
- L. Dong, Y. Liu, Y. Lu, L. Zhang, N. Man, L. Cao, K. Ma, D. An, J. Lin, Y.-J. Xu, W.-P. Xu, W.-B. Wu, S.-H. Yu and L.-P. Wen, Adv. Funct. Mater., 2013, 23, 5930–5940 CrossRef CAS.
- H. Jin, Y. Bu, J. Li, J. Liu, X. Fen, L. Dai, J. Wang, J. Lu and S. Wang, Adv. Mater., 2018, 30, 1707424 CrossRef PubMed.
- Q. Li and Y.-S. Jun, Commun. Chem., 2018, 1, 56 CrossRef.
- H. Zhao, S. Sen, T. Udayabhaskararao, M. Sawczyk, K. Kučanda, D. Manna, P. K. Kundu, J.-W. Lee, P. Král and R. Klajn, Nat. Nanotechnol., 2016, 11, 82–88 CrossRef CAS PubMed.
- V. Polshettiwar, B. Baruwati and R. S. Varma, ACS Nano, 2009, 3, 728–736 CrossRef CAS PubMed.
- I. T. Papadas, I. Vamvasakis, I. Tamiolakis and G. S. Armatas, Chem. Mater., 2016, 28, 2886–2896 CrossRef CAS.
- A. O. Govorov, G. W. Bryant, W. Zhang, T. Skeini, J. Lee, N. A. Kotov, J. M. Slocik and R. R. Naik, Nano Lett., 2006, 6, 984–994 CrossRef CAS.
- J. Lee, A. O. Govorov, J. Dulka and N. A. Kotov, Nano Lett., 2004, 4, 2323–2330 CrossRef CAS.
- D. Luo, X. Qin, Q. Song, X. Qiao, Z. Zhang, Z. Xue, C. Liu, G. Mo and T. Wang, Adv. Funct. Mater., 2017, 27, 1701982 CrossRef.
- B. Dong, N. Mansour, Y. Pei, Z. Wang, T. Huang, S. L. Filbrun, M. Chen, X. Cheng, M. Pruski, W. Huang and N. Fang, J. Am. Chem. Soc., 2020, 142, 13305–13309 CrossRef CAS PubMed.
- B. Dong, Y. Pei, F. Zhao, T. W. Goh, Z. Qi, C. Xiao, K. Chen, W. Huang and N. Fang, Nat. Catal., 2018, 1, 135–140 CrossRef.
- Q. Zhang, W.-Z. Wang, J.-J. Yu, D.-H. Qu and H. Tian, Adv. Mater., 2017, 29, 1604948 CrossRef PubMed.
- A. B. Grommet, M. Feller and R. Klajn, Nat. Nanotechnol., 2020, 15, 256–271 CrossRef CAS PubMed.
- K. Hou, J. Han and Z. Tang, ACS Mater. Lett., 2020, 2, 95–106 CrossRef CAS.
- S. Wintzheimer, T. Granath, M. Oppmann, T. Kister, T. Thai, T. Kraus, N. Vogel and K. Mandel, ACS Nano, 2018, 12, 5093–5120 CrossRef CAS PubMed.
- D. Luo, C. Yan and T. Wang, Small, 2015, 11, 5984–6008 CrossRef CAS PubMed.
- S. Whitelam and R. L. Jack, Annu. Rev. Phys. Chem., 2015, 66, 143–163 CrossRef CAS PubMed.
- A. Guillaussier, Y. Yu, V. R. Voggu, W. Aigner, C. S. Cabezas, D. W. Houck, T. Shah, D.-M. Smilgies, R. N. Pereira, M. Stutzmann and B. A. Korgel, Langmuir, 2017, 33, 13068–13076 CrossRef CAS PubMed.
- J. Gong, R. S. Newman, M. Engel, M. Zhao, F. Bian, S. C. Glotzer and Z. Tang, Nat. Commun., 2017, 8, 14038 CrossRef CAS PubMed.
- D. Gerstner and T. Kraus, Nanoscale, 2018, 10, 8009–8013 RSC.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- S. Sun, C. B. Murray, D. Weller, L. Folks and A. Moser, Science, 2000, 287, 1989–1992 CrossRef CAS PubMed.
- X. Ye, L. Jin, H. Caglayan, J. Chen, G. Xing, C. Zheng, V. Doan-Nguyen, Y. Kang, N. Engheta, C. R. Kagan and C. B. Murray, ACS Nano, 2012, 6, 2804–2817 CrossRef CAS PubMed.
- L. Wu, J. J. Willis, I. S. McKay, B. T. Diroll, J. Qin, M. Cargnello and C. J. Tassone, Nature, 2017, 548, 197–201 CrossRef CAS PubMed.
- B. Abécassis, F. Testard and O. Spalla, Phys. Rev. Lett., 2008, 100, 115504 CrossRef PubMed.
- E. V. Yakovlev, K. A. Komarov, K. I. Zaytsev, N. P. Kryuchkov, K. I. Koshelev, A. K. Zotov, D. A. Shelestov, V. L. Tolstoguzov, V. N. Kurlov, A. V. Ivlev and S. O. Yurchenko, Sci. Rep., 2017, 7, 13727 CrossRef PubMed.
- Y. Yu, D. Yu, B. Sadigh and C. A. Orme, Nat. Commun., 2018, 9, 4211 CrossRef PubMed.
- Y. Yu, D. Yu and C. A. Orme, Nano Lett., 2017, 17, 3862–3869 CrossRef CAS PubMed.
- D. A. Weitz, J. S. Huang, M. Y. Lin and J. Sung, Phys. Rev. Lett., 1985, 54, 1416–1419 CrossRef CAS PubMed.
- J. Lee, E. Nakouzi, M. Song, B. Wang, J. Chun and D. Li, ACS Nano, 2018, 12, 12778–12787 CrossRef CAS PubMed.
- J. Park, H. Zheng, W. C. Lee, P. L. Geissler, E. Rabani and A. P. Alivisatos, ACS Nano, 2012, 6, 2078–2085 CrossRef CAS PubMed.
- G. Lin, S. W. Chee, S. Raj, P. Král and U. Mirsaidov, ACS Nano, 2016, 10, 7443–7450 CrossRef CAS PubMed.
- A. S. Powers, H.-G. Liao, S. N. Raja, N. D. Bronstein, A. P. Alivisatos and H. Zheng, Nano Lett., 2017, 17, 15–20 CrossRef CAS PubMed.
- Z. Ou, L. Yao, H. An, B. Shen and Q. Chen, Nat. Commun., 2020, 11, 4555 CrossRef CAS PubMed.
- Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Nat. Mater., 2020, 19, 450–455 CrossRef CAS PubMed.
- C. Liu, Z. Ou, F. Guo, B. Luo, W. Chen, L. Qi and Q. Chen, J. Am. Chem. Soc., 2020, 142, 11669–11673 CrossRef CAS PubMed.
- E. Cepeda-Perez, D. Doblas, T. Kraus and N. de Jonge, Sci. Adv., 2020, 6, eaba1404 CrossRef CAS PubMed.
- Y. Wang, L. Li, H. Liang, Y. Xing, L. Yan, P. Dai, X. Gu, G. Zhao and X. Zhao, ACS Nano, 2019, 13, 2901–2912 CrossRef CAS PubMed.
- M. Wang, A. C. Leff, Y. Li and T. J. Woehl, ACS Nano, 2021, 15, 2578–2588 CrossRef CAS PubMed.
- T. J. Woehl, T. Moser, J. E. Evans and F. M. Ross, MRS Bull., 2020, 45, 746–753 CrossRef.
- T. J. Woehl and P. Abellan, J. Microsc., 2017, 265, 135–147 CrossRef CAS PubMed.
- M. Wang, C. Park and T. J. Woehl, Chem. Mater., 2018, 30, 7727–7736 CrossRef CAS.
- M. N. Yesibolati, K. I. Mortensen, H. Sun, A. Brostrøm, S. Tidemand-Lichtenberg and K. Mølhave, Nano Lett., 2020, 20, 7108–7115 CrossRef CAS PubMed.
- R. Viswanatha and D. D. Sarma, in Nanomaterials Chemistry, 2007, pp. 139–170, DOI:10.1002/9783527611362.ch4.
- R. Hunter, Foundations of Colloid Science, Oxford UP, Oxford, 2009 Search PubMed.
- D. Alloyeau, W. Dachraoui, Y. Javed, H. Belkahla, G. Wang, H. Lecoq, S. Ammar, O. Ersen, A. Wisnet, F. Gazeau and C. Ricolleau, Nano Lett., 2015, 15, 2574–2581 CrossRef CAS PubMed.
- J. Korpanty, L. R. Parent and N. C. Gianneschi, Nano Lett., 2021, 21, 1141–1149 CrossRef CAS PubMed.
- D. Subramanian, C. T. Boughter, J. B. Klauda, B. Hammouda and M. A. Anisimov, Faraday Discuss., 2013, 167, 217–238 RSC.
- D. Verdin, Int. J. Radiat. Phys. Chem., 1970, 2, 201–208 CrossRef CAS.
- R. S. Bauer and W. W. Spooncer, J. Polym. Sci., Part A-1: Polym. Chem., 1970, 8, 2971–2977 CrossRef CAS.
- M. Matusiak, S. Kadłubowski and P. Ulański, Appl. Sci., 2021, 11, 10142 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr05416c |
| This journal is © The Royal Society of Chemistry 2022 |