Open Access Article
Open Access ArticleNitrogen-doped molecular bowls as electron donors in photoinduced electron transfer reactions†
O. A.
Stasyuk
 ab,
A. J.
Stasyuk
ab,
A. J.
Stasyuk
 *ab,
M.
Solà
*ab,
M.
Solà
 *a and
A. A.
Voityuk
*a and
A. A.
Voityuk
 *a
*a
aInstitut de Química Computacional, Departament de Química, Universitat de Girona, C/ Maria Aurèlia Capmany 69, 17003 Girona, Spain. E-mail: antony.stasuk@gmail.com; miquel.sola@udg.edu; alexander.voityuk@gmail.com
bFaculty of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
First published on 30th March 2022
Abstract
In recent years, the chemistry of curved π-conjugated molecules has experienced a sharp rise. The inclusion of a heteroatom in the carbon network significantly affects its semiconducting properties. In this work, we computationally study the photoinduced electron transfer in a series of C60 fullerene complexes with experimentally established nitrogen-doped molecular bowls. Our results demonstrate that introducing nitrogen into pentagonal rings of the bowl-shaped π-conjugated molecules and extending the π-conjugation can modulate their electron-transfer properties. Among the studied complexes, the hub-NCor⊃C60 complex exhibits the most desirable combination of ultrafast charge separation and slow charge recombination, suggesting its potential use in photovoltaics.
Introduction
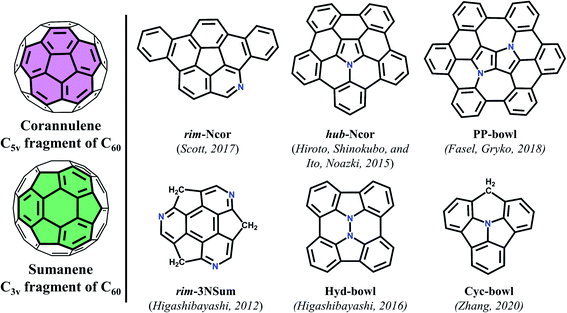
Significant advances in the chemistry of curved π-conjugated molecules observed in the last few decades are the result of the progress in their synthesis.1,2 The bowl-shaped compounds can be considered as structural parts of fullerenes and have attracted great attention3 since the discovery of fullerenes4 and nanotubes.5 Historically, the first synthesized buckybowl with C5v symmetry is corannulene (Cor). In 1966, Barth and Lawton reported on the multistage synthesis of dibenzo[ghi,-mno]fluoranthene called corannulene.6 Synthesis of sumanene (Sum) – a fullerene segment with C3v symmetry – was carried out almost 40 years later by Sakurai and Hirao (Fig. 1).7 In the early 1990s the development of the flash vacuum pyrolysis (FVP) method enabled materials scientists to evaluate these compounds.8–11 This attention to bowl-shaped molecules arises not only from aesthetic pleasure of curved π-conjugated systems, but also from the fact that they contribute to fundamental research of aromaticity,12 complexation with molecules and metal ions,13,14 and strain energy.1,15,16 It is known that the introduction of heteroatoms into a carbon π-conjugated system can dramatically affect its properties. Doping with nitrogen or boron atoms influences the semiconducting and luminescent properties of carbon materials due to changes in the band structure.17 Also, the introduction of the heteroatom can create “special areas” due to their electronegative or electropositive characteristics.18 Moreover, nitrogen-embedded bowl-shaped molecules are used as model compounds for azafullerenes and nitrogen-doped nanotubes.19–21There are two main types of heteroatom positions within bowl-shaped π-conjugated molecules: the rim position, in which a CH unit on the rim of a bowl is replaced by a heteroatom; and the hub position where a heteroatom is embedded in the central part and connects with three other atoms of the bowl. To date there have only been limited reports on the synthesis of such bowl-shaped compounds.
The first example of azabuckybowl–triazasumanene (rim-3NSum) – was reported by Higashibayashi and co-workers in 2012.20 This is the only synthesized nitrogen-doped sumanene derivative.
The synthesis of azapentabenzocorannulene bearing a nitrogen atom in the core of corannulene (hub-NCor) was independently reported in 2015 by Ito and Nozaki, as well as by Hiroto and Shinokubo.22,23 Azadibenzocorannulene with a nitrogen on the rim position (rim-NCor) was described by Scott two years later.24 Very recently, Krzeszewski et al. reported a new nitrogen-containing bowl-shaped molecule (PP-bowl) consisting of a pyrrolo[3,2-b]pyrrole core substituted with six arene rings linked in a circle.25 In contrast to the “classical” azabuckybowls, the presented bowl features two pentagonal rings located between two heptagons. This molecule could be used as an optoelectronic material due to the electron-rich nature of the pyrrolo[3,2-b]pyrrole fragment.26 Hydrazinobuckybowl, a diaza analog of diindenochrysene (Hyd-bowl) with a particularly electron-rich nature, was reported by Higashibayashi and co-workers.27 More recently, the structure of the nitrogen-embedded π-extended cyclazine (Cyc-bowl) was described in 2020 by Deng and Zhang.28 In general, the introduction of nitrogen or other heteroatoms into bowl-shaped π-conjugated molecules can be used as an effective strategy for modulating their physicochemical and electronic properties, which greatly expands the diversity and hence the use of such molecules in functional materials.
Here, we study electronic and photoinduced electron transfer (PET) properties of complexes based on C60 with a number of previously synthesized nitrogen-doped molecular bowls of different topologies. Using the time-dependent density functional theory (TD-DFT), we investigate the efficiency of PET in a particular complex as a function of the structural features of the bowl. The results can be used in the design of N-doped carbon nanomaterials for photovoltaic applications.
Computational methods
Geometry optimizations were performed by employing the DFT B3LYP29–31 hybrid exchange–correlation functional with Ahlrichs' def2-SVP basis set.32,33 The empirical dispersion D3 correction was included using the Becke–Johnson damping scheme.34,35 Vertical excitation energies were calculated using the TDA formalism36 with the range-separated CAM-B3LYP37,38 functional and the def2-SVP basis set,32,33 as implemented in the Gaussian 16 (rev. A03) program.39 The same program was used for population analysis in terms of Mulliken,40 Löwdin,41 Hirshfeld,42 iterative Hirshfeld43 and CM5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 charges. The formation energy of the complexes and their strain energy were computed with the B3LYP-D3(BJ)/def2-TZVP//B3LYP-D3(BJ)/def2-SVP scheme.45 A Morokuma-like energy decomposition analysis (EDA)46–48 was performed using the Amsterdam Density Functional (ADF) program at the B3LYP-D3(BJ)/TZP//B3LYP-D3(BJ)/def2-SVP.49 The topological analysis of the electron density distribution was conducted using the “Quantum Theory of Atoms in Molecules” (QTAIM).50 The AIMALL suite of programs51 was applied to evaluate the bond critical points and associated bond descriptors. Molecular structures and frontier molecular orbitals were visualized using the Chemcraft 1.8 program.52 Details on the analysis of excited states, calculation of solvent effects, electron transfer rates, reorganization and interaction energies can be found in the ESI.†
44 charges. The formation energy of the complexes and their strain energy were computed with the B3LYP-D3(BJ)/def2-TZVP//B3LYP-D3(BJ)/def2-SVP scheme.45 A Morokuma-like energy decomposition analysis (EDA)46–48 was performed using the Amsterdam Density Functional (ADF) program at the B3LYP-D3(BJ)/TZP//B3LYP-D3(BJ)/def2-SVP.49 The topological analysis of the electron density distribution was conducted using the “Quantum Theory of Atoms in Molecules” (QTAIM).50 The AIMALL suite of programs51 was applied to evaluate the bond critical points and associated bond descriptors. Molecular structures and frontier molecular orbitals were visualized using the Chemcraft 1.8 program.52 Details on the analysis of excited states, calculation of solvent effects, electron transfer rates, reorganization and interaction energies can be found in the ESI.†
Results and discussion
Ground state properties
The complementary concave–convex interaction between C60 fullerene and pristine corannulene leads to the formation of an 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
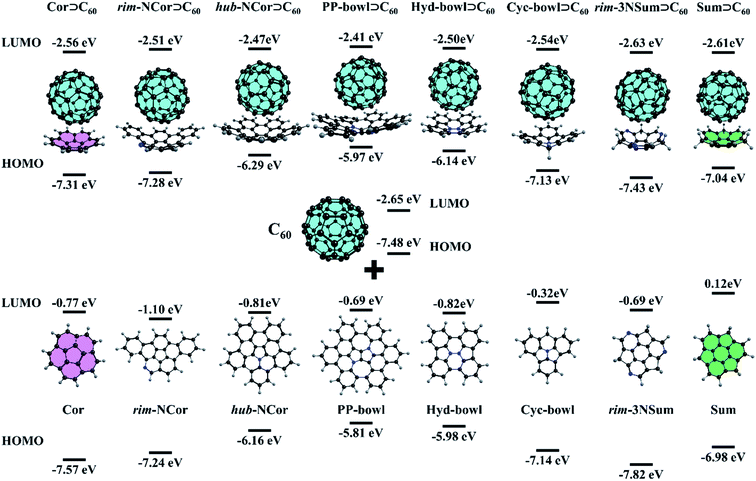
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Although the complex was observed in the gas-phase and on a metal surface, its binding constant is not high. Yokoi et al. found that enhanced electron donating properties of the molecular bowl cause its closer association with electron-deficient C60 both in solution and in the solid state. In particular, the binding constant between the tert-butyl derivative of hub-NCor and C60 was measured to be 3.8 × 103 L mol−1,23 in contrast to the binding constant values of 280–475 L mol−1 for substituted corannulenes.53 The pronounced electron-rich character of the nitrogen-containing bowls and the electron-deficient nature of C60 encouraged us to study the ground state (GS) properties of six van der Waals (vdW) complexes, rim-NCor⊃C60, hub-NCor⊃C60, PP-bowl⊃C60, Hyd-bowl⊃C60, Cyc-bowl⊃C60, and rim-3NSum⊃C60 (Fig. 2), and their response to photoexcitation compared with the reference systems Cor⊃C60 and Sum⊃C60. The selected bowls are synthesized derivatives of corannulene and sumanene with the nitrogen atom located at different positions. Rim-NCor⊃C60 and rim-3NSum⊃C60 contain pyridinic N atoms on the periphery, and Cyc-bowl⊃C60 has a pyramidal amine N atom, while pyrrolic N atoms are contained in the central part of other bowls. Each type of N atom has a different effect on the electronic and photophysical properties of the bowls and their complexes.
1 complex. Although the complex was observed in the gas-phase and on a metal surface, its binding constant is not high. Yokoi et al. found that enhanced electron donating properties of the molecular bowl cause its closer association with electron-deficient C60 both in solution and in the solid state. In particular, the binding constant between the tert-butyl derivative of hub-NCor and C60 was measured to be 3.8 × 103 L mol−1,23 in contrast to the binding constant values of 280–475 L mol−1 for substituted corannulenes.53 The pronounced electron-rich character of the nitrogen-containing bowls and the electron-deficient nature of C60 encouraged us to study the ground state (GS) properties of six van der Waals (vdW) complexes, rim-NCor⊃C60, hub-NCor⊃C60, PP-bowl⊃C60, Hyd-bowl⊃C60, Cyc-bowl⊃C60, and rim-3NSum⊃C60 (Fig. 2), and their response to photoexcitation compared with the reference systems Cor⊃C60 and Sum⊃C60. The selected bowls are synthesized derivatives of corannulene and sumanene with the nitrogen atom located at different positions. Rim-NCor⊃C60 and rim-3NSum⊃C60 contain pyridinic N atoms on the periphery, and Cyc-bowl⊃C60 has a pyramidal amine N atom, while pyrrolic N atoms are contained in the central part of other bowls. Each type of N atom has a different effect on the electronic and photophysical properties of the bowls and their complexes.
First, we consider such effects in the bowls by analyzing the frontier molecular orbitals: the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). For the bowls with pyrrolic N in a hub position, we found a significant reduction in the HOMO–LUMO (HL) gap compared to the undoped bowls (Fig. 2). This can be explained by the formation of an aromatic sextet in pentagonal rings and by increasing π-electron delocalization in the bowls. The electron-donating character of the bowls can be described by the HOMO energy. The donating effects decrease by passing from the PP-bowl and Hyd-bowl with two N atoms to hub-NCor with one pyrrolic N atom. The lowest donating properties are found for rim-NCor and rim-3NSum bowls having pyridinic N.
It is important to note that the LUMO of complexes is localized on the C60 fragment in each case, while the localization of the HOMO depends on the complex. Because the HOMO of Cor and rim-3NSum bowls is lower than that of C60, the HOMO of their complexes is localized on the fullerene. In other complexes, the HOMO is localized on the bowls. The HL gap (Table S1, ESI†) also depends on the complex. For example, hub-NCor⊃C60, PP-bowl⊃C60, and Hyd-bowl⊃C60 have a relatively small HL gap (3.6 to 3.8 eV), while it is about 1 eV larger (ranging from 4.4 to 4.8 eV) in rim-NCor⊃C60, rim-3NSum⊃C60, and Cyc-bowl⊃C60, as well as in the reference systems Cor⊃C60 and Sum⊃C60. Thus, the HL gap is modulated by the nitrogen content and topology of the π-conjugated system. A larger number of pyrrolic N atoms and an increase in π-conjugation promote narrowing of the HL gap. The formation of the vdW complexes has a rather small effect on the orbital energies of their fragments. In particular, the LUMO energy of the C60 fragment changes within only 0.25 eV compared to the isolated C60, while the variation in the HOMO energy located on bowls does not exceed 0.17 eV. The population analysis does not reveal any significant charge transfer between the host (Bowl) and the guest (C60) in the GS (Table S2, ESI†). Because of that, only minor changes are found in the HOMO and LUMO energies of the molecules by the formation of their complexes.
The stability of the complexes was evaluated by calculating the interaction energy (ΔEint) between the bowls and C60 (see Table 1). Using a Morokuma-type energy decomposition method, the interaction energy is divided into four components: Pauli repulsion (ΔEPauli), electrostatic (ΔEelstat), orbital interactions (ΔEoi), and dispersion correction (ΔEdisp) (see computational details in the ESI†).
| Complex | d Bowl⋯C60 | Energy components | ||||
|---|---|---|---|---|---|---|
| ΔEint | ΔEPauli | ΔEelstat | ΔEoi | ΔEdisp | ||
| a The energy values are in kcal mol−1. The percentage contributions to the sum of attraction energies (ΔEelstat + ΔEoi + ΔEdisp) are given in parentheses. b Distances between the centers of C60 and Bowl fragments are in Å. | ||||||
| Cor⊃C60 | 5.949 | −18.84 | 35.51 | −17.54 (32.3%) | −8.20 (15.1%) | −28.62 (52.6%) |
| rim-NCor⊃C60 | 5.599 | −24.52 | 42.35 | −20.42 (30.5%) | −10.00 (15.0%) | −36.45 (54.5%) |
| hub-NCor⊃C60 | 5.462 | −30.79 | 48.41 | −23.36 (29.5%) | −11.45 (14.5%) | −44.40 (56.1%) |
| PP-bowl⊃C60 | 5.370 | −33.51 | 49.06 | −23.94 (29.0%) | −11.77 (14.3%) | −46.85 (56.7%) |
| Hyd-bowl⊃C60 | 5.746 | −24.40 | 40.83 | −20.40 (31.3%) | −10.10 (15.5%) | −34.73 (53.2%) |
| Cyc-bowl⊃C60 | 5.995 | −18.52 | 34.04 | −16.66 (31.7%) | −8.47 (16.1%) | −27.43 (52.2%) |
| rim-3NSum⊃C60 | 6.114 | −17.98 | 30.37 | −14.21 (29.4%) | −7.53 (15.6%) | −26.61 (55.0%) |
| Sum⊃C60 | 5.943 | −19.71 | 37.95 | −18.25 (31.6%) | −9.29 (16.1%) | −30.13 (52.2%) |
As seen in Table 1, the least stable complex is rim-3NSum⊃C60 due to the larger bowl-depth and weaker dispersion interactions. More extended and less curved buckybowls (hub-NCor and PP-bowl) form the most stable complexes with C60. In these complexes, there are shorter distances between the centers of C60 and Bowl fragments, more stabilizing dispersion interactions and more destabilizing Pauli repulsions. ΔEPauli varies from 30.4 kcal mol−1 for rim-3NSum⊃C60 to 49.1 kcal mol−1 for PP-bowl⊃C60. Among the intermolecular attractions (electrostatic, orbital, and dispersion interactions), the last term dominates contributing from 52 to 57%. It is followed by the electrostatic (about 30%) and orbital (14 to 16%) interactions. We note that the HL gap increases with ΔEoi (Fig. 2). A similar picture was found earlier in vdW complexes of C60 with phosphangulene oxide derivatives.54
The topological analysis based on Bader's atoms in molecules theory (QTAIM) was used to obtain additional information about the host–guest interactions. The electron density, its Laplacian, and other topological parameters at the bond critical points (BCPs) were calculated (see Table S3†). The analysis revealed that there are only π⋯π interactions between the host and guest units in Cor⊃C60, rim-NCor⊃C60, hub-NCor⊃C60, PP-bowl⊃C60, Hyd-bowl⊃C60, and Cyc-bowl⊃C60. Additional interactions of the CH⋯π type are found in rim-3NSum⊃C60 and Sum⊃C60. QTAIM molecular graphs for the complexes are given in Fig. S1, ESI.† The topology of the host–guest interactions in the complexes was also described using the non-covalent interaction index (NCI).55 The NCI isosurfaces are fairly evenly distributed between the Bowl and C60 fragments and have a similar shape in all complexes. The reduced density gradient (RDG) plots and NCI isosurfaces are presented in Fig. S2 and S3, ESI.†
Singlet excited states
The strong electron-accepting properties of fullerene and the relatively small HL gap in the complexes suggest promising PET properties of the systems. To describe the properties of excited states, all systems were divided into 2 fragments: guest (acceptor) C60 and host (donor) bowls. The electron density distribution was analyzed for the 100 lowest-lying excited states. Three types of excited states were identified: (1) locally excited (LE) states, in which the excitation is mostly localized either on the guest (LE1) or on the host molecule (LE2) and charge transfer is less than 0.1e (CT < 0.1e); (2) charge transfer (CT) states showing a significant charge separation (CT > 0.8e); and (3) mixed states, where both LE and CT states contribute substantially (0.1e < CT < 0.8e).14,56In the gas-phase, the 100 lowest vertical singlet excitation energies of the complexes are found in the range from 2.55 to 5.25 eV. The analysis revealed two types of LE states (LE1 and LE2) but only one type of CT state. This CT type corresponds to electron transfer from Bowl to C60, leading to Bowl+⊃C60−. CT states with opposite charge separation, Bowl−⊃C60+, were not found in the studied energy range. We note that in all complexes the lowest LE states localized on C60 are dark. Thus, they can only be populated due to the fast internal conversion of absorbing states of C60.
| Supramolecular host–guest systems Bowl⊃C60 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cor | rim-NCor | hub-NCor | PP-bowl | Hyd-bowl | Cyc-bowl | rim-3NSum | Sum | |
| a LE2 state is partially delocalized over the C60 unit. b Mixed state with significant contributions of LE and CT. | ||||||||
| LE 1 (fullerene C60 ) | ||||||||
| Ex | 2.561 | 2.570 | 2.563 | 2.560 | 2.557 | 2.551 | 2.566 | 2.552 |
| Trans. (W) | H–L (0.27) | H−1–L+1 (0.22) | H−2–L+2 (0.32) | H−3–L+2 (0.20) | H−1–L (0.28) | H−2–L+1 (0.16) | H–L (0.46) | H−4–L+1 (0.21) |
| f | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| χ | 0.974 | 0.974 | 0.898 | 0.952 | 0.967 | 0.955 | 0.979 | 0.928 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| LE 2 (Bowl) | ||||||||
| Ex | 3.976 | 3.883 | 3.245 | 2.984 | 3.284 | 4.152a | 4.171 | 4.143 |
| Trans. (W) | H−6–L+6 (0.36) | H−5–L+3 (0.22) | H–L+7 (0.42) | H–L+7 (0.69) | H–L+7 (0.90) | H–L+6 (0.37) | H−5–L+6 (0.39) | H–L+6 (0.21) |
| f | <0.001 | 0.019 | 0.048 | 0.003 | 0.001 | 0.019 | 0.019 | <0.001 |
| χ | 0.856 | 0.796 | 0.925 | 0.879 | 0.950 | 0.543 | 0.848 | 0.788 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Most absorptive transition | ||||||||
| Ex | 4.393 | 4.391 | 4.388 | 4.399 | 4.404 | 4.369 | 4.390 | 4.389b |
| Trans. (W) | H–L+5 (0.22) | H−1–L+4 (0.16) | H−3–L+4 (0.14) | H−7–L+3 (0.14) | H−5–L+3 (0.18) | H–L+5 (0.23) | H–L+3 (0.19) | H−2–L+3 (0.14) |
| f | 0.357 | 0.255 | 0.251 | 0.306 | 0.297 | 0.385 | 0.303 | 0.199 |
| Localiz. | C60 | C60 | C60 | C60 | C60 | C60 | C60 | C60 |
| χ | 0.946 | 0.811 | 0.910 | 0.884 | 0.913 | 0.903 | 0.897 | 0.684 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| CT (Bowl → fullerene C60 ) | ||||||||
| Ex | 3.835 | 3.413 | 2.310 | 2.078 | 2.120 | 3.214 | 3.913 | 3.137 |
| Trans. (W) | H−6–L (0.62) | H−5–L+2 (0.69) | H–L+1 (0.81) | H–L+1 (0.63) | H–L (0.73) | H−5–L+1 (0.49) | H−6–L+1 (0.32) | H−1–L (0.58) |
| f | 0.002 | 0.003 | 0.008 | <0.001 | <0.001 | <0.001 | 0.005 | 0.008 |
| CT | 0.856 | 0.968 | 0.871 | 0.966 | 0.904 | 0.804 | 0.854 | 0.870 |
Depending on the nature of the first excited state, the complexes can be divided into two groups. The first group includes hub-NCor⊃C60, PP-bowl⊃C60, and Hyd-bowl⊃C60, in which the CT state is the lowest-lying excited state with the energy ranging from 2.08 to 2.31 eV (Table 2). The second group includes Cor⊃C60, rim-NCor⊃C60, Cyc-bowl⊃C60, rim-3NSum⊃C60, and Sum⊃C60. In this group, the LE1 state with the excitation on C60 is the lowest one, and the energy of CT states varies from 3.14 to 3.91 eV. We note that in all complexes the energy of LE2 states with the exciton localized on Bowl is higher than that of LE1 and CT states. For each system, the excited states with a significant oscillator strength are almost completely localized on the C60 fragment. The selected LE and CT states were additionally analyzed in terms of natural transition orbitals (NTOs), which are shown in Fig. S4–S11 in the ESI.† The NTOs corresponding to local excitations in the C60 and Bowl fragments are of π type and rather evenly distributed over the entire fragment. The occupied and vacant NTOs associated with CT are localized on the bowls and the fullerene, respectively. The main contributions of the Kohn–Sham orbitals to the NTOs are provided in Table S4, ESI.†
Effects of the environment
A well-proven COSMO-like model14,57–59 with dichloromethane (DCM) as a solvent was applied to estimate the effect of the polar environment on electronic excitations. The GS dipole moment of the studied complexes is in the range of 0.2 to 1.9 D. The small dipole moments can be explained by the high symmetry of the units (bowls and fullerene) and their mutual arrangement. The GS solvation energy varies from −0.15 to −0.28 eV. The reference corannulene and sumanene complexes have the lowest solvation energies. The higher solvation energy of the complexes with nitrogen-containing bowls is due to the polar C–N bonds. A change in the dipole moment (Δμ) due to GS → LE excitations is rather small and does not exceed 3.9 D. The solvation energies of the GS, LE1, and LE2 states are found to be similar. Detailed solvation data including the analysis of excited states in DCM are given in Tables S5 and S6, ESI.† As expected, the dipole moment of CT states is significantly larger than that of GS and LE states. Depending on a particular complex, ΔμCT varies from 21.4 to 26.4 D. The solvation energy of the Bowl+⊃C60− CT states is significantly larger. Note that the solvent stabilization of CT states in Cor⊃C60 and rim-3NSum⊃C60 is not strong enough to energetically enable the LE1 →CT transition. In contrast, the stabilization of the CT state in rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 is sufficient to reduce the gap between CT and LE1 to less than 0.3 eV (Fig. 3).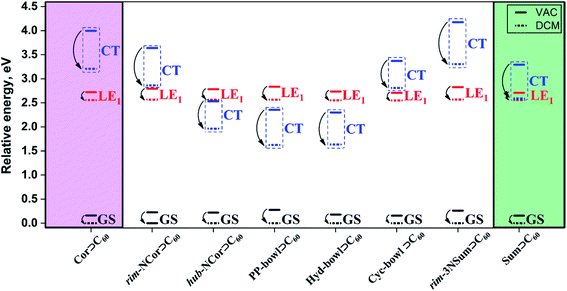 | ||
| Fig. 3 Relative energies (in eV) of GS, LE1, and CT states for the complexes of interest computed in a vacuum (VAC) and dichloromethane (DCM). | ||
Electron transfer rates and the effect of excited state geometry relaxation
CT states in the complexes are characterized by a very weak oscillator strength and can therefore not be directly populated by light absorption. However, they can be generated by the decay of LE states. Our calculations showed that excitations with the highest probability of absorption are localized on the fullerene unit. The rates of charge separation (kCS) and charge recombination (kCR) were calculated using the semi-classical method proposed by Ulstrup and Jortner.60 Within this approach, the intramolecular relaxation associated with ET is described by an effective vibrational mode, and the rate is controlled by four parameters: electronic coupling of the initial and final states Vij, solvation reorganization energy λs, reaction Gibbs energy ΔG0, and the effective Huang–Rhys factor Seff. A two-state coupling scheme was employed in all cases. The rates were estimated using the effective frequency of 1600 cm−1, which corresponds to the stretching of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. Previously, we demonstrated that the rate of charge separation for similar systems does not change significantly by varying the effective frequency from 1400 to 1800 cm−1.54 Our tests for the representative complexes Cor⊃C60, Sum⊃C60, and hub-NCor⊃C60 confirm the small effect of the effective frequency on the CS rate (Table S7 and Fig. S12, ESI†). The computed parameters and kCS in DCM are listed in Table 3.
C bonds. Previously, we demonstrated that the rate of charge separation for similar systems does not change significantly by varying the effective frequency from 1400 to 1800 cm−1.54 Our tests for the representative complexes Cor⊃C60, Sum⊃C60, and hub-NCor⊃C60 confirm the small effect of the effective frequency on the CS rate (Table S7 and Fig. S12, ESI†). The computed parameters and kCS in DCM are listed in Table 3.
| Complex | ΔG0a, eV | |Vij|, eV | Reorg. energy, eV | S eff | ΔEac, eV | k CS, s−1 | |
|---|---|---|---|---|---|---|---|
| λ i | λ s | ||||||
| a Gibbs energy difference between CT and LE1 states. b Effective value of the Huang–Rhys factor Seff = λi/ħωeff, where ħωeff is set to 1600 cm−1. c Activation energy barrier for the LE1 → CT reaction. | |||||||
| Cor⊃C60 | 0.652 | 9.35 × 10−3 | 0.170 | 0.413 | 0.857 | 0.686 | 5.67 × 100 |
| rim-NCor⊃C60 | 0.296 | 4.93 × 10−3 | 0.151 | 0.338 | 0.761 | 0.297 | 6.63 × 106 |
| hub-NCor⊃C60 | −0.598 | 1.98 × 10−3 | 0.165 | 0.246 | 0.832 | 0.017 | 3.89 × 1012 |
| PP-bowl⊃C60 | −0.942 | 2.22 × 10−3 | 0.250 | 0.322 | 1.260 | 0.016 | 2.29 × 1010 |
| Hyd-bowl⊃C60 | −0.918 | 2.20 × 10−3 | 0.277 | 0.345 | 1.396 | 0.015 | 3.16 × 1010 |
| Cyc-bowl⊃C60 | 0.260 | 1.91 × 10−2 | 0.218 | 0.312 | 1.099 | 0.262 | 4.06 × 108 |
| rim-3NSum⊃C60 | 0.736 | 1.17 × 10−2 | 0.212 | 0.407 | 1.069 | 0.802 | 9.82 × 10−2 |
| Sum⊃C60 | 0.034 | 1.96 × 10−3 | 0.166 | 0.410 | 0.836 | 0.120 | 9.39 × 108 |
As seen in Table 3, the electron transfer reactions in the complexes are characterized by moderate internal reorganization energies, which range from 0.15 to 0.28 eV. The LE1 → CT charge separation process in Cor⊃C60 and rim-3NSum⊃C60 is unlikely because of its highly positive Gibbs energy. In turn, the modest activation energy barrier is responsible for the rather slow charge separation in rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60. Electron transfer in these complexes occurs in the normal Marcus regime (|ΔG0| < λ) on the nanosecond timescale or even slower. The characteristic time (τ) was found to be 151.94, 2.46, and 1.07 ns, respectively. At the same time, PET in hub-NCor⊃C60, PP-bowl⊃C60, and Hyd-bowl⊃C60 is almost barrierless. The calculated rate constants unambiguously confirm the ultrafast charge separation between the C60 and Bowl fragments. Thus, the complexes with the bowls containing the pyrrolic nitrogen atoms and extended π-conjugation demonstrate better PET properties.
Usually, the generated CT states are deactivated by charge recombination to the ground state. For large conjugated systems, the effect of internal geometry reorganization on ΔG0 is rather small and can be safely neglected.61,62 However, in the studied complexes, the Bowl fragment is relatively small, and the relaxation effect can be significant. Thus, we studied the effect of geometry relaxation on the rate of charge recombination in DCM for rim-NCor⊃C60, hub-NCor⊃C60, PP-bowl⊃C60, Hyd-bowl⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 (Table 4). The Cor and rim-3NSum based complexes were not considered because the formation of CT states is unlikely for them.
| Complex | ΔG0a, eV | |Vij|, eV | Reorg. energy, eV | S eff | ΔEac, eV | k CR, s−1 | |
|---|---|---|---|---|---|---|---|
| λ i | λ s | ||||||
| a Gibbs energy difference between CT and GS. b Effective value of the Huang–Rhys factor Seff = λi/ħωeff, where ħωeff is set to 1600 cm−1. c Activation energy barrier for the CT → GS reaction. | |||||||
| Vertical Frank–Condon geometries | |||||||
| rim-NCor⊃C60 | −2.863 | 6.62 × 10−2 | 0.140 | 0.338 | 0.706 | 0.058 | 2.46 × 103 |
| hub-NCor⊃C60 | −1.965 | 4.10 × 10−2 | 0.145 | 0.246 | 0.731 | 0.036 | 3.98 × 107 |
| PP-bowl⊃C60 | −1.623 | 4.22 × 10−2 | 0.147 | 0.322 | 0.741 | 0.036 | 7.22 × 109 |
| Hyd-bowl⊃C60 | −1.635 | 3.44 × 10−3 | 0.183 | 0.345 | 0.923 | 0.033 | 1.64 × 108 |
| Cyc-bowl⊃C60 | −2.590 | 7.40 × 10−2 | 0.164 | 0.312 | 0.827 | 0.047 | 3.96 × 105 |
| Sum⊃C60 | −3.304 | 1.22 × 10−2 | 0.165 | 0.410 | 0.832 | 0.066 | 4.28 × 100 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Relaxed in CT geometries | |||||||
| rim-NCor⊃C60 | −2.614 | 5.82 × 10−2 | 0.138 | 0.328 | 0.696 | 0.054 | 4.49 × 104 |
| hub-NCor⊃C60 | −1.548 | 2.31 × 10−2 | 0.130 | 0.350 | 0.655 | 0.039 | 3.98 × 109 |
| PP-bowl⊃C60 | −1.262 | 1.09 × 10−2 | 0.136 | 0.326 | 0.686 | 0.030 | 1.39 × 1010 |
| Hyd-bowl⊃C60 | −0.956 | 3.46 × 10−2 | 0.218 | 0.415 | 1.099 | 0.017 | 6.91 × 1012 |
| Cyc-bowl⊃C60 | −2.252 | 3.89 × 10−2 | 0.240 | 0.321 | 1.210 | 0.035 | 1.74 × 108 |
| Sum⊃C60 | −2.877 | 6.47 × 10−2 | 0.167 | 0.337 | 0.842 | 0.053 | 1.27 × 104 |
In contrast to the charge separation, the charge recombination reactions take place in the inverted Marcus region (|ΔG0| > λ). Thus, the relaxation of the CT geometry leads to a decrease in the |ΔG0| and accordingly increases kCR. Moreover, the geometry relaxation reduces the activation barrier of the CT → GS reaction.
Since the electron transfer in the rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 complexes is characterized by ΔG0 > 0 (Table 3), the charge recombination CT → LE1 state can be considered as an alternative deactivation channel of the CT state. As seen in Table 5, the back electron transfer from the CT to the LE1 state in the rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 complexes is rather fast. Thus, we infer that the CT states in these complexes can hardly be observed.
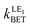 (in s−1), Gibbs energy ΔG0 (in eV), electronic coupling Vij (in eV), solvent (λs) and internal (λi) reorganization energy (in eV), Huang–Rhys factor (Seff) and activation energy barrier (ΔEa, eV) for the rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 complexes computed in DCM
(in s−1), Gibbs energy ΔG0 (in eV), electronic coupling Vij (in eV), solvent (λs) and internal (λi) reorganization energy (in eV), Huang–Rhys factor (Seff) and activation energy barrier (ΔEa, eV) for the rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 complexes computed in DCM
| Complex | ΔG0a, eV | |Vij|, eV | Reorg. energy, eV | S eff | ΔEac, eV | , s−1 | |
|---|---|---|---|---|---|---|---|
| λ i | λ s | ||||||
| a Gibbs energy difference between LE1 and CT states. b Effective value of the Huang–Rhys factor Seff = λi/ħωeff, where ħωeff is set to 1600 cm−1. c Activation energy barrier for the CT → LE1 reaction. | |||||||
| rim-NCor⊃C60 | −0.296 | 4.93 × 10−3 | 0.151 | 0.338 | 0.761 | 0.004 | 7.15 × 1012 |
| Cyc-bowl⊃C60 | −0.260 | 1.91 × 10−2 | 0.218 | 0.312 | 1.099 | 0.005 | 1.06 × 1013 |
| Sum⊃C60 | −0.034 | 1.96 × 10−3 | 0.166 | 0.410 | 0.836 | 0.087 | 3.53 × 109 |
In summary, for PP-bowl⊃C60, Hyd-bowl⊃C60, Cyc-bowl⊃C60, rim-NCor⊃C60, Cyc-bowl⊃C60, and Sum⊃C60 complexes, kCR was found to be similar to or even higher than the corresponding charge separation rates. Fast charge recombination is a significant disadvantage as it prevents the efficient extraction of electrons and holes and, consequently, the potential application of these complexes in photovoltaic devices. Only hub-NCor⊃C60 demonstrates ultrafast photoinduced electron transfer on the picosecond timescale (τ = 0.25 ps) and slow charge recombination (kCR is smaller by 3 orders of magnitude than kCS).
Conclusions
In this work, we studied in detail the ground and excited-state properties of several complexes formed by C60 fullerene and nitrogen-doped molecular bowls of different topologies using the DFT/TD-DFT approach. The propensity of a particular complex to photoinduced electron transfer is mainly determined by the electron-donating properties of the bowl. The low HOMO energy of the rim-3NSum bowl results in a high activation barrier for electron transfer in rim-3NSum⊃C60, and thus inhibits this process. PET in the rim-NCor⊃C60 and Cyc-bowl⊃C60 complexes occurs in the normal Marcus regime on the nanosecond timescale. In turn, the hub-NCor⊃C60, PP-bowl⊃C60, and Hyd-bowl⊃C60 complexes reveal ultrafast PET occurring on the picosecond timescale. However, the practical application of PP-bowl⊃C60, Hyd-bowl⊃C60, and Cyc-bowl⊃C60 may be limited due to fast charge recombination. Only the hub-NCor⊃C60 complex demonstrates the desirable combination of ultrafast charge separation (τ = 0.25 ps) and relatively slow charge recombination. This makes it a promising candidate for applications in organic photovoltaics.Author contributions
O. A. S.: investigation, formal analysis, writing – original draft, writing – review & editing. A. J. S.: investigation, formal analysis, writing – original draft, writing – review & editing. M. S.: supervision, writing – review & editing, funding acquisition. A. A. V.: supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Spanish MINECO (Network RED2018-102815-T, project PID2020-113711GB-I00, and Juan de la Cierva contract IJC2019-039846-I to A. J. S.), the Catalan DIUE (2017SGR39), and the University of Girona (POSTDOC-UdG 2021/31 to O. A. S.). This research was supported in part by PLGrid Infrastructure.References
- S. H. Pun and Q. Miao, Acc. Chem. Res., 2018, 51, 1630–1642 CrossRef CAS PubMed.
- J. M. Fernández-García, P. J. Evans, S. Filippone, M. Á. Herranz and N. Martín, Acc. Chem. Res., 2019, 52, 1565–1574 CrossRef PubMed.
- M. Saito, H. Shinokubo and H. Sakurai, Mater. Chem. Front., 2018, 2, 635–661 RSC.
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- W. E. Barth and R. G. Lawton, J. Am. Chem. Soc., 1966, 88, 380–381 CrossRef CAS.
- H. Sakurai, T. Daiko and T. Hirao, Science, 2003, 301, 1878 CrossRef CAS PubMed.
- A. Borchardt, A. Fuchicello, K. V. Kilway, K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 1992, 114, 1921–1923 CrossRef CAS.
- L. T. Scott, M. M. Hashemi and M. S. Bratcher, J. Am. Chem. Soc., 1992, 114, 1920–1921 CrossRef CAS.
- L. T. Scott, M. M. Hashemi, D. T. Meyer and H. B. Warren, J. Am. Chem. Soc., 1991, 113, 7082–7084 CrossRef CAS.
- G. Zimmermann, U. Nuechter, S. Hagen and M. Nuechter, Tetrahedron Lett., 1994, 35, 4747–4750 CrossRef.
- S. Escayola, A. Poater, A. Muñoz-Castro and M. Solà, Chem. Commun., 2021, 57, 3087–3090 RSC.
- S. N. Spisak, Z. Zhou, S. Liu, Q. Xu, Z. Wei, K. Kato, Y. Segawa, K. Itami, A. Y. Rogachev and M. A. Petrukhina, Angew. Chem., Int. Ed., 2021, 60, 25445–25453 CrossRef CAS PubMed.
- S. Zank, J. M. Fernández-García, A. J. Stasyuk, A. A. Voityuk, M. Krug, M. Solà, D. M. Guldi and N. Martín, Angew. Chem., Int. Ed., 2022, 61, e202112834 CrossRef CAS PubMed.
- A. S. Filatov, A. V. Zabula, S. N. Spisak, A. Y. Rogachev and M. A. Petrukhina, Angew. Chem., Int. Ed., 2014, 53, 140–145 CrossRef CAS PubMed.
- C. Liu, Y. Ni, X. Lu, G. Li and J. Wu, Acc. Chem. Res., 2019, 52, 2309–2321 CrossRef CAS PubMed.
- O. Stephan, P. M. Ajayan, C. Colliex, P. Redlich, J. M. Lambert, P. Bernier and P. Lefin, Science, 1994, 266, 1683–1685 CrossRef CAS PubMed.
- S. Hiroto, Chem. Lett., 2021, 50, 1146–1155 CrossRef CAS.
- S. Maldonado, S. Morin and K. J. Stevenson, Carbon, 2006, 44, 1429–1437 CrossRef CAS.
- Q. Tan, S. Higashibayashi, S. Karanjit and H. Sakurai, Nat. Commun., 2012, 3, 891 CrossRef PubMed.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- S. Ito, Y. Tokimaru and K. Nozaki, Angew. Chem., Int. Ed., 2015, 54, 7256–7260 CrossRef CAS PubMed.
- H. Yokoi, Y. Hiraoka, S. Hiroto, D. Sakamaki, S. Seki and H. Shinokubo, Nat. Commun., 2015, 6, 8215 CrossRef PubMed.
- V. M. Tsefrikas, A. K. Greene and L. T. Scott, Org. Chem. Front., 2017, 4, 688–698 RSC.
- S. Mishra, M. Krzeszewski, C. A. Pignedoli, P. Ruffieux, R. Fasel and D. T. Gryko, Nat. Commun., 2018, 9, 1714 CrossRef PubMed.
- M. Krzeszewski, Ł. Dobrzycki, A. L. Sobolewski, M. K. Cyrański and D. T. Gryko, Angew. Chem., Int. Ed., 2021, 60, 14998–15005 CrossRef CAS PubMed.
- S. Higashibayashi, P. Pandit, R. Haruki, S.-i. Adachi and R. Kumai, Angew. Chem., Int. Ed., 2016, 55, 10830–10834 CrossRef CAS PubMed.
- N. Deng and G. Zhang, Org. Lett., 2019, 21, 5248–5251 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- L. W. S. H. Vosko and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- P. Besalú-Sala, A. A. Voityuk, J. M. Luis and M. Solà, Phys. Chem. Chem. Phys., 2021, 23, 5376–5384 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- P. O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P. Bultinck, C. V. Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- G. Frenking and F. M. Bickelhaupt, The EDA Perspective of Chemical Bonding, in The Chemical Bond, ed. G. Frenking and S. Shaik, Wiley, Weinheim, 2014, pp. 121–157 Search PubMed.
- ADF 2018, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. A. Keith, AIMAll, Version 14.06.21, TK Gristmill Software, Overland Park, KS, 2014 Search PubMed.
- G. A. Zhurko, Chemcraft 1.80 (build 523b) – graphical program for visualization of quantum chemistry computations, https://chemcraftprog.com Search PubMed.
- S. Mizyed, P. E. Georghiou, M. Bancu, B. Cuadra, A. K. Rai, P. Cheng and L. T. Scott, J. Am. Chem. Soc., 2001, 123, 12770–12774 CrossRef CAS PubMed.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Dalton Trans., 2021, 50, 16214–16222 RSC.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- M. Izquierdo, B. Platzer, A. J. Stasyuk, O. A. Stasyuk, A. A. Voityuk, S. Cuesta, M. Solà, D. M. Guldi and N. Martin, Angew. Chem., Int. Ed., 2019, 131, 7006–7011 CrossRef.
- A. Klamt, J. Phys. Chem., 1996, 100, 3349–3353 CrossRef CAS.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem.–Eur. J., 2019, 25, 2577–2585 CrossRef CAS PubMed.
- O. A. Stasyuk, A. J. Stasyuk, M. Solà and A. A. Voityuk, Phys. Chem. Chem. Phys., 2021, 23, 2126–2133 RSC.
- J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358–4368 CrossRef CAS.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem. Commun., 2020, 56, 12624–12627 RSC.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, J. Mater. Chem. C, 2021, 9, 9436–9445 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2na00150k |
| This journal is © The Royal Society of Chemistry 2022 |