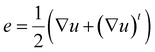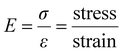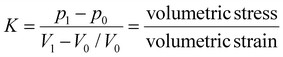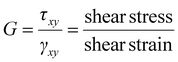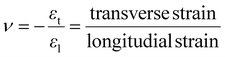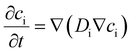Open Access Article
Open Access ArticleReview of foundational concepts and emerging directions in metamaterial research: design, phenomena, and applications
Jade E.
Holliman
Jr
 ,
H. Todd
Schaef
,
H. Todd
Schaef
 ,
B. Peter
McGrail
,
B. Peter
McGrail
 and
Quin R. S.
Miller
and
Quin R. S.
Miller
 *
*
Pacific Northwest National Laboratory, Richland, Washington 99354, USA. E-mail: quinrs.miller@pnnl.gov
First published on 8th November 2022
Abstract
In the past two decades, artificial structures known as metamaterials have been found to exhibit extraordinary material properties that enable the unprecedented manipulation of electromagnetic waves, elastic waves, molecules, and particles. Phenomena such as negative refraction, bandgaps, near perfect wave absorption, wave focusing, negative Poisson's ratio, negative thermal conductivity, etc., all are possible with these materials. Metamaterials were originally theorized and fabricated in electrodynamics, but research into their applications has expanded into acoustics, thermodynamics, seismology, classical mechanics, and mass transport. In this Research Update we summarize the history, current state of progress, and emerging directions of metamaterials by field, focusing the unifying principles at the foundation of each discipline. We discuss the different designs and mechanisms behind metamaterials as well as the governing equations and effective material parameters for each field. Also, current and potential applications for metamaterials are discussed. Finally, we provide an outlook on future progress in the emerging field of metamaterials.
I. Introduction
Metamaterials are artificial materials composed of unit cells that work collectively to produce unusual, unique physical properties not found in natural materials or traditional composite materials. In turn, these properties enable metamaterials to manipulate propagating waves as well as the transport of matter, thus opening the door to a world of new devices with extraordinary abilities and potential applications. Over the years several definitions of metamaterials have been provided in literature, ranging from broad to narrow. The broader view is that a metamaterial is composed of artificial unit cells or atoms that act as one to produce properties not seen in natural materials.1–3 More narrow definitions include but are not limited to ones that emphasize that effective material parameters are present4 or that classify metamaterials based on mathematical properties.5 Generally, the unit cells are arranged in a periodic array that is a key component to most metamaterials; however, this is not a requirement for all metamaterials. Depending on the operating wavelength, metamaterials can be constructed to be as small as nanoscale, with units of atomic lattices, to as large as meter-scale with units composed of strategically placed resonators. Over the past two decades many advancements have been made in the metamaterial field, but the idea was originally conceived in 1967 by physicist Victor Veselago.6 Veselago wondered what if the electromagnetic parameters electric permittivity (ε) and magnetic permeability (μ) in Maxwell's equations were simultaneously negative. He then realized that one would still get a propagating wave, however, it would be backwards meaning it has antiparallel wave vector and Poynting vectors.7 Natural material with these parameters does not exist so Veselago further hypothesized possibilities for materials having such parameters. Veselago called these materials “left-handed substances” because when ε and μ are simultaneously negative, electric field vector E, magnetic field vector H, and wave vector k form a left-handed set of vectors. They are also known as double negative (DNG) materials. He proposed that when a material has simultaneous negative ε and μ, an electromagnetic wave incident on the material will exhibit negative phase velocity and the material will have a negative index of refraction, a reversal of Snell's law. He also proposed that the Doppler effect and Cherenkov radiation would be reversed. In the late 1990s J. B. Pendry and colleagues began preliminary work in the steps to realizing this left-handed material. Pendry et al.8 theorized and computationally verified a cubic lattice structure made a of extremely thin wires capable of effective plasma frequency in the GHz regime with ε of negative one Experimental verification of such a structure came soon after.9 Pendry et al.10 then achieved negative permeability using very thin, periodically arranged nonmagnetic conducting sheets that formed cylindrical microstructures known as split ring resonators (SRRs). From these discoveries, D. R. Smith et al.11 created a composite material consisting of periodically placed thin wires and SRRs that exhibited simultaneous negative permittivity and permeability. A negative index of refraction was experimentally proven at microwave frequencies the next year by R. A Shelby et al.,12 just as Veselago predicted.Metamaterials are not the only artificial materials created to manipulate wave propagation. Photonic crystals (PTCs),13,14 artificial crystals comprised of periodically varying dielectric lattice structures with high index contrast, can manipulate electromagnetic waves and create band gaps. The idea of PTCs originates from two separate papers published in 1987 by Eli Yablonovitch15 and Sajeev John.16 They proposed material designs that affect photons in the same way semiconductor crystals affect electrons and create an electromagnetic bandgap. Although their approaches were different in that Yablonovitch intended to control spontaneous emission while John wanted to create strong photon localization, both researchers wanted to find the photonic bandgap. PTCs can behave as metamaterials17 by exhibiting effective propagation properties18,19 or possessing effective parameters20,21 but, they are generally classified separately. There is one key difference that sets them apart; PTCs and other artificial crystals (i.e., phononic crystals [PNCs]22,23 and platonic crystals [PLTCs]24) can only manipulate waves that are of comparable size to their lattice constant, which typically results in a lattice constant about half the size of the operating wavelength. However, metamaterials can manipulate waves much larger than their lattice constant, giving metamaterials a much wider range of application. Metamaterials tend to employ geometry and resonance, among other mechanisms, to help achieve their novel properties. For example, electromagnetic metamaterials (EMs) often use magnetic resonance25–28 while a class of metamaterials known as hyperbolic metamaterials29–31 utilize high anisotropy instead of resonance.
Metamaterial research began in the electromagnetic field but has expanded to cover many physical domains (i.e., acoustics, thermodynamics, classical mechanics, seismology, and mass transport). Following the success of EMs researchers wondered if the metamaterial concept could be applied to other waves, leading to the first acoustic metamaterial in 2000.32 Several years later coordinate invariant mathematical methods for creating EMs were developed opening the door for other physical domains possessing coordinate invariant governing equations. This realization lead to thermal metamaterials in 2008,33,34 seismic metamaterials in 2012,35,36 and mass transport metamaterials in 2016.37,38 Mechanical metamaterials do not have as clear of an origin, but materials classified as mechanical metamaterials today have been around for many years.39,40 Due to the vast amount of information on metamaterials, we provide review articles for each category, excluding mass transport. In this research update, we identify the established and emerging metamaterial fields. We discuss the different designs and mechanisms behind metamaterials as well as the governing equations and effective material parameters in each field. We will discuss the many interesting phenomena that occur such as negative refraction, bandgaps, wave attenuation, wave absorption, wave focusing, negative Poisson's ratio, negative stiffness, etc. Over the past two decades, the metamaterial field has grown significantly so we divide it into six fundamental categories: (1) electromagnetic, (2) acoustic, (3) thermal, (4) seismic, (5) mechanical, and (6) mass transport. Fig. 1 shows these six categories in a circular diagram that is read from the center outward. The center of the circle contains effective parameters that help produce the physical phenomena in the second, middle section. The third, outer section shows current and potential applications. The parameters and phenomena with blended colors are shared between two or more categories. Furthermore, this review summarizes the current progress and highlights existing work in each area.
II. Electromagnetic metamaterials
EMs operate at several different frequencies depending on the operating wavelength and target application. Thus, EMs are comprised of several types of metamaterials that apply to specific wavelengths including radio waves,41 microwaves,42 terahertz,43,44 infrared,45 and visible light (i.e., photonic metamaterials).46,47 EMs are made possible through the manipulation of Maxwell's equations (Table 1). The equations describe how electric and magnetic fields propagate and interact with one another and with different mediums; therefore, being able to manipulate these equations subsequently allows electromagnetic waves also to be manipulated. Two fundamental parameters within these equations determine the electromagnetic properties of a medium: (1) electric permittivity (ε) and (2) magnetic permeability (μ). These properties are the effective parameters of EMs and give rise to their unique properties. Most materials have positive permittivity and permeability, a few have negative permittivity and positive permeability or vice versa, but no natural material has negative permittivity and permeability simultaneously. As theorized and later proven, a material that possesses negative permittivity and permeability simultaneously has a negative index of refraction. In nature, all mediums have a positive index of refraction in which incident electromagnetic waves are refracted at a positive angle to the normal. A negative index of refraction means that incident waves are refracted at a negative angle to the normal, in other words, on the same side of the normal as the incident wave. These materials are known as negative index materials (NIMs) and can serve as metamaterials by themselves or can be combined with other materials to form a metamaterial. In 2000, Pendry et al.48 gave practical use to NIMs by proposing that a slab of NIM can be a perfect lens that can produce near-field subwavelength images beyond the diffraction to which traditional optical lenses are limited. The diffraction limit does not allow details that are smaller than half the wavelength of light to be resolved. These extremely fine details are carried by evanescent waves that exponentially decay in space. However, in theory, a perfect lens made of a NIM can amplify evanescent waves and focus them with the propagating waves, creating an image with greater detail than one from an optical lens. A schematic drawing of the perfect lens is shown in Fig. 2. The perfect lens concept was proven a few years later49,50; however, evanescent waves were observed to decay again at a certain material thickness, calling for improved lens designs. Also, these lenses are referred to as superlenses and not perfect lenses because of the inherent energy loss associated with NIMs.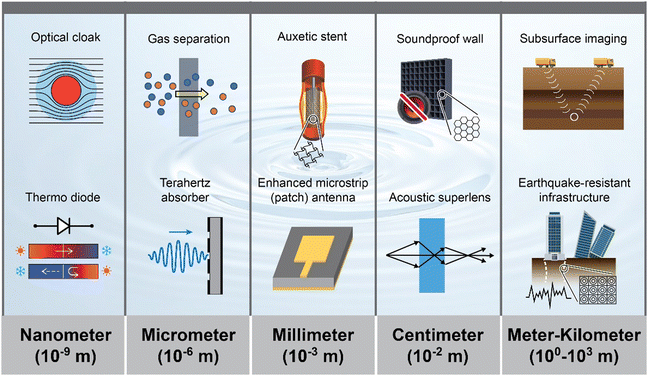 | ||
| Fig. 2 Examples of different characteristic length scales for metamaterial phenomena and applications. Metamaterials are fabricated in varying sizes depending on the operating wavelength and their intended function. Optical cloaks51,52 and thermal diodes53,54 are constructed on a nanometer scale to manipulate particles such as photons and phonons. Gas separation membranes37,55 and terahertz absorbers56,57 operate on a micrometer scale to manipulate molecules and high frequency terahertz waves. Auxetic stents58 and microstrip (patch) antennas59,60 are constructed with millimeter dimensions to manipulate mechanical motion and electromagnetic waves. The soundproof wall61,62 and acoustic superlens63,64 have periodic structures on the centimeter scale to manipulate sound waves. Subsurface imaging65 and earthquake-resistant infrastructure66,67 are constructed on the meter to kilometer scale to manipulate seismic waves. | ||
Superlenses have since been experimentally demonstrated at optical,68,69 microwave,70 and infrared frequencies71–74 with different designs. These lenses are capable of imaging as small as 60 nm, but high energy losses still significantly reduce their efficiency. Because of the design of the slab of NIM superlens, it is limited to near-field applications. To bring the subwavelength image into the far-field, far-field superlenses have been proposed and experimentally achieved.75–77 The far-field lens enhances and then converts evanescent waves into propagating waves, thus allowing the details they carry to be seen in the far-field. Hyperlenses in the far-field78–81 also are capable of subwavelength imaging. A hyperlens is an alternative to a superlens that is anisotropic with hyperbolic dispersion. Lenses82–84 also can be created from the transformation method discussed below. More information on the physics and types of metamaterial lenses is given in the reviews.85,86
Perhaps more interesting than a lens with subwavelength capability is the electromagnetic cloak. An electromagnetic cloak redirects incident electromagnetic waves around an object and recombines them on the other side in the same direction they entered, as if the object is not there (Fig. 2 and 3a). At optical frequencies, this is perceived as invisibility to an observer. Such a device was theoretically conceived using coordinate transformations by U. Leonhardt87 and Pendry et al.88 Maxwell's equations are invariant under coordinate transformation meaning the equations remain true after being transformed to another coordinate system. This is the foundation of the transformation method known as transformation optics89 for light waves. This method began in optics as a strategy to create EMs that allows any deformation of an electromagnetic field to be physically created with the corresponding spatial distribution of material based on the coordinate transformation. The resulting material usually is highly anisotropic, spatially complex, and has varying indices of refraction, which makes them extremely hard to fabricate. A microwave cloak consisting of SRRs is one of the earliest experimentally achieved cloaks.90 The cloak is created by squeezing space from an arbitrary volume into an annular shell leaving an opening in the center. The shell is the transformed space made to redirect the incident light and surrounds the object being concealed. A cloak also can be created by squeezing the space into either a line91 or a sheet.92,93 Based on the coordinate transformation, required electromagnetic properties are determined, and the cloak is created. Optical cloaks able to cloak objects on the micrometer scale have been experimentally achieved using transformation optics.51,52,94 Electromagnetic cloaks have come a long way but require more research for practical applications. In addition to transformation optics, there are other methods for creating cloaks and EMs in general. Many involve implementing metasurfaces95–97 that do not rely on the bulk constitutive properties of a composite material. A metasurface is an extremely thin material, smaller than the wavelength, made up of periodic units capable of manipulating wavefronts. A popular design technique known as inverse design98–100 aims to achieve optimal metamaterial structure based on the desired characteristics. This is done using numerical optimizations (i.e., shape optimization, topology optimization, and genetic algorithms) and numerical analyses (i.e., finite element method and finite-difference time-domain) which solve Maxwell's equations providing the parameters required to fabricate the desired metamaterial and provide computational simulations of the resulting metamaterial. Antennas transmit and receive electromagnetic waves and have been used in televisions, telephones, radios, etc., for years. The range and efficiency of antennas always have been limited; however, with metamaterials, their capability and performance can be improved. Metamaterial antennas are comprised solely of metamaterials, or metamaterial components and techniques are implemented (Fig. 2). In general, metamaterial antennas can be broken down into four categories: (1) metamaterial loaded, (2) composite right/left handed (CRLH)-based, (3) metasurface loaded, and (4) metamaterial inspired. Metamaterial loading involves loading the antenna with effective media that interact with the antenna to produce the desired metamaterial properties. Effective media include resonators, PTCs, negative permittivity/permeability material, or extreme permittivity/permeability material. CRLH-based antennas implement left- and right-handed material properties depending on the frequency. They are created through transmission line and resonator methods and often use a CRLH unit cell to produce the desired properties. Metasurface loading involves loading the antenna with metasurfaces with properties such as bandgaps, high impedance surfaces, and reactive impedance surfaces.101–103 Metamaterial inspired antennas use one or more than two unit cells arranged in a particular array to produce the desired metamaterial properties.59,104,105 These unit cells can be SSRs or can be engraved into the actual antenna surface.60 All design methods have been experimentally proven to miniaturize antennas and improve gain and bandwidth. Electromagnetic wave absorption and sensing is another important application of EMs. Absorbers can be used for radar echo reduction, reducing unwanted radiation in antennas, protecting people from harmful radiation in medical devices, and reducing any other electromagnetic interference.106 There are two types of absorbers: (1) resonant and (2) broadband. Resonant absorbers use resonance to interact with the incident waves at a certain frequency, while broadband absorbers have properties that are frequency independent, allowing them to operate over a wider bandwidth. Perfect absorption that allows no scattering or reflection can be obtained through metamaterial absorbers. Landy et al.107 developed a perfect electromagnetic wave absorber in the microwave frequency range that was able to absorb nearly 100% of the incident wave. Soon metamaterial absorbers were expanded to other frequency ranges including terahertz,56,57,108 infrared,109,110 and visible light.111 More recently, W. Jiang et al.112 used three-dimensional printing to develop a metamaterial absorber that is capable of more than 90% absorption in the radio wave frequency. Metamaterial sensors113 mainly are used for material characterization114,115 and non-destructive evaluation.116 Generally, sensors must absorb some of the incident waves to detect them, so metamaterial absorbers and sensors are often one in the same.117,118 They can detect extremely small chemical and biological attributes or changes as well as pressure changes. They commonly are applied in microwave and terahertz frequencies119 but also have been tested for other frequencies.
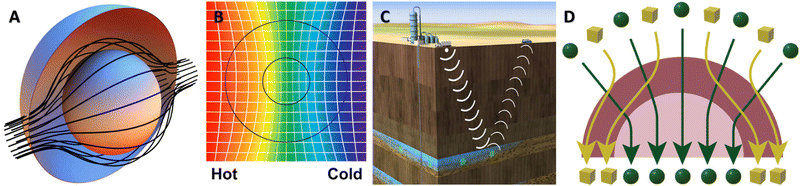 | ||
| Fig. 3 (A) Optical cloak: a three-dimensional view of the optical cloak. The light rays are guided within the annulus of the cloaking material contained within R1 < r < R2 and emerge from the opposite side uninterrupted from their original course. (B) Thermal concentrator: a constant heat source is applied to the left of the concentrator. The mesh formed by streamlines of thermal flux (vertical) and isothermal values (horizontal) illustrates the deformation of the transformed thermal space which is squeezed into the central disc. (C) Seismic metamaterial sensing: Enhanced monitoring of subsurface fluids and structures (e.g., fractures) after injection of contrast agents that form periodic meta-structures. (D) Mass separation: Anisotropic membrane consisting of an isotropic cylindrical core of radius R1 covered by an anisotropic cylindrical shell with internal radius R1 and external radius R2. The two molecules permeate in the membrane where one compound is directed around the core and the other compound is directed towards the core. Graphics inspired by Pendry et al.88 (A), Guenneau et al.120 (B), Miller et al.65 (C), and Restrepo-Florez and Maldovan55 (D). Panel (A) adapted from J. B. Pendry, D. Schurig and D. R. Smith, Controlling Electromagnetic Fields, Science, 2006, 312(5781), 1780–1782, reprinted with permission from AAAS. Panel (D) adapted from J.-M. Restrepo-Florez and M. Maldovan, Breaking separation limits in membrane technology, J. Membr. Sci., 2018, 566, 301–306, reprinted with permission from Elsevier. | ||
All the metamaterials mentioned so far are classified as passive and static meaning that once fabricated, the metamaterial cannot be altered and possesses a narrow field of operation. Active metamaterials121 are a class of metamaterials with functionalities that can be actively tuned or switched. They can be tuned in real time to fit a changing environment and respond accordingly. There are two general classes of active metamaterials: (1) mechanical reconfiguration materials and (2) active materials. Mechanical reconfiguration refers to altering structural qualities such as lattice constants, resonator shapes, or spatial arrangements using external stimuli that change the response of the metamaterial. Commonly used external stimuli include heat,122,123 electricity,124 and light.125–127 Alternatively, active materials can be implemented into the structure of metamaterials to create an active metamaterial. Active materials are sensitive to external stimuli, thus enabling their active control. Active materials include devices like varactor diodes,128–130 semiconductors,131,132 liquid crystals,133,134 phase change materials,135,136etc. Active metamaterials are seen across physical domains so others will be discussed in their respective sections.
III. Acoustic metamaterials
Advances in metamaterials caused researchers to wonder if the theory of EMs can be applied to other fields. Soon enough, these methods were carried over to the acoustic field and applied to sound waves. This started a whole new class of metamaterials called acoustic metamaterials (AMs).1,137 Like EMs, AMs have effective parameters that give rise to their extreme properties. Those properties are the bulk modulus (κ) and the mass density (ρ), which are mathematically analogous to permittivity and permeability, respectively. Negative bulk modulus and/or negative mass density gives rise to negative refraction and other unnatural effects. The acoustic wave equation (Table 1) is the governing equation for acoustic wave propagation and contains the effective parameters. Negative refraction can be used to create an acoustic band gap like the electromagnetic band gap seen in EMs. PNCs also were created to manipulate sound waves in the same way that PTCs manipulate electromagnetic waves. Phonons are units of vibrational energy analogous to photons. The first PNCs were introduced in the early 1990s by Sigalas and Economou138 and Kushwaha et al.139 Phononic crystals achieve sound wave control through Bragg scattering while many AMs use a mechanism known as local resonance to control wave propagation. Local resonance refers to wave coupling that occurs when resonators are arranged periodically with oscillators or other resonators. In addition, Helmholtz resonance, which also is used in AMs, refers to the resonance phenomenon of air in a cavity. Acoustic metamaterials and PNCs are similar, but the range of frequencies effected by PNCs is limited by anisotropy and the lattice constant of the crystal while the range of AMs is unrestricted. AMs can manipulate waves of a much larger wavelength than their lattice size, allowing a wider range of application. The limitation of PNCs is due to their use of Bragg scattering that only produces a band gap of the same order as the lattice constant.Acoustic metamaterials originally focused on sound attenuation, which was achieved by Z. Y. Liu et al.32 in 2000. Their AM was sonic crystals comprised of centimeter-sized lead spheres coated in rubber and arranged in a square lattice with a lattice constant of 1.5 cm. This device uses local resonance to produce negative elastic constants, subsequently causing attenuation. In addition to attenuation AMs are capable of cloaking, subwavelength imaging, absorption, and sensing and are engineered at macroscale and microscale levels. Macroscale AMs involve periodic structures or transformation acoustics while microscale AMs involve the manipulation of phonons. Acoustic attenuation often is achieved through mechanisms such as Bragg scattering and local resonance. Membrane-type AMs have been shown to implement these mechanisms and achieve high attenuation for low-frequency sound (<500 Hz).61,62,140,141 In addition, there are groups working on active acoustic metamaterials with some promising applications for sound attenuation.142,143 For example, Xia et al.142 theorized a thermally tunable acoustic metamaterial for underwater sound blocking application.
The function of the acoustic cloak is similar to that of electromagnetic cloak, but instead of visual invisibility, audible invisibility is achieved. Using transformation acoustics, it was theorized in two dimensions144 and then in three dimensions145 due to the realization of the form-invariant linear acoustic equations. Many cloaks implement the traditional transformation method in which there is an annular shell structure that protects objects within the shell from outside sound waves by redirecting the waves around the shell. The waves then continue along their original propagation path effectively exhibiting acoustic invisibility. Many groups have fabricated functioning acoustic cloaks146–149; however, practical applications have yet to be realized because of the cloak's ability to perform only at small scale and the fabricating the cloaks is challenging because of their properties. Metasurface acoustic cloaks150–152 are a promising alternative to transformation-based cloaks. These cloaks use very little material with less extreme properties. The acoustic lens (Fig. 2), like the electromagnetic lens, is used for subwavelength imaging beyond the diffraction limit. Near-field superlenses63,64,153 amplify evanescent waves while far-field hyperlenses154,155 convert evanescent waves to propagating waves. Other far-field lenses that do not use high anisotropy have also been designed.156,157 Acoustic lenses show great promise for applications such as medical imaging or building structure imaging. For example, Zhu et al. developed a superlens with holes in its structure to amplify evanescent waves in the near-field through resonant tunneling.158 Such a lens could be used to improve ultrasonic imaging or detect cracks in building components. Sound absorption AMs are another popular use. Acoustic metamaterial absorbers have overlapping application with attenuation AMs; however, they are fundamentally different. Absorbers use resonators that couple with incoming waves, thus effectively trapping them with little to no reflection or transmission. They can absorb both low- and high-frequency waves depending on the design. Many of these materials are capable of >90% absorption making them excellent candidates for sound insulation or sound proofing159–163 (Fig. 2). Acoustic metamaterial sensors are used for pressure and sound sensing164–166 and non-destructive evaluation.167
IV. Thermal metamaterials
Thermal metamaterials168,169 (TMs) manipulate the flow of heat. Heat transfer (i.e., conduction, convection, and radiation) is less ordered than wave propagation so achieving control is more difficult, which in turn makes the fabrication of TMs difficult. Heat naturally travels from higher temperatures to lower temperatures unless work is done on the system to reverse this process. This is a diffusive process that is different from wave propagation so coordinate invariant heat diffusion equations are required to create TMs with the transformation method. The effective parameters for TMs are thermal conductivity (κ), mass density (ρ), and specific heat capacity (cρ). In 2008, Fan et al.34 and Chen et al.33 discovered form-invariant thermal conduction equations (Table 1) and achieved control of heat flow by using extreme thermal conductivity values not seen in natural materials. All natural materials have fixed, positive thermal conductivities so achieving extreme or negative thermal conductivity gives rise to interesting heat flow phenomena. Fan et al. used transformation thermodynamics to develop a material capable of transferring heat from a lower temperature to a higher temperature in a process known as “apparent negative thermal conductivity.” Soon after, Chen et al. proved that transformation thermodynamics still works in curvilinear anisotropic backgrounds and developed a cloaking device. Fan and Chen only worked with steady-state systems, but most heat phenomena involve transient systems that switch between unsteady and steady states. In 2012, Guenneau et al.120 developed a transformation method, known as “transformation thermodynamics,” for steady-state and transient systems that was later experimentally verified by Narayana and Sato,170 Narayana et al.,171 and Schittny et al.120,172 In addition to TMs, PNCs also can be used to manipulate heat flow.22,23 Remember that phonons are units of vibrational energy, and vibrations produce sound as well as heat. This relationship between vibrations, sound, and heat allows PNCs to be used in both acoustics and thermodynamics. Similar to AMs, TMs can be constructed on the macro- or microscales depending on the method and target application. At the microscale, heat is carried by phonons that oscillate at THz frequencies, so they behave more like particles than waves. This makes it difficult to control thermal phonons with PNCs.Despite fabrication challenges, many groups have created transformation thermodynamics-based devices such as thermal cloaks, concentrators,173 rotators,174 and camouflage.175,176 A thermal cloak keeps its cloaked region at a constant temperature while under a thermal gradient, thereby appearing to be thermally invisible. A thermal concentrator focuses thermal flux from a finite volume to a smaller one (Fig. 3B). A thermal rotator can reverse the direction of heat flux within a region. Thermal camouflage has a similar result to the cloak but, instead, mimics the thermal properties of another object, effectively making the camouflaged object look like another object. Practical applications for devices like these are needed, but some groups have proposed good potential applications. Dede et al.177 proposed using thermal cloaks, concentrators, and rotators in printed circuit boards for heat control in electronics. Also, active versions of these devices that are sensitive to voltage178 and light179 stimuli are being investigated. Most devices, such as those mentioned above, are meant to control thermal conduction due to the use of form-invariant conduction equations for transformation thermodynamics. Metamaterials for thermal convection180–182 and radiation183,184 control currently are being studied. TMs also are being studied and fabricated on the microscopic level through phonon or photon manipulation. Thermal diodes53,54,185,186 (Fig. 2), thermal transistors,187 thermal logic gates,188–190 and thermal memories191 are all possible through phonon and photon manipulation.
V. Seismic metamaterials
Seismic metamaterials192,193 (SMs) have gained much attention in the past several years as an emerging metamaterial field. Elastic metamaterials always have been of interest in the acoustic and seismic fields, but SMs are tailored to low-frequency elastic waves. Seismic metamaterials manipulate the propagation of seismic waves through deflection, attenuation, and absorption. The main goals of SMs are wave attenuation and wave redirection to protect buildings and other structures from seismic waves produced by earthquakes. The effective parameters giving SMs their unique properties are mass density (ρ) and the Lamé parameters (λ and μ) that when negative, give rise to negative refraction. Local resonance and Bragg scattering are the two main mechanisms for inducing negative or extreme properties in SMs. Seismic wave propagation is governed by elastodynamic equations called the Navier equations. In 2006, Milton et al.35 investigated form-invariant elastodynamic equations and discovered that the standard Navier equations are not coordinate invariant in their general form. Instead, they must be altered to Willis equations to be form invariant (Table 1). However, at times, the Navier equations do hold under coordinate transformation,194 and other sets of elastodynamic equations have been shown to be coordinate invariant.195 Because of the difficulty of using coordinate-invariant equations, many groups implement local resonance and Bragg scattering through periodic arrangement of effective parameter materials. In 2012, Farhat et al.36 proposed a cylindrical elastic cloak for elastic waves propagating through thin plates that through numerical simulation, successfully controlled propagation of the waves. This led to experiments on seismic waves carried out by Brule et al.196,197 in 2014 and 2017 in which they successfully demonstrated that periodically structured soils are able to attenuate seismic waves through inclusions, or holes, in the soil. In addition to SMs, PLTCs24 and certain AMs are used for seismic wave manipulation. PLTCs are analogous to PTCs and PNCs but implement a periodic structure of thin elastic plates that manipulate vibrations. However, PLTCs are in the early stages of research so they are not as widely used as PTCs or PNCs.Seismic metamaterials have been classified in different ways, usually based on characteristics such as wave cloaking, attenuation, and deflection. Because of the size of seismic waves (tens to hundreds of meters), many SMs are physically and spatially large enough to be able to manipulate seismic waves. Other metamaterials have small lattice constants while SMs tend to have lattice constants on the meter scale. In general, we will be classifying SMs into two main groups192: (1) outer shield metamaterials and (2) foundation metamaterials. Outer shields refer to the metamaterials that interact with seismic waves outside of the structure they are meant to protect, ultimately preventing the seismic waves from reaching the building. Foundation metamaterials implement metamaterial designs or devices into the foundations of buildings to combat seismic waves (Fig. 2). Seismic soil metamaterials are an example of outer shields that implement periodic design based on transformation methods. Brule et al.196–198 developed seismic soils consisting of cylindrical voids and rigid inclusions that interfere with seismic wave propagation. Voids and inclusions (i.e., holes) dug into the ground in a periodic, in some cases non-periodic, array cause seismic bandgaps, complete reflection, wave-path control, or attenuation by energy dissipation depending on their arrangement in the soil. Resonators buried in the soil are used to reduce the response of the soil to seismic waves. Such resonators consist of a mass, a spring, and a damper that are tuned to the structural frequency of the building. When excited, the damper resonates out of phase with the structural motion of the building, thus dissipating the energy caused by seismic waves.198 The shape, size, and position of the resonators are directly linked to bandwidth and attenuation efficiency of the bandgaps so these qualities can vary. Some have suggested burying cross-shaped, locally resonant cylinders,199 some have tried resonant cylinders with differing eigenfrequencies,200 and others have tested cubic arrays of resonant spheres.201 Above-surface resonators are resonators placed on the ground around a designated structure to interfere with incoming seismic waves. These resonators can be artificial (i.e., like the seismic metawedge202) or natural (i.e. such as trees in a forest203,204). The metawedge attenuates the wave as it passes through or converts it to a much less harmful bulk shear wave. Trees can attenuate seismic waves by creating bandgaps through local resonance. Metamaterial foundations are the other classification of SMs in which the foundation of the building, or parts of it, is a metamaterial or has a metamaterial design. Many designs consist of periodic, layered sections of material like the one developed by Xiang et al.,205 which implement layers of concrete and rubber and Cheng and Shi206 which uses steel, concrete, and rubber. Other groups67,207 have tested periodic plate foundations to successfully produce seismic bandgaps. Auxetic materials, discussed in further detail in the next section, can be buried in the soil underneath a building to act as a part of the foundation and create bandgaps.208 Chiral materials (i.e., materials that cannot be superimposed upon themselves) also can be used to mitigate seismic wave activity. Carta et al.209 proposed using gyro-elastic beams arranged in a chiral design to reduce the vibrations on a building and the concept successfully created bandgaps. Implementing metamaterials into the foundation is a promising form of SM that protects a structure from incoming waves, thus reducing the effects of displacement and stress.
In addition to the civil engineering applications of SMs, there are also long-range subsurface sensing applications (Fig. 2 and 3C). Porous and/or flexible metal–organic framework (MOF) composites and nanoparticles are acoustic metamaterials with tunable sound adsorption and resonances.210 Injectable MOF suspensions have been shown to alter the distinct elastic and anelastic properties of rocks, resulting in decreased seismic wave velocities and amplitudes.65,211 The ability to disperse the contrast agent nanoparticles212,213 throughout a fluid-rock system allows for the possibility of imposing a 2D or 3D km-scale subsurface meta-structure (Fig. 3C). Overall, these attributes make injectable seismic contrast agents a potentially transformational technology for enabling geophysical sensing and lends new perspective to the burgeoning field of seismic metamaterials.193,214
VI. Mechanical metamaterials
Mechanical metamaterials2 (MMs) are another emerging field that in recent years, has received much attention because of their potential uses and ability to be implemented in other fields like AMs and SMs. Mechanical metamaterials are periodic, sometimes aperiodic, structures that use mechanical motion, energy, deformations, and stresses in unconventional ways to give these metamaterials extraordinary moveability. Initially MMs exploited geometry to achieve negative or extreme effective parameters, but recently, designs have extended beyond this. The effective parameters of MMs are mass density (ρ) and the elastic moduli (i.e., Young's modulus [E], bulk modulus [K], shear modulus [G], and Poisson's ratio [ν]) (Table 1). When these parameters are made negative or extreme the metamaterial possessing these qualities can exhibit extraordinary mechanical movement. Individual unit cells in MMs move together and/or in response to one another to produce behavior not seen in the constituent materials. A prime example is an auxetic MM. Auxetic materials possess a negative Poisson's ratio, giving them the ability to expand or contract in all directions when force is applied.39,215 Normally when a material is pulled or stretched in one direction it will become thinner in the perpendicular directions exhibiting a positive Poisson's ratio; however, this is not the case for auxetic materials that expand radially when pulled transversely. Chiral, extremal, and pentamode metamaterials are more examples of MMs. Chirality is useful for not only elastic wave manipulation but also for mechanical deformations. MMs capable of converting uniaxial compression into torsion216 or inducing their own global rotational motion217 are possible through chirality. Extremal metamaterials can resist one specific deformation. For example, an extremal metamaterial can greatly resist isotropic compression but will buckle under shear compression. Pentamode metamaterials,218 or metafluids, possess fluid-like properties. They are known as pentamode metamaterials because they possess five very small eigenvalues making them extremely compliant to deformation in five of six primary directions. This results in a small shear modulus and large bulk modulus when compared to one another. A large bulk modulus allows the volume of the metamaterial to remain the same under deformation that can be interpreted as a Poisson's ratio of 0.5. A small shear modulus gives the metamaterial the ability to flow like water. These elastic moduli give pentamode materials their fluid-like properties. Most pentamode metamaterials use the atomic lattice developed by Milton and Cherkaev40 in which two conical beams connected at their base are arranged in a diamond lattice structure. This design219 and others220–224 have been fabricated and tested yet all still are only approximations of an ideal pentamode metamaterial. Pentamode metamaterials can be used to manipulate elastic waves in acoustics and seismology. They also are good candidates for additive manufacturing224,225 of metamaterials that require a complex distribution of mechanical properties.Bertoldi et al.2 breaks MMs down into three categories: (1) mechanism-based, (2) instability-based, and (3) topological metamaterials. Mechanism-based MMs are the most straightforward. A mechanism is a group of moving parts connected by hinges or some other type of linkage that perform one motion or action together. Origami and kirigami principles are commonly used in mechanism-based MMs. Origami involves precise folding that allows materials to contract, expand, and bend without breaking. Kuribayashi et al.58 developed flexible medical stents (Fig. 2) using this technique that can expand and contract when needed. Two-dimensional metasheets also have been fabricated.226 Kirigami involves making precise cuts that allow the shape and elastic properties of the material to be controlled.227 Isobe et al.228 fabricated stretchable sheets from stiff materials. Instability-based MMs use elastic instabilities and large deformations to create strong nonlinear relationships between the stresses and strains of the MM. There are many buckling-based MMs that rely on elastic instability. A simple example is an elastomeric sheet of material possessing a square array of holes that allows the sheet to compress more than traditional material. The thin pieces of material formed from the addition of holes behave like beams buckling under compression.229 Elastic instability also is used in snapping-based MMs that have units able to snap into certain positions based on the compression or extension of the metamaterial. Topological MMs possess topologically protected properties meaning their geometric properties remain the same though deformations such as stretching, bending, and twisting. Mechanical metamaterials with topologically protected properties have a topological index that is unchanged, which allows the materials to manipulate mechanical wave propagation and absorb energy.
VII. Mass transport metamaterials
Mass transport metamaterials (MTMs) are an emerging field of metamaterials that can manipulate mass flow in diffusion processes. Like TMs, MTMs are designed based on diffusion laws rather than wave propagation laws. In fact, a group of researchers has theorized metamaterials capable of controlling mass or heat flow due to the mathematical similarities of their governing equations.230 Fick's laws dictate mass diffusion and Fick's second law is invariant under coordinate transformation, which is required for using the transformation method (Table 1). For MTMs, the effective parameter is the chemical potential gradient of the system. Classically, the driving force for diffusion is the concentration gradient; however, for MTMs, Restrepo-Flórez and Maldovan37,38,55,231 realized it is chemical potential gradient due to the non-homogeneous nature of metamaterials. Also, MTMs usually are non-homogenous and highly anisotropic due to the spatial distribution of diffusivity required for guided mass flow. However, this area of metamaterials still is mostly unexplored because the fundamentals of mass diffusion are not well understood.Current MTMs aim to control mass flow to assist in separation (Fig. 2) and catalysis processes. Restrepo-Flórez and Maldovan have developed several MTMs capable of concentrating and/or cloaking mass flux. There is no standard coordinate transformation method for mass flow manipulation so multiple metamaterial configurations have been tested. For example, one device is a multilayered structure consisting of concentric rings that separate a binary mixture of oxygen and nitrogen diffusing through a polymeric matrix by cloaking nitrogen and concentrating oxygen.37 Another separation device performs the same task but uses an anisotropic cylindrical membrane consisting of an isotropic core and an anisotropic shell55 (Fig. 3D). Traditionally isotropic membranes are used to separate compounds by permeating one species and rejecting the other, but anisotropic membranes allow both species to permeate while guiding them to different spatial locations.55 However non-homogenous, anisotropic materials are extremely difficult to fabricate and manufacture so layers of homogeneous, isotropic material are used to achieve the desired anisotropic properties. Very few groups are working on MTMs37,38,55,230–237 and even fewer can successfully fabricate them because of the difficulties encountered. Improved coordinate transformation techniques for mass flow control are needed for this field to progress.
VIII. Outlook
Over the past 20 years, significant progress has been made in the design and fabrication of metamaterials. The field has expanded beyond electrodynamics to acoustics, thermodynamics, seismology, mechanics, and mass transport. Phenomena such as negative refraction, bandgaps, near perfect wave absorption, wave focusing, negative Poisson's ratio, negative thermal conductivity, etc., all are possible with these metamaterials. Improvements in metamaterial design, fabrication, and manufacturing are crucial to finding more practical applications. Electromagnetic and acoustic metamaterials are perhaps the most researched and understood materials but require better fabrication and manufacturing methods. Thermal metamaterials require further research on heat transfer and phonons. Real-world scenarios involving heat are more complicated than current TMs are capable of, and phonon transfer still is not quite fully understood. Seismic metamaterials are relatively new metamaterials with the first field experiments occurring in the 2010s. The applications are obvious and abundant for SMs; however, more field testing needs to be done to better understand their effectiveness on seismic waves. Current MMs perform novel functions, but real applications are scarce. MTMs require a better transformation technique to standardize the fabrication and realize the many possible applications for MTMs. This Research Update has thoroughly summarized the history, current state of progress, and emerging directions of metamaterials by field. Practical metamaterial devices and structures will soon be available with continued research in metamaterials.Abbreviations
| AM | Acoustic metamaterial |
| EM | Electromagnetic metamaterial |
| MM | Mechanical metamaterials |
| MTM | Mass transport metamaterials |
| NIM | Negative index materials |
| PTC | Photonic crystal |
| PNC | Phononic crystal |
| PLTC | Platonic crystal |
| SM | Seismic metamaterial |
| TM | Thermal metamaterial |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based on work supported by the U.S. Department of Energy Office of Fossil Energy at PNNL through the National Energy Technology Laboratory, Morgantown, West Virginia. We thank Darin Damiani (DOE HQ) for support. JEH was partially supported by the U.S. Department of Energy National Nuclear Security Administration MSIIP program. HTS acknowledges support from the Carbon Utilization and Storage Partnership (CUSP). We thank the Editor and two anonymous reviewers for their thorough and helpful reviews. We especially thank Reviewer 2 for their thoroughness and dedication to helping us improve this manuscript.References
- S. A. Cummer, J. Christensen and A. Alu, Controlling sound with acoustic metamaterials, Nat. Rev. Mater., 2016, 1(3), 16001 CrossRef.
- K. Bertoldi, et al., Flexible mechanical metamaterials, Nat. Rev. Mater., 2017, 2(11), 17066 CrossRef CAS.
- G. Ma and P. Sheng, Acoustic metamaterials: From local resonances to broad horizons, Sci. Adv., 2016, 2(2), e1501595 CrossRef PubMed.
- M. Kadic, et al., 3D metamaterials, Nat. Rev. Phys., 2019, 1(3), 198–210 CrossRef.
- N. Kim, Y.-J. Yoon and J. B. Allen, Generalized metamaterials: Definitions and taxonomy, J. Acoust. Soc. Am., 2016, 139(6), 3412–3418 CrossRef PubMed.
- V. G. Veselago, Electrodynamics of Substances with Simultaneously Negative Values of Sigma and Mu, Soviet Phys. Uspekhi, 1968, 10(4), 509 Search PubMed.
- P. A. Belov, Backward waves and negative refraction in uniaxial dielectrics with negative dielectric permittivity along the anisotropy axis, Microwave Opt. Technol. Lett., 2003, 37(4), 259–263 CrossRef.
- J. B. Pendry, et al., Extremely Low Frequency Plasmons in Metallic Mesostructures, Phys. Rev. Lett., 1996, 76(25), 4773–4776 CrossRef CAS PubMed.
- J. B. Pendry, et al., Low frequency plasmons in thin-wire structures, J. Phys.: Condens. Matter, 1998, 10(22), 4785 Search PubMed.
- J. B. Pendry, et al., Magnetism from conductors and enhanced nonlinear phenomena, IEEE Trans. Microwave Theory Tech., 1999, 47(11), 2075–2084 CrossRef.
- D. R. Smith, et al., Composite Medium with Simultaneously Negative Permeability and Permittivity, Phys. Rev. Lett., 2000, 84(18), 4184–4187 CrossRef CAS PubMed.
- R. A. Shelby, D. R. Smith and S. Schultz, Experimental verification of a negative index of refraction, Science, 2001, 292(5514), 77–79 CrossRef CAS PubMed.
- E. Yablonovitch, Photonic Crystals, J. Mod. Opt., 1994, 41(2), 173–194 CrossRef CAS.
- J. D. Joannopoulos, P. R. Villeneuve and S. Fan, Photonic crystals: putting a new twist on light, Nature, 1997, 386(6621), 143–149 CrossRef CAS.
- E. Yablonovitch, Inhibited Spontaneous Emission in Solid-State Physics and Electronics, Phys. Rev. Lett., 1987, 58(20), 2059–2062 CrossRef CAS PubMed.
- S. John, Strong localization of photons in certain disordered dielectric superlattices, Phys. Rev. Lett., 1987, 58(23), 2486–2489 Search PubMed.
- S. Foteinopoulou, Photonic crystals as metamaterials, Phys. B, 2012, 407(20), 4056–4061 Search PubMed.
- R. Moussa, et al., Negative refraction and superlens behavior in a two-dimensional photonic crystal, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(8), 085106 CrossRef.
- K. Ren, et al., Three-dimensional light focusing in inverse opal photonic crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(11), 115108 Search PubMed.
- V. Yannopapas, Negative refraction in random photonic alloys of polaritonic and plasmonic microspheres, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(3), 035112 Search PubMed.
- W. Park and Q. Wu, Negative effective permeability in metal cluster photonic crystal, Solid State Commun., 2008, 146(5), 221–227 Search PubMed.
- M. Maldovan, Sound and heat revolutions in phononics, Nature, 2013, 503(7475), 209–217 CrossRef CAS PubMed.
- M. I. Hussein, M. J. Leamy and M. Ruzzene, Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook, Appl. Mech. Rev., 2014, 66(4), 040802 Search PubMed.
- R. C. McPhedran, A. B. Movchan and N. V. Movchan, Platonic crystals: Bloch bands, neutrality and defects, Mech. Mater., 2009, 41(4), 356–363 CrossRef.
- C. Enkrich, et al., Magnetic Metamaterials at Telecommunication and Visible Frequencies, Phys. Rev. Lett., 2005, 95(20), 203901 CrossRef CAS PubMed.
- A. K. Sarychev, G. Shvets and V. M. Shalaev, Magnetic plasmon resonance, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73(3), 036609 CrossRef PubMed.
- Z.-G. Dong, et al., Plasmonically induced transparent magnetic resonance in a metallic metamaterial composed of asymmetric double bars, Opt. Express, 2010, 18(17), 18229–18234 CrossRef CAS PubMed.
- J. Zhang, K. F. MacDonald and N. I. Zheludev, Near-infrared trapped mode magnetic resonance in an all-dielectric metamaterial, Opt. Express, 2013, 21(22), 26721–26728 CrossRef PubMed.
- A. Poddubny, et al., Hyperbolic metamaterials, Nat. Photonics, 2013, 7(12), 948–957 CrossRef CAS.
- C. Shen, et al., Broadband acoustic hyperbolic metamaterial, Phys. Rev. Lett., 2015, 115(25), 254301 CrossRef PubMed.
- J. Zhou, et al., Experiment and Theory of the Broadband Absorption by a Tapered Hyperbolic Metamaterial Array, ACS Photonics, 2014, 1(7), 618–624 CrossRef CAS.
- Z. Y. Liu, et al., Locally resonant sonic materials, Science, 2000, 289(5485), 1734–1736 CrossRef CAS PubMed.
- T. Chen, C.-N. Weng and J.-S. Chen, Cloak for curvilinearly anisotropic media in conduction, Appl. Phys. Lett., 2008, 93(11), 114103 CrossRef.
- C. Fan, Y. Gao and J. Huang, Shaped graded materials with an apparent negative thermal conductivity, Appl. Phys. Lett., 2008, 92(25), 251907 Search PubMed.
- G. W. Milton, M. Briane and J. R. Willis, On cloaking for elasticity and physical equations with a transformation invariant form, New J. Phys., 2006, 8(10), 248 Search PubMed.
- M. Farhat, S. Guenneau and S. Enoch, Broadband cloaking of bending waves via homogenization of multiply perforated radially symmetric and isotropic thin elastic plates, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(2), 020301 Search PubMed.
- J. M. Restrepo-Florez and M. Maldovan, Mass Separation by Metamaterials, Sci. Rep., 2016, 6, 21971 CrossRef CAS PubMed.
- J. M. Restrepo-Florez and M. Maldovan, Rational design of mass diffusion metamaterial concentrators based on coordinate transformations, J. Appl. Phys., 2016, 120(8), 084902 CrossRef.
- R. Lakes, Foam structures with a negative Poisson's ratio, Science, 1987, 235(4792), 1038–1040 Search PubMed.
- G. W. Milton and A. V. Cherkaev, Which elasticity tensors are realizable?, 1995 Search PubMed.
- S. Abdullah, G. Xiao and R. E. Amaya, A review on the history and current literature of metamaterials and its applications to antennas & radio frequency identification (RFID) devices, IEEE J. Radio Freq. Identif., 2021, 5(4), 427–445 Search PubMed.
- T. Chen, et al., Microwave metamaterials, Ann. Phys., 2019, 531(8), 1800445 CrossRef.
- J. He, et al., Recent progress and applications of terahertz metamaterials, J. Phys. D: Appl. Phys., 2022, 55(12), 123002 Search PubMed.
- W. Xu, L. Xie and Y. Ying, Mechanisms and applications of terahertz metamaterial sensing: a review, Nanoscale, 2017, 9(37), 13864–13878 RSC.
- S. Ogawa and M. Kimata, Metal-Insulator-Metal-Based Plasmonic Metamaterial Absorbers at Visible and Infrared Wavelengths: A Review, Materials, 2018, 11(3), 458 CrossRef PubMed.
- C. M. Soukoulis and M. Wegener, Past achievements and future challenges in the development of three-dimensional photonic metamaterials, Nat. Photonics, 2011, 5(9), 523–530 Search PubMed.
- Y. Xiong, et al., Microscopies Enabled by Photonic Metamaterials, Sensors, 2022, 22(3), 1086 CrossRef CAS PubMed.
- J. B. Pendry, Negative refraction makes a perfect lens, Phys. Rev. Lett., 2000, 85(18), 3966–3969 CrossRef CAS PubMed.
- Z. Liu, et al., Rapid growth of evanescent wave by a silver superlens, Appl. Phys. Lett., 2003, 83(25), 5184–5186 CrossRef CAS.
- N. Fang, et al., Regenerating evanescent waves from a silver superlens, Opt. Express, 2003, 11(7), 682–687 CrossRef CAS PubMed.
- T. Ergin, et al., Three-Dimensional Invisibility Cloak at Optical Wavelengths, Science, 2010, 328(5976), 337–339 Search PubMed.
- M. Gharghi, et al., A carpet cloak for visible light, Nano Lett., 2011, 11(7), 2825–2828 CrossRef CAS PubMed.
- A. Fiorino, et al., A thermal diode based on nanoscale thermal radiation, ACS Nano, 2018, 12(6), 5774–5779 CrossRef CAS PubMed.
- Z. Chen, et al., A photon thermal diode, Nat. Commun., 2014, 5(1), 1–6 CrossRef.
- J. M. Restrepo-Florez and M. Maldovan, Breaking separation limits in membrane technology, J. Membr. Sci., 2018, 566, 301–306 CrossRef CAS.
- H. Tao, et al., A dual band terahertz metamaterial absorber, J. Phys. D: Appl. Phys., 2010, 43(22), 225102 CrossRef.
- J. Zhu, et al., Ultra-broadband terahertz metamaterial absorber, Appl. Phys. Lett., 2014, 105(2), 021102 CrossRef.
- K. Kuribayashi, et al., Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil, Mater. Sci. Eng., A, 2006, 419(1–2), 131–137 Search PubMed.
- D. Li, et al., A high gain antenna with an optimized metamaterial inspired superstrate, IEEE Trans. Antennas Propag., 2012, 60(12), 6018–6023 Search PubMed.
- L. W. Li, et al., A broadband and high-gain metamaterial microstrip antenna, Appl. Phys. Lett., 2010, 96(16), 164101 Search PubMed.
- N. Sui, et al., A lightweight yet sound-proof honeycomb acoustic metamaterial, Appl. Phys. Lett., 2015, 106(17), 171905 CrossRef.
- Y. Li, Y. Zhang and S. Xie, A lightweight multilayer honeycomb membrane-type acoustic metamaterial, Appl. Acoust., 2020, 168, 107427 CrossRef.
- J. J. Park, et al., Acoustic superlens using membrane-based metamaterials, Appl. Phys. Lett., 2015, 106(5), 051901 CrossRef.
- X. Yang, et al., Acoustic superlens using Helmholtz-resonator-based metamaterials, Appl. Phys. Lett., 2015, 107(19), 193505 CrossRef.
- Q. R. S. Miller, et al., Geophysical Monitoring with Seismic Metamaterial Contrast Agents, Unconventional Resources Technology Conference (URTeC) Proceedings, 2019, vol. 1123.
- A. Colombi, et al., Mitigation of seismic waves: Metabarriers and metafoundations bench tested, J. Sound Vib., 2020, 485, 115537 CrossRef.
- Y. Yan, et al., Seismic isolation of two dimensional periodic foundations, J. Appl. Phys., 2014, 116(4), 044908 CrossRef.
- N. Fang, et al., Sub–diffraction-limited optical imaging with a silver superlens, Science, 2005, 308(5721), 534–537 CrossRef CAS PubMed.
- R. Dhama, et al., Super-Resolution Imaging by Dielectric Superlenses: TiO2 Metamaterial Superlens versus BaTiO3 Superlens, Photonics, 2021, 8(6), 222 CrossRef CAS.
- A. Grbic and G. V. Eleftheriades, Overcoming the diffraction limit with a planar left-handed transmission-line lens, Phys. Rev. Lett., 2004, 92(11), 117403 CrossRef PubMed.
- T. Taubner, et al., Near-field microscopy through a SiC superlens, Science, 2006, 313(5793), 1595 Search PubMed.
- P. Li, et al., Graphene-enhanced infrared near-field microscopy, Nano Lett., 2014, 14(8), 4400–4405 Search PubMed.
- M. Fehrenbacher, et al., Plasmonic superlensing in doped GaAs, Nano Lett., 2015, 15(2), 1057–1061 CrossRef CAS PubMed.
- S. C. Kehr, et al., Near-field examination of perovskite-based superlenses and superlens-enhanced probe-object coupling, Nat. Commun., 2011, 2(1), 1–9 Search PubMed.
- Z. Liu, et al., Far-field optical superlens, Nano Lett., 2007, 7(2), 403–408 Search PubMed.
- S. Durant, et al., Theory of the transmission properties of an optical far-field superlens for imaging beyond the diffraction limit, J. Opt. Soc. Am. B, 2006, 23(11), 2383–2392 Search PubMed.
- G. Yuan, et al., Far-field superoscillatory metamaterial superlens, Phys. Rev. Appl., 2019, 11(6), 064016 CrossRef CAS.
- Z. Jacob, L. V. Alekseyev and E. Narimanov, Optical hyperlens: Far-field imaging beyond the diffraction limit, Opt. Express, 2006, 14(18), 8247–8256 Search PubMed.
- Z. Liu, et al., Far-field optical hyperlens magnifying sub-diffraction-limited objects, Science, 2007, 315(5819), 1686 CrossRef CAS PubMed.
- D. Lee, et al., Realization of wafer-scale hyperlens device for sub-diffractional biomolecular imaging, ACS Photonics, 2017, 5(7), 2549–2554 CrossRef.
- T.-J. Huang, et al., Amplifying Evanescent Waves by Dispersion-Induced Plasmons: Defying the Materials Limitation of the Superlens, ACS Photonics, 2020, 7(8), 2173–2181 Search PubMed.
- N. Kundtz and D. R. Smith, Extreme-angle broadband metamaterial lens, Nat. Mater., 2010, 9(2), 129–132 CrossRef CAS PubMed.
- H. F. Ma and T. J. Cui, Three-dimensional broadband and broad-angle transformation-optics lens, Nat. Commun., 2010, 1(1), 1–7 CAS.
- S. So and J. Rho, Geometrically flat hyperlens designed by transformation optics, J. Phys. D: Appl. Phys., 2019, 52(19), 194003 Search PubMed.
- X. Zhang and Z. Liu, Superlenses to overcome the diffraction limit, Nat. Mater., 2008, 7(6), 435–441 CrossRef CAS PubMed.
- D. Lu and Z. Liu, Hyperlenses and metalenses for far-field super-resolution imaging, Nat. Commun., 2012, 3(1), 1–9 Search PubMed.
- U. Leonhardt, Optical conformal mapping, Science, 2006, 312(5781), 1777–1780 Search PubMed.
- J. B. Pendry, D. Schurig and D. R. Smith, Controlling electromagnetic fields, Science, 2006, 312(5781), 1780–1782 Search PubMed.
- J. B. Pendry, et al., Transformation Optics and Subwavelength Control of Light, Science, 2012, 337(6094), 549–552 Search PubMed.
- D. Schurig, et al., Metamaterial electromagnetic cloak at microwave frequencies, Science, 2006, 314(5801), 977–980 CrossRef CAS PubMed.
- W. X. Jiang, et al., Invisibility cloak without singularity, Appl. Phys. Lett., 2008, 93(19), 194102 Search PubMed.
- J. S. Li and J. B. Pendry, Hiding under the Carpet: A New Strategy for Cloaking, Phys. Rev. Lett., 2008, 101(20), 203901 Search PubMed.
- R. Liu, et al., Broadband Ground-Plane Cloak, Science, 2009, 323(5912), 366–369 Search PubMed.
- J. Valentine, et al., An optical cloak made of dielectrics, Nat. Mater., 2009, 8(7), 568–571 Search PubMed.
- A. Alù, Mantle cloak: Invisibility induced by a surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(24), 245115 Search PubMed.
- X. Ni, et al., An ultrathin invisibility skin cloak for visible light, Science, 2015, 349(6254), 1310–1314 Search PubMed.
- H. Chu, et al., A hybrid invisibility cloak based on integration of transparent metasurfaces and zero-index materials, Light: Sci. Appl., 2018, 7(1), 1–8 Search PubMed.
- J. S. Jensen and O. Sigmund, Topology optimization for nano-photonics, Laser Photonics Rev., 2011, 5(2), 308–321 CrossRef CAS.
- O. Sigmund, On the usefulness of non-gradient approaches in topology optimization, Struct. Multidiscip. Optim., 2011, 43(5), 589–596 Search PubMed.
- M. M. Elsawy, et al., Numerical optimization methods for metasurfaces, Laser Photonics Rev., 2020, 14(10), 1900445 CrossRef CAS.
- M. E. Badawe, T. S. Almoneef and O. M. Ramahi, A true metasurface antenna, Sci. rep., 2016, 6(1), 1–8 CrossRef PubMed.
- W. E. Liu, et al., Miniaturized wideband metasurface antennas, IEEE Trans. Antennas Propag., 2017, 65(12), 7345–7349 Search PubMed.
- J. Noh, et al., Design of a transmissive metasurface antenna using deep neural networks, Opt. Mater. Express, 2021, 11(7), 2310–2317 CrossRef CAS.
- M. Alibakhshikenari, et al., Metamaterial-Inspired Antenna Array for Application in Microwave Breast Imaging Systems for Tumor Detection, IEEE Access, 2020, 8, 174667 Search PubMed.
- H. M. AlSabbagh, et al., A compact triple-band metamaterial-inspired antenna for wearable applications, Microwave Opt. Technol. Lett., 2020, 62(2), 763–777 CrossRef.
- C. M. Watts, X. L. Liu and W. J. Padilla, Metamaterial Electromagnetic Wave Absorbers, Adv. Mater., 2012, 24(23), Op98–Op120 Search PubMed.
- N. I. Landy, et al., Perfect metamaterial absorber, Phys. Rev. Lett., 2008, 100(20), 207402 CrossRef CAS PubMed.
- H. Tao, et al., A metamaterial absorber for the terahertz regime: design, fabrication and characterization, Opt. Express, 2008, 16(10), 7181–7188 Search PubMed.
- Y. Avitzour, Y. A. Urzhumov and G. Shvets, Wide-angle infrared absorber based on a negative-index plasmonic metamaterial, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(4), 045131 CrossRef.
- X. Liu, et al., Infrared spatial and frequency selective metamaterial with near-unity absorbance, Phys. Rev. Lett., 2010, 104(20), 207403 CrossRef PubMed.
- K. Aydin, et al., Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers, Nat. Commun., 2011, 2(1), 1–7 Search PubMed.
- W. Jiang, et al., Electromagnetic wave absorption and compressive behavior of a three-dimensional metamaterial absorber based on 3D printed honeycomb, Sci. Rep., 2018, 8, 4817 CrossRef PubMed.
- J. J. Yang, et al., Metamaterial Sensors, Int. J. Antennas Propag., 2013, 2013, 637270 Search PubMed.
- W. Withayachumnankul, et al., Metamaterial-based microfluidic sensor for dielectric characterization, Sens. Actuators, A, 2013, 189, 233–237 CrossRef CAS.
- A. Ebrahimi, et al., High-Sensitivity Metamaterial-Inspired Sensor for Microfluidic Dielectric Characterization, IEEE Sens. J., 2014, 14(5), 1345–1351 Search PubMed.
- Y. Zhang, et al., Microwave metamaterial absorber for non-destructive sensing applications of grain, Sensors, 2018, 18(6), 1912 CrossRef PubMed.
- L. Cong, et al., Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: A comparison with the metasurfaces, Appl. Phys. Lett., 2015, 106(3), 031107 CrossRef.
- A. S. Saadeldin, et al., Highly sensitive terahertz metamaterial sensor, IEEE Sens. J., 2019, 19(18), 7993–7999 CAS.
- T. Chen, S. Li and H. Sun, Metamaterials application in sensing, Sensors, 2012, 12(3), 2742–2765 CrossRef PubMed.
- S. Guenneau, C. Amra and D. Veynante, Transformation thermodynamics: cloaking and concentrating heat flux, Opt. Express, 2012, 20(7), 8207–8218 CrossRef PubMed.
- S. Y. Xiao, et al., Active metamaterials and metadevices: a review, J. Phys. D: Appl. Phys., 2020, 53(50), 503002 CrossRef CAS.
- P. Pitchappa, et al., Bidirectional reconfiguration and thermal tuning of microcantilever metamaterial device operating from 77 K to 400 K, Appl. Phys. Lett., 2017, 111(26), 261101 CrossRef.
- H. Tao, et al., MEMS based structurally tunable metamaterials at terahertz frequencies, J. Infrared, Millimeter, Terahertz Waves, 2011, 32(5), 580–595 CrossRef.
- X. Zhao, et al., Voltage-tunable dual-layer terahertz metamaterials, Microsyst. Nanoeng., 2016, 2(1), 1–8 Search PubMed.
- A. Karvounis, et al., Nano-optomechanical nonlinear dielectric metamaterials, Appl. Phys. Lett., 2015, 107(19), 191110 CrossRef.
- J. Zhang, K. F. MacDonald and N. I. Zheludev, Nonlinear dielectric optomechanical metamaterials, Light: Sci. Appl., 2013, 2(8), e96 CrossRef.
- I. V. Shadrivov, et al., Metamaterials Controlled with Light, Phys. Rev. Lett., 2012, 109(8), 083902 CrossRef PubMed.
- X. G. Zhang, et al., Light-Controllable Digital Coding Metasurfaces, Adv. Sci., 2018, 5(11), 1801028 Search PubMed.
- X. G. Zhang, W. X. Jiang and T. J. Cui, Frequency-dependent transmission-type digital coding metasurface controlled by light intensity, Appl. Phys. Lett., 2018, 113(9), 091601 CrossRef.
- J. Zhao, et al., A tunable metamaterial absorber using varactor diodes, New J. Phys., 2013, 15(4), 043049 Search PubMed.
- M. Gupta, Y. K. Srivastava and R. Singh, A Toroidal Metamaterial Switch, Adv. Mater., 2018, 30(4), 1704845 Search PubMed.
- C. Zou, et al., Resonant dielectric metasurfaces: active tuning and nonlinear effects, J. Phys. D: Appl. Phys., 2019, 52(37), 373002 CrossRef CAS.
- L. Wang, et al., Broadband tunable liquid crystal terahertz waveplates driven with porous graphene electrodes, Light: Sci. Appl., 2015, 4(2), e253–e253 Search PubMed.
- A. Komar, et al., Electrically tunable all-dielectric optical metasurfaces based on liquid crystals, Appl. Phys. Lett., 2017, 110(7), 071109 Search PubMed.
- Y. Qu, et al., Dynamic Thermal Emission Control Based on Ultrathin Plasmonic Metamaterials Including Phase-Changing Material GST, Laser Photonics Rev., 2017, 11(5), 1700091 CrossRef.
- A. Tittl, et al., A Switchable Mid-Infrared Plasmonic Perfect Absorber with Multispectral Thermal Imaging Capability, Adv. Mater., 2015, 27(31), 4597–4603 Search PubMed.
- J. Liu, H. Guo and T. Wang, A Review of Acoustic Metamaterials and Phononic Crystals, Crystals, 2020, 10(4), 305 CrossRef CAS.
- M. M. Sigalas and E. N. Economou, Elastic and Acoustic-Wave Band-Structure, J. Sound Vib., 1992, 158(2), 377–382 Search PubMed.
- M. S. Kushwaha, et al., Acoustic band structure of periodic elastic composites, Phys. Rev. Lett., 1993, 71(13), 2022 CrossRef CAS PubMed.
- K. Lu, et al., A lightweight low-frequency sound insulation membrane-type acoustic metamaterial, AIP Adv., 2016, 6(2), 025116 Search PubMed.
- F. Ma, M. Huang and J. H. Wu, Ultrathin lightweight plate-type acoustic metamaterials with positive lumped coupling resonant, J. Appl. Phys., 2017, 121(1), 015102 CrossRef.
- B. Xia, et al., Temperature-controlled tunable acoustic metamaterial with active band gap and negative bulk modulus, Appl. Acoust., 2016, 112, 1–9 CrossRef.
- K. Yi, et al., Active metamaterials with broadband controllable stiffness for tunable band gaps and non-reciprocal wave propagation, Smart Mater. Struct., 2019, 28(6), 065025 Search PubMed.
- S. A. Cummer and D. Schurig, One path to acoustic cloaking, New J. Phys., 2007, 9(3), 45 Search PubMed.
- H. Chen and C. Chan, Acoustic cloaking in three dimensions using acoustic metamaterials, Appl. Phys. Lett., 2007, 91(18), 183518 Search PubMed.
- S. Zhang, C. G. Xia and N. Fang, Broadband Acoustic Cloak for Ultrasound Waves, Phys. Rev. Lett., 2011, 106(2), 024301 Search PubMed.
- B. I. Popa, L. Zigoneanu and S. A. Cummer, Experimental Acoustic Ground Cloak in Air, Phys. Rev. Lett., 2011, 106(25), 253901 CrossRef PubMed.
- L. Zigoneanu, B. I. Popa and S. A. Cummer, Three-dimensional broadband omnidirectional acoustic ground cloak, Nat. Mater., 2014, 13(4), 352–355 Search PubMed.
- Y. Bi, et al., Experimental demonstration of three-dimensional broadband underwater acoustic carpet cloak, Appl. Phys. Lett., 2018, 112(22), 223502 Search PubMed.
- H. Esfahlani, et al., Acoustic carpet cloak based on an ultrathin metasurface, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94(1), 014302 Search PubMed.
- F. Ma, et al., Bilayer synergetic coupling double negative acoustic metasurface and cloak, Sci. Rep., 2018, 8(1), 5906 CrossRef PubMed.
- J. Guo and J. Zhou, An ultrathin acoustic carpet cloak based on resonators with extended necks, J. Phys. D: Appl. Phys., 2020, 53(50), 505501 CrossRef CAS.
- H. Jia, et al., Subwavelength imaging by a simple planar acoustic superlens, Appl. Phys. Lett., 2010, 97(17), 173507 CrossRef.
- Y. Gu, Y. Cheng and X. Liu, Acoustic planar hyperlens based on anisotropic density-near-zero metamaterials, Appl. Phys. Lett., 2015, 107(13), 133503 CrossRef.
- C. Hu, et al., Experimental demonstration of a three-dimensional acoustic hyperlens for super-resolution imaging, Appl. Phys. Lett., 2021, 118(20), 203504 CrossRef CAS.
- G. Y. Song, et al., Acoustic Magnifying Lens for Far-Field High Resolution Imaging Based on Transformation Acoustics, Adv. Mater. Technol., 2017, 2(9), 1700089 CrossRef.
- Y.-X. Shen, et al., Ultrasonic super-oscillation wave-packets with an acoustic meta-lens, Nat. Commun., 2019, 10(1), 1–7 Search PubMed.
- J. Zhu, et al., A holey-structured metamaterial for acoustic deep-subwavelength imaging, Nat. Phys., 2011, 7(1), 52–55 Search PubMed.
- N. Jimenez, et al., Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption, Appl. Phys. Lett., 2016, 109(12), 121902 CrossRef.
- J. Mei, et al., Dark acoustic metamaterials as super absorbers for low-frequency sound, Nat. Commun., 2012, 3(1), 1–7 Search PubMed.
- X. Wu, et al., High-efficiency ventilated metamaterial absorber at low frequency, Appl. Phys. Lett., 2018, 112(10), 103505 CrossRef.
- Y. Tang, et al., Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound, Sci. Rep., 2017, 7(1), 1–11 CrossRef PubMed.
- Z.-x Xu, et al., Tunable low-frequency and broadband acoustic metamaterial absorber, J. Appl. Phys., 2021, 129(9), 094502 CrossRef CAS.
- Y. Xie, et al., Single-sensor multispeaker listening with acoustic metamaterials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(34), 10595–10598 CrossRef CAS PubMed.
- T. Chen, et al., Weak Signals Detection by Acoustic Metamaterials-Based Sensor, IEEE Sens. J., 2021, 21(15), 16815–16825 Search PubMed.
- T. Chen, W. Li and D. Yu, A tunable gradient acoustic metamaterial for acoustic sensing, Extreme Mech. Lett., 2021, 49, 101481 Search PubMed.
- R. Fleury, D. Sounas and A. Alu, An invisible acoustic sensor based on parity-time symmetry, Nat. Commun., 2015, 6(1), 1–7 Search PubMed.
- S. R. Sklan and B. W. Li, Thermal metamaterials: functions and prospects, Natl. Sci. Rev., 2018, 5(2), 138 Search PubMed.
- J. Wang, G. L. Dai and J. Huang, Thermal Metamaterial: Fundamental, Application, and Outlook, Iscience, 2020, 23(10), 101637 CrossRef CAS PubMed.
- S. Narayana and Y. Sato, Heat Flux Manipulation with Engineered Thermal Materials, Phys. Rev. Lett., 2012, 108(21), 214303 Search PubMed.
- S. Narayana, S. Savo and Y. Sato, Transient heat flux shielding using thermal metamaterials, Appl. Phys. Lett., 2013, 102(20), 201904 Search PubMed.
- R. Schittny, et al., Experiments on Transformation Thermodynamics: Molding the Flow of Heat, Phys. Rev. Lett., 2013, 110(19), 195901 Search PubMed.
- D.-P. Liu, P.-J. Chen and H.-H. Huang, Realization of a thermal cloak–concentrator using a metamaterial transformer, Sci. Rep., 2018, 8(1), 2493 CrossRef PubMed.
- E. M. Dede, et al., Heat flux cloaking, focusing, and reversal in ultra-thin composites considering conduction-convection effects, Appl. Phys. Lett., 2013, 103(6), 063501 CrossRef.
- T. Han, et al., Full control and manipulation of heat signatures: cloaking, camouflage and thermal metamaterials, Adv. Mater., 2014, 26(11), 1731–1734 Search PubMed.
- R. Hu, et al., Illusion Thermotics, Adv. Mater., 2018, 30(22), 1707237 Search PubMed.
- E. M. Dede, et al., Thermal Metamaterials for Heat Flow Control in Electronics, J. Electron. Packag., 2018, 140(1), 010904 Search PubMed.
- D. M. Nguyen, et al., Active thermal cloak, Appl. Phys. Lett., 2015, 107(12), 121901 Search PubMed.
- Z. Zhou, et al., Programmable thermal metamaterials based on optomechanical systems, ES Energy, Environ., 2019, 6(3), 85–91 Search PubMed.
- G. Dai, J. Shang and J. Huang, Theory of transformation thermal convection for creeping flow in porous media: Cloaking, concentrating, and camouflage, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2018, 97(2), 022129 CrossRef CAS PubMed.
- G. Dai and J. Huang, A transient regime for transforming thermal convection: Cloaking, concentrating, and rotating creeping flow and heat flux, J. Appl. Phys., 2018, 124(23), 235103 CrossRef.
- M. Imran, L. Zhang and A. K. Gain, Advanced thermal metamaterial design for temperature control at the cloaked region, Sci. Rep., 2020, 10(1), 11763 CrossRef CAS PubMed.
- L. Xu and J. Huang, Metamaterials for Manipulating Thermal Radiation: Transparency, Cloak, and Expander, Phys. Rev. Appl., 2019, 12(4), 044048 CrossRef CAS.
- L. Xu, G. Dai and J. Huang, Transformation multithermotics: controlling radiation and conduction simultaneously, Phys. Rev. Appl., 2020, 13(2), 024063 CrossRef CAS.
- B. Li, L. Wang and G. Casati, Thermal Diode: Rectification of Heat Flux, Phys. Rev. Lett., 2004, 93(18), 184301 Search PubMed.
- M. Schmotz, et al., A thermal diode using phonon rectification, New J. Phys., 2011, 13(11), 113027 CrossRef.
- P. Ben-Abdallah and S.-A. Biehs, Near-field thermal transistor, Phys. Rev. Lett., 2014, 112(4), 044301 Search PubMed.
- L. Wang and B. Li, Thermal logic gates: computation with phonons, Phys. Rev. Lett., 2007, 99(17), 177208 CrossRef PubMed.
- C. Kathmann, et al., Scalable radiative thermal logic gates based on nanoparticle networks, Sci. Rep., 2020, 10(1), 3596 Search PubMed.
- P. Ben-Abdallah and S.-A. Biehs, Towards Boolean operations with thermal photons, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94(24), 241401 CrossRef.
- L. Wang and B. Li, Thermal memory: a storage of phononic information, Phys. Rev. Lett., 2008, 101(26), 267203 Search PubMed.
- D. Mu, et al., A Review of Research on Seismic Metamaterials, Adv. Eng. Mater., 2020, 22(4), 1901148 Search PubMed.
- S. Br û lé, S. Enoch and S. Guenneau, Emergence of seismic metamaterials: Current state and future perspectives, Phys. Lett. A, 2020, 384(1), 126034 CrossRef.
- M. Brun, S. Guenneau and A. B. Movchan, Achieving control of in-plane elastic waves, Appl. Phys. Lett., 2009, 94(6), 061903 CrossRef.
- S. Br û lé, et al., Metamaterial-like transformed urbanism, Innovative Infrastruct. Solutions, 2017, 2(1), 20 CrossRef.
- S. Brule, et al., Experiments on Seismic Metamaterials: Molding Surface Waves, Phys. Rev. Lett., 2014, 112(13), 133901 CrossRef CAS PubMed.
- S. Brule, et al., Flat lens effect on seismic waves propagation in the subsoil, Sci. Rep., 2017, 7, 18066 CrossRef PubMed.
- S. Brûlé, S. Enoch and S. Guenneau, Structured soils under dynamic loading: The metamaterials in Geotechnics, Revue Française de Géotechnique, 2017 Search PubMed.
- M. Miniaci, et al., Large scale mechanical metamaterials as seismic shields, New J. Phys., 2016, 18(8), 083041 Search PubMed.
- S. Krödel, N. Thomé and C. Daraio, Wide band-gap seismic metastructures, Extreme Mech. Lett., 2015, 4, 111–117 Search PubMed.
- Y. Achaoui, et al., Seismic waves damping with arrays of inertial resonators, Extreme Mech. Lett., 2016, 8, 30–37 CrossRef.
- A. Colombi, et al., A seismic metamaterial: The resonant metawedge, Sci. Rep., 2016, 6, 27717 Search PubMed.
- A. Colombi, et al., Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances, Sci. Rep., 2016, 6, 19238 Search PubMed.
- A. Maurel, et al., Conversion of Love waves in a forest of trees, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98(13), 134311 CrossRef CAS.
- H. Xiang, et al., Periodic materials-based vibration attenuation in layered foundations: experimental validation, Smart Mater. Struct., 2012, 21(11), 112003 CrossRef.
- Z. Cheng and Z. Shi, Novel composite periodic structures with attenuation zones, Eng. Struct., 2013, 56, 1271–1282 CrossRef.
- Y. Zeng, et al., Subwavelength seismic metamaterial with an ultra-low frequency bandgap, J. Appl. Phys., 2020, 128(1), 014901 Search PubMed.
- B. Ungureanu, et al., Auxetic-like metamaterials as novel earthquake protections, EPJ Appl. Metamaterials, 2015, 2, 17 Search PubMed.
- G. Carta, et al., Gyro-elastic beams for the vibration reduction of long flexural systems, Proc. R. Soc. A, 2017, 473(2203), 20170136 Search PubMed.
- Q. R. S. Miller, et al., Microporous and Flexible Framework Acoustic Metamaterials for Sound Attenuation and Contrast Agent Applications, ACS Appl. Mater. Interfaces, 2018, 10, 44226–44230 CrossRef CAS PubMed.
- H. T. Schaef, et al., Injectable contrast agents for enhanced subsurface mapping and monitoring, Energy Procedia, 2017, 114, 3764–3770 Search PubMed.
- S. K. Nune, et al., Transport of Polymer–Coated Metal–Organic Framework Nanoparticles in Porous Media, Sci. Rep., 2022, 12, 13962 Search PubMed.
- Q. R. S. Miller, M. Pohl, K. Livo, H. Asgar, S. K. Nune, M. A. Sinnwell, M. Prasad, G. Gadikota, B. P. McGrail and H. T. Schaef, Porous Colloidal Nanoparticles as Injectable Multimodal Contrast Agents for Enhanced Geophysical Sensing, ACS Appl. Mater. Interfaces, 2022, 14, 23420–23425 Search PubMed.
- D. Mu, et al., A review of research on seismic metamaterials, Adv. Eng. Mater., 2020, 22(4), 1901148 CrossRef.
- J. N. Grima and K. E. Evans, Auxetic behavior from rotating squares, J. Mater. Sci. Lett., 2000, 19(17), 1563–1565 CrossRef CAS.
- R. Zhong, et al., A novel three-dimensional mechanical metamaterial with compression-torsion properties, Compos. Struct., 2019, 226, 111232 Search PubMed.
- K. K. Dudek, New type of rotation of chiral mechanical metamaterials, Smart Mater. Struct., 2020, 29(11), 115027 Search PubMed.
- A. A. Zadpoor, Mechanical meta-materials, Mater. Horiz., 2016, 3(5), 371–381 RSC.
- M. Kadic, et al., On the practicability of pentamode mechanical metamaterials, Appl. Phys. Lett., 2012, 100(19), 191901 CrossRef.
- M. Kadic, et al., On anisotropic versions of three-dimensional pentamode metamaterials, New J. Phys., 2013, 15(2), 023029 CrossRef CAS.
- C. N. Layman, et al., Highly anisotropic elements for acoustic pentamode applications, Phys. Rev. Lett., 2013, 111(2), 024302 Search PubMed.
- G. F. Méjica and A. D. Lantada, Comparative study of potential pentamodal metamaterials inspired by Bravais lattices, Smart Mater. Struct., 2013, 22(11), 115013 Search PubMed.
- X. Cai, et al., The mechanical and acoustic properties of two-dimensional pentamode metamaterials with different structural parameters, Appl. Phys. Lett., 2016, 109(13), 131904 CrossRef.
- S. Wu, et al., Topological design of pentamode metamaterials with additive manufacturing, Comput. Methods Appl. Mech. Eng., 2021, 377, 113708 Search PubMed.
- R. Hedayati, A. Leeflang and A. Zadpoor, Additively manufactured metallic pentamode meta-materials, Appl. Phys. Lett., 2017, 110(9), 091905 Search PubMed.
- S. Waitukaitis, et al., Origami multistability: From single vertices to metasheets, Phys. Rev. Lett., 2015, 114(5), 055503 Search PubMed.
- Y. Cho, et al., Engineering the shape and structure of materials by fractal cut, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(49), 17390–17395 CrossRef CAS PubMed.
- M. Isobe and K. Okumura, Initial rigid response and softening transition of highly stretchable kirigami sheet materials, Sci. Rep., 2016, 6(1), 1–6 Search PubMed.
- K. Bertoldi, et al., Negative Poisson's ratio behavior induced by an elastic instability, Adv. Mater., 2010, 22(3), 361–366 CrossRef CAS PubMed.
- S. Guenneau, et al., Transformed Fourier and Fick equations for the control of heat and mass diffusion, AIP Adv., 2015, 5(5), 053404 CrossRef.
- J. M. Restrepo-Florez and M. Maldovan, Mass diffusion cloaking and focusing with metamaterials, Appl. Phys. Lett., 2017, 111(7), 071903 Search PubMed.
- J. M. Restrepo-Florez and M. Maldovan, Metamaterial membranes, J. Phys. D: Appl. Phys., 2017, 50(2), 025104 CrossRef.
- J. M. Restrepo-Florez and M. Maldovan, Permeabilities and selectivities in anisotropic planar membranes for gas separations, Sep. Purif. Technol., 2019, 228, 115762 CrossRef CAS.
- L. W. Zeng and R. X. Song, Controlling chloride ions diffusion in concrete, Sci. Rep., 2013, 3, 3359 Search PubMed.
- L. Zeng, et al., Experimental measure mass diffusion transparency, Solid State Commun., 2014, 186, 23–27 CrossRef CAS.
- S. Guenneau and T. M. Puvirajesinghe, Fick’s second law transformed: one path to cloaking in mass diffusion, J. R. Soc., Interface, 2013, 10(83), 20130106 CrossRef CAS PubMed.
- S. Guenneau, et al., Cloaking and anamorphism for light and mass diffusion, J. Opt., 2017, 19(10), 103002 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |





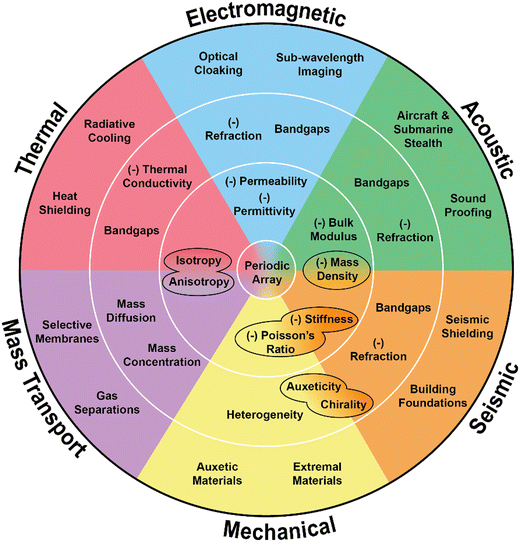
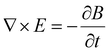
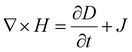
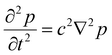
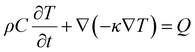
![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif)