Microfluidic acoustic sawtooth metasurfaces for patterning and separation using traveling surface acoustic waves†
Mingxin
Xu
 ,
Peter V. S.
Lee
and
David J.
Collins
,
Peter V. S.
Lee
and
David J.
Collins
 *
*
Department of Biomedical Engineering, University of Melbourne, Melbourne, Victoria, Australia. E-mail: david.collins@unimelb.edu.au
First published on 3rd December 2021
Abstract
We demonstrate a sawtooth-based metasurface approach for flexibly orienting acoustic fields in a microfluidic device driven by surface acoustic waves (SAW), where sub-wavelength channel features can be used to arbitrarily steer acoustic fringes in a microchannel. Compared to other acoustofluidic methods, only a single travelling wave is used, the fluidic pressure field is decoupled from the fluid domain's shape, and steerable pressure fields are a function of a simply constructed polydimethylsiloxane (PDMS) metasurface shape. Our results are relevant to microfluidic applications including the patterning, concentration, focusing, and separation of microparticles and cells.
Introduction
Acoustofluidic devices are used for the manipulation of cells, bacteria, and other biological particles, with applications including tissue engineering,1–3 drug delivery,4,5 diagnosis,6–8 single-cell studies,9–11 and nanoscale manipulation.12,13 Compared with manipulation methods such as magnetic,14,15 dielectrophoretic,16,17 hydrodynamic,18 optical19 approaches, acoustic methods are particularly useful for manipulating biological particles because they are contactless, label-free, biocompatible, and compact.20–23Surface acoustic wave (SAW)24 piezoelectric transducers are commonly used to manipulate micron-scale objects due to their small wavelengths (∼3–300 μm) and planar structure, simplifying fabrication.25–27 Typical standing wave SAW devices generate uniform acoustic fields in microchannels,28–30 where patterns are restricted to half-wavelength periodic distances between nodes or anti-nodes.31 Travelling surface acoustic waves, in contrast, can be used to generate translational forces that push particles along the acoustic propagation direction,32,33 though recent work has demonstrated that diffractive time-averaged acoustic patterns can be generated when the transducer domain is bounded by a channel wall.34–40 This SAW diffractive approach results in acoustic fields that are automatically aligned to the channel features, rather than the underlying substrate oscillations, greatly simplifying device setup. Using this diffractive approach further permits generation of acoustic fields that are angled to the SAW propagation axis, where the resulting acoustic field can be arbitrarily designed by tuning the channel shape.40 A limitation, however, of such diffraction-based methods is that the acoustic fields are inseparably parallel to channel interfaces, with the overall shape of the fluidic domain being intrinsically coupled to acoustic domain, limiting its applicability for continuous throughput and the generation of more complex acoustic fields.
Acoustic metasurfaces are an alternative approach to modulating acoustic fields, where metasurfaces are comprised of wavelength-scale structures that can modulate acoustic fields41,42via wavefront modulation and redirection,43–46 acoustic absorption,42,47 and frequency-selective acoustic transmission.48–50 Metasurfaces include those based on arrangements of topological features, including coiled structures that result in acoustic absorption or phase shifts,51–53 Helmholtz resonators46,54–56 and membrane-bound cavities.57,58 These approaches, however, often rely on the fabrication of complex 3D structures, which is complicated by the micrometer structure resolutions required for the >10 MHz frequencies necessary for cell-scale micromanipulation, limiting their use in microfluidic systems.
In this work we demonstrate an acoustic metasurface based on diffractive effects, where sub-wavelength channel shapes are used to define and steer acoustic fields in microfluidic devices, permitting acoustic field steering without the use of complex microstructures. Here, an interfacial microchannel-based metasurface converts a traveling surface acoustic wave (TSAW) into a flexibly defined time-averaged period acoustic field. Compared to microchannel diffractive effects examined elsewhere,38,39 this metasurface approach yields acoustic fields whose orientation is decoupled from the shape of the fluid domain. The metasurface is composed of sawtooth-like sub-wavelength microstructures defined via a polydimethylsiloxane (PDMS) channel wall in the path of a travelling SAW, requiring no unique fabrication steps or complex geometries with minimal impact on fluid flow streamlines. This approach is dissimilar from other acoustic metasurface approaches that spatially modulate a wavefront's phase or amplitude42–45,47,56,59–61 in that the apparent acoustic field orientation is steered via diffractive effects, effectively changing the shape of the transducer domain via a shaped channel, and creates time-averaged steerable patterns along the propagation direction with the application of only a single propagating travelling wave. This is compared to acoustic metasurface beam-steering approaches in which no such propagation-direction periodicity occurs. The metasurface demonstrated in this work is able to generate a periodic, spatially localized acoustic field, where the channel features dictate the acoustic field orientation. Moreover, whereas only one set of orientations is possible using standing waves from opposing IDTs,62–64 with the acoustic field orientation intrinsically coupled with the underlying substrate oscillation variations, we demonstrate that our channel-based metasurface can produce a range of different orientations across the same device with the same transducer, showing how flexibly acoustic fields can be generated and employed. The outcome of this work is a metasurface approach that can arbitrarily define acoustic field orientations and is highly appropriate for use in microfluidic devices. In examining this approach, we present analytical and simulation models to predict acoustic field orientation and periodic spacing as a function of metasurface dimensions. We further demonstrate example applications of the metasurface in particle patterning and continuous sorting.
System design and principles
An understanding of the operating principle of diffractive patterning is important for modelling this metasurface approach. In creating diffractive effects, acoustic fringes are generated according to the Huygens–Fresnel principle, which indicates that the acoustic field at a specified point in the fluid is equal to the superposition of all contributing spherically propagating wavefronts from the transducer domain.37 When a microchannel is placed on an oscillating substrate, the geometry of the channel–fluid interface defines the transducer extent that interacts with the fluid, resulting in time-averaged acoustic field gradients that are coincident with the channel walls. The resulting fringe spacing is represented by λθ, which in the case of a flat channel wall is expressed in the transducer (x–y) plane as:38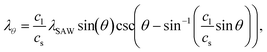 | (1) |
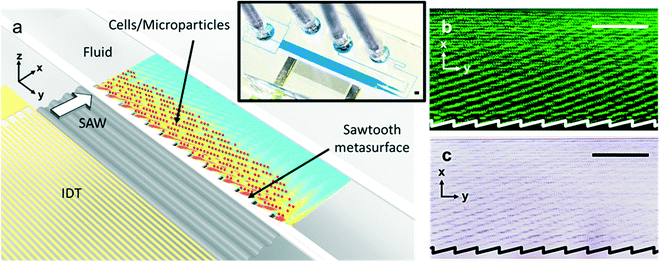
Rather than using a flat wall that can only generate fringes parallel to channel walls, here we investigate the use of a sawtooth-shaped channel interface, whose wavelength-scale features can be used to arbitrarily orient diffractive fringes irrespective of the bulk fluidic domain. The sawtooth metasurface is composed of a series of triangular features, as shown in Fig. 1(a). This figure conceptually encapsulates the phenomenon, where an interdigital transducer (IDT) generates a SAW, whereafter the metasurface interface modifies the transducer boundary in the fluid domain to produce time-averaged acoustic field gradients, and therefore particle patterns, at steered angles to the propagation direction. The inset shows an image of a physical device. Fig. 1(b) and (c) show example photos of fluorescence and brightfield 2 μm polystyrene particles, respectively.
Fig. 2(a) shows the coordinates and parameters that we use to describe this system. Firstly, the SAW propagates along the +x axis, whereupon it intersects with sawtooth features characterized by the sawtooth angle θst and sawtooth height hst, as shown in Fig. 2(a). The result of this is an angle of the generated time-average acoustic field in the fluid, θdiv, where this subscript notes that this is an angle that can diverge from θst. The spacing between adjoining acoustic minima is defined as λθ, and the height of the sawtooth in the direction of λθ is represented by hθ. These parameters are represented in Fig. 2(a).
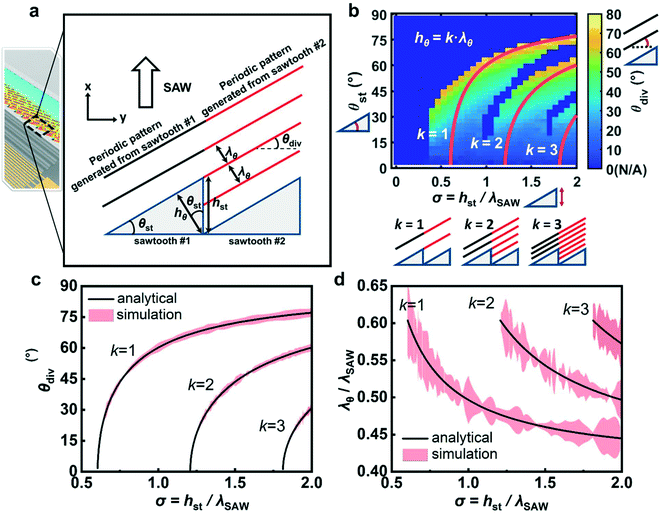 | ||
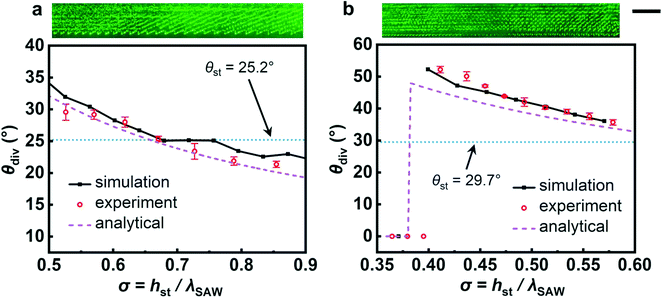
| Fig. 2 Coordinate system and mapping of acoustic field reorientation (θdiv) as a function of metasurface shape. (a) The mechanism by which sawtooth metasurfaces generate oblique acoustic fields. (b) Simulation results (scatter plot) and analytical results (red lines) corresponding to different k values, for k = 1, 2, and 3. Pictograms adjoining each axes/colorbar denote the angle or dimension measured. (c) Plot of analytical (eqn (2)) and simulation results for the acoustic field angle, θdiv, against σ, and for (d) the fringe spacing (eqn (1)), plotting λθ/λSAW as a function of σ. | ||
We first examine the case where hθ is an integer multiple of λθ, as in Fig. 2(a), with
| hθ = k·λθ, | (2) |
hθ = hst![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θst. θst. | (3) |
The acoustic field orientation is not necessarily the same as the angle of the sawtooth surfaces, however, due to the complex interplay between the incoming SAW and the sawtooth feature dimensions. The contour plot in Fig. 2(b) shows the simulation results of this relationship between sawtooth dimensions, angle and θdiv, in which we define σ as the ratio between the sawtooth height and the SAW wavelength (σ = hst/λSAW), plotting this here from σ = 0 to σ = 2. The red lines in Fig. 2(b) show the analytical solutions by combining eqn (1)–(3) for k equal to 1, 2, and 3. This figure shows that θdiv increases as σ increases for a given k value, though θdiv is not constant for a given θst, and only equal to θst in cases exactly where k = 1, 2, 3, etc. Examining this situation in particular, the comparisons between the analytical results and the simulation results for different integer k values are shown in Fig. 2(c) and (d), which shows good agreement between the analytical results and simulation results (difference <1°). The analytical model described in eqn (1)–(3) corresponding to the red lines in Fig. 2(b), can therefore be readily used to design sawtooth dimensions based on the required acoustic field angle (θdiv) with integer k values.
For the case where hθ is not an integer multiple of λθ, namely where k in eqn (2) is a positive non-integer, Fig. 3 demonstrates how θdiv varies from the metasurface's θst values. Fig. 3(a), for example, shows a case where hθ is slightly decreased, i.e. k < 1, while keeping θst constant. To delineate k values either slightly less than or greater than 1 in this figure, we annotate hθ here as h−θ or h+θ, respectively. Since hθ decreases while λθ is a constant, the fringes produced by a given sawtooth feature are located further along the SAW propagation direction than those produced to their left. Therefore, θdiv increases and is larger than θst (for h−θ). This corresponds to the higher θdiv values in Fig. 2(b) to the left of each red line. The converse is the case for h+θ, in which θdiv is smaller than θst (Fig. 3(c)). Fig. 3(b), as in Fig. 2(a), shows the case where hθ is an integer multiple of λθ, where θdiv is the same as θst. The outcome of this is an interesting, if counterintuitive result, that larger sawtooth features result in a less angled acoustic field for a given sawtooth angle. The description of the analytical model, its derivation, and the resulting θdiv are shown in ESI† Note S1, Fig. S1 and S2. Equivalently, a generalized Snell's law for these sawtooth metasurfaces is also derived in ESI† Note S2.
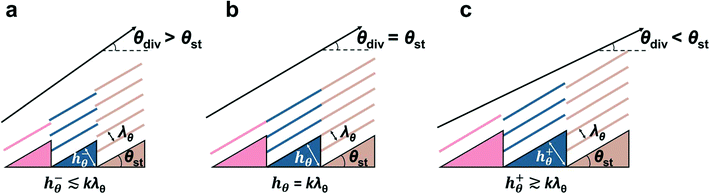 | ||
| Fig. 3 Principle of shifting acoustic fringes orientation as a function of hθ. For (a) h−θ ≲ kλθ, (b) hθ = kλθ, and (c) h+θ ≳ kλθ. | ||
To ensure the effective generation of time-averaged interference patterns, the following conditions need to be considered. First, total internal reflection ideally occurs at the channel–fluid interface to yield a transducer domain that is effectively bounded by the channel geometry,38 such that the Rayleigh angle (θR) is less than the critical angle of total internal reflection (θc). This is accomplished with a lithium niobate transducer, a polydimethylsiloxane (PDMS) channel and water fluid. Further, reflections from the channel roof leads to acoustic field periodicity in the vertical direction,34,38 with the result that particles can be captured at different heights in the vertical direction. As the channel heights used in this work are on the order of the acoustic wavelength in the fluid, however, there are only a limited number of vertical positions at which particles can aggregate. Moreover, recent results suggest that for systems with wavelength-scale heights that acoustic streaming effects will result in preferential aggregation at one height in the vertical direction.65 The drag force caused by acoustic streaming has further been reported to be a function of channel geometry, particle size, and viscosity,66,67 where larger channel heights, especially those on the order of several acoustic wavelengths, result in higher fluid velocities and therefore drag forces.65 Accordingly, this metasurface approach is ideally employed in systems where the channel height is on the order of the acoustic wavelength in the fluid, where larger channel heights may result in higher streaming velocities that will tend to defocus particle aggregations.
Methods
The experimental devices comprise a SAW substrate and a PDMS microchannel. The SAW is generated by an interdigital transducer (IDT) is patterned on a piezoelectric 128° Y-cut lithium niobate (LN) substrate, consisting of a 150 nm thick Au conductive layer on a 10 nm thick Cr adhesion layer. The substrate (excepting electrode pads) is subsequently covered by a 300 nm SiO2 layer to enhance the corrosion resistance and the adhesion of the PDMS channel. The IDTs are 6 mm wide with a SAW wavelength (λSAW) of 100 μm. The PDMS microchannels, with heights of 50 μm and widths (along the flow direction) of 1000 μm are defined by SU-8 molds manufactured by conventional photolithography processes and bonded to the substrate by plasma surface treatment. An examination of the fabricated metasurface channel features demonstrates that they match their design to a tolerance of less than 4 μm. The SAW is driven by a 39.31 MHz sinusoidal signal (Rigol DG4162, Beijing, China) amplified to 0.1 W. An inverted microscope (Olympus IX73, Tokyo, Japan) is used to observe the behavior of fluorescent polystyrene particles, where the polystyrene particles are captured at the position with the minimum acoustic potential. Fluorescent polystyrene particles (Magsphere, CA, USA) were suspended in 1% w/w Pluronic F-127 (Sigma-Aldrich, MO, USA) solution to prevent the particles from attaching to the channel walls.A program adapted from previous literature was used to simulate the resulting pressure field (running in MATLAB R2017b, MathWorks, MA, USA), based on the Huygens–Fresnel principle, where O'Rorke et al. describes the simulation process used to calculate the acoustic force field generated by a given channel geometry.68 In order to detect θdiv and verify the relationship between sawtooth geometry and the angle of the resulting acoustic field, a Hough transform69 is used to identify the geometric features of the generated acoustic field by detecting the lines or shapes in the resulting acoustic field. An example of Hough transform is shown in ESI† Fig. S4.
Results and discussion
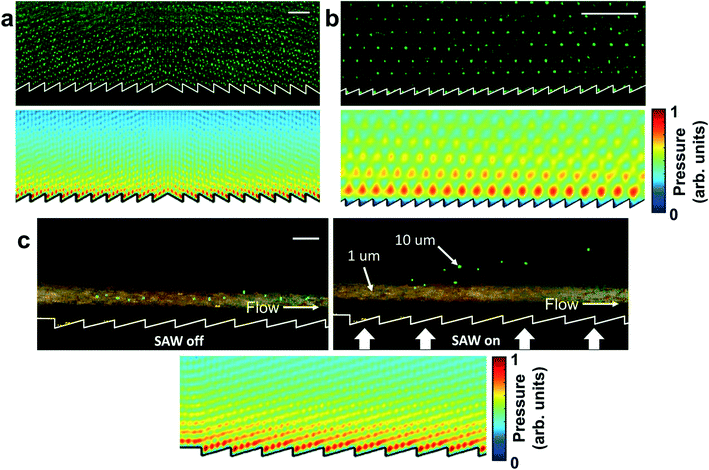
We first experimentally examine the sawtooth metasurface approach in the context of periodically spaced identical features to characterize the resulting acoustic fields. Fig. 4 shows the experiment (top) and simulation (bottom) results from different sawtooth metasurface designs. The experimental results show patterned 2 μm diameter fluorescent polystyrene particles, subject to a SAW excited at 0.1 W and 39.31 MHz. The red area and blue regions in the simulation results represent pressure maxima and minima, respectively, where polystyrene particles (with a positive contrast coefficient) migrate from the high-pressure to the low-pressure areas. All experimental and simulation images clearly show the central premise of this metasurface approach, where a series of sawtooth features subject to a travelling SAW (whose propagation direction is indicated by the arrow at the right of Fig. 4) results in a similarly angled acoustic field, despite the use of a single, uniform travelling wave and the overall rectilinear morphology of the fluidic channel domain, except for the small sub-wavelength angled metasurface features along the SAW path.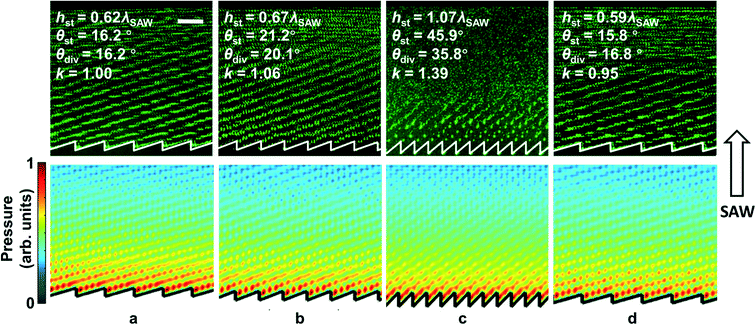 | ||
| Fig. 4 Experimental (top) and simulation (bottom) results for different sawtooth designs, and the corresponding k values from eqn (2). This includes results for θdiv = θst, with (a) k = 1, θdiv < θst (the corresponding video is in ESI† Video S1), with (b) k = 1.06 and (c) k = 1.39, and θdiv > θst, with (d) k = 0.95. Scale bar (top left) is 2λSAW (200 μm). | ||
Each set of images in Fig. 4 shows the geometric parameters for each metasurface, namely hst, θst, θdiv (from simulations), and k. As we are particularly interested in generating angled features with minimum alteration to the fluidic domain, we focus our investigation on interfaces near k = 1, where larger integer values of k correspond to larger channel features with hθ equal to multiple λθ; such larger sawtooth features would more significantly impact the shape of the fluid domain without improving the acoustic field. Fig. 4(a) shows experimental and simulation results in the case where θdiv is equal to θst (k = 1), corresponding to Fig. 3(b). As per the geometric model in eqn (2) (corresponding to the k = 1 line in Fig. 2(b)), the diffractive fringes produced by each sawtooth are continuous with the fringes produced by the previous sawtooth. Other images examine cases where k > 1 and k < 1. Fig. 4(b) and (c) show the case with h+θ (corresponding to Fig. 3(c)), for instance, where the diffractive fringes produced by a given sawtooth are slightly lower (towards the channel wall) than the fringes produced by the sawtooth on its left side, corresponding to the right side of the k = 1 red line in Fig. 2(b), such that the resulting θdiv is smaller than θst. This is especially notable for the case in Fig. 4(c), where the larger k value results in a pressure field that is angled ≈10° less than the channel features. When k, and therefore the divergence of θdiv from θst, increases, the attenuation of the resulting diffraction fringes in the SAW propagation direction becomes more apparent, equating to a less defined pressure field farther from the transducer; while the aggregate acoustic field is still angled, the misalignment between diffraction fringes results in greater destructive interference. Fig. 4(d), however, shows a design corresponding to Fig. 3(a) and a thus a position to the left of the k = 1 red line in Fig. 2(b), with a θdiv greater than θst. The locations of these designs within the parameter space from Fig. 2(b) are shown in ESI† Fig. S5. For the designs with λSAW = 100 μm in this work, the periodicity of the acoustic patterns is on the order of ∼0.45–0.6λSAW, equating to spacings between 45 μm and 60 μm. ESI† Fig. S6 indicates that that relationship holds true for different wavelengths, with the periodicity scaling proportionally with the SAW wavelength. Particles align along discrete acoustic minima, with the finite-width of the particle patterning locations (the thickness of the particle bands in the experimental images) dictated by the particle loading in the initial state.
ESI† Fig. S7 further shows experimental results with various input powers, up to 0.1 W. Unique to acoustofluidic devices generating periodic fields, the effective extent of the acoustic field can be modulated by varying the input power. ESI† Fig. S8 shows that filling readily occurs in our devices without the formation of air bubbles, bubbles that may be introduced at higher perfusion flow rates during filling can be eliminated by slightly pressurizing the channels and/or using degassed fluids.70,71
Fig. 5 examines the relationship between θst and θdiv in finer detail, further demonstrating how the acoustic fringe angle can diverge from that of the metasurface. We show this in Fig. 5 by presenting experimental, simulation, and analytical results for sawtooth designs with constant θst but gradually increasing hst, effectively moving in the horizontal axis across Fig. 2(b). The horizontal position in each of the micrographs at the top of Fig. 5(a) and (b) corresponds to the value of the horizontal axis (i.e., σ) in the plot below. Fig. 5(a and b) shows the results for θst = 25.2° and θst = 29.7°, where the hst of each sawtooth increases by 2% and 1% between subsequent features, respectively. The experimental θdiv angle here corresponds to the angle of the patterned particles measured directly above the neighboring sets of sawtooth features, with error bars representing ±1 standard deviation. The metasurface has no significant effect on the apparent acoustic field angle for σ ≲ 0.4. However, when σ ≳ 0.4, a tilted acoustic field with a negative correlation between θdiv and σ is observed. For σ ≲ 0.65, an angled acoustic field with θdiv > θst appears, corresponding to h−θ, with θdiv decreasing until θdiv = θst when σ ≈ 0.65 (with k = 1). Further increases in σ yield further θdiv decreases below θst (with k < 1) for each of the simulation, modeling and experimental cases shown. Highlighting the importance of the metasurface dimensions relative to the acoustic wavelength, the angle of the acoustic field can diverge more than 50% from the sawtooth angles.
Fig. 6(a) and (b) show example applications and simulation results of this metasurface approach beyond generating arbitrary acoustic field orientations. Fig. 6(a), for instance, shows that these orientations can be inverted as well, where arranging the sawtooth features in opposite generates a V-shaped periodic acoustic field pattern, in this case where σ = 0.93 and θst = 29.7° (k = 1.4). Fig. 6(b) shows the experimental results for the same θst (29.7°), but where σ increases from 0.29 to 0.35 (left to right). While this domain does not result in an appreciably angled field, this range of σ nevertheless yields unique patterning phenomena. This pattern is a result of the small sawtooth dimensions, resulting in periodically overlapping interference fringes from each of these sub-wavelength features, and where different hexagonal/pentagonal interference patterns result as σ increases.
In Fig. 6(c) further demonstrates the combination of this metasurface approach with continuous flow, where the experimental image here shows the particle separation activity in the case where θst = 16.2° and σ = 0.65 (k = 1.05). In the top left image, 10 μm particles (green) and 1 μm particles (orange) are hydrodynamically focused in a flow with a particle flow rate of 1 μL min−1 and a sheath flow rate of 3.5 μL min−1 prior to SAW excitation, the focused particle solution continues unperturbed by the neighboring sawtooth channel features. The top right figure in Fig. 6(c) shows that after SAW is excited at 0.1 W and 39.31 MHz, 10 μm particles are separated from smaller 1 μm particles, and migrate along the acoustic field acoustic minima at an angle to the fluid direction. The bottom figures in Fig. 6 show the simulated acoustic fields. We note that for particles with a particle size much smaller than acoustic wavelength, the acoustic radiation force arising from time-averaged field gradients dominates particle trajectories and the directional action of the traveling wave force is comparatively small72 (for κ < 1.28 ± 0.10;73 here κ < 0.84 for all particles). Interestingly, this setup is essentially equivalent to highly effective setups employing angled acoustic fields for particle sorting,74,75 though with the beneficial characteristics that both only a single transducer is utilized and that the acoustic field can be arbitrarily limited, tuned and reoriented by modifying the channel features independently of the acoustic actuation source.
The diffractive metasurface approach is further expanded from sawtooth metasurfaces to additional sawtooth-like metasurfaces and other channel interface shapes. Example simulation results of the acoustic pressure fields from such shapes are shown in ESI† Fig. S9. For ease of interpretation, features with widths larger than the SAW wavelength are presented here. A sawtooth-like metasurface, one with curved rather than straight interface features, can also produce a spatially continuous acoustic field pattern. The principle of sawtooth-like metasurfaces is similar in that the patterns generated by each element combine to generate a shaped field that corresponds to the shape of the interface elements (Fig. S9(a)–(e)†). Other interface element shapes (staired features, circular shapes in Fig. S9(f)–(i)†) yield complex fields as well, while still generating acoustic fields whose overall morphology matches that or the underlying interface elements. There is future potential for more complex such acoustic fields to be obtained through the combination of different metasurface shapes, including through the use of algorithmic and machine-learning based design approaches.
Conclusion
In this work we have presented an acoustic metasurface approach ideal for use in microfluidic systems. This is comprised of a straightforward implementation of sawtooth features though sub-wavelength modification of a microchannel interface. Compared to other acoustic metasurfaces based on complex geometries, this approach is uniquely suitable for high frequency actuation and use in microfluidic systems, with only conventional soft-lithography methods used to define the metasurface features. These benefits are partly driven by the physics relevant to this form of acoustic field manipulation, where the metasurface features determine the shape and orientation of the diffractive acoustic fringes. We find here that the acoustic field orientation is also related to metasurface dimensions relative to the SAW wavelength, permitting the steering of an acoustic field without changing the metasurface sub-unit angle. Compared to previous diffractive acoustic implementations, using such a sub-wavelength metasurface decouples the acoustic field from the bulk shape of the fluid domain, permitting varied acoustic fields to be generated without substantially altering fluid flow. Even though the channel shape is varied only within a region smaller than the SAW wavelength, the reoriented acoustic field that is generated can span an entire channel. This method also has significant advantages compared with typical SAW approaches, which generally create a uniform standing wave over the entire IDT aperture, where we can instead generate multiple acoustic field orientations in the same device while using only one transducer. Additionally, as the traveling wave magnitude attenuates along the propagation direction, the magnitude and effective extent of the acoustic field can be arbitrarily tuned. This also uniquely appropriate for use microfluidic devices compared to other metasurface approaches, where sawtooth metasurfaces can be defined and the resulting acoustic fields arbitrarily oriented, all while requiring one transducer, and without the need for complex sub-wavelength 3D metamaterial fabrication, aiding miniaturization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed in part at the Melbourne Centre for Nanofabrication (MCN) in the Victorian Node of the Australian National Fabrication Facility (ANFF). Dr. Collins is the recipient of a Discovery Early Career Researcher Award from the Australian Research Council (DECRA, DE200100909), and funding from the National Health and Medical Research Council (Ideas, APP2003446).References
- V. Goranov, T. Shelyakova, R. De Santis, Y. Haranava, A. Makhaniok and A. Gloria, et al., 3D Patterning of cells in Magnetic Scaffolds for Tissue Engineering, Sci. Rep., 2020, 10(1), 2289 CrossRef CAS PubMed.
- J. Kobayashi, A. Kikuchi, T. Aoyagi and T. Okano, Cell sheet tissue engineering: Cell sheet preparation, harvesting/manipulation, and transplantation, J. Biomed. Mater. Res., Part A, 2019, 107(5), 955–967 CrossRef CAS PubMed.
- I. Calejo, R. Costa-Almeida, R. L. Reis and M. E. Gomes, A Physiology-Inspired Multifactorial Toolbox in Soft-to-Hard Musculoskeletal Interface Tissue Engineering, Trends Biotechnol., 2020, 38(1), 83–98 CrossRef CAS PubMed.
- K. Kooiman, H. J. Vos, M. Versluis and N. de Jong, Acoustic behavior of microbubbles and implications for drug delivery, Adv. Drug Delivery Rev., 2014, 72, 28–48 CrossRef CAS.
- K. Villa, L. Krejčová, F. Novotný, Z. Heger, Z. Sofer and M. Pumera, Cooperative Multifunctional Self-Propelled Paramagnetic Microrobots with Chemical Handles for Cell Manipulation and Drug Delivery, Adv. Funct. Mater., 2018, 28(43), 1804343 CrossRef.
- P. Li, Z. Mao, Z. Peng, L. Zhou, Y. Chen and P.-H. Huang, et al., Acoustic separation of circulating tumor cells, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(16), 4970–4975 CrossRef CAS.
- M. Wu, P.-H. Huang, R. Zhang, Z. Mao, C. Chen and G. Kemeny, et al., Circulating Tumor Cell Phenotyping via High-Throughput Acoustic Separation, Small, 2018, 14(32), 1801131 CrossRef.
- M. Tayebi, D. Yang, D. J. Collins and Y. Ai, Deterministic Sorting of Submicrometer Particles and Extracellular Vesicles Using a Combined Electric and Acoustic Field, Nano Lett., 2021, 21(16), 6835–6842 CrossRef CAS PubMed.
- Y. Zhou, S. Basu, E. Laue and A. A. Seshia, Single cell studies of mouse embryonic stem cell (mESC) differentiation by electrical impedance measurements in a microfluidic device, Biosens. Bioelectron., 2016, 81, 249–258 CrossRef CAS PubMed.
- L. Huang, F. Liang, Y. Feng, P. Zhao and W. Wang, On-chip integrated optical stretching and electrorotation enabling single-cell biophysical analysis, Microsyst. Nanoeng., 2020, 6(1), 57 CrossRef CAS.
- Y. Xie, H. Bachman and T. J. Huang, Acoustofluidic methods in cell analysis, TrAC, Trends Anal. Chem., 2019, 117, 280–290 CrossRef CAS PubMed.
- P. Zhang, J. Rufo, C. Chen, J. Xia, Z. Tian and L. Zhang, et al., Acoustoelectronic nanotweezers enable dynamic and large-scale control of nanomaterials, Nat. Commun., 2021, 12(1), 3844 CrossRef CAS.
- M. Tayebi, R. O'Rorke, H. C. Wong, H. Y. Low, J. Han and D. J. Collins, et al., Massively Multiplexed Submicron Particle Patterning in Acoustically Driven Oscillating Nanocavities, Small, 2020, 16(17), 2000462 CrossRef CAS PubMed.
- L. Zwi-Dantsis, B. Wang, C. Marijon, S. Zonetti, A. Ferrini and L. Massi, et al., Remote Magnetic Nanoparticle Manipulation Enables the Dynamic Patterning of Cardiac Tissues, Adv. Mater., 2020, 32(6), 1904598 CrossRef CAS PubMed.
- X. Wang, C. Ho, Y. Tsatskis, J. Law, Z. Zhang and M. Zhu, et al., Intracellular manipulation and measurement with multipole magnetic tweezers, Sci. Robot., 2019, 4(28), eaav6180 CrossRef PubMed.
- S.-I. Han, C. Huang and A. Han, In-droplet cell separation based on bipolar dielectrophoretic response to facilitate cellular droplet assays, Lab Chip, 2020, 20(20), 3832–3841 RSC.
- P.-E. Thiriet, J. Pezoldt, G. Gambardella, K. Keim, B. Deplancke and C. Guiducci, Selective Retrieval of Individual Cells from Microfluidic Arrays Combining Dielectrophoretic Force and Directed Hydrodynamic Flow, Micromachines, 2020, 11(3), 322 CrossRef PubMed.
- C.-K. He, Y.-W. Chen, S.-H. Wang and C.-H. Hsu, Hydrodynamic shuttling for deterministic high-efficiency multiple single-cell capture in a microfluidic chip, Lab Chip, 2019, 19(8), 1370–1377 RSC.
- Y. Liang, G. Liang, Y. Xiang, J. Lamstein, R. Gautam and A. Bezryadina, et al., Manipulation and Assessment of Human Red Blood Cells with Tunable “Tug-of-War” Optical Tweezers, Phys. Rev. Appl., 2019, 12(6), 064060 CrossRef CAS.
- W. T. Coakley, D. W. Bardsley, M. A. Grundy, F. Zamani and D. J. Clarke, Cell Manipulation in Ultrasonic Standing Wave Fields, J. Chem. Technol. Biotechnol., 1989, 44(1), 43–62 CrossRef.
- T. Luo, L. Fan, R. Zhu and D. Sun, Microfluidic single-cell manipulation and analysis: Methods and applications, Micromachines, 2019, 10(2), 1–31 CrossRef.
- T. Laurell, F. Petersson and A. Nilsson, Chip integrated strategies for acoustic separation and manipulation of cells and particles, Chem. Soc. Rev., 2007, 36(3), 492–506 RSC.
- K. Kolesnik, M. Xu, P. V. S. Lee, V. Rajagopal and D. J. Collins, Unconventional acoustic approaches for localized and designed micromanipulation, Lab Chip, 2021, 21(15), 2837–2856 RSC.
- X. Ding, P. Li, S.-C. S. Lin, Z. S. Stratton, N. Nama and F. Guo, et al., Surface acoustic wave microfluidics, Lab Chip, 2013, 13(18), 3626 RSC.
- F. Li, Y. Xiao, J. Lei, X. Xia, W. Zhou and L. Meng, et al., Rapid acoustophoretic motion of microparticles manipulated by phononic crystals, Appl. Phys. Lett., 2018, 113(17), 173503 CrossRef.
- M. Gedge and M. Hill, Acoustofluidics 17: Theory and applications of surface acoustic wave devices for particle manipulation, Lab Chip, 2012, 12, 2998–3007 RSC.
- M. C. Jo and R. Guldiken, Particle manipulation by phase-shifting of surface acoustic waves, Sens. Actuators, A, 2014, 207, 39–42 CrossRef CAS.
- C. Han, Y. Wang and D. Mei, Acoustofluidic waveguides for fabrication of localized polymeric microstructure arrays, Appl. Phys. A: Mater. Sci. Process., 2020, 126(8), 651 CrossRef CAS.
- A. Chaalane, M. Addouche, R. Zeggari, D. Guneysu, F. Lardet-Vieudrin and A. Bermak, et al., Tunable Separation of Nanoparticles in a Continuous Flow Using Standing Surface Acoustic Wave, Sens. Transducers, 2019, 238(11), 72–79 Search PubMed.
- D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves, Nat. Commun., 2015, 6, 8686 CrossRef CAS.
- X. Tao, T. D. Nguyen, H. Jin, R. Tao, J. Luo and X. Yang, et al., 3D patterning/manipulating microparticles and yeast cells using ZnO/Si thin film surface acoustic waves, Sens. Actuators, B, 2019, 299, 126991 CrossRef CAS.
- Z. Ma, D. J. Collins and Y. Ai, Single-actuator Bandpass Microparticle Filtration via Traveling Surface Acoustic Waves, Colloid Interface Sci. Commun., 2017, 16, 6–9 CrossRef CAS.
- D. J. Collins, A. Neild and Y. Ai, Highly focused high-frequency travelling surface acoustic waves (SAW) for rapid single-particle sorting, Lab Chip, 2016, 16(3), 471–479 RSC.
- C. Devendran, D. J. Collins, Y. Ai and A. Neild, Huygens-Fresnel acoustic interference and the development of robust time-averaged patterns from traveling surface acoustic waves, Phys. Rev. Lett., 2017, 118(15), 154501 CrossRef.
- D. J. Collins, R. O'Rorke, C. Devendran, Z. Ma, J. Han and A. Neild, et al., Self-Aligned Acoustofluidic Particle Focusing and Patterning in Microfluidic Channels from Channel-Based Acoustic Waveguides, Phys. Rev. Lett., 2018, 120(7), 074502 CrossRef CAS.
- A. Fakhfouri, C. Devendran, T. Albrecht, D. J. Collins, A. Winkler and H. Schmidt, et al., Surface acoustic wave diffraction driven mechanisms in microfluidic systems, Lab Chip, 2018, 18(15), 2214–2224 RSC.
- H. G. Kraus, Huygens–Fresnel–Kirchhoff wave-front diffraction formulation: spherical waves, J. Opt. Soc. Am. A, 1989, 6(8), 1196 CrossRef.
- D. J. Collins, R. O'Rorke, A. Neild, J. Han and Y. Ai, Acoustic fields and microfluidic patterning around embedded micro-structures subject to surface acoustic waves, Soft Matter, 2019, 15(43), 8691–8705 RSC.
- C. Devendran, K. Choi, J. Han, Y. Ai, A. Neild and D. J. Collins, Diffraction-based acoustic manipulation in microchannels enables continuous particle and bacteria focusing, Lab Chip, 2020, 20(15), 2674–2688 RSC.
- S. J. Raymond, D. J. Collins, R. O'Rorke, M. Tayebi, Y. Ai and J. Williams, A deep learning approach for designed diffraction-based acoustic patterning in microchannels, Sci. Rep., 2020, 10(1), 1–12 CrossRef.
- B. Assouar, B. Liang, Y. Wu, Y. Li, J.-C. Cheng and Y. Jing, Acoustic metasurfaces, Nat. Rev. Mater., 2018, 3(12), 460–472 CrossRef CAS.
- Y. Zhu, K. Donda, S. Fan, L. Cao and B. Assouar, Broadband ultra-thin acoustic metasurface absorber with coiled structure, Appl. Phys. Express, 2019, 12(11), 114002 CrossRef CAS.
- W. Wang, Y. Xie, B.-I. Popa and S. A. Cummer, Subwavelength diffractive acoustics and wavefront manipulation with a reflective acoustic metasurface, J. Appl. Phys., 2016, 120(19), 195103 CrossRef.
- Y. Zhu, X. Fan, B. Liang, J. Cheng and Y. Jing, Ultrathin acoustic metasurface-based Schroeder diffuser, Phys. Rev. X, 2017, 7(2), 21034 Search PubMed.
- S.-D. Zhao, A.-L. Chen, Y.-S. Wang and C. Zhang, Continuously Tunable Acoustic Metasurface for Transmitted Wavefront Modulation, Phys. Rev. Appl., 2018, 10(5), 054066 CrossRef CAS.
- J. Xia, X. Zhang, H. Sun, S. Yuan, J. Qian and Y. Ge, Broadband Tunable Acoustic Asymmetric Focusing Lens from Dual-Layer Metasurfaces, Phys. Rev. Appl., 2018, 10(1), 014016 CrossRef CAS.
- Y. Li and B. M. Assouar, Acoustic metasurface-based perfect absorber with deep subwavelength thickness, Appl. Phys. Lett., 2016, 108(6), 063502 CrossRef.
- Y. Li, C. Shen, Y. Xie, J. Li, W. Wang and S. A. Cummer, et al., Tunable Asymmetric Transmission via Lossy Acoustic Metasurfaces, Phys. Rev. Lett., 2017, 119(3), 035501 CrossRef PubMed.
- L. Ye, C. Qiu, J. Lu, K. Tang, H. Jia and M. Ke, et al., Making sound vortices by metasurfaces, AIP Adv., 2016, 6(8), 85007 CrossRef.
- X. Jiang, Y. Li, B. Liang, J. Cheng and L. Zhang, Convert Acoustic Resonances to Orbital Angular Momentum, Phys. Rev. Lett., 2016, 117(3), 034301 CrossRef PubMed.
- R. Ghaffarivardavagh, J. Nikolajczyk, R. Glynn Holt, S. Anderson and X. Zhang, Horn-like space-coiling metamaterials toward simultaneous phase and amplitude modulation, Nat. Commun., 2018, 9(1), 1349 CrossRef PubMed.
- H. Wu, H. Zhang and C. Hao, Reconfigurable spiral underwater sound-absorbing metasurfaces, Extreme Mech. Lett., 2021, 47, 101361 CrossRef.
- S. Chen, Y. Fan, F. Yang, Y. Jin, Q. Fu and J. Zheng, et al., Engineering Coiling-Up Space Metasurfaces for Broadband Low-Frequency Acoustic Absorption, Phys. Status Solidi RRL, 2019, 13(12), 1900426 CrossRef CAS.
- X. Zhao, L. Cai, D. Yu, Z. Lu and J. Wen, A low frequency acoustic insulator by using the acoustic metasurface to a Helmholtz resonator, AIP Adv., 2017, 7(6), 065211 CrossRef.
- S. Tang, B. Ren, Y. Feng, J. Song and Y. Jiang, Broadband acoustic focusing via binary rectangular cavity/Helmholtz resonator metasurface, J. Appl. Phys., 2021, 129(15), 155307 CrossRef CAS.
- Z. Tian, C. Shen, J. Li, E. Reit, Y. Gu and H. Fu, et al., Programmable Acoustic Metasurfaces, Adv. Funct. Mater., 2019, 29(13), 1808489 CrossRef PubMed.
- P. Liu, X. Chen, W. Xu and Y. Pei, Magnetically controlled multifunctional membrane acoustic metasurface, J. Appl. Phys., 2020, 127(18), 185104 CrossRef CAS.
- K. Watanabe, M. Fujita and K. Tsuruta, Design of non-circular membranes metasurfaces for broadband sound absorption, Jpn. J. Appl. Phys., 2020, 59(SK), SKKA06 CrossRef CAS.
- Y. Xie, W. Wang, H. Chen, A. Konneker, B.-I. Popa and S. A. Cummer, Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface, Nat. Commun., 2014, 5, 5553 CrossRef CAS PubMed.
- F. Ma, M. Huang, Y. Xu and J. H. Wu, Bilayer synergetic coupling double negative acoustic metasurface and cloak, Sci. Rep., 2018, 8(1), 5906 CrossRef.
- H. Esfahlani, S. Karkar, H. Lissek and J. R. Mosig, Acoustic carpet cloak based on an ultrathin metasurface, Phys. Rev. B, 2016, 94(1), 014302 CrossRef.
- S. Li, X. Ding, Z. Mao, Y. Chen, N. Nama and F. Guo, et al., Standing surface acoustic wave (SSAW)-based cell washing, Lab Chip, 2015, 15(1), 331–338 RSC.
- X. Ding, S.-C. S. Lin, M. I. Lapsley, S. Li, X. Guo and C. Y. Chan, et al., Standing surface acoustic wave (SSAW) based multichannel cell sorting, Lab Chip, 2012, 12(21), 4228 RSC.
- L. Zhao, P. Niu, E. Casals, M. Zeng, C. Wu and Y. Yang, et al., Phase separation of a nonionic surfactant aqueous solution in a standing surface acoustic wave for submicron particle manipulation, Lab Chip, 2021, 21(4), 660–667 RSC.
- K. Kolesnik, P. Hashemzadeh, D. Peng, M. E. M. Stamp, W. Tong and V. Rajagopal, et al., Periodic Rayleigh streaming vortices and Eckart flow arising from traveling-wave-based diffractive acoustic fields, Phys. Rev. E, 2021, 104(4), 45104 CrossRef CAS.
- P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces, Lab Chip, 2012, 12(22), 4617–4627 RSC.
- B. Tiller, J. Reboud, M. Tassieri, R. Wilson and J. M. Cooper, Frequency dependence of microflows upon acoustic interactions with fluids, Phys. Fluids, 2017, 29(12), 122008 CrossRef.
- R. O'Rorke, D. Collins and Y. Ai, A rapid and meshless analytical model of acoustofluidic pressure fields for waveguide design, Biomicrofluidics, 2018, 12(2), 024104 CrossRef.
- L. A. F. Fernandes and M. M. Oliveira, Real-time line detection through an improved Hough transform voting scheme, Pattern Recognit., 2008, 41(1), 299–314 CrossRef.
- J. H. Kang, Y. C. Kim and J.-K. Park, Analysis of pressure-driven air bubble elimination in a microfluidic device, Lab Chip, 2008, 8(1), 176–178 RSC.
- I. Pereiro, A. Fomitcheva Khartchenko, L. Petrini and G. V. Kaigala, Nip the bubble in the bud: a guide to avoid gas nucleation in microfluidics, Lab Chip, 2019, 19(14), 2296–2314 RSC.
- Z. Ma, Y. Zhou, D. J. Collins and Y. Ai, Fluorescence activated cell sorting via a focused traveling surface acoustic beam, Lab Chip, 2017, 17(18), 3176–3185 RSC.
- V. Skowronek, R. W. Rambach, L. Schmid, K. Haase and T. Franke, Particle Deflection in a Poly(dimethylsiloxane) Microchannel Using a Propagating Surface Acoustic Wave: Size and Frequency Dependence, Anal. Chem., 2013, 85(20), 9955–9959 CrossRef CAS PubMed.
- H. Ahmed, G. Destgeer, J. Park, M. Afzal and H. J. Sung, Sheathless Focusing and Separation of Microparticles Using Tilted-Angle Traveling Surface Acoustic Waves, Anal. Chem., 2018, 90(14), 8546–8552 CrossRef CAS , Available from: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85048821087&doi=10.1021%2Facs.analchem.8b01593&partnerID=40&md5=484e850ed1d3a059a01ba87e516fdd3f.
- D. J. Collins, T. Alan and A. Neild, Particle separation using virtual deterministic lateral displacement (vDLD), Lab Chip, 2014, 14(9), 1595–1603 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc00711d |
| This journal is © The Royal Society of Chemistry 2022 |