Ionic liquids for renewable thermal energy storage – a perspective

Abstract

Thermal energy storage systems utilising phase change materials have the potential to overcome the intermittency issues associated with most renewable energy sources, significantly contributing to the decarbonisation of the energy sector. While the concept of storing energy in the latent heat of a phase transition is not new, large scale systems employing this concept have not yet realised their full potential. This is in large part due to the shortcomings of conventionally used materials – whether it be issues with their flammability, chemical and thermal instability, corrosivity, poor cycling stability, or a combination of these. Ionic liquids offer a suite of inherent “green” properties that translate well into the field of phase change materials, namely low volatility, low flammability, and good thermal and chemical stability, alongside the potential to tune their chemical and phase properties. In this Perspective, we discuss the evolution and promise of the emerging field of ionic liquids for renewable thermal energy storage. Systems are considered from a holistic, sustainable point of view, demonstrating the importance of assessing material origins and synthetic pathways as well as system performance through lifecycle assessment. We elucidate the emerging design rules for optimising thermal properties, and in doing so attempt to provide an overview of promising emerging systems and future directions.

---

1. Introduction

Warming of the climate,¹ compromised ecosystems,² and threats to public health caused by depleted air quality³ are all crises frequently attributed to our continued use of fossil fuels for energy. Couple these realities with the inherent unsustainability of fossil fuels due to rapidly depleting reserves⁴ and we are confronted with the reality that transitioning to a carbon-free energy sector is not only a necessity, but that it must be done fast – delays in mitigation efforts will only amplify the challenge.⁵ The good news is that the solutions are within reach; renewable energy sources are abundant and can aid this transition, foreseeing a reduction in global CO₂ emissions of over 30 billion tonnes annually.⁶ To accommodate renewable energy systems, however, sustainable energy storage technologies must be developed to facilitate their continuous use during natural fluctuations of availability. It has been estimated that anywhere between a six- and 17-fold increase in deployed battery storage would be needed to accommodate a doubling of renewable energy generation.⁷ The requirement for alternative energy storage technologies that can complement renewable energy systems is thus ever-pressing.

Thermal energy storage (TES) systems represent a favourable emerging solution in a number of contexts, as not only do they provide the option to store and deliver energy in the form it is globally most used,⁷ the capture-storage mechanism in TES systems need not convert the energy between forms (e.g. thermal to electrical). This theoretically allows the design of non-complex and highly efficient systems. Current TES technologies most commonly use molten salts which have high specific heat capacities, allowing the storage of large quantities of sensible heat (defined as heat used only to increase the temperature of a system, without inducing any change of phase). These systems are most commonly used in concentrated solar plants, allowing the continuous discharge of energy during solar downtimes as the “charged” salts transfer heat to a heat transfer fluid, which is used to drive a steam turbine. This type of TES system is effective and can have a large impact – in 2013, the Gemasolar concentrated solar plant in Spain used molten salt technology to deliver a consistent baseload of electricity for 36 days. This single plant generates sufficient energy to power 25 000 homes, reducing CO₂ emissions by 30 000 tonnes per year.⁸

Molten salts are typically mixtures of nitrate, chloride, carbonate, or fluoride alkali salts. The most commonly used combination is a non-eutectic mixture of 60% NaNO₃ and 40% KNO₃ (wt%), dubbed Solar Salt. Within its operating range of 240 °C–565 °C, this salt can reversibly store thermal energy at 901 MJ m⁻³ at a cost of 2.65 $ MJ⁻¹.⁹ This compares favourably with other current energy storage technologies, with lithium ion batteries currently averaging ∼38 $ MJ⁻¹ of stored electrical energy.¹⁰ While effective in this context, the typically high melting temperatures of inorganic salts limits these materials to high temperature cycles, excluding them from important lower temperature TES applications (e.g. space and water heating, waste heat recovery, etc.). Furthermore, these systems require precise temperature control, as solidification can cause damage to equipment.⁷ For lower temperature applications, water is commonly used as a sensible heat storage medium, which is attractive for a plethora of obvious reasons (low cost and low toxicity etc.), as well as its high specific heat capacity (C_p = 4.2 J g⁻¹), but is limited to temperatures around 100 °C and below.

The performance of TES systems can be considerably improved if the operating temperature range includes a phase transition in the thermal energy storage material, allowing additional energy to be stored in the form of latent heat. The latent heat describes the amount of energy absorbed by a material during a phase change, which is in turn released when the reverse transition occurs. Materials used for this purpose are suitably named phase change materials (PCMs), and while many phase transitions (liquid–gas, solid–gas, etc.) may be utilised, solid to liquid transitions are particularly desirable, as containment vessels need not account for a substantial change in volume upon transition. For solid to liquid PCMs, the energy storage density is dictated by the enthalpy of fusion (ΔH_f) of the material. In contrast to purely sensible heat storage systems, latent heat storage systems can offer high energy storage density within a narrow temperature range. For example, in the case of water, while the high specific heat capacity allows dense storage of sensible heat, its high enthalpy of fusion (333 J g⁻¹) means that the amount of energy released by cooling the material by 1 °C through its liquid–solid transition is ∼80 times greater than the energy released from cooling liquid water by 1 °C if no solidification is induced by the cooling.

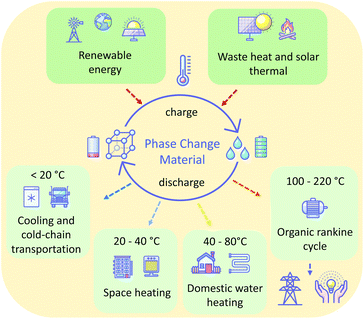
Furthermore, by choice of a material having an appropriate melting temperature (T_m), PCMs can operate over any temperature range. This allows their use in a range of contexts. In general, low melting point PCMs (<20 °C) are used in cooling and cold-chain transportation applications,¹¹ ambient (20–40 °C) melting PCMs in space heating,¹² above ambient (40–80 °C) melting PCMs in domestic water heating,¹³ and higher temperature PCMs (>200 °C) for waste heat recovery¹⁴ and solar energy storage¹⁵ (Fig. 1). A wide range of materials are used as PCMs for these various applications, including paraffins, metal-salt hydrates, sugar alcohols, and polymers. Unfortunately, many of these materials suffer from drawbacks, inherent to the nature of the materials, that make their practical application challenging. Such drawbacks variously include flammability, corrosivity, supercooling tendencies, and poor cycling stability as a result of phase separation or instability. The latter of these is prohibitive: cycling stability is critical for the PCM to offer a long-term storage solution. For these reasons, there is a demand for new materials that offer ideal thermal properties and are safe, economical and stable in the context of use for given applications. Additionally, perhaps owing to the conventional (but restrictive) definition of ILs as salts with melting temperatures below 100 °C, there is a lack of reported liquid salts that melt in the intermediate temperature range (100–220 °C), despite the possibility of PCMs that melt in this range offering a new solution for the storage of renewable thermal energy.¹⁶

Fig. 1 Concept and application of solid to liquid phase change materials, where the “charging” consists of melting the PCM material, and the energy released by the crystallisation process during “discharge” can be used in many diverse applications, depending on the T_m of the PCM.

Around the same time that the world was coming to terms with the stark consequences of a carbon-based energy sector, the field of ionic liquids (ILs) was emerging and developing apace as researchers strived for greener chemical processes. Initial work in the IL field focussed on the potential for ILs to act as “green” solvents,¹⁷ owing to a collection of inherent properties including low volatility, low flammability/flame retardancy, and generally good thermal and chemical stability. These properties have seen the application of ILs propelled beyond their use as solvents, into applications including electrochemistry,¹⁸ pharmaceuticals,¹⁹ and lubricants.²⁰ More recently, it has been realised that these properties are advantageous for the field of PCMs – drawbacks of the present PCM materials (e.g. flammability, volatility, corrosivity) are suitably negligible in many ionic liquids. Furthermore, their typically high densities allow high volumetric energy storage capacities (MJ m⁻³), and structural alterations to cations and anions provides scope to tune chemical and phase properties to suit the desired application.

In this Perspective, through a “green” lens, we describe the evolution of the emerging field of ionic liquids for thermal energy storage. We develop a view that to accelerate this field further, an enhanced understanding of the structure–property relationships that underpin the melting properties of ILs is needed. This can be challenging, as previous research into their applications as solvents, electrolytes, etc. has focussed almost solely on the properties of the liquid state. As such, while there is an abundance of data reported on properties such as liquid density and viscosity, and while melting temperatures are often included, data on other melting properties (e.g. ΔH_f, volume change (ΔV_f), and entropy change (ΔS_f)) is scarcely reported.^21,22

Nonetheless, in this Perspective we highlight emerging understanding of common structural features that can be incorporated into the design of ILs to promote favourable interactions and tailor melting properties. Furthermore, we illustrate the importance of constructing the “whole picture” to assess the sustainability of materials in thermal energy storage applications – specifically through lifecycle assessment (LCA) methods that establish environmental footprints by consideration of material origins and synthetic pathways alongside system performance.

2. Ionic liquids as PCMs

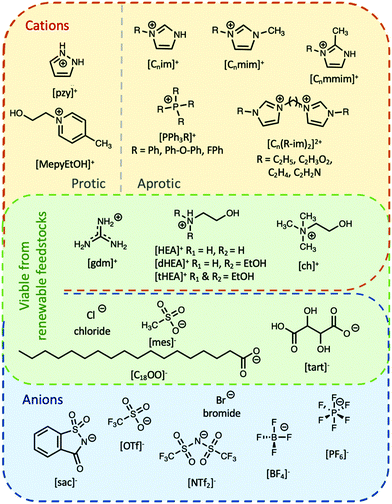
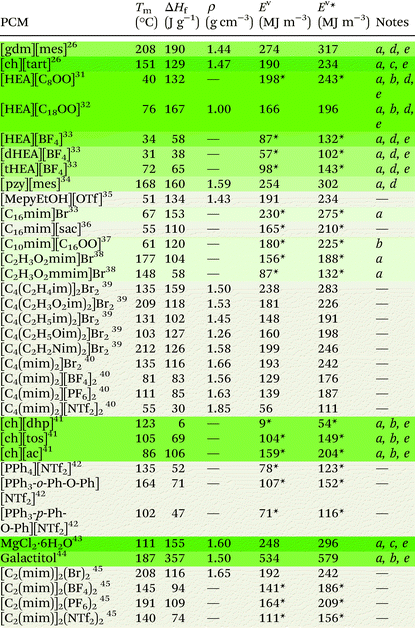
Ionic liquids can be broadly divided into two categories: protic and aprotic. Both have advantages and disadvantages that influence their suitability for any of the diverse range of applications of ILs. For example, a benefit of protic ionic liquids is their facile synthesis, as they form via a simple proton transfer reaction between a Brønstead acid and a Brønstead base. However, this labile proton can lead to non-negligible vapour pressures,²³ which may constitute a drawback for some applications; notably, evaporation of some aprotic ILs has also been shown to be possible.²⁴ Common cations and anions used in ILs that have been studied for use as PCMs are presented in Fig. 2. The thermal properties of some ionic liquids discussed herein are detailed in Table 1, alongside some known PCMs for comparison of properties. Table 1 also indicates the potential for the material to be considered a sustainable component, based on a number of criteria including the nature of the synthesis approach, whether one or both of the components are sourced from renewable feedstocks, and the expected degree of environmental toxicity. Aspects of these assessments will be further discussed in the sections below.

Fig. 2 Chemical structures of some of the main cations and anions used in ILs that have been studied for use as PCMs or are discussed in the text. C₂H₅ = ethyl, C₂H₃O₂ = carboxymethyl, C₂H₄ = ethylene, C₂H₂N = cyanomethyl.

Table 1 Thermal properties of the main PCMs discussed in the text. Rows are colour coded from neutral to dark green (most sustainable) to indicate an estimation of the material's sustainability based on the criteria listed in the notes

E ^v = latent volumetric energy storage. E^v* = volumetric energy storage within 20 °C of T_m (T_m ± 10 °C). This value accounts for the small but significant additional energy stored in the form of sensible heat. We have assumed a specific heat capacity (C_p) value of 1.5 J mol⁻¹ K⁻¹ for the calculation because of the absence of data in the solid and liquid state. When density data is not provided, we assume a value of 1.5 g cm⁻³ for the calculation. Values that have been calculated with this assumed density are denoted with an asterisk (*) following the numbers in the E^v and E^v* columns. The Notes column provides information regarding the materials sustainability, where a indicates the material is formed in a one-step synthesis from commonly available starting materials, b indicates one component is sourced from renewable feedstocks, c indicates both components are sourced from renewable feedstocks, d indicates one or more component is viable from renewable feedstocks, and e indicates the material has low environmental toxicity. Rows are colour coded from neutral to dark green (most sustainable) to give an estimation of the materials sustainability based on these criteria.

---

2.1 Protic ionic liquids

Protic ionic liquids have sustainable appeal owing to their 100% atom economical synthesis via a proton transfer reaction. This synthetic route encompasses some of the classic Principles of Green Chemistry²⁵ as waste is minimised, chemical derivatives are avoided, and atom economy is optimised, with the reaction yielding no by-products and often performed using neat conditions. In 2013, we first studied protic organic salts for use as PCMs, investigating the thermal properties of protic salts based on a range of cations including guanidinium and cholinium, with various anions including methanesulfonate (mesylate) trifluoro-methanesulfonate (triflate) and tartrate, among others. Guanidinium mesylate was identified as an attractive candidate for intermediate temperature TES as it melts with an enthalpy of fusion of 190 J g⁻¹ at 208 °C.²⁶ The large enthalpy of fusion of this salt is attributed to extensive hydrogen bonding in the crystal lattice,²⁷ which resembles the interactions found in metal-salt hydrates (see section 3.1).^28,29 Metal-salt hydrates are the oldest and most extensively studied type of PCM, with high enthalpies of fusion but prohibitive drawbacks; in particular, these materials undergo incongruent melting, which leads to phase separation and hinders cyclability. Replicating the extended H-bond networks found in metal-salt hydrates in materials that do not undergo phase separation may thus be a key to achieving PCMs with ideal thermal properties that are stable upon cycling. We subsequently demonstrated that guanidinium mesylate is stable upon cycling, with no change to thermal properties observed over 400 heating/cooling cycles.¹⁶ The high density of this salt (1.44 g cm⁻³) allows high volumetric energy storage, storing 274 MJ m⁻³ during the phase transition (E^v) and 317 MJ m⁻³ in cycles within T_m ± 10 °C (denoted here as E^v*). Cholinium tartrate was also identified as a potential candidate for PCM applications, melting with an enthalpy of fusion of 129 J g⁻¹ at 151 °C (E^v = 190 MJ m⁻³, E^v* = 234 MJ m⁻³). While this energy density is less than that of guanidinium mesylate, both the cation and anion can be sourced from renewable feedstocks and are well recognised to be environmentally benign – both are even considered safe for ingestion by humans.³⁰ As is often the case, identifying an ideal PCM requires a compromise, with a balanced consideration of energy storage density and material origins/synthetic pathways being required to achieve the most sustainable energy storage technology (see section 5).

In the context of providing negative carbon technologies, the benefit of using renewable feedstocks in emerging materials is clear. The conversion of (or some of) the 170 billion tonnes of plant biomass produced annually by nature into useful chemicals via low-energy and non-toxic process pathways is key to reducing greenhouse gases.⁴⁶ Fatty acid-based ILs are an avenue through which this may be achieved, and are appealing for the PCM application as they could conceivably be designed to have large enthalpies of fusion through the cumulative contributions of coulombic, hydrogen bonding, and van der Waals interactions. In striving to understand the complex thermal behaviour, rheology and self-assembly of fatty acid protic ionic liquids, Toledo Hijo et al.³¹ studied a range protic ILs with (mono-, di- and tri-substituted) ethanolamine cations and various fatty acid anions derived from vegetable oils. The study reports enthalpies of fusion as high as 132 J g⁻¹ for [HEA][C₈OO] (T_m = 40 °C) (see Fig. 2 for abbreviations). The stearate ([C₁₈OO]⁻) analogue of this salt has been found to have an enthalpy of fusion of 167 J g⁻¹ upon melting at 76 °C,³² making it a promising candidate for PCM applications in this temperature range (E^v = 166 MJ m⁻³, E^v* = 196 MJ m⁻³). For these ethanolamine fatty acid ILs, melting temperatures were lowest for salts with the di-substituted cation and/or unsaturated anions, likely owing to asymmetry promoting disorder and reducing cation–anion interactions. This is consistent with the findings of Zhu et al.,³³ who studied the same three substituted ethanolamine cations with the tetrafluoroborate ([BF₄]⁻) anion. T_m and ΔH_f were found to be lowest for the di-substituted cation ([dHEA][BF₄], 31 °C and 38 J g⁻¹ respectively). The melting temperature of [HEA][BF₄] was also low (34 °C), while the enthalpy of fusion was found to be substantially higher (58 J g⁻¹). The tri-substituted analogue [tHEA][BF₄] displayed both the highest T_m and ΔH_f (72 °C and 65 J g⁻¹ respectively). Low melting points have also been observed for organic salts with the cholinium cation, where it is postulated that the asymmetry of the cation contributes to the hindrance of regular packing arrangements, resulting in low melting temperatures.⁴⁷ These observations provide a toolbox of structural variations that can allow tuning of melting points to a particular PCM application.

Since our initial study on protic ILs as PCMs, we have studied a range of protic organic salts of the pyrazolium cation, again finding the methanesulfonate analogue to have the highest enthalpy of fusion, melting at 168 °C with an enthalpy of fusion of 160 J g⁻¹ (E^v = 255 MJ m⁻³, E^v* = 302 MJ m⁻³).³⁴ We showed that this material exhibits no changes to thermal properties after more than 130 heating/cooling cycles, demonstrating the possibility of protic organic salts overcoming the stability issues associated with other PCM materials.

Recently, Shi et al.³⁵ studied small pyridinium and imidazolium protic organic salts with the triflate anion for use as PCMs. The authors approached the design phase with computer-aided molecular design (CAMD) methods. This approach, alongside other computational methods (see section 4), is likely to become increasingly common in the design of IL PCMs as it allows the direction of synthetic efforts towards the most promising materials. When predicting PCM performance, the authors considered density, heat capacity and thermal conductivity as well as enthalpy of fusion, and of the nine salts studied, they identified [MepyEtOH][OTf] to be the best material (ΔH_f = 134 J g⁻¹, T_m = 51 °C). This material has a volumetric latent energy storage density of 191 MJ m⁻³, and 234 MJ m⁻³ when operating in a range ± 10 °C of T_m. It is important to note of course that the triflate anion is relatively expensive due to its fluorine content compared to other bio-sourced anions.

2.2 Aprotic ionic liquids

2.2.1 Monocationic imidazolium-based ILs. The synthesis of aprotic ILs can be split into two main steps: formation of the desired cation, followed by an anion exchange (where necessary) to produce the desired salt.⁴⁸ The majority of reported aprotic ILs for thermal energy storage incorporate the imidazolium cation, with structural variations to achieve (or approach) the desired thermal properties. In 2009, Zhu et al.³³ reported a range of alkyl-imidazolium bromides and chlorides, with ΔH_f as high as 153 J g⁻¹ for [C₁₆mim]Br (T_m = 64 °C). The authors found that for three analogous 1-alkyl-2,3-methylimidazolium bromide salts (n = 4, 10, 16), ΔH_f increased with increasing alkyl chain length. For the [C_nmmim]Br salts, T_m increased in the order C₁₀ < C₄ < C₁₆. This is consistent with the trend typically observed for alkyl-substituted imidazolium ILs: lengthening (e.g. from n = 0 to n = 10) initially reduces T_m through destabilisation of coulombic contributions to packing, followed by a steady increase with chain length above ∼n = 8–10, as attractive van der Waals interactions between alkyl chains increase structural ordering in the solid state.⁴⁸ Čanji et al.³⁶ also studied ILs with the [C₁₆mim]⁺ cation for potential use as PCMs, finding the saccharinate analogue [C₁₆mim][sac] to have an enthalpy of fusion of 110 J g⁻¹ (or 98 J g⁻¹, depending on the DSC method used) upon melting at 55 °C. The authors note that the phase behaviour is more complex than simple melting/crystallisation, appearing to have a liquid crystalline phase prior to melting (which was also observed for [C₁₆mim]Cl and is typical for alkyl-imidazolium salts with n > 12 (ref. 49–51)). They further note that feasibility studies, including lifecycle analysis (see section 5), are required to confirm the viability of the material as a PCM. Interestingly, shorter (n = 4–10) 1-alkyl-3-methyl-imidazolium saccharinates have also been studied for use in TES, but in the context of sensible heat storage, owing to the high specific heat capacities of the salts and the fact that they are liquids at RT.⁵²

Another relevant study that offers an interesting new research direction is that of Biswas et al.,³⁷ which investigated the phase behaviour of a range of 1-alkyl-3-methylimidazolium ionic liquids with various fatty acid anions. While these materials were not studied in the context of TES, 1-decyl-3-methylimidazolium palmitate ([C₁₀mim][C₁₆OO]) was reported to melt with an enthalpy of fusion of 120 J g⁻¹ at 61 °C. The authors used density functional methods to examine the molecular structure and ion pair interactions, finding the dominant cation–anion interaction to be hydrogen bonding, where the C2 proton and a proton from the 3-methyl group in the cation each form a hydrogen bond with an oxygen atom on the anionic head group (Fig. 3). Presumably, the cumulative contributions of these interactions, as well as van der Waals attractive forces between the alkyl substituents, is responsible for the relatively high ΔH_f of [C₁₀mim][C₁₆OO]. Comparing [C₁₀mim][C₁₆OO] and [C₁₀mim]Br, (ΔH_f = 120 J g⁻¹ and 67 J g⁻¹ (ref. 33) respectively), it appears that substitution of Br⁻ with palmitate results in a near doubling of ΔH_f due to the long chain van der Waals interactions. It will be interesting, in the future, to see if a higher ΔH_f can be achieved by substituting Br⁻ with palmitate in [C₁₆mim]Br (or other fatty acids with any other long chain alkyl-substituted imidazolium halide salts with high ΔH_f). Notably these long chain fatty acid based materials have bio-material origins and are generally non-toxic.

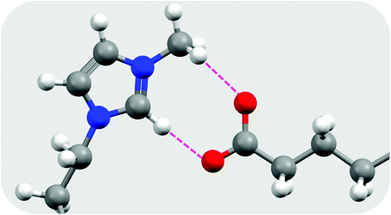Fig. 3 Hydrogen bonding interactions in [C₁₀mim][C₁₆OO] as determined from the optimised geometry at the B3LYP/6-31G(d) level of theory, redrawn from Biswas et al.³⁷ Hydrogen atoms are shown as white spheres, carbon as grey, nitrogen as blue, and oxygen as red. Hydrogen bonds are shown as broken pink lines.

Other studies have also demonstrated the role of hydrogen bonding in imidazolium-based ILs in increasing ΔH_f. For example, methylation at the C2 carbon typically results in decreased enthalpies of fusion, which is attributed to the absence of hydrogen bonds from the C2 proton (see section 3.1). Differences between 2-methylated and non-2-methylated analogues of imidazolium salts have been reported to be as high as 79% for [C₂H₃O₂mim]Br (1-carboxyl-3-methylimidazolium bromide) and [C₂H₃O₂mmim]Br (ΔH_f = 104 J g⁻¹ and 58 J g⁻¹ respectively).³⁸ The same study, which investigated the effects of different functional group substituents on the imidazolium cation on the thermal behaviour of the salts, found that those capable of hydrogen bonding led to higher ΔH_f materials, with higher decomposition temperatures than their alkyl-substituted analogues.

2.2.2 Dicationic imidazolium-based ILs. Other research into aprotic imidazolium-based ILs has focused on dicationic imidazolium cations, where two cationic imidazolium moieties are separated by an alkyl linker chain (Fig. 2). While data on these compounds is limited, dicationic ILs provide scope to tune the thermal properties through increasing the length of the alkyl linker chain, as well as substitution of both cationic moieties with long chain alkyl or other functional groups.⁵³ Furthermore, recent studies have suggested that these dicationic ILs are more thermally stable and have lower toxicity profiles compared to monocationic imidazolium ILs.^54,55 Studies have also found that their heat of fusion is typically higher than their monocationic analogues.^39,40,45 This has been attributed to increased electrostatic and hydrogen bonding interactions between cations and anions in these compounds.³⁹ Similar to monocationic ILs, the 2-methylimidazolium derivatives typically have lower enthalpies of fusion due to the absence of hydrogen bonding interactions from the C2 proton of the imidazolium cations.^40,45 Interestingly, in contrast to monocationic imidazolium-based ILs, methylation at the C2 carbon seems to most often lead to depression of melting points for these materials.^40,45,56

Shorter side chains on the cationic imidazolium moieties have been found to be beneficial to ΔH_f by centralising the positive charge on the imidazolium ring, increasing the interaction energy between ions.⁴⁰ This is consistent with observations that introducing electronegative functional groups into imidazolium rings increases the enthalpy of fusion.³⁸ Zhang et al.³⁹ studied the effects of different side-chain functionalities on the thermal properties and interactions in dicationic imidazolium ILs. The authors found that substitution with functional groups capable of hydrogen bonding leads to increased ΔH_f for the materials. Through NMR studies, they conclude that these functionalities supress hydrogen bonding from the C2 proton as hydrogen bonds from the substituted functional group occur preferentially. Interestingly, of the five functional groups studied (vinyl, carboxyl, ethyl, ether and cyanomethyl – Table 1) the enthalpy of fusion is highest for the vinyl (ethylene) derivative [C₄(C₂H₃im)₂]Br₂ (ΔH_f = 159 J g⁻¹).

In a study by Liu et al.,⁴⁰ that investigated geminal dicationic ILs with methyl substituents on the second nitrogen of the imidazolium cations ([C₄(mim)₂]⁺), the effect of charge dispersity of the anion was found to have significant effects on ΔH_f. In line with other studies,³⁸ the authors found that smaller, less charge disperse anions increased the thermal energy storage density of the salts. The heat of fusion was greatest for the bromide derivative (ΔH_f = 116 J g⁻¹), roughly the same for salts with the [BF₄]⁻ and [PF₆]⁻ anions (ΔH_f = 83 J g⁻¹ and 85 J g⁻¹ respectively), and lowest for the bistriflamide ([NTf₂]⁻) derivative (ΔH_f = 30 J g⁻¹). A similar trend was observed for melting temperatures, although [C₄(mim)₂][PF₆]₂ had a melting temperature 30 °C higher than [C₄(mim)₂][BF₄]₂ (T_m = 111 °C and 81 °C respectively). Since T_m and ΔH_f are thermodynamically linked via the entropy of fusion, ΔS_f = ΔH_f /T_m, the consistency of ΔH_f but higher temperature melting of [C₄(mim)₂][PF₆]₂ suggests that there is less entropic change (ΔS_f) during the melting transition of [C₄(mim)₂][PF₆]₂ compared to [C₄(mim)₂][BF₄]₂.

The highest ΔH_f reported for geminal dicationic ILs is that of [C₄(C₂H₃im)₂]Br₂, which melts at 135 °C with an enthalpy of fusion of 159 J g⁻¹.³⁹ For this dicationic salt, the energy storage density is E^v = 238 MJ m⁻³ (E^v* = 283 MJ m⁻³). This volumetric energy density is competitive among other materials. However, we have been unable to locate thermal cycling data for this material, which is crucial in determining its suitability for PCM applications.

2.2.3 Other aprotic ILs. While the above thermophysical data presents imidazolium-based ILs as promising PCM candidates, some concerns arise regarding their toxicity and complete biodegradability, both of which are significant concerns when large quantities of these materials will be manufactured and distributed. Alternatively, ionic liquids and deep eutectic systems based on the cholinium cation have emerged as being low-cost, non-toxic and biocompatible in nature,⁵⁷ making them promising candidates as PCMs. Recently, the thermophysical properties of a series of cholinium-based ILs were investigated by Parajó et al.⁴¹ The melting point of three different ILs i.e., cholinium dihydrogen phosphate ([ch][dhp]), cholinium tosylate ([ch][tos]) and cholinium acetate ([ch][ac]) were reported to be 123 °C, 105 °C, 86 °C respectively. The enthalpy of fusion was highest for [ch][ac] (106 J g⁻¹), which also produced the highest heat capacity C_p, a property that is governed by the molar mass of a material. In this case, however, the authors attribute such high C_p to the additional ability of the cholinium cation and acetate anion to form hydrogen bonds. [ch][tos] also showed a reasonable enthalpy of fusion (69 J g⁻¹), while that of [ch][dhp] was substantially lower (6 J g⁻¹). Despite encouraging results demonstrated in this work, their application as PCMs is yet to be determined.

In most cases the tuning of anions or cations in aprotic ILs can play a key role in the thermophysical properties. For example, the introduction of an ethereal group in either the cation or the anion has been shown to reduce the melting point, attributed to an increase in the motion and rotation of the ion, inhibiting close packing of the ions.⁵⁸ On the other hand, introducing bulky symmetric groups can often increase the melting temperature and thermal stability of ILs. Recently, a new family of phosphonium-based ILs, particularly those comprised of tetraarylphosphonium cations, show melting points in the range of 100–150 °C, with superior thermal stabilities (>400 °C) (with a few exceptions), making them highly suitable candidates as intermediate PCMs for solar thermal and excess wind energy storage applications.^42,59–61 Cassity et al.⁶⁰ demonstrated that structural modifications of the phosphonium cation can play a key role in the melting point of the IL. For example, in a series of bistriflamide ([NTf₂]⁻) salts, in comparison to salts with the tetraphenylphosphonium cation [PPh₄]⁺ (T_m = 135 °C, ΔH_f = 52 J g⁻¹), a higher T_m and ΔH_f was observed when one phenyl group was replaced with a ortho-phenoxyphenyl functional group, i.e. the [PPh₃-o-Ph-O-Ph]⁺ cation (T_m = 164 °C, ΔH_f = 71 J g⁻¹) (Fig. 4b). Both quantum calculations and molecular dynamics simulations indicate that the introduction of the phenoxyphenyl moiety results in a bent configuration, reducing the electrostatic exposure of the lone pairs of the oxygen atom. This can further increase the cation–cation repulsion, and the authors postulate that the more compact arrangement presumably results in more efficient packing in the crystal lattice, thereby increasing the T_m and ΔH_f. Interestingly, moving the position of the phenoxyphenyl moiety from the ortho- to the para-position (Fig. 4c), reduces both the melting point and ΔH_f (102 °C, and 47 J g⁻¹ respectively). In the para-position, the electronegative phenoxy oxygen is placed further away from the positive phosphorous centre. This results in an increase in the dipole moment, reducing cation–cation repulsion and thus decreasing the melting point of the IL.⁶⁰

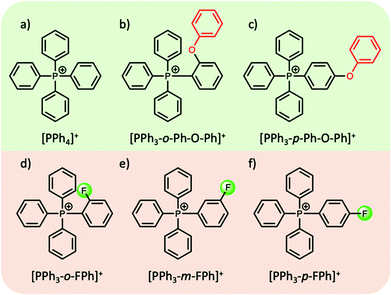Fig. 4 Examples of structural modifications to alter the dipole moment of tetraarylphosphonium cations; (a–c)⁶⁰ (d–f).⁴²

In efforts to lower the melting points in ILs, Rabideau et al.⁴² demonstrated that the replacement of hydrogen atoms with fluorine in certain tetraarylphosphonium cations can further increase the dipole moment (Fig. 4d–f). As mentioned above, the increase in dipole moment can increase cation–cation interactions in the crystalline state, while obstructing cation–anion interactions. However, the cation–anion interactions, which are energetically favoured, are recovered upon melting, lowering the overall ΔH_f and T_m of the IL. Once again, the position of the substituent on the phenyl group, i.e. ortho-, meta-, para-, plays a key role in these interactions and does not always show the expected correlation between the dipole moment and the melting point. Nevertheless, such careful alterations of IL cations (and anions), complemented by computational studies, can be highly beneficial in designing aprotic ILs with thermal properties suitable for their use as PCMs.

3. Tailoring thermal properties

It is well recognised that more work is needed to determine how the properties of ILs change as a function of their ion structures and substitution patterns.⁴⁸ This is especially relevant for their use as PCMs, as data on melting and thermochemical properties is scarcely available. On top of this, the exposition of structure–property relationships that can be used to design new ILs with the desired thermal properties is hindered by discrepancies in the data: reported values can differ tremendously from one source to another.²¹ The main suspects for these discrepancies are impurities – residual synthetic precursors or water absorbed during handling may lead to considerable deviations among data reported for the same compounds.^36,62 Beyond impurities, if melting transitions are determined by visual means, the tendency of ILs to form glasses may lead to confusion,^21,48 or decomposition products may be liquids (or mixtures of the material and solid decomposition products). Both of these possibilities may result in an unrecognised but problematic mismatch between the reported data and true values.⁶³ A related issue stems from partial or complete decomposition during melting; an endotherm due to volatilisation of products can be misinterpreted as a promisingly high ΔH_f. This requires that T_m and ΔH_f data must always be reported for three or more stable cycles. Where this is not the case, literature data must be treated with caution. Nonetheless, from the melting data that is available on ILs, in combination with some data from non-ionic PCM materials, we can elucidate the role that some structural components and their interactions can play in influencing thermal properties.

3.1 Hydrogen bonding

Materials with typically high enthalpies of fusion include metal-salt hydrates (e.g. MgCl₂·6H₂O: T_m = 111 °C, ΔH_f = 155 J g⁻¹),⁴³ sugar alcohols (e.g. galactitol: T_m = 187 °C, ΔH_f = 357 J g⁻¹),⁴⁴ and water (T_m = 0 °C, ΔH_f = 333 J g⁻¹). In the solid state, these materials all form extended hydrogen bond networks (see Fig. 5 for examples). Our research has shown that H-bond networks are also favourable for increasing ΔH_f in protic ionic materials.^26,27,34,64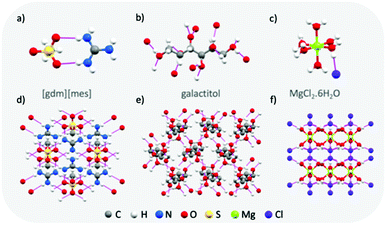

Fig. 5 Examples of the extended hydrogen bond networks found in high enthalpy of melting materials: crystal structures of guanidinium mesylate (a and d), galactitol⁶⁵ (b and e) and MgCl₂·6H₂O⁶⁶ (c and f). Hydrogen bonds are shown as pink lines.

It is important to note that hydrogen bonds are not completely disrupted during melting; it is to be expected that transient H-bonding will remain a feature of the liquid phase. Hence it is the change in average H-bond interaction that represents a contribution to ΔH_f. Being both length and angle dependent the H-bond energy is readily lowered by the loss of rigidity and symmetry of the crystalline structure; nonetheless the extent of H-bonding that is retained in the liquid state remains an important, and difficult to quantify, aspect of understanding and predicting ΔH_f.

Hydrogen bonds have also been shown to be favourable for increasing ΔH_f in aprotic ILs, with imidazolium-based ILs substituted with functional groups capable of hydrogen bonding showing higher ΔH_f than their alkyl-substituted analogues.³⁸ Higher ΔH_f is also observed for imidazolium-based ILs without substitution at the C2 carbon, which is attributed to H-bonding interactions from the C2 proton.³⁸ Interestingly, despite removing the main hydrogen bonding site, methylation at the C2 carbon usually leads to increased melting points (although not always³⁸).^42,67 Fumino et al.⁶⁸ offered an explanation for this counterintuitive increase in T_m, suggesting the methylated derivatives form more stable coulombic networks, whereas hydrogen bonds from the C2 proton introduce “defects” to this network and destabilise the system by increasing the dynamics of the ions (resulting in lower T_m). A different explanation proposed the change in T_m to be entropically driven, as methylation at the C2 carbon decreases the entropy of the liquid state.^67,69 Further studies have suggested that these theories are complementary, and that additional to entropic contributions, C2 methylation leads to redistribution of electron density about the imidazolium ring such that configurational variation is decreased, leading to higher order and tighter packing of molecules in the solid state.⁷⁰ Nonetheless, while an unambiguous explanation of this phenomenon still eludes us,^71–73 this example demonstrates the complexities of establishing structure–property relationships that can aid a rational design process.

3.2 Ion size and charge dispersity

Salts comprised of less charge disperse and/or smaller ions typically have higher enthalpies of fusion and melting points. For substituted methylimidazolium ILs, those functionalised with electron withdrawing groups that centralise the positive charge on the imidazolium ring lead to higher enthalpies of fusion than those observed for their alkyl-substituted analogues.³⁸ When varying the anion between Br⁻, [BF₄]⁻, [PF₆]⁻, and [NTf₂]⁻ for salts with the dicationic imidazolium cation [C₂(mim)₂], Zhang et al.⁴⁵ found T_m and ΔH_f to be highest for the Br⁻ analogue (116 J g⁻¹, 208 °C) and lowest for the [NTf₂]⁻ analogue (74 J g⁻¹, 140 °C). Interestingly, the T_m and ΔH_f of the [PF₆]⁻ analogue was higher than that of the [BF₄]⁻ analogue (ΔH_f = 109 J g⁻¹, T_m = 191 °C and ΔH_f = 94 J g⁻¹, T_m = 145 °C respectively), despite the increased size of the anion. Increased melting points for imidazolium salts with [PF₆]⁻ anions when compared to [BF₄]⁻ salts have also been reported by other authors.^48,50

The trend in increasing ΔH_f and T_m with decreased ion size and charge dispersity is also evident when varying the anion between different halides – for the same cation, ILs with Cl⁻ anions typically have higher ΔH_f and T_m than those with Br⁻ anions.³⁸ These trends have been attributed to increased ion sizes and charge dispersity reducing coulombic attraction contributions to lattice energies.⁴⁸ Furthermore, the symmetry of charge distribution about the ion can have a substantial effect on ΔH_f and T_m. For example, in the phosphonium ILs studied by Rabideau et al.,⁴² greater dipole moments in the phosphonium cation leads to decreased enthalpies of fusion and melting points. This is attributed to an increased free energy of the solid state, as cation–cation repulsion is minimised, leading to cationic domains in the crystalline lattice. The melting process, which recovers these cation–anion interactions, thus includes a negative component into the otherwise positive enthalpy process. Increased ion sizes may also work to lower ΔH_f and T_m if the steric hinderance is sufficient to separate H-bond donor and acceptor sites to distances beyond which hydrogen bonds may be formed.³⁸

3.3 Alkyl branching

For ions with small alkyl substituents, branching may increase ΔH_f and T_m by increasing packing efficiency and atom density, and decreasing free rotation in the solid lattice.⁴⁸ For example, for three isomeric 1-butyl-3-methylimidazolium hexafluorophosphates, the ΔH_f of the tert-butyl isomer (ΔH_f = 292 J g⁻¹) is more than double that of the n-butyl isomer (ΔH_f = 109 J g⁻¹), and the melting point is >20 times higher (T_m = 160 °C and 6 °C respectively).⁴⁸ This trend of increased melting temperatures for branched isomers, which is inverse to the behaviour observed for simple alkane molecules, has also been reported for other imidazolium-based ILs.^74,75 Higher melting points for imidazolium-based ILs with cyclo-alkyl substituents, when compared to their n-alkyl-substituted analogues, has also been reported.⁷⁶ This is likely because the branched- or cyclo-alkyl substituents can have more compact arrangement in the solid lattice. Furthermore, conformational flexibility leads to smaller lattice enthalpies and larger entropy changes on melting that lower melting points.⁷⁷ Molecular dynamics (MD) simulations have shown that branched side chains lead to more stable packing between cations and anions in the liquid phase of branched ILs.⁷⁸ This presumably results in a lower entropy of fusion for these materials, which would also contribute to higher melting points.

3.4 Ion symmetry

Ion symmetry plays an important role in crystal packing and thus also in dictating ΔH_f and T_m. Asymmetry distorts ideal close packing of charges, depressing both T_m and ΔH_f. This has been reported in both dicationic imidazolium-based ILs⁴⁵ and fatty acid-based ILs.³¹ For the latter category, when the fatty acids are unsaturated, chain symmetry is decreased and reduced packing efficiencies lead to depressed melting points. For the fatty acid ILs studied by Toledo Hijo et al.³¹ with mono- di- and tri-substituted ethanolamine cations, the oleic acid ([C_18:1OO]⁻) analogues consistently melt at temperatures >40 °C lower than the stearate ([C₁₈OO]⁻) analogues. When the anion alkyl chains are doubly unsaturated ([C_18:2OO]⁻), T_m is again lower (ΔH_f is also >4 times lower for [tHEA][C_18:2OO] compared to [tHEA][C₁₈OO], but not enough data is available to elucidate the consistency of this trend among the [HEA] and [dHEA] analogues). These differences in melting points may be explained with reference to Carnelley's rule, which postulates that for isomeric compounds, the most symmetrical isomer will have the highest melting point owing to more compact arrangement of atoms in the solid state.⁷⁹

While these insights are helpful in guiding the design of new ILs with favourable thermal properties for the PCM application, it should be noted that several structural elements can interact with one another – both synergistically and antagonistically.⁸⁰ As a result, it is not uncommon for ILs to display unexpected thermal properties, the reasons for which are sometimes ambiguous (the 2-methylimidazoliums discussed in section 3.1 above provide an apt example). We expect that a better-informed approach to the design of ILs as PCMs will become achievable as more data becomes available for the elucidation of structure–property relationships, alongside the development of computational methods for property screening. The latter is discussed in more detail in the next section.

4. Computational methods for IL design

As often pointed out by the late Professor Ken Seddon, the vast number of cations and anions that can be used to make ILs produces around a trillion possible materials with an extremely wide range of properties.⁸¹ Considering this, the synthesis and study of every cation and anion combination is an impossible task. The basic screening of properties via computational methods is therefore a valuable tool to save time and resources, narrowing synthetic focus to the most promising materials. While this is not an easy task, vast progress has already been made in this field. Computational techniques that have been used to study various properties include Quantum Structure Property Relationship (QSPR), Conductor-like Screening Model for Realistic Solvation (COSMO-RS), Volume-Based Thermodynamics (VBT), quantum chemical calculations of single ion pairs, Molecular Dynamics (MD) simulations and Machine Learning (ML).⁸² These techniques have been used to predict a range of properties including density, melting point, heat capacity, and enthalpy of fusion, as well as to give insight into intermolecular forces and their interplay.⁸² As mentioned, however, much focus in this field has been on liquid state properties, and ILs have typically been desired as liquids at room temperature. The approach to these materials has been to use bulky, charge delocalised ions. On the other hand, for PCM applications, materials that form highly ordered crystalline structures are the most interesting. Thus, for this application, slightly different parameters need to be addressed, as the most important properties for ILs as PCMs are T_m and ΔH_f. Here, we present a short overview of computational techniques that have been used to study these properties in ILs.

4.1 Melting points

Melting point values of ILs vary broadly, with some grouping according to cation type as illustrated by Fig. 6.^83,84 While conventional definitions of ILs that limit melting temperatures to 100 °C and below may exclude some of the higher melting temperature organic salts from being classified as ILs, here we take a less restrictive definition that considers a broader scope of liquid salts. The main factors known to affect the melting points of ILs include charge distribution on the ions and the ability of the ions to form hydrogen bonds.⁸³ There have been several attempts to predict melting point values using a variety of techniques. QSPR models have been found to give the maximum deviation in a range between 25 and 100 °C.⁸⁵ This high error can be decreased when quantum chemical descriptors are applied.⁸² Extensive research to predict T_m using COSMO-RS has been performed by the Krossing group.^63,86–88 The errors obtained were also high (33.5 °C) when a wide range of ILs were screened. Many attempts to apply quantum chemical calculations of single ion pairs to predict T_m have concluded that there is no direct correlation between the ion pair interaction energy and melting points, and that treatment of the many-body effects are required to achieve accurate predictions.^82,89,90 Recently, research into the application of machine learning to predict T_m has increased. This technique is an interesting alternative to other computational methods as it requires lower computation times, making it especially attractive for high-throughput screening. A study of 2212 ILs with diverse cations and anions showed an error of 29 °C in predicted T_m.⁸⁴ Thus it is clear that melting point assessment through computational techniques is a challenging task, and still requires increased knowledge and improvement of tools.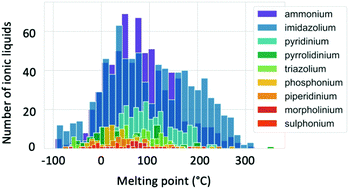

Fig. 6 Distribution of the ionic liquid melting points separated by cation type. Reproduced from Low et al.⁸⁴ with the permission of AIP Publishing.

4.2 Enthalpy of fusion

The possibility of predicting ΔH_f by computational methods would be extremely beneficial for PCM applications. Research in this area is currently scarce, not only among ionic liquids, but in the PCM field in general. The first attempt to predict ΔH_f for ionic liquids was by Bai et al.,³³ who used a six-descriptor QSPR model to predict the heat of fusion of 44 ILs with imidazolium cations and various anions. The authors reported “reasonable” correlation and prediction accuracy (R² of linear regression model for experimental vs. calculated ΔH_f = 0.9047) and found the cation–anion interaction energy to be the most important descriptor. In 2011, the same authors formulated QSPR models using 30 ILs in “training sets”, and determined the most effective descriptors for the models by means of a stepwise method (that is, identifying an initial model, repeatedly altering it by addition of variables one at a time, and removing variables when they do not improve the model).⁹¹ The models again gave “reasonable” correlation and prediction accuracy, with mean relative errors between 12% and 20% (R² > 0.9 for all models). It was found that increased molecular weight and increased energy of the lowest occupied molecular orbital (E_LUMO) led to lower ΔH_f, while increased dipole moments and molecular volumes increased ΔH_f. These studies demonstrate the potential of QSPR methods in predicting ΔH_f, potentially as a component of more sophisticated machine learning approaches.

One of the fundamental challenges in a priori calculation of ΔH_f, which to our knowledge has never been successfully demonstrated, is that it depends critically on an accurate prediction of the crystal structure. While melting points can be approximately derived from melting of estimated crystal structures in molecular dynamics simulations (a valuable starting point in this endeavour), the value of ΔH_f is expected to be much more sensitive than T_m to the exact details of the crystal symmetry and packing. Prediction/calculation of crystal structures is an important theoretical challenge across many disciplines of chemistry and materials science⁹² and it becomes especially challenging in the ionic liquids field because of the complex structures that exhibit a variety of intermolecular interactions. In our opinion progress in this area would represent a tremendous step forward in the PCM field.

4.3 Probing and calculating intermolecular interactions

Determining the key intermolecular interactions present in ILs is an important task, as it is these interactions that govern the chemical and physical properties of the IL. How the strengths of these interactions are affected by the melting process is especially important in the case of PCMs, as these changes govern T_m and ΔH_f.⁹³ As there is no experimental method available to directly measure the strength of the components of intermolecular interactions, support from computational techniques is crucial in this aspect. The wide range of possible cations and anions gives rise to a diverse range of possible interactions that can exist in a particular system. In ILs the dominant interactions are electrostatic in nature (i.e. coulombic).⁸² In addition, dispersion forces and hydrogen bonding can be extensive.^82,94 The main difference between prior IL studies and those specifically looking at their use as PCMs is that the value of ΔH_f is determined from the differences in these interactions between the two phases. Therefore, in order to understand the type of interactions that most affect ΔH_f, it is important to understand the nature and strength of interactions present in both the solid and liquid state.^95,96 Electrostatic forces, though very strong, are long-range interactions (falling away as 1/r where r is the distance between the charged centres), and therefore may not change substantially during melting. Shorter range forces, especially van der Waals forces between alkyl chains, are expected to be much more disrupted and diminished by melting.

In principle these nuances are accessible by appropriate MD simulations as long as the crystal structure is known, as discussed above. The sophistication and accuracy of MD in the ILs field has been advancing rapidly in recent years^97,98 and certainly seems capable of approaching a highly meaningful outcome. The growing number of crystal structures that are available on the CCDC database⁹⁹ for ionic liquids can support this computational endeavour, giving insights into the solid state. Thus, further simulations of both phases, and comparison of their energy components, could enable a breakthrough in the design of novel ILs for PCM applications. In our own work we have been collaborating with the group of Agilio Padua and co-workers to investigate and develop these techniques for PCMs and hope to be able to report on progress shortly.

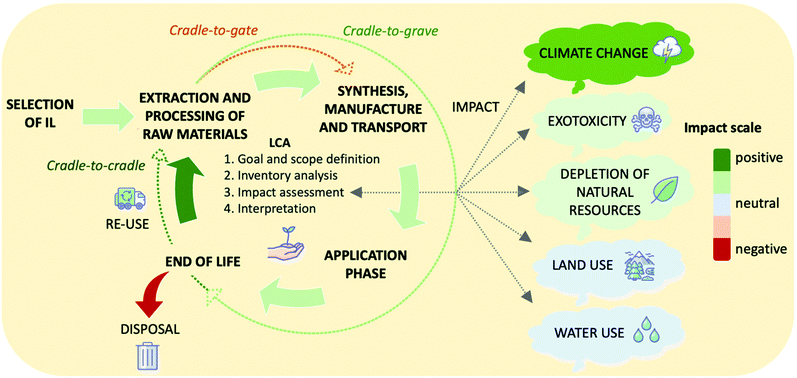
5. Design of systems with low environmental and economic cost

As well as designing new materials with high energy storage densities, it is important to consider how a system will perform, as a whole and over its lifetime, to determine if the environmental benefits will outweigh the environmental and economic cost of manufacturing and recycling/disposal. Lifecycle assessment (LCA), a process for developing environmental profiles of products and systems that is governed by international standards ISO4040/4044,¹⁰⁰ is a valuable tool for quantifying the environmental and economic impacts of all stages in a product or system's lifetime. The international standards require detailed data of all energy and material inputs, from extraction and transport of raw materials through to impact assessments, energy pay-back time, and decommissioning of products. The LCA framework has four stages: goal and scope definition, inventory analysis, impact assessment, and interpretation. The impact profile may be derived by consideration of only the development phase (cradle-to-gate), or preferably include impacts that span the lifetime and further-life of the system, from development through to eventual disposal or re-use (cradle-to-grave and cradle-to-cradle, respectively) (Fig. 7). The LCA method is used extensively worldwide to allow educated decisions to be made by governments and private organisations on new products and systems,^101,102 and necessarily requires large data inputs, capable software, and considerable time contributions. For ILs, such studies are comparatively absent in the literature relative to the growing number of papers that are published on the topic. This is in large part owing to the shortage of inventory databases available on ILs and their precursors.¹⁰³ Their often-complex syntheses further complicate the challenge,¹⁰⁴ all the while having negative contributions to the environmental impact of the material.¹⁰⁵ As such, while not feasible to be performed within the scope of this Perspective, we recommend that promising IL PCM materials be subjected to this assessment at an early stage and certainly prior to their actualisation in large-scale systems.

Fig. 7 The lifecycle assessment process, showing the four stages of the LCA, and the steps that are considered for cradle-to-gate, cradle-to-grave, and cradle-to-cradle analyses. Five impact categories are shown as examples of the impacts considered by LCA analysis. The stages and impact categories are colour coded to show the potential impact of using ionic liquids as PCMs in TES systems.

To help inform this process, we provide here some insight into the economic and environmental production costs of IL PCMs through review of the relevant literature. In 2014, Chen et al.¹⁰⁶ demonstrated the commercial viability of protic ionic liquids for large-scale IL-based processes, estimating the cost of production for triethylammonium hydrogen sulfate [TEA][HSO₄] to be as low as 1.24 $ kg⁻¹; cheaper than the price of many common organic solvents (e.g. acetone and ethyl acetate). Aspen Plus software (widely used in the literature and suitable for economic and environmental system modelling of this type) was used to model two production processes. It was found that an “intensified” process using high surface area flow reactors is energetically favourable compared to conventional processes using scaled-up laboratory conditions. A follow up study by Baaqel et al.¹⁰¹ further improved this manufacturing process (Fig. 8), resulting in a direct production cost of just 0.78 $ kg⁻¹ for [TEA][HSO₄]. This study modelled the environmental costs of the production of this ionic liquid, finding it less environmentally damaging than the production of both acetone and glycerol, the latter of which is typically considered a “green” solvent.^107,108 For this process, the authors attribute a majority of the production costs to the triethylamine and sulfuric acid starting materials. A reasonable assumption can be made that other protic ILs formed via Brønstead acid/base neutralisation reactions could be produced by this process, with the cost scaled relative to those of the different raw materials.

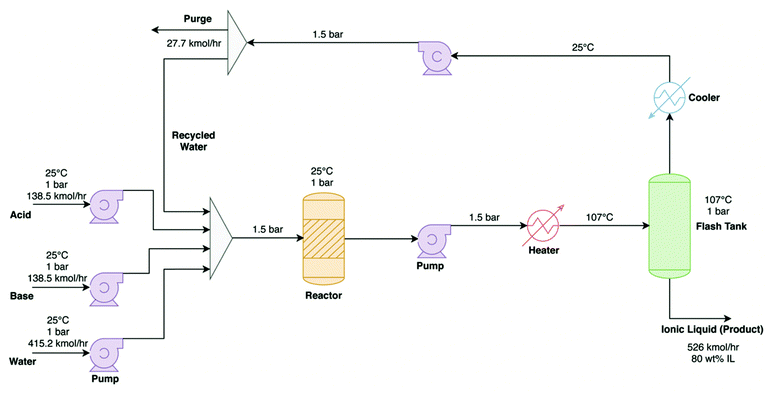Fig. 8 Process flow diagram for the production process of [TEA][HSO₄], reproduced from Baaqel et al.¹⁰¹

Similarly, we have shown that salts containing the methanesulfonate anion have desirable properties for PCM applications; in the future, the substitution of sulfuric acid with methanesulfonic acid, which is of comparable price but safer and less toxic,¹⁰⁹ could make this process more environmentally friendly. Furthermore, a newly developed route to methanesulfonic acid via the direct reaction of methane with sulfur trioxide under mild conditions¹¹⁰ provides scope for a carbon negative production process if the methane is sourced from biological waste – LCA analysis suggests this new route has an environmental impact 3 times less than that of the conventional method, with the potential to be further improved.¹¹¹

Alongside economic cost, a large contributor to the environmental impact of ILs is related to their ecotoxicity. Although ILs have the advantage of not being released into the environment through evaporation, thanks to their negligible vapour pressures, ILs are often water-soluble and can persist in the environment when released through other avenues as their typically high stability contributes to poor bio-degradability.¹¹² LCA highlights the environmental impact of the toxicity of ILs and where applicable the detriment this can have to the sustainability of the system. For example, Amado Alviz and Alvarez¹¹³ found that when comparing [C₄mim]Br and conventionally used toluene as solvents for the production of acetylsalicylic acid (aspirin), [C₄mim]Br has the greater environmental impact of the two, attributed largely to its ecotoxicity. Toxicological information on ILs is thus paramount in the determination of their “green” potential, whether in replacing conventionally used materials or for their use in new processes – there is limited benefit in tackling one environmental challenge to the detriment of another. While experimental determination of the toxicity of all ILs would be both time and chemically laborious,¹¹⁴ there are nonetheless ways to proactively approach the design of ILs to direct synthetic efforts to materials with lower toxicity. For example, quantitative structure–activity relationship (QSAR) modelling can be used for pre-synthesis or pre-application “screening”, filling in data gaps where experimental data is missing.¹¹⁵ The QSAR method facilitates predictions of the toxicity of ILs through the relationship between chemical structure and biological activity, and is widely recognised as a valuable risk management technique, including by the Registration, Evaluation, Authorisation, and Restriction of Chemicals (REACH) regulation.¹¹⁶ Peric et al.¹¹⁷ used this method to study the ecotoxicity of a range of protic and aprotic ILs, with good correlation between experimental and predicted results. The authors found that protic ILs generally have lower toxicity than aprotic ILs, largely due to the nature of the cations used in aprotic ILs, with amines in particular having considerable contributions to toxicity. This is in agreement with other research that has found cations to be the more significant contributor to toxicity in ILs.^118,119 Montalbán et al.,⁵⁴ who studied the toxicity of a range of mono- and di-cationic ILs, found “very good” agreement between experimental toxicity values and those estimated using the QSAR method. The toxicity of the dicationic ILs was found to be lower than that observed for the homologous monocationic ILs. For the cations discussed in this Perspective, toxicity generally increases in the order of cholinium < imidazolium (protic < aprotic) < phosphonium.¹²⁰ Increases to cation alkyl side-chain length/lipophilicity are also known to contribute to toxicity.^120–123

While anions are known to play a lesser role in toxicity, those derived from natural sources (e.g. tartrate and fatty acids) are surely the most benign, with high bio-degradability circumventing environmental concern upon their release. Similarly, the methanesulfonate anion is of low toxicological concern, typically forming highly soluble, non-hazardous salts.¹¹¹ Furthermore, while fluorinated anions such as [BF₄]⁻ and [PF₆]⁻ may have toxicological concerns during operation, due to the potential release of HF upon decomposition by hydrolysis, these are of less environmental concern as the evolving compounds (i.e. fluoride, borate and phosphate salts) are not harmful to the environment in moderate concentrations.¹²³ Even without the direct use of QSAR modelling of potential new materials, these insights, alongside those from studies of structure–activity relationships, can aid in the design of more sustainable IL PCM systems.

The discussion above has attempted to provide detailed examples of LCA information relevant to certain ionic liquids, where relevant data is available. In the absence of such data more broadly, we have colour coded the entries in Table 1 according to our best guess estimates of the potential sustainability of the material involved in large scale use as a PCM, on the basis of the main LCA criteria.

Looking forward, for prospective IL PCM systems, we can make two key recommendations to aid effective environmental impact evaluations via LCA methods:

Firstly, for the formulation of a precise definition of the product and its lifecycle (which comes under stage one of the LCA method), understanding the thermal and cycling stability of the IL PCM is paramount. If the IL PCM undergoes slight decomposition or contamination over its operating lifetime, can it be regenerated, for example by recrystallisation or other purification methods? The main drawback that has deterred major industrial uptake of ILs is the cost of the IL itself, rather than the capital cost of the associated technology/systems, as well as a lack of efficient recovery strategies.¹²⁴ Any extension to their life through reuse or recycling will thus help to minimise the cost of the system, with clear environmental benefits. Ultrafiltration¹²⁵ and distillation¹²⁶ methods have proven highly effective for recovering imidazolium-based ILs. For protic ILs, a hinderance to the system may be a reverse proton transfer reaction (relative to the synthetic route), which can lead to separation of the starting materials.²⁴ In this case, remixing in situ may be a route to regeneration that extends the lifetime of the material, provided no decomposition has occurred.

Secondly, to determine the true sustainability of the system, a cradle-to-grave (or cradle-to-cradle for systems with recycling prospects) analysis is much preferred over cradle-to-gate analysis to ensure the long-term positive impacts of the renewable energy application of the PCM are brought into the analysis. Furthermore, a common limitation of many IL LCA studies is a lack of consideration of the environmental impact of directly releasing the IL into the environment,¹⁰³ which in some cases may be higher than the conventional materials they are replacing.^127,128 LCA should thus be used to highlight the important areas needing improvement to ensure that the IL PCM really is the greener choice, as well as the best PCM in terms of cyclability, performance, etc. Fundamentally, the environmental performance of IL PCMs will improve significantly if stability and regeneration methods are improved. These factors should thus be a key focus of future work in the field.

6. Conclusion and future perspectives

The emerging application of ionic liquids for renewable thermal energy storage brings with it great potential for meaningful, green and sustainable impact. But how green and sustainable can they be? Inevitably, in its infancy, the field bears knowledge gaps that leave this question not fully answerable. Among these gaps is a lack of understanding of the fundamental structure–property relationships that underpin ΔH_f. This results in challenges in optimising ΔH_f in desirable (i.e. stable, renewable, economical) materials, as well as in developing a more fundamental understanding of the maximum storage potential of systems using these materials. In the present literature, there is also an absence of thermal cycling data on proposed materials, which considerably limits our ability to determine the feasibility of the materials for PCM applications – a high enthalpy of fusion is of little value if it is not retained through multiple heating/cooling cycles. It would be an oversight to omit this data on the presumption of stability; the broad acceptance of ILs as highly thermally and chemically stable does not mean all ILs convey these properties.¹²⁹ In fact, the stability (and other properties, e.g. flammability), of ILs is dependent on their structures, and is thus influenced by the type of ions used (as well as by structural modifications to these ions).^130,131 The measurement protocol is also critical to the quantitative determination of meaningful thermal stability information.^131,132 It is therefore essential that data is reported on these properties and protocols as part of assessment is made as to their suitability for the PCM application. QSPR approaches have been developed in order to predict heats of combustion and thereby evaluate fire hazard potential for ionic liquid materials,¹³³ and this approach could be very valuable in the present context.

Machine learning and simulation techniques clearly have an increasing role to play in developing a predictive approach to understanding structure–property relationships and developing new materials. The computational community in the ILs field is close to this goal; molecular dynamics simulation techniques are already well developed for the liquid state and the intermolecular interaction energies are moderately well understood and modelled. What is frustratingly missing is an a priori approach to predicting and calculating the crystal structure for a given salt. Machine learning applied to iterative approaches to finding low energy crystal structures may provide a way forward; notably this is a goal of major significance in many branches of chemistry. We commend to the computational community this important task.

In optimising the sustainability of proposed IL PCM systems, LCA analysis is a valuable tool, constructing the “whole picture” by quantifying the impacts of the system at all stages throughout the lifecycle of the material. The key to a sustainable energy storage solution is clearly to minimise the initial impact of material and energy input into their synthesis, ensuring the return impact is more valuable than those of production. Ideally, a renewable material source is used and as such could even represent a carbon sink for as long as the material is not decomposed into volatile carbonaceous compounds. These LCA methods repeatedly demonstrate vast advantages to system sustainability if materials can be re-used or regenerated at their “end-of-life”. This should thus be a key focus of future research in this field. Furthermore, the environmental impacts of direct, unintentional release into the environment are a principal consideration, and target materials should have minimal impact in this case. This places bio-derived cations and anions among those at the centre of the most sustainable systems.

A final and important note is that the operating range of a PCM will vary depending on the application, and this can affect the storage capabilities of the materials, as larger operating ranges result in additional energy being stored in the form of sensible heat. As a conservative estimate, we have assumed here an operating range of 10 °C ± T_m. In reality, renewable thermal energy storage systems can operate in a temperature range starting substantially lower than 10 °C below their melting temperature and heat to substantially higher than T_m.¹⁶ As such, for this application, the energy storage densities (E^v*) are likely to be substantially higher than our approximations; actual values are dependent on the feasible operating range, as well as the specific heat capacity and density of the material.

In summary, new ILs for PCM applications should be readily accessible through facile synthetic pathways, have low environmental toxicity, high chemical stability to support long-lifetime in use, and be designed with functionalities capable of promoting favourable interactions for optimising ΔH_f, as well as achieving a melting temperature that suits the desired application. With these considerations in mind, and with the help of ever-improving computational techniques, we expect to see this field continue to grow, yielding new and sustainable energy storage systems that will certainly contribute strongly to the global transition to renewable energy sources.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge funding from the Australian Research Council through its Linkage Project scheme (LP190100522) and collaborating organisation Energy Storage Pty Ltd.

References

1. Intergovernmental Panel on Climate Change (IPCC), Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2021.
2. W. Thuiller, Nature, 2007, 448, 550–552.
3. L. Wang, B. Zhong, S. Vardoulakis, F. Zhang, E. Pilot, Y. Li, L. Yang, W. Wang and T. Krafft, Int. J. Environ. Res. Public Health, 2016, 13, 1196.
4. M. Höök and X. Tang, Energy Policy, 2013, 52, 797–809.
5. O. Edenhofer, Climate Change 2014: Mitigation of Climate Change, Cambridge University Press, 2015, vol. 3.
6. International Energy Agency (IEA), Global Energy & CO₂ Status Report 2019, Paris, 2019.
7. International Renewable Energy Agency, Innovation Outlook: Thermal Energy Storage, Abu Dhabi, 2020.
8. Gemasolar celebrates its second anniversary with an excellent operational record, https://www.group.sener/press-releases/gemasolar-celebrates-its-second-anniversary-with-an-excellent-operational-record, (accessed September 7, 2021).
9. A. Caraballo, S. Galán-Casado, Á. Caballero and S. Serena, Energies, 2021, 14, 1197–1212.
10. V. Henz, Bloom. New Energy Finance Dec. 16^th, https://about.bnef.com/blog/battery-pack-prices-cited-below-100-kwh-for-the-first-time-in-2020-while-market-average-sits-at-137-kwh/(accessed August 10, 2021).
11. Y. Zhao, X. Zhang and X. Xu, J. Therm. Anal. Calorim., 2020, 139, 1419–1434.
12. M. Song, F. Niu, N. Mao, Y. Hu and S. Deng, Energy Build., 2018, 158, 776–793.
13. E. Douvi, C. Pagkalos, G. Dogkas, M. K. Koukou, V. N. Stathopoulos, Y. Caouris and M. Gr. Vrachopoulos, Int. J. Thermofluids, 2021, 10, 100075–100099.
14. T. Nomura, N. Okinaka and T. Akiyama, Resour., Conserv. Recycl., 2010, 54, 1000–1006.
15. C. Zhou and S. Wu, Int. J. Energy Res., 2019, 43, 621–661.
16. K. Matuszek, R. Vijayaraghavan, M. Kar, S. Mahadevan and D. R. MacFarlane, ChemSusChem, 2021, 14, 2757–2652.
17. R. D. Rogers and K. R. Seddon, Division of Industrial and Engineering Chemistry Staff American Chemical Society and Meeting Staff American Chemical Society, Ionic liquids as green solvents, ACS Publications, Washington, DC, 2003.
18. D. S. Silvester and R. G. Compton, Z. Phys. Chem., 2006, 220, 1247–1274.
19. I. Marrucho, L. Branco and L. Rebelo, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 527–546.
20. M.-D. Bermúdez, A.-E. Jiménez, J. Sanes and F.-J. Carrión, Molecules, 2009, 14, 2888–2908.
21. J. O. Valderrama and R. A. Campusano, C. R. Chim., 2016, 19, 654–664.
22. J. A. Coutinho, P. J. Carvalho and N. M. Oliveira, RSC Adv., 2012, 2, 7322–7346.
23. T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237.
24. M. J. Earle, J. M. Esperança, M. A. Gilea, J. N. C. Lopes, L. P. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831–834.
25. P. T. Anastas and J. C. Warner, Frontiers, 1998, 640, 1998.
26. R. Vijayraghavan, U. A. Rana, G. D. Elliott and D. R. MacFarlane, Energy Technol., 2013, 1, 609–612.
27. K. Matuszek, R. Vijayaraghavan, M. Kar and D. R. MacFarlane, Cryst. Growth Des., 2019, 20, 1285–1291.
28. J. S. Ricci, R. C. Stevens, R. K. McMullan and W. T. Klooster, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 381–386.
29. H. A. Levy and G. C. Lisensky, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3502–3510.
30. CFR – Code of Federal Regulations Title 21, https://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfcfr/CFRSearch.cfm?fr=182.8250, (accessed August 25, 2021).
31. A. A. C. Toledo Hijo, G. J. Maximo, M. C. Costa, R. L. Cunha, J. F. B. Pereira, K. A. Kurnia, E. A. C. Batista and A. J. A. Meirelles, J. Phys. Chem. B, 2017, 121, 3177–3189.
32. D. Santos, F. Costa, E. Franceschi, A. Santos, C. Dariva and S. Mattedi, Fluid Phase Equilib., 2014, 376, 132–140.
33. J. Zhu, L. Bai, B. Chen and W. Fei, Chem. Eng. J., 2009, 147, 58–62.
34. K. Matuszek, R. Vijayaraghavan, C. M. Forsyth, S. Mahadevan, M. Kar and D. R. MacFarlane, ChemSusChem, 2020, 13, 159–164.
35. H. Shi, X. Zhang, K. Sundmacher and T. Zhou, Green Energy Environ., 2020, 6, 392–404.
36. M. Čanji, M. Bendová, M. G. Bogdanov, Z. Wagner, N. Zdolšek, F. Quirion, V. Jandová and P. Vrbka, J. Mol. Liq., 2019, 292, 111222–111230.
37. M. Biswas, M. Dule, P. N. Samanta, S. Ghosh and T. K. Mandal, Phys. Chem. Chem. Phys., 2014, 16, 16255–16263.
38. Z. Zhang, A. A. Salih, M. Li and B. Yang, Energy Fuels, 2014, 28, 2802–2810.
39. H. Zhang, J. Liu, M. Li and B. Yang, J. Mol. Liq., 2018, 269, 738–745.
40. J. Liu, W. Yang, Z. Li, F. Ren and H. Hao, J. Mol. Liq., 2020, 307, 112994–113003.
41. J. Parajó, M. Villanueva, J. Troncoso and J. Salgado, J. Chem. Thermodyn., 2020, 141, 105947–105957.
42. B. D. Rabideau, M. Soltani, R. A. Parker, B. Siu, E. A. Salter, A. Wierzbicki, K. N. West and J. H. Davis, Phys. Chem. Chem. Phys., 2020, 22, 12301–12311.
43. S. Höhlein, A. König-Haagen and D. Brüggemann, Materials, 2017, 10, 444–459.
44. G. Barone, G. D. Gatta, D. Ferro and V. Piacente, J. Chem. Soc., Faraday Trans., 1990, 86, 75–79.
45. H. Zhang, W. Xu, J. Liu, M. Li and B. Yang, J. Mol. Liq., 2019, 282, 474–483.
46. Principles of Green Chemistry, https://www.acs.org/content/acs/en/greenchemistry/principles/12-principles-of-green-chemistry.html, (accessed August 13, 2021).
47. D. Rengstl, V. Fischer and W. Kunz, Phys. Chem. Chem. Phys., 2014, 16, 22815–22822.
48. P. Wasserscheid and T. Welton, Ionic liquids in synthesis, Wiley-VCH, Weinheim, 2nd edn, 2008.
49. C. M. Gordon, J. D. Holbrey, A. R. Kennedy and K. R. Seddon, J. Mater. Chem., 1998, 8, 2627–2636.
50. J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133–2140.
51. Y. Ji, R. Shi, Y. Wang and G. Saielli, J. Phys. Chem. B, 2013, 117, 1104–1109.
52. M. Bendová, M. Čanji, Z. Wagner and M. G. Bogdanov, J. Solution Chem., 2019, 48, 949–961.
53. L. Guglielmero, A. Mezzetta, L. Guazzelli, C. S. Pomelli, F. D'Andrea and C. Chiappe, Front. Chem., 2018, 6, 612–628.
54. M. G. Montalbán, G. Víllora and P. Licence, Ecotoxicol. Environ. Saf., 2018, 150, 129–135.
55. S. Steudte, S. Bemowsky, M. Mahrova, U. Bottin-Weber, E. Tojo-Suarez, P. Stepnowski and S. Stolte, RSC Adv., 2014, 4, 5198–5205.
56. H. Zhang, M. Li and B. Yang, J. Phys. Chem. C, 2018, 122, 2467–2474.
57. I. F. Mena, E. Diaz, J. Palomar, J. J. Rodriguez and A. F. Mohedano, Chemosphere, 2020, 240, 124947–124956.
58. N. Terasawa, S. Tsuzuki, T. Umecky, Y. Saito and H. Matsumoto, Chem. Commun., 2010, 46, 1730–1732.
59. C. G. Cassity, A. Mirjafari, N. Mobarrez, K. J. Strickland, R. A. O'Brien and J. H. Davis, Chem. Commun., 2013, 49, 7590–7592.
60. C. A. Cassity, B. Siu, M. Soltani, J. L. McGeehee, K. J. Strickland, M. Vo, E. A. Salter, A. C. Stenson, A. Wierzbicki, K. N. West, B. D. Rabideau and J. H. Davis, Phys. Chem. Chem. Phys., 2017, 19, 31560–31571.
61. B. D. Rabideau, K. N. West and J. H. Davis, Chem. Commun., 2018, 54, 5019–5031.
62. J. Troncoso, C. A. Cerdeirina, Y. A. Sanmamed, L. Romaní and L. P. N. Rebelo, J. Chem. Eng. Data, 2006, 51, 1856–1859.
63. U. P. Preiss, W. Beichel, A. M. Erle, Y. U. Paulechka and I. Krossing, ChemPhysChem, 2011, 12, 2959–2972.
64. S. L. Piper, C. M. Forsyth, M. Kar, D. R. MacFarlane, K. Matuszek and J. M. Pringle, Mater. Adv., 2021 10.1039/D1MA00603G.
65. H. M. Berman and R. Rosenstein, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 435–441.
66. P. Agron and W. Busing, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1969, 25, 118.
67. T. Endo, T. Kato and K. Nishikawa, J. Phys. Chem. B, 2010, 114, 9201–9208.
68. K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734.
69. P. A. Hunt, J. Phys. Chem. B, 2007, 111, 4844–4853.
70. K. Noack, P. S. Schulz, N. Paape, J. Kiefer, P. Wasserscheid and A. Leipertz, Phys. Chem. Chem. Phys., 2010, 12, 14153–14161.
71. E. I. Izgorodina, R. Maganti, V. Armel, P. M. Dean, J. M. Pringle, K. R. Seddon and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14688–14697.
72. A. S. M. C. Rodrigues, C. F. R. A. C. Lima, J. A. P. Coutinho and L. M. N. B. F. Santos, Phys. Chem. Chem. Phys., 2017, 19, 5326–5332.
73. Y. Zhang and E. J. Maginn, Phys. Chem. Chem. Phys., 2012, 14, 12157–12164.
74. H. L. Ngo, K. LeCompte, L. Hargens and A. B. McEwen, Thermochim. Acta, 2000, 357, 97–102.
75. L. Xue, E. Gurung, G. Tamas, Y. P. Koh, M. Shadeck, S. L. Simon, M. Maroncelli and E. L. Quitevis, J. Chem. Eng. Data, 2016, 61, 1078–1091.
76. T. Mandai, H. Masu, M. Imanari and K. Nishikawa, J. Phys. Chem. B, 2012, 116, 2059–2064.
77. I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingärtner, J. Am. Chem. Soc., 2006, 128, 13427–13434.
78. Y. Zhang, L. Xue, F. Khabaz, R. Doerfler, E. L. Quitevis, R. Khare and E. J. Maginn, J. Phys. Chem. B, 2015, 119, 14934–14944.
79. S. H. Yalkowsky, J. Pharm. Sci., 2014, 103, 2629–2634.
80. F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021.
81. M. Kar, K. Matuszek and D. MacFarlane, Ionic Liquids in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Hoboken, 2019.
82. E. I. Izgorodina, Z. L. Seeger, D. L. Scarborough and S. Y. Tan, Chem. Rev., 2017, 117, 6696–6754.
83. V. Venkatraman, S. Evjen, H. K. Knuutila, A. Fiksdahl and B. K. Alsberg, J. Mol. Liq., 2018, 264, 318–326.
84. K. Low, R. Kobayashi and E. I. Izgorodina, J. Chem. Phys., 2020, 153, 104101–104111.
85. J. O. Valderrama, Ind. Eng. Chem. Res., 2014, 53, 1004–1014.
86. W. Beichel, U. P. Preiss, S. P. Verevkin, T. Koslowski and I. Krossing, J. Mol. Liq., 2014, 192, 3–8.
87. U. Preiss, S. P. Verevkin, T. Koslowski and I. Krossing, Chem. – Eur. J., 2011, 17, 6508–6517.
88. U. Preiss, S. Bulut and I. Krossing, J. Phys. Chem. B, 2010, 114, 11133–11140.
89. E. I. Izgorodina, D. Golze, R. Maganti, V. Armel, M. Taige, T. J. Schubert and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2014, 16, 7209–7221.
90. U. L. Bernard, E. I. Izgorodina and D. R. MacFarlane, J. Phys. Chem. C, 2010, 114, 20472–20478.
91. L. Bai, J. Zhu and B. Chen, Fluid Phase Equilib., 2011, 312, 7–13.
92. A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Nat. Rev. Mater., 2019, 4, 331–348.
93. H. Mehling, Sol. Energy, 2013, 95, 290–299.
94. P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288.
95. T. Inagaki and T. Ishida, J. Phys. Chem. C, 2016, 120, 7903–7915.
96. T. Inagaki and T. Ishida, J. Am. Chem. Soc., 2016, 138, 11810–11819.
97. K. Goloviznina, Z. Gong and A. A. Padua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 15, 5858–5871.
98. D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell Jr., B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995.
99. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
100. M. Finkbeiner, A. Inaba, R. Tan, K. Christiansen and H.-J. Klüppel, Int. J. Life Cycle Assess., 2006, 11, 80–85.
101. H. Baaqel, I. Díaz, V. Tulus, B. Chachuat, G. Guillén-Gosálbez and J. P. Hallett, Green Chem., 2020, 22, 3132–3140.
102. W. Klöpffer, Int. J. Life Cycle Assess., 2008, 13, 89–95.
103. V. G. Maciel, D. J. Wales, M. Seferin, C. M. L. Ugaya and V. Sans, J. Cleaner Prod., 2019, 217, 844–858.
104. R. M. Cuéllar-Franca, P. García-Gutiérrez, S. F. R. Taylor, C. Hardacre and A. Azapagic, Faraday Discuss., 2016, 192, 283–301.
105. A. Mehrkesh and A. T. Karunanithi, ACS Sustainable Chem. Eng., 2013, 1, 448–455.
106. L. Chen, M. Sharifzadeh, N. Mac Dowell, T. Welton, N. Shah and J. P. Hallett, Green Chem., 2014, 16, 3098–3106.
107. A. Wolfson, C. Dlugy and Y. Shotland, Environ. Chem. Lett., 2007, 5, 67–71.
108. Y. Gu and F. Jérôme, Green Chem., 2010, 12, 1127–1138.
109. T. Palden, B. Onghena, M. Regadío and K. Binnemans, Green Chem., 2019, 21, 5394–5404.
110. M. Mccoy, Chem. Eng. News, 2016, 94, 10.
111. S. Kappenthuler, S. Olveira, J. Wehrli and S. Seeger, J. Cleaner Prod., 2018, 202, 1179–1191.
112. J. Flieger and M. Flieger, Int. J. Mol. Sci., 2020, 21, 6267–6308.
113. P. L. Amado Alviz and A. J. Alvarez, J. Cleaner Prod., 2017, 168, 1614–1624.
114. K. S. Khoo, W. Y. Chia, K. Wang, C.-K. Chang, H. Y. Leong, M. N. B. Maaris and P. L. Show, Sci. Total Environ., 2021, 793, 148705–148715.
115. N. Abramenko, L. Kustov, L. Metelytsia, V. Kovalishyn, I. Tetko and W. Peijnenburg, J. Hazard. Mater., 2020, 384, 121429–121443.
116. K. Chinen and T. Malloy, Integr. Environ. Assess. Manage., 2020, 16, 745–760.
117. B. Peric, J. Sierra, E. Martí, R. Cruañas and M. A. Garau, Ecotoxicol. Environ. Saf., 2015, 115, 257–262.
118. J. Arning, S. Stolte, A. Böschen, F. Stock, W.-R. Pitner, U. Welz-Biermann, B. Jastorff and J. Ranke, Green Chem., 2008, 10, 47–58.
119. A. Romero, A. Santos, J. Tojo and A. Rodríguez, J. Hazard. Mater., 2008, 151, 268–273.
120. M. Amde, J.-F. Liu and L. Pang, Environ. Sci. Technol., 2015, 49, 12611–12627.
121. S. Stolte, J. Arning, U. Bottin-Weber, A. Müller, W.-R. Pitner, U. Welz-Biermann, B. Jastorff and J. Ranke, Green Chem., 2007, 9, 760–767.
122. A. S. Wells and V. T. Coombe, Org. Process Res. Dev., 2006, 10, 794–798.
123. M. Matzke, S. Stolte, K. Thiele, T. Juffernholz, J. Arning, J. Ranke, U. Welz-Biermann and B. Jastorff, Green Chem., 2007, 9, 1198–1207.
124. J. F. Fernandez, J. Neumann and J. Thoming, Curr. Org. Chem., 2011, 15, 1992–2014.
125. X. Liang, J. Wang and H. Liu, Bioresour. Technol., 2021, 325, 124726–124735.
126. K. Huang, R. Wu, Y. Cao, H. Li and J. Wang, Chin. J. Chem. Eng., 2013, 21, 577–584.
127. S. P. F. Costa, P. C. A. G. Pinto, M. L. M. F. S. Saraiva, F. R. P. Rocha, J. R. P. Santos and R. T. R. Monteiro, Chemosphere, 2015, 139, 288–294.
128. Y. Zhang, B. R. Bakshi and E. S. Demessie, Environ. Sci. Technol., 2008, 42, 1724–1730.
129. A. O. Diallo, C. Len, A. B. Morgan and G. Marlair, Sep. Purif. Technol., 2012, 97, 228–234.
130. D. M. Fox, W. H. Awad, J. W. Gilman, P. H. Maupin, C. Hugh and P. C. Trulove, Green Chem., 2003, 5, 724–727.
131. Y. Cao and T. Mu, Ind. Eng. Chem. Res., 2014, 53, 8651–8664.
132. K. J. Baranyai, G. B. Deacon, D. R. MacFarlane, J. M. Pringle and J. L. Scott, Aust. J. Chem., 2004, 57, 145–147.
133. A.-O. Diallo, G. Fayet, C. Len and G. Marlair, Ind. Eng. Chem. Res., 2012, 51, 3149–3156.

---