Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterization of nano-scale mineral dust aerosols in snow by single particle inductively coupled plasma mass spectrometry†
Aaron J.
Goodman
 a,
Alexander
Gundlach-Graham
a,
Alexander
Gundlach-Graham
 *b,
Shaun G.
Bevers
a and
James F.
Ranville
*b,
Shaun G.
Bevers
a and
James F.
Ranville
 a
a
aDepartment of Chemistry, Colorado School of Mines, USA
bDepartment of Chemistry, Iowa State University, USA. E-mail: alexgg@iastate.edu
First published on 1st June 2022
Abstract
Although natural atmospheric nanomaterials are ubiquitous and highly influential in environmental systems, they have only recently begun to be studied. We analyzed sub-micron and nano-scale mineral dust aerosols (MDAs) in wet deposition (snowfall) from two storms in Colorado, USA using single particle inductively coupled plasma mass spectrometry (spICP-MS). We found high particle number concentrations (PNCs) of MDAs (up to 108 particles per mL) and observed an order of magnitude difference in number concentrations related consistent with storm strength and meteorological conditions. We applied novel data processing to particle size distributions (PSDs) obtained with spICP-MS and determined that all PSDs followed the Pareto distribution despite differences in number concentration. We characterized multi-element MDA particle types with single particle ICP-time-of-flight MS (spICP-TOFMS) using particle type-specific detection limits based on crustal abundance ratios, and supplemented this approach with an unsupervised hierarchical clustering algorithm. Both methods confirmed that the median MDA composition largely followed elemental crustal abundance ratios, with a minor class of titanium-rich particles identified. We conclude that the particle size and composition of MDAs can be effectively analyzed in wet deposition by spICP-MS, but quantifying the particle number has greater uncertainty. Characterization of nano-scale MDAs can be used to better understand particle dynamics in the atmosphere, which can affect climate. Analysis of natural particle composition informs studies related to nanogeochemical cycling and can provide background particle data to further advance methods of detecting engineered nanomaterials in the environment.
Environmental significanceCharacterization of natural nanomaterials in the atmosphere is vital for understanding their role in earth's climate through their effect on radiative forcing, as well as their input to biogeochemical nutrient cycling. Advancement in the study of these materials requires significant method development. We analyzed mineral dust aerosols (MDAs) in wet deposition using single particle inductively coupled plasma mass spectrometry (spICP-MS), and determined that the measured particle concentrations were reflective of meteorological conditions. We processed spICP-MS data with machine learning to identify mineralogically distinct groups of particles. Knowledge of MDA concentrations can inform future studies of atmospheric particles and their effect on climate, while detailed mineralogical compositions of MDA can be of value to nutrient cycling studies. |
Introduction
Particulate matter (PM) is ubiquitous in the earth's atmosphere, and affects environmental systems on all scales from global to local.1 PM affects global climate through changes in radiative forcing, as well as decreasing the albedo of glaciers through deposition.2 On a local scale, increases in PM can cause respiratory health concerns, as well as influence aquatic chemistry through deposition of nutrients and metals.3,4 By mass, 88% of atmospheric PM is of natural origin, and mineral dust aerosols (MDAs) comprise up to 75% of this fraction.1,5 MDAs primarily enter the atmosphere in arid regions through eolian transport, with size-dependent residence times ranging from tens of seconds to hundreds of days.5 MDAs >1 μm in diameter dominate volume and mass fluxes; however, by particle number, the majority are PM1.0 (d < 1 μm) and nanoparticles (NPs; d < 100 nm).6 Due to their small size, and consequently higher fraction of surface atoms, NPs have a disproportionately large effect on atmospheric chemistry, as well as an increased environmental reactivity and toxicity.7 It is necessary not only to characterize MDAs to advance the knowledge of nanoscale geochemical cycling, but also to improve analysis related to engineered NPs (ENPs). In this regard, TiO2 NPs have been of particular interest due to their release as ENPs from products such as paints and sunscreens, as well as their incidental release to the environment from coal burning.8,9 Studies have characterized the direct release of TiO2 NPs from these products and processes, but a reliable method for discrimination between Ti-bearing natural nanoparticles (NNPs) and ENPs in environmental samples has not been fully established.10,11 MDAs provide a diverse NNP background population, which can be characterized to further refine methods for detection of some ENPs.While the in situ detection and characterization of MDAs is the most effective for atmospheric chemistry studies, laboratory analysis of MDA in wet or dry deposition is highly relevant for ecotoxicity applications and for comparisons of NNPs to ENPs.12 Wet deposition and dry deposition occur in the presence and absence of precipitation (rain, snow), respectively.13 Characterization of MDA has often been performed using high temperature combustion, scanning electron microscopy (SEM), and X-ray diffraction (XRD), which determine the organic/inorganic fractions,14 particle size/morphology/elemental composition,15 and mineralogy,16 respectively. SEM is time consuming and requires extensive sample preparation (drying, mounting, exposure to a vacuum), which can introduce artifacts that obscure particle size analysis.17 Despite developments in automated image analysis, SEM often does not characterize enough particles to generate statistically accurate particle number concentrations (PNCs) or particle size distributions (PSDs), leading to the need for alternative approaches.
Single particle inductively coupled plasma mass spectrometry (spICP-MS) has demonstrated a superior ability to measure large numbers of NPs by quantifying individual particles in aqueous suspensions.17,18 In spICP-MS, particles are detected as isotope/element-specific transient signal spikes above a background generated by the dissolved form of the element of interest and detector noise. These spikes are individually integrated to determine the mass of the element in each particle, and subsequent data processing calculates a spherical size for each particle, assuming a specific metallic composition (oxide form of a metal or similar). Being a high throughput technique, spICP-MS can produce element-specific PSDs with several thousand particles analyzed per minute. Size detection limits are as small as 5–20 nm depending on the instrument sensitivity, particle composition, and density.19,20 The unique ability of spICP-MS to rapidly count and size particles makes it an ideal tool for characterization of the nano-scale fraction of MDAs.
With appropriate data processing, widely available quadrupole mass spectrometry (QMS) can provide PSDs for individual elements.21 Recent developments in ICP-time-of-flight mass spectrometry (TOFMS) have made it possible to quantify more than one element in individual particles.22,23 Both spICP-QMS and spICP-TOFMS have been used to characterize NPs in precipitation, but studies have been limited to proof of concept, concluding that spICP-MS is suitable for this analysis.24 We examined the influence of meteorological conditions on atmospheric MDA deposition by sampling at three sites along the Colorado Front Range (USA) during two strong storm events that occurred in March 2021. In particular, the submicron fraction of MDAs was examined by spICP-MS. Atmospheric NP numbers and PSDs were measured using spICP-QMS, and elemental associations provided by spICP-TOFMS were used to identify groups of particles representative of different mineral classes. The first objective of the study was to investigate whether particle populations analyzed by spICP-MS were related to meteorological conditions. Furthermore, the study investigated the sources of error in the size distributions of these highly polydisperse natural samples, and the effect on PSD shape of both data processing and sample dilution. Finally, the study compared different particle classification schemes applied to atmospheric NP data generated by spICP-TOFMS.
Methods
Sample collection
Wet deposition, in this case, in the form of snowfall collected on March 16 and March 23, 2021, was provided by the National Atmospheric Deposition Program (NADP), which monitors both wet and dry deposition across the U.S. and Canada.25 Sampling occurred in downtown Denver (S1, S2), in the Rocky Mountain National Park (RMNP) (S3, S4), and in Boulder Canyon (BC) (S5, S6). A map of sample locations is provided in the ESI† (Fig. S1). An Aerochem Metrics 301 deposition collector (ACM) with wet-side and dry-side polyethylene collectors was used.26 NADP samples are collected each week on Tuesday mornings. Subsamples in 1 L polyethylene bottles (Nalgene) were shipped to the laboratory at the Colorado School of Mines (CSM) where they were stored at 4 °C in the dark prior to analysis. All samples were analyzed on the same day for each element of interest, but the time between sample collection, receipt at CSM, and spICP-MS analysis was variable. The stability of the NPs with respect to the particle number and size was examined over the course of one month by collecting an additional wet deposition sample for immediate analysis (Fig. S2†). Mineral specimens of biotite (K(Fe2+/Mg)2(Al/Fe3+/Mg/Ti)([Si/Al/Fe]2Si2O10)(OH/F)2), ilmenite ((Fe,Ti)2O3), and rutile ((Ti)O2) were obtained from the Colorado School Mines Earth Science Museum.27 Gram quantities were hand-ground in a porcelain mortar and pestle prior to spICP-MS analysis, which was cleaned with Milli-Q water (18.2 MΩ cm, Barnstead International) between grinding of each mineral specimen. It is unlikely that a mass of porcelain sufficient to affect results was introduced into the ground mineral powder. This is supported by the different element ratios observed by spICP-TOFMS analysis for each mineral (Fig. 4).Sample preparation and analysis
A NexIon 300D quadrupole mass spectrometer (Perkin Elmer) equipped with a Meinhard nebulizer (Model TR-50-C0.5) and a glass cyclonic spray chamber was used for spICP-QMS analysis of 27Al. Transport efficiency (TE) was calculated using a mass-based approach, using citrate-stabilized 50 nm NanoXact gold nanospheres (NanoComposix).29 Elemental response was measured by preparing a dissolved gold calibration curve (0 to 100 μg L−1) from a 100 mg L−1 stock (Aristar) that was diluted in Milli-Q water, and acidified with 5 drops of concentrated HCl. The TE and sample flow rate were used along with dissolved elemental calibration curves to determine the number concentration, as well as the mass and size distributions. Gold NPs, dissolved standards, and samples were analyzed using a 60 s acquisition time, 100 μs dwell time, and a liquid flow rate of 0.3 mL min−1. Various dilutions (10–1000×) of the precipitation samples were performed using Milli-Q water to examine the effect of concentration on the reported PSDs. Particle events were detected and integrated using the Perkin Elmer Syngistix 2.5 Nano module, employing a 3σ iterative process to determine a baseline (dissolved background) and the sample-specific critical value (minimum particle-derived signal) used for particle detection.30 Previous studies refer to this value as the threshold.29 Signal pulses above the critical value were integrated to determine the mass of a particular element, and a formula for a hypothetical mineral containing Al at crustal abundance was used to estimate particle mass. Density was estimated at 2.5 g cm−3 to represent an aluminosilicate mineral, and a spherical shape was assumed to calculate particle diameter. Particle number concentrations (PNCs) are reported as particles per mL, and were determined by correcting the observed pulse frequency for transport efficiency, flow rate, and dilution. The total concentration of each element (μg L−1) was determined through integration of the full 60 second spICP-MS signal.
To extend the upper range of PSD determination, data were obtained by single particle optical sensing (SPOS). An Accusizer Model 770 (Particle Sizing Systems) calibrated with polystyrene spheres was used to determine the particle size from 1 to 500 μm. Samples were diluted to <104 particles per mL with Milli-Q water to avoid coincidence.
Samples were introduced into the ICP via a microFAST MC autosampler (Elemental Scientific, NE, USA) at a liquid flow rate of 45 μL min−1. A PFA pneumatic nebulizer (PFA-ST, Elemental Scientific, NE, USA) and cyclonic spray chamber were used. Particle mass and number concentration calibrations were achieved according to the particle mass method.29 Ultra-uniform 50 nm diameter Au nanospheres (Nanocomposix, San Diego, USA) and dissolved-Au standards of 0, 0.5, 1, 2, and 5 μg L−1 were used to determine the plasma uptake rate (qplasma). A multi-elemental solution of Al, Ti, Mn, Fe, Cu, Zn, Y, Zr, Nb, La, Ce, Nd, Pb, Th, and U in 1% nitric acid (in-house, sub-boil distilled) was used to establish absolute detection sensitivities (counts per g) for element-mass quantification in single particles. In the ESI,† we provide the operating conditions for the ICP-TOFMS in single-particle mode, isotopes used for mass quantification, sensitivities, and critical values for particle finding in terms of mass.
spICP-TOFMS data were analyzed with in-house developed software written in LabVIEW (ver2018, National Instruments Corp., Austin, TX, USA). Critical values to separate dissolved background signals from particle-derived signals were automatically calculated for each analyte element according to the compound-Poisson distribution established for ICP-TOF data, and are defined as LC,sp.31,32 The LC,sp values were calculated with dynamic alpha values to limit the contribution of dissolved-signal false-positive events to <1% that of true particle events.33 Split particle-events were corrected as previously reported.34 Two-stage hierarchical clustering analysis (HCA) was performed with a custom script in MatLab (v2019b, Mathworks) and followed a similar process to that reported previously.33 In our two-stage HCA approach, first, intra-sample hierarchical clustering for each sample was performed with the correlation distance metric and a correlation cutoff threshold of 0.6 to establish the main clusters. The correlation cutoff was user defined and established by inspecting resultant dendrograms for each sample. For each identified cluster, the mean mass of each element detected in at least 10% of the particle events was multiplied by its occurrence frequency to produce occurrence-normalized mean element masses. These normalized mean element masses were stored as the representative multi-metal nanoparticle (mmNP) signature of each cluster. The representative mmNP signatures were named based on the element symbols of up to the three most frequently detected elements in the cluster. In the second stage of HCA, the representative mmNP signatures from each sample were clustered with the correlation distance metric and a distance cutoff of 0.5 to define inter-sample clusters. The occurrence-normalized element masses and PNCs of each cluster were then plotted along with the inter-sample clustering dendrogram (see the ESI†). The MatLab script and data used for the two-stage HCA are available on GitHub (https://github.com/TOFMS-GG-Group).
Results and discussion
Meteorological influence on MDA deposition
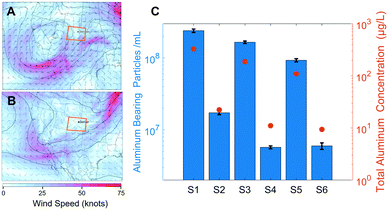
Two strong winter storms delivered MDAs to the Colorado Front Range, with the first storm depositing sufficient dust to warrant mention by local news sources.35 Wind speeds and directions for the two sampling events are presented in Fig. 1A and B. Specifically, on March 12th, 2021, a low-pressure system was located over the Intermountain West region of the United States, deepening as it underwent cyclogenesis. Strong cyclonic flow developed, extending well south of the United States–Mexico border, advecting dust-rich air from the Chihuahuan Desert and transporting it to the Front Range of Colorado. The system moved east along the Colorado/New Mexico border, where it developed into an extratropical cyclone by March 14th before tracking into the American Midwest on March 15th. On March 21st, an upper-atmospheric trough over the western United States closed off and formed a center of low pressure which strengthened and underwent cyclogenesis. This system tracked east over northern Arizona and New Mexico on March 22nd, with strong cyclonic flow that advected dust-rich air from the American desert southwest region and Chihuahuan Desert into the Front Range region of Colorado until the system had tracked east of the state by March 23rd.Aluminum was chosen as an indicator element for the MDAs due to its high abundance in aluminosilicate minerals (the main constituent of soil-derived MDAs) and for its suitability over silicon for ICP-MS.36,37 Particles were estimated to contain 10.5% Al by mass, corresponding to the approximate crustal abundance; this was used to convert counts of 27Al into particle diameter.36 While the abundance of Al in individual MDA particles is highly variable, the median element ratios of all particles detected followed the crustal abundance ratios (see the spICP-TOFMS section). Because the single element capability of QMS necessitates a single chemical formula to establish particle size, the crustal abundance value was chosen. Additionally, in a collection of papers studying MDA geochemistry, the average crustal abundance of elements is used as a benchmark to determine enrichment on a particle by particle basis.38 This is because MDAs arise from weathered crustal material; this coupled with large geographical areas of generation and subsequent homogenization in the atmosphere indicates that the crustal abundance is a suitable average parameter to determine size.39 The PNC and PSD results for the MDAs are affected by both sample properties and the limits on the size range measured by spICP-MS. As such, the PNCs and PSDs primarily reflect the submicron size range of MDAs.
The PNCs at each location were significantly different between the two precipitation events (p < 0.001), with the March 13th event containing on average 17.3× more particles compared to the March 22nd event (Fig. 1C). This increase can likely be attributed to the different meteorological conditions between the events (Fig. 1A and B), specifically, the stronger lofting of MDAs due to high surface winds over arid portions of the American southwest and northern Mexico during the March 13th event. Because the March 22nd system followed a similar track over arid regions, MDAs were also seen in the precipitation from this event. However, lower surface wind speeds, and a wind direction tangential to Colorado resulted in fewer MDA particles being lofted and transported to the Front Range. The differences in PNC among locations were similar for each storm event, with Denver containing 1.5–3× more particles than BC and RMNP (Fig. 1C). Patterns in the temporal and spatial differences in the total Al mass concentration (Fig. 1C) are very similar to that seen for the PNC, which is a first indication that no major differences in PSDs might be present among the samples. These two storm events provide a window into the abundance of NNPs associated with MDAs, but deposition of exceptional amounts of MDAs (even seen on the macro-scale as brown dust) likely masked the influence of local geography and land cover type on the atmospheric NP presence. While we are confident in the observed difference in PNC between meteorological events, the numerical values provide only an estimate, as the uncertainty is large in quantifying the PNC as discussed in the following section.
PNC and PSD from spICP-QMS data processing
The higher sensitivity of spICP-QMS for 27Al compared to that of spICP-TOFMS allowed us to detect smaller particles (i.e., lower-mass Al-particles) with this method. This was in part due to the TOFMS being tuned for all masses rather than being optimized for low-mass elements. After a correction for dilution, a close agreement was found between the total number of particles detected by spICP-TOFMS and the number of particles detected by spICP-QMS above the critical value (LC,sp,Al) for spICP-TOFMS (Table S1†). This agreement supports the interpretation that different but overlapping size regions of the same particle population were analyzed by both instruments. Key characteristics of MDAs as determined by spICP-QMS analysis of 27Al are given in Table 1.| Sample | Location/GPS | Precipitation event | Number of particles analyzed | Peak detection critical value (counts) | Mode (nm) | “Dissolved” background from 0.02 μm filtration (μg L−1) | Pareto slope (eqn (1)) |
|---|---|---|---|---|---|---|---|
| Column 6 refers to the mode particle size of the samples-specific particle size distribution (PSD). Column 7 refers to the approximation of dissolved background obtained through analysis of 0.02 μm filtrate, where all detectable particles are removed. a Elevated concentration may be an artifact of ineffective filtration. | |||||||
| S1 | Denver (39.73949, −104.94231) | 3/12–13 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 400 200 ± 400 |
12.5 ± 0.4 | 98 | 0.11 ± 0.01 | −3.83 |
| S2 | 3/23 | 9800 ± 400 | 4.3 ± 0.0 | 70 | 0.91 ± 0.13 | −2.93 | |
| S3 | Rocky Mountain National Park (40.3658872, −105.5602764) | 3/12–13 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 300 000 ± 300 |
8.1 ± 0.1 | 86 | 0.33 ± 0.09 | −3.49 |
| S4 | 3/23 | 3600 ± 200 | 3.5 ± 0.1 | 66 | 0.70 ± 0.07 | −2.20 | |
| S5 | Boulder Canyon (39.99389, −105.47970) | 3/12–13 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 100 600 ± 100 |
4.2 ± 0.0 | 68 | 0.21 ± 0.16 | −3.04 |
| S6 | 3/23 | 4600 ± 300 | 3.1 ± 0.1 | 62 | 4.41 ± 0.15a | −2.64 | |
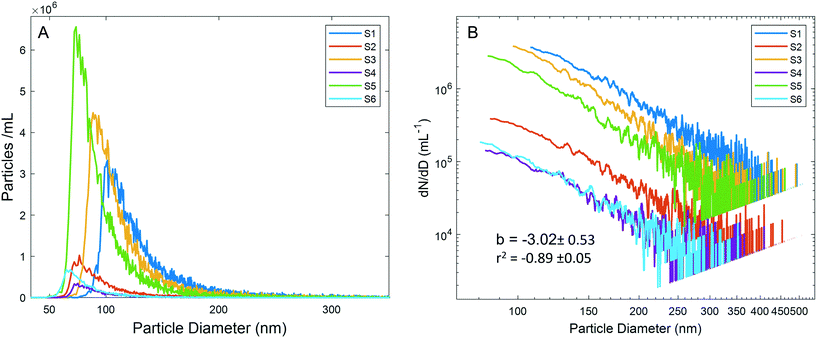
The PSDs for diluted precipitation samples (3/13 samples, 250× dilution; 3/23 samples, 50× dilution) are presented in Fig. 2A. Generating accurate PSDs for natural samples from spICP-MS raw data is complex, yet most studies take a simple approach of providing size histograms with bin widths of several nm. These histograms are generally plotted in linear space, and the particle number in each bin is used to draw conclusions regarding differences in PSDs among samples. This is an acceptable approach for routine analysis of known NP compositions such as in commercial products, where particles are synthesized to be monodisperse. Differences between such PSDs have been used to examine particle transformation processes.21,40 However, in a natural sample where particle characteristics are unknown, differences in PSDs between samples are possibly artifactual, necessitating a more rigorous treatment of the data.
The conventional approach for peak detection described by Pace et al. was used, in which a critical value (based on the 3σ iterative process) identifies particle derived signals over a dissolved background.29 However, even at a high dilution factor, large numbers of very small particles (non-resolved particles) generate a signal that software can mistake for a dissolved background, which then results in an elevated NP detection critical value. We therefore used 0.02 μm filtration to remove most NPs and thus provide a truer measurement of the dissolved background.28 This dissolved background in undiluted samples S1–S5 was 0.45 ± 0.3 μg L−1 (2% of the total Al in these samples). 4.4 μg L−1 Al was recorded in sample 6, which was likely due to a sample preparation error such as a broken filter (data were not examined for several months, preventing replicate analysis). The dissolved background from 0.02 μm filtrate was measured in undiluted samples, while 10 μm filtrate was diluted 50–250× for analysis. Applying this high dilution to the 0.02 μm filtrate would have generated background Al signals below the instrument detection limit (Table S2†). We are therefore confident that the background signals recorded in the 10 μm filtrate were artifactual, a consequence of non-resolved particles.
Plotting the PSDs without additional data processing (Fig. 2A) resulted in large differences between samples despite following the same general trends, with a sharp increase in the particle number as size increases to a mode, followed by a long-tailed distribution. Reporting the data as such would lead to the false conclusion that the PSDs were significantly different between samples. Because of the low dissolved background across all samples, the particle detection critical values should have been similar. However, substantially different critical values were observed among samples, likely due to varying numbers of non-resolved particles. To further explore how the particle number affects the critical value and PSD shape, a dilution experiment (10× to 1000×) for sample S1 was performed. As the dilution factor increased, the number of particles detected did not decrease in proportion to the dilution factor, a consequence of more particles being quantified as the critical value decreased (Table S3†). The experiment concluded that attempting to perform dilutions to mitigate the effects of differing critical values is not trivial for a complex and polydisperse natural sample, and that finding an ideal dilution may not be possible. Critical values were not only different among the 6 samples, but were highly correlated with the mode of each PSD (r2 = 0.98, Fig. S3†), indicating that the mode was likely an analytical artifact, and not a property of the sample-specific PSDs. Based on this correlation as well as the additional sources of error discussed below, we report final PSDs (Fig. 2B) only for sizes above the sample-specific mode. This issue persists in spICP-MS studies, where despite careful treatment of the data processing regarding peak detection and integration, this analytical artifact in the PSD shape is often ignored.41
MDAs, as well as aquatic particles, are described by many distributions in the literature, but the Pareto distribution (inverse power law, sometimes called the Junge distribution) has been commonly used to describe particle sizes between 100 nm and 10 μm.42,43 The Pareto distribution is linear when plotted in log space, and follows eqn 1, where dN is the particle number (or PNC) in a given size bin, D is the particle diameter (dD being the width of the size bin), a is the intercept in log space (related to total particle number), and b is the slope in log space:
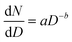 | (1) |
While PSDs at sizes larger than the mode follow the Pareto distribution, particle numbers rapidly decrease at smaller sizes between the mode and the critical value. This is because the critical value provides a fixed value in counts proportional to the baseline signal but does not account for the noise associated with measuring the particles themselves. At a particle size near the critical value, only a fraction (up to 50%) of the true particle number at that size can be detected, following detection limit theory that has been adapted to spICP-MS metrology.46,47 Therefore, at the smallest end of the PSD, the number concentration is underreported. However, the fraction of detectable particles in a given size range increases with particle size, and beyond the mode of the PSD, it is assumed that the entire population is being detected (evidenced by PSDs following the Pareto distribution at sizes larger than the mode). The error associated with particle detection near the critical value is not the only source of error when considering particle sizes below the mode. While the PSD mode is the smallest size at which the power law is observed in each sample, it is possible that this relationship extends to smaller sizes. Should this occur, the increase in particle numbers below the mode would result in extremely large particle numbers (e.g., 1010 ml−1 at 20 nm). These particles would be coincident, resulting in additional undercounting of the small end of the PSD. Modeling particle coincidence in any polydisperse sample is difficult, and the unknown lower size limit of the power law relationship makes this impossible. Therefore, in natural samples governed by a power law distribution, the PSD mode provides a practical approach for determining where particle sizes are representative of the true population.
The agreement among slopes across all samples, and the comparable slopes between spICP-MS and SPOS indicate that the particle size distributions of the six samples were similar. While differences in the particle number are clearly visible in the vertical spacing between PSDs in log space, and supported by the total PNC (Fig. 1C), the parallel slopes indicate that the PSDs themselves were similar. This additional data processing prevented false conclusions being drawn based on PSD positions in linear space (Fig. 2A).
The effect of the particle number on the PSD slope was explored through the S1 dilution experiment. Slopes (dN/dD vs. diameter) in log space of the lower dilution factors are as high as 8, but at higher dilutions (200–1000×), the slopes become approximately 3 (Fig. S5†). Data for lower dilution factors are clearly affected by coincidence and thus are not valid. The data are presented as a contrast to the dilution factors where Pareto behavior is observed, which indicates that despite an elevated critical value (due to non-resolved particles), the shape of the PSD above the mode still approximates Pareto behavior. The agreement with the Pareto distribution at several dilution factors (200, 500, 600, 800, and 1000×) indicates that despite a dilution-dependent effect on the total PNC, the shape of the PSD can still be effectively analyzed above the mode. Consideration of this effect is critical in highly concentrated samples that span orders of magnitude in size and are governed by the Pareto distribution. Attempting to optimize a dilution where coincidence is avoided at the small end of the PSD while maintaining statistically significant numbers of particles at the large end is often not possible. To analyze trends among such samples, examining data at several dilutions where Pareto behavior is observed represents the most feasible process. The dilution experiment also suggests that the dilution factor of 250× used for the 3/13 precipitation event (S1, S3, S5) likely resulted in undercounting particles for these samples. This does not influence the finding that higher MDA particle numbers were reflective of meteorological conditions, and in fact understates this impact.
The Pareto distribution for atmospheric aerosols between 100 nm and 10 μm is thought to result from the addition of multiple log-normal particle distributions corresponding to different particle species.48 The largest particles (1–10 μm) are typically referred to as “Coarse Particles” and previous studies have primarily recorded MDAs in this size range, with coarse particles becoming significantly less frequent below 1 μm.44,48 Mechanical weathering is not thought to generate significant numbers of particles below this size.39 Between 100 nm and 1 μm, the “accumulation mode” is thought to dominate particle numbers; these particles arise in situ from the precipitation and aggregation of sulfates, and other salt particles.44 However, the power law increase in the number of Al-bearing particles (an elemental mineral dust tracer) as size decreases to 100 nm indicates that there may be more overlap between the coarse particle mode and accumulation mode. Accumulation mode particles are soluble salts, and likely do not contain appreciable 27Al, eliminating the possibility that we measured these particle types by spICP-MS.
Particles larger than 550 nm were not observed in any sample by spICP-QMS, but were detected by SPOS and SEM. Samples were sonicated prior to all three modes of analysis, ruling out aggregates as the cause of larger particles detected with SPOS. This discrepancy might be explained in part if the upper size limit for both particle transport in the spray chamber and vaporization in the plasma was reached at 550 nm. This is unlikely as studies have vaporized particles in the micron range, although not all particle compositions (e.g. metal oxides, silicates, etc.) have been examined.49 The results might be better explained by the total number of particles we measured in each sample following the Pareto distribution. With roughly 106 particles per mL observed at the smaller end of the PSD (<100 nm), the probability of observing a particle under our conditions approaches 0 beyond 500 nm. As noted in the discussion regarding the effect of dilution on the critical value, a low dilution to analyze larger numbers of particles could enable detection of larger sizes but would sacrifice detection at the small-size end of the PSD as discussed above.
Given the analytical artifacts discussed above that effected the PSDs, the software-generated total particle number typically used to calculate PNC is inappropriate. Therefore, to accurately compare PNCs between samples, sizes above the largest recorded mode (98 nm, S1) were considered. While this underrepresents the true PNC, inclusion of smaller sizes based on individual sample modes would not provide accurate number comparisons. Fig. 1C presents the PNC for each sample, correlating with the differing strengths of the two storms described. Through the appropriate data processing, the PSD position on the Y axis in Fig. 2B reflects these differences in PNC, supporting the approach.
spICP-TOFMS results
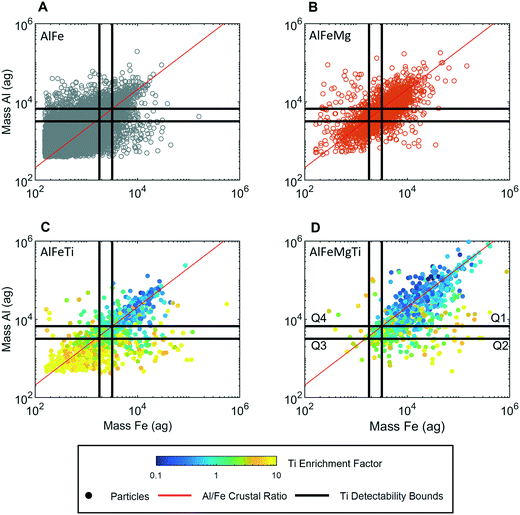
The use of spICP-TOFMS provided the simultaneous detection of single-metal (sm) and multi-metal (mm) NPs in high concentrations (106–108 mL−1) in all samples. We define smNP and mmNP as containing only one or multiple elements detectable by spICP-TOFMS, respectively. Other non-detectable elements such as S and O may be present in any particle. A plot of the total recorded PNCs of smNPs and mmNPs from each sample by spICP-TOFMS is provided in Fig. S6.† spICP-QMS was used to compare PNCs and PSDs between samples, whereas data from all six samples were combined for spICP-TOFMS detection limit filtering. We justify this approach based on the agreement among the PSDs from QMS analysis, the similarity in the source of storm-generated MDAs, and the storm strength that likely masked local geographic variations. Further support comes from the low variance in the normalized PNC across the samples for the major elements considered (Fig. S7†). Additionally, HCA was performed on samples individually, yielding similar elemental fingerprints (Fig. 4). We therefore combined data for simplicity in the detection limit filtering analysis.spICP-TOFMS identified 46% of the particles as mmNPs and over 99% of these mmNPs contained some combination of aluminum (Al), iron (Fe), magnesium (Mg), and titanium (Ti), which are the most abundant elements in the earth's crust suitable for ICP-MS, as Si, Ca, Na, and K have high detection limits resulting from isobaric and polyatomic interferences.36,50 In Fig. 3, we plot the mass correlation of Al and Fe in the four most frequent elemental combinations recorded as single particles: recorded by spICP-TOFMS: AlFe (A), AlFeMg (B), AlFeTi (C), and AlFeMgTi (D).
Across these four mmNP combinations, the Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratios follow the crustal ratio (CR) of 2.08 (red line)36 with the AlFe group displaying increased variance at lower particle masses. A large spread around the CR was observed for precipitation samples, likely indicating the presence of multiple minerals. This was supported by spICP-TOF-MS analysis of ground pure minerals, with the element ratios for biotite, rutile, and ilmenite showing a significantly lower variation than those for samples (Fig. 4). The agreement with the crustal ratio, as well as the presence of multiple minerals, strongly suggests that the particles measured in the precipitation were MDAs.
Fe ratios follow the crustal ratio (CR) of 2.08 (red line)36 with the AlFe group displaying increased variance at lower particle masses. A large spread around the CR was observed for precipitation samples, likely indicating the presence of multiple minerals. This was supported by spICP-TOF-MS analysis of ground pure minerals, with the element ratios for biotite, rutile, and ilmenite showing a significantly lower variation than those for samples (Fig. 4). The agreement with the crustal ratio, as well as the presence of multiple minerals, strongly suggests that the particles measured in the precipitation were MDAs.
The multi-element combinations observed in the MDA particles is a function of both real particle composition heterogeneity and inherent limitations and characteristics of spICP-MS measurements. With spICP-TOFMS, low-abundance (or low-sensitivity) elements in a particle type are only quantitatively measured in larger particles, whereas major elements (or ones with high sensitivity) can be measured in smaller particles. Simply put, from small NPs, we will most likely record only major elements, whereas from large particles, we are more likely to record a more complete element composition. To determine at what signal levels we expect to record given multi-elemental compositions, we must consider two detection criteria: the critical value and the detection limit. In spICP-TOFMS, the single-particle critical value (LC,sp) is the value above which we define a signal as particle-derived and methods for establishing these values are reported.32 At the critical value, particles with average mass that should produce a signal equal to LC,sp will only be detected 50% of the time, i.e. there will be a 50% false negative rate.46,51 For quantitative detection of a particle population, we define a detection limit (LD,sp) above which we expect particles with an average signal equal to LD,sp to be detected 95% of the time (a 5% false-negative rate). As demonstrated by Szakas et al., spICP-TOFMS data follows Poisson statistics and LD,sp values can be calculated based on element-specific LC,sp values and Poisson-normal statistics.52 While critical values and detection limits are fundamental to the ion-signal (counts) domain, we can also express the LC,sp and LD,sp in terms of mass by applying a calibration function (instrument sensitivity). For the remaining discussion, we express all LC,sp and LD,sp values in mass of the element(s) under consideration.
We can define the LC,sp and LD,sp values for any analyte element. However, when considering the absence or presence of specific elements in mmNPs, it is useful to consider which elements limit the detection of a particular mmNP composition. The detection limit (LD,sp) of low-abundance or low-sensitivity elements in a given mmNP composition actually determines whether all the elements from a mmNP will be recorded. To decide whether a given particle signal is large enough to measure all elements of interest (major elements, i, and minor elements, j) if they were present at a known mass ratio, we define two particle-type-specific detection criteria: a particle-specific critical value (LC,sp,i,i–j) and a particle-specific detection limit (LD,sp,i,i–j).52Lc,sp,i,i–j and LD,sp,i,i–j represent the lowest mass of i that we need to detect j above its critical value (LC,sp,j) and detection limit (LD,sp,j), respectively, given the known mass ratio. We assume that this mass ratio between i and j is the crustal abundance ratio (i.e. CRi:j); to obtain the particle-type-specific detection criteria, the critical value and detection limit of j are multiplied by CRi:j according to eqn (2) and (3), respectively. We use the CR to establish the detection criteria because this ratio is conserved between major elements recorded in MDA particles (see Fig. 3 and 4), and because the CR is used extensively in the MDA literature.38 All LC,sp or LD,sp values are first calculated in the signal domain and then converted to equivalent values in mass amount via the known sensitivities of elements.
| LC,sp,i,i–j = LC,sp,j × CRi:j | (2) |
| LD,sp,i,i–j = LD,sp,j × CRi:j | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti = 10.20; iron is ten times more abundant than titanium. This means that from small MDA particles, we are likely to measure Fe and not Ti, and as such falsely classify the particle as not having Ti. To determine whether undetected Ti could be present in a given particle at the CR, we first consider the critical value of Ti, which is 175 ag (∼8.5 counts) in our spICP-TOFMS measurements. Based on the CRFe:Ti, the critical value for detecting an Fe–Ti MDA (LC,Fe,Fe–Ti) is 10.20 × 175 ag = 1785 ag. Therefore, if a measured particle has <1.785 fg of Fe and no detectable Ti, then we cannot say whether Ti is present at the CR or lower. If Ti is measured in a particle with less than 1785 ag of Fe, then that particle must be enriched in Ti compared to the CRFe:Ti. We do not expect all MDA particles with Fe above LC,Fe,Fe–Ti = 1.785 fg to have a measurable amount of titanium. At the critical value, only 50% of Ti signals will be detected. Therefore, we also define the detection limit for Fe–Ti MDA particles. The detection limit for Ti (LD,sp,Ti) is 300 ag, as predicted by Poisson statistics. The detection limit for Fe in a Fe–Ti MDA particle (LD,sp,Fe,Fe–Ti) is thus 3.06 fg. At this detection limit, we estimate that 95% of Fe–Ti MDA particles can be accurately recorded as Fe–Ti mmNPs. So, for detected particles with an Fe mass above 3.06 fg, we should measure Ti if it is present at or above the CRFe–Ti. If we measure an Fe-bearing particle with more than 3.06 fg Fe but no Ti, then we can be certain (with 95% confidence) that Ti was either absent or depleted compared to CRFe:Ti. Similar detection criteria can be applied for Al-bearing MDA using a CRAl:Ti of 21.27.
Ti = 10.20; iron is ten times more abundant than titanium. This means that from small MDA particles, we are likely to measure Fe and not Ti, and as such falsely classify the particle as not having Ti. To determine whether undetected Ti could be present in a given particle at the CR, we first consider the critical value of Ti, which is 175 ag (∼8.5 counts) in our spICP-TOFMS measurements. Based on the CRFe:Ti, the critical value for detecting an Fe–Ti MDA (LC,Fe,Fe–Ti) is 10.20 × 175 ag = 1785 ag. Therefore, if a measured particle has <1.785 fg of Fe and no detectable Ti, then we cannot say whether Ti is present at the CR or lower. If Ti is measured in a particle with less than 1785 ag of Fe, then that particle must be enriched in Ti compared to the CRFe:Ti. We do not expect all MDA particles with Fe above LC,Fe,Fe–Ti = 1.785 fg to have a measurable amount of titanium. At the critical value, only 50% of Ti signals will be detected. Therefore, we also define the detection limit for Fe–Ti MDA particles. The detection limit for Ti (LD,sp,Ti) is 300 ag, as predicted by Poisson statistics. The detection limit for Fe in a Fe–Ti MDA particle (LD,sp,Fe,Fe–Ti) is thus 3.06 fg. At this detection limit, we estimate that 95% of Fe–Ti MDA particles can be accurately recorded as Fe–Ti mmNPs. So, for detected particles with an Fe mass above 3.06 fg, we should measure Ti if it is present at or above the CRFe–Ti. If we measure an Fe-bearing particle with more than 3.06 fg Fe but no Ti, then we can be certain (with 95% confidence) that Ti was either absent or depleted compared to CRFe:Ti. Similar detection criteria can be applied for Al-bearing MDA using a CRAl:Ti of 21.27.
In Fig. 3, the detectability bounds for Al in an Al–Ti MDA (LC,sp,Al,Ti–Al and LD,sp,Al,Ti–Al) and for Fe in an Fe–Ti MDA (LC,sp,Fe,Ti–Fe and LD,sp,Fe,Ti–Fe) are plotted as horizontal and vertical black lines, respectively. These detectability bounds divide each Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe correlation plot into 4 quadrants: Q1, Q2, Q3, and Q4. A zone of uncertainty is established by the area between the lower and upper detectability bounds. In Q3, Ti is not expected to be detected because the amount of Al and Fe is so low that Ti present at the CR would be below the LC,sp,Ti. Therefore any particle with a measurable amount of Ti in Q3 must be enriched in Ti with respect to the CR. Following a similar argument, particles in Q2 and Q4 that have measurable Ti must be enriched in Ti compared to the CRAl:Ti and CRFe:Ti, respectively. As the masses of the major elements increase (i.e. the particle gets bigger), it becomes possible to assess whether Ti is enriched or depleted relative to the crustal ratio in question. For example, at 10 × LC,sp,i,i–Ti, Ti at 10% of the CR can be determined in a single particle. In Q1, there is a sufficient mass of both Al and Fe to measure Ti in all particles in which Ti is present at the CR. Therefore, any particles in Q1 without measurable amounts of Ti (reported in AlFe and AlFeMg groups) are either correctly characterized as not containing Ti, or contain Ti at a lower ratio than the CR.
Fe correlation plot into 4 quadrants: Q1, Q2, Q3, and Q4. A zone of uncertainty is established by the area between the lower and upper detectability bounds. In Q3, Ti is not expected to be detected because the amount of Al and Fe is so low that Ti present at the CR would be below the LC,sp,Ti. Therefore any particle with a measurable amount of Ti in Q3 must be enriched in Ti with respect to the CR. Following a similar argument, particles in Q2 and Q4 that have measurable Ti must be enriched in Ti compared to the CRAl:Ti and CRFe:Ti, respectively. As the masses of the major elements increase (i.e. the particle gets bigger), it becomes possible to assess whether Ti is enriched or depleted relative to the crustal ratio in question. For example, at 10 × LC,sp,i,i–Ti, Ti at 10% of the CR can be determined in a single particle. In Q1, there is a sufficient mass of both Al and Fe to measure Ti in all particles in which Ti is present at the CR. Therefore, any particles in Q1 without measurable amounts of Ti (reported in AlFe and AlFeMg groups) are either correctly characterized as not containing Ti, or contain Ti at a lower ratio than the CR.
Particle-specific detection-limit filtering helps us make sense of the multi-element particle combinations recorded from the Fe–Al particles. In Fig. 3A, particles with detectable amounts of only Al and Fe are reported. However, since 89% of these particles fall outside of Q1, the recorded element composition of most of these particles is likely incomplete. The high percentage of particles outside of Q1 in the AlFe group indicates that AlFe particles should not be considered a unique class of particles, but rather small particles from which minor elements cannot be accurately detected. In Fig. 3B, AlFeMg particles are reported. On average, these particles are larger than AlFe particles because the lower CR of Mg prevents its detection in smaller particles. In our spICP-TOFMS measurements, we did not determine the Mg sensitivity, and as such we cannot draw particle-specific detection-limit boundary lines like those for the detection of Ti. Nonetheless, detection of particulate Mg is useful in defining mmNP groups. As is the case for the AlFe group, we can be confident that particles in Q1 do not contain Ti ≥ CR but could contain depleted levels of Ti.
In Fig. 3C and D, we report the AlFeTi and AlFeTiMg particles, respectively. For these particles, we can assess the enrichment or depletion of Ti with respect to the CR. Here, we define an enrichment factor (EF) (eqn 4), which is plotted by color in Fig. 3C and D. Importantly, in Q3, the Fe and Al mass per particle is so low that depleted levels of Ti are not measurable. Likewise, in Q2 and Q4, measurement of depletion of Ti with respect to Al and Fe, respectively, is not possible. In Q1, we can measure depleted, normal (at the CR), and enriched levels of Ti in single particles.
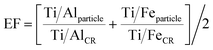 | (4) |
Detection-limit filtering can be used to identify some distinctions between particle groups; however, this method only allows us to predict the signal levels at which we expect to measure certain mmNP compositions based on a set element ratio. The approach does not account for the variance in element ratios observed or allow for differentiation of mmNPs with the same nominal element compositions, but different stoichiometries. This limitation is seen in Fig. 3C and D, in which some of the AlFeTi or AlFeMgTi particles in Q1 show an EF > 1 and others have an EF < 1. These particles with different EFs are likely different types, i.e. different minerals. To gain more insight into how to further differentiate particle groups, we used an unsupervised two-stage hierarchical clustering analysis (HCA) to find major groups; the complete results of this clustering are provided in Fig. S8.† Details about this clustering approach are provided in the Methods and materials section. Two-stage HCA is an unsupervised data reduction approach that groups NPs based on their intra- and inter-sample multi-element signatures.
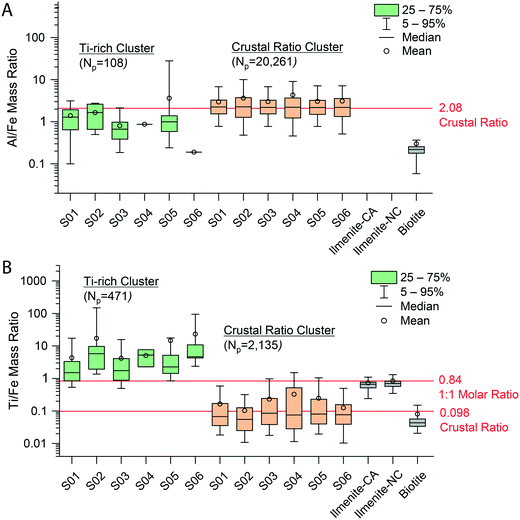
As seen in Fig. S8,† inter-sample clustering of the mmNP signatures of the six snow samples produced 8 distinct NP groups. These groups are discriminated based on the presence and relative amounts of 19 elements. Five of the HCA-developed clusters are present in all six samples, and—by far—most recorded particles are part of one of two clusters, which we name the “Ti-rich Cluster” and the “Crustal Ratio Cluster.” In Fig. 4, we plot the distributions of the Al/Fe and Ti/Fe ratios from individual particles composing the two major HCA clusters. We find that the Al/Fe values in both the Ti-rich Cluster and Crustal Ratio Cluster are not significantly different from the CR (p = 0.22, 0.88 respectively), in agreement with the slope presented in Fig. 3. On the other hand, the Ti/Fe ratios differ by 10–100× between clusters, with the “Crustal Ratio Cluster” (CRC) not differing significantly from the CR (p = 0.77) and the “Ti-rich Cluster” (Ti-RC) showing high enrichment in Ti. This indicates the presence of two particle classes: one class of minerals that has elemental ratios constrained to the CR, and a second that contains Ti at ratios well above the CR. CRC particles likely contain silicate minerals (indicated by the presence of Mg) with various substitutions of Fe and Ti, while Ti-RC likely contains rutile, ilmenite, and other Ti rich minerals. This approach appears to provide a robust clustering of particles, as the same groups are identified in all samples despite differences in the particle number. Additionally, although the model was unsupervised, it constrained CRC to the CR for both Ti/Fe and Al/Fe, aligning it with geochemical principles. Only 3% of particles in the Ti-RC contained Mg, supporting the conclusion provided by DL filtering that the absence of Mg was related to the enrichment of Ti. However, because clustering included relative element amounts rather than just the absence or presence of an element, these 3% of particles were correctly classified by HCA. The particle numbers in each cluster also support the conclusions drawn from detection limit filtering. Ti-RC contains 537 particles, in the range of the particle numbers outside of Q1 in Fig. 3C and D (680). Because the clustering approach was completely independent, we did not expect to see a perfect overlap between the two approaches. In fact, we expected the same general trends to be seen (a class of Ti-rich particles, and a class of particles near the CR), with more accurate placement of individual particles in the groups generated. We therefore conclude that while a computationally simple geochemical approach based on the crustal abundance of elements (detection limit filtering) can be used to approximate particle groups, HCA enables more robust and accurate particle-type grouping. Additionally, detection limit filtering is necessary for accurate smNP characterization (see below).
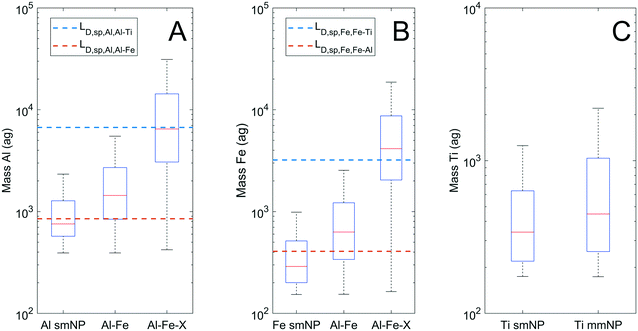
Interestingly, 54% of particles detected by spICP-TOF-MS contained only one element. The true composition of these smNPs may have been different than that observed, and the multi-element capability of TOFMS allows for informed decision making on smNP classification. Because only one element was measured, elemental ratios cannot be applied to classify particles by clustering. Therefore, DL filtering was used. Fig. 5 presents the mass distributions of Al, Fe, and Ti bearing particles as smNPs and mmNPs, plotting LD,sp,Al,Al–X and LD,sp,Fe,Fe–X, for the detection of Al (A), Fe (B), and Ti (C). The AlFe group of particles is plotted separately from other mmNP classes, as we lack confidence for the true composition (i.e., presence of Ti) in nearly 90% of this group (Fig. 3A).
Fig. 5A and B indicate that roughly half of Al smNPs contain insufficient mass to detect Fe at the CR, and the majority of Fe smNPs contain insufficient mass to detect Al. Thus, while some Al and Fe smNPs may be truly devoid of the other major element, we cannot be confident in this for the majority. More significantly, nearly all Al and Fe smNPs lack sufficient mass to detect Ti at the CR (outliers not plotted). We therefore cannot classify either group as true smNPs, because we are not confident in their lack of Ti. Particle-type specific detection limits prevent mischaracterizing particles as smNPs when the element mass is insufficient for accurate detection of minor elements.
Fig. 5C plots the Ti mass distributions for Ti smNPs and the groups of Ti-bearing mmNPs identified in Fig. 3. Because Ti is the least abundant element in the mmNP groups, the mass distributions of the Ti smNPs and mmNPs are similar. This is because the LD,sp lines for Ti as a function of Fe or Al for Fig. 5C would fall below the instrument critical value for measuring a Ti-bearing particle. There is always a sufficient mass of Ti for the accurate detection of Al and Fe if they are present at the CR, so we are therefore confident that Ti smNPs do not contain Al or Fe in appreciable amounts. However, the contribution of trace metals to smNPs cannot be ignored. Ti-rich minerals nearly always have trace impurities of Nb, Ta, or W.53 However, the relative abundance of these elements is so low that the mass of Ti needed to confidently detect them is more than two orders of magnitude above the median Ti mmNP mass. Indeed, we did detect 87 Ti–Nb particles, but due to the extremely high Ti/Nb CR (Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nb = 320), our results were biased towards detecting only Nb-enriched particles.36,54 Therefore, while we are confident that Ti smNPs did not contain major elements such as Al or Fe, we cannot determine whether they contain trace elements such as Nb, Ta, or W.
Nb = 320), our results were biased towards detecting only Nb-enriched particles.36,54 Therefore, while we are confident that Ti smNPs did not contain major elements such as Al or Fe, we cannot determine whether they contain trace elements such as Nb, Ta, or W.
While particle type detection limit filtering can inform the characterization of smNPs detected by spICP-TOFMS, a limitation in this approach lies in the inability to detect certain elements by ICP-MS. Si, Ca, and K are highly abundant in the earth's crust, but cannot be effectively analyzed by ICP-TOFMS due to large polyatomic/isobaric interferences.50 This primarily affected the analysis of Al smNPs, as these elements (primarily Si) are often associated with Al in MDAs.
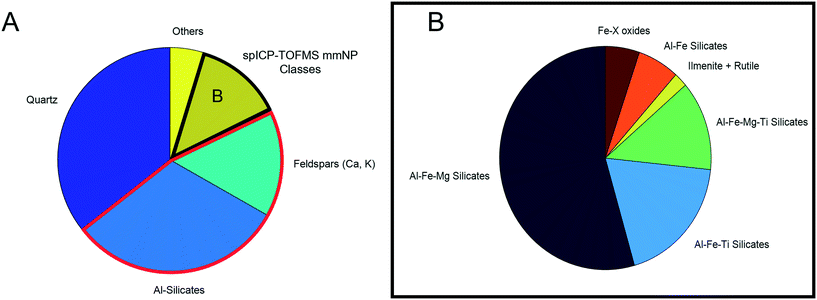
Automated mineralogy analysis
Automated mineralogy (AM) identified particles ranging from 5–100 μm, with the 1 μm EDX spot size limiting the chemical analysis of small particles. The result is a size analysis range that does not overlap with spICP-TOFMS characterization. However, all major particle chemical/mineralogical types were detected across the entire range of particles scanned by AM (Fig. S9†), indicating that the particle composition was not dependent on size. The relative proportions of each particle type may have been different between the sizes due to factors such as shape and density, which could have influenced the atmospheric transport of minerals. However, for the purpose of this study, SEM simply provided support for spICP-TOFMS's ability to detect mineralogically distinct particle classes, so specific particle numbers were not important for this comparison. Fig. 6 presents the mass percent of each particle type detected.To simplify the results, the full suite of minerals detected by AM are not presented; particles are grouped into major categories. Quartz was the most abundant mineral, followed by a group of Al-silicates (primarily kaolinite and other clays), with feldspars also detected in significant numbers. Quartz (SiO2) was not detectable by spICP-TOFMS, while clays and feldspars primarily would have been detected as Al smNPs due to the low sensitivity of Ca, Na, and K by spICP-MS. Additionally, a small number of titanite particles ((Ca,Ti(SiO4)O)) were detected by AM.27 These particles would be detected as smNPs by spICP-TOFMS and based on detection-limit filtering could be erroneously identified as “true” Ti-smNPs.
All four major mmNP types detected by spICP-TOFMS (Fig. 3) were detected by SEM/AM. However, there are similar issues regarding element-specific detection limits. The advantage of spICP-TOFMS is that these limits are more precisely quantified, and detection-limit filtering can be applied. Furthermore, element masses are more precisely quantified on a particle-by-particle basis using spICP-TOFMS compared to AM. Therefore, the agreement in particle classes between both instruments provides a validation that spICP-TOFMS can be used to characterize mmNPs. Additionally, the data for one sample required several hours of analysis and subsequent data reduction, while spICP-MS analyzed a far greater number of particles in a 90s analysis.
Conclusion
Atmospheric particles are dominated by MDAs, and understanding their composition and sizes is relevant to nutrient cycling, climate change, and anthropogenic NP flux. spICP-MS has emerged as the preferred technique to rapidly count and size particles. This study analyzed MDAs in wet deposition transported to Colorado from two storms. An observed 17× increase in average Al-bearing PNC in the stronger storm indicated that the MDA particle number was consistent with meteorological conditions. Application of unique data processing to PSD analysis minimized analytical artifacts, and revealed that despite large differences in particle numbers, all PSDs followed the Pareto distribution observed for aerosols in the literature.42 Al-bearing particles were detected in high numbers at sizes as small as 100 nm, which is smaller than those reported in many previous studies of MDAs. Characterization of MDA sizes is important for modeling earth's albedo, impacting radiative forcing through both light absorption and scattering.55spICP-TOFMS was used to characterize mmNPs, and particle type detection-limit filtering identified groups based on the presence of Ti and Mg. Hierarchical clustering analysis, a data-driven approach, improved upon these groups, and enabled the use of element ratios to identify a class of Ti-rich particles. Natural Ti-rich particles are important in atmospheric chemistry because they influence micronutrient speciation and, consequently, micronutrient bioavailability.56 Therefore, quantification of Ti in natural sources such as MDAs is critical. In our study, Ti smNPs were identified, but, due to their low masses, largely could not be confirmed as true smNPs, i.e. the particles had insufficient mass to measure minor or trace elements such as Nb in them. As ENPs often contain only one metal, accurate detection of Ti smNPs (such as commercially produced TiO2) is essential in determining anthropogenic impacts on the nanoscale.57 The study concluded that MDAs contain a diverse range of minerals with particle sizes that extend into the nanoscale, and can be detected by spICP-MS. Characterization of this particle-rich natural background is essential for future studies of the earth's nanogeochemical cycle.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Edna Bailey Sussman fund, and by the Colorado School of Mines Department of Chemistry. A. G.-G. would like to acknowledge Iowa State University for faculty start-up funds. The authors would like to acknowledge Greg Wetherbee (USGS) for providing NADP snow samples, and Thomas Horner for providing meteorology data and storm descriptions. We acknowledge the contribution of minerals by the Colorado School of Mines Geology Museum. Automated mineralogy analysis was performed by Kelsey Livingston and Katharina Pfaff in the Mineral and Materials Characterization (MMC) Facility at the Colorado School of Mines.References
- S. Fuzzi, U. Baltensperger, K. Carslaw, S. Decesari, H. Denier Van Der Gon and M. C. Facchini, et al. Particulate matter, air quality and climate: Lessons learned and future needs. Atmos, Chem. Phys., 2015, 15(14), 8217–8299 CAS.
- T. E. Shaw, G. Ulloa, D. Farías-Barahona, R. Fernandez, J. M. Lattus and J. Mcphee, Glacier albedo reduction and drought effects in the extratropical Andes, J. Glaciol., 2021, 67(261), 158–169 CrossRef , Available from: https://explorador.cr2.cl/.
- D. Voutsa and C. Samara, Labile and bioaccessible fractions of heavy metals in the airborne particulate matter from urban and industrial areas, Atmos. Environ., 2002, 36(22), 3583–3590 CrossRef CAS.
- J. Brahney, A. P. Ballantyne, C. Sievers and J. C. Neff, Increasing Ca2+ deposition in the western US: The role of mineral aerosols, Aeolian Res., 2013, 10, 77–87, DOI:10.1016/j.aeolia.2013.04.003.
- C. Anastasio and S. T. Martin, Atmospheric nanoparticles, Rev. Mineral. Geochem., 2001, 44, 293–349 CrossRef CAS.
- M. F. Hochella, D. W. Mogk, J. Ranville, I. C. Allen, G. W. Luther and L. C. Marr, et al. Natural, incidental, and engineered nanomaterials and their impacts on the Earth system, Science, 2019, 363(6434), eaau8299 CrossRef PubMed.
- S. C. Sahu and A. W. Hayes, Toxicity of nanomaterials found in human environment, Toxicol. Res. Appl., 2017, 1, 239784731772635 Search PubMed.
- J. Wu, F. Tou, Y. Yang, C. Liu, J. C. Hower and M. Baalousha, et al. Metal-Containing Nanoparticles in Low-Rank Coal-Derived Fly Ash from China: Characterization and Implications toward Human Lung Toxicity, Environ. Sci. Technol., 2021, 55(10), 6644–6654 CrossRef CAS PubMed.
- Y. Dan, H. Shi, X. Liang and C. Stephan, ICP - Mass Spectrometry Measurement of Titanium Dioxide Nanoparticles in Sunscreen using Single Particle ICP-MS, Perkin Elmer Application Note, 2015, vol. 4, pp. 1–4 Search PubMed.
- S. Wagner, A. Gondikas, E. Neubauer, T. Hofmann and F. Von Der Kammer, Spot the difference: Engineered and natural nanoparticles in the environment-release, behavior, and fate, Angew. Chem., Int. Ed., 2014, 53(46), 12398–12419 CAS.
- M. M. Nabi, J. Wang and M. Baalousha, Episodic surges in titanium dioxide engineered particle concentrations in surface waters following rainfall events, Chemosphere, 2021, 263, 128261, DOI:10.1016/j.chemosphere.2020.128261.
- J. Sun, Q. Zhang, M. R. Canagaratna, Y. Zhang, N. L. Ng and Y. Sun, et al. Highly time- and size-resolved characterization of submicron aerosol particles in Beijing using an Aerodyne Aerosol Mass Spectrometer, Atmos. Environ., 2010, 44(1), 131–140, DOI:10.1016/j.atmosenv.2009.03.020.
- P. Zannetti, Dry and Wet Deposition, Springer, Boston, MA, 1990, pp. 249–262 Search PubMed.
- J. M. Prospero, Long-term measurements of the transport of African mineral dust to the southeastern United States: Implications for regional air quality, J. Geophys. Res.: Atmos., 1999, 104(D13), 15917–15927 CrossRef CAS.
- K. Slezakova, J. C. M. Pires, M. C. Pereira, F. G. Martins and M. C. Alvim-Ferraz, Influence of traffic emissions on the composition of atmospheric particles of different sizes-Part 2: SEM-EDS characterization, J. Atmos. Chem., 2008, 60(3), 221–236 CrossRef CAS.
- S. Nowak, S. Lafon, S. Caquineau, E. Journet and B. Laurent, Quantitative study of the mineralogical composition of mineral dust aerosols by X-ray diffraction, Talanta, 2018, 186, 133–139, DOI:10.1016/j.talanta.2018.03.059.
- G. Cornelis, J. Tuoriniemi, M. Montaño, S. Wagner, J. A. Gallego-Urrea and K. Mattsson, et al. Challenges and current approaches toward environmental monitoring of nanomaterials, Monitoring Environmental Contaminants, 2021, pp. 73–108 Search PubMed.
- M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Single Particle ICP-MS: Advances toward routine analysis of nanomaterials, Anal. Bioanal. Chem., 2016, 408(19), 5053–5074, DOI:10.1007/s00216-016-9676-8.
- S. Lee, X. Bi, R. B. Reed, J. F. Ranville, P. Herckes and P. Westerhoff, Nanoparticle size detection limits by single particle ICP-MS for 40 elements, Environ. Sci. Technol., 2014, 48(17), 10291–10300 CrossRef CAS PubMed.
- J. Kocic, D. Günther and B. Hattendorf, Improving detection capability for single particle inductively coupled plasma mass spectrometry with microdroplet sample introduction, J. Anal. At. Spectrom., 2021, 36(1), 233–242 RSC.
- M. Mansor, H. Alarcon, J. Xu, J. F. Ranville and M. D. Montaño, Simultaneous Insight into Dissolution and Aggregation of Metal Sulfide Nanoparticles through Single-Particle Inductively Coupled Plasma Mass Spectrometry, ACS Earth Space Chem., 2022, 541–550 CrossRef CAS.
- M. D. Montan, C. W. Cuss, H. M. Holliday, M. B. Javed, W. Shotyk and K. L. Sobocinski, et al. Exploring Nanogeochemical Environments: New Insights from Single Particle ICP-TOFMS and AF4-ICPMS, ACS Earth Space Chem., 2022, 943–952 CrossRef PubMed.
- L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, Characterization of a new ICP-TOFMS instrument with continuous and discrete introduction of solutions, J. Anal. At. Spectrom., 2017, 32(3), 548–561, 10.1039/C6JA00400H.
- A. Azimzada, I. Jreije, M. Hadioui, P. Shaw, J. M. Farner and K. J. Wilkinson, Quantification and Characterization of Ti-, Ce-, and Ag-Nanoparticles in Global Surface Waters and Precipitation, Environ. Sci. Technol., 2021, 55(14), 9836–9844 CrossRef CAS PubMed.
- About NADP, 2014, Available from: https://nadp.sws.uiuc.edu/NADP/.
- S. Dossett, National Trends Network Site Operation Manual, National Atmospheric Deposition Program Office, 1999, https://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:NATIONAL+TRENDS+NETWORK+SITE+OPERATION+MANUAL#0 Search PubMed.
- J. D. Dana and E. Dana, The System of Mineralogy of James Dwight Dana, ed. J. W. Sons, 1892 Search PubMed.
- S. Bevers, M. D. Montaño, L. Rybicki, T. Hofmann, F. von der Kammer and J. F. Ranville, Quantification and Characterization of Nanoparticulate Zinc in an Urban Watershed, Front. Environ. Sci., 2020, 8, 1–16 CrossRef.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Determining Transport Efficiency for the Purpose of Counting and Sizing Nanoparticles via Single Particle Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2011, 83(24), 9361–9369 CrossRef CAS PubMed.
- S. Bazargan and H. Badiei, U.S. Patent: Systems and Methods for Automated Analysis of Output in SP-ICP-MS, 2019 Search PubMed.
- L. Hendriks, A. Gundlach-Graham and D. Günther, Performance of sp-ICP-TOFMS with signal distributions fitted to a compound Poisson model, J. Anal. At. Spectrom., 2019, 34(9), 1900–1909 RSC.
- A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Monte Carlo Simulation of Low-Count Signals in Time-of-Flight Mass Spectrometry and Its Application to Single-Particle Detection, Anal. Chem., 2018, 90(20), 11847–11855 CrossRef CAS PubMed.
- K. Mehrabi, R. Kaegi, D. Günther and A. Gundlach-Graham, Emerging investigator series: Automated single-nanoparticle quantification and classification: A holistic study of particles into and out of wastewater treatment plants in Switzerland, Environ. Sci.: Nano, 2021, 8(5), 1211–1225 RSC.
- A. Gundlach-Graham and K. Mehrabi, Monodisperse microdroplets: A tool that advances single-particle ICP-MS measurements, J. Anal. At. Spectrom., 2020, 35(9), 1727–1739 RSC.
- J. Gray, Mexican dust found in Colorado blizzard – CNN, 2021, Available from: https://www.cnn.com/2021/03/15/weather/mexican-dust-in-colorado-snow/index.html.
- R. L. Rudnick, The Crust, 2005 Search PubMed.
- H. Maring, D. L. Savoie, M. A. Izaguirre, L. Custals and J. S. Reid, Mineral dust aerosol size distribution change during atmospheric transport, J. Geophys. Res.: Atmos., 2003, 108(19), 1–6 Search PubMed.
- M. Leinmen and M. Sarnthein, Paleoclimatology and Paleometeorology: Modern and Past Patterns of Golbal Atmospheric Transport, Kluwer Academic Publishers, 1987 Search PubMed.
- F. Luis and G. Moncayo, Desert Aerosol: Characteristics and Effects on Climate, 1989 Search PubMed.
- D. M. Mitrano, J. F. Ranville, A. Bednar, K. Kazor, A. S. Hering and C. P. Higgins, Tracking dissolution of silver nanoparticles at environmentally relevant concentrations in laboratory, natural, and processed waters using single particle ICP-MS (spICP-MS), Environ. Sci.: Nano, 2014, 1(3), 248–259, 10.1039/C3EN00108C.
- M. Hadioui, G. Knapp, A. Azimzada, I. Jreije, L. Frechette-Viens and K. J. Wilkinson, Lowering the Size Detection Limits of Ag and TiO2 Nanoparticles by Single Particle ICP-MS, Anal. Chem., 2019, 91(20), 13275–13284 CrossRef CAS PubMed.
- C. Junge, The Size Distribution and Aging of Natural Aerosols as Determined From Electrical and Optical Data on the Atmosphere, J. Atmos. Sci., 1955, 12(1), 13–25 Search PubMed.
- R. Jaenicke, Chapter 1 Tropospheric Aerosols, International Geophysics. Academic Press Inc., 1993, vol. 54, pp. 1–31, Available from: DOI:10.1016/S0074-6142(08)60210-7.
- W. C. Hinds, Aerosol Technoloy: Properties, Behavior, and Measurement of Airborne Particles, John Wiley and Sons, Los Angeles, CA, 2nd edn, 1999 Search PubMed.
- Incorporated TSI. AEROSOL STATISTICS LOGNORMAL DISTRIBUTIONS AND dN/dlogD p.
- L. A. Currie, Limits for Qualitative Detection and Quantitative Determination: Application to Radiochemistry, Anal. Chem., 1968, 40(3), 586–593 CrossRef CAS.
- F. Laborda, A. C. Gimenez-Ingalaturre, E. Bolea and J. R. Castillo, About detectability and limits of detection in single particle inductively coupled plasma mass spectrometry, Spectrochim. Acta, Part B, 2020, 169, 105883, DOI:10.1016/j.sab.2020.105883.
- K. Whitby, On the multimodal nature of atmospheric aerosol size distribution, in VIII international conference on nucleation, leningrad, 1973 Search PubMed.
- F. Laborda, C. Trujillo and R. Lobinski, Analysis of microplastics in consumer products by single particle-inductively coupled plasma mass spectrometry using the carbon-13 isotope, Talanta, 2021, 221, 121486, DOI:10.1016/j.talanta.2020.121486.
- T. W. May and R. H. Wiedmeyer, A Table of Polyatomic Interferences in ICP-MS, 1998, vol. 19 Search PubMed.
- L. A. Currie, Nomenclature in evaluation of analytical methods including detection and quantification capabilities, Pure Appl. Chem., 1995, 67(10), 1699–1723 CrossRef CAS.
- S. Szakas, R. Lancaster, R. Kaegi and A. Gundlach-graham, Quantification and Classification of Engineered, Incidental, and Natural Cerium-Containing Particles by spICP-TOFMS, Environ. Sci.: Nano, 2022, 1627–1638 RSC.
- T. Zack, A. Kronz, S. F. Foley and T. Rivers, Trace element abundances in rutiles from eclogites and associated garnet mica schists, Chem. Geol., 2002, 184(1–2), 97–122 CrossRef CAS.
- D. Lide, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, Fl, 104th edn, 2021 Search PubMed.
- G. Foret, G. Bergametti, F. Dulac and L. Menut, An optimized particle size bin scheme for modeling mineral dust aerosol, J. Geophys. Res.: Atmos., 2006, 111(17), 1–15 Search PubMed.
- E. Hettiarachchi and G. Rubasinghege, Mechanistic Study on Iron Solubility in Atmospheric Mineral Dust Aerosol: Roles of Titanium, Dissolved Oxygen, and Solar Flux in Solutions Containing Different Acid Anions, ACS Earth Space Chem., 2020, 4(1), 101–111 CrossRef CAS.
- M. D. Montaño, G. V. Lowry, F. Von Der Kammer, J. Blue and J. F. Ranville, Current status and future direction for examining engineered nanoparticles in natural systems, Environ. Chem., 2014, 11(4), 351–366 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2en00277a |
| This journal is © The Royal Society of Chemistry 2022 |