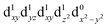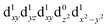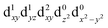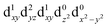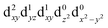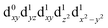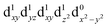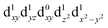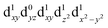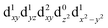Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photoinduced Jahn–Teller switch in Mn(III) terpyridine complexes†
Kyle
Barlow
 a,
Julien
Eng
a,
Julien
Eng
 b,
Iona
Ivalo
b,
Iona
Ivalo
 a,
Marco
Coletta
a,
Marco
Coletta
 a,
Euan K.
Brechin
a,
Euan K.
Brechin
 a,
Thomas J.
Penfold
b and
J. Olof
Johansson
a,
Thomas J.
Penfold
b and
J. Olof
Johansson
 *a
*a
aEaStCHEM School of Chemistry, University of Edinburgh, David Brewster Road, EH9 3FJ, Edinburgh, UK. E-mail: olof.johansson@ed.ac.uk
bChemistry, School of Natural and Environmental Sciences, Newcastle University, Newcastle Upon Tyne, UK
First published on 10th May 2022
Abstract
Ultrafast transient absorption spectra were recorded for [Mn(terpy)X3], where X = Cl, F, and N3, to explore photoinduced switching from axial to equatorial Jahn–Teller (JT) distortion. Strong oscillations were observed in the transients, corresponding to a wavepacket on the excited-state potential energy surface with oscillation frequency around 115 cm−1 for all three complexes. Multireference quantum chemistry calculations indicate that the reaction coordinate is a pincer-like motion of the terpyridine ligand arising from bond length changes in the excited state due to the JT switch. We observed long dephasing times of the wavepacket, with times of 620 fs for [Mn(terpy)Cl3], 450 fs for [Mn(terpy)F3], and 370 fs for [Mn(terpy)(N3)3]. The dephasing time of these coherences decreases with an increasing number of vibrational modes at lower energy than the mode dominating the reaction coordinate, suggesting they act as an effective bath to dissipate the excess energy obtained from photoexcitation.
1. Introduction
The early dynamics after photoexcitation in many inorganic complexes feature vibrational coherences that can be identified as oscillations in transient absorption signals. The wavepackets arise due to coherent nuclear motion after population of sigma-antibonding eg orbitals, which highlights the strong coupling between nuclear and electronic degrees of freedom in these complexes.1–3 These coherences can act as signatures of the main reaction coordinates involved in a photophysical transformation. Recently, Paulus et al. have used the information contained in vibrational coherences to synthetically modify a Fe(II) polypyridyl-based complex to control the excited state dynamics.4 By adding structural rigidity to restrict the normal mode involved in the decay of a charge-transfer state into a metal-centred state, they extended the lifetime of the charge-transfer state 20-fold. Coherent nuclear motion has also been shown to have a significant effect on intersystem crossing rates for a range of Ru(II)5 and Cr(III)1 complexes. Similarly, two branching intersystem crossing processes have been identified in binuclear Pt(II) complexes with different ligands through analysis of vibrational wavepackets.6,7High-spin Mn(III) ions with t32ge1g electron configuration are often used as building blocks for single-molecule magnets (SMMs), for example in the well-studied Mn6,8 because the half-filled eg orbitals lead to a Jahn–Teller (JT) distortion, which in turn leads to a zero-field splitting of the magnetic sublevels and a uniaxial magnetic anisotropy.9 It is the JT distortion and spin–orbit coupling in these 3d metal complexes that lead to the magnetic anisotropy. Modulating the JT distortion by exciting nuclear wavepackets using femtosecond laser pulses will transiently change the magnetic anisotropy which could lead to methods of ultrafast magnetisation control in SMMs. For example, there are reports of ultrafast spin state switching in Cu(II) molecule-based chain magnets arising from a photoinduced change of the JT axis.10,11 In our previous work, ultrafast excitation of ligand-field transitions in Mn(acac)3 was shown to change the JT distortion from elongation to compression, which will switch the sign of the axial zero-field splitting parameter D leading to a change from easy-axis to easy-plane anisotropy.12 The JT switch is generated by exciting an electron from the dz2 to the dx2−y2 orbital. Upon photoexcitation, a nuclear wavepacket was launched in the excited state along the JT normal modes with frequencies ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 170 and 208 cm−1 and a dephasing time τd = 325 fs. The reversed JT state lived for more than 400 ps. The SMM [Mn(III)3O(Et-sao)3(β-pic)3(ClO4)] (Mn3),13 where saoH2 is salicylaldoxime and β-pic is 3-picoline, was also studied. Mn3 has three Mn(III) ions arranged in a triangle and are connected with a single strong, central μ3-oxo bridge and three peripheral –N–O– bonds with the JT axes of the Mn ions perpendicular to the plane of the triangle. Only one vibrational component
= 170 and 208 cm−1 and a dephasing time τd = 325 fs. The reversed JT state lived for more than 400 ps. The SMM [Mn(III)3O(Et-sao)3(β-pic)3(ClO4)] (Mn3),13 where saoH2 is salicylaldoxime and β-pic is 3-picoline, was also studied. Mn3 has three Mn(III) ions arranged in a triangle and are connected with a single strong, central μ3-oxo bridge and three peripheral –N–O– bonds with the JT axes of the Mn ions perpendicular to the plane of the triangle. Only one vibrational component ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 181 cm−1 with a dephasing time τd = 360 fs was observed after photoexcitation of Mn3 corresponding to the in-phase, out-of-plane motion of all three ions along the JT axis. The μ3-oxo bridges inhibits equatorial elongation and restricts wavepacket motion to one direction. This restriction shortens the excited state lifetime significantly in comparison to Mn(acac)3 with the return to the ground state occurring with a time constant of 9 ps. However, the restriction also simplifies the reaction coordinate.
= 181 cm−1 with a dephasing time τd = 360 fs was observed after photoexcitation of Mn3 corresponding to the in-phase, out-of-plane motion of all three ions along the JT axis. The μ3-oxo bridges inhibits equatorial elongation and restricts wavepacket motion to one direction. This restriction shortens the excited state lifetime significantly in comparison to Mn(acac)3 with the return to the ground state occurring with a time constant of 9 ps. However, the restriction also simplifies the reaction coordinate.
An important aspect to consider is the vibrational dephasing time of the coherent motion. Given that the dephasing time of Mn3, with more restricted JT axes, was longer than Mn(acac)3, we have in this work investigated three terpyridine-based monomeric Mn(III) complexes with a more restricted/well-defined JT axis in contrast to the dynamic JT distortion in Mn(acac)3. We have carried out femtosecond transient absorption (TA) spectroscopy on [Mn(terpy)F3], [Mn(terpy)Cl3], and [Mn(terpy)(N3)3], where terpy = 2,2′:6′,2′′-terpyridine. The terpy ligand introduces a well-defined JT axis in the molecule, as seen in Fig. 1A. Our results show that the JT axis is switched upon photoexcitation from the dz2 to the dx2−y2 orbitals, and that this leads to a wavepacket in the excited state with dephasing times that are significantly longer than Mn(acac)3. The vibrational mode of the wavepacket is attributed to a pincer-like motion of the terpyridine ligand in all three complexes. We observe that the dephasing time of these coherences decreases with an increasing number of vibrational states of lower energy than the mode dominating the reaction coordinate. These findings represent a possible design criterion to increase vibrational dephasing times in transition metal complexes.
2. Experimental
2.1 Synthesis and characterisation
The syntheses of [Mn(terpy)Cl3], [Mn(terpy)F3], and [Mn(terpy)(N3)3] were carried out according to literature procedures.14–16 The ultraviolet-visible spectra were measured using a Shimadzu UV-1800 photospectrometer using a 1 cm quartz cuvette. Raman spectra were measured using a Renishaw Raman microscope with a laser wavelength of 785 nm.2.2 Time-resolved measurements
The TA set-up is based on ref. 12. The output from a Light Conversion Pharos-PH2 regenerative amplifier with central wavelength 1030 nm, a pulse duration of 270 fs and repetition rate of 1 kHz was split into pump and probe lines using a 90/10 beam splitter. The stronger arm of the beam was used to pump a Light Conversion Orpheus-F non-collinear optical parametric amplifier, which produced the ca. 40 fs pulses that were used to excite the sample. The timing between the pump and probe pulses was controlled by a corner retroreflector mounted on an Areotech PRO115LM motorised delay stage in the pump path. A mechanical chopper was running at 500 Hz to remove every second pump pulse so that each consecutive probe measures the spectra of a pumped and unpumped sample. The pump pulse is then focussed on the sample using a spherical concave mirror with beam diameters ranging from 200–240 μm depending on wavelength.The weaker arm of the fundamental beam from the amplifier was directed into a 5 mm thick CaF2 window to produce a supercontinuum spectrum. The CaF2 crystal is continuously moved in a circular motion to prevent damage.17 A dichroic mirror is used to separate the supercontinuum from the near-infrared. The probe wavelength range used in these experiments spanned 320 to 720 nm. The beam was split into a sample probe and a reference beam. The sample probe was focused into the sample with a diameter of 100 μm using a spherical concave mirror. The relative polarisations of the pump and probe was set to magic angle (54.7 degrees) and the angle between the pump and probe was 1.1 degrees. After the sample, the beam was collimated and directed into a prism which dispersed the supercontinuum onto fast charge coupled device (CCD) cameras (Entwicklungsbuero Stresing) equipped with Hamamatsu S7031-0907 sensors with 512 × 58 active pixels. The reference beam was directed into an identical spectrometer. Both cameras binned the 58 vertical pixels which allowed for synchronous read out of both the sample probe and reference at 1 kHz. 1500 difference spectra were measured at each time delay and five scans were carried out meaning each spectrum is an average of 7500 individual difference spectra.
The samples were flowed through a Starna flow cuvette with a 0.2 mm path length at a rate of 16 μL min−1. [Mn(terpy)F3] and [Mn(terpy)(N3)3] were dissolved in ethanol with concentrations 25 and 15 mmol, respectively. [Mn(terpy)Cl3] was dissolved in dimethylformamide (DMF) with a concentration of 35 mmol as the complex was nearly insoluble in ethanol. With this cuvette, we achieve a temporal cross-correlation in the pure solvent of ca. 180 fs in the UV range (at 350 nm) and 110 fs in the visible range (at 460 nm).
2.3 Computational details
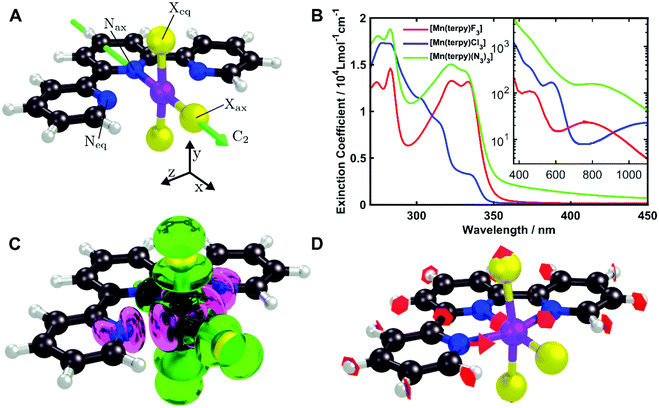
All calculations were performed using the quantum chemistry package Orca 4.2.18 Ground state geometries for all three complexes were optimised with the density functional theory (DFT) method using the PBE0 functional19 and the def2-TZVP basis set20 with the Douglas Kroll Hess (DKH2) correction21 as implemented in the Orca software. The vibrational normal modes were computed in the electronic ground state to ensure the optimised geometry is a minimum. The ground state normal modes are assumed to be a good approximation of the normal modes of the excited states minimum due to the rigidity of the molecules. For [Mn(terpy)Cl3], the electronic structure was calculated using the CASSCF/NEVPT2 approach with an active space of 14 electrons in 10 orbitals and the DKH2-def2-TZVP basis set. This allowed us to take into account both the bonding and anti-bonding orbitals involving the metal centre. The RIJCOSX approximation for integral calculation was employed to speed up the calculations.22 The geometrical parameters are given in Table 1 and the structure is shown in Fig. 1A.| Dimension | X = Cl | X = F | X = N3 |
|---|---|---|---|
| Mn–Xax/Å | 2.227 | 1.78 | 1.92 |
| Mn–Xeq/Å | 2.260 | 1.78 | 1.96/1.94 |
| Mn–Nax/Å | 2.118 | 1.89 | 2.14 |
| Mn–Neq/Å | 2.252 | 1.97 | 2.27/2.28 |
| ∠Xax–Mn–Xeq/° | 93.9 | 90.9 | 92.1 |
| ∠Xax–Mn–Neq/° | 106.3 | 99.8 | 89.28 |
| Symmetry | C 2v | C 2v | C1 |
3. Results and discussion
[Mn(terpy)Cl3] and [Mn(terpy)F3] were optimised in their C2v symmetry ground state minimum. [Mn(terpy)(N3)3] optimisation led to a non-symmetric minimum due to rotation of the N3 ligands. The main dimensions that describe the first coordination sphere of the Mn atom are shown in Table 1. The terms axial and equatorial are defined with respect to the C2 symmetry axis for [Mn(terpy)Cl3] and [Mn(terpy)F3] (see Fig. 1A). For [Mn(terpy)(N3)3], the “axial” axis is defined similarly to the other two complexes even though there is strictly no C2 axis.The electronic structure of [Mn(terpy)Cl3] was investigated with the CASSCF/NEVPT2 approach. The NEVPT2 energies and nature of the lowest excited states are reported in Table 2. The energies of the lowest quintet states are in good agreement with experimentally measured transitions. The first excited quintet state (Q1) occurs at 925 nm (≃1100 nm experimentally). The three other ligand field transitions (Q2–Q4) are higher in energy at 566, 506 and 490 nm, respectively. Q1 (Fig. 1C) involves an excitation of the electron from orbital 100 to orbital 101 (see Fig. S1†), corresponding to exciting from a dz2 to dx2−y2 orbital. Orbital 100 has antibonding character on the Mn–Neq bonds (and on the Mn–Clax and Mn–Nax to a lower extent) and non-bonding character on the Mn–Cleq bonds. In contrast, orbital 101 has non-bonding character on the Mn–Neq bonds and anti-bonding character on the others. We therefore expect a decrease of the Mn–Neq bond lengths and an increase of the four other bond lengths after population of the Q1 state, which corresponds to a JT switch from axial to equatorial (Fig. 1D).
The UV/VIS spectra are presented in Fig. 1B. The transitions in the visible and near-infrared spectral region can be assigned to ligand-field transitions, as identified in the calculations. The peak position of the lowest ligand-field transition changes because the ligand-field strength changes for the three different molecules. These transitions have an extinction coefficient between 10–100 dm3 mol−1 cm−1, which firmly places them as ligand-field transitions. We observe three ligand-field transitions in the spectrum of each complex because Q3 and Q4 are quasi-degenerate.
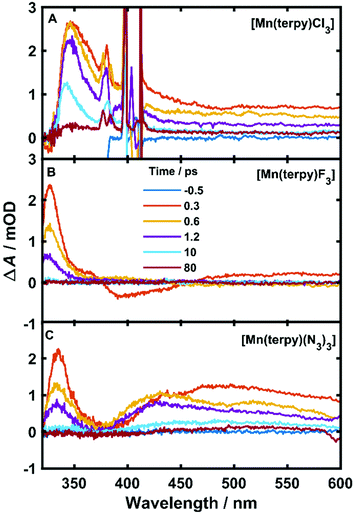
The TA data are presented in Fig. 2 after exciting at the lowest ligand-field transition, which for [Mn(terpy)F3] and [Mn(terpy)(N3)3] corresponds to exciting at 750 and 800 nm, respectively. It was not possible to excite [Mn(terpy)Cl3] at the lowest ligand-field transition as we did encounter some issues with obtaining a good signal. The sample did not dissolve in ethanol and the highest solubility was found in DMF. However, even with this solvent, we were not able to achieve high enough concentrations to produce large enough absorption at the lowest ligand-field transition. This was made worse because the lowest ligand-field transition was not an accessible pump wavelength and so we had to pump at the red-edge of the peak, which resulted in even lower absorption (and therefore weak TA signal). The data for [Mn(terpy)Cl3] excited at the lowest ligand-field transition are presented in the ESI (Fig. S2†) but it is dominated by the solvent and cuvette response. Therefore, we decided to pump at 400 nm, which corresponds to the Q3/4 transitions.
An excited-state absorption (ESA) band in the TA spectra was observed in the UV for all three molecules, as seen in Fig. 2. Kinetic traces at the peak of the UV band are plotted in Fig. 3, where strong oscillations in the data are observed. The data were fitted to two exponential decays with time constants τi and amplitude Ai with an additional damped oscillatory component with frequency ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , amplitude AO and a characteristic dephasing time τd to model the vibronic coherence. This was convoluted with a Gaussian instrument response function IRF(t,σ) = e−t2/2σ2 to model the effect of the finite pump and probe pulse durations as shown in eqn (1).
, amplitude AO and a characteristic dephasing time τd to model the vibronic coherence. This was convoluted with a Gaussian instrument response function IRF(t,σ) = e−t2/2σ2 to model the effect of the finite pump and probe pulse durations as shown in eqn (1).
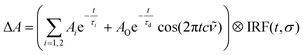 | (1) |
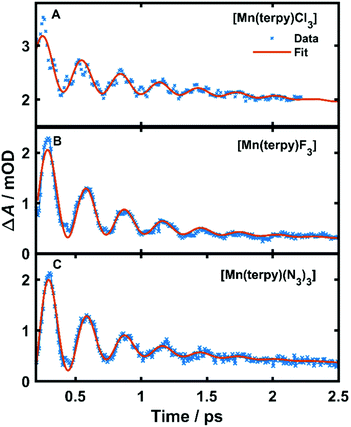 | ||
| Fig. 3 Kinetic trace data and fit at the peak of the excited state absorption. (A) Kinetic trace at 350 nm in TA spectrum of [Mn(terpy)Cl3] after exciting at 400 nm, (B) kinetic trace at 340 nm in TA spectrum of [Mn(terpy)F3] after exciting at 750 nm. (C) Kinetic trace at 343 nm in TA spectrum of [Mn(terpy)(N3)3] after exciting at 400 nm. The data have been fitted with the sum of 2 exponential decays and a single-frequency oscillatory component with dephasing time τd as shown in eqn (1). | ||
The fit gave oscillation frequencies of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 113 ± 1, 115 ± 1, and 115 ± 1 cm−1 for [Mn(terpy)Cl3], [Mn(terpy)F3], and [Mn(terpy)(N3)3], respectively. The corresponding dephasing times were τd = 620 ± 40, 450 ± 20 and 370 ± 10 fs. The kinetics in the UV decayed with two components with time constants τ1 = 330 ± 40 fs and τ2 = 11.7 ± 0.1 ps for [Mn(terpy)Cl3]; τ1 = 450 ± 20 fs and τ2 = 4.0 ± 0.2 ps for [Mn(terpy)F3]; and τ1 = 850 ± 60 fs and τ2 = 9 ± 1 ps for [Mn(terpy)(N3)3]. These parameters are summarised in Table 3. The fit to longer times is shown in Fig. S3.† The TA of [Mn(terpy)F3] showed no signal in the visible, and none of the complexes showed significant oscillations in the visible region from the sample. The visible ESA must originate from a different transition than the UV peak observed in [Mn(terpy)Cl3] and [Mn(terpy)F3] and the visible region is only marginally sensitive to the wavepacket in [Mn(terpy)(N3)3] at 460 nm (Fig. S5†). The visible traces, fits and FFT of residues are shown in Fig. S4–S6.† The time constants for traces at 460 nm were the same as the peak of the ESA apart from [Mn(terpy)Cl3] where τ2 was smaller 2.4 ± 0.3 ps.
= 113 ± 1, 115 ± 1, and 115 ± 1 cm−1 for [Mn(terpy)Cl3], [Mn(terpy)F3], and [Mn(terpy)(N3)3], respectively. The corresponding dephasing times were τd = 620 ± 40, 450 ± 20 and 370 ± 10 fs. The kinetics in the UV decayed with two components with time constants τ1 = 330 ± 40 fs and τ2 = 11.7 ± 0.1 ps for [Mn(terpy)Cl3]; τ1 = 450 ± 20 fs and τ2 = 4.0 ± 0.2 ps for [Mn(terpy)F3]; and τ1 = 850 ± 60 fs and τ2 = 9 ± 1 ps for [Mn(terpy)(N3)3]. These parameters are summarised in Table 3. The fit to longer times is shown in Fig. S3.† The TA of [Mn(terpy)F3] showed no signal in the visible, and none of the complexes showed significant oscillations in the visible region from the sample. The visible ESA must originate from a different transition than the UV peak observed in [Mn(terpy)Cl3] and [Mn(terpy)F3] and the visible region is only marginally sensitive to the wavepacket in [Mn(terpy)(N3)3] at 460 nm (Fig. S5†). The visible traces, fits and FFT of residues are shown in Fig. S4–S6.† The time constants for traces at 460 nm were the same as the peak of the ESA apart from [Mn(terpy)Cl3] where τ2 was smaller 2.4 ± 0.3 ps.
| X = Cl | X = F | X = N3 | |
|---|---|---|---|
| Q1 exp./nm | 1100 | 750 | 800 |
| Q2 exp./nm | 580 | 510 | 520 |
| Q3/Q4 exp./nm | 460 | 470 | 450 |
| τ 1/fs | 330 | 450 | 850 |
| τ 2/ps | 11.7 | 4 | 9 |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1 /cm−1 |
113 | 115 | 115 |
| τ d/fs | 620 | 450 | 370 |
| No. of vib. modes below pincer-mode | 9 | 11 | 17 |
Considering the pump excited the complexes to only the first excited state for [Mn(terpy)F3] and [Mn(terpy)(N3)3] it is expected that the only possible electronic change that can occur during relaxation can be an internal conversion to the ground state. We do not expect intersystem crossing as the calculations suggest there are no states of different spin multiplicities that lie between the ground and first excited quintet state (Table 2). The shortest time constant (τ1) observed in all three complexes is accompanied with a blue-shift and narrowing of the ESA band. These changes in a TA spectrum are often indicative of cooling a vibrationally hot state,23 and so we assign τ1 to this process. We did not observe any additional time constant after exciting [Mn(terpy)Cl3] at the Q3/4 transition, suggesting that the internal conversion to Q1 is within the pump–probe cross correlation time. After the vibrational relaxation the entire spectrum monotonically decays with the second longer time constant, which suggests the second time constant for all three complexes is related to internal conversion back to the ground state. In [Mn(terpy)F3] and [Mn(terpy)(N3)3] the return to the ground state is complete within 80 ps. [Mn(terpy)Cl3] has a small offset above 80 ps suggesting there is not a full return to the ground state for this complex within the measurement time.
Oscillations in the kinetic traces can arise through both ground state wavepacket motion, where the wavepacket is launched through an impulsive Raman scattering mechanism or excited state wavepacket motion where the Franck–Condon region is displaced from the potential minima.24 Normally, these two scenarios are differentiated by observing where in the TA spectra these occur (ground state bleach (GSB) for ground state and ESA for excited state) and if the vibrational frequency measured in the TA spectra is invariably shifted from the ground state spectra. In all three of the complexes there are peaks in the absorption spectra from 400 nm and below and therefore the oscillations are in a region of overlapping GSB and ESA, which makes the ground state versus excited state assignment more complicated. Furthermore, the oscillation frequencies are close to peaks in the ground state Raman spectra shown in Fig. 4, although they are consistently red-shifted. However, plotting the amplitude of the oscillations as a function of wavelength together with the ground state and transient spectra in Fig. 5, we see that the oscillation amplitudes follow the ESA from the difference spectra much more closely than the ground state spectra, which indeed suggests it is an excited state coherence.
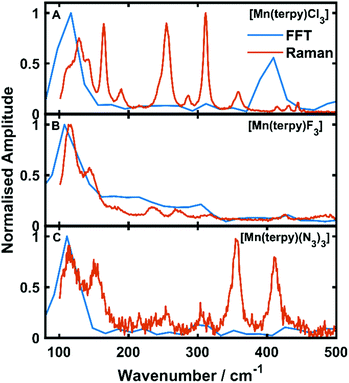 | ||
| Fig. 4 Fast Fourier transforms of the residuals of the kinetic fit plotted with the low frequency Raman spectra. (A–C) refer to [Mn(terpy)Cl3], [Mn(terpy)F3] and [Mn(terpy)(N3)3], respectively. The peak in the FFT at 110 cm−1 matches well with the frequencies from the kinetic trace fitting. The second peak in the Raman in [Mn(terpy)Cl3] occurring at 400 cm−1 is a response from the solvent (Fig. S8†). | ||
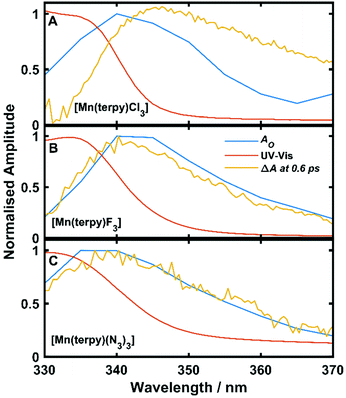 | ||
| Fig. 5 Ground state UV-Vis spectra, ΔA at 0.6 ps and oscillation amplitude AO as a function of wavelength. AO was found by fitting eqn (1) to the data across kinetic traces in the range 330–370 nm. (A) Data from [Mn(terpy)Cl3]. (B) Data from [Mn(terpy)F3]. (C) Data from [Mn(terpy)(N3)3]. In all cases AO can be seen to follow ΔA more closely than the ground state spectrum suggesting the coherence is exists on the electronic excited state. | ||
In the excited state, the electron density is moved from the ground state dz2 to the dx2−y2 orbital (Fig. 1C), both of which are antibonding orbitals. This means that the Mn–Neq bonds will shorten and the Mn–Nax and Mn–X bonds will increase. In addition to this, the excited state coherence has approximately the same frequency in the three complexes regardless of what other ligand is used, which suggests the normal mode is primarily localised on the terpyridine ligand. Putting these two observations together leads to assignment of a pincer-like motion of the terpyridine ligand as shown in Fig. 1D. This mode has previously been observed in [Co(terpy)2]2+ in an ultrafast X-ray scattering experiment with a frequency of 150 cm−1,25 and in the ground state of [Pt(terpy)(S-glutathionato)]2+ (ref. 26) and [Ru(terpy)2]2+ (ref. 27) with frequencies of 111 cm−1 and 80 cm−1, respectively. The values of 113 and 115 cm−1 therefore seem reasonable for this normal mode. To verify this, we have performed electronic structure calculations along the normal modes (q) that decrease the energy gap the most between Q1 and Q0 (ΔEQ0/Q1). We found that two normal modes mainly take part in decreasing ΔEQ0/Q1: q10 (ω10 = 97.861 cm−1) and q21 (ω21 = 273.370 cm−1). q10 corresponds to the pincer-like motion that involves a “closing” of the terpyridine ligand around the Neq–Nax–Neq angle, effectively modulating the Mn–Neq bond lengths. This normal mode also involves a variation of the Cleq–Mn–Cleq angle. The second normal mode q21 is composed of a symmetrical breathing mode of the terpyridine, modulating the Mn–Neq bond lengths, in combination with a symmetric stretch of the Mn–Cleq bonds. This mode was not observed in the TA spectra, although it can be seen in the Raman spectrum. We expect these two motions to be the main distortions that occur upon relaxation in Q1, they are shown in Fig. S9.† The gain in potential energy will thus be mainly converted in kinetic energy in those two modes. To further support this, we have optimised the conical intersection between Q0 and Q1 (i.e. geometry of degeneracy) using DFT/TDDFT with the PBE0 functional. DFT is not accurate enough to handle the multi-configurational nature of the ground state, however, it gives an idea of the distortions. A frequency analysis at this point reveals one imaginary frequency, that corresponds to a combination of q10 and q21 (see Fig. 1D). The frequency of the pincer-like motion was computed to be 97.4 cm−1 which is close to the experimental value of 113 cm−1. It corresponds to mode q10 for [Mn(terpy)Cl3], mode q12 for [Mn(terpy)F3] and mode q18 for [Mn(terpy)(N3)3].
We argue that the decoherence occurs via intramolecular vibrational energy redistribution (IVR) in the prepared excited electronic states, rather than pure dephasing.28 Most of the kinetic energy gained during the relaxation along the Q1 potential energy surface will be concentrated in the pincer-like motion in [Mn(terpy)X3]. This energy will be preferentially dissipated to vibrations of lower frequency via IVR (Fig. S10†). [Mn(terpy)Cl3] shows the fewest vibrational modes below the pincer-like motion, and exhibits the longest dephasing time τd = 620 fs. [Mn(terpy)F3] has two more vibrational modes below mode q12 and has a slightly shorter dephasing time τd = 450 fs. Finally, [Mn(terpy)(N3)3] has the most flexible structure due to the three N3 ligands and exhibits the shortest dephasing time τd = 370 fs. The interpretation of decoherence via IVR is consistent with the number of modes, but a full analysis taking into account the coupling constants between different modes would be required to confirm this.
In comparison to Mn(acac)3, the [Mn(terpy)X3] complexes have a simpler reaction coordinate in the excited state. In [Mn(terpy)X3] only one frequency is observed in the TA spectra which corresponds to the pincer-like mode of the terpyridine ligand. Whereas in Mn(acac)3 two frequencies are observed in the spectrum. This is likely due to Mn(acac)3 possessing dynamic JT distortion where the JT axis can lie along any of the three bond axes due to all the coordination sites being equivalent. [Mn(terpy)X3] does not have equivalent ligands at every coordination site and therefore the JT axis in the ground state is fixed along the Neq–Mn–Neq bonds. When excited there are two separate nuclear trajectories that the Mn(acac)3 can take to reach the compressed state. The axial bonds can compress and the equatorial bonds can expand or only two of the equatorial bonds that lie opposite each other can elongate. Both these trajectories lead to the same geometry for the compressed JT distortion in the excited state but involve different trajectories to do so. Since [Mn(terpy)X3] has a fixed JT axis there is only one main trajectory for the nuclear relaxation. This may explain the observation of two frequency components in the dynamics in Mn(acac)3 but only one in [Mn(terpy)X3] suggesting a simpler reaction coordinate can be generated via restriction of the JT axis similar to the strong oxide and oxime bonds which constrained the wavepacket motion in Mn3.12
4. Conclusion
We have measured the femtosecond transient absorption spectra of [Mn(terpy)X3] where X = Cl, F, and N3 after exciting ligand-field transitions. The pump transition was assigned using multiconfigurational calculations and corresponds to an excitation from the dz2 to the dx2−y2 orbital, which leads to a change in the Jahn–Teller distortion from axial elongation to compression. During this subsequent nuclear motion, all three complexes show evidence of a vibrational wavepacket with frequencies around 115 cm−1, which corresponds to a pincer-like motion of the terpyridine ligand which is identified in the computation as one of the main reaction coordinates along the Q1 potential. The dephasing times are inversely correlated with the number of normal modes with energy lower than that of the pincer-mode, which suggest that the coherent motion dephases primarily due to intramolecular vibrational redistribution. These results represent a strategy to increase vibrational dephasing times in transition metal complexes by limiting the number of low-frequency vibrational modes. Extending these coherence lifetimes may lead to methods of optical control of magnetic anisotropy in SMMs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded in whole, or in part, by EPSRC (EP/S018824/1 and EP/V010573/1). For the purpose of open access, the authors have applied a creative commons attribution (CC BY) licence to any author accepted manuscript version arising.References
- J. N. Schrauben, K. L. Dillman, W. F. Beck and J. K. McCusker, Chem. Sci., 2010, 1, 405–410 RSC.
- G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. Van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647–656 CrossRef CAS.
- C. Consani, M. Prémont-Schwarz, A. Elnahhas, C. Bressler, F. Van Mourik, A. Cannizzo and M. Chergui, Angew. Chem., Int. Ed., 2009, 48, 7184–7187 CrossRef CAS PubMed.
- B. C. Paulus, S. L. Adelman, L. L. Jamula and J. K. McCusker, Nature, 2020, 582, 214–218 CrossRef CAS PubMed.
- J. W. Kim, D. G. Kang, S. K. Kim and T. Joo, Phys. Chem. Chem. Phys., 2020, 22, 25811–25818 RSC.
- R. Monni, G. Capano, G. Auböck, H. B. Gray, A. Vlcek, I. Tavernelli and M. Chergui, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6396–E6403 CrossRef CAS.
- P. Kim, A. J. S. Valentine, S. Roy, A. W. Mills, A. Chakraborty, F. N. Castellano, X. Li and L. X. Chen, J. Phys. Chem. Lett., 2021, 12, 6794–6803 CrossRef CAS PubMed.
- R. Inglis, C. J. Milios, L. F. Jones, S. Piligkos and E. K. Brechin, Chem. Commun., 2012, 48, 181–190 RSC.
- J. Conradie, Inorg. Chim. Acta, 2019, 486, 193–199 CrossRef CAS.
- W. Kaszub, A. Marino, M. Lorenc, E. Collet, E. G. Bagryanskaya, E. V. Tretyakov, V. I. Ovcharenko and M. V. Fedin, Angew. Chem., 2014, 126, 10812–10816 CrossRef.
- X. Dong, M. Lorenc, E. V. Tretyakov, V. I. Ovcharenko and M. V. Fedin, J. Phys. Chem. Lett., 2017, 8, 5587–5592 CrossRef CAS PubMed.
- F. Liedy, J. Eng, R. McNab, R. Inglis, T. J. Penfold, E. K. Brechin and J. O. Johansson, Nat. Chem., 2020, 12, 452–458 CrossRef CAS PubMed.
- R. Inglis, S. M. Taylor, L. F. Jones, G. S. Papaefstathiou, S. P. Perlepes, S. Datta, S. Hill, W. Wernsdorfer and E. K. Brechin, Dalton Trans., 2009, 9157–9168 RSC.
- C. Mantel, A. K. Hassan, J. Pécaut, A. Deronzier, M. N. Collomb and C. Duboc-Toia, J. Am. Chem. Soc., 2003, 125, 12337–12344 CrossRef CAS PubMed.
- C. Mantel, H. Chen, R. H. Crabtree, G. W. Brudvig, J. Pécaut, M. N. Collomb and C. Duboc, ChemPhysChem, 2005, 6, 541–546 CrossRef CAS PubMed.
- J. Limburg, J. S. Vrettos, R. H. Crabtree, G. W. Brudvig, J. C. De Paula, A. Hassan, A. L. Barra, C. Duboc-Toia and M. N. Collomb, Inorg. Chem., 2001, 40, 1698–1703 CrossRef CAS PubMed.
- U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Appl. Phys. B: Lasers Opt., 2009, 96, 215–231 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- E. A. Juban and J. K. McCusker, J. Am. Chem. Soc., 2005, 127, 6857–6865 CrossRef CAS PubMed.
- L. Dhar, J. A. Rogers and K. A. Nelson, Chem. Rev., 1994, 94, 157–193 CrossRef CAS.
- K. Kjær, R. Hartsock, M. Pápai, A. Britz, M. Christensen, A. Dohn, K. Gaffney, R. Alonso-Mori, W. Liang, J. Uhlig, T. Assefa, A. Galler, J. Glownia, V. Sundström, D. Sokaras, T. VanDriel, S. Canton, K. Wärnmark, M. Chollet, K. Møller, E. Biasin, S. Nelson, Z. Németh, W. Gawelda, C. Bressler, J. Zhang, M. Nielsen, G. Vankó, Y. Liu, P. Chabera, H. Lemke, K. Haldrup and T. Harlang, Phys. Rev. Lett., 2016, 117, 130021–130026 Search PubMed.
- W. Huang, C. Li, J. Wang and L. Zhu, Spectrosc. Lett., 1998, 31, 1793–1809 CrossRef CAS.
- S. Schneider, G. Brehm, C. J. Prenzel, W. Jäger, M. I. Silva, H. D. Burrows and S. T. Formosinho, J. Raman Spectrosc., 1996, 27, 163–175 CrossRef CAS.
- K. S. Schweizer and D. Chandler, J. Chem. Phys., 1982, 76, 2296–2314 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt00889k |
| This journal is © The Royal Society of Chemistry 2022 |