Examining the gas-phase homodimers of 3,3,3-trifluoro-1,2-epoxypropane using quantum chemistry and microwave spectroscopy

Abstract

Gas phase homodimers of 3,3,3-trifluoro-1,2-epoxypropane (TFO), a molecule which has shown promise as an effective chiral tag for determining the absolute stereochemistry and the enantiomeric composition of chiral analytes, are explored using a variety of quantum chemistry models and rotational spectroscopy. The potential surface governing the interaction of the two molecules is rapidly explored using the artificial bee colony algorithm for homodimer candidates that are subsequently optimized by quantum chemistry methods. Although all model chemistries employed agree that the lowest energy form of the heterochiral homodimer of TFO (RS or SR) is lower in energy than that of the homochiral dimer (RR or SS), the energy spacings among the lower energy isomers of each and indeed the absolute energy ordering of the isomers of each are very model dependent. The experimental results suggest that the B3LYP-D3BJ/def2-TZVP model chemistry is the most reliable and provides excellent estimates of spectroscopic constants. In accord with theoretical predictions the non-polar lowest energy form of the heterochiral homodimer is not observed, while two isomers of the homochiral dimer are observed and spectroscopically characterized. Observation and assignment of the spectra for all three unique singly-substituted ¹³C isotopologues, in addition to that of the most abundant isotopologue for the lowest energy isomer of the homochiral homodimer of TFO, provide structural information that compares very favorably with theoretical predictions, most notably that the presence of three fluorine atoms on the trifluoromethyl group removes their direct participation in the intermolecular interactions, which instead comprise two equivalent pairs of CH⋯O hydrogen bonds between the two epoxide rings augmented by favorable dispersion interactions between the rings themselves.

---

I. Introduction

Recently, the phenomenon of chiral recognition, where the manner of interaction of one chiral species with another depends on the relative handedness of the two,^1,2 is being developed into an analytical tool for the determination of not only enantiomeric excess, but also the absolute stereochemistry of a sample.^3–8 This method, known as chiral tagging, relies on the conversion of enantiomers, which have identical microwave rotational spectra, into spectroscopically distinct and readily identifiable diastereomers upon complexation via non-covalent interactions to form a heterodimer with a tag molecule of known chirality.

The success of the chiral tagging method relies on the availability of suitable chiral tags. Three small molecules, 3,3,3-trifluoro-1,2-epoxypropane [CH₂CH(CF₃)O], 3,3-difluoro-1,2-epoxypropane [CH₂CH(CHF₂)O], and 3-fluoro-1,2-epoxypropane [CH₂CH(CH₂F)O], also known as 2-(trifluoromethyl)-oxirane, 2-(difluoromethyl)-oxirane, and 2-(fluoromethyl)-oxirane and abbreviated as TFO, DFO, and FO, respectively, are among those that have been found to be potentially useful. They have strong and simple microwave spectra (i.e., without hyperfine structure, internal rotation, or tunneling motion), their structures have been determined through a combination of experimental data and theoretical calculations, and their ability to participate in non-covalent interactions has been observed through the rotational spectra of their argon complexes.^9–11 The availability of multiple functional groups – electronegative O and F atoms and electropositive H atoms – should facilitate intermolecular interactions between each of these molecules and chiral analytes. Here, we use TFO as a chiral tag to explore its utility in providing the absolute configuration of a chiral molecule, and the species to be tagged is TFO itself. In other words, this is a self-tagging experiment where we employ a racemic mixture of TFO and explore the rotational spectroscopy of homochiral and heterochiral dimers of TFO.

The existence of multiple functional groups points to a rather complicated complex-forming landscape; thus, we must turn to theoretical methods to guide our spectral assignments. We have employed several computational methods and will compare the results with our experimental findings in an effort to determine the ones that can well predict both the relative energies and the isomers of a complex formed by small organic molecules.

II. Theoretical calculations

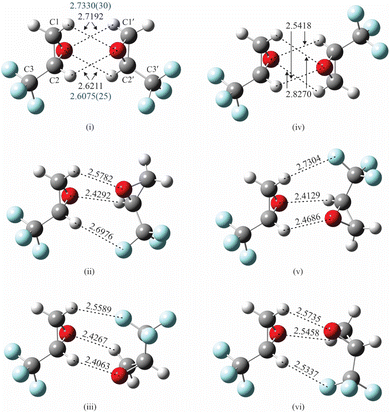
As indicated previously, the presence of electronegative O and F atoms and electropositive H atoms in TFO may lead to the existence of many stable isomers for (TFO)₂. Consequently, it is important that the configuration space available to the two subunits is carefully and efficiently explored to identify candidates for possible isomers. We found the ABCluster program, developed by Zhang and Dolg, which uses the artificial bee colony algorithm,^12,13 to be effective for this work. A set of 30 structures for each type of dimer – homochiral and heterochiral (TFO)₂ – was identified by the program, and each structure was then optimized to minimize the energy using density functional theory (DFT) as implemented in GAUSSIAN 16.¹⁴ All the GAUSSIAN calculations reported here are complete optimizations where all structural parameters are floated. The subunits are not restricted to their average or equilibrium monomeric structure.

The B3LYP functional with the def2-TZVP basis set¹⁵ was employed with the addition of D3 dispersion correction with Becke–Johnson (BJ) damping.¹⁶ Indeed, all DFT calculations presented here include this dispersion correction. The initial set of 30 structures converged to roughly a dozen unique minimum energy structures after the DFT calculations. The three lowest energy structures are labeled (i)–(iii) for homochiral (TFO)₂ and (iv)–(vi) for heterochiral (TFO)₂, and are shown in Fig. 1, with important intermolecular interactions and their lengths labeled. The atomic positions for each isomer in its principal axis system are available as ESI.†

Fig. 1 The optimized structures (B3LYP/def2-TZVP, with GD3BJ dispersion) for the three lowest energy isomers of homochiral (TFO)₂ (i–iii) and the three lowest energy isomers of heterochiral (TFO)₂ (iv–vi). Important interaction distances (in Å and from theory) are labeled in black while experimental distances (also in Å) from the fit to experimentally determined moments of inertia are in blue. Atom colors: C, dark gray; H, light gray; F, blue, O, red.

Isomers (i)–(iii) in Fig. 1 show homochiral (TFO)₂ as formed by two (S)-TFO subunits; those formed by two (R)-TFO subunits are simply the mirror images of these structures and have the same intermolecular interactions. In isomer (i), each O atom in one subunit interacts with two H atoms in the other subunit, while in isomers (ii) and (iii), each O atom interacts with only one H atom, and the third interaction is an F⋯H bond. A noncovalent interaction (NCI) analysis¹⁷ performed using Multiwfn¹⁸ and visualized in Fig. 2 using Chimera¹⁹ confirms the conclusions reached on the basis of the interatomic distances shown in Fig. 1, and in addition reveals the existence of attractive dispersion interactions between the two epoxide rings for each isomer. An intramolecular CF⋯H hydrogen bond is found in each monomer as well as what appears to be exchange repulsion between the same fluorine atom and the pseudo-π electron density of the ring C–C bond.

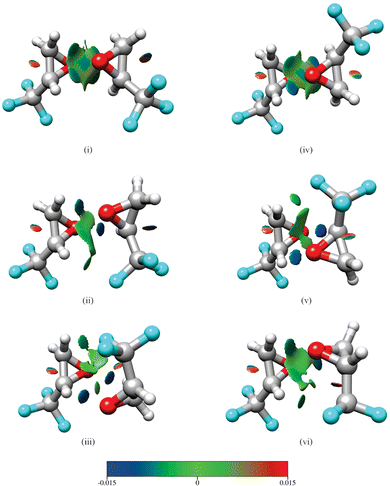Fig. 2 Results of a noncovalent interaction (NCI) analysis performed for the three lowest energy isomers of homochiral (TFO)₂ (i–iii) and the three lowest energy isomers of heterochiral (TFO)₂ (iv–vi). The legend displays the color scale (in a.u.) used for the value of sign(λ₂)ρ. Surfaces rendered in blue and green represent regions of attractive hydrogen-bonding and dispersion interactions, respectively, while those in red show areas of steric repulsion. The same atom color scheme is used as in Fig. 1.

To gain a better understanding of the efficacy of different theoretical methods, these six structures were optimized using the same functional (B3LYP-D3), but with two different additional basis sets [6-311++G(p,d) and 6-311++G(2p,2d)] and also via the ab initio MP2 level of theory utilizing all three basis sets. This last method is chosen here because when used in conjunction with the 6-311++G(2p,2d) basis set it has proven to be an adequate method for the smaller complexes studied at Amherst.²⁰ These calculations were also carried out using GAUSSIAN 16.¹⁴ The relative zero-point corrected energies, rotational constants, and magnitudes of the dipole moment components resulting from each method are listed in Tables 1 and 2, respectively, for three isomers of homochiral and of heterochiral (TFO)₂. To further investigate the significance of basis set superposition error (BSSE) in the theoretical calculations, we carried out additional calculations using the counterpoise correction^21,22 (at each point of the optimization) and these relative zero-point corrected energies are also listed in Tables 1 and 2 for each method. The rotational constants and dipole moment components from the BSSE-corrected calculations are included in the ESI,† together with those from the uncorrected calculations for comparison.

Table 1 Rotational constants, dipole moment components, and relative energies (zero-point corrected) for three conformers of homochiral (TFO)₂ obtained from several levels of theory and basis sets^a

Isomer	B3LYP/6-311++G(p,d)			B3LYP/6-311++G(2p,2d)			B3LYP/def2-TZVP
	(i)	(ii)	(iii)	(i)	(ii)	(iii)	(i)	(ii)	(iii)
a GD3BJ dispersion is included in calculations that use the B3LYP model. b The energies for each calculation method are given relative to the values obtained using the same calculation method for the most stable isomer. These are −981.877788 Hartree, −981.904115 Hartree, −982.001825 Hartree, −979.610230 Hartree, −979.837120 Hartree, and −980.180542 Hartree for B3LYP/6-311++G(p,d), B3LYP/6-311++G(2p,2d), B3LYP/def2-TZVP, MP2/6-311++G(p,d), MP2/6-311++G(2p,2d), and MP2/def2-TZVP, respectively. c The energies for each calculation method are given relative to the values obtained using the same calculation method for the most stable isomer. These are −981.876564 Hartree, −981.903134 Hartree, −982.000957 Hartree, −979.606523 Hartree, −979.833876 Hartree, and –980.178500 Hartree for B3LYP/6-311++G(p,d), B3LYP/6-311++G(2p,2d), B3LYP/def2-TZVP, MP2/6-311++G(p,d), MP2/6-311++G(2p,2d), and MP2/def2-TZVP, respectively. d Isomer (ii) converges to isomer (i) upon attempted optimization with this model chemistry.
A/MHz	1280	1190	1369	1285	1168	1334	1290	1171	1375
B/MHz	270	305	285	269	316	294	266	311	282
C/MHz	249	273	272	248	282	280	245	278	269
|μa|/D	0.00	2.17	2.06	0.00	1.89	1.92	0.00	1.74	1.87
|μb|/D	3.35	3.27	0.11	3.21	3.51	0.10	2.99	3.36	0.12
|μc|/D	0.00	0.06	0.74	0.00	0.01	0.80	0.00	0.01	0.63
Energy^b/cm^−1	17.78	41.26	0.00	3.51	21.51	0.00	0.00	38.63	42.36
BSSE corrected energy^c/cm^−1	0.66	26.56	0.00	0.00	27.00	22.39	0.00	38.41	36.43

---

Isomer	MP2/6-311++G(p,d)			MP2/6-311++G(2p,2d)			MP2/def2-TZVP
	(i)	(ii)	(iii)	(i)	(ii)	(iii)	(i)	(ii)	(iii)
A/MHz	1279	1152	1321	1289	1162	1315	1299	—	1337
B/MHz	277	338	304	278	353	312	273	—	299
C/MHz	254	298	288	256	313	295	252	—	284
|μa|/D	0.00	1.93	1.93	0.00	2.19	1.82	0.00	—	1.73
|μb|/D	3.22	3.83	0.18	3.09	3.86	0.25	2.98	—	0.16
|μc|/D	0.00	0.09	0.79	0.00	0.11	0.75	0.00	—	0.09
Energy^b/cm^−1	0.00	56.62	32.04	0.00	55.75	52.02	0.00	(i)^d	124.00
BSSE corrected energy^c/cm^−1	0.00	(i)^d	49.82	0.00	72.65	73.30	0.00	—	75.72

---

Table 2 Rotational constants, dipole moment components, and relative energies (zero-point corrected) for three conformers of heterochiral (TFO)₂ obtained from several levels of theory and basis sets^a

Isomer	B3LYP/6-311++G(p,d)			B3LYP/6-311++G(2p,2d)			B3LYP/def2-TZVP
	(iv)	(v)	(vi)	(iv)	(v)	(vi)	(iv)	(v)	(vi)
a GD3BJ dispersion is included in calculations that use the B3LYP model. b The energies for each calculation method are given relative to the values obtained using the same calculation method for the most stable isomer. These are −981.878078 Hartree, −981.904413 Hartree, −982.002076 Hartree, −979.610427 Hartree, −979.837274 Hartree, and −980.180716 Hartree for B3LYP/6-311++G(p,d), B3LYP/6-311++G(2p,2d), B3LYP/def2-TZVP, MP2/6-311++G(p,d), MP2/6-311++G(2p,2d), and MP2/def2-TZVP respectively. c The energies for each calculation method are given relative to the values obtained using the same calculation method for the most stable isomer. These are −981.876949 Hartree, −981.903466 Hartree, −982.001208 Hartree, –979.606756 Hartree, −979.834074 Hartree, and –980.178687 Hartree for B3LYP/6-311++G(p,d), B3LYP/6-311++G(2p,2d), B3LYP/def2-TZVP, MP2/6-311++G(p,d), MP2/6-311++G(2p,2d), and MP2/def2-TZVP, respectively. d Isomer (v) converges to isomer (iv) upon attempted optimization with this model chemistry.
A/MHz	1713	1422	1164	1721	1462	1157	1719	1475	1163
B/MHz	228	266	314	228	259	319	227	256	313
C/MHz	222	250	281	222	245	284	221	242	280
|μa|/D	0.00	1.45	2.46	0.00	1.33	2.32	0.00	1.26	2.27
|μb|/D	0.00	0.99	3.24	0.00	1.13	3.25	0.00	1.07	3.07
|μc|/D	0.00	0.16	0.55	0.00	0.09	0.60	0.00	0.10	0.56
Energy^b/cm^−1	17.78	0.00	142.00	16.46	0.00	114.57	0.00	3.73	134.98
BSSE corrected energy^c/cm^−1	19.09	0.00	156.49	15.58	0.00	142.44	2.19	0.00	133.88

---

Isomer	MP2/6-311++G(p,d)			MP2/6-311++G(2p,2d)			MP2/def2-TZVP
	(iv)	(v)	(vi)	(iv)	(v)	(vi)	(iv)	(v)	(vi)
A/MHz	1741	—	1164	1755	1536	1161	1759	—	1175
B/MHz	230	—	324	231	255	339	229	—	320
C/MHz	224	—	289	226	243	300	223	—	285
|μa|/D	0.00	—	2.38	0.00	1.38	2.38	0.00	—	2.24
|μb|/D	0.00	—	3.37	0.00	1.52	3.37	0.00	—	3.14
|μc|/D	0.00	—	0.67	0.00	0.01	0.73	0.00	—	0.66
Energy^b/cm^−1	0.00	(iv)^d	126.42	0.00	75.94	127.95	0.00	(iv)^d	170.09
BSSE corrected energy^c/cm^−1	0.00	—	137.17	0.00	42.14	146.39	0.00		131.25

---

All of the MP2 calculations as well as the B3LYP-D3/def2-TZVP calculation, with or without the inclusion of BSSE correction, agree on isomer (i) being the global minimum structure for the homochiral case. These same methods, again regardless of the BSSE correction, predict that the zero-point corrected energies of isomers (ii) and (iii) are either higher (at least 32 cm⁻¹) than isomer (i), or in the case of MP2/def2-TZVP (BSSE corrected or not) and BSSE corrected MP2/6-311++G(p,d) that isomer (ii) is not a stable minimum on the surface, optimizing instead to isomer (i). Typically in an expansion using argon as a carrier gas, unless the barriers between isomers are fairly large, only the lowest energy isomer of a complex is observed, although there are exceptions.^23–25 Thus, based on these model chemistries, in an argon expansion we should expect to observe isomer (i) experimentally, and the other isomers are likely too high in energy to observe, although they might be seen using helium or neon as the carrier gas.

In contrast, it is difficult to see any consistency in the energy ordering among these three isomers when using the B3LYP-D3 functional with the 6-311++G(p,d) and 6-311++G(2p,2d) basis sets. B3LYP-D3/6-311++G(p,d) predicts isomer (iii) as the global minimum and isomer (ii) as the highest energy of the three both with or without BSSE correction, but the energies of isomers (i) and (ii) relative to isomer (iii) are lowered (15–17 cm⁻¹) by the inclusion of the correction, making isomer (i) nearly isoenergetic with isomer (iii). B3LYP-D3/6-311++G(2p,2d) predicts isomer (iii) as the global minimum without BSSE corrections with isomer (i) 3.5 cm⁻¹ higher in energy, but reverses the order and increases the separation to 22 cm⁻¹ with the correction and results in isomers (ii) and (iii) having similar energies. Thus, these calculations would suggest that there is a good chance, although not a certainty, of observing isomer (iii) in addition to isomer (i) experimentally.

The interactions in the three lowest energy isomers for heterochiral (TFO)₂, (S)-TFO–(R)-TFO, are similar to those for their homochiral counterpart as revealed by both interatomic distances (Fig. 1) and the NCI analysis (Fig. 2). Specifically, in isomer (iv), each O atom interacts with two H atoms in the other subunit, while isomers (v) and (vi) show each O atom interacting with one H atom with the subunits oriented to allow for an F⋯H interaction. All of the computational methods (uncorrected for BSSE) show that isomer (vi) is much higher in energy compared to (iv) and (v). Isomer (iv) has no dipole moment and is not observable while isomer (v) is polar, but has a smaller dipole moment than any of the three homochiral (TFO)₂ dimers listed in Table 1. Similar to the homochiral dimer, for two of the model chemistries [MP2/def2-TZVP and MP2/6-311++G(p,d)], isomer (v) is not a stable minimum, converging to isomer (iv) upon optimization. Ultimately, no spectra for any isomers of the heterochiral dimer were observed, making it impossible to provide any experimental evidence for the energy ordering of the isomers.

III. Experiment

The rotational spectrum of (TFO)₂ was collected using four different spectrometers, located at Amherst College, University of Alberta, and Deutsches Elektronen-Synchrotron (DESY), covering the region from 2 GHz up to 18.1 GHz for isomer (i) (and 2–8 GHz for its minor isotopologues) and up to 20.0 GHz for isomer (iii). At Amherst, the vapor pressure over a room-temperature liquid sample of TFO (SynQuest Laboratories, Achala, FL) was used to form a 1% gas mixture, in argon and first run neon, respectively, for the detection of isomers (i) and (iii). With a backing pressure of 1–2 atm, the spectrum was collected from 6.0 GHz to 18.1 GHz using a broadband, chirped pulse Fourier transform microwave spectrometer^26–28 and 6.0–20.0 GHz using a narrowband, Balle–Flygare spectrometer.^27,29 The broadband spectrometer utilizes two pulsed valves, each with a 0.8 mm diameter nozzle. After expansion through the pulsed valve, the sample is polarized using a chirped microwave polarization pulse of 4 μs duration and 20–25 W of power. Four separately acquired segments of 2.0 or 4.0 GHz bandwidth are obtained by mixing the output of an arbitrary waveform generator (AWG) with carrier frequencies of 10.6, 12.6, 14.6, or 18.6 GHz (generated using phase locked dielectric resonator oscillators) and isolating the lower sideband. The resulting free induction decay (FID) is digitized at 50 Gs s⁻¹ for 10 μs beginning 0.5 μs after the end of the excitation pulse. Ten FIDs are collected during each 800 μs opening of the pulsed valves, which operate at 4 Hz. 618 000 to 900 000 FIDs are averaged for each segment, and as described previously,²⁷ the average is Fourier transformed to give a frequency domain spectrum with a resolution element of 23.84 kHz and typical line widths (FWHM) of 200 kHz. This allows us to assign line centers with an estimated measurement uncertainty of 10 to 20 kHz. The narrowband instrument uses only one pulsed valve. The background-corrected time domain signal is digitized for 1024 data points and zero-filled to a 2048-point record length before Fourier transformation to give a frequency domain signal with a resolution element of 4.8 kHz and an estimated measurement uncertainty of 2 kHz.

A chirped-pulse microwave spectrum was obtained at the University of Alberta^30,31 using mixtures of 0.1% TFO in helium and also in neon with backing pressures similar to those at Amherst, but utilizing only one pulsed valve operating at 2.5 Hz. These spectra are obtained from 2.0–6.0 GHz using direct generation of the 1.0 μs polarizing pulse via an AWG which is amplified to approximately 400 W with a traveling wave tube (TWT) amplifier. The resulting FID is digitized at 25 Gs s⁻¹ for 20 μs, with 6 FIDs obtained per gas pulse, and 650 000 to 732 000 FIDs are averaged prior to Fourier transformation to give a frequency domain spectrum with a resolution element of 25 kHz, linewidths of approximately 120 kHz (FWHM), and an estimated measurement uncertainty of 12.5 kHz. At DESY³² a 2.0–8.0 GHz chirped pulse spectrum was obtained by flowing neon with a backing pressure of 2.5 atm over a heated reservoir containing liquid TFO. The 4.0 μs polarization pulse covering 2.0–8.0 GHz, generated via direct digital synthesis with an AWG, is obtained from the output of a 300 W TWT amplifier. The FIDs are digitized at 25 Gs s⁻¹ for 40 μs, and 7 200 000 averages are obtained before Fourier transformation. These spectra have a resolution element of 12.5 kHz, a 60 kHz linewidth (FWHM), and a measurement uncertainty of approximately 6 kHz.

IV. Results

A. Spectral analysis

We initially took the chirped pulse spectrum of (TFO)₂ at Amherst using argon as a carrier gas and were unable to assign transitions to any species, but spectra from the Alberta instrument, in a helium expansion, allowed us to do so for isomer (iii) of homochiral (TFO)₂. The spectrum was then further refined at DESY through deep averaging. Using the DESY spectrum and with the prediction using ABCluster of isomers that had been previously missed, in addition to isomer (iii), we were able to assign transitions to isomer (i) for the first time. Thereafter, we were able to identify lines due to this species in the Alberta and Amherst chirped pulse spectra. Puzzled by the absence of isomer (iii) in the Amherst spectrum, we turned to the higher resolution and higher sensitivity Balle–Flygare instrument, and discovered that with extensive signal averaging at known frequencies, transitions for isomer (iii) could be observed with very low intensity, which became much stronger when argon is replaced by first run neon, suggesting that isomer (iii) is higher in energy than isomer (i) and explaining why we could not observe it in the Amherst chirped pulse spectrum.

Because much more signal averaging was performed in obtaining the DESY spectrum than the Alberta spectrum, our final data analyses, using Kisiel's AABS package,^33,34 for both isomers [(i) and (iii)] utilize transitions measured from the former for the lower frequency range (2–8 GHz). For higher frequencies (8–18 GHz), the Amherst data are used.

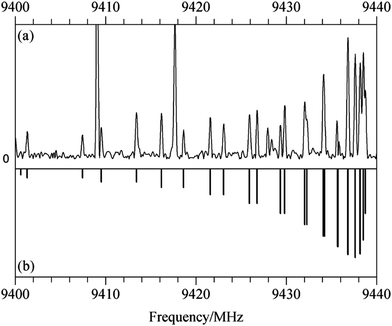
For the spectrum of isomer (i) of homochiral (TFO)₂, only b type transitions were observed, a result of the existence of a C₂ rotational axis in the species. With a predicted dipole moment of about 3 D, these transitions are experimentally quite intense. Fig. 3(a) shows a 40 MHz portion of the spectrum containing the K_a = 5–4 Q branch with transitions arising from J = 5 to 18. The simulated spectrum appears in Fig. 3(b). For the most abundant species, transitions from 2 to 8 GHz, measured using the DESY data, and those from 8 to 18 GHz, obtained at Amherst, were first separately analyzed using the Watson A-reduced Hamiltonian³⁵ in the I^r representation with Pickett's nonlinear least squares SPFIT program.³⁶ After the weight of each set of lines was adjusted to be the same as the standard deviation of each separate fit, the lines were combined to give a global fit. There are a total of 561 transitions, sampling a J range of 1–29 and a K_a range of 0–9. The spectroscopic constants (with uncertainties adjusted using Kisiel's PIFORM program³³) are reported in Table 3.

Fig. 3 (a) A 40 MHz segment of the chirped pulse spectrum taken with the Amherst spectrometer showing Q branch, K_a = 5–4 transitions for isomer (i) of homochiral (TFO)₂. The strong transition at 9409.07 MHz is due to Ar–TFO (11_{0 11}–10_{1 9}); (b) simulated stick spectrum calculated using experimental spectroscopic constants. The intensities of both the experimental and calculated spectra are given in arbitrary units.

Table 3 Experimental spectroscopic constants (in MHz, unless as otherwise noted) for four isotopologues of the lowest energy isomer [isomer (i)] of TFO dimer^a

	CH2CH(CF3)O–CH2CH(CF3)O	^13CH2CH(CF3)O–CH2CH(CF3)O	CH2^13CH(CF3)O–CH2CH(CF3)O	CH2CH(^13CF3)O–CH2CH(CF3)O
a 1σ standard deviations in the parameters are given in parentheses. b All transitions are b type.
A	1305.785412(94)	1294.60882(31)	1305.04415(31)	1305.08646(39)
B	267.046922(28)	266.54268(15)	266.61656(13)	265.80017(14)
C	246.774746(28)	245.95982(15)	246.40261(13)	245.68431(15)
ΔJ/10^−3	0.075235(35)	0.07465(42)	0.07471(37)	0.07498(36)
ΔJK/10^−3	−0.54008(23)	−0.5377(26)	−0.5385(26)	−0.5366(27)
ΔK/10^−3	1.8501(10)	1.816(11)	1.892(17)	1.844(21)
δ J/10^−3	0.0112057(55)	0.01132(18)	0.01089(16)	0.01109(16)
δ K/10^−3	0.16148(64)	0.151(35)	0.170(31)	0.177(35)
No. of rotational transitions^b	561	77	68	79
J range	1–29	2–15	1–15	1–16
K a range	0–9	0–6	0–4	0–4
rms/kHz	7.19	5.01	3.81	5.22

---

Because of the symmetry of isomer (i), there are only three unique isotopologues singly substituted with ¹³C, and they are observed in the DESY spectrum. We assigned 68–79 b type transitions for each isotopologue, sampling J from 1 or 2 up to 15 or 16 and K_a from 0 to at least 4. These spectra were also analyzed with the Watson A-reduced Hamiltonian³⁵ in the I^r representation and Pickett's nonlinear SPFIT program,³⁶ and the spectroscopic constants are listed in Table 3.

For each of the four isotopologues of isomer (i), we determined three rotational constants and five quartic centrifugal distortion constants. The rms deviation is between 3.8 and 7.2 kHz, commensurate with the resolution element of the spectrometers (at DESY and Amherst). Tables of observed and calculated transition frequencies with assignments for all isotopologues studied are in the ESI.†

According to theory (Table 1), isomer (iii) has a smaller dipole moment than isomer (i). Additionally, the a dipole moment component (∼2 D) is greater than the c component (∼0.6–0.8 D) while the b component is very small (0.1–0.3 D). It is therefore not surprising that the transitions observed for this species were in general weaker than those for isomer (i). In fact, despite careful searching for b type transitions using the cavity spectrometer, we were able to observe only a and c type transitions of the most abundant isotopologue totaling 284 transitions. These transitions also sample large J and K_a ranges (J = 1–18 and K_a = 0–8). The transitions from 2–6 GHz (DESY data) and from 6–20 GHz (Amherst narrowband data) were initially analyzed separately, as we did with the most abundant isotopologue of isomer (i), using the Watson A-reduced Hamiltonian³⁵ in the I^r representation and Pickett's nonlinear SPFIT program.³⁶ After adjusting the weights of the two sets of lines with their respective rms uncertainties from the two separate fits, a global fit was carried out, yielding three rotational constants, five quartic centrifugal distortion constant, and five sextic centrifugal distortion constants. We attribute the need for higher order centrifugal distortion constants in fitting transitions in this isomer as likely arising from it being of higher energy, and therefore less strongly bound than isomer (i). The rms deviation of the fit is 3.63 kHz. The spectroscopic constants are listed in Table 4, and a table of observed and calculated transition frequencies with assignments is in the ESI.†

Table 4 Experimental spectroscopic constants (in MHz, unless as otherwise noted) for the most abundant isotopologue of a higher energy [isomer (iii)] TFO dimer^a

	CH2CH(CF3)O–CH2CH(CF3)O
a 1σ standard deviations in the parameters are given in parentheses. b 146 transitions are a type and 138 transitions are c type.
A	1352.20264(18)
B	290.382088(63)
C	276.378481(63)
ΔJ/10^−3	0.23282(29)
ΔJK/10^−3	−1.9286(22)
ΔK/10^−3	6.9717(65)
δ J/10^−3	0.01526(15)
δ K/10^−3	0.373(10)
ΦJ/10^−6	−0.04196(48)
Φ JK/10^−6	0.4155(62)
Φ KJ/10^−6	−2.473(38)
Φ K/10^−6	7.908(86)
ϕ J/10^−6	−0.00439(32)
No. of rotational transitions^b	284
J range	1–18
K a range	0–8
rms/kHz	3.63

---

Despite our efforts, we were not able to assign transitions to any isomers of heterochiral (TFO)₂. Given the vanishing dipole moment of the lowest energy isomer predicted by theory, this is not unexpected.

B. Structure determination

Because we were able to detect only the most abundant isotopologue of isomer (iii), a near prolate asymmetric top with an asymmetry parameter of −0.97, we are not able to extract structural information from its experimental spectroscopic constants. The availability of spectroscopic constants of four isotopologues of isomer (i), however, supply us with intermolecular structural information. This is also a near prolate asymmetric top and has an asymmetry parameter of −0.96 for each of the isotopologues. Treating the most abundant species as the parent, each of the three minor isotopologues contains a single ¹³C substitution in the C1, C2, and C3 positions respectively (these are equivalent to substitutions at C1′, C2′, and C3′). The labeling scheme for the C atoms can be found in Fig. 1. The coordinates of the substituted atom in the principal axis system of the parent can then be determined with a Kraitchman analysis,³⁷ and are listed in Table 5. The relative signs are assigned based on reasonable chemical distances. These values compare very well with the theoretically predicted coordinates given by B3LYP-D3/def2-TZVP calculation (listed also in Table 5), the respective values agreeing to within 0.05 Å. The Kraitchman c coordinate of C3 is nonphysical, indicating that the atom is in (or nearly in) the a–b inertial plane and that the zero-point vibrational motions are different between the most abundant species and its isotopologue when C3 is substituted with ¹³C. Indeed, this is confirmed by the theoretical coordinate of 0.0450 Å.

Table 5 The coordinates of the carbon atoms in homochiral (TFO)₂ [isomer (i)] determined by theory and experimental data^a

	a/Å	b/Å	c/Å
a The a and c coordinates of the carbon atoms C1′, C2′, and C3′ are the negatives of their counterparts listed in the table while the b coordinates are the same as those listed. b Obtained from solving the Kraitchman equations.^37 Costain errors^45 in the parameters are given in parentheses. c Although only the absolute values of the substitution coordinates can be determined from the Kraitchman analysis, the relative signs are assigned using physically reasonable atomic distances. d Obtained from a fit to experimentally determined moments of inertia. See text for details.
B3LYP/def2tzvp with GD3BJ dispersion
C1	1.8384	−1.8288	0.2893
C2	1.7714	−0.3716	0.2935
C3	2.9967	0.4704	0.0450
Substitution coordinates^b^c
C1	1.87303(80)	−1.81194(83)	0.2640(57)
C2	1.72246(87)	−0.3597(42)	0.3019(50)
C3	2.98131(50)	0.4599(33)	Nonphysical
Structure fit^d
C1	1.8348(14)	−1.82815(92)	0.2346(20)
C2	1.78394(92)	−0.3758(11)	0.3154(10)
C3	2.97921(9)	0.45478(9)	0.04998(13)

---

More structural detail for isomer (i) can be determined by fixing each TFO subunit at its average structure⁹ and fitting intermolecular geometric parameters. Because of the symmetry of the complex, only four parameters are necessary in determining its structure. In the following, the unprimed atoms and center of mass belong to one subunit where the primed ones belong to the second subunit. We chose to fit the distance between the centers of mass of the two subunits (COM′–COM), two angles that specify the orientation of COM′ with respect to the first subunit, namely, COM′–COM–O and COM′–COM–O–C2, and a dihedral angle that specifies the orientation of the second subunit in the complex, O′–COM′–COM–O. The symmetry of the complex requires that the orientation of COM with respect to the second unit is equivalent to that of COM′ with respect to the first. This is accomplished by enforcing the equality of COM′–COM–O with COM–COM′–O′ and COM′–COM–O–C2 with COM–COM′–O′–C2′ in the fit. (These parameters are shown in Fig. S1 in the ESI†). Because the last parameter, O′–COM′–COM–O, is correlated with the others, it is fixed to a value (74.9°) empirically adjusted to minimize the rms deviation of the fit. (We were not able to find alternative sets of four parameters that removed the correlation.) Using Kisiel's STRFIT program,³⁸ the three parameters are determined to be, respectively, 5.305942(88) Å, 44.027(53)°, and −42.78(16)°, and the rms deviation of the fit is 0.120 amu Ų. The principal coordinates of C atoms are listed in Table 5 (and those for the rest of the atoms are available as ESI†), agreeing within 0.05 Å of theoretical values (B3LYP-D3/def2-TZVP) and to 0.06 Å with the substitution coordinates. Fig. S2 in the ESI† provides a visual comparison of the theoretically predicted and experimentally determined positions of the carbon atoms. We use Kisiel's EVAL program to determine bond distances,^33,39 and find that the O atom of one subunit interacts somewhat unequally with two H atoms of the other subunit: for the H connected to C1 (or C1′), O⋯H is 2.7330(30) Å, which is 0.126 Å (or 4.81%) longer than that of 2.6075(25) Å for the H connected to C2 (or C2′).

V. Discussion

We are well served by the bee colony algorithm in identifying possible candidates for the isomers of (TFO)₂, and are also well guided by subsequent DFT and MP2 calculations in this work. Experimentally in the Amherst narrowband spectrometer, we found that isomer (iii) of homochiral (TFO)₂ shows weaker transitions in an argon expansion than in a first run neon expansion. It is, therefore, of higher energy than isomer (i). Of course, the larger dipole moment of isomer (i) also contributes to stronger transitions as observed in the Amherst narrowband spectrometer using an argon expansion, but we believe the intensity also derives from the fact that this is the global minimum energy structure, and as a result, is the dominant form of homochiral (TFO)₂. It follows then that all of the MP2 calculations as well as B3LYP-D3/def2-TZVP, regardless of the application of BSSE correction or not, are able to locate the global minimum on the interaction potential surface of two homochiral TFO molecules. These methods, however, also indicate that isomer (iii) is 32–124 cm⁻¹ higher in energy than isomer (i), an amount that in our experience, would likely render it unobservable using an argon expansion,^23–25 contrary to what we found unless the barrier between the two isomers, about which we have no information, is sufficiently high. The two methods, B3LYP-D3/6-311++G(p,d) and B3LYP-D3/6-311++G(2p,2d) do suggest that isomers (i) and (iii) are similar in energy, while isomer (ii) is sufficiently higher to be unobservable, in line with our experimental results. However, the magnitude of the difference in their energies changes depending on whether the BSSE correction is made or not, and for the calculation using the 6-311++G(2p,2d) basis set, the energy ordering changes as well. For the BSSE corrected B3LYP-D3/6-311++G(p,d) calculation and the BSSE uncorrected B3LYP-D3/6-311++G(2p,2d) calculation the energy difference between the two isomers (0.66 or 3.51 cm⁻¹, respectively) is so small that we consider it to be within the uncertainty of the methods.

As we are not able to observe spectra for any heterochiral (TFO)₂ isomers, it is difficult to judge the soundness of the theoretical methods for these species, except to say that negative evidence may once again show that B3LYP-D3/def2-TZVP and MP2 with any of the basis sets utilized here, do well in predicting the global minimum regardless of the inclusion of BSSE correction. For all three basis sets, B3LYP-D3 gives very similar energies for isomers (iv) and (v), both significantly lower than that of isomer (vi), but not a consistent ordering. All the MP2 calculations unambiguously give isomer (iv) as the global minimum. Isomer (iv) is nonpolar, and an absence of a rotational spectrum, in accord to our experimental observation, is expected. Overall, it is difficult to judge the soundness of the energy ordering and the relative energies of different isomers for both homochiral and heterochiral (TFO)₂ using these model chemistries. This is certainly not surprising, as intermolecular interactions are results of delicate balances of rather complicated attractive and repulsive forces.

The experimentally determined rotational constants, which are averaged over the zero-point motion of the dimer, for both structures of homochiral (TFO)₂ are better reproduced by the equilibrium rotational constants from the three DFT calculations than by the MP2 method. The DFT calculated rotational constants differ from the experimental ones by no more than 3% when BSSE correction is not considered, and by 5% or less with BSSE correction. The differences are greater for the MP2 method: by up to 8% without and 20% with BSSE correction. Consequently, although MP2/6-311++G(2p,2d) identifies correctly the global minimum structure, it is computationally much more expensive and does not reproduce the experimental rotational constants of isomers (i) and (iii) as well as the other methods. This is not too surprising, as MP2 is known to overestimate intermolecular binding energy. All three basis sets provide similar structural predictions, and consequently, predictions for rotational constants of comparable utility for assigning and interpreting microwave spectra of the observed TFO dimer conformers. The improvement afforded to these predictions by the inclusion of the BSSE corrections does not justify the additional time it required for this purpose. However, aside from the 6-311++G(2p,2d) basis set result for the homochiral dimer where the energy difference (3.5 cm⁻¹) is so small to render the significance questionable, reliable energy ordering in the absence of BSSE correction was only achieved with the def2-TZVP basis, leaving the B3LYP-D3/def2-TZVP model chemistry as the best choice for obtaining routine guidance in assigning microwave spectra of these complexes.

The effect of the various contributions to the intermolecular interactions on the relative stabilities of the various isomers of (TFO)₂ can be examined using symmetry adapted perturbation theory (SAPT)⁴⁰ as implemented in the PSI4 program package.⁴¹ We choose the def2-TZVP basis for this analysis. The results are summarized in Table 6. The greatest contribution to stability for each species comes from electrostatics (>50%), followed by dispersion (34–40%), and then induction (9–10%). The exchange energy represents a repulsive contribution with magnitudes 43–47% of the sum of the three attractive contributions. Although electrostatic interactions are the strongest contributors to the stability of the isomers of TFO dimer considered here, the relative energies of the species are a result of a balance among the four interactions resulting from the SAPT analysis. Neither the lowest energy forms of the homochiral nor the heterochiral TFO dimer are the ones most stabilized by electrostatic interactions. It is a combination of favorable dispersion interactions and an exchange repulsion that is a smaller fraction of the total stabilization energy (and for the homochiral dimer the smallest absolute value of destabilization) that combine to compensate for the smaller amount of stabilization due to electrostatics and induction to make isomers (i) and (iv) lowest in energy.

Table 6 Contributions to SAPT binding energy (in kJ mol⁻¹ and % of total stabilization energy^a) for three lowest energy homochiral and heterochiral isomers for (TFO)₂

	Electrostatics		Induction		Dispersion		Exchange		SAPT binding energy
	kJ mol^−1	%	kJ mol^−1	%	kJ mol^−1	%	kJ mol^−1	%	kJ mol^−1
a The stabilization energy is the sum of electrostatics, induction, and dispersion energies. Percentages are relative to this total stabilization energy. In the case of exchange energy, the negative percentage indicates that it is destabilizing.
Homochiral
(i)	−21.55	51.37	−3.78	9.00	−16.62	39.63	17.92	−42.72	−24.03
(ii)	−21.92	53.01	−4.11	9.94	−15.32	37.05	18.91	−45.72	−22.45
(iii)	−23.33	54.33	−4.47	10.42	−15.14	35.25	20.30	−47.26	−22.65
Heterochiral
(iv)	−22.74	52.69	−3.96	9.17	−16.46	38.14	18.53	−42.93	−24.62
(v)	−24.39	55.49	−4.51	10.26	−15.06	34.25	20.32	−46.23	−23.64
(vi)	−20.57	52.36	−3.60	9.17	−15.11	38.46	17.40	−44.28	−21.89

---

The observation of two isomers of homochiral (TFO)₂ shows that the presence of multiple functional groups in TFO, a potentially useful chiral tag, does facilitate intermolecular interactions. Additionally, we can readily identify the configuration of its binding partner, this time, another TFO. The experimental structure for isomer (i) shows that the two O⋯H bonds formed by the same O atom are of different lengths, with the one involving H connected to C2 (or C2′) to be slightly shorter, and hence stronger than that connected to C1 (or C1′). This is likely due to the location of the three F atoms, which are closer to (three bonds away from) the former H atom and can remove electron density from it more easily than that for the latter H atom (four bonds away). The presence of four interactions probably makes this complex lower in energy than does the three in isomer (iii), but not significantly so because the two subunits in isomer (iii) can approach each other closer in forging those interactions, as indicated by calculations (Fig. 1).

It is interesting to compare the observed isomers of TFO dimer with the six isomers observed for the dimers of propylene oxide (PO),⁴² which has a methyl (–CH₃) group in place of a fluoromethyl group (–CF₃). All of the observed PO dimers, three heterochiral (RS2, RS4, RS5) and three homochiral (RR2, RR4, RR5) contain at least one hydrogen bond between a ring oxygen and a methyl hydrogen, which cannot occur in (TFO)₂. However, the lowest energy isomers of heterochiral and homochiral (TFO)₂ have structures very similar to the unobserved RS6 and RR6 isomers of (PO)₂. These TFO dimers are additionally stabilized by hydrogen bonds formed between a ring hydrogen donor and a –CF₃ fluorine acceptor that are impossible in (PO)₂. Indeed, we find that the replacement of the PO methyl group by the TFO fluoromethyl group changes the interaction potential landscape of these two molecules. This was additionally seen in the differences in the lowest energy, observed isomers of the argon complexes of the two. With TFO, argon locates above the epoxide ring with the –CF₃ group below the ring,⁹ while in Ar–PO, the argon locates to the side of the ring, forming a close contact with the methyl group carbon atom as well as a carbon atom and the oxygen atom in the ring.^9,43,44

Although we cannot observe a heterochiral (TFO)₂, it is clear that in this self-tagging experiment, we are able to form one or more dimers between a tag and an analyte, and that straightforward applications of theoretical methods and rotational spectroscopy can readily identify them.

VI. Conclusion

Multiple potential, low energy isomers for homodimers of 3,3,3-trifluoro-1,2-epoxypropane (TFO), both heterochiral and homochiral, are located using the ABCluster program^12,13 and further characterized using various quantum chemistry model calculations. Both steps are necessary as the lowest energy homochiral dimer was not found when exploring the configuration space available to the interacting species in a simplistic and time-consuming scan of the two subunits about each other, while not all configurations located by the artificial bee colony algorithm optimized to unique minima on the potential surface. However, the combination of the ABCluster algorithm with a low-cost density functional calculation, B3LYP-D3/def2-TZVP, provides a rapid and reliable method of identifying low energy configurations and provides predictions of spectroscopic constants of sufficient accuracy for straightforward assignment of rotational spectra.

The lowest energy heterochiral homodimer predicted by such calculations of TFO contains a center of inversion, and lacking a permanent dipole moment, cannot be observed using microwave spectroscopy. Attempts to assign spectra of higher energy isomers, using a variety of carrier gases, were unsuccessful. Spectra for two low-energy isomers of the homochiral dimer were assigned, including all three unique ¹³C isotopologues for the lowest energy isomer, based on the carrier gas dependence of transition intensities. Comparison of the experimental structural parameters provided by analysis of the rotational constants for all four isotopologues of this isomer with quantum chemical predictions confirms that B3LYP-D3/def2-TZVP provides a good estimate of the dimer's structure. This suggests that this model chemistry will find useful application in predicting the spectra of the diastereometric chiral tag-analyte pairs required for chiral analysis.

Conflicts of interest

The are no conflicts of interest to declare.

Acknowledgements

This material is based on work supported by the National Science Foundation under Grant No. CHE-1856637 to HOL and MDM. HOL and MDM gratefully acknowledge the H. Axel Schupf ’57 Fund for Intellectual Life for support of the Faculty Research Awards Program at Amherst College and of sabbatical leaves, and they also thank their hosts in Edmonton and Hamburg for their hospitality while collecting data at the University of Alberta and at DESY. This work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Projektnummer 328961117 – SFB 1319 ELCH. SRD acknowledges FCT Portugal for funding through the CEEC-IND program (2018), Grant No. UIDB/04564/2020 and UIDP/04564/2020. YX and WJ acknowledge funding from the Natural Sciences and Engineering Research Council of Canada and the University of Alberta. YX is a Tier 1 Canada Research Chair in Chirality and Chirality Recognition.

References

1. N. Borho and Y. Xu, Molecular Recognition in 1:1 Hydrogen-Bonded Complexes of Oxirane and Trans-2,3-Dimethyloxirane with Ethanol: A Rotational Spectroscopic and Ab Initio Study, Phys. Chem. Chem. Phys., 2007, 9, 4514–4520.
2. N. Borho and Y. Xu, Lock-and-Key Principle on a Microscopic Scale: The Case of the Propylene Oxide⋯Ethanol Complex, Angew. Chem., Int. Ed., 2007, 46, 2276–2279.
3. L. Evangelisti, W. Caminati, D. Patterson, J. Thomas, Y. Xu, C. West and B. Pate, A Chiral Tagging Strategy for Determining Absolute Configuration and Enantiomeric Excess by Molecular Rotational Spectroscopy, The 72nd International Symposium on Molecular Spectroscopy, Talk RG-03, Urbana-Champaign, IL, 2017.
4. B. H. Pate, L. Evangelisti, W. Caminati, Y. Xu, J. Thomas, D. Patterson, C. Pérez and M. Schnell, Quantitative Chiral Analysis by Molecular Rotational Spectroscopy, Chiral Analysis, 2nd edn, Elsevier, 2018, pp. 679–729.
5. S. R. Domingos, C. Pérez, M. D. Marshall, H. O. Leung and M. Schnell, Assessing the Performance of Rotational Spectroscopy in Chiral Analysis, Chem. Sci., 2020, 11, 10863–10870.
6. M. D. Mills, R. E. Sonstrom, Z. P. Vang, J. L. Neill, H. N. Scolati, C. T. West, B. H. Pate and J. R. Clark, Enantioselective Synthesis of Enantioisotopomers with Quantitative Chiral Analysis by Chiral Tag Rotational Spectroscopy, Angew. Chem., Int. Ed., 2022, 61, e202207275.
7. R. E. Sonstrom, J. L. Neill, A. V. Mikhonin, R. Doetzer and B. H. Pate, Chiral Analysis of Pantolactone with Molecular Rotational Resonance Spectroscopy, Chirality, 2022, 34, 114–125.
8. F. Xie, N. A. Seifert, W. Jäger and Y. Xu, Conformational Panorama and Chirality Controlled Structure–Energy Relationship in a Chiral Carboxylic Acid Dimer, Angew. Chem., Int. Ed., 2020, 59, 15703–15710.
9. M. D. Marshall, H. O. Leung, K. Wang and M. D. Acha, Microwave Spectrum and Molecular Structure of the Chiral Tagging Candidate, 3,3,3-Trifluoro-1,2-Epoxypropane and Its Complex with the Argon Atom, J. Phys. Chem. A, 2018, 142, 4670–4680.
10. M. D. Marshall and H. O. Leung, The Microwave Spectrum and Molecular Structure of 3,3-Difluoro-1,2-Epoxypropane and Its Complex with the Argon Atom, J. Mol. Spectrosc., 2018, 350, 18–26.
11. H. O. Leung, M. D. Marshall and D. J. Stuart, Microwave Spectrum and Molecular Structure of 3-Fluoro-1,2-Epoxypropane and the Unexpected Structure of Its Complex with the Argon Atom, J. Phys. Chem. A, 2020, 124, 1798–1810.
12. J. Zhang and M. Dolg, ABCluster: The Artificial Bee Colony Algorithm for Cluster Global Optimization, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
13. J. Zhang and M. Dolg, Global Optimization of Rigid Molecular Clusters by the Artificial Bee Colony Algorithm, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Wallingford, CT, 2016.
15. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
16. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
17. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506.
18. T. Lu and F. W. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592.
19. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferring, UCSF Chimera – a Visualization System for Exploratory Research and Analysis, J. Comput. Chem., 2004, 25, 1605–1612.
20. H. O. Leung and M. D. Marshall, Exploring the Forces Contributing to Non-Covalent Bonding by Microwave Spectroscopy and Structural Characterization of Gas-Phase Heterodimers of Protic Acids with Haloethylenes, J. Phys. Chem. A, 2019, 123, 10846–10861.
21. S. F. Boys and F. Bernardi, The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors, Mol. Phys., 1970, 19, 553–566.
22. S. Simon, M. Duran and J. J. Dannenberg, How Does Basis Set Superposition Error Change the Potential Surfaces for Hydrogen Bonded Dimers?, J. Chem. Phys., 1996, 105, 11024–11031.
23. T. D. Klots, R. S. Ruoff and H. S. Gutowsky, Rotational Spectrum and Structure of the Linear CO₂-HCN Dimer: Dependence of Isomer Formation on Carrier Gas, J. Chem. Phys., 1989, 90, 4216–4221.
24. R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, Relaxation of Conformers and Isomers in Seeded Supersonic Jets of Inert Gases, J. Chem. Phys., 1990, 93, 3142–3150.
25. T. Emilsson, T. C. Germann and H. S. Gutowsky, Kinetics of Molecular Association and Relaxation in a Pulsed Supersonic Expansion, J. Chem. Phys., 1992, 96, 8830–8839.
26. M. D. Marshall, H. O. Leung, B. Q. Scheetz, J. E. Thaler and J. S. Muenter, A Chirped Pulse Fourier Transform Microwave Study of the Refrigerant Alternative 2,3,3,3-Tetrafluoropropene, J. Mol. Spectrosc., 2011, 266, 37–42.
27. M. D. Marshall, H. O. Leung and C. E. Calvert, Molecular Structure of the Argon-(Z)-1-Chloro-2-Fluoroethylene Complex from Chirped-Pulse and Narrow-Band Fourier Transform Microwave Spectroscopy, J. Mol. Spectrosc., 2012, 280, 97–103.
28. H. O. Leung, M. D. Marshall, J. P. Messinger, G. S. Knowlton, K. M. Sundheim and J. C. Cheung-Lau, The Microwave Spectra and Molecular Structures of 2-Chloro-1,1-Difluoroethylene and Its Complex with the Argon Atom, J. Mol. Spectrosc., 2014, 305, 25–33.
29. H. O. Leung, D. Gangwani and J. U. Grabow, Nuclear Quadrupole Hyperfine Structure in the Microwave Spectrum of Ar–N₂O, J. Mol. Spectrosc., 1997, 184, 106–112.
30. C. D. Carlson, N. A. Seifert, M. Heger, F. Xie, J. Thomas and Y. Xu, Conformational Dynamics of 1-Phenyl-2,2,2-Trifluoroethanol by Rotaional Spectroscopy and Ab Initio Calculations, J. Mol. Spectrosc., 2018, 351, 62–67.
31. N. A. Seifert, J. Thomas, W. Jäger and Y. Xu, Rotational Spectra and Theoretical Study of Tetramers and Trimers of 2-Fluoroethanol: Dramatic Intermolecular Compensation for Intramolecular Instability, Phys. Chem. Chem. Phys., 2018, 20, 27630–27637.
32. D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, Multi-Resonance Effects within a Single Chirp in Broadband Rotational Spectroscopy: The Rapid Adiabatic Passage Regime for Benzonitrile, J. Mol. Spectrosc., 2012, 280, 77–84.
33. Z. Kisiel, Prospe – Programs for Rotational Spectroscopy. http://info.ifpan.edu.pl/~kisiel/prospe.htm (accessed June 17, 2021).
34. Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. deLucia and E. Herbst, Rotational Spectrum of Trans–Trans Diethyl Ether in the Ground and Three Excited Vibrational States, J. Mol. Spectrosc., 2005, 233, 231–243.
35. J. K. G. Watson, Aspects of Quartic and Sextic Centrifugal Effects on Rotational Energy Levels, in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier Scientific Publishing, Amsterdam, 1977, vol. 6, pp. 1–89.
36. H. M. Pickett, The Fitting and Prediction of Vibration-Rotation Spectra with Spin Interactions, J. Mol. Spectrosc., 1991, 148, 371–377.
37. J. Kraitchman, Determination of Molecular Structure from Microwave Spectroscopic Data, Am. J. Phys., 1953, 21, 17–24.
38. Z. Kisiel, Least-Squares Mass-Dependence Molecular Structures for Selected Weakly Bound Intermolecular Clusters, J. Mol. Spectrosc., 2003, 218, 58–67.
39. Z. Kisiel, Assignment and Analysis of Complex Rotational Spectra, in Spectroscopy from Space, ed. J. Demaison, K. Sarka and E. A. Cohen, Kluwer Academic Publishers, Dordrecht, 2001.
40. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of Van Der Waals Complexes, Chem. Rev., 1994, 94, 1887–1930.
41. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. De Prince, III, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, III, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability, J. Chem. Theory Comput., 2017, 13, 3185–3197.
42. Z. Su, N. Borho and Y. Xu, Chiral Self-Recognition: Direct Spectroscopic Detection of the Homochiral and Heterochiral Dimers of Propylene Oxide in the Gas Phase, J. Am. Chem. Soc., 2006, 128, 17126–17131.
43. S. Blanco, S. Melandri, A. Maris, W. Caminati, B. Velino and Z. Kisiel, Free Jet Rotational Spectrum of Propylene Oxide-Krypton and Modelling and Ab Initio Calculations for Propylene Oxide-Rare Gas Dimers, Phys. Chem. Chem. Phys., 2003, 5, 1359–1364.
44. S. Blanco, A. Maris, A. Millemaggi and W. Caminati, The Most Stable Conformer of the Propylene Oxide-Argon Complex, J. Mol. Struct., 2002, 612, 309–313.
45. C. C. Costain, Determination of Molecular Structures from Ground State Rotational Constants, J. Chem. Phys., 1958, 29, 864–874.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04663f

‡ Present address: CFisUC, Department of Physics, University of Coimbra, 3004-516 Coimbra, Portugal.

§ Present address: Center for Science and Peace Research, University of Hamburg, Bogenallee 11, 20144 Hamburg, Germany.

¶ Present address: Department of Chemistry and Chemical & Biomedical Engineering, University of New Haven, 300 Boston Post Rd, West Haven, CT, 06516, USA.

---