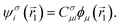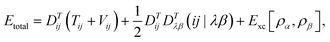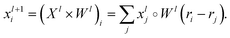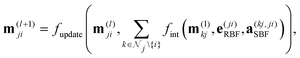nablaDFT: Large-Scale Conformational Energy and Hamiltonian Prediction benchmark and dataset
Kuzma
Khrabrov
 *a,
Ilya
Shenbin
*a,
Ilya
Shenbin
 c,
Alexander
Ryabov
c,
Alexander
Ryabov
 de,
Artem
Tsypin
de,
Artem
Tsypin
 a,
Alexander
Telepov
a,
Alexander
Telepov
 a,
Anton
Alekseev
a,
Anton
Alekseev
 cg,
Alexander
Grishin
cg,
Alexander
Grishin
 a,
Pavel
Strashnov
a,
Pavel
Strashnov
 a,
Petr
Zhilyaev
d,
Sergey
Nikolenko
a,
Petr
Zhilyaev
d,
Sergey
Nikolenko
 cf and
Artur
Kadurin
cf and
Artur
Kadurin
 *ab
*ab
aAIRI, Kutuzovskiy prospect house 32 building K.1, Moscow, 121170, Russia. E-mail: kadurin@airi.net; khrabrov@airi.net
bKuban State University, Stavropolskaya Street, 149, Krasnodar 350040, Russia
cSt. Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences, nab. r. Fontanki 27, St. Petersburg 191011, Russia
dCenter for Materials Technologies, Skolkovo Institute of Science and Technology, Bolshoy Boulevard 30, bld. 1, Moscow, 121205, Russia
eMoscow Institute of Physics and Technology (National Research University), Institutsky lane, 9, Dolgoprudny, Moscow Region 141700, Russia
fISP RAS Research Center for Trusted Artificial Intelligence, Alexander Solzhenitsyn st. 25, Moscow, 109004, Russia
gSt. Petersburg University, 7-9 Universitetskaya Embankment, St Petersburg, 199034, Russia
First published on 24th October 2022
Abstract
Electronic wave function calculation is a fundamental task of computational quantum chemistry. Knowledge of the wave function parameters allows one to compute physical and chemical properties of molecules and materials. Unfortunately, it is infeasible to compute the wave functions analytically even for simple molecules. Classical quantum chemistry approaches such as the Hartree–Fock method or density functional theory (DFT) allow to compute an approximation of the wave function but are very computationally expensive. One way to lower the computational complexity is to use machine learning models that can provide sufficiently good approximations at a much lower computational cost. In this work we: (1) introduce a new curated large-scale dataset of electron structures of drug-like molecules, (2) establish a novel benchmark for the estimation of molecular properties in the multi-molecule setting, and (3) evaluate a wide range of methods with this benchmark. We show that the accuracy of recently developed machine learning models deteriorates significantly when switching from the single-molecule to the multi-molecule setting. We also show that these models lack generalization over different chemistry classes. In addition, we provide experimental evidence that larger datasets lead to better ML models in the field of quantum chemistry.
1 Introduction
The solution of the many-particle Schrödniger equation (SE) for electrons makes it possible to describe matter at the level of chemical bonds for molecules and band structure for crystals. In turn, the electronic system of matter determines a large number of its equilibrium and transport properties, which opens up vast opportunities in the search for new molecules such as prospective drugs or catalysts and new materials such as novel superhard, superconducting, low-dimensional, and other materials.Solving the many-particle SE is a complex task that has attracted a lot of attention from several generations of researchers, but, unfortunately, its analytical solution is still unknown. However, there exist a wide variety of numerical methods that solve it on different levels of precision. These methods comprise a hierarchy that trades off accuracy against computational cost and the number of electrons whose motion one can calculate in reasonable time using a particular technique.
At the top of the hierarchical pyramid are two families of Post-Hartree–Fock1 and quantum Monte Carlo methods.2 They are very accurate (approximately 1 kcal mol−1) but computationally expensive, allowing to consider systems of up to tens of electrons. All of them are based on manipulating the many-body wave function, which is represented as an expansion of one-electron orbitals with adjustable coefficients. Optimization search is performed in the space of these adjustable coefficients to a find a multi-particle wave function that provides the minimum energy of the system. Therefore, it most closely corresponds to the “real” multi-particle wave function of the ground state (the minimum energy state).
The second step of the hierarchical pyramid is taken by the density functional theory (DFT) method,3–5 which is currently the primary approach for solving the many-particle SE for electrons.
DFT is a mean-field method, where the many-particle problem is divided into several single-particle problems, and one solves SE for a single electron in the effective field of other electrons. The main difference between this method and more accurate ones is that it manipulates not the many-particle wave function but electron density, which is an observable quantity. DFT makes it possible to consider systems on a scale of 1000 electrons6 with satisfactory accuracy (approximately 10 kcal mol−1), thus scaling up to systems that are already nano-objects such as nanotubes and fullers, pieces of proteins, or parts of catalytic surfaces. Accuracy of the DFT is determined by the so-called exchange-correlation (XC) functional,7–9 which again has an accuracy/complexity tradeoff hierarchy within itself. It is believed that by looking for a fast and accurate exchange-correlation functional it may be possible to improve DFT's accuracy up to 1 kcal mol−1, thus making it almost equal in accuracy to the methods at the very top.
On the nominal third step of the hierarchy are the so-called parametric methods such as the tight-binding method,10 which require a parameterization of the Hamiltonian. They make calculations possible for extensive systems up to a tens of thousand electrons.11 However, the non-deterministic pre-parameterization step and large volatility in the resulting accuracy make this method less popular than DFT.
In addition to traditional numerical methods for solving the many-body SE for electrons, machine learning (ML) methods have emerged in abundance, looking for their own place in the hierarchy of accuracy/complexity. One promising direction to incorporate ML into the field is to develop a family of trial wave functions based on deep neural networks (NN); recent results show that it can outperform the best highly accurate quantum Monte–Carlo methods.12,13 Another direction is to directly predict the wave-function, electron densities, and/or the Hamiltonian matrix from atom coordinates (system configuration).14–18 The third direction is to use neural networks to model the XC functional for high accuracy DFT.19–26
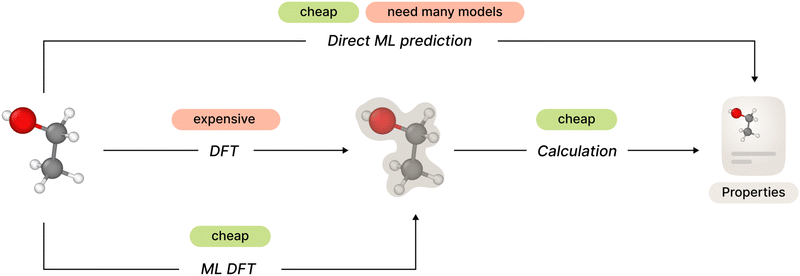
The general framework of ab initio molecular property prediction consists of two steps: first compute the electron structure of a specific molecular conformation or a set of conformations, and then calculate desired properties based on the results of the first step. The second step is relatively simple, but total computational complexity could be too high depending on the method used on the first step.
One straightforward approach to avoid this complexity is to train a machine learning model to predict desired molecular properties directly, shortcutting around the electron structure part. However, this approach may lack generalization since one would need to develop and train a separate new model for each new property.
Recent studies have shown promising results in the field of electron structure prediction using a number of different ML methods. It avoids costly computations of DFT (or higher order) methods by substituting it with a relatively simple ML model but keeping the generalized property computation framework. In this way, the method only needs a single ML model for all necessary properties (Fig. 1).
Though there exist recent advances in Hamiltonian matrix approximation using ML (see Section 2), these studies suffer from two serious drawbacks. First, all models were trained and tested in the single-molecule setup (both training and testing on different conformations of the same molecule), and all models have problems with scaling up to larger molecular structures. In our study we focus on exploring these drawbacks.
An important inspiration for this work comes from the lack of datasets that could be used to train such models. The expressive power of machine learning models is meaningless unless supported by the size and variability of training data. Related fields are seeing the rise of large-scale datasets of small molecules and compounds where the necessary properties have been established by accurate and computationally expensive methods; for example, t6 he MOSES benchmarking platform27 has compared molecular generation models for drug discovery based on a subset of the ZINC clean leads dataset.28 Other examples of large-scale datasets with results of DFT calculations are Open Catalyst 2020 (OC20) and 2022 (OC22).29,30 These datasets together contain 1.3 million molecular relaxations with results from over 260 million DFT calculations.
Large-scale datasets have allowed to achieve impressive results in the field of Natural Language Processing. One of the key reasons of the success of the Transformer-based models,31 such as BERT32 or GPT-3,33 was the access to a huge training corpus. It has been shown in the domain of medicinal chemistry34 that degradation in the accuracy from the full dictionary to a 30% of the dictionary is significant for disease linking in clinical trials. Apart from the quality increase, bigger and more diverse datasets are important for models robustness. Work of Tutubalina et al.35 elaborates that the generalization ability of machine learning models is influenced by whether the test entity/relation has been presented in the training set.
In this work, we introduce a new large-scale dataset that contains structures and Hamiltonian matrices for about million conformations of about 6 million conformations of about 1 million molecular structures, with electronic properties computed with the Kohn–Sham method. This dataset allows for comparisons between DFT-based models in different settings, in particular generalization tests where the training and test sets contain different molecules. In the way of benchmarking, we adapt several classical and state of the art DFT-based models and compare their results on our dataset, drawing important conclusions about their expressivity, generalization power, and sensitivity to data size and training regimes. The models considered in this work come in two varieties, either estimating the potential energy estimation or predicting the Hamiltonian coefficients.
The paper is organized as follows. Section 2 describes related prior art, including datasets and methods as well as modern AI applications. Section 3 introduces the terminology used throughout this paper and sets up the mathematical foundations. Section 4 describes our new dataset, and Section 5 introduces the models used in our benchmark. Section 6 shows benchmark setup and results and discusses the outcomes of our experimental study, and Section 7 concludes the paper.
2 Related work
DFT allows to predict the behaviour of complex systems of atoms (molecules, materials) ab initio, based directly on quantum mechanics. However, accurate quantum-chemical computations have prohibitive computational costs. One possible solution is to use sufficiently simple analytic approximations to overly complex functions such as the total energy of the system.36 Another approach, which has been rapidly gaining prominence over the last decade, is to learn such approximations in the form of various machine learning models.2.1 Datasets
Several datasets with DFT calculations have been released.The Quantum Machines 9 (QM9) dataset presents molecular structures and properties obtained from quantum chemistry calculations for the first 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 molecules of the chemical universe GDB-17 database.37 The dataset corresponds to the GDB-9 subset of all neutral molecules with up to nine heavy atoms (CONF), not counting hydrogen. Additionally, the dataset includes 6095 constitutional isomers of C7H10O2. For all molecules, calculated parameters include equilibrium geometries, frontier orbital eigenvalues, dipole moments, harmonic frequencies, polarizabilities, and thermochemical energetics corresponding to atomization energies, enthalpies, and entropies at ambient temperature. These properties have been obtained at the B3LYP/6-31G(2df,p) level of theory. For a subset of 6095 constitutional isomers, these parameters were calculated at the more accurate G4MP2 level of theory.
885 molecules of the chemical universe GDB-17 database.37 The dataset corresponds to the GDB-9 subset of all neutral molecules with up to nine heavy atoms (CONF), not counting hydrogen. Additionally, the dataset includes 6095 constitutional isomers of C7H10O2. For all molecules, calculated parameters include equilibrium geometries, frontier orbital eigenvalues, dipole moments, harmonic frequencies, polarizabilities, and thermochemical energetics corresponding to atomization energies, enthalpies, and entropies at ambient temperature. These properties have been obtained at the B3LYP/6-31G(2df,p) level of theory. For a subset of 6095 constitutional isomers, these parameters were calculated at the more accurate G4MP2 level of theory.
Along with their Accurate NeurAl networK engINe for Molecular Energies (ANAKIN-ME, or ANI), Smith et al.38 released ANI-1,39 a dataset of non-equilibrium DFT total energy calculations for organic molecules that contains ≈20m molecular conformations for 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462 molecules from the GDB-11 database.40,41 Atomic species are limited to C,N,O atoms (with hydrogens added separately with RDKit), and the number of heavy atoms varies from 1 to 8. All electronic structure calculations in the ANI-1 dataset are carried out with the ωB97x42 density functional and the 6-31 G(d) basis set in the Gaussian 09 electronic structure package.
462 molecules from the GDB-11 database.40,41 Atomic species are limited to C,N,O atoms (with hydrogens added separately with RDKit), and the number of heavy atoms varies from 1 to 8. All electronic structure calculations in the ANI-1 dataset are carried out with the ωB97x42 density functional and the 6-31 G(d) basis set in the Gaussian 09 electronic structure package.
Quantum-Mechanical Properties of Drug-like Molecules (QMugs) is a data collection of over 665k curated molecular structures extracted from the ChEMBL database.43 Three conformers per compound were generated, and the corresponding geometries were optimized using the GFN2-xTB method,44–46 with a comprehensive array of quantum properties computed at the DFT level of theory using the ωB97X-D functional47 and the def2-SVP Karlsruhe basis set.48
2.2 Methods and applications
The field was opened by Snyder et al.49 who used traditional machine learning models to approximate density functionals in Kohn–Sham DFT for a small number of fermions (up to 4 electrons). The SchNet model by Schütt et al.15 introduced a deep neural network approach to physical chemistry problems, specifically to the prediction of molecular conformation energy. This served as a starting point for a plethora of publications addressing different tasks in the field. Hermann et al.50 and Pfau et al.51 proposed PauliNet and Ferminet respectively, two different deep learning wave function ansatzes that achieve nearly exact solutions of the electronic Schrödinger equation for single atoms or small molecules such as LiH, ethanol, or bicyclobutane. Gao and Günnemann52 PESNet outperformed previous works in terms of computational cost while matching or surpassing their accuracy. However, these approaches are very hard to scale both with the size of the molecular system and with the number of molecules. As reported by Gao and Günnemann,52 it takes 854, 4196, and 89 hours of training on an NVidia A100 GPU for PauiliNet, FermiNet, and PESNet respectively for a system of only two nitrogen atoms, so further research is needed to make this approach scalable.Advances in the field of AI for fundamental problem solving have shown promising results in a series of domains. In particular, Eremin et al.53 recently designed, synthesized and tested a novel quasicrystal with the help of state-of-the-art machine learning models. Yakubovich et al.54 used deep generative models to search for molecules suitable for triplet–triplet fusion with potential applications in blue OLED devices, finding significantly increased performance in terms of generated lead quality. Wan et al.55 applied a hybrid DFT-ML approach to study catalytic activity of materials. Schleder et al.56 used machine learning techniques and DFT to identify thermodynamically stable 2D materials. Recently, Ritt et al.57 elucidated key mechanisms for ion selectivity in nanoporous polymeric membranes by combining first-principles simulations with machine learning. Janet et al.58 developed a ML-based approach for accelerated discovery of transition-metal complexes which allows to evaluate a large chemical compound space in a matter of minutes. Ye et al.59 reviewed recent advances in applying DFT in molecular modeling studies of COVID-19 pharmaceuticals.
2.3 Importance
Mata and Suhm60 pointed out the importance of benchmarking for computational quantum chemistry methods. Following them, we believe that it is crucial to establish a reliable and comprehensive benchmark procedure for machine learning methods in quantum chemistry. A transparent and reproducible assessment of accuracy and generalization power for novel ML approaches represents an important stepping stone towards future successes in many applied fields of quantum chemistry.3 Theoretical foundations
3.1 Conformations
Conformations are structural arrangements of the same molecule that differ by rotation around single bonds and bond stretching. In molecular modeling, conformational analysis is a crucial step because it helps to cut down the time spent screening compounds for activity. For example, most drugs are flexible molecules that can take on various conformations, so conformations are crucial in the prediction of a drug's biological activity as well as its physico-chemical characteristics. Conformational analysis is related to the investigation of the total energies of different conformations for a given molecule (conformational energies). These energies represent important chemical properties that require benchmarking of various DFT methods.3.2 DFT
Anti-symmetrized products of single-electron functions or molecular orbitals are frequently used in quantum chemistry to express the electronic wave function Ψ associated with the electronic time-independent Schrödinger equation| ĤΨ = EΨ, |
These single-particle functions are usually defined in a local atomic orbital basis of spherical atomic functions 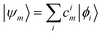 , where |ϕi〉 are the basis functions and cim are the coefficients. As a result, one can represent the electronic Schrödinger equation in matrix form as
, where |ϕi〉 are the basis functions and cim are the coefficients. As a result, one can represent the electronic Schrödinger equation in matrix form as
| Fσcσ = εσScσ, |
| Hij = 〈ϕi|Ĥ|ϕj〉, |
S is the overlap matrix:
| Sij = 〈ϕi|ϕj〉, |
In matrix form, the single-particle wave function expansion can be represented by using Einstein summation as
Therefore, the density matrix is represented as
| Dσij = CσikCσjk |
In DFT, the matrix F corresponds to the Kohn–Sham matrix:
| Fσij = Hcσij + Jσij + Vxcij |
In DFT, the total energy of the system (e.g., total energy of a conformation) can be expressed as
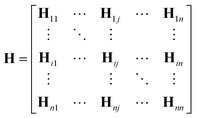
One can represent the Hamiltonian matrix in block form:16
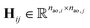 and the choice of nao,i and nao,j atomic orbitals depend on the atoms i,j within their chemical environments. This fact underlies the construction of interaction modules in the models described in Section 5: they construct representations of atom pairs from representations of atomic environments.
and the choice of nao,i and nao,j atomic orbitals depend on the atoms i,j within their chemical environments. This fact underlies the construction of interaction modules in the models described in Section 5: they construct representations of atom pairs from representations of atomic environments.
Unfortunately, eigenvalues and wave function coefficients are not well-behaved or smooth functions because they depend on atomic coordinates and changing molecular configurations. This problem can be addressed by deep learning architectures that directly define the Hamiltonian matrix.
In this work, we propose a benchmark for both scalar parameter prediction, such as the conformation energy, and prediction of matrix parameters such as the core Hamiltonian and overlap matrices.
4 Dataset
The first primary contribution of this work is a large-scale ∇DFT dataset suitable for training expressive models for quantum chemical properties prediction. Our dataset is based on a subset of the Molecular Sets (MOSES) dataset.27 The resulting dataset contains 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 004
004![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 918 molecules with atoms C, N, S, O, F, Cl, Br, and H. It contains 226
918 molecules with atoms C, N, S, O, F, Cl, Br, and H. It contains 226![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 unique Bemis–Murcko scaffolds61 and 34
424 unique Bemis–Murcko scaffolds61 and 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 unique BRICS fragments.62
572 unique BRICS fragments.62
For each molecule from the dataset, we have run the conformation generation method from the RDKit software63,64 suite proposed in Wang et al.65 Next, we clustered the resulting conformations with the Butina clustering method,66 finally taking the clusters that cover at least 95% conformations and using their centroids as the set of conformations. This procedure has resulted in 1 to 62 unique conformations for each molecule, with 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340
340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 total conformations in the full dataset. For each conformation, we have calculated its electronic properties including the energy (E), DFT Hamiltonian matrix (H), and DFT overlap matrix (S) (see the full list in Table 2). All properties were calculated using the Kohn–Sham method67 at ωB97X-D/def2-SVP levels of theory using the quantum-chemical software package Psi4,68 version 1.5. Default PSI4 parameters were used for DFT computations, i.e. Lebedev–Treutler grid with a Treutler partition of the atomic weights, 75 radial points and 302 spherical points, the criterion for the SCF cycle termination was the convergence of energy and density up to 10−6 threshold, integral calculation threshold was 10−12.
152 total conformations in the full dataset. For each conformation, we have calculated its electronic properties including the energy (E), DFT Hamiltonian matrix (H), and DFT overlap matrix (S) (see the full list in Table 2). All properties were calculated using the Kohn–Sham method67 at ωB97X-D/def2-SVP levels of theory using the quantum-chemical software package Psi4,68 version 1.5. Default PSI4 parameters were used for DFT computations, i.e. Lebedev–Treutler grid with a Treutler partition of the atomic weights, 75 radial points and 302 spherical points, the criterion for the SCF cycle termination was the convergence of energy and density up to 10−6 threshold, integral calculation threshold was 10−12.
We provide several splits of the dataset that can serve as the basis for comparison across different models. First, we fix the training set that consists of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with 436
000 molecules with 436![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 conformations and its smaller subsets with 10
581 conformations and its smaller subsets with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 5000, and 2000 molecules and 38
000, 5000, and 2000 molecules and 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364, 20
364, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349, and 5768 conformations respectively; these subsets can help determine how much additional data helps various models. We choose another 100
349, and 5768 conformations respectively; these subsets can help determine how much additional data helps various models. We choose another 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random molecules as a structure test set. The scaffold test set has 100
000 random molecules as a structure test set. The scaffold test set has 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules containing a Bemis–Murcko scaffold from a random subset of scaffolds which are not present in the training set. Finally, the conformation test set consists of 91
000 molecules containing a Bemis–Murcko scaffold from a random subset of scaffolds which are not present in the training set. Finally, the conformation test set consists of 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182 (resp., 10
182 (resp., 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 5000, 2000) molecules from the training set with new conformations, numbering in total 92
000, 5000, 2000) molecules from the training set with new conformations, numbering in total 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 (8892, 4897, 1724) conformations; this set can be used for the single-molecule setup.
821 (8892, 4897, 1724) conformations; this set can be used for the single-molecule setup.
As part of the benchmark, we provide separate databases for each subset and task and a complete archive with wave function files produced by the Psi4 package that contains quantum chemical properties of the corresponding molecule and can be used in further computations.
A formal comparison of our dataset's parameters with previously available datasets such as QM9, ANI-1, and QMugs is presented in Table 1.
| Statistic | QM9 | ANI-1 | QMugs | ∇DFT |
|---|---|---|---|---|
| a Hamiltonian matrices for QMugs dataset can be calculated from density matrices by one step of DFT cycle. | ||||
| Number of molecules | 134k | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462 462 |
665k | 1m |
| Number of conformers | 134k | 20m | 2m | 5m |
| Number of atoms | 3–29 | 2–26 | 4–228 | 8–62 |
| Number of heavy atoms | 1–9 | 1–8 | 4–100 | 8–27 |
| Atomic species | H, C, N, O, F | H, C, N, O | H, C, N, O, P, S, Cl, F, Br, I | H, C, N, O, Cl, F, Br |
| Hamiltonian matrices | No | No | Noa | Yes |
| Level of theory | B3LYP/6-31G(2df,p)+G4MP2 | ωB97X/6-31G(d) | ωB97X-D/def2-SVP+GFN2-xTB | ωB97X-D/def2-SVP |
| Storage size | 230 Mb | 5.29 Gb | 7 Tb | 100 Tb |
| QM9 | DFT + partially G4MP2: rotational constants, dipole moment, isotropic polarizability, HOMO/LUMO/gap energies, electronic spatial extent, zero point vibrational energy, internal energy at 0 K, internal energy at 298.15 K, enthalpy at 298.15 K, free energy at 298.15 K, heat capacity at 298.15 K, Mulliken charges, harmonic vibrational frequencies |
| ANI-1 | DFT: total energy |
| QMugs | GFN2 + DFT: total, internal atomic and formation energies, dipole, rotational constants, HOMO/LUMO/gap energies, Mulliken partial charges |
| GFN2: total enthalpy, total free energy, quadrupole, enthalpy, heat capacity, entropy, Fermi level, covalent coordination number, molecular dispersion coefficient, atomic dispersion coefficients, molecular polarizability, atomic polarizabilities, Wiberg bond orders, total Wiberg bond orders | |
| DFT: electrostatic potential, Löwdin partial charges, exchange correlation energy, nuclear repulsion energy, one-electron energy, two-electron energy, mayer bond orders, Wiberg–Löwdin bond orders, total mayer bond orders, total Wiberg–Löwdin bond orders, density/orbital matrices, atomic-orbital-to-symmetry-orbital transformer matrix | |
| ∇DFT | DFT: electrostatic potential, Löwdin partial charges, exchange correlation energy, nuclear repulsion energy, one-electron energy, two-electron energy, mayer bond orders, Wiberg–Löwdin bond orders, total mayer bond orders, total Wiberg–Löwdin bond orders, density/orbital matrices, atomic-orbital-to-symmetry-orbital transformer matrix, Hamiltonian matrix |
5 Methods
The goal of this benchmark is to advance and standardize studies in the field of machine learning methods for computational quantum chemistry. We focus on the class of models that predict quantum chemistry properties from the spatial representation of molecules. More precisely, we study models for two tasks:• Conformational energy prediction and
• DFT Hamiltonian prediction
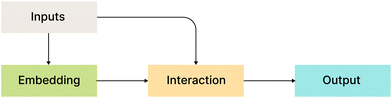
Fig. 2 shows a bird's eye overview of the general architecture for the models that we compare in this work. It consists of four main blocks:
• Inputs: all considered models use atom types, coordinates, or their functions as input.
• Embedding layers: MLP or a single linear layer.
• Interaction layers: this is usually the main part with model-specific architecture.
• Output layers: depending on the model, output layers are designed to convert internal representations into specific desired values.
5.1 Linear regression
We propose the linear regression model (LR) as a simple baseline for molecular properties prediction, in particular energy prediction. It takes the numbers of each atom type in the molecule as an input representation and predicts energy as its weighed sum. While it is clear that more sophisticated handcrafted features may increase a model's accuracy and generalization power, in this work we focus on deep models that can learn such features automatically.5.2 SchNet15
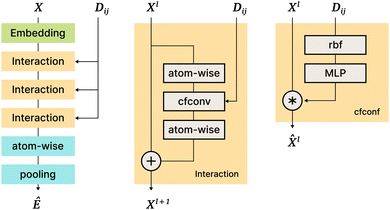
The SchNet model was one of the first works that suggested a neural architecture for atomic forces and molecular energy prediction. The key contribution here is the cfconv, a continuous-filter convolutional layer for modeling objects with arbitrary positions. The model is schematically represented in Fig. 3.Given feature representations of n objects 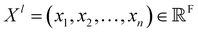 Xl = (x1,x2,…,xn) ∈F (at layer l), which are at positions
Xl = (x1,x2,…,xn) ∈F (at layer l), which are at positions 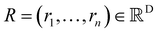 , and a special function Wl that maps R's domain to X's domain, i.e.,
, and a special function Wl that maps R's domain to X's domain, i.e., 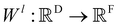 , the output of the proposed cfconv layer is defined as
, the output of the proposed cfconv layer is defined as
The use of cfconv and the overall network architecture design ensure an important property: energy and force predictions are rotationally invariant and equivariant respectively. For instance, in the cfconv layer Wl is a combination of ||ri − rj||, radial basis functions, dense feedforward layers, and a shifted softplus activation function ssp(x) = ln(0.5ex + 0.5).
The model takes nuclear charges and atomic positions as inputs. Nuclear charges are first embedded into 64-dimensional representations, After that, they are processed with an “Interaction” block of layers that includes 3 applications of cfconv (cf.Fig. 3, thus enriching the feature representation with positional information). Then more atom-wise modifications follow to be pooled in a final layer to obtain the energy prediction. Differentiating the energy with respect to atom positions yields the forces, hence force predictions can be and are also added to the loss function.
The resulting method has been tested on three datasets: QM9,37,69 MD17,70 and ISO17 (introduced in the original work15). For more details we refer to Schutt et al.15
5.3 DimeNet71
A major contribution of DimeNet is that it takes into account not only the distances between pairs of atoms, but also angles formed by triples of atoms. The authors note that the pairwise distance matrix is sufficient to describe the full geometric information of the molecule. However, in order to keep computational costs reasonable graph neural networks (GNN) ignore connections between atoms that are more than a certain cutoff distance apart. One possible result of this simplification could be that the GNN would not be able to distinguish between some molecules.
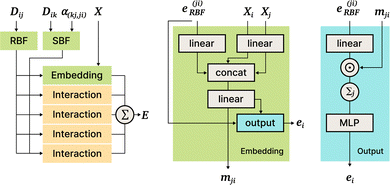
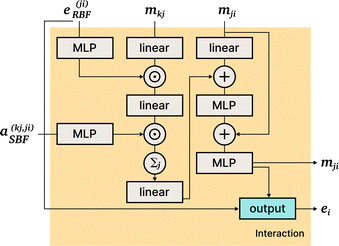
DimeNet is inspired by the PhysNet model72 and expands it with message passing and additional directional information. A general overview of the architecture is shown in Fig. 4 (left). The core of DimeNet is the Interaction block: a message mji from atom j to atom i takes into account information about the angles ∠xixjxk obtained via messages from the corresponding atoms k that are neighbors of atom j. Specifically, it is defined as follows:
 is the set of neighbors of atom j, e(ji)RBF is the radial basis interatomic distance, and a(kj,ji)SBF is the directional information represented by spherical Bessel functions and spherical harmonics.
is the set of neighbors of atom j, e(ji)RBF is the radial basis interatomic distance, and a(kj,ji)SBF is the directional information represented by spherical Bessel functions and spherical harmonics.
The Interaction block is visualized in Fig. 5. A message mji is initialized with learnable embeddings h(0)i and h(0)j that depend on the relative position of corresponding atoms (Fig. 4, middle). Finally, the messages are combined together to form the atom embedding
The resulting model is invariant to permutations, translation, rotation, and inversion. Evaluation on QM9 and MD17 shows that DimeNet significantly outperforms SchNet on the prediction of most targets. An extension of this model was later proposed in DimeNet++;73 it further improved performance and reduced computational costs.
5.4 SchNOrb16
This model is a direct continuation of the SchNet model15; the SchNet sub-architecture is used as a “first step” in the SchNOrb model. The most important differences are the following: (1) SchNOrb is designed to predict molecular energy, forces, the overlap matrix, and the Hamiltonian matrix; (2) directions (angles and normalized position differences) are used explicitly to capture the interaction information and model various symmetries; (3) the loss function is a sum of errors in the prediction of energy, forces, Hamiltonian, and the overlap matrix (Fig. 6).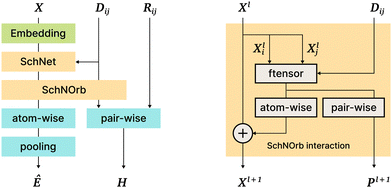 | ||
| Fig. 6 The SchNOrb architecture. On the left: general architecture overview; on the right: the Interaction block in SchNOrb. In addition to the SchNet Interaction block, SchNOrb uses the factorized tensor layer74 to produce pairwise atom features and predict the basis coefficients for the Hamiltonian. | ||
The inputs for this neural network are the charges Z and position differences ||rij|| (norm of the vector pointing from atom i to atom j); the model also uses normalized directions 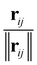 . The representations Z and ||rij|| are then processed with the SchNet step as described in Section 5.2.
. The representations Z and ||rij|| are then processed with the SchNet step as described in Section 5.2.
On the next SchNOrb step, SchNet outputs (a vector per atom) are combined with ||rij|| using a factorised tensor layer,74 feedforward layers, shifted softplus, and simple sums. The outputs include: (1) rotationally invariant per-atom embeddings Xl, which are then transformed and aggregated to predict the energy value; (2) embeddings Pl for atom pairs that are multiplied by different powers of directional cosines, aggregated and passed to fully connected layers to predict blocks of the Hamiltonian and overlap matrices; (3) finally, similar to SchNet, forces are predicted via graph differentiation.
The datasets used in this work are based on MD1770 and include water, ethanol, malondialdehyde, and uracil. Reference calculations were performed with Hartree–Fock (HF) and density functional theory (DFT) with the PBE exchange correlation functional. For more details regarding data preparation and augmentation we refer to Schütt et al.16
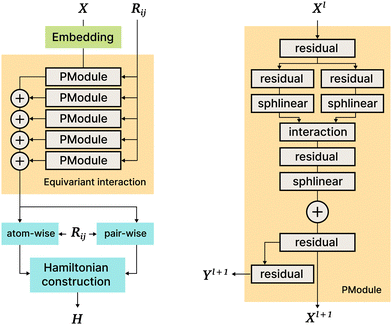
5.5 SE3 (PhiSNet)
The PhiSNet model was suggested by Unke et al.17 The authors presented an SE(3)-equivariant architecture for predicting Hamiltonian matrices. The model improves over the results of SchNOrb both in terms of equivariance (SchNOrb is not SE(3)-equivariant, so its predictions for the same conformation in a different reference coordinate system may differ in unpredictable ways) and in terms of accuracy metrics for single compound datasets.The main building blocks of PhiSNet are the following: (1) feature representation both for input and intermediate layers is of the form 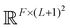 , where F corresponds to feature channels and (L + 1)2 corresponds to all possible spherical harmonics of degree l ∈ {0,…,L}; (2) all layers except the last one apply SE(3)-equivariant operations on features; matrix multiplication, tensor product contractions, and tensor product expansions are mixed together to make equivariant updates for the features of every atom and atom pair; on the last layer, the Hamiltonian and overlap matrices are constructed from pairwise features (Fig. 7).
, where F corresponds to feature channels and (L + 1)2 corresponds to all possible spherical harmonics of degree l ∈ {0,…,L}; (2) all layers except the last one apply SE(3)-equivariant operations on features; matrix multiplication, tensor product contractions, and tensor product expansions are mixed together to make equivariant updates for the features of every atom and atom pair; on the last layer, the Hamiltonian and overlap matrices are constructed from pairwise features (Fig. 7).
We have made several minor modifications to the original model implementation of PhiSNet in order to allow it to work with the ∇DFT dataset; in particular, we have applied batchization similar to Pytorch Geometric, where molecules inside a single batch are treated as one molecule with no bonds between atoms of different molecules.
6 Benchmark setup and results
We focus on two different tasks: DFT Hamiltonian matrix prediction and molecular conformation energy prediction. All models have been trained on 2k, 5k, 10k, and 100k subsets of ∇DFT. For the first task we compare SchNOrb and PhiSNet models, while for the second task we compare linear regression, SchNet, SchNOrb, and Dimenet++ models. In both tasks, our main goal is to measure the ability of state of the art models to generalize across a diverse set of molecules.Metrics for energy prediction and prediction of Hamiltonian matrices are reported in Tables 3 and 4 respectively. These results lead us to the following observations.
| Model | MAE for energy prediction, × 10−2Eh | |||
|---|---|---|---|---|
| 2k | 5k | 10k | 100k | |
| a Training SchNOrb model did not converge for the 10k, and 100k train split, for SchNet model did not converge for the 100k train split. | ||||
| Structure test split | ||||
| LR | 4.6 | 4.7 | 4.7 | 4.7 |
| SchNet | 151.8 | 66.1 | 29.6 | —a |
| Dimenet++ | 24.1 | 21.1 | 10.6 | 3.2 |
| SchNOrb | 5.9 | 3.7 | 13.3a | —a |
| Scaffolds test split | ||||
| LR | 4.6 | 4.7 | 4.7 | 4.7 |
| SchNet | 126.5 | 68.3 | 27.4 | —a |
| Dimenet++ | 21.6 | 20.9 | 10.1 | 3.0 |
| SchNOrb | 5.9 | 3.4 | 14.8a | —a |
| Conformations test split | ||||
| LR | 4.0 | 4.2 | 4.0 | 4.0 |
| SchNet | 79.1 | 67.3 | 21.4 | —a |
| Dimenet++ | 18.3 | 33.7 | 5.2 | 2.5 |
| SchNOrb | 5.0 | 3.6 | 14.5a | —a |
| Model | MAE for Hamiltonian matrix prediction, × 10−3Eh | MAE for overlap matrix prediction, × 10−5 | ||||
|---|---|---|---|---|---|---|
| 2k | 5k | 10k | 2k | 5k | 10k | |
| a While the relative difference between metrics for SchNOrb and PhiSNet is similar to the one reported by phisnet2021, we believe that there are still some problems with SchNOrb training in the multi-molecule setup, e.g., gradient explosion. | ||||||
| Structure test split | ||||||
| SchNOrb | 386.5 | 383.4 | 382.0 | 1550 | 1571 | 3610 |
| PhiSNet | 7.4 | 3.2 | 2.9 | 5.1 | 4.3 | 3.5 |
| Scaffolds test split | ||||||
| SchNOrb | 385.3 | 380.7 | 383.6 | 1543 | 1561 | 3591 |
| PhiSNet | 7.2 | 3.2 | 2.9 | 5.0 | 4.3 | 3.5 |
| Conformations test split | ||||||
| SchNOrb | 385.0 | 384.8 | 392.0 | 1544 | 1596 | 3576 |
| PhiSNet | 6.5 | 3.2 | 2.8 | 5.1 | 4.6 | 3.6 |
First and foremost, we see that all models in both tasks, except SchNOrb and Linear Regression, benefit from increasing the dataset size. This indicates that even already published models may not have hit the limit of their expressive power and may further benefit from larger scale datasets. We suppose that linear model has almost identical scores trained on train sets of different sizes because of small expressiveness. Training has not converged in the case of SchNOrb model for 10k and 100k splits.
Second, as expected, the models perform better on the conformations test split that contains the same set of structures but with different conformations; in this case, the training set is most similar to the test set so this behaviour is expected. On the other hand, on the structures test split and the scaffolds test split the models show nearly equivalent performance. This may imply that models generalized on different structures automatically generalize on different scaffolds.
Third, interestingly, deep models that were trained on small dataset splits (2k, 5k, and 10k) only to predict energy show results worse than a simple linear regression. On the positive side, the DimeNet++ model trained on the 100k subset performs better, which may imply that the same model trained on the full training set may show much better results. Moreover SchNOrb models trained on 2k and 5k splits perform better than linear regression and other models trained on corresponding splits, which may imply that energy prediction benefits from multi-target (Hamiltonian matrix, overlap matrix and energy) learning.
Fourth, in our setup deep models for energy prediction perform much worse than they do on previously known benchmarks such as QM9 or MD17 (e.g. DimeNet++ has MAE 0.00023Eh on QM973). This may be caused by the diversity of the ∇DFT dataset and small size of splits. The latter point holds for models for predicting Hamiltonian matrices as well; in this case, we see that as an indication that more care needs to be taken in hyperparameter tuning and construction of new architectures.
7 Conclusions
In this work, we present a unique molecular dataset containing results of DFT computations along with a number of deep neural network models designed to predict the computed properties. We have designed a number of different tests to assess the generalization capabilities of machine learning models across the chemistry domain, specifically the domain of medicinal chemistry. We have modified several publicly available neural network models to make them able to learn from conformations of multiple molecules instead of a single molecule. We share the code for modified models as well as their pertrained versions to simplify future research in this field.Results of our experimental evaluation show the ability of modern deep neural networks to generalize, both for energy prediction and estimation of Hamiltonian matrices. We also see that increasing amount of data leads to better metrics, especially in the case of the PhiSNet model. Unfortunately, training with a limited amount of computational resources or small dataset size often leaves deep neural networks undertrained and exhibiting comparatively bad performance. In particular, model errors grow significantly in the multi-molecular setting compared to a single molecule. It still remains a challenge to obtain models that are superior to chemical accuracy.
Data and code accessibility
The code and links to the full dataset and its parts can be found at https://github.com/AIRI-Institute/nablaDFT.Author contributions
Conceptualization: K. K., A. K. Methodology: K. K., S. N., A. K. Software: K. K., I. S., A. G., A. Ts., A. Tel., A. A. Validation: K. K., A. G. Investigation: K. K., I. S., A. Ts., A. Tel., A. A. Data curation: K. K. Writing – original draft: K. K., I. S., A. R., P. Z., S. N., A. K. Writing – review & editing: K. K., I. S., A. R., A. G., A. Ts., A. A., P. Z., S. N., A. K., P. S. Visualization: A.K. Supervision: A. K. Project administration: A.K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work of S. N. was supported by a grant for research centers in the field of artificial intelligence, provided by the Analytical Center for the Government of the Russian Federation in accordance with the subsidy agreement (agreement identifier 000000D730321P5Q0002) and the agreement with the Ivannikov Institute for System Programming of the Russian Academy of Sciences dated November 2, 2021 No. 70-2021-00142.Notes and references
- R. J. Bartlett and J. F. Stanton, Rev. Comput. Chem., 1994, 65–169 CAS.
- B. L. Hammond, W. A. Lester and P. J. Reynolds, Monte Carlo methods in ab initio quantum chemistry, World Scientific, 1994, vol. 1 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 Search PubMed.
- R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge university press, 2020 Search PubMed.
- A. Erba, J. Baima, I. Bush, R. Orlando and R. Dovesi, J. Chem. Theory Comput., 2017, 13, 5019–5027 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- C. Goringe, D. Bowler and E. Hernandez, Rep. Prog. Phys., 1997, 60, 1447 CrossRef CAS.
- C. W. Groth, M. Wimmer, A. R. Akhmerov and X. Waintal, New J. Phys., 2014, 16, 063065 Search PubMed.
- K. Choo, A. Mezzacapo and G. Carleo, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- G. Hegde and R. C. Bowen, Sci. Rep., 2017, 7, 1–11 CrossRef PubMed.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Advances in neural information processing systems, 2017, vol. 30, pp. 992–1002 Search PubMed.
- K. T. Schütt, M. Gastegger, A. Tkatchenko, K.-R. Müller and R. J. Maurer, Nat. Commun., 2019, 10, 1–10 CrossRef PubMed.
- O. Unke, M. Bogojeski, M. Gastegger, M. Geiger, T. Smidt and K.-R. Müller, Advances in Neural Information Processing Systems, 2021, vol. 34, pp. 14434–14447 Search PubMed.
- H. Li, Z. Wang, N. Zou, M. Ye, W. Duan and Y. Xu, arXiv, 2021, preprint arXiv:2104.03786.
- R. Nagai, R. Akashi, S. Sasaki and S. Tsuneyuki, J. Chem. Phys., 2018, 148, 241737 CrossRef PubMed.
- R. Nagai, R. Akashi and O. Sugino, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- X. Lei and A. J. Medford, Phys. Rev. Mater., 2019, 3, 063801 CAS.
- P. Ramos and M. Pavanello, arXiv, 2019, preprint arXiv:1906.06661.
- A. Ryabov, I. Akhatov and P. Zhilyaev, Sci. Rep., 2020, 10, 1–7 CrossRef PubMed.
- L. Li, S. Hoyer, R. Pederson, R. Sun, E. D. Cubuk, P. Riley and K. Burke, et al. , Phys. Rev. Lett., 2021, 126, 036401 CrossRef CAS PubMed.
- J. Kirkpatrick, B. McMorrow, D. H. Turban, A. L. Gaunt, J. S. Spencer, A. G. Matthews, A. Obika, L. Thiry, M. Fortunato and D. Pfau, et al. , Science, 2021, 374, 1385–1389 CrossRef CAS PubMed.
- A. Ryabov, I. Akhatov and P. Zhilyaev, Sci. Rep., 2022, 12, 1–10 CrossRef PubMed.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy, M. Veselov, A. Kadurin, S. Johansson, H. Chen, S. Nikolenko, A. Aspuru-Guzik and A. Zhavoronkov, Front. Pharmacol., 2020, 11, 565644 CrossRef CAS PubMed.
- J. Irwin, T. Sterling, M. Mysinger, E. Bolstad and R. Coleman, J. Chem. Inf. Model., 2012, 52(7), 1757–1768 CrossRef CAS PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- R. Tran, J. Lan, M. Shuaibi, B. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, Z. Ulissi and C. L. Zitnick, arXiv, 2022, preprint arXiv:2206.08917.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. U. Kaiser and I. Polosukhin, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, Minnesota, 2019, pp. 4171-4186.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever and D. Amodei, Advances in Neural Information Processing Systems, 2020, pp.1877–1901 Search PubMed.
- Z. Miftahutdinov, A. Kadurin, R. Kudrin and E. Tutubalina, Bioinformatics, 2021, 37, 3856–3864 CAS.
- E. Tutubalina, A. Kadurin and Z. Miftahutdinov, Proceedings of the 28th International Conference on Computational Linguistics, 2020, pp. 6710-6716.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 Search PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 1–8 Search PubMed.
- T. Fink, H. Bruggesser and J.-L. Reymond, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS PubMed.
- T. Fink and J.-L. Reymond, J. Chem. Inf. Model., 2007, 47, 342–353 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- D. Mendez, A. Gaulton, A. P. Bento, J. Chambers, M. De Veij, E. Félix, M. P. Magariños, J. F. Mosquera, P. Mutowo and M. Nowotka, et al. , Nucleic Acids Res., 2019, 47, D930–D940 CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. C. Snyder, M. Rupp, K. Hansen, K.-R. Müller and K. Burke, Phys. Rev. Lett., 2012, 108, 253002 CrossRef PubMed.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- D. Pfau, J. S. Spencer, A. G. D. G. Matthews and W. M. C. Foulkes, Phys. Rev. Res., 2020, 2, 033429 CrossRef CAS.
- N. Gao and S. Günnemann, arXiv preprint arXiv:2110.05064, 2021.
- R. A. Eremin, I. S. Humonen, P. N. Zolotarev, I. V. Medrish, L. E. Zhukov and S. A. Budennyy, Cryst. Growth Des., 2022, 22, 4570–4581 CrossRef CAS.
- A. Yakubovich, A. Odinokov, S. I. Nikolenko, Y. Jung and H. Choi, Front. Chem., 2021, 9, 800133 CrossRef CAS PubMed.
- X. Wan, Z. Zhang, W. Yu and Y. Guo, Materials Reports: Energy, 2021, 1, 100046 CrossRef.
- G. R. Schleder, C. M. Acosta and A. Fazzio, ACS Appl. Mater. Interfaces, 2020, 12, 20149–20157 CrossRef CAS PubMed.
- C. L. Ritt, M. Liu, T. A. Pham, R. Epsztein, H. J. Kulik and M. Elimelech, Sci. Adv., 2022, 8, eabl5771 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, A. Nandy, F. Liu and H. J. Kulik, Acc. Chem. Res., 2021, 54, 532–545 CrossRef CAS PubMed.
- N. Ye, Z. Yang and Y. Liu, Drug Discovery Today, 2022, 27, 1411–1419 CrossRef CAS PubMed.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS PubMed.
- G. W. Bemis and M. A. Murcko, J. Med. Chem., 1996, 39, 2887–2893 CrossRef CAS PubMed.
- J. Degen, C. Wegscheid-Gerlach, A. Zaliani and M. Rarey, ChemMedChem, 2008, 3, 1503–1507 CrossRef CAS PubMed.
- RDKit: Open-source cheminformatics, https://www.rdkit.org.
- G. Landrum, P. Tosco, B. Kelley, Ric, sriniker, gedeck, R. Vianello, NadineSchneider, E. Kawashima, A. Dalke, D. N, D. Cosgrove, B. Cole, M. Swain, S. Turk, Alexander-Savelyev, G. Jones, A. Vaucher, M. Wójcikowski, I. Take, D. Probst, K. Ujihara, V. F. Scalfani, guillaume godin, A. Pahl, F. Berenger, JLVarjo, strets123, JP and DoliathGavid, rd-kit/rdkit: 2022_03_1 (Q1 2022) Release, 2022, DOI:10.5281/zenodo.6388425.
- S. Wang, J. Witek, G. A. Landrum and S. Riniker, J. Chem. Inf. Model., 2020, 60, 2044–2058 CrossRef CAS PubMed.
- J. M. Barnard and G. M. Downs, J. Chem. Inf. Comput. Sci., 1992, 32, 644–649 CrossRef CAS.
- L. J. Sham and W. Kohn, Phys. Rev., 1966, 145, 561 CrossRef CAS.
- D. G. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio and A. Alenaizan, et al. , J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 1–7 Search PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- J. Gasteiger, C. Yeshwanth and S. Günnemann, Advances in Neural Information Processing Systems, 2021, pp.15421–15433 Search PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- J. Gasteiger, S. Giri, J. T. Margraf and S. Günnemann, Machine Learning for Molecules Workshop, NeurIPS, 2020.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 1–8 CrossRef PubMed.
| This journal is © the Owner Societies 2022 |