Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A semiempirical potential for alkali halide diatoms with damped interactions I. Rittner potential
Xiaowei
Sheng
a,
Kwong Tin
Tang
 b and
J. Peter
Toennies
b and
J. Peter
Toennies
 *c
*c
aDepartment of Physics, Anhui Normal University, Anhui, Wuhu 24100, China
bDepartment of Physics, Pacific Lutheran University, Tacoma, Washington 98447, USA
cMax-Planck-Institut für Dynamik und Selbstorganisation, Am Fassberg 17, D-37077, Göttingen, Germany. E-mail: jtoenni@gwdg.de
First published on 29th September 2022
Abstract
A new semiempirical potential is described for the ground state X1Σ+ of the alkali halide diatoms. The model potential is the first to account for the damping of all the electrostatic and induction potential terms as well as of the long-range dispersion potential. Accordingly, the potential does not have a negative singularity at vanishingly small internuclear distances and is the first Rittner-type model with a realistic dependence of the repulsion at short distances. The new potential is tested by comparing with ab initio potentials, which presently are only available in the well region for the molecules LiF, LiCl and CsI. The three parameters of the new potential are determined by fitting the latest experimental parameters for the well depth De, bond distance Re and vibrational frequency ωe. The new potential is in good agreement with the ab initio potentials.
I. Introduction
A. Alkali halides
The alkali halide solids and diatoms are among the most widely studied with ionic bonding. The solids have served as ideal model systems both in the bulk and also at the surface.1 In 1946 Seitz remarked “In the field of solids, the properties of alkali halides have an enduring interest, since these crystals have continuously yielded to persistent investigation and have gradually provided us with a better and better understanding of the most interesting properties of all solids”.2 The alkali halides also play an important role in many areas of biology and medicine and in industry.3 The molecules have been important prototype systems in the development of molecular physics4 and in crossed beam scattering studies of bimolecular reactions.5 In recent years, due to their large dipole moments, polar molecules have opened up new perspectives in the preparation of ultra-cold gases.6B. Alkali halide diatoms
The understanding of the alkali halide diatoms has a long history essentially because of the simple classical Coulomb interactions between the constituent ions. In 1898 and probably much earlier it was realized that NaCl crystals consisted of a regular periodic array of positive and negative ions.7,8 In 1917 Kossel, well before the discovery of quantum mechanics, realized that the strong polar bonding of ions could explain the binding in many molecules.9 Then in 1932 shortly after London published his paper on the dispersion forces, Born and Mayer proposed that the binding in the alkali halide solids could be described by the following simple formula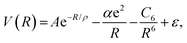 | (1) |
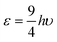 .11
.11
Rittner in 1951 added the classical charge induction and dipole terms already introduced by Born and Heisenberg in 1924.12 Furthermore, Rittner proposed that the interaction energy between the ions in the dimer is given by (in atomic units)13
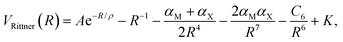 | (2) |
In 1973 Brumer and Karplus used quantum-mechanical exchange perturbation theory to analyze the interactions in alkali halide diatoms. They demonstrated that higher multipole contributions are quenched by exchange and that a consistent second-order perturbation treatment requires that the 2αMαX/R7 term in the Rittner potential be neglected.15,16 The resulting potential, denoted as the truncated Rittner (T-Rittner) model, is given by
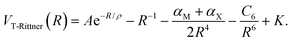 | (3) |
In 1986 Kumar, Kaur and Shankar implemented the T-Rittner model and demonstrated that it reproduced the experimental potential data reasonably well at the equilibrium separation of 25 diatomic alkali halide and the alkali hydride molecules.16 Although several potential models have since been introduced14,17,18 the T-Rittner potential model or minor variants thereof are presently considered to be the best models for the diatomic molecules.
A problem with the T-Rittner model and most all of the variant potential models is that they have an unphysical negative singularity at vanishing internuclear distances and fail in describing the repulsive potential which is well known to tend to a large positive value in the limit of R ≥ 0.19–21 Therefore, the T-Rittner model is valid only at large R corresponding to the well region. Frequently, the Rittner type potential models, even those for the solid22 used in connection with high pressure experiments,23 have an incorrect shape in the repulsive region resulting from the spurious singularity at small internuclear distances.
To a large extent the predominant literature on the potentials is from the previous century. One of the most recent publication is from Walz et al. in 2018.3 In a comprehensive review of the efforts to find a phase transferable force field for all three phases of the alkali halides Waltz et al. have used potential models with simple repulsive terms without the Coulomb singularity. These include the well-known, but ultra-simple Lennard-Jones, Buckingham and modified Buckingham potentials. Thus, even today the overall situation in finding a universal potential model is not satisfactory.
In the present article the T-Rittner model is modified by taking account of the damping of the electrostatic, induction and dispersion terms in the T-Rittner model for the potential of the lowest X1Σ+ state. The article is organized as follows. First, it is demonstrated that the values of the available dispersion coefficients and polarizabilities on which previous models have relied differ by large amounts. Then the new model, denoted TTT-R, is introduced. The available experimental data on the bond distance, dissociation energies and vibrational constant on which the TTT-R model is based are surveyed. The more realistic behavior of the TTT-R model in the repulsive region compared to the T-Rittner model is analyzed next. The results are then compared with the available ab initio calculations. A survey of the literature reveals that only for LiF, and LiCl reliable, reproducible calculations of the potential curves of the X1Σ+ and A1Σ+ states have been reported. Only a single ab initio calculation is available for the third system CsI. Fig. 1 shows a recent ab initio calculation for the potential curves of both the ground X1Σ+ ion state and the A1Σ+ covalent state of LiCl.24 The accuracy of the TTT-R model is then evaluated by a quantitative comparison of the reduced potentials with the corresponding ab initio potentials for the X1Σ+ state for the three systems. The agreement is better than a few percent. The implications of the TTT-R repulsive potential for which there are no previous model- and ab initio-calculations, for analyzing and understanding high pressure experiments is discussed in the concluding section.
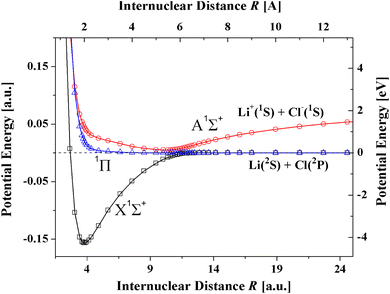 | ||
| Fig. 1 Ab initio potential curves of LiCl showing the avoided crossing between the ionic X1Σ+ state and the A1Σ+ covalent state.24 In a collision of an alkali atom with an halogen atom at the avoided crossing the outer electron of the alkali atom transfers to the halogen atom thereby producing two oppositely charged ions which attract each other and form a strong ionic bond. | ||
C. Dispersion coefficients and polarizabilities
Surprisingly, even presently little is known about the properties of the constituent alkali halide ions. For example, the dispersion coefficients between the constituent ions are not theoretically accurately known, at least compared to the rare gas dimers and solids which have the same electronic structure. In the extensive compilations of Jiang et al.25 and Gould et al.26 the long-range dispersion coefficients between oppositely charged ions are not explicitly included. Table 1 summarizes some of the literature values for the dispersion coefficients. These have been estimated by using various approximations and differ by more than an order of magnitude. The last entry, which is used here, is based on the assumption that the dispersion coefficients are the same as that of the corresponding isoelectronic rare gas dimers created after transfer of the electron from the alkali to the halogen atom, but without consideration of the charges.27The polarizabilities of the ions to be used in the Rittner models are also not accurately known. In the literature there is no agreement as to whether the free ion polarizabilities or special polarizabilities, which account for the electric field emanating from the partner ion, are to be used in eqn (3). The long discussion in the literature is concisely summarized by the following discussion between two of the protagonists. Shanker et al. have argued that the polarizability depends on the environment of the atom on which there is evidence from condensed systems.29 This has been questioned by Donald et al.30 in response to which Shanker and Kushwah wrote “a detailed investigation is required to resolve the question of potential dependent polarizability”.31
Table 2 provides a comparison of recent state of the art ab initio calculations of the free ion polarizabilities32 with some recent literature values of the ion-in-molecule polarizabilities. These recent values for the ion-in-molecule polarizabilities in Table 2 differ also by similar large amounts from earlier published results.15,16,33 Presently there is no unanimity as to the values of the polarizabities of the ions in the diatoms. Generally the ion-in-molecule polarizabilities are smaller, while in some cases they are about the same or even larger with no obvious trend. One of the aims of the present investigation is the experimental determination of the effective polarizability in the alkali halide molecules under investigation.
| LiF | LiCl | CsI | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| α M | α X | C 4 | α M | α X | C 4 | α M | α X | C 4 | |
| Free ion polarizabilities | |||||||||
| 0.0285 | 2.462 | 17.931 | 0.0285 | 5.356 | 38.767 | 2.384 | 10.400 | 92.043 | 32 |
| 0.1923 | 16.614 | 8.4034 | 0.1923 | 36.144 | 18.168 | 16.088 | 70.183 | 43.135 | |
| Molecular state polarizabilities | |||||||||
| 0.0360 | 0.6320 | 4.8095 | 0.0340 | 2.1500 | 15.724 | 2.9100 | 5.3700 | 59.615 | 34 |
| 0.2429 | 4.2650 | 2.2539 | 0.2294 | 14.509 | 7.3692 | 19.638 | 36.239 | 27.938 | |
| 0.0530 | 1.1920 | 8.9638 | 0.0530 | 2.3140 | 17.042 | 3.3960 | 5.3070 | 62.660 | 35 |
| 0.3577 | 8.0440 | 4.2008 | 0.3577 | 15.616 | 7.9867 | 22.917 | 35.813 | 29.365 | |
II. A new potential model for the alkali halide diatoms with damped interactions
A. Theory
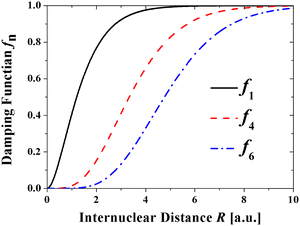
The unphysical shortrange behavior of the Rittner-type potentials can be avoided by introducing a damping function to reduce the R−n terms to zero at small distances. This was first demonstrated for the London dispersion energy in the Tang–Toennies model (TT).36 The universal damping function introduced by Tang and Toennies is given by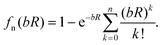 | (4) |
It has the advantage that it can be applied to all powers of n and depends only on the exponent of the repulsive Born Mayer term. The TT damping function has been shown to reproduce well the ab initio calculated damping of the R−6 dispersion potential of two hydrogen atoms by Koide et al37 and Wheatley and Meath.38 Theoretical calculations have demonstrated that they are remarkably accurate for He239 and HeH.40 It has also been shown to reproduce the direct calculation of the damping of the R−4 induction potential.41
The TT damping function for the Coulomb potential is given by
| f1(bR) = 1 − e−bR(1 + bR). | (5) |
We are not aware of formal calculations of the damping of the Coulomb potential with which to compare eqn (5) although it has been adopted at least in one other publication.42 In a related problem Stone in his book The Theory of Intermolecular Forces has calculated the correction of the electrostatic multipole energy at short distances, which he denotes the “penetration energy”.43 Accordingly, the energy of a proton as a function of distance from a hydrogen-like atom of nuclear charge Z is given by: V(R) = −1/2[1 − exp(−2ZR)(1 + RZ)], where the term in brackets is the damping function and exp(−2ZR) is the charge density of the atom. Substituting α = 2Z the damping function becomes f1 = 1 − exp(−αR)(1−αR/2), which is very similar in form to eqn (5). See also Slipchenko and Gordon.44
The TTT-R potential model can be written in atomic units compactly as
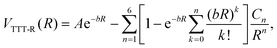 | (6) |
In eqn (6) it is implicitly assumed that the alkali halide diatom is completely ionized. It is however known that the alkali halide molecules have a small covalent character. See for example.45 The ionicity can be estimated from the ratio of the experimental dipole moment to the theoretical dipole moment calculated assuming a 100% ionic bond. The corresponding ionicities of LiF, LiCl and CsI are 84.2, 73.4 and 73.4%, respectively.3 Inclusion of the ionicities would require consideration of a corresponding covalent contribution which could compensate the reduction in the ionicity. Since the ionicity was not included in the T-Rittner models it has not been included here.
B. Experimental and TTT-R potential parameters
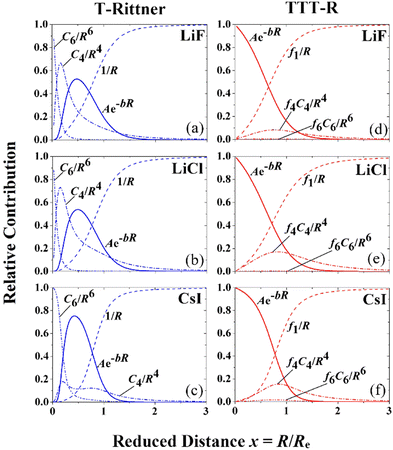
As in the Rittner model and similar models the potential parameters A and b in eqn (6) are customarily determined by a self-consistent least squares fit of two experimental parameters, usually the bond distance Re and the vibrational constant ωe. In the present case considering the uncertainty in C4 it was also fitted. Since the dispersion term C6 makes a contribution of at most 1.2% to the total potential in the case of CsI and even less in the lithium containing LiF and LiCl molecules (see Fig. 3) it was assumed to be the same as that of an isoelectronic dimer of rare gas atoms obtained by transferring an electron from the halogen atom to the alkali metal (Table 1, last entry). A, b and C4 are determined from the experimental values for the well depth De in addition to the bond distance Re and the vibrational frequency ωe.The experimental values used in the fit are listed in Table 3. The experimental dissociation energies of LiF and LiCl date back to 1961 from thermodynamic considerations. That of CsI should be more reliable since it was measured directly by photodissociation. Since it is only possible to measure the dissociation energy to atoms D0, the classical energy for dissociation to ions De was calculated from the equation De = D0 + 0.5ωe – 0.25ωeχe + (EIE − EEA), where χe is the anharmonicity parameter, EIE is the ionization potential of the neutral alkali atom and EEA is the electron affinity of the neutral halogen atom. The corresponding parameters are listed in the Appendix.
| Dimer | Bond distance Re47 | Dissociation energy (to atoms) D0 | Classical dissociation energy (to ions) De | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vibrational constant49,50ωe | C 6 25 | |||||||||
| Å | a.u. | eV | a.u. | eV | a.u. | cm−1 | a.u. | eV Å6 | a.u. | |
| a The values are the average of D0 reported in the two references. The errors are estimated to be ±3%. | ||||||||||
| 7Li19F | 1.563 | 2.955 | 5.9305a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51,52 51,52 |
0.2179 | 7.9772 | 0.2931 | 910.57 | 0.00415 | 1.8116 | 3.0319 |
| 7Li35Cl | 2.020 | 3.818 | 4.8720a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51,52 51,52 |
0.1790 | 6.690 | 0.2458 | 642.95 | 0.00293 | 5.7076 | 9.5519 |
| 133Cs127I | 3.314 | 6.262 | 3.467053 | 0.1274 | 4.3092 | 0.15836 | 119.19 | 0.00054 | 170.82 | 285.87 |
The three unknowns A, b and C4 of the TTT-R model are determined by simultaneously solving the following three equations self-consistently for the experimental values for Re, De and ωe:
| V(Re) = De, | (7) |
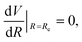 | (8) |
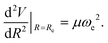 | (9) |
The best fit potential parameters are listed in Table 4 where they are compared with the T-Rittner values based on nearly the same experimental values for Re and ωe but with assumed values of C4. The different approach has a big effect on the TTT-R values for the preexponential factor A. They are reduced to about one half of the T-Rittner values, and the b values are smaller than the T-Rittner values by 6, 14 and 12% for LiF, LiCl and CsI, respectively. Whereas for LiF the present value for C4 of 3.8800 is close to the T-Rittner value of 3.6407 the TTT-R values for LiCl and CsI are about a factor two larger than the T-Rittner values.
| Dimer | Potential | A | b | C 4 | |||
|---|---|---|---|---|---|---|---|
| eV | a.u. | Å−1 | a.u. | eV Å4 | a.u. | ||
| LiF | TTT-R | 419.96 | 15.433 | 3.4605 | 1.8312 | 8.2796 | 3.8802 |
| T-Rittner13 | 728.81 | 28.768 | 3.6697 | 1.9419 | 7.7686 | 3.6407 | |
| LiCl | TTT-R | 411.40 | 15.119 | 2.6468 | 1.4006 | 46.150 | 21.628 |
| T-Rittner13 | 998.25 | 36.685 | 3.0211 | 1.5987 | 26.776 | 12.549 | |
| CsI | TTT-R | 2078.5 | 76.383 | 2.3055 | 1.2200 | 123.45 | 57.856 |
| T-Rittner13 | 4311.4 | 158.44 | 2.5880 | 1.3695 | 69.118 | 32.392 | |
C. The effects of damping on the potential terms
The dramatic effect of damping on the potential parameters is shown in Fig. 3 where the contributions of the individual terms to the T-Rittner potential are compared with the contributions of the damped terms of the TTT-R potential. On the left-hand side of Fig. 3 the three frames (a)–(c) illustrate the relative absolute contributions of the four interaction terms to the original T-Rittner model for LiF, LiCl and CsI, respectively. To facilitate the comparison of the three systems the contributions are plotted against the reduced distance x = R/Re. The T-Rittner contribution from the attractive Coulomb potential gradually decreases with decreasing internuclear distance from 100% at about x ≈ 1.5 to zero at x = 0. At about x ≈ 0.6 it is overtaken by the repulsive Born–Mayer term which first goes through a maximum and then turns over and also goes to zero. This complete suppression of this important term is caused by the increasingly large negative (attractive) contribution at small internuclear distances from the undamped C4 term, which also goes through a maximum as it is replaced by the more negative C6 term. Thus, these two long range undamped negative terms by virtue of their large negative powers n contribute the most at very small distances. Together with the negative Coulomb term they pull the entire potential down to negative infinity.The corresponding damped TTT-R potential terms are shown in the right-hand frames (d)–(f). Perhaps surprisingly the contribution from the negative Coulomb shows about the same behavior as with the T-Rittner potential. This is attributed to the strong similarity of the damping curve (Fig. 2) and the undamped Coulomb contribution curves in Fig. 3(a)–(c). The damping of the negative long-range terms C4 and C6 serves to largely reduce their influence and allows the positive Born Mayer term to dominate the potential at small distances. This provides the overall potential with the usual repulsive wall. The middle frames also show the almost negligible contribution of the C6 dispersion term referred to in Section II B.
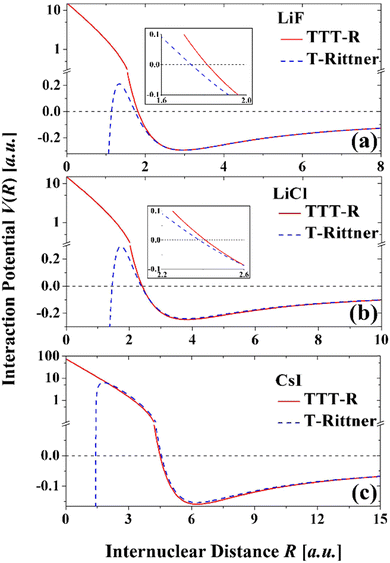
The potential curves based on the two models are shown in Fig. 4. The attractive well regions are nearly identical and there the damping has little effect. Small differences occur at internuclear distance less than the minimum, which are especially apparent in LiF and LiCl. In the repulsive region the damping raises the potentials so that they show the expected behavior. In contrast the T-Rittner potentials pass through a maximum of about 0.2 a.u. (∼5.5 eV) and then become strongly negative. CsI behaves differently due to the extended range of the Born–Mayer term (Fig. 3(f)) and in this system the T-Rittner potential turns over at much higher energies.
The potential parameters A, b and C4 also depend on the damping of each of the attractive terms of the TTT-R model. This is shown in Table 5 where the parameters are listed following successive removal of the damping of the Coulomb potential (second line), removal of damping of the C4 (third line) and finally removal of all damping functions (last line). The damping of the Coulomb potential does not have a large effect on the potential parameters, but without damping of the attractive C4 term the preexponential Born Mayer terms A increases significantly and approaches the T-Rittner values. The damping has a much smaller effect on the parameter b and C4 of LiF but a larger effect on the heavier diatoms LiCl and CsI. It is of interest that the surprisingly large value of C4 of the present TTT-R potential compared to the assumed T-Rittner value is not affected by damping.
| Model | LiF | LiCl | CsI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | b | C 4 | A | b | C 4 | A | b | C 4 | |
| Present | 15.432 | 1.8312 | 3.8802 | 15.119 | 1.4006 | 21.628 | 76.382 | 1.2200 | 57.856 |
| f 1 = 1 | 18.098 | 1.8411 | 3.8352 | 17.165 | 1.4064 | 21.519 | 78.078 | 1.2200 | 58.038 |
| f 4 = f1 = 1 | 27.909 | 1.9404 | 3.3099 | 37.469 | 1.5388 | 18.703 | 96.562 | 1.2370 | 57.379 |
| f 6 = f4 = f1 = 1 | 31.104 | 1.9757 | 3.1130 | 39.822 | 1.5538 | 18.375 | 107.232 | 1.2489 | 56.847 |
III. TTT-R potential curves of LiF, LiCl and CsI
A. Comparison of TTT-R potentials with ab initio potential curves
Table 6 provides an overview of the available ab initio calculations of the potential curves of LiF, LiCl and CsI, which presently are the only ones available for the alkali halide molecules. The ab initio predicted well parameters De and Re and the vibrational frequencies ωe are compared with the latest experimental values (Table 3) which are listed in the bottom entry for each system. The most recent theories predict the well parameters De and Re and the vibrational frequencies within a few percent of the experimental values.| Method | R e (Å) | R e (a.u) | D e (eV) | D e (a.u.) | ω e (cm) | Ref. | |
|---|---|---|---|---|---|---|---|
| a CI with generalized valence-bond orbitals from ground state MCSCF calculation. b Coulomb energy calculated from electron density of the combined system assumed as the sum of the separate ionic electron densities. Non-Coulombic energy calculated from electron gas approximation. c MCSCF with optimized wave functions. d Covalent-ionic resonance model together with valence-bond method. e Multireference CI based on complete-active-space SCF wave functions. f Multireference single-and double-excitation CI. g Quantum mechanical exchange perturbation theory similar to used in ref. 15. | |||||||
| LiF | GVB/IVO-CIa | 1.5637 | 2.9550 | 7.1875 | 0.2487 | — | Kahn et al.54 |
| EDC-SSDb | 1.5000 | 2.8346 | 8.0225 | 0.2948 | 1010 ± 20 | Kim and Gordon55 | |
| MCSCFc | 1.5890 | 3.0028 | 7.8305 | 0.2878 | 896.1 | Werner and Meyer56 | |
| CIR-VBd | 1.6000 | 3.0236 | 8.0605 | 0.2962 | — | Zeiri and Balint-Kurti57 | |
| MRCIe | 1.5991 | 3.0219 | 7.7864 | 0.2861 | — | Varandas58 | |
| Expt. | 1.563 | 2.995 | 7.9772 | 0.2931 | 910.57 | Table 3 | |
| LiCl | EDC-SSDb | 1.9400 | 3.6661 | 6.2532 | 0.22980 | 690 ± 10 | Kim and Gordon55 |
| CIR-VBd | 2.0000 | 3.7795 | 6.5489 | 0.24067 | — | Zeiri and Balint-Kurti57 | |
| MRSDCIf | 2.0215 | 3.832 | 6.7742 | 0.24894 | 644.09 | Weck et al.59 | |
| MRSDCIf | 2.0327 | 3.8112 | 6.3672 | 0.2340 | 630.62 | Kurosaki and Yokoyama24 | |
| Expt. | 2.0207 | 3.8185 | 6.690 | 0.2458 | 642.95 | Table 3 | |
| CsI | QMEPTg | 3.2650 | 6.170 | 4.3267 | 0.15900 | — | Patil27 |
| MRSDCIf | 3.4000 | 6.4251 | 3.6679 | 0.13479 | 116.6 | Kurosaki et al.60 | |
| Expt. | 3.3142 | 6.2629 | 4.3092 | 0.15836 | 119.19 | Table 3 | |
Fig. 5(a), 6(a) and 7(a) display comparisons of the present TTT-R reduced potential curves with the corresponding ab initio reduced potentials for LiF, LiCl and CsI, respectively. Alternatively the absolute potentials (V in a.u., R in a.u.) could be compared. But in this case each of the different theoretical potential curves would be slightly shifted in both the x- and y-coordinate depending on the corresponding values of De and Re and the comparison would be difficult. For this reason the reduced curves normalized to the corresponding well parameters, which show the shape of the potential, are compared in the following figures. The well parameters are compared separately in Table 6.
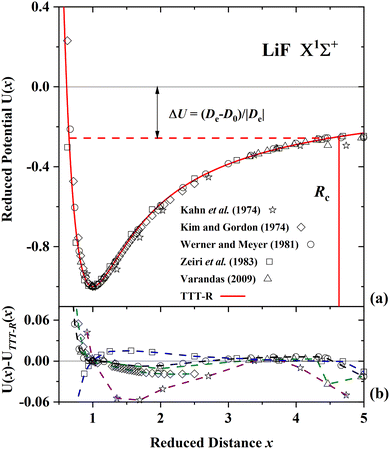 | ||
| Fig. 5 Comparison of the present reduced potential (red line curve) with five ab initio reduced potential curves for LiF in the ground state.54–58 (a) Shows the ab initio energy-distance points on a reduced scale. The zero reduced potential corresponds to dissociation to ions, the dashed red line corresponds to dissociation to atoms. ΔU denotes the difference between the two dissociation limits. Rc denotes the reduced distance at which the covalent and Coulombic potentials cross each other. (b) The differences in the ab initio reduced potentials with respect to the present potential are plotted as a function of the reduced distance. The agreement among the ab initio potentials and with the present potential is better than 3% with the exception of the potential of ref. 53 and the agreement with the TTT-R potential is better than about 2%. | ||
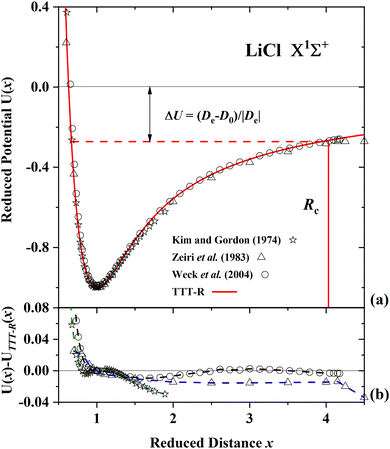 | ||
| Fig. 6 Comparison of the present reduced potential (red line curve) with 3 ab initio reduced potential curves for LiCl in the ground state.55,57,59 (a) Shows the ab initio energy-distance points on a reduced scale. The zero reduced potential corresponds to dissociation to ions, the dashed red line corresponds to dissociation to atoms. ΔU denotes the difference between the two dissociation limits. Rc denotes the reduced distance at which the covalent and Coulombic potentials cross each other. (b) The differences in the ab initio reduced potentials with respect to the present potential are plotted as a function of the reduced distance. The present potential agrees with the latest ab initio potential of Weck et al.59 to better than 1% and agrees to better than 2% with the earlier potential of Zieri et al.57 | ||
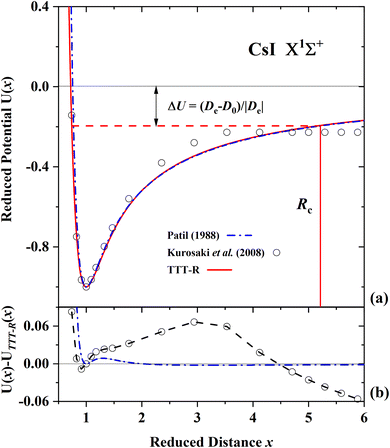 | ||
| Fig. 7 Comparison of the present reduced potential (red line curve) with the ab initio reduced potential of Kurosaki et al.60 and the semi-ab initio reduced potential of Patil27 for CsI in the ground state. (a) Shows the ab initio energy-distance points on a reduced scale. The zero reduced potential corresponds to dissociation to ions, the dashed red line corresponds to dissociation to atoms. ΔU denotes the difference between the two dissociation limits. Rc denotes the reduced distance at which the covalent and Coulombic potentials cross each other. (b) The differences in the ab initio reduced potentials with respect to the present potential are plotted as a function of the reduced distance. The present potential differs by up to 6% with the ab initio potential60 and differs only by less than 0.5% with the semi-ab initio potential of Patil.27 | ||
For LiF and LiCl the different ab initio potentials and the predicted TTT-R potential all follow closely the same potential curve. In the case of CsI there is only one ab initio potential from Kurosaki et al.60 In this case the agreement is not so good. In lieu of other calculations the semi-ab initio potential of Patil27 is also shown. In this case the agreement with the TTT-R potential is excellent. This suggests that the TTT-R potential is more reliable than the ab initio potentials.
Since the differences between the TTT-R and the ab initio potential curves are too small to be clearly resolved in Fig. 5(a), 6(a) and 7(a) they are shown in the bottom parts of each of the figures. In the case of LiF and LiCl the agreement with the ab initio potentials is better than about 2% and mostly about 1%. The only exception is the 1974 CI potential of Kahn et al.54 for LiF. The large differences in the case of CsI and the fact that there is only one ab initio potential for this system appears to be related with the large spin–orbit (SO) coupling which leads to a splitting between the 2P1/2 and 2P1/2 states of the halogen atom. Iodine stands out among the halogen atoms by having the largest splitting of 7603 cm−1 compared to 404 cm−1 and 881 cm−1 for fluorine and chlorine, respectively. As stated by Kurosaki et al. in their article:60 “The atomic SO splittings greatly affect the nature of the potential energy curves especially around the avoided crossing point. Also substantial are the relativistic effects on the inner shell electrons in heavy elements.” This illustrates another advantage of the model potentials, which are not affected by these complications.
As indicated by Fig. 4 similarly good agreement with the ab initio potentials in the well region is also expected for the T-Rittner potentials based on the parameters in Table 4. Since most of the modern ab initio potentials have appeared in the present century and the model calculations are mostly from the end of the last century the good agreement provides belated justification of the T-Rittner model for the attractive well region of the potentials.
IV. Summary and discussion
The present article describes the effects of the damping due to charge overlap at short distances on the popular T-Rittner potential13 for the alkali halide diatoms. The damping function used is based on the original damping function of Tang and Toennies which was developed and tested first for the London dispersion potential. Without damping the long range negative R−4 induction and R−6 dispersion terms are shown to dominate the T-Rittner potential at the expense of the Born–Mayer repulsion so that the potential tends to minus infinity at distances below the zero crossing point. Thus the damping of the attractive Coulomb potential, induction and dispersion terms has the important effect that it eliminates the negative singularity at short distances. Instead, at short ranges the new potential with damping, denoted TTT-R, exhibits the expected increase of the repulsive potential with decreasing internuclear distances.In addition to having the proper short range behavior it is demonstrated that the TTT-R potential curve also agrees within a few percent over the full range of distance from the zero passage distance R0 out to very large distances with the ab initio potentials for LiF and LiCl. Since the damping affects only the potential at short distances near the zero crossing point the 1973 T- Rittner potential on which the TTT-R potential is based provides a nearly equally good agreement with the ab initio potentials over most of the well region. The comparison with the only ab initio potential for CsI is not satisfactory, but this could be due to inaccuracies of the ab initio potential related to the large spin–orbit coupling and relativistic effects. On the other hand comparison with a semi ab initio perturbation calculation26 appears to provide confirmation of the model potentials.
In the early T-Rittner-type investigations the C4 induction term was assumed to be known. In view of the wide range of the polarizabilities of the ions in the many previous reports the C4 term was also fitted in the present investigation. Thus the parameters of TTT-R model are based on a fit not only of the well distance Re, and vibrational frequency ωe but also of the experimental determined well depth De. Whereas the so determined value for C4 in the case of LiF is in reasonable agreement with an earlier theoretical value for the ion-in-molecule polarizabilities35 the best fit C4 value for LiCl is about a three times larger and CsI is about twice larger as the theoretical values in the early literature.34,35 Compared to the free ion polarizabilities for LiF they are about one half as large and for LiCl about the same and about 50% larger for CsI. Also in view of the uncertainties of the theory in treating the effects of strong Coulomb forces on the ion polarizabilities, further work is necessary.
With the availability of realistic potentials it is possible to compare the potentials for the three systems with the potentials of the isoelectronic rare gas diatoms HeNe, HeAr, and XeXe61 over nearly the full range of internuclear distances (Fig. 8). The much wider attractive bowls of the alkali halide potentials derive from the damped Coulomb and induction C4 terms. The strong attraction of these terms can also explain that the bond distances are smaller by 51, 58 and 76% and that the dissociation energies are much greater by factors of 103 to 102.
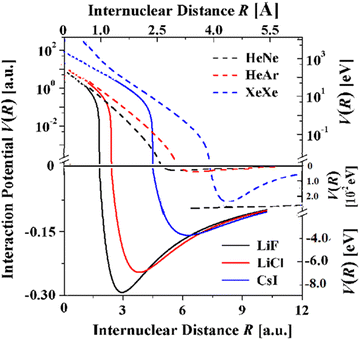 | ||
| Fig. 8 Comparison of the TTT-R potentials of the three alkali halide diatoms with the corresponding isoelectronic rare gas diatoms. The rare gas potentials are highly accurate and have recently been shown to be conformal.61 Their repulsive potentials extend to R = 0 since the proper united atom limit has been taken into account.61 | ||
Whereas the attractive wells of the rare gas dimers are much smaller Fig. 8 shows that the repulsive potentials are similar. In particular, in the case of CsI and XeXe this trend is in agreement with high pressure equation of state studies which reveal that at pressures above 15 GPa the volumes per atom are nearly identical.62Fig. 8 suggests that this may also be true for the lighter alkali halide and isoelectronic rare gas dimers. The comparison of the repulsive regions in Fig. 8 suffers somewhat from the fact that the united atom limit has not been accounted for in the TTT-R potentials but have been included in the rare gas dimers. Thus, the extent of agreement of the repulsive potentials at distance less than 1.5 a.u. is only approximate. More accurate models and experiments are required before it can be shown that the alkali halide reduced potentials are conformal as it has been recently shown for the rare gas diatoms.61
In future investigations several improvements of damped T-Rittner models can be envisaged. The polarizabilities of the cations and anions can be improved by accounting for the large differences in the free anion and cation polarizabilities and their different internuclear distance dependencies. The T-Rittner type models including the present TTT-R model have the disadvantage that they are based on experimental parameters related only to the minimum of the potential. By including additional ab initio parameters such as the distance dependence of the dipole moments better models could be developed. The repulsive region can also be improved by taking account of the united atom limit.20,61 Future refined models will provide accurate force field models for treating condensed systems such as solids and liquid alkali halides.
Author contributions
Xiaowei Sheng carried out the calculations and made the figures. K. T. Tang had the idea and made valuable advice. Peter Toennies wrote the final version.Conflicts of interest
There are no conflicts of interest.Appendix
| Dimer | ω e χ e 48 | Ionization energies EIE47 | Electron affinities ELA63 | ΔE = EIE − EEA | ||||
|---|---|---|---|---|---|---|---|---|
| cm−1 | a.u. | eV | a.u. | eV | a.u. | eV | a.u. | |
| LiF | 8.2080 | 3.74 × 10−5 | 5.392 | 0.1981 | 3.401 | 0.1250 | 1.991 | 0.07314 |
| LiCl | 4.4725 | 2.04 × 10−5 | 5.392 | 0.1981 | 3.613 | 0.1328 | 1.779 | 0.06538 |
| CsI | 0.2542 | 1.16 × 10−6 | 3.894 | 0.1431 | 3.051 | 0.1124 | 0.8349 | 0.03068 |
Acknowledgements
X. W. S. acknowledges and appreciates the support of the National Natural Science Foundation of China (No. 12174003) and the Anhui Provincial Natural Natural Science Foundation (No. 2008085MA25). J. P. T. thanks his colleagues for generous support: He also thanks Katrin Glormann for careful assistance in preparing the manuscript. Open Access funding provided by the Max Planck Society.References
- G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer, New York, 2018 Search PubMed.
- F. Seitz, Color Centers in Alkali Halide Crystals, Rev. Mod. Phys., 1946, 18(3), 384 CrossRef CAS.
- M. M. Walz, M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, Phase-Transferable Force Field for Alkali Halides, J. Chem. Theory Comput., 2018, 14(11), 5933 CrossRef CAS PubMed.
- C. W. Townes and A. L. Schawlow, Microwave Spectroscopy McGraw Hill, New York, 1955 Search PubMed.
- D. Herschbach, Molecular collisions, from warm to ultracold, Faraday Discuss., 2009, 142, 9 RSC.
- P. D. Gregory, J. A. Blackmore, S. L. Bromley, J. M. Hutson and S. L. Cornish, Robust storage qubits in ultracold polar molecules, Nat. Phys., 2021, 17(10), 1149 Search PubMed.
- W. Barlow, The Architecture of Molecules, Z. Kristallogr, 1898, 29, 433 Search PubMed.
- L. Pauling, The theoretical prediction of the physical properties of many-electron atoms and ions. Mole refraction, diamagnetic susceptibility, and extension in space, Proc. R. Soc. A., 1927, 114, 181 CAS.
- W. Kossel, Sitzungsbericht d. Bayr. Akad., meth.-naturw. Kl., 1917, 127 Search PubMed.
- E. Madelung, Das elektrische Feld in Systemen von regelmäßig angeordneten Punktladungen, Phys. Z., 1918, 19, 524 Search PubMed.
- M. Born and J. E. Mayer, Zur Gittertheorie der Ionenkristalle, Z. Phys., 1932, 75, 1 CrossRef CAS.
- M. Born and W. Heisenberg, Über den Einfluß der Deformierbarkeit der Ionen auf optische und chemischen Konstanten, Z. Phys., 1924, 23, 388 CrossRef CAS.
- E. S. Rittner, Binding Energy and Dipole Moment of Alkali Halide Molecules, J. Chem. Phys., 1951, 19(8), 1030 CrossRef CAS.
- B. T. Gowda, B. S. Sherigara and S. W. Benson, Potential Functions for Alkali-Halide Molecules, J. Comput. Chem., 1985, 6(2), 93 CrossRef CAS.
- P. Brumer and M. Karplus, Perturbation-Theory and Ionic Models for Alkali-Halide Systems. 1. Diatomics, J. Chem. Phys., 1973, 58(9), 3903 CrossRef CAS.
- M. Kumar, A. J. Kaur and J. Shanker, Spectroscopic Constants of Alkali-Halides and Hydrides Using Modified T-Rittner Model, J. Chem. Phys., 1986, 84(10), 5735 CrossRef CAS.
- M. J. L. Sangster and M. Dixon, Interionic Potentials in Alkali-Halides and Their Use in Simulations of Molten-Salts, Adv. Phys., 1976, 25(3), 247 CrossRef CAS.
- R. N. Yardley and G. G. Balintkurti, Ab-Initio Valence-Bond Calculations on HF, LiH, LiH+ and LiF, Mol. Phys., 1976, 31(3), 921 CrossRef CAS.
- R. A. Buckingham, The Repulsive Interaction of Atoms in S States, Trans. Faraday Soc., 1958, 54(4), 453 RSC.
- S. Warnecke, K. T. Tang and J. P. Toennies, Communication: A simple full range analytical potential for H(2)b(3)Sigma(+)(u), H-He (2)Sigma(+), and He-2 (1)Sigma(+)(g), J. Chem. Phys., 2015, 142, 13 CrossRef.
- R. K. Pathak and A. J. Thakkar, Very Short-Range Interatomic Potentials, J. Chem. Phys., 1987, 87(4), 2186 CrossRef CAS.
- A. J. Kaur, W. N. Bhende, P. S. Bakhshi and J. Shanker, Analysis of the Short-Range Repulsive Potential in Alkali-Halides, Phys. Status Solidi B, 1984, 123(1), 71 CrossRef CAS.
- A. Dewaele, A. B. Belonoshko, G. Garbarino, F. Occelli, P. Bouvier, M. Hanfland and M. Mezouar, High-pressure high-temperature equation of state of KCl and KBr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(21), 214105 CrossRef.
- Y. Kurosaki and K. Yokoyama, Ab initio MRSDCI study on the low-lying electronic states of the lithium chloride molecule (LiCl), J. Chem. Phys., 2012, 137(17), 064305 CrossRef.
- J. Jiang, J. Mitroy, Y. Cheng and M. W. J. Bromley, Effective oscillator strength distributions of spherically symmetric atoms for calculating polarizabilities and long-range atom-atom interactions, At. Data Nucl. Data Tables, 2015, 101, 158 CrossRef CAS.
- T. Gould and T. Bucko, C-6 Coefficients and Dipole Polarizabilities for All Atoms and Many Ions in Rows 1-6 of the Periodic Table, J. Chem. Theory Comput., 2016, 12(8), 3603 CrossRef CAS PubMed.
- S. H. Patil, Interionic Potentials in Alkali-Halides, J. Chem. Phys., 1987, 86(1), 313 CrossRef CAS.
- Y. P. Varshni and R. C. Shukla, Potential Energy Functions for Alkali Halide Molecules, J. Mol. Spectrosc., 1965, 16(1), 63 CrossRef CAS.
- J. Shanker, G. G. Agrawal and N. Dutt, Electronic Polarizabilities and Photoelastic Behavior of Ionic-Crystals, Phys. Status Solidi B, 1986, 138(1), 9 CrossRef CAS.
- K. J. Donald, W. H. Mulder and L. von Szentpaly, Comment on “A potential dependent polarizability?” [J. Chem. Phys. 96, 5289 (1992)], J. Chem. Phys., 2000, 113(8), 3477 CrossRef CAS.
- J. Shanker and S. S. Kushwah, Response to “Comment on A potential dependent polarizability?” [J. Chem. Phys. 113, 3477 (2000)], J. Chem. Phys., 2000, 113(8), 3479 CrossRef CAS.
- A. S. McNeill, K. A. Peterson and D. A. Dixon, Polarizabilities of neutral atoms and atomic ions with a noble gas electron configuration, J. Chem. Phys., 2020, 153(17), 174304 CrossRef CAS PubMed.
- J. Shanker and H. B. Agrawal, Electronic Polarizabilities, Ionic-Radii, and Repulsive Potential Parameters for Diatomic Alkali-Halide Molecules, Can. J. Phys., 1980, 58(7), 950 CrossRef CAS.
- M. Kumar and J. Shanker, Electronic Polarizabilities, Potential Functions, and Spectroscopic Constants for Diatomic-Molecules of Alkali-Halides and Alkali Hydrides, J. Chem. Phys., 1992, 96(7), 5289 CrossRef CAS.
- S. Hati, B. Datta and D. Datta, Polarizability of an ion in a molecule. Applications of Rittner's model to alkali halides and hydrides revisited, J. Phys. Chem., 1996, 100(51), 19808 CrossRef CAS.
- K. T. Tang and J. P. Toennies, An Improved Simple-Model for the van der Waals Potential Based on Universal Damping Functions for the Dispersion Coefficients, J. Chem. Phys., 1984, 80(8), 3726 CrossRef CAS.
- A. Koide, W. J. Meath and A. R. Allnatt, 2nd Order Charge Overlap Effects and Damping Functions for Isotropic Atomic and Molecular-Interactions, Chem. Phys., 1981, 58(1), 105 CrossRef CAS.
- R. J. Wheatley and W. J. Meath, Dispersion Energy Damping Functions, and Their Relative Scale with Interatomic Separation, for (H,He,Li)-(H,He,Li) Interactions, Mol. Phys., 1993, 80(1), 25 CrossRef CAS.
- M. Gutowski, J. Verbeek, J. H. Vanlenthe and G. Chalasinski, The Impact of Higher Polarization Functions on 2nd-Order Dispersion Energy - Partial-Wave Expansion and Damping Phenomenon for He-2, Chem. Phys., 1987, 111(2), 271 CrossRef CAS.
- W. Meyer and L. Frommhold, Long-Range Interactions in H-He: ab-initio Potential, Hyperfine Pressure Shift and Collision-Induced Absorption in the Infrared, Theor. Chim. Acta, 1994, 88(3), 201 CrossRef CAS.
- K. T. Tang and J. P. Toennies, Asymptotic Theory of the Chemical-Bond in H-2+ Based on a Simple Physical Model, J. Phys. Chem., 1990, 94(20), 7880 CrossRef CAS.
- R. Nikhar and K. Szalewicz, Reliable crystal structure predictions from first principles, Nat. Commun., 2022, 13, 3095 CrossRef CAS PubMed.
- A. J. Stone, The Theory of Intermolecular Forces, Clarendon Press, Oxford, 1996 Search PubMed.
- L. V. Slipchenko and M. S. Gordon, Electrostratic Energy in the Effective Fragment Potential Method: Theory and Application to Benzene Dimer, I. Wiley Periodicals, 2006 Search PubMed.
- K. Jug, E. Fasold and A. M. Koster, Charge and Valence in Lithium Compounds, Chem. Phys. Lett., 1992, 188(3–4), 294 CrossRef CAS.
- The atomic masses for these isotopes are m(7Li) = 7.016004 u, m(19F) = 18.993105 u, m(35Cl) = 34.968852729 u, m(127I) = 126.904070 u, m(133Cs) = 132.905433 u.
- K. T. Tang and J. P. Toennies, New Combining Rules for Well Parameters and Shapes of the van der Waals Potential of Mixed Rare-Gas Systems, Z. Phys. D – Atoms Molec. Clusters, 1986, 1(1), 91 CrossRef CAS.
- Online available at https://physics.nist.gov/cgi-bin/MolSpec/diperiodic.pl.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, IV Constants of Diatomic Molecules, Van Nostrand Rheinhold Co., New York, 1979 Search PubMed.
- K. K. Irikura, Experimental vibrational zero-point energies: Diatomic molecules, J. Phys. Chem. Ref. Data, 2007, 36(2), 389 CrossRef CAS.
- L. Brewer and E. Brackett, The Dissociation Energies of Gaseous Alkali Halides, Chem. Rev., 1961, 61(4), 425 CrossRef CAS.
- E. M. Bulewicz, L. F. Phillips and T. M. Sugden, Determination of Dissociation Constants and Heats of Formation of Simple Molecules by Flame Photometry.8. Stabilities of Gaseous Diatomic Halides of Certain Metals, Trans. Faraday Soc., 1961, 57(6), 921 RSC.
- T. M. R. Su and S. J. Riley, Alkali-Halide Photofragment Spectra.1. Alkali Iodide Bond-Energies and Excited-State Symmetries at 266 Nm, J. Chem. Phys., 1979, 71(8), 3194 CrossRef CAS.
- L. R. Kahn and P. J. Hay, Theoretical Study of Curve Crossing - Ab-Initio Calculations on 4 Lowest 1sigma+ States of Lif, J. Chem. Phys., 1974, 61(9), 3530 CrossRef CAS.
- Y. S. Kim and R. G. Gordon, Ion-Ion Interaction Potentials and Their Application to Theory of Alkali-Halide and Alkaline-Earth Dihalide Molecules, J. Chem. Phys., 1974, 60(11), 4332 CrossRef CAS.
- H. J. Werner and W. Meyer, Mcscf Study of the Avoided Curve Crossing of the 2 Lowest Sigma-1+ States of Lif, J. Chem. Phys., 1981, 74(10), 5802 CrossRef CAS.
- Y. Zeiri and G. G. Balint-kurti, Theory of Alkali-Halide Photofragmentation - Potential-Energy Curves and Transition Dipole-Moments, J. Mol. Spectrosc., 1983, 99(1), 1 CrossRef CAS.
- A. J. C. Varandas, Accurate ab initio potential energy curves for the classic Li-F ionic-covalent interaction by extrapolation to the complete basis set limit and modeling of the radial nonadiabatic coupling, J. Chem. Phys., 2009, 131(12), 124128 CrossRef CAS PubMed.
- P. F. Weck, K. Kirby and P. C. Stancil, Ab initio configuration interaction study of the low-lying (1)Sigma(+) electronic states of LiCl, J. Chem. Phys., 2004, 120(9), 4216 CrossRef CAS PubMed.
- Y. Kurosaki, L. Matsuoka, K. Yokoyama and A. Yokoyama, Ab initio study on the ground and low-lying excited states of cesium iodide (CsI), J. Chem. Phys., 2008, 128(2), 024301 CrossRef PubMed.
- X. W. Sheng, J. P. Toennies and K. T. Tang, Conformal Analytical Potential for All the Rare Gas Dimers over the Full Range of Internuclear Distances, Phys. Rev. Lett., 2020, 125(25), 253402 CrossRef CAS PubMed.
- A. N. Zisman, I. V. Aleksandrov and S. M. Stishov, X-Ray Study of Equations of State of Solid Xenon and Cesium Iodide at Pressures up to 55-Gpa, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32(1), 484 CrossRef CAS PubMed.
- T. Andersen, H. K. Haugen and H. Hotop, Binding energies in atomic negative ions: III, J. Phys. Chem. Ref. Data, 1999, 28(6), 1511 CrossRef CAS.
| This journal is © the Owner Societies 2022 |