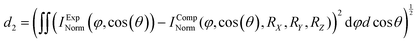Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new route for enantio-sensitive structure determination by photoelectron scattering on molecules in the gas phase
Kilian
Fehre
*a,
Nikolay M.
Novikovskiy
 bc,
Sven
Grundmann
bc,
Sven
Grundmann
 a,
Gregor
Kastirke
a,
Sebastian
Eckart
a,
Gregor
Kastirke
a,
Sebastian
Eckart
 a,
Florian
Trinter
a,
Florian
Trinter
 ad,
Jonas
Rist
a,
Alexander
Hartung
a,
Daniel
Trabert
a,
Christian
Janke
a,
Martin
Pitzer
a,
Stefan
Zeller
a,
Florian
Wiegandt
a,
Miriam
Weller
a,
Max
Kircher
a,
Giammarco
Nalin
ad,
Jonas
Rist
a,
Alexander
Hartung
a,
Daniel
Trabert
a,
Christian
Janke
a,
Martin
Pitzer
a,
Stefan
Zeller
a,
Florian
Wiegandt
a,
Miriam
Weller
a,
Max
Kircher
a,
Giammarco
Nalin
 a,
Max
Hofmann
a,
Lothar Ph. H.
Schmidt
a,
André
Knie
b,
Andreas
Hans
a,
Max
Hofmann
a,
Lothar Ph. H.
Schmidt
a,
André
Knie
b,
Andreas
Hans
 b,
Ltaief
Ben Ltaief
b,
Ltaief
Ben Ltaief
 b,
Arno
Ehresmann
b,
Arno
Ehresmann
 b,
Robert
Berger
e,
Hironobu
Fukuzawa
b,
Robert
Berger
e,
Hironobu
Fukuzawa
 f,
Kiyoshi
Ueda
f,
Horst
Schmidt-Böcking
a,
Joshua B.
Williams
g,
Till
Jahnke
f,
Kiyoshi
Ueda
f,
Horst
Schmidt-Böcking
a,
Joshua B.
Williams
g,
Till
Jahnke
 h,
Reinhard
Dörner
a,
Philipp V.
Demekhin
h,
Reinhard
Dörner
a,
Philipp V.
Demekhin
 *b and
Markus S.
Schöffler
*b and
Markus S.
Schöffler
 *a
*a
aInstitut für Kernphysik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, 60438, Frankfurt am Main, Germany. E-mail: fehre@atom.uni-frankfurt.de; schoeffler@atom.uni-frankfurt.de
bInstitut für Physik und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132, Kassel, Germany. E-mail: demekhin@physik.uni-kassel.de
cInstitute of Physics, Southern Federal University, 344090, Rostov-on-Don, Russia
dMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195, Berlin, Germany
eDepartment of Chemistry, Philipps-Universität Marburg, Hans-Meerwein-Straße 4, 35032, Marburg, Germany
fInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai, 980-8577, Japan
gDepartment of Physics, University of Nevada, Reno, Nevada 89557, USA
hEuropean XFEL GmbH, Holzkoppel 4, 22869, Schenefeld, Germany
First published on 28th October 2022
Abstract
X-Ray as well as electron diffraction are powerful tools for structure determination of molecules. Studies on randomly oriented molecules in the gas phase address cases in which molecular crystals cannot be generated or the interaction-free molecular structure is to be addressed. Such studies usually yield partial geometrical information, such as interatomic distances. Here, we present a complementary approach, which allows obtaining insight into the structure, handedness, and even detailed geometrical features of molecules in the gas phase. Our approach combines Coulomb explosion imaging, the information that is encoded in the molecular-frame diffraction pattern of core–shell photoelectrons and ab initio computations. Using a loop-like analysis scheme, we are able to deduce specific molecular coordinates with sensitivity even to the handedness of chiral molecules and the positions of individual atoms, e.g., protons.
Introduction
During the last decade, the determination of the three-dimensional structure of molecules using electron crystallography developed into a complementary analysis method to the well-established X-ray crystallography.1–3 In particular, for the structural investigation of micro- and nano-crystalline materials, where sufficiently large single crystals for X-ray diffraction cannot be obtained4 or crystalline-sponge approaches for X-ray diffraction5,6 fail, electron diffraction is the method of choice.7 It yields Ångstrom resolution even when applied to large systems8 or systems involving weak scatterers such as hydrogen atoms.9 For cases in which molecular crystals cannot be obtained or the interaction-free molecular structure is to be addressed, corresponding electron-scattering approaches on gas-phase molecules exist.10,11 Such electron diffraction studies on randomly oriented molecules, however, can only provide information on interatomic distances, which is, in addition, challenging to extract in case of overlapping distance parameters. Furthermore, they do not reveal the handedness of chiral systems.12 In order to overcome the drawback of a random orientation of the molecules under investigation, several experiments have been performed utilizing electron13,14 and X-ray diffraction15 in combination with sophisticated two-dimensional and three-dimensional laser-alignment schemes.An alternative approach employs electrons that are created from within the molecule as a probe. In these experiments, highly energetic single photons or strong-field laser pulses ionize isolated molecules in the gas phase. The emitted photoelectron is scattered by the molecular potential, yielding a very complex interference pattern, in which the structural information is encoded. Using table-top laser systems, laser-induced electron diffraction (LIED) has, for example, proven its capability determining internuclear distances with high accuracy for small molecules.16–18 In general, photoelectron diffraction by molecules in the gas phase has been successfully applied for determining molecular constituents,19 mapping bond lengths20,21 and simple chemical reactions22 on ultrafast timescales.17 Until now, however, corresponding studies were restricted to linear17,19,22 or mostly symmetric molecules23–25 such as, e.g., CO, CO2, H2O, or CH4.
Apart from measuring the electron-diffraction pattern (in terms of an electron angular emission distribution), the key to electron diffraction experiments on molecules is the knowledge of each individual molecule's orientation in space.26 A possible approach is to adsorb the molecule to a surface13 or (as indicated above) to utilize weak laser pulses in various schemes (and in 2D or 3D arrangements) to orient27,28 or align15,27–31 the molecule. Single-cycle pulses in the THz were also used in the past to orient/align molecules.32 An alternative approach for detecting the molecule's spatial orientation is Coulomb explosion imaging,33 which, in addition, provides structural information, as well. Here, molecular ions or molecules are rapidly charged up by foil-induced electron stripping,33 multiple ionization by a short and strong laser pulse, or by photoionization and subsequent Auger decay (cascades).34 After the charge-up, the ionic fragments are driven apart rapidly by Coulomb repulsion. Intriguingly, if more than three molecular fragments are generated in the Coulomb explosion, the triple product of three of their momentum vectors allows for identifying whether a chiral molecule was right- or left-handed.35 However, despite the absolute configuration of chiral molecules can be determined in principle using this method,35,36 it has been restricted, so far, to small molecules with only a few atoms. So far, the largest molecule investigated using this approach was halothane consisting of eight atoms,37 but just recently iodopyridine (11 atoms) has been addressed in an experiment.38 Seribal et al. have shown in a simulation that Coulomb explosion imaging in combination with a spatial orientation of the gas-phase target substance allows for retrieving the molecules’ handedness even for systems as large as camphor.39 In detail, however, gathering structural information of larger molecules with the help of Coulomb explosion techniques faces yet multiple technical challenges. These are, for example, the initial generation of high charge states, the rapidly declining detection efficiency for the coincident detection of multiple molecular fragments,40 and uncertainties in their correct m/q assignment. In addition, the inversion of the measured momentum-space information to position-space is far from trivial as soon as the charge-up of the molecule and/or its fragmentation is governed by nuclear dynamics. Already when examining small molecules as H2O, support from sophisticated theory is required for the interpretation of Coulomb explosion data, which in turn provides valuable details on the fragmentation dynamics and processes.41
In this article, we demonstrate in a proof-of-principle study how to overcome these obstacles. With a combination of the concepts of Coulomb explosion imaging, photoelectron diffraction imaging and support from ab initio modelling, we developed a method for addressing isolated molecules in the gas phase to determine their structure and their handedness. Our scheme is applicable without the need for advanced laser-alignment schemes or elaborate abilities for detecting a multitude of ionic fragments in coincidence. We will show, furthermore, that our approach allows to determine even tiny details, as, for example, a slight displacement of a hydrogen atom in a methyloxirane molecule.
Experimental method
In our study, we target methyloxirane molecule and examine its ionic fragments (occurring after photoionization and subsequent Auger decay) and the angular distributions of the emitted photoelectrons. The measurements were performed employing Cold Target Recoil Ion Momentum Spectroscopy (COLTRIMS), which is a multi-coincidence momentum-imaging technique.42,43 In brief, ions and electrons created in the interaction of single photons from the SOLEIL synchrotron with single methyloxirane molecules were guided by electric and magnetic fields onto two time- and position-sensitive microchannel-plate detectors. From the particles’ positions of impact and times-of-flight the individual trajectories inside the COLTRIMS spectrometer were reconstructed in an offline analysis of the data. This information yielded the particles’ momenta and accordingly all derived observables as emission directions and kinetic energies. As a coincidence measurement has been performed, relative quantities are retrieved, as well, as, for example, relative emission angles. The experimental data were recorded at the same beamtime as the data from a previous publication. Accordingly, the identical experimental setup was used and further details on the exact parameters of the COLTRIMS reaction microscope can be found there.44 The employed photon energy of 550 eV addressed the O 1s shell of the methyloxirane molecule leading to a photoelectron energy of about 11.5 eV, and we restricted our analysis to electrons with kinetic energy of 11.5 ± 1.5 eV in order to suppress possible background. Furthermore, we employed the aforementioned photon energy as photoelectrons of this specific kinetic energy showed a large chiral response and this electron energy is amenable for accurate calculations.44 The measurements were performed using circularly polarized light with left and right helicity. In order to cross-check the data and the analysis, the results from both helicities were compared, taking into account the corresponding symmetries. The data shown below contain both helicities added. Several fragmentation pathways occur after the oxygen–K-shell ionization of the molecule and subsequent Auger decay(s). As detailed below, we employ for our study cases where the molecule fragmented into at least three parts of which two were charged. In order to increase statistics, the data presented in this study consists of a combination of the fragmentation channels C3H6O → C2H3+ + CH2+ + OH0 + 2e− and C3H6O → C2H2+ + CH2+ + H2O0 + 2e−. About 3 × 106 events were recorded for both enantiomers of the molecule and both light helicities. Two other breakup channels, namely C3H6O → C2H3+ + CH3+ + O0 + 2e− and C3H6O → C2H2+ + CH3+ + OH0 + 2e−, cannot be used because of the following reasons: It turns out that for the latter fragmentation channels the CH3+ group stems from the methyl group of methyloxirane. This different fragmentation dynamics manifests itself in the fact that the measured momenta of the ions define a completely different molecular coordinate system. In addition, the interference patterns for these fragmentation channels are washed out. We suspect that this is due to a weaker correlation between the measured ionic momenta and the molecular orientation at the instant of ionization due to complex fragmentation dynamics.Theoretical method
In order to extract information on the molecular geometry from the experimental data, we performed a modelling of the electron diffraction pattern, i.e., of the molecular-frame angular emission distributions of the photoelectrons. The ionization transition amplitudes for the emission of O 1s photoelectrons of the methyloxirane enantiomers were computed by using the single-center method and code45,46 in the relaxed-core Hartree–Fock approximation, as described in our previous work on this molecule44 (please see the ESI document of this reference for more details, as well).The averaging of the molecular-frame photoelectron angular emission distributions over all incident directions of the ionizing light, required for the present study, was performed analytically. The average differential cross section reads:
Here, θ and φ are the photoelectron emission angles in the frame of molecular reference, YLM are spherical harmonics, and Aε![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) mk are the dipole transition amplitudes for the emission of the partial photoelectron waves with the angular-momentum quantum numbers
mk are the dipole transition amplitudes for the emission of the partial photoelectron waves with the angular-momentum quantum numbers ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and m via the absorption of a photon of polarization k, as defined in the frame of the molecule. Because of the mutual orthogonality of the Wigner rotational matrices (which transform the ionizing light of a given polarization from the laboratory to the molecular frame), the average molecular-frame photoelectron angular distribution is independent of the polarization of the ionizing light that is used in the experiment.
and m via the absorption of a photon of polarization k, as defined in the frame of the molecule. Because of the mutual orthogonality of the Wigner rotational matrices (which transform the ionizing light of a given polarization from the laboratory to the molecular frame), the average molecular-frame photoelectron angular distribution is independent of the polarization of the ionizing light that is used in the experiment.
Results and discussion
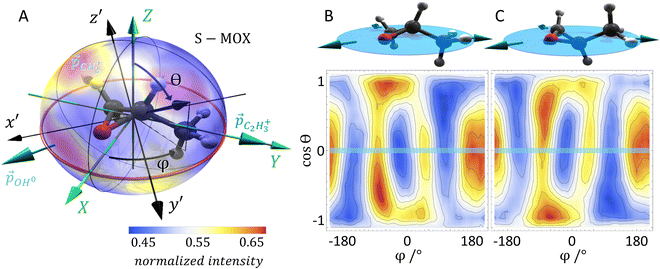
As mentioned above, we use synchrotron light to ionize the molecule by emission of a core electron. The emerging photoelectron is diffracted by the molecular potential and serves as a messenger providing the molecular structure information in its angular emission pattern. Molecules are in most cases unstable after the emission of a core electron. Typically, at least one more additional electron is released in an Auger decay process and, subsequently, the molecule fragments into charged and neutral pieces. It turns out that the detection of the fragmentation direction (i.e., the momentum vectors) of two charged fragments of a breakup of the molecule into at least three pieces is sufficient to gather the information on the spatial orientation of the molecule, which is needed for evaluating the photoelectron interference pattern. Dictated by conservation of linear momentum, the momentum vectors of three molecular fragments lie within a plane (turquoise arrows in Fig. 1A). They can be employed to form a fragment coordinate frame (X, Y, Z) in Fig. 1A, which was built as follows:![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) C3H3+ (
C3H3+ (![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) C2H2+, respectively) points in the direction of the Y axis,
C2H2+, respectively) points in the direction of the Y axis, ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) C2H3+ ×
C2H3+ × ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) CH2+ (
CH2+ (![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) C2H2+ ×
C2H2+ × ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) CH2+) in the direction of the Z axis, and
CH2+) in the direction of the Z axis, and ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) =
= ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) ×
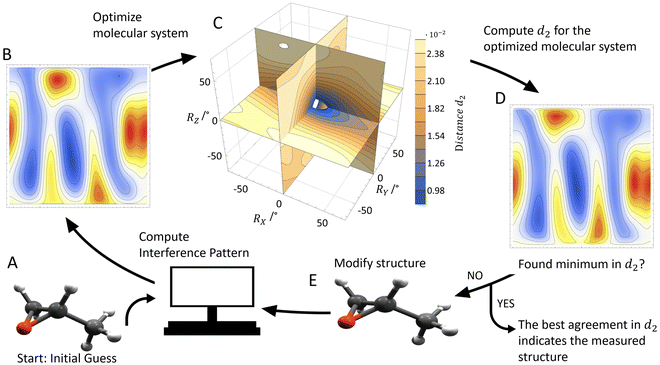
× ![[Z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_005a_20d1.gif) . The actual spatial orientation of the molecule within this fragment coordinate frame at the instant of photoionization remains, however, unknown. In larger systems, the fragments’ emission directions are typically only loosely connected to the direction of the molecular bonds prior to the fragmentation, in particular if only few fragments are generated. Thus, the fragment frame (X, Y, Z) deduced from the ion-direction measurement and a desired molecular coordinate frame (x′, y′, z′) linked to its structure are typically skewed by some unknown angles (RX, RY, and RZ, i.e., the rotation angles with respect to the X, Y, and Z axes). In addition, the measured ion momentum vectors alone do not provide any information on the handedness of the ionized molecule, as they define a plane and thus leave the sign of the Z axis open, as depicted in Fig. 1B and C. Both, this information and the information on the skew-angles are, however, encoded in the electron diffraction pattern.
. The actual spatial orientation of the molecule within this fragment coordinate frame at the instant of photoionization remains, however, unknown. In larger systems, the fragments’ emission directions are typically only loosely connected to the direction of the molecular bonds prior to the fragmentation, in particular if only few fragments are generated. Thus, the fragment frame (X, Y, Z) deduced from the ion-direction measurement and a desired molecular coordinate frame (x′, y′, z′) linked to its structure are typically skewed by some unknown angles (RX, RY, and RZ, i.e., the rotation angles with respect to the X, Y, and Z axes). In addition, the measured ion momentum vectors alone do not provide any information on the handedness of the ionized molecule, as they define a plane and thus leave the sign of the Z axis open, as depicted in Fig. 1B and C. Both, this information and the information on the skew-angles are, however, encoded in the electron diffraction pattern.
To extract the structural information from the experimental data, we use the procedure that is outlined in Fig. 2. We start with an initial guess for the molecular structure and compute the photoelectron interference pattern in a guessed molecular frame (x′, y′, z′), which is assumed to coincide with the fragment frame. Then, we compare this pattern to the pattern obtained in our experiment, which is provided in the fragment frame (X, Y, Z). To quantify the agreement, we introduce the distance parameter d2 between the renormalized experimental and computed interference patterns. This parameter depends, as well, on the relative rotation between (x′, y′, z′) and (X, Y, Z) quantified by the rotation angles RX, RY, and RZ and the guess of the handedness.
We now determine the skew between the coordinate frames (x′, y′, z′) and (X, Y, Z) varying the three rotation angles in order to obtain the smallest distance parameter d2 (Fig. 2C). The minimized value of d2 (i.e., after applying the rotation) is then used to quantify the overall agreement between the measured and the computed interference pattern for the initially hypothesized molecular structure and handedness. This procedure is then repeated with a slightly adjusted molecular structure in terms of bond length or angles as an input in order to further minimize d2. The model structure, which provides the smallest distance parameter d2, is assumed to be responsible for the measured interference patterns, thus providing the molecular structure and coordinate system at the instant of ionization.
In more detail, in order to actually calculate the distance parameter d2, we apply the following procedure: The minimum value occurring in the interference pattern is first subtracted from the pattern and then the pattern's integral is normalized to one. In this way, one compares two stretched two-dimensional distributions. For each calculated molecular structure, the molecular system in coordinate space used in the calculation must be connected to the measured fragment momentum vectors. To do this, we rotate the measured and calculated interference pattern with respect to each other, applying the X–Y–Z convention (roll, pitch, and yaw angle: RX, RY, and RZ). We determine the transformation that connects the fragment system defined by the measured ionic momenta and a molecular system used in the computation by performing a full scan of the global minimum of d2 in the whole three-dimensional rotational space of the yaw, pitch, and roll angles (see Fig. 2C). We scan all angles in steps of one degree. This step size is small enough to ensure that the residual error in the molecular frame does not influence the result presented in the following.
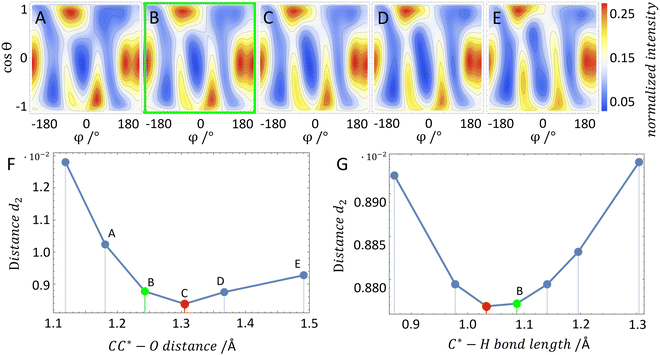
In order to test our approach, we employ the two enantiomers of methyloxirane as benchmark systems. As outlined in the Experimental method section, we are using a photoelectron of 11.5 eV kinetic energy emitted from the oxygen K-shell for the diffraction imaging and a naturally occurring subsequent Auger decay for the generation of two ionic and one neutral fragments. As shown in Fig. 1B and C, the observed interference pattern is vastly different for the two enantiomers making chiral discrimination straightforward. A comparison to the modelled pattern shown in Fig. 2D provides the information on the absolute configuration. As the geometry of methyloxirane is well known in the literature,47 we employ the algorithm described above (and illustrate the high sensitivity of our approach) in order to extract the exact location of distinct atoms inside the molecule. A corresponding table of the atomic coordinates at its equilibrium can be found in the ESI of ref. 44. As a first example, we show in Fig. 3A–F the effect of a modification of the CC*–O distance (i.e., the distance of the oxygen atom to the CC* bond) in the oxirane ring around the equilibrium structure. The resulting variation of d2 is shown in Fig. 3F and implies that we are sensitive to a change of 5% of the geometry-optimized CC*–O distance. For comparison, a similar relative accuracy of a few percent for a bond-length measurement has been demonstrated recently employing LIED examining OCS molecules.48 Particularly challenging for other methods of structure determination is the assignment of the location of hydrogen atoms. Electron scattering is known to be sensitive also to such weak scatterers. Accordingly, in a second demonstration, we investigate the sensitivity of our approach to a change of the C*–H bond length. The corresponding results are depicted in Fig. 3G, which confirms that within 5% discrepancy, the correct bond length between the chiral carbon atom and the adjacent proton attached to it has been found via the smallest value of d2.
The experimental statistical error is smaller than the plotted dot size; however, different sources of systematic errors might alter the exact value of d2. The quality of the reconstruction as well as the achievable resolution depends on multiple factors, which cannot be easily quantified. For example, the recorded interference pattern has a finite experimental resolution. It is, however, not easy to estimate how resolving fine details of the interference pattern affects the reconstruction of geometrical features in the end. First estimates on the presented data suggest that the experimental resolution is not limiting the accuracy of the geometrical reconstruction. Furthermore, background from other fragmentation channels or a complex interplay between areas of reduced detection efficiency on the electron and ion detectors might affect the geometry reconstruction, as well. Yet, we expect that the statistics of the recorded datasets has a stronger impact on the reconstruction quality in our present study. An additional source of errors is connected to the approximation that is made in the ab initio computations. Each molecular configuration was calculated only for fixed internuclear distances (i.e., a single fixed molecular geometry) and only for a single photoelectron energy. In the experiment, however, the signal is averaged over a certain distribution of photoelectron energies and real-life molecules exhibit vibrational motion. In the case of a non-linear relationship between the influencing parameters and the observed variable, the mean value of the observed variable generally does not correspond to the mean value of the influencing factors. Therefore, an estimate of our resolution when determining the three-dimensional position of the atoms is provided by considering how close the minimum in d2 comes to the result of the geometry-optimized structure when scanning across different molecular structures. Thus, the resolution is estimated to be of similar magnitude as our chosen step size of ∼6 × 10−12 m. Please note that with our technique the spatial resolution is not limited by the photoelectron's wavelength of 3.6 Å.
Conclusion
Combining partial Coulomb explosion imaging of a large molecule with the measurement of the photoelectron diffraction pattern in the molecular frame and quantum chemical computation allows for precise structural analysis and chiral discrimination of molecules in the gas phase. Unlike established X-ray or several of the electron diffraction techniques, our approach does not require a molecular crystal. Contrary to traditional Coulomb explosion imaging, it is scalable, so that larger molecules can be examined, as well. The only requirement is that the molecule breaks sufficiently fast into at least three fragments (of which at least two are charged), so that the measured ion momentum vectors are linked to the molecular orientation at the time of ionization. In addition, by adjusting the photon energy, distinct atoms of the molecule can be addressed and the emission source of the probing electron wave inside the molecule can be selected. By applying pump–probe schemes, the method will allow for tracking changes in the molecular structure on a femtosecond time scale49,50 in the future. The described approach is in principle general and can be extended to larger molecules. If necessary, required calculations can rely on density functional theory (DFT) based methods, which are usually not limited by molecular size, like, e.g. the TDDFT B-spline LCAO formalism.51Data availability
All data needed to evaluate the conclusions in the paper are present in the paper. Additional data related to this paper may be requested from the authors. Correspondence and requests for materials should be addressed to K. F. (fehre@atom.uni-frankfurt.de), P. V. D. (demekhin@physik.uni-kassel.de), or M. S. S. (schoeffler@atom.uni-frankfurt.de).Author contributions
The experiment was conceived by M. S. S. and R. D. The experiment was prepared and carried out by S. G., G. K., S. E., F. T., J. R., A. H., D. T., C. J., M. P., S. Z., F. W., M. W., M. K., M. H, L. Ph. H. S., A. K., A. H., L. B. L., A. E., R. B., H. F., K. U., T. J., J. B. W., and M. S. S. Data analysis was performed by K. F. and M. S. S. Theoretical calculations were performed by P. V. D. and N. M. N. All authors discussed the results and commented on the manuscript. K. F., P. V. D., R. D., T. J., and M. S. S. wrote the paper.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
We acknowledge synchrotron SOLEIL (Saint-Aubin, France) for the provision of experimental facilities. The experiment was carried out at the beamline SEXTANTS. We thank D. Reich for discussion. We thank A. Czasch und O. Jagutzki from Roentdek GmbH for support with the detectors. We thank the staff of SOLEIL for running the facility and providing beamtimes under projects 20140056 and 20141178 and especially SEXTANTS beamline for their excellent support. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) – Project No. 328961117 – SFB 1319 ELCH (Extreme light for sensing and driving molecular chirality). K. F. and A. H. acknowledge support by the German National Merit Foundation. M. S. S. thanks the Adolf-Messer Foundation for financial support. H. F. and K. U. acknowledge the XFEL Priority Strategy Program of MEXT, the Research Program of “Dynamic Alliance for Open Innovations Bridging Human, Environment and Materials”, and the IMRAM project for support.References
- X. Zou and S. Hovmöller, Electron crystallography: imaging and single-crystal diffraction from powders, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 149–160 CrossRef CAS PubMed.
- D. P. Woodruff, Photoelectron diffraction: from phenomenological demonstration to practical tool, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 439–445 CrossRef CAS.
- T. Kunde and B. M. Schmidt, Microcrystal Electron Diffraction (MicroED) for Small-Molecule Structure Determination, Angew. Chem., Int. Ed., 2019, 58, 666–668 CrossRef CAS PubMed.
- J. M. Zuo, I. Vartanyants, M. Gao, R. Zhang and L. A. Nagahara, Atomic Resolution Imaging of a Carbon Nanotube from Diffraction Intensities, Science, 2003, 300, 1419–1421 CrossRef CAS PubMed.
- L. Palatinus, P. Brázda, P. Boullay, O. Perez, M. Klementová, S. Petit, V. Eigner, M. Zaarour and S. Mintova, Hydrogen positions in single nanocrystals revealed by electron diffraction, Science, 2017, 355, 166–169 CrossRef CAS PubMed.
- K. Hedberg, L. Hedberg, D. S. Bethune, C. A. Brown, H. C. Dorn, R. D. Johnson and M. de Vries, Bond Lengths in Free Molecules of Buckminsterfullerene, C60, from Gas-Phase Electron Diffraction, Science, 1991, 254, 410–412 CrossRef CAS PubMed.
- A. A. Fokin, et al., Intramolecular London Dispersion Interaction Effects on Gas-Phase and Solid-State Structures of Diamondoid Dimers, J. Am. Chem. Soc., 2017, 139, 16696–16707 CrossRef CAS PubMed.
- M. Centurion, Ultrafast imaging of isolated molecules with electron diffraction, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 062002 CrossRef.
- H. N. Chapman, et al., Femtosecond X-ray protein nanocrystallography, Nature, 2011, 470, 73–77 CrossRef CAS PubMed.
- Y. Inokuma, S. Yoshioka, J. Ariyoshi, T. Arai, Y. Hitora, K. Takada, S. Matsunaga, K. Rissanen and M. Fujita, X-ray analysis on the nanogram to microgram scale using porous complexes, Nature, 2013, 495, 461–466 CrossRef CAS PubMed.
- S. Lee, E. A. Kapustin and O. M. Yaghi, Coordinative alignment of molecules in chiral metal-organic frameworks, Science, 2016, 353, 808–811 CrossRef CAS PubMed.
- T. Gruene, et al., Rapid Structure Determination of Microcrystalline Molecular Compounds Using Electron Diffraction, Angew. Chem., Int. Ed., 2018, 57, 16313–16317 CrossRef CAS PubMed.
- C. J. Hensley, J. Yang and M. Centurion, Imaging of Isolated Molecules with Ultrafast Electron Pulses, Phys. Rev. Lett., 2012, 109, 133202 CrossRef PubMed.
- J. Yang, et al., Diffractive imaging of a rotational wavepacket in nitrogen molecules with femtosecond megaelectronvolt electron pulses, Nat. Commun., 2016, 7, 11232 CrossRef CAS PubMed.
- T. Kierspel, et al., X-ray diffractive imaging of controlled gas-phase molecules: Toward imaging of dynamics in the molecular frame, J. Chem. Phys., 2020, 152, 084307 CrossRef CAS PubMed.
- C. I. Blaga, et al., Imaging ultrafast molecular dynamics with laser-induced electron diffraction, Nature, 2012, 483, 194–197 CrossRef CAS PubMed.
- B. Wolter, et al., Ultrafast electron diffraction imaging of bond breaking in di-ionized acetylene, Science, 2016, 354, 308–312 CrossRef CAS PubMed.
- A. Sanchez, et al., Molecular structure retrieval directly from laboratory-frame photoelectron spectra in laser-induced electron diffraction, Nat. Commun., 2021, 12, 1520 CrossRef CAS PubMed.
- A. Landers, et al., Photoelectron Diffraction Mapping: Molecules Illuminated from Within, Phys. Rev. Lett., 2001, 87, 013002 CrossRef CAS PubMed.
- H. Fukuzawa, et al., Probing molecular bond-length using molecular-frame photoelectron angular distributions, J. Chem. Phys., 2019, 150, 174306 CrossRef PubMed.
- M. Meckel, et al., Laser-Induced Electron Tunneling and Diffraction, Science, 2008, 320, 1478–1482 CrossRef CAS PubMed.
- P. Hockett, C. Z. Bisgaard, O. J. Clarkin and A. Stolow, Time-resolved imaging of purely valence-electron dynamics during a chemical reaction, Nat. Phys., 2011, 7, 612–615 Search PubMed.
- R. Boll, et al., Femtosecond photoelectron diffraction on laser-aligned molecules: Towards time-resolved imaging of molecular structure, Phys. Rev. A, 2013, 88, 061402(R) CrossRef.
- J. B. Williams, et al., Imaging Polyatomic Molecules in Three Dimensions Using Molecular Frame Photoelectron Angular Distributions, Phys. Rev. Lett., 2012, 108, 233002 CrossRef CAS PubMed.
- M. Yamazaki, J.-i Adachi, T. Teramoto, A. Yagishita, M. Stener and P. Decleva, 3D mapping of photoemission from a single oriented H2O molecule, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 051001 CrossRef.
- R. Fasel, J. Wider, C. Quitmann, K.-H. Ernst and T. Greber, Determination of the Absolute Chirality of Adsorbed Molecules, Angew. Chem., Int. Ed., 2004, 43, 2853–2856 CrossRef CAS PubMed.
- I. Nevo, L. Holmegaard, J. H. Nielsen, J. L. Hansen, H. Stapelfeldt, F. Filsinger, G. Meijer and J. Küpper, Laser-induced 3D alignment and orientation of quantum state-selected molecules, Phys. Chem. Chem. Phys., 2009, 11, 9912–9918 RSC.
- K. Amini, et al., Alignment, orientation, and Coulomb explosion of difluoroiodobenzene studied with the pixel imaging mass spectrometry (PImMS) camera, J. Chem. Phys., 2017, 147, 013933 CrossRef PubMed.
- J. J. Larsen, K. Hald, N. Bjerre, H. Stapelfeldt and T. Seideman, Three Dimensional Alignment of Molecules Using Elliptically Polarized Laser Fields, Phys. Rev. Lett., 2000, 85, 2470 CrossRef CAS PubMed.
- J. Küpper, et al., X-Ray Diffraction from Isolated and Strongly Aligned Gas-Phase Molecules with a Free-Electron Laser, Phys. Rev. Lett., 2014, 112, 083002 CrossRef.
- D. Rolles, et al., Femtosecond x-ray photoelectron diffraction on gas-phase dibromobenzene molecules, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124035 CrossRef.
- S. Fleischer, Y. Zhou, R. W. Field and K. A. Nelson, Molecular Orientation and Alignment by Intense Single-Cycle THz Pulses, Phys. Rev. Lett., 2011, 107, 163603 CrossRef PubMed.
- Z. Vager, R. Naaman and E. P. Kanter, Coulomb Explosion Imaging of Small Molecules, Science, 1989, 244, 426–431 CrossRef CAS PubMed.
- Z. Bao, R. F. Fink, O. Travnikova, D. Céolin, S. Svensson and M. N. Piancastelli, Detailed theoretical and experimental description of normal Auger decay in O2, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 125101 CrossRef.
- M. Pitzer, et al., Direct Determination of Absolute Molecular Stereochemistry in Gas Phase by Coulomb Explosion Imaging, Science, 2013, 341, 1096–1100 CrossRef CAS PubMed.
- K. Fehre, et al., Enantioselective fragmentation of an achiral molecule in a strong laser field, Sci. Adv., 2019, 5, eaau7923 CrossRef CAS PubMed.
- M. Pitzer, et al., Stereochemical configuration and selective excitation of the chiral molecule halothane, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 234001 CrossRef.
- R. Boll, et al., X-ray multiphoton-induced Coulomb explosion images complex single molecules, Nat. Phys., 2022, 18, 423–428 Search PubMed.
- C. Saribal, A. Owens, A. Yachmenev and J. Küpper, Detecting handedness of spatially oriented molecules by Coulomb explosion imaging, J. Chem. Phys., 2021, 154, 071101 CrossRef CAS PubMed.
- K. Fehre, et al., Absolute ion detection efficiencies of microchannel plates and funnel microchannel plates for multi-coincidence detection, Rev. Sci. Instrum., 2018, 89, 045112 CrossRef CAS PubMed.
- T. Jahnke, et al., Inner-Shell-Ionization-Induced Femtosecond Structural Dynamics of Water Molecules Imaged at an X-Ray Free-Electron Laser, Phys. Rev. X, 2021, 11, 041044 CAS.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. Ph. H. Schmidt and H. Schmidt-Böcking, Recoil-ion and electron momentum spectroscopy: reaction-microscopes, Rep. Prog. Phys., 2003, 66, 1463 CrossRef CAS.
- T. Jahnke, Th. Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. Ph. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, Multicoincidence studies of photo and Auger electrons from fixed-in-space molecules using the COLTRIMS technique, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS.
- M. Tia, et al., Observation of Enhanced Chiral Asymmetries in the Inner-Shell Photoionization of Uniaxially Oriented Methyloxirane Enantiomers, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- Ph. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, Single center method: A computational tool for ionization and electronic excitation studies of molecules, J. Chem. Phys., 2011, 134, 024113 CrossRef PubMed.
- S. A. Galitskiy, A. N. Artemyev, K. Jänkälä, B. M. Lagutin and Ph. V. Demekhin, Hartree-Fock calculation of the differential photoionization cross sections of small Li clusters, J. Chem. Phys., 2015, 142, 034306 CrossRef CAS PubMed.
- M. C. Tam, N. J. Russ and T. D. Crawford, Coupled cluster calculations of optical rotatory dispersion of (S)-methyloxirane, J. Chem. Phys., 2004, 121, 3550 CrossRef CAS PubMed.
- E. T. Karamatskos, G. Goldsztejn, S. Raabe, Ph. Stammer, T. Mullins, A. Trabattoni, R. R. Johansen, H. Stapelfeld, S. Trippel, M. J. J. Vrakking, J. Küpper and A. Rouzée, Atomic-resolution imaging of carbonyl sulfide by laser-induced electron diffraction, J. Chem. Phys., 2019, 150, 244301 CrossRef PubMed.
- G. Kastirke, et al., Photoelectron Diffraction Imaging of a Molecular Breakup Using an X-Ray Free-Electron Laser, Phys. Rev. X, 2020, 10, 021052 CAS.
- J. Yang, et al., Simultaneous observation of nuclear and electronic dynamics by ultrafast electron diffraction, Science, 2020, 368, 885–889 CrossRef CAS PubMed.
- M. Stener, G. Fronzoni and P. Decleva, Time-dependent density-functional theory for molecular photoionization with noniterative algorithm and multicenter B-spline basis set: CS2 and C6H6 case studies, J. Chem. Phys., 2005, 122, 234301 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |

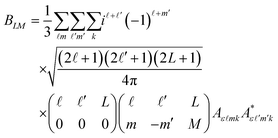
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)