Photoelectron–photoion(s) coincidence studies of molecules of biological interest
P.
Bolognesi
 and
L.
Avaldi
and
L.
Avaldi
 *
*
CNR-Istituto di Struttura della Materia, Area della Ricerca di Roma 1, CP 10 00015 Monterotondo Scalo, Italy. E-mail: Lorenzo.avaldi@ism.cnr.it
First published on 9th September 2022
Abstract
Photoelectron–photoion(s) coincidence, PEPICO, experiments with synchrotron radiation have become one of the most powerful tools to investigate dissociative photoionization thanks to their selectivity. In this paper their application to the study of molecular species of biological interest in the gas phase is reviewed. Some applications of PEPICO to the study of potential radiosensitizers, amino acids and small peptides and opportunities offered by the advent of novel methods for the production of beams of these molecules are discussed.
1. Introduction
The interaction of VUV and/or soft X-ray radiation with a molecule in the gas phase results in a single or multiple ionization event. The experiments to characterize this event therefore must involve the detection of electrons and ions. Photoelectron spectra at fixed incident wavelength yields information on the binding energies of the different valence and core orbitals and within the frame of the Franck–Condon approximation allow to unveil changes in the molecular structure occurring in the ionization event. The measurement of the mass-selected ion yields as a function of the photon energy provide information on the onset of the ionization and fragmentation channels. The two methods have been applied to a large class of molecules, free radicals, clusters and nanoaggregates and strongly benefitted of the advent of sources tunable over a broad energy range like the synchrotron radiation sources. Already in 1967 Brehm and Von Puttkamer1 realized that combining photoelectron spectroscopy with mass analysis in a photoelectron–photoion coincidence, PEPICO, experiment provides information which goes beyond the simple combination of the photoelectron and mass spectra, but via the time-correlation between the two particles allows to explore in detail the dissociation dynamics. As shown by the broad existing literature2–4 PEPICO experiments give the possibility to determine the branching ratios to various decay channels, the absolute rate decay and the energy partitioning among the products. These experiments have given an invaluable contribution to present understanding of unimolecular dissociation reactions.5 The field then benefitted by the development of techniques for the detection of threshold electrons,6,7i.e. electrons with a kinetic energy of a few meV. These techniques are characterized by a high efficiency thanks to the almost 4π detection and a high energy resolution. PEPICO and threshold PEPICO, TPEPICO,8 experiments probe different ionization mechanisms. While PEPICO experiments performed at fixed photon energy rely on direct ionization, apart from accidental resonant excitation of the target at the chosen photon energy, in the TPEPICO experiments, which involve a photon energy scan, the “threshold” electrons are often produced by autoionization processes of neutral excited states of the target, which in some cases cannot be accessed by direct ionization. As the photon energy increases above the double or multiple ionization thresholds two or more ions can be produced in the ionization process. This “multi-ion” production is enhanced in the region of inner shell ionizations, where the Auger decay of the core ionized species populates dication states. Dications are reactive species, usually formed with a certain internal energy, which easily fragment in two cations. In the final state of a double ionization event therefore there are four charged particles (two electrons and two ions), and this number increases when even more highly charged states are formed. A plethora of coincidence schemes which involve the simultaneous detections of few charged particles or charged particles and photons have been envisaged to study multiionized molecules.9,10 J. H. Eland, to whom this festschrift is dedicated, gave an unvaluable contribution to the field of multicoicidence experiments9,11 and their applications in chemical physics.The understanding of the physics and chemistry of isolated molecules of biological interest is fundamental not only for biology, where the damage of ionizing radiation strongly depends on the structural and chemical properties of the biomolecular constituents of life matter and can be related to processes initiated at the atomic and molecular level, but also in biotechnological applications, such as biosensors and molecular electronics. In astrochemistry and astrobiology, key information on the origin of life is provided by the understanding of the chemistry of relatively simple molecules in an environment resembling primordial conditions, either on Earth or extraterrestrial objects. In this multidisciplinary field, molecular physics can provide a valuable contribution both experimentally and theoretically. Photoelectron and ion spectroscopies have been used to investigate spectroscopy and dynamics of amino acids and peptides, nucleobases and their building blocks, pharmaceuticals, antibiotics and their elementary components, radiosensitizers for radiotherapy, sugars and lipids with a view to understanding their electronic properties, and modelling their chemical behavior.12 Here we will present examples of the specific contribution that electron–ion coincidences can and have provided to this field. The PEPICO experiments described in this brief review do not aim to represent a complete survey of the field. Most of them have been carried out by our group and they have been chosen to show some achievements and to point out future opportunities.
The review is organized as follows. A description of the experimental set-up used at Elettra for PEPICO experiments is done in Section 2. Then in Section 3 four different applications are discussed. Ionization via inner shell excitation and direct valence photoionization of halogenated pyrimidines are used to tackle the topic of site selectivity and bond breakage in Section 3.1. The use of PEPICO data from valence photoionization of thymidine and furan to extract information on the energy distribution in collision experiments is illustrated in Section 3.2. Some examples of the large variety of electron–ion coincidence experiments performed on amino acids and peptides, going from energy unselected measurements with Helium I discharge lamp to photoelectron–photoion–photoion studies following core ionization, are reported in Section 3.3. The attempt to go beyond experiments on model systems is discussed in Section 3.4 using as an example the PEPICO studies of nitroimidazole compounds. Finally some conclusions and future perspectives are presented in Section 4.
2. Schematics of a PEPICO set-up
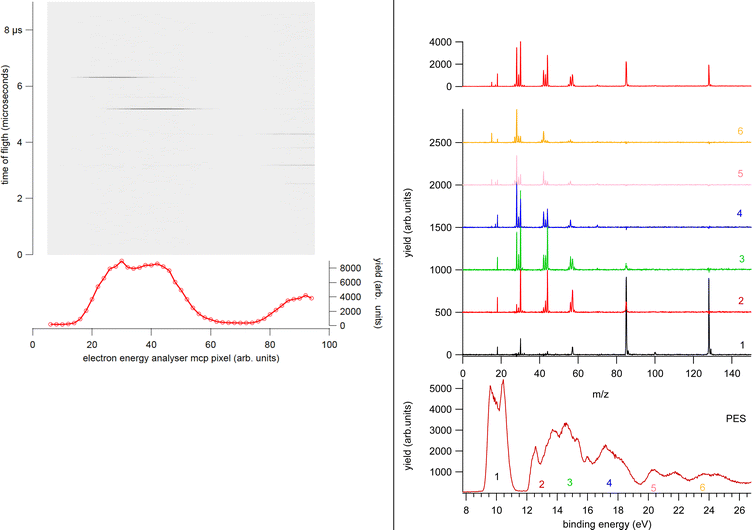
In a PEPICO experiment an energy resolved electron and an ion produced in the photoionization of the target are detected in a time correlated mode. As an example of a PEPICO set-up, we will describe the one in operation at the Gas Phase beamline at Elettra.13The end-station (Fig. 1) is equipped with a 150 mm radius hemispherical electron energy analyser (VG 220i) and a time-of-flight (TOF) ion mass spectrometer. The two spectrometers are mounted opposite to each other at approximately 55° with respect to the direction of the linear polarization of the photon beam, in order to cancel out angular effects in the measurements. They can be operated independently for photoelectron (PE) spectroscopy or photoion mass spectrometry (MS) measurements, or ‘in conjunction’ for PEPICO experiments.
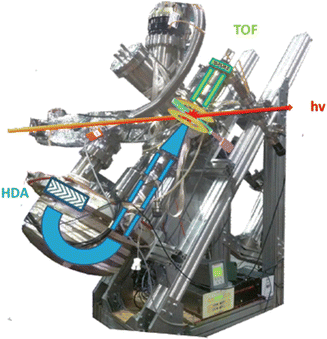 | ||
| Fig. 1 Set-up for electron–ion coincidence at Elettra14 (S. Maclot courtesy). | ||
The electron analyzer hosts a 2D position-sensitive detector (PSD) built by Sincrotrone Trieste15,16 characterized by an acquisition window and an energy resolution of about 10% and 2% of the pass energy, respectively. To detect the ion, the repeller and extractor electrodes of the TOF spectrometer are polarized with antisymmetric voltages (Directed Energy Inc., model PVM4210) to produce a field up to 370 V cm−1. At the time resolution of typical PEPICO experiments, the synchrotron photon beam can be considered as a continuous source, therefore the ion extraction is operated in pulsed mode.
In the experiment the ion extraction is triggered either by the detection of a photoelectron or by a pulse running at a frequency of 100 Hz. The latter is used for the measurement of the ‘false electron–ion coincidence spectrum’, due to ions residing in the interaction zone and uncorrelated with the detected photoelectron. This spectrum has to be subtracted from the measured electron–ion coincidence one. The coincidence measurement is performed at fixed photon energy by scanning the electron kinetic energy (KE) over the range of interest in regular steps guaranteeing a good superposition between adjacent regions. An example of the procedure is shown in Fig. 2. First the PE spectrum is measured using the hemispherical analyzer, then considering the width of the acquisition window of the position-sensitive detector the PE spectrum is divided in a few regions. After selecting a region of binding energies a coincidence mass spectrum is measured. Fig. 2 clearly shows that (i) each energy-selected mass spectrum is characterized by only a few fragments as compared to the total mass spectrum of the molecule; (ii) it strongly depends on the selected region of binding energies and (iii) only a few fragmentation channels at a time are associated with the bands in the selected region of binding energies although lower energy fragmentation channels may be already energetically open. Finally, by a fine binning of the data in each region the branching ratios of the different fragmentation channels as a function of binding energy can be derived. Schematically, the coincidence data acquisition is based on a 8-channels time-to-digital converter (TDC) that records the arrival times of the signals from the four ends of the PSD of the electron detector and the one from the ion detector, as well as the triggering signal for the ion extraction. The system operates with a master clock running at 1 Hz that drives the time scale for all acquired signals and allows to reconstruct the x, y coordinates of the electrons on the PSD, the ions time of flight with respect to the extraction pulse as well as the ‘flag’ identifying the extraction pulse as triggered by either a random pulse or an electron. This mode of operation17 is particularly suitable in the case of continuous or quasi-continous sources, like synchrotron radiation, high count rates and broad TOF range. Indeed, the ion extraction can be triggered by either the detection of an electron or an external pulse. These two signals are combined into an OR logic unit whose output controls the power supplies for the antisymmeric repeller/extraction voltages. The output of this OR unit as well as an analogue signal where an arbitrary time delay has been added to the external trigger signal are recorded into two separate TDC channels, providing respectively the time-zero for the scale of the ions's flight time and a flag to sort ‘true + false’ and ‘false’ coincidence events. In this set-up, due to the high angular and energy selectivity in the hemispherical electron spectrometer, the ion signal is typically two orders of magnitude larger than that of electrons, resulting in a significant unbalance in the number of detected electrons and ions. This often represents the bottleneck for the coincidence experiment, resulting in long acquisition time. A technical development, which can overcome this bottleneck, is represented by the advent of velocity map imaging (VMI),18 which guarantees high collection efficiency and simultaneous detection of particles with different velocity and at all emission angles. Since its introduction VMI has found application in electron–ion(s) and ion–ion coincidence techniques.19,20 While in the first applications with lasers mainly threshold and/or low energy electrons were detected,8 more recent developments have seen VMI coincidence spectrometers used in conjunction with synchrotron radiation.21,22 In such a case, the opportunities opened up by the higher photon energies require the detection of particles with higher kinetic energy, which in turns require modification of the standard VMI design (larger size of the PSD, reduction of the time of flights by biasing the drift tube and the adoption of extra focusing lenses). The ability of VMI to study the angular distribution of the electrons and ions released in the photoionization and the kinetic energy released, adds to the state selectivity of PEPICO experiments further potentialities to disentangle the complex fragmentation following ionization in large molecules where several dissociation paths may compete.
The large majority of the molecules of biological interest is in the form of crystalline powders. Thus the set-up is equipped with a noncommercial, noninductively wound oven where the sample under study is thermally evaporated to produce an effusive beam. The oven is equipped with a chromel/alumel thermocouple. The materials used are aluminum or stainless steel for the crucible, stainless steel for the heated parts of the furnace and heat shield, and machinable glass ceramic for thermal and electrical insulation.23 The set-up is equipped by an inlet system which allows to insert/remove the crucible without breaking the vacuum of the main chamber. This provision speeds up any maintenance operation of the crucible (cleaning, refilling, change of sample under study). The temperature of the crucible can vary in the range from room temperature to about 200 °C. The sublimation temperature of each sample is usually determined via off-line photoionization mass spectrometry with a VUV rare gas discharge lamp. The mass spectra are monitored for long time, using the ratio of the fragment ions as a figure of merit to check for the stable operational conditions or any indication of thermal decomposition in the case of too high temperature. Typically, samples of biomolecules degas water at low temperature as well as sometimes other contaminants, like residual precursors of the molecular synthesis. During the long PEPICO experiments the photoelectron spectrum is monitored before and after each coincidence scan. This allows to identify impurities, such as water, and spurious signals due for example to carbon dioxide, ammonia or other small molecules that provide hints of thermal decomposition of the sample. These small species give rise to sharp peaks, often with vibrational structure, easily recognizable in high resolution PES spectra. Another possible artifact to be monitored is the charging up effect, due to the deposition of the evaporated sample on the meshes delimiting the extraction and acceleration zone of the TOF, which shifts in energy the photoelectron peaks. Plekan et al.23 estimated the local vapor pressure by comparing the photoemission signal of the amino acids they were studying with the signal from nitrogen gas admitted to the chamber by a separate inlet and measuring the nitrogen pressure with an ion gauge. The local pressures were estimated in the range of a few 10−6 mb with a possible error of a factor of 2, mainly attributed to a systematic error because the nitrogen gas is distributed uniformly, whereas the effusive source is inhomogeneous.
3. Application to molecules of biological interest
3.1 Halogenated pyrimidines: site selectivity and bond breakage
The ability to manipulate selective bond cleavage in molecules, via proper ‘‘molecular knife/scissors’’,24 has attracted interest because it offers unique chances to manage the local site physics and chemistry. Inner shell photo-excitation and ionization have been proposed as suitable candidates for selective bond cleavage because core electrons are localized close to the nucleus of one particular atom.25–28 In terms of biological applications and in particular of the radiation damage, selective bond cleavage can be exploited for the damaging/destruction of certain molecules, the selective production of reactive radicals or the splitting of the two moieties of a theranostic agent, for example.As an example of an experiment devoted to investigate the selective bond cleavage in a molecule of biological interest here the PEPICO experiments on 2Br-pyrimidine (C4H3BrN2, 158/160 amu)29 are described. Pyrimidine is the building block of some of the letters of the DNA/RNA alphabet and halopyrimidines are the basic constituents of an important class of radiosensitizers, such as bromo- and iodo-deoxyuridine (UdR) or the 5-fluorouracil (5-FU).30
In the experiment the fragmentation of the 2Br-pyrimidine molecule following inner shell photoexcitation at the C and N 1s and Br 3d thresholds or via direct valence photoionization has been studied by electron–ion coincidence experiments. The inner shell excitations of the Br, C and N atoms in molecules are separated by more than 100 eV. This guarantees a site-selective excitation. A core excited state is unstable, in a few fs undergoes either a fluorescence decay or more likely a non-radiative decay with the emission of a resonant Auger electron. The selection of the incident photon energy to excite a specific atom, i.e. a specific site, in the molecule and the detection of the resonant Auger electron, which marks the final cation state, in coincidence with the formed ions completely define the fragmentation process. The leading fragmentation channels in 2Br-pyrimidine31 (Fig. 3) are the HCN loss (m/z = 131/133), the Br loss (m/z = 79), the BrCN loss (m/z = 53) and then the sequential or concerted loss of the HCN group and the Br atom or of the BrCN group and the H atom (m/z = 52). In the mass spectrum other features at m/z < 40 are observed. The main ones are assigned to C3H2+, HCN+ and CN+ at m/z = 38, 27 and 26, respectively.
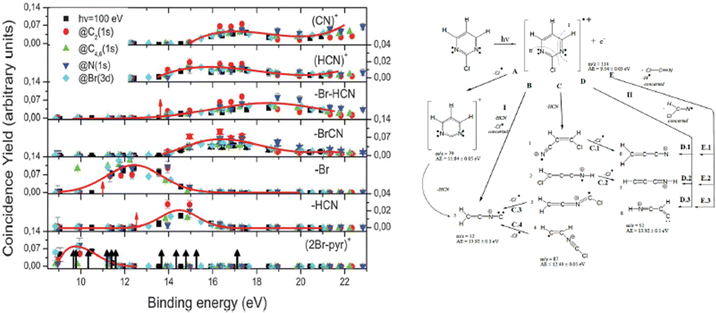 | ||
| Fig. 3 The energy-selected coincidence yield for several 2Br-pyrimidine fragments as a function of the binding energy of the singly charged ion state (left panel). The black arrows in the bottom panel indicate the position of the ion states calculated by O’Keeffe et al.,32 while the red ones indicate the appearance energy of the fragments measured by Castrovilli et al.31 (right panel) The scheme of fragmentation of the 2Br-pyrimidine cation as proposed by Castrovilli et al.31 | ||
The coincidence yields of seven fragments (from m/z = 158/160 down to m/z = 26) produced at photon energies corresponding to the excitation of the C(1s), N(1s) and Br(3d) to the LUMO state as well as from direct photoionization at 100 eV measured as a function of the binding energy of the singly charged final state are shown in Fig. 3, where also the ion states32 of the molecule are indicated. The PEPICO yields show that, independently of the excitation channel, the parent ion is only formed in correspondence with the three lower ion states, while the channel of the loss of the Br atom opens close to 11 eV. The HCN loss channel is mainly active for the states between 13 and 16 eV and appears to be a minor channel. At about 14 eV also the (BrCN + H) loss and the HCN+ channels open up. The PEPICO yields measured in the direct valence photoionization experiment follows the same trend of the ones measured at the different inner shell excitation energies.
The similar behavior of the fragmentation observed in valence photoionization and inner shell excitation, independently of the excited atom, can be explained by the fact that the fragmentation occurs on a timescale longer than the non-radiative relaxation of the inner shell vacancy. Thus, it is the internal energy stored in the singly charged ion and/or the charge distribution of different cation states that control the fragmentation. The site selectivity of the inner shell excitation appears to affect only the yield of the fragments, because depending on the overlap between the neutral inner shell excited state and the final singly charged ion states, the population of the singly charge ion states and in turn the fragmentation channels preferentially associated with those states, vary.
However site-specific fragmentation results to be strongly molecule dependent as shown by the study of the fragmentation following Cl 2p excitation in a similar molecule, the 2Cl-pyrimidine.33 In this molecule the core hole localization on the Cl atom of 2Cl-pyrimidine, occurring by the choice of a photon energy equal to the Cl(2p3/2 → σ*) excitation, triggers an ultrafast molecular dissociation proved by the emission of atomic autoionizing electrons from the decay of the Cl+ 3s23p4 (3P,1D and 1S) states as well as by the production of the Cl+ ions in coincidence with these electrons.
In summary the PEPICO experiments in these molecules, prototype of an important class of radiosensitizers, show that the combination of selective soft X-ray excitation together with a change of the local chemistry can enhance the production of certain fragments. In the radiation damage language this means to target either directly malignant molecules or chemical agents that can release toxic species, like HCN, or extremely reactive radicals like halogen and H atoms that act as secondary source of radiation damage.
3.2 PEPICO and energy distribution in ion collisions
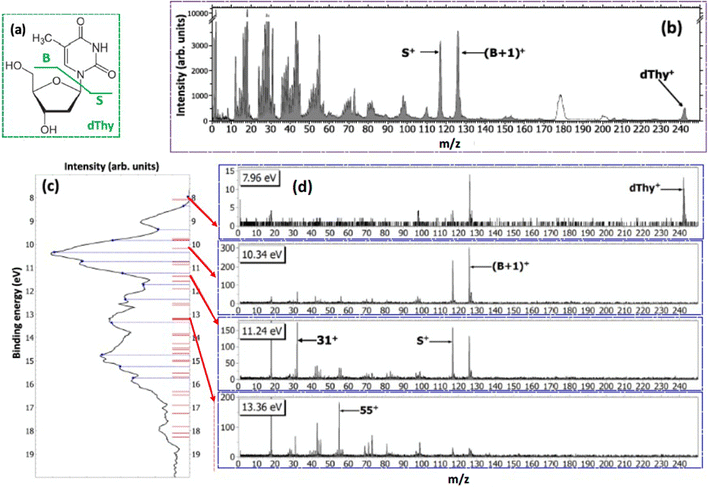
With the development of cancer therapies based on ionizing particles, such as hadrotherapy,34 the understanding of the radiation damage via a multiscale and multidisciplinary approach has become a must.35 At the molecular scale, this relies on the investigation of ionization or fragmentation of molecules of biological interest in different energy ranges.36–39 The excitation energy distribution of complex molecular ions produced in collisions with fast ions is the key parameter in order to evaluate the energy deposition and therefore the damage in the tissues. In ion collision the energy transferred by the ion projectile to the target molecules is expected to be represented by a wide distribution due to interactions at different impact parameters. Some information on the internal energy distribution of the target has been obtained by measuring the energy loss of the scattered particle,40 but the method implies the knowledge of the initial and final state of the incident ion, which is achievable only in specific cases.40Maclot et al.41 proposed a procedure that combines ion collision with state-selected photoionization experiments and quantum chemistry calculations to estimate the excitation energy distribution in ion collision. As target, the thymidine, a nucleoside composed of deoxyribose (a pentose sugar) and the pyrimidinic base thymine, has been used. Fig. 4 shows the mass spectrum of thymidine after the ionization by 48 keV O6+ ions and the state-selected mass spectra measured in the PEPICO experiments at 50 eV photon energy.
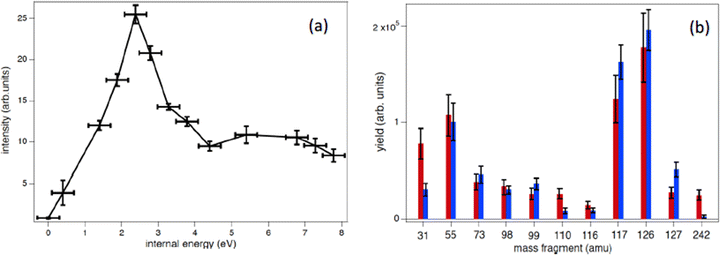
In the procedure a series of PEPICO spectra is measured at different binding energies. These spectra are normalized to the same total area and then their combination is fitted via a constrained linear least-square regression to the ion-induced mass spectrum, considering the most relevant features. In the case of thymidine, the eleven most intense fragments have been considered. The fit parameters are the weighting factors of each PEPICO mass spectrum used in the linear regression. The value of these parameters represents the contribution of each PEPICO mass spectrum, i.e. the contribution of the fragmentation of a bunch of excited states in a specific binding energy of the singly charged ion region, to the ion spectrum.41 The result is displayed in Fig. 5a as a function of the excitation energy defined as the difference between the energy left in the target and the ionization potential. The energy distribution increases smoothly up to a maximum around 2–3 eV and then it decreases towards 8 eV and most likely extends above this energy, as suggested by the presence of a larger amount of small fragments in the ion-induced mass spectrum. Collisions at closer impact parameters can explain the extended tail towards larger deposited energies,42 because penetrating trajectories are associated with large deposit energy of several tens of eV.41 The quality of the fit is shown in Fig. 5b where the comparison between the measured intensity of the selected charged species in the ion spectrum and the one reconstructed by the fit is reported.
The form of the distribution shown in Fig. 5 is qualitatively similar to those obtained by fitting theoretical fragmentation probabilities to experimental measured branching ratios in small carbon clusters43 and fullerenes,44 in which the energy distribution was the fitting parameter. This shows that the present results are also consistent with previous empirical estimations. Notice that, although the set of accessible target states can, in principle, be different in photoionization and collision processes, due to the different conservation rules that can apply in each case, this is not a problem in thymidine because the absence of any symmetry in the molecular target does not restrict the number of accessible states in either process. Moreover, the single-electron capture, which is the dominant process at impact energies considered in this work, is not accompanied by excitation of target and projectile electrons.44 Therefore, one can safely assume that the mass spectra resulting from the collision involves the same target states as the PEPICO spectra.
In a further work the PEPICO fragmentation branching ratios in furan ionized by 60 eV photons have been compared with the ones predicted by a combination of high level quantum chemical calculations and the statistical Microcanonical Metropolis Monte Carlo method (M3C).45 The M3C assumes the excess energy being randomly distributed among all internal degrees of freedom and the fragmentation independent of the excitation process, i.e. the applied excitation and ionization method. The found good agreement between calculated and measured branching ratios45 suggests that the internal energy distribution function is the main parameter which determines the fragmentation pattern. Therefore, from the calculated breakdown curves the internal energy distribution function for the ion–molecule collision induced by Xe25+ and Ar+ ions and electron impact experiments have been determined backwards as the one which generates the best fit to each measured mass spectrum (Fig. 6). The obtained results are consistent with the fact that single electron capture occurs at much larger ion–molecule distances for higher projectile charges, hence leading to a much lower energy transfer, while in Ar+ collisions and electron impact ionization occurs in close or penetrating collisions by either electron capture or direct ionization.
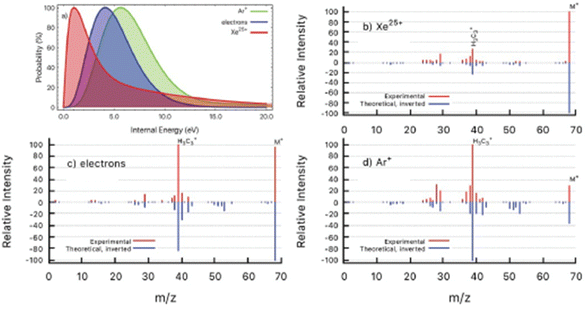 | ||
| Fig. 6 (a) Determined distributions of internal energy in the ion collision and electron impact experiments. (b–d) Experimental mass spectra (red) detected after the interaction of Xe25+ (b), electrons (c) and Ar+ (d) with furan molecule. Inverted peaks (blue) are theoretical mass spectra obtained by convolution of M3C breakdown curves with the corresponding internal energy function from panel (a). Reproduced from ref. 45 with permission from the Royal Society of Chemistry, copyright 2021. | ||
The proposed approach displays promising applications in the modelling of radiation damage and may guide new efforts to unravel the molecular fragmentation of more complex systems like large biomolecules.
3.3 Amino acids and peptides
The twenty amino acids have primary importance in living organisms since they participate in protein synthesis. The knowledge of their structure and reactivity is crucial to understand the role of transient species involved in protein radical catalysis as well as the effects of oxidative damage in proteins, which can be initiated by agents like radicals or ionizing radiation. They also play a role in the search for prebiotic molecules in interstellar media and Altwegg et al.46 recently reported the observation of volatile glycine, the simplest amino acid, in the coma of a comet by the Rosetta Orbiter mass spectrometer for ion and neutral analysis.The first coincidence experiments on amino acids have been performed using a Helium I (21.21 eV) discharge lamp and an energy unselected electron to trigger the mass/charge analysis by a TOF mass spectrometer. Glycine, alanine, proline and valine47 have been studied. In the mass spectra the most intense fragment observed corresponds to the loss of a neutral fragment (COOH) by the parent molecule. The dominance of the COOH loss channel due to the backbone break over the entire outer valence region has been attributed to the most energetically favorable process which involves the removal of one electron from the nitrogen lone pair. As a consequence ionization mainly results in the charge being localized on the nitrogen and on the adjacent α-carbon atom.
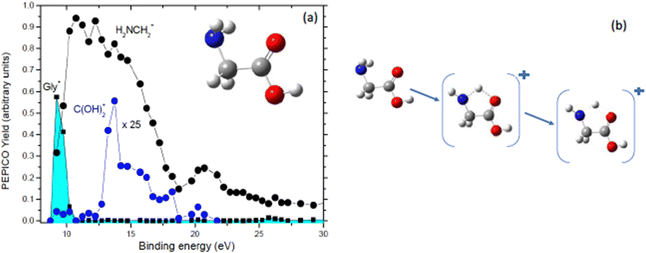
Further PEPICO experiments with synchrotron radiation on glycine48 confirmed the relevance of the COOH loss, but also allowed to unravel traces of minor processes like the isomerization with H transfer and dehydration of the parent ion.47 As an example, Fig. 7 reports the state-selected branching ratios for the formation of the H2NCH2+m/z 30 fragment, which corresponds to the COOH loss channel, and the C(OH)2+m/z 46 one. The observation of this latter fragment clearly indicates that a hydrogen migration from the H2NCH2 moiety to the carboxylic group has occurred. The C(OH)2+ fragment has been observed only in a quite narrow region of BEs. According to C. T. Falzon and F. Wang49 in this binding energy region are located a few cation states (the 3a′′, 14a′, 13a′, and 2a′′ orbitals) significantly affected by the conformational process induced by rotations of the C–C, C–O(H) and C–N bonds. A rotation around the Cα–N bond may change the orientation of the NH2 moiety, turning from the bifurcated configuration, the most stable neutral structure of glycine, to an in-plane one stabilizing the hydrogen bond between the NH2 and the carboxylic oxygen atom. Then a H transfer from the amino group directly to the carboxylic oxygen atom may occur. Theoretical studies on the migration of hole charge during the ionization in glycine50,51 show that on a fs time scale the hole charge migrates from the orbital 14a′, spread over the entire molecule but with its most significant part located on the N-terminal moiety, to the orbital 13a′, localized mainly on the carboxyl group. The hole charge then returns back to its original position in a cyclic way. The electronic dynamics may also affect the nuclear dynamics, because at least within the Born–Oppenheimer approximation, the electronic motion determines the effective potential seen by the nuclei. Evidence of this nuclear dynamics has been given more recently by a pump–probe experiment with a XUV attosecond pulse that assigned a time constant of about 50 fs to the intramolecular hydrogen transfer in the glycine cation.52
As already outlined in Section 3.1 core excitation and ionization represent useful tools to localize the energy transfer on a particular molecular site. In the case of amino acids these tools can be exploited in the study of the effect of varying the carbon backbone length, different stereoisomers and addition/removal of functional groups.53,54 In the case of light elements (C, N, O and S), like the ones composing amino acids, the ionization of a core shell leads to the formation of an intermediate cation state with a short life time of a few fs, which rapidly decays via an Auger process forming a dication, often in a highly excited state. This state then suffers a fragmentation in two momentum correlated singly charged ionic fragments, in some cases accompanied by neutral species. The most appropriate approaches to characterize the fragmentation via inner shell ionization process are either a photoelectron–photoion–photoion coincidence (PEPIPICO) experiment, where a photoelectron, which marks the ionized atom, triggers the collection of the ions or the Auger electron–ion–ion coincidence, where the Auger electron selects both the ionized atom and the final dication state. The results of these experiments are usually reported in the form of 2D maps which display the flight time of the slower ion in the pair versus the time of the faster ion. The shape of the patterns of the correlated ion pairs, their slope and intensity can be used to extract information about the fragmentation dynamics and the relative probabilities of different fragmentation channels.9 The Turku group has exploited both methods to investigate the photofragmentation of a few amino acids: glycine, methionine, cysteine and serine.53–56 Their results show that core ionization induced fragmentation is mainly governed by the rupture of C–Cα bond, usually followed by a secondary dissociation. Correlations between the localized core ionization and the molecular fragmentation have been observed with some channels stronger at one specific core hole. The site-specific effect can be as strong as to change the dominant dissociation pathway. The site-specific core–hole localization effects however could not be related to particular bond breakages or charge localization in a straightforward way. Instead, fast Auger decay populates dication states with electron charge density depending on the hole creation in particular molecular orbitals, which can be strongly core hole dependent. It is the final dication state that determines the preferential bond breakages and fragmentation pathway. This latter observation is consistent with the one reported in ref. 29 and in Section 3.1 in the case the dissociation following inner shell excitation, where, of course, in that case the final state was a cation.
In all the reported studies on amino acids the observation of the large contribution of dissociation channels which involve the carboxylic acid, either as an ion or a neutral species, has a direct relevance to the medical fields. Organic acids are intermediate metabolites of all major groups of organic cellular components and it has been repeatedly proven that their presence in excess in various fluids of the human body is linked to the manifestation of certain diseases as stated in ref. 57 “More than sixty-five disorders well-known these days are due to enzyme deficiency in the amino acids degradation pathways”.
The simplest combination of two amino acids, a dipeptide, is achieved via the formation of peptide bonds between the carboxylic and amino groups of the two respective amino acids and the elimination of one or two water molecules, resulting in a linear or cyclic structure, respectively. While almost all amino acids have been investigated in the gas phase by valence and core photoemission spectroscopy23,58–62 as well as by mass spectrometry†,63,64 the studies of both linear65 and cyclo66–69 dipeptides, are quite scarce. This is probably due to the thermal lability of most of these biomolecules which can undergo structural changes during the desorption, particularly in linear dipeptides.63,70 The driving force for the investigation of dipeptides spans from the need to answer questions concerning the origin of life and the biological activities of larger peptides and proteins, to their exploitation in therapeutic and technological applications.
In a recent study,68 where PEPICO experiments have been combined with ab initio molecular dynamics (MD) simulations and calculations of the potential energy surface, the photofragmentation of cyclo-AlanilAlanine (cAA) by VUV radiation has been investigated. The molecule (Fig. 8) is formed by the diketopiperazine ring and two methyl groups. In the PEPICO spectrum, among others, the 71+ fragment observed in the BE region of 12–16 eV, is particularly intriguing. This fragment, with a mass, which is half of the cAA mass, is produced in a symmetric breakup of cAA and may be related to the [alanine–H–OH]+ fragment.
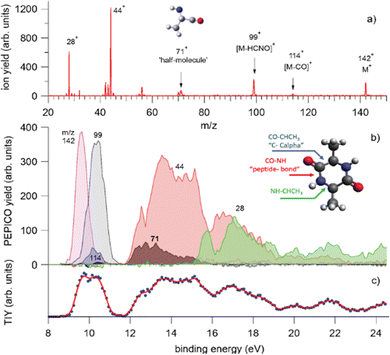 | ||
| Fig. 8 PEPICO spectra and ion yields. (a) Sum of all PEPICO spectra of cAA up to BE of 24 eV; all the fragments relevant to this work and the structure of the 71+ fragment are indicated. (b) PEPICO breakdown curves of the fragment ions indicated by arrows in panel (a). In the inset, the structure of the cAA molecule and the bond breaks responsible for the ring opening are indicated. (c) Total ion yield (dots) obtained by adding up the breakdown curves for all fragment ions shown in panel (a) and its three-point smoothing. Reproduced from ref. 68 under the license CC BY 4.0. | ||
The theoretical investigation of the cAA fragmentation lead to two relevant observations involving this fragment. On the one hand they predict that this fragment can drive the reconstruction of the dipeptide itself through reaction with a similar neutral fragment. Then they show that the cAA+ fragmentation in the near-ionization threshold region is always initiated by a ring opening which likely leads to the formation of stable oxazolidinone structures. The reactivity between the neutral 71 and cationic 71+ products can also produce the oxazolidinone obtained after ring opening and with the addition of a further a neutral 71 fragment can lead to the formation and elongation of a linear peptide as the reactive side is repristinated each time (Fig. 9).
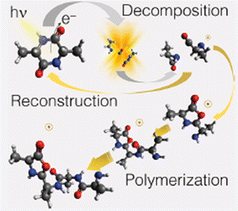 | ||
| Fig. 9 Artistic view reproduced from ref. 68 of the theoretically proposed pathways leading to the reconstruction or polimerization of cAA following the fragmentation of cAA+. Reproduced from ref. 68 under the license CC BY 4.0. | ||
These findings demonstrate that a cyclic dipeptide via a smart decomposition can recycle its fragments into a cyclic-dipeptide structure or provide the seed for linear polymerization and suggest that the identified pathways may have played a role in the early stages of the chemical evolution of life.
3.4 From model system to real drug: the case of the nitroimidazoles
Highly sensitive experimental techniques and among them PEPICO experiments, which due to their energy selectivity, provide insights on state-selected fragmentation, and accurate computational methods have been developed to provide a detailed description of model molecules and to link their electronic and geometric structure to their functions. The question is whether the fragmentation mechanisms and properties identified in the model systems are still active at macroscopic level in more complex and realistic systems. Nitroimidazole derived compounds offer the opportunity to follow a bottom-up approach starting from their building blocks, the 2- or 5-nitroimidazole up to the more complex species misonidazole, nimorazole and metronidazole (Fig. 10) which are used in clinical applications.These molecules are known for their capability to sensitize hypoxic tumor cells to radiation by “mimicking” the effects of the presence of oxygen as a damaging agent.71–75 In an aerobic environment, free oxygen, produced by for example radiolysis of water, falsely repairs damaged DNA reducing the survival rate of tumor cells. Nitroimidazoles are oxygen mimetics compounds that, activated by irradiation during radiotheraphy, can trigger mechanisms matching the chemical characteristic of molecular oxygen. However, at variance with the direct injection of oxygen, they can be driven to the tumor site and activated in conjunction with a radiotheraphy. Despite some successful applications the detailed mechanisms of nitroimidazole operation at molecular levels are still unknown, making difficult for example to understand while some isomers have better performances as radiosensitizer than others and hampering a rational design of more efficient and less toxic drugs for treatment.
A series of studies on nitroimidazole derivatives based mainly on PEPICO experiments and accompanied by quantum theory calculations76–80 have been reported in the literature. The first objective of these studies has been the identification of the possible microscopic physical chemical mechanisms that could explain not only the known radiosensiting capabilities of nitroimidazole, but also the different efficacy reported for the different isomers. Indeed, three regio-isomers of nitroimidazole (Fig. 10) exist depending where the nitro group is attached to the imidazole ring. The 4-nitroimidazole, 4NI, isomer was found to be more stable than 5-nitroimidazole, 5NI, in water81 and in crystalline state,82 while in gas phase they coexist in a tautomeric equilibrium.81
The first observation from VUV photofragmentation measurements has been that the intensity of the NO-loss channel (m/z 83) appears to be a dominant channel in both the non-coincidence and PEPICO mass spectra of 2NI, while it is strongly suppressed in the case of 4(5)NI.76 At first glance, these experimental results may lead to the conclusion that 2NI releases a significant amount of NO, while 4(5)NI does not, explaining the enhanced performance of 2NI as radiosensitizer. Indeed, similarly to oxygen nitric oxide is a potent radiosensitiser and highly reactive species, but also an essential signaling molecule in the cardiovascular system acting as regulator of vasodilation.83 However, the theoretical calculations76 reveal very similar energetics for the NO-loss channel in the three isomers. Indeed the potential energy surfaces76 for the fragmentation of the 5NI, 4NI (not shown, but very similar to 5NI), and 2NI radical cation isomers (Fig. 11) show that in all isomers the most stable structure of the radical cation corresponds to a quasi-planar arrangement with the nitro group out of plane with respect to the neutral molecule. This structure allows the easy NO-loss following intramolecular rearrangement in the nitro group, with energy barriers of 1.35, 1.52 and 1.37 eV for 4NI, 5NI, and 2NI, respectively. Therefore, in all isomers, the NO-loss from the [83–30]+ adduct can produce the C3H3N2O+ ion at m/z 83, which preserves the ring structure, or the NO+ ion at m/z 30. From the energetic point of view, the three isomers show a very similar behavior in the formation of the m/z 83 fragment, while the subsequent fate of this ion is profoundly different. While in 4NI and 5NI (Fig. 11) the intermediate fragment is unstable and, by overcoming an energy barrier of 0.58 and 1.14 eV respectively, it undergoes a ring opening and fragmentation with the final release of CO and HCN, in the case of 2NI the m/z 83 ion has to overcome a large barrier of 2.75 eV before the final fragmentation into HCN and CO molecules and the HCNH+ ion can take place. A further PEPICO experiment79 focused on the study of the NO-loss channel in 1-methyl-5-nitroimidazole. The results show that adding a methyl group to the N1 site in 5NI suppresses even further the NO release and totally inhibits the NO+ production. This work also outlined the role of density of effective dissociative states in determining the relative yields of the NO loss and NO+ channel.
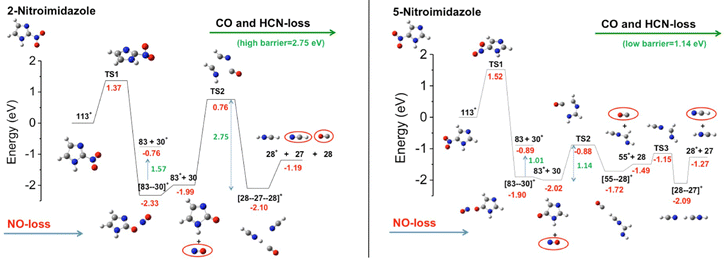 | ||
| Fig. 11 Potential energy surfaces of the 2NI and 5NI, respectively, for the fragmentation of their corresponding molecular ions M+ (m/z 113) calculated at the CCSD/6-311++G**//B3LYP/6-311++G** level of theory.76 The molecular ion M+ as well as the fragments [M–O]+, NO2+, HCN2+, NO+, and HCNH+ are all radical ions; the radical symbol • has been omitted for sake of simplicity. | ||
The more complex misonidazole, metronidazole and nimorazole molecules are characterized by linear side chain attached to the N1 atom in misonidazole and metronidazole and by the morpholine group at the end of the side chain in nimorazole, which creates a double ring structure. Both metronidazole and nimorazole are built on 5NI, while misonidazole on 2NI. The results of the PEPICO experiments in the case of misonidazole and metronidazole78 indicate that the main reaction/fragmentation channels correspond to the elimination of the NO2 and HONO groups in both molecules. Although both metronidazole and misonidazole contain the imidazole ring in their backbone, the side branches of these molecules appear to lead to different bonding mechanisms and properties. Metronidazole is very fragile and a complex fragmentation follows the initial ionization. Misonidazole on the other hand is relatively robust. Ionization and fragmentation may occur simultaneously, as the intensity of the molecular ion in the mass spectrum is very small. Then the preferential loss of part of the tail, acts as a ‘protection’ of the ring against its opening and successive fragmentations. The dissociation of nimorazole80 is strongly characterized by a single fragment C5H10NO+ (m/z 100), which results from the fragmentation of the molecule in two moieties with the cleavage of the H2C–CH2 bond of the side tail. In this molecule neither NO2 nor NO loss are observed.
The fact that the NO loss, the most relevant channel involved76,77,79 in the 2-NI and 4(5)-NI molecules, is a minor, if any, channel in these large compounds, prevents a direct extension of the chemical physics mechanisms identified in the building block molecules to the more complex species adopted as drugs in clinical use. The preferential elimination of the nitro-group in the metronidazole and misonidazole molecules may support the hypothesis84 that the radiosensitizer effect is due to the complex redox chemistry, which, occurring after the selective binding of the nitroaromatic compounds to hypoxic cells, involves the reduction of the nitro-group to an amine (–NH2).
In summary the results of this set of extensive studies on nitroimidazoles, which has followed a bottom-up approach, indicate that the translation of the chemical physics findings from the prototype molecules to the chemotherapeutic compounds is neither straightforward nor an easy task.
4. Conclusions and future perspectives
This brief review illustrates how the selectivity of PEPICO experiments combined with the tunability and broad energy range of synchrotron radiation can be exploited for the characterization of the structure and the dynamic processes that lead to the redistribution of the energy absorbed by some molecules of biological interest, such as radiosensitizers, amino acids and small peptides. It has been shown that the obtained information on energy distribution can found useful application in the modeling of radiation damage in hadrotherapy and the accurate study of the fragmentation pathways can lead to a better understanding of the effectiveness of some molecules and may suggest pathways to the origin of life in the early universe. It has also shown, however that a direct bottom-up approach to transpose the findings in prototype molecules to the compounds used in clinical application is still a challenge.While most of the work performed up to now and all the work done by the authors has been restricted to molecules produced by thermal evaporation, a promising research area is the examination of larger molecules, brought into the gas phase by sophisticated and softer methods. The state-of-the-art technique to bring unfragmented nucleotides, proteins or peptides from solution into the gaseous phase is represented by the Electrospray Ionization (ESI) technique.85,86 Since the commercial development of ESI sources, mass spectrometry has become the most popular tool for the study of very large organic molecules. The coupling of this versatile ion source with spectroscopic techniques implies that the mass selected ions generated in the gas phase by an ESI source are collected in an ion trap and then excited with a proper radiation. For example, Gonzalez-Magana et al.87 used a combination of an ESI source, tandem mass spectrometer and Paul trap to measure partial ion yield NEXAFS spectrum at the carbon edge of protonated leucine enkephalin, a peptide containing five amino acid residues and more recently the same group studied the VUV photoabsorption in multiply deprotonated gas-phase oligonucleotides containing a long telomere sequence.88 Using similar methods to produce the sample, Milosavljevic et al.89 produced free protonated cytochrome ions (consisting of 104 amino acids, and charge state-selected), and performed VUV photoionization mass spectrometry. An improvement of the throughput of the sources is needed in order to make them suitable for electron spectroscopies and eventually for photoelectron–photoion coincidence experiments. However in the case of an ESI source used in negative mode to produce anions and coupled to a hexapole accumulation ion trap the Weitzel group90,91 has investigated laser-induced photodetachment from gramicidin anions, a peptide consisting of 15 amino acids and Gibbard and Continetti92 proved that photoelectron–photofragment coincidence spectroscopy of the dissociative photodetachment of negative ions can be done.
In the ESI process biomolecules are produced as multicharged ions in small charged droplets so that the spectroscopy and photon-induced processes involving neutral species cannot be assessed. A possibility to overcome this issue is represented by the aerosol mass thermo-desorption method which combines the aerodynamic lens systems, typically used in mass spectrometry of aerosols93 with the thermal desorption from a heated surface.94 This approach has been followed by Gaie-Levrel et al.95 at Soleil synchrotron where such a source has been coupled to a Velocity Map Imaging (VMI) analyzer operated in coincidence with a Wiley–McLaren Time of Flight spectrometer. With this set-up the thermochemistry of some aminoacids95 and DNA bases96 has been investigated by measuring their ionization energies and fragmentation paths via threshold photoionization spectroscopy (TPEPICO) at high resolution and the chiroptical properties of gas phase pure enantiomers of biomolecules and especially their photoelectron circular dichroism (PECD) have been characterized.
Chirality plays a fundamental role in the bio world, for example in determining the functions of different molecules as well as the molecular recognition processes. Methods probing simultaneously chirality and molecular conformation are therefore crucially needed. The photoelectron circular dichroism (PECD),97 which results from the forward–backward asymmetry in the photoelectron angular distribution with respect to the light axis for randomly oriented chiral molecules photoionized by circularly polarized radiation, is well suited for studying gas-phase molecules. Unlike to others chiroptical spectroscopy methods which lack sensitivity (the measured effect is about ∼10−3 of the total absorption), PECD is allowed in the electric dipole approximation, which explains its intense relative magnitude, up to almost 40% of the average photoelectron intensity.98 The combination of PECD with ion mass spectrometry in an electron–ion coincidence experiment can find interesting analytical applications like the quantitative determination of enantiomeric excess, as shown by the first pioneering experiments99–101 using double imaging electron–ion coincidence spectrometers, as well as enable the predicted identification of the absolute molecular configuration from the experimental observations.97
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This paper is based upon work from COST action CA18212 –Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). This work was also partially supported by PRIN 20173B72NB project ‘‘Predicting and controlling the fate of bio-molecules driven by extreme-ultraviolet radiation’’.References
- B. Brehm and E. V. Puttkamer, Z. Naturforsch., 1967, 22A, 8 CrossRef.
- J. H. Eland, Int. J. Mass Spectrom. Ion Processes, 1972, 8, 143 CrossRef CAS.
- T. Baer, J. Booze and K. M. Weitzel, in Vacuum Ultraviolet Photoionization and Photodissociation of Molecules and Clusters, ed. C. Y. Ng, World Scientific, Singapore, 1991, p. 259 Search PubMed.
- T. Baer, A. Bodi and B. Sztaray, Encyclopedia of Spectroscopy and Spectrometry, 3rd edn, Academic Press Ltd-Elsevier Science Ltd, 2017, vol. 3, p. 635 Search PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, New York, 1996 Search PubMed.
- G. C. King, M. Zubek, P. M. Rutter and F. H. Read, J. Phys. E: Sci. Instrum., 1987, 20, 440 CrossRef CAS.
- R. I. Hall, A. McConkey, K. Ellis, G. Dawber, L. Avaldi, M. A. MacDonald and G. C. King, Meas. Sci. Technol., 1992, 3, 316 CrossRef.
- T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19, 9698 RSC.
- J. H. Eland in Vacuum Ultraviolet Photoionization and Photodissociation of Molecules and Clusters, ed. C. Y. Ng, World Scientific, Singapore, 1991, p. 297 and references therein Search PubMed.
- T. Arion and U. Herghenhahn, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 222 CrossRef CAS.
- J. H. Eland, Adv. Chem. Phys., 2009, 141, 153 Search PubMed and references therein.
- K. C. Prince, P. Bolognesi, V. Feyer, O. Plekan and L. Avaldi, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 335 CrossRef CAS.
- R. R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, J. Slezak, K. C. Prince, R. Richter, M. Vondracek, R. Camilloni, L. Avaldi, M. Coreno, G. Stefani, C. Furlani, M. De Simone, S. Stranges and M. Y. Adam, J. Electron Spectrosc. Relat. Phenom., 1999, 101–103, 959–964 CrossRef CAS.
- S. Maclot, “Stabilitè de Systemes complexes d’interet biologique sous rayonnements ionisants”, PhD thesis, Universitè de Normandie, 2014 Search PubMed.
- G. Cautero, R. Sergo, L. Stebel, P. Lacovig, P. Pittana, M. Predonzani and S. Carrato, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 447–459 CrossRef CAS.
- R. H. Menk, M. Antonelli, G. Brajnik, J. Bufon, C. Dri, D. Giuressi, A. Gubertini, C. Nichetti, G. Pinaroli, P. Pittana, S. Schillani, R. Sergo, L. Stebel and G. Cautero, AIP Conf. Proc., 2019, 2054, 060071 CrossRef.
- A. Bodi, B. Sztaray, T. Baer, M. Johnson and T. Gerber, Rev. Sci. Instrum., 2007, 78, 084102 CrossRef PubMed.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477 CrossRef CAS.
- A. G. Suits and R. E. Continetti, Imaging in Chemical Dynamics, American Chemical Society, Washington, DC, 2000 Search PubMed.
- M. Takahashi, J. P. Cave and J. H. D. Eland, Rev. Sci. Instrum., 2000, 71, 1337 CrossRef CAS.
- D. Rolles, Z. D. Pesic, M. Perri, R. C. Bilodeau, G. D. Ackerman, B. S. Rude, A. L. D. Kilcoyne, J. D. Bozek and N. Berrah, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 170–174 CrossRef CAS.
- J. Adachi, M. Kazama, T. Teramoto, N. Miyauch, T. Mizuno, M. Yamazaki, T. Fujikawa and A. Yagishita, J. Phys. B: At. Mol. Phys., 2012, 45, 194007 CrossRef.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2007, 111, 10998 CrossRef CAS PubMed.
- K. Tanaka, H. Kizaki, R. Sumii, Y. Matsumoto and S. Wada, Radiat. Phys. Chem., 2006, 75, 2076–2079 CrossRef CAS.
- W. Eberhardt, T. K. Sham, R. Carr, S. Krummacher, M. Strongin, S. L. Weng and D. Wesner, Phys. Rev. Lett., 1983, 50, 1038 CrossRef CAS.
- W. Eberhardt, E. W. Plummer, I.-W. Lyo, R. Carr and W. K. Ford, Phys. Rev. Lett., 1987, 58, 207–210 CrossRef CAS PubMed.
- J. H. D. Eland, P. Linusson, M. Mucke and R. Feifel, Chem. Phys. Lett., 2012, 548, 90–94 CrossRef CAS.
- P. Salén, M. Kaminska, R. J. Squibb, R. Richter, M. Alagia, S. Stranges, P. van der Meulen, J. H. D. Eland, R. Feifeld and V. Zhaunerchyk, Phys. Chem. Chem. Phys., 2014, 16, 15231 RSC.
- P. Bolognesi, J. A. Kettunen, A. Cartoni, R. Richter, S. Tosic, S. Maclot, P. Rousseau, R. Delaunay and L. Avaldi, Phys. Chem. Chem. Phys., 2015, 17, 24063 RSC.
- R. Watanabe and H. Nikjoo, Int. J. Radiat. Biol., 2002, 78, 953 CrossRef CAS.
- M. C. Castrovilli, P. Bolognesi, A. Cartoni, D. Catone, P. O’Keeffe, A. Casavola, S. Turchini, N. Zema and L. Avaldi, J. Am. Soc. Mass Spectrom., 2014, 25, 351 CrossRef CAS PubMed.
- P. O’Keeffe, P. Bolognesi, A. Casavola, D. Catone, N. Zema, S. Turchini and L. Avaldi, Mol. Phys., 2009, 107, 2025 CrossRef.
- P. Bolognesi, A. Kettunen, P. O’Keeffe, R. Richter, A. Cartoni, A. R. Casavola, M. C. Castrovilli, S. Tosic, B. P. Marinkovic and L. Avaldi, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 244004 CrossRef.
- M. Durante and J. S. Loeffler, Nat. Rev. Clin. Oncol., 2010, 7, 37 CrossRef PubMed.
- A. V. Solov’yov, E. Surdutovich, E. Scifoni, I. Mishustin and W. Greiner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011909 CrossRef.
- P. López-Tarifa, M.-A. Hervé du Penhoat, R. Vuilleumier, M.-P. Gaigeot, I. Tavernelli, A. Le Padellec, J.-P. Champeaux, M. Alcamí, P. Moretto-Capelle, F. Martín and M.-F. Politis, Phys. Rev. Lett., 2011, 107, 023202 CrossRef.
- B. Liu, S. B. Nielsen, P. Hvelplund, H. Zettergren, H. Cederquist, B. Manil and B. A. Huber, Phys. Rev. Lett., 2006, 97, 133401 CrossRef CAS PubMed.
- S. Ptasińska, S. Denifl, V. Grill, T. D. Märk, E. Illenberger and P. Scheier, Phys. Rev. Lett., 2005, 95, 093201 CrossRef PubMed.
- E. C. Montenegro, M. B. Shah, H. Luna, S. W. J. Scully, A. L. F. de Barros, J. A. Wyer and J. Lecointre, Phys. Rev. Lett., 2007, 99, 213201 CrossRef CAS.
- L. Chen, S. Martin, J. Bernard and R. Brédy, Phys. Rev. Lett., 2007, 98, 193401 CrossRef CAS PubMed.
- S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero and P. Rousseau, Phys. Rev. Lett., 2016, 117, 073201 CrossRef CAS PubMed.
- A. Rentenier, L. F. Ruiz, S. Díaz-Tendero, B. Zarour, P. Moretto-Capelle, D. Bordenave-Montesquieu, A. Bordenave-Montesquieu, P. A. Hervieux, M. Alcamí, M. F. Politis, J. Hanssen and F. Martín, Phys. Rev. Lett., 2008, 100, 183401 CrossRef CAS PubMed.
- G. Martinet, S. Díaz-Tendero, M. Chabot, K. Wohrer, S. Della Negra, F. Mezdari, H. Hamrita, P. Désesquelles, A. L. Padellec, D. Gardés, L. Lavergne, G. Lalu, X. Grave, J. F. Clavelin, P.-A. Hervieux, M. Alcamí and F. Martín, Phys. Rev. Lett., 2004, 93, 06340 CrossRef PubMed.
- A. Rentenier, L. F. Ruiz, S. Díaz-Tendero, B. Zarour, P. Moretto-Capelle, D. Bordenave-Montesquieu, A. Bordenave-Montesquieu, P. A. Hervieux, M. Alcamí, M. F. Politis, J. Hanssen and F. Martín, Phys. Rev. Lett., 2008, 100, 18340 CrossRef.
- E. Erdmann, N. F. Aguirre, S. Indrajith, J. Chiarinelli, A. Domaracka, P. Rousseau, B. A. Huber, P. Bolognesi, R. Richter, L. Avaldi, S. Diaz-Tendero, M. Alcami and M. Łabuda, Phys. Chem. Chem. Phys., 2021, 23, 1859 RSC.
- K. Altwegg, H. Balsiger, A. Bar-Nun, J.-J. Berthelier, A. Bieler, P. Bochsler, C. Briois, U. Calmonte, M. R. Combi and H. Cottin, et al. , Sci. Adv., 2016, 2, 1600285 CrossRef.
- A. F. Lago, L. H. Coutinho, R. R. T. Marinho, A. Naves de Brito and G. G. B. de Souza, Chem. Phys., 2004, 307, 9 CrossRef CAS.
- J. Chiarinelli, P. Bolognesi, A. Domaracka, P. Rousseau, M. C. Castrovilli, R. Richter, S. Chatterjee, F. Wang and L. Avaldi, Phys. Chem. Chem. Phys., 2018, 20, 22841 RSC.
- C. T. Falzon and F. Wang, J. Chem. Phys., 2005, 123, 214307 CrossRef PubMed.
- A. I. Kuleff and L. S. Cederbaum, Chem. Phys., 2007, 338, 320 CrossRef CAS.
- A. I. Kuleff, J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2005, 123, 044111 CrossRef PubMed.
- M. C. Castrovilli, A. Trabattoni, P. Bolognesi, P. O’Keeffe, L. Avaldi, M. Nisoli, F. Calegari and R. Cireasa, J. Phys. Chem. Lett., 2018, 9, 6012 CrossRef CAS PubMed.
- J. Laksman, K. Kooser, H. Levola, E. Itälä, D. T. Ha, E. Rachlew and E. Kukk, J. Phys. Chem. B, 2014, 118, 11688 CrossRef CAS PubMed.
- E. Itälä, H. Levola, D. Trinh Ha, K. Kooser, E. Rachlew and E. Kukk, J. Phys. Chem. A, 2016, 120, 5419 CrossRef.
- D. T. Ha, Y. Wang, M. Alcamí, E. Itälä, K. Kooser, S. Urpelainen, M. A. Huels, E. Kukk and F. Martín, J. Phys. Chem. A, 2014, 118, 1374 CrossRef CAS PubMed.
- E. Itälä, K. Kooser, E. Rachlew, M. A. Huels and E. Kukk, J. Chem. Phys., 2014, 140, 234305 CrossRef PubMed.
- R. Chalmers, Organic Acids in Man, 1st edn, Springer, Netherlands, 1982 Search PubMed.
- O. Plekan, V. Feyer, R. Richter, M. Coreno and K. C. Prince, Mol. Phys., 2008, 106, 1143 CrossRef CAS.
- I. Powis, E. E. Rennie, U. Hergenhahn, O. Kugeler and R. Bussy-Socrate, J. Phys. Chem. A, 2003, 107, 25 CrossRef CAS.
- W. Zhang, V. Carravetta, O. Plekan, V. Feyer, R. Richter, M. Coreno and K. C. Prince, J. Chem. Phys., 2009, 131, 07B611 Search PubMed.
- O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. Prince and V. Carravetta, Chem. Phys. Lett., 2007, 442, 429 CrossRef CAS.
- J. Chiarinelli, P. Bolognesi, A. Domaracka, P. Rousseau, M. C. Castrovilli, R. Richter, S. Chatterjee, F. Wang and L. Avaldi, Phys. Chem. Chem. Phys., 2018, 20, 22841 RSC.
- H. J. Svec and G. A. Junk, J. Am. Chem. Soc., 1964, 86, 2278 CrossRef CAS.
- H.-W. Jochims, M. Schwell, J.-L. Chotin, M. Clemino, F. Dulieu, H. Baumgårtel and S. Leach, Chem. Phys., 2004, 298, 279 CrossRef CAS.
- V. Feyer, O. Plekan, R. Richter, M. Coreno, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2009, 113, 10726 CrossRef CAS PubMed.
- A. P. W. Arachchilage, F. Wang, V. Feyer, O. Plekan and K. C. Prince, J. Chem. Phys., 2010, 133, 174319 CrossRef PubMed.
- A. P. Wickrama Arachchilage, F. Wang, V. Feyer, O. Plekan and K. C. Prince, J. Chem. Phys., 2012, 136, 124301 CrossRef.
- D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Diaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379 CrossRef CAS PubMed.
- J. Chiarinelli, D. Barreiro-Lage, P. Bolognesi, R. Richter, H. Zettergren, M. H. Stockett, S. Diaz-Tendero and L. Avaldi, Phys. Chem. Chem. Phys., 2022, 24, 5855 RSC.
- L. Carlini, J. Chiarinelli, G. Mattioli, C. Mattea, V. Valentini, A. De Stefanis, E. Bauer, P. Bolognesi and L. Avaldi, J. Phys. Chem. B, 2022, 126, 2968–2978 CrossRef CAS PubMed and references therein.
- P. Wardman, K. Rothkamm, L. K. Folkes, M. Woodcock and P. Johnston, J. Radiat. Res., 2007, 167, 475 CrossRef CAS PubMed.
- S. Rockwell, I. T. Dobrucki, E. Y. Kim, S. T. Marrison and V. T. Vu, Curr. Mol. Med., 2009, 9, 442 CrossRef CAS PubMed.
- P. Sonveaux, B. F. Jordan, B. Gallez and O. Feron, Eur. J. Cancer, 2009, 45, 1352 CrossRef CAS PubMed.
- W. R. Wilson and M. P. Hay, Nat. Rev. Cancer, 2011, 11, 393 CrossRef CAS PubMed.
- G. S. Higgins, S. M. O’Cathail, R. J. Muschel and W. G. McKenna, Cancer Treat. Rev., 2015, 41, 105 CrossRef PubMed.
- P. Bolognesi, A. R. Casavola, A. Cartoni, R. Richter, P. Markus, S. Borocci, S. Tosic, H. Sa’adeh, M. Masic, B. P. Marinkovic, K. C. Prince and L. Avaldi, J. Chem. Phys., 2016, 145, 191102 CrossRef CAS PubMed.
- A. Cartoni, A. R. Casavola, P. Bolognesi, M. C. Castrovilli, D. Catone, J. Chiarinelli, R. Richter and L. Avaldi, J. Phys. Chem. A, 2018, 122, 4031–4041 CrossRef CAS PubMed.
- J. Chiarinelli, A. R. Casavola, M. C. Castrovilli, P. Bolognesi, A. Cartoni, F. Wang, R. Richter, D. Catone, S. Tosic, B. P. Marinkovic and L. Avaldi, Front. Chem., 2019, 7, 329 CrossRef CAS PubMed.
- E. Itala, H. Myllynen, J. Niskanen, J. Gonzalez-Vazquez, Y. Wang, D. Trinh Ha, S. Denifl and E. Kukk, J. Phys. Chem. A, 2019, 123, 3074 CrossRef CAS PubMed.
- E. Itala, J. Niskanen, L. Pihlava and E. Kukk, J. Phys. Chem. A, 2020, 124, 5555 CrossRef CAS PubMed.
- P. Jimenez, J. Laynez, R. M. Claramunt, D. Sanz, J. P. Fayet, M. C. Vertut, J. Catalán, J. L. G. de Paz, G. Pfister-Guillouzo, C. Guimon, R. Flammang, A. Maquestiau and J. Elguero, New J. Chem., 1989, 13, 151 CAS.
- A. I. Vokin, L. V. Sherstyannikova, I. G. Krivoruchka, T. N. Aksamentova, O. V. Krylova and V. K. Turchaninov, Russ. J. Gen. Chem., 2003, 73, 973 CrossRef CAS.
- https://www.nobelprize.org/prizes/medicine/1998/press-release/ .
- G. E. Adams, I. R. Flockhart, C. E. Smithern, I. J. Stratford, P. Wardman and M. E. Watts, Radiat. Res., 2012, 178, AV183 CrossRef CAS PubMed.
- M. Yamashita and J. B. Fenn, J. Phys. Chem., 1984, 88, 4451 CrossRef CAS.
- J. B. Fenn, M. Mann, C. K. Meng, S. F. Wong and C. M. Whitehouse, Science, 1989, 246, 164 CrossRef.
- O. Gonzalez-Magan, G. Reitsma, M. Tiemens, L. Boschman, R. Hoekstra and T. Schlatholter, J. Phys. Chem. A, 2012, 116, 10745 CrossRef PubMed.
- W. Li, E. Mjekiqi, W. Douma, X. Wang, O. Kavatsyuk, R. Hoekstra, J.-C. Poully and T. Schlatholter, Chem. – Eur. J., 2019, 25, 16114–16119 CrossRef CAS PubMed.
- A. R. Milosavljevic, C. Nicolas, J. Lemaire, L. Nahon and A. Giuliani, Phys. Chem. Chem. Phys., 2011, 13, 15432 RSC.
- P. Krüger and K.-M. Weitzel, Angew. Chem., Int. Ed., 2021, 60, 17861 CrossRef.
- P. Krüger, J. H. Both, U. Linne, F. Chirot and K. M. Weitzel, J. Phys. Chem. Lett., 2022, 13, 6110 CrossRef PubMed.
- J. A. Gibbard and R. E. Continetti, Faraday Discuss., 2019, 217, 203 RSC.
- X. Wang and P. H. McMurry, Aerosol Sci. Technol., 2006, 40, 320 CrossRef CAS.
- D. C. Sykes, E. Woods, G. D. Smith, T. Baer and R. E. Miller, Anal. Chem., 2002, 74, 2048 CrossRef CAS.
- F. Gaie-Levrel, G. A. Garcia, M. Schwell and L. Nahon, Phys. Chem. Chem. Phys., 2011, 13, 7024 RSC.
- D. Touboul, F. Gaie-Levrel, G. A. Garcia, L. Nahon, L. Poisson, M. Schwell and M. Hochlaf, J. Chem. Phys., 2013, 138, 094203 CrossRef CAS PubMed.
- I. Powis in Adv. Chem. Phys. ed. J. C. Light, Wiley, 2008, vol. 138, p. 267 Search PubMed.
- H. Ganjitabar, R. Hadidi, G. A. Garcia, L. Nahon and I. Powis, J. Mol. Spectrosc., 2018, 353, 11 CrossRef CAS.
- A. Bodi, P. Hemberger, D. L. Osborn and B. Sztaray, J. Phys. Chem. Lett., 2013, 4, 2948 CrossRef CAS.
- M. Tia, B. Cunha de Miranda, S. Daly, F. Gaie-Levrel, G. A. Garcia, L. Nahon and I. Powis, J. Phys. Chem. A, 2014, 118, 2765 CrossRef CAS PubMed.
- M. M. R. Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Nat. Commun., 2015, 6, 7511 CrossRef CAS PubMed.
Footnote |
| † The cited references represent just a few examples, far from being an exhaustivereview of the vast amount of work present in the literature. |
| This journal is © the Owner Societies 2022 |