Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced elastic scattering of He2 and He3 from solids by multiple-edge diffraction
Lee Yeong
Kim
 a,
Sanghwan
Park
b,
Chang Young
Lee
a,
Sanghwan
Park
b,
Chang Young
Lee
 b,
Wieland
Schöllkopf
b,
Wieland
Schöllkopf
 *c and
Bum Suk
Zhao
*c and
Bum Suk
Zhao
 *ad
*ad
aDepartment of Physics, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, South Korea. E-mail: zhao@unist.ac.kr
bDepartment of Chemical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, South Korea
cFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: wschoell@fhi-berlin.mpg.de
dDepartment of Chemistry, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, South Korea
First published on 9th August 2022
Abstract
We report on a method of enhanced elastic and coherent reflection of 4He2 and 4He3 from a micro-structured solid surface under grazing incidence conditions. The van der Waals bound ground-state helium clusters exhibit fundamental quantum effects: 4He2, characterized by a single ro-vibrational bound state of 10−7 eV dissociation energy, is known to be a quantum halo state; and 4He3 is the only electronic ground-state triatomic system possessing an Efimov state in addition to the ro-vibrational ground state. Classical methods to select and manipulate these clusters by interaction with a solid surface fail due to their exceedingly fragile bonds. Quantum reflection under grazing incidence conditions was demonstrated as a viable tool for elastic scattering from a solid surface but suffers from small reflection probabilities for typical conditions. Here we demonstrate that multiple-edge diffraction enables enhanced elastic scattering of the clusters from a solid. A dual-period reflection grating, where the strips consist of micro-structured edge arrays, shows an up to ten fold increased reflection probability as compared to its conventional counterpart where the strips are plane patches enabling quantum reflection of the clusters. The observed diffraction patterns of the clusters provide evidence of the coherent and elastic nature of scattering by multiple-edge diffraction.
1 Introduction
Helium is the least reactive of all elements in the periodic table. Due to the closed-shell structure of its electronic ground state, text-book molecular orbital theory tells us that the diatomic, 4He2, cannot be formed by covalent bonding. There is, however, an attractive van der Waals (vdW) dispersion interaction between two He atoms. In combination with the steep repulsive interaction at short internuclear distances, where electron clouds start to overlap, the vdW interaction results in a He–He pair interaction characterized by a potential well of ≈11 K depth at an internuclear distance of ≈0.3 nm. This weak He–He interaction, in conjunction with the small mass of the He atom lies at the origin of macroscopic and microscopic quantum effects. The most important macroscopic quantum effect in helium is arguably superfluidity, which has fascinated and challenged scientists since its first observation in 1937. Helium is the only known naturally occurring substance forming this peculiar quantum-fluid phase when cooled to cryogenic temperatures where other liquids, including hydrogen, freeze out forming solids.Quantum effects in helium also occur on a microscopic scale turning the He diatomic and triatomic systems into unique quantum clusters. The dimer, formed by weak vdW forces, exhibits an extremely small binding energy on the order of ≈1 mK (100 neV).1,2 This is just a fraction of 10−4 of the He–He potential well depth indicating the dominant effect of zero-point energy of the only bound ro-vibrational state. The vibrational wavefunction of 4He2 spreads out to tens of nm and is characterized by an exceptionally large mean internuclear separation of 5.2 nm.1 The wavefunction reveals that 4He2 is found with more than 80% probability in a classically-forbidden tunnelling state, where the internuclear separation is larger than the pair potential's classical outer turning point. This is why 4He2 has been termed a quantum-halo state.2,3
Another intriguing microscopic quantum effect has been observed in the triatomic 4He3, which was found to support a weakly bound Efimov excited state in addition to its ro-vibrational ground state.4 The Efimov effect predicts additional bound excited states occurring in a three-particle system (here 4He3) when the binding energy in the corresponding two-particle system (here 4He2) is vanishingly small.5 Efimov physics has been studied intensively throughout the last decade within the field of ultracold gases. In those systems the Efimov regime in the vicinity of a 2-body binding resonance can be reached by tuning the interaction strength in the gas via externally applied magnetic fields. In 4He3, on the other hand, the given interaction strength just happens to be such that a single Efimov excited state is present in the trimer.
Their exceeding fragility makes the experimental investigation of helium dimers and trimers challenging. First experimental observations of 4He2 and 4He3 present in molecular beams of helium were reported in the 1990's.6–8 An essential prerequisite in experimental studies of weakly bound helium clusters is a method to separate them from the dominant atomic component present in a helium molecular beam. Conventional methods based on scattering from gases or surfaces, or on electron scattering are of limited use, because collisions at realistic kinetic energies lead to break-up of the fragile vdW bonds. This limitation has been overcome by exploiting the wave-nature of atoms and clusters. Based on their different de Broglie wavelengths He atoms and clusters of different mass travelling with the same speed in a supersonic beam can be non-destructively manipulated and separated by diffraction from periodic structures. Owing to the minute de Broglie wavelengths on the order of tenths of nm only, diffractive elements typically need to be structured on length scales of 1 micron or even less. The dimer's binding energy and bond length, for instance, were determined by diffraction from a 100 nm period transmission grating.1 The diffraction peak intensities depend on the size of the dimer, allowing to deduce the mean bond length from detailed analysis of diffraction intensities.
Diffraction from a nanoscale transmission grating also allowed for the observation of 4He3 in its ro-vibrational ground state,7,8 which is bound by 11 μeV, but did not provide evidence of the elusive Efimov excited state.9 Experimental evidence of the Efimov state of 4He3 was eventually found in Coulomb explosion imaging of helium trimers pre-selected by the diffraction technique.4 In addition, that method was successfully applied to mapping out the above-mentioned quantum-halo wavefunction of 4He22 as well as the ground-state wavefunctions of 4He3 and of the isotope-mixed trimer 3He4He2.10
In all these experiments small clusters entrained in a helium molecular beam were separated by diffraction from a nanoscale transmission grating. This method suffers from an enormous sacrifice of flux introduced by narrow collimation slits needed to achieve the spatial coherence which is prerequisite for resolving diffraction peaks. In addition, still today fabrication of the delicate free-standing nanoscale gratings is far from trivial and only possible by sophisticated nano-fabrication techniques available in specialised labs. This motivates the development of alternative experimental techniques for non-destructive manipulation of weakly-bound vdW clusters. Possible future experiments include studying the interaction of He2 or He3 with external fields or with a surface. The effects of intense laser fields11–14 and external electric fields15 on the helium-helium interaction potential have been studied theoretically. Very recently, an experimental study on the interaction of He2 with a short laser pulse was reported.16 Such investigations could benefit from experimental techniques which do not depend on the use of free-standing nanoscale transmission gratings.
To this end our group has been investigating techniques of non-destructive scattering of 4He2 and 4He3 from solids. Two quantum-mechanical phenomena have been found to mediate elastic scattering from solids under grazing incidence conditions; quantum reflection (QR) from a solid surface17,18 and reflection due to diffraction from multiple half-plane edges referred to as multiple-edge-diffraction reflection (MEDR).19,20 Both effects take advantage of the wave nature of particles and enable coherent non-destructive manipulation of the clusters. In combination with periodic structuring of the surface this permits observation of well resolved diffraction patterns. In this work we demonstrate that multiple-edge diffraction can be exploited to obtain enhanced scattering intensities of 4He2 and 4He3 as compared to quantum reflection.
Quantum reflection from a solid is mediated by the attractive particle–surface interaction.18,21–26 Near a surface, a neutral atom or molecule experiences a long-range attractive potential U, approximated by the van der Waals potential UvdW = −C3/z3 at z ≪ l or the Casimir–Polder potential UCP = −C4/z4 at z ≫ l. Here, C3 is the van der Waals coefficient, z is the distance between the particle and the surface, and C4 = C3l with l the parameter associated with the retardation effect. In a classical picture, a particle approaching the solid surface will be accelerated by the attractive potential and will gain kinetic energy corresponding to the potential-well depth. Subsequently, it will smash into the steep repulsive branch of the potential where it scatters back at the classical turning point. In a quantum-mechanical picture, however, an alternative way of reflection can occur. If the incident de Broglie wavelength is exceedingly large, the wave's reflection coefficient at the attractive potential branch will be non-vanishing. This is reminiscent of the reflection of a wave from a sharp step in a one-dimensional potential, as it is often described in quantum mechanics text books.27 As a result, a helium cluster can scatter back elastically without probing the classical turning point at the repulsive branch of the particle–surface potential.
For typical conditions of thermal kinetic energies at normal incidence the QR probability is exceedingly small. However, it increases towards unity as the normal component kperp of the incident particle's wave number k approaches zero. This is why QR of atoms from a solid surface was first observed with ultracold atoms at grazing incidence angles of 1–10 mrad.28 Later, QR was also observed for thermal-energy beams of 3He29 and 4He atoms,17,30 where sufficiently small kperp values where achieved by grazing incidence geometry. Subsequently, non-destructive quantum reflection and diffraction of 4He2 and 4He3 was observed.31,32
The second non-classical reflection mechanism, based on multiple-edge diffraction (MEDR), was first reported by Oberst et al.19 who studied the scattering of metastable He atoms from a ridged micro-structured surface. The incident wave is diffracted by each thin ridge in the same way as it occurs at the edge of a half plane (also referred to as Fresnel diffraction19). The physics of reflection and diffraction by multiple-edge diffraction is summarized in Fig. 1. As indicated in the figure, for a periodic array of half planes, the outgoing diffracted wavelets from all edges will coherently add up in the directions of grating-diffraction maxima including the 0th diffraction order which forms the specular beam. A theoretical model considering a periodic array of half planes, grazing-incidence conditions, and multiple outgoing diffraction beams shows a dependence on a single parameter that depends on wavelength, period of the array, and incidence angle.33 Our recent previous study with He atoms confirmed that model and provided evidence for a transition from the regime of multiple-edge diffraction to quantum reflection with increasing width of the fine ridges constituting the half-plane array.20
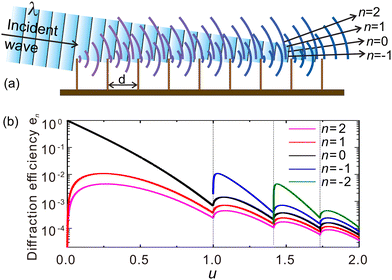 | ||
Fig. 1 Multiple-edge-diffraction reflection (MEDR) from a periodic array of half planes of period d. (a) Schematic of the configuration leading to MEDR. The wavefronts of an incoming beam are diffracted at each half-plane edge (edge diffraction, also referred to as Fresnel diffraction) resulting in diffracted wavelets indicated by curved wavefronts. For the sake of visibility their angular span is grossly exaggerated in the graph; appreciable intensity is only found in an exceedingly small angular range centered around the incident beam direction. As such, MEDR is only observable for extreme grazing-incidence conditions as achieved in our setup. In the far field the diffracted wavelets add up constructively at the well known diffraction angles of a grating of period d labeled by the diffraction order n. (b) The anticipated diffraction intensities (normalized to the incident-beam intensity) have been calculated for diffraction orders n = −2,…, 2 using the Bogomolny–Schmit calculus.33 The intensities are a function of a single variable u which depends on the wavelength, period, and incidence angle as 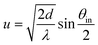 . The decaying-sawtooth shape of the curves and the intensity hierarchy (increasing intensity with decreasing order n) are the fingerprints of MEDR and have been observed experimentally.20 At the smallest incidence angles only non-negative diffraction orders are present; with increasing incidence angle negative-order diffraction beams emerge successively at threshold angles indicated by vertical dashed lines. . The decaying-sawtooth shape of the curves and the intensity hierarchy (increasing intensity with decreasing order n) are the fingerprints of MEDR and have been observed experimentally.20 At the smallest incidence angles only non-negative diffraction orders are present; with increasing incidence angle negative-order diffraction beams emerge successively at threshold angles indicated by vertical dashed lines. | ||
In this work we report on multiple-edge diffraction of He2 and He3 from half-plane arrays. Our results indicate that small helium clusters can scatter elastically and coherently via the MEDR mechanism. In our experiment we observe reflection and diffraction of helium atoms and clusters from two square-wave reflection gratings; a conventional one and a dual-period grating of identical material. Both gratings are characterised by a period of 1.8 mm and strips of 0.9 mm width. Although this is a comparatively large period it still makes it possible to resolve and separate diffraction peaks of monomers, dimers and trimers under extreme grazing-incidence conditions. In the conventional grating the strips are simply plane homogenous parallel patches, whereas in the dual-period grating the strips are micro-structured with each strip consisting of an array of 2.3 μm-wide micro-strips with 20 μm micro-period. (The micro-strips are parallel to each other and to the main strip orientation, see Fig. 3(a) and (b).) For both gratings we observe diffraction patterns of atoms and clusters where He2 and He3 peaks are identified from their different diffraction angles. Comparison of the reflection probabilities observed for the two gratings indicates that quantum reflection at the conventional grating is much more efficient to reflect He atoms than multiple edge-diffraction at the dual-period grating. This is in agreement with our previous results.20 For He2 and He3, however, we observe a significant enhancement of coherent reflectivity for the dual-period grating as compared to the conventional grating. Comparison of our experimental results with theoretical model calculations confirms that reflection by multiple-edge diffraction is responsible for the increased reflectivity observed for the dual-period grating.
2 Experimental
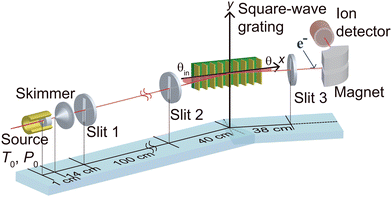
A schematic diagram of the experimental setup is shown in Fig. 2. Details of the apparatus have been described in previous publications.17,27,31,32 In brief, a continuous molecular beam is formed by expansion of pure 4He gas from a cryogenic source cell through a 5 μm-diameter orifice into a high vacuum. The stagnation temperature and pressures in the source cell are T0 = 9.0 K and P0 = 0.5, 1.0, or 2.0 bar, respectively. At P0 = 0.5 bar the helium beam primarily consists of helium atoms, whereas appreciable fractions of small helium clusters, namely ground-state dimers He2 and trimers He3, are present at P0 = 1.0 and 2.0 bar, respectively.34 Atoms and clusters in the beam share the most probable velocity and the velocity width of about 304 m s−1 and 2 m s−1, respectively. The beam is collimated by two 20 μm-wide slits (Slit 1 and Slit 2 in Fig. 2) separated by 100 cm. The atoms' and clusters' mean incident wave vector k is oriented along the line connecting the centers of the two slits. The incident helium beam scatters off the grating under grazing incidence conditions (glancing angle θin). A part of the scattered beam is transmitted to the detector which is equipped with an entrance slit (Slit 3, 25 μm wide) located 38 cm downstream from the grating. The detector pivot axis serves as the y-axis of our coordinate system. The grating is mounted such that the y-axis is parallel to its grooves and passes through the center of its surface. The centers of the three slits are on the incident plane formed by k and the grating normal. The detection angle θ is defined by the line from the coordinate origin to the center of Slit 3, which is on the plane of incidence. We vary θin and θ, which are measured with respect to the grating surface, by rotating the grating and the detector around the y-axis, respectively. A diffraction pattern is obtained by recording the detector signal at different values of θ for a given θin. Furthermore, to characterise the incident beam, angular profiles can also be measured with the grating fully removed from the beam path. The full widths at half maximum (FWHM) of incident-beam profiles are observed to be about 120 μrad resulting from beam collimation and the angular resolution of the detector, and present the angular resolution of the apparatus.The detector is a non-commercial mass-spectrometer. Neutral atoms or clusters entering the detector are first ionized by electron bombardment. The resulting ions are accelerated by a voltage of 1 kV and mass-to-charge selected in a 90° sector-field electro magnet, before the ion signal is recorded by a multiplier tube. Due to their weak binding energies the neutral clusters He2 and He3 can easily fragment in the ionization step. As a result neutral clusters He2 and He3 can both be detected on the He+ (4 mass units) and on the He2+ (8 mass units) channel of the detector,8 whereas neutral He atoms can only be observed when the detector is set to the He+ (4 mass units) channel. It will be shown below how this feature of the detector can be exploited to assign diffraction peaks in angular spectra to atoms and clusters.
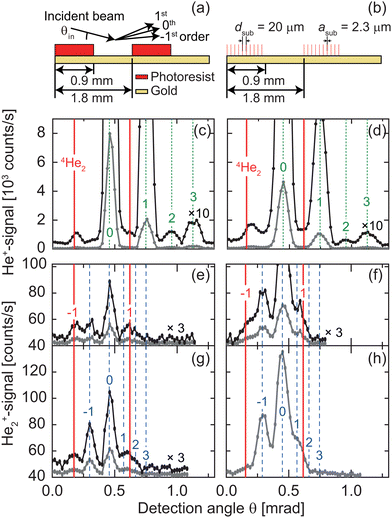
We use two plane square-wave gratings, referred to as conventional and dual-period grating, the schematics of which are shown in Fig. 3(a) and (b), respectively. These gratings consist of one-dimensional periodic arrays of parallel strips made of 1.01 μm-thick photoresist patterned on a commercial gold mirror. The conventional grating has a period of d = 1.8 mm (1.790 ± 0.002 mm) and a strip width of a = 0.9 mm (0.894 ± 0.002 mm). In the dual-period grating, each 0.9 mm-wide strip is replaced by a sub-grating composed of 45 photoresist strips that have a width of asub = 2.3 μm (2.08 ± 0.04 μm) and are separated by dsub = 20 μm (20.1 ± 0.1 μm). The values in parentheses give the dimensions measured using an optical microscope in addition to the nominal values.
3 Results and discussion
3.1 Diffraction patterns measured at different ion-mass channels
Fig. 3(c)–(h) shows the diffraction patterns of helium cluster beams from the conventional and dual-period gratings at θin = 0.48 mrad. To make it easier to assign diffraction peaks to atoms or clusters, the predicted diffraction angles θn for He, He2, and He3 are indicated by green dotted, red solid, and blue dashed vertical lines, respectively. These were calculated for de Broglie wavelengths of λ = 0.326, 0.163, and 0.109 nm, respectively. The diffraction patterns for T0 = 9.0 K and P0 = 1.0 bar, measured with the detector set to 4 atomic mass units (4 u), are shown in Fig. 3(c) and (d). The He+ signal results predominantly from ionizing neutral He monomers, but, as described above, due to fragmentation in the ionizer it can as well stem from neutral clusters in the beam.In both spectra, intense specular and diffraction peaks are found at the calculated diffraction angles of the He atoms. Therefore, we assign these peaks, which appear to be more intense for the conventional grating than for the dual-period grating, to the He monomer. In addition to the monomer peaks, the −1st-order diffraction peak of He2 is clearly visible. Unlike the monomer peaks, its intensity is larger for the dual-period grating than for the conventional grating. The signal occurring in between the specular peak and the dimer −1st-order diffraction peak, which is larger for the dual-period grating, can be tentatively attributed to contributions from He3.
To learn more about the diffraction probabilities of He2 and He3, we repeated the measurement with the detector set to the He2+ (8 mass units) channel for otherwise identical conditions (Fig. 3(e) and (f)). The absence of the monomer signal in this ion-channel mode of the detector makes the −1st-order diffraction peak of the trimer, a specular peak of the clusters, and the 1st-order diffraction peak of the dimers distinctive. The dimer signal (≈5 counts/s) appears weaker than the corresponding one in the spectra measured at the mass 4 channel (≈100 counts/s). This reflects the branching probabilities of He+ and He2+ being formed upon electron-impact ionization of neutral He2.8 The overall signals for the dual-period grating (Fig. 3(f)) are clearly higher compared with those for the conventional grating (Fig. 3(e)). The peak height of the trimer −1st-order beam from the dual-period grating (13 counts/s) is 2.6 times larger than that from the conventional grating (5 counts/s). The corresponding peak height ratio for the dimer is approximately 1.5.
When P0 is increased from 1.0 to 2.0 bar (Fig. 3(g) and (h)), the He2+ signals of the diffraction patterns increase, and the enhancement of the He3 reflection probability by the dual-period grating becomes clearly visible. The larger signal at the higher P0 is due to the increased mole fraction xN of trimers and larger clusters (HeN with N ≥ 3) in the helium beam. The mole fractions of helium clusters formed in the molecular beam expansion vary with P0.34 At T0 = 9.0 K the mole fraction of trimers and larger clusters rises within the pressure range from 1.0 to 2.0 bar, whereas the dimer mole fraction x2 starts to decreases in this pressure range. At P0 = 2.0 bar the He3 signal at θ−1 for the dual-period grating is 5.7 times stronger than that for the conventional grating. The different values of these factors for the two stagnation conditions, 2.6 and 5.7, indicate that the corresponding signals originate from He3 and larger clusters as well.
These results indicate that by replacing the flat strips of the conventional grating by the sub-grating structures in the dual-period grating, we can alter the reflection probabilities of helium atoms and clusters. Apparently, the atoms exhibit a reduced probability of reflection from the dual-period grating, whereas for He2 and, in particular, for He3 it is increased.
3.2 Reflection probabilities of He, He2, and He3 as a function of incidence angle
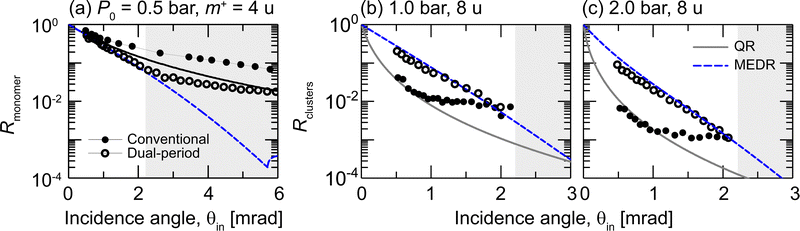
To study the reflection probability quantitatively and to check the different reflection mechanisms at play, we analyze the coherent reflection probabilities of helium atoms and clusters, Rmonomer and Rclusters, respectively, as a function of the incidence angle θin and compare them to calculated reflection probabilities in Fig. 4. Experimental values of Rmonomer and Rclusters are determined from the integrated areas of the diffraction peaks (including specular peak) measured at the He+ and He2+ ion-mass channel, respectively. The resulting data are normalized to the incident beam area at each ion-mass channel and eventually multiplied by 2 to compensate for the duty cycle of 1/2 of both conventional and dual-period gratings. We measure Rmonomer at reduced stagnation pressure of P0 = 0.5 bar to avoid contributions from helium clusters, while the beam-source conditions for Fig. 4(b) and (c) are identical to those for Fig. 3(e), (f) and (g), (e), respectively.The experimental reflectivities of He atoms, plotted in Fig. 4(a), are found to increase with decreasing incidence angle approaching unity in the limit θin → 0. While both gratings exhibit atomic reflectivities greater than 1% over the full range of incidence angles, the reflectivity from the conventional grating appears to be significantly larger than the one for the dual-period grating. This is in agreement with our previous results and has been explained in terms of quantum reflection from the conventional grating being more efficient, for atoms, than reflection resulting from multiple-edge diffraction.20
The experimental reflection probabilities of helium clusters plotted in Fig. 4(b) and (c) are overall smaller than those of the monomers and, for the dual-period grating, exhibit a steeper decay with increasing incidence angle. Most notably, the cluster reflection probabilities show the opposite hierarchy as compared to the atoms; they are greater for the dual-period grating than for the conventional grating. This is found for P0 = 1.0 bar (Fig. 4(b)), where mainly dimers constitute the clusters in the beam, and it appears to be even more pronounced for P0 = 2.0 bar (Fig. 4(c)), where trimers are the dominant cluster component. For instance, for P0 = 2.0 bar at θin ≃ 1 mrad the reflection probability from the dual-period grating is about 1 order of magnitude larger than the one of the conventional grating. This observation is in line with the basic picture of quantum reflection decreasing with increasing particle–surface interaction strength. As the latter increases steadily with cluster size, dimers and, more so, trimers exhibit much smaller quantum reflection probabilities than helium atoms.17 This is not the case for reflection mediated by multiple-edge diffraction, because it only depends on the particle's de Broglie wavelength (although it can also get somewhat reduced by the particle–surface interaction35). For the dual-period grating we observe reflection probabilities of small helium clusters at the smallest incidence angles in excess of 20% at P0 = 1.0 bar (predominantly He2) and in excess of 10% at P0 = 2.0 bar (predominantly He3).
3.3 Reflection probabilities calculated with two different models; quantum reflection and reflection by multiple-edge diffraction
To check this interpretation we quantitatively model the data by quantum reflection and by the multiple-edge-diffraction reflection model. The solid lines in Fig. 4 represent the reflection probabilities calculated for quantum reflection from a flat surface. The dashed lines represent reflection probabilities calculated within the model of multiple-edge diffraction at an array of parallel half-planes. In either model the calculation of Rclusters requires a weighted summation over the relevant cluster sizes by considering the contribution of each cluster size to the He2+ signal. This is achieved by the following equation,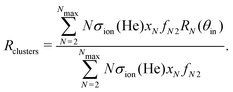 | (1) |
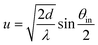 | (2) |
| e0,MEDR = G(u)2, | (3) |
 | (4) |
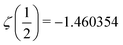 is given by the Riemann zeta function ζ(s).
is given by the Riemann zeta function ζ(s).
Reflection due to multiple-edge diffraction is also affected by the particle–surface interaction. It was shown by Kouznetsov and Oberst35 that the van der Waals interaction between an incident particle and a strip of non-negligible width (asub = 2.3 μm in our dual-period grating) causes a reduction of the reflection efficiency, which can be described by an attenuation factor A(θin). To approximate the interaction potential we use the Casimir–van der Waals potential, UCvdW = −lC3/(z + l)z3 with the same C(N)3 and l(N) parameters used in the QR model described above. This interaction induces an additional phase shift to the matter-wave and thereby reduces the specular reflection probability. We derive A(θin) using eqn (55) of ref. 35. The reflection probabilities RN of HeN scattering from the dual-period grating within the MEDR model corrected for the influence of the van der Waals interaction follow as the product of e0,MEDR(θin) and A(θin).
To check the assumption that reflection based on multiple-edge diffraction is responsible for the increased cluster reflectivity from the dual-period grating we compare the experimental data with results from MEDR calculations. Despite a number of uncertainties that enter eqn (1), including the mole fractions xN, the ionization cross sections σion(HeN), and the fragmentation probabilities fNK, the MEDR calculations show a reasonable agreement with the cluster reflectivities observed with the dual-period grating. The smaller cluster reflectivities observed with the conventional grating can be reasonably well described by the quantum reflection calculation only at small incidence angles below about 1 mrad. At larger incidence angles the observed cluster reflectivities are greater than what is predicted by the QR model. The reason for this deviation is not yet understood.
Regarding the He atom reflectivity, it is apparent from Fig. 4(a) that the model calculations do not provide an accurate description of the measured reflectivities. For the dual-period grating the MEDR calculation is in reasonable agreement with the experimental probability for small θin < 2.2 mrad only. At larger incidence angles, θin > 2.2 mrad, parts of the incident beam can scatter off from the gold substrate of the grating and contribute to Ratom. Thus, both models necessarily break down in this regime indicated by the shaded area in the plots. The measured atomic reflectivity from the conventional grating, on the other hand, are poorly described by the calculated QR probability. Reasonable agreement is only found at the smallest values of θin (<1 mrad). At larger incidence angles the calculated QR probability clearly underestimates the observed reflectivity.
4 Conclusions
Our results demonstrate reflection and diffraction of fragile He2 and He3 from a conventional square-wave grating and a dual-period grating under grazing incidence conditions. The observation of diffraction peaks at different ion-mass channels of the mass-spectrometer detector provides evidence for coherent and elastic (non-destructive) scattering of the weakly bound van der Waals clusters. Total coherent reflection probabilities of mixed-size helium clusters from the two gratings are explained in terms of quantum reflection for the conventional grating and reflection based on multiple-edge diffraction (MEDR) for the dual-period grating. Our results indicate that reflection by multiple-edge diffraction allows for much increased reflection probabilities and, hence, diffraction efficiencies of He2 and He3 as compared with those found for quantum reflection from the conventional grating.Within the MEDR model the reflection probability is a function of a single universal parameter u, which is proportional to the root of the half-plane-array's period and to the sine of the glancing angle. This opens the possibility to further increase the total coherent reflection probability from a dual-period grating in future experiments by (i) decreasing the period and width of the sub-grating ridges and/or by (ii) going to even smaller angles of incidence. The latter approach will require large area (many cm wide) dual-period gratings of excellent macroscopic flatness. Elastic coherent reflection probabilities of He2 and He3 in excess of 25% can be expected. For He3, for instance, this corresponds to an increase by a factor of 2.5 bringing the −1st-order diffraction peak intensity at the He2+ ion-mass channel from presently ≈80 counts/s (Fig. 3(h)) up to 200 counts/s for otherwise identical conditions. The latter is about the same signal as what has been observed by diffraction from state-of-the-art 100 nm-period transmission gratings using one and the same detector as in the present work.34 In those experiments the level of angular collimation (70 μrad FWHM) was almost a factor of two better than in the present setup (120 μrad FWHM), and the helium-beam source was operated at 6 K, where the flux of He3 is about 50% greater than at the presently used 9 K. From this we conclude that the flux of helium trimers per radian that can be achieved by MEDR from a taylor-made dual-period grating at grazing incidence can realistically reach about the same level as what has been achieved with a nanoscale transmission grating.
Furthermore, with a reflection probability as large as 25%, experiments with preselected beams of He2, and He3 will be feasible. In these experiments, a pure beam of helium dimers or trimers can be prepared by diffraction from a nanoscale transmission grating. Subsequently, the reflection of a selected cluster size from the structured surface of interest can be investigated. In this approach a dual-period grating structure is no longer needed to study multiple-edge diffraction; the large-scale grating, needed to mass select clusters and atoms in the present experiments, can then be omitted. Instead a flat surface structured by ridges of width asub with period dsub can be used. Reflectivity measurements of He2 or He3 from that kind of surface can serve as clean bench tests for model descriptions. In particular, this will make it possible to investigate how the van der Waals interaction between He2 or He3 and the structured surface affects reflection by multiple-edge diffraction.
Author contributions
B. S. Z. conceived and supervised the experiment. L. Y. K. performed the measurements. S. P. and C. Y. L. prepared the micro-structured gratings. L. Y. K. made the simulations. L. Y. K., W. S., and B. S. Z. analyzed the data. B. S. Z. and W. S. wrote the manuscript with input from all co-authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT, and Future Planning (Grant No. NRF-2019R1A2C1086215, NRF-2020R1A2C3003701, NRF-2019R1A2C1084928, and NRF-2017H1A2A1042369). Open Access funding provided by the Max Planck Society.Notes and references
- R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt, T. Köhler and M. Stoll, Phys. Rev. Lett., 2000, 85, 2284–2287 CrossRef CAS PubMed.
- S. Zeller, M. Kunitski, J. Voigtsberger, A. Kalinin, A. Schottelius, C. Schober, M. Waitz, H. Sann, A. Hartung, T. Bauer, M. Pitzer, F. Trinter, C. Goihl, C. Janke, M. Richter, G. Kastirke, M. Weller, A. Czasch, M. Kitzler, M. Braune, R. E. Grisenti, W. Schöllkopf, L. Ph. H. Schmidt, M. S. Schöffler, J. B. Williams, T. Jahnke and R. Dörner, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14651–14655 CrossRef CAS PubMed.
- A. S. Jensen, K. Riisager, D. V. Fedorov and E. Garrido, Rev. Mod. Phys., 2004, 76, 215–261 CrossRef CAS.
- M. Kunitski, S. Zeller, J. Voigtsberger, A. Kalinin, L. Ph. H. Schmidt, M. Schöffler, A. Czasch, W. Schöllkopf, R. E. Grisenti, T. Jahnke, D. Blume and R. Dörner, Science, 2015, 348, 551–555 CrossRef CAS PubMed.
- V. Efimov, Phys. Lett. B, 1970, 33, 563–564 CrossRef CAS.
- F. Luo, G. Kim, G. C. McBane, C. F. Giese and W. R. Gentry, J. Chem. Phys., 1993, 98, 9687–9690 CrossRef CAS.
- W. Schöllkopf and J. P. Toennies, Science, 1994, 266, 1345–1348 CrossRef PubMed.
- W. Schöllkopf and J. P. Toennies, J. Chem. Phys., 1996, 104, 1155–1158 CrossRef.
- R. Brühl, A. Kalinin, O. Kornilov, J. P. Toennies, G. C. Hegerfeldt and M. Stoll, Phys. Rev. Lett., 2005, 95, 063002 CrossRef PubMed.
- J. Voigtsberger, S. Zeller, J. Becht, N. Neumann, F. Sturm, H.-K. Kim, M. Waitz, F. Trinter, M. Kunitski, A. Kalinin, J. Wu, W. Schöllkopf, D. Bressanini, A. Czasch, J. B. Williams, K. Ullmann-Pfleger, L. Ph. H. Schmidt, M. S. Schöffler, R. E. Grisenti, T. Jahnke and R. Dörner, Nat. Commun., 2014, 5, 5765 CrossRef CAS PubMed.
- B. Friedrich, M. Gupta and D. Herschbach, Collect. Czech. Chem. Commun., 1998, 63, 1089–1093 CrossRef CAS.
- M. Lemeshko and B. Friedrich, Phys. Rev. Lett., 2009, 103, 053003 CrossRef PubMed.
- M. Lemeshko and B. Friedrich, J. Phys. Chem. A, 2010, 114, 9848–9854 CrossRef CAS PubMed.
- Q. Wei, S. Kais, T. Yasuike and D. Herschbach, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E9058–E9066 CAS.
- Q. Guan and D. Blume, Phys. Rev. A, 2019, 99, 033416 CrossRef CAS.
- M. Kunitski, Q. Guan, H. Maschkiwitz, J. Hahnenbruch, S. Eckart, S. Zeller, A. Kalinin, M. Schöffler, L. Ph. H. Schmidt, T. Jahnke, D. Blume and R. Dörner, Nat. Phys., 2021, 17, 174–178 Search PubMed.
- B. S. Zhao, S. A. Schulz, S. A. Meek, G. Meijer and W. Schöllkopf, Phys. Rev. A, 2008, 78, 010902(R) CrossRef.
- G. Rojas-Lorenzo, J. Rubayo-Soneira, S. Miret-Artés and E. Pollak, Phys. Rev. A, 2018, 98, 063604 CrossRef CAS.
- H. Oberst, D. Kouznetsov, K. Shimizu, J. Fujita and F. Shimizu, Phys. Rev. Lett., 2005, 94, 013203 CrossRef PubMed.
- J. H. Lee, L. Y. Kim, Y.-T. Kim, C. Y. Lee, W. Schöllkopf and B. S. Zhao, Phys. Rev. Lett., 2019, 122, 040401 CrossRef CAS PubMed.
- R. B. Doak and A. V. G. Chizmeshya, Europhys. Lett., 2000, 51, 381–387 CrossRef CAS.
- A. Mody, M. Haggerty, J. M. Doyle and E. J. Heller, Phys. Rev. B, 2001, 64, 085418 CrossRef.
- H. Friedrich, G. Jacoby and C. G. Meister, Phys. Rev. A, 2002, 65, 032902 CrossRef.
- S. Miret-Artés and E. Pollak, J. Phys. Chem. Lett., 2017, 8, 1009–1013 CrossRef PubMed.
- J. Petersen, E. Pollak and S. Miret-Artés, Phys. Rev. A, 2018, 97, 042102 CrossRef CAS.
- G. Rojas-Lorenzo, J. Rubayo-Soneira, S. Miret-Artés and E. Pollak, Phys. Rev. A, 2020, 101, 022506 CrossRef CAS.
- W. Zhang, J. H. Lee, H. A. Kim, B. G. Jin, B. J. Kim, L. Y. Kim, B. S. Zhao and W. Schöllkopf, ChemPhysChem, 2016, 17, 3670–3676 CrossRef CAS PubMed.
- F. Shimizu, Phys. Rev. Lett., 2001, 86, 987–990 CrossRef CAS PubMed.
- V. Druzhinina and M. DeKieviet, Phys. Rev. Lett., 2003, 91, 193202 CrossRef CAS PubMed.
- B. S. Zhao, H. C. Schewe, G. Meijer and W. Schöllkopf, Phys. Rev. Lett., 2010, 105, 133203 CrossRef PubMed.
- B. S. Zhao, G. Meijer and W. Schöllkopf, Science, 2011, 331, 892–894 CrossRef CAS PubMed.
- B. S. Zhao, W. Zhang and W. Schöllkopf, Mol. Phys., 2013, 111, 1772–1780 CrossRef CAS.
- E. Bogomolny and C. Schmit, Nonlinearity, 2003, 16, 2035–2059 CrossRef.
- L. W. Bruch, W. Schöllkopf and J. P. Toennies, J. Chem. Phys., 2002, 117, 1544–1566 CrossRef CAS.
- D. Kouznetsov and H. Oberst, Phys. Rev. A, 2005, 72, 013617 CrossRef.
- C. Hättig, H. Larsen, J. Olsen, P. Jørgensen, H. Koch, B. Fernández and A. Rizzo, J. Chem. Phys., 1999, 111, 10099–10107 CrossRef.
| This journal is © the Owner Societies 2022 |