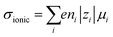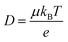Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploiting mixed conducting polymers in organic and bioelectronic devices
Scott T.
Keene†
a,
Viktor
Gueskine†
 bc,
Magnus
Berggren
bc,
Magnus
Berggren
 bc,
George G.
Malliaras
bc,
George G.
Malliaras
 a,
Klas
Tybrandt
a,
Klas
Tybrandt
 bc and
Igor
Zozoulenko
bc and
Igor
Zozoulenko
 *bc
*bc
aElectrical Engineering Division, Department of Engineering, Cambridge University, 9 JJ Thompson Ave., CB3 0FA Cambridge, UK
bLaboratory of Organic Electronics, Department of Science and Technology, Linköping University, SE-601 74, Norrköping, Sweden. E-mail: igor.zozoulenko@liu.se
cWallenberg Wood Science Center, Linköping University, SE-601 74, Norrköping, Sweden
First published on 2nd August 2022
Abstract
Efficient transport of both ionic and electronic charges in conjugated polymers (CPs) has enabled a wide range of novel electrochemical devices spanning applications from energy storage to bioelectronic devices. In this Perspective, we provide an overview of the fundamental physical processes which underlie the operation of mixed conducting polymer (MCP) devices. While charge injection and transport have been studied extensively in both ionic and electronic conductors, translating these principles to mixed conducting systems proves challenging due to the complex relationships among the individual materials properties. We break down the process of electrochemical (de)doping, the basic feature exploited in mixed conducting devices, into its key steps, highlighting recent advances in the study of these physical processes in the context of MCPs. Furthermore, we identify remaining challenges in further extending fundamental understanding of MCP-based device operation. Ultimately, a deeper understanding of the elementary processes governing operation in MCPs will drive the advancement in both materials design and device performance.
1. Introduction
Mixed ionic-electronic conduction is a critical feature in a wide range of emerging electrochemical devices which utilize their unique ability to modulate the charge carrier concentration through the bulk of the active material. Mixed ionic-electronic conductors (MIECs) based on conjugated polymers (CPs) have recently emerged as a promising class of materials due to their relatively large free volume facilitating ion transport with relatively low activation energy barriers. These materials have been utilized for a wide range of breakthrough organic electrochemical devices (OECDs) including organic batteries,1 supercapacitors,2 wearable and implantable biosensors,3,4 printed electronic circuits,5 amplifiers,6 electrochromic displays,7 and neuromorphic devices.8The common functionality of all OECDs is the intimate coupling of ionic and electronic charges throughout the bulk of the CP film. Along a typical CP–electrolyte interface, charge polarization and compensation are stabilized by dipole moments extending only over short charge separation distances. For mixed conducting polymers (MCPs) which allow transport of both electronic and ionic charges through the bulk of the material, the CP–electrolyte interface extends through the bulk of the material allowing for OECDs which operate at low voltages and respond to chemical, physical, or biological features. In addition, this tight coupling of ions and electronic charges allows for the construction of devices which operate volumetrically rather than at a nanoscale interface. This volumetric operation facilitates production of “robust” OECDs and systems which operate at low voltages. Thus, the overall performance and device parameters of OECDs are to a large extent dependent on the energetics for injection, transport, and coupling of electronic and ionic charges.
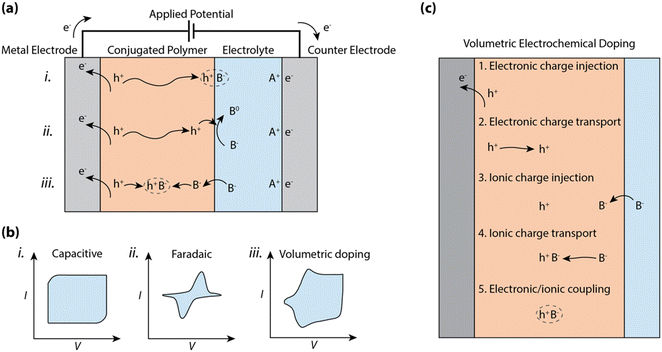
So, how is charge polarization established in CP–electrolyte systems? At one extreme, the ions of the electrolyte can only compensate and polarize the electronic charges of the CP along the planar CP–electrolyte interface, akin to a double layer capacitive electrode (see (i) in Fig. 1a). In this case, the charge polarization is preceded by displacement of ions in the electrolyte along with injection and transport of electronic charges within the CP towards the interface. The boundary at the CP–electrolyte interface, which prevents motion of either electronic or ionic carriers, leads to the formation of an electric double layer, typically reaching an areal capacitance value in the range of 1 to 10 μF cm−2.9 This double-layer formation results in a box-like characteristic in the cyclic voltammogram (see (i) in Fig. 1b) due to the linear relationship between surface charge density and voltage. Such double layer formation at the electrode–electrolyte interface, including the accumulated 2-D interface of electronic charges residing in the CP, defines the mode of operation of electrolyte-gated organic field effect transistors (EGOFETs)10–12 and EGOFET sensors.13,14
In addition to the case described above, one should also account for possible charge transfer between the CP phase and components of the electrolyte system (see (ii) in Fig. 1a). Such a faradaic process (relative to the solution components) can include any reduction or oxidation (redox) process with reactants present in the electrolyte system. If a redox molecule is added to the electrolyte in contact with a CP electrode, the electric double layer stores charge, while the charges at the CP–electrolyte interface can be transferred to the redox molecule. The resulting CP electrode thus expresses the permutation of capacitive and redox characteristics, where a distinct redox peak can be observed in the cyclic voltammogram (see (ii) in Fig. 1b) due to both the exponential dependence between current and potential as well as the diffusion-limited current of the redox-active molecule. CP films have also been explored as the faradaic electrode in various electrocatalytic experiments and systems, exemplified by the electrocatalytic production of hydrogen (H2)15,16 and as the cathodic catalyst for the reduction of hydrogen peroxide (H2O2) to water.17
In organic mixed conducting materials, the CP bulk includes percolating pathways for ions. In many cases, the CP is complexed or decorated with hydrophilic moieties to favor ion transport and/or electrolyte uptake.2,18,19 Then, the transport of ions and electrons occurs within a bi-continuous conducting network, where double layers are formed along the boundary between the two phases. The shape and size of this two-phase system depends on the morphology of the amalgam, often resulting in very large specific surface areas reaching far beyond 100 m2 g−1.20 Thus for MCPs, charge accumulation and ion compensation occur within a 3D network and produces a bulk capacitance of typical values in the range of ca. 10 to 1000 F g−1 and scales with volume instead of the area of the CP film (see (iii) in Fig. 1a).21,22 The reversible accumulation–depletion switching and charge polarization of the CP thus include injection and transport of both electrons and ions into and within the CP bulk volume, respectively (see (iii) in Fig. 1a). Such bulk switching allows reversible control of the electronic carrier density of the CP bulk, a phenomenon that is utilized in electrochromic displays,23 organic electrochemical transistors,24 polymer supercapacitors,25 and conjugated polymer actuators.26
The performance of a CP film while operating in an electrochemical device is to a large extent dictated by the charging-discharging properties, following any of the processes in Fig. 1c. The wide range of physical processes involved in bulk ionic doping of CPs complicates the analysis of the cyclic voltammogram, which tends to include both box-like capacitive features as well as diffusion limited peaks (see (iii) in Fig. 1b). These non-linearities due to charge injection, ionic/electronic diffusion, non-constant electron mobility, and/or redox potentials distributed over large voltage regions make a simple description of the bulk charging process invalid.
Here, we scrutinize the individual physical processes involved in bulk electrochemical doping, and identify the effect of CP morphology/organization on the process, and the impact of each process on the performance of OECDs. In the following sections, we will examine the following processes required for bulk electrochemical doping, noting the interdependence of the individual steps: (1) electronic charge injection across the CP/metal interface, (2) electronic charge transport through the CP, (3) ionic charge injection at the CP/electrolyte interface, (4) ionic charge transport, and (5) charge coupling between ionic and electronic carriers within the CP (Fig. 1c). Finally, we will compare the electrochemical reactions observed for MCPs to classical capacitive and faradaic electrodes and describe how the pseudocapacitive and faradaic properties of MCPs can be exploited in heterogeneous electrocatalysis. With this thorough examination, we aim to summarize the state-of-the-art understanding of conjugated polymer–electrolyte systems and its bearing on some of the critical device parameters of OECDs. Additionally, the outlooks aim to provide direction for further characterization and understanding of the operational mechanics of MCP devices and systems.
2. Electronic charge injection
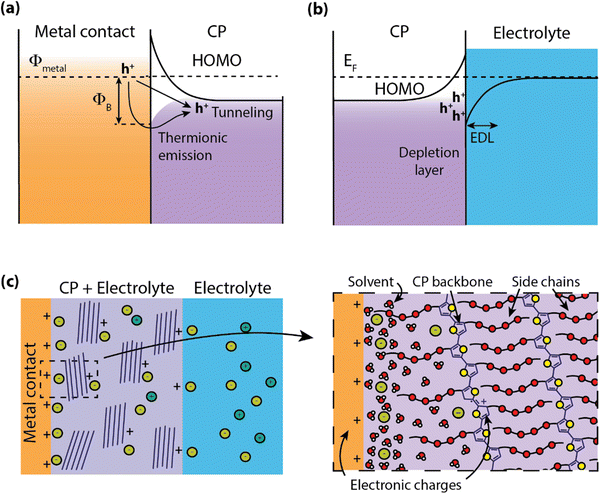
Electronic state energy alignment has long been an important direction of study to understand the physics of organic devices such as organic field-effect transistors (OFETs),27 organic light-emitting devices (OLEDs),28 and organic photovoltaics (OPVs).29 By understanding how charges move across conjugated polymer (CP)–metal heterojunctions, the field of organic electronics has achieved significant advancements in device design and performance. For instance, interfacial engineering has played a significant role in the improvement of OPV power conversion efficiencies.30,31 While it is apparent that charge injection will certainly dictate the operation of organic electrochemical devices (OECDs) as well, there are far fewer studies on these systems. In this section, we explore how the models and descriptions of metal–organic interfaces can extend to “wet” systems.When CPs are put in contact with metals, such as in OLEDs or OFETs, a barrier for charge transport is formed do to the band-bending of electronic states at heterojunction, leading to a device contact resistance (RC)32 for electronic charge injection (Fig. 2a). In addition to the mismatch of Fermi levels between the metal and CP, the misalignment at the interface can be greatly affected by the formation of surface dipoles,33 hybridization of molecular orbitals with the metal electronic states,34 and, for the case of surface monolayers, covalent bonding at the metal surface.35 Often contact engineering can improve performance of these organic optoelectronic devices using materials layers which ease the barrier for charge injection or extraction.36 However, this picture of electronic energy alignment is complicated by the inclusion of an electrolyte in the CP.
Water–semiconductor interfaces (Fig. 2b) can largely be described with similar band bending models considering the polarizability of water molecules and the electrolyte. Polarization between the solid electrode and liquid electrolyte is described by the formation of an electric double layer (EDL) that screens the potential difference between the two phases. This EDL is roughly analogous to the depletion region in semiconductors, where a local electric field is screened by the local rearrangement of charges and/or dipoles. The structure and charge distribution of the EDL can be estimated using models with increasing complexity to account for the arrangement of ions and solvent dipoles at the interface (e.g. Helmholtz, Gouy-Chapman), solvent and/or ion electrosorption to the surface,37,38 and the accumulation/depletion of charges at the semiconductor surface.39
Many OECDs operate with aqueous electrolytes and are designed to readily uptake water into the bulk of the material, easing the transport of ionic species through the CP.19 This presence of water in the bulk introduces complications to understanding the band alignment at the CP–electrode heterojunction (Fig. 2c). For example, the inclusion of ions and solvent (water) in the CP can result in the formation of an EDL at the heterojunction, further altering the electron energetic landscape. This has been explored for light-emitting electrochemical cells, which were observed to have charge injection voltages near the bandgap of the emitter without the use of charge injection layers.40 Further investigation revealed that the presence of ions in the polymer shrink the width of the depletion region at the contact due to the formation of an EDL, thereby reducing the tunneling distance and facilitating charge injection.41 Recent organic electrochemical transistor (OECT) models have predicted nonuniform ion distribution within the CP during steady-state operation,42 indicating that an accurate description of ion distributions could assist in understanding both electronic charge injection as well as transport.
While many OECDs demonstrate ohmic electronic contact, it is still critical to characterize electronic charge injection to understand and improve OECD engineering. First, polarization of electrolyte in the CP could have implications for the maximum speed of operation in OECDs. For amplifiers43 and memory devices44 where speed is a critical metric, understanding the time associated with internal EDL formation at the contact is crucial. Furthermore, parasitic charge injection plays a significant role in OECD operational stability.45 Thus, understanding the parasitic reactions between the electrolyte and contact could be leveraged to further design contacts for more stable OECDs. Finally, the contact resistance and ion accumulation at the contacts could play a significant role in modulation in gated (transistor-like) OECDs.46,47 For example, the use of contact passivating layers has proven to significantly improve the performance of organic electrochemical transistors.48 While there is a great wealth of knowledge regarding contact engineering from research on OLEDs, OFETs, and OPVs, a better understanding charge injection in OECDs would inform device design and reveal which strategies are relevant.
Characterizing the energy landscape of the three-phase interface between the metal, CP, and solvent/electrolyte has proven challenging. The large degrees of molecular freedom for the solvent and electrolyte introduce computational complexity for first principles modeling of the interface. Additionally, the presence of water complicates traditional measurements of electronic energies such as with ultraviolet photoelectron spectroscopy/low energy inverse photoelectron spectroscopy (UPS/LEIPS) due to the requirement of a high vacuum. Traditional electrochemical analysis is also somewhat convoluted due to the presence of two polarizable interfaces – one at the electrode–CP junction and one at the CP–water interface. Electrochemical techniques such as spectroelectrochemistry, cyclic voltammetry, chronopotentiometry, and chronoamperometry can reveal information about electronic doping profile, injection potentials, and injection rates; however, these techniques do not differentiate between ion and electron limited injection. There are numerous other effects associated with water such as deep traps sites49 and parasitic redox reactions,50 which further convolutes measurements of electronic charge injection.
To overcome these challenges associated with characterizing electronic charge injection, it is critical to consider the full electrochemical doping process when analyzing experimental results. When possible, the specific electrochemical processes being investigated (i.e., ionic/electronic ejection or expulsion, faradaic reactions) should be isolated. This isolation can also be achieved by combining traditional electrochemical measurements with orthogonal measurements such as optical microscopy51/spectroscopy,52 mapping potential across the material,42 characterizing the contact resistance,53 electron spin resonance,54 Raman spectroscopy55/microscopy,56 quartz crystal microbalance,57,58 ellipsometry,59 neutron reflection,60 grazing-incidence X-ray diffraction,61etc. These in situ and operando techniques allow for characterization of the evolving microstructure, chemical bonding environment, solvation of ions/polymers, mass uptake across a wide range of time and length scales, which improves the microscopic and energetic understanding of ion and electronic injection kinetics and greatly advances physical models of OECD operation.
3. Electronic structure and charge transport
Electron transport in CPs has been the subject of intensive studies for many decades62 and has become the primary metric for quantifying CP material performance in optoelectronic devices. It is generally accepted that electronic charge carriers in CPs are transported via phonon-assisted hopping consisting of both intra- and interchain jumps. This conclusion is based on the character of the temperature dependence of the conductivity (σ) in most conductive polymers, where σ increases with temperature, which is the characteristic feature of the hopping transport.63,64 However, we note that in some rare cases, CPs can also exhibit semi-metallic, band-like transport where the conductivity decreases with increasing temperature,65 which, however, still can be attributed to the hopping transport.64 The intense study of the electronic structure and transport in CPs has led to the emergence of a “traditional,” widely accepted polaronic picture66 where charges are localized on a polymer chain over several monomer units due to a strong electron-lattice interactions.67The hopping transport of polarons in CPs consists of a series of jumps between localized states along the CP backbone and/or between neighboring chains (Fig. 3a–d). The charge carrier hopping can be qualitatively described in either real space (Fig. 3c) or in energy space (Fig. 3d) where the localized states have different energies due to the disordered electrostatic potential due to the local surroundings (counterions, neighboring chains, water molecules, etc.). The phonon-assisted hopping probability between localized states, as described by the Miller–Abrahams formula,68 depends on the distance between the localized states and their energy difference. In order to account for the reorganization energy of the polymer chains during the hopping event, the Marcus hopping rate is often used.69 To capture charge transport in disordered organic conductors and CPs, Bässler et al. developed Monte Carlo simulations to analyze the dependence of the carrier mobility on temperature, electric field, and carrier concentration.70 These ideas were further developed by Arkhipov et al. who utilized the concept of the transport energy (Etransp), which represents the energy to promote a carrier from the tail of the DOS to a mobile (i.e. conducting) electronic state (Fig. 3d).71 The energy from phonons is needed to promote carriers from the lowest energy electronic states into higher energy states which exist at a much higher concentration in the film. Then, from this higher energy state, charges can perform a random walk over the sites centered at Etransp in the energy space.
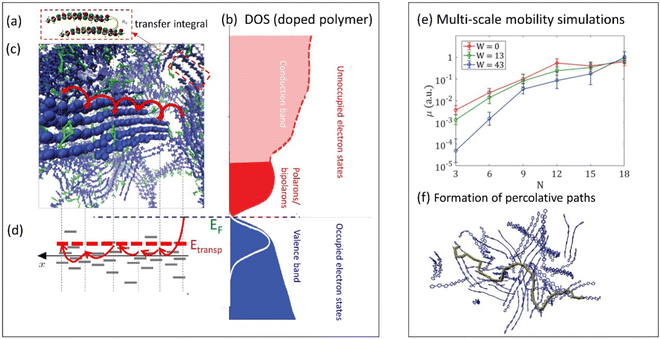 | ||
| Fig. 3 (a) Illustration of the transfer integral defining a hopping probability between two polymer chains in the film (adapted from ref. 79 with permission from American Physical Society, copyright 2018). (b) Schematic density of states (DOS) of doped conductive polymers (adapted from ref. 80 with permission from John Wiley and Sons, copyright 2018). (c) Snapshot of molecular dynamics simulations of PEDOT:TOS illustrating a charge hopping between the chains in the film (adapted from ref. 81), and (d) corresponding charge hopping in the energy space illustrating hopping between localized states on polymer chains. EF and Etransp define the Fermi energy and the transport energy respectively. (e) Multi-scale calculations of the mobility in conductive polymers as a function of the chain length N and water content W (adapted from ref. 79 with permission from American Physical Society, copyright 2018). The inset to the right illustrates a formation of percolative paths in polymer film (marked in green) (adapted from ref. 82). | ||
In these and further works, various semi-analytical models for charge transport (often combined with Monte Carlo calculations) were developed, providing quantitative description of the experimental temperature and the concentration dependences of the electronic mobility in a wide range of CP systems.72–74 For example, the experimental conductivity and the Seebeck coefficient in PEDOT:PSS and PEDOT:Tos65,75 were modeled in ref. 64, 73 and 74. In these works, the experimental results were successfully fitted using a hopping model of localized polarons extending over 2–3 monomer units, with typical jumps over a distance of 3–4 units, with energetic disorder (i.e. broadening of the DOS) estimated to be ca. 0.1 eV.73,74 When extended to mixed conducting systems, the model has predicted that, for low carrier concentrations, the number of mobile carriers contributing to the transport is only a small fraction of the total carriers.73,74 A possible explanation offered for this observation is that the electron percolation network is broken by the morphological changes to the polymer film during ion injection/expulsion, causing a transition to non-conductive state.
Many MCPs consist of both ordered and disordered phases, and it is therefore important for the material and device design to understand how (or whether) crystallinity and the polymerization degree affect the charge transport. Based on the analysis of reported mobilities for a wide range of CPs, Noriega et al. concluded that mobility is rather insensitive to the polymerization degree at high molecular weights, but shows a rapid decrease for CPs with short chain lengths.76 They argued that a high degree of crystallinity (i.e. long-range crystalline order) is of less importance for efficient charge transport; instead, it is the short-range connection between local aggregates or crystallites that are important for the enhancement of charge transport in the entire film. One critical pathway for this inter-grain transport is via long chains which bridge crystallites (i.e. tie chains).76 Similar conclusions were reached by Zhang et al. and Wang et al., who demonstrated that CPs lacking significant long-range order can outperform highly ordered CPs.77,78
Achieving a detailed microscopic understanding of the morphology-mobility dependence in MCPs requires approaches that go beyond simplified cubic-grid Monte Carlo or idealized semi-analytical models developed in earlier works. Such understanding can be achieved by modern multi-scale computational approaches that start with the calculations of the realistic material morphology using the molecular dynamics simulations.64,79,83–85 Based on this morphology, the calculation of the hopping rates is then performed, followed by the mobility calculations utilizing the Monte Carlo or master equation techniques. Such calculations were recently performed for PEDOT:Tos and analyzed in terms of transfer integral distributions and percolation thresholds.64,79,83 The percolative analysis shows that it is the effective π–π stacking, not the long-range order, which is essential for formation of the percolative paths across the film. In the same analysis, exponential growth of the electronic mobility with increasing chain length was shown for low degrees of polymerization, providing theoretical support for the findings of Noriega et al.76
For mixed conducting systems, it is also critical to account for the change in charge transport properties in the presence of ions and electrolyte. Recently, density functional theory (DFT) was applied to the description of the electronic structure of MCPs in the presence of ionic charges which resulted in a qualitatively different picture as compared to the “traditional” one (Fig. 4a–c).67,86–88 At low oxidation levels, the presence of negatively charged counterions in the vicinity of a polymer chain gives rise to the formation of an unoccupied polaron state above the valence band (Fig. 4a and d). As more counterions/dopants are present, the oxidation level of polymer increases and more polaronic states appear in the gap (Fig. 4b, e and f). As the oxidation level increases further, the overlapping polaronic states start to form an (unoccupied) polaronic band in the film (Fig. 4c and g). At high enough oxidation states, the polaronic band may even reach the filled valence band edge, leading to the observation of semi-metallic behavior.65,89
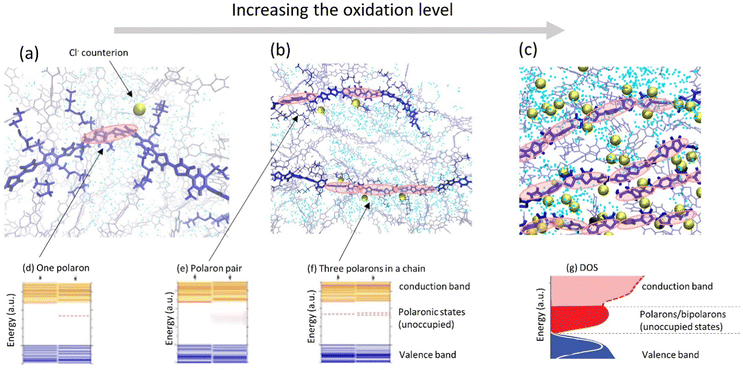 | ||
| Fig. 4 (a–c) Representative snapshots of molecular dynamics simulations of a conducting polymer illustrating morphological changes and ion intake during cyclic voltammetry as the oxidation level is progressively increases (adapted from ref. 90). Polymer backbones are shown in blue, Cl− counterions are shown as golden spheres; water molecules are shown as blue dots. Polaronic states in the polymer (depicted by red ovals) are schematic illustration. (d–f) Evolution of the electronic structure of a polymer as the oxidation level increases showing schematically the electronic structure of (d) one polaron, (e) a polaron pair, and (f) three polarons in a chain, respectively (adapted from ref. 88). (g) As the oxidation level increases, unoccupied polaronic states in the gap transforms into the polaron/bipolaron band in the DOS of the thin film (adapted from ref. 80 with permission from John Wiley and Sons, copyright 2018). | ||
While intuitively one might expect a change in the electronic transport properties of CPs in the presence of water, recent findings by Wieland et al. show that the electrical conductivity of PEDOT:PSS films are essentially unaffected by increasing water content.91 Multiscale transport models provide further insight into performance of CP films in the aqueous environment. For example, it is predicted that the mobility of holes in PEDOT-based MCPs is independent of the water content, which is explained in terms of formation of the extended network of π–π stacking connections throughout the system which remain unimpacted by water penetration.79,83 Multiscale mobility calculations for MCPs can also be used to predict side-chain distributions which optimize the performance of mixed ionic–electronic conductors.84,85 For example, Khot et al. predicted that electronic mobility is maximized when all of the side-chains are hydrophilic rather than form a mixture of randomly distributed hydrophilic and hydrophobic side chains.85 However, the results found for PEDOT-based MCPs is not generalized to other systems where, at some threshold, increasing water content/degree of swelling has been shown to reduce carrier mobility.92 Thus, further investigation of the effects of ions and water inclusion on electronic charge transport for a wide range of MCPs is necessary to develop generalized transport models in these systems.
4. Ion injection and water intake
During recent years, the effect of the ion injection, water intake, and swelling on the electronic and ionic conductivities of MCPs has attracted considerable attention. Most devices relying on the mixed conductivity such as sensors, transducers of biological activity, and drug delivery devices operate in aqueous solution or other electrolytes which permeate into the MCP film. However, increasing the ionic injection and transport in MCPs can result in reduced electrical mobilities and conductivities. Thus, the microstructure of MCPs must be tuned to allow for water intake without substantial disruption of the percolative electronic conduction pathways. For example, Rivnay et al. demonstrated that a solvent treatment of PEDOT:PSS can result in improved ionic transport but reduced electronic,93 suggesting that there is a trade-off when tuning film morphology for either electronic or ionic transport.While PEDOT:PSS has traditionally been the material of choice for mixed conductors94 and the subject of studies of morphological and electrical properties during the water and moisture intake,57,91 a lot of attention has been recently turned to ethylene glycol functionalized polythiophenes.19,90,92,95–99 Decorating the CP backbone of various polythiophenes with polar ethylene glycol side-chains enhances the intake of ions and water significantly, resulting in a shift from gating CP at the polymer/electrolyte interface (i.e. EGOFET operation) to bulk gating of the material (i.e. OECT operation).19 This observation may lead one to assume that increasing the water uptake should enhance the performance in MCP applications. However, while ion uptake is necessary for bulk doping, Savva et al. demonstrated that increasing the degree of swelling of the CP is not de facto beneficial for OECT performance.57 Following this result, Moser et al. carefully designed glycolated polythiophenes with different distributions of side chains to optimize water intake and swelling. The resulting materials displayed unprecedented performance and stability in an organic electrochemical transistor (OECT).95
MCPs can also undergo significant structural changes during bulk electrochemical gating. For example, Bischak et al. demonstrated that a conjugated polymer with glycolated side chains (PB2T-TEG), undergoes reversible structural phase transitions during water intake and voltage-driven ion injection.96 Using molecular dynamics simulations, Ghosh et al. provided an atomistic understanding of the structural phase transitions in the (PB2T-TEG) system.90 They showed that the observed phase transition arises due to the interplay between several factors, including the effect of the underlying surface favoring the edge-on orientation of the polymer chains and formation of lamella structure; unzipping of the interdigitated polymer chains during oxidation; and formation of the π–π stacking at the high oxidation level facilitating the electron mobility in the polymer film.
Another phenomenon observed in MCPs is a transition between the solid state and the gel phase accompanied by gigantic swelling,97 where the first irreversible volume change reaches 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000%, followed by subsequent cycles with reversible swelling in the range from 280% to 330% (Fig. 5a). Using the molecular dynamics simulation, the microscopic origin of the swelling behavior was unraveled and attributed to the total water intake, where the counterions injected into the film electrochemically carry water molecules in their hydration shells. During swelling, the polymer morphology transforms from a solid phase to a gel with large pores filled by water, while the CP backbone maintains a percolated network allowing for high electrical conductivity (Fig. 5b and c). Further studies outlined the effect of the side chain length on the electrochemically induced swelling in glycolated polythiophenes and on the performance of the OECT.98,99 It is interesting to note that both PEDOT:PSS and PEDOT:Tos, in contrast to ethylene glycol functionalized polythiophenes, practically do not swell during electrochemical cycling. However, PEDOT:PSS strongly swells when a dry film is immersed into water, which is attributed to the deprotonation of PSS chains with the consequent water intake due to the hydration shells of hydronium ions.100 PEDOT:Tos undergoes pronounced changes in morphology and chemical composition during electrochemical cycling when tosylate counterions are exchanged by counterions from the electrolyte.101,102
000%, followed by subsequent cycles with reversible swelling in the range from 280% to 330% (Fig. 5a). Using the molecular dynamics simulation, the microscopic origin of the swelling behavior was unraveled and attributed to the total water intake, where the counterions injected into the film electrochemically carry water molecules in their hydration shells. During swelling, the polymer morphology transforms from a solid phase to a gel with large pores filled by water, while the CP backbone maintains a percolated network allowing for high electrical conductivity (Fig. 5b and c). Further studies outlined the effect of the side chain length on the electrochemically induced swelling in glycolated polythiophenes and on the performance of the OECT.98,99 It is interesting to note that both PEDOT:PSS and PEDOT:Tos, in contrast to ethylene glycol functionalized polythiophenes, practically do not swell during electrochemical cycling. However, PEDOT:PSS strongly swells when a dry film is immersed into water, which is attributed to the deprotonation of PSS chains with the consequent water intake due to the hydration shells of hydronium ions.100 PEDOT:Tos undergoes pronounced changes in morphology and chemical composition during electrochemical cycling when tosylate counterions are exchanged by counterions from the electrolyte.101,102
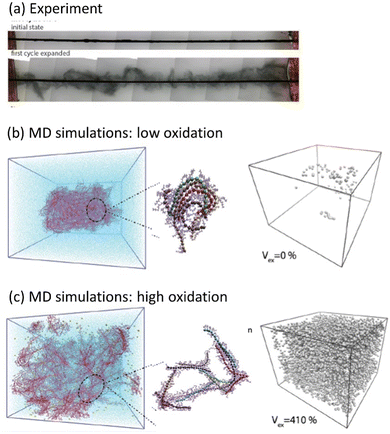 | ||
| Fig. 5 Water intake and swelling in glycolated polythiophene p(gT2) (adapted from ref. 97). (a) Swelling of the polymer during the first cycle (The black rod is a working electrode which is coated with the polymer). Molecular Dynamics (MD) simulations of a polymer film at (b) low (5%) and (c) high (30%) oxidation levels. Images to the left show representative snapshots of the polymer film with counterions, and the images to the right show void volume inside the polymer matrix filled with water. | ||
While there are clear design rules for promoting or inhibiting solvent and/or ion uptake, the energetics for injection of ions across the electrolyte/MCP interface remain unclear. While polar side chains or polyelectrolytes clearly reduce the barrier for ion injection and transport, understanding ionic charge injection requires further characterization of the electrochemical potential of ionic species in the CP relative to the interfacing water or solvent. Furthermore, recent work by Quill et al. demonstrated that, in addition to ions swelling MCPs during doping, MCPs can undergo swelling via neutral ion pair uptake.103 Thus, a crucial aspect in better understanding ion injection in MCPs is quantifying the relative concentrations of unpaired ions vs. neutral ion pairs injected during electrochemical cycling and characterizing whether ionic doping redox reactions are a result of ion uptake or expulsion.
5. Ionic charge transport
Ionic conductivities vary substantially among different classes of CPs,104,105 with densely packed hydrophobic CPs typically exhibiting very poor ionic conductivities, while CP–polyelectrolyte blends, like PEDOT:PSS, show ionic conductivities that matche those of ion exchange membranes.106 Ion transport is a complex phenomenon, as it can include many different ionic species of fixed or varying charge, and it depends strongly on the ionic interactions within the system, which are affected by the solvation of ions, ion–ion interactions and interactions with the polymer matrix. Further, the ion transport within a CP film can depend strongly on the doping level and on the history of solvent exposure and doping cycles. The ionic conductivity (σionic) is given by the sum of the ionic conductivities of all the mobile ionic species i:where μi is the mobility, ni the number density, e the elementary charge, and zi the ion charge. The ion mobility and diffusivity can be related by the Einstein relation:
where T is temperature and kB is Boltzmann's constant. This simplistic representation of ionic conductivities can be rather misleading, as it disguises the fact that the ionic mobility, or diffusivity, depends strongly on both internal and external factors that can vary over time. It is thus not granted that the ionic conductivity increases with the concentration of ionic species, in some cases it is actually the opposite.107 To achieve a deeper understanding of the ion transport within various types of MCPs, one therefore needs to go beyond the simplistic representation above and investigate the different ion transport mechanisms that can be present in MCPs. As the ion transport in MCP films typically does not occur in the conjugated phase of the material, knowledge from previous studies on ion transport in non-conjugated polymer systems can be applied to many MCP systems. Examples of relevant non-conjugated polymer systems are polymer electrolytes and polyelectrolytes, the latter often in the form of crosslinked membranes.
In dry polymer systems without solvent and solvation of ions, ion transport can be facilitated by segmental motion of polymer side chains or the polymer backbone.109 Here, the ion–polymer interaction is of uttermost importance, often resulting in large differences in mobilities for cations and anions. This type of ion transport is also sensitive to temperature which strongly affects the segmental motion in polymers.109 In solvated polymer systems, the full or partial solvation of the ions render them mobile within the solvated phase of the material. The swollen polymer matrix can either be neutral, e.g. poly(ethylene glycol) (PEG) gels, or containing fixed charges, e.g. polyelectrolytes and crosslinked ion exchange membranes. The degree of swelling and solvation of ions has a huge influence on the ionic conductivity and is often more important than other materials parameters, e.g. the concentration of ions in the system. From conventional electrolytes, it is well known that the ionic mobility decreases with increasing concentration, as the ionic interactions increase. In crosslinked polyelectrolytes, this can happen to the extent that the ionic conductivity can decrease with increasing concentrations of fixed charges and/or counterions. The conduction of protons, however, does not behave similarly to conventional electrolytes, and is instead a special case which is governed by the Grotthuss mechanism, in which protons hop from hydronium ions to water molecules across a hydrogen bonded network.110 This results in a significantly higher ionic mobility for protons than other cations or anions.
MCPs can be classified into three groups based on how the ion transport is facilitated within the materials: pure CPs, CP–polymer electrolytes, and CP–polyelectrolytes (Fig. 6). Pure CPs do not incorporate an internal polymer phase intended to facilitate the transport of ions. Within this category one finds many of the CPs not intended for electrochemical devices in the first place. Even a CP like P3HT, which is not generally considered as a MCP, can be electrochemically doped/dedoped;111 however, the ion transport is typically slow, thereby limiting device performance. There are, however, pure CPs that are widely used in electrochemical applications, the prime example being polypyrrole (PPy).26 PPy is a better ion conductor than many other pure CPs due to its relatively hydrophilic nature. The ion transport in PPy is improving after the first electrochemical doping/dedoping cycle, as this process incorporates significant amounts of solvent and ions into the polymer (Fig. 6a).
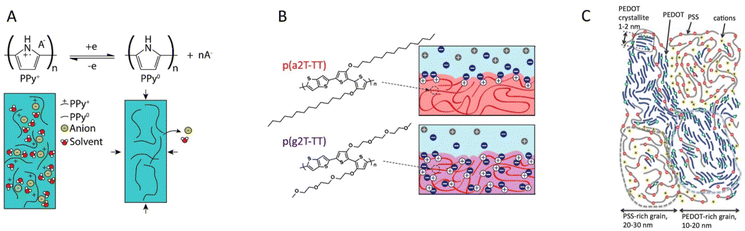 | ||
| Fig. 6 Classes of mixed conducting polymers. (a) The pure CP polypyrrole is popular in electrochemical applications as its hydrophilic backbone allows for incorporation of ions and solvent upon doping (recreated from ref. 108). (b) Glycolated side chains grafted to the CP backbone provides an ion conducting phase that allows bulk ion conduction (reproduced from ref. 19). (c) PEDOT:PSS is a common CP–polyelectrolyte blend, which exhibits excellent selective ion transport within the polyelectrolyte phase (reproduced from ref. 22 with permission from John Wiley and Sons, copyright 2017). | ||
CP–polymer electrolytes systems comprise a polymer phase which facilitate ion transport, either by segmental motion or solvated transport (Fig. 6b). PEG chains are often incorporated for this purpose, either in polymer blends,112 CP–polyelectrolyte co-polymers,113 or conjugated polymer electrolytes.114 The method of incorporation has implications on the morphology of the material as it dictates the length scale of the CP–polymer electrolyte phase separation. When CP–polymer electrolytes with PEG chains are brought in contact with electrolyte, the swelling of the polymer electrolyte phase is mechanically restricted by the CP phase. The ion concentration within the CP is determined by the equilibrium with the external electrolyte, which also depends on the doping level.
A widely used and popular class of materials is the CP–polyelectrolyte systems. In similarity to the polymer electrolytes, polyelectrolytes can be incorporated as blends115 or copolymers116 with CPs or as conjugated polyelectrolytes.117 While the early success of aqueous PEDOT:PSS dispersions (Fig. 6c) paved the way for this class of materials, more recent work has often taken advantage of the excellent ionic conductivity of CP–polyelectrolyte systems, which can be similar to that of ion exchange membranes. The ion conduction within these materials is dominated by mobile counterions compensating fixed charges of the polyelectrolyte component. As the concentration of counterions does not depend much on electrolyte concentration or the doping level, the ionic conductivity within these materials tends to be rather stable with respect to these factors.
Characterization of the ion conductivity within CPs can be quite challenging since the ionic and electronic transport are coupled. The ionic conductivity is typically well below 1 S cm−1, thus for doped CPs the electronic conductivity is often orders of magnitude higher than the ionic conductivity. For a MCP electrode immersed in electrolyte, the frequency of an applied voltage perturbation can affect which ionic transport process is probed. This phenomenon can be picked up by electrochemical impedance spectroscopy (EIS) and the ionic conductivity can be extracted by the application of equivalent circuit models.118 The latter step is however far from trivial, as the use of various complex circuit elements, like Warburg diffusion elements or constant phase elements, is often require to fit the resulting EIS data making the physical interpretation of the data difficult. Another challenge for the analysis of thin CP films is that the electrolyte resistance can dominate the measured ionic resistance, thereby preventing the measurement of the ionic conductivity within the MCP film itself. A useful way around this problem is to create lateral encapsulated CP films that are only in contact with the electrolyte at one end.51,93 This creates the equivalence of a very thick CP film with low electrolyte resistance, thus enabling the analysis of the lateral movement of ions within the film. The measurement and optimization of ionic conductivity in CPs will help to elucidate the relationship between ionic and electronic transport, leading to improved device design and performance.
6. Coupling of ionic and electronic charge transport
Electrochemical applications of CPs can involve many different electrodes, redox species, and ions. There exist extensive reviews on the fundamentals and applications of the electrochemistry of CPs.119,120 Our aim here is to focus on the understanding of the electronic and ionic movements involved in the electrochemical transformations of CPs (Fig. 7a). For a detailed understanding of CPs in these applications, it is necessary to consider the coupling of the electrostatic potentials, energy levels, and doping levels throughout the whole system. Tybrandt et al.121 proposed a model for immersed PEDOT:PSS electrodes which included the work function of the gold contact and the Ag/AgCl reference electrode, and a Gaussian DOS tail of the PEDOT (Fig. 7b). By analyzing the system in steady state for different applied potentials, it was concluded that the Au-PEDOT and the PEDOT-PSS interface voltages varied with the applied potential. The model reproduced the experimental doping vs. voltage characteristics of PEDOT:PSS electrodes, indicating that for low doping levels the change in chemical potential in the DOS tail of the CP dictated the behavior, while for higher doping levels capacitive charging of the electric double layer was dominant.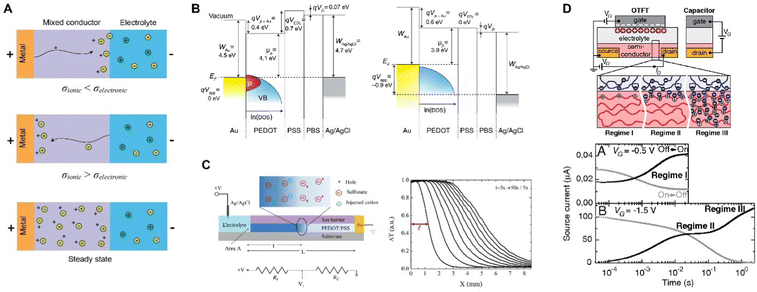 | ||
| Fig. 7 Coupling of ionic and electronic transport. (A) Schematic of distribution of electronic and ionic charge upon application of a voltage for different situations. (B) Schematic of the energy levels in a gold-PEDOT:PSS-electrolyte stack for doped and undoped systems (reproduced from ref. 121). (C) Lateral doping fronts can be utilized to study coupled electronic and ionic transport (reproduced from ref. 51 with permission from John Wiley and Sons, copyright 2013). (D) In ion transport limited systems, different portions of a film can be accessible depending on the frequency of the applied voltage (reproduced from ref. 122). | ||
To describe the transient characteristics of CP systems, the coupled ionic and electronic transport of the CP should be added to the steady state description (Fig. 7a). The ionic and electronic transport, described in preceding sections, occurs in different parts of the materials (electrons are exchanged with the electrode, ions with the electrolyte) but are coupled through the charge compensation between ionic and electronic charge carriers. In the case of ion-free domains in the CP, electronic charge carriers can exist as space charge (OFETs, CP diodes), however at lower concentrations than for ion compensated electronic charges.123 The local changes in doping level will be determined by the ionic and electronic transport, in combination with the energetic cost of doping (charging) the material. One should note that since CP electrodes interact with many different ionic species, they will typically not be screened by a supporting electrolyte. Therefore, migration rather than diffusion is often the dominating ionic transport mechanism within CP systems. The geometry of electrochemical CP devices dictates the directions and length scales over which the electronic and ionic transport occurs. Indeed, the rate limiting factors for the ionic and electronic movements accompanying electrochemical switching of a CP are fundamentally different. The accessibility of the bulk for ions, most likely solvated, depends on morphology and mechanical relaxation of the MCP. Its accessibility for electrons (or holes) is determined by electronic conductivity, drastically changing over the course of doping/de-doping of the CP. However, electroneutrality requires that the rates of both processes being equal.
Devices with parallel ionic/electronic transport within the material can either have vertical architecture (e.g. electrodes, supercapacitors,124 and LEECs125), which results in shorter transport distances through the film thickness, or lateral architecture (e.g. lateral LEECs,126 LETs,127 electrochromic moving front devices51), in which the transport occurs over longer distances. Devices with parallel ionic/electronic transport are often limited by ionic transport, as the ionic conductivity typically is orders of magnitude lower than the electronic conductivity of doped CPs. Electrochromic moving front studies in lateral devices are useful for analyzing the mixed transport in CPs (Fig. 7c). The configuration allows for optical measurements of the electrochromic response of the film, providing a direct measurement of the moving doping front within the film, which has been used to analyze the ionic transport.51,93 For PEDOT:PSS electrodes, the PEDOT is initially reduced at the electrolyte interface,51 indicating that the ionic transport is limiting. One should notice that the broad transition region in the doping level in such experiments not only arises due to diffusion but also the changes in the Fermi level within the CP resulting from different doping levels. Inhomogeneous ion transport within CPs93 has not been widely studied but recent results indicate that it might be responsible for some of the non-idealities found in the characterization of CP electrodes.128 For example, electrochemical quartz crystal microbalance measurements have been used to explore the timescales for coupling of ions, solvent uptake, and polymer reconfiguration.129–131 As ionic transport often is the limiting factor in electrochemical CP devices, including energy devices, electrodes, OECTs, and electrochromic displays, it is one of the most critical material parameters to consider when designing novel materials for these applications. This can be demonstrated by the long-term success of PEDOT:PSS and recent activities in the development of pegylated19 CPs with high ionic conductivity. For undoped CPs, limitations in the ionic transport can also result in that different portions of a film are accessible depending on the frequency of the applied voltage (Fig. 7d).122 For high frequencies, only the EDL at the CP–electrolyte interface is charged, while for lower frequencies a larger portion of the bulk of the film is affected.122
For devices with orthogonal electronic/ionic transport (electrodes with side contact, OECTs, and some neuromorphic devices)132 electronic transport can be limiting despite significantly higher electronic than ionic conductivity within the CP. Since the CP film thickness often is below 1 μm, the lateral electronic transport path can be many orders of magnitude longer than the ionic path. For OECTs and electrolyte-gated OFETs, this effect is manifested as an increase in switching speed with the reduction of the channel length.133,134
For CP electrodes with side contact, moving front experiments by Aoki et al. made the electronic insulator/conductor (I/C) transitions limiting, while allowing for unhindered vertical ion transport between the film and the solution.135,136 These spectroelectrochemical experiments revealed that I/C switching proceeds directly from the current lead and from the surface of microscopic conductor clusters in electric contact with the lead. However, trapped conducting clusters surrounded by insulator during the conductor-to-insulator transition leaves behind in the film a notable share of the conductive species, forming fractal geometry (Fig. 8).
 | ||
| Fig. 8 CP microstructural evolution during conductor-to-insulator transitions. (A) Schematic showing the trapping of conductive clusters (C, light blue) within the insulating domain (I, dark blue) during rapid conductor-to-insulator transitions and (B) the subsequent insulator-to-conductor conversion where the conductive domains can rapidly connect to the electrode (recreated from ref. 135). | ||
This behavior is not limited to a single polymer and manifests in both p- and n-doping.137 Such conductor-clusters, not even related to morphology, can be detected by scanning Kelvin probe microscopy (SKPM) on the surface of a CP.138,139 Nevertheless, fluctuations, due to thermal movement or charge transfer, tend to rearrange the clusters and restore some of their connections to the electrode, allowing the reduction to advance slowly. And this builds a bridge to such a manifestation of electrochemical doping/de-doping asymmetry in CP as “the first scan” or “slow relaxation” effect:140 the CV doping (insulator-to-conductor transition) peak overpotential manifests the logarithmic dependence on time the film had spent in the insulating state. The effect has been observed for various CPs,141 and reveals that equilibrium in conductor-to-insulator transition is not attained for at least 9 decades of time.142 These observations underscore the fundamental asymmetry between doping (insulator-to-conductor) and de-doping (conductor-to-insulator) processes and help to understand the electrochemical behavior of CP. A similar two-phase model was recently and independently put forward143 to explain the so-called pseudocapacitive behavior of an inorganic material.
The shape of CP CVs has created a lot of confusion and debate over the years. For an electrochemically reversible system not limited by ion movements, this implies symmetric oxidation and reduction I–V characteristics in steady state and a well understood shift between oxidation and reduction peaks of the same shape in a cyclic voltammogram. This simple behavior is indeed observed at electrodes modified with polymers that contain well-defined localized, electrochemically independent redox sites either as pendant groups or as part of non-conjugated backbone144,145 called redox polymers. Electronic conductivity of redox polymers is assured by redox hopping between these sites and remains orders of magnitude lower than that of the CP in doped states. Further discussion of redox polymers is beyond the scope of this Perspective. The distinctive feature of a CP is its conjugated backbone that undergoes multiple redox itself, so that separate electroactive sites cannot be delimited. Furthermore, this electrochemical doping and de-doping is accompanied by drastic increase and decrease, respectively, in electronic conductivity, implying the same backbone. One probably should not be surprised that even at very low scan rates, when one would normally expect electrochemical reversibility, a CP displays manifestly asymmetric CV. This CV typically comprises a box-like region, associated with capacitive charging, and asymmetric redox-like peaks close to the undoped state, which has often led to the conclusion that there are two different charging mechanism in CPs which either faradaic or capacitive. Though this debate is beyond the scope of this Perspective, it is worth noting that for any nanoporous material in a conducting state, the very conceptual boundary between the processes becomes blurred. This ambiguity is because faradaic (redox) reactions of redox centers located near the material surface (i.e. at a distance l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≪
≪ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2Dt)1/2, where D is the diffusion coefficient for charge-compensating ions) are electrochemically indistinguishable from purely capacitive, double-layer charging.146
(2Dt)1/2, where D is the diffusion coefficient for charge-compensating ions) are electrochemically indistinguishable from purely capacitive, double-layer charging.146
Over the years a variety of models have been proposed to describe ion-electron coupling in MCP devices. Early models were based on the classical electrochemical Butler–Volmer equations but had to add a phenomenological term to account for capacitive currents.147–149 More recently, drift-diffusion approaches have been popular and have managed to reproduce some aspects of mixed organic conductors;150–152 however, such approaches have often failed to reproduce the experimentally observed volumetric capacitance as they have not included the energetic cost of charging the material. A theoretical formalism for the calculations of the volumetric capacitance based on the density functional theory (DFT) was developed by Sahalianov et al.153,154 and applied to two archetypical conducting polymers: PEDOT and polypyrrole (PPy). The volumetric capacitance of PEDOT and PPy was calculated to be ca. 100 F cm−3 and ca. 300 F cm−3, respectively, which is within the range of the corresponding reported experimental results. The DFT calculations unraveled that the volumetric capacitance is originated from charges stored in the atomistic Stern layers between oxidized polymeric chains and counterions. Hence, MCPs were classified as double-layer supercapacitors rather than pseudo-capacitors.
OECTs have been successfully modelled at moderate carrier concentrations by combining volumetric capacitance with the standard OFET equations.155,156 Simulations of CP nanopores have shown that volumetric capacitance can arise from the interface between the electronic and ionic phases within CP materials.22 This concept has been further extended to the device level drift-diffusion framework by introducing separate electronic and ionic phases coupled by an EDL. To properly account for the doping of the material at low doping levels, the tail of the DOS of the semiconductor had to be considered. This approach reproduces a wide range of different device and material characteristics, including those of PEDOT:PSS OECTs. The approach has also been coupled to conventional electrochemical reactions of redox molecules to describe redox enhanced supercapacitors.124,154 This modeling approach is expected to be useful for capturing a wider range of MCP such as intrinsic semiconductors which do not include an internal polyelectrolyte and are expected to transport both anions and cations.
7. Redox reactions using CP electrodes
From electrochemical response of CP themselves it is logical to proceed to considering redox reactions at CP based or containing electrodes. It is well known that the rate of an electrochemical reaction can vary by orders of magnitude depending on the material of the electrode at which it takes place. In a wide and relative sense, catalysis of an electrochemical reaction is often understood as its acceleration at one electrode compared to another. Note, however, that an electrochemical reaction is overall a complex process comprising heterogeneous electron transfer and mass transport of reactants and products, including compensating ion transport. Therefore, the observed acceleration may be due to improved accessibility and increased real surface of the electrode; these subtle differences are not always clearly distinguished in the literature.157 Nevertheless, it is useful to distinguish electrocatalysis in the strict sense and redox mediation. Electrocatalysis, the electrochemical counterpart of heterogeneous catalysis in chemistry, refers to the increase of the reaction rate constant (at a given potential) due to chemisorption of the reactant or an intermediate at the electrode. Redox mediation implies indirect electron transfer from the electrode to the reactant via an additional moiety, a mediator, and does not include chemisorption. A redox mediator can be either immobilized at the electrode or soluble and play the role of shuttle. To underscore the difference from electrocatalyst, the term outer-sphere redox mediator can be used.158 Conducting polymers are notable for undergoing reversible redox transformations in the form of doping, without making or breaking chemical bonds. Their role in electrochemical reactions at electrodes is usually discussed in term of redox mediation.159 However, design and optimization of a catalyst should rather extend beyond the molecular level to the device scale, and MCPs with their intrinsic molecular porosity and ion exchange ability naturally allow for this.In the context of composing an electrode material to drive an electrochemical reaction, MCPs can serve as an additive to boost the performance of the catalyst proper, which itself may be not sufficiently electronically and ionically conductive.160,161 This role of a CP, however important, can still be considered passive. The ability of a CP itself to drive a target electrochemical reaction also attracts attention, a notable milestone here being the demonstration by Winther-Jensen et al.162 of efficient oxygen reduction reaction (ORR) at PEDOT. This behavior was later confirmed163,164 and a theoretical framework was successful in describing the role of a CP in the ORR.165,166
Quinone/hydroquinone (Q/HQ) redox reactions are omnipresent in living nature and are being extensively studied for organic redox flow batteries.167 Electrocatalysis of Q/HQ transformations by CPs was noticed and attracted attention to polythiophenes,168 in particular in the context of biosensors.169 However, the molecular mechanism of such activity remains unclear. In a recent study,170 we went a step further by taking a polythiophene analog PEDOT as electrode material, choosing an ionic quinoid reactant, and making use of the ion exchange properties of the CP to allow or not the reacting ions to penetrate its bulk (Fig. 9). When PEDOT:PSS is used as the electrode film, an anionic reactant in solution (tiron) was repelled from the bulk due to the immobile doping anions on PSS (Fig. 9A). In contrast, when the electrode film is PEDOT doped with mobile anions (Tos), tiron anions are involved in the congruent ionic transport along with the dopant anions, leading to enhanced redox currents linearly scaling with the film thickness (Fig. 9B). This novel phenomenon, called Ion-Selective ElectroCatalysis (ISEC), was used in an all-organic redox flow battery to improve device performance.
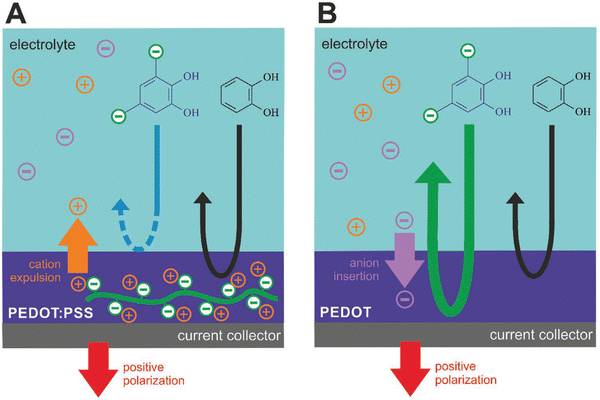 | ||
| Fig. 9 Ion-selective electrocatalysis selecting for the (A) cation or (B) anion transport (reproduced from open access article ref. 170). | ||
The unique offerings of MCPs make these materials a promising choice for heterogeneous electrocatalysis. Not only do MCPs increase the effective surface area of catalysts because of their porosity, but they also add functionality and/or selectivity for redox reactions. For example, the careful design of the internal charge or electronic energy levels helps select for reduction or oxidation reactions as discussed above. Finally, the excellent electronic transport properties can improve electrically connectivity between catalytic sites and the electrode without impeding diffusion of redox species.
8. Conclusions and outlook
Mixed conducting polymers (MCPs) present a highly promising materials system for organic electrochemical devices (OECDs) including bioelectronic devices, electrochemical charge storage, printed electronics, electrochromics, and emerging memory devices. The unique behavior of MCPs is a result of both their ability to intimately couple with interfacing electrolytes, ideal for biological systems which are governed by largely by ionic rather than electronic transport, as well as their ability to go beyond the surface doping modulation found in most electronic materials, undergoing bulk doping which gives rise to high gain. While these materials are already emerging into commercial application, the widespread use is still limited by the lack of well-established engineering constraints resulting from the limited fundamental understanding of the electrochemical doping process. A deeper understanding of the individual processes which govern OECD operation as well as the co-dependence of these processes would greatly improve device performance and stability.As outlined in this Perspective, the operational mechanism for electrochemical doping in MCPs is complex and is the result of a cascade of processes rather than just one step. This complexity makes traditional experimental data difficult to interpret. Thus, the path forward for understanding ionic doping in MCPs requires isolation and investigation of elementary processes from the injection of ionic or electronic charges, their transport through the bulk, to their electrostatic coupling. Creative experimental protocols which target specific elementary steps can provide insight into the key parameters governing such processes. Then, these individual pieces can be reassembled to gain insight to the full picture of electrochemical doping in MCPs. Through fundamental understanding of the polymer energetics and the spatial distributions of electrons, ions, and electric fields, OECDs could be optimized for performance metrics such as gain, operational frequency, and sensitivity while mitigating undesirable characteristics which lead to instability.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
S. T. K. gratefully acknowledges funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 101022365. V. G. and I. Z. gratefully acknowledge funding from the Knut and Alice Wallenberg Foundation through the project “H2O2” and Wallenberg Wood Science Center (program 1, 3). K. T. gratefully acknowledges funding from the Swedish Government Strategic Research Area in Materials Science on Advanced Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971) and by the Swedish Foundation for Strategic Research. G. G. M. and M. B. acknowledge support from H2020-EU-FET Open MITICS (964677). The computations were conducted on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N.References
- D. Moia, A. Giovannitti, A. A. Szumska, I. P. Maria, E. Rezasoltani, M. Sachs, M. Schnurr, P. R. F. Barnes, I. McCulloch and J. Nelson, Design and evaluation of conjugated polymers with polar side chains as electrode materials for electrochemical energy storage in aqueous electrolytes, Energy Environ. Sci., 2019, 12, 1349–1357 RSC.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, An Organic Mixed Ion-Electron Conductor for Power Electronics, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed.
- S. T. Keene, D. Fogarty, R. Cooke, C. D. Casadevall, A. Salleo and O. Parlak, Wearable Organic Electrochemical Transistor Patch for Multiplexed Sensing of Calcium and Ammonium Ions from Human Perspiration, Adv. Healthcare Mater., 2019, 8, 1901321 CrossRef CAS PubMed.
- C. Cea, G. D. Spyropoulos, P. Jastrzebska-Perfect, J. J. Ferrero, J. N. Gelinas and D. Khodagholy, Enhancement-mode ion-based transistor as a comprehensive interface and real-time processing unit for in vivo electrophysiology, Nat. Mater., 2020, 19, 679–686 CrossRef CAS PubMed.
- P. Andersson Ersman, R. Lassnig, J. Strandberg, D. Tu, V. Keshmiri, R. Forchheimer, S. Fabiano, G. Gustafsson and M. Berggren, All-printed large-scale integrated circuits based on organic electrochemical transistors, Nat. Commun., 2019, 10, 5053 CrossRef CAS PubMed.
- M. Braendlein, T. Lonjaret, P. Leleux, J.-M. Badier and G. G. Malliaras, Voltage Amplifier Based on Organic Electrochemical Transistor, Adv. Sci., 2017, 4, 1600247 CrossRef PubMed.
- R. Brooke, J. Edberg, X. Crispin, M. Berggren, I. Engquist and M. P. Jonsson, Greyscale and Paper Electrochromic Polymer Displays by UV Patterning, Polymers, 2019, 11, 267 CrossRef PubMed.
- A. Melianas, T. J. Quill, G. LeCroy, Y. Tuchman, H. V. Loo, S. T. Keene, A. Giovannitti, H. R. Lee, I. P. Maria, I. McCulloch and A. Salleo, Temperature-resilient solid-state organic artificial synapses for neuromorphic computing, Sci. Adv., 2020, 6, eabb2958 CrossRef CAS PubMed.
- M. J. Panzer, C. R. Newman and C. D. Frisbie, Low-voltage operation of a pentacene field-effect transistor with a polymer electrolyte gate dielectric, Appl. Phys. Lett., 2005, 86, 103503 CrossRef.
- A. S. Dhoot, J. D. Yuen, M. Heeney, I. McCulloch, D. Moses and A. J. Heeger, Beyond the metal-insulator transition in polymer electrolyte gated polymer field-effect transistors, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 11834–11837 CrossRef CAS PubMed.
- E. Said, X. Crispin, L. Herlogsson, S. Elhag, N. D. Robinson and M. Berggren, Polymer field-effect transistor gated via a poly(styrenesulfonic acid) thin film, Appl. Phys. Lett., 2006, 89, 143507 CrossRef.
- L. Kergoat, L. Herlogsson, D. Braga, B. Piro, M.-C. Pham, X. Crispin, M. Berggren and G. Horowitz, A Water-Gate Organic Field-Effect Transistor, Adv. Mater., 2010, 22, 2565–2569 CrossRef CAS PubMed.
- S. Casalini, F. Leonardi, T. Cramer and F. Biscarini, Organic field-effect transistor for label-free dopamine sensing, Org. Electron., 2013, 14, 156–163 CrossRef CAS.
- M. Magliulo, A. Mallardi, M. Y. Mulla, S. Cotrone, B. R. Pistillo, P. Favia, I. Vikholm-Lundin, G. Palazzo and L. Torsi, Electrolyte-Gated Organic Field-Effect Transistor Sensors Based on Supported Biotinylated Phospholipid Bilayer, Adv. Mater., 2013, 25, 2090–2094 CrossRef CAS PubMed.
- B. Winther-Jensen, K. Fraser, C. Ong, M. Forsyth and D. R. MacFarlane, Conducting Polymer Composite Materials for Hydrogen Generation, Adv. Mater., 2010, 22, 1727–1730 CrossRef CAS PubMed.
- J. Kosco, S. Gonzalez-Carrero, C. T. Howells, W. Zhang, M. Moser, R. Sheelamanthula, L. Zhao, B. Willner, T. C. Hidalgo, H. Faber, B. Purushothaman, M. Sachs, H. Cha, R. Sougrat, T. D. Anthopoulos, S. Inal, J. R. Durrant and I. McCulloch, Oligoethylene Glycol Side Chains Increase Charge Generation in Organic Semiconductor Nanoparticles for Enhanced Photocatalytic Hydrogen Evolution, Adv. Mater., 2021, 2105007 Search PubMed.
- E. Miglbauer, P. J. Wójcik and E. D. Głowacki, Single-compartment hydrogen peroxide fuel cells with poly(3,4-ethylenedioxythiophene) cathodes, Chem. Commun., 2018, 54, 11873–11876 RSC.
- C. B. Nielsen, A. Giovannitti, D.-T. Sbircea, E. Bandiello, M. R. Niazi, D. A. Hanifi, M. Sessolo, A. Amassian, G. G. Malliaras, J. Rivnay and I. McCulloch, Molecular Design of Semiconducting Polymers for High-Performance Organic Electrochemical Transistors, J. Am. Chem. Soc., 2016, 138, 10252–10259 CrossRef CAS PubMed.
- A. Giovannitti, D.-T. Sbircea, S. Inal, C. B. Nielsen, E. Bandiello, D. A. Hanifi, M. Sessolo, G. G. Malliaras, I. McCulloch and J. Rivnay, Controlling the mode of operation of organic transistors through side-chain engineering, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12017–12022 CrossRef CAS PubMed.
- L. Cheng, X. Du, Y. Jiang and A. Vlad, Mechanochemical assembly of 3D mesoporous conducting-polymer aerogels for high performance hybrid electrochemical energy storage, Nano Energy, 2017, 41, 193–200 CrossRef CAS.
- C. M. Proctor, J. Rivnay and G. G. Malliaras, Understanding volumetric capacitance in conducting polymers, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1433–1436 CrossRef CAS.
- A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Understanding the Capacitance of PEDOT:PSS, Adv. Funct. Mater., 2017, 27, 1700329 CrossRef.
- P. Andersson, D. Nilsson, P.-O. Svensson, M. Chen, A. Malmström, T. Remonen, T. Kugler and M. Berggren, Active Matrix Displays Based on All-Organic Electrochemical Smart Pixels Printed on Paper, Adv. Mater., 2002, 14, 1460–1464 CrossRef CAS.
- J. Rivnay, S. Inal, A. Salleo, R. M. Owens, M. Berggren and G. G. Malliaras, Organic electrochemical transistors, Nat. Rev. Mater., 2018, 3, 17086 CrossRef CAS.
- S. Ghosh and O. Inganäs, Conducting Polymer Hydrogels as 3D Electrodes: Applications for Supercapacitors, Adv. Mater., 1999, 11, 1214–1218 CrossRef CAS.
- E. W. H. Jager, E. Smela and O. Inganäs, Microfabricating Conjugated Polymer Actuators, Science, 2000, 290, 1540–1545 CrossRef CAS PubMed.
- C. Liu, Y. Xu and Y.-Y. Noh, Contact engineering in organic field-effect transistors, Mater. Today, 2015, 18, 79–96 CrossRef CAS.
- B. Geffroy, P. le Roy and C. Prat, Organic light-emitting diode (OLED) technology: materials, devices and display technologies, Polym. Int., 2006, 55, 572–582 CrossRef CAS.
- E. L. Ratcliff, B. Zacher and N. R. Armstrong, Selective Interlayers and Contacts in Organic Photovoltaic Cells, J. Phys. Chem. Lett., 2011, 2, 1337–1350 CrossRef CAS PubMed.
- L. Meng, Y. Zhang, X. Wan, C. Li, X. Zhang, Y. Wang, X. Ke, Z. Xiao, L. Ding, R. Xia, H.-L. Yip, Y. Cao and Y. Chen, Organic and solution-processed tandem solar cells with 17.3% efficiency, Science, 2018, 361, 1094–1098 CrossRef CAS PubMed.
- A. Distler, C. J. Brabec and H. Egelhaaf, Organic photovoltaic modules with new world record efficiencies, Prog. Photovoltaics, 2021, 29, 24–31 Search PubMed.
- D. Natali and M. Caironi, Charge Injection in Solution-Processed Organic Field-Effect Transistors: Physics, Models and Characterization Methods, Adv. Mater., 2012, 24, 1357–1387 CrossRef CAS PubMed.
- M. Knupfer and G. Paasch, Origin of the interface dipole at interfaces between undoped organic semiconductors and metals, J. Vac. Sci. Technol. Vac. Surf. Films, 2005, 23, 1072–1077 CrossRef CAS.
- F. Flores, J. Ortega and H. Vázquez, Modelling energy level alignment at organic interfaces and density functional theory, Phys. Chem. Chem. Phys., 2009, 11, 8658 RSC.
- J. K. Wenderott and P. F. Green, Self-Assembled Monolayers at the Conjugated Polymer/Electrode Interface: Implications for Charge Transport and Band-Bending Behavior, ACS Appl. Mater. Interfaces, 2018, 10, 21458–21465 CrossRef CAS PubMed.
- X. Qi, N. Li and S. R. Forrest, Analysis of metal-oxide-based charge generation layers used in stacked organic light-emitting diodes, J. Appl. Phys., 2010, 107, 014514 CrossRef.
- B. E. Conway, Transition from “Supercapacitor” to “Battery” Behavior in Electrochemical Energy Storage, J. Electrochem. Soc., 1991, 138, 1539–1548 CrossRef CAS.
- J. O. Bockris, M. A. V. Devanathan and K. Müller, On the structure of charged interfaces, Proc. R. Soc. Lond. Ser. Math. Phys. Sci., 1963, 274, 55–79 CAS.
- M. Green, Electrochemistry of the Semiconductor-Electrolyte Electrode. I. The Electrical Double Layer, J. Chem. Phys., 1959, 31, 200–203 CrossRef CAS.
- Q. Pei, G. Yu, C. Zhang, Y. Yang and A. J. Heeger, Polymer Light-Emitting Electrochemical Cells, Science, 1995, 269, 1086–1088 CrossRef CAS PubMed.
- J. C. deMello, N. Tessler, S. C. Graham and R. H. Friend, Ionic space-charge effects in polymer light-emitting diodes, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12951–12963 CrossRef CAS.
- V. Kaphle, P. R. Paudel, D. Dahal, R. K. Radha Krishnan and B. Lüssem, Finding the equilibrium of organic electrochemical transistors, Nat. Commun., 2020, 11, 2515 CrossRef CAS PubMed.
- F. Torricelli, P. Romele, P. Gkoupidenis, D. A. Koutsouras, K. Lieberth, Z. M. Kovács-Vajna and P. W. M. Blom, in Integrated Sensors for Biological and Neural Sensing, ed. H. Mohseni, SPIE, Online Only, USA, 2021, p. 37 Search PubMed.
- E. J. Fuller, S. T. Keene, A. Melianas, Z. Wang, S. Agarwal, Y. Li, Y. Tuchman, C. D. James, M. J. Marinella, J. J. Yang, A. Salleo and A. A. Talin, Parallel programming of an ionic floating-gate memory array for scalable neuromorphic computing, Science, 2019, 364, 570–574 CrossRef CAS PubMed.
- A. Giovannitti, R. B. Rashid, Q. Thiburce, B. D. Paulsen, C. Cendra, K. Thorley, D. Moia, J. T. Mefford, D. Hanifi, D. Weiyuan, M. Moser, A. Salleo, J. Nelson, I. McCulloch and J. Rivnay, Energetic Control of Redox-Active Polymers toward Safe Organic Bioelectronic Materials, Adv. Mater., 2020, 32, 1908047 CrossRef CAS PubMed.
- V. Kaphle, S. Liu, A. Al-Shadeedi, C.-M. Keum and B. Lüssem, Contact Resistance Effects in Highly Doped Organic Electrochemical Transistors, Adv. Mater., 2016, 28, 8766–8770 CrossRef CAS PubMed.
- P. R. Paudel, V. Kaphle, D. Dahal, R. K. Radha Krishnan and B. Lüssem, Tuning the Transconductance of Organic Electrochemical Transistors, Adv. Funct. Mater., 2021, 31, 2004939 CrossRef CAS.
- A. F. Paterson, H. Faber, A. Savva, G. Nikiforidis, M. Gedda, T. C. Hidalgo, X. Chen, I. McCulloch, T. D. Anthopoulos and S. Inal, On the Role of Contact Resistance and Electrode Modification in Organic Electrochemical Transistors, Adv. Mater., 2019, 31, 1902291 CrossRef PubMed.
- G. Zuo, M. Linares, T. Upreti and M. Kemerink, General rule for the energy of water-induced traps in organic semiconductors, Nat. Mater., 2019, 18, 588–593 CrossRef CAS PubMed.
- S. T. Keene, A. Melianas, Y. van de Burgt and A. Salleo, Mechanisms for Enhanced State Retention and Stability in Redox-Gated Organic Neuromorphic Devices, Adv. Electron. Mater., 2019, 5, 1800686 CrossRef.
- E. Stavrinidou, P. Leleux, H. Rajaona, D. Khodagholy, J. Rivnay, M. Lindau, S. Sanaur and G. G. Malliaras, Direct Measurement of Ion Mobility in a Conducting Polymer, Adv. Mater., 2013, 25, 4488–4493 CrossRef CAS PubMed.
- T. F. Otero and M. Bengoechea, UV-Visible Spectroelectrochemistry of Conducting Polymers. Energy Linked to Conformational Changes, Langmuir, 1999, 15, 1323–1327 CrossRef CAS.
- F. Bonafè, F. Decataldo, B. Fraboni and T. Cramer, Charge Carrier Mobility in Organic Mixed Ionic–Electronic Conductors by the Electrolyte-Gated van der Pauw Method, Adv. Electron. Mater., 2021, 7, 2100086 CrossRef.
- J. C. Scott, P. Pfluger, M. T. Krounbi and G. B. Street, Electron-spin-resonance studies of pyrrole polymers: Evidence for bipolarons, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 2140–2145 CrossRef CAS.
- T. Berzina, V. Erokhin and M. P. Fontana, Spectroscopic investigation of an electrochemically controlled conducting polymer-solid electrolyte junction, J. Appl. Phys., 2007, 101, 024501 CrossRef.
- C. Francis, D. Fazzi, S. B. Grimm, F. Paulus, S. Beck, S. Hillebrandt, A. Pucci and J. Zaumseil, Raman spectroscopy and microscopy of electrochemically and chemically doped high-mobility semiconducting polymers, J. Mater. Chem. C, 2017, 5, 6176–6184 RSC.
- A. Savva, S. Wustoni and S. Inal, Ionic-to-electronic coupling efficiency in PEDOT:PSS films operated in aqueous electrolytes, J. Mater. Chem. C, 2018, 6, 12023–12030 RSC.
- A. Robert Hillman and A. Glidle, Electroactive bilayers employing conducting polymers. Part 6. Kinetic electrochemical quartz crystal microbalance measurements, Phys. Chem. Chem. Phys., 2001, 3, 3447–3458 RSC.
- P. A. Christensen and A. Hamnett, In situ spectroscopic investigations of the growth, electrochemical cycling and overoxidation of polypyrrole in aqueous solution, Electrochim. Acta, 1991, 36, 1263–1286 CrossRef CAS.
- A. Glidle, A. R. Hillman, K. S. Ryder, E. L. Smith, J. Cooper, N. Gadegaard, J. R. P. Webster, R. Dalgliesh and R. Cubitt, Use of Neutron Reflectivity to Measure the Dynamics of Solvation and Structural Changes in Polyvinylferrocene Films During Electrochemically Controlled Redox Cycling, Langmuir, 2009, 25, 4093–4103 CrossRef CAS PubMed.
- B. D. Paulsen, R. Wu, C. J. Takacs, H. Steinrück, J. Strzalka, Q. Zhang, M. F. Toney and J. Rivnay, Time-Resolved Structural Kinetics of an Organic Mixed Ionic–Electronic Conductor, Adv. Mater., 2020, 32, 2003404 CrossRef CAS PubMed.
- J. Lee, Physical modeling of charge transport in conjugated polymer field-effect transistors, J. Phys. Appl. Phys., 2021, 54, 143002 CrossRef CAS.
- P. Stadler, Isotropic metallic transport in conducting polymers, Synth. Met., 2019, 254, 106–113 CrossRef CAS.
- N. Rolland, J. F. Franco-Gonzalez and I. Zozoulenko, Can Mobility Negative Temperature Coefficient Be Reconciled with the Hopping Character of Transport in Conducting Polymers?, ACS Appl. Polym. Mater., 2019, 1, 2833–2839 CrossRef CAS.
- O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J.-B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Semi-metallic polymers, Nat. Mater., 2014, 13, 190–194 CrossRef CAS PubMed.
- W. R. Salaneck, R. H. Friend and J. L. Brédas, Electronic structure of conjugated polymers: consequences of electron–lattice coupling, Phys. Rep., 1999, 319, 231–251 CrossRef CAS.
- G. Heimel, The Optical Signature of Charges in Conjugated Polymers, ACS Cent. Sci., 2016, 2, 309–315 CrossRef CAS PubMed.
- A. Miller and E. Abrahams, Impurity Conduction at Low Concentrations, Phys. Rev., 1960, 120, 745–755 CrossRef CAS.
- S. D. Baranovskii, Theoretical description of charge transport in disordered organic semiconductors: Charge transport in disordered organic semiconductors, Phys. Status Solidi B, 2014, 251, 487–525 CrossRef CAS.
- H. Bässler, Charge Transport in Disordered Organic Photoconductors a Monte Carlo Simulation Study, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef.
- V. I. Arkhipov, E. V. Emelianova and G. J. Adriaenssens, Effective transport energy versus the energy of most probable jumps in disordered hopping systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125125 CrossRef.
- R. Schmechel, Hopping transport in doped organic semiconductors: A theoretical approach and its application to p -doped zinc-phthalocyanine, J. Appl. Phys., 2003, 93, 4653–4660 CrossRef CAS.
- G. Kim and K. P. Pipe, Thermoelectric model to characterize carrier transport in organic semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085208 CrossRef.
- S. Ihnatsenka, X. Crispin and I. V. Zozoulenko, Understanding hopping transport and thermoelectric properties of conducting polymers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035201 CrossRef.
- O. Bubnova, M. Berggren and X. Crispin, Tuning the Thermoelectric Properties of Conducting Polymers in an Electrochemical Transistor, J. Am. Chem. Soc., 2012, 134, 16456–16459 CrossRef CAS PubMed.
- R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, A general relationship between disorder, aggregation and charge transport in conjugated polymers, Nat. Mater., 2013, 12, 1038–1044 CrossRef CAS PubMed.
- X. Zhang, H. Bronstein, A. J. Kronemeijer, J. Smith, Y. Kim, R. J. Kline, L. J. Richter, T. D. Anthopoulos, H. Sirringhaus, K. Song, M. Heeney, W. Zhang, I. McCulloch and D. M. DeLongchamp, Molecular origin of high field-effect mobility in an indacenodithiophene–benzothiadiazole copolymer, Nat. Commun., 2013, 4, 2238 CrossRef PubMed.
- S. Wang, S. Fabiano, S. Himmelberger, S. Puzinas, X. Crispin, A. Salleo and M. Berggren, Experimental evidence that short-range intermolecular aggregation is sufficient for efficient charge transport in conjugated polymers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10599–10604 CrossRef CAS PubMed.
- N. Rolland, J. F. Franco-Gonzalez, R. Volpi, M. Linares and I. V. Zozoulenko, Understanding morphology-mobility dependence in PEDOT:Tos, Phys. Rev. Mater., 2018, 2, 045605 CrossRef CAS.
- W. A. Muñoz, X. Crispin, M. Fahlman and I. V. Zozoulenko, Understanding the Impact of Film Disorder and Local Surface Potential in Ultraviolet Photoelectron Spectroscopy of PEDOT, Macromol. Rapid Commun., 2018, 39, 1700533 CrossRef PubMed.
- M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Morphology and ion diffusion in PEDOT:Tos. A coarse grained molecular dynamics simulation, Phys. Chem. Chem. Phys., 2018, 20, 17188–17198 RSC.
- J. F. Franco-Gonzalez, E. Pavlopoulou, E. Stavrinidou, R. Gabrielsson, D. T. Simon, M. Berggren and I. V. Zozoulenko, Morphology of a self-doped conducting oligomer for green energy applications, Nanoscale, 2017, 9, 13717–13724 RSC.
- N. Rolland, M. Modarresi, J. F. Franco-Gonzalez and I. Zozoulenko, Large scale mobility calculations in PEDOT (Poly(3,4-ethylenedioxythiophene)): Backmapping the coarse-grained MARTINI morphology, Comput. Mater. Sci., 2020, 179, 109678 CrossRef CAS.
- A. Khot and B. M. Savoie, Top–Down Coarse-Grained Framework for Characterizing Mixed Conducting Polymers, Macromolecules, 2021, 54, 4889–4901 CrossRef CAS.
- A. Khot and B. M. Savoie, How side-chain hydrophilicity modulates morphology and charge transport in mixed conducting polymers, J. Polym. Sci., 2022, 60, 610–620 CrossRef CAS.
- U. Salzner, Investigation of Charge Carriers in Doped Thiophene Oligomers through Theoretical Modeling of their UV/Vis Spectra, J. Phys. Chem. A, 2008, 112, 5458–5466 CrossRef CAS PubMed.
- I. Zozoulenko, A. Singh, S. K. Singh, V. Gueskine, X. Crispin and M. Berggren, Polarons, Bipolarons, And Absorption Spectroscopy of PEDOT, ACS Appl. Polym. Mater., 2019, 1, 83–94 CrossRef CAS.
- I. Sahalianov, J. Hynynen, S. Barlow, S. R. Marder, C. Müller and I. Zozoulenko, UV-to-IR Absorption of Molecularly p-Doped Polythiophenes with Alkyl and Oligoether Side Chains: Experiment and Interpretation Based on Density Functional Theory, J. Phys. Chem. B, 2020, 124, 11280–11293 CrossRef CAS PubMed.
- W. A. Muñoz, S. K. Singh, J. F. Franco-Gonzalez, M. Linares, X. Crispin and I. V. Zozoulenko, Insulator to semimetallic transition in conducting polymers, Phys. Rev. B, 2016, 94, 205202 CrossRef.
- S. Ghosh and I. Zozoulenko, Effect of Substrate on Structural Phase Transition in a Conducting Polymer during Ion Injection and Water Intake: A View from a Computational Microscope, ACS Appl. Electron. Mater., 2020, 2, 4034–4041 CrossRef CAS.
- M. Wieland, C. Dingler, R. Merkle, J. Maier and S. Ludwigs, Humidity-Controlled Water Uptake and Conductivities in Ion and Electron Mixed Conducting Polythiophene Films, ACS Appl. Mater. Interfaces, 2020, 12, 6742–6751 CrossRef CAS PubMed.
- A. Savva, R. Hallani, C. Cendra, J. Surgailis, T. C. Hidalgo, S. Wustoni, R. Sheelamanthula, X. Chen, M. Kirkus, A. Giovannitti, A. Salleo, I. McCulloch and S. Inal, Balancing Ionic and Electronic Conduction for High-Performance Organic Electrochemical Transistors, Adv. Funct. Mater., 2020, 30, 1907657 CrossRef CAS.
- J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Structural control of mixed ionic and electronic transport in conducting polymers, Nat. Commun., 2016, 7, 11287 CrossRef PubMed.
- M. Berggren, X. Crispin, S. Fabiano, M. P. Jonsson, D. T. Simon, E. Stavrinidou, K. Tybrandt and I. Zozoulenko, Ion Electron–Coupled Functionality in Materials and Devices Based on Conjugated Polymers, Adv. Mater., 2019, 31, 1805813 CrossRef PubMed.
- M. Moser, T. C. Hidalgo, J. Surgailis, J. Gladisch, S. Ghosh, R. Sheelamanthula, Q. Thiburce, A. Giovannitti, A. Salleo, N. Gasparini, A. Wadsworth, I. Zozoulenko, M. Berggren, E. Stavrinidou, S. Inal and I. McCulloch, Side Chain Redistribution as a Strategy to Boost Organic Electrochemical Transistor Performance and Stability, Adv. Mater., 2020, 32, 2002748 CrossRef CAS PubMed.
- C. G. Bischak, L. Q. Flagg, K. Yan, T. Rehman, D. W. Davies, R. J. Quezada, J. W. Onorato, C. K. Luscombe, Y. Diao, C.-Z. Li and D. S. Ginger, A Reversible Structural Phase Transition by Electrochemically-Driven Ion Injection into a Conjugated Polymer, J. Am. Chem. Soc., 2020, 142, 7434–7442 CrossRef CAS PubMed.
- J. Gladisch, E. Stavrinidou, S. Ghosh, A. Giovannitti, M. Moser, I. Zozoulenko, I. McCulloch and M. Berggren, Reversible Electronic Solid–Gel Switching of a Conjugated Polymer, Adv. Sci., 2020, 7, 1901144 CrossRef CAS PubMed.
- M. Moser, J. Gladisch, S. Ghosh, T. C. Hidalgo, J. F. Ponder, R. Sheelamanthula, Q. Thiburce, N. Gasparini, A. Wadsworth, A. Salleo, S. Inal, M. Berggren, I. Zozoulenko, E. Stavrinidou and I. McCulloch, Controlling Electrochemically Induced Volume Changes in Conjugated Polymers by Chemical Design: from Theory to Devices, Adv. Funct. Mater., 2021, 31, 2100723 CrossRef CAS.
- A. A. Szumska, I. P. Maria, L. Q. Flagg, A. Savva, J. Surgailis, B. D. Paulsen, D. Moia, X. Chen, S. Griggs, J. T. Mefford, R. B. Rashid, A. Marks, S. Inal, D. S. Ginger, A. Giovannitti and J. Nelson, Reversible Electrochemical Charging of n-Type Conjugated Polymer Electrodes in Aqueous Electrolytes, J. Am. Chem. Soc., 2021, 143, 14795–14805 CrossRef CAS PubMed.
- M. Modarresi, A. Mehandzhiyski, M. Fahlman, K. Tybrandt and I. Zozoulenko, Microscopic Understanding of the Granular Structure and the Swelling of PEDOT:PSS, Macromolecules, 2020, 53, 6267–6278 CrossRef CAS.
- S. Rudd, J. F. Franco-Gonzalez, S. Kumar Singh, Z. Ullah Khan, X. Crispin, J. W. Andreasen, I. Zozoulenko and D. Evans, Charge transport and structure in semimetallic polymers, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 97–104 CrossRef CAS PubMed.
- N. Delavari, J. Gladisch, I. Petsagkourakis, X. Liu, M. Modarresi, M. Fahlman, E. Stavrinidou, M. Linares and I. Zozoulenko, Water Intake and Ion Exchange in PEDOT:Tos Films upon Cyclic Voltammetry: Experimental and Molecular Dynamics Investigation, Macromolecules, 2021, 54, 6552–6562 CrossRef CAS.
- T. J. Quill, G. LeCroy, A. Melianas, D. Rawlings, Q. Thiburce, R. Sheelamanthula, C. Cheng, Y. Tuchman, S. T. Keene, I. McCulloch, R. A. Segalman, M. L. Chabinyc and A. Salleo, Ion Pair Uptake in Ion Gel Devices Based on Organic Mixed Ionic–Electronic Conductors, Adv. Funct. Mater., 2021, 31, 2104301 CrossRef CAS.
- B. D. Paulsen, K. Tybrandt, E. Stavrinidou and J. Rivnay, Organic mixed ionic–electronic conductors, Nat. Mater., 2020, 19, 13–26 CrossRef CAS PubMed.
- B. D. Paulsen, S. Fabiano and J. Rivnay, Mixed Ionic-Electronic Transport in Polymers, Annu. Rev. Mater. Res., 2021, 51, 73–99 CrossRef CAS.
- M. Lefebvre, Z. Qi, D. Rana and P. G. Pickup, Chemical Synthesis, Characterization, and Electrochemical Studies of Poly(3,4-ethylenedioxythiophene)/Poly(styrene-4-sulfonate) Composites, Chem. Mater., 1999, 11, 262–268 CrossRef CAS.
- D. J. Poxson, E. O. Gabrielsson, A. Bonisoli, U. Linderhed, T. Abrahamsson, I. Matthiesen, K. Tybrandt, M. Berggren and D. T. Simon, Capillary-Fiber Based Electrophoretic Delivery Device, ACS Appl. Mater. Interfaces, 2019, 11, 14200–14207 CrossRef CAS PubMed.
- W. Zheng, P. G. Whitten and G. M. Spinks, Polypyrrole actuators: the effects of polymer thickness and voltage scan rate on fractional charging and isotonic actuation strain, Multifunct. Mater., 2018, 1, 014002 CrossRef CAS.
- S. B. Aziz, T. J. Woo, M. F. Z. Kadir and H. M. Ahmed, A conceptual review on polymer electrolytes and ion transport models, J. Sci. Adv. Mater. Devices, 2018, 3, 1–17 CrossRef.
- T. Miyake and M. Rolandi, Grotthuss mechanisms: from proton transport in proton wires to bioprotonic devices, J. Phys.: Condens. Matter, 2016, 28, 023001 CrossRef PubMed.
- D. Neusser, C. Malacrida, M. Kern, Y. M. Gross, J. van Slageren and S. Ludwigs, High Conductivities of Disordered P3HT Films by an Electrochemical Doping Strategy, Chem. Mater., 2020, 32, 6003–6013 CrossRef CAS.
- Y. Cao, G. Yu, A. J. Heeger and C. Y. Yang, Efficient, fast response light-emitting electrochemical cells: Electroluminescent and solid electrolyte polymers with interpenetrating network morphology, Appl. Phys. Lett., 1996, 68, 3218–3220 CrossRef CAS.
- S. N. Patel, A. E. Javier, K. M. Beers, J. A. Pople, V. Ho, R. A. Segalman and N. P. Balsara, Morphology and Thermodynamic Properties of a Copolymer with an Electronically Conducting Block: Poly(3-ethylhexylthiophene)- block -poly(ethylene oxide), Nano Lett., 2012, 12, 4901–4906 CrossRef CAS PubMed.
- A. Giovannitti, C. B. Nielsen, D.-T. Sbircea, S. Inal, M. Donahue, M. R. Niazi, D. A. Hanifi, A. Amassian, G. G. Malliaras, J. Rivnay and I. McCulloch, N-type organic electrochemical transistors with stability in water, Nat. Commun., 2016, 7, 13066 CrossRef CAS PubMed.
- C.-Y. Yang, M.-A. Stoeckel, T.-P. Ruoko, H.-Y. Wu, X. Liu, N. B. Kolhe, Z. Wu, Y. Puttisong, C. Musumeci, M. Massetti, H. Sun, K. Xu, D. Tu, W. M. Chen, H. Y. Woo, M. Fahlman, S. A. Jenekhe, M. Berggren and S. Fabiano, A high-conductivity n-type polymeric ink for printed electronics, Nat. Commun., 2021, 12, 2354 CrossRef CAS PubMed.
- H. Erothu, J. Kolomanska, P. Johnston, S. Schumann, D. Deribew, D. T. W. Toolan, A. Gregori, C. Dagron-Lartigau, G. Portale, W. Bras, T. Arnold, A. Distler, R. C. Hiorns, P. Mokarian-Tabari, T. W. Collins, J. R. Howse and P. D. Topham, Synthesis, Thermal Processing, and Thin Film Morphology of Poly(3-hexylthiophene)–Poly(styrenesulfonate) Block Copolymers, Macromolecules, 2015, 48, 2107–2117 CrossRef CAS.
- H. Jiang, P. Taranekar, J. R. Reynolds and K. S. Schanze, Conjugated Polyelectrolytes: Synthesis, Photophysics, and Applications, Angew. Chem., Int. Ed., 2009, 48, 4300–4316 CrossRef CAS PubMed.
- X. Ren and P. G. Pickup, Ion transport in polypyrrole and a polypyrrole/polyanion composite, J. Phys. Chem., 1993, 97, 5356–5362 CrossRef CAS.
- J. Heinze, B. A. Frontana-Uribe and S. Ludwigs, Electrochemistry of Conducting Polymers—Persistent Models and New Concepts, Chem. Rev., 2010, 110, 4724–4771 CrossRef CAS PubMed.
- J. G. Ibanez, M. E. Rincón, S. Gutierrez-Granados, M. Chahma, O. A. Jaramillo-Quintero and B. A. Frontana-Uribe, Conducting Polymers in the Fields of Energy, Environmental Remediation, and Chemical–Chiral Sensors, Chem. Rev., 2018, 118, 4731–4816 CrossRef CAS PubMed.
- K. Tybrandt, I. V. Zozoulenko and M. Berggren, Chemical potential–electric double layer coupling in conjugated polymer–polyelectrolyte blends, Sci. Adv., 2017, 3, eaao3659 CrossRef PubMed.
- A. Laiho, L. Herlogsson, R. Forchheimer, X. Crispin and M. Berggren, Controlling the dimensionality of charge transport in organic thin-film transistors, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15069–15073 CrossRef CAS PubMed.
- H. Shimotani, G. Diguet and Y. Iwasa, Direct comparison of field-effect and electrochemical doping in regioregular poly(3-hexylthiophene), Appl. Phys. Lett., 2005, 86, 022104 CrossRef.
- M. O. Bamgbopa, J. Edberg, I. Engquist, M. Berggren and K. Tybrandt, Understanding the characteristics of conducting polymer-redox biopolymer supercapacitors, J. Mater. Chem. A, 2019, 7, 23973–23980 RSC.
- S. B. Meier, D. Tordera, A. Pertegás, C. Roldán-Carmona, E. Ortí and H. J. Bolink, Light-emitting electrochemical cells: recent progress and future prospects, Mater. Today, 2014, 17, 217–223 CrossRef CAS.
- T. Sakanoue, J. Li, H. Tanaka, R. Ito, S. Ono, S. Kuroda and T. Takenobu, High Current Injection into Dynamic p-n Homojunction in Polymer Light-Emitting Electrochemical Cells, Adv. Mater., 2017, 29, 1606392 CrossRef PubMed.
- J. Zaumseil, R. H. Friend and H. Sirringhaus, Spatial control of the recombination zone in an ambipolar light-emitting organic transistor, Nat. Mater., 2006, 5, 69–74 CrossRef CAS.
- M. O. Bamgbopa, D. Belaineh, D. A. Mengistie, J. Edberg, I. Engquist, M. Berggren and K. Tybrandt, Modelling of heterogeneous ion transport in conducting polymer supercapacitors, J. Mater. Chem. A, 2021, 9, 2184–2194 RSC.
- A. R. Hillman, S. J. Daisley and S. Bruckenstein, Kinetics and mechanism of the electrochemical p-doping of PEDOT, Electrochem. Commun., 2007, 9, 1316–1322 CrossRef CAS.
- S. Bruckenstein, J. Chen, I. Jureviciute and A. R. Hillman, Ion and solvent transfers accompanying redox switching of polypyrrole films immersed in divalent anion solutions, Electrochim. Acta, 2009, 54, 3516–3525 CrossRef CAS.
- E. Pater, S. Bruckenstein and A. R. Hillman, Theory for Solvent and Salt Transfer Accompanying Partial Redox Conversion of Electroactive Polymer Films under Permselective and Nonpermselective Conditions, J. Phys. Chem. B, 2006, 110, 14761–14769 CrossRef CAS PubMed.
- Y. van de Burgt, E. Lubberman, E. J. Fuller, S. T. Keene, G. C. Faria, S. Agarwal, M. J. Marinella, A. Alec Talin and A. Salleo, A non-volatile organic electrochemical device as a low-voltage artificial synapse for neuromorphic computing, Nat. Mater., 2017, 16, 414–418 CrossRef CAS PubMed.
- D. Khodagholy, M. Gurfinkel, E. Stavrinidou, P. Leleux, T. Herve, S. Sanaur and G. G. Malliaras, High speed and high density organic electrochemical transistor arrays, Appl. Phys. Lett., 2011, 99, 163304 CrossRef.
- L. Herlogsson, Y. Noh, N. Zhao, X. Crispin, H. Sirringhaus and M. Berggren, Downscaling of Organic Field-Effect Transistors with a Polyelectrolyte Gate Insulator, Adv. Mater., 2008, 20, 4708–4713 CrossRef CAS.
- K. Aoki, J. Cao and Y. Hoshino, Coulombic irreversibility at polyaniline-coated electrodes by electrochemical switching, Electrochim. Acta, 1993, 38, 1711–1716 CrossRef CAS.
- Y. Tezuka, K. Aoki, H. Yajima and T. Ishii, Concentration profiles of conducting species in polypyrrole films in cyclic voltammetry by means of a diode array detector, J. Electroanal. Chem., 1997, 425, 167–172 CrossRef CAS.
- N. M. Alpatova, O. A. Semenikhin, E. V. Ovsyannikova, M. R. Erenburg, O. N. Efimov, M. Y. Belov and V. E. Kazarinov, Two types of retarded charge in the electron-conducting thiophene polymers, Russ. J. Electrochem., 2000, 36, 919–925 CrossRef CAS.
- O. A. Semenikhin, L. Jiang, T. Iyoda, K. Hashimoto and A. Fujishima, Atomic Force Microscopy and Kelvin Probe Force Microscopy Evidence of Local Structural Inhomogeneity and Nonuniform Dopant Distribution in Conducting Polybithiophene, J. Phys. Chem., 1996, 100, 18603–18606 CrossRef CAS.
- M. Ortuño, E. Escasain, E. Lopez-Elvira, A. M. Somoza, J. Colchero and E. Palacios-Lidon, Conducting polymers as electron glasses: Surface charge domains and slow relaxation, Sci. Rep., 2016, 6, 21647 CrossRef PubMed.
- C. Odin and M. Nechtschein, Slow relaxation in conducting polymers, Phys. Rev. Lett., 1991, 67, 1114–1117 CrossRef CAS PubMed.
- G. M. Abou-Elenien, A. A. El-Maghraby and G. M. El-Abdallah, Electrochemical relaxation study of polythiophene as conducting polymer (I), Synth. Met., 2004, 146, 109–119 CrossRef CAS.
- J. Cao and K. Aoki, Percolation threshold potentials at quasi-static electrochemical switching of polyaniline films, Electrochim. Acta, 1996, 41, 1787–1792 CrossRef CAS.
- C. Costentin, T. R. Porter and J.-M. Savéant, Nature of Electronic Conduction in “Pseudocapacitive” Films: Transition from the Insulator State to Band-Conduction, ACS Appl. Mater. Interfaces, 2019, 11, 28769–28773 CrossRef CAS PubMed.
- R. H. Terrill, J. E. Hutchison and R. W. Murray, Solid State Electron-Hopping Transport and Frozen Concentration Gradients in a Mixed Valent Viologen−Tetraethylene Oxide Copolymer, J. Phys. Chem. B, 1997, 101, 1535–1542 CrossRef CAS.
- N. Casado, G. Hernández, H. Sardon and D. Mecerreyes, Current trends in redox polymers for energy and medicine, Prog. Polym. Sci., 2016, 52, 107–135 CrossRef CAS.
- Y. Gogotsi and R. M. Penner, Energy Storage in Nanomaterials – Capacitive, Pseudocapacitive, or Battery-like?, ACS Nano, 2018, 12, 2081–2083 CrossRef CAS PubMed.
- T. Yeu, T. V. Nguyen and R. E. White, A Mathematical Model for Predicting Cyclic Voltammograms of Electronically Conductive Polypyrrole, J. Electrochem. Soc., 1988, 135, 1971–1976 CrossRef CAS.
- S. W. Feldberg, Reinterpretation of polypyrrole electrochemistry. Consideration of capacitive currents in redox switching of conducting polymers, J. Am. Chem. Soc., 1984, 106, 4671–4674 CrossRef CAS.
- T. Yeu, K. Yin, J. Carbajal and R. E. White, Electrochemical Characterization of Electronically Conductive Polypyrrole on Cyclic Voltammograms, J. Electrochem. Soc., 1991, 138, 2869–2877 CrossRef CAS.
- X. Wang, B. Shapiro and E. Smela, Development of a Model for Charge Transport in Conjugated Polymers, J. Phys. Chem. C, 2009, 113, 382–401 CrossRef CAS.
- M. Modestov, V. Bychkov, D. Valiev and M. Marklund, Internal Structure of Planar Electrochemical Doping Fronts in Organic Semiconductors, J. Phys. Chem. C, 2011, 115, 21915–21926 CrossRef CAS.
- V. N. Prigodin, F. C. Hsu, J. H. Park, O. Waldmann and A. J. Epstein, Electron-ion interaction in doped conducting polymers, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035203 CrossRef.
- I. Sahalianov, S. K. Singh, K. Tybrandt, M. Berggren and I. Zozoulenko, The intrinsic volumetric capacitance of conducting polymers: pseudo-capacitors or double-layer supercapacitors?, RSC Adv., 2019, 9, 42498–42508 RSC.
- I. Sahalianov, M. G. Say, O. S. Abdullaeva, F. Ahmed, E. Glowacki, I. Engquist, M. Berggren and I. Zozoulenko, Volumetric Double-Layer Charge Storage in Composites Based on Conducting Polymer PEDOT and Cellulose, ACS Appl. Energy Mater., 2021, 4, 8629–8640 CrossRef CAS.
- D. A. Bernards and G. G. Malliaras, Steady-State and Transient Behavior of Organic Electrochemical Transistors, Adv. Funct. Mater., 2007, 17, 3538–3544 CrossRef CAS.
- J. T. Friedlein, S. E. Shaheen, G. G. Malliaras and R. R. McLeod, Optical Measurements Revealing Nonuniform Hole Mobility in Organic Electrochemical Transistors, Adv. Electron. Mater., 2015, 1, 1500189 CrossRef.
- J. N. Hansen, H. Prats, K. K. Toudahl, N. Mørch Secher, K. Chan, J. Kibsgaard and I. Chorkendorff, Is There Anything Better than Pt for HER?, ACS Energy Lett., 2021, 6, 1175–1180 CrossRef CAS PubMed.
- S. Lhenry, Y. R. Leroux and P. Hapiot, Use of Catechol As Selective Redox Mediator in Scanning Electrochemical Microscopy Investigations, Anal. Chem., 2012, 84, 7518–7524 CrossRef CAS PubMed.
- G. O. Ybarra, C. A. Moina, M. Inés Florit and D. Posadas, Redox mediation at electroactive polymer coated electrodes: Mechanistic diagnosis criteria from steady state polarization curves, J. Electroanal. Chem., 2007, 609, 129–139 CrossRef CAS.
- A. D. Chowdhury, N. Agnihotri, P. Sen and A. De, Conducting CoMn2O4 - PEDOT nanocomposites as catalyst in oxygen reduction reaction, Electrochim. Acta, 2014, 118, 81–87 CrossRef CAS.
- J. A. Vigil, T. N. Lambert and K. Eldred, Electrodeposited MnOx/PEDOT Composite Thin Films for the Oxygen Reduction Reaction, ACS Appl. Mater. Interfaces, 2015, 7, 22745–22750 CrossRef CAS PubMed.
- B. Winther-Jensen, O. Winther-Jensen, M. Forsyth and D. R. MacFarlane, High Rates of Oxygen Reduction over a Vapor Phase–Polymerized PEDOT Electrode, Science, 2008, 321, 671–674 CrossRef CAS PubMed.
- E. Mitraka, M. J. Jafari, M. Vagin, X. Liu, M. Fahlman, T. Ederth, M. Berggren, M. P. Jonsson and X. Crispin, Oxygen-induced doping on reduced PEDOT, J. Mater. Chem. A, 2017, 5, 4404–4412 RSC.
- E. Mitraka, M. Gryszel, M. Vagin, M. J. Jafari, A. Singh, M. Warczak, M. Mitrakas, M. Berggren, T. Ederth, I. Zozoulenko, X. Crispin and E. D. Głowacki, Electrocatalytic Production of Hydrogen Peroxide with Poly(3,4-ethylenedioxythiophene) Electrodes, Adv. Sustain. Syst., 2019, 3, 1800110 CrossRef.
- V. Gueskine, A. Singh, M. Vagin, X. Crispin and I. Zozoulenko, Molecular Oxygen Activation at a Conducting Polymer: Electrochemical Oxygen Reduction Reaction at PEDOT Revisited, a Theoretical Study, J. Phys. Chem. C, 2020, 124, 13263–13272 CrossRef CAS.
- F. Sarrami, V. Gueskine and I. Zozoulenko, Electrochemical oxygen reduction reaction at conductive polymer PEDOT: Insight from ab initio molecular dynamics simulations, Chem. Phys., 2021, 551, 111308 CrossRef CAS.
- M. Miroshnikov, K. P. Divya, G. Babu, A. Meiyazhagan, L. M. Reddy Arava, P. M. Ajayan and G. John, Power from nature: designing green battery materials from electroactive quinone derivatives and organic polymers, J. Mater. Chem. A, 2016, 4, 12370–12386 RSC.
- A. Malinauskas, Electrocatalysis at conducting polymers, Synth. Met., 1999, 107, 75–83 CrossRef CAS.
- N. F. Atta, I. Marawi, K. L. Petticrew, H. Zimmer, H. B. Mark and A. Galal, Electrochemistry and detection of some organic and biological molecules at conducting polymer electrodes. Part 3. Evidence of the electrocatalytic effect of the heteroatom of the poly(hetetroarylene) at the electrode/electrolyte interface, J. Electroanal. Chem., 1996, 408, 47–52 CrossRef.
- M. Vagin, C. Che, V. Gueskine, M. Berggren and X. Crispin, Ion-Selective Electrocatalysis on Conducting Polymer Electrodes: Improving the Performance of Redox Flow Batteries, Adv. Funct. Mater., 2020, 30, 2007009 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2022 |