Quantitative molecular simulations

Abstract

All-atom simulations can provide molecular-level insights into the dynamics of gas-phase, condensed-phase and surface processes. One important requirement is a sufficiently realistic and detailed description of the underlying intermolecular interactions. The present perspective provides an overview of the present status of quantitative atomistic simulations from colleagues’ and our own efforts for gas- and solution-phase processes and for the dynamics on surfaces. Particular attention is paid to direct comparison with experiment. An outlook discusses present challenges and future extensions to bring such dynamics simulations even closer to reality.

---

1 Introduction

In principle, quantum mechanics (QM) exactly describes the energetics of chemical systems of any size. However, despite the ever increasing computational power available, determining the interactions and forces for large systems required to follow their molecular dynamics becomes computationally prohibitive. This is due to the unfavourable scaling of electronic structure calculations with the number of electrons and the large number of basis functions required for accurately solving the Schrödinger equation although linear scaling methods provide some remedies for these disadvantages.¹ A quantum mechanical treatment for the nuclear degrees of freedom is even more computationally demanding and typical system sizes are ∼10 heavy atoms for which rigorous calculations are feasible.²

On the other hand, empirical molecular mechanics (MM) energy functions (“force fields”) are computationally advantageous to evaluate. Propagating the dynamics based on Newton's equations of motion allows to access long time scales for large molecular systems. In this context, “long time scale” is sub-microsecond and “large systems” means 10⁹ atoms for which performance of up to 8 ns day⁻¹ can be achieved.^3,4 Such molecular dynamics (MD) simulations have been used to investigate processes ranging from protein folding,^5,6 ligand binding^7–11 crowding in cellular environments¹² to characterizing spectroscopic properties of solutes and peptides and reactions in the gas phase and in solution.^13–15 However one of the challenges remains to develop suitable energy functions that retain the precision of the QM methods they are often based on and that are suitable to follow bond breaking and bond formation.

One- or multi-dimensional vibrational spectroscopy is a powerful means to characterize the structural dynamics of complex systems.^16,17 Experiments greatly benefit and often require accompanying MD simulations for their molecular-level interpretation. Such atomistic simulations rely on the bonded and non-bonded interactions to be described in a meaningful way for making direct contact with experiments. Traditionally, empirical energy functions use harmonic springs for chemical bonds and valence angles, periodic functions for dihedrals, an atom-centered point charge-based model for charges and a Lennard-Jones representation for van der Waals interactions together with additional, more purpose-tailored terms.¹⁸ For applications in spectroscopy the chemical bonds (stretching vibration) need to be described somewhat more realistically to account for mechanical anharmonicity for which Morse-oscillators are often sufficient because experiments at ambient temperatures are not sensitive to highly vibrationally excited states. Nevertheless, there is scope to use more accurate representations, for example based on machine learning-type approaches, in particular if reference data from high-level electronic structure calculations are available. For the non-bonded interactions – which include electrostatic and van der Waals terms – more physics-based models that go beyond the standard representations have been developed.

The first-order treatment of the electrostatic interaction is based on atom-centered point charges for Coulomb interactions. Such pair interactions can be rapidly computed but lack the accuracy for describing anisotropic contributions to the charge density.¹⁹ Including higher-order atomic multipoles improves the accuracy but at the expense of increased computational cost and implementation complexity.^20–23 Accounting for polarizability is another contribution that has been recently included in empirical force fields and shows much promise for further improvements of the computational models.²⁴ From an empirical force field perspective the van der Waals interactions are often represented as Lennard-Jones terms with ad hoc (Lorentz–Berthelot) combination rules. Alternative and potentially improved representations are the buffered 14–7 parametrization²⁵ and modified combination rules.^26,27

Current methods to investigate reactive systems in the gas- and condensed-phase include mixed quantum mechanical/molecular mechanics (QM/MM),^28–30 reactive force fields ReaxFF³¹ and reactive MD (RMD).³² The general ansatz for reactive force fields is to describe reactant and product states with a separate energy function and to connect the two either by mixing functions or by diagonalizing an n × n matrix, where n is the number of states considered. This reactive part is embedded in an environment that is described by a more empirical energy function, akin to mixed QM/MM calculations and simulations. In recent years, a variety of sophisticated Machine Learning (ML) potentials were developed to accurately represent ab initio results from high level reference calculations (see ref. 33, 34 and references therein). Such ML-based energy functions were also extended to reactive systems in the gas phase,³⁵ for simulations in solution³⁶ and on surfaces,³⁷ and recently they were also presented for composite systems in the gas phase to study complex combustion processes.³⁸

Computational investigations of surface reactions are of particular interest from a technological perspective. A substantial amount of heterogeneous catalytic reactions are performed in chemical industry and make up an important economic factor.³⁹ The focus of theoretical and experimental investigation are not only on formation and breaking of chemical bonds but also the diffusion processes as well as the prediction of scattering experiments.^40–42 The systems considered range from monocrystalline surfaces of metals, metal oxides, minerals or ionic compounds to graphene sheets, amorphous porous carbon⁴³ and water surfaces.^44,45 They can be modified by adsorbing ultra-thin layers on metal support, using metal alloy or nanostructuring by metal cluster or single atoms or vacancies.^46–48 Of particular relevance are surface sites with coordination-unsaturated atoms on surface edges, kinks or vacancies which have been found to be sites of increased reactivity.^49,50 However, modeling such surfaces with impurities from high-level electronic quantum methods is still a challenging task, in particular if dynamics information is sought.

A combination of methods with the accuracy of a quantum mechanical treatment with a computational performance comparable to an empirical force field would open up possibilities to investigate reactive processes and spectroscopic properties at a quantitative level. Advances in this direction were acknowledged by the 2013 Nobel Prize in Chemistry.^51,52 However, application of accurate, physics-based force fields for condensed-phase simulations is still not routine. The present work highlights specific applications from our own work and from colleagues in the field, demonstrates the opportunities of such approaches, and discusses future prospects and reasons which slow down more rapid adaptation of such methods in a broader sense. This overview of the field of quantitative MD simulations focuses on applications to questions arising in physical chemistry and biophysics. In the current context, the quantitative aspect is judged as from comparing with available experimental data. Therefore, the close relationship between experimental and computational characterization of the systems is essential.

2 Computational methods for quantitative MD

Following the time evolution of a chemical system by means of atomistic simulations is in principle possible through ab initio MD (AIMD) simulations. However, computational feasibility and the limited accuracy of density functional theory (DFT) methods for certain applications, such as reactions, often preclude using such an approach for quantitative studies. Production runs for full AIMD simulations are typically limited to tens or hundreds of trajectories with simulation times up to hundreds of picoseconds at the semiempirical or DFT level.^53–55 On the other hand, empirical force fields provide a computationally efficient way to determine the total energy and forces of systems in the condensed phase to carry out MD simulations. However, such (parametrized) representations are often not sufficiently accurate for quantitative comparisons or even predictions.

2.1 Potential energy surfaces for gas- and condensed-phase processes

With the advent of computationally efficient and accurate electronic structure calculations, empirical potential energy surfaces (PESs) for small molecules can now be replaced with more accurate representations. It is now possible to determine energies for ∼10⁴ geometries at the coupled cluster singles/doubles and perturbative triples (CCSD(T)) or at the multi reference configuration interaction (MRCI) levels of theory. This shifted the main problem to representing this information such that the PES can be evaluated efficiently and with comparable accuracy as the underlying quantum chemical calculations. With this, even “spectroscopically accurate” calculations are now possible for small molecules.⁵⁶

For small molecules, in particular atom–diatom or diatom–diatom van der Waals complexes, expansions in terms of products of Legendre polynomials P_λ(cos θ), single Y_l,m(θ, ϕ) or coupled Y^l_l1,l2,m (θ₁, θ₂, ϕ) spherical harmonics together with radial functions V (R) is convenient.^57,58 Such an approach was used together with explicit fits to experimental data or to reference electronic structure calculations. Alternatively, for the long-range, distance-dependent part explicit electrostatics using experimentally determined or computed atomic and molecular multipoles and polarizabilities and hyperpolarizabilities^59,60 provides very accurate PESs.

Alternatively, permutationally invariant polynomials (PIPs) can be used to describe the total PES.⁶¹ This has the added benefit that it lends itself to more straightforward generalization to globally reactive PESs as has been done to study reactive collisions for N₂ + N₂ → N₂ + 2N and N₂ + N₂ → 4N.⁶² PIPs use a basis of Morse-type functions and fit products of such basis functions to the reference electronic structure data. Recently, PIPs have been used for systems as large as N-methyl acetamide⁶³ or tropolone.⁶⁴

PESs can also be represented by kernel-based approaches such as a reproducing kernel Hilbert space (RKHS).^65–67 By construction, the RKHS reproduces the reference energies from electronic structure calculations exactly on the grid points. In addition, the physical long-range decay for large separations → ∞ can be explicitly included in the functional dependence of the kernel. Such RKHS-based representations have been used for entire PESs⁶⁸ or in a QM/MM-type approach to treat part of an extended system with higher accuracy.^69–71

Finally, recent efforts for high-accuracy representations of energy functions for individual molecules have revolved around machine learning techniques including neural networks (NNs),^72,73 PIPs combined with NNs,⁷⁴ Gaussian processes,⁷⁵ or kernel-based methods.^76,77 Recent reviews provide a concise status of this field.^34,78–83

For condensed phase simulations accurate electrostatic and van der Waals interactions are essential. The most widely adopted approximation for electrostatics is to represent the molecular charge distribution as a superposition of point charges located on the atoms.¹⁸ However, such an approach neglects the local anisotropy of the electrostatic potential (ESP) which can be particularly relevant for halogens or charged groups. Specifically for halogen atoms the σ-hole requires particular attention.^84,85 For such problems, and for more generally representing a molecule's ESP in a realistic fashion, multipolar^21,86 or distributed charge models (DCM)^87,88 were developed over the past 20 years. A non-exhaustive list of notable efforts in this direction are the “Sum of Interactions Between Fragments Ab Initio” (SIBFA),⁸⁹ “atomic multipole optimized energetics for biomolecular applications” (AMOEBA),⁹⁰ and the “atomic multipole” (MTP)⁹¹ approaches. In addition, energy functions accounting for polarizability have been developed which also allow to obtain more realistic, physics-based models, in particular for condensed-phase simulations.^90,92

The charge distribution ρ(x) also depends on the geometry x. Developing charge models capturing this variation can be challenging. For one, fluctuating point charges based on the charge equilibration scheme have been developed for this purpose.^93,94 They have been mainly applied to simulate the structure and diffusivity of water, ions or amides in water but not for infrared (IR) spectroscopy. Recently, a charge equilibration scheme using a high dimensional NN to learn chemical hardness and electronegativities was presented.⁹⁵ Furthermore, generalizations to simulating larger molecules are difficult and no such extensions are available for multipolar charge models although their conformational dependence has been investigated.⁹⁶ For CO in myoglobin⁹⁷ and CN⁻ in water⁹⁸ conformationally dependent MTPs have demonstrated to perform very well. For larger molecules than diatomics fluctuating charge models have been reported by using ML methods to predict point charges for an ensemble of structures to match their molecular dipole moment, e.g. within the PhysNet neural network approach.⁷³

2.2 Dynamics and reactions on surfaces

The two established ways for computations involving surfaces are by periodic and cluster embedding models. The first model uses the periodicity of a unit cell to describe the electronic wave function of an infinite system. Periodic models allow meaningful computations for metal surfaces. Care has to be taken to minimize finite size effects such as self interaction of surface modifications or reactive sites. Increasing the size of the unit cell lowers the self interactions but leads to higher computational cost.⁹⁹ As realistic systems contain at least ∼10² atoms, simulations for reactions typically use generalized gradient approximation (GGA) functionals.¹⁰⁰ For non-reactive systems also meta-GGA and hybrid density functionals were already applied.^101,102 However, the accuracy can be increased by the specific reaction parameter (SRP) approach to density functional theory that optimizes the mix of exchange and correlation energies.¹⁰³ Surface systems are also modeled by a limited cluster surrounded by a sufficiently sized grid of point charges corresponding to the charge of cluster atoms or ions. Cluster embedding is usually restricted to insulators and semi conductors but is well suited for modelling surface impurities, supported surface clusters or reactants of low concentration.^104–106 Thus, with the cluster embedding method even coupled cluster calculations can be carried out.¹⁰⁵

As for MD simulations in general, the quality of the potential energy surface but also the validity of the Born–Oppenheimer approximation for the surface process significantly determines the accuracy of the simulation.¹⁰⁷ The accuracy of potential energy surface is important for adiabatic processes such as elastic intramolecular energy redistribution within the adsorbate when interacting with the surface and inelastic energy transfer between adsorbate and surface. Experimentally, adsorbate–surface interaction can be probed by state-to-state scattering experiments^108,109 or time dependent desorption.^110–112

Non-adiabatic effects on the dynamics must be considered for simulations especially for processes on metal surfaces. Here, one “weakly” non-adiabatic effect is called “electronic friction” that is the coupling between moving adsorbate atoms with a manifold of electronic states of the surface via electron–hole pair transitions. It is labelled “weakly” as the effect can be treated perturbatively as a damping force on the adsorbate movement.^{107,113–115} Additionally a random force applies on the adsorbate for surfaces of finite temperatures. Effects on the dynamics by coupling between two or more PES of multiple electronic states are accounted for in the “strong” non-adiabatic regime.

3 Vibrational spectroscopy and dynamics in solution

Vibrational spectroscopy is particularly suitable for quantitative comparisons between experiments and simulations. This is primarily due to the precision with which such (laser-based) experiments can be carried out. In the context of experiments, atomistic simulations also yield positions and velocities of all atoms at all times. This provides necessary information to relate experimental observables, such as the IR spectrum, with specific structural features of a system. Even small peptides at ambient conditions can sample multiple conformations each of which exhibits potentially conformer-specific IR spectra. This applies to both, peptides in the gas phase and in solution.^116–118 Thus it is of interest to determine (a) what conformational substate leads to a particular spectroscopic response and (b) whether there exists a unique correspondence (“fingerprint”) between structure and spectroscopy. One possibility is to use extensive electronic structure calculations. This is, however, time consuming and usually only possible for gas-phase systems.^117,119 Alternatively, MD simulations with physics-based and improved force fields can be used to determine the underlying structural features by comparing computed and experimentally measured IR spectra.^120,121

N-Methyl acetamide (NMA) is a topical example for which substantial experimental and computational work has been carried out. In a recent effort the frequency correlation function for NMA in water was determined from an energy function based on reproducing kernel Hilbert space representation for the [CONH] moiety and atomic multipoles up to quadrupole for the electrostatics.¹⁵ Depending on the technique used to determine the amide-I stretch frequency (scanning along the –CO local mode or along the CONH normal mode) the three time scales τ₁ to τ₃ for the decay of the frequency–frequency correlation function (FFCF) were [0.02; 0.21; 1.00] ps or [0.02; 0.20; 0.81] ps compared with two time scales from experiments [(0.05 to 0.1); 1.6] ps and [0.01; 1.0] ps^122,123 and [0.06; 0.66] ps from simulations¹²³ from using a standard force field. The simulation results using a multipolar representation favour a larger value for the decay times which is more consistent with the experimental findings.

A slightly larger and equally well-studied system is trialanine (Ala₃).^{120,121,124–133} Most experiments were carried out under conditions that prefer the cationic species and agree that the conformational ensemble is dominated by the poly-proline II (ppII) structure, often together with some population of the β-sheet conformation and rare sampling of a right-handed α-helical structure. From 1-d and 2-d IR experiments in the amide-I region a notable study used spectroscopic data to refine the underlying conformational ensemble generated from MD simulations. For this, the experimentally measured IR spectra was reproduced best from Bayesian ensemble refinement¹²⁰ which effectively reweights a reference distribution with corresponding conformer-specific IR spectra. Interestingly, the final ensemble generated from such an approach was similar to the Ramachandran maps from explicit MD simulations using a multipolar representation which also correctly described the IR spectroscopy.¹²¹

IR spectroscopy can also be used to follow protein assembly and disassembly. Insulin binds to the insulin receptor in its monomeric form but is stored in the body as a zinc-bound hexamer each of which consists of three homodimers. Hence, the stability of the dimer to decay into two monomers is a physiologically relevant property. For human WT insulin the experimentally determined stabilization of the dimer with respect to two separated monomers is ΔG = −7.2 kcal mol⁻¹.¹³⁴ Thermodynamic stabilities from free energy simulations are between −8.4 and −11.9 kcal mol⁻¹ and simulations along the minimum energy path yield −12.4 kcal mol⁻¹.^135–137 For pharmaceutical applications modified insulins have been synthesized but their dimerization free energies are unknown and challenging to be determined by standard experimental protocols. Hence, alternative means to assess the thermodynamic stability of insulin dimer are required. One possibility is to use infrared spectroscopy because the insulin dimerization interface involves breaking of several hydrogen bonds involving contacts with the –CO unit that give rise to amide-I spectra.^138,139 Atomistic simulations using multipolar force fields confirm that changes in the association state result in modified amide-I spectra.¹⁴⁰ Based on this, attempts can be made to relate changes in the spectroscopic response with the thermodynamic stability of insulin dimer.

The IR spectroscopy and reaction dynamics of diatomic ligands – including CO and NO – bound to and within Myoglobin (Mb) have been thoroughly investigated.¹⁴² Most characteristically, the CO infrared spectrum is split with the two peaks separated by ∼10 cm⁻¹. The spectroscopic signatures were associated with two distinct conformational substates but their structural assignment remained elusive despite dedicated efforts.^143,144 MD simulations with sufficiently detailed electrostatic models for photodissociated CO provided the necessary accuracy^145,146 and together with experimental mutation studies¹⁴⁷ the more red-shifted peak was associated with the Fe–OC orientation whereas the less red-shifted peak corresponds to the Fe–CO state.¹⁴⁸Fig. 1 shows the structure of unligated CO in Mb together with the IR spectrum of the free CO ligand (dashed line). State-specific spectra for the two conformational substates (Fe–CO in green; Fe–OC in blue) are shown as solid lines. It is found that the total spectrum, which is the experimental observable, agrees favourably with the measured spectrum and that the substate-specific spectra allow assignment to an Fe–CO and Fe–OC motif. However, although the spectra provide an identification of the two states, the results also imply that while sampling the Fe–CO conformation the spectroscopy is still sensitive to the presence of the Fe–OC state and vice versa. This is due to the low isomerization barrier between the two states. They are separated by a barrier of ∼0.7 kcal mol⁻¹ which is close to the experimentally reported barrier of 0.5 kcal mol⁻¹.¹⁴⁹

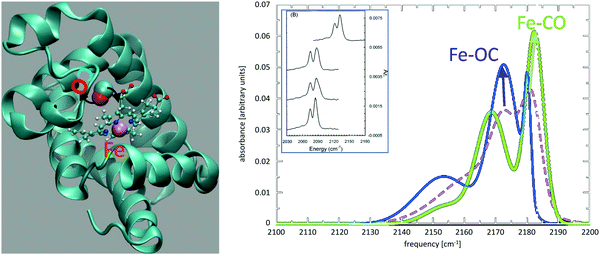Fig. 1 Photodissociated CO and its infrared spectrum in myoglobin (Mb). Left panel: Mb secondary structure in green with heme (ball-and-stick) and CO (van der Waals spheres) and the heme-Fe (green). The black arrows indicate rotation of the photodissociated ligand in the active site. Right panel: The IR spectrum for photodissociated CO from simulations with a multipolar representation of the electrostatics. The spectrum from the entire trajectory (dashed line) is compared with the spectrum from parts of the trajectory sampling the Fe–CO (green) and the Fe–OC (blue) substates. The inset shows experimental spectra for ¹²CO in human Mb (glycerol/water), ¹³CO in human Mb (D₂O), ¹³CO in sperm whale Mb (D₂O), and ¹³CO in Hb (D₂O).¹⁴¹ Reproduced from ref. 141 with permission from American Institute of Physics, copyright 1995.

By their very nature, classical MD simulations neglect nuclear quantum effects such as zero point energy or tunneling. Rigorous treatment of quantum effects in the nuclear dynamics is only possible for small systems with ∼10 heavy atoms.¹⁵⁰ Even for such system sizes the calculations need to make approximations because already for 4 atoms using a product basis set with 10 basis functions per degree of freedom leads to a 10⁶ × 10⁶ dense matrix to be diagonalized. Approximate schemes for including quantum effects for spectroscopic applications include path integral approaches or ring polymer MD (RPMD)^151,152 or centroid MD (CMD) simulations.^153–155 Although computationally convenient, care has to be exercised that the computed spectra do not suffer from artifacts. For example, unusually large red shifts have been found from CMD simulations of liquid water which were ultimately traced back to the so called “curvature problem” in CMD.¹⁵⁶ Similarly, RPMD simulations have been applied to the infrared spectroscopy of a range of systems^157–160 but again care has to be taken to avoid and/or remedy artifacts.^161,162 Also, the infrared lineshapes from RPMD simulations have been found to be unusually broad.¹⁶³ In the words of a recent review: “[T]he difference between the various methods [for describing nuclear quantum effects] are comparable to those one should expect from performing simulations on an imperfect potential energy surface.”¹⁶⁴ Although quantum mechanical methods can obtain spectroscopically accurate results for small systems in the gas phase,¹⁶⁵ extending this to larger molecules and systems in solution is highly nontrivial. An interesting recent development are on-the-fly quantum dynamics simulations without precomputed PESs which have been applied, e.g., to the nonadiabatic dynamics of pyrazine.¹⁶⁶ Also, non-equilibrium RPMD and CMD simulations may provide effective routes to improved spectroscopic characterizations of systems in the condensed phase.^167,168

Quantitative simulations are also possible for thermodynamic properties, such as pure liquid densities or hydration free energies. Such validated parametrizations are required for protein–ligand binding studies, for a molecular-level understanding of chromatography, or for reactions in solvents other than water. Recent progress has been made in the automated parametrization for a library of 430 molecules by focusing on the electrostatic, Lennard-Jones, torsional and 1–4 nonbonded interactions.¹⁶⁹ For the density of the pure liquid the experimental reference values were reproduced with an averaged unsigned error of 1.8% whereas for the enthalpy of vaporization it is 5.9% which both are considerable improvements over earlier parametrizations.^170,171 Nevertheless, to remove systematic differences (∼2 kcal mol⁻¹) between experimental and computed hydration free energies (which were determined with the TIP3P model for water) required introducing an overall solute–solvent scaling factor to increase the solute–solvent by 15% on average.¹⁶⁹ Following a similar optimization protocol for the polarizable Drude model the errors on the pure liquid density and heats of vaporization were 2% and 6%, respectively, whereas for the hydration free energies the error decreased to 0.5 kcal mol⁻¹ together with the SWM4-NDP water model.^172,173

One recurring theme in assessing the quality of (empirical) energy functions is that a particular parametrization may yield favourable comparison for only one or a few experimentally determined properties (e.g. pure liquid density and vaporization energy) – even for a class or library of compounds – but not yield satisfactory results for other observables (hydration free energy).¹⁷² Such transferability has been explicitly considered for cyanide in water.^98,174,175 Using one single parametrization based on fluctuating multipolar electrostatics²¹ it was possible to obtain quantitative results for vibrational energy relaxation, the 1d- and 2d-IR spectroscopy, and the hydration free energy. The computed T₁ times were T₁ = 22 ± 2 ps and 68 ± 11 ps in H₂ O and D₂O, respectively, compared with 28 ± 7 ps and 71 ± 3 ps from experiments with T₁(H₂O)/T₁(D₂O) = 0.33 vs. T₁(H₂O)/T₁(D₂O) = 0.39.^174,176 For the 1d- and 2d-infrared spectroscopy the computed blue shift was 35 cm⁻¹ compared with 44 cm⁻¹ from experiments, the full width at half maximum of 13 cm⁻¹vs. 15 cm⁻¹ from experiment, and the tilt angle depending on waiting time agreed between experiment and simulations.^98,176 The computed hydration free energy of −76 kcal mol⁻¹ compared with −72 to −77 kcal mol⁻¹ from experiment.^175,177 Additional improvements can be obtained from using PES-morphing techniques.^178,179

For pure water a range of force fields has been developed in the recent past. One of them is the AMOEBA model which uses atomic multipoles.^180,181 The iAMOEBA parametrization is very successful for a wide range of ∼30 properties¹⁸¹ for which the majority of the computed values are within a few percent of the experimentally reported data. The E3B model follows a different strategy by adding explicit three-body terms, akin to a many body expansion.¹⁸² Similarly, the HBB (Huang, Braams, Bowman) force field also uses a many-body expansion.¹⁸³ Finally, the most comprehensive water force field in various phases is probably the MB-Pol model which also builds on multipolar interactions and many-body polarization.¹⁸⁴

4. Reaction dynamics

4.1 Reactions in the gas phase

One recent field which has witnessed quantitative simulations concerns small-molecule reactions relevant to hypersonics and atmospheric re-entry.^185–188 For this, a simulation strategy involving high-level electronic structure calculations, global and reactive RKHS-based PESs and QCT simulations has been successfully developed and used for a range of atom + diatom reactions.^68,189,190 The focus was primarily on computing thermal reaction rates, final state distributions and vibrational relaxation times over a wide temperature range, up to 20 000 K. A typical PES for one electronic state is based on 10⁴ energies and the reference energies are typically reproduced within a few cm⁻¹ by the RKHS interpolation. Computed thermal and vibrational relaxation rates agree to within a few percent with those measured experimentally which is a good basis for developing more coarse grained models.^191–193

Malonaldehyde (MA), acetylacetone, and formic acid dimer (FAD) are topical systems for quantitative simulations of gas-phase spectroscopy and reactions. In particular MA and FAD have attracted considerable interest and quantitatively accurate results are available for tunneling splittings. The experimentally determined¹⁹⁴ splitting for MA is 21.6 cm⁻¹ which compares with 23.8 cm⁻¹ from MCTDH calculations and 21.6 cm⁻¹ from Monte Carlo simulations on the same full dimensional PES.¹⁹⁵ For acetylacetone, which is related to MA by substituting hydrogen atoms by methyl-groups, the IR spectroscopy is of particular interest as the barrier for proton transfer is low and leads to signatures in the spectra.¹⁹⁶ Morphing^178,179 a parametrized PES suitable for following proton transfer and comparing the resulting infrared spectrum with that from experiments yields an estimated barrier for proton transfer of 2.35 kcal mol⁻¹; see Fig. 2. Subsequent machine learning found a barrier of 3.25 kcal mol⁻¹ from transfer learning to the PNO-LCCSDT(T)-F12 level of theory.³⁵

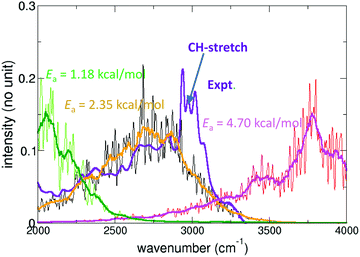Fig. 2 Experimental infrared (blue) and computed (green, black/orange, red) power spectrum in the region of the H-transfer mode of acetylacetone. For the computations PESs featuring different barrier heights (1.18, 2.35, 4.70) kcal mol⁻¹ were used in a morphing-type approach¹⁷⁸ to assess the position of the proton transfer band. Best agreement between experimentally measured and computed IR spectra is for a barrier height of 2.35 kcal mol⁻¹, compared with 3.2 kcal mol⁻¹ from CCSD(T) calculations.¹⁹⁶ The signatures around 3000 cm⁻¹ in the experimentally measured spectra are due to the CH stretch vibrations.

For FAD the gas phase infrared spectroscopy contained signatures for double proton transfer (DPT).¹⁹⁷ Comparing computed IR spectra from MD simulations on a morphed PES¹⁷⁸ with those measured experimentally yielded an estimated barrier for DPT of 7.2 kcal mol^−1 197 which compares with 7.3 kcal mol⁻¹ from a subsequent analysis of microwave spectra¹⁹⁸ and 8.2 kcal mol⁻¹ from fitting CCSD(T)-F12a energies calculated with the cc-pVTZ and aug-cc-pVTZ basis sets for H and C/O atoms (CCSD(T)-F12a/haTZ) to permutationally invariant polynomials.¹⁹⁹ A recent full dimensional PES which was transfer learned from the MP2 level of theory to CCSD(T) energies reported²⁰⁰ a barrier for DPT of 7.92 kcal mol⁻¹ and a dissociation energy for FAD in the gas phase from diffusion Monte Carlo simulations of D₀ = −14.23 ± 0.08 kcal mol⁻¹ in excellent agreement with an experimentally determined value of −14.22 ± 0.12 kcal mol⁻¹.²⁰¹ These examples illustrate the benefit of accurate, reactive and full-dimensional PESs for quantitative simulations of gas phase processes.

QCT simulations were also applied to the photodissociation of formaldehyde (H₂CO) following excitation of the 2¹4³ band. The results from QCT simulations on a PIP-represented PES determined at the MRCI/cc-pVTZ level of theory compared with experiments yielded excellent results.²⁰² The properties considered included the speed distributions for state-selected CO, and the rotational and vibrational distributions of the CO and H₂ products.²⁰² In a more recent study the kinetic energy release of the three-body breakup from Coulomb explosion experiments was compared with that from QCT simulations. For high kinetic energy particularly good agreement was found whereas for lower energies the agreement was rather more qualitative.²⁰³

Atomistic simulations can also be successfully used for determining vibrational relaxation rates. This was done²⁰⁴ for the CO + CO collision based on an accurate 6-dimensional PES (frozen monomers) validated for 68 rovibrational levels with a root mean square error of 0.29 cm⁻¹ between experiment and calculations.²⁰⁵ The vibrational relaxation rates from QCT simulations for the v = 10 and v = 16 vibrational levels were 2.6 × 10¹⁰ cm³ s⁻¹ and 3.1 × 10¹⁰ cm³ s⁻¹ compared with 1.9 × 10¹⁰ cm³ s⁻¹ and 5.0 × 10¹⁰ cm³ s⁻¹ from experiments.²⁰⁶ Such information is paramount for combustion processes and hypersonics and was also determined in near-quantitative agreement for the N + NO and O + CO systems.^190,207 Also, for the H + O₃ → OH + O₂ reaction, QCT simulations based on a PIP + NN representation of energies calculated at the MRCI level of theory reported final state vibrational distributions for the OH product peaking at v′ = 8, in near-quantitative agreement with available experiments.²⁰⁸

Finally, thermal rates for reactions have also been determined for bimolecular processes. As an example, the kinetics of the OH + HO₂ reaction to form O₂ + H₂O was determined from QCT simulations using a full dimensional PES based on PIP + NN.²⁰⁹ Over a temperature range between 250 K and 3000 K the computed rate is in good agreement with a range of experiments and reproduces in particular the negative temperature dependence reported at low temperatures.

4.2 Reactions in solution

For reactions in solution the additional complication is the presence of an environment that needs to be described by a separate energy function. The most common solvent, water, is particularly challenging to represent and despite immense effort to date no single parametrization outperforming all others is available.²¹⁰ In addition, many empirical energy functions which are a common starting point for investigating reactions in solution have been parametrized with one of the simpler water force fields such as TIP3P²¹¹ or SPC/E.²¹²

Despite the challenges, meaningful quantitative simulations for certain reaction types in solution are available. One of them concerns the Claisen rearrangement reaction.²¹³ Using multi state adiabatic reactive dynamics (MS-ARMD) simulations, the transformation from chorismate to prephenate and corresponding smaller molecular systems was investigated,²¹⁴ whereas the actual activation free energy did not reproduce the experimentally observed results. This can be achieved from using a dedicated parametrization as was done for EVB-based simulations of the same reaction.²¹⁵ With a model parametrized to reproduce the activation free energy in water the barrier height in the protein environment was reproduced to within 0.6 kcal mol⁻¹ compared with experiment.

Another class of reactions that has been investigated in great detail in solution are S_N2 reactions. One example is the S_N2 reaction of haloalkane dehalogenase (DhlA) in which the nucleophile carboxylate from Asp124 replaces one of the halides of the CH₂Cl–CH₂Cl substrate, i.e. –COO⁻ + (CH₂Cl)₂ → –OCO–CH₂–CH₂Cl + Cl⁻.²¹⁶ Following the empirical valence bond (EVB) approach,¹⁴ first the reference reaction in water was parametrized to reproduce the experimentally observed activation free energy. This model was then used for simulations in the protein DhlA and the computed catalytic effect of 11.6 kcal mol⁻¹ was in good agreement with the experimentally observed value of 11.7 kcal mol⁻¹.²¹⁶ For the [Br–CH₃–Cl]⁻ reaction in solution parametrizations within the MS-VALBOND²¹⁷ and MS-ARMD²¹⁸ frameworks have been successfully used.²¹⁹ The catalytic effect in going from the gas phase to solution for the forward [Br–CH₃ + Cl]⁻ → [Br + CH₃–Cl]⁻ reaction is 17.4 kcal mol⁻¹ using MS-ARMD at the MP2 level, compared with 15.2 kcal mol⁻¹ from experiment.

Phosphate hydrolysis reactions have also been investigated at a quantitative level. For a number of substituted methyl phenyl phosphate diesters activation free energies were determined from EVB calculations and compared with experiment.²²⁰ Typical differences between computed and measured activation free energies were below 1 kcal mol⁻¹. From analysis of the MD trajectories it was concluded that phosphate transfer in these systems followed an associative rather than a dissociative pathway. For methyl transfer reactions, recent MS-ARMD simulations also found that the pathway is associative. For one of the systems, Pyr + MeBr experimentally determined barrier heights for acetonitrile and hexane as the solvent were 22.5 kcal mol⁻¹ and 27.6 kcal mol⁻¹ which compare with 23.2 kcal mol⁻¹ and 28.1 kcal mol⁻¹ from MS-ARMD simulations.²²¹

4.3 Surface reactions

Molecular beam scattering experiments are an important tool to investigate the reaction dynamics at the gas–surface interface and yield information about reaction mechanisms, topological features and the gas–surface interaction potential. Their characterization and accurate prediction of suitable observables such as the final vibrational, rotational or translational energy distribution of the reaction products, reaction rates, or desorption energies from simulations is of great importance not only for understanding but also for designing new heterogeneous catalysts.^222–225

One prominent process is the scattering of NO from a metal Au(111) surfaces that is focus of research for the past 20 years.²²⁶ The scattering of initially highly vibrationally excited NO molecules (ν_ini = 15) has shown vibrational relaxation of about 36 kcal mol⁻¹ (150 kJ mol⁻¹) or up to 10 vibrational quanta. This differs significantly for NO scattering from insulators such as LiF(001) for which negligible vibrational energy loss was observed which is indicative of non-adiabatic relaxation channels rather than purely mechanical ones.^226,227

Early simulations by Tully and coworker based on the independent electron surface hopping (IESH) model allow metal-to-molecule charge transfer by including two electronic states in the model Hamiltonian.^228,229 Such an approach only qualitatively captures the large experimentally observed vibrational relaxation. As an example, simulations for the scattering of NO(ν_ini = 16) with an incident energy of E_ini = 0.5 eV lead to a most probable population of the ν_fin = 14 final vibrational state whereas experiments report pronounced relaxation to ν_fin,exp = 6.¹⁰⁹ Including electron friction in the model to perturbatively describe vibration–electron coupling yields relaxation to ν_fin = 13.^{108,109,113,230} These differences between experiment and simulations were primarily attributed to inaccuracies in the PES which also may explain the observed overestimation of multibounce events in the simulations.^228,231

Fig. 3a shows one of the most recent improvements towards a quantitative study of NO-vibrational relaxation using accurate energy functions in MD simulations including electron friction (MDEF, open green squares).²³² Vibrational relaxation of scattered NO(ν_ini = 16, E_ini = 0.52 eV) on Au(111) leads to a loss of 9 quanta to yield ν_fin = 7 which is close to the experimental peak at ν_fin,exp = 6.²²⁶ This corresponds to a vibrational energy loss of ∼23 kcal mol⁻¹ (∼1.0 eV) compared with the experimentally observed 36 kcal mol⁻¹ (150 kJ mol⁻¹). Even without electronic friction (red bars) QCT simulations with the embedded atom neural network (EANN) potential model already predicts a considerably more pronounced relaxation with a peak at ν_fin = 11. Conversely, when NO(ν_ini = 12, E_ini = 0.42 eV) scatters from LiF(001), the product state distribution P (ν_fin) strongly peaks at ν_fin = 12 and no vibrational relaxation takes place, see Fig. 3b. This finding primarily reflects the rather isotropic interaction between NO and the LiF surface that governs the dynamics.²³² Similarly, the predicted translational energy loss of scattered NO(ν_ini = 1, E_ini = 0.31 eV) of 〈ΔE_trans〉 = 4.8 kcal mol⁻¹ (0.21 eV) agrees well with the experimentally determined value of 4.4 kcal mol⁻¹ (0.19 eV).²³³ Hence, a quantitative understanding of such experiments is possible.

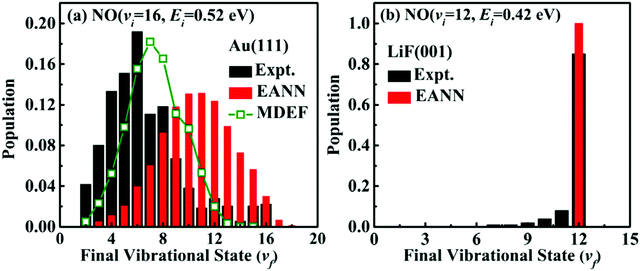Fig. 3 Final vibrational distribution of highly vibrationally excited NO scattered from (a) Au(111) and (b) LiF(001) from adiabatic (red) and non-adiabatic MD simulations including electronic friction (open green squares). Experimental data of are shown in black.^226,227 Reproduced from ref. 232 with permission from American Physical Society, copyright 2021.

These results emphasize the need for high-dimensional and accurate PESs to describe energy transfer between the surface and the impacting molecules together with including non-adiabatic effects especially for simulation on metal surfaces. In the present case the improvement is due to using a machine-learned, reactive PES that correctly captures the decrease in the NO dissociation barrier from ∼161 kcal mol⁻¹ (7.0 eV) in the gas phase to 66 kcal mol⁻¹ (2.86 eV)²³² on Au(111) which is below the vibrational energy at ν = 16 (corresponding to 78 kcal mol⁻¹ or 3.4 eV).^109,234,235 The NO bond elongation up to 1.89 Å leads to softening of the molecular vibration and increased coupling with other surface degrees of freedom.

For CO on Au(111) a NN representation of the Behler–Parrinello type fitted to DFT reference data was used together with QCT simulations to investigate the scattering of vibrationally excited CO(v_ini = 2) from the surface. The simulation shows predominantly specular scattering with no significant deviation between incidence angle (9°) and scattering angle (peak at 10°), consistent with an experimentally observed scattering angle of 9°. More importantly, the experimentally observed CO(v_fin = 1) product could be attributed to rapid nonadiabatic relaxation of chemisorbed CO.²³⁶ The vibrationally relaxed CO can either desorb rapidly or transfer into a long living physisorbed state giving raise to the fast and slow component in the experimental time of flight spectra.²³⁷

Achieving quantitative simulation of surface reactions is still challenging but highly relevant for developing and improving heterogeneous catalysts.^100,238,239 Although the prediction of the reaction probability for the dissociative chemisorption of molecular H₂ on metal surfaces is possible with high accuracy,²⁴⁰ for practical application reliable prediction of heavier atoms are required. Neglecting surface atom motion, simulations of H₂ on Cu(111) yield a reaction probability curve that is shifted by less than 1 kcal mol⁻¹ along the collision energy range up to 19.1 kcal mol⁻¹ (80 kJ mol⁻¹).²⁴¹

One limitation in such simulations concerns the level at which the electronic structure calculations can be carried out due to the system size and time scales required for meaningful simulations. The current state-of-the art for modeling molecule–metal reactions is still DFT with GGA functionals.¹⁰⁰ GGA density functionals have shown good performance for predicting sticking probabilities of dissociative adsorptions if the work function of the metal surface exceeds 7 eV.²⁴² One successful example is the match between ab initio MD simulations of the dissociative adsorption of CH₄ on Ni(111) surfaces at 550 K with molecular beam experiments. The SRP approach on density functionals was used for an accurate interpolation of the dissociation barrier height.^103,243 They achieved chemical accuracy for low incident energies ranging from 24.1 kcal mol⁻¹ up to 28.7 kcal mol⁻¹ (101–120 kJ mol⁻¹).²⁴³ At higher incident energies the differences between simulation and experiment increased. It was argued that this is due to a deficiency in the classical dynamics description to account for quasi-resonant energy transfer. However, quantitative agreement was found with initially excited CH-stretch vibrations (ν = 1) at incident energies up to 38.2 kcal mol⁻¹ (160 kJ mol⁻¹). Subsequently, the development of a 15-dimensional PIP-based PES for CH₄ on Ni(111) fitted to nearly 200 000 reference data points has opened up the possibility for statistically quantitative description.²⁴⁴ Chemical accuracy for the dissociative adsorption of CHD₃ on Pt(111) by ab initio MD simulations was also achieved.^245–247

For metal surface systems with low work functions pure density functionals perform less well for reaction barriers and sticking probabilities of dissociatively adsorbed molecules.²⁴² One well-studied example system is the adsorption of O₂ on Al(111) surfaces. Here, experiments have shown small initial sticking probabilities of 1% at low incident energies (∼0.7 kcal mol⁻¹, 30 meV) and an increase to ∼90% at high incident energies (>13.8 kcal mol⁻¹, 600 meV).²⁴⁸ Adiabatic MD simulations on PESs from GGA density functionals yield a barrier-less O₂ dissociation on the Al(111) surface and predict a 100% sticking probability even for the lowest simulated incident energy of 0.6 kcal mol⁻¹ (25 meV). Only energy surfaces from spin-constrained density functional computations with O₂ in the electronic triplet state yield qualitative agreement for the sticking probabilities.²⁴⁹ Nearly quantitative agreement has been achieved by using a PES determined from embedded correlated wave function theory²⁵⁰ that treats a molecule–surface embedded subsystem with more accurate electron correlation methods and the extended surface at the DFT level. MD simulations were carried out on a fitted 6-dimensional London–Eyring–Polanyi–Sato PES^251,252 using 700 reference points for O₂ on a 10 to 14 atoms embedded Al(111) slab in a periodic supercell on MP2 level. The results yield a simulated probability sticking curve that is about 1.1 kcal mol⁻¹ (0.05 eV) shifted towards higher incident energies.²⁵³

In another recent effort²⁵⁴ the vibrationally induced isomerization of CO on NaCl surfaces was investigated from QCT simulations. Experiments have reported the isomerization of OC–NaCl to CO–NaCl for highly vibrationally excited CO. For the largest cluster considered, containing 13 CO molecules adsorbed onto the NaCl surface, isomerization starts with v = 22 quanta in the CO stretch, consistent with experiment. Even after isomerization, the CO adsorbate remains vibrationally excited which is also what experiments report.

Quantitative MD simulations have also been possible for chromatographic systems. The dynamics of single molecules at the solid/liquid interface plays important roles in surface science (adsorption/desorption), material science, and interfacial chemistry. The molecular mechanisms underlying retention in RPLC depends on both, specific and non-specific interactions between the analyte and its environment.^255–260 The non-polar stationary phase is often a functionalized silica surface to which alkyl chains of various lengths are tethered, and the typical mobile phase is a water/methanol or water/acetonitrile mixture. Despite the superficially “simple” chemical composition of such systems, a molecular understanding underlying the separation process is challenging as the system is highly dynamical, heterogeneous and disordered.^261–264 Experimentally determined capacity factors which can be converted into retention times and free energies of binding are available for toluene, benzene, chlorobenzene, and phenol.²⁶⁵ Using multipolar force fields that reproduce the hydration free energies for the probe molecules,²⁶⁶ free energy differences ΔΔG_PhCl→PhR for mutating –Cl in chlorobenzene to –H (benzene), –OH (phenol), and –CH₃ (toluene) were determined inside the chromatographic column. With a 20 : 80 MeOH/H₂O solvent mixture these computed free energy changes for toluene, benzene, and phenol are [0.05; 0.57; 1.25] kcal mol⁻¹ compared with [0.06; 0.60; 1.43] kcal mol⁻¹ from experiment and for the 50 : 50 MeOH/H₂O mixture they are [0.08; 0.51; 1.01] kcal mol⁻¹ compared with [0.20; 0.61; 1.16] kcal mol⁻¹.²⁶⁷

5 Outlook

In this outlook a number of possible future developments are described. They include conceptual and practical aspects of force fields and further refinements to better capture the underlying physics of the molecules considered.

The majority of atomistic simulations in solution are carried out with rather empirical energy functions for the solvent. This is particularly obvious for protein dynamics using TIP3P²¹¹ or SPC/E²¹² models for the solvent which are convenient but not quantitative. One of the main reasons for this is the fact that the corresponding energy functions for the proteins have been parametrized with such water models early on. Only replacing the underlying water model will lead to an imbalance between the water–water and water–protein interactions which is not desirable. Hence, only a rigorous “bottom-up” reparametrization of protein force fields using improved but still computationally efficient water energy functions can address this. Recently, an effort has been made to emulate a wide range of rigid, fixed-charge and polarizable water parametrizations using the minimally distributed charge model⁸⁸ within the same implementation.²⁶⁸ This can serve as a proxy for a unified parametrization platform for small molecules and protein fragments in solution based on improved energy functions for water. Together with ongoing efforts to improve energy functions for small molecules and protein building blocks^90,172 such approaches hold promise to make atomistic simulations quantitative in a broader sense and lead to computing platforms that even allow predictive simulations for large systems.

For chemical reactions in solution the reorganization of the electrons makes an important contribution to the solute–solvent interaction. In the gas phase such effects can be absorbed in the total energy if a global representation of the total energy function is possible. However, in solution, the charge reorganization needs to be included explicitly as a function of geometry because the solvent–solute interaction is described by explicit electrostatics in one or the other way. A recent example concerns the recombination dynamics of CO and oxygen atoms. For the process in gas phase all necessary interactions are accounted for in one global energy function¹⁹⁰ whereas for the process on amorphous solid water the reorganization of the electrons between the CO + O reactant and the CO₂ product needs to be included explicitly.^45,269

Conformationally dependent electrostatics has already been explored to some extent in the past.²⁷⁰ However, the applications were often restricted to water⁹³ with the exception of the fluctuating charge implementation in CHARMM.²⁷¹ The model itself is based on charge equilibration between bonded atoms based on their electronegativity and chemical hardness rather than first principles electrostatic potentials from electronic structure calculations. For additional accuracy, multipolar energy functions can include conformational dependence of the MTPs which has, however, only been done for diatomics.^97,98

As an example for the influence of conformationally dependent charges, Fig. 4 reports the CO₂ formation probability for different initial conditions of the reactive MD simulations. Recombination simulations were initiated from a CO(center of mass)–O separation of (i) R = 4.0 Å for a previously used⁴⁵ fixed point charge model in the collinear OC–O (θ = 180°) conformation and (ii) for separations ranging from R = 4.0 Å to R = 8.0 Å with a fluctuating charge model. With fixed charges^45,269 the oxygen atom interacts more strongly with the water hydrogen atoms due to its charge of q_O = −0.2 e. Although some charge transfer between the water surface and the oxygen atom is expected from electronic structure calculations⁴⁵ the magnitude of the charge is probably too high. On the other hand, with the fluctuating charge model it is possible to correctly describe the change in the charges of the CO and O moieties as they approach one another. In this model, the magnitude of the point charges depends on the OC–O distance. Charges from reference electronic structure calculations were found to change in a sigmoidal fashion between the CO₂ product geometry and the CO + O reactant state.

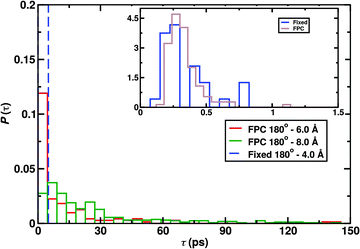Fig. 4 Normalized reaction time distributions for CO + O recombination from 500 simulations, for reactions initiated from θ = 180° and R = 4.0, 6.0, 8.0 Å using fixed^45,269 and fluctuating point charge (FPC) models. The inset reports the distribution for R = 4.0 Å and almost all recombination takes place within 1 ps. The reaction probability found with R = 4.0 Å is 32% and 99.2% with fixed and fluctuating charges respectively.

As is shown in the inset of Fig. 4, for the shortest separation the normalized reaction time distributions for the two charge models are close but the total product formation probability differs considerably. It is 32% for fixed charges and 99% for fluctuating charges from running 500 simulations. As in the reactant geometry the CO and O fragments are close to electrically neutral they interact weakly with the surface and diffusion is facile (diffusional barrier of 0.2 kcal mol⁻¹ to 2 kcal mol⁻¹ for atomic oxygen)²⁷² which increases the probability for reactive encounters. Hence, recombination from short distances R is almost 100% and recombination from further away is still possible on the 100 ps time scale, see Fig. 4. The desorption energy for atomic oxygen with q_O = −0.2 e is ∼7 kcal mol⁻¹ which also explains its slow surface diffusion with fixed charges. Experimentally, the desorption energy ranges from 2.4 to 3.5 kcal mol^−1 273 compared with 2.2 kcal mol⁻¹ from simulations with neutral oxygen (q_O = 0 e).²⁷² For molecular oxygen (O₂) atomistic simulations found²⁷⁴ desorption energies of 1.5 to 2.0 kcal mol⁻¹ which compares favourably with experiments that report a value of 1.8 kcal mol⁻¹.²⁷⁵ In summary, with fluctuating charges correctly describing the asymptotic states of the OC + O → CO₂ reaction the diffusional and desorption barriers for the oxygen atom are in quantitative agreement with experiment and allow to realistically model recombination on amorphous solid water.

For energy transfer and spectroscopy the coupling between internal degrees of freedom is important. However, in most empirical energy functions this mechanical coupling is implicit and primarily governed by coordinate transformations between Cartesian coordinates which are used for following the molecular dynamics and the internal coordinates in which the energy function itself is described. There are examples for force fields such as the Merck Molecular Force Field (MMFF),²⁷⁶ which include cross terms, e.g. between neighboring bonds, bonds and valence angles. However, the number of parameters to be determined increases considerably and the additional number of terms affects the computational performance. ML-based techniques provide an opportunity to include such couplings from rigorous electronic structure data and first examples demonstrate their accuracy for chemical reactions and spectroscopy.^200,277

Dynamical simulations and the chemical understanding of surface processes are a crucial factor for innovations in heterogeneous catalysis. The difficulties and large effort in performing accurate, high-level quantum electronic computations together with incorporating non-adiabatic effects during molecule–surface interactions has often hindered quantitative agreement between simulations and experimental observations. Increased understanding in surface effects, sophisticated models for accurate potential energy surfaces and ML potentials that allow the simulation of adsorbate and surface atom dynamics have lead to increasing success of reproducing experimental results. However, there are examples like the dissociative chemisorption of HCl on Au(111) for which quantitative molecular dynamics simulation could not successfully achieved yet.^37,278–281

Quantitative atomistic simulations provide considerable scope for molecular-level understanding of complex chemical and biological systems. For this, computationally efficient, versatile and implementations of sufficiently accurate representations of the total energy of the systems are required. The “quantitative” nature of such simulations is ultimately judged from comparison with experiments which in itself has measurement errors associated with it. An integrated approach combining knowledge from experiment and simulation together with a realistic assessment of the uncertainties involved in both will be of particular interest to arrive at a comprehensive description and understanding of complex systems. In this regard, ML-based techniques will contribute to both, the representation of the energy function and the molecular simulations themselves, and the quantification of the underlying uncertainties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Swiss National Science Foundation through grants 200021-117810, 200020-188724, the NCCR MUST, AFOSR, and the University of Basel (to MM). This project also received funding (to KT) from the European Unions Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 801459 – FP-RESOMUS.

References

1. D. R. Bowler and T. Miyazaki, Methods in Electronic Structure Calculations, Rep. Prog. Phys., 2012, 75, 036503.
2. H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional Quantum Dynamics: MCTDH Theory and Applications, John Wiley & Sons, 2009.
3. J. Jung, C. Kobayashi, K. Kasahara, C. Tan, A. Kuroda, K. Minami, S. Ishiduki, T. Nishiki, H. Inoue and Y. Ishikawa, et al., New Parallel Computing Algorithm of Molecular Dynamics for Extremely Huge Scale Biological Systems, J. Comput. Chem., 2021, 42, 231–241.
4. A. Dommer, L. Casalino, F. Kearns, M. Rosenfeld, N. Wauer, S.-H. Ahn, J. Russo, S. Oliveira, C. Morris and A. Bogetti, et al., # COVIDisAirborne: AI-Enabled Multiscale Computational Microscopy of Delta SARS-CoV-2 in a Respiratory Aerosol, bioRxiv, 2021 DOI:10.1101/2021.11.12.468428.
5. M. Levitt and A. Warshel, Computer Simulation of Protein Folding, Nature, 1975, 253, 694–698.
6. S. Piana, J. L. Klepeis and D. E. Shaw, Assessing the Accuracy of Physical Models Used in Protein-folding Simulations: Quantitative Evidence from Long Molecular Dynamics Simulations, Curr. Opin. Struct. Biol., 2014, 24, 98–105.
7. W. L. Jorgensen and C. Ravimohan, Monte Carlo Simulation of Differences in Free Energies of Hydration, J. Chem. Phys., 1985, 83, 3050–3054.
8. C. F. Wong and J. A. McCammon, Dynamics and Design of Enzymes and Inhibitors, J. Am. Chem. Soc., 1986, 108, 3830–3832.
9. T. Simonson, G. Archontis and M. Karplus, Free Energy Simulations Come of Age: Protein- Ligand Recognition, Acc. Chem. Res., 2002, 35, 430–437.
10. Z. Cournia, B. Allen and W. Sherman, Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations, J. Chem. Inf. Model., 2017, 57, 2911–2937.
11. S. Decherchi and A. Cavalli, Thermodynamics and Kinetics of Drug-Target Binding by Molecular Simulation, Chem. Rev., 2020, 120, 12788–12833.
12. M. Feig and Y. Sugita, Whole-cell Models and Simulations in Molecular Detail, Annu. Rev. Cell Dev. Biol., 2019, 35, 191–211.
13. M. Karplus, R. D. Sharma and R. N. Porter, Dynamics of Reactive Collisions - H + H₂ Exchange Reaction, J. Chem. Phys., 1964, 40, 2033–2034.
14. A. Warshel and R. M. Weiss, An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes, J. Am. Chem. Soc., 1980, 102, 6218–6226.
15. D. Koner, S. M. Salehi, P. Mondal and M. Meuwly, Non-conventional Force Fields for Applications in Spectroscopy and Chemical Reaction Dynamics, J. Chem. Phys., 2020, 153, 010901.
16. E. T. Nibbering, H. Fidder and E. Pines, Ultrafast Chemistry: Using Time-resolved Vibrational Spectroscopy for Interrogation of Structural Dynamics, Annu. Rev. Phys. Chem., 2005, 56, 337–367.
17. P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, 2011.
18. A. D. Mackerell, Empirical Force Fields for Biological Macromolecules: Overview and Issues, J. Comput. Chem., 2004, 25, 1584–1604.
19. A. Stone, The Theory of Intermolecular Forces, OUP, Oxford, 2013.
20. C. M. Handley, G. I. Hawe, D. B. Kell and P. L.-A. Popelier, Optimal Construction of a Fast and Accurate Polarisable Water Potential Based on Multipole Moments Trained by Machine Learning, Phys. Chem. Chem. Phys., 2009, 11, 6365.
21. T. Bereau, C. Kramer and M. Meuwly, Leveraging Symmetries of Static Atomic Multipole Electrostatics in Molecular Dynamics Simulations, J. Chem. Theory Comput., 2013, 9, 5450–5459.
22. M. Devereux, S. Raghunathan, D. G. Fedorov and M. Meuwly, A Novel, Computationally Efficient Multipolar Model Employing Distributed Charges for Molecular Dynamics Simulations, J. Chem. Theory Comput., 2014, 10, 4229.
23. T. Bereau and M. Meuwly, Many-Body Effects and Electrostatics in Biomolecules, Jenny Stanford Publishing, 2016, pp. 251–286.
24. Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J.-P. Piquemal and P. Ren, Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications, Annu. Rev. Biochem., 2019, 48, 371–394.
25. T. A. Halgren, The Representation of van der Waals (vdW) Interactions in Molecular Mechanics Force Fields: Potential Form, Combination Rules, and vdW Parameters, J. Am. Chem. Soc., 1992, 114, 7827–7843.
26. J. Bzowski, E. Mason and J. Kestin, On Combination Rules for Molecular van der Waals Potential-well Parameters, Int. J. Thermophys., 1988, 9, 131–143.
27. J. Delhommelle and P. Millié, Inadequacy of the Lorentz-berthelot Combining Rules for Accurate Predictions of Equilibrium Properties by Molecular Simulation, Mol. Phys., 2001, 99, 619–625.
28. A. Warshel and M. Levitt, Theoretical Studies of Enzymic Reactions: Dielectric, Electrostatic and Steric Stabilization of the Carbonium Ion in the Reaction of Lysozyme, J. Mol. Biol., 1976, 103, 227–249.
29. G. Alagona, C. Ghio and P. A. Kollman, Simple Model for the Effect of Glu165 - Asp165 Mutation on the Rate of Catalysis in Triose Phosphate Isomerase, J. Mol. Biol., 1986, 191, 23–27.
30. M. J. Field, P. A. Bash and M. Karplus, A Combined Quantum Mechanical and Molecular Mechanical Potential for Molecular Dynamics Simulations, J. Comput. Chem., 1990, 11, 700–733.
31. A. C.-T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, Reaxff: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409.
32. D. Nutt and M. Meuwly, Studying Reactive Processes with Classical Dynamics: Rebinding Dynamics in MbNO, Biophys. J., 2006, 90, 1191–1201.
33. S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Towards Exact Molecular Dynamics Simulations with Machine-learned Force Fields, Nat. Commun., 2018, 9, 3887.
34. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine Learning Force Fields, Chem. Rev., 2021, 121, 10142–10186.
35. S. Käser, O. T. Unke and M. Meuwly, Reactive Dynamics and Spectroscopy of Hydrogen Transfer from Neural Network-based Reactive Potential Energy Surfaces, New J. Phys., 2020, 22, 055002.
36. K. Töpfer; S. Käser and M. Meuwly, Double Proton Transfer in Hydrated Formic Acid Dimer: Interplay of Spatial Symmetry and Solvent-generated Force on Reactivity, 2022, PCCP, in print.
37. Q. Liu, X. Zhou, L. Zhou, Y. Zhang, X. Luo, H. Guo and B. Jiang, Constructing High-dimensional Neural Network Potential Energy Surfaces for Gas-surface Scattering and Reactions, J. Phys. Chem. C, 2018, 122, 1761–1769.
38. J. Zeng, L. Cao, M. Xu, T. Zhu and J. Z. Zhang, Complex Reaction Processes in Combustion Unraveled by Neural Network-based Molecular Dynamics Simulation, Nat. Commun., 2020, 11, 1–9.
39. I. Chorkendorff and J. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, Germany, 3rd edn, 2017.
40. A. W. Kleyn, Molecular Beams and Chemical Dynamics at Surfaces, Chem. Soc. Rev., 2003, 32, 87–95.
41. C. Liu, Y. Tan, S. Lin, H. Li, X. Wu, L. Li, Y. Pei and X. C. Zeng, CO Self-promoting Oxidation on Nanosized Gold Clusters: Triangular Au₃ Active Site and CO Induced O-O Scission, J. Am. Chem. Soc., 2013, 135, 2583–2595 , PMID: 23343464.
42. D. Faras and R. Miranda in Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, ed. R. Díez Muiño and H. F. Busnengo, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 51–73.
43. B. Singh, M. B. Gawande, A. D. Kute, R. S. Varma, P. Fornasiero, P. McNeice, R. V. Jagadeesh, M. Beller and R. Zbořil, Single-atom (iron-based) Catalysts: Synthesis and Applications, Chem. Rev., 2021, 121, 13620–13697.
44. M. Pezzella, D. Koner and M. Meuwly, Formation and Stabilization of Ground and Excited-state Singlet O₂ upon Recombination of 3p Oxygen on Amorphous Solid Water, J. Phys. Chem. Lett., 2020, 11, 2171–2176.
45. M. Upadhyay, M. Pezzella and M. Meuwly, Genesis of Polyatomic Molecules in Dark Clouds: CO₂ Formation on Cold Amorphous Solid Water, J. Phys. Chem. Lett., 2021, 12, 6781–6787.
46. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, Gold Catalysts Prepared by Coprecipitation for Low-temperature Oxidation of Hydrogen and of Carbon Monoxide, J. Catal., 1989, 115, 301–309.
47. T. Bernhardt, U. Heiz and U. Landman in Nanocatalysis, ed. U. Heiz and U. Landman, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 1–191.
48. X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-atom Catalysts: A New Frontier in Heterogeneous Catalysis, Acc. Chem. Res., 2013, 46, 1740–1748 , PMID: 23815772.
49. H. S. Taylor and E. F. Armstrong, A Theory of the Catalytic Surface, Proc. R. Soc. London, Ser. A, 1925, 108, 105–111.
50. A. Gutiérrez-González and R. D. Beck, Quantum State and Surface-site-resolved Studies of Methane Chemisorption by Vibrational Spectroscopies, Phys. Chem. Chem. Phys., 2020, 22, 17448–17459.
51. M. Karplus, Development of Multiscale Models for Complex Chemical Systems: From H + H₂ to Biomolecules (nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 9992–10005.
52. A. Warshel, Multiscale Modeling of Biological Functions: From Enzymes to Molecular Machines (nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 10020–10031.
53. M. Meuwly and M. Karplus, Simulation of Proton Transfer along Ammonia Wires: An “Ab Initio” and Semiempirical Density Functional Comparison of Potentials and Classical Molecular Dynamics, J. Chem. Phys., 2002, 116, 2572–2585.
54. G. Vogt, P. Nuernberger, T. Brixner and G. Gerber, Femtosecond Pump-shaped-dump Quantum Control of Retinal Isomerization in Bacteriorhodopsin, Chem. Phys. Lett., 2006, 433, 211–215.
55. V. Hänninen, G. Murdachaew, G. M. Nathanson, R. B. Gerber and L. Halonen, Ab Initio Molecular Dynamics Studies of Formic Acid Dimer Colliding with Liquid Water, Phys. Chem. Chem. Phys., 2018, 20, 23717–23725.
56. J. Tennyson, Perspective: Accurate Ro-vibrational Calculations on Small Molecules, J. Chem. Phys., 2016, 145, 120901.
57. J. M. Hutson, Intermolecular Forces from the Spectroscopy of van der Waals Molecules, Annu. Rev. Phys. Chem., 1990, 41, 123–154.
58. A. van der Avoird, P. E. Wormer and R. Moszynski, From Intermolecular Potentials to the Spectra of van der Waals Molecules, and Vice Versa, Chem. Rev., 1994, 94, 1931–1974.
59. T. Karman, A. van der Avoird and G. C. Groenenboom, Potential energy and dipole moment surfaces of the triplet states of the O₂ (X³Σ_g⁻) - O₂ (X³Σ_g⁻, a¹Δ_g, b¹Σ_g⁺) complex, J. Chem. Phys., 2017, 147, 084306.
60. D. Koner, J. C.-S. V. Veliz, A. van der Avoird and M. Meuwly, Near Dissociation States for H₂⁺-He on MRCI and FCI Potential Energy Surfaces, Phys. Chem. Chem. Phys., 2019, 21, 24976–24983.
61. B. J. Braams and J. M. Bowman, Permutationally Invariant Potential Energy Surfaces in High Dimensionality, Int. Rev. Phys. Chem., 2009, 28, 577–606.
62. J. D. Bender, S. Doraiswamy, D. G. Truhlar and G. V. Candler, Potential Energy Surface Fitting by a Statistically Localized, Permutationally Invariant, Local Interpolating Moving Least Squares Method for the Many-body Potential: Method and Application to N₄, J. Chem. Phys., 2014, 140, 054302.
63. A. Nandi, C. Qu and J. M. Bowman, Full and Fragmented Permutationally Invariant Polynomial Potential Energy Surfaces for Trans and Cis N-methyl Acetamide and Isomerization Saddle Points, J. Chem. Phys., 2019, 151, 084306.
64. P. Houston, R. Conte, C. Qu and J. M. Bowman, Permutationally Invariant Polynomial Potential Energy Surfaces for Tropolone and H and D Atom Tunneling Dynamics, J. Chem. Phys., 2020, 153, 024107.
65. T.-S. Ho and H. Rabitz, A General Method for Constructing Multidimensional Molecular Potential Energy Surfaces from Ab Initio Calculations, J. Chem. Phys., 1996, 104, 2584–2597.
66. T. Hollebeek, T.-S. Ho and H. Rabitz, Constructing Multidimensional Molecular Potential Energy Surfaces from Ab Initio Data, Annu. Rev. Phys. Chem., 1999, 50, 537–570.
67. O. T. Unke and M. Meuwly, Toolkit for the Construction of Reproducing Kernel-based Representations of Data: Application to Multidimensional Potential Energy Surfaces, J. Chem. Inf. Model., 2017, 57, 1923–1931.
68. D. Koner, R. J. Bemish and M. Meuwly, The C(³P) + NO(X²Π) → O(³P) + CN(X²Σ⁺), N(²D)/N(⁴S) + CO(X¹Σ⁺) Reaction: Rates, Branching Ratios, and Final States from 15 K to 20000 K, J. Chem. Phys., 2018, 149, 094305.
69. M. Soloviov and M. Meuwly, Co-dynamics in the Active Site of Cytochrome C Oxidase, J. Chem. Phys., 2014, 140, 145101.
70. M. Soloviov, A. K. Das and M. Meuwly, Structural Interpretation of Metastable States in Myoglobin-NO, Angew. Chem., Int. Ed., 2016, 55, 10126–10130.
71. A. K. Das and M. Meuwly, Kinetic Analysis and Structural Interpretation of Competitive Ligand Binding for NO Dioxygenation in Truncated Hemoglobinn, Angew. Chem., Int. Ed., 2018, 57, 3509–3513.
72. K. T. Schuett, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Mueller, Schnet - a Deep Learning Architecture for Molecules and Materials, J. Chem. Phys., 2018, 148, 241722.
73. O. T. Unke and M. Meuwly, Physnet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15, 3678–3693.
74. B. Jiang, J. Li and H. Guo, Potential Energy Surfaces from High Fidelity Fitting of Ab Initio Points: The Permutation Invariant Polynomial-neural Network Approach, Int. Rev. Phys. Chem., 2016, 35, 479–506.
75. Y. Guan, S. Yang and D. H. Zhang, Construction of Reactive Potential Energy Surfaces with Gaussian Process Regression: Active Data Selection, Mol. Phys., 2018, 116, 823–834.
76. A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, FCHL Revisited: Faster and More Accurate Quantum Machine Learning, J. Chem. Phys., 2020, 152, 044107.
77. S. Käser, D. Koner, A. S. Christensen, O. A. von Lilienfeld and M. Meuwly, Machine Learning Models of Vibrating H₂ CO: Comparing Reproducing Kernels, FCHL, and PhysNet, J. Phys. Chem. A, 2020, 124, 8853–8865.
78. S. Manzhos and T. Carrington Jr, Neural Network Potential Energy Surfaces for Small Molecules and Reactions, Chem. Rev., 2021, 121, 10187–10217.
79. M. Meuwly, Machine Learning for Chemical Reactions, Chem. Rev., 2021, 121, 10218–10239.
80. J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev., 2021, 121, 10037–10072.
81. B. Jiang, J. Li and H. Guo, High-fidelity Potential Energy Surfaces for Gas-Phase and Gas-Surface Scattering Processes from Machine Learning, J. Phys. Chem. Lett., 2020, 11, 5120–5131.
82. R. Krems, Bayesian Machine Learning for Quantum Molecular Dynamics, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410.
83. C. Qu, Q. Yu and J. M. Bowman, Permutationally Invariant Potential Energy Surfaces, Annu. Rev. Phys. Chem., 2018, 69, 151–175.
84. T. Clark, M. Hennemann, J. Murray and P. Politzer, Halogen Bonding: The σ-hole, J. Mol. Model., 2007, 13, 291–296.
85. K. El Hage, T. Bereau, S. Jakobsen and M. Meuwly, Impact of Quadrupolar Electrostatics on Atoms Adjacent to the Sigma-hole in Condensed-phase Simulations, J. Chem. Theory Comput., 2016, 12, 3008–3019.
86. C. Kramer, P. Gedeck and M. Meuwly, Atomic Multipoles: Electrostatic Potential Fit, Local Reference Axis Systems and Conformational Dependence, J. Comput. Chem., 2012, 33, 1673–1688.
87. M. Devereux, S. Raghunathan, D. G. Fedorov and M. Meuwly, A Novel, Computationally Efficient Multipolar Model Employing Distributed Charges for Molecular Dynamics Simulations, J. Chem. Theory Comput., 2014, 10, 4229–4241.
88. O. T. Unke, M. Devereux and M. Meuwly, Minimal Distributed Charges: Multipolar Quality at the Cost of Point Charge Electrostatics, J. Chem. Phys., 2017, 147, 161712.
89. J.-P. Piquemal, H. Chevreau and N. Gresh, Toward a Separate Reproduction of the Contributions to the Hartree- Fock and DFT Intermolecular Interaction Energies by Polarizable Molecular Mechanics with the SIBFA Potential, J. Chem. Theory Comput., 2007, 3, 824–837.
90. Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, Polarizable Atomic Multipole-based Amoeba Force Field for Proteins, J. Chem. Theory Comput., 2013, 9, 4046–4063.
91. F. Hédin, K. El Hage and M. Meuwly, A Toolkit to Fit Nonbonded Parameters from and for Condensed Phase Simulations, J. Chem. Inf. Model., 2016, 56, 1479–1489.
92. J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell Jr, An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications, Chem. Rev., 2016, 116, 4983–5013.
93. S. Rick, S. Stuart and B. Berne, Dynamical Fluctuating Charge Force-fields - Applications to Liquid Water, J. Chem. Phys., 1994, 101, 6141–6156.
94. P. E.-M. Lopes, B. Roux and A. D. MacKerell Jr., Molecular Modeling and Dynamics Studies with Explicit Inclusion of Electronic Polarizability: Theory and Applications, Theor. Chem. Acc., 2009, 124, 11–28.
95. T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, A Fourth-Generation High-Dimensional Neural Network Potential with Accurate Electrostatics Including Non-Local Charge Transfer, Nat. Chem., 2021, 12, 398.
96. U. Kich, P. Popelier and A. Stone, Conformational Dependence of Atomic Multipole Moments, Chem. Phys. Lett., 1995, 238, 253–260.
97. N. Plattner and M. Meuwly, The Role of Higher CO-multipole Moments in Understanding the Dynamics of Photodissociated Carbonmonoxide in Myoglobin, Biophys. J., 2008, 94, 2505–2515.
98. M. W. Lee, J. K. Carr, M. Goellner, P. Hamm and M. Meuwly, 2D IR Spectra of Cyanide in Water Investigated by Molecular Dynamics Simulations, J. Chem. Phys., 2013, 139, 054506.
99. J. Carrasco, N. Lopez and F. Illas, On the Convergence of Isolated Neutral Oxygen Vacancy and Divacancy Properties in Metal Oxides Using Supercell Models, J. Chem. Phys., 2005, 122, 224705.
100. G.-J. Kroes, Computational Approaches to Dissociative Chemisorption on Metals: Towards Chemical Accuracy, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048.
101. N. Gerrits, J. Geweke, D. J. Auerbach, R. D. Beck and G.-J. Kroes, Highly Efficient Activation of HCl Dissociation on Au(111) Via Rotational Preexcitation, J. Phys. Chem. Lett., 2021, 12, 7252–7260.
102. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215.
103. Y.-Y. Chuang, M. L. Radhakrishnan, P. L. Fast, C. J. Cramer and D. G. Truhlar, Direct Dynamics for Free Radical Kinetics in Solution: Solvent Effect on the Rate Constant for the Reaction of Methanol with Atomic Hydrogen, J. Phys. Chem. A, 1999, 103, 4893–4909.
104. S. A. French, A. A. Sokol, S. T. Bromley, C. R.-A. Catlow, S. C. Rogers, F. King and P. Sherwood, From CO₂ to Methanol by Hybrid QM/MM Embedding, Angew. Chem., Int. Ed., 2001, 40, 4437–4440.
105. A. M. Burow, M. Sierka, J. Döbler and J. Sauer, Point Defects in CaF₂ and CeO₂ Investigated by the Periodic Electrostatic Embedded Cluster Method, J. Chem. Phys., 2009, 130, 174710.
106. K. Töpfer, G. Füchsel and J. C. Tremblay, Energy Transfers in a Weakly Coupled Gas-Surface System: The Scattering of CO from MgO(001), Surf. Sci., 2021, 706, 121767.
107. P. Saalfrank, G. Füchsel, S. Monturet, J. C. Tremblay and T. Klamroth, in Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, ed. R. Díez Muiño and H. F. Busnengo, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 323–348.
108. S. Monturet and P. Saalfrank, Role of Electronic Friction during the Scattering of Vibrationally Excited Nitric Oxide Molecules from Au(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075404.
109. B. C. Krüger, N. Bartels, C. Bartels, A. Kandratsenka, J. C. Tully, A. M. Wodtke and T. Schäfer, NO Vibrational Energy Transfer on a Metal Surface: Still a Challenge to First-principles Theory, J. Phys. Chem. C, 2015, 119, 3268–3272.
110. D. N. Denzler, C. Frischkorn, C. Hess, M. Wolf and G. Ertl, Electronic Excitation and Dynamic Promotion of a Surface Reaction, Phys. Rev. Lett., 2003, 91, 226102.
111. S. Wagner, C. Frischkorn, M. Wolf, M. Rutkowski, H. Zacharias and A. C. Luntz, Energy Partitioning in the Femtosecond-laser-induced Associative D₂ Desorption from Ru(0001), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205404.
112. J. Gladh, T. Hansson and H. Öström, Electron- and Phonon-coupling in Femtosecond Laser-induced Desorption of CO from Ru(0001), Surf. Sci., 2013, 615, 65–71.
113. M. Head-Gordon and J. C. Tully, Molecular Dynamics with Electronic Frictions, J. Chem. Phys., 1995, 103, 10137–10145.
114. W. Dou and J. E. Subotnik, Perspective: How to Understand Electronic Friction, J. Chem. Phys., 2018, 148, 230901.
115. A. J. Coffman and J. E. Subotnik, When Is Electronic Friction Reliable for Dynamics at a Molecule-metal Interface?, Phys. Chem. Chem. Phys., 2018, 20, 9847–9854.
116. T. S. Zwier, Laser Probes of Conformational Isomerization in Flexible Molecules and Complexes, J. Phys. Chem. A, 2006, 110, 4133–4150.
117. T. R. Rizzo, J. A. Stearns and O. V. Boyarkin, Spectroscopic Studies of Cold, Gas-phase Biomolecular Ions, Int. Rev. Phys. Chem., 2009, 28, 481–515.
118. A. Amadei, I. Daidone, A. Di Nola and M. Aschi, Theoretical-computational Modelling of Infrared Spectra in Peptides and Proteins: A New Frontier for Combined Theoretical-experimental Investigations, Curr. Opin. Struct. Biol., 2010, 20, 155–161.
119. E. G. Buchanan, W. H. James III, S. H. Choi, L. Guo, S. H. Gellman, C. W. Müller and T. S. Zwier, Single-conformation Infrared Spectra of Model Peptides in the Amide I and Amide II Regions: Experiment-based Determination of Local Mode Frequencies and Inter-mode Coupling, J. Chem. Phys., 2012, 137, 094301.
120. C. J. Feng, B. Dhayalan and A. Tokmakoff, Refinement of Peptide Conformational Ensembles by 2D IR Spectroscopy: Application to Ala-Ala-Ala, Biophys. J., 2018, 114, 2820–2832.
121. P. Mondal, P.-A. Cazade, A. K. Das, T. Bereau and M. Meuwly, Multipolar Force Fields for Amide-I Spectroscopy from Conformational Dynamics of the Alanine Trimer, J. Phys. Chem. B, 2021, 125, 10928–10938.
122. S. Woutersen, R. Pfister, P. Hamm, Y. Mu, D. S. Kosov and G. Stock, Peptide Conformational Heterogeneity Revealed from Nonlinear Vibrational Spectroscopy and Molecular Dynamics Simulations, J. Chem. Phys., 2002, 117, 6833–6840.
123. M. F. Decamp, L. Deflores, J. M. Mccracken, A. Tokmakoff, K. Kwac and M. Cho, Amide I Vibrational Dynamics of N-methylacetamide in Polar Solvents: The Role of Electrostatic Interaction, J. Phys. Chem. B, 2005, 109, 11016–11026.
124. S. Woutersen and P. Hamm, Structure Determination of Trialanine in Water Using Polarization Sensitive Two-dimensional Vibrational Spectroscopy, J. Phys. Chem. B, 2000, 104, 11316–11320.
125. S. Woutersen, R. Pfister, P. Hamm, Y. Mu, D. S. Kosov and G. Stock, Peptide Conformational Heterogeneity Revealed from Nonlinear Vibrational Spectroscopy and Molecular-dynamics Simulations, J. Chem. Phys., 2002, 117, 6833–6840.
126. S. Woutersen, Y. Mu, G. Stock and P. Hamm, Subpicosecond Conformational Dynamics of Small Peptides Probed by Two-dimensional Vibrational Spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11254–11258.
127. R. Schweitzer-Stenner, F. Eker, Q. Huang and K. Griebenow, Dihedral Angles of Trialanine in D₂O Determined by Combining FTIR and Polarized Visible Raman Spectroscopy, J. Am. Chem. Soc., 2001, 123, 9628–9633.
128. S. Woutersen and P. Hamm, Isotope-edited Two-dimensional Vibrational Spectroscopy of Trialanine in Aqueous Solution, J. Chem. Phys., 2001, 114, 2727.
129. Y. Mu and G. Stock, Conformational Dynamics of Trialanine in Water: A Molecular Dynamical Study, J. Phys. Chem. B, 2002, 106, 5294–5301.
130. J. Graf, P. H. Nguyen and H. Schwalbe, Structure and Dynamics of the Homologous Series of Alanine Peptides: A Joint Molecular Dynamics/NMR Study, J. Am. Chem. Soc., 2007, 129, 1179–1189.
131. R. D. Gorbunov, P. H. Nguyen, M. Kobus and G. Stock, Quantum-classical Description of the Amide I Vibrational Spectrum of Trialanine, J. Chem. Phys., 2007, 126, 054509.
132. K. I. Oh, K. K. Lee and M. Cho, Circular Dichroism Eigen Spectra of Polyproline II and β-strand Conformers of Trialanine in Water: Singular Value Decomposition Analysis, Chirality, 2010, 22, E186–E201.
133. X. Xiao, N. Kallenbach and Y. Zhang, Peptide Conformation Analysis Using an Integrated Bayesian Approach, J. Chem. Theory Comput., 2014, 10, 4152–4159.
134. S. Strazza, R. Hunter, E. Walker and D. W. Darnall, The Thermodynamics of Bovine and Porcine Insulin and Proinsulin Association Determined by Concentration Difference Spectroscopy, Arch. Biochem. Biophys., 1985, 238, 30–42.
135. V. Zoete, M. Meuwly and M. Karplus, Study of the Insulin Dimerization: Binding Free Energy Calculations and Per-residue Free Energy Decomposition, Proteins: Struct., Funct., Bioinf., 2005, 61, 79–93.
136. S. Raghunathan, K. El Hage, J. L. Desmond, L. Zhang and M. Meuwly, The Role of Water in the Stability of Wild-type and Mutant Insulin Dimers, J. Phys. Chem. B, 2018, 122, 7038–7048.
137. P. Banerjee, S. Mondal and B. Bagchi, Effect of Ethanol on Insulin Dimer Dissociation, J. Chem. Phys., 2019, 150, 084902.
138. Z. Ganim, K. C. Jones and A. Tokmakoff, Insulin Dimer Dissociation and Unfolding Revealed by Amide I Two-dimensional Infrared Spectroscopy, Phys. Chem. Chem. Phys., 2010, 12, 3579–3588.
139. X.-X. Zhang, K. C. Jones, A. Fitzpatrick, C. S. Peng, C.-J. Feng, C. R. Baiz and A. Tokmakoff, Studying Protein-protein Binding through T-jump Induced Dissociation: Transient 2D IR Spectroscopy of Insulin Dimer, J. Phys. Chem. B, 2016, 120, 5134–5145.
140. S. M. Salehi, D. Koner and M. Meuwly, Dynamics and Infrared Spectrocopy of Monomeric and Dimeric Wild Type and Mutant Insulin, J. Phys. Chem. B, 2020, 124, 11882–11894.
141. M. Lim, T. A. Jackson and P. A. Anfinrud, Mid-infrared Vibrational Spectrum of CO After Photodissociation from Heme: Evidence for a Ligand Docking Site in the Heme Pocket of Hemoglobin and Myoglobin, J. Chem. Phys., 1995, 102, 4355.
142. H. Frauenfelder, B. McMahon and P. Fenimore, Myoglobin: the Hydrogen Atom of Biology and a Paradigm of Complexity, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8615–8617.
143. J. Meller and R. Elber, Computer Simulations of Carbon Monoxide Photodissociation in Myoglobin: Structural Interpretation of the B States, Biophys. J., 1998, 74, 789–802.
144. M. Anselmi, M. Aschi, A. Di Nola and A. Amadei, Theoretical Characterization of Carbon Monoxide Vibrational Spectrum in Sperm Whale Myoglobin Distal Pocket, Biophys. J., 2007, 92, 3442–3447.
145. D. R. Nutt and M. Meuwly, Theoretical Investigation of Infrared Spectra and Pocket Dynamics of Photodissociated Carbonmonoxy Myoglobin, Biophys. J., 2003, 85, 3612–3623.
146. N. Plattner and M. Meuwly, The Role of Higher CO-multipole Moments in Understanding the Dynamics of Photodissociated Carbonmonoxide in Myoglobin, Biophys. J., 2008, 94, 2505–2515.
147. K. Nienhaus, J. Olson, S. Franzen and G. Nienhaus, The Origin of Stark Splitting in the Initial Photoproduct State of MbCO, J. Am. Chem. Soc., 2005, 127, 40–41.
148. M. Meuwly, On the Influence of the Local Environment on the CO Stretching Frequencies in Native Myoglobin: Assignment of the B-states in MbCO, ChemPhysChem, 2006, 7, 2061–2063.
149. J. M. Kriegl, K. Nienhaus, P. Deng, J. Fuchs and G. U. Nienhaus, Ligand Dynamics in a Protein Internal Cavity, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7069–7074.
150. J. M. Bowman, T. Carrington and H.-D. Meyer, Variational Quantum Approaches for Computing Vibrational Energies of Polyatomic Molecules, Mol. Phys., 2008, 106, 2145–2182.
151. I. R. Craig and D. E. Manolopoulos, Quantum Statistics and Classical Mechanics: Real Time Correlation Functions from Ring Polymer Molecular Dynamics, J. Chem. Phys., 2004, 121, 3368–3373.
152. B. J. Braams and D. E. Manolopoulos, On the Short-time Limit of Ring Polymer Molecular Dynamics, J. Chem. Phys., 2006, 125, 124105.
153. J. Cao and G. A. Voth, The Formulation of Quantum Statistical Mechanics Based on the Feynman Path Centroid Density. I. Equilibrium Properties, J. Chem. Phys., 1994, 100, 5093–5105.
154. J. Cao and G. A. Voth, The Formulation of Quantum Statistical Mechanics Based on the Feynman Path Centroid Density. II. Dynamical Properties, J. Chem. Phys., 1994, 100, 5106–5117.
155. Y. Ohta, K. Ohta and K. Kinugawa, Ab Initio Centroid Path Integral Molecular Dynamics: Application to Vibrational Synamics of Diatomic Molecular Systems, J. Chem. Phys., 2004, 120, 312–320.
156. S. D. Ivanov, A. Witt, M. Shiga and D. Marx, Communications: On Artificial Frequency Shifts in Infrared Spectra Obtained from Centroid Molecular Dynamics: Quantum Liquid Water, J. Chem. Phys., 2010, 132, 031101.
157. X. Huang, S. Habershon and J. M. Bowman, Comparison of Quantum, Classical, and Ring-Polymer Molecular Dynamics Infra-red Spectra of Cl⁻ (H₂O) and H⁺ (H₂O)₂, Chem. Phys. Lett., 2008, 450, 253–257.
158. M. Shiga and A. Nakayama, Ab Initio Path Integral Ring Polymer Molecular Dynamics: Vibrational Spectra of Molecules, Chem. Phys. Lett., 2008, 451, 175–181.
159. A. Kaczmarek, M. Shiga and D. Marx, Quantum Effects on Vibrational and Electronic Spectra of Hydrazine Studied by “On-The-Fly” Ab Initio Ring Polymer Molecular Dynamics, J. Phys. Chem. A, 2009, 113, 1985–1994.
160. M. Rossi, H. Liu, F. Paesani, J. Bowman and M. Ceriotti, Communication: On the Consistency of Approximate Quantum Dynamics Simulation Methods for Vibrational Spectra in the Condensed Phase, J. Chem. Phys., 2014, 141, 181101.
161. M. Rossi, M. Ceriotti and D. E. Manolopoulos, How to Remove the Spurious Resonances from Ring Polymer Molecular Dynamics, J. Chem. Phys., 2014, 140, 234116.
162. M. Rossi, V. Kapil and M. Ceriotti, Fine Tuning Classical and Quantum Molecular Dynamics using a Generalized Langevin Equation, J. Chem. Phys., 2018, 148, 102301.
163. Z.-H. Xu and M. Meuwly, Vibrational Spectroscopy and Proton Transfer Dynamics in Protonated Oxalate, J. Phys. Chem. A, 2017, 121, 5389–5398.
164. M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges, Chem. Rev., 2016, 116, 7529–7550.
165. O. L. Polyansky, A. G. Császár, S. V. Shirin, N. F. Zobov, P. Barletta, J. Tennyson, D. W. Schwenke and P. J. Knowles, High-Accuracy Ab Initio Rotation-Vibration Transitions for Water, Science, 2003, 299, 539–542.
166. G. W. Richings and S. Habershon, MCTDH On-the-fly: Efficient Grid-based Quantum Dynamics without Pre-computed Potential Energy Surfaces, J. Chem. Phys., 2018, 148, 134116.
167. R. Welsch, K. Song, Q. Shi, S. C. Althorpe and T. F. Miller III, Non-Equilibrium Dynamics from RPMD and CMD, J. Chem. Phys., 2016, 145, 204118.
168. T. Begušić, X. Tao, G. A. Blake and T. F. Miller III, Equilibrium-Nonequilibrium Ring-Polymer Molecular Dynamics for Nonlinear Spectroscopy, J. Chem. Phys., 2022, 156, 131102.
169. E. Boulanger, L. Huang, C. Rupakheti, A. D. MacKerell Jr and B. Roux, Optimized Lennard-Jones Parameters for Druglike Small Molecules, J. Chem. Theory Comput., 2018, 14, 3121–3131.
170. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and Testing of a General Amber Force Field, J. Comput. Chem., 2004, 25, 1157–1174.
171. D. L. Mobley, É. Dumont, J. D. Chodera and K. A. Dill, Comparison of Charge Models for Fixed-charge Force Fields: Small-Molecule Hydration Free Energies in Explicit Solvent, J. Phys. Chem. B, 2007, 111, 2242–2254.
172. C. R. Rupakheti, A. D. MacKerell Jr and B. Roux, Global Optimization of the Lennard-Jones Parameters for the Drude Polarizable Force Field, J. Chem. Theory Comput., 2021, 17, 7085–7095.
173. G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell Jr, A Polarizable Model of Water for Molecular Dynamics Simulations of Biomolecules, Chem. Phys. Lett., 2006, 418, 245–249.
174. M. W. Lee and M. Meuwly, On the Role of Nonbonded Interactions in Vibrational Energy Relaxation of Cyanide in Water, J. Phys. Chem. A, 2011, 115, 5053–5061.
175. M. W. Lee and M. Meuwly, Hydration Free Energies of Cyanide and Hydroxide Ions from Molecular Dynamics Simulations with Accurate Force Fields, Phys. Chem. Chem. Phys., 2013, 15, 20303–20312.
176. P. Hamm, M. Lim and R. M. Hochstrasser, Vibrational Energy Relaxation of the Cyanide Ion in Water, J. Chem. Phys., 1997, 107, 10523–10531.
177. R. G. Pearson, Ionization Potentials and Electron Affinities in Aqueous Solution, J. Am. Chem. Soc., 1986, 108, 6109–6114.
178. M. Meuwly and J. M. Hutson, Morphing Ab Initio Potentials: A Systematic Study of Ne-HF, J. Chem. Phys., 1999, 110, 8338–8347.
179. J. M. Bowman and B. Gazdy, A Simple Method to Adjust Potential Energy Surfaces: Application to HCO, J. Chem. Phys., 1991, 94, 816–817.
180. P. Ren and J. Ponder, Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation, J. Phys. Chem. B, 2003, 107, 5933–5947.
181. L.-P. Wang, T. Head-Gordon, J. W. Ponder, P. Ren, J. D. Chodera, P. K. Eastman, T. J. Martinez and V. S. Pande, Systematic Improvement of a Classical Molecular Model of Water, J. Phys. Chem. B, 2013, 117, 9956–9972.
182. R. Kumar and J. L. Skinner, Water Simulation Model with Explicit Three-molecule Interactions, J. Phys. Chem. B, 2008, 112, 8311–8318.
183. X. Huang, B. Braams and J. Bowman, Ab Initio Potential Energy and Dipole Moment Surfaces of (H₂O)₂, J. Phys. Chem. A, 2006, 110, 445–451.
184. V. Babin, C. Leforestier and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient, J. Chem. Theory Comput., 2013, 9, 5395–5403.
185. G. Sarma, Physico-chemical Modelling in Hypersonic Flow Simulation, Prog. Aerospace Sci., 2000, 36, 281–349.
186. J. Bertin and R. Cummings, Fifty Years of Hypersonics: Where We’ve Been, Where We’re Going, Prog. Aerospace Sci., 2003, 39, 511–536.
187. I. D. Boyd and T. E. Schwartzentruber, Nonequilibrium Gas Dynamics and Molecular Simulation, Cambridge University Press, New York, 2017.
188. D. Koner, R. J. Bemish and M. Meuwly, Dynamics on Multiple Potential Energy Surfaces: Quantitative Studies of Elementary Processes Relevant to Hypersonics, J. Phys. Chem. A, 2020, 124(31), 6255–6269.
189. J. C. San Vicente Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, The N(⁴S) + O₂(X³Σ_g⁻) ↔ O(³P) + NO(X²Π) Reaction: Thermal and Vibrational Relaxation Rates for the 2A′, 4A′ and 2A′′ States, Phys. Chem. Chem. Phys., 2020, 22, 3927–3939.
190. J. C.-S. V. Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, The C (³P)+ O₂ (³Σ_g⁻) ↔ CO₂ ↔ CO (¹Σ⁺) + O(¹D)/O(³P) Reaction: Thermal and Vibrational Relaxation Rates from 15 K to 20000 K, Phys. Chem. Chem. Phys., 2021, 23, 11251–11263.
191. D. Koner, O. T. Unke, K. Boe, R. J. Bemish and M. Meuwly, Exhaustive State-to-state Cross Sections for Reactive Molecular Collisions from Importance Sampling Simulation and a Neural Network Representation, J. Chem. Phys., 2019, 150, 211101.
192. J. Arnold, D. Koner, S. Käser, N. Singh, R. J. Bemish and M. Meuwly, Machine Learning for Observables: Reactant to Product State Distributions for Atom-Diatom Collisions, J. Phys. Chem. A, 2020, 124, 7177–7190.
193. J. Arnold, J. C. San Vicente Veliz, D. Koner, N. Singh, R. J. Bemish and M. Meuwly, Machine Learning Product State Distributions from Initial Reactant States for a Reactive Atom-Diatom Collision System, J. Chem. Phys., 2021, 156, 034301.
194. D. Firth, K. Beyer, M. Dvorak, S. Reeve, A. Grushow and K. Leopold, Tunable Far-infrared Spectroscopy of Malonaldehyde, J. Chem. Phys., 1991, 94, 1812–1819.
195. Y. Wang, B. J. Braams, J. M. Bowman, S. Carter and D. P. Tew, Full-dimensional Quantum Calculations of Ground-state Tunneling Splitting of Malonaldehyde Using an Accurate Ab Initio Potential Energy Surface, J. Chem. Phys., 2008, 128, 224314.
196. D. L. Howard, H. G. Kjaergaard, J. Huang and M. Meuwly, Infrared and Near-infrared Spectroscopy of Acetylacetone and Hexafluoroacetylacetone, J. Phys. Chem. A, 2015, 119, 7980–7990.
197. K. Mackeprang, Z.-H. Xu, Z. Maroun, M. Meuwly and H. G. Kjaergaard, Spectroscopy and Dynamics of Double Proton Transfer in Formic Acid Dimer, Phys. Chem. Chem. Phys., 2016, 18, 24654–24662.
198. W. Li, L. Evangelisti, Q. Gou, W. Caminati and R. Meyer, The Barrier to Proton Transfer in the Dimer of Formic Acid: A Pure Rotational Study, Angew. Chem., Int. Ed., 2019, 58, 859–865.
199. C. Qu and J. M. Bowman, An Ab Initio Potential Energy Surface for the Formic Acid Dimer: Zero-point Energy, Selected Anharmonic Fundamental Energies, and Ground-state Tunneling Splitting Calculated in Relaxed 1-4-mode Subspaces, Phys. Chem. Chem. Phys., 2016, 18, 24835–24840.
200. S. Käser and M. Meuwly, Transfer Learned Potential Energy Surfaces: Accurate Anharmonic Vibrational Dynamics and Dissociation Energies for the Formic Acid Monomer and Dimer, Phys. Chem. Chem. Phys., 2022, 24, 5269–5281.
201. F. Kollipost, R. W. Larsen, A. Domanskaya, M. Nörenberg and M. Suhm, Communication: The Highest Frequency Hydrogen Bond Vibration and an Experimental Value for the Dissociation Energy of Formic Acid Dimer, J. Chem. Phys., 2012, 136, 151101.
202. P. L. Houston, X. Wang, A. Ghosh, J. M. Bowman, M. S. Quinn and S. H. Kable, Formaldehyde Roaming Dynamics: Comparison of Quasi-Classical Trajectory Calculations and Experiments, J. Chem. Phys., 2017, 147, 013936.
203. T. Endo, S. P. Neville, V. Wanie, S. Beaulieu, C. Qu, J. Deschamps, P. Lassonde, B. E. Schmidt, H. Fujise and M. Fushitani, et al., Capturing Roaming Molecular Fragments in Real Time, Science, 2020, 370, 1072–1077.
204. J. Chen, J. Li, J. M. Bowman and H. Guo, Energy Transfer Between Vibrationally Excited Carbon Monoxide Based on a Highly Accurate Six-Dimensional Potential Energy Surface, J. Chem. Phys., 2020, 153, 054310.
205. L. A. Surin, D. N. Fourzikov, T. F. Giesen, S. Schlemmer, G. Winnewisser, V. A. Panfilov, B. S. Dumesh, G. W. Vissers and A. van der Avoird, Higher Energy States in the CO Dimer: Millimeter-Wave Spectra and Rovibrational Calculations, J. Phys. Chem. A, 2007, 111, 12238–12247.
206. R. L. DeLeon and J. W. Rich, Vibrational Energy Exchange Rates in Carbon Monoxide, Chem. Phys., 1986, 107, 283–292.
207. D. Koner, J. C. San Vicente Veliz, R. J. Bemish and M. Meuwly, Accurate Reproducing Kernel-based Potential Energy Surfaces for the Triplet Ground States of N₂O and Dynamics for the N + NO ↔ O + N₂ Reaction, Phys. Chem. Chem. Phys., 2020, 22, 18488–18498.
208. Q. Chen, X. Hu, H. Guo and D. Xie, Insights into the Formation of Hydroxyl Radicals with Nonthermal Vibrational Excitation in the Meinel Airglow, J. Phys. Chem. Lett., 2021, 12, 1822–1828.
209. Y. Liu, M. Bai, H. Song, D. Xie and J. Li, Anomalous kinetics of the reaction between OH and HO₂ on an accurate triplet state potential energy surface, Phys. Chem. Chem. Phys., 2019, 21, 12667–12675.
210. O. Demerdash, L.-P. Wang and T. Head-Gordon, Advanced Models for Water Simulations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1355.
211. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79, 926–935.
212. H. Berendsen, J. Grigera and T. Straatsma, The Missing Term in Effective Pair Potentials, J. Phys. Chem., 1987, 91, 6269–6271.
213. L. Claisen, Über Umlagerung Von Phenol-allyläthern in C-allyl-phenole, Ber. Dtsch. Chem. Ges., 1912, 45, 3157–3166.
214. S. Brickel and M. Meuwly, Molecular Determinants for Rate Acceleration in the Claisen Rearrangement Reaction, J. Phys. Chem. B, 2019, 123, 448–456.
215. M. Štrajbl, A. Shurki, M. Kato and A. Warshel, Apparent NAC Effect in Chorismate Mutase Reflects Electrostatic Transition State Stabilization, J. Am. Chem. Soc., 2003, 125, 10228–10237.
216. M. H. Olsson and A. Warshel, Solute Solvent Dynamics and Energetics in Enzyme Catalysis: The S_N2 Reaction of Dehalogenase As a General Benchmark, J. Am. Chem. Soc., 2004, 126, 15167–15179.
217. M. H. Schmid, A. K. Das, C. R. Landis and M. Meuwly, Multi-state Valbond for Atomistic Simulations of Hypervalent Molecules, Metal Complexes, and Reactions, J. Chem. Theory Comput., 2018, 14, 3565–3578.
218. T. Nagy, J. Yosa Reyes and M. Meuwly, Multisurface Adiabatic Reactive Molecular Dynamics, J. Chem. Theory Comput., 2014, 10, 1366–1375.
219. S. Brickel, A. K. Das, O. T. Unke, H. T. Turan and M. Meuwly, Reactive Molecular Dynamics for the [Cl-CH₃-Br]⁻ Reaction in the Gas Phase and in Solution: A Comparative Study Using Empirical and Neural Network Force Fields, Electron. Struct., 2019, 1, 024002.
220. E. Rosta, S. C. Kamerlin and A. Warshel, On the Interpretation of the Observed Linear Free Energy Relationship in Phosphate Hydrolysis: A Thorough Computational Study of Phosphate Diester Hydrolysis in Solution, Biochemistry, 2008, 47, 3725–3735.
221. H. T. Turan, S. Brickel and M. Meuwly, Solvent Effects on the Menshutkin Reaction, J. Phys. Chem. B, 2022, 126, 1951–1961.
222. M. Bonn, A. Kleyn and G. Kroes, Real Time Chemical Dynamics at Surfaces, Surf. Sci., 2002, 500, 475–499.
223. J. Libuda and H.-J. Freund, Molecular Beam Experiments on Model Catalysts, Surf. Sci. Rep., 2005, 57, 157–298.
224. A. M. Wodtke, Electronically Non-adiabatic Influences in Surface Chemistry and Dynamics, Chem. Soc. Rev., 2016, 45, 3641–3657.
225. X. Yang and A. M. Wodtke, Surface Reaction Dynamics, Chem. Soc. Rev., 2016, 45, 3573–3575.
226. Y. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Vibrational Promotion of Electron Transfer, Science, 2000, 290, 111–114.
227. A. M. Wodtke, Y. Huang and D. J. Auerbach, Interaction of NO(v = 12) with LiF(001): Evidence for Anomalously Large Vibrational Relaxation Rates, J. Chem. Phys., 2003, 118, 8033–8041.
228. N. Shenvi, S. Roy and J. C. Tully, Nonadiabatic Dynamics at Metal Surfaces: Independent-electron Surface Hopping, J. Chem. Phys., 2009, 130, 174107.
229. S. Roy, N. A. Shenvi and J. C. Tully, Model Hamiltonian for the Interaction of NO with the Au(111) Surface, J. Chem. Phys., 2009, 130, 174716.
230. J. I. Juaristi, M. Alducin, R. D. Muiño, H. F. Busnengo and A. Salin, Role of Electron-hole Pair Excitations in the Dissociative Adsorption of Diatomic Molecules on Metal Surfaces, Phys. Rev. Lett., 2008, 100, 116102.
231. K. Golibrzuch, P. R. Shirhatti, I. Rahinov, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, The Importance of Accurate Adiabatic Interaction Potentials for the Correct Description of Electronically Nonadiabatic Vibrational Energy Transfer: A Combined Experimental and Theoretical Study of NO(v = 3) Collisions with a Au(111) Surface, J. Phys. Chem., 2014, 140, 044701.
232. R. Yin and B. Jiang, Mechanical Vibrational Relaxation of NO Scattering from Metal and Insulator Surfaces: When and Why They Are Different, Phys. Rev. Lett., 2021, 126, 156101.
233. J. Misewich, H. Zacharias and M. M.-T. Loy, State-to-state Molecular-beam Scattering of Vibrationally Excited NO from Cleaved LiF(100) Surfaces, Phys. Rev. Lett., 1985, 55, 1919–1922.
234. B. C. Krüger, S. Meyer, A. Kandratsenka, A. M. Wodtke and T. Schäfer, Vibrational Inelasticity of Highly Vibrationally Excited NO on Ag(111), J. Phys. Chem. Lett., 2016, 7, 441–446.
235. R. Yin, Y. Zhang and B. Jiang, Strong Vibrational Relaxation of NO Scattered from Au(111): Importance of the Adiabatic Potential Energy Surface, J. Phys. Chem. Lett., 2019, 10, 5969–5974.
236. M. Huang, X. Zhou, Y. Zhang, L. Zhou, M. Alducin, B. Jiang and H. Guo, Adiabatic and Nonadiabatic Energy Dissipation During Scattering of Vibrationally Excited CO from Au (111), Phys. Rev. B, 2019, 100, 201407.
237. P. R. Shirhatti, I. Rahinov, K. Golibrzuch, J. Werdecker, J. Geweke, J. Altschäffel, S. Kumar, D. J. Auerbach, C. Bartels and A. M. Wodtke, Observation of the Adsorption and Desorption of Vibrationally Excited Molecules on a Metal Surface, Nat. Chem., 2018, 10, 592–598.
238. B. Jiang and H. Guo, Dynamics in Reactions on Metal Surfaces: A Theoretical Perspective, J. Chem. Phys., 2019, 150, 180901.
239. D. J. Auerbach, J. C. Tully and A. M. Wodtke, Chemical Dynamics from the Gas-phase to Surfaces, Nat. Sci., 2021, 1, e10005.
240. G.-J. Kroes and C. Díaz, Quantum and Classical Dynamics of Reactive Scattering of H₂ from Metal Surfaces, Chem. Soc. Rev., 2016, 45, 3658–3700.
241. C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G. J. Kroes, Chemically Accurate Simulation of a Prototypical Surface Reaction: H₂ Dissociation on Cu(111), Science, 2009, 326, 832–834.
242. N. Gerrits, E. W.-F. Smeets, S. Vuckovic, A. D. Powell, K. Doblhoff-Dier and G.-J. Kroes, Density Functional Theory for Molecule-Metal Surface Reactions: When Does the Generalized Gradient Approximation Get It Right, and What to Do If It Does Not, J. Phys. Chem. Lett., 2020, 11, 10552–10560.
243. F. Nattino, D. Migliorini, G.-J. Kroes, E. Dombrowski, E. A. High, D. R. Killelea and A. L. Utz, Chemically Accurate Simulation of a Polyatomic Molecule-metal Surface Reaction, J. Phys. Chem. Lett., 2016, 7, 2402–2406.
244. X. Zhou, F. Nattino, Y. Zhang, J. Chen, G.-J. Kroes, H. Guo and B. Jiang, Dissociative Chemisorption of Methane on Ni(111) Using a Chemically Accurate Fifteen Dimensional Potential Energy Surface, Phys. Chem. Chem. Phys., 2017, 19, 30540–30550.
245. H. Chadwick, D. Migliorini and G. J. Kroes, CHD₃ Dissociation on Pt(111): A Comparison of the Reaction Dynamics Based on the PBE Functional and on a Specific Reaction Parameter Functional, J. Chem. Phys., 2018, 149, 044701.
246. F. Nattino, D. Migliorini, M. Bonfanti and G.-J. Kroes, Methane Dissociation on Pt(111): Searching for a Specific Reaction Parameter Density Functional, J. Chem. Phys., 2016, 144, 044702.
247. F. Nattino, H. Ueta, H. Chadwick, M. E. van Reijzen, R. D. Beck, B. Jackson, M. C. van Hemert and G.-J. Kroes, Ab Initio Molecular Dynamics Calculations Versus Quantum-state-resolved Experiments on CHD₃ + Pt(111): New Insights into a Prototypical Gas-surface Reaction, J. Phys. Chem. Lett., 2014, 5, 1294–1299.
248. L. Österlund, I. Zoric-acute and B. Kasemo, Dissociative Sticking of O₂ on Al(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15452–15455.
249. J. Behler, K. Reuter and M. Scheffler, Nonadiabatic Effects in the Dissociation of Oxygen Molecules at the Al(111) Surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421.
250. F. Libisch, C. Huang and E. A. Carter, Embedded Correlated Wavefunction Schemes: Theory and Applications, Acc. Chem. Res., 2014, 47, 2768–2775.
251. L. Martin-Gondre, C. Crespos, P. Larregaray, J. Rayez, B. van Ootegem and D. Conte, Is the LEPS Potential Accurate Enough to Investigate the Dissociation of Diatomic Molecules on Surfaces?, Chem. Phys. Lett., 2009, 471, 136–142.
252. L. Martin-Gondre, C. Crespos, P. Larrégaray, J. Rayez, D. Conte and B. van Ootegem, Detailed Description of the Flexible Periodic London-Eyring-Polanyi-Sato Potential Energy Function, Chem. Phys., 2010, 367, 136–147.
253. R. Yin, Y. Zhang, F. Libisch, E. A. Carter, H. Guo and B. Jiang, Dissociative Chemisorption of O₂ on Al(111): Dynamics on a Correlated Wave-function-based Potential Energy Surface, J. Phys. Chem. Lett., 2018, 9, 3271–3277.
254. A. Nandi, P. Zhang, J. Chen, H. Guo and J. M. Bowman, Quasiclassical Simulations Based on Cluster Models Reveal Vibration-Facilitated Roaming in the Isomerization of CO Adsorbed on NaCl, Nat. Chem., 2021, 13, 249–254.
255. J. G. Dorsey and K. A. Dill, The Molecular Mechanism of Retention in Reversed-phase Liquid Chromatography, Chem. Rev., 1989, 89, 331–346.
256. J. G. Dorsey and W. T. Cooper, Retention Mechanisms of Bonded-phase Liquid Chromatography, Anal. Chem., 1994, 66, 857A–867A.
257. F. Gritti, G. Félix, M. F. Achard and F. Hardouin, Laterally Attached Liquid Crystalline Polymers As Stationary Phases in Reversed-phase High-performance Liquid Chromatography: V. Study of Retention Mechanism Using Linear Solvation Energy Relationships, J. Chromatogr. A, 2001, 922, 51–61.
258. R. G. Wolcott, J. W. Dolan, L. R. Snyder, S. R. Bakalyar, M. A. Arnold and J. A. Nichols, Control of Column Temperature in Reversed-phase Liquid Chromatography, J. Chromatogr. A, 2000, 869, 211–230.
259. K. Krupczyńska, B. Buszewski and P. Jandera, Characterizing HPLC Stationary Phases, Anal. Chem., 2004, 76, 227A–234A.
260. B. Buszewski and S. Noga, Hydrophilic Interaction Liquid Chromatography (HILIC)-a Powerful Separation Technique, Anal. Bioanal. Chem., 2012, 402, 231–247.
261. A. Fouqueau, M. Meuwly and R. Bemish, Adsorption of Acridine Orange at a C_8,18/water/acetonitrile Interface, J. Phys. Chem. B, 2007, 111, 10208–10216.
262. M. Orzechowski and M. Meuwly, Dynamics of Water Filaments in Disordered Environments, J. Phys. Chem. B, 2010, 114, 12203–12212.
263. P. K. Gupta and M. Meuwly, Dynamics of Water/Methanol Mixtures at Functionalized Chromatographic Interfaces, J. Phys. Chem. B, 2012, 116, 10951–10959.
264. P. K. Gupta and M. Meuwly, Structure and Dynamics of Water/Methanol Mixtures at Hydroxylated Silica Interfaces Relevant to Chromatography, ChemPhysChem, 2016, 17, 2938–2944.
265. B. Buszewski, Z. Suprynowicz, P. Staszczuk, K. Albert, B. Pfleiderer and E. Bayer, Effect of Coverage Density of the Retention Mechanism in Reversed-phase High-performance Liquid Chromatography, J. Chromatogr. A, 1990, 499, 305–316.
266. K. El Hage, T. Bereau, S. Jakobsen and M. Meuwly, Impact of Quadrupolar Electrostatics on Atoms Adjacent to the Sigma-hole in Condensed-phase Simulations, J. Chem. Theory Comput., 2016, 12, 3008–3019.
267. K. El Hage, P. K. Gupta, R. Bemish and M. Meuwly, Molecular Mechanisms Underlying Solute Retention at Heterogeneous Interfaces, J. Phys. Chem. Lett., 2017, 8, 4600–4607.
268. M. Devereux, M. Pezzella, S. Raghunathan and M. Meuwly, Polarizable Multipolar Molecular Dynamics Using Distributed Point Charges, J. Chem. Theory Comput., 2020, 16, 7267–7280.
269. M. Upadhyay and M. Meuwly, Energy Redistribution Following CO₂ Formation on Cold Amorphous Solid Water, Front. Chem., 2022, 9, 827085.
270. A. K. Rappe and W. A. Goddard III, Charge Equilibration for Molecular Dynamics Simulations, J. Phys. Chem., 1991, 95, 3358–3363.
271. S. Patel and C. L. Brooks III, Charmm Fluctuating Charge Force Field for Proteins: I Parameterization and Application to Bulk Organic Liquid Simulations, J. Comput. Chem., 2004, 25, 1–16.
272. M. Pezzella, O. T. Unke and M. Meuwly, Molecular Oxygen Formation in Interstellar Ices Does Not Require Tunneling, J. Phys. Chem. Lett., 2018, 9, 1822–1826.
273. M. Minissale, E. Congiu and F. Dulieu, Direct Measurement of Desorption and Diffusion Energies of O and N Atoms Physisorbed on Amorphous Surfaces, Astron. Astrophys., 2016, 585, A146.
274. M. Pezzella and M. Meuwly, O₂ Formation in Cold Environments, Phys. Chem. Chem. Phys., 2019, 21, 6247–6255.
275. J. Noble, E. Congiu, F. Dulieu and H. Fraser, Thermal Desorption Characteristics of CO, O₂ and CO₂ on Non-Porous Water, Crystalline Water and Silicate Surfaces at Submonolayer and Multilayer Coverages, Month. Not. Roy. Acad. Sci., 2012, 421, 768–779.
276. T. A. Halgren, Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94, J. Comput. Chem., 1996, 17, 490–519.
277. S. Käser, O. T. Unke and M. Meuwly, Isomerization and Decomposition Reactions of Acetaldehyde Relevant to Atmospheric Processes from Dynamics Simulations on Neural Network-based Potential Energy Surfaces, J. Chem. Phys., 2020, 152, 214304.
278. B. Kolb and H. Guo, Communication: Energy Transfer and Reaction Dynamics for DCl Scattering on Au(111): An Ab Initio Molecular Dynamics Study, J. Chem. Phys., 2016, 145, 011102.
279. G. Füchsel, M. del Cueto, C. Díaz and G.-J. Kroes, Enigmatic HCl + Au(111) Reaction: A Puzzle for Theory and Experiment, J. Phys. Chem. C, 2016, 120, 25760–25779.
280. G. Füchsel, X. Zhou, B. Jiang, J. I. Juaristi, M. Alducin, H. Guo and G.-J. Kroes, Reactive and Nonreactive Scattering of HCl from Au(111): An Ab Initio Molecular Dynamics Study, J. Phys. Chem. C, 2019, 123, 2287–2299.
281. N. Gerrits, J. Geweke, E. W.-F. Smeets, J. Voss, A. M. Wodtke and G.-J. Kroes, Closing the Gap between Experiment and Theory: Reactive Scattering of HCl from Au(111), J. Phys. Chem. C, 2020, 124, 15944–15960.

---